1 Introduction

PMSM drives become more and more attractive in motion-control applications such as High Speed Trains and electric vehicles. Its high performances: high efficiency, low inertia and high torque-to-volume ratio, high power factor and almost no need for maintenance are the main advantages. Compared to induction and reluctance motors, PMSM is lower in weight and smaller in size [1]. The previous features make it the most preferable for high performances motion control application. Several control strategies have been carried on to unsure the highest dynamic electrical machine drive performances. The most popular one is the IFOC which requires an accurate knowledge of the rotor shaft position. This implies the need of a speed or position sensors, such as an absolute encoders or magnetic resolvers mounted to the rotating shaft. However, these sensors present several drawbacks, such as reduced reliability, susceptibility to noise, additional cost and weight, and increased complexity of the installation [2]. Therefore, sensorless drive system is crucial for many applications, not only to reduce cost of the equipment, but also to improve system reliability. So the idea is to replace the real speed encoder by a software one. This last is an observer or an estimator which is built upon measured variables. Effectively, the simplest measured PMSM variables are stator voltages and currents. Many sensorless based schemes have been proposed in the literatures [3]. Some methods are based on the back-EMF voltage. These are simple and yield well position estimation at average and rated speeds, but fail at low operating speeds. Two basic deficiencies let these methods degrade as the speed reduces: pure integration drift and sensitivity to parameter uncertainty. To overcome this problem, several authors have used other techniques, either based on state observers, like Extended Kalman Filter in [4], High-gain Observer in [5] and Extended Luenberger Observer in [6], or based on the intelligent techniques, like the neuronal network estimators as presented in [7]. For its good performance proved in [8], the artificial neural architecture is used to replace the real speed encoder in this application.

The PMSM control problems present an extended research sector. Many authors, who look for the PMSM robustness drive, use the field oriented control (FOC) strategy as a reliable method, which is characterized by a simple architecture based on three proportional plus integral controllers as described in [2]. But the problems that occur in this last method are mainly: calculation of controller parameters and the robustness performances. Some works propose the adaptive control scheme as a robust control strategy, as the Model Reference Adaptive Control (MRAC) method. Effectively, the MRAC approach was able to compensate the system parameters variations, such as inertia and torque constant as explained in [9, 10]. Some other authors relied on the artificial intelligence techniques in their robustness control problems as presented in [11]. In the mean time, these methods need an exact mathematical identification for the learning system’s starting phase, in the artificial case, and for adjusting the controller parameters in the MRAC case.

The Internal Model Control (IMC) is classified as a robust control strategy which principle simulates the human style. Thus, in the manual mode, the operator attempts to tune the desired variable close to the desired goal, based on their spontaneous representation. This act is designed by the internal model in the IMC architecture. Therefore, some authors aim to replace the internal model system by an intelligent one, as neuron, fuzzy, or ANFIS technique, as supported in [12] and [13–17]. However, the inverse model stability problem appeared as explained in [17]. Meanwhile, the contributions in the internal model control strategy are limited and the IMC filter parameter tuning presents another critical point which hardly can influences the IMC control performances.

Many researches are based on the heuristics algorithms in their optimization problems, as given in [18], where the authors are based on the Ant-Colony Algorithm in the satellite control problem, or as done in [19], where the authors use the Particle Swarm Optimization technique in the Fuzzy inferences system tuning. These algorithms prove their effectiveness in these optimization problems. Therefore, based on the heuristic algorithms, an intelligent optimization method based on bacterial foraging algorithm (BFO) is used here for tuning the IMC controller parameter and for enhancing its robustness. The BFO approach choice is based on its powerful optimization algorithms in terms of convergence speed and final precision [18]. In the proposed PMSM control method, the BFO-IMC is used as current controllers in the IFOC drive strategy. In order to improve the overall PMSM control scheme, a robust speed controller is required. This one should enable the drive to follow any reference speed, taking into account the high speed mode and the effects of load dynamic impact and parameter variations. In [7] and [19], the performance and robustness of the recurrent neural network are noted. So the recurrent neural network type is selected as the speed controller in this method. In the electrical vehicle application, the high speed range is required and to perform this working mode, a filed weakening algorithm [20] is added for generating the needed direct reference stator current.

This paper is organized as follows: Sect. 2 presents the mathematical model of the PMSM, the principles of the field weakening and the IFOC strategies. The use of the neural network as a speed controller and as a speed observer is developed in Sect. 3. Section 4 is designed for the development of two internal model current controllers and the stability analysis. The intelligent optimization approach using the BFO is explained in Sect. 5. Sections 9 and 7 present the simulation results and the conclusion, respectively.

2 Mathematical modeling of the PMSM

The dynamic model of the PMSM written in the (d-q) reference frame can be described by the system (1) of nonlinear differential equations [7, 21]:

$$ \left \{ \begin{array}{l} \displaystyle v_{d} = R_{s}i_{d} + L_{d}\frac{di_{d}}{dt} - \omega L_{q}i_{q} \\[6pt] \displaystyle v_{q} = R_{s}i_{q} + L_{q}\frac{di_{q}}{dt} + \omega L_{d}i_{d} + \omega\lambda_{m} \end{array} \right . $$
(1)

where v d ,v q and i d ,i q are respectively direct and quadratic stator voltage and current comportments. R s is the stator resistance, L d ,L q are the d and q axis self stator inductances, ω is the rotor speed and λ m is the permanent magnet flux linkage.

The electromagnetic torque expression can be formulated as Eqs. (2) or (3):

$$ T_{e} = \frac{3}{2}p \bigl( \lambda_{m}i_{q} + ( L_{d} - L_{q} )i_{d}i_{q} \bigr) $$
(2)
$$ T_{e} = \frac{3}{2}p ( \lambda_{d}i_{q} + \lambda_{q}i_{d} ) $$
(3)

where λ d =L d i d +λ m and λ q =L q i q . For a non salient pole PMSM the quadratic and the direct inductances are equal then L d =L q =L s , so the torque expression becomes: \(T_{e} = \frac{3}{2}p( \lambda_{m}i_{q} )\).

Hence the electromagnetic torque depends only on the q axis current.

The mechanical equation for the motor dynamics is given in Eq. (4):

$$ T_{e} - T_{l} = \biggl( \frac{J}{p} \biggr) \biggl( \dot{\omega} + \frac{fv}{J}\omega \biggr) $$
(4)

where, T l , p, J and fv are respectively the load torque, the motor pole pairs number, the moment of inertia and the viscous friction coefficient.

2.1 Field weakening operation FWO

In general, a PMSM is fed by a Voltage Source Inverter (VSI). When the drive reaches nominal speed, the inverter generates maximum voltage magnitude. Without field weakening control algorithm, the torque rapidly decreases to zero and can be even negative for speed range above the nominal one [20]. The maximum electromagnetic torque and output power developed by PMSM are ultimately dependent on the allowable inverter current rating and the maximum output voltage. The stator current is limited by the VSI current rating. Then the stator d and q components and corresponding limit value are given in Eq. (5).

$$ i_{d}^{2} + i_{q}^{2} \le i_{s\max}^{2} $$
(5)

This expression represents a current-limited circle centering at the origin, but with the radius of i smax as shown in Fig. 1. It should be noticed that this current-limited circle remains constant for any speed. Assume that the voltage applied to the PMSM reaches its limit, the maximum stator voltage v smax is determined by the available DC bus voltage. Considering this limit, the stator voltage equations should satisfy the following condition:

$$ v_{s}^{2} = v_{d}^{2} + v_{d}^{2} \le v_{s\max}^{2} $$
(6)

Neglecting the stator resistance voltage drop, assuming steady state operation and substituting v d and v q from system 1 and dividing by ω squared, the stator voltage equation can then be written as indicated in Eq. (7):

$$ ( L_{d}i_{d} + \lambda_{m} )^{2} + ( L_{q}i_{q} )^{2} = \biggl( \frac{v_{s}}{\omega} \biggr)^{2} \le \biggl( \frac{v_{s\max}}{\omega} \biggr)^{2} $$
(7)

As illustrated, the constraint Eq. (7) determines a series of concentrated ellipses, centering at Point \(C( - \frac{\lambda_{m}}{L_{d}},0 )\) in the (i d ,i q ) plane. As the maximum voltage v smax is fixed, the ellipsis shrinks inversely with rotor speed. Figure 1 illustrates the voltage-limit ellipses (ω 1<ω 2<ω 3) and the current-limit circle which are plotted in the (i d ,i q ) plane.

Fig. 1
figure 1

Current-limit circle and voltage-limit ellipses of the PMSM

Full size image

It should be noted that the ellipse shape depends on the saliency ratio, which is defined as \(\frac{L_{q}}{L_{d}}\). For all non-saliency PMSM (L d =L q =L s ), the voltage-limited shape (Eq. (8)) change to circles.

$$ \biggl( i_{d} + \frac{\lambda_{m}}{L_{s}} \biggr)^{2} + ( i_{q} )^{2} = \biggl( \frac{v_{s}}{\omega L_{s}} \biggr)^{2} \le \biggl( \frac{v_{s\max}}{\omega L_{s}} \biggr)^{2} $$
(8)

Here is proposed a new field weakening algorithm as illustrated in Fig. 2. Effectively, if the target speed is less than the nominal one, the reference direct stator current is equal to zero. However if the desired target speed is higher than the nominal value, the reference direct stator current is generated from Eq. (8).

Fig. 2
figure 2

The proposed Field weakening algorithm

Full size image

2.2 Field oriented control (FOC)

Field oriented control (FOC) strategy has been widely used in various industrial applications. It is one of the most popular schemes for high performance of electrical machine drives. It is originally introduced for induction machines and it is easily extended to PMSM drives. The FOC-PMSM strategy in its standard scheme incorporates one outer loop for speed control and two inner loops for d and q current components regulation. These loops are usually built all around PI conventional regulators. In this strategy the direct reference current is fixed to a zero value. Hence, the PMSM drive behaves typically as a separately excited DC machine. However, if the reference speed exceeds the rated one, the d current reference value is derived from the field weakening algorithm. The q-axis reference current i q is generated as the speed regulator output Fig. 6.

3 Neural networks controller and estimator

The neural networks application is highly useful as controller estimator. Neural networks architecture can be classified into recurrent and non recurrent categories. Every architecture is required for a specific application. In the non recurrent networks the output is calculated directly from the input through feed forward connections. In the recurrent networks, the output is calculated from the actual input value of the network, and the actual or the previous outputs or states of the total network. It is clear that the recurrent one is dynamic versus the non recurrent one. In this work, two NNs are used together as a speed controller, and estimator.

The non recurrent neuron network architecture is used as estimator for its simple and easy usage versus the recurrent. The estimator is ANN and the recurrent one as a dynamic is used as a controller. This last contains more mathematical expressions in the running algorithm; this why the ANN is selected for identification problem [21].

3.1 Recurrent neural networks speed controller

Recurrent neural networks (RNN) have been an interesting and important part of neural network research during the 1990’s. Much architecture is presented in the literature, where some is characterized by the total connection and other by a partial connection. In this work, the proposed and used recurrent neural networks Speed Controller (RNNSC) architecture is given in Fig. 3. The structure corresponds to 3 neurons at input layer, two neurons in hidden layer and one in output layer. Refers to Fig. 3 as describing the connecting, S j is the input signals of the hidden layer, X is the output signal of the hidden layer, \(i_{q}^{*}\) is the final output signal of the RNNSC and I i (k) is the input vector. \(W_{j,j}^{D}(k)\) is the weight between the same neuron in the hidden layer, \(W_{j,j}^{L}(k)\) is the weight between two successive neurons in the hidden layer, \(W_{j,i}^{I}(k)\) is the weight from the input layer to the hidden layer and \(W_{j}^{O}(k)\) is the weight from the hidden layer to the output layer. f(.) is a sigmoid activation function.

Fig. 3
figure 3

Recurrent neural network global architecture

Full size image

The mathematical relations [7] between the different neurons in the different layers are given by Eqs. (9), (10) and (11):

(9)
(10)
(11)

Equation (12) gives the error function for the proposed RNNSC:

$$ E_{I} ( k ) = \frac{1}{2} \bigl[ i_{q} ( k ) - i_{q}^{*} ( k ) \bigr]^{2} = \frac{1}{2}e_{I}^{2} ( k ) $$
(12)

The error e I is the difference between the desired actual i q current and the RNNSC output as a reference one. The gradient method is used for adjusting the weights. The mathematical expressions used to update the different weights are in Eq. (13):

$$ \left \{ \begin{array}{l} \displaystyle W_{j}^{O} ( k + 1 ) = W_{j}^{O} ( k ) + \Delta W_{j}^{O} ( k )\\[6pt] \displaystyle \phantom{W_{j}^{O} ( k + 1 )}= W_{j}^{O} ( k ) - \eta_{I}^{O} ( k )\frac{\partial E_{I} ( k )}{\partial W_{j}^{O} ( k )} \\[12pt] \displaystyle W_{j,i}^{I} ( k + 1 ) = W_{j,i}^{I} ( k ) + \Delta W_{j,i}^{I} ( k )\\[6pt] \displaystyle \phantom{W_{j,i}^{I} ( k + 1 )} = W_{j,i}^{I} ( k ) - \eta_{I}^{I} ( k )\frac{\partial E_{I} ( k )}{\partial W_{j,i}^{I} ( k )} \\[12pt] \displaystyle W_{j,j - 1}^{L} ( k + 1 ) = W_{j,j - 1}^{L} ( k ) + \Delta W_{j,j - 1}^{L} ( k )\\[6pt] \phantom{W_{j,j - 1}^{L} ( k + 1 )}\displaystyle = W_{j,j - 1}^{L} ( k ) - \eta_{I}^{L} ( k )\frac{\partial E_{I} ( k )}{\partial W_{j,j - 1}^{L} ( k )} \\[12pt] \displaystyle W_{j,j}^{D} ( k + 1 ) = W_{j,j}^{D} ( k ) + \Delta W_{j,j}^{D} ( k )\\[6pt] \phantom{W_{j,j}^{D} ( k + 1 )}\displaystyle = W_{j,j}^{D} ( k ) - \eta_{I}^{D} ( k )\frac{\partial E_{I} ( k )}{\partial W_{j,j}^{D} ( k )} \end{array} \right . $$
(13)

The gradient expressions are shown in Eq. (14):

$$ \left\{ \begin{array}{l} \left\{ \begin{array}{l} \displaystyle \frac{\partial E_{I} ( k )}{\partial W_{j}^{O} ( k )} = - e_{I} ( k )X_{j} ( k ) \\[12pt] \displaystyle \frac{\partial E_{I} ( k )}{\partial W_{j,j}^{D} ( k )} = - e_{I} ( k )W_{j}^{O} ( k )P_{j,j} ( k ) \\[12pt] \displaystyle \frac{\partial E_{I} ( k )}{\partial W_{j,i}^{I} ( k )} = - e_{I} ( k )W_{j}^{O} ( k )Q_{j,i} ( k ) \\[12pt] \displaystyle \frac{\partial E_{I} ( k )}{\partial W_{j,j - 1}^{L} ( k )} = - e_{I} ( k )W_{j}^{O} ( k )R_{j,j - 1} ( k ) \end{array} \right. \\\\ \left\{ \begin{array}{l} \displaystyle P_{j,j} ( k ) = X_{j} ( k ) ( 1 - X_{j} ( k ) ) \\[6pt] \phantom{P_{j,j} ( k ) =}{}\times( X_{j} ( k - 1 ) + W_{j,j}^{D} ( k )P_{j,j} ( k - 1 ) ) \\[6pt] \displaystyle Q_{j,i} ( k ) = X_{j} ( k ) ( 1 - X_{j} ( k ) ) \\[6pt] \phantom{Q_{j,i} ( k ) =}{}\displaystyle \times( I_{i} ( k ) + W_{j,j}^{D} ( k )Q_{j,i} ( k - 1 ) ) \\[6pt] \displaystyle R_{j,j - 1} ( k ) = X_{j} ( k ) ( 1 - X_{j} ( k ) )\\[6pt] \phantom{R_{j,j - 1} ( k ) =}{}\displaystyle \times ( W_{j,j}^{D} ( k )R_{j,j - 1} ( k - 1 ) + X_{j - 1} ( k - 1 ) ) \end{array} \right. \\ \end{array} \right. $$
(14)

The coefficients \(\eta_{I}^{I}\), \(\eta_{I}^{D}\), \(\eta_{I}^{L}\), \(\eta_{I}^{O}\) design the RNNSC learning rates.

3.2 Artificial neural networks speed estimator

For the Artificial Neural Networks Speed Estimator (ANNSE), the relations between the different neurons in the input, hidden and the output layer are given by the mathematical expressions as depicted in Eqs. (15), (16), and (17) [8].

$$ S_{j} ( k ) = \sum_{i = 1}^{m} V_{j,i}^{I} ( k )I_{i} ( k ) $$
(15)
$$ X_{j} ( k ) = f \bigl( S_{j} ( k ) \bigr) = \frac{1}{1 + \exp ( - S_{j} ( k ) )} $$
(16)
$$ \hat{\omega} ( k ) = \sum_{j = 1}^{n} V_{j}^{O} ( k )X_{j} ( k ) $$
(17)

where, S j is the hidden layer input signals. X j is the hidden layer output signals. \(\hat{\omega}\) is the output signal of the ANNSE. \(V_{j,i}^{I}(k)\) is the weight from the input layer to the hidden layer and \(V_{j}^{O}(k)\) is the weight from the hidden layer to the output layer. I i (k) is the input data vector and f(.) is the sigmoid function. The error function is defined in Eq. (18):

(18)

e ω (k) is the error between the desired actual speed and the ANNSE output. We use the gradient method for adjusting the weights. The mathematical expressions for the weights update are given in Eq. (19), and the gradient expressions are reported in Eq. (20):

(19)
(20)

The coefficients \(\eta_{\omega}^{I}, \eta_{\omega}^{O}\)are the learning ANNSE rates. The used ANNSE structure corresponds to 3 neurons at input layer, two neurons in hidden layer and one in output layer.

4 The internal model current controller

The internal Model control strategy can be a challenge for the PMSM drive, as reported in [12]. The general IMC structure is presented in Fig. 4, where Gi(s) represents the internal model, C(s) the controller and G(s) the real model. The reference stator currents \(i^{*} = [ i_{d}^{*},i_{q}^{*} ]\) are compared with the output error between the real, “” and the observed, “” stator currents. The output errors are applied as inputs to the controller to generate the stator reference voltages v ∗=[v d ,v q ].

Fig. 4
figure 4

The IMC structure

Full size image

The used PMSM voltages are deduced as depicted in Eq. (21):

(21)

then

(22)

The inverse model can be expressed by the Eq. (23)

(23)

4.1 IMC stability analysis

From Fig. 4, if the internal model is perfect, then Gi(s)=G(s). So, there is no more feedback occurring in Fig. 4. The closed loop system can be expressed as: F(s)=Gi(s)C(s).

F(s) is stable if and only if Gi(s) and C(s) are stable. However, if Gi(s) is not minimum phase, then Gi −1(s) is unstable. If Gi −1(s) numerator degree is higher than the denominator, then Gi −1(s) cannot be implemented. These two constraints can be resolved as: In the present application Gi(s) has no right half plane zero. So refers to H 2 optimization procedure we can let: C(s)=Gi −1(s). This solution resolves only the first cited constraint. The second one is resolved with a low pass filter L(s). Then the IMC controller can be expressed by:

$$\left \{ \begin{array}{l} \displaystyle C ( s ) = L ( s )Gi^{ - 1} \\ L ( s ) = \left [ \begin{array}{c@{\quad}c} \frac{\alpha}{s + \alpha} & 0 \\ 0 & \frac{\alpha}{s + \alpha} \\\end{array} \right ] \\ \end{array} \right . $$

This IMC regulator parameter is adjusted online, using an intelligent optimization algorithm based on the bacterial research food principle. The detail of the proposed intelligent optimization algorithm is given in the next section.

5 Bacteria foraging optimization: a brief overview

According to the Escherichia coli (E. coli) bacterial which is present in the human intestine, the bacterial foraging optimization support a new method based on foraging behavior for solving optimization problems. So according to the bacteria behavior law, all the elements support the best species which have the ability for searching food and eliminate the other. The bacteria foraging strategy can be expressed generally by three processes, the first is the chemotaxis step. The second is called the reproduction and the last is the elimination-dispersal step [18]. Some authors divide the chemotaxis step into two other, swimming and tumbling, then four steps are obtained.

The bacterial foraging optimization algorithm is illustrated in Fig. 5. We define J(i,j,k,l) the value function coast and θ i (j,k,l) the ith bacteria position. In the present algorithm, the most important loop is the chemotaxis, designed by “B”. In this one, each bacterium will be passed through the tumbling and the swimming step “F”. Where the corresponding objective value will be calculated and compared to the less saved one. After assuring that all the bacteria, “G”, are executing the entire chemotaxis step, “B”, the reproduction one will start. Effectively, this action is characterized by, the reproduction of the best bacteria half. Where, the worst bacteria half that corresponding to the highest objective function coast will be dead. However, the other best half with the lowest coast function, split. The obtained copies are placed at the same location as their parent. After, the reproduction step is achieved, the last one, which called “elimination-dispersal”, start. Effectively, with a probability P ed , an elimination and dispersion for each bacterium (this keeps the number of bacteria in the population constant) occur [18, 22]. The elimination and dispersal events assist chemotaxis progress by placing the bacteria to the nearest required values. Each bacterium according to a fixed probability dispersed from their original position and move to best position within the search space. These events may prevent the local optima trapping but lead to disturb the optimization process.

Fig. 5
figure 5

The bacterial foraging optimization algorithm

Full size image

In the chemotaxis step, the bacterium is said swimming if it moves in a predefined direction and tumbling if it moves in an altogether different direction. The bacterial position is updated mathematically by Eq. (24):

  • C(i)=C(i)+d1 in swimming

  • C(i)=C(i)−d2 in the tumbling

(24)

θ i (j,k,l) represents the position of the ith bacterial in the jth chemotaxis step, the kth reproduction step and the lth elimination step. The parameters d1 and d2 are two positive elements. C(i) shows the swim size taken in the random direction specified by the tumble. Δs(i) depicts the vector direction of the jth chemotaxis step. When the bacterial movement is run or swim, Δs(i) takes the same that was available in the last chemotaxis step; otherwise, Δs(i) is a random vector elements in the interval [−1,1]. This swimming action is continued as long as it continues to reduce the cost, but only up to a maximum number of steps, Ns. If not, this action will be stopped.

Several optimization coast functions are commonly used, such as:

  • The Integral Absolute Error and (IAE): \(\mathit{IAE} = \int_{0}^{\infty} | \mathit{error}( t ) | dt\)

  • The Integral of Time-weighted-Absolute Error (ITAE): \(\mathit{ITAE} = \int_{0}^{\infty} t| \mathit{error}( t ) | dt\)

  • The Integral of the Squared Error (ISE): \(\mathit{ISE} = \int_{0}^{\infty} | \mathit{error}^{2}( t ) | dt\)

In this work the ISE is used in the optimization problem as written in Eq. (25).

(25)

The BFO IMC tuning algorithm is running for the proposed control structure taking into account the most of load disturbances and stator resistance variations. Up on this condition the BFO converge on the best filter parameter to be used.

6 Simulations results

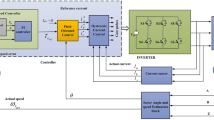
In order to verify the effectiveness and the robustness of the proposed control scheme for the PMSM drives at a high speed working region, Matlab/Simulink software package is used to perform simulation tests of the overall drive schema illustrated in Fig. 6. The proposed control scheme based on the IFOC strategy; regroups two inner loops IMC current controllers, a RNNSC outer loop controller and an ANNSE to estimate the shaft speed. The field weakening Algorithm is synthesized to generate the direct stator reference current. The Bacterial Foraging algorithm is carefully applied for adjusting the IMC filter parameters.

Fig. 6
figure 6

The PMSM high performance sensorless drive scheme

Full size image

The PMSM parameters are: P=400 W, the rated current I rat=2 A, the maximum current I max=2.I rat, the rated speed ω=2500 rpm, the rated torque T l =1.5 N m, L d =L q =21.5 mH, R s =5.2 Ω, λ m =0.24 Wb, J=85e −6 kg m2. The inverter parameters are: the DC bus voltage is fixed to 660 V and the switching frequency is 10 kHz.

In the traction and the electric vehicle applications, the load torque decreases if the motor speed exceeds the rated value. In this work the electric vehicle typical drive cycle is supporting the speed reference trajectory. The used target speed trajectory begins with T l =1.5 N m from 0 rpm at t=0 s to 2500 rpm at t=0.075 s, then to 4000 rpm with T l =0.9 N m at t=0.575 s as indicated to Fig. 10.

For the proposed PMSM control drive system, the two neural blocs, speed estimator and controller, need a significant database for the learning phase. This data base is containing a variable reference speed with many load appliances, as presented in Fig. 7. The vectors input data used for the two neural blocs are:

  • For the ANNSE: \(I(k)=\bigl[i_{d}(k)\ i_{q} (k)\ v_{d} (k) v_{q}(k)\bigr]^{T}\)

  • For the RNNSC: \(I(k)=\bigl[e(k-1) e(k) i^{*}_{q}(k-1)\bigr]^{T}\)

Fig. 7
figure 7

Learning data base for the RNNSC case

Full size image

Figures 8a and 8b show the viewer’s windows of the learning step. The iterations number is fixed to 200 and 700 for RNNSC and ANNSE respectively. Good performances are obtained after the learning operation.

Fig. 8
figure 8figure 8

The learning viewer’s windows

Full size image

After obtaining the desired neural blocs, the IMC parameters BFO tuning is started. The objective function to be minimized is presented in Eq. (25). The coefficients β 1 and β 2 are two positive numbers chosen in this application as β 1=β 2=100. The speed error and overshoot are respectively denoted by e and Δ. The BFO architecture parameters specifications are chosen those of the test yielding to a minimum of computational and keeping good performance. The best obtained BFO characteristics are given as the follow:

  • The bacteria number: S=6

  • The chemotaxis steps number: N c =4

  • The swim length: N s =4

  • The reproduction steps number: N re =2

  • The elimination-dispersal events number: N ed =2

  • The number of bacteria reproductions (splits) per generation S r =S/2

  • The probability that each bacteria will be eliminated/dispersed: P ed =0.25

  • The run length c(:,1)=0.05_ones(s,1)

  • The initial fitness cost; calculated by the ISE method for the initial random parameter.

The simulation results in Fig. 9 show the evolution of the fitness coast function and the IMC parameter according to the S bacteria and the chemotaxis event, in the entire reproduction and elimination loop. As presented in this figure, the obtained results demonstrate that the coast function value decrease in the last elimination and reproduction event. Where, in the first stage, presented in Fig. 9a, the cost value is approximated to 15×105. However in the last one, Fig. 9d, the value is decreased to 3×104. The corresponding IMC parameters are also highlighted at the same figures. It should be noticed that the obtained minimum coast function can be more reduced if the reproduction and the elimination iterations are increased. However, a compromise between simulation time reduction and a precise results, inquires the use of previously cited BFO configuration.

Fig. 9
figure 9figure 9figure 9figure 9

Evolution of the coast and the IMC parameter values according to the chemotaxis, reproduction and elimination entire loop. (a) BFO results in N ed =1, N re =1. (b) BFO results in N ed =1, N re =2. (c) BFO results in N ed =2, N re =1. (d) BFO results in N ed =2, N re =2

Full size image

In these figures, are illustrated the obtained coast function value and IMC parameter for each bacterium and for every part of chemotaxis step. It is clear that the best objective function cost value, is always obtained in the first chemotaxis step. That is due to the reproduction loop, where the present bacteria are cloned from the best previous one. So, the new chemotaxis event will be started with the best bacterium. It is clear here to deduce that the last chemotaxis loop presents the highly coast function and this is due to the worst half of bacteria, that will be eliminated.

Finally, the BFO generate the best IMC parameter that equivalent to the minimum of both speed error and overshoot. In this case, the best value is obtained for N re =2, N ed =2, N c =1. Where, all the S bacteria locate the same optimum IMC parameter.

6.1 Comparative and discussion studies

Figures 10 and 11 present the speed and stator flux simulation results for five control methods defined as:

  • The conventional IFOC strategy with three PI (PI method),

  • The IFOC strategy with a PI speed regulator and two standard IMC current regulators (IMC without BFO method),

  • The IFOC strategy with a neural network speed controller and two PI current controllers (NN method),

  • The IFOC strategy with a PI speed regulator and two BFO IMC current regulators (IMC with BFO method),

  • The proposed IFOC strategy with a RNNSC speed controller and two BFO IMC current regulators (IMC with BFO and NN method).

Fig. 10
figure 10

Evolution of the PMSM speed response for the five cited methods and zooms at the load torque and parameter variations and overshoots

Full size image
Fig. 11
figure 11

Comparative study of five methods based on flux components phase plane

Full size image

Effectively, five dynamic speed and flux responses are respectively reported in Figs. 10 and 11. Each of these responses is obtained for each method separately and under the same test conditions. Speed targets are fixed at first to the rated one (2500 rpm) and consequently to a high speed one (4000 rpm) and all of them have a slope change dynamic. At rated speed region a load torque of 0.1 N m is applied at t=0.15 s and removed at t=0.4 s. The same load torque crisp value (0.1 N.m) is added in the high speed region, at a time t=0.9 s. An added 100 % abrupt stator resistance variation is introduced at a time t=1 s. In Fig. 10, many zooms are presented to highlight PMSM speeds dynamic response performances according to the five previously cited methods. These zooms concern the load torque and parameter variations as same as the speeds overshoots. For the same methods and conditions, the Fig. 11 reports the phase plane stator flux components. It can be easily noticed that the IFOC decoupling and different magnetic regimes behavior are highly better for the proposed method (IMC with BFO and NN method). A comparison of different methods performances are extracted and summarized in Table 1. Where one easily notices the highest performances of the proposed method compared to others. The worst method (IMC without BFO) is not reported in this table and in the zooms too. The IFOC strategy with a PI speed regulator and two standard IMC current regulators (IMC without BFO method) gives the worst performances and the speed signal becomes unstable when a stator resistance variation occurs at a high speed regimes.

Table 1 A comparative study between the four drive methods
Full size table

The speeds dynamic responses reported in Fig. 10 confirm that the dynamic performances of the proposed method are much higher versus the four candidate methods. From Fig. 11 the NN and IMC-BFO method phase plane trajectory of the motor flux, indicates the superiority in IFOC decoupling at different speed regimes and in its high performances dynamic trajectory behavior.

The major drawback of the PMSM is the ripple in the produced torque which is critical. The important torque ripple source is generated by the interaction of the stator current magnetomotive forces and the permanent magnetic field produced. In order to reduce this, good performance current regulation is the challenge. Figure 14b, confirms the obtained high performances in stator current regulation against load torque and resistance variations for a large speed working range. Therefore, the use of IMC with BFO (Fig. 14b) in current regulation is better than that of conventional PI (Fig. 14a). From the IMC with BFO current regulation response which is robust and precise, it can be concluded that the IFOC used strategy will have good decoupling, the drive scheme is of energy saving and the torque ripple is then reduced. For a high performance drives the speed regulation performance is not sufficient because this can induces lost of FOC decoupling, worst efficiency and higher torque ripple. For that the use of IMC with BFO is very helpful to enhance the PMSM drive performances.

As previously highlighted the robustness and the effectiveness of the proposed overall control scheme (IMC with BFO and NN method) is proven. The simulation of the overall PMSM drive system yields to Figs. 12 and 13 illustrations. The two operating regimes are depicted one for the rated speed (2500 rpm) and the field weakening one for (4000 rpm). The motor stator current components are acting in a way that i q generates the torque and i d is generated by the field weakening algorithm accordingly to the speed working regime. It can be seen the agreement of the estimated speed with the reference one. A stator resistance and torque variations are applied and the system response is immune to that.

Fig. 12
figure 12

Estimated speed and electromagnetic torque responses (IMC with BFO and NN method)

Full size image
Fig. 13
figure 13

Stator current components dynamic responses (IMC with BFO and NN method)

Full size image
Fig. 14
figure 14

Robustness comparison between PI without IMC-BFO and PI with IMC-BFO methods; (a) PI without IMC-BFO, (b) IMC with BFO and (c) the applied load and parameters variations. PMSM current controllers (regulation) performances against load torque and parameter (stator resistance) variations

Full size image

7 Conclusion

In this paper, a high performances sensorless PMSM drives based on the recurrent neuronal networks and the bacteria foraging algorithm IMC tuning is developed to control the PMSM at wide speed range. The Internal model control based on the bacteria foraging algorithm for adjusting the parameters of the IMC controller, was applied as a robust command in the IFOC strategy. The recurrent neural network algorithm was described and the bacteria foraging algorithm was presented. The simulation results prove the good performances obtained for the proposed control scheme under load torque and stator resistance variations.