Abstract
We study the Yoneda lemma for arbitrary simplicial spaces. We do that by introducing left fibrations of simplicial spaces and studying their associated model structure, the covariant model structure. In particular, we prove a recognition principle for covariant equivalences over an arbitrary simplicial space and invariance of the covariant model structure with respect to complete Segal space equivalences.
Similar content being viewed by others
1 Introduction
1.1 Fibrations and the Yoneda Lemma
The Yoneda lemma is a fundamental result in classical category theory. It states that the value of a set-valued functor  at an object c is uniquely determined by natural transformations
at an object c is uniquely determined by natural transformations  . Using the Yoneda lemma we can embed every category into a larger category via the Yoneda embedding, that shares many pleasant features with the category of sets. As a concrete example, we can use the Yoneda lemma and our understanding of limits in the category of sets, to give a precise description of limits in an arbitrary category [45, 63].
. Using the Yoneda lemma we can embed every category into a larger category via the Yoneda embedding, that shares many pleasant features with the category of sets. As a concrete example, we can use the Yoneda lemma and our understanding of limits in the category of sets, to give a precise description of limits in an arbitrary category [45, 63].
In recent decades there has been an effort to generalize the notion of a category to an \((\infty ,1)\)-category, which satisfies the conditions of a category only up to coherent homotopies and is thus better suited to study objects that arise naturally in homotopy theory. This first happened via several models: quasi-categories [11], complete Segal spaces [58], Kan enriched categories [3], and many other models [4, 6]. More recent developments have focused on general concepts that incorporate these models, such as \(\infty \)-cosmoi [65].
Given the important role of the Yoneda lemma for classical categories, we would expect a similarly important role for the Yoneda lemma for \((\infty ,1)\)-categories. However, unlike the 1-categorical case, the study of the Yoneda lemma for \((\infty ,1)\)-categories depends on the particular model we are working with. When we are using the model of Kan enriched categories, we can rely on the extensive literature regarding enriched categories to obtain a Yoneda lemma for Kan enriched categories [63, Lemma 7.3.5], [41, 1.9]. However, other common models of \((\infty ,1)\)-categories, such as quasi-categories or complete Segal spaces, are not strict categories and so we need to use an alternative approach. Indeed, even trying to define an analogue to the representable functor  would require us to choose compositions, which are only defined up to a contractible choice.
would require us to choose compositions, which are only defined up to a contractible choice.
Here we can take another look at the historical development of the Yoneda lemma in the setting of classical categories. Starting with ideas of Grothendieck [28], but also important figures such as Gray [27] and Bénabou [68], a certain full subcategory of  , now known as discrete Grothendieck opfibrations over
, now known as discrete Grothendieck opfibrations over  , was recognized as an alternative characterization of the functor category, meaning it is equivalent to the category of set-valued functors out of the category
, was recognized as an alternative characterization of the functor category, meaning it is equivalent to the category of set-valued functors out of the category  , via the Grothendieck construction. In particular, this means there is also a fibrational Yoneda lemma, which states that for every object c there exists a representable Grothendieck opfibration
, via the Grothendieck construction. In particular, this means there is also a fibrational Yoneda lemma, which states that for every object c there exists a representable Grothendieck opfibration  such that for every discrete Grothendieck opfibration
such that for every discrete Grothendieck opfibration  a morphism
a morphism  over
over  (a “natural transformation”) is uniquely determined by an element in the fiber of p over c (the “value of c”).
(a “natural transformation”) is uniquely determined by an element in the fiber of p over c (the “value of c”).
Such discrete Grothendieck opfibrations are characterized via a lifting property and are hence much more amenable to generalizations to the \((\infty ,1)\)-categorical setting. It was in fact Joyal who first realized that the lifting condition can be generalized to quasi-categories, introducing left fibrations of simplicial sets [38, 39]. Since then, many other approaches to left fibrations and the Yoneda lemma have been studied for several models of \((\infty ,1)\)-categories:
-
Quasi-categories: After Joyal also studied by Lurie [42]. Has since been reworked using different methods by Heuts–Moerdijk [31, 33], Stevenson [67], Cisinski [16] and Nguyen [49].
-
\(\infty \)-Cosmoi: Introduced and proven by Riehl and Verity [65, Chapter 5].
-
Segal spaces: Studied by de Brito [19] and Kazhdan–Varshavsky [40].
In this work we want to focus on left fibrations and Yoneda lemma for general simplicial spaces. Concretely we want to tackle the following previously unanswered questions:
-
(1)
How can we define left fibrations over an arbitrary simplicial space?
-
(2)
For a given simplicial space X can we define a homotopy theory of left fibrations over X (in the form of a model structure)?
-
(3)
For a given simplicial space X and a choice of point x can we construct a representable left fibration \(L_x \rightarrow X\) and prove the Yoneda lemma for simplicial spaces: A morphism of left fibrations \(L_x \rightarrow L\) over X is uniquely determined by a choice of element in the fiber of \(p: L \rightarrow X\) over x?
-
(4)
Given an arbitrary simplicial space X, what is the relation between left fibrations over X and left fibrations over its free complete Segal space (i.e. the fibrant replacement)?
Answering these questions (and many more) is the goal of this work, the major outcomes of which have been summarized more precisely in Sect. 0.4.
1.2 Why Simplicial Spaces?
Given that most results here appeared in one form or another in the language of quasi-categories or \(\infty \)-cosmoi why present the material in the language of simplicial spaces? Here we will list several valuable implications:
Simplified Arguments: Using the approach via simplicial spaces permits very straightforward definitions and proofs, a key example being the Grothendieck construction for left fibrations over categories. In the simplicial space approach we can simply use the classical Grothendieck construction level-wise, as we prove in Theorem 4.18, thus giving a computationally much more feasible description. In particular, one aspect of the Grothendieck construction is its naturality. This is stated without proof in [42, Proposition 2.2.1.1], only to be recently proven (using an intricate argument) in [30, Sect. 6]. The simplified construction given here enables us to give a similar naturality proof in a much more straightforward manner.
Internalization: The study of left fibrations via simplicial sets are build on the specific combinatorial properties of the category of simplicial sets. In the simplicial space approach, however, we characterize left fibrations as morphisms of simplicial spaces, which are simplicial diagrams in spaces. Hence this approach does not rely on the same combinatorial techniques (beyond possibly what is necessary to construct Kan complexes in the first place). As a result this approach can be effectively generalized to many settings beyond spaces. An elegant example is recent work by Martini, who studies left fibrations (using the definition given here) via simplicial diagrams in an arbitrary Grothendieck \(\infty \)-topos [47].
Synthetic \(\infty \)-Category Theory: Homotopy Type Theory is a new foundation for mathematics that is axiomatically homotopy invariantFootnote 1 and thus in many ways better suited for homotopical constructions [69]. One long term goal is to use Homotopy Type Theory to introduce a synthetic notion of \(\infty \)-categories. A first step in this regard has been taken by Riehl and Shulman [64] who introduced a notion of a Rezk type as a way to define \((\infty ,1)\)-categories in Homotopy Type Theory. The notion of a Rezk type is motivated by complete Segal spaces and so in particular their approach to fibrations and the Yoneda lemma corresponds to fibrations of complete Segal spaces rather than quasi-categories. Recently there has been new development, which takes ideas regarding left fibrations of Segal spaces to study higher category theory (such as limits and adjunctions) in the setting of Homotopy Type Theory [12, 46, 71].
Completeness: One defining property of \((\infty ,1)\)-categories is completeness, first introduced by Rezk [58] and then also by Voevodsky in the context of Homotopy Type Theory, where it is introduced as the univalence axiom [69]. A more precise comparison between the univalence axiom in a type theory and completeness of the corresponding Segal object can be found in [66].
From a foundational perspective we want to determine which results in \((\infty ,1)\)-category theory depend on the univalence axiom (i.e. require completeness) and which ones hold in a more general foundation. However, we cannot directly use quasi-categories to address this problem as quasi-categories are automatically complete. Rather it would require us to use technical tools such as flagged \(\infty \)-categories [1]. On the other hand complete Segal spaces can be easily generalized to Segal spaces and so give us a direct computational way to study the necessity of completeness: We simply have to check whether a result only holds for complete Segal spaces or can be generalized to Segal spaces.
Let us give two concrete examples to illustrate possible results. In Sect. 5.2 we observe that we can define and study limits and colimits in a Segal space without any reference to the completeness condition. On the other hand, in order to establish the equivalence of several notions of left adjoints, Riehl and Shulman need to explicitly require the completeness condition [64, Theorem 11.23].
Decomposition Spaces: Decomposition spaces, also known as 2-Segal spaces, are a generalization of Segal spaces with relevance in algebraic K-theory [10], combinatorics [23, 24] and representation theory [22]. This has motivated the study of decomposition spaces and their relevant morphisms, known as CULF morphisms. It was proven by Hackney and Kock [29] that the \(\infty \)-category of CULF morphisms over a given simplicial space is equivalent to right fibrations over its edge-wise subdivision (which is generally not a Segal space). Hence, studying right fibrations over general simplicial spaces provides us with effective tools to better understand decomposition spaces and CULF morphisms as well.
Fibrations of \((\infty ,n)\)-Categories: The same way that 1-categories have been generalized to \((\infty ,1)\)-categories, strict n-categories have been generalized to \((\infty ,n)\)-categories. Similar to the \((\infty ,1)\)-categorical case there is now a long list of models [5], however, unlike in the \((\infty ,1)\)-categorical case, many important questions about \((\infty ,n)\)-categories have remained unanswered.
First of all it is not yet proven that the common models of \((\infty ,n)\)-category that appear in the literature are actually equivalent. For example, it is known that \(\Theta _n\)-spaces [60] are equivalent to n-fold complete Segal spaces [2] as proven by Bergner and Rezk [8, 9]. However, it is not known whether they are equivalent to complicial sets [70] and both of those are not known to be equivalent to comical sets [14]. These are just some of the models that appear in the literature and clearly illustrate the challenges that lie ahead.
On the other hand each model has its own applications in various branches of mathematics. For example, n-fold complete Segal spaces have been the primary model in the study of topological field theories and the cobordism hypothesis [13, 43] and thus merit a theory of fibrations. However, given the difficulties we currently face comparing different models and the fact that the theory of fibrations has not been developed for any of the models, transferring results from one model to another (the way we could for \((\infty ,1)\)-categories) is currently not possible. It is thus imperative to study fibration of n-fold complete Segal spaces in their own right.
The fact that n-fold complete Segal spaces are a direct generalization of complete Segal spaces thus means that an important first step towards realizing this goal is to study left fibrations of complete Segal spaces.
In all three examples, what is important is not just to know that a certain result holds, but rather how to prove the desired results. For example, the study of fibrations of n-fold complete Segal spaces is expected to be a direct generalization of the results for simplicial spaces proven here.
1.3 Relation to Other Work
The idea of working on a Yoneda lemma for simplicial spaces was suggested to me by my advisor Charles Rezk in 2015, as at that time the literature had mostly focused on the study of quasi-categories. Since then however, significant progress has been made:
-
De Brito developed left fibrations of Segal spaces in [19] and so several result proven here (independently) already appear in [19], which have been pointed out when appropriate.
-
Building on the ideas of this paper, several subsequent papers have been written studying (Cartesian) fibrations of complete Segal spaces by the author [52, 53, 55].
-
The key ideas of this paper have also been generalized in [54] to the setting of \((\infty ,n)\)-categories in the particular model of n-fold complete Segal spaces (and various other models of \((\infty ,n)\)-categories introduced by Bergner and Rezk [9]).
-
Independently Nuiten [50] has also studied fibrations of n-fold complete Segal spaces, which imply certain results proven here, when restricting to \(n=1\).
The main benefit of this work consists in uniting different results that have already appeared before, as well as generalizing them to arbitrary simplicial spaces. This in particular includes, but is not limited to, the recognition principle for covariant equivalences (Theorem 4.41) and the invariance of the covariant model structure under CSS equivalences (Theorem 5.1).
1.4 Main Results
The paper focuses on the study of left fibrations. A left fibration is a Reedy fibration of simplicial spaces \(p:Y \rightarrow X\) such that for all \(n \ge 0\) the commutative square

is a homotopy pullback square of spaces (Definition 3.2). It generalizes the unique lifting condition of a discrete Grothendieck opfibration for categories (Definition 1.15). It is well-established that discrete Grothendieck opfibrations model covariant functors valued in sets (Proposition 1.10) and by analogy we think of left fibrations as a model for covariant functors valued in spaces, which guides our work throughout this paper.Footnote 2
Unlike Grothendieck opfibrations, the study of left fibrations requires \((\infty ,1)\)-categorical techniques, which is why we will use the theory of model categories (Appendix A). Concretely, we will show that for each simplicial space X there is a unique simplicial model structure on the category of simplicial spaces over X, denoted  and called the covariant model structure, such that the cofibrations are exactly monomorphisms and fibrant objects are precisely the left fibrations (Theorem 3.12).
and called the covariant model structure, such that the cofibrations are exactly monomorphisms and fibrant objects are precisely the left fibrations (Theorem 3.12).
One important model of an \((\infty ,1)\)-category is a complete Segal space, which is a simplicial space that satisfies the certain lifting conditions that endows it with the structure of a homotopy-coherent generalization of a category (Definition 2.21). As a first step, we thus expect that left fibrations over complete Segal spaces share some of the attributes of discrete Grothendieck opfibrations over categories. We will in fact take a more general step and study left fibrations over Segal spaces (Definition 2.15), getting the following generalization of the Yoneda lemma (here F(n) is the representable simplicial discrete space Sect. 2.3(5)).
Theorem
3.49 Let W be a Segal space and \(x: F(0) \rightarrow W\) be an object. Let

be the under-category projection, which is a left fibration (Theorem 3.44). Then the map

is a covariant equivalence over the Segal space W and so in particular for every left fibration \(L \rightarrow W\) the induced map
is a Kan equivalence (Corollary 3.50).
If the Segal space is the nerve of a category  , then we can give a very precise relationship between left fibrations over
, then we can give a very precise relationship between left fibrations over  (Notation 2.23) and functors out of
(Notation 2.23) and functors out of  valued in spaces.
valued in spaces.
Theorem
4.18 Let  be a small category. The two simplicially enriched adjunctions
be a small category. The two simplicially enriched adjunctions

are Quillen equivalences, which are (up to equivalence) natural in  . Moreover, the derived counit map
. Moreover, the derived counit map  is in fact a Reedy equivalence. Here
is in fact a Reedy equivalence. Here  has the projective model structure and
has the projective model structure and  has the covariant model structure over
has the covariant model structure over  .
.
The result in particular implies (Corollary 4.22) that a morphism of simplicial spaces \(X \rightarrow Y\) over  is a covariant equivalence if and only if for all objects c in
is a covariant equivalence if and only if for all objects c in  the morphism
the morphism

is a diagonal equivalence. One new and important aspect of this work is that we generalize this last result from nerves of categories to arbitrary simplicial spaces. The key input is the following natural zig-zag of equivalences.
Theorem
4.39 Let \(p:Y \rightarrow X\) be a map of simplicial spaces. For every \(\{x\}: F(0) \rightarrow X\), there is a natural zig-zag of diagonal equivalences (Theorem 2.11)
Here \(i: Y \rightarrow \hat{Y}\) is a choice of a left fibrant replacement of Y over X and \(R_x \rightarrow X\) is a contravariant fibrant replacement of \(\{ x \}: F(0) \rightarrow X\) (Remark 4.25).
Building on this zig-zag we can now establish the recognition principle, classifying general covariant equivalences.
Theorem
4.41 (Recognition principle) For every morphism \(\{x\}:F(0) \rightarrow X\) fix a contravariant fibrant replacement \(R_x \rightarrow X\). Let \(g: Y \rightarrow Z\) be a morphism over X. Then \(g:Y \rightarrow Z\) over X is a covariant equivalence over X if and only if for every \(\{x\}: F(0) \rightarrow X\)
is a diagonal equivalence.
The second is the invariance property of the covariant model structure.
Theorem
5.1 (Invariance property) Let \(f: X \rightarrow Y\) be a CSS equivalence (Theorem 2.22). Then the adjunction

is a Quillen equivalence. Here both sides have the covariant model structure.
Using the invariance property, we can finally establish the Yoneda lemma for simplicial spaces (Corollary 5.10), generalizing the Yoneda lemma for Segal spaces (Corollary 3.50). For a simplicial space X fix a CSS fibrant replacement \( i: X \hookrightarrow \hat{X}\). Then, for any point \(x: F(0) \rightarrow X\) and left fibration \(L \rightarrow X\), there is an equivalence of Kan complexes
where \(X_{x/} = X \times _{\hat{X}} \hat{X}^{F(1)} \times _{\hat{X}} F(0)\). Finally, relying on these results we can establish the following further facts.
Theorem
5.11 The covariant model structure is a localization of the CSS model structure on  .
.
Theorem
5.15 Base change by left fibrations preserves CSS equivalences.
1.5 Outline
In Sect. 1 we review the classical Yoneda lemma in Sect. 1.1, the Grothendieck construction in Sect. 1.2 and the fibrational Yoneda lemma for categories in Sect. 1.3 with an eye towards a generalization to simplicial spaces.
Section 2 is a review of necessary background concepts: Joyal–Tierney calculus (Sect. 2.1), spaces (Sect. 2.2), simplicial spaces (Sect. 2.3), the Reedy model structure (Sect. 2.4) and complete Segal spaces (Sect. 2.6).
In Sect. 3 we begin the study of left fibrations. In Sect. 3.1 we introduce left fibrations and give various alternative characterizations. We then move on in Sect. 3.2 to define a model structure for left fibrations, the covariant model structure, over arbitrary simplicial spaces (Theorem 3.12). Finally, in Sect. 3.3 we study left fibrations over Segal spaces and in particular prove the Yoneda lemma for Segal spaces (Theorem 3.49).
In the next section, Sect. 4, we first take a technical digression in Sect. 4.1 and focus on the covariant model structure over nerves of categories and in particular prove the Grothendieck construction in Theorem 4.18. We then use these new technical results in Sect. 4.2 to prove the recognition principle for covariant equivalences (Theorem 4.41).
In the final section, Sect. 5, we study the relation between left fibrations and complete Segal spaces. In particular, in Sect. 5.1 we prove the invariance of the covariant model structure (Theorem 5.1) and several important implications. Finally, in Sect. 5.2 we apply these result to the study of colimits in Segal spaces.
There are two appendices. In Appendix A we review some key lemmas about model categories. In Appendix B we prove that the covariant model structure for simplicial spaces is Quillen equivalent to the covariant model structure for simplicial sets studied in [42].
1.6 Background
The main language here is the language of model categories and complete Segal spaces. So, we assume familiarity with both throughout. Only a few results are explicitly stated here. For a basic introduction to the theory of model categories see [21, 34, 35]. For an introduction to complete Segal spaces see the original source [58].
1.7 Notation
We mostly follow the notation as introduced in [58] and will be reviewed in Sect. 2. We use categories with different enrichments and use the following notation to distinguish between them. Fix a category  and two objects x, y.
and two objects x, y.
-
We denote the set of maps between them by
 . For a further object z and maps \(g: y \rightarrow x, f:z \rightarrow x\), we will denote the set of maps
. For a further object z and maps \(g: y \rightarrow x, f:z \rightarrow x\), we will denote the set of maps  by \(\textrm{Hom}_{/x}(y,z)\).
by \(\textrm{Hom}_{/x}(y,z)\). -
There is one exception to the previous rule. If
 is a category of functors, then we denote the set of natural transformations from F to G by \(\textrm{Nat}(F,G)\), following conventional notation.
is a category of functors, then we denote the set of natural transformations from F to G by \(\textrm{Nat}(F,G)\), following conventional notation. -
If
 is enriched over the category of simplicial sets, we denote the mapping simplicial set by
is enriched over the category of simplicial sets, we denote the mapping simplicial set by 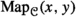 or, if
or, if  is clear from the context, by \(\textrm{Map}(x,y)\). Similar to the last one we will, instead of
is clear from the context, by \(\textrm{Map}(x,y)\). Similar to the last one we will, instead of  , use \(\textrm{Map}_{/x}(y,z)\).
, use \(\textrm{Map}_{/x}(y,z)\). -
If
 is Cartesian closed, we denote the internal mapping object by \(y^x\).
is Cartesian closed, we denote the internal mapping object by \(y^x\). -
There is one exception to the previous rule. For two categories
 ,
,  , we denote the category of functors by
, we denote the category of functors by  , following conventional notation.
, following conventional notation. -
If W is a Segal space, then for two objects x, y in W there is a mapping space, which we denote by \(\textrm{map}_W(x,y)\) (Definition 2.17).
For a functor between small categories  and a bicomplete category
and a bicomplete category  we use the following notation for the induced functors at the level of functor categories:
we use the following notation for the induced functors at the level of functor categories:

Here \(F^*\) is defined by precomposition, \(F_!\) is the left Kan extension and \(F^*\) the right Kan extension.
Similarly, for a given morphism \(f:c \rightarrow d\) in a locally Cartesian closed category  with small limits and colimits we denote the adjunctions
with small limits and colimits we denote the adjunctions

where \(f_!\) is the postcomposition functor, \(f^*\) the pullback functor and \(f_*\) is the right adjoint to \(f^*\).
Finally, let  be a category with final object 1. Then for a given morphism \(\{y\}: 1 \rightarrow Y\), we use the notation \(\{y\}: X \rightarrow Y\) for the unique map that factors through the map \(\{y\}:1 \rightarrow Y\) that picks out the element y in Y.
be a category with final object 1. Then for a given morphism \(\{y\}: 1 \rightarrow Y\), we use the notation \(\{y\}: X \rightarrow Y\) for the unique map that factors through the map \(\{y\}:1 \rightarrow Y\) that picks out the element y in Y.
2 Another Look at the Yoneda Lemma for Classical Categories
The Yoneda lemma is an important result in classical category theory and is thus well known among practitioners of category theory. A lesser known aspect of the Yoneda lemma is that it can be expressed in several different ways. Concretely we want to review four different faces of the Yoneda lemma, which are summarized in this table:
Let us start with the most common form of the Yoneda lemma, which can be found in any introductory book on classical category theory. Here is a version that appears in [45, Page 61].
Lemma 1.1
(Hom version of Yoneda for functors) If  is a functor fand
is a functor fand  an object, then the natural map
an object, then the natural map

is a bijection.
There is, however, a different way this equivalence can be phrased. It relies on the Hom-Tensor Adjunction.
2.1 Tensor Product of Functors and Yoneda Lemma
Most of the material in this subsection can be found in greater detail in [44, VII.2]. For this subsection let  be a fixed category and
be a fixed category and  and
and  be two functors. Then we define the tensor product as the following colimit diagram
be two functors. Then we define the tensor product as the following colimit diagram 

where \(\varphi (a,f,b) = (P(f)(a),b)\) and \(\psi (a,f,b) = (a,F(f)(b))\). So the tensor product of two functors is the product of the values quotiented out by the mapping relations. This definition generalizes the tensor product of a right and left module over a ring, which is the motivation for this notation. Similar to the case of rings this definition of a tensor product fits into a hom-tensor adjunction.
Theorem 1.2
Let  be a category and
be a category and  a functor. Then we have the adjunction
a functor. Then we have the adjunction

where the left adjoint takes P to  and the right adjoint takes a set S to the functor which takes an object C to
and the right adjoint takes a set S to the functor which takes an object C to  .
.
Remark 1.3
Note that we could have made the same construction for the case where  is replaced with any category which has all colimits. However, here we do not need to work at this level of generality. For more details on the general construction see [44, Page 358].
is replaced with any category which has all colimits. However, here we do not need to work at this level of generality. For more details on the general construction see [44, Page 358].
With the tensor product at hand we can state another version of the Yoneda lemma.
Lemma 1.4
(Tensor version of Yoneda for functors) If  is a functor and
is a functor and  an object, then the natural map
an object, then the natural map

is a bijection.
This version of the Yoneda lemma has the following basic corollaries, which should look quite familiar.
Corollary 1.5
Let  be a category and \(C,C'\) two objects. Then we have the following isomorphism.
be a category and \(C,C'\) two objects. Then we have the following isomorphism.

Corollary 1.6
Let  be a category and
be a category and  be two functors. Then a natural transformation \(\alpha : P \rightarrow Q\) is a natural isomorphism if and only if
be two functors. Then a natural transformation \(\alpha : P \rightarrow Q\) is a natural isomorphism if and only if

is a bijection for every object  .
.
2.2 From Functors to Fibrations: The Grothendieck Construction
We want to now translate the Yoneda lemma from a statement about set-valued functors to a statement about fibrations. This requires us to translate between functors and fibrations which we will do via the Grothendieck construction.
Remark 1.7
We will need a careful understanding of the Grothendieck construction in the coming sections. Thus the review in this section is self-contained. However, the ideas are in no way new and a more detailed approach can be found in many places, such as [44, I.5], or [36, A1.1.7, B1.3.1].
Definition 1.8
Let  be a category. Define
be a category. Define

as the functor that takes  to the category
to the category  with
with
-
Objects: Pairs (c, x) where c is an object in
 and \(x \in F(c)\).
and \(x \in F(c)\). -
Morphisms: For two objects (c, x), (d, y) we have

It comes with an evident projection map  . Moreover, for a natural transformation \(\alpha : F \Rightarrow G\), the functor
. Moreover, for a natural transformation \(\alpha : F \Rightarrow G\), the functor  is given as \((c,x) \mapsto (c,\alpha _cx)\).
is given as \((c,x) \mapsto (c,\alpha _cx)\).
Notice, by construction the fiber of  over an object c is the discrete category with object set F(c). This functor has a left adjoint and a right adjoint that we want to define in detail.
over an object c is the discrete category with object set F(c). This functor has a left adjoint and a right adjoint that we want to define in detail.
Definition 1.9
Let  be a category. We define the functor
be a category. We define the functor

that takes an object to the over-category  and a morphism \(f:c \rightarrow d\) to the post-composition
and a morphism \(f:c \rightarrow d\) to the post-composition  .
.
Similarly, define the functor

that takes an object to the under-category  and a morphism \(f: c \rightarrow d\) to the precomposition
and a morphism \(f: c \rightarrow d\) to the precomposition  .
.
For a given category over  ,
,  define
define

as the composition

in other words we have  . Similarly, define
. Similarly, define

as the composition

meaning we have  . We claim that
. We claim that  is the left adjoint and
is the left adjoint and  is the right adjoint to
is the right adjoint to  .
.
Proposition 1.10
We have the following diagram of adjunctions

Proof
We first prove the right adjoint. First of all notice  commutes with colimits. Indeed, for a given diagram
commutes with colimits. Indeed, for a given diagram  it is direct computation that the induced cocone
it is direct computation that the induced cocone  satisfies the universal property of the universal cocone. Now, by [44, Corollary I.5.4], every colimit preserving functor out of
satisfies the universal property of the universal cocone. Now, by [44, Corollary I.5.4], every colimit preserving functor out of  is the left Kan extension of its restriction to
is the left Kan extension of its restriction to  , meaning we have the following left Kan extension
, meaning we have the following left Kan extension

which means it has a right adjoint given by  .
.
For the left adjoint, we first show that  commutes with colimits. As colimits are computed point-wise this means we have to prove that for every object c the functor
commutes with colimits. As colimits are computed point-wise this means we have to prove that for every object c the functor

commutes with colimits. This functor is a composition and so we check separately that both are left adjoints:
-
(1)
 is a left adjoint because
is a left adjoint because  is a Conduché functor [17].
is a Conduché functor [17]. -
(2)
\(\pi _0\) is the left adjoint of the inclusion functor
 .
.
Now, we prove that  is the left adjoint. Recall that [n] is the category given via the poset structure \(\{0 \le 1 \le \ldots \le n \}\) and that every category over
is the left adjoint. Recall that [n] is the category given via the poset structure \(\{0 \le 1 \le \ldots \le n \}\) and that every category over  is a colimit of functors
is a colimit of functors  and so the result follows from the following natural isomorphisms:
and so the result follows from the following natural isomorphisms:

Let us explain the various natural isomorphisms that require a justification.
Notice a morphism in  is of the form \(f:(c,x) \rightarrow (d,G(f)(x))\), where \(f: c \rightarrow d\) is a morphism in
is of the form \(f:(c,x) \rightarrow (d,G(f)(x))\), where \(f: c \rightarrow d\) is a morphism in  . Hence, for a given functor
. Hence, for a given functor  , which we can depict by a chain of n morphisms in
, which we can depict by a chain of n morphisms in  , \(c_0\xrightarrow { \ f_1 \ } c_1 \xrightarrow { \ f_2 \ } \ldots \xrightarrow { \ f_n \ } c_n\), a functor
, \(c_0\xrightarrow { \ f_1 \ } c_1 \xrightarrow { \ f_2 \ } \ldots \xrightarrow { \ f_n \ } c_n\), a functor  over
over  that lifts \(\alpha \) is of the form \((c_0,x) \xrightarrow { \ f_0 \ } (c_1,G(f_0)(x)) \xrightarrow { \ f_1 \ } \ldots \xrightarrow { \ f_n \ } (c_1,G(f_n \circ \ldots \circ f_1 \circ f_0)(x))\), meaning it is uniquely determined by the value of the object 0 in [n].
that lifts \(\alpha \) is of the form \((c_0,x) \xrightarrow { \ f_0 \ } (c_1,G(f_0)(x)) \xrightarrow { \ f_1 \ } \ldots \xrightarrow { \ f_n \ } (c_1,G(f_n \circ \ldots \circ f_1 \circ f_0)(x))\), meaning it is uniquely determined by the value of the object 0 in [n].
The third isomorphism is the Yoneda lemma. The fourth isomorphism follows from the fact that  . Finally, for the last isomorphism we observe that two objects of the form \(\alpha (0) \rightarrow \alpha (1) \rightarrow \ldots \rightarrow \alpha (n) \rightarrow c\) in
. Finally, for the last isomorphism we observe that two objects of the form \(\alpha (0) \rightarrow \alpha (1) \rightarrow \ldots \rightarrow \alpha (n) \rightarrow c\) in  are in the same path-component if they compose to the same morphism \(\alpha (0) \rightarrow c\) giving us the desired bijection
are in the same path-component if they compose to the same morphism \(\alpha (0) \rightarrow c\) giving us the desired bijection  . \(\square \)
. \(\square \)
In fact  has even more desirable properties.
has even more desirable properties.
Lemma 1.11
 is fully faithful.
is fully faithful.
Proof
Let  be two functors. We need to prove that the map
be two functors. We need to prove that the map

is a bijection of sets. For that we will construct an inverse. Concretely, we define

as follows. For a given functor  over
over  we define the natural transformation
we define the natural transformation  . The functoriality of H implies that
. The functoriality of H implies that  is natural.
is natural.
It remains to show these are inverses. For a given natural transformation\(\alpha : F \Rightarrow G\) we have

and on the other side

finishing the proof. \(\square \)
This has a direct implication for  and
and  .
.
Corollary 1.12
 is a localization functor and
is a localization functor and  is a colocalization functor.
is a colocalization functor.
We end this subsection by observing that while  is fully faithful, it is in fact not essentially surjective.
is fully faithful, it is in fact not essentially surjective.
Definition 1.13
A functor  is conservative if it reflects isomorphisms.
is conservative if it reflects isomorphisms.
Lemma 1.14
Let  be a functor. Then
be a functor. Then  is conservative.
is conservative.
Proof
Let \(f: (c,x) \rightarrow (d,y)\) be a morphism in  such that the underlying morphism \(\pi _F(f): c \rightarrow d\) is an isomorphism. We need to show that f in
such that the underlying morphism \(\pi _F(f): c \rightarrow d\) is an isomorphism. We need to show that f in  is an isomorphism and we will do so by providing an inverse. Let \(f^{-1}: d \rightarrow c\) in
is an isomorphism and we will do so by providing an inverse. Let \(f^{-1}: d \rightarrow c\) in  be the inverse of \(\pi _F(f)\) in
be the inverse of \(\pi _F(f)\) in  . The inverse is now given by the lift \(f^{-1}: (d,y) \rightarrow (c,x)\). \(\square \)
. The inverse is now given by the lift \(f^{-1}: (d,y) \rightarrow (c,x)\). \(\square \)
Thus we need to restrict our attention to the essential image of  , which leads us to discrete Grothendieck fibrations.
, which leads us to discrete Grothendieck fibrations.
2.3 Yoneda Lemma for Grothendieck Fibrations
In this subsection we want to use the fully faithful functor  to translate both versions of the Yoneda lemma from a functorial statement to a fibrational one.
to translate both versions of the Yoneda lemma from a functorial statement to a fibrational one.
This might not be a major improvement when studying 1-categories, however, in the world of higher categories functors can be difficult to study, because of the homotopy coherence. On the other hand, fibrations can be defined and studied in a straightforward manner. Thus a fibrational approach to the Yoneda lemma is an excellent first step for a generalization to a Yoneda lemma for simplicial spaces.
As we observed in Lemma 1.11,  is fully faithful, however, it is not essentially surjective!
is fully faithful, however, it is not essentially surjective!
Definition 1.15
A functor  is a discrete Grothendieck opfibration over
is a discrete Grothendieck opfibration over  if it is in the essential image of
if it is in the essential image of  , meaning there exists a functor
, meaning there exists a functor  and isomorphism
and isomorphism  over
over  .
.
Fortunately, there is also an internal characterization of discrete Grothendieck opfibrations.
Lemma 1.16
A functor  is a discrete Grothendieck opfibration over
is a discrete Grothendieck opfibration over  if and only if for any map \(f: c \rightarrow c'\) in
if and only if for any map \(f: c \rightarrow c'\) in  and object d in
and object d in  such that \(P(d) = c\), there exists a unique lift \(\hat{f}:d \rightarrow d'\) such that \(P(\hat{f}) =f\).
such that \(P(d) = c\), there exists a unique lift \(\hat{f}:d \rightarrow d'\) such that \(P(\hat{f}) =f\).
Proof
Let  be a functor. Then
be a functor. Then  satisfies the lifting condition stated in the lemma. Indeed, for a morphism \(f: c \rightarrow c'\) and a lift (c, x) where \(x \in F(c)\), there is a unique lift given by the morphism \(f: (c,x) \rightarrow (c',F(f)(x))\).
satisfies the lifting condition stated in the lemma. Indeed, for a morphism \(f: c \rightarrow c'\) and a lift (c, x) where \(x \in F(c)\), there is a unique lift given by the morphism \(f: (c,x) \rightarrow (c',F(f)(x))\).
On the other hand let us assume that  satisfies the lifting condition of the lemma. Then we will construct a functor
satisfies the lifting condition of the lemma. Then we will construct a functor  such that
such that  over
over  .
.
First note that the unique lifting condition implies that the fiber of P over every given point c, \(P^{-1}(c)\), is a discrete category i.e. a set. Indeed let f be a morphism in  such that \(P(f) = \textrm{id}_C\). Then by the uniqueness assumption \(f = \textrm{id}\).
such that \(P(f) = \textrm{id}_C\). Then by the uniqueness assumption \(f = \textrm{id}\).
Now define F as follows:
-
Objects: For an object c in
 define \(F(c) = P^{-1}(c)\)
define \(F(c) = P^{-1}(c)\) -
Morphisms: For a morphism \(f: c \rightarrow c'\) define \(F(f): F(c) \rightarrow F(c')\) as the map that takes \(x \in F(c)\) to the target of the unique lift of f in
 .
.
The standard projection  exactly recovers
exactly recovers  . \(\square \)
. \(\square \)
The previous characterization allows us to give a contravariant version of Grothendieck opfibrations.
Definition 1.17
 is called a discrete Grothendieck fibration if for any map \(f: c \rightarrow c'\) in
is called a discrete Grothendieck fibration if for any map \(f: c \rightarrow c'\) in  and object \(d'\) in
and object \(d'\) in  such that \(P(d') = c'\), there exists a unique lift \(\hat{f}:d \rightarrow d'\) such that \(P(\hat{f}) = f\).
such that \(P(d') = c'\), there exists a unique lift \(\hat{f}:d \rightarrow d'\) such that \(P(\hat{f}) = f\).
Remark 1.18
Note that it is very rare that a functor  is a discrete Grothendieck fibration as well as a discrete Grothendieck opfibration. Concretely it only happens if
is a discrete Grothendieck fibration as well as a discrete Grothendieck opfibration. Concretely it only happens if  over
over  where
where  takes every morphism to an isomorphism.
takes every morphism to an isomorphism.
Remark 1.19
Discrete Grothendieck fibrations are a special case of more general Grothendieck fibrations that correspond to functors valued in categories. See [68] for a readable introduction to general Grothendieck fibrations.
We now want to move on to the Yoneda lemma for discrete Grothendieck fibrations, but for that we need the analogue of representable functors.
Example 1.20
Let us determine the category  . Its objects are pairs \((d,f: c \rightarrow d)\) and a morphism \((d,f: c \rightarrow d) \rightarrow (d',f':c \rightarrow d')\) is a morphism \(g: d \rightarrow d'\) such that \(gf = f': c \rightarrow d'\). Thus we just rediscovered the projection from the under-category
. Its objects are pairs \((d,f: c \rightarrow d)\) and a morphism \((d,f: c \rightarrow d) \rightarrow (d',f':c \rightarrow d')\) is a morphism \(g: d \rightarrow d'\) such that \(gf = f': c \rightarrow d'\). Thus we just rediscovered the projection from the under-category  .
.
With the previous remarks at hand we can now phrase the first fibered version of the Yoneda Lemma.
Lemma 1.21
(Hom version of Yoneda for fibered categories) Let  be a discrete Grothendieck opfibration. Then the natural map between the sets of functors
be a discrete Grothendieck opfibration. Then the natural map between the sets of functors

is a bijection. Here  denotes the hom set in the category
denotes the hom set in the category  and \(\textrm{id}_c:c \rightarrow c\) is seen as an object in
and \(\textrm{id}_c:c \rightarrow c\) is seen as an object in  .
.
Proof
Let  be a functor such that
be a functor such that  over
over  . We now have the following commutative diagram
. We now have the following commutative diagram

Here the left morphism is a bijection as  is fully faithful and the bottom morphism is a bijection by the Yoneda lemma. \(\square \)
is fully faithful and the bottom morphism is a bijection by the Yoneda lemma. \(\square \)
Similar to the previous part we also have a tensor version of the Yoneda lemma for fibered categories. First, however, we have to define a notion of tensor product for fibered categories. Recall that the tensor product of two functors  ,
,  is given by a quotient on the set
is given by a quotient on the set  , which reminds us of a fibered product. Hence the fibrational analogue of the tensor product of a discrete Grothendieck opfibration
, which reminds us of a fibered product. Hence the fibrational analogue of the tensor product of a discrete Grothendieck opfibration  and discrete Grothendieck fibration
and discrete Grothendieck fibration  is given by
is given by

where \(\pi _0\) is the set of connected components. With this definition we can state our last version of the Yoneda lemma.
Lemma 1.22
(Tensor version of Yoneda for fibered categories) Let  be a discrete Grothendieck opfibration. Then the natural map
be a discrete Grothendieck opfibration. Then the natural map

is a bijection (here \(\hat{f}\) is the unique lift of f with domain \(d'\)).
Proof
Notice  is a discrete Grothendieck opfibration and so the fiber
is a discrete Grothendieck opfibration and so the fiber  is already a discrete category, and so we can directly establish a bijection of sets. For every arbitrary morphism \((f:c' \rightarrow c, d')\), the elements \((f:c' \rightarrow c, d')\) and \((\textrm{id}_c:c \rightarrow c, Codomain(\hat{f}))\) are in the same equivalence class of
is already a discrete category, and so we can directly establish a bijection of sets. For every arbitrary morphism \((f:c' \rightarrow c, d')\), the elements \((f:c' \rightarrow c, d')\) and \((\textrm{id}_c:c \rightarrow c, Codomain(\hat{f}))\) are in the same equivalence class of  . Moreover, \((\textrm{id}_c:c \rightarrow c, d)\) and \((\textrm{id}_c:c \rightarrow c, d')\) are in the same equivalence class if and only if \(d= d'\). This proves that the assignment \((\textrm{id}_c,d) \mapsto d\) induces the desired bijection. \(\square \)
. Moreover, \((\textrm{id}_c:c \rightarrow c, d)\) and \((\textrm{id}_c:c \rightarrow c, d')\) are in the same equivalence class if and only if \(d= d'\). This proves that the assignment \((\textrm{id}_c,d) \mapsto d\) induces the desired bijection. \(\square \)
Our goal in the coming sections is to build the necessary machinery to generalize these statements to the setting of simplicial spaces. In particular, we will define the correct analogue to discrete Grothendieck opfibrations, study their properties and prove the Yoneda lemma.
Concretely, we have the following generalizations:
3 Basics and Conventions
In this section we review some basic concepts that we will need in the coming sections. In particular, we review the Joyal–Tierney calculus (Sect. 2.1) [37] as a powerful notational tool. Moreover, we review notation for simplicial sets (Sect. 2.2), simplicial spaces (Sect. 2.3) and its associated Reedy model structure (Sect. 2.4) along with two localizations of the Reedy model structure (Sect. 2.5). Finally, we use complete Segal spaces as our model of higher categories and thus will end the section with a quick review following [58] (Sect. 2.6).
3.1 Joyal–Tierney Calculus
As we primarily work with simplicial spaces it is helpful to first set up some notation that will simplify many statements. The notation introduced here is due to Joyal and Tierney [37, Sect. 7].
Notation 2.1
For this subsection let  be a locally Cartesian closed bicomplete category.
be a locally Cartesian closed bicomplete category.
Definition 2.2
Let \(f: A \rightarrow B\) and \(g: C \rightarrow D\) be two maps in  . We define the pushout product as the universal map out of the pushout
. We define the pushout product as the universal map out of the pushout
induced by the commutative square

Moreover, for two sets of maps \(\mathcal {A}\) and \(\mathcal {B}\) we use the notation
Definition 2.3
For two maps \(f: A \rightarrow B\) and \(p: Y \rightarrow X\) we define the pullback exponential
induced by the commutative square

Moreover, for two sets of maps \(\mathcal {A}\) and \(\mathcal {X}\) we use the notation
These two functors give us an adjunction of arrow categories:

The key result about these two constructions is that they can help us better understand lifting conditions.
Notation 2.4
Let \(\mathcal {L}\) and \(\mathcal {R}\) be two sets of morphisms in  . If every morphism in \(\mathcal {L}\) has the left lifting property with respect to morphisms in \(\mathcal {R}\) then we use the notation \(\mathcal {L} \pitchfork \mathcal {R}\).
. If every morphism in \(\mathcal {L}\) has the left lifting property with respect to morphisms in \(\mathcal {R}\) then we use the notation \(\mathcal {L} \pitchfork \mathcal {R}\).
Proposition 2.5
( [37, Proposition 7.6]) Let \(\mathcal {A}\), \(\mathcal {B}\) and \(\mathcal {X}\) be three sets of morphisms in  . Then:
. Then:
3.2 Simplicial Sets
 will denote the category of simplicial sets. Following [58, 2.1] we will also use the terminology spaces. We will use the following notation with regard to spaces:
will denote the category of simplicial sets. Following [58, 2.1] we will also use the terminology spaces. We will use the following notation with regard to spaces:
-
(1)
 is the indexing category with objects posets \([n] = \{0,1,\ldots ,n \} \) and mappings maps of posets.
is the indexing category with objects posets \([n] = \{0,1,\ldots ,n \} \) and mappings maps of posets. -
(2)
We will denote a morphism \([n] \rightarrow [m]\) by a sequence of numbers \(< a_0,\ldots ,a_n>\), where \(a_i\) is the image of \(i \in [n]\).
-
(3)
\(\Delta [n]\) denotes the simplicial set representing [n] i.e. \(\Delta [n]_k = \textrm{Hom}_{\Delta }([k], [n])\).
-
(4)
\(\partial \Delta [n]\) denotes the boundary of \(\Delta [n]\) i.e. the largest sub-simplicial set which does not include \(id_{[n]}: [n] \rightarrow [n]\). Similarly \(\Lambda [n]_l\) denotes the largest simplicial set in \(\Delta [n]\) which does not include the \(l^{th}\) face.
-
(5)
For a simplicial set S we denote the face maps by \(d_i: S_{n} \rightarrow S_{n-1} \) and the degeneracy maps by \(s_i: S_n \rightarrow S_{n+1}\).
-
(6)
Let I[l] be the category with l objects and one unique isomorphism between any two objects. Then we denote the nerve of I[l] as J[l]. It is a Kan fibrant replacement of \(\Delta [l]\) and comes with an inclusion \(\Delta [l] \rightarrowtail J[l]\), which is a Kan equivalence.
-
(7)
We say a space K is discrete if for each n, \(K_n = K_0\) and all simplicial operators are identity maps.
3.3 Simplicial Spaces
 denotes the category of simplicial spaces (bisimplicial sets). We have the following basic notations with regard to simplicial spaces:
denotes the category of simplicial spaces (bisimplicial sets). We have the following basic notations with regard to simplicial spaces:
-
(1)
We embed the category of spaces inside the category of simplicial spaces as constant simplicial spaces (i.e. the simplicial spaces S such that \(S_n = S_0\) for all n and all simplicial operator maps are identities).
-
(2)
More generally we say a simplicial space is homotopically constant if all simplicial operator maps \(X_n \rightarrow X_m\) are weak equivalences (and in particular \(X_n\) are all equivalent to \(X_0\)).
-
(3)
On the other hand we say a simplicial space X is a simplicial discrete space if for all n, the space \(X_n\) is discrete.
-
(4)
For a given simplicial space X we use the notation s, the source map, for \(d_1: X_1 \rightarrow X_0\) and t, the target map, for \(d_0: X_1 \rightarrow X_0\). This is motivated by thinking of a simplicial diagram as a generalization of a directed graph.
-
(5)
Denote F(n) to be the simplicial discrete space defined as
$$\begin{aligned} F(n)_k = \textrm{Hom}_{\Delta }([k],[n]). \end{aligned}$$ -
(6)
Similar to Sect. 2.2(3) we denote a morphism \(F(n) \rightarrow F(m)\) by \(< a_0,\ldots ,a_n>\).
-
(7)
\(\partial F[n]\) denotes the boundary of F(n). Similarly \(L(n)_l\) denotes the largest simplicial space in F(n) which lacks the \(l^{th}\) face.
-
(8)
The category
 is enriched over spaces via
is enriched over spaces via 
-
(9)
The category
 is also enriched over itself via
is also enriched over itself via 
-
(10)
By the Yoneda lemma, for a simplicial space X we have an isomorphism of spaces

3.4 Reedy Model Structure
The category of simplicial spaces has a Reedy model structure [56], which is defined as follows:
- (F):
-
A map \(f: Y \rightarrow X\) is a (trivial) Reedy fibration if for each \(n\ge 0\) the following map of spaces is a (trivial) Kan fibration

- (W):
-
A map \(f:Y \rightarrow X\) is a Reedy weak equivalence if it is a level-wise Kan weak equivalence.
- (C):
-
A map \(f:Y \rightarrow X\) is a Reedy cofibration if it is an inclusion.
The Reedy model structure is very helpful as it enjoys many features that can help us while doing computations. In particular, it is cofibrantly generated, simplicial and proper. Moreover, it is also compatible with Cartesian closure, by which we mean that if \(i: A \rightarrow B\) and \(j: C \rightarrow D\) are cofibrations and \(p: X \rightarrow Y\) is a fibration then the map \(i \square j\) is a cofibration and \(\textrm{exp}(i,p)\) is a fibration, which are trivial if any of the involved maps are trivial.
These properties in particular imply that we can apply Bousfield localizations to the Reedy model structure. See Appendix A for more details.
3.5 Diagonal and Kan Model Structure
In the coming sections we will use various localizations of simplicial spaces with the Reedy model structure that are equivalent to the Kan model structure. Although these results have been studied before, we will make ample use of the notation and thus will do a careful review here.
First we need two adjunctions between spaces and simplicial spaces.
Notation 2.6
Let

be the diagonal functor that takes an object [n] to the pair ([n], [n]) and let

be the projection functors that take an object ([n], [m]) to the projections [n] or [m], respectively. Finally, let

be the inclusion functors that take an object [n] to ([n], 0) or (0, [n]), respectively.
These functors give us three adjunctions

Remark 2.7
These adjunctions \((\textrm{Diag}^*,\textrm{Diag}_*)\), \(((\pi _1)^*, (\pi _1)_*)\) and \(((i_1)^*,(i_1)^*)\) are in fact enriched adjunctions, meaning that we have a natural isomorphism of spaces

Remark 2.8
Our notation convention, Sect. 2.3(1), implies that for a space K we denote the simplicial space \((\pi _1)^*(K)\) by K as well.
Remark 2.9
Notice we have \(\pi _1 \circ i_1 = \textrm{id}\) and so \((i_1)^* \circ (\pi _1)^* = \textrm{id}\). More importantly, for every simplicial set X

hence \((\pi _1)_* = (i_1)^*\). Thus, we can also think of \((i_1)_*\) as the right adjoint to \((\pi _1)_*\).
Before we move on we want to give very detailed descriptions of these functors.
For a simplicial space X we have:
Also, for a simplicial set K we have:
Remark 2.10
The direct computation above in particular implies that for a given Kan complex K there is a natural map
that is a Reedy trivial cofibration. Indeed, we have a retract diagram \(K \rightarrow K^{\Delta [n]} \rightarrow K\), that we can make into a deformation retract via morphism \(\Delta [n] \times \Delta [1] \rightarrow \Delta [n]\) induced by the morphism \([n] \times [1] \rightarrow [n]\) given by \((i,0) \mapsto i\) and \((i,1) \mapsto n\).
We want to show that the category of simplicial spaces has two model structures that makes the three adjunctions above into Quillen equivalences and that will play an important role in the coming sections.
The first one is the diagonal model structure on simplicial spaces. Given its prominent role in homotopy theory, it has already been considered in a variety of settings, such as, among others, by Moerdijk [48, Proposition 1.2], Rezk–Schwede–Shipley [61, Lemma 4.3], Dugger [20, Example 5.6], and Cisinski [15, Corollary 3.16].
Theorem 2.11
There is a unique, cofibrantly generated, simplicial model structure on  , called the diagonal model structure and denoted by
, called the diagonal model structure and denoted by  , with the following specifications.
, with the following specifications.
- (W):
-
A map \(f:X \rightarrow Y\) is a weak equivalence if the diagonal map of spaces
$$\begin{aligned} \textrm{Diag}^*(f): \textrm{Diag}^*(X) \rightarrow \textrm{Diag}^*(Y) \end{aligned}$$is a Kan equivalence.
- (C):
-
A map \(f:X \rightarrow Y\) is a cofibration if it is an inclusion.
- (F):
-
A map \(f:X \rightarrow Y\) is a fibration if it satisfies the right lifting condition for trivial cofibrations.
In particular, an object W is fibrant if and only if it is Reedy fibrant and a homotopically constant simplicial space.
Proof
Let \(\mathcal {L}\) be the following set of cofibrations

Then by Theorem A.7 there is a localized model structure on  such that cofibrations are inclusions and fibrant objects are Reedy fibrant simplicial spaces K such that
such that cofibrations are inclusions and fibrant objects are Reedy fibrant simplicial spaces K such that

is a Kan equivalence.
In order to finish the proof we only need to prove that \(f: X \rightarrow Y\) is a weak equivalence in the localized model structure if and only if \(\textrm{Diag}^*(f)\) is a Kan equivalence. For that we first observe that for a given fibrant simplicial space K, we have the following diagram

Here the left hand morphism is the Reedy trivial cofibration described in Remark 2.10, implying the existence of a lift \(\gamma _K: \textrm{Diag}_*K_0 \rightarrow K\), which by 2-out-of-3 is a Reedy equivalence as well.
Now, notice also that \(\textrm{Diag}_*(K_0)\) is Reedy fibrant, as the Reedy morphism is given by the Kan fibration \((K_0)^{\Delta [n]} \rightarrow (K_0)^{\partial \Delta [n]}\). Hence, for the fibrant simplicial space K we have the following diagram

Here the vertical morphisms in the top square are equivalences, because \(\gamma _K: \textrm{Diag}_*K_0 \rightarrow K\) is a Reedy equivalence between Reedy fibrant objects and the vertical morphisms in the bottom square are isomorphisms because of the simplicially enriched adjunction \((\textrm{Diag}^*,\textrm{Diag}_*)\).
Now the map \(f: X \rightarrow Y\) is an equivalence in this localized model structure if and only if the top horizontal map is a Kan equivalence for all fibrant objects K (as the model structure is simplicial), which by the diagram above is equivalent to the bottom map being a Kan equivalence for all Kan complexes \(K_0\).
The equivalence above holds in particular when K is a simplicial space of the form \(\textrm{Diag}_*L\), where L is an arbitrary Kan complex, which, combined with the fact that the Kan model structure is simplicial, implies that this is equivalent to
being a Kan equivalence, which is exactly the desired statement and finishes the proof. \(\square \)
Theorem 2.12
There is a unique, cofibrantly generated, simplicial model structure on  , called the Kan model structure and denoted by
, called the Kan model structure and denoted by  , with the following specifications.
, with the following specifications.
- (W):
-
A map \(f: X \rightarrow Y\) is a weak equivalence if
$$\begin{aligned} (\pi _1)_*f: (\pi _1)_*X \rightarrow (\pi _1)_*Y \end{aligned}$$is a Kan equivalence.
- (C):
-
A map \(f: X \rightarrow Y\) is a cofibration if it is an inclusion.
- (F):
-
A map \(f: X \rightarrow Y\) is a fibration if it satisfies the right lifting condition for trivial cofibrations.
In particular, an object W is fibrant if and only if it is Reedy fibrant and the map

is a trivial Kan fibration for \(n >0\).
Proof
Let \(\mathcal {L}\) be the following set of cofibrations

Then by Theorem A.7 there is a localized model structure on  such that cofibrations are inclusions and fibrant objects are Reedy fibrant simplicial spaces K such that
such that cofibrations are inclusions and fibrant objects are Reedy fibrant simplicial spaces K such that

is a Kan equivalence.
Before we can finish the proof, we need a better understanding of the fibrant objects in this model structure. A Reedy fibrant simplicial space X is fibrant if and only if the map \(X_n \rightarrow (X_0)^{n+1}\) is an equivalence. Thus a Reedy fibrant simplicial space X is fibrant in this model structure if and only if the natural map \(X \rightarrow (i_1)_*(X_0)\) is a Reedy equivalence.
In order to finish the proof we only need to prove that \(f: X \rightarrow Y\) is a weak equivalence in this localized model structure if and only if \((\pi _1)_*(f)\) is a Kan equivalence. Fix a map of simplicial spaces \(X \rightarrow Y\) and a fibrant simplicial space Z. Then we have the following diagram of spaces:

The vertical maps in the top square are Kan equivalences as Z and \((i_1)_*(Z_0)\) are both Reedy fibrant, and moreover, by the explanation in the previous paragraph, \(Z \rightarrow (i_1)_*(Z_0)\) is a Reedy equivalence. Indeed, \((i_1)_*(Z_0)_0= Z_0\) is Kan fibrant and for \(n>0\), the morphism  is the identity. The vertical maps in the bottom square are isomorphisms because \((i_1)_*\) is the right adjoint to \((\pi _1)_*\) as explained in Remark 2.9.
is the identity. The vertical maps in the bottom square are isomorphisms because \((i_1)_*\) is the right adjoint to \((\pi _1)_*\) as explained in Remark 2.9.
Now the map \(f: X \rightarrow Y\) is an equivalence in this localized model structure if and only if the top horizontal map is a Kan equivalence for all fibrant objects Z (as the model structure is simplicial), which by the diagram above is equivalent to the bottom map being a Kan equivalence for all Kan complexes \(Z_0\).
We can in particular apply this equivalence to the fibrant simplicial space \((i_1)_*(L)\) for an arbitrary Kan complex L, meaning the result holds for an arbitrary Kan complex and the Kan model structure is simplicial. Hence this is equivalent to
being a Kan equivalence of simplicial sets. \(\square \)
We are finally in a position to prove the existence of the chain of Quillen equivalences.
Theorem 2.13
The following three simplicially enriched adjunctions

are Quillen equivalences.
Proof
Quillen Adjunctions: The fact that these three adjunctions are Quillen adjunctions is similar for all three cases and so we will combine the argument. In all three cases we observe that the left adjoint \(\textrm{Diag}^*, (\pi _1)^*, (i_1)^*\) preserve inclusions and weak equivalences and thus preserves cofibrations and trivial cofibrations, which imply they are left Quillen functors.
Indeed, the fact that they preserve inclusions is immediate. The fact that they preserve weak equivalences is an immediate observation for \((\pi _1)^*\) and \((i_1)^*\) and for \(\textrm{Diag}^*\) follows from Theorem 2.11.
Quillen Equivalence: We move on to prove that these are Quillen equivalences. First we prove that \((\pi _1)^*\) and \((i_1)^*\) are derived inverses of each other. Notice that for every simplicial set K, \((i_1)^*(\pi _1)^*(K)=K\). So, in order to prove they are derived inverses it suffices to prove there is a natural equivalence
for every simplicial space X fibrant in the Kan model structure on simplicial spaces. This will then imply that \(((\pi _1)^*, (\pi _1)_*)\) and \(((i_1)^*, (i_1)_*)\) are Quillen equivalences and in fact are inverses of each other.
We have \((\pi _1)^*(i_1)^*(X)_n = X_0\) and so the natural map \((\pi _1)^*(i_1)^*(X) \rightarrow X\) is an equivalence in the Kan model structure on simplicial spaces.
Next we move on to prove that \((\textrm{Diag}^*,\textrm{Diag}_*)\) is a Quillen equivalence. Based on Lemma A.4 it suffices to prove that \(\textrm{Diag}^*\) reflects weak equivalences and the derived counit map (which is the actual counit map as all objects are cofibrant) \(\textrm{Diag}^*\textrm{Diag}_*K \rightarrow K\) is a Kan equivalence of simplicial sets, for K a Kan complex.
The fact that \(\textrm{Diag}^*\) reflects weak equivalences is part of Theorem 2.11. Before we move on to the second part we first observe that
This in particular means that \(\textrm{Diag}^*\textrm{Diag}_*K\) is a Kan complex. Indeed, we need to witness that for all \(n \ge 0\) and \(0 \le l \le n\) \(\textrm{Hom}(\Delta [n],\textrm{Diag}^* \textrm{Diag}_*K) \rightarrow \textrm{Hom}( \Lambda [n]_l,\textrm{Diag}^* \textrm{Diag}_*K)\) is surjective, which is equivalent to \(\textrm{Hom}(\Delta [n] \times \Delta [n],K) \rightarrow \textrm{Hom}(\Lambda [n]_l \times \Lambda [n]_l,K)\) being surjective, which follows from the fact that \(\Lambda [n]_l \times \Lambda [n]_l \rightarrow \Delta [n] \times \Delta [n]\) is a trivial cofibration in the Kan model structure [26, Corollary 4.6].
Now, the counit map
is induced by the diagonal map \(\Delta :\Delta [\bullet ] \rightarrow \Delta [\bullet ] \times \Delta [\bullet ]\). By 2-out-of-3 it suffices to show that the morphism \((\pi _1)^*:\textrm{Hom}(\Delta [\bullet ],K) \rightarrow \textrm{Hom}(\Delta [\bullet ] \times \Delta [\bullet ],K)\) is a Kan equivalence as \((\pi _1)^*\) and \(\Delta ^*\) compose to the identity.
We will now construct an explicit deformation retract of Kan complexes for
finishing the proof. As \(\pi _1 \circ i_1\) is the identity, we only need a morphism \(\gamma :\Delta [\bullet ] \times \Delta [\bullet ] \times \Delta [1] \rightarrow \Delta [\bullet ] \times \Delta [\bullet ]\), which satisfies \(\gamma (-,-,0) = i_1\pi _1\) and \(\gamma (-,-,1) = \textrm{id}\). We can obtain such a morphism, by defining the morphism of posets \(g:[n] \times [n] \times [1] \rightarrow [n] \times [n]\) with \(g(i,j,0) = g(i,0,0)\) and \(g(i,j,1) = (i,j)\) and then applying nerves. \(\square \)
Remark 2.14
Composing the two Quillen equivalences \((\textrm{Diag}^*,\textrm{Diag}_*)\) and \(((\pi _1)^*, (\pi _1)_*)\) we get a Quillen equivalence

however, this Quillen equivalence is not the identity adjunction. Thus the Kan model structure and diagonal model structure on simplicial spaces are Quillen equivalent, but not the same model structures (as their set of weak equivalences and fibrations differ).
3.6 Complete Segal Spaces
The Reedy model structure can be localized such that it models \((\infty ,1)\)-categories [58]. This is done in two steps. First we define Segal spaces. For that let \(\alpha _i:[1] \rightarrow [n]\) be the morphism given by \(\alpha _i(0) = i\) and \(\alpha _i(1) = i+1\), where \(0 \le i < n\).
Definition 2.15
[58, Page 11] A Reedy fibrant simplicial space X is called a Segal space if the map
is a Kan equivalence for \(n \ge 2\).
Segal spaces come with a model structure, namely the Segal space model structure.
Theorem 2.16
[58, Theorem 7.1] There is a simplicial closed model category structure on the category  of simplicial spaces called the Segal space model category structure, and denoted
of simplicial spaces called the Segal space model category structure, and denoted  , with the following properties.
, with the following properties.
-
(1)
The cofibrations are precisely the monomorphisms.
-
(2)
The fibrant objects are precisely the Segal spaces.
-
(3)
The weak equivalences are precisely the maps f such that
 is a weak equivalence of spaces for every Segal space W.
is a weak equivalence of spaces for every Segal space W. -
(4)
A Reedy weak equivalence between any two objects is a weak equivalence in the Segal space model category structure, and if both objects are themselves Segal spaces then the converse holds.
-
(5)
For two cofibrations i and j, \(i \square j\) is a cofibration, which is trivial if either of i or j are.
-
(6)
The model structure is the localization of the Reedy model structure with respect to the maps
$$\begin{aligned} G(n) = F(1) \coprod _{F(0)} \ldots \coprod _{F(0)} F(1) \rightarrow F(n) \end{aligned}$$for \(n \ge 2\).
A Segal space already has many characteristics of a category, such as objects and morphisms.
Definition 2.17
Let W be a Segal space. Then an object x in W is a point in \(W_0\). Moreover for two objects x, y we define the mapping space as the pullback

Unlike classical categories, the mapping spaces of a Segal space do not come with strict composition maps. Rather there is a natural zig-zag. For more details see [58, Sect. 5]. On the other hand we do get an actual homotopy category:
Definition 2.18
Let W be a Segal space. We define the homotopy category of W, denoted \(\textrm{Ho}W\), as the following category:
-
(1)
Objects of \(\textrm{Ho}W\) are objects of W.
-
(2)
For two objects x, y we have
$$\begin{aligned} \textrm{Hom}_{\textrm{Ho}W}(x,y) = \pi _0(\textrm{map}_W(x,y)). \end{aligned}$$
This indeed gives us a category [58, 5.5]. Moreover, a morphism f in W is a weak equivalence precisely if the morphism [f] in \(\textrm{Ho}W\) is an isomorphism.
Segal spaces do not give us a model of \((\infty ,1)\)-categories. For that we need complete Segal spaces.
Definition 2.19
Let J[n] be the fibrant replacement of \(\Delta [n]\) in the Kan model structure on simplicial sets (Sect. 2.2(6)). We define the simplicial discrete space E(n) as \(E(n) = (\pi _2)^*J[n].\) where \((\pi _2)^*\) was defined in Notation 2.6. In particular, E(1) is the free invertible arrow, meaning a morphism of Segal spaces \(E(1) \rightarrow W\) is precisely given by a choice of weak equivalence in W.
Definition 2.20
Let W be a Segal space. We define the space of weak equivalences \(W_{hoequiv}\) as

Notice \(W_{hoequiv} \rightarrow W_1\) is an equivalence when restricted to each path component in \(W_{hoequiv}\). Moreover, for any two objects x, y in W define \(\textrm{hoequiv}_W(x,y) = W_{hoequiv} \times _{W_0\times W_0} \Delta [0]\) and notice the morphism \(\textrm{hoequiv}_W(x,y) \rightarrow \textrm{map}_W(x,y)\) is also an equivalence on each path component of \(\textrm{hoequiv}_W(x,y)\).
Definition 2.21
A Segal space W is called a complete Segal space if it satisfies one of the following equivalent conditions.
-
(1)
The inclusion map
$$\begin{aligned} W_0 \hookrightarrow W_{hoequiv} \end{aligned}$$is a weak equivalence.
-
(2)
The map
$$\begin{aligned} < 0 >^*: W_{hoequiv}= Map(E(1),W) \rightarrow Map(F(0),W) = W_0 \end{aligned}$$is a trivial Kan fibration.
-
(3)
The map
$$\begin{aligned} < 1 >^*: W_{hoequiv}= Map(E(1),W) \rightarrow Map(F(0),W) = W_0 \end{aligned}$$is a trivial Kan fibration.
Complete Segal spaces come with their own model structure, the complete Segal space model structure.
Theorem 2.22
[58, Theorem 7.2] There is a simplicial closed model category structure on the category  of simplicial spaces, called the complete Segal space model category structure, and denoted
of simplicial spaces, called the complete Segal space model category structure, and denoted  , with the following properties.
, with the following properties.
-
(1)
The cofibrations are precisely the monomorphisms.
-
(2)
The fibrant objects are precisely the complete Segal spaces.
-
(3)
The weak equivalences are precisely the maps f such that
 is a weak equivalence of spaces for every complete Segal space W.
is a weak equivalence of spaces for every complete Segal space W. -
(4)
A Reedy weak equivalence between any two objects is a weak equivalence in the complete Segal space model category structure, and if both objects are themselves complete Segal spaces then the converse holds.
-
(5)
For two cofibrations i and j, \(i \square j\) is a cofibration, which is trivial if either of i or j are.
-
(6)
The model structure is the localization of the Segal space model structure with respect to the map
$$\begin{aligned} < 0 >: F(0) \rightarrow E(1). \end{aligned}$$
A complete Segal space is a model for an \((\infty ,1)\)-category. For a better understanding of complete Segal spaces see [58, 6] and for a comparison with other models see [7, 37].
We end this section with reviewing the relationship between categories and (complete) Segal spaces. For that we first establish the following notational conventions.
Notation 2.23
For a given category  , following our notational convention (Remark 2.8)
, following our notational convention (Remark 2.8)  . Hence, we introduce the notation
. Hence, we introduce the notation  , called the horizontal nerve and note the resulting simplicial space is a Segal space with
, called the horizontal nerve and note the resulting simplicial space is a Segal space with  a discrete space.
a discrete space.
While  is a Segal space (and in fact the Kan equivalences in Definition 2.15 are isomorphisms of discrete simplicial sets), it is usually not complete. That is why there is an alternative construction, the classifying diagram, given as follows.
is a Segal space (and in fact the Kan equivalences in Definition 2.15 are isomorphisms of discrete simplicial sets), it is usually not complete. That is why there is an alternative construction, the classifying diagram, given as follows.
Definition 2.24
Let  be a category. Then the classifying diagram of
be a category. Then the classifying diagram of  is the simplicial space defined as
is the simplicial space defined as  .
.
We now have the following results in [58, Proposition 6.1].
Proposition 2.25
Let  be a category, then
be a category, then  is a complete Segal space, moreover, the evident morphism
is a complete Segal space, moreover, the evident morphism  is a complete Segal space equivalence of Segal spaces.
is a complete Segal space equivalence of Segal spaces.
4 Left Fibrations and the Covariant Model Structure
This section is focused on the study of left fibrations. We first focus on various characterizations of left fibrations (Sect. 3.1). Then we show that left fibrations can be seen as fibrant objects in a model structure, the covariant model structure (Sect. 3.2). Finally, we do a careful analysis of left fibrations over Segal spaces (Sect. 3.3).
Remark 3.1
Historical note on left fibrations for simplicial spaces: Left fibrations for complete Segal spaces were first considered by Charles Rezk, motivated by his paper on complete Segal spaces [58], however, he never published those ideas.
The first record of left fibrations for Segal spaces can be found in the work of de Brito [19, 0.1] and Kazhdan-Varshavsky [40, Definition 2.1.1], where both authors (independently) give the same definition of a left fibration for Segal spaces.
The definition of left fibration given here was suggested to the author by Charles Rezk and generalizes those definitions from Segal spaces to an arbitrary simplicial space.
4.1 The Many Faces of Left Fibrations
In this section we first define left fibrations (Definition 3.2) and then prove they can be characterized in several alternative ways: Lemmas 3.5, 3.6, Proposition 3.7, Lemma 3.10. There is one final characterization of left fibrations, Lemma 3.20, which we relegate to the next section.
We want to generalize the definition of a discrete Grothendieck opfibration (Definition 1.15) to simplicial spaces. The guiding principle towards a working definition is the following idea:
Thus we need to find an appropriate contractibility condition. Using our intuition from Segal spaces for a given simplicial space X we should think of the space \(X_0\) as the space of objects, \(X_1\) as the space of morphisms and the simplicial map \(s: X_1 \rightarrow X_0\) as map that takes a morphism to its source (Sect. 2.3(4)).
This motivates the following definition:
Definition 3.2
A map of simplicial spaces \(p: L \rightarrow X\) is called a left fibration if it is a Reedy fibration such that the following square is a homotopy pullback square for all \(n \ge 0\)

where the horizontal maps come from the map \(< 0 >: [0] \rightarrow [n]\) taking the point to \(0 \in [n]\). More generally, a morphism of simplicial spaces is a left morphism if it satisfies the pullback condition in 3.3.
Remark 3.4
As we observed in Lemma 1.16, for a given category  , discrete Grothendieck opfibrations over
, discrete Grothendieck opfibrations over  correspond to functors
correspond to functors  . Given that left fibrations are the homotopical analogue of Grothendieck opfibrations they are expected to model functors valued in spaces. We will in fact prove this statement for the specific case where
. Given that left fibrations are the homotopical analogue of Grothendieck opfibrations they are expected to model functors valued in spaces. We will in fact prove this statement for the specific case where  (Theorem 4.18) and use this idea as a guide towards studying left fibrations over general simplicial spaces.
(Theorem 4.18) and use this idea as a guide towards studying left fibrations over general simplicial spaces.
The proof of the general case can be found for quasi-categories in [42, Theorem 2.2.1.2], [31, Theorem C].
Let us start with a simple, alternative way of characterizing left fibrations.
Lemma 3.5
Let \(p: Y \rightarrow X\) be a Reedy fibration. The following are equivalent:
-
(1)
p is a left fibration.
-
(2)
For each \(n \ge 0\), the map
$$\begin{aligned} (p_n, < 0 >^*): Y_n \rightarrow X_n \underset{X_0}{\times }\ Y_0 \end{aligned}$$is a Kan equivalence.
-
(3)
For each \(n \ge 0\), the map
$$\begin{aligned} (p_n, < 0 >^*): Y_n \twoheadrightarrow X_n \underset{X_0}{\times }\ Y_0 \end{aligned}$$is a trivial Kan fibration.
Proof
\((1 \Leftrightarrow 2)\) This follows from the definition of a homotopy pullback and right-properness of the Kan model structure.
\((2 \Leftrightarrow 3)\) The map \(< 0 >: F(0) \rightarrow F(n)\) is a cofibration, which implies that

or, equivalently, the map
is a Kan fibration. Thus it is a weak equivalence if and only if it is a trivial Kan fibration. \(\square \)
Next we give an alternative, inductive characterization of left fibrations.
Lemma 3.6
Let \(p: Y \rightarrow X\) be a Reedy fibration. The following two are equivalent:
-
(1)
The commutative square

is a homotopy pullback square for all \(n \ge 0\), meaning p is a left fibration.
-
(2)
The commutative square

is a homotopy pullback square for all \(n \ge 1\).
Proof
We have the following diagram:

\(( 1 \Rightarrow 2)\) In this case the rectangle and the right square is a homotopy pullback and therefore the left hand square is also a homotopy pullback.
\((2 \Rightarrow 1)\) For this case we use induction. The case \(n=1\) is clear. If it is true for \(n-1\) then this means that in the diagram above the right hand square is a homotopy pullback. By assumption the left hand square is a homotopy pullback and so the whole rectangle has to be a homotopy pullback and we are done. \(\square \)
Next we give a characterization of left fibrations via lifting conditions.
Proposition 3.7
Let \(p: Y \rightarrow X\) be a Reedy fibration. Then the following are equivalent:
-
(1)
p is a left fibration.
-
(2)
p satisfies the right lifting property with respect to maps of the form
$$\begin{aligned} (< 0 >: F(0) \rightarrow F(n)) \square (\partial \Delta [l] \rightarrow \Delta [l]), \end{aligned}$$for all \(n \ge 0\) and \(l \ge 0\).
-
(3)
The map of simplicial sets \((\pi _1)^*(\textrm{exp}(< 0 >:F(0) \rightarrow F(n),p))\) (where \(\pi _1\) was introduced in Notation 2.6) satisfies the right lifting property with respect to maps of the form
$$\begin{aligned} \partial \Delta [l] \rightarrow \Delta [l], \end{aligned}$$for all \(n \ge 0\) and \(l \ge 0\).
Proof
By Lemma 3.5, the map \(p: Y \rightarrow X\) is a left fibration if and only if
is a trivial fibration, where \(\pi _1\) was introduced in Notation 2.6. This is equivalent to \((\pi _1)_*(\textrm{exp}(< 0 >:F(0) \rightarrow F(n),p: Y \rightarrow X))\) having the right lifting property with respect to the inclusion maps \(\partial \Delta [l] \rightarrow \Delta [l]\). Using the adjunction \(((\pi _1)^*,(\pi _1)_*)\), this is equivalent to \(\textrm{exp}(< 0 >:F(0) \rightarrow F(n),p: Y \rightarrow X)\) having the right lifting property with respect to \((\pi _1)^*(\partial \Delta [l]) \rightarrow (\pi _1)^*\Delta [l]\), which by our notation convention (Remark 2.8) we denote by \(\partial \Delta [l] \rightarrow \Delta [l]\).
Thus, \(p:Y \rightarrow X\) is a left fibration is and only if
Now using Proposition 2.5 with the set of morphisms:
-
\(\mathcal {A} = \{ < 0 >: F(0) \rightarrow F(n): n \ge 0 \} \)
-
\(\mathcal {B} = \{ \partial \Delta [l] \rightarrow \Delta [l]: l \ge 0 \}\)
-
\(\mathcal {L} = \{ \text {left fibrations} \}\)
we have
Hence we are done. \(\square \)
The pullback characterization of left fibrations (Lemma 3.5) immediately has the following implication.
Lemma 3.8
Let \(f:Y \rightarrow X\), \(g:Z \rightarrow Y\) and \(h: W \rightarrow V\) be three Reedy fibrations.
-
(1)
If f and g are left fibrations then fg is also a left fibration.
-
(2)
If f and fg are left fibrations then g is also a left fibration.
-
(3)
If f and h are weakly equivalent Reedy fibrations, then f is a left fibration if and only if h is a left fibration.
The fact that left fibrations are given via a right lifting property has the following formal consequence.
Lemma 3.9
The pullback of a left fibration is a left fibration.
We can use the pullback stability of left fibrations to give several local characterizations of left fibrations.
Lemma 3.10
Let \(p: L \rightarrow X\) be a Reedy fibration. Then the following are equivalent:
-
(1)
p is a left fibration.
-
(2)
For every map \(F(n) \times \Delta [l] \rightarrow X\) the pullback \(L \times _X (F(n) \times \Delta [l]) \rightarrow F(n) \times \Delta [l]\) is a left fibration.
-
(3)
For every map \(F(n) \rightarrow X\) the pullback \(L \times _X F(n) \rightarrow F(n)\) is a left fibration.
Proof
\((1 \Rightarrow 3)\) This follows from Lemma 3.9.
\((2 \Rightarrow 1)\) By Proposition 3.7 it suffices to prove that the map p has the right lifting property with respect to the maps \((F(0) \rightarrow F(n)) \square (\partial \Delta [l] \rightarrow \Delta [l])\), meaning we have to show the following diagram has a lift

We can now take a pullback of p along f to obtain the following diagram

By assumption \(f^*L \rightarrow F(n) \times \Delta [l]\) is a left fibration, which means the lift \(\hat{f}\) exists. Hence, \(p^*f \circ \hat{f}\) is the desired lift for the original diagram.
\((3 \Rightarrow 2)\) Fix a map \(f: F(n) \times \Delta [l] \rightarrow X\). The map \(< 0 >: \Delta [0] \rightarrow \Delta [l]\) gives us the following pullback square

The bottom map is a Reedy equivalence, which implies the top map is also a Reedy equivalence. The maps \(f^*p\) and \((f \circ (id \times 0))^*(p)\) are Reedy fibrations and so, by Lemma 3.8(3), \(f^*p\) is a left fibration if and only if \((f \circ (id \times 0))^*(p)\) is a left fibration, which holds by assumption. \(\square \)
Using the same argument as in the previous proof we can prove the analogous statement about diagonal fibrations that will become useful later on.
Lemma 3.11
Let \(p: Y \rightarrow X\) be a Reedy fibration. Then the following are equivalent:
-
(1)
p is a diagonal fibration.
-
(2)
For every map \(F(n) \times \Delta [l] \rightarrow X\) the pullback \(Y \times _X (F(n) \times \Delta [l]) \rightarrow F(n) \times \Delta [l]\) is a diagonal fibration.
-
(3)
For every map \(F(n) \rightarrow X\) the pullback \(Y \times _X F(n) \rightarrow F(n)\) is a diagonal fibration.
Proof
Following [61, Definition 3.3, Lemma 4.3] a morphism \(p:Y \rightarrow X\) is a fibration in the diagonal model structure if and only if p is a Reedy fibration and for all \(d_i: [n] \rightarrow [n+1]\) the induced morphism \((d_i,p_{n+1}): Y_{n+1} \rightarrow Y_n \times _{X_n} X_{n+1}\) is a weak equivalence, where \(0 \le i \le n\). This means p is a diagonal fibration if it is a Reedy fibration and satisfies the right lifting property with respect to morphisms \(d_i \square (\partial \Delta [l] \rightarrow \Delta [l])\). The result now follows from applying the same proof as the one given in Lemma 3.10 with the set of morphisms \(d_i \square (\partial \Delta [l] \rightarrow \Delta [l])\), where \(0 \le i \le n\). \(\square \)
4.2 The Covariant Model Structure
Let X be a simplicial space. In this subsection we define a model structure on the over-category  , the covariant model structure, which has fibrant objects precisely the left fibrations over X (Theorem 3.12). We end the subsection by giving a useful criterion for determining covariant equivalences by generalizing deformation retracts from classical homotopy theory (Theorem 3.27).
, the covariant model structure, which has fibrant objects precisely the left fibrations over X (Theorem 3.12). We end the subsection by giving a useful criterion for determining covariant equivalences by generalizing deformation retracts from classical homotopy theory (Theorem 3.27).
Theorem 3.12
Let X be a simplicial space. There is a unique simplicial left proper model structure on the over-category  , called the covariant model structure and denoted by
, called the covariant model structure and denoted by  , which satisfies the following conditions:
, which satisfies the following conditions:
-
(1)
The fibrant objects are the left fibrations over X.
-
(2)
Cofibrations are monomorphisms.
-
(3)
A map \(f: A \rightarrow B\) over X is a covariant weak equivalence if

is a Kan equivalence for every left fibration \(L \rightarrow X\).
-
(4)
A weak equivalence (covariant fibration) between fibrant objects is a level-wise equivalence (Reedy fibration).
Proof
Let \(\mathcal {L}\) be the collection of maps of the following form
Note that \(\mathcal {L}\) is a set of cofibrations in  with the Reedy model structure. This allows us to use the theory of Bousfield localizations (Theorem A.7) with respect to \(\mathcal {L}\) on the category
with the Reedy model structure. This allows us to use the theory of Bousfield localizations (Theorem A.7) with respect to \(\mathcal {L}\) on the category  . The resulting model structure immediately satisfies all the conditions above and in particular the fibrant objects are precisely the left fibrations by Lemma A.12. \(\square \)
. The resulting model structure immediately satisfies all the conditions above and in particular the fibrant objects are precisely the left fibrations by Lemma A.12. \(\square \)
Remark 3.13
This model structure is also constructed in [19, Proposition 1.10] for the particular case where the base X is a Segal space, and so the theorem could be deduced from that result as well.
We can actually say more about the fibrations in the covariant model structure.
Lemma 3.14
Let \(p: L \rightarrow X\) and \(q: L' \rightarrow X\) be two left fibrations. A map \(f: L \rightarrow L'\) over X is a fibration in the covariant model structure if and only if it is a left fibration.
Proof
As p and q are fibrant, f is a fibration if and only if it is a Reedy fibration (Theorem 3.12(4)). The statement now follows from Lemma 3.8 as \(qf = p\). \(\square \)
Note the covariant model structure behaves well with respect to base change.
Theorem 3.15
Let \(f: X \rightarrow Y\) be map of simplicial spaces. Then the following adjunction

is a Quillen adjunction, which is a Quillen equivalence if f is a Reedy equivalence. Here \(f_!\) is the composition map and \(f^*\) is the pullback map.
Proof
This is the special case of Lemma A.9 when \(\mathcal {L} = \{ < 0 >: F(0) \rightarrow F(n): n \ge 0 \}\). \(\square \)
Remark 3.16
Later we will prove a much stronger result, namely if f is an equivalence in the CSS model structure then the Quillen adjunction is actually a Quillen equivalence (Theorem 5.1).
Theorem 3.17
The following is a Quillen adjunction

which is a Quillen equivalence if X is a homotopically constant simplicial space. Here the left side has the covariant model structure and the right side has the induced diagonal model structure (Proposition A.5). This implies that the diagonal model structure over X is a localization of the covariant model structure over X.
Proof
If we localize the Reedy model structure on  with respect to maps of the form \(F(0) \rightarrow F(n) \rightarrow X\) we get the covariant model structure (Theorem 3.12) whereas if we localize the Reedy model structure on
with respect to maps of the form \(F(0) \rightarrow F(n) \rightarrow X\) we get the covariant model structure (Theorem 3.12) whereas if we localize the Reedy model structure on  with respect to maps \(< 0 >: F(0) \rightarrow F(n)\) we get the diagonal model structure (Theorem 2.11). This means we can apply Theorem A.13 to deduce that this a Quillen adjunction.
with respect to maps \(< 0 >: F(0) \rightarrow F(n)\) we get the diagonal model structure (Theorem 2.11). This means we can apply Theorem A.13 to deduce that this a Quillen adjunction.
Now let us assume X is homotopically constant. Let \(j: X \rightarrow \hat{X}\) be a Reedy fibrant replacement of X. Then \(\hat{X}\) is also homotopically constant, which means it is fibrant in the diagonal model structure (Theorem 2.11). We now have the following diagram of Quillen adjunctions

The left hand vertical adjunction is a Quillen equivalence as j is a Reedy equivalence and by Lemma A.9. The right hand Quillen adjunction is a Quillen equivalence as the diagonal model structure is right proper and [59, Proposition 2.5]. The bottom horizontal adjunction is a Quillen equivalence because \(\hat{X}\) is fibrant in the diagonal model structure and Theorem A.13. Thus, 2-out-of-3 implies that the top adjunction is a Quillen equivalence as well. \(\square \)
Remark 3.18
The theorem implies that every covariant equivalence is a diagonal equivalence, whereas the opposite direction is obviously not true. On the other hand, in Sect. 4.2 we will prove that we can determine whether a map is a covariant equivalence by checking whether a certain collection of maps consists of diagonal equivalences (Theorem 4.41).
Example 3.19
One very important instance is the case \(X=F(0)\). The theorem shows that  is the same as
is the same as  .
.
Using the covariant model structure we can add one final alternative characterization of left fibrations.
Lemma 3.20
Let \(p: L \rightarrow X\) be a Reedy fibration. Then the following are equivalent:
-
(1)
p is a left fibration.
-
(2)
For all \(n \ge 0\)
 (3.21)
(3.21)is a homotopy pullback square.
-
(3)
\(\textrm{exp}(< 0 >:F(0) \rightarrow F(1),p)\) is a trivial Reedy fibration.
Proof
\((1 \Rightarrow 2)\) First, let us assume p is a left fibration. Fix a morphism \(p:F(n) \times F(1) \rightarrow X\). We can write \(F(n) \times F(1)\) as a colimit of a diagram
over X such that all maps \(F(n) \rightarrow F(n+1)\) take 0 to 0 (for a more detailed description of this diagram see [58, Diagram 10.4]). Thus, by applying 2-out-of-3 to the diagram \(F(0) \rightarrow F(n) \rightarrow F(n+1)\) over X, the maps in 3.22 are covariant equivalences over X. As the covariant model structure is left proper (Theorem 3.12) this implies that \(F(n) \times \{ 0 \} \rightarrow F(n) \times F(1)\) is a covariant equivalence over X. As the covariant model structure is simplicial, this implies that the morphism \(\textrm{Map}_{/X}(F(n)\times F(1),L) \rightarrow \textrm{Map}_{/X}(F(n),L)\) is a Kan equivalence. As the morphism is precisely the fiber of the diagram of Kan fibrations

over the point \(p: F(n)\times F(1) \rightarrow X\), this proves, by Corollary A.2, that the square 3.21 is a homotopy pullback square for all \(n \ge 0\).
\((2 \Rightarrow 1)\) Let 3.21 be a homotopy pullback square for all \(n\ge 0\), which means

a trivial Kan fibration.
Let \(r: [n] \times [1] \rightarrow [n+1]\) be the functor given by \(r(i,0) = i\), \(r(i,1) = n+1\). Then notice the following is a retract diagram

Let us denote \(i=< (0,0) ,... ,(n ,0) ,(n ,1)>: F(n+1) \rightarrow F(n) \times F(1)\). The diagram gives us the following retract diagram of morphisms

As the middle horizontal diagram is a weak equivalence, by 3.23, it follows that the top morphism is a weak equivalence. By Lemma 3.6, this implies that \(p:L \rightarrow X\) is a left fibration.
\((2 \Leftrightarrow 3)\) The map \(\textrm{exp}(< 0 >:F(0) \rightarrow F(1),p)\) is a trivial Reedy fibration if and only if it is a level-wise weak equivalence, meaning the maps 3.21 are Kan equivalences for all \(n\ge 0\). \(\square \)
Remark 3.24
One interesting implication of this lemma is that we can get the covariant model structure on  (Theorem 3.12) also by localizing with respect to the maps
(Theorem 3.12) also by localizing with respect to the maps
Indeed, Lemma 3.20 implies that the left Bousfield localization with respect to the two sets of morphisms \(\{ < (0,0) >:F(0) \rightarrow F(1) \times F(n) \rightarrow X: n \ge 0 \}.\) and \(\{< 0 >:F(0) \rightarrow F(n) \rightarrow X: n \ge 0 \}\) have the same cofibrations (monomorphisms) and fibrant objects (left fibrations) and hence are the same model structure (the covariant model structure over X).
We can apply this argument inductively to conclude that we can also obtain the covariant model structure by localizing with respect to
One important goal in the coming sections is to give a recognition principle for covariant equivalences. This will be done in Theorem 4.41 and needs us to first discuss the simplicial Grothendieck construction (Theorem 4.18). However, there are certain instances, motivated by classical homotopy theory, where recognizing covariant equivalences is quite easy. First we need to prove an important lemma about closure properties of some covariant equivalences.
Lemma 3.25
Let \(\mathcal {L}\) be the class of monomorphisms of simplicial spaces that have the left lifting property with respect to all left fibrations.
-
(1)
If \(i:A \rightarrow B \in \mathcal {L}\) and j is a cofibration then \(i\square j\) is in \(\mathcal {L}\).
-
(2)
If p is a left fibration and j a cofibration then \(\textrm{exp}(j,p)\) is a left fibration.
-
(3)
If \(i:A \rightarrow B \in \mathcal {L}\) and \(B \rightarrow X\) is an arbitrary morphism, then i over X is a covariant equivalence.
Proof
(1), (2) By Proposition 2.5 and the fact that left fibrations are described via right lifting property (Proposition 3.7), the first two statements are equivalent and so it suffices to prove the second one. Following Lemma 3.20, we only have to prove that \(\textrm{exp}(< 0 >:F(0) \rightarrow F(1),\textrm{exp}(j,p))\) is a trivial fibration. Now, we have the following chain of isomorphisms
By Lemma 3.20, \(\textrm{exp}(< 0 >:F(0) \rightarrow F(1),p)\) is a trivial fibration. Moreover, as the Reedy model structure is Cartesian closed (Sect. 2.4), \(\textrm{exp}(j,\textrm{exp}(< 0 >,p))\) is also a trivial fibration. Hence, \(\textrm{exp}(< 0 >:F(0) \rightarrow F(1),\textrm{exp}(j,p))\) is a trivial fibration and we are done.
(3) We need to prove that for every \(g:B \rightarrow X\) and left fibration \(p:L \rightarrow X\), the induced morphism \(\textrm{Map}_{/X}(B,L) \rightarrow \textrm{Map}_{/X}(A,L)\) is a Kan equivalence. This morphism is obtained by considering the morphism \(t:\textrm{Map}(B,L) \rightarrow \textrm{Map}(B,X) \times _{\textrm{Map}(A,X)} \textrm{Map}(A,L)\) over \(\textrm{Map}(B,X)\) and then taking the fiber over g. Hence, by Corollary A.2, it suffices to show that t is a Kan equivalence.
By Sect. 2.3(9) and the definition of pullback exponentials (Definition 2.3), we have \(t = \textrm{exp}(i,p)_0\), meaning in order to complete this proof it suffices to show that \(\textrm{exp}(i,p)\) is a Reedy weak equivalence. We will in fact prove it is a trivial fibration, by establishing it has the right lifting property with respect to all cofibrations j. By Proposition 2.5, this claim is equivalent to \(i \square j\) having the left lifting property with respect to p, which holds by (1). \(\square \)
This lemma has a useful corollary.
Corollary 3.26
Let \(L \rightarrow X\) be a left fibration and Y a simplicial space, then \(L^Y \rightarrow X^Y\) is a left fibration.
Proof
This follows from the previous result if we use the cofibration \(\emptyset \rightarrow Y\). \(\square \)
With the technical lemma at hand, we can give a helpful characterization of covariant equivalences.
Theorem 3.27
Let \(i:A \rightarrow B\) be a monomorphism over X. Then i is a trivial cofibration in the covariant model structure on  if there exists a retraction \(r: B \rightarrow A\) (not necessarily over X) and a \(H:B \times F(1) \rightarrow B\) (relative to A) such that \(H(-,0) = ir\) and \(H(-,1) = \textrm{id}_B\).
if there exists a retraction \(r: B \rightarrow A\) (not necessarily over X) and a \(H:B \times F(1) \rightarrow B\) (relative to A) such that \(H(-,0) = ir\) and \(H(-,1) = \textrm{id}_B\).
Proof
For the proof we simply adapt the argument in [33, Lemma 2.1] to simplicial spaces. Let \(Z \xrightarrow { \ p \ } Y \rightarrow X\) be a fibration in the covariant model structure over X. We need to prove that a lift of the following diagram exists:

Let \(j = (< 0 >: F(0) \rightarrow F(1)) \square (i: A \rightarrow B)\). Using the homotopy H and the map j, we can factor this diagram as follows:

It suffices to show the right hand square has a lift. For that we need to show that j is a trivial cofibration in the covariant model structure over X. However, this follows immediately from the fact that \(< 0 >:F(0) \rightarrow F(1)\) has the left lifting property with respect to all left fibrations (Proposition 3.7) and so, by Lemma 3.25, j is a covariant equivalence over X. \(\square \)
Remark 3.28
As already stated in the proof, this theorem was stated and proven for simplicial sets by Heuts and Moerdijk [33, Lemma 2.1].
We will use this result in the next subsection to study left fibrations of Segal spaces.
4.3 Yoneda Lemma for Segal Spaces
In this subsection we want to use the results we have proven until now to study left fibrations over Segal spaces. In particular, we prove the Yoneda lemma for Segal spaces (Theorem 3.49).
We will start by simplifying the definition of a left fibration over Segal spaces.
Lemma 3.29
Let \(p:Y \rightarrow X\) be a Reedy fibration and X a Segal space. The following are equivalent:
-
(1)
Y is a Segal space and the following is a homotopy pullback square:

-
(2)
p is a fibration in the Segal space model structure and the following is a homotopy pullback square:

-
(3)
p is a left fibration.
Proof
\((1 \Leftrightarrow 2)\) This follows immediately from the fact that a Reedy fibration between Segal spaces is a Segal fibration (Theorem 2.16).
\((3 \Leftrightarrow 1)\) For all \(n \ge 2\) we have the following diagram:

We have the following facts about this diagram:
-
The bottom square is a homotopy pullback for all \(n \ge 1\) if and only if X is a Segal space.
-
Similarly, the top square is a homotopy pullback for all \(n \ge 1\) if and only if Y is a Segal space.
-
The four squares around the cube are homotopy pullback squares if and only if p is a left fibration (Lemma 3.6).
The result now follows from checking homotopy pullback squares. The bottom square is always a homotopy pullback square.
If we assume (2) then the top square and the right hand square are homotopy pullback squares, which directly implies that left hand square is a homotopy pullback square (by the cancellation property of homotopy pullbacks) and so, by Lemma 3.6, p is a left fibration.
If we assume (3) then all four squares around are homotopy pullback squares which implies that the top square is a homotopy pullback square as well. \(\square \)
Remark 3.30
Note that [19] and [40] use the characterization in Lemma 3.29 as a definition of left fibrations rather than the definition we have given here (Definition 3.2). Hence this lemma proves that our definition agrees with theirs when the base is a Segal space and thus is a proper generalization of their definition.
Note that a left fibration of Segal spaces generalizes a discrete Grothendieck opfibration between categories.
Lemma 3.31
Let W be a Segal space and \(p: L \rightarrow W\) be a left fibration. Then the induced functor on homotopy categories \(\textrm{Ho}(p): \textrm{Ho}(L) \rightarrow \textrm{Ho}(W)\) is a discrete Grothendieck opfibration.
Proof
By Lemma 3.29L is a Segal space. Thus \(\textrm{Ho}(p): \textrm{Ho}(L) \rightarrow \textrm{Ho}(W)\) is a functor. We want to prove it is a discrete Grothendieck opfibration. Let \([f]: x \rightarrow y\) be a morphism in \(\textrm{Ho}(W)\) and \(\hat{x}\) be a lift of x in \(\textrm{Ho}(L)\). We need to prove there is a unique lift \(\hat{[f]}\) of f such that \(\textrm{Ho}(p)(\hat{[f]}) = [f]\).
Let f in \(W_1\) be a representative for the class \([f] \in \pi _0(W_1)\). Then \((\hat{x},f)\) is a point in \(L_0 \times _{W_0} W_1\). The fact that \(p:L \rightarrow W\) is a left fibration implies that
is a trivial Kan fibration and so the fiber over \((\hat{x},f)\), which we denote by \(F_f\), is contractible. This means \(\pi _0(F_f) = \{\hat{[f]} \}\) has a single element, which is precisely the unique lift. \(\square \)
There is an inverse argument to Lemma 3.31.
Lemma 3.32
Let  be a Grothendieck opfibration. Then
be a Grothendieck opfibration. Then  is a left fibration.
is a left fibration.
Proof
Notice  and
and  are simplicial discrete spaces, which means \(\textrm{N}^h(p)\) is a Reedy fibration. Moreover, \(\textrm{N}^h\mathscr {D}\) and
are simplicial discrete spaces, which means \(\textrm{N}^h(p)\) is a Reedy fibration. Moreover, \(\textrm{N}^h\mathscr {D}\) and  are nerves of categories and hence Segal spaces. Thus by Lemma 3.29 we have to show that the square
are nerves of categories and hence Segal spaces. Thus by Lemma 3.29 we have to show that the square

is a pullback square. However, this is precisely the lifting condition of a Grothendieck opfibration (Lemma 1.16). \(\square \)
We will see later (Proposition 5.20) that this result also holds when we replace the nerve with the classifying diagram (Definition 2.24). We can use the connection between left fibrations and Grothendieck opfibrations to study conservativity of left fibrations.
Definition 3.33
A map of Segal spaces \(p: V \rightarrow W\) is conservative if the square

is a homotopy pullback square.
We can characterize conservativity via the homotopy category.
Lemma 3.35
Let \(p:V \rightarrow W\) be a morphism of Segal spaces. Then the following are equivalent:
-
(1)
p is conservative.
-
(2)
For all objects x, y in V, the square
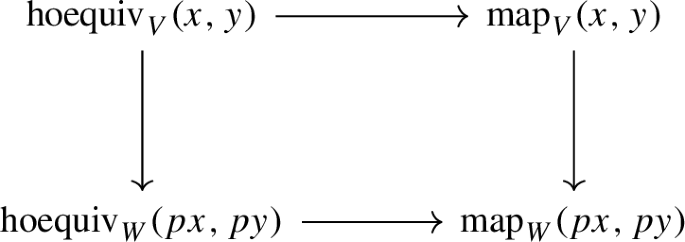
is a homotopy pullback square.
-
(3)
The functor of categories
 is conservative.
is conservative.
Proof
\((1)\Leftrightarrow (2)\) The square 3.34 is a homotopy pullback square if and only if the morphism \(V_{hoequiv} \rightarrow W_{hoequiv} \times _{W_1} V_1\) is a weak equivalence, which is equivalent to being a weak equivalence over \(W_0 \times W_0\) in the following diagram

Now, as both legs of the triangle are Kan fibrations, by Corollary A.2, the top morphism is an equivalence if and only if it is a fiber-wise equivalence. However, by Definition 2.17 and Definition 2.20 for a given point \((x,y): \Delta [0] \rightarrow W_0 \times W_0\), the fiber is precisely given by the morphism
finishing the proof.
\((2)\Leftrightarrow (3)\) Fix two arbitrary objects x, y in W. By Definition 2.20, the morphism \(\textrm{hoequiv}_W(x,y) \rightarrow \textrm{map}_W(x,y)\) is an equivalence when restricted to each path-component and so
is a weak equivalence if and only if
is a bijection of sets. However, by definition \(\pi _0\textrm{map}_W(x,y) = \textrm{Hom}_{\textrm{Ho}W}(x,y)\) \(\pi _0\textrm{hoequiv}_W(x,y) = \mathscr {I}\textrm{so}_{\textrm{Ho}W}(x,y)\), meaning this is equivalent to  being a bijection, which by Definition 1.13, is equivalent to \(\textrm{Ho}(p)\) being conservative. \(\square \)
being a bijection, which by Definition 1.13, is equivalent to \(\textrm{Ho}(p)\) being conservative. \(\square \)
We can finally relate conservativity and left fibrations.
Lemma 3.36
Let W be a Segal space and \(p:L \rightarrow W\) a left fibration. Then p is conservative.
Proof
By Lemma 3.29, L is a Segal space and so p is a map of Segal spaces. Thus, by Lemma 3.35, p is conservative if and only if the functor \(\textrm{Ho}p: \textrm{Ho}W \rightarrow \textrm{Ho}V\) is conservative. However, by Lemma 3.31, p is a discrete Grothendieck opfibration and thus is conservative. \(\square \)
Remark 3.37
This result was proven for quasi-categories in [39, Proposition 4.9], which could give us the analogous argument for complete Segal spaces. However, this proof generalizes the result to arbitrary Segal spaces.
We can use conservativity to characterize left fibrations over complete Segal spaces.
Lemma 3.38
Let W be a complete Segal space and \(p: V \rightarrow W\) be a left fibration. Then V is a complete Segal space.
Proof
We have the diagram

The left hand square is a homotopy pullback square as p is a left fibration and thus conservative (Lemma 3.36). The right hand square is a pullback square because of p is a left fibration. Hence the whole rectangle is a homotopy pullback.
Now completeness of W implies that the bottom map is an equivalence (Definition 2.21) and, as the square is a homotopy pullback, this means \(V_{hoequiv} \rightarrow V_0\) is an equivalence. Hence, again by Definition 2.21, this means that V is a complete Segal space. \(\square \)
We can combine Lemmas 3.29 and 3.38 into the following very useful result.
Proposition 3.39
Let W be a Segal space. Then the adjunction

is a Quillen adjunction, where the left hand side has the induced Segal space model structure and the right hand side has the covariant model structure.
Moreover, if W is also complete then the adjunction

is a Quillen adjunction, where the left hand side has the CSS model structure and the right hand side has the covariant model structure.
Proof
Let us focus on the case for Segal spaces first. As, following Theorem A.13, the induced and the localized Segal space model structures coincide when W is a Segal space, we can apply Corollary A.10. This means it suffices to prove that the left adjoint preserves monomorphisms and the right adjoint preserves Reedy fibrations and fibrant objects. It is evident that the identity functor preserves monomorphisms and Reedy fibrations. For the last part, observe that fibrant objects in the induced Segal space model structure are precisely Segal fibrations over W. Thus we only have to prove that if W is a Segal space and \(p: V \rightarrow W\) is a left fibration then p is a Segal fibration, which is precisely the statement of Lemma 3.29.
The case for complete Segal spaces is identical except in the last step we use the fact that a left fibration over a complete Segal space is a complete Segal space fibration as shown in Lemma 3.38. \(\square \)
Remark 3.40
The assumption that the base simplicial space is fibrant is not necessary and this proposition can be generalized to arbitrary simplicial spaces as we will do in Theorem 5.11. However, before we can do that we need to understand invariance properties of the covariant model structure (Theorem 5.1).
Having a better understanding of left fibrations over Segal spaces, we can move on to prove the Yoneda lemma for Segal spaces.
Definition 3.41
Let W be a Segal space and x an object in W. Then we define the under-Segal space \(W_{x/}\) as

Remark 3.42
In the particular case when W is a complete Segal space, it comes with an underlying quasi-category, denoted \(i_1^*W\) [37] (see Appendix B for more details regarding \(i_1^*\)). This suggests the natural question how \(i_1^*(W_{x/})\) compares with \((i_1^*W)_{x/}\).
The common definition of an under-quasi-category (for example the one that can be found in [42]) relies on the join of simplicial sets. Hence, \(i_1^*(W_{x/})\) (as constructed in Definition 3.41) would not be isomorphic as a simplicial set to \((i_1^*W)_{x/}\), as constructed in [42, Proposition 1.2.9.2] via the join. However, in Appendix B we prove that \(i_1^*\) in fact induces a Quillen equivalence of covariant model structures, which in particular implies that the quasi-categories \((i_1^*W)_{x/}\), \(i_1^*(W_{x/})\) are equivalent left fibrations over \(i_1^*W\).
An alternative argument that shows that the constructions of under-categories via joins and pullbacks are equivalent (in a general \(\infty \)-cosmos) can be found in [62, Corollary 4.2.8].
Notice the under-Segal space is in fact a Segal space.
Lemma 3.43
For a Segal space W and an object x, the projection \(W_{x/} \rightarrow W\) is a Segal space fibration and so the under-Segal space \(W_{x/}\) is a Segal space.
Proof
We have the following pullback diagram

The right hand map is a fibration in the Segal space model structure as it is the pullback exponential of a cofibration and a fibrant object (Theorem 2.16). Thus the pullback is a Segal fibration. The result now follows from the fact that W itself is a Segal space. \(\square \)
We have shown that the projection map \(W_{x/} \rightarrow W\) that takes each morphism to its target is a fibration in the Segal space model structure. We want to show that it is actually a left fibration.
Theorem 3.44
Let W be a Segal space and x an object in W. Then the projection map \(W_{x/} \rightarrow W\) is a left fibration.
Proof
In order to simplify notation we will denote the four vertices \(F(1) \times F(1)\) by \(\{ 00\), 01, 10, \(11 \}\).
By Lemma 3.29 it suffices to prove that the map
is a trivial Kan fibration.
Notice

and

Thus, (recalling the definition of G(2) in Theorem 2.16) it suffices to prove the map

is a trivial Kan fibration, or, equivalently, the map
is a trivial cofibration in the Segal space model structure (as W is a Segal space).
This map factors as
and so we only need to show the second map is a Segal equivalence. Using the isomorphism

the map \(< 00,01,11>\) is the pushout of the following diagram:

So, the result follows from knowing that the left hand map is a trivial cofibration, as the Segal space model structure is left proper by Theorem 2.16. The left hand map itself is the pushout of the following diagram:

As all vertical arrows are equivalences in the Segal space model structure and the Segal space model structure is left proper, the pushout is a Segal space equivalence as well. Hence we are done. \(\square \)
Remark 3.46
In order to better understand the proof it might be helpful to visualize the map 3.45 as:

Remark 3.47
The fact that the left fibration \(W_{x/} \rightarrow W\) happened to be a Segal fibration is not a coincidence. We will later see that every left fibration is indeed a Segal fibration (Theorem 5.11).
Remark 3.48
The Segal space condition in Theorem 3.44 is in fact a key condition and the theorem does not hold for general Reedy fibrant simplicial spaces, as we will show with G(2). We want to prove that \(G(2)_{0/} \rightarrow G(2)\) is not a left fibration. For that it suffices to observe that the map
is not a trivial Kan fibration.
Notice that
On the other hand we have
and the map \(\pi \) simply restricts \(\alpha : F(1) \times F(1) \rightarrow G(2)\) to the pair \((\alpha \circ< (0,0),(0,1)>, \alpha \circ < (0,1),(1,1) >)\). Hence, the point (01, 12) has no lift along \(\pi \) as any choice of lift \(\alpha \) necessarily satisfies \(\alpha (1,1) = 2\), which is impossible.
We are now at the point where we can prove the Yoneda lemma for Segal spaces.
Theorem 3.49
Let W be a Segal space and x an object. Then the map \(\{id_x\}: F(0) \rightarrow W_{x/}\) is a covariant equivalence over W.
Proof
Let \(\textrm{mul}: F(1) \times F(1) \rightarrow F(1)\) be the map defined by \(\textrm{mul}(i,j) = ij\) where \(i,j = 0,1\). Moreover, let \(\textrm{mul}^*: W^{F(1)} \rightarrow W^{F(1) \times F(1)}\). Using the adjunction between product and exponential, we get a morphism \(\widehat{\textrm{mul}^*}: F(1) \times W^{F(1)} \rightarrow W^{F(1)}\), which fits into the following diagram:

Now, notice we have the following diagram

as \(\textrm{mul}^*\) takes a morphism \(f:x \rightarrow y\) to the square

This means we can restrict the diagram via the inclusion \(W_{x/}\hookrightarrow W^{F(1)}\) to get the following diagram

Notice, by definition of \(\widehat{\textrm{mul}^*}\) we have the commutative diagram

meaning \(\widehat{\textrm{mul}^*}\) is a homotopy between \(\textrm{id}\) and \(\{\textrm{id}_x\}:W_{x/} \rightarrow W_{x/}\) relative to \(\{\textrm{id}_x\}\). Hence, by Theorem 3.27, the map \(\{ \textrm{id}_x \}: F(0)\rightarrow W_{x/}\) over W is a covariant equivalence. \(\square \)
Why do we call this the Yoneda lemma? The next corollary makes the connection more clear:
Corollary 3.50
Let W be a Segal space and \(L \rightarrow W\) be a left fibration. Then the map of spaces
is a trivial Kan fibration.
Proof
Follows from Theorem 3.49 and the fact that the covariant model structure is simplicial (Theorem 3.12). \(\square \)
Remark 3.51
This Yoneda lemma for Segal spaces has also been proven (independently) by Boavida [19, Lemma 1.31]. The analogous version for quasi-categories, meaning a Kan equivalence \(\textrm{Map}_{/S}(S_{x/},L) \rightarrow \textrm{Map}_{/S}(\Delta [0],L)\), where \(L \rightarrow S\) is a left fibration of quasi-categories and \(S_{x/} \rightarrow S\) is the under-quasi-category projection, has also been established in the literature. It was proven directly by Joyal [39, Chapter 11], but is also an implication of the straightening construction by Lurie [42, Theorem 2.2.1.2]. Finally, there is an analogous statement in an arbitrary \(\infty \)-cosmos, meaning a Kan equivalence \(\textrm{Map}_{/S}(S_{x/},L) \rightarrow \textrm{Map}_{/S}(\Delta [0],L)\), where S is an \(\infty \)-category in an \(\infty \)-cosmos \(\mathcal {K}\), \(L \rightarrow S\) a left fibration (there called discrete coCartesian fibration [62, Definition 5.5.3]) and \(S_{x/} \rightarrow S\) the under-\(\infty \)-category [62, Theorem 5.7.3].
We can use this result to study the relation between initial objects and representable functors. Let W be a Segal space. Then for two objects x, y we can define the mapping space \(\textrm{map}_W(x,y)\) (Definition 2.17). We would hope that this choice is functorial, meaning we get a functor \(\textrm{map}_W(x,-)\). This would require an actual composition map
for any map \(f: y \rightarrow z\) in W. However, composition of morphisms in a Segal space is only defined up to contractible ambiguity. For more details on composition in Segal spaces see [58, Sect. 5]
We will thus take a fibrational approach. We observed in Example 1.20 that the Grothendieck opfibration associated to the representable functor  is the under-category
is the under-category  . This motivates the following definition:
. This motivates the following definition:
Definition 3.52
A left fibration \(p:V \rightarrow W\) is called representable if there exists an object x in W and a Reedy equivalence \(f: W_{x/} \rightarrow V\) over X.
Using covariant equivalences we can relate representable left fibrations with the concept of initiality.
Definition 3.53
Let W be a Segal space. An object x in W is called initial if the map \(\{x\}:F(0) \rightarrow W\) is a covariant equivalence over W.
Remark 3.54
Initial objects are a special kind of colimit as we shall see in Sect. 5.2. Initial objects were thus studied in the context of colimits in quasi-categories [42, 1.2.12], [38, 10.1].
Theorem 3.55
Let \(p:L \rightarrow W\) be a left fibration. Then the following are equivalent:
-
(1)
p is representable.
-
(2)
L has an initial object
Proof
\((1) \Rightarrow (2)\) If p is representable then L is Reedy equivalent to \(W_{x/}\) for some object x in W. Thus it suffices to prove \(W_{x/}\) has an initial object. We have the following diagram.

\(W_{x/}\) is a left fibration over W. By Lemma 3.8\((W_{x/})_{id_x/}\) is also a left fibration over W as the composition of left fibrations is a left fibration. By Theorem 3.49, the map \(\{ \textrm{id}_x \}\) is a covariant equivalence over W. By the same argument the map \(\{ \textrm{id}_{\textrm{id}_x} \}\) is a covariant equivalence over \(W_{x/}\), which implies it is also a covariant equivalence over W (Theorem 3.15). By 2-out-of-3, we get that \(\pi \) is a covariant equivalence over W. But \(\pi \) is a map between left fibrations over W and thus must be a trivial Reedy fibration (Theorem 3.12).
\((2) \Rightarrow (1)\) Let \(\{ x \}:F(0) \rightarrow L\) be a covariant equivalence over L. Then, by Theorem 3.15, \(\{ l \}:F(0) \rightarrow L\) is a covariant equivalence over W. By Theorem 3.49, \(F(0) \rightarrow W_{p(l)/}\) is a trivial covariant cofibration over W and, by assumption, \(L \rightarrow W\) is a left fibration and thus a covariant fibration over W and so we can lift the diagram below

As the top map is a covariant equivalence over W, by 2-out-of-3, the lift \(W_{p(l)/} \rightarrow L\) is a covariant equivalence over W. As both are left fibrations, by Theorem 3.12, this map is a Reedy equivalence. \(\square \)
Remark 3.56
Notice the second condition only depends on L. Thus representability of a left fibration \(p:L \rightarrow W\) is independent of the map p and base W.
5 From the Grothendieck Construction to the Yoneda Lemma
In Sect. 3.3 we studied many important features of the covariant model structure over Segal spaces. The goal is to generalize all those results to the covariant model structure over an arbitrary simplicial space. An important step is to have a precise characterization of left fibrations over F(n) and a computationally feasible way for characterizing covariant equivalences over an arbitrary simplicial space. The goal of this section is to address both these concerns.
In Sect. 4.1 we prove the simplicial Grothendieck construction for categories (Theorem 4.18), which in particular gives us a characterization of left fibrations over F(n). In Sect. 4.2, we will then use this characterization to prove the recognition principle for covariant equivalences (Theorem 4.41).
Notation 4.1
For this section, recall that for a given category  ,
,  is the simplicial space given as
is the simplicial space given as  , which is a (generally non-complete) Segal space with
, which is a (generally non-complete) Segal space with  being a discrete simplicial set given by the set
being a discrete simplicial set given by the set  (Notation 2.23).
(Notation 2.23).
5.1 Grothendieck Construction over Categories
In Proposition 1.10 we constructed an adjunction between set-valued functors out of  and functors over
and functors over  , which gives us an equivalence when we restrict to discrete Grothendieck opfibrations.
, which gives us an equivalence when we restrict to discrete Grothendieck opfibrations.
In this subsection we generalize this result and prove two Quillen equivalences between a model category of space valued functors out of  and a model category of left fibrations over
and a model category of left fibrations over  . We will then use this result to give a precise characterization of left fibrations over F(n).
. We will then use this result to give a precise characterization of left fibrations over F(n).
Definition 4.2
Let  be a small category. We define the projective model structure on the functor category
be a small category. We define the projective model structure on the functor category  as follows.
as follows.
- (F):
-
A natural transformation \(\alpha : G \rightarrow H\) is a projective fibration if and only if for every object c in
 the map \(\alpha _c: G(c) \rightarrow H(c)\) is a Kan fibration.
the map \(\alpha _c: G(c) \rightarrow H(c)\) is a Kan fibration. - (W):
-
A natural transformation \(\alpha : G \rightarrow H\) is a projective equivalence if and only if for every object c in
 the map \(\alpha _c: G(c) \rightarrow H(c)\) is a Kan equivalence.
the map \(\alpha _c: G(c) \rightarrow H(c)\) is a Kan equivalence. - (C):
-
A natural transformation is a projective cofibration if it satisfies the left lifting property with respect to all trivial projective fibrations.
The projective model structure on  exists [42, Proposition A.2.8.2]. Recall that for a given simplicial set S we denote the constant functor as
exists [42, Proposition A.2.8.2]. Recall that for a given simplicial set S we denote the constant functor as  (Sect. 0.7).
(Sect. 0.7).
Remark 4.3
The projective model structure has many desirable properties.
-
(1)
It is proper.
-
(2)
It is combinatorial.
-
(3)
It is a simplicial model category, with simplicial enrichment given by
$$\begin{aligned} \textrm{Map}(F,G)_n = \textrm{Nat}(F \times \{ \Delta [n] \},G). \end{aligned}$$ -
(4)
It is compatible with Cartesian closure of the underlying category: If \(A \rightarrow B\) and \(C \rightarrow D\) are cofibrations then \((A \rightarrow B) \square (C \rightarrow D)\) is a cofibration, which is trivial if either is trivial.
Remark 4.4
Using the isomorphism of functor categories

we can think of a space valued functor  as a simplicial object in set valued functors
as a simplicial object in set valued functors  . Thus we will often switch between those when required.
. Thus we will often switch between those when required.
Our first step is to generalize the adjunction from Proposition 1.10.
Definition 4.5
Let

be the functor that applies  level-wise to the functor
level-wise to the functor  , meaning
, meaning  .
.
Remark 4.6
By direct computation, the simplicial space  is level-wise equal to
is level-wise equal to

with projection  taking an element \((c_0 \rightarrow \cdots \rightarrow c_n, x)\) to \(c_0 \rightarrow \cdots \rightarrow c_n\).
taking an element \((c_0 \rightarrow \cdots \rightarrow c_n, x)\) to \(c_0 \rightarrow \cdots \rightarrow c_n\).
Definition 4.7
Let

be the functor defined as the left Kan extension of the functor

Definition 4.8
Let

be the functor that takes a map  to the functor
to the functor

meaning that for an object c in  the value is given by
the value is given by

Lemma 4.9
The functors  give us two adjunctions
give us two adjunctions 

Moreover, the adjunction  is simplicially enriched.
is simplicially enriched.
Proof
By definition  commutes with colimits. Hence it suffices to observe that we have the following natural bijections
commutes with colimits. Hence it suffices to observe that we have the following natural bijections

which establishes the adjunction  (here
(here  is as described in Remark 4.4).
is as described in Remark 4.4).
On the other hand we have

which establishes the adjunction  .
.
Following [63, Proposition 3.7.10], in order to show the adjunction is simplicially enriched it suffices to show that the adjunction preserves the simplicial tensor. Following the explicit description of the tensor given in Sect. 2.3 and Remark 4.3, this means we need to prove  . However, it is an immediate computation that
. However, it is an immediate computation that  . Moreover,
. Moreover,  is a right adjoint and hence commutes with products and so we have
is a right adjoint and hence commutes with products and so we have  over
over  and hence we are done. \(\square \)
and hence we are done. \(\square \)
We would like to prove that if a functor  is valued in Kan complexes then the map of simplicial spaces
is valued in Kan complexes then the map of simplicial spaces  is a left fibration. However, this does not hold in general and so we instead have the following lemma.
is a left fibration. However, this does not hold in general and so we instead have the following lemma.
Lemma 4.10
Let  be a functor. Then
be a functor. Then  is a left morphism. Moreover, let
is a left morphism. Moreover, let  be a Reedy fibrant replacement of
be a Reedy fibrant replacement of  . Then
. Then  is a left fibration.
is a left fibration.
Proof
First we observe that  is a left morphism. Notice the square
is a left morphism. Notice the square

is a pullback as an element in \(\coprod _{c_0 \rightarrow \ldots \rightarrow c_n} G(c_0)_k\) is precisely a choice of \(c_0 \rightarrow \ldots \rightarrow c_n\) in  along with a choice of element in \(G(c_0)_k\). Moreover, the diagram is already a homotopy pullback square as
along with a choice of element in \(G(c_0)_k\). Moreover, the diagram is already a homotopy pullback square as  is a Kan fibration.
is a Kan fibration.
Now, let  be a Reedy fibrant replacement. Notice, it is a Reedy fibration by definition and so we only need to verify the locality condition. As
be a Reedy fibrant replacement. Notice, it is a Reedy fibration by definition and so we only need to verify the locality condition. As  is a discrete simplicial space, the map
is a discrete simplicial space, the map  is a Kan fibration for all n, and so by right properness of the Kan model structure the induced map on pullbacks
is a Kan fibration for all n, and so by right properness of the Kan model structure the induced map on pullbacks  is a Kan equivalence. Hence, for every \(n \ge 1\), we have the following commutative diagram where three sides are weak equivalences
is a Kan equivalence. Hence, for every \(n \ge 1\), we have the following commutative diagram where three sides are weak equivalences

and so the desired result follows from 2-out-of-3. \(\square \)
We can use this observation to determine when  is a covariant equivalence.
is a covariant equivalence.
Lemma 4.11
Let \(\alpha : G \rightarrow H\) be a natural transformation. Then \(\alpha \) is a projective equivalence if and only if  is a covariant equivalence.
is a covariant equivalence.
Proof
Let  be a Reedy fibrant replacement of
be a Reedy fibrant replacement of  . By the previous lemma
. By the previous lemma  ,
,  are left fibrations and so
are left fibrations and so  is an equivalence if and only if
is an equivalence if and only if  is a Kan equivalence. We now have the following diagram
is a Kan equivalence. We now have the following diagram

The vertical maps are Kan equivalences as Reedy equivalences are level-wise Kan equivalences. Hence the top map is an equivalence (which is equivalent to \(\alpha \) being a projective equivalence) if and only if the bottom map is an equivalence (which is equivalent for  to be a covariant equivalence). \(\square \)
to be a covariant equivalence). \(\square \)
Although  has many desirable properties it is generally not a left fibration, because it is not a Reedy fibration. Hence, we need to define an alternative, yet equivalent, functor that takes projectively fibrant functors to left fibrations. The following remark can help guide us towards a working definition.
has many desirable properties it is generally not a left fibration, because it is not a Reedy fibration. Hence, we need to define an alternative, yet equivalent, functor that takes projectively fibrant functors to left fibrations. The following remark can help guide us towards a working definition.
Remark 4.12
In Proposition 1.10 the left adjoint of  , denoted
, denoted  , was defined as
, was defined as  . This exactly coincides with the left Kan extension of the functor that takes the functor
. This exactly coincides with the left Kan extension of the functor that takes the functor  to the representable functor \(\textrm{Hom}(p(0),-)\).
to the representable functor \(\textrm{Hom}(p(0),-)\).
This would suggest that the correct simplicial generalization should take  to the functor which takes c to the simplicial set
to the functor which takes c to the simplicial set  , as in that case we would have an isomorphism of set valued functors
, as in that case we would have an isomorphism of set valued functors  . Indeed for any category
. Indeed for any category  we have a bijection
we have a bijection  .
.
However, this is clearly not the case. Indeed, as we proved in Lemma 4.9, the left adjoint is given by the functor  , which, following Definition 4.7, satisfies
, which, following Definition 4.7, satisfies  , which is clearly not the same as
, which is clearly not the same as  .
.
Building on this remark, we want to define an appropriate analogue of  with the correct values, which we will label
with the correct values, which we will label  .
.
Definition 4.13
Let

be the functor that takes a map  to the functor
to the functor

concretely meaning the values are given as follows

For the next definition we use the fact that a map  corresponds to a functor
corresponds to a functor  .
.
For the next definition recall that there is an isomorphism of categories  [44, Page 157]. Here
[44, Page 157]. Here  is the full subcategory of
is the full subcategory of  with objects
with objects  .
.
Definition 4.14
Define

as the functor that via the adjunction between products and exponentials corresponds to

using the isomorphism  . Unwinding this definition, it takes G to the simplicial space
. Unwinding this definition, it takes G to the simplicial space  , whose morphisms from
, whose morphisms from  over
over  are given by
are given by

Here  is the functor that corresponds to the map
is the functor that corresponds to the map  .
.
It will follow from Theorem 4.18 that for a projectively fibrant functor G,  is in fact a left fibration and equivalent to
is in fact a left fibration and equivalent to  , giving us a fibrant replacement.
, giving us a fibrant replacement.
We now establish that these functors are in fact adjoints.
Proposition 4.15
The functors  form a simplicially enriched adjunction
form a simplicially enriched adjunction

that is natural up to isomorphism in  .
.
Proof
First we show the functor  commutes with colimits. As colimits in
commutes with colimits. As colimits in  are evaluated point-wise, we only need to confirm that for every object c in
are evaluated point-wise, we only need to confirm that for every object c in  , the functor
, the functor  preserves colimits. This follows immediately from the fact that \(\textrm{Diag}^*\) preserves colimits (it is a left adjoint) and that
preserves colimits. This follows immediately from the fact that \(\textrm{Diag}^*\) preserves colimits (it is a left adjoint) and that  preserves colimits (
preserves colimits ( is locally Cartesian closed). Now, following [44, Corollary I.5.4], every colimit preserving functor out of
is locally Cartesian closed). Now, following [44, Corollary I.5.4], every colimit preserving functor out of  is uniquely determined by its restriction to
is uniquely determined by its restriction to  and has a right adjoint, which is by definition given by
and has a right adjoint, which is by definition given by  .
.
We now move on to show the adjunction is enriched. Again, by [63, Proposition 3.7.10], we need to prove that  preserves the simplicial tensor. Based on Sect. 2.3 and Remark 4.3 we need to prove that for a given simplicial set K,
preserves the simplicial tensor. Based on Sect. 2.3 and Remark 4.3 we need to prove that for a given simplicial set K,  . This is a direct computation as for every object c in
. This is a direct computation as for every object c in  we have
we have

Hence, giving us the desired isomorphism of functors  .
.
Finally, we move on to show the adjunction is natural. Fix a functor  . We want to show the diagram of adjunctions
. We want to show the diagram of adjunctions

commutes up to isomorphism. By uniqueness of right adjoints it suffices to show that the diagram of left adjoints commute. As left adjoints commute with colimits it suffices to prove that  . We have shown that
. We have shown that  are simplicially enriched. Moreover
are simplicially enriched. Moreover  is also simplicially enriched [42, Proposition A.3.3.6]. Hence, we can reduce the computation to showing that
is also simplicially enriched [42, Proposition A.3.3.6]. Hence, we can reduce the computation to showing that  .
.
We will start with the case \(n=0\). In that case a morphism  is given by a choice of object in
is given by a choice of object in  and by direct computation (Definition 4.13)
and by direct computation (Definition 4.13)  and
and  thought of as a discrete simplicial sets. The desired result
thought of as a discrete simplicial sets. The desired result  is now a direct computation (see also [45, Page 236]).
is now a direct computation (see also [45, Page 236]).
We move on to the case \(n>0\). Fix a morphism  given by a chain \(c_0 \rightarrow \ldots \rightarrow c_n\). Notice for \(k \ge 0\), we have
given by a chain \(c_0 \rightarrow \ldots \rightarrow c_n\). Notice for \(k \ge 0\), we have

Hence, we can repeat the argument of the previous paragraph level-wise (using the fact that left adjoints commute with coproducts) to deduce the desired isomorphism  , finishing the proof. \(\square \)
, finishing the proof. \(\square \)
We now want to prove that these adjunctions are Quillen adjunctions. For that we first need to show that they interact well with the model structures.
Lemma 4.16
The functor  takes (trivial) projective cofibrations to (trivial) covariant cofibrations.
takes (trivial) projective cofibrations to (trivial) covariant cofibrations.
Proof
It suffices to check  preserves the generating cofibrations and trivial cofibrations, which, following [42, Remark A.2.8.5], are given by the cofibrations
preserves the generating cofibrations and trivial cofibrations, which, following [42, Remark A.2.8.5], are given by the cofibrations  and the trivial cofibrations
and the trivial cofibrations  .
.
Observe that  takes the generating cofibrations
takes the generating cofibrations

to the cofibrations

and similarly the generating trivial cofibrations

to the morphisms

which is a trivial cofibration in the Reedy model structure over  and hence also a covariant equivalence. \(\square \)
and hence also a covariant equivalence. \(\square \)
Lemma 4.17
The functor  takes (trivial) projective fibrations to (trivial) fibrations in the covariant model structure over
takes (trivial) projective fibrations to (trivial) fibrations in the covariant model structure over  .
.
Proof
Let \(\alpha : G \rightarrow H\) be a projective fibration. We need to prove that  has the right lifting property with respect to maps
has the right lifting property with respect to maps
-
 ,
, -
 .
.
Using the adjunction  this is equivalent to proving that
this is equivalent to proving that
-
 ,
, -

are trivial projective cofibrations in  .
.
By direct computation these are equal to
-
 ,
, -
 .
.
The map \(\{\Lambda [l]_i\} \rightarrow \{\Delta [l]\}\) is a trivial projective cofibration and \(\{\partial \Delta [l]\} \rightarrow \{\Delta [l]\}\) is a projective cofibration. Hence, by Remark 4.3, it suffices to prove that  is a projective cofibration and
is a projective cofibration and  is a projective trivial cofibration.
is a projective trivial cofibration.
Fix a morphism  and notice it comes from a functor
and notice it comes from a functor  , which we also denote by \(\alpha \). By Proposition 4.15, we now have the following commutative diagram of adjunctions
, which we also denote by \(\alpha \). By Proposition 4.15, we now have the following commutative diagram of adjunctions

The right hand adjunction is a Quillen adjunction of projective model structures [42, Proposition A.2.8.7], meaning \(\alpha _!\) preserves (trivial) cofibrations. Hence it suffices to prove \(s\mathbb {T}_{[n]}(\partial F(n) \rightarrow F(n) \rightarrow F(n))\) is a cofibration and \(s\mathbb {T}_{[n]}(F(0) \rightarrow F(n) \rightarrow F(n))\) is a trivial cofibration. By direct computation for \(i<n\) we have
and for \(i = n\) we have
This means we have the following pushout square in 

proving the desired morphism is a projective cofibration.
Finally, by direct computation
giving us the desired equivalence.
Now, let us assume that \(\alpha : G \rightarrow H\) is a trivial projective fibration. We need to prove that  has the right lifting property with respect to maps of the form
has the right lifting property with respect to maps of the form  , which is equivalent to establishing that
, which is equivalent to establishing that

is a projective cofibration. However, we already showed above that  is a projective cofibration and so the desired result follows from the fact that the projective model structure is simplicial. \(\square \)
is a projective cofibration and so the desired result follows from the fact that the projective model structure is simplicial. \(\square \)
Theorem 4.18
Let  be a small category. The two simplicially enriched adjunctions
be a small category. The two simplicially enriched adjunctions

are Quillen equivalences, which are (up to equivalence) natural in  . Moreover, the derived counit map
. Moreover, the derived counit map  is in fact a Reedy equivalence. Here
is in fact a Reedy equivalence. Here  has the projective model structure and
has the projective model structure and  has the covariant model structure over
has the covariant model structure over  .
.
Proof
First we show both are Quillen adjunctions. By Lemma 4.16,  preserves cofibrations and trivial cofibrations and so is a left Quillen functor. On the other hand, by Lemma 3.14, a fibration between fibrant objects in the covariant model structure is a left fibration. By Lemma 4.17,
preserves cofibrations and trivial cofibrations and so is a left Quillen functor. On the other hand, by Lemma 3.14, a fibration between fibrant objects in the covariant model structure is a left fibration. By Lemma 4.17,  takes projective fibrations to left fibrations, which means it takes projective fibrations between fibrant objects to covariant fibrations. By the same lemma,
takes projective fibrations to left fibrations, which means it takes projective fibrations between fibrant objects to covariant fibrations. By the same lemma,  takes trivial projective fibrations to trivial covariant fibrations. Hence, by Lemma A.3, it is a right Quillen functor.
takes trivial projective fibrations to trivial covariant fibrations. Hence, by Lemma A.3, it is a right Quillen functor.
We move on to prove they are Quillen equivalences. Notice, the composition functor  is a colimit preserving functor that takes \(\textrm{Hom}(c,-) \times \{\Delta [l]\}\) to the functor
is a colimit preserving functor that takes \(\textrm{Hom}(c,-) \times \{\Delta [l]\}\) to the functor  , which is naturally equivalent to \(\textrm{Hom}(c,-) \times \{\Delta [l]\}\). Hence, the composition functor is naturally weakly equivalent to the identity and so a Quillen equivalence. Thus in order to prove both adjunctions are Quillen equivalences by 2-out-of-3 it suffices to prove
, which is naturally equivalent to \(\textrm{Hom}(c,-) \times \{\Delta [l]\}\). Hence, the composition functor is naturally weakly equivalent to the identity and so a Quillen equivalence. Thus in order to prove both adjunctions are Quillen equivalences by 2-out-of-3 it suffices to prove  is a Quillen equivalence.
is a Quillen equivalence.
By Lemma A.4, it suffices to prove that the derived counit map is an equivalence and  reflects weak equivalences. We already proved that
reflects weak equivalences. We already proved that  reflects weak equivalences in Lemma 4.11. Let
reflects weak equivalences in Lemma 4.11. Let  be a left fibration. We want to prove that
be a left fibration. We want to prove that  is a covariant equivalence, where
is a covariant equivalence, where  is a cofibrant replacement of
is a cofibrant replacement of  in the projective model structure on
in the projective model structure on  . We will in fact prove the derived counit is a Reedy equivalence, hence also proving the second statement of the theorem and so finishing the proof. It suffices to do so fiber-wise.
. We will in fact prove the derived counit is a Reedy equivalence, hence also proving the second statement of the theorem and so finishing the proof. It suffices to do so fiber-wise.
Fix a map  that we can represent by a diagram \(c_0 \rightarrow \ldots \rightarrow c_n\). As L is a left fibration we have an equivalence of spaces
that we can represent by a diagram \(c_0 \rightarrow \ldots \rightarrow c_n\). As L is a left fibration we have an equivalence of spaces

that restricts along the inclusion \(< 0 >:F(0) \rightarrow F(n)\). Moreover, by Remark 4.6,

which also restricts a morphism  along \(< 0 >:F(0) \rightarrow F(n)\) to an element in
along \(< 0 >:F(0) \rightarrow F(n)\) to an element in  . Hence, in order to establish the Quillen equivalence, we only have to show that the composition map
. Hence, in order to establish the Quillen equivalence, we only have to show that the composition map

is a Kan equivalence. However, tracing through these morphisms, this morphism is induced by restricting along  . Hence, this is an equivalence precisely by the statement of the Yoneda lemma for Segal spaces (Theorem 3.49).
. Hence, this is an equivalence precisely by the statement of the Yoneda lemma for Segal spaces (Theorem 3.49).
Let  be a functor. In order to finish the proof, we need to show that the diagram of adjunctions
be a functor. In order to finish the proof, we need to show that the diagram of adjunctions

commutes up to natural equivalence. We have shown in Proposition 4.15 that the right hand square commutes up to natural isomorphism, so we only need to prove the left hand square commutes up to weak equivalence. We will prove that the right Quillen functors  and
and  are naturally equivalent for fibrant objects.
are naturally equivalent for fibrant objects.
Fix a left fibration  . Then
. Then

Hence, in order to establish a natural projective equivalence  it suffices to prove that the natural morphism
it suffices to prove that the natural morphism  is a Kan equivalence. However, this again follows from the Yoneda lemma for Segal spaces (Theorem 3.49) combined with 2-out-of-3, as the morphism
is a Kan equivalence. However, this again follows from the Yoneda lemma for Segal spaces (Theorem 3.49) combined with 2-out-of-3, as the morphism  induces a commutative diagram
induces a commutative diagram

where the two left hand morphisms are Kan equivalences. \(\square \)
Remark 4.19
It is interesting to note how this result compares to a similar result in [33, Theorem C]. There the authors study a functor very similar to  using quasi-categories, however, as they are using simplicial sets, their functor \(h_!\) is the diagonal of the level-wise Grothendieck construction. Thus, they cannot simply take a Reedy fibrant replacement (as we did in Lemma 4.11) to get a left fibration and thus have to apply more complicated techniques.
using quasi-categories, however, as they are using simplicial sets, their functor \(h_!\) is the diagonal of the level-wise Grothendieck construction. Thus, they cannot simply take a Reedy fibrant replacement (as we did in Lemma 4.11) to get a left fibration and thus have to apply more complicated techniques.
Remark 4.20
The left side of the two Quillen equivalences has also been proven to be an equivalence by de Brito [19, Theorem A]. Moreover, both equivalences have been generalized to the \((\infty ,n)\)-categorical setting, which in particular would restrict to the equivalences given here [54, Theorem 5.50]
The Quillen equivalence can help us find fibrant replacements.
Corollary 4.21
Let  be a map of simplicial spaces. Then the derived unit map
be a map of simplicial spaces. Then the derived unit map  is the covariant fibrant replacement of
is the covariant fibrant replacement of  .
.
There is one key example which we want to consider more explicitly. Let  . Then
. Then  (using Notation 4.1). and so the result implies that we have Quillen equivalences
(using Notation 4.1). and so the result implies that we have Quillen equivalences

The main result (Theorem 4.18) and this diagram has important corollaries that we will use extensively.
Corollary 4.22
A morphism of simplicial spaces \(X \rightarrow Y\) over  is a covariant equivalence if and only if for all objects c in
is a covariant equivalence if and only if for all objects c in  the morphism
the morphism

is a diagonal equivalence. In particular, a map of simplicial spaces \(X \rightarrow Y\) over F(n) is a covariant equivalence if and only if for all maps \(< 0,\ldots ,i >:F(i) \rightarrow F(n)\) the induced map
is a diagonal equivalence for all \(0 \le i \le n\).
Proof
By Theorem 4.18,  reflects weak equivalences meaning a morphism \(X \rightarrow Y\) over
reflects weak equivalences meaning a morphism \(X \rightarrow Y\) over  is a weak equivalence if and only if
is a weak equivalence if and only if  is a projective equivalence. By definition of projective weak equivalences (Definition 4.2) this is equivalent to
is a projective equivalence. By definition of projective weak equivalences (Definition 4.2) this is equivalent to  being a Kan equivalence for all objects c in
being a Kan equivalence for all objects c in  , which is the same as
, which is the same as  being a Kan equivalence, which, by Theorem 2.11, means
being a Kan equivalence, which, by Theorem 2.11, means  is a diagonal equivalence for all objects c in
is a diagonal equivalence for all objects c in  .
.
Finally, by direct computation \(\textrm{N}^h([n]_{/i}) \rightarrow \textrm{N}^h([n])\) is exactly the map \(< 0,\ldots ,i >:F(i) \rightarrow F(n)\). This means for a given morphism \(X \rightarrow F(n)\), we have \(s\mathbb {T}_{[n]}(X \rightarrow F(n))(i) = \textrm{Diag}^*(F(i) \times _{F(n)} X)\) and so the result follows from the previous paragraph. \(\square \)
Corollary 4.23
Every left fibration \(L \rightarrow F(n)\) is Reedy equivalent to a colimit (and hence a homotopy colimit) of left morphisms \((< 0,\ldots ,i > \circ \pi _1): F(i) \times \Delta [l] \rightarrow F(n)\).
Proof
Let \(L \rightarrow F(n)\) be a left fibration. Then by Theorem 4.18 there exists a functor  and a Reedy equivalence \(L \simeq s\hspace{-0.04in}\int _{[n]} G\) over F(n) (concretely we can take
and a Reedy equivalence \(L \simeq s\hspace{-0.04in}\int _{[n]} G\) over F(n) (concretely we can take  ). But G is a simplicial presheaf and so there is an isomorphism \(G \cong \textrm{colim}(\textrm{Hom}([i],-) \times \Delta [l])\) and so
). But G is a simplicial presheaf and so there is an isomorphism \(G \cong \textrm{colim}(\textrm{Hom}([i],-) \times \Delta [l])\) and so
giving us the desired result. \(\square \)
Corollary 4.24
Let \(L \rightarrow F(n) \times \Delta [l]\) be a left fibration. Then there is a Reedy equivalence
over \(F(n) \times \Delta [l] \).
Proof
The projection map \(\pi _1: F(n) \times \Delta [l] \rightarrow F(n)\) is a Reedy equivalence and so by Theorem 3.15 gives us a Quillen equivalence

which implies that the derived unit map \(L \rightarrow \hat{L} \times \Delta [l]\) is a Reedy equivalence of left fibrations over \(F(n) \times \Delta [l]\). Here \(\hat{L}\) is given as the left fibrant replacement of the morphism \(L \rightarrow F(n) \times \Delta [l] \rightarrow F(n)\). Now, by the previous corollary we have a Reedy equivalence \(\hat{L} \simeq \textrm{colim}((< 0,\ldots ,i > \circ \pi _1): F(i) \times \Delta [l] \rightarrow F(n))\) over F(n). We can pull back this equivalence along \(F(n) \times \Delta [l] \rightarrow F(n)\) to get an equivalence \(\hat{L} \times \Delta [l] \simeq \textrm{colim}((< 0,\ldots ,i > \circ \pi _1): F(i) \times \Delta [l] \rightarrow F(n)) \times \Delta [l])\), using the fact that  preserves weak equivalences between non-fibrant simplicial sets. Finally, the desired result follows from the fact that colimits commute with products, giving us
preserves weak equivalences between non-fibrant simplicial sets. Finally, the desired result follows from the fact that colimits commute with products, giving us
over \(F(n) \times \Delta [l]\). \(\square \)
In the coming sections we will need the contravariant version of fibrations, right fibrations.
Remark 4.25
Until now we have focused on the covariant approach to fibrations. However, there is also a contravariant analogue. A morphism of simplicial spaces \(p:R \rightarrow X\) is a right fibration if the morphism \(p^{op}:R^{op} \rightarrow X^{op}\) is a left fibration. Explicitly this means a right fibration \(p:R \rightarrow X\) is a Reedy fibration such that for all \(n \ge 0\), the induced morphism \((p_n,< n >): Y_n \xrightarrow { \ \simeq \ } X_n \times _{X_0} Y_0\) is a Kan equivalence.
We can now repeat all the results in Sects. 3 and 4.1 using the fact that we can define right fibrations in terms of left fibrations. However, instead of repeating all theorems for right fibrations we introduce the following table, which simply states the terminology relevant to right fibrations.
Left Fibration (Morphism) | Right Fibration (Morphism) |
|---|---|
\((p_n, < 0 >^*): Y_n \xrightarrow { \ \simeq \ } X_n \times _{X_0} Y_0\) | \((p_n, < n >^*): Y_n \xrightarrow { \ \simeq \ } X_n \times _{X_0} Y_0\) |
Covariant Model Structure | Contravariant Model Structure |
Under-Segal Space | Over-Segal Space |
| |
initial object | final object |
|
Having defined left and right fibrations, we can use our previous results to generalize Remark 1.18 from categories to simplicial spaces.
Theorem 4.26
Let \(p: L \rightarrow X\) be a left fibration. Then the following are equivalent:
-
(1)
p is a right fibration.
-
(2)
For every map \(f: F(1) \rightarrow X\) the map \(f^*L \rightarrow F(1)\) is a right fibration.
-
(3)
p is a diagonal fibration.
-
(4)
For every map \(f: F(1) \rightarrow X\) the map \(f^*L \rightarrow F(1)\) is a diagonal fibration.
Proof
By Lemmas 3.10, 3.11p is a left, right or diagonal fibration if and only if \(f^*p: f^*L \rightarrow F(n)\) is such a fibration for every map \(F(n) \rightarrow X\). We will hence assume that \(X = F(n)\).
(1 \(\Leftrightarrow \) 2) One side is a special case. For the other side, as F(n) is a Segal space, by Lemma 3.29, it suffices to show that \((p_1,< 1 >^*):L_1 \rightarrow L_0 \times _{F(n)_0} \times F(n)_1\) is an equivalence over \(F(n)_1\). By Corollary A.2, this is equivalent to a fiber-wise equivalence, meaning we need to show that for every \(\alpha \) in \(F(n)_1\) the induced map on fibers
is a Kan equivalence. Fix one \(\alpha \) in \(F(n)_1\) and notice this corresponds to a morphism of simplicial spaces \(\{\alpha \}:F(1) \rightarrow F(n)\), meaning \(\alpha \) is precisely the image of the identity \(\{\alpha \}_1:F(1)_1 \rightarrow F(n)_1\). Hence, by the pasting property of pullbacks, the map above is isomorphic to the map
which is an equivalence as \(\{\alpha \}^*L \rightarrow F(1)\) is a right fibration.
(1 \(\Leftrightarrow \) 3) Every diagonal fibration is a left fibration and right fibration. Before we prove the opposite direction, we make the following observation regarding diagonal fibrations. Let K be a Kan complex, then, by Remark 2.10, \(\textrm{Diag}_*K\) gives us a Reedy fibrant replacement of K and so \(F(n) \times \textrm{Diag}_*K \rightarrow F(n)\) is a Reedy fibration that is in fact a diagonal fibration, as it satisfies the conditions given in [61, Definition 3.3], which precisely describe the diagonal fibrations by [61, Lemma 4.3]. Hence, in order to prove a Reedy fibration \(L \rightarrow F(n)\) is a diagonal fibration, it suffices to show it is Reedy equivalent to a morphism of the form \(F(n) \times K \rightarrow F(n)\) for some Kan complex K.
Now, let \(L \rightarrow F(n)\) be a right and left fibration. As it is a left fibration, by Theorem 4.18, there exists a functor  such that \(s\hspace{-0.04in}\int _{[n]} G\) is Reedy equivalent to L over F(n). We can assume without loss of generality that G takes value in Kan complexes (by fibrantly replacing in the projective model structure).
such that \(s\hspace{-0.04in}\int _{[n]} G\) is Reedy equivalent to L over F(n). We can assume without loss of generality that G takes value in Kan complexes (by fibrantly replacing in the projective model structure).
Following the argument in the first paragraph, in order to finish the proof we only need to prove there is a Reedy weak equivalence \(F(n) \times G(0) \xrightarrow { \ \simeq \ } s\hspace{-0.04in}\int _{[n]} G\) over F(n). Let  be the constant functor and notice it comes with an evident natural transformation \(\alpha : \{G(0)\} \Rightarrow G\). Moreover, \(s\hspace{-0.04in}\int _{[n]} \{G(0)\} = G(0) \times F(n)\), hence we need to establish that \(s\hspace{-0.04in}\int _{[n]}\alpha \) is a Reedy weak equivalence. By Remark 4.6, at level k the morphism is given by \(\coprod _{c_0 \rightarrow \ldots \rightarrow c_k} G(0) \rightarrow \coprod _{c_0 \rightarrow \ldots \rightarrow c_k} G(c_0)\) and Kan equivalences are closed under coproducts, meaning we only have to show that the morphisms \(G(0) \rightarrow G(i)\) are equivalences for all \(0\le i \le n\).
be the constant functor and notice it comes with an evident natural transformation \(\alpha : \{G(0)\} \Rightarrow G\). Moreover, \(s\hspace{-0.04in}\int _{[n]} \{G(0)\} = G(0) \times F(n)\), hence we need to establish that \(s\hspace{-0.04in}\int _{[n]}\alpha \) is a Reedy weak equivalence. By Remark 4.6, at level k the morphism is given by \(\coprod _{c_0 \rightarrow \ldots \rightarrow c_k} G(0) \rightarrow \coprod _{c_0 \rightarrow \ldots \rightarrow c_k} G(c_0)\) and Kan equivalences are closed under coproducts, meaning we only have to show that the morphisms \(G(0) \rightarrow G(i)\) are equivalences for all \(0\le i \le n\).
Let \(f:0 \rightarrow i\) be the unique morphism in [n] from 0 to i. Taking fiber of the commutative diagram

over f in \(F(n)_1\) gives us the diagram

Here the vertical morphisms are equivalences because \(s\hspace{-0.04in}\int _{[n]}G \rightarrow L\) is a Reedy equivalence and the bottom vertical morphism is a weak equivalence because \(L \rightarrow F(n)\) is a right fibration, it hence follows that the top morphism is also a weak equivalence.
(2 \(\Leftrightarrow \) 4) We can use the same argument as in the previous part. \(\square \)
5.2 The Yoneda Lemma
We are finally in a position to prove the recognition principle for covariant equivalences. The proof has three main steps:
-
(1)
Study how right and left fibrations interact: Theorem 4.29.
-
(2)
Characterize covariant equivalences between left fibrations: Theorem 4.35.
-
(3)
Prove the recognition principle for covariant equivalences: Theorem 4.41.
However, before we can start we need one technical lemma.
Lemma 4.27
Let  be a set of monomorphisms in
be a set of monomorphisms in  . For every simplicial space X denote by
. For every simplicial space X denote by  the left Bousfield localization of the induced Reedy model structure with respect to the set of monomorphisms
the left Bousfield localization of the induced Reedy model structure with respect to the set of monomorphisms  in
in  . Then the following are equivalent:
. Then the following are equivalent:
-
(1)
For every simplicial space X and every right fibration \(p: R \rightarrow X\) over X, the adjunction

is a Quillen adjunction.
-
(2)
For every \(j \in J\), every object c in
 and map
and map  in \(\mathcal {L}\) the pullback map
in \(\mathcal {L}\) the pullback map 
is a trivial cofibration in
 . Here
. Here  is the projection map.
is the projection map.
Proof
\( (1 \Rightarrow 2)\) This is just the special case of (1) applied to the right fibration  .
.
\((2 \Rightarrow 1)\) The proof consists of several reduction steps.
(I) Reduce to Fibrant Objects: First, by Corollary A.10 it suffices to show \(p_!p^*\) preserves cofibrations, \(p_*p^*\) preserves Reedy fibrations and fibrant objects \(Y \rightarrow X\). The fact that \(p_!p^*\) preserves cofibrations and that \(p_*p^*\) preserves Reedy fibrations follows from the fact that \((p_!p^*,p_*p^*)\) is a Quillen adjunction when both sides just have the induced Reedy model structure, as the Reedy model structure is right proper (Sect. 2.4). So, we only have to prove that for every fibrant object \(Y \rightarrow X\), \(p_*p^*(Y) \rightarrow X\) is also fibrant.
(II) Reduce to Local Objects: Next notice that \(p_*p^*(Y) \rightarrow X\) is fibrant if and only if it is Reedy fibrant and local with respect to maps  , where
, where  is in \(\mathcal {L}\). Again the Reedy fibrancy follows from the previous paragraph and so it suffices to prove that \(p_*p^*(Y) \rightarrow X\) is local. Thus we need to prove that
is in \(\mathcal {L}\). Again the Reedy fibrancy follows from the previous paragraph and so it suffices to prove that \(p_*p^*(Y) \rightarrow X\) is local. Thus we need to prove that

is a Kan equivalence for all j and all morphisms  .
.
(III) Reduce to Local Trivial Cofibration: Using the fact that \(p_*p^*\) has a left adjoint this is equivalent to

being a Kan equivalence. As the model structure  is simplicial and \(Y \rightarrow X\) is an arbitrary fibrant object, this is equivalent to
is simplicial and \(Y \rightarrow X\) is an arbitrary fibrant object, this is equivalent to

being a weak equivalence in  for all \(j \in J\) and
for all \(j \in J\) and  . Here the morphism
. Here the morphism  is given as
is given as  , where the first morphism is the counit.
, where the first morphism is the counit.
(IV) Reduce to Categorical base: Fix a \(j \in J\) and morphism  . Then we have the following pullback square
. Then we have the following pullback square

Now the Beck-Chevalley condition for pullback squares [25, 1.2] implies that we have an isomorphism \(p^*m_!(i) \cong k_!q^*(i)\). However, notice \(k_!\) preserves weak equivalences. Thus to prove that \(p_!p^*i\) is a weak equivalence over X it suffices to prove that  is a weak equivalence over
is a weak equivalence over  in the
in the  model structure.
model structure.
(V) Reduce to Representable Right Fibrations: By Lemma 3.9, right fibrations are stable under pullback and so  is also a right fibration. However, by the contravariant analogue of Corollary 4.23, every right fibration over
is also a right fibration. However, by the contravariant analogue of Corollary 4.23, every right fibration over  is Reedy equivalent to
is Reedy equivalent to  (and so a homotopy colimit). Thus we can reduce the argument to proving that for all \(j \in J\) and object c in
(and so a homotopy colimit). Thus we can reduce the argument to proving that for all \(j \in J\) and object c in 

is a weak equivalence in  .
.
(VI) Reduce to the desired condition: Finally, using the fact that  is a simplicial model structure with all objects cofibrant, for every object
is a simplicial model structure with all objects cofibrant, for every object  , the induced morphism \(\textrm{id}_X \times < 0 >: X \times \Delta [0] \rightarrow X \times \Delta [n]\) is a weak equivalence over
, the induced morphism \(\textrm{id}_X \times < 0 >: X \times \Delta [0] \rightarrow X \times \Delta [n]\) is a weak equivalence over  in the
in the  model structure. Hence the previous condition is equivalent to
model structure. Hence the previous condition is equivalent to

being a trivial cofibration in  in the
in the  model structure, for all \(j \in J\) and objects c in
model structure, for all \(j \in J\) and objects c in  . \(\square \)
. \(\square \)
Remark 4.28
We can use the same argument to prove an analogous result for pulling back along left fibrations. Concretely,

is a Quillen adjunction for every left fibration \(p: L \rightarrow X\) if and only if

is a trivial cofibration in  for every \(j \in J\) and object c in
for every \(j \in J\) and object c in  .
.
We can now use this result to give the desired connection between right fibrations and covariant equivalences.
Theorem 4.29
Let \(p: R \rightarrow X\) be a right fibration. Then the adjunction

is a Quillen adjunction where both sides have the covariant model structure.
Proof
The covariant model structure is given by localization with respect to maps \(F(0) \xrightarrow { < 0 > } F(n) \rightarrow X\), where \(n \ge 1\). The over-category \([n]_{/i} \rightarrow [n]\) is given by the map of simplicial spaces \(< 0,\ldots ,i >: F(i) \rightarrow F(n)\). Thus, by the previous lemma, we only need to prove that the pullback map \(F(0)= F(0) \times _{F(n)} F(i) \rightarrow F(i)\) is a covariant equivalence over F(n). However, that is true by definition. \(\square \)
Remark 4.30
By Remark 4.28 and the analogous argument to Theorem 4.29, for every left fibration \(p: L \rightarrow X\), we get a Quillen adjunction \((p_!p^*,p_*p^*)\) between contravariant model structures.
Remark 4.31
The analogous result for quasi-categories (namely that pulling back along right fibrations of simplicial sets preserves equivalences in the model structure for quasi-categories) was proven independently by Lurie [42, Proposition 4.1.2.15], Joyal [39, Theorem 11.9], and Nguyen [49, Proposition 4.12].
We can also use this lemma to prove a relationship between right fibrations and complete Segal spaces.
Theorem 4.32
Let W be a Segal space and \(p: R \rightarrow W\) be a right or left fibration. Then the adjunction

is a Quillen adjunction where both sides have the induced Segal space model structure (Proposition A.5).
If W is also complete, then the same statement holds for the adjunction

where now both sides have the induced complete Segal space model structure (Proposition A.5).
Proof
We will assume p is a right fibration. The argument for left fibrations follows similarly, using the adjustment in Remark 4.28.
Let W be a Segal space. We can extend the adjunction above as follows

In order to show that \((p^*,p_*)\) is a Quillen adjunction, we have to prove \(p^*\) preserves cofibrations and trivial cofibrations in the Segal space model structure. It is evident that \(p^*\) preserves cofibrations, as they are just monomorphisms. Moreover, by Proposition A.5, \(p_!\) preserves and reflects trivial Segal cofibrations. Hence \(p^*\) preserves trivial cofibrations if and only if \(p_!p^*\) preserves trivial cofibrations, which is equivalent to proving that

is a Quillen adjunction, where both sides have the Segal space model structure. We can thus apply Lemma 4.27.
By Theorem A.13 the induced Segal space model structure over a Segal space is just given by localizing with respect to the maps \(G(n) \rightarrow F(n) \rightarrow W\), where \(n \ge 2\). Thus we only need to check the map \(G(n) \rightarrow F(n)\) satisfies the desired condition in Lemma 4.27. We know the over-category over i is given by \(< 0,\ldots ,i >: F(i) \rightarrow F(n)\). Thus we only need to show that \(G(i) = G(n) \times _{F(n)} F(i) \rightarrow F(i)\) is an equivalence in the Segal space model structure, which is true by definition.
Now let us assume also in addition that W is complete. By the explanation given at the beginning of the proof, it suffices to show that

is a Quillen adjunction, where both sides have the complete Segal space model structure. This means we can again use Lemma 4.27.
By Theorem A.13 the induced complete Segal space model structure is given by localizing with respect to maps \(G(n) \rightarrow F(n) \rightarrow W\) and \(F(0) \rightarrow E(1) \rightarrow W\). We already observed that \(G(n) \rightarrow F(n)\) satisfies the condition of Lemma 4.27 so we only need to prove the same statement for the map \(F(0) \rightarrow E(1)\).
However, \(E(1) = \textrm{N}^h(I[1])\), where I[1] is the category with two objects and one unique isomorphism (Definition 2.19). By direct computation \(I[1]_{/0} = I[1]_{/1} = I[1]\) and so the projection map from the over-category is just the identity map. Hence we are done. \(\square \)
This theorem has the following useful corollary.
Corollary 4.33
Let the following diagram be given

where W is a complete Segal space, \(p:L \rightarrow W\) is a left or right fibration and f is a complete Segal space weak equivalence. Then \(p^*f: p^*X \rightarrow L\) is a complete Segal space weak equivalence.
Remark 4.34
The assumptions in the previous theorem seem too strong, the result should also hold if the base simplicial space W is not a Segal space. This is in fact correct and we will prove this in Theorem 5.15 / Theorem 5.16. However, before we can do that we need to understand the invariance of left fibrations with respect to complete Segal space equivalences, which is the goal of Theorem 5.1.
We can now move on to the second step and characterize covariant equivalences between left fibrations.
Theorem 4.35
Let \(L \rightarrow X\) and \(L' \rightarrow X\) be left fibrations and \(f:L \rightarrow L'\) a map over X. The following are equivalent:
-
(1)
f is a covariant equivalence.
-
(2)
f is a Reedy equivalence.
-
(3)
f is a Kan equivalence.
-
(4)
f is a fiber-wise Reedy equivalence (\(f \times _X F(0): L \times _X F(0) \rightarrow L' \times _X F(0)\) is a Reedy equivalence for every map \(F(0) \rightarrow X\)).
-
(5)
f is a fiberwise Kan equivalence (\(f \times _X F(0): L \times _X F(0) \rightarrow L' \times _X F(0)\) is a Kan equivalence for every map \(F(0) \rightarrow X\)).
-
(6)
f is a fiberwise diagonal equivalence (\(f \times _X F(0): L \times _X F(0) \rightarrow L' \times _X F(0)\) is a diagonal equivalence for every map \(F(0) \rightarrow X\)).
Remark 4.36
By Theorem 4.18, a left fibration  is Reedy equivalent to
is Reedy equivalent to  for some functor
for some functor  . Thus a map of left fibrations \(L \rightarrow L'\) over
. Thus a map of left fibrations \(L \rightarrow L'\) over  is an equivalence if and only if the corresponding natural transformation \(G \rightarrow G'\) is an equivalence.
is an equivalence if and only if the corresponding natural transformation \(G \rightarrow G'\) is an equivalence.
Theorem 4.35 can thus be seen as a generalization of this observation to an arbitrary simplicial space X: We are comparing two left fibrations over X, by comparing their fibers, which we should think of as their “values”.
Proof
(1 \(\Leftrightarrow \) 2) Follows from the definition of localization as left fibrations are the fibrant objects in the covariant model structure (Theorem 3.12).
(2 \(\Leftrightarrow \) 3) Clearly (2) implies (3). For the other side let f be a Kan equivalence, then \(f_0: L_0 \rightarrow L'_0\) is a Kan equivalence of spaces. This implies that in the diagram

the two vertical maps and the bottom horizontal map are Kan equivalences. Thus \(f_n: Y_n \rightarrow Z_n\) is a Kan equivalence as well, which implies that f is a Reedy equivalence.
(3 \(\Leftrightarrow \) 5) This is precisely the statement of Corollary A.2.
(4 \(\Leftrightarrow \) 5) By Example 3.19, left fibrations over F(0) are diagonal fibrations and hence homotopically constant, which means \(f \times _X F(0): L \times _X F(0) \rightarrow L' \times _X F(0)\) is a Kan equivalence if and only if it is a Reedy equivalence.
(4 \(\Leftrightarrow \) 6 ) By Lemma 3.9, \(F(0) \times _X L \rightarrow F(0)\) is a left fibration, which by Example 3.19 means that \(L \times _X F(0)\) is diagonally fibrant. Thus \(f \times _X F(0): L\times _X F(0) \rightarrow L' \times _X F(0)\) is a Reedy equivalence if and only if it is a diagonal equivalence (Theorem 2.11). \(\square \)
Remark 4.37
Note we can reduce condition (5) in Theorem 4.35 to proving that there exists \(x: F(0) \rightarrow X\) such that \(f \times _X F(0)\) is a fiberwise Kan equivalence for every path component of \(X_0\). Indeed, if x and y are in the same path-component then we have an equivalence of fibers \(f_0 \underset{X_0}{\times }^x \Delta [0] \simeq f_0 \underset{X_0}{\times }^y\Delta [0]\).
Remark 4.38
Covariant equivalences of left fibrations have also been studied by de Brito, Moerdijk and Heuts [19, Proposition 1.10], [18, Lemma 4.3], [32, Proposition 13.8].
We can now move on to the general case.
Theorem 4.39
Let \(p:Y \rightarrow X\) be a map of simplicial spaces. For every \(\{x\}: F(0) \rightarrow X\), there is a natural zig-zag of diagonal equivalences
Here \(i: Y \rightarrow \hat{Y}\) is a choice of a left fibrant replacement of Y over X and \(R_x \rightarrow X\) is a contravariant fibrant replacement of \(\{ x \}: F(0) \rightarrow X\).
Proof
Fix a covariant fibrant replacement \(i: Y \rightarrow \hat{Y}\) over X. Then we have the following zig-zag of equivalences
By Theorem 4.29 the first map is a covariant equivalence because \(R_x \rightarrow X\) is a right fibration. By the covariant version of the same lemma the second map is a contravariant equivalence because \(\hat{Y} \rightarrow X\) is a left fibration. So, by Theorem 3.17, both are diagonal equivalences. \(\square \)
In the case X is a Segal space, we can replace the zig-zag of equivalences with an actual map.
Remark 4.40
Let X be a Segal space. Let \(p: Y \rightarrow X\) be a map of simplicial spaces and \(Y \xrightarrow { \ i \ } \hat{Y} \xrightarrow { \ \hat{p} \ } X\) its fibrant replacement in the covariant model structure. Then, by Theorem 3.49, \(\{\textrm{id}_x \}:F(0) \rightarrow F(0)\times _X X^{F(1)}\) is a covariant fibrant replacement of \(\{x\}:F(0) \rightarrow X\) over X. Now we have the following diagram:

By Lemma 3.20, the map \(\hat{Y}^{F(1)} \rightarrow \hat{Y} \times _X X^{F(1)}\) is a trivial Reedy fibration and so we can pick a section
By Theorem 4.39, \(\hat{Y}\underset{X}{\times }\ \{ id_x \}\) is a diagonal equivalence and so, by 2-out-of-3, s is a diagonal equivalence. Hence
is the desired diagonal equivalence.
We can finally prove the recognition principle for covariant equivalences.
Theorem 4.41
(Recognition principle) For every morphism \(\{x\}:F(0) \rightarrow X\) fix a contravariant fibrant replacement \(R_x \rightarrow X\). Let \(g: Y \rightarrow Z\) be a morphism over X. Then \(g:Y \rightarrow Z\) over X is a covariant equivalence over X if and only if for every \(\{x\}: F(0) \rightarrow X\)
is a diagonal equivalence.
Proof
Let the diagram

be a left fibrant replacement of g over X. By Theorem 3.12, \(g:Y \rightarrow Z\) is a covariant equivalence if and only if \(\hat{g}:\hat{Y} \rightarrow \hat{Z}\) is a Reedy equivalence. We now have the following diagram:

By Theorem 4.39, all vertical maps are diagonal equivalences and so the top horizontal map is a diagonal equivalence if and only if the bottom horizontal map is one. But the bottom map is a diagonal equivalence for every \(x: F(0) \rightarrow X\) if and only if \(\hat{Y} \rightarrow \hat{Z}\) is a Reedy equivalence (Theorem 4.35). Hence, we are done. \(\square \)
In the case of Segal spaces the equivalence takes on a very simple form.
Corollary 4.42
Let X be a Segal space and \(f:Y \rightarrow Z\) a map over X. Then f is a covariant equivalence if and only if
is a diagonal equivalence for every object x.
Proof
By Theorem 3.49, \(X_{/x} \rightarrow X\) is the contravariant fibrant replacement of \(\{ x \}: F(0) \rightarrow X\). The result now follows from Theorem 4.41. \(\square \)
Remark 4.43
A similar result has been established by Heuts and Moerdijk [33, Proposition G] using quasi-categories, to characterize covariant equivalences of simplicial sets over a given quasi-category. Notice, we cannot use the Quillen equivalence between complete Segal spaces and quasi-categories to prove Corollary 4.42 using [33, Proposition G] as the proof here holds for all Segal spaces.
Remark 4.44
Corollary 4.42 should very much remind us of the behavior of  , which takes a map
, which takes a map  to the functor
to the functor  with value
with value  . The functor
. The functor  was only defined over nerves of categories, but Corollary 4.42 suggests that a map of Segal spaces \(Y \rightarrow X\) should via the covariant model structure correspond to a functor with value \(\textrm{Diag}^*(Y \times _{X} X_{/x} )\).
was only defined over nerves of categories, but Corollary 4.42 suggests that a map of Segal spaces \(Y \rightarrow X\) should via the covariant model structure correspond to a functor with value \(\textrm{Diag}^*(Y \times _{X} X_{/x} )\).
6 Complete Segal Spaces and Covariant Model Structure
In this section we want to study the relation between complete Segal spaces and left fibrations. Concretely, while the covariant model structure is invariant under Reedy equivalences, meaning a Reedy equivalence induces a Quillen equivalence of covariant model structures, we will prove (the very non-trivial fact) that the covariant model structure is invariant under CSS equivalences as well (Theorem 5.1). We further witness that (although not initially defined this way) the covariant model structure is a Bousfield localization of the complete Segal space model structure (Theorem 5.11), which in particular implies that every left fibration is a complete Segal space fibration (Corollary 5.13). We will use this connection to generalize results regarding Segal spaces proven in Sect. 3.3 to arbitrary simplicial spaces, and in particular establish the Yoneda lemma for simplicial spaces (Corollary 5.10). Finally, we apply our new understanding of left fibrations to study colimits in Segal spaces (Definition 5.26) and establish Quillen’s Theorem A (Theorem 5.40) in this setting in Sect. 5.2.
6.1 Invariance of the Covariant Model Structure
Until now we have seen several results that suggest a deep connection between complete Segal spaces and left fibrations, in particular over a Segal space. For example the left fibration \(W_{/x} \rightarrow W\) is in fact a Segal fibration (Lemma 3.43). Or pulling back a right fibration of complete Segal spaces \(R \rightarrow X\) preserves CSS equivalences (Theorem 4.32). In this subsection we want to prove that these types of results generalize to an arbitrary simplicial space. The key input is the invariance theorem for the covariant model structure, which proves that the covariant model structure is invariant under equivalences in the complete Segal space model structure.
Theorem 5.1
(Invariance property) Let \(f: X \rightarrow Y\) be a CSS equivalence. Then the adjunction

is a Quillen equivalence. Here both sides have the covariant model structure.
Remark 5.2
As the proof is quite long here is an overview of the essential steps:
-
(1)
By the diagram in 5.3, we can reduce the proof to a fibrant replacement morphism obtained via the small object argument \(i: X \rightarrow \hat{X}\).
-
(2)
We first prove the derived counit map is an equivalence in 5.4.
-
(3)
We then move on to the derived unit map. By the small object argument the proof reduces to checking for a generating set of trivial cofibrations for the Reedy model structure (1), the morphisms characterizing Segal spaces (2), and the morphisms giving us the completeness condition (1), of which only the case of morphisms for the Segal condition (2) require a longer argument.
-
(4)
By direct computation we can reduce the case for Segal maps to proving that \(F(0) \rightarrow G(n)\) is a covariant equivalence over G(n) (5.5).
-
(5)
We prove this by induction in (5.6).
Proof
As the first step of the proof we fix a fibrant replacement for X in the complete Segal space model structure. By Theorem 2.22 a complete Segal space is characterized via right lifting property with respect to three sets of morphisms, which we explicitly name as the Reedy, Segal and completeness maps:
-
(1)
Reedy: \((\partial F(n) \rightarrow F(n)) \square (\Lambda [l]_i \rightarrow \Delta [l])\)
-
(2)
Segal: \((G(n) \rightarrow F(n)) \square (\partial \Delta [l] \rightarrow \Delta [l])\)
-
(3)
Completeness: \((F(0) \rightarrow E(1)) \square (\partial \Delta [l] \rightarrow \Delta [l])\)
Hence, applying the small object argument [34, Proposition 10.5.16] to the morphism \(X \rightarrow F(0)\) in  gives us a factorization \(X \xrightarrow {i } \hat{X} \rightarrow F(0)\) that satisfies the following properties:
gives us a factorization \(X \xrightarrow {i } \hat{X} \rightarrow F(0)\) that satisfies the following properties:
-
\(i: X \rightarrow \hat{X}\) is a cell complex, meaning it is transfinite composition of pushouts of coproducts of the three sets of morphisms.
-
The morphism \(\hat{X} \rightarrow F(0)\) satisfies the right lifting property with respect to the three classes of morphisms, which means \(\hat{X}\) is a complete Segal space.
Use the same argument on Y to obtain a morphism \(i': Y \rightarrow \hat{Y}\) with the same properties. For the remainder of the proof we will use the fixed \(i: X \rightarrow \hat{X}\) and \(i':Y \rightarrow \hat{Y}\) obtained via this argument.
Now, pick a morphism \(\hat{f}:\hat{X} \rightarrow \hat{Y}\) that makes the following diagram commute (using the lifting property of i against \(\hat{Y}\))

Then all maps in the diagram are equivalences in the CSS model structure and so the bottom horizontal map is a Reedy equivalence as \(\hat{X}\) and \(\hat{Y}\) are themselves complete Segal spaces (Theorem 2.22).
This diagram gives us the following diagram of adjunctions:

By Theorem 3.15, all four are Quillen adjunctions and the bottom horizontal Quillen adjunction is a Quillen equivalence. So, if we proved that the two vertical Quillen adjunctions are Quillen equivalences, it would then follow from 2-out-of-3 that the top horizontal adjunction is a Quillen equivalence as well. As both vertical Quillen adjunctions are given by a fibrant replacement map, it suffices to prove the left vertical Quillen adjunction \((i_!,i^*)\) is a Quillen equivalence.
We will prove that the derived unit and derived counit maps are weak equivalences. First we prove that the derived counit map \(i_!i^*L \rightarrow L\) is a covariant equivalence for every left fibration \(p:L \rightarrow \hat{X}\) (notice again that the derived counit map is the actual counit map as all objects are cofibrant).
The counit map comes from the diagram

As p is a left fibration over a complete Segal space and i is a CSS equivalence, it follows from Theorem 4.32 that \(i^*L \rightarrow L\) is a CSS equivalence. Finally, by Proposition 3.39, a CSS equivalence over the CSS \(\hat{X}\) is also a covariant equivalence over \(\hat{X}\) finishing this part of the proof.
We move on to prove that the derived unit map is an equivalence. As explained in the beginning of the proof i is given as the transfinite composition of pushouts of coproducts of the three sets of morphisms, the Reedy, Segal and completeness morphisms, specified in the beginning of the proof. We claim it suffices to check these three cases separately to deduce that \((i_!,i^*)\) is a Quillen equivalence. Indeed, let \(\mathcal {P}\) be the collection of cofibrations \(f:A \rightarrow B\) such that \((f_!,f^*)\) is a Quillen equivalence between covariant model structures. It suffices to show that \(\mathcal {P}\) is closed under transfinite composition, coproducts and pushouts.
-
Let \(A_0 \xrightarrow { \ f_0 \ } A_1 \xrightarrow { \ f_1 \ } \ldots \) be a chain of morphisms such that \(f_i \in \mathcal {P}\) for all i. Then, the transfinite composition \(f_\infty : A_0 \rightarrow A = \textrm{colim}(A_0 \rightarrow A_1 \rightarrow \ldots )\) is in \(\mathcal {P}\) as the \((f_\infty )^*\) is given as the projection from the limit of the tower
 and so if every functor in the diagram is a right Quillen equivalence, \((f_\infty )^*\) is a Quillen equivalence as well. Hence, \(\mathcal {P}\) is closed under transfinite composition.
and so if every functor in the diagram is a right Quillen equivalence, \((f_\infty )^*\) is a Quillen equivalence as well. Hence, \(\mathcal {P}\) is closed under transfinite composition. -
For a collection of morphisms \(\{f_j: A_j \rightarrow B_j\}_{j \in J}\) we have an isomorphism between
 and
and  and so if all \((f_j)^*\) are right Quillen equivalences then so is \((\coprod _j f_j)^*\). Hence, \(\mathcal {P}\) is closed under arbitrary coproducts.
and so if all \((f_j)^*\) are right Quillen equivalences then so is \((\coprod _j f_j)^*\). Hence, \(\mathcal {P}\) is closed under arbitrary coproducts. -
If \(k:A \rightarrow B\) is a monomorphism of simplicial spaces and \(f:A \rightarrow C\) a morphism, then we have a pullback square
So, if \(k^*\) is a right Quillen equivalence, then so is the induced functor \((\iota _2)^*\). Hence, \(\mathcal {P}\) is closed under pushouts.
We now prove the three types of maps give us Quillen equivalences. The case for Reedy maps follows from Theorem 3.15. The case for the completeness maps follows from the fact that in the diagram of Quillen adjunctions induced by the functor \([0] \rightarrow I[1]\)

the horizontal maps are Quillen equivalences (Theorem 4.18) and the left hand side is also a Quillen equivalence (\(\{ 0 \}: [0] \rightarrow I[1]\) is an equivalence of categories) and so by 2-out-of-3 the right hand vertical adjunction is also a Quillen equivalence. Hence we only need to focus on the case of Segal maps.
To simplify notation we denote the map \((G(n) \rightarrow F(n)) \square (\partial \Delta [l] \rightarrow \Delta [l])\) by \(j_n:G(n,l) \rightarrow F(n,l)\). Let \(p:L \rightarrow G(n,l)\) be a left fibration. We want to prove the derived unit map \(L \rightarrow j_n^*R(j_n)_!L\) is a covariant equivalence over G(n, l). Here \(L \rightarrow R(j_n)_!L\) is a fibrant replacement in the covariant model structure over F(n, l). The key idea towards the proof is the appropriate fibrant replacement. The morphism \(\pi _1: F(n) \times \Delta [l] \rightarrow F(n)\) is a Reedy equivalence and so, by Theorem 3.15, we have an equivalence \(R(j_n)_!L \simeq (\pi _1)^*R(\pi _1j_n)_!L\), meaning we can obtain a fibrant replacement of L over F(n, l) by taking the fibrant replacement over F(n) and pulling back the replacement via \(\pi _1:F(n,l) \rightarrow F(n)\).
Now, by Corollary 4.21, a fibrant replacement of \((\pi _1j_n)_!p: L \rightarrow F(n)\) is given by the derived unit map \(L \rightarrow s\mathbb {I}_{[n]}Rs\mathbb {T}_{[n]} L\), where \(Rs\mathbb {T}_{[n]} L\) is the fibrant replacement of the functor  in the projective model structure. Hence, the derived unit map of \(p:L \rightarrow G(n,l)\) is given by the morphism \(L \rightarrow j_n^*(\pi _1)^*(s\mathbb {I}_{[n]}Rs\mathbb {T}_{[n]} L)\) over G(n, l). We can summarize this construction in the following diagram:
in the projective model structure. Hence, the derived unit map of \(p:L \rightarrow G(n,l)\) is given by the morphism \(L \rightarrow j_n^*(\pi _1)^*(s\mathbb {I}_{[n]}Rs\mathbb {T}_{[n]} L)\) over G(n, l). We can summarize this construction in the following diagram:

By Theorem 4.35, it suffices to prove that \(L \rightarrow j_n^*(\pi _1)^*(s\mathbb {I}_{[n]}Rs\mathbb {T}_{[n]} L)\) is fiber-wise a Kan equivalence. Fix an object \(m: F(0) \rightarrow G(n,l)\). On the one hand, as \(L \rightarrow G(n,l)\) is a left fibration, the fiber over \(m: F(0) \rightarrow G(n,l)\) is homotopically constant (Example 3.19) and so \((L \times _{G(n,l)} F(0))_0 \rightarrow \textrm{Diag}^*(L \times _{G(n,l)} F(0))\) is a Kan equivalence. On the other hand, we have the following chain of equivalences:

where \(\textrm{Map}\) denotes the mapping space of the functor category, using the fact that the projective model structure is simplicial (Remark 4.3).
Notice, if we compose the chain of morphisms we get an equivalence \(\textrm{Diag}^*(L \times _{F(n)} F(n)_{/m}) \rightarrow ((\pi _1j_n)^*(s\mathbb {I}_{[n]}Rs\mathbb {T}_{[n]} L ) \times _{G(n,l)} F(0))_0\), which takes an element \(\sigma \in \textrm{Diag}^*(L \times _{F(n)} F(n)_{/m})_l\) to the natural transformation

where the middle natural transformation is uniquely determined via the Yoneda lemma (Lemma 1.1) by the element \(\sigma \in (s\mathbb {T}_{[n]}L)(m)_l = \textrm{Diag}^*(L \times _{F(n)} F(n)_{/m})_l\).
Now, by Proposition 4.15, we have that \(s\mathbb {T}_{[n]}(\{m\}:\Delta [l] \rightarrow F(n)) = N([0]^{\{m\}} \times _{[n]} [n]_{/-}) \times \{\Delta [l]\}\). This means the second line in the chain of equivalences above is precisely given via the adjunction between \(s\mathbb {T}_{[n]}\) and \(s\mathbb {I}_{[n]}\). Hence, by definition of the unit of an adjunction, the unit map \((L \times _{G(n,l)} F(0))_0 \rightarrow (s\mathbb {I}_{[n]}R s\mathbb {T}_{[n]} L)_0\) at the level of l-simplices is also given via the morphism

that takes an element \(\sigma \) to the natural transformation  described above. This means if we restrict the chain of equivalences above via the evident inclusion \(\iota :(L \times _{G(n,l)} F(0))_0 \rightarrow \textrm{Diag}^*(L \times _{F(n)} F(n)_{/m})\) it becomes equal to the unit map. In other words, we have established that the following diagram commutes, where the top map is induced by the unit map
described above. This means if we restrict the chain of equivalences above via the evident inclusion \(\iota :(L \times _{G(n,l)} F(0))_0 \rightarrow \textrm{Diag}^*(L \times _{F(n)} F(n)_{/m})\) it becomes equal to the unit map. In other words, we have established that the following diagram commutes, where the top map is induced by the unit map

We already observed above that the two vertical morphisms are equivalences. So, by 2-out-of-3, in order to show that the top morphism is a Kan equivalence is suffices to show that the bottom morphism is a Kan equivalence, or in other words, the map of fibers given as
is a diagonal equivalence.
It suffices to prove that \(F(0) \rightarrow G(n,l) \times _{F(n)} F(n)_{/m}\) is a contravariant equivalence over G(n, l). Indeed, in that case, by Theorem 4.29, the map 5.5 is also a contravariant equivalence (as \(L \rightarrow G(n,l)\) is a left fibration) and hence a diagonal equivalence by Theorem 3.17.
By direct computation \(F(n)_{/m} \rightarrow F(n)\) is given by \(< 0,\ldots ,m >: F(m) \rightarrow F(n)\) and so we have an isomorphism
Now, the map \(F(0) \rightarrow G(m,l)\) factors as \(F(0) \rightarrow F(0) \times \Delta [l] \rightarrow G(m,l)\). The first map is a Reedy equivalence (as \(\Delta [l]\) is contractible) and so we need to show that \(F(0) \times \Delta [l] \rightarrow G(m,l)\) is a covariant equivalence over G(n, l). The map is the homotopy pushout (in the Reedy model structure) of the diagram

Thus it suffices to prove the vertical maps are contravariant equivalences over G(n, l) (as the contravariant model structure is left proper by Theorem 3.12).
The contravariant model structure is simplicial (Theorem 3.12) and so we can reduce it to checking that \(< 0 >: F(0) \rightarrow G(m)\) is a contravariant equivalence over G(n, l). The map is a composition of maps \(g: G(i) \rightarrow G(i+1)\) and thus it suffices to show that g is a contravariant equivalence over G(n, l). By Theorem 3.15, we can reduce that to proving that \(g:G(i) \rightarrow G(i+1)\) is a contravariant equivalence over \(G(i+1)\).
Finally, we have the following pushout square:

The top horizontal map is a covariant equivalence by definition, which implies that the bottom horizontal map is a contravariant equivalence over \(G(i+1)\). \(\square \)
Remark 5.7
This result is also proven by Lurie [42, Remark 2.1.4.11], however, there it relies on translating the problem into the world of simplicial categories and then proving it there, which we managed to avoid. On the other side, it is also proven by Heuts and Moerdijk [33, Proposition F] with simplicial sets, using a very similar approach. In the special case where the domain and codomain are Segal spaces, the result also follows from [19, Proposition 5.5].
Remark 5.8
Interestingly enough the result does not hold if we replace “CSS equivalence” with covariant or contravariant equivalence. For that it suffices to look at the simple case of \(F(0) \rightarrow F(1)\), as the covariant model structure over F(0) is just the diagonal model structure, which is certainly not equivalent to the covariant or contravariant model structure over F(1). Note, following [59, Proposition 2.5], this in particular implies that the covariant model structure is not right proper.
Remark 5.9
Notice, there are maps which are not CSS equivalences, but still induce a Quillen equivalence of covariant model structures, as we shall explain. In Appendix B we prove that the covariant model structure over a simplicial set S (as defined in [42, Proposition 2.1.4.7]) is equivalent, via a left Quillen equivalence \(p_1^*\), to the covariant model structure over the simplicial space \(p_1^*S\) (Theorem B.12). Hence, it suffices to witness a morphism of simplicial sets that is not an equivalence in the Joyal model structure (the model structure for quasi-categories), but induces an equivalence of covariant model structures over simplicial sets.
Examples of such maps can be found in [42, Sects. 4.4.5 and 5.1.4]. Indeed, [42, Sect. 5.1.4] studies idempotent completions of \(\infty \)-categories and proves in [42, Proposition 5.1.4.9, Corollary 4.4.5.15] that any such idempotent completion induces an equivalence on \(\infty \)-categories of presheaves. Hence, the same argument given in [42, Remark 2.1.4.11] (that relies on the straightening construction [42, Theorem 2.2.1.2]) implies that any non-trivial idempotent completion \(S \rightarrow \hat{S}\) is a map of simplicial sets that is not an equivalence in the Joyal model structure, but induces an equivalence on covariant model structures.
We can now use this theorem to finally establish a Yoneda lemma for simplicial spaces generalizing Theorem 3.49.
Corollary 5.10
Let X be a simplicial space and \( i: X \hookrightarrow \hat{X}\) be a chosen CSS fibrant replacement of X. Then for any point \(x: F(0) \rightarrow X\) the covariant fibrant replacement is given by \(\{ s_0(x)\}:F(0) \rightarrow X_{x/} =F(0) \times _{\hat{X}} \hat{X}^{F(1)} \times _{\hat{X}} X\) induced by the composition \(i\{x\}: F(0) \rightarrow \hat{X}\). In particular, for any left fibration \(L \rightarrow X\) there is an equivalence of Kan complexes
Proof
For the first part, according to Theorem 3.49, \(F(0) \times _{\hat{X}} \hat{X}^{F(1)} \rightarrow \hat{X}\) is the covariant fibrant replacement of \(x: F(0) \rightarrow \hat{X}\) and then by Theorem 5.1 the covariant equivalence is preserved by pulling back along i. Now, the second part follows from the fact that the covariant model structure is simplicial (Theorem 3.12). \(\square \)
In Proposition 3.39 we proved that a left fibration over a complete Segal space is a complete Segal space fibration. Using the invariance theorem, Theorem 5.1, we can now generalize it to left fibrations over every simplicial space.
Theorem 5.11
Let X be a simplicial space. Then the following adjunction

is a Quillen adjunction. Here the left hand side has the induced CSS model structure (Definition A.5) and the right hand side has the covariant model structure.
This implies that the covariant model structure over X is a localization of the induced CSS model structure over X.
Proof
We want to prove that the left adjoint preserves cofibrations and trivial cofibrations. Clearly it preserves cofibrations as they are just the monomorphisms. Let \(i: Y \rightarrow Z\) be a trivial CSS cofibration over X. Then, Theorem 5.1 gives us a Quillen equivalence

Thus, in particular, the counit map \(i_!i^*Z \rightarrow Z\) is a covariant equivalence over Z. However, we have \(i_!i^*(\textrm{id}_Z) = i: Y \rightarrow Z\), which means i is a covariant equivalence over Z. Finally, by Theorem 3.15, i is also a covariant equivalence over X. \(\square \)
Remark 5.12
Note that we can use the same proofs with the contravariant model structure to show that the contravariant model structure is a localization of the CSS model structure as well.
The result above has the following very important corollary.
Corollary 5.13
Every left (and right) fibration is a CSS fibration.
Remark 5.14
This result generalizes [19, Sect. 1.4], which proved that left fibrations over Segal spaces are CSS fibrations. Lurie proves the same result over an arbitrary simplicial set [42, Theorem 3.1.5.1], but relies on the straightening construction.
In Theorem 4.32 we proved that pulling back along right and left fibrations over a complete Segal space preserves CSS equivalences. Using the invariance theorem, Theorem 5.1, we can generalize this to arbitrary right and left fibrations.
Theorem 5.15
Let \(p:R \rightarrow X\) be a right or left fibration. Then the adjunction

is a Quillen adjunction. Here both sides have the induced CSS model structure (Proposition A.5).
Proof
We will assume that p is a right fibration, the case for left fibrations follows similarly.
In order to prove \((p^*,p_*)\) is a Quillen adjunction is suffices to prove \(p^*\) preserves cofibrations and trivial cofibrations. Evidently, \(p^*\) preserves cofibrations as they are just monomorphisms. Hence we are left with proving that for a given CSS equivalence \(Y \rightarrow Z\) over X, the map \(Y \times _X R \rightarrow Z \times _X R\) is a CSS equivalence over R.
First of all, observe that this property is invariant under Reedy equivalences, meaning if \(g:R \xrightarrow { \ \simeq \ } R'\) are Reedy equivalent fibrations over X, and pulling back along R preserves CSS equivalences, then so does pulling back along \(R'\). Indeed, for an arbitrary CSS equivalence \(f:Y \rightarrow Z\) over X we have the following diagram

The horizontal morphisms are Reedy equivalences, as the Reedy model structure is right proper and \(R \rightarrow X, R' \rightarrow X\) are fibrations [34, Proposition 13.3.9]. Hence, the left hand morphism is a CSS equivalence if and only if the right hand morphism is a CSS equivalence.
Now, let \(R \rightarrow X\) be a right fibration and fix a CSS fibrant replacement \(i: X \rightarrow \hat{X}\). Then, by Theorem 5.1, there is a Reedy equivalence of right fibrations \(R \rightarrow i^*\widehat{i_!R}\) over X, where \(\widehat{i_!R}\) is the contravariant fibrant replacement of \(i_!R \rightarrow \hat{X}\). So by the previous paragraph it suffices to show that pulling back along \(i^*R\widehat{i_!R} \rightarrow X\) preserves CSS equivalences.
In order to simplify notation we denote \(\widehat{i_!R} \rightarrow \hat{X}\) by \(\hat{R} \rightarrow \hat{X}\) and \(i^*R\widehat{i_!R} \rightarrow X\) by \(R \rightarrow X\) and notice we now have the following pullback square

Now, by the Beck-Chevalley condition for pullback squares, we have a natural isomorphism \(j_!p^* \cong \hat{p}^*i_!\) [25, 1.2]. By Proposition A.5, \(j_!\) reflects weak equivalences and so \(p^*\) preserves weak equivalences if and only if \(j_!p^*\) does, which, by the natural isomorphism is equivalent to \(\hat{p}^*i_!\) preserving weak equivalences. However, this follows directly from the fact that \(i_!\) always preserves weak equivalences and \(\hat{p}^*\) does so by Theorem 4.32. \(\square \)
The exact same proof can be used to prove the following theorem.
Theorem 5.16
Let \(p:R \rightarrow X\) be a right or left fibration. Then the adjunction

is a Quillen adjunction. Here both sides have the induced Segal space model structure (A.5).
Remark 5.17
This same result is stated in [39, Remark 11.10] in the language of quasi-categories, however without a proof.
The theorem has the following helpful corollary.
Corollary 5.18
Let \(X \rightarrow Y\) be a CSS equivalence and \(F \rightarrow Y\) either a right or left fibration over Y. Then the map \(X \times _Y F \rightarrow F\) is also a CSS equivalence.
This result is indeed helpful, as the CSS model structure is not right proper i.e. generally weak equivalences are not preserved by pullbacks along fibrations in the complete Segal space model structure. We can easily see this in the following example.
Example 5.19
The map \(G(2) \rightarrow F(2)\) is a Segal equivalence. Let \(F(1) \rightarrow F(2)\) be the unique map that takes 0 to 0 and 1 to 2. Note that this map is a CSS fibration but neither a left fibration nor a right fibration. Now the pullback
is clearly not a Segal equivalence as the left hand side is just \(F(0) \coprod F(0)\).
We will end this subsection with a generalization of Lemma 3.32 using Theorem 5.1. For that recall the classifying diagram  defined in Definition 2.24.
defined in Definition 2.24.
Proposition 5.20
Let  be a discrete Grothendieck opfibration. Then
be a discrete Grothendieck opfibration. Then  is a left fibration of complete Segal spaces.
is a left fibration of complete Segal spaces.
Proof
It follows from the same argument as in [58, Lemma 3.9] that  is a Reedy fibration. We now have a pullback diagram
is a Reedy fibration. We now have a pullback diagram

The horizontal morphisms are equivalences in the complete Segal space model structure (Proposition 2.25). Hence, by Theorem 5.1, the left hand morphism is a left fibration if and only if the right hand map is a left fibration. However, we established in Lemma 3.32 that the left hand morphism is a left fibration and so we are done. \(\square \)
6.2 Colimits, Cofinality and Quillen’s Theorem A
One intricate subject in the theory of \((\infty ,1)\)-categories is the study of limits and colimits. Accordingly, there are now many sources dedicated to the study of colimits of quasi-categories, such as [38, 42]. Thus if we are interested in understanding colimits in a complete Segal space, we can translate those results from quasi-categories to complete Segal spaces using the work of Joyal and Tierney [37], or specialize the model independent approach to colimits via \(\infty \)-cosmoi to the case of complete Segal spaces [65].
In Sect. we discussed how we want to understand whether results about \((\infty ,1)\)-categories, such as various results about their colimits, still hold if we drop the completeness condition. This cannot be directly translated from the corresponding results about quasi-categories or \(\infty \)-cosmoi and needs to be proven directly.
In this final section we will apply our knowledge about left fibrations of Segal spaces to prove several classical results about colimits in the context of Segal spaces. In particular, we prove that a cocone out of a diagram corresponds to a map out of its colimit (Theorem 5.29), that final maps give us equivalent colimits (Theorem 5.37), and Quillen’s theorem A for simplicial spaces (Theorem 5.40) and in particular Segal spaces (Corollary 5.41).
Remark 5.21
In this section we focus on using left fibrations to study colimits. We can analogously study limits via right fibrations.
Definition 5.22
Let X be a Segal space and \(p:K \rightarrow X\) be a map of simplicial spaces. We define the Segal space of cocones under K, denoted by \(X_{p/}\), as the pullback

where \(\Delta : X \rightarrow X^K\) is the map induced by the final map \(K \rightarrow F(0)\).
Remark 5.23
Recall that if X is a complete Segal space, then the underlying quasi-category of the under-complete Segal space \(i_1^*(W_{x/})\) is equivalent to the under-quasi-category \(i_1^*(W)_{x/}\) (as defined in [42, Proposition 1.2.9.2]), but not isomorphic (Remark 3.42). Again, by [42, Proposition 1.2.9.2], the same applies to the Segal space of cocones. Concretely, this means that if X is a complete Segal space and \(p: K \rightarrow X\) a morphism of simplicial spaces, then the equivalence of covariant model structures established in Appendix B implies an equivalence of left fibrations \(i_1^*(W_{p/}) \simeq i_1^*(W)_{i_1^*(p)/}\) although the constructions will not be isomorphic.
Example 5.24
If X is a Segal space and \(K = F(0)\) then p is determined by a choice of point x in X and we have \(X_{p/} = X_{x/}\), the Segal space of objects under x, as defined in Definition 3.41.
Lemma 5.25
Let X be a Segal space and \(p: K \rightarrow X\) be a map of simplicial spaces. The projection map
is a left fibration.
Proof
In the following pullback diagram

the right vertical map is a left fibration, by Theorem 3.44, and so the left vertical map must be a left fibration as well, as left fibrations are closed under pullbacks (Lemma 3.9). \(\square \)
Definition 5.26
Let X be a Segal space and \(p:K \rightarrow X\) a map of simplicial spaces. We say p has a colimit if the Segal space \(X_{p/}\) has an initial object (Definition 3.53).
Remark 5.27
This approach to colimits has already been studied for quasi-categories [42, Definition 1.2.13.4].
The next lemma can help us better understand the definition of a colimit.
Lemma 5.28
Let X be a Segal space and \(p: K \rightarrow X\) be a map of simplicial spaces. Then the following are equivalent:
-
(1)
p has a colimit.
-
(2)
There is a covariant equivalence \(\{ \sigma \}: F(0) \rightarrow X_{p/}\) over X.
-
(3)
There is a Reedy equivalence
$$\begin{aligned} X_{v/} \rightarrow X_{p/} \end{aligned}$$where v is an object in X.
Proof
\((1 \Rightarrow 2)\) If p is a colimit, then \(X_{p/}\) has an initial object \(\sigma \) which, by Definition 3.53, means \(\{ \sigma \}: F(0) \rightarrow X_{p/}\) is a covariant equivalence over X.
\((2 \Rightarrow 3)\) Assume we have a covariant equivalence \(\{ \sigma \}: F(0) \rightarrow X_{p/}\) over X and let \(\{ v \} = \pi \circ \{ \sigma \}: F(0) \rightarrow X\). Then the commutative square

has a lift. Indeed, \(X_{p/} \rightarrow X\) is a left fibration (Lemma 5.25) and so a fibration in the covariant model structure and \(F(0) \rightarrow X_{v/}\) is a covariant equivalence over X (Theorem 3.49). As the top and left hand maps are covariant equivalences over X, the map \(X_{v/} \rightarrow X_{p/}\) is also a covariant equivalence over X. Finally, as both \(X_{v/}\) and \(X_{p/}\) are left fibrations over X, the covariant equivalence is in fact a Reedy equivalence (Theorem 3.12).
\((3 \Rightarrow 1)\) By Theorem 3.55, \(X_{v/}\) has an initial object and so by the Reedy equivalence \(X_{p/}\) also has an initial object. \(\square \)
We call the object \(\sigma \) in \(X_{p/}\) the universal cocone and, by abuse of language, the object v in X the colimit.
For the remainder of this section we want to use our knowledge of left fibrations to study colimits of Segal spaces. First, we prove the Segal space analogue to the fact that maps out of a colimit are equivalent to maps of cocones.
Theorem 5.29
Let X be a Segal space and \(p: K \rightarrow X\) be a map of simplicial spaces and assume it has universal cocone \(\sigma : F(0) \rightarrow X_{p/}\) with colimit v. Then for any object y in X we have a natural equivalence
Proof
By Lemma 5.28, we have a Reedy equivalence \(X_{v/} \rightarrow X_{p/}\) over X. Fix an object \(y: F(0) \rightarrow X\), which gives us a point \(y: \Delta [0] \rightarrow X_0\). Then, using Definition 2.17, we get a Kan equivalence
and hence we are done. \(\square \)
We now move on to study computational aspects of colimits in Segal spaces. In particular, we introduce final maps and prove they give us equivalent colimits.
Definition 5.30
A map \(f: X \rightarrow Y\) is called final if f is a contravariant equivalence over Y. Similarly, \(f: X \rightarrow Y\) is called initial if f is a covariant equivalence over Y.
Remark 5.31
The notion of final maps of quasi-categories was first studied in [38, 8.11]. They also have been studied by Lurie [42, Definition 4.1.1.1] where they are called cofinal.
Initial and final maps are a generalization of initial and final objects.
Example 5.32
A map \(\{x\}: F(0) \rightarrow X\) is initial in the sense of Definition 5.30 if and only if the object x is initial in the sense of Definition 3.53.
Lemma 5.33
Let \(f: X \rightarrow Y\) be a map of simplicial spaces. The following are equivalent:
-
(1)
f is a final map.
-
(2)
For any map \(g:Y \rightarrow Z\) the map f is a contravariant equivalence over Z.
-
(3)
For any right fibration \(R \rightarrow Y\) the induced map
$$\begin{aligned} \textrm{Map}_{/Y}(Y,R) \rightarrow \textrm{Map}_{/Y}(X,R) \end{aligned}$$is a Kan equivalence.
Proof
(1 \(\Rightarrow \) 2) As \(f: X \rightarrow Y\) is a covariant equivalence over Y, \(g_!(X \rightarrow Y)\) is a covariant equivalence over Z (Theorem 3.15).
(2 \(\Rightarrow \) 1) This is just a special case where \(g = \textrm{id}_Y\).
(1 \(\Leftrightarrow \) 3) Follows from the definition of contravariant equivalence (Theorem 3.12). \(\square \)
Remark 5.34
Although final maps are defined as certain contravariant equivalences, they do not always behave similar to weak equivalences in the model categorical sense. In particular, they do not satisfy the 2-out-of-3 property. For example, in the chain
the map \(< 0,0>\) and the composition \(< 0>\) are final, but \(< 0 >: F(0) \rightarrow F(1)\) is not.
Corollary 5.35
If \(f:X \rightarrow Y\) is a CSS equivalence then it is final.
Proof
This follows directly from Theorem 5.11. \(\square \)
Before we move on let us note that this gives us one exception to Remark 5.34.
Lemma 5.36
Let \(X \xrightarrow { \ f \ } Y \xrightarrow { \ g \ } Z\) be a chain of maps such that g is a CSS equivalence. Then f is a final map if and only if gf is a final map.
Proof
First note that g is a final map. So, if f is final then it is a contravariant equivalence over Z (Lemma 5.33) and so the composition gf is also a covariant equivalence over Z, which by definition means it is final.
On the other side, let us assume \(gf= g_!(f)\) is a final map. Then, by Theorem 5.1, the following adjunction is a Quillen equivalence:

which implies that \(f: X \rightarrow Y\) is a contravariant equivalence over Y if and only if \(g_!(f): X \rightarrow Y\) is a contravariant equivalence over Z, and so f is a final map as well. \(\square \)
Having discussed final maps we can now show how it allows us to simplify colimit diagrams.
Theorem 5.37
Let \(g: A \rightarrow B\) be a final map and X be a Segal space. Then for any map \(f:B \rightarrow X\) the induced map
is a Reedy equivalence.
Proof
Fix an object x in the Segal space X. Using adjunctions between products and exponentials, we have the following isomorphism
Let \(\textrm{Map}^{res}(F(1) \times B,X)\) be the full subspace of \(\textrm{Map}(F(1) \times B,X)\) consisting of maps \(H: F(1) \times B \rightarrow X\) such that \(H|_{\{0\}} = f: B \rightarrow X\) and \(H|_{\{1\}} = \{x\}: B \rightarrow X\). Then restricting the two isomorphisms in 5.38 gives us the isomorphisms
This isomorphism is natural is B and hence the map \(g: A \rightarrow B\) gives us a commutative diagram:

By the explanation above the vertical maps are isomorphisms. Moreover, \(X_{/x} \rightarrow X\) is a right fibration (Theorem 3.44) and so, by Definition 5.30, the bottom map is a Kan equivalence. Hence the top map is a Kan equivalence for every map \(x: F(0) \rightarrow X\). As \(g_*: X_{f/} \rightarrow X_{fg/}\) is a map of left fibrations over X, this implies that it is a Reedy equivalence (Theorem 4.35). \(\square \)
Notice, this statement has also been proven in the context of quasi-categories in [42, Proposition 4.1.1.7].
Corollary 5.39
Let X be a Segal space and \(g: A \rightarrow B\) be a final map of simplicial spaces. Then a map \(f: B \rightarrow X\) has a colimit if and only if \(gf: A \rightarrow X\) has a colimit and in that case they are equivalent objects in X.
We end this section by giving a useful criterion for classifying final maps of simplicial spaces, motivated by Quillen’s Theorem A [51].
Theorem 5.40
Let \(f: X \rightarrow Y\) be a map of simplicial spaces and \(\{L_y \rightarrow Y\}_{\{y\}:F(0)\rightarrow Y}\) a collection of covariant fibrant replacements of \(\{y\}:F(0) \rightarrow Y\). The following are equivalent:
-
(1)
f is a final map.
-
(2)
For any \(y:F(0) \rightarrow Y\), the simplicial space \(L_y \times _Y X\) is diagonally contractible.
Proof
By Theorem 4.41, \(f:X \rightarrow Y\) is a contravariant equivalence over Y if and only if
is a diagonal equivalence for all \(y: F(0) \rightarrow Y\). By assumption \(F(0) \rightarrow L_y\) is a covariant equivalence over Y and thus, by Theorem 3.17, a diagonal equivalence. Hence, \(L_y \times _Y f\) is a diagonal equivalence if and only if \(L_y \times _Y X\) is diagonally contractible. \(\square \)
In the case of Segal spaces we can simplify the statement.
Corollary 5.41
Let Y be a Segal space and \(f: X \rightarrow Y\) be a map of simplicial spaces. Then f is final if and only if for every object y in Y the simplicial space \(Y_{y/} \times _Y X\) is diagonally contractible.
Remark 5.42
This result was proven for quasi-categories in [42, Theorem 4.1.3.1] where it is attributed to Joyal. Thus, Corollary 5.41 generalizes Quillen’s theorem A to Segal spaces.
Availability of Data and Materials
Data sharing not applicable to this article as no datasets were generated or analysed during the current study.
Notes
More precisely, type theoretic constructors are invariant under identities, which by the univalence axiom correspond to equivalences.
Left fibrations are a special case of coCartesian fibrations, which themselves can be thought of as \((\infty ,1)\)-categorical analogues of general Grothendieck opfibrations.
References
Ayala, D., Francis, J.: Flagged higher categories. In: Topology and Quantum Theory in Interaction, vol. 718 of Contemp. Math., pp. 137–173. American Mathematical Society, Providence, RI (2018)
Barwick, Cl.: (infinity, n)-Cat as a closed model category. ProQuest LLC. Ann Arbor, MI (2005). Thesis (Ph.D.)–University of Pennsylvania
Bergner, J.E.: A model category structure on the category of simplicial categories. Trans. Am. Math. Soc. 359(5), 2043–2058 (2007)
Bergner, J.E.: A survey of \((\infty ,1)\)-categories. In: Towards Higher Categories, vol. 152 of IMA Vol. Math. Appl., pp. 69–83. Springer, New York (2010)
Bergner, J.E.: A survey of models for \((\infty , n)\)-categories. Handbook of Homotopy Theory, edited by Haynes Miller, Chapman & Hall/CRC, pp. 263–295 (2020)
Bergner, J.E.: The homotopy theory of \((\infty , 1)\)-categories. London Mathematical Society Student Texts, vol. 90. Cambridge University Press, Cambridge (2018)
Bergner, J.E.: Three models for the homotopy theory of homotopy theories. Topology 46(4), 397–436 (2007)
Bergner, J.E., Rezk, C.: Comparison of models for \((\infty , n)\)-categories. I. Geom. Topol. 17(4), 2163–2202 (2013)
Bergner, J.E., Rezk, C.: Comparison of models for \((\infty , n)\)-categories. II. J. Topol. 13(4), 1554–1581 (2020)
Bergner, J.E., Osorno, A.M., Ozornova, V., Rovelli, M., Scheimbauer, C.I.: 2-Segal sets and the Waldhausen construction. Topology Appl. 235, 445–484 (2018)
Boardman, J.M., Vogt, R.M.: Homotopy Invariant Algebraic Structures on Topological Spaces. Lecture Notes in Mathematics, vol. 347. Springer, Berlin (1973)
Buchholtz, U., Weinberger, J.: Synthetic fibered \((\infty ,1)\)-category theory. arXiv preprint (2021). arXiv:2105.01724
Calaque, D., Scheimbauer, C.: A note on the \((\infty, n)\)-category of cobordisms. Algebr. Geom. Topol. 19(2), 533–655 (2019)
Campion, T., Kapulkin, K., Maehara, Y.: Comical sets: a cubical model for \((\infty ,n)\)-categories. arXiv preprint (2020). arXiv:2005.07603v2
Cisinski, D.-C.: Batanin higher groupoids and homotopy types. In: Categories in Algebra, Geometry and Mathematical Physics, vol. 431 of Contemp. Math., pp. 171–186. American Mathematical Society, Providence, RI (2007)
Cisinski, D.-C.: Higher categories and homotopical algebra. Cambridge Studies in Advanced Mathematics, vol. 180. Cambridge University Press, Cambridge (2019)
Conduché, F.: Au sujet de l’existence d’adjoints à droite aux foncteurs “image réciproque’’ dans la catégorie des catégories. C. R. Acad. Sci. Paris Sér. A-B 275, A891–A894 (1972)
de Brito, P.B., Moerdijk, I.: Dendroidal spaces, \(\Gamma \)-spaces and the special Barratt–Priddy–Quillen theorem. J. Reine Angew. Math. 760, 229–265 (2020)
de Brito, P.B.: Segal objects and the Grothendieck construction. In: An Alpine Bouquet of Algebraic Topology, vol. 708 of Contemp. Math., pp 19–44. American Mathematical Society, Providence, RI (2018)
Dugger, D.: Universal homotopy theories. Adv. Math. 164(1), 144–176 (2001)
Dwyer, W.G., Spalinski, J.: Homotopy theories and model categories. Handb. Algebraic Topol. 73, 126 (1995)
Dyckerhoff, T., Kapranov, M.: Higher Segal spaces. Lecture Notes in Mathematics, vol. 2244. Springer, Cham (2019)
Gálvez-Carrillo, I., Kock, J., Tonks, A.: Corrigendum to Decomposition spaces, incidence algebras and Möbius inversion II: completeness, length filtration, and finiteness. [Adv. Math. 333 (2018) 1242–1292]. Adv. Math., 371, 107267 (2020)
Gálvez-Carrillo, I., Kock, J., Tonks, A.: Decomposition spaces, incidence algebras and Möbius inversion I: basic theory. Adv. Math. 331, 952–1015 (2018)
Gambino, N., Kock, J.: Polynomial functors and polynomial monads. Math. Proc. Camb. Philos. Soc. 154(1), 153–192 (2013)
Goerss, P.G., Jardine, J.F.: Simplicial homotopy theory. Modern Birkhäuser Classics. Birkhäuser Verlag, Basel (2009). Reprint of the 1999 edition [MR1711612]
Gray, J.W.: Fibred and cofibred categories. In: Proceedings of Conference Categorical Algebra (La Jolla, Calif., 1965), pp. 21–83. Springer, New York (1966)
Grothendieck, A.: Revêtements étales et groupe fondamental. Institut des Hautes Études Scientifiques, Paris, 1963. Troisième édition, corrigée, Séminaire de Géométrie Algébrique (1960/61)
Hackney, P., Kock, J.: Culf maps and edgewise subdivision. arXiv preprint (2022). arXiv:2210.11191
Hebestreit, F., Heuts, G., Ruit, J.: A short proof of the straightening theorem. arXiv preprint (2021). arXiv:2111.00069
Heuts, G., Moerdijk, I.: Left fibrations and homotopy colimits II. arXiv preprint (2016). arXiv:1602.01274v1
Heuts, G., Moerdijk, I.: Simplicial and Dendroidal Homotopy Theory. 2022. To appear in Ergebnisse der Mathematik
Heuts, G., Moerdijk, I.: Left fibrations and homotopy colimits. Math. Z. 279(3–4), 723–744 (2015)
Hirschhorn, P.S.: Model Categories and their Localizations. Mathematical Surveys and Monographs, vol. 99. American Mathematical Society, Providence, RI (2003)
Hovey, M.: Model Categories. Mathematical Surveys and Monographs, vol. 63. American Mathematical Society, Providence, RI (1999)
Johnstone, P.T.: Sketches of an Elephant: A Topos Theory Compendium. Vol. 1, vol. 43 of Oxford Logic Guides. The Clarendon Press, Oxford University Press, New York (2002)
Joyal, A., Tierney, M.: Quasi-categories vs Segal spaces. In: Categories in algebra, geometry and mathematical physics, volume 431 of Contemp. Math., pp. 277–326. American Mathematical Society, Providence, RI (2007)
Joyal, A.: Notes on quasi-categories. preprint (2008). https://www.math.uchicago.edu/~may/IMA/Joyal.pdf. Accessed 08 Feb 2021
Joyal, A.: The theory of quasi-categories and its applications (2008). https://mat.uab.cat/~kock/crm/hocat/advanced-course/Quadern45-2.pdf. Accessed 08 Feb 2021
Kazhdan, D., Varshavskiĭ, Y.: The Yoneda lemma for complete Segal spaces. Funktsional. Anal. i Prilozhen. 48(2), 3–38 (2014)
Kelly, G.M.: Basic Concepts of Enriched Category Theory. London Mathematical Society Lecture Note Series, vol. 64. Cambridge University Press, Cambridge, New York (1982)
Lurie, J.: Higher Topos Theory. Annals of Mathematics Studies, vol. 170. Princeton University Press, Princeton (2009)
Lurie, J.: On the classification of topological field theories. In: Current Developments in Mathematics, 2008, pp. 129–280. Int. Press, Somerville, MA (2009)
Mac Lane, S., Moerdijk, I.: Sheaves in geometry and logic. Universitext. Springer, New York, (1994). A first introduction to topos theory, Corrected reprint of the (1992) edition
Mac Lane, S.: Categories for the Working Mathematician, vol. 5 of Graduate Texts in Mathematics, second edition. Springer, New York (1998)
Martínez, C.B.: Limits and colimits of synthetic \(\infty \)-categories. arXiv preprint (2022). arXiv:2202.12386
Martini, L.: Yoneda’s lemma for internal higher categories. arXiv preprint (2021). arXiv:2103.17141
Moerdijk, I.: Bisimplicial sets and the group-completion theorem. In: Algebraic \(K\)-Theory: Connections with Geometry and Topology (Lake Louise, AB, 1987), vol. 279 of NATO Adv. Sci. Inst. Ser. C: Math. Phys. Sci., pp. 225–240. Kluwer Acad. Publ., Dordrecht (1989)
Nguyen, H.K.: Covariant and contravariant homotopy theories. arXiv preprint, (2019). arXiv:1908.06879v1
Nuiten, J.: On straightening for Segal spaces. arXiv preprint (2021). arXiv:2108.11431
Quillen, D.: Higher algebraic \(K\)-theory. I. In: Algebraic \(K\)-Theory, I: Higher \(K\)-Theories (Proc. Conf., Battelle Memorial Inst., Seattle, Wash., 1972), pp. 85–147. Lecture Notes in Math., Vol. 341 (1973)
Rasekh, N.: Cartesian fibrations of complete Segal spaces. High. Struct. 7(1), 40–73 (2023)
Rasekh, N.: Quasi-categories vs. Cartesian edition. J. Homotopy Relat. Struct, Segal spaces (2021)
Rasekh, N.: Yoneda lemma for \(\cal{D}\)-simplicial spaces. arXiv preprint (2021). arXiv:2108.06168
Rasekh, N.: Cartesian fibrations and representability. Homology Homotopy Appl. 24(2), 135–161 (2022)
Reedy, C.L.: Homology of algebraic theories. ProQuest LLC, Ann Arbor, MI (1974). Thesis (Ph.D.)–University of California, San Diego
Rezk, C.: Stuff about quasicategories (2017). http://www.math.illinois.edu/rezk/595-fal16/quasicats.pdf
Rezk, C.: A model for the homotopy theory of homotopy theory. Trans. Am. Math. Soc. 353(3), 973–1007 (2001)
Rezk, C.: Every homotopy theory of simplicial algebras admits a proper model. Topology Appl. 119(1), 65–94 (2002)
Rezk, C.: A Cartesian presentation of weak \(n\)-categories. Geom. Topol. 14(1), 521–571 (2010)
Rezk, C., Schwede, S., Shipley, B.: Simplicial structures on model categories and functors. Am. J. Math. 123(3), 551–575 (2001)
Riehl, E., Verity, D.: Elements of \(\infty \)-Category Theory. Cambridge Studies in Advanced Mathematics. Cambridge University Press (2022)
Riehl, E.: Categorical Homotopy Theory. New Mathematical Monographs, vol. 24. Cambridge University Press, Cambridge (2014)
Riehl, E., Shulman, M.: A type theory for synthetic \(\infty \)-categories. High. Struct. 1(1), 147–224 (2017)
Riehl, E., Verity, D.: Fibrations and Yoneda’s lemma in an \(\infty \)-cosmos. J. Pure Appl. Algebra 221(3), 499–564 (2017)
Stenzel, R.: Univalence and completeness of segal objects. J. Pure Appl. Algebra 227(4), 107254 (2023)
Stevenson, D.: Covariant model structures and simplicial localization. North-West. Eur. J. Math. 3, 141–203 (2017)
Streicher, T.: Fibred categories à la jean bénabou. arXiv preprint (2018). arXiv:1801.02927v11
The Univalent Foundations Program. Homotopy Type Theory: Univalent Foundations of Mathematics. https://homotopytypetheory.org/book, Institute for Advanced Study (2013)
Verity, D.R.B.: Weak complicial sets. I. Basic homotopy theory. Adv. Math. 219(4), 1081–1149 (2008)
Weinberger, J.: A synthetic perspective on \((\infty ,1)\)-category theory: fibrational and semantic aspects. arXiv preprint (2022). arXiv:2202.13132
Acknowledgements
I want to thank my advisor Charles Rezk who has guided me through every step of the work. I want to in particular thank him for many helpful remarks on previous drafts. I also want to thank Matt Ando for many fruitful conversations and suggestions. Moreover, I want to thank the first referee for many helpful comments and suggestions on how to improve and simplify the theorems. Finally, I want to sincerely thank the second referee for several very extensive lists of comments that have significantly improved the results and presentation.
Funding
Open Access funding enabled and organized by Projekt DEAL. No funding was received to assist with the preparation of this manuscript. The author did not receive support from any organization for the submitted work.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors have no relevant financial or non-financial interests to disclose.
Additional information
Communicated by Nicola Gambino.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: Some Facts about Model Categories
We primarily used the theory of model categories to tackle issues of higher category theory. In this section we will not introduce model categories as there are already several excellent sources. For instance, we refer the reader to [21] for a short introduction to this subject and to [34, 35] for a more detailed discussion. Here we will only state some technical lemmas we have used throughout.
First, we make ample use of the following very classical result about trivial Kan fibrations.
Lemma A.1
Let \(p: S \rightarrow T\) be a Kan fibration in  . Then p is a trivial Kan fibration if and only if each fiber of p is contractible.
. Then p is a trivial Kan fibration if and only if each fiber of p is contractible.
For a readable proof of this statement see [57, Sect. 38]. This lemma has the following important corollary.
Corollary A.2
Let \(p:S \rightarrow K\) and \(q:T \rightarrow K\) be two Kan fibrations. A map \(f: S \rightarrow T\) over K is a Kan equivalence if and only if for each point \(\{ k \}: \Delta [0] \rightarrow K\) the map between fibers
is a Kan equivalence.
Next we have two important results that help us study Quillen adjunctions.
Lemma A.3
( [37, Proposition 7.15], [34, Proposition 8.5.4]) Let \(\mathcal {M}\) and \(\mathcal {N}\) be two model categories and

be an adjunction of model categories, then the following are equivalent:
-
(1)
(F, G) is a Quillen adjunction.
-
(2)
F takes cofibrations to cofibrations and G takes fibrations between fibrant objects to fibrations.
-
(3)
G preserves trivial fibrations and takes fibrations between fibrant objects to fibrations.
Lemma A.4
(Special case of [37, Proposition 7.17, Proposition 7.22]) Let

be a Quillen adjunction of model categories. Then the following are equivalent:
-
(1)
(F, G) is a Quillen equivalence.
-
(2)
F reflects weak equivalences between cofibrant objects and the derived counit map \(FLG(n) \rightarrow n\) is an equivalence for every fibrant-cofibrant object \(n \in \mathcal {N}\) (Here LG(n) is a cofibrant replacement of G(n) inside \(\mathcal {M}\)).
-
(3)
G reflects weak equivalences between fibrant objects and the derived unit map \(m \rightarrow GRF(m)\) is an equivalence for every fibrant-cofibrant object \(m \in \mathcal {M}\) (Here RF(m) is a fibrant replacement of F(m) inside \(\mathcal {N}\)).
We move on to the main topic of this appendix, namely the existence of two localized model structures on the category of simplicial spaces over a fixed simplicial space and their comparison.
Proposition A.5
[34, Theorem 7.6.5] Let \(\mathcal {M}\) be a model structure on  . Let X be a simplicial space. There is a simplicial model structure on
. Let X be a simplicial space. There is a simplicial model structure on  , which we call the induced model structure and denote by
, which we call the induced model structure and denote by  , and which satisfies the following conditions:
, and which satisfies the following conditions:
- (F):
-
A map \(f: Y \rightarrow Z\) over X is a (trivial) fibration if \(Y \rightarrow Z\) is a (trivial) fibration in \(\mathcal {M}\).
- (W):
-
A map \(f:Y \rightarrow Z\) over X is a weak equivalence if \(Y \rightarrow Z\) is a weak equivalence in \(\mathcal {M}\).
- (C):
-
A map \(f:Y \rightarrow Z\) over X is a (trivial) cofibration if \(Y \rightarrow Z\) is a (trivial) cofibration in \(\mathcal {M}\).
Remark A.6
The induced model structure can be defined for any model category and not just for model structures on  , but for our work there is no need for further generality.
, but for our work there is no need for further generality.
Theorem A.7
Let X be a simplicial space and \(\mathcal {L}\) be a set of monomorphisms in  . There exists a cofibrantly generated, simplicial model category structure on
. There exists a cofibrantly generated, simplicial model category structure on  with the following properties:
with the following properties:
-
(1)
The cofibrations are exactly the monomorphisms.
-
(2)
The fibrant objects (called \(\mathcal {L}\)-local objects) are exactly the Reedy fibrations
 such that $$\begin{aligned} \textrm{Map}_{/X}(B, W) \rightarrow \textrm{Map}_{/X}(A, W) \end{aligned}$$
such that $$\begin{aligned} \textrm{Map}_{/X}(B, W) \rightarrow \textrm{Map}_{/X}(A, W) \end{aligned}$$is a weak equivalence of spaces for all maps \(f: A \rightarrow B\) over X in \(\mathcal {L}\).
-
(3)
The weak equivalences (called \(\mathcal {L}\)-local weak equivalences) are exactly the maps \(g: Y \rightarrow Z\) over X such that for every \(\mathcal {L}\)-local object \(W\rightarrow X\), the induced map
$$\begin{aligned} \textrm{Map}_{/X}(Z, W) \rightarrow \textrm{Map}_{/X}(Y, W) \end{aligned}$$is a weak equivalence.
-
(4)
Let \(f: Y \rightarrow Z\) be a map over X.
-
If f is a Reedy weak equivalence over X then it is a \(\mathcal {L}\)-local weak equivalence.
-
If f is a \(\mathcal {L}\)-local fibration then it is a Reedy fibration.
The opposite of both statements hold if Y and Z are \(\mathcal {L}\)-local.
-
We call this model category the localized model structure.
The model structure is given as the left Bousfield localization of the induced Reedy model structure on  . For a careful and detailed proof of the existence of left Bousfield localizations see [34, Theorem 4.1.1] (notice we are using the fact that the induced Reedy model structure on
. For a careful and detailed proof of the existence of left Bousfield localizations see [34, Theorem 4.1.1] (notice we are using the fact that the induced Reedy model structure on  is proper and cellular [34, Proposition 12.1.6]). For a nice summary of this proof that goes over the main steps see [58, Proposition 9.1].
is proper and cellular [34, Proposition 12.1.6]). For a nice summary of this proof that goes over the main steps see [58, Proposition 9.1].
Remark A.8
Notice, we can in particular take X to be the final object in which case the theorem gives us a localization model structure of the Reedy model structure on  .
.
Note any such model structure is invariant under Reedy equivalences.
Lemma A.9
Let \(\mathcal {L}\) be a set of monomorphisms in  and let \(f: X \rightarrow Y\) be a map of simplicial spaces. Then the adjunction
and let \(f: X \rightarrow Y\) be a map of simplicial spaces. Then the adjunction

is a Quillen adjunction which is a Quillen equivalence if f is a Reedy equivalence. Here the left hand side has the localization model structure with respect to maps \(A \rightarrow B \rightarrow X\) for all maps \(A \rightarrow B\) in \(\mathcal {L}\) and the right hand side has the localization model structure with respect to maps \(A \rightarrow B \rightarrow Y\) for all maps \(A \rightarrow B\) in \(\mathcal {L}\).
Proof
First we use Lemma A.3 to prove it is a Quillen adjunction. Clearly the left adjoint \(f_!\) preserves monomorphisms and thus cofibrations. On the other hand, fibrations between fibrant objects are just Reedy fibrations, which are preserved by \(f^*\). Thus we only need to prove that \(f^*\) preserves fibrant objects. However, the fibrant objects are just Reedy fibrations which satisfy the right lifting property with respect to maps \(A \rightarrow B\) in \(\mathcal {L}\) and the class of such maps is clearly closed under pullback.
Next we assume that f is a Reedy equivalence and prove that the adjunction is a Quillen equivalence. We will prove that the derived unit and derived counit maps are equivalences. Before we can analyze the derived unit map we need to better understand fibrant replacements. Let \(p: Z \rightarrow X\) be a fibrant object (meaning p is a local Reedy fibration) and let \(Z \xrightarrow { \ i \ } \hat{Z} \xrightarrow { \ \widehat{f_!(p)} \ } Y\) be a Reedy fibrant replacement of \(f_!(p):Z \rightarrow Y\). As p and \(\widehat{f_!(p)}\) are Reedy equivalent and p is local, it follows that \(\widehat{f_!(p)}\) is a local fibration as well, meaning that \(i: Z \rightarrow \hat{Z}\) is in fact already a fibrant replacement in the localized Reedy model structure.
Now, the derived unit map, \(f^*Rf_!\), is given by taking the fibrant replacement in the localized model structure of the map \(Z \rightarrow X \rightarrow Y\) in  and then pulling it back along \(f: X \rightarrow Y\). This can be depicted as the following diagram:
and then pulling it back along \(f: X \rightarrow Y\). This can be depicted as the following diagram:

where (as we explained in the previous paragraph) \(i: Z \rightarrow \hat{Z}\) is taken to be the Reedy fibrant replacement. The map \(f^*\hat{Z} \rightarrow \hat{Z}\) is a Reedy equivalence as Reedy equivalences are preserved by pullbacks along fibrations. Thus, by 2-out-of-3, the derived unit map \(u: Z \rightarrow f^*\hat{Z}\) is a Reedy weak equivalence.
We move on to the derived counit map. As all objects are cofibrant the derived counit map is simply given by the actual counit map. Let \(W \rightarrow Y\) be a fibrant object (meaning a fibration). Then we have the diagram

As the Reedy model structure is right proper (Sect. 2.4) and thus Reedy weak equivalences are preserved by pullback, the counit map \(f^*W \rightarrow W\) is a Reedy equivalence and so also an equivalence in the localized model structure (Theorem A.7). \(\square \)
Our precise understanding of the fibrant objects in the localized model structure allows us to simplify the conditions in Lemma A.3.
Corollary A.10
Let X be a simplicial space and let  and
and  be two localized model structures of the induced Reedy model structure. Then an adjunction
be two localized model structures of the induced Reedy model structure. Then an adjunction

is a Quillen adjunction if it satisfies the following conditions:
-
(1)
F takes cofibrations to cofibrations.
-
(2)
G takes fibrant objects to fibrant objects.
-
(3)
G takes Reedy fibrations to Reedy fibrations.
Remark A.11
Let X be a simplicial space and \(\mathcal {L}\) be a set of monomorphisms over X. Then we can construct two model structures on  using \(\mathcal {L}\):
using \(\mathcal {L}\):
-
(1)
Using Theorem A.7 we can construct a localized model structure on the induced model structure
 . This is the localized model structure on
. This is the localized model structure on  .
. -
(2)
We can project \(\mathcal {L}\) to
 to get a set of monomorphisms in
to get a set of monomorphisms in  and then use Theorem A.7 to construct a localized model structure on
and then use Theorem A.7 to construct a localized model structure on  and finally take the induced model structure on
and finally take the induced model structure on  . We call this the induced localized model structure on
. We call this the induced localized model structure on  .
.
We want to understand how these two model structures compare to each other. Before we can do that we need a precise characterization of the fibrant objects in the localized model structure on  in terms of the Reedy model structure on
in terms of the Reedy model structure on  .
.
Lemma A.12
Let X be a simplicial space and \(\mathcal {L}\) a set of monomorphisms. An object \(p: Y \rightarrow X\) in  is fibrant in the localized model structure if and only if it is a Reedy fibration and for every morphism \(f: A \rightarrow B\) in \(\mathcal {L}\) the commutative square
is fibrant in the localized model structure if and only if it is a Reedy fibration and for every morphism \(f: A \rightarrow B\) in \(\mathcal {L}\) the commutative square

is a homotopy pullback square of spaces.
Proof
The square is a homotopy pullback square if and only if the horizontal map below is an equivalence

By Corollary A.2, this is equivalent to proving that for each map \(g: B \rightarrow X\) the induced map
is an equivalence, which is exactly the condition of being fibrant in the localized model structure (Theorem A.7). \(\square \)
Theorem A.13
Let X be a simplicial space and \(\mathcal {L}\) be a set of monomorphisms in  . Then the adjunction
. Then the adjunction

is a Quillen adjunction, which is a Quillen equivalence if X is fibrant in the localized model structure. In fact, in this case the two model structures are isomorphic. Here the left hand side has the localized model structure and the right hand side has the induced localized model structure (Remark A.11).
Proof
Both sides have the same set of cofibrations. By [42, Corollary A.3.7.2], in order to finish the proof it suffices to show that every fibrant object in the induced localized model structure on  is fibrant in the localized model structure on
is fibrant in the localized model structure on  and that the opposite holds if X is fibrant in the localized model structure.
and that the opposite holds if X is fibrant in the localized model structure.
Let \(p: Y \rightarrow X\) be a Reedy fibration and \(f: A \rightarrow B\) a morphism in \(\mathcal {L}\). Then we have the following diagram:

If p is fibrant in the induced localized model structure on  , then the square above is a homotopy pullback square as the induced localized model structure on
, then the square above is a homotopy pullback square as the induced localized model structure on  is a simplicial model structure and \(f: A \rightarrow B\) is a trivial cofibration in the localized model structure on
is a simplicial model structure and \(f: A \rightarrow B\) is a trivial cofibration in the localized model structure on  . However, by Lemma A.12, this is equivalent to \(p: Y \rightarrow X\) being fibrant in the localized model structure on
. However, by Lemma A.12, this is equivalent to \(p: Y \rightarrow X\) being fibrant in the localized model structure on  . This finishes one side and proves the adjunction above is a Quillen adjunction.
. This finishes one side and proves the adjunction above is a Quillen adjunction.
On the other hand, let us assume X is fibrant in the localized model structure on  and \(p: Y \rightarrow X\) is fibrant in the localized model structure on
and \(p: Y \rightarrow X\) is fibrant in the localized model structure on  . The fibrancy of \(p: Y \rightarrow X\) implies, again by Lemma A.12, that the square
. The fibrancy of \(p: Y \rightarrow X\) implies, again by Lemma A.12, that the square

is a homotopy pullback square for all morphisms \(f: A \rightarrow B\) in \(\mathcal {L}\) and the fibrancy of X implies the bottom map is a Kan equivalence. Hence the top map is a Kan equivalence as well. This means that Y is fibrant in the localized model structure on  . Thus, by Theorem A.7, the map \(p: Y \rightarrow X\) is a fibration in the localized model structure on
. Thus, by Theorem A.7, the map \(p: Y \rightarrow X\) is a fibration in the localized model structure on  , as Reedy fibrations between fibrant objects are fibrations in the localized model structure. \(\square \)
, as Reedy fibrations between fibrant objects are fibrations in the localized model structure. \(\square \)
Appendix B: Comparison with Quasi-Categories
In this part we confirm that the covariant model structure on simplicial sets coincides with the covariant model structure on simplicial spaces, by proving they are Quillen equivalent, via two different Quillen equivalences.
The trick is to realize that the Quillen equivalences between the model structure for quasi-categories (which we will henceforth call the Joyal model structure) and the model structure for complete Segal spaces constructed by Joyal and Tierney [37] descend to Quillen equivalences between their respective covariant model structures.
We will thus start by giving a quick review of the relevant results in [37] and review the relevant definitions of the covariant model structure on simplicial sets. We will only focus on specific results that we need in this section and refer the reader to the vast literature for any details [33, 42].
Notation B.1
This section focuses on the interaction between complete Segal spaces and quasi-categories and more specifically relies on [37]. We will hence use different notation in this section alone to match existing literature. Concretely, we use the following notation:
-
We use
 for the Joyal model structure on the category of simplicial sets (with fibrant objects quasi-categories) and, for a given simplicial set S, use the notation
for the Joyal model structure on the category of simplicial sets (with fibrant objects quasi-categories) and, for a given simplicial set S, use the notation  for the covariant model structure on simplicial sets over S (defined in Definition B.3).
for the covariant model structure on simplicial sets over S (defined in Definition B.3). -
Following the notation in [37, Sect. 2] we denote
 defined as \(p_1([n],[m])=[n]\) and
defined as \(p_1([n],[m])=[n]\) and  defined as \(i_1([n]) = ([n],[0])\).
defined as \(i_1([n]) = ([n],[0])\).
Definition B.2
[42, Definition 2.0.0.3] A map \(f:S \rightarrow T\) of simplicial sets is a left fibration if it satisfies the right lifting property with respect to all horn conclusions of the form \(\displaystyle \Lambda ^n_i \rightarrow \Delta [n]\), where \( 0 \le i < n\).
Definition B.3
[42, Definition 2.1.4.5, Proposition 2.1.4.7, Proposition 2.1.4.8] Let S be a simplicial set. There is a left proper, combinatorial, simplicial model structure on  , called the covariant model structure and denoted by
, called the covariant model structure and denoted by  , which satisfies the following conditions:
, which satisfies the following conditions:
-
(1)
A map \(T \rightarrow U\) over S is a cofibration if it is a monomorphism.
-
(2)
The fibrant objects are the left fibrations
We can also characterize the fibrations between fibrant objects.
Corollary B.4
[42, Corollary 2.2.3.14] A map between left fibrations is a fibration in the covariant model structure if and only if it is a left fibration.
There are several important theorems about the covariant model structure we are going to need later on.
Theorem B.5
[42, Theorem 3.1.5.1] Let S be a simplicial set. Then the following adjunction

is a Quillen adjunction, where the left hand side has the Joyal model structure and the right hand side has the covariant model structure. This implies that the covariant model structure is a localization of the Joyal model structure.
Theorem B.6
[42, Proposition 2.1.4.10, Remark 2.1.4.11] Let \(f: S \rightarrow T\) be a map of simplicial sets. Then the adjunction

is a Quillen adjunction, which is a Quillen equivalence if f is a categorical equivalence. Here both sides have the covariant model structure.
We now move on to review the main results in [37]. We will hence use the notation given in [37, Sect. 2] instead of the notation we have used before. Concretely,  is given by \(p_1*([n],[m]) = [n]\)
is given by \(p_1*([n],[m]) = [n]\)
Theorem B.7
[37, Theorem 4.11] The functors \(p_1, i_1\) (Notation B.1) induce the following adjunction

which is a Quillen equivalence, where  has the Joyal model structure and
has the Joyal model structure and  has the CSS model structure.
has the CSS model structure.
Theorem B.8
[37, Theorem 4.12] Let  be the left Kan extension of the map which is defined on the generators \(F(n) \times \Delta [l]\) as \(t_!(F(n) \times \Delta [l]) = \Delta [n] \times J[l]\). Let
be the left Kan extension of the map which is defined on the generators \(F(n) \times \Delta [l]\) as \(t_!(F(n) \times \Delta [l]) = \Delta [n] \times J[l]\). Let  be the right adjoint of this construction, i.e.
be the right adjoint of this construction, i.e.  . Then this defines a Quillen equivalence
. Then this defines a Quillen equivalence

with  having the CSS model structure and
having the CSS model structure and  having the Joyal model structure.
having the Joyal model structure.
The two adjunctions \((p_1^*,i_1^*)\), \((t_!,t^!)\) do interact well with each other.
Lemma B.9
[37, Proposition 4.10] Let S be a quasi-category. Then the natural map
is an equivalence in the CSS model structure.
There is an analogous statement for complete Segal spaces.
Lemma B.10
Let X be a complete Segal space, then the natural map
induced by applying \(t_!\) to the counit map \(p_1^*i_1^*X \rightarrow X\) and using \(t_!p_1^* = id\) is a categorical equivalence.
We now move on to the main topic of this section: the two Quillen equivalences (Theorems B.12 and B.14).
Remark B.11
Let  be a category with pullbacks and let
be a category with pullbacks and let

be an adjunction of categories and C an object in  . Then we get an adjunction
. Then we get an adjunction

where the left adjoint takes a map \(f: D \rightarrow C\) to \(Ff: FD \rightarrow FC\) and the right adjoint takes a map \(f:D \rightarrow FC\) to the pullback \(u^*(G(f)): u^*G(D) \rightarrow C\), where \(u: C \rightarrow GFC\) is the unit map.
Theorem B.12
Let S be a simplicial set. The adjunction

is a Quillen equivalence, where both sides have the covariant model structure.
Proof
We break down the proof in several steps. In Lemma B.15 we prove the adjunction is a Quillen adjunction. Then, in Remark B.17 we reduce the proof of the Quillen equivalence to the case when S is a quasi-category. Finally, we show the Quillen adjunction is a Quillen equivalence when S is a quasi-category in Lemma B.18 and hence we are done. \(\square \)
Remark B.13
In the particular case where the base is of the form \(i_1^*X\), where X is a complete Segal space, the adjunction \((p_1^*,u^*i_1^*)\) has been shown to be a Quillen equivalence independently by de Brito [19, Theorem 1.22].
Theorem B.14
Let X be a simplicial space. The adjunction

is a Quillen equivalence, where both sides have the covariant model structure.
Proof
The proof involves several separate steps. In Lemma B.15 we prove the adjunction is a Quillen adjunction. Then, again in Remark B.17 we reduce the proof of the Quillen equivalence to the case when X is a complete Segal space. Finally, we show the Quillen adjunction is a Quillen equivalence when X is a complete Segal space in Lemma B.19 finishing the proof. \(\square \)
We start with the Quillen adjunctions.
Lemma B.15
Let S be a simplicial set. The adjunction

is a Quillen adjunction, where both sides have the covariant model structure.
Proof
We use Lemma A.3. Clearly, \(p_1^*\) takes cofibrations to cofibrations as they are just inclusions. So, all that is left is to show that \(u^*i_1^*\) takes fibrations between fibrant objects to fibrations. By Lemma 3.14 a fibration between fibrant objects is just a left fibration. Thus it suffices to prove that \(u^*i_1^*\) preserves left fibrations. The map \(u^*\) just pulls back along the unit, which preserves left fibrations, as it is given by a right lifting property (Definition B.2). So it suffices to prove that \(i_1^*\) preserves left fibrations.
Let \(p:L \rightarrow p_1^*S\) be a left fibration. We have to show that \(i_1^*(p)\) satisfies the right lifting property with respect to horns \(\Lambda [n]_i \rightarrow \Delta [n]\) where \(0 \le i < n\) (Definition B.2). Using the adjunction \((p_1^*,i_1^*)\) This is equivalent to p having the right lifting property with to the maps \(j: L(n)_i \rightarrow F(n)\), which means we have to prove j is a trivial cofibration in  with respect to the covariant model structure over \(p_1^*S\).
with respect to the covariant model structure over \(p_1^*S\).
From Corollary 4.22 and the fact that \(< 0,\ldots ,k > \times _{\textrm{id}_{F(n)}} j: F(k) \times _{F(n)} L(n)_i \rightarrow F(k)\) is a diagonal equivalence (both sides are diagonally contractible), we deduce that j is a covariant equivalence over F(n) and so is a covariant equivalence over \(p_1^*S\) as well (Theorem 3.15). \(\square \)
Lemma B.16
For a left fibration of simplicial sets \(p:L \rightarrow S\), \(t^!L \rightarrow t^!S\) is a left fibration of simplicial spaces. In particular, for every simplicial space X the adjunction

is a Quillen adjunction where both sides have the covariant model structure.
Proof
By Theorem B.5, \(p: L \rightarrow S\) is a fibration in the Joyal model structure and so \(t^!(p)\) is a CSS fibration, by Theorem B.8, and so in particular a Reedy fibration. Thus we only have to prove that for every map \(F(n) \rightarrow X\) the induced map
is a Kan equivalence. By adjunction, this is equivalent to proving that \(< 0 >: \Delta [0] = t_!(F(0)) \rightarrow t_!(F(n))= \Delta [n]\) is a covariant equivalence over \(t^!S\). However, it is a well-established fact that the map \(< 0 >: \Delta [0] \rightarrow \Delta [n]\) is a covariant equivalence over \(\Delta [n]\) and so in particular over S (by Theorem 3.15). For an elegant proof of this fact see [33, Lemma 2.5].
We now move on to the adjunction. We will show the adjunction satisfies the three conditions of Lemma A.3. Clearly, \(t_!\) takes cofibrations to cofibrations as they are just monomorphisms. Thus we only need to prove that \(u^*t^!\) preserves fibrant objects and fibrations between fibrant objects. By Corollary B.4, a fibration between fibrant objects is a left fibration, thus it suffices to prove that \(u^* t^!\) preserves left fibrations. By Lemma 3.9, it suffices to prove that \(t^!\) preserves left fibrations, which we established in the previous paragraph. \(\square \)
Next we will reduce the proof to the case of complete Segal spaces and quasi-categories.
Remark B.17
Let S be a simplicial set and choose a quasi-category fibrant replacement \(i:S \rightarrow \hat{S}\) and let X be a simplicial space and choose a complete Segal space fibrant replacement \(j: X \rightarrow \hat{X}\). Then we have the following diagram of Quillen adjunctions:

All vertical Quillen adjunctions are Quillen equivalences (Theorems B.6, 5.1) thus the top horizontal Quillen adjunctions are Quillen equivalences if and only if the bottom Quillen adjunctions are Quillen equivalences.
We are now ready to move on to the last step.
Lemma B.18
Let S be a quasi-category. Then the adjunction

is a Quillen equivalence, where both sides have the covariant model structure.
Proof
We prove that the derived unit and counit maps are equivalences.
First we prove the derived counit map is an equivalence. Let \(p: L \rightarrow p_1^*S\) be a left fibration. We need to prove that the map \(p_1^*u^*i_1^*L \rightarrow L\) is a covariant equivalence over \(p_1^*S\). By Theorem B.7, \(u: S \rightarrow i_1^* p_1^* S\) is the identity map. Hence we only need to prove that \(p_1^*i_1^*L \rightarrow L\) is a covariant equivalence over \(p_1^*S\). However, this follows immediately from the fact that \(p_1^*i_1^*L \rightarrow L\) is a complete Segal space equivalence (by Theorem B.7) and hence a covariant equivalence over \(p_1^*S\) (Theorem 5.11).
We move on to prove that the derived unit map is an equivalence. Let \(p:L \rightarrow S\) be a left fibration. Then \(p_1^*L \rightarrow p_1^*S\) is generally not a left fibration and so we need to find a left fibrant replacement. We have the following diagram:

By Lemma B.16, \(t^!L \rightarrow t^!S\) is a left fibration and so \((g_S)^*(t_!L) \rightarrow p_1^*S\) is a left fibration (Lemma 3.9). Moreover, \((g_S)^*t^!L \rightarrow t^!L\) is a CSS equivalence, as pulling back along left fibrations preserves CSS equivalences (Theorem 5.15) and \(g_L\) is a CSS equivalence by Lemma B.9. Thus \(p_1^*L \rightarrow (g_S)^*t^!L\) is a CSS equivalence over \(p_1^*S\) and so a covariant equivalence over \(p_1^*S\) (by Theorem 5.11). Hence, \(p_1^*L \rightarrow (g_S)^*t^!L\) is a fibrant replacement of \(p_1^*p\) in  .
.
Thus, in order to prove the derived unit is an equivalence we only need to show that
is a covariant equivalence over \(p_1^*S\). However, both maps are just the identity map and hence we are done. \(\square \)
Lemma B.19
Let X be a complete Segal space. Then the adjunction

is a Quillen equivalence, where both sides have the covariant model structure.
Proof
We have the following chain of Quillen adjunctions:

Here \(c: p_1^*i_1^*X \rightarrow X\) is the counit map of the adjunction.
The first adjunction is a Quillen equivalence by Lemma B.18. The middle one is a Quillen equivalence by Theorem 5.1, as c is an equivalence of complete Segal spaces (as proven in Theorem B.7). Finally, the composition takes a morphism \(S \xrightarrow { p } i_1^*X\) to \(t_!p_1^*S \rightarrow t_!p_1^*i_1^*X \rightarrow t_!X\). By definition of \(h_X\) (Lemma B.10) this morphism is equal to \(S \xrightarrow { p } i_1^*X \xrightarrow {h_X} t_!X\) meaning the composition is precisely the Quillen adjunction

Now, by Lemma B.10, \(h_X\) is a categorical equivalence and so \(((h_X)_!,(h_X)^*)\) is a Quillen equivalence and so by 2-out-of-3, the Quillen adjunction \((t_!,u^*t^!)\) is also a Quillen equivalence. \(\square \)
The Quillen equivalence in Theorem B.12 has an interesting corollary.
Corollary B.20
The covariant model structure on  is the localization of the Joyal model structure with respect to the set of maps \(< 0 >:\Delta [0] \rightarrow \Delta [n] \rightarrow S\).
is the localization of the Joyal model structure with respect to the set of maps \(< 0 >:\Delta [0] \rightarrow \Delta [n] \rightarrow S\).
Remark B.21
Essentially we proved that the two Quillen equivalences that Joyal and Tierney introduced remain an equivalence after we localize at both sides. Theoretically, we could have just proven these theorems using the fact that localizing with respect to the "same" maps on both sides preserves Quillen equivalences. However, the issue is that we did not have a good enough understanding of the localization of the Joyal model structure (i.e. it is not clear which maps we are localizing with respect to). It is just after this proof that we get a clear sense of the localizing maps.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Rasekh, N. Yoneda Lemma for Simplicial Spaces. Appl Categor Struct 31, 27 (2023). https://doi.org/10.1007/s10485-023-09734-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10485-023-09734-z


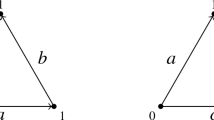

 . For a further object z and maps
. For a further object z and maps  by
by  is a category of functors, then we denote the set of natural transformations from F to G by
is a category of functors, then we denote the set of natural transformations from F to G by  is enriched over the category of simplicial sets, we denote the mapping simplicial set by
is enriched over the category of simplicial sets, we denote the mapping simplicial set by 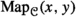 or, if
or, if  is clear from the context, by
is clear from the context, by  , use
, use  is Cartesian closed, we denote the internal mapping object by
is Cartesian closed, we denote the internal mapping object by  ,
,  , we denote the category of functors by
, we denote the category of functors by  , following conventional notation.
, following conventional notation.



 and
and 
 is a left adjoint because
is a left adjoint because  is a Conduché functor [
is a Conduché functor [ .
. define
define  .
. is the indexing category with objects posets
is the indexing category with objects posets  is enriched over spaces via
is enriched over spaces via 
 is also enriched over itself via
is also enriched over itself via 


 is a weak equivalence of spaces for every Segal space W.
is a weak equivalence of spaces for every Segal space W. is a weak equivalence of spaces for every complete Segal space W.
is a weak equivalence of spaces for every complete Segal space W.





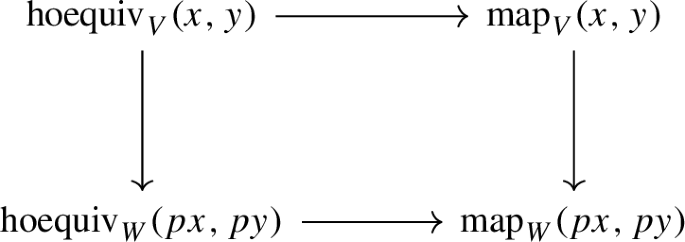
 is conservative.
is conservative. the map
the map  the map
the map  ,
, .
. ,
,
 ,
, .
.




 and map
and map  in
in 
 . Here
. Here  is the projection map.
is the projection map. and so if every functor in the diagram is a right Quillen equivalence,
and so if every functor in the diagram is a right Quillen equivalence,  and
and  and so if all
and so if all 
 such that
such that  . This is the localized model structure on
. This is the localized model structure on  .
. to get a set of monomorphisms in
to get a set of monomorphisms in  and then use Theorem
and then use Theorem  and finally take the induced model structure on
and finally take the induced model structure on  . We call this the induced localized model structure on
. We call this the induced localized model structure on  .
. for the Joyal model structure on the category of simplicial sets (with fibrant objects quasi-categories) and, for a given simplicial set S, use the notation
for the Joyal model structure on the category of simplicial sets (with fibrant objects quasi-categories) and, for a given simplicial set S, use the notation  for the covariant model structure on simplicial sets over S (defined in Definition
for the covariant model structure on simplicial sets over S (defined in Definition  defined as
defined as  defined as
defined as