Optimal pricing and financing decision of dual-channel green supply chain considering product differentiation and blockchain

Abstract

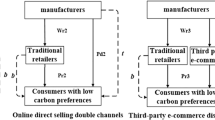
This paper constructs a dual-channel green supply chain model that includes a well-capitalized retailer and e-commerce platform, as well as a capital-constrained manufacturer. The manufacturer sells two different green quality products through the e-commerce platform and the retailer. There are two portfolio financing strategies for the manufacturer to choose and decide whether to use blockchain. We establish four models of whether to use blockchain under the EP financing strategy (e-commerce platform financing and prepayment financing) and the EB financing strategy (e-commerce platform financing and bank financing). By comparing the optimal solutions under four models, we discover some results. Firstly, we discover that the wholesale price will be higher than the selling price of the online channel when the product greenness difference between the two channels is large, and the optimal expected profit of the retailer is not related to product green differences. Secondly, the EP financing strategy is the optimal financing strategy choice for the manufacturer regardless of whether blockchain is used or not. Thirdly, when the cost per unit of using blockchain is greater than a certain threshold, the manufacturer should choose not to use blockchain. Finally, the manufacturer's acceptable blockchain usage threshold under the EP financing strategy is higher than under the EB financing strategy, and it decreases with the smaller product greenness difference between the two channels under the EP financing strategy. In addition, we also make an extension that verifies our model and findings are robust.

Appendices

Appendix A

Proof of Proposition 1

In the model PN, the expected profits of supply chain members are

$$\begin{array}{c}E\left({\pi }_{r}^{PN}\right)=\left({p}_{r}^{PN}-{w}^{PN}\right)\left(1-{p}_{r}^{PN}+\theta {p}_{m}^{PN}+\beta \right)+{r}_{1}\left[c\left(1-{p}_{r}^{PN}+\theta {p}_{m}^{PN}+\beta \right)+\frac{1}{2}\rho \right]\end{array}$$

(A.1)

$$E\left({\pi }_{m}^{PN}\right)=\left({w}^{PN}-c\right)\left(1-{p}_{r}^{PN}+\theta {p}_{m}^{PN}+\beta \right)+\left({p}_{m}^{PN}-c\right)\left(1-{p}_{m}^{PN}+\theta {p}_{r}^{PN}+\beta t\right)-\frac{1}{2}\rho $$

$$\begin{array}{c}-{r}_{0}c\left(1-{p}_{m}^{PN}+\theta {p}_{r}^{PN}+\beta t\right)-{r}_{1}\left[c\left(1-{p}_{r}^{PN}+\theta {p}_{m}^{PN}+\beta \right)+\frac{1}{2}\rho \right]-G\end{array}$$

(A.2)

$$\begin{array}{c}{E( \pi }_{f}^{PN})= G+{r}_{0}c\left(1-{p}_{m}^{PN}+\theta {p}_{r}^{PN}+\beta t\right)\end{array}$$

(A.3)

In the EP financing strategy, when not using blockchain, we obtain $\frac{\partial {E\left({\pi }_{r}^{PN}\right)}^{2}}{\partial {{p}_{r}^{PN}}^{2}}=-2<0$, so $E\left({\pi }_{r}^{PN}\right)$ is a strictly concave function concerning ${p}_{r}^{PN}$. According to the inverse inductive solution method, let $\frac{\partial E\left({\pi }_{r}^{PN}\right)}{\partial {p}_{r}^{PN}}=0$, we can obtain the optimal pricing for the retail channel ${p}_{r}^{PN}$ concerning ${w}^{PN}$ and ${p}_{m}^{PN}$ as follows:

$$\begin{array}{c}{p}_{r}^{PN}\left({w}^{PN},{p}_{m}^{PN}\right)=\frac{\beta -{r}_{1}c+\theta {p}_{m}^{PN}+1+{w}^{PN}}{2}\end{array}$$

(A.4)

Place ${p}_{r}^{PN}\left({w}^{PN},{p}_{m}^{PN}\right)$ substitute into $E\left({\pi }_{m}^{PN}\right)$, we will obtain the expression of $E\left({\pi }_{m}^{PN}\right)$ concerning ${w}^{PN}$ and ${p}_{m}^{PN}$. The Hessian matrix of $E\left({\pi }_{m}^{PN}\right)$ concerning ${w}^{PN}$ and ${p}_{m}^{PN}$ is obtained by calculating as follows:

$$\begin{array}{c}{H}_{E\left({\pi }_{m}^{PN}\right)\left({w}^{PN},{p}_{m}^{PN}\right)}=\left[\begin{array}{cc}{\theta }^{2}-2& \theta \\ \theta & -1\end{array}\right]\end{array}$$

(A.5)

Due to $0<\theta <1$, $\frac{\partial {E\left({\pi }_{m}^{PN}\right)}^{2}}{\partial {{p}_{m}^{PN}}^{2}}={\theta }^{2}-2<0$, and ${H}_{E\left({\pi }_{m}^{PN}\right)\left({w}^{PN},{p}_{m}^{PN}\right)}=2-2{\theta }^{2}>0$, therefore ${H}_{E\left({\pi }_{m}^{PN}\right)\left({w}^{PN},{p}_{m}^{PN}\right)}$ is a negative definite matrix. $E\left({\pi }_{m}^{PN}\right)$ is a strictly combinatorial concave function on ${w}^{PN}$ and ${p}_{m}^{PN}$.

Let$\frac{\partial E\left({\pi }_{m}^{PN}\right)}{\partial {p}_{m}^{PN}}=0$, $\frac{\partial E\left({\pi }_{m}^{PN}\right)}{\partial {w}^{PN}}=0$, we get

$$\begin{array}{c}{p}_{m}^{PN}\left({w}^{PN}\right)=\frac{c\left({r}_{0}+1\right){\theta }^{2}+\left[\left({2r}_{2}+1\right)c-\left(\beta +1+2{w}^{PN}\right)\right]\theta -2\left({r}_{0}+1\right)c-2\beta t-2}{2\left({\theta }^{2}-2\right)}\end{array}$$

(A.6)

$$\begin{array}{c}{w}^{PN}\left({p}_{m}^{PN}\right)=\frac{1+c-c\theta -{r}_{0}c\theta +{r}_{1}c+2\theta {p}_{m}^{PN}+\beta }{2}\end{array}$$

(A.7)

Substituting ${p}_{m}^{PN}\left({w}^{PN}\right)$ and ${w}^{PN}\left({p}_{m}^{PN}\right)$ into each other to solve for

$$\begin{array}{c}{p}_{m}^{PN*}=\frac{c\left({r}_{0}+1\right){\theta }^{2}-\left(\beta +1\right)\theta -\left({r}_{0}+1\right)c-\beta t-1}{2\left({\theta }^{2}-1\right)}\end{array}$$

(A.8)

$$\begin{array}{c}{w}^{PN*}=\frac{c\left(2{r}_{1}+1\right){\theta }^{2}-\left(\beta t+1\right)\theta -\left(2{r}_{1}+1\right)c-\beta -1}{2\left({\theta }^{2}-1\right)}\end{array}$$

(A.9)

Substituting ${p}_{m}^{PN}$ and ${w}^{PN}$ into ${p}_{r}^{PN}\left({w}^{PN},{p}_{m}^{PN}\right)$ obtains

$$\begin{array}{c}{p}_{r}^{PN*}=\frac{c\left({r}_{0}+1\right){\theta }^{3}+\left(\beta +1+c\right){\theta }^{2}-\left[\left({r}_{0}+1\right)c+2\beta t+2\right]\theta -3\beta -3-c}{4\left({\theta }^{2}-1\right)}\end{array}$$

(A.10)

Substituting ${p}_{m}^{PN}$, ${w}^{PN}$, and ${p}_{r}^{PN}$ into $E\left({\pi }_{r}^{PN}\right),E\left({\pi }_{m}^{PN}\right),\mathrm{ and }E\left({\pi }_{f}^{PN}\right)$, we obtain

$$\begin{array}{c}{E\left({\pi }_{r}^{PN}\right)}^{*}=\frac{{\left[\left({r}_{0}+1\right)\theta -1\right]}^{2}{c}^{2}+2c\left(\beta +1\right)\left[\left({r}_{0}+1\right)\theta -1\right]+{\beta }^{2}+2\beta +8{r}_{1}\rho +1}{16}\end{array}$$

(A.11)

$$\begin{array}{c}{E\left({\pi }_{m}^{PN}\right)}^{*}=\frac{{A}_{1}{\theta }^{3}+{B}_{1}{\theta }^{2}+{C}_{1}\theta -\left(2{{r}_{0}}^{2}+4{r}_{0}+3\right){c}^{2}+{D}_{1}c+{E}_{1}+8G}{8\left({\theta }^{2}-1\right)}\end{array}$$

(A.12)

$$\begin{array}{c}{E\left({\pi }_{f}^{PN}\right)}^{*}=\frac{\left[\left({\theta }^{2}-2\right){r}_{0}+{\theta }^{2}+\theta -2\right]{r}_{0}{c}^{2}+{r}_{0}c\left[\left(\beta +1\right)\theta +2\beta t+2\right]}{4} +G\end{array}$$

(A.13)

(${A}_{1}=-{c}^{2}{\left({r}_{0}+1\right)}^{2}{\theta }^{4}-2c\left({r}_{0}+1\right)\left(\beta +1+c\right)$; ${B}_{1}=\left(3{{r}_{0}}^{2}+6{r}_{0}+4\right){c}^{2}-\left[4\beta \left({r}_{0}t+t+\frac{1}{2}\right)+\left(4{r}_{0}+6\right)\right]c-{\beta }^{2}-2\beta -1-\left(4{r}_{1}+4\right)\rho -8G$; ${C}_{1}=\left(2{r}_{0}+2\right){c}^{2}+2\left({r}_{0}+1\right)\left(\beta +1\right)c-4\left(\beta +1\right)\left(\beta t+1\right)$; ${D}_{1}=4\beta \left({r}_{0}t+t+\frac{1}{2}\right)+\left(4{r}_{0}+6\right)$; ${E}_{1}=-\left(2{t}^{2}+1\right){\beta }^{2}-4\beta \left(t+\frac{1}{2}\right)-3{a}^{2}+\left(4{r}_{1}+4\right)\rho$).

Proof of Corollary 1

• (1) $\frac{\partial {w}^{PN*}}{\partial t}=-\frac{\theta \beta }{2\left({\theta }^{2}-1\right)}>0$

• (2) $\frac{\partial {p}_{m}^{PN*}}{\partial t}=-\frac{\beta }{2\left({\theta }^{2}-1\right)}>0$

• (3) $\frac{\partial {p}_{r}^{PN*}}{\partial t}=-\frac{\theta \beta }{2\left({\theta }^{2}-1\right)}>0$

• (4) $\frac{\partial {E\left({\pi }_{r}^{PN}\right)}^{*}}{\partial t}=0$

• (5) $\frac{\partial {E\left({\pi }_{m}^{PN}\right)}^{*}}{\partial t}=-\frac{\beta \left[c\left({r}_{0}+1\right){\theta }^{2}+\left(\beta +1\right)\theta -c\left({r}_{0}+1\right)+\beta t+1\right]}{2\left({\theta }^{2}-1\right)}>0$

• (6) $\frac{\partial {{E( \pi }_{f}^{PN})}^{*}}{\partial t}=\frac{{r}_{0}c\beta }{2}>0$

Proof of Proposition 2

In the model PB, the expected profits of supply chain members are

$$\begin{aligned} E\left({\pi }_{r}^{PB}\right)&=\left({p}_{r}^{PB}-{w}^{PB}-b\right)\left(1+\frac{h}{2}-{p}_{r}^{PB}+\theta {p}_{m}^{PB}+\beta \right)\\ &\quad +{r}_{1}\left[\left(c+b\right)\left(1+\frac{h}{2}-{p}_{r}^{PB}+\theta {p}_{m}^{PB}+\beta \right)+\frac{1}{2}\rho \right]\end{aligned}$$

(A.14)

$$\begin{aligned} E\left({\pi }_{m}^{PB}\right)&=\left({w}^{PB}-c-b\right)\left(1+\frac{h}{2}-{p}_{r}^{PB}+\theta {p}_{m}^{PB}+\beta \right)\\ &\quad +\left({p}_{m}^{PB}-c-2b\right)\left(1+\frac{h}{2}-{p}_{m}^{PB}+\theta {p}_{r}^{PB}+\beta t\right)-\frac{1}{2}\rho \end{aligned}$$

$$\begin{array}{c}-{r}_{0}\left(c+2b\right)\left(1+\frac{h}{2}-{p}_{m}^{PB}+\theta {p}_{r}^{PB}+\beta t\right)-{r}_{1}\left[\left(c+b\right)\left(1+\frac{h}{2}-{p}_{r}^{PB}+\theta {p}_{m}^{PB}+\beta \right)+\frac{1}{2}\rho \right]-G\end{array}$$

(A.15)

$$\begin{array}{c}E\left({\pi }_{f}^{PB}\right)= G+{r}_{0}\left(c+2b\right)\left(1-{p}_{m}^{PB}+\theta {p}_{r}^{PB}+\beta t\right)\end{array}$$

(A.16)

In the EP financing strategy, when using blockchain, we obtain $\frac{{\partial E\left({\pi }_{r}^{PB}\right)}^{2}}{\partial {{p}_{r}^{PB}}^{2}}=-2<0$, so $E\left({\pi }_{r}^{PB}\right)$ is a strictly concave function concerning ${p}_{r}^{PB}$. According to the inverse inductive solution method, let $\frac{\partial E\left({\pi }_{r}^{PB}\right)}{\partial {p}_{r}^{PB}}=0$, we can obtain the optimal pricing for the retail channel ${p}_{r}^{PB}$ concerning ${w}^{PB}$ and ${p}_{m}^{PB}$ as follows:

$$\begin{array}{c}{p}_{r}^{PB}\left({w}^{PB},{p}_{m}^{PB}\right)=\frac{\beta -{r}_{1}b-{r}_{1}c+\theta {p}_{m}^{PB}+1+{w}^{PB}+b}{2}+\frac{h}{4}\end{array}$$

(A.17)

Place ${p}_{r}^{PB}\left({w}^{PB},{p}_{m}^{PB}\right)$ substitute into $E\left({\pi }_{m}^{PB}\right)$, we will obtain the expression of $E\left({\pi }_{m}^{PB}\right)$ concerning ${w}^{PB}$ and ${p}_{m}^{PB}$. The Hessian matrix of $E\left({\pi }_{m}^{PB}\right)$ concerning ${w}^{PB}$ and ${p}_{m}^{PB}$ is obtained by calculating as follows:

$$\begin{array}{c}{H}_{E\left({\pi }_{m}^{PB}\right)\left({w}^{PB},{p}_{m}^{PB}\right)}=\left[\begin{array}{cc}{\theta }^{2}-2& \theta \\ \theta & -1\end{array}\right]\end{array}$$

(A.18)

Due to $0<\theta <1$,$\frac{\partial {E\left({\pi }_{m}^{PB}\right)}^{2}}{\partial {{p}_{m}^{PB}}^{2}}={\theta }^{2}-2<0$, and ${H}_{E\left({\pi }_{m}^{PB}\right)\left({w}^{PB},{p}_{m}^{PB}\right)}=2-2{\theta }^{2}>0$, therefore ${H}_{E\left({\pi }_{m}^{PB}\right)\left({w}^{PB},{p}_{m}^{PB}\right)}$ is a negative definite matrix. $E\left({\pi }_{m}^{PB}\right)$ is a strictly combinatorial concave function on ${w}^{PB}$ and ${p}_{m}^{PB}$.

Let$\frac{\partial E\left({\pi }_{m}^{PB}\right)}{\partial {p}_{m}^{PB}}=0$, $\frac{\partial E\left({\pi }_{m}^{PB}\right)}{\partial {w}^{PB}}=0$,we get

$$\begin{array}{c}{p}_{m}^{PB}\left({w}^{PB}\right)=\frac{4\left({r}_{0}+1\right)\left(\frac{c}{2}+b\right){\theta }^{2}+\left[\left(4{r}_{1}+2\right)c+4{r}_{1}b-\left(2\beta +2+h+4{w}^{PB}\right)\right]\theta -8\left({r}_{0}+1\right)b-4\left({r}_{0}+1\right)c-4\left(\beta t+1\right)-2h}{4\left({\theta }^{2}-2\right)}\end{array}$$

(A.19)

$$\begin{array}{c}{w}^{PB}\left({p}_{m}^{PB}\right)=\frac{1+c-2\theta b-c\theta -2{r}_{0}\theta b-{r}_{0}c\theta +2{r}_{1}c+2\theta {p}_{m}^{PB}+\beta +2{r}_{1}b}{2}+\frac{h}{4}\end{array}$$

(A.20)

Substituting ${p}_{m}^{PB}\left({w}^{PB}\right)$ and ${w}^{PB}\left({p}_{m}^{PB}\right)$ into each other to solve for

$$\begin{array}{c}{w}^{PB*}=\frac{\left[4\left(b+c\right){r}_{1}+2c\right]{\theta }^{2}-\left(2\beta t+2+h\right)\theta -4\left(b+c\right){r}_{1}-2-2\beta t-2c-h}{4\left({\theta }^{2}-1\right)}\end{array}$$

(A.21)

$$\begin{array}{c}{p}_{m}^{PB*}=\frac{4\left({r}_{0}+1\right)\left(\frac{c}{2}+b\right){\theta }^{2}-\left(2\beta +2+h\right)\theta -4\left({r}_{0}+1\right)b-2\left({r}_{0}+1\right)c-2\left(\beta t+1\right)-h}{4\left({\theta }^{2}-1\right)}\end{array}$$

(A.22)

Substituting ${p}_{m}^{PB}$ and ${w}^{PB}$ into ${p}_{r}^{PB}\left({w}^{PB},{p}_{m}^{PB}\right)$ obtains

$$\begin{array}{c}{p}_{r}^{PB*}=\frac{\left[4\left({r}_{0}+1\right)\left(\frac{c}{2}+b\right)\right]{\theta }^{3}+\left(2\beta +2+4b+2c+h\right){\theta }^{2}-{A}_{2}\theta -6\beta -6-4b-2c-3h}{12\left({\theta }^{2}-1\right)}\end{array}$$

(A.23)

Substituting ${p}_{m}^{PB}$, ${w}^{PB}$, and ${p}_{r}^{PB}$ into $E\left({\pi }_{r}^{PB}\right),E\left({\pi }_{m}^{PB}\right),\mathrm{ and }E\left({\pi }_{f}^{PB}\right)$, we obtain

$$\begin{array}{c}{E\left({\pi }_{r}^{PB}\right)}^{*}=\frac{{\left(\frac{c}{2}+b\right)}^{2}{\left({r}_{0}+1\right)}^{2}{\theta }^{2}+\left(\beta +1-2b-c+\frac{h}{2}\right)\left(\frac{c}{2}+b\right)\left({r}_{0}+1\right)\theta +{b}^{2}+4{B}_{2}+4{C}_{2}}{4}\end{array}$$

(A.24)

$$\begin{array}{c}{E\left({\pi }_{m}^{PB}\right)}^{*}=\frac{{D}_{2}{\theta }^{3}+{E}_{2}{\theta }^{2}{+F}_{2}\theta -\left(32{{r}_{0}}^{2}+64{r}_{0}+48\right){b}^{2}+{H}_{2}b-\left(8{{r}_{0}}^{2}+16{r}_{0}+12\right){c}^{2}+{I}_{2}c+{J}_{2}}{32{\theta }^{2}-32}\end{array}$$

(A.25)

$$\begin{array}{c}{E\left({\pi }_{f}^{PB}\right)}^{*}= \left(\frac{c}{2}+b\right)\left({\theta }^{2}-2\right){{r}_{0}}^{2}+{K}_{2}\left(\frac{c}{2}+b\right){r}_{0}+G\end{array}$$

(A.26)

$$ \begin{aligned} & (A_{2} = 4\left( {r_{0} + 1} \right)b + 2\left( {r_{0} + 1} \right)c + 4\beta t + 4 + 2h;\;B_{2} \\ &\qquad = \frac{{\left( {2 + h} \right)\beta }}{{16}} + \frac{{8r_{1} \rho + 1 + h}}{{16}} + \frac{{h^{2} }}{{64}};\;C_{2} = \frac{{4c^{2} - \left( {8\beta + 8 + 4h} \right)c + 4\beta ^{2} }}{{16}} \\ &\qquad\quad + \frac{{\left( { - 16\beta - 16 + 16c - 8h} \right)b}}{{64}};\\ &D_{2} = - 16\left( {\frac{c}{2} + b} \right)^{2} \left( {r_{0} + 1} \right)^{2} \theta ^{4} - 16\left( {\beta + 1 + 2b + c + \frac{h}{2}} \right)\left( {\frac{c}{2} + b} \right)\left( {r + 1} \right); \\ & E_{2} = \left( {48r_{0}^{2} + 96r_{0} + 64} \right)b^{2}\\ &\qquad\quad + \left[ {\left( {48r_{0}^{2} + 96r_{0} + 64} \right)c - \left( {32\beta t + 32 + 16h} \right)r_{0} - \left( {32t + 16} \right)\beta - 48 - 24h} \right]b\\ &\qquad\quad + \left( {12r_{0}^{2} + 24r_{0} + 16} \right)c^{2} - \left[ {\left( {16\beta t + 16 + 8h} \right)r_{0} + \left( {16t + 8} \right)\beta + 24 + 12h} \right]c\\ &\qquad\quad - 4\beta ^{2} - 8\beta \left( {1 + \frac{h}{2}} \right) - 4 - 4h - h^{2} - \left( {16r_{1} + 16} \right)\rho - 32G \\ & F_{2} = \left({32r_{0} + 32} \right)b^{2} + 16b\left({\beta + 1 + 2c + \frac{h}{2}} \right)\left( {r_{0} + 1} \right) + \left( {8r + 8} \right)c^{2} + 8c\left( {\beta + 1 + \frac{h}{2}} \right)\left( {r_{0} + 1} \right)\\ &\qquad\quad - 16\left( {\beta + 1 + \frac{h}{2}} \right)\left( {\beta t + 1 + \frac{h}{2}} \right) \\ & H_{2} = - \left({32r_{0}^{2} + 64r_{0} + 48} \right)c + \left( {32\beta t + 32 + 16h} \right)r_{0} + \left( {32t + 16} \right)\beta + 48 + 24h;\\ & I_{2} = \left( {16\beta t + 16 + 8h} \right)r_{0} + \left( {16t + 8} \right)\beta + 24 + 12h \\ & J_{2} = - \left( {8t^{2} + 4} \right)\beta ^{2} - 16\beta \left( {1 + \frac{h}{2}} \right)\left( {t + \frac{1}{2}} \right) - 12 - 12h - 3h^{2} + \left( {16r_{1} + 16} \right)\rho + 32G;\\ & K_{2} = [(\theta ^{2} + \theta - 2)b + \frac{{\theta ^{2} + \theta - 2}}{2}c + \theta \frac{{2\beta + 2 + h}}{4} + \beta t + 1 + \frac{h}{2}]) \\ \end{aligned} $$

Proof of Corollary 2

• (1) $\frac{\partial {w}^{PB*}}{\partial t}=-\frac{\theta \beta }{2\left({\theta }^{2}-1\right)}>0$

• (2) $\frac{\partial {p}_{m}^{PB*}}{\partial t}=-\frac{\beta }{2\left({\theta }^{2}-1\right)}>0$

• (3) $\frac{\partial {p}_{r}^{PB*}}{\partial t}=-\frac{\theta \beta }{2\left({\theta }^{2}-1\right)}>0$

• (4) $\frac{\partial {E\left({\pi }_{r}^{PB}\right)}^{*}}{\partial t} =0$

• (5) $\frac{\partial {E\left({\pi }_{m}^{PB}\right)}^{*}}{\partial t}=-\frac{2\beta \left[2\left(\frac{c}{2}+b\right)\left({r}_{0}+1\right){\theta }^{2}+\left(\beta +1+\frac{h}{2}\right)\theta -\left(2b+c\right)\left({r}_{0}+1\right)+\beta t+1+\frac{h}{2}\right]}{4\left({\theta }^{2}-1\right)}>0$

• (6) $\frac{\partial E{\left({\pi }_{f}^{PB}\right)}^{*}}{\partial t}=\beta {r}_{0}\left(\frac{c }{2}+b\right)>0$

Proof of Corollary 3

• (1) $\frac{\partial {w}^{PB*}}{\partial b}={r}_{1}>0$

• (2) $\frac{\partial {p}_{m}^{PB*}}{\partial b}={r}_{0}+1>0$

• (3) $\frac{\partial {p}_{r}^{PB*}}{\partial b}=\frac{\left(1+{r}_{0}\right)\theta +1}{2}>0$

• (4) When $0<b<{b}_{1}$, $\frac{\partial {E\left({\pi }_{r}^{PB}\right)}^{*}}{\partial b}<0$; $b>{b}_{1}$, $\frac{\partial {E\left({\pi }_{r}^{PB}\right)}^{*}}{\partial b}>0$.

• (5) When $0<b<{b}_{2}$, $\frac{\partial {E\left({\pi }_{m}^{PB}\right)}^{*}}{\partial b}<0$; $b>{b}_{2}$, $\frac{\partial {E\left({\pi }_{m}^{PB}\right)}^{*}}{\partial b}>0$.

• (6) When $0<b<{b}_{3}$,$\frac{\partial {E\left({\pi }_{f}^{PB}\right)}^{*}}{\partial b}>0$; $b>{b}_{3}$, $\frac{\partial {E\left({\pi }_{f}^{PB}\right)}^{*}}{\partial b}<0.$

  $$ \begin{gathered} \left( {b_{1} = \frac{{2\theta r_{0} c + 2\beta + 2\theta c + h - 2c + 2}}{{4\left( {1 - \theta - r_{0} \theta } \right)}}; } \right. \hfill \\ b_{2} = \frac{\begin{array}{c} - 2c( {r_{0} + 1} )\theta^{2} - ( {2\beta + 2 + 4c + h} )( {r_{0} + 1} )\theta + 4r_{0}^{2} c\\ - ({4\beta t + 4 - 8c + 2h} )r_{0} + 6c - 4\beta t - 2\beta - 6 - 3h\end{array}}{{4( {r_{0} + 1} )^{2} \theta^{2} + ( {8r_{0} + 8} )\theta - 8r_{0}^{2} - 16r_{0} - 12}}; \hfill \\ \left. {b_{3} = \frac{{ - 4c\left( {r_{0} + 1} \right)\theta^{2} - \left( {2\beta + 2 + 4c + h} \right)\theta + \left( {8r_{0} + 8} \right)c - 4\beta t - 4 - 2h}}{{8\left( {r_{0} \theta^{2} + \theta^{2} - 2r_{0} + \theta - 2} \right)}}} \right) \hfill \\ \end{gathered} $$

Proof of Proposition 3

Under the model BN, the expected profits of supply chain members are

$$\begin{array}{c}E\left({\pi }_{r}^{BN}\right)=\left({p}_{r}^{BN}-{w}^{BN}\right)\left(1-{p}_{r}^{BN}+\theta {p}_{m}^{BN}+\beta \right)\end{array}$$

(A.27)

$$\begin{array}{c}E\left({\pi }_{m}^{BN}\right)=\left({w}^{BN}-c\right)\left(1-{p}_{r}^{BN}+\theta {p}_{m}^{BN}+\beta \right)+\left({p}_{m}^{BN}-c\right)\left(1-{p}_{m}^{BN}+\theta {p}_{r}^{BN}+\beta t\right)\\ -\frac{1}{2}\rho -{r}_{0}c\left(1-{p}_{m}^{BN}+\theta {p}_{r}^{BN}+\beta t\right)-{r}_{2}\left[c\left(1-{p}_{r}^{BN}+\theta {p}_{m}^{BN}+\beta \right)+\frac{1}{2}\rho \right]-G\end{array}$$

(A.28)

$$\begin{array}{c}{E( \pi }_{f}^{BN})= G+{r}_{0}c\left(1-{p}_{m}^{BN}+\theta {p}_{r}^{BN}+\beta t\right)\end{array}$$

(A.29)

In the EB financing strategy, when not using blockchain, we obtain $\frac{\partial {E\left({\pi }_{r}^{BN}\right)}^{2}}{\partial {{p}_{r}^{BN}}^{2}}=-2<0$, so $E\left({\pi }_{r}^{BN}\right)$ is a strictly concave function concerning ${p}_{r}^{BN}$. According to the inverse inductive solution method, let $\frac{\partial E\left({\pi }_{r}^{BN}\right)}{\partial {p}_{r}^{BN}}=0$, we can obtain the optimal pricing for the retail channel ${p}_{r}^{BN}$ concerning ${w}^{BN}$ and ${p}_{m}^{BN}$ as follows:

$$\begin{array}{c}{p}_{r}^{BN}\left({w}^{BN},{p}_{m}^{BN}\right)=\frac{\beta +\theta {p}_{m}^{BN}+1+{w}^{BN}}{2}\left(A.30\right)\end{array}$$

Place ${p}_{r}^{BN}\left({w}^{BN},{p}_{m}^{BN}\right)$ substitute into $E\left({\pi }_{m}^{BN}\right)$, we will obtain the expression of $E\left({\pi }_{m}^{BN}\right)$ concerning ${w}^{BN}$ and ${p}_{m}^{BN}$. The Hessian matrix of $E\left({\pi }_{m}^{BN}\right)$ concerning ${w}^{BN}$ and ${p}_{m}^{BN}$ is obtained by calculating as follows:

$$\begin{array}{c}{H}_{E\left({\pi }_{m}^{BN}\right)\left({w}^{BN},{p}_{m}^{BN}\right)}=\left[\begin{array}{cc}{\theta }^{2}-2& \theta \\ \theta & -1\end{array}\right]\end{array}$$

(A.31)

Due to $0<\theta <1$, $\frac{\partial {E\left({\pi }_{m}^{BN}\right)}^{2}}{\partial {{p}_{m}^{BN}}^{2}}={\theta }^{2}-2<0$, and ${H}_{E\left({\pi }_{m}^{BN}\right)\left({w}^{BN},{p}_{m}^{BN}\right)}=2-2{\theta }^{2}>0$, therefore ${H}_{E\left({\pi }_{m}^{BN}\right)\left({w}^{BN},{p}_{m}^{BN}\right)}$ is a negative definite matrix. $E\left({\pi }_{m}^{BN}\right)$ is a strictly combinatorial concave function on ${w}^{BN}$ and ${p}_{m}^{BN}$.

Let $\frac{\partial E\left({\pi }_{m}^{BN}\right)}{\partial {p}_{m}^{BN}}=0$, $\frac{\partial E\left({\pi }_{m}^{BN}\right)}{\partial {w}^{BN}}=0$, we get

$$\begin{array}{c}{p}_{m}^{BN}\left({w}^{BN}\right)=\frac{c\left({r}_{0}+1\right){\theta }^{2}+\left[\left({r}_{2}+1\right)c-\left(\beta +1+2{w}^{BN}\right)\right]\theta -2\left({r}_{0}+1\right)c-2\beta t-2}{2\left({\theta }^{2}-2\right)}\end{array}$$

(A.32)

$$\begin{array}{c}{w}^{BN}\left({p}_{m}^{BN}\right)=\frac{1+c-c\theta -{r}_{0}c\theta +{r}_{2}c+2\theta {p}_{m}^{BN}+\beta }{2}\end{array}$$

(A.33)

Substituting ${p}_{m}^{BN}\left({w}^{BN}\right)$ and ${w}^{BN}\left({p}_{m}^{BN}\right)$ into each other to solve for

$$\begin{array}{c}{p}_{m}^{BN*}=\frac{c\left({r}_{0}+1\right){\theta }^{2}-\left(\beta +1\right)\theta -\left({r}_{0}+1\right)c-\beta t-1}{2\left({\theta }^{2}-1\right)}\end{array}$$

(A.34)

$$\begin{array}{c}{w}^{BN*}=\frac{c\left({r}_{2}+1\right){\theta }^{2}-\left(\beta t+1\right)\theta -\left({r}_{2}+1\right)c-\beta -1}{2\left({\theta }^{2}-1\right)}\end{array}$$

(A.35)

Substituting ${p}_{m}^{BN}$ and ${w}^{BN}$ into ${p}_{r}^{BN}\left({w}^{BN},{p}_{m}^{BN}\right)$, we get

$$\begin{array}{c}{p}_{r}^{BN*}=\frac{c\left({r}_{0}+1\right){\theta }^{3}+{\left[\beta +1+\left({r}_{2}+1\right)c\right]\theta }^{2}-\left[\left({r}_{0}+1\right)c+2\beta t+2\right]\theta -3\left(\beta +1\right)-\left({r}_{2}+1\right)c}{4\left({\theta }^{2}-1\right)}\end{array}$$

(A.36)

Substituting ${p}_{m}^{BN}$, ${w}^{BN}$, and ${p}_{r}^{BN}$ into $E\left({\pi }_{r}^{BN}\right)$, $E\left({\pi }_{m}^{BN}\right)$, and $E\left({\pi }_{f}^{BN}\right)$, we obtain

$$\begin{array}{c}{E\left({\pi }_{r}^{BN}\right)}^{*}=\frac{{\left[c\left({r}_{0}+1\right)\theta -\left({r}_{2}+1\right)c+\beta +1\right]}^{2}{\left(\theta +1\right)}^{2}{\left(\theta -1\right)}^{2}}{16{\left({\theta }^{2}-1\right)}^{2}}\end{array}$$

(A.37)

$$\begin{array}{c}{E\left({\pi }_{m}^{BN}\right)}^{*}=\frac{{A}_{3}{c}^{2}-2c{B}_{3}-{C}_{3}{\theta }^{2}-{D}_{3}+4{r}_{2}\rho -3+4\rho +8G}{8\left({\theta }^{2}-1\right)}\end{array}$$

(A.38)

$$\begin{array}{c}{E\left({\pi }_{f}^{BN}\right)}^{*}=\frac{{r}_{0}{c}^{2}\left[\left({\theta }^{2}-2\right){r}_{0}-2+{\theta }^{2}+\left({r}_{2}+1\right)\theta \right]+{r}_{0}c\left[\left(\beta +1\right)\theta +2\beta t+2\right]}{4}+G\end{array}$$

(A.39)

$$ \begin{gathered} \left( {A_{3} = \left( {\theta + 1} \right)\left( {\theta - 1} \right)\left[ { - \left( {r_{0} + 1} \right)^{2} \theta^{2} - 2\theta \left( {r_{0} + 1} \right)\left( {r_{2} + 1} \right) + r_{2}^{2} + 2r_{0}^{2} + 2r_{2} + 4r_{0} + 3} \right];} \right. \hfill \\ B_{3} = \left( {\theta + 1} \right)\left( {\theta - 1} \right)\left[ {\left( {r_{0} + 1} \right)\left( {\beta + 1} \right)\theta + \beta \left( {2r_{0} t + 2t + r_{2} + 1} \right) + \left( {r_{2} + 2r_{0} + 3} \right)} \right]; \hfill \\ \left. {C_{3} = \beta^{2} + 4r_{2} \rho + 2\beta + 4\rho + 1 + 8G;\;D_{3} = 4\theta \left( {\beta + 1} \right)\left( {\beta t + 1} \right) + \beta^{2} \left( {2t^{2} + 1} \right) + 4\beta \left( {t + \frac{1}{2}} \right)} \right) \hfill \\ \end{gathered} $$

Proof of Corollary 4

• (1) $\frac{\partial {w}^{BN*}}{\partial t}=-\frac{\theta \beta }{2\left({\theta }^{2}-1\right)}>0$

• (2) $\frac{\partial {p}_{m}^{BN*}}{\partial t}=-\frac{\beta }{2\left({\theta }^{2}-1\right)}>0$

• (3) $\frac{\partial {p}_{r}^{BN*}}{\partial t}=-\frac{\theta \beta }{2\left({\theta }^{2}-1\right)}>0$

• (4) $\frac{\partial {E\left({\pi }_{r}^{BN}\right)}^{*}}{\partial t}=0$

• (5) $\frac{\partial E{\left({\pi }_{m}^{BN}\right)}^{*}}{\partial t}=-\frac{\beta \left[c\left({r}_{0}+1\right){\theta }^{2}+\left(\beta +1\right)\theta -c\left({r}_{0}+1\right)+\beta t+1\right]}{2\left({\theta }^{2}-1\right)}>0$

• (6) $\frac{\partial {{E( \pi }_{f}^{BN})}^{*}}{\partial t}=\frac{{r}_{0}c\beta }{2}>0$

Proof of Proposition 4

Under the model BB, the expected profits of supply chain members are

$$\begin{array}{c}E\left({\pi }_{r}^{BB}\right)=\left({p}_{r}^{BB}-{w}^{BB}-b\right)\left(1+\frac{h}{2}-{p}_{r}^{BB}+\theta {p}_{m}^{BB}+\beta \right)\end{array}$$

(A.40)

$$\begin{array}{c}E\left({\pi }_{m}^{BB}\right)=\left({w}^{BB}-c-b\right)\left(1+\frac{h}{2}-{p}_{r}^{BB}+\theta {p}_{m}^{BB}+\beta \right)+\left({p}_{m}^{BB}-c-2b\right)\left(1+\frac{h}{2}-{p}_{m}^{BB}+\theta {p}_{r}^{BB}+\beta t\right)-\frac{1}{2}\rho \\ -{r}_{0}\left(c+2b\right)\left(1+\frac{h}{2}-{p}_{m}^{BB}+\theta {p}_{r}^{BB}+\beta t\right)-{r}_{2}\left[\left(c+b\right)\left(1+\frac{h}{2}-{p}_{r}^{BB}+\theta {p}_{m}^{BB}+\beta \right)+\frac{1}{2}\rho \right]-G\end{array}$$

(A.41)

$$\begin{array}{c}E\left({\pi }_{f}^{BB}\right)= G+ {r}_{0}\left(c+2b\right)\left(1+\frac{h}{2}-{p}_{m}^{BB}+\theta {p}_{r}^{BB}+\beta t\right)\end{array}$$

(A.42)

In the EB financing strategy, when using blockchain, we obtain $\frac{\partial {E\left({\pi }_{r}^{BB}\right)}^{2}}{\partial {{p}_{r}^{BB}}^{2}}=-2<0$, so $E\left({\pi }_{r}^{BB}\right)$ is a strictly concave function concerning ${p}_{r}^{BB}$. According to the inverse inductive solution method, let $\frac{\partial E\left({\pi }_{r}^{BB}\right)}{\partial {p}_{r}^{BB}}=0$, we can obtain the optimal pricing for the retail channel ${p}_{r}^{BB}$ concerning ${w}^{BB}$ and ${p}_{m}^{BB}$ as follows:

$$\begin{array}{c}{p}_{r}^{BB}\left({w}^{BB},{p}_{m}^{BB}\right)=\frac{\beta +\theta {p}_{m}^{BB}+1+{w}^{BB}+b}{2}+\frac{h}{4}\end{array}$$

(A.43)

Place ${p}_{r}^{BB}\left({w}^{BB},{p}_{m}^{BB}\right)$ substitute into $E\left({\pi }_{m}^{BB}\right)$, we will obtain the expression of $E\left({\pi }_{m}^{BB}\right)$ concerning ${w}^{BB}$ and ${p}_{m}^{BB}$. The Hessian matrix of $E\left({\pi }_{m}^{BB}\right)$ concerning ${w}^{BB}$ and ${p}_{m}^{BB}$ is obtained by calculating as follows:

$$\begin{array}{c}{H}_{E\left({\pi }_{m}^{BB}\right)\left({w}^{BB},{p}_{m}^{BB}\right)}=\left[\begin{array}{cc}{\theta }^{2}-2& \theta \\ \theta & -1\end{array}\right]\end{array}$$

(A.44)

Due to$0<\theta <1$,$\frac{\partial {E\left({\pi }_{m}^{BB}\right)}^{2}}{\partial {{p}_{m}^{BB}}^{2}}={\theta }^{2}-2<0$, and ${H}_{E\left({\pi }_{m}^{BB}\right)\left({w}^{BB},{p}_{m}^{BB}\right)}=2-2{\theta }^{2}>0$, therefore ${H}_{E\left({\pi }_{m}^{BB}\right)\left({w}^{BB},{p}_{m}^{BB}\right)}$ is a negative definite matrix. $E\left({\pi }_{m}^{BB}\right)$ is a strictly combinatorial concave function on ${w}^{BB}$ and${p}_{m}^{BB}$.

Let $\frac{\partial E\left({\pi }_{m}^{BB}\right)}{\partial {p}_{m}^{BB}}=0$, and $\frac{\partial E\left({\pi }_{m}^{BB}\right)}{\partial {w}^{BB}}=0$,we get

$$\begin{array}{c}{p}_{m}^{BB}\left({w}^{BB}\right)=\frac{4\left({r}_{0}+1\right)\left(\frac{c}{2}+b\right){\theta }^{2}-\left[\left(2{r}_{2}+2\right)c+2{r}_{2}b-\left(2\beta +2+h+4{w}^{BB}\right)\right]\theta -8\left({r}_{0}+1\right)b-4\left({r}_{0}+1\right)c-4\left(\beta t+1\right)-2h}{4\left({\theta }^{2}-2\right)}\end{array}$$

(A.45)

$$\begin{array}{c}{w}^{BB}\left({p}_{m}^{BB}\right)=\frac{1+c-2\theta b-c\theta -2{r}_{0}\theta b-{r}_{0}c\theta +{r}_{2}c+2\theta {p}_{m}^{BB}+\beta +{r}_{2}b}{2}+\frac{h}{4}\end{array}$$

(A.46)

Substituting ${p}_{m}^{BB}\left({w}^{BB}\right)$ and ${w}^{BB}\left({p}_{m}^{BB}\right)$ into each other to solve for

$$\begin{array}{c}{p}_{m}^{BB*}=\frac{\left[4\left({r}_{0}+1\right)\left(\frac{c}{2}+b\right)\right]{\theta }^{2}-\left(2\beta +2+h\right)\theta -4\left({r}_{0}+1\right)b-2\left({r}_{0}+1\right)c-2\left(\beta t+1\right)-h}{4\left({\theta }^{2}-1\right)}\end{array}$$

(A.47)

$$\begin{array}{c}{w}^{BB*}=\frac{\left[\left(2b+2c\right){r}_{2}+2c\right]{\theta }^{2}-\left(2\beta t+2+h\right)\theta -2\left(b+c\right){r}_{2}-2\left(1+c\right)-2\beta -h}{4\left({\theta }^{2}-1\right)}\end{array}$$

(A.48)

Substituting ${p}_{m}^{BB}$ and ${w}^{BB}$ into ${p}_{r}^{BB}\left({w}^{BB},{p}_{m}^{BB}\right)$ obtains

$$\begin{array}{c}{p}_{r}^{BB*}=\frac{{A}_{4}{\theta }^{2}-{B}_{4}\theta -6\beta -6-\left(2{r}_{2}+4\right)b-\left(2{r}_{2}+2\right)c-3h}{8\left({\theta }^{2}-1\right)}\end{array}$$

(A.49)

Substituting ${p}_{m}^{BB}$, ${w}^{BB}$, and ${p}_{r}^{BB}$ into $E\left({\pi }_{r}^{BB}\right)$, $E\left({\pi }_{m}^{BB}\right)$, and $E\left({\pi }_{f}^{BB}\right)$, we obtain

$$\begin{array}{c}{E\left({\pi }_{r}^{BB}\right)}^{*}=\frac{{\left[2\left({r}_{0}+1\right)\left(\frac{c}{2}+b\right)\theta -b\left({r}_{2}+2\right)-c\left({r}_{2}+1\right)+\beta +1+\frac{h}{2}\right]}^{2}}{16}\end{array}$$

(A.50)

$$\begin{array}{c}{E\left({\pi }_{m}^{BB}\right)}^{*}=\frac{{C}_{4}{\theta }^{4}+{D}_{4}{\theta }^{3}+{E}_{4}{\theta }^{2}+{F}_{4}\theta +{H}_{4}{b}^{2}+{I}_{4}b+{J}_{4}{c}^{2}+{K}_{4}c+{L}_{4}}{32\left({\theta }^{2}-1\right)}\end{array}$$

(A.51)

$$\begin{array}{c}{E\left({\pi }_{f}^{BB}\right)}^{*}=\left({\theta }^{2}-2\right) {\left(\frac{c}{2}+b\right)}^{2}{{r}_{0}}^{2}+\left(\frac{c}{2}+b\right){M}_{4}{r}_{0}+G\end{array}$$

(A.52)

$$ \begin{aligned} & (A_{4} = [2(r_{0} + 1)(c + 2b)]\theta^{3} + [2\beta + 2 + (2r_{2} + 4)b + (2r_{2} + 2)c + h];\\ &B_{4} = 4(r_{0} + 1)b + 2(r_{0} + 1)c + 4\beta t + 4 + 2h;\\ &C_{4} = - 8(r_{0} + 1)^{2} (c + 2b)^{2} ;\\ &D_{4} = - 8(r_{0} + 1)(c + 2b)\left[ {(r_{2} + 2)b + (r_{2} + 1)c + \beta + 1 + \frac{h}{2}} \right]; \\ & E_{4} = \left( {48r_{0}^{2} + 4r_{2}^{2} + 96r_{0} + 16r_{2} + 64} \right)b^{2} + \left[ {\left( {48r_{0}^{2} + 8r_{2}^{2} + 96r_{0} + 24r_{2} + 64} \right)c} \right. \\ & \left.\qquad { - \left( {32\beta t + 32 + 16h} \right)r_{0} - \left( {8\beta + 8 + 4h} \right)r_{2} - \left( {32t + 16} \right)\beta - 48 - 24h} \right]b\\ &\qquad + (12r_{0}^{2} + 4r_{2}^{2} + 24r_{0} + 8r_{2} + 16)c^{2} + [( - 16\beta t - 16 - 8h)r_{0}\\ &\qquad - (8\beta + 8 + 4h)r_{2} + ( - 16t - 8)\beta - 24 - 12h]c - 16r_{2} \rho - 4\beta^{2}\\ &\qquad - 8\left( {1 + \frac{h}{2}} \right)\beta - 16\rho - 4 - 4h - h^{2} - 32G; \\ &F_{4} = 16\left( {r_{0} + 1} \right)\left( {r_{2} + 2} \right)b^{2} + 24\left( {r_{0} + 1} \right)b\left[ {\left( {r_{2} + \frac{4}{3}} \right)c + \frac{2\beta }{3} + \frac{2}{3} + \frac{h}{3}} \right]\\ &\qquad + 8\left( {r_{0} + 1} \right)\left( {r_{2} + 2} \right)c^{2} + 8c\left( {r_{0} + 1} \right)\left( {\beta + 1 + \frac{h}{2}} \right) - 16\left( {\beta t + 1 + \frac{h}{2}} \right)\left( {\beta + 1 + \frac{h}{2}} \right); \\ & H_{4} = - 32r_{0}^{2} - 4r_{2}^{2} - 64r_{0} - 16r_{2} - 48;\\ &I_{4} = \left( { - 32r_{0}^{2} - 8r_{2}^{2} - 64r_{0} - 24r_{2} - 48} \right)c + \left( {32\beta t + 32 + 16h} \right)r_{0} + \left( {8\beta + 8 + 4h} \right)r_{2}\\ &\qquad + \left( {32t + 16} \right)\beta + 48 + 24h; \\ & J_{4} = - 8r_{0}^{2} - 4r_{2}^{2} - 16r_{0} - 8r_{2} - 12;\\ &K_{4} = \left( {16\beta t + 16 + 8h} \right)r_{0} + \left( {8\beta + 8 + 4h} \right)r_{2} + \left( {16t + 8} \right)\beta + 24 + 12h; \\ & L_{4} = - 16r_{2} \rho - \left( { - 8t^{2} - 4} \right)\beta^{2} - 16\beta \left( {t + \frac{1}{2}} \right)\left( {1 + \frac{h}{2}} \right) + 16\rho - 12 - 12h - 3h^{2} + 32G;\\ &M_{4} = \left( {\frac{c}{2} + b} \right)\theta^{2} + \left[ {\left( {\frac{{r_{2} }}{2} + 1} \right)b + \left( {\frac{{r_{2} }}{2} + \frac{1}{2}} \right)c + \frac{\beta }{2} + \frac{1}{2} + \frac{h}{2}} \right]\theta\\ &\qquad + \beta t + 1 - 2b - c + \frac{h}{2} \\ \end{aligned} $$

Proof of Corollary 5

• (1) $\frac{\partial {w}^{BB*}}{\partial t}=-\frac{\theta \beta }{2\left({\theta }^{2}-1\right)}>0$

• (2) $\frac{\partial {p}_{m}^{BB*}}{\partial t}=-\frac{\beta }{2\left({\theta }^{2}-1\right)}>0$

• (3) $\frac{\partial {p}_{r}^{BB*}}{\partial t}=-\frac{\theta \beta }{2\left({\theta }^{2}-1\right)}>0$

• (4) $\frac{\partial {E\left({\pi }_{r}^{BB}\right)}^{*}}{\partial t}=0$

• (5) $\frac{\partial {E\left({\pi }_{m}^{BB}\right)}^{*}}{\partial t}=-\frac{2\beta \left[2\left({r}_{0}+1\right)\left(\frac{c}{2}+b\right){\theta }^{2}+\left(\beta +1+\frac{h}{2}\right)\theta -\left(2b+c\right)\left({r}_{0}+1\right)+\beta t+1+\frac{h}{2}\right]}{4{\theta }^{2}-4}>0$

• (6) $\frac{\partial {E\left({\pi }_{f}^{BB}\right)}^{*}}{\partial t}=\left(\frac{c}{2}+b\right)\beta {r}_{0}>0$

Proof of Corollary 6

• (1) $\frac{\partial {w}^{BB*}}{\partial b}=\frac{{r}_{2}}{2}>0$

• (2) $\frac{\partial {p}_{m}^{BB*}}{\partial b}={r}_{0}+1>0$

• (3) $\frac{\partial {p}_{r}^{BB*}}{\partial b}=\frac{2\left(1+{r}_{0}\right)\theta +{r}_{2}+2}{4}>0$

  When $0<b<{b}_{4}$, $\frac{\partial {E\left({\pi }_{r}^{BB}\right)}^{*}}{\partial b}<0$; $b>{b}_{4}$, $\frac{\partial {E\left({\pi }_{r}^{BB}\right)}^{*}}{\partial b}>0$;

  When $0<b<{b}_{5}$, $\frac{\partial {E\left({\pi }_{m}^{BB}\right)}^{*}}{\partial b}<0$; $b>{b}_{5}$, $\frac{\partial {E\left({\pi }_{m}^{BB}\right)}^{*}}{\partial b}>0$;

  When $0<b<{b}_{6}$, $\frac{\partial E{\left({\pi }_{f}^{BB}\right)}^{*}}{\partial b}>0$; $b>{b}_{6}$, $\frac{\partial E{\left({\pi }_{f}^{BB}\right)}^{*}}{\partial b}<0.$

  (${b}_{4}=\frac{2\theta \left({r}_{0}+1\right)c-\left(2{r}_{2}+2\right)c+2\beta +2+h}{4\left(1-\theta -{r}_{0}\theta \right)+2{r}_{0}}$; ${b}_{6}=-\frac{4c\left({r}_{0}+1\right){\theta }^{2}-\left[2\beta +2+\left(3{r}_{2}+4\right)c+h\right]\theta +\left(8{r}_{0}+8\right)c-4\beta t-4-2h}{8\left({r}_{0}{\theta }^{2}+{\theta }^{2}\right)+\left(4{r}_{2}+8\right)\theta -16{r}_{0}-16}$;

  ${b}_{5}=\frac{-4c\left({r}_{0}+1\right){\theta }^{2}-\left[4\beta +4+\left(6{r}_{2}+8\right)c+2h\right]\left({r}_{0}+1\right)\theta +8{{r}_{0}}^{2}c-\left(8\beta t+8-16c+4h\right){r}_{0}+\left(2{{r}_{2}}^{2}+6{r}_{2}+12\right)c-\left(2\beta +2+h\right){r}_{2}-\left(8t+4\right)\beta -12-6h}{8{\left({r}_{0}+1\right)}^{2}{\theta }^{2}+\left(8{r}_{0}+8\right)\left({r}_{2}+2\right)\theta -16{{r}_{0}}^{2}-2{{r}_{2}}^{2}-32{r}_{0}-8{r}_{2}-24}$)

Proof of Corollary 7

The results of the manufacturer's optimal wholesale price comparison are as follows:

• (1) When using the EP financing strategy ${w}^{PB*}-{w}^{PN*}=\frac{4b{r}_{1}\left(\theta -1\right)-h}{4\theta -4}>0$.

• (2) When using the EB financing strategy ${w}^{BB*}-{w}^{BN*}=\frac{2b{r}_{2}\left(\theta -1\right)-h}{4\theta -4}>0$.

• (3) When blockchain is not used ${w}^{PN*}-{w}^{BN*}=\frac{\left(2{r}_{1}-{r}_{2}\right)c}{2}$, when using the blockchain${w}^{PB*}-{w}^{BB*}=\left(b+c\right)\left({r}_{1}-\frac{{r}_{2}}{2}\right)$; therefore, when${r}_{1}>\frac{{r}_{2}}{2}$,${w}^{PN*}>{w}^{BN*}$,${w}^{PB*}>{w}^{BB*}$; when${r}_{1}<\frac{{r}_{2}}{2}$,${w}^{BN*}>{w}^{PN*}$,${w}^{BB*}>{w}^{PB*}$. Since${w}^{BB*}-{w}^{PN*}=\frac{4\left(\theta -1\right)\left(b+c\right){r}_{2}-2c\theta {r}_{1}+2c{r}_{1}-h}{4\theta -4}>0$, so when${r}_{1}>\frac{{r}_{2}}{2}$,${w}^{PB*}>{w}^{BB*}>{w}^{PN*}>{w}^{BN*}$. Since${w}^{PB*}-{w}^{BN*}=\frac{2\left(\theta -1\right)\left(b+c\right){r}_{2}-4c\theta {r}_{1}+4c{r}_{1}-h}{4\theta -4}>0$, so when${r}_{1}>\frac{{r}_{2}}{2}$,${w}^{BB*}>{w}^{PB*}>{w}^{BN*}>{w}^{PN*}$.

Proof of Corollary 8

The results of the comparison of optimal pricing for products in the retail channel are as follows:

• (1) When using the EP financing strategy ${p}_{r}^{PB*}-{p}_{r}^{PN*}=\frac{4b{\theta }^{2}\left({r}_{0}+1\right)-\left(4b{r}_{0}+h\right)\theta -4b-3h}{8\theta -8}>0$

• (2) When using the EB financing strategy ${p}_{r}^{BB*}-{p}_{r}^{BN*}=\frac{4b{\theta }^{2}\left({r}_{0}+1\right)+\left[\left(-4{r}_{0}+2{r}_{2}\right)b+h\right]\theta -\left(2{r}_{2}+4\right)b-3h}{8\theta -8}>0$

• (3) When blockchain is not used ${p}_{r}^{PN*}-{p}_{r}^{BN*}=-\frac{c{r}_{2}}{4}<0$, when using the blockchain ${p}_{r}^{PB*}- {p}_{r}^{BB*}=-\frac{(b+c){r}_{2}}{4}<0$;${p}_{r}^{PB*}-{p}_{r}^{BN*}=\frac{4b\left({r}_{0}+1\right){\theta }^{2}-\left(4b{r}_{0}+2c{r}_{2}-h\right)\theta +2c{r}_{2}-4b-3h}{8\theta -8}>0$, so ${p}_{r}^{BB*}>{p}_{r}^{PB*}>{p}_{r}^{BN*}>{p}_{r}^{PN*}$.

Proof of Corollary 9

The results of the comparison of the optimal pricing of products in the online channel are as follows:

• (1) When using the EP financing strategy ${p}_{m}^{PB*}-{p}_{m}^{PN*}=\frac{4b\left(\theta -1\right)\left({r}_{0}+1\right)-h}{4\theta -4}>0$.

• (2) When using the EB financing strategy ${p}_{m}^{BB*}-{p}_{m}^{BN*}=\frac{4b\left(\theta -1\right)\left({r}_{0}+1\right)-h}{4\theta -4}>0$.

• (3) ${p}_{m}^{PN*}-{p}_{m}^{BN*}=0$, and ${p}_{m}^{PB*}-{p}_{m}^{BB*}=0$, therefore ${p}_{m}^{PB*}={p}_{m}^{BB*}>{p}_{m}^{PN*}={p}_{m}^{BN*}$.

Appendix B

The optimal pricing and the optimal expected profits under the model KPN are in Table 7.

Table 7 The optimal solutions of model KPN

Where ${A}_{5}=\left(3{{r}_{0}}^{2}+6{r}_{0}+4\right){c}^{2}-\left[\left(4{r}_{0}+2t+4\right)\beta +4{r}_{0}+6\right]c-{\beta }^{2}{t}^{2}-4{r}_{0}\rho -2\beta t-8G-4\rho -1$, ${B}_{5}=\left(2{r}_{0}+2\right){c}^{2}+2c\left(\beta t+1\right)\left({r}_{0}+1\right)-4\left(\beta +1\right)\left(\beta t+1\right)$, ${C}_{5}=\left(-2{{r}_{0}}^{2}-4{r}_{0}-3\right){c}^{2}+\left[\left(4{r}_{0}+2t+4\right)\beta +4{r}_{0}+6\right]c-\left({t}^{2}+2\right){\beta }^{2}-\left(2t+4\right)\beta +4{r}_{0}\rho +8G+4\rho -3$.

The optimal pricing and the optimal expected profits under the model KPB are in Table 8.

Table 8 The optimal solutions of model KPB

Where ${A}_{6}=4(2\beta t+4b+2c+h+2)(c+2b)({r}_{0}+1)$, ${B}_{6}=\left(48{{r}_{0}}^{2}+96{r}_{0}+64\right){b}^{2}+\left[\left(48{{r}_{0}}^{2}+96{r}_{0}+64\right)c-\left(16h+32\beta +32\right){r}_{0}-\left(16t+32\right)\beta -24h-48\right]b+\left(12{{r}_{0}}^{2}+24{r}_{0}+16\right){c}^{2}+\left[\left(-8h-16\beta -16\right){r}_{0}-\left(8t+16\right)\beta -12h-24\right]c-16{r}_{0}\rho -4{\beta }^{2}{t}^{2}-4t\beta \left(h+2\right)-{h}^{2}-32G-4h-16\rho -4$, ${C}_{5}=\left(32{r}_{0}+32\right){b}^{2}+8\left(2\beta t+4c+h+2\right)\left({r}_{0}+1\right)b+\left(8{r}_{0}+8\right){c}^{2}+4\left({r}_{0}+1\right)\left(2\beta t+h+2\right)c-4(2\beta +h+2)(2\beta t+h+2)$, ${D}_{5}=-\left(32{{r}_{0}}^{2}+64{r}_{0}+48\right){b}^{2}+\left[\left(32{{r}_{0}}^{2}+64{r}_{0}+48\right)c+\left(16h+32\beta +32\right){r}_{0}+\left(16t+32\right)\beta +24h+48\right]b-\left(8{{r}_{0}}^{2}+16{r}_{0}+12\right){c}^{2}+\left[\left(8h+16\beta +16\right){r}_{0}+\left(8t+16\right)\beta +12h+24\right]c+16{r}_{0}\rho -4{\beta }^{2}{t}^{2}-8{\beta }^{2}-4\beta \left(t+2\right)\left(h+2\right)-3{h}^{2}+32G-12h+16\rho -12$, ${E}_{5}={r}_{0}\big\{\left(8{\theta }^{2}+8\theta -16\right){b}^{2}+\big[\left(8{\theta }^{2}+8\theta -16\right)c+\left(4\beta t+2h+4\right)\theta +4h+8\beta +8\big]b+\left(2{\theta }^{2}+2\theta -4\right){c}^{2}+\big[\left(2\beta t+h+2\right)\theta +2h+4\beta +4\big]c+4\rho \big\}$.

The optimal pricing and the optimal expected profits under the model KBN are in Table 9.

Table 9 The optimal solutions of model KBN

Where ${A}_{7}=(1-{\theta }^{2})\left[{({r}_{0}+1)}^{2}{\theta }^{2}+2\left({r}_{0}+1\right)\left({r}_{2}+1\right)\theta -2{{r}_{0}}^{2}-{{r}_{2}}^{2}-4{r}_{0}-2{r}_{2}-3\right])$, ${B}_{7}=(1-{\theta }^{2})\left[\left(\beta t+1\right)\left({r}_{0}+1\right)\theta +\left(2{r}_{0}+2+t+{r}_{2}t\right)\beta +2{r}_{0}+{r}_{2}+3\right]$, ${C}_{7}={\beta }^{2}{t}^{2}+2\beta t+4{r}_{0}\rho +8G+4\rho +1$.

The optimal pricing and the optimal expected profits under the model KBB are in Table 10.

Table 10 The optimal solutions of model KBB

Where ${A}_{8}=(2{r}_{2}+4)b+(2{r}_{2}+2)c+2\beta t+h+2$, ${B}_{8}=(2b+c)(2{r}_{0}+2)-2h-4\beta -4$, ${C}_{8}=4(c+2b)({r}_{0}+1)[2({r}_{2}+2)b+2({r}_{2}+1)c+2\beta t+h+2]$, ${D}_{5}=(48{{r}_{0}}^{2}+4{{r}_{2}}^{2}+96{r}_{0}+16{r}_{2}+64){b}^{2}+[(48{{r}_{0}}^{2}+8{{r}_{2}}^{2}+96{r}_{0}+24{r}_{2}+64)c-(16h+32\beta +32){r}_{0}-(8t{r}_{2}+16t+32)\beta -4(h+2)({r}_{2}+6)]b+(12{{r}_{0}}^{2}+4{{r}_{2}}^{2}+24{r}_{0}+8{r}_{2}+16){c}^{2}-[(8h+16\beta +16){r}_{0}+(8t{r}_{2}+8t+16)\beta +4(h+2)({r}_{2}+3)]c-16{r}_{0}\rho -4{\beta }^{2}{t}^{2}-4\beta t(h+2)-{h}^{2}-32G-4h-16\rho -4$, ${E}_{8}=16({r}_{0}+1)({r}_{2}+2){b}^{2}+8[(3{r}_{2}+4)c+2\beta t+h+2]({r}_{0}+1)b+8({r}_{0}+1)({r}_{2}+2){c}^{2}+4({r}_{0}+1)(2\beta t+h+2)-4(2\beta t+h+2)(2\beta +h+2)$, ${F}_{8}=-(32{{r}_{0}}^{2}+4{{r}_{2}}^{2}+64{r}_{0}+16{r}_{2}+48){b}^{2}+[-(32{{r}_{0}}^{2}+8{{r}_{2}}^{2}+64{r}_{0}+24{r}_{2}+48)c+(16h+32\beta +32){r}_{0}+(8t{r}_{2}+8t+32)\beta +4(h+2)({r}_{2}+6)]b-(8{{r}_{0}}^{2}+4{{r}_{2}}^{2}+16{r}_{0}+8{r}_{2}+12){c}^{2}+[(8h+16\beta +16){r}_{0}+(8t{r}_{2}+8t+16)\beta +4(h+2)({r}_{2}+3)]c+16{r}_{0}\rho -(4{t}^{2}+8){\beta }^{2}-4\beta (h+2)(t+2)-{3h}^{2}+32G-12h+16\rho -12$, ${H}_{8}=2{(c+2b)}^{2}{\theta }^{2}+(c+2b)[2({r}_{2}+2)b+2({r}_{2}+1)c+2\beta t+h+2]-16{b}^{2}+(-16c+4h+8\beta +8)b-4{c}^{2}+(2h+4\beta +4)c+4\rho$.