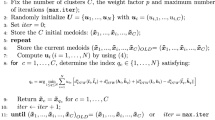1 Introduction

Grouping complex objects into a partition that satisfies the principle of maximum internal cohesion is still an ongoing research topic and a challenging task in the specific literature on clustering techniques. Multivariate time series, which are characterized by multiple features, belong to this class of objects. They can be thought of as three-way data arrays where the third dimension is time so that they are a collection of observations on the same units and the same variables indexed by time. Thanks to the growing amount of this type of data, time series are becoming widespread and are used in a wide range of fields, including climate, economic, and social research, as well as healthcare and finance, among others. Due to the complexity of the features space, more attention must be paid to the choice of an appropriate proximity measure to be used in the clustering process and to the consideration of relaxing the rigid crisp assignment of each object to only one cluster. This study addresses both issues by proposing a fuzzy clustering method that allows units to belong to more than one cluster and embeds a suitable dissimilarity measure robust against “anomalous” time series, as discussed in detail later.

In the specific literature on this subject, including both robust and non-robust techniques, three main approaches can be distinguished (D’Urso, 2015): observation-based, features-based and model-based. The first group uses dissimilarity measures based on the observed values of the time series (D’Urso et al., 2018, 2021) while second group those based on several features like quantile cross-spectral densities (López-Oriona et al. 2022a, b, c), quantile autocovariance (Lafuente-Rego et al., 2020; Vilar et al., 2018), autocorrelation function (Alonso and Maharaj, 2006) and generalized cross-correlation (Alonso et al., 2021), cepstral coefficients (Maharaj and D’Urso, 2011), periodogram (Caiado et al., 2006, 2009), wavelets decomposition (D’Urso and Maharaj, 2012; D’Urso et al., 2023; Maharaj et al., 2010).

The third group uses suitable dissimilarity measures among the parameter estimates arising from suitable fitted time series models like ARIMA models (D’Urso et al., 2015; Piccolo, 1990; Xiong and Yeung, 2004), GARCH and INGARCH models (Caiado and Crato, 2010; Cerqueti et al., 2022; D’Urso et al., 2013a; Otranto, 2008, 2010), extreme value analysis (D’Urso et al., 2017a), splines coefficients (D’Urso et al., 2021) and copulas (De Luca and Zuccolotto, 2011, 2017; Disegna et al., 2017; Durante et al., 2015).

As far as robust techniques are concerned, they can be further classified into the following four approaches:

  • noise approach: given C clusters, it assigns the outlier time series to the \((C+1)\)-th cluster, the so-called noise cluster (D’Urso et al., 2013b);

  • metric approach: the objective function is characterized by a distance satisfying robust properties (D’Urso et al., 2015, 2016);

  • trimmed approach: the clustering technique is applied to a subset of objects, those who remain after a fixed number of outliers is deleted (D’Urso et al., 2017b);

  • influence weighting approach: a weighting system is proposed that assigns low weights to the outliers objects (D’Urso, 2005b).

With the aim of defining a clustering technique able to identify natural groups of multivariate time series even when some of them are noisy time-varying units, following a metric approach, we propose a robust fuzzy medoids-based clustering method characterized by an entropy regularization term. In general, the fuzzy clustering with entropy regularization (Li and Mukaidono, 1995, 1999; Miyamoto and Mukaidono, 1997) answers the need to address the criticism made by some researchers on the role of the exponent “m”, i.e. the fuzziness coefficient that controls the extent of membership shared among the fuzzy clusters in the well-known Fuzzy C-Means (FCM) clustering method (Bezdek, 1974, 1981; Dunn, 1974).

The main advantage of the maximum entropy principle is that it offers a new perspective on the problem of fuzzifying the partition while ensuring the maximum compactness of the obtained clusters (Coppi and D’Urso, 2006; D’Urso et al., 2023; Gao et al., 2019; Kahali et al., 2019). The objective function includes an entropy term i.e. the Shannon entropy, called fuzzy entropy when applied to the membership degrees. Fuzziness is controlled by this term; specifically, the minimization of the functional is regularized by maximizing the total amount of information (Coppi and D’Urso, 2006).

In our proposal, the objective function is further characterized by a suitable robust dissimilarity measure that can detect natural groups even in the presence of outliers. As pointed out by García-Escudero et al. (2008), “the precise detection of the outliers is an important task due to the serious troubles they introduce in standard clustering procedures as well as the appealing interest that outliers could have by themselves after explaining why they depart from general behaviour”.

García-Escudero et al. (2003) also distinguish between clustered and radial outliers: the former could be a smaller group of objects than the main clusters while the latter could be isolated objects, each forming its own group. In both definitions, however, they significantly differ from all other objects belonging to the natural groups.

In the context of time series clustering, an outlier can have different specifications. In this paper, we name “outlier” a time series with an anomalous behaviour, more specifically, with dynamics that deviate markedly from that of all other objects.

Following the metric approach, we propose an exponential transformation of the chosen dissimilarity (Wu and Yang, 2002; Zhang and Chen, 2004), i.e. we define a suitable exponential transformation of the Dynamic Time warping based on the Euclidean distance.

The proposed clustering method can identify natural group structures counteracting the negative effect of some anomalous and time-switching units.

We must point out that a considerable amount of the literature has already been devoted to the same purposes, although it essentially focuses on robust versions of the fuzzy prototype-based clustering methods based on the “m” exponent. To the best of our knowledge, no other robust version of the fuzzy clustering medoids-based techniques with entropy regularization for time series has been already introduced.

The implementation of a medoids-based clustering method (FCMd, Krishnapuram et al. 1999, 2001) provides an additional advantage since the prototype, i.e. the medoid, is an observed unit in the dataset rather than a “fictitious” prototype time series as in the fuzzy C-means. Specifically, the medoids are objects whose overall distance with respect to all other objects within the same cluster is minimal. It is noteworthy that the identification of representative non-fictitious prototypes is of great importance in practical applications, in particular for the interpretation of clusters.

Moreover, the main advantage of the FCMd is related to a series of computational aspects: it is more efficient since the distance matrix needs to be computed once at the beginning of the iterative process and it is less affected by getting stuck in a local optima or by convergence problems (Everitt et al., 2001; Hwang et al., 2007). Furthermore, FCMd is considered more robust than FCM if noise or outliers occur in the data, being the medoid less influenced by such extreme values than the mean.

Summing up, we argue that the main contribution of this research study lies in the definition of a comprehensive and unified methodological framework that exploits the single advantages of each approach. Specifically, the new proposal benefits from (a) the use of the observation-based methodology, which is easy to apply and, thanks to the DTW, can handle time series of different lengths; (b) the relatively lower complexity of the non-hierarchical approach; (c) the PAM approach, which allows the identification of real observed prototypes; (d) the fuzzy framework which provides the degree of uncertainty in the process of assigning objects to clusters, particularly useful in the case of complex data; (e) the use of entropy as a regularization term in the objective function and (f) the metric approach which allows outliers to be dealt with. All this represents an improvement in terms of overall information gain, and thus a strength compared to other robust time series clustering methods proposed in the literature.

The outline of the article is as follows. In Sect. 2, after the introduction to DTW, we describe in detail the proposed robust fuzzy clustering method with entropy regularization. Section 3 reports the results of the simulation studies. In Sect. 4, we report and discuss the results of the application to air pollution data. Section 5 concludes.

2 Research method

In this Section, we introduce the reader to the instruments and the proposed method for handling three-way data. A further source of complexity arises from the presence of some anomalous or switching time series: this issue has been addressed by defining a robust fuzzy clustering method. In the next paragraphs, we provide a formal description of a three-way data array (paragraph 2.1), then introduce DTW and its exponential transformation (paragraph 2.2), the proposed robust method (paragraph 2.3) and the validity measure used, i.e. the Fuzzy Silhouette index (paragraph 2.4).

2.1 The three-way data array

A three-way data array of type “same objects \(\times \) same quantitative variables \(\times \) times”, can be algebraically formalized as follows (D’Urso, 2000, 2004, 2005b):

$$\begin{aligned} {\textbf{X}}\equiv \{x_{ijt}:i=1,\ldots ,I;\;j=1,\ldots ,J;\;t=1,\ldots ,T\} \end{aligned}$$
(1)

where the indices i, j and t stand, respectively, for the units, the quantitative variables and the times and \(x_{ijt}\) is the value of the j-th variable observed for the i-th unit at time t. In this paper, we take into account the case in which \({\textbf{X}}\) is represented in the space of the “units” thus \(\Re ^{J+1}\) (J dimensions corresponding to the J variables plus one dimension corresponding to the time). Thus, the matrix \({\textbf{X}}_i\equiv \{{\textbf{x}}_{it}:\;t=1,\ldots ,T\}\) represents the i-th multivariate time series where \({\textbf{x}}_{it}\equiv (x_{i1t},\ldots ,x_{ijt},\ldots ,x_{iJt}),\;i=1,\ldots ,I,\;t=1,\ldots ,T\).

2.2 Dynamic time warping

The Dynamic Time Warping (DTW, Berndt 1994; Velichko and Zagoruyko 1970) allows to find an optimal alignment between two given time sequences under certain restrictions. Properly, the sequences are warped in a nonlinear way to match each other. Let \({\textbf{X}}_{i}\equiv \lbrace {{\textbf{x}}_{i1},\ldots , {\textbf{x}}_{it},\ldots , {\textbf{x}}_{iT}}\rbrace \) and \({\textbf{X}}_{i^{'}}\equiv \lbrace {{\textbf{x}}_{i^{'}1},\ldots , {\textbf{x}}_{i^{'}t^{'}},\ldots , {\textbf{x}}_{i^{'}T^{'}}}\rbrace \) two multivariate time series for which T and \(T^{'}\) could be not equal. The total distance between \({\textbf{X}}_{i}\) and \({\textbf{X}}_{i^{'}}\) is computed through the so-called “warping path” that “realigns” the time indices of the multivariate time series so that each data point in \({\textbf{X}}_{i}\) is compared to the “closest” data point in \({\textbf{X}}_{i^{'}}\).

The warping path is defined as follows. Let

$$\begin{aligned} \varPhi _{l} = (\varphi _{l},\psi _{l}), \quad l = 1,\ldots , L \end{aligned}$$

be a set of realigned indices \(1,\ldots , T\) and \(1,\ldots , T^{'}\) under the following constraints:

  1. 1.

    Boundary condition: \(\varPhi _{1}=(1, 1), \varPhi _{L}=(T, T^{'})\);

  2. 2.

    Monotonicity condition: \(\varphi _{1}\le \cdots \le \varphi _{l}\le \cdots \le \varphi _{L} \, and \, \psi _{1}\le \cdots \le \psi _{l} \le \cdots \le \psi _{L}.\)

The warping curve applied to the two multivariate time series \({\textbf{X}}_{i}\) and \({\textbf{X}}_{i^{'}}\) realigns their time indices through the functions \(\varphi \) and \(\psi \). The total dissimilarity between the two “warped” multivariate time series is:

$$\begin{aligned} \sum _{l=1}^{L}d({\textbf{x}}_{i,\varphi _{l}},{\textbf{x}}_{i',\psi _{l}})m_{l,\varPhi } \end{aligned}$$
(2)

where \(m_{l,\varPhi }\) is a local weighting coefficient and d(., .) is, usually, the Euclidean distance for multivariate time series.

Among several warping curves, DTW is the one that minimizes the total dissimilarity between \({\textbf{X}}_{i}\) and \({\textbf{X}}_{i^{'}}\). By preserving the time ordering of the sequence, DTW goes beyond the instantaneous features of time data and satisfies the following properties: it allows the comparison of multivariate time series of different lengths and does not require any assumption concerning the properties of the multivariate time series. Moreover, it takes into account the non-linear rate at which each component of a multivariate time series can vary.

Even if the DTW algorithm could be problematic with long time series, when used in the Partitioning around Medoids (PAM) method, its computational burden is reduced since the distance or the dissimilarity matrix is computed only once in the iterative process. We also specify that, in this study, we used as constraints the Itakura parallelogram (Itakura, 1975).

2.2.1 The exponential transformation of the dynamic time warping based on the Euclidean distance

As pointed out by García-Escudero and Gordaliza (2005), the medoids-based fuzzy methods represent only a “timid” robustification with respect to centroids-based clustering techniques. To cope with this issue, as suggested by Wu and Yang (2002) and D’Urso et al. (2018), we apply the following exponential transformation:

$$\begin{aligned} dtw_{d^2_{exp}}({\textbf{X}}_{i},{\textbf{X}}_{i^{'}})=1-exp \lbrace - \beta \cdot \left[ D({\textbf{X}}_i,{\textbf{X}}_{i^{'}})\right] ^{2}\rbrace _{i \ne i^{'}} \quad \text {with} \quad i,i^{'}=1 \ldots n, \end{aligned}$$
(3)

where \(\left[ D({\textbf{X}}_i,{\textbf{X}}_{i^{'}})\right] ^{2}\) is the squared dissimilarity based on DTW between the i-th and the \(i^{'}\)-th time series, respectively.

Since \(\beta \) must be set as the inverse of some measure of data variability, we adapt in the context of the entropy-based fuzzy clustering methods the \(\beta \)’s formulation proposed by D’Urso et al. (2018) for the same scopes and denoted here by \(\widetilde{\beta }\). By considering a multiplicative factor, k, we have:

$$\begin{aligned} \beta =k\cdot \widetilde{\beta }, \,\,\, \text {with} \,\, k \in \lbrace 1,2 \rbrace \end{aligned}$$
(4)

where

$$\begin{aligned} \widetilde{\beta }= \left[ \frac{\sum _{i=1}^{n} \left[ D({\textbf{X}}_i,\tilde{{\textbf{X}}}_q)\right] ^{2}}{n} \right] ^{- 1} \end{aligned}$$
(5)

and \(\tilde{{\textbf{X}}}_q: q=arg\, min_{1 \le i\le n}\sum _{i^{'}=1}^{n} \left[ D({\textbf{X}}_i,\tilde{{\textbf{X}}}_{i^{'}})\right] ^{2}\).

The dissimilarity based on the exponential transformation lies in the interval [0, 1] and is sensitive to the \(\beta \)’s value: it tends to its maximum more rapidly as the \(\beta \)’s value increases. The most important characteristic to note is that it assigns the outliers to the C clusters with the same membership degree (approximately 1/C), treating them as fuzzy units.

This smoothing effect on the membership degrees also depends on the characteristics of the clusters. If they are well-separated, all units far from the medoids are candidates as outliers; in the case of overlapping clusters or well-separated clusters but with a large number of anomalous units, the method tends to assign approximately equal membership degrees to the units that are only slightly separated from the bulk of data (D’Urso et al., 2018). As far as the role of k is concerned, we refer to Sect. 3 for a more detailed analysis.

The next paragraph provides the mathematical formalization of the fuzzy C-medoids clustering method with the entropy term and the exponential transformation of DTW, henceforth called DTW-Exp-FCMd-E.

2.3 The robust DTW-based entropy fuzzy clustering method

The robust DTW-based entropy fuzzy clustering method (DTW-Exp-FCMd-E) allows to identify C prototypes, i.e. the subset of medoids (\({\textbf{X}}_1,\ldots ,{\textbf{X}}_C\)) where C is the number of clusters, and the matrix of the fuzzy coefficients \({\textbf{U}}_{n \times C}\), by minimizing the following objective function:

$$\begin{aligned} \left\{ \begin{array}{ll} min: \quad &{}\sum _{i=1}^{n} \sum _{c=1}^{C} u_{ic}\,{_{dtw}} {d^{2}}_{exp}({\textbf{X}}_i,\widetilde{{\textbf{X}}}_c)+p \sum _{i=1}^{n} \sum _{c=1}^{C} u_{ic} ln(u_{ic})\\ &{}=\sum _{i=1}^{n} \sum _{c=1}^{C} u_{ic}\left( 1-exp\left\{ -\beta \left[ D({\textbf{X}}_i,\widetilde{{\textbf{X}}}_c)\right] ^{2} \right\} \right) +p \sum _{i=1}^{n} \sum _{c=1}^{C} u_{ic} ln(u_{ic}) \\ \text {s.t.} \quad &{} \sum _{c=1}^{C} u_{ic}=1, \, u_{ic}\ge 0.\\ \end{array} \right. \end{aligned}$$
(6)

\({\textbf{X}}_i\) and \(\widetilde{{\textbf{X}}}_c\) are the multivariate time series of the i-th unit and the c-th medoid respectively, while D(\(\cdot \)) is the dissimilarity based on DTW for multivariate time series. The second addend in the objective function represents the entropy regularization term: the Shannon entropy (pre-multiplied by \(-1\)) is multiplied by the weight factor p that controls the contribution of the regularization function to the clustering criterion and is called the degree of fuzzy entropy.

Therefore the total functional is optimized by both maximizing the internal cohesion and the given measure of entropy.

The \(u_{ic}\) denotes the membership degree of the i-th unit to the c-th cluster. The solutions for each \(u_{ic}\), for \(i=1,\ldots , I\) and \(c=1,\ldots ,C\), is:

$$\begin{aligned} u_{ic} = \dfrac{1}{\sum _{c^{'}=1}^{C} \left[ \dfrac{exp\left( \dfrac{1}{p}{\left[ 1-exp\left\{ -\beta \left[ D({\textbf{X}}_i,\widetilde{{\textbf{X}}}_c) \right] ^{2}\right\} \right] }\right) }{exp\left( \dfrac{1}{p}{\left[ 1-exp\left\{ -\beta \left( D({\textbf{X}}_i,\widetilde{{\textbf{X}}}_{c^{'}}) \right) ^{2}\right\} \right] }\right) }\right] } \end{aligned}$$
(7)

Proof

We consider the Lagrangian function:

$$\begin{aligned} L_p({\textbf{u}}_i,\lambda ){} & {} =\sum _{i=1}^{n}\sum _{c=1}^{C}u_{ic} \left[ 1-exp\left\{ -\beta \left( D({\textbf{X}}_i,\widetilde{{\textbf{X}}}_c) \right) ^{2} \right\} \right] \nonumber \\{} & {} \quad +p\sum _{i=1}^{n}\sum _{c=1}^{C} u_{ic} ln(u_{ic}) -\lambda \left( \sum _{c=1}^{C}u_{ic}-1\right) \end{aligned}$$
(8)

where \({\textbf{u}}_i=(u_{i1},\ldots ,u_{ic},\ldots ,u_{iC})^{\prime }\) and \(\lambda \) is the Lagrange multiplier. Therefore, we set the first derivatives of (8) with respect to \(u_{ic}\) and \(\lambda \) equal to zero, yielding:

$$\begin{aligned} \frac{\partial L_p({\textbf{u}}_i,\lambda )}{\partial u_{ic}}=0 \,&\Leftrightarrow \, \left[ 1-exp\left\{ -\beta \left( D({\textbf{X}}_i,\widetilde{{\textbf{X}}}_c) \right) ^{2} \right\} \right] +p \left[ ln(u_{ic})+1\right] -\lambda =0 \end{aligned}$$
(9)
$$\begin{aligned} \frac{\partial L_p({\textbf{u}}_i,\lambda )}{\partial \lambda }=0\,&\Leftrightarrow \, \sum _{c=1}^{C}u_{ic}-1=0 \end{aligned}$$
(10)

From (9) we obtain:

$$\begin{aligned} ln(u_{ic})=\dfrac{1}{p}\left( \lambda -\left[ 1-exp\left\{ -\beta \left( D({\textbf{X}}_i,\widetilde{{\textbf{X}}}_c \right) ^{2} \right\} \right] \right) -1 \end{aligned}$$
(11)

and, then:

$$\begin{aligned} u_{ic}=exp \left\{ \dfrac{\lambda }{p}-\dfrac{1}{p}\left( \left[ 1-exp\left\{ -\beta \left( D({\textbf{X}}_i,\widetilde{{\textbf{X}}}_c\right) ^{2} \right\} \right] \right) -1\right\} \end{aligned}$$
(12)

By considering (10):

$$\begin{aligned} exp \left( \dfrac{\lambda }{p}-1\right) =\frac{1}{\sum _{c=1}^{C}\left( \frac{1}{exp \left\{ (1/p)\left[ 1-exp\left\{ -\beta \left( D({\textbf{X}}_i,\widetilde{{\textbf{X}}}_c \right) ^{2} \right\} \right] \right\} }\right) }. \end{aligned}$$
(13)

and by replacing Eq. (13) in (12), we have the solution as in (7). \(\square \)

The fuzzy clustering algorithm that minimizes the objective function is built by adopting an estimation strategy based on the Fu and Albus heuristic algorithm (Fu and Albus, 1977; Krishnapuram et al., 1999, 2001). Indeed, the alternating optimization estimation procedure cannot be adopted because the necessary conditions cannot be derived by differentiating the objective function with respect to the medoids.

The next paragraph describes the internal validity criterion used in this work to choose the number of groups. It is a fuzzy extension of the Average Silhouette Width Criterion, originally defined to assess crisp data partitions.

2.4 The fuzzy silhouette index

In order to choose the best solution in terms of the number of groups, in this study we adopt the Fuzzy Silhouette (FS) index (Campello and Hruschka, 2006), one of the most known cluster internal validity criteria based on the weighted average of the individual silhouettes width, \(\lambda _i\), as follows:

$$\begin{aligned} FS=\frac{\sum _{i=1}^{I}(u_{ip}-u_{iq})^{\alpha }\cdot \lambda _i}{\sum _{i=1}^{I}(u_{ip}-u_{iq})^{\alpha }}, \qquad \lambda _i=\frac{(b_{ip}-a_{ip})}{\max \{b_{ip},a_{ip}\}} \end{aligned}$$
(14)

where \(a_{ip}\) is the average distance of object i to all other objects belonging to the same cluster p (\(p=1\),...,C) and \(b_{ip}\) is the minimum (over clusters) average distance of the i-th unit to all units belonging to the cluster q with \(q\ne p\). \((u_{ip}-u_{iq})^{\alpha }\) is the weight of each \(\lambda _i\), where \(u_{ip}\) and \(u_{iq}\) correspond to the first and second largest element of the i-th row of the fuzzy partition matrix \({\textbf{U}}\), respectively; \(\alpha \ge 0\) is an optional user-defined weighting coefficient. Setting \(\alpha =0\), it reduces to the crisp Silhouette measure.

A higher value of FS means a better assignment of the units to the clusters which implies that, simultaneously, the intra-cluster distance is minimized while the inter-clusters distance is maximized.

The next section shows our simulation results highlighting the strengths and weaknesses of the proposed method.

3 Simulation study

This Section includes two simulation studies, the former explicitly defined to investigate the performances of the proposed clustering method in a setting similar to the application proposed; the latter implemented to investigate the performances in a more complex and general setting.

3.1 First simulation

In this simulation study, 30 bivariate time series have been generated and clustered in 3 equally sized groups, i.e. \(I=30\) and \(J=2\); in order to account for time series of different lengths, those belonging to the first and second group have a length equal to \(T=12\), while those belonging to the third group have a length \(T=10\). Moreover, a switching time series and 3 anomalous time series have been added, always fixing \(J=2\) and \(T=12\). This configuration can be seen in Fig. 1, randomly selected from the 100 simulated. For both variables, the time series belonging to the first and third clusters have similar longitudinal patterns, but different cross-sectional features. Moreover, the first and third clusters are only well-separated in the second dimension.

In detail, along the first dimension, the time series belonging to the three groups have been generated according to the following scheme:

  • First group: \(x_t=t+w_t\) for \(t=1,2,\ldots ,T\) and \(w_t \sim N(0,1)\)

  • Second group: \(y_t=T+1-t+w_t\) for \(t= 1,2,\ldots ,T\) and \(w_t \sim U(0,3)\)

  • Third group: \(z_t=y_t+5+w_t\) for \(t=1,2,\ldots ,(T-2)\) and with \(w_t \sim N(0,1).\)

The switching time series is “switching” between the first and the third group so that the first T/2 observations have been generated from the same generative model of the first group, the last T/2 from that of the third group.

The three outliers have been generated as follows:

  • \(g_{1,t}=sin(2\pi (t-1)/T)+w_t\) with \(w_t \sim N(20,25)\) for \(t=1, 2,\ldots ,T/2\) and \(g_{1,t}=cos(2\pi (t-1)/T)+w_t\) with \(w_t \sim N(-5,9)\) for \(t=(T/2)+1,(T/2)+2,\ldots ,T\)

  • \(g_{2,t}=cos(2\pi (t-1)/T)+w_t\) with \(w_t \sim N(2,4)\) for \(t=1,2,\ldots ,T\)

  • \(g_{3,t}=cos(2\pi (t-1)/T)+w_t\) with \(w_t \sim N(-10,25)\) for \(t=1, 2,\ldots ,T\).

Along the second dimension, the time series have been generated according to:

  • First group: \(x_t=T+1-t+w_t\) for \(t=1,2,\ldots , T\) and \(w_t \sim N(0,1)\)

  • Second group: \(y_t=t+w_t\) for \(t=1,2,\ldots ,T\) and \(w_t \sim U(0,5)\)

  • \(z_t=y_t-10-w_t\) for \(t =1,2,\ldots ,T-2\) and with \(w_t \sim N(0,1)\).

The switching time series is “switching” again between the first and the third group so that the first T/2 observations have been generated from the same generative model of the first group, the last T/2 from that of the third group.

The three outliers have been generated as follows:

  • \(g_{1,t}=sin(2\pi (t-1)/T)+w_t+20\) with \(w_t \sim N(0,1)\) for \(t= 1,2,\ldots ,T\)

  • \(g_{2,t}=sin(2\pi (t-1)/T)+w_t\) with \(w_t \sim N(-2,4)\) for \(t= 1,2,\ldots ,T\)

  • \(g_{3,t}=cos(2\pi (t-1)/T)+w_t\) with \(w_t \sim N(-15,25)\) for \(t=1,2,\ldots ,T\)

Fig. 1
figure 1

The simulated scenario with respect to the first (on the left) and the second dimension (on the right)

Full size image

Both robust (DTW-Exp-FCMd-E) and non-robust (DTW-FCMd-E) methods have been applied to the 100 simulated datasets, the latter easily obtained by replacing the exponential transformation of DTW with the non-robust original DTW. For comparison purposes, the fuzzy C-Medoids method based on the exponential transformation of DTW and the fuzziness parameter m, henceforth referred to as DTW-Exp-FCMd, has also been applied, together with its non-robust version, henceforth referred to as DTW-FCMd.

We applied all the methods by setting \(C=3\), according to the number of simulated groups. To assess the impact of fuzziness parameters on the final partition, we ran the DTW-Exp-FCMd-E and DTW-FCMd-E varying \(p \in \left\{ 0.05,0.10,0.15,0.20,0.25\right\} \) and \(k \in \left\{ 1,2\right\} \) while the DTW-Exp-FCMd and DTW-FCMd varying \(m \in \left\{ 1.1,1.3,1.5,1.7,2\right\} \) and, as usual, \(k=1\). For each setting, we considered 100 random restarts and as the maximum number of iterations 100.

Furthermore, for fixed values of p and k, three different scenarios have been simulated starting from a basic one with 3 natural clusters and then contaminating it with the presence of one switching time series and an increasing number of outliers. Thus, the simulation schemes are in order as follows: (i) 3 natural groups, 0 outliers and 0 switching time series (ii) 3 natural groups, 1 outlier and 1 switching time series and (iii) 3 natural groups, 3 outliers and 1 switching time series.

Robustness to outliers has been analysed by studying the effect of the anomalous and switching time series on the membership degrees in the final partition.

To this end, the 100 fuzzy partitions of the 30 bivariate time series (only those belonging to the natural groups excluding the outliers and the switching time series) are compared with the reference crisp partition, by means of the Fuzzy Adjusted Rand Index (ARI) (Campello, 2007), a well-known external validation criterion. Lying in the range \([-1,1]\), it is equal to 1 in the case of perfect correspondence between the two partitions. So, the higher is the value, the better is the agreement between the two partitions.

Table 1 The lower and upper bounds of the confidence interval for the mean of the Fuzzy ARI index, at a level of 95% for DTW-FCMd-E, DTW-Exp-FCMd-E (with k = 1) and DTW-Exp-FCMd-E (with k = 2) considering the three simulated scenarios: (i) 3 natural groups, 0 outliers and 0 switching time series (ii) 3 natural groups, 1 outlier and 1 switching time series and (iii) 3 natural groups, 3 outliers and 1 switching time series
Full size table

The lower and upper bounds of the confidence interval for the mean of the Fuzzy ARI index, at a confidence level of \(95\%\), have been given in Table 1 for both DTW-FCMd-E and DTW-Exp-FCMd-E.

As expected, as the level of fuzziness increases, and, consequently, as the value of p increases, the Fuzzy ARI index decreases because the membership degrees become smoother. The presence of the outliers and one switching time series has a great effect on the identification of the natural groups as far as the non-robust method is concerned especially when three outliers are added while it shows good behaviour in the first scenario without outliers and a low value of p, as expected.

Both robust methods outperform the DTW-FCMd-E method but the one based on \(k=2\) performs the best: in fact, it is not only able to recover the natural structure of groups but is also less sensitive to different values of the weight factor p. Moreover, looking at the width of each confidence interval, particularly in the third scenario, one can notice that DTW-Exp-FCMd-E with \(k=2\) is also much less variable.

Table 2 shows the same confidence intervals of the Fuzzy ARI index considering the DTW-FCMd and DTW-Exp-FCMd methods according to different values of the fuzziness parameter m with reference to the same three scenarios. Although DTW-Exp-FCMd and DTW-Exp-FCMd-E cannot be directly compared at all, i.e. given the same values of the fuzziness parameter, one can notice that they behave almost the same; in fact, also DTW-Exp-FCMd outperforms the non-robust version in almost all setups and is also more stable, thus showing a performance similar to that of DTW-Exp-FCMd-E with \(k=2\).

Table 2 The lower and upper bounds of the confidence interval for the mean of the Fuzzy ARI index, at a level of \(95\%\) for DTW-FCMd and DTW-Exp-FCMd considering the three simulated scenarios: (i) 3 natural groups, 0 outliers and 0 switching time series (ii) 3 natural groups, 1 outlier and 1 switching time series and (iii) 3 natural groups, 3 outliers and 1 switching time series
Full size table

From these comparisons, we argue that the multiplicative factor k of the \(\beta \) parameter is necessary to ensure that the robust method based on the entropy achieves the same level of performance as its competitor, i.e. the robust method based on the fuzziness parameter m. This correction is needed to avoid the membership degrees matrix becoming blurrier as the number of noisy time series and the value of p increase. To investigate with more detail the performances of the proposed methods, we also computed the average correct classification rate (ACR) of the 30 bivariate time series over the 100 trials together with the average fuzzy units rate (FCR) according to the different values of p (see Table 3, columns 1–2) and m (see Table 4, columns 1–2) respectively, focusing on the most contaminated setup, the third one.

Table 3 Average correct classification rate (ACR), average fuzzy units rate (FCR) with reference to the 30 bivariate time series over 100 replications, frequency of times over 100 replications the clustering method identifies the switching time-series (SWF), no outliers (OUT0F), only 1 outlier (OUT1F), only 2 outliers (OUT2F) and both 3 outliers (OUT3F), respectively
Full size table
Table 4 Average correct classification rate (ACR), average fuzzy units rate (FCR) with reference to the 30 bivariate time series over 100 replications, frequency of times over 100 replications the clustering method identifies the switching time-series (SWF), no outliers (OUT0F), only 1 outlier (OUT1F), only 2 outliers (OUT2F) and both 3 outliers (OUT3F), respectively
Full size table

With this aim, the following cut-off value has been chosen to assign a multivariate time series to a given cluster: for each of the thirty bivariate time series, if the \(u_{ic}>=0.6\), then the i-th time series is assigned to cluster c, otherwise it becomes a fuzzy unit. Both the standard methods (DTW-FCMd-E and DTW-FCMd) as well as the DTW-Exp-FCMd-E with \(k=1\) are not stable as the value of the fuzziness parameter increases. The partitions become too blurred so that, for example, when \(p=0.25\) the average fuzzy units rate is equal to 0.81 for DTW-FCMd-E and 0.41 for DTW-Exp-FCMd-E with \(k=1\) respectively. The same happens for the standard method DTW-FCMd. In contrast, DTW-Exp-FCMd-E with \(k=2\) and DTW-Exp-FCMd are both able to recover the natural structure in three groups without being affected by the degree of fuzziness.

A second, no less relevant task is to analyse the capability of the robust method to correctly identify the switching time series and the outliers too.

For this purpose, the same above cut-off value has been chosen. Therefore, the outliers are correctly handled when \(u_{ic} < 0.6\) for all c, i.e. when the series exhibits similar membership degrees in all the C clusters. The switching time series is correctly identified when its membership degrees are more or less equally distributed on two of the three clusters.

For each of the 100 trials in the third scenario, we computed the frequency of times out of 100 replications the clustering method identifies the switching time-series (SWF), no outlier (OUT0F), 1 outlier (OUT1F), 2 outliers (OUT2F) and 3 outliers (OUT3F), respectively. All these results are shown in the same aforementioned Tables 3, 4. The first thing to note is that, for lower values of p, the standard clustering method and the robust one with \(k=1\) fail to correctly identify the outliers while the non-anomalous series are more often well-assigned (see the ACR value). Increasing the value of p generates a seemingly strange behaviour: the outliers and the switching time series are well-identified while the non-anomalous time series are not. Actually, this is only due to the fact that, as p becomes larger, the boundaries between clusters become more blurred and the switching series (or the outlier) becomes a fuzzy unit too. But, as already shown by looking at the FCR, this implies the higher risk that many other non-switching time series might become fuzzy too. After all, as already highlighted, this is the main drawback of the robust clustering method with \(k=1\).

As far as the robust method with \(k=2\) is concerned, we argue that its performance increases as the value of p increases, since the clustering method produces softer boundaries between clusters and hence membership degrees of outliers closer to 0.3 while keeping the membership degrees of non-outliers still high.

Essentially, this method is always able to correctly identify all 30 non-anomalous time series and all three outliers. The same considerations hold for the robust clustering method based on m, the DTW-Exp-FCMd. One can argue for a better performance of the latter to identify the switching time series than the DTW-Exp-FCMd-E. Actually, by increasing the cut-off value to 0.7 (see Table 5), one can notice that DTW-Exp-FCMd-E shows almost the same performance than DTW-Exp-FCMd.

Table 5 Average correct classification rate (ACR), average fuzzy units rate (FCR) with reference to the 30 bivariate time series over 100 replications, frequency of times over 100 replications the clustering method identifies the switching time-series (SWF), no outliers (OUT0F), only 1 outlier (OUT1F), only 2 outliers (OUT2F) and both 3 outliers (OUT3F), respectively
Full size table

Lastly, to give more insight to the reader, we show two examples of obtained partitions focusing on the three most interesting methods: the standard DTW-FCMd-E and the robust methods DTW-Exp-FCMd-E with k = 2 and DTW-Exp-FCMd.

Table 6 Example of a Membership degree matrix for the DTW-FCMd-E and DTW-Exp-FCMd-E (\(k=2\)) with \(p=0.15\) and for DTW-Exp-FCMd with \(m=1.5\)
Full size table
Table 7 A second example of a Membership degree matrix for DTW-FCMd-E and DTW-Exp-FCMd-E (\(k=2\)) with \(p=0.15\) and for DTW-Exp-FCMd with \(m=1.5\)
Full size table

To this purpose, we show two possible typical situations, when \(p=0.15\) and \(m=1.5\), in the Tables 6 and  7 respectively. The former reports the case in which the standard clustering method fails to assign all units while the robust ones are able to identify both non-anomalous units as well as switching time series and outliers. In fact, the last three units are all fuzzy units, as expected by using the exponential transformation.

The latter reports another possible configuration in which even the standard method is able to correctly assign units to the cluster they belong to but outliers are incorrectly assigned to a cluster. The switching time series is assigned to the two clusters it belongs to but one needs a cut-off value greater than 0.75 to be identified as switching. This is not the case with the robust methods that well assign all 34 units instead.

In addition, focusing on the most contaminated setup, we ran DTW-FCMd-E and DTW-Exp-FCMd-E with 100 Random restarts and a number of iterations equal to 100 by setting \(C=2\). We computed the number of times the two clustering methods chose the correct number of groups based on the Fuzzy Silhouette (FS) index.

As can be seen by looking at the results in Table 8, for \(p=0.05\), the standard method chooses the correct number of groups \(C=3\)Footnote 1 only 18 times out of 100 and in general this percentage is not greater than 0.28, considering the different values of p. In contrast, the robust method with \(k=2\) always chooses the correct number of groups.

Simulation results clearly showed the excellent performance of the proposed robust clustering method based on entropy regularization and a value of \(k=2\); as a further result, it provides almost the same level of performance as its competitor, the robust clustering method based on the fuzziness parameter m. Moreover, robust methods in general allow to distinguish between outliers and switching time series since in the latter case the membership degrees are not equally distributed over all C clusters as in the former case.

Table 8 The percentage of times the clustering methods DTW-FCMd-E and DTW-Exp-FCMd-E (\(k=2\)) choose the correct number of groups, i.e. \(C=3\), based on the FS index
Full size table

3.2 Second simulation

We considered the following simulation plan to evaluate the proposed clustering method in a more complex scenario with longer time series. Therefore, we simulated again 30 bivariate time series clustered in 3 equally sized groups, i.e. \(I=30\) and \(J=2\), with length \(T=200\) for all time series. Moreover, a switching time series and 3 outliers trajectories have been added, always fixing \(J=2\) and \(T=200\). This configuration can be seen in Fig. 2, randomly selected from the 100 simulated.

Fig. 2
figure 2

The simulated scenario with respect to the first (on the left) and the second dimension (on the right)

Full size image

Along the first dimension, the time series have been generated from the following scheme:

  • First group: \(x_t = cos(8 \pi (t-1)/T)+a_t+w_t\) for \(t=1,2,\ldots ,200\); where \(a_t\) belongs to the sequence of the T equally-spaced values in the interval [1, 6] and \(w_t\sim N(0,0.25)\)

  • Second group: \(y_t = cos(4 \pi (t-1)/T)+w_t\) for \(t=1,2,\ldots ,200\) and with \(w_t \sim N(-2,0.25)\)

  • Third group: \(z_t = sin(15 \pi (t-1)/T)+w_t\) for \(t=1,2,\ldots ,200\) and with \(w_t \sim N(0,0.5)\).

The switching time series is “switching” between the first and the third group so that the first T/2 observations have been generated from the same generative model of the first group, the last T/2 from that of the third group.

The three outliers have been generated, respectively, from:

  • A random walk with drift \(g_{1,t} = -0.01 + g_{1,t-1} + w_t\) with \(\sigma _{w_t}=0.05\) for \(t=2,\ldots ,201\)

  • A random walk with drift \(g_{2,t} = 0.01 + g_{2,t-1} + w_t\) with \(\sigma _{w_t}=0.05\) for \(t=2,\ldots ,201\)

  • \(g_{3,t}=6.025-0.025 \cdot t+a_t\) with \(a_t\sim N(0,0.04)\) and for \(t=1,2,\ldots ,200\).

Along the second dimension, the time series have been generated from the following scheme:

  • First group: \(x_t = cos(8 \pi (t-1)/T)+a_t+w_t\) for \(t=1,2,\ldots ,200\) where \(a_t\) belongs to the sequence of the T equally-spaced values in the interval [0, 7] and \(w_t \sim N(0,0.25)\)

  • Second group: \(y_t = cos(4 \pi (t-1)/T)+a_t+w_t\) for \(t=1,2,\ldots ,200\) here \(a_t\) belongs to the sequence of the T equally-spaced values in the interval [1, 7] with decreasing order and \(w_t \sim N(-1,0.25)\)

  • Third group: \(z_t = sin(5 \pi (t-1)/T)+w_t\) for \(t=1,2,\ldots ,200\) with \(w_t \sim N(1,0.25)\).

The switching time series is again “switching” between the first and the third group. The three outliers have been generated, respectively, from:

  • A random walk with drift \(g^{*}_{1,t} = -0.05 + g^{*}_{1,t-1} + w_t\) with \(\sigma _{w_t}=0.1\) for \(t=2,\ldots ,201\); then, we shifted it by 5 so that \(g_{1,t} = g^{*}_{1,t} + 5\);

  • A random walk \(g_{2,t} = g_{2,t-1} + w_t\) with \(\sigma _{w_t}=0.5\) for \(t=2,\ldots ,201\);

  • A random walk with drift \(g_{3,t} = 0.01 + g_{3,t-1} + w_t\) with \(\sigma _{w_t}=0.5\) for \(t=2,\ldots ,201\).

In this second simulation, DTW-Exp-FCMd-E has been applied to the 100 simulated datasets and, for comparison purposes, in addition to its non-robust version, i.e. DTW-FCMd-E, and the fuzzy C-Medoids method based on the exponential transformation of DTW and the fuzziness parameter m, i.e. DTW-Exp-FCMd, we considered further benchmarks: a) the fuzzy C-medoids based on the fuzziness parameter m and a generalization of the dissimilarity introduced by D’Urso and Maharaj (2009b), based on auto and cross-correlations as implemented in the R package mlmts (Ángel López-Oriona and Vilar, 2023) fixing the maximum lag to 50, henceforth referred to as COR-FCMd and b) the fuzzy clustering procedure proposed by He and Tan (2018) implemented in the R package mlmts, fixing the rate of retained variability to 0.94, henceforth referred to as VPCA-FCM.

In this simulation, we applied all the methods by varying \(C \in \lbrace 2,3,4\}\), \(p \in \{0.015,0.02,0.03,0.05\}\) for DTW-FCMd-E, \(p \in \lbrace 0.05,0.10,0.15,0.20\}\) and \(k \in \left\{ 1,2\right\} \) for DTW-Exp-FCMd-EFootnote 2 while, for the models based on the “m” coefficient, varying \(m \in \left\{ 1.1,1.3,1.5,1.7\right\} \).

For DTW-FCMd-E, DTW-Exp-FCMd-E, DTW-Exp-FCMd and VPCA-FCM, data have been standardized according to Coppi et al. (2010).

For each setting, we considered 100 random restarts (except for VPCA-FCM) and as the maximum number of iterations 100. Furthermore, for fixed values of p and k, the same three scenarios have been simulated starting from the basic one with 3 natural clusters and then contaminating it with one switching time series and an increasing number of outliers.

For fixed values of p and k, the final partition, and therefore the optimal number of clusters among the solutions with 2, 3 and 4 groups, has been chosen by means of the Fuzzy silhouette index (Campello and Hruschka, 2006).

Robustness against outliers has been tested by comparing the fuzzy partitions of the 30 bivariate time series with the reference crisp partition by means of the fuzzy ARI (Campello and Hruschka, 2006)

The main evidences from the simulation can be inferred by observing the distribution of fuzzy ARI across the methods and scenarios as the degree of fuzziness increases. To this end, we show the corresponding plots in Figs. 3, 4, 5, 6, 7, and 8. While the performance in case of no outliers, or with one outlier and a switching time series is almost the same for all clustering techniques (but DTW-FCMd-E more sensitive to p), if we consider the third scenario, the best performance is associated with DTW-Exp-FCMd-E with \(k=2\) and VPCA-FCM, that could be considered a competitor. Both methods are more stable with respect to the degree of fuzziness.

Furthermore, in Tables 9 and 10, we computed the number of times, over 100 simulated data sets, the FS index leads to choose the correct number of groups,i.e. \(C=3\), for all clustering techniques and for all scenarios.

We can state that, in the first and second scenarios, for almost all methods, except for VPCA-FCM, in \(100\%\) of the cases the choice of the best C is correctly identified while, in the third scenario, the best performance is associated with our robust method with \(K=2\), which shows the highest percentages. For VPCA-FCM, we should point out that the lower values in the second and third scenarios are motivated by the fact that the method tends to choose \(C=4\), where the additional cluster acts as a noise cluster since, often, it includes only one unit that is one of the outliers.

Fig. 3
figure 3

Distribution of the Fuzzy Adjusted Rand Index for DTW-FCMd-E method according to the three simulated scenarios, with \(p \in \lbrace 0.015, 0.02, 0.03, 0.05\rbrace \)

Full size image
Fig. 4
figure 4

Distribution of the Fuzzy Adjusted Rand Index for DTW-Exp-FCMd-E method according to the three simulated scenarios, with \(k=1\) and \(p \in \lbrace 0.05,0.10,0.15,0.20\rbrace \)

Full size image
Fig. 5
figure 5

Distribution of the Fuzzy Adjusted Rand Index for DTW-Exp-FCMd-E method according to the three simulated scenarios, with \(k=2\) and \(p \in \lbrace 0.05,0.10,0.15,0.20\rbrace \)

Full size image
Fig. 6
figure 6

Distribution of the Fuzzy Adjusted Rand Index for DTW-Exp-FCMd method according to the three simulated scenarios, with \(m \in \lbrace 1.1,1.3,1.5,1.7\rbrace \)

Full size image
Fig. 7
figure 7

Distribution of the Fuzzy Adjusted Rand Index for COR-FCMd method according to the three simulated scenarios, with \(m \in \lbrace 1.1,1.3,1.5,1.7\rbrace \)

Full size image
Fig. 8
figure 8

Distribution of the Fuzzy Adjusted Rand Index for VPCA-FCM method according to the three simulated scenarios, with \(m \in \lbrace 1.1,1.3,1.5,1.7\rbrace \)

Full size image

We conclude by highlighting that the choice of the best value of the fuzziness parameter p, as well as of k,Footnote 3 strictly depends on the scaling of the dissimilarity used and the degree of separation among groups; thus in practical applications, we recommend taking into account all these issues and selecting the best combinations of C, p and k based on some internal validation criterion.

4 An application to real data: air pollution in the Province of Rome

A large number of anthropogenic activities result in the release of a significant number of chemical substances into the atmosphere, some already present in small quantities, others not at all, which are potentially harmful to man, flora and fauna if present in quantities and/or with properties that alter normal atmospheric conditions. It is therefore particularly important to analyse spatial (monitoring site characteristics) and dynamic trends in air (and soil) concentrations of different types of pollutants. In this study, based on data availability and their relevance to the serious health effects associated with long-term exposure, we considered three pollutants: the particulate matter with diameter less than 10 micrometers (PM10), the nitrogen oxide (NO) and nitrogen dioxide (NO2). Particulate matter (PM), in general, is a highly heterogeneous collection of solid or liquid particles (aerosols) that remain suspended in lower troposphere air for longer or shorter durations due to their characteristic small size. Particles are of various sizes and contain a wide range of substances such as sand, ash, dust, soot, silica, vegetable matter, metal compounds, salts, elements such as lead and other heavy metals, inorganic and organic chemical compounds. Particulate matter is present in the air as a result of both natural causes and human activities. It is a primary pollutant (emitted directly by the various emission sources present in the area) in the former case while in the latter it can be both a primary pollutant and a secondary pollutant (i.e. formed by the chemical interaction of other substances which react to form an aerosol which is then dispersed in the air). Because its presence in the air can adversely affect human health, it is considered, along with nitrogen dioxide and ozone, a major cause of concern for air quality. With reference to the nitrogen oxides, NO and NO\(_2\) are the two most relevant ones for air pollution which originate in the lower layers of the atmosphere mainly from combustion processes and, in urban areas, from car emissions and domestic heating.

Table 9 Number of times, over 100 simulated data sets, the correct number of groups, i.e \(C=3\), is chosen based on the maximization of the FS index, for DTW-FCMd-E and DTW-Exp-FCMd-E methods (with \(k=1\) and \(k=2\))
Full size table
Table 10 Number of times, over 100 simulated data sets, the correct number of groups, i.e \(C=3\), is chosen based on the maximization of the FS index, for DTW-Exp-FCMd, COR-FCMd and VPCA-FCM methods
Full size table

Although NO\(_2\), like NO, is a primary pollutant, it is also one of the most important secondary pollutants, i.e. it results from the reaction of different chemical species in the atmosphere and is therefore not emitted directly. NO\(_2\) is an acidic and highly corrosive gas and prolonged exposure to elevated levels may contribute to the development of asthma and may increase susceptibility to respiratory infections. NO is a colourless, tasteless and odourless gas, much less toxic than NO\(_2\). However, they play a role in the formation of both smog and acid rain.

In this study, we consider the daily mean concentrations (in \(\upmu \)g/m\(^3\)) of PM10, NO and NO\(_2\), measured at 23Footnote 4 monitoring stations belonging to the Province of Rome, with reference to the year 2022, i.e the array dimension is I = 23, J = 3 and T = 365.

Missing values, for each time series, have been replaced by simple moving averages using the function \(na\_ma()\) implemented in the R package imputeTS. The data from the monitoring stations are collected, processed and disseminated by the Regional Air Quality Centre (downloaded from https://www.arpalazio.net/main/aria/sci/basedati/chimici/chimici.php). Table 11 shows the monitoring stations and their type (U-urban, S-suburban, R-rural, I-industrial, B-background, T-traffic) while the time series of daily pollution concentrations for each monitoring station are shown in Fig. 9 (each with a different y-scale).

Table 11 Monitoring stations and associated type (U-urban, S-suburban, R-rural, I-industrial, B-background, T-traffic)
Full size table
Fig. 9
figure 9

Time series showing the daily mean concentrations of the three pollutants at each monitoring station (different y-scale)

Full size image
Fig. 10
figure 10

Fuzzy Silhouette index based on the combination of C and the p values

Full size image

The multivariate time series have been pre-processed by applying the following standardization as proposed in Coppi and D’Urso (2006) so that \(z_{ijt}=\frac{(x_{ijt} -\overline{x}_{.jt})}{ \sqrt{\frac{\sum _i (x_{ijt} -\overline{x}_{.jt})^2}{I}}}, \quad i=1,\ldots ,I, \quad j=1,\ldots ,J \quad t=1,\ldots ,T\). We applied both DTW-FCMd-E and DTW-Exp-FCMd-E (with \(k=2\)) clustering methods to the transformed data The best solution, i.e. the optimal number of clusters C, has been chosen based on the combination of C and the p that maximizes the Fuzzy Silhouette index. In this regard, we computed the FS index for each combination of \(C \in \lbrace 2, \ldots 6 \rbrace \) and \(p \in \lbrace 0.05, 0.08, 0.10, 0.12, 0.15 \rbrace \) for DTW-Exp-FCMd-E (with \(k=2\)) while \(p \in \lbrace 0.08, 0.13, 0.16, 0.20, 0.24 \rbrace \) for DTW-FCMd-E (to account for the different magnitude of the dissimilarity measure).

Looking at the two plots in Fig. 10 referred to as the DTW-FCMd-E on the left and DTW-Exp-FCMd-E on the right, it is observed that, in both cases, the FS index exhibits a slight increase with p, attaining its maximum value when \(C=2\).

Consequently, we choose the solution with two groups and \(p=0.12\) for DTW-Exp-FCMd-E and \(p=0.20\) for DTW-FCMd-E.

The membership degrees matrix for both cases has been reported in Table 12. The column subheadings correspond to the medoid units of the clusters.

As can be observed, both methods result in similar partitions with identical medoids, specifically Arenula and Guidonia, the former being situated in an urban area and the latter in a suburban one. Figure 11 displays the corresponding time series for each pollutant, based on standardized data. As expected, they vary in terms of trend and fluctuations and NO\(_2\) clearly exhibits a significant difference in magnitude.

However, for the purposes of this analysis, it should be noted that the two partitions are nearly identical, except for three stations, namely Allumiere, Fermi and Tiburtina, where the membership degrees show significant differences. The robust method assigns almost identical membership degree to both clusters while the non-robust method assigns a clear high membership to one of the two clusters.

From Fig. 12, which displays the time series of the medoids and the three stations for each pollutant, it is clear that Allumiere, Fermi and Tiburtina exhibit an atypical and ambiguous behaviour (or magnitude) for at least one of the three pollutants, qualifying them as outlying stations. This leads to the conclusion that the non-robust method fails to identify outlying units. Rather, it assigns them to a cluster with a high membership degree.

It is worth noting that both partitions are quite fuzzy. This is due to the complexity of the features space involved in the clustering process. Infact, many units show fuzzy behaviour, four of them (Allumiere, Colleferro Oberdan, Fermi and Tiburtina) are anomalous. Using a cut-off value for the degree of membership of 0.7, the crisp partition for both methods is shown in the maps in Fig. 13.

Table 12 Membership degrees matrix for DTW-FCMd-E and DTW-Exp-FCMd-E (\(k=2\))
Full size table

With the only scope of showing the advantages and effectiveness of our proposed methodology in several real cases, we also report the best solutions based on the FS index when another type of standardization is used for pre-processing the data. In detail, the standardization is based on the following formula as suggested in Coppi et al. (2010): \(z_{ijt}=\frac{x_{ijt} -\overline{x}_{.j.}}{ \sqrt{\frac{\sum _i (x_{ijt} -\overline{x}_{.j.})^2}{IT}}}, \quad i=1,\ldots ,I, \quad j=1,\ldots ,J \quad t=1,\ldots ,T\). Both membership degrees matrices for the best solution \(C=2\), with \(p=0.07\) for DTW-FCMd-E and \(p=0.08\) for DTW-Exp-FCMd-E (\(k=2\)), are reported in Table 13 with column subheadings corresponding to the medoid units of the clusters while the maps of the crisp partition based on the same cut-off as above are shown in Fig. 14.

Fig. 11
figure 11

Time series of medoids (standardized data)

Full size image
Fig. 12
figure 12

Time series of the medoids and the three outliers, i.e Allumiere, Fermi and Tiburtina (standardized data)

Full size image
Fig. 13
figure 13

Map of the crisp partition for a DTW-FCMd-E and b DTW-Exp-FCMd-E (k = 2). Pink identifies units belonging to the first cluster, green those belonging to the second cluster, blue fuzzy units while the medoids are coloured dark pink and dark green respectively. (Color figure online)

Full size image
Table 13 Membership degrees matrix for DTW-FCMd-E and DTW-Exp-FCMd-E (\(k=2\)) according to the second type of data standardization
Full size table
Fig. 14
figure 14

Map of the crisp partition for a DTW-FCMd-E and b DTW-Exp-FCMd-E (k = 2) according to the second type of data standardization. Pink identifies units belonging to the first cluster, green those belonging to the second cluster, blue fuzzy units, while the medoids are coloured dark pink and dark green respectively. (Color figure online)

Full size image

Looking at the results in Table 13, also with the help of the maps, we can see that in this case the partitions are very different and the effect of some outlying and\(\backslash \)or switching time series leads to the identification of a different medoid for the first group. Even though Arenula and Fiumicino Villa Guglielmi are both classified as urban background stations, it can be argued that the robust method is not only able to identify as fuzzy units the anomalous time series (such as Fermi), but it is also more accurate in distinguishing between the group of stations located inside the ring road highway that surrounds the city of Rome and those outside; the non-robust method, instead, selects as medoids two units that are both located outside the ring road highway. It is worth noting that in all cases the solutions identify many series showing a fuzzy behaviour, which supports the usefulness of the fuzzy approach for complex data, such as those used in this work.

5 Conclusion

The clustering of complex data, especially three-way data arrays, is one of the most discussed topics in the literature, with new methods and applications being proposed in a wide variety of research fields. To address the specific problem of robustness against outliers in clustering techniques, this paper proposes a robust fuzzy C-medoids method based on entropy regularization. To this purpose, as suggested in the seminal paper of Wu and Yang (2002), we introduce in the objective function a suitable robust dissimilarity measure based on the exponential transformation of the original DTW. The fuzzy framework allows greater flexibility accounting for the complexity of the features space. It allows a time series to be assigned to more than one group, considering potential switching behaviours. The outliers act as fuzzy units being assigned to the C clusters with approximately the same membership degree. Specifically, fuzziness is controlled by the entropy regularization term so that the minimization of the functional is regularized by maximizing the total amount of information (Coppi and D’Urso, 2006). Moreover, it also inherits the same nice properties of its baseline, since it can manage time series of different lengths thanks to DTW and selects as cluster prototypes a subset of observed time series typical of a partition around medoids approach.

The performance of the proposed clustering method has been evaluated through simulations involving scenarios with different types of contamination. Based on the simulation results, we conclude that the robust method has a good performance even when compared with other benchmark methods when some fewer time series markedly deviate from all others assuming anomalous behaviour. In particular, the robust method with \(k=2\) is able to neutralize the effect of the anomalous series recovering the true clustering structure as well as being much less affected by the value of the weight factor p. The proposed robust fuzzy clustering method has been applied to real data by using a dataset consisting of the daily time series of the mean concentrations of three air pollutants throughout 2022 in the Province of Rome. As in the case of simulated data, the application to real data shows the effectiveness and robustness of the proposed clustering procedure.

Therefore, we believe the paper meets a twofold objective: dealing with the issue of clustering complex data such as multivariate time series and neutralizing the negative effect of anomalous time series that can lead to erroneous assignments of the units to a group.

Furthermore, as already highlighted, this study defines a comprehensive and unified methodological framework that exploits the single advantages of each approach resulting in an improvement in terms of overall information gain. Also in light of these promising results, we argue that there are still interesting methodological challenges for further research. For instance, other robust approaches like those based on the noise cluster and the trimming procedure could be adapted to the fuzzy C-medoids clustering method with entropy regularization and based on DTW. As a further development, we would take into account other types of dissimilarities among the warped series, like those considering the inter-correlation structure.

Furthermore, one might be interested in defining other validity measures than the FS index to provide an alternative internal validity criterion for choosing the correct number of groups even in the presence of outliers.