Resilient and social health service network design to reduce the effect of COVID-19 outbreak

Abstract

With the severe outbreak of the novel coronavirus (COVID-19), researchers are motivated to develop efficient methods to face related issues. The present study aims to design a resilient health system to offer medical services to COVID-19 patients and prevent further disease outbreaks by social distancing, resiliency, cost, and commuting distance as decisive factors. It incorporated three novel resiliency measures (i.e., health facility criticality, patient dissatisfaction level, and dispersion of suspicious people) to promote the designed health network against potential infectious disease threats. Also, it introduced a novel hybrid uncertainty programming to resolve a mixed degree of the inherent uncertainty in the multi-objective problem, and it adopted an interactive fuzzy approach to address it. The actual data obtained from a case study in Tehran province in Iran proved the strong performance of the presented model. The findings show that the optimum use of medical centers’ potential and the corresponding decisions result in a more resilient health system and cost reduction. A further outbreak of the COVID-19 pandemic is also prevented by shortening the commuting distance for patients and avoiding the increasing congestion in the medical centers. Also, the managerial insights show that establishing and evenly distributing camps and quarantine stations within the community and designing an efficient network for patients with different symptoms result in the optimum use of the potential capacity of medical centers and a decrease in the rate of bed shortage in the hospitals. Another insight drawn is that an efficient allocation of the suspect and definite cases to the nearest screening and care centers makes it possible to prevent the disease carriers from commuting within the community and increase the coronavirus transmission rate.

1 Introduction

Rapid progression, a worldwide epidemic, and chronic disorders make infectious diseases different from other diseases. An outbreak of the disease leads to unforeseen consequences. On the other hand, irreparable damages come to health care, social, and economic systems with no effective control of the disease (Zhu et al., 2020). As a result of the differences in the symptoms of the disease and its rate of spread, the healthcare systems face serious challenges at the management level (Ivanov, 2020a). The first coronavirus (COVID-19/SARS-COV-2) case observed in Wuhan, China, in December 2019, has reached epidemic proportions worldwide and is of great concern to public health (Liu et al., 2020). According to the latest World Health Organization (WHO) report, about 230 countries, and more than 684,900,000 people have been infected by COVID-19, from which about 6.8 million people have died by late April 2023. The United States, with more than 106 million infected cases and around 1,150,000 dead, has the highest number of infected people with COVID-19 worldwide. The number of infected people and the mortality rate in Iran are 7,592,255 and 145,391, respectively. It is worth mentioning that information resource is the official statistics till late April 2023, and the number of infected people is steadily increasing (WHO, 2023).

Coronavirus is a new infectious disease, and its symptoms vary from person to person, among which fever, fatigue, and dry cough are the most common (Huang et al., 2019). Infected people may also exhibit a runny nose or nasal congestion, sore throat, or diarrhea. The symptoms appear with moderate severity and may worsen gradually. Some infected people may have no symptoms, which makes them unaware of being virus carriers. About 17% of the infected people with COVID-19 have short breath. Elders suffering from an underlying disease, such as diabetes or hypertension, are at a greater risk (Rothan & Byrareddy, 2020). Thus, infected people need to take special medical services based on the type and severity of symptoms and their underlying disease.

Infected people with severe symptoms of the underlying disease need to receive special medical services usually offered in specialized hospitals. On the other hand, due to the limited capacity of specialized hospitals, infected people having severe symptoms with no underlying disease should undergo medical treatment in general hospitals. Meanwhile, infected people with mild symptoms need medical treatment but are in no emergency (Cao et al., 2020). A proper decision on the medical treatment of such infected people is to set up camps used as a place for settling improved infected people who lack the necessary qualifications for staying home.

Social distance is one of the most significant factors in controlling the spread of infectious diseases (Govindan et al., 2020). As health providers have rightly pointed out, contact between infected people and healthy people is one of the main transmission routes of such infectious diseases as coronavirus, which increases the rate of spread (Aloi et al., 2020). On the other hand, infected people need to receive medical services in medical centers, which necessitates their commute in society. Accordingly, the healthcare systems face the challenge of (a) providing the infected people with medical services in such a way that the patients’ commute in society reduces and (b) establishing medical centers for the infected people with mild symptoms, the improved cases, and the uninformed carriers or the infected people with a variety of symptoms.

Limited healthcare facilities, daily increase in cases, and patients in an emergency (such as cancer, diabetes, and heart disease) place the medical centers under added pressure during the outbreak of pandemic diseases such as COVID-19 (Samani & Hosseini-Motlagh, 2021). Also, the issue of preventing infectious disease transmission from infected people to healthy people is of great importance in healthcare systems. In these circumstances, adaptation between the health system and increasing demand becomes a vital necessity, which is interpreted as resilience. Thus, the health system network must have a proper design to deal with risky situations and carry out efficient operations for these situations. It also must be capable of easily or quickly recovering from sudden disruptions (Djalante et al., 2020). This potential is the reason behind the importance of resiliency in healthcare systems facing infectious diseases. In general, the resiliency of a system is regarded as its ability to overcome particular difficulties and become strengthened and more resourceful in the face of adversity (Holling, 1973). To have a resilient healthcare system during the outbreak of COVID-19 disease, the architectural style of the medical center's network needs to minimize bed shortage, population density, and as a result, the rate of spread.

With the essential motivation for addressing the problem the Ministry of Health and Medical Education (MHME) of Iran faces, this study presents a mixed-integer linear programming (MILP) model to design a resilient health system for improving medical services to the infected people with COVID-19. The proposed model has the potential capability to make the appropriate decision regarding the number and location of health providers, such as screening centers, camps, or quarantine stations, the distribution of infected people in different kinds of medical centers and camps, the distribution of improved infected people in quarantine stations, and the distribution of infected people in each of the medical centers. Thus, it seeks to decrease the spread rate of the virus, considering the lowest rate of movement of infected people in the community.

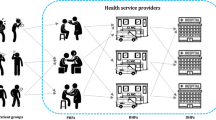
In this network, suspected COVID-19 cases undergo a test, and then they are admitted to the medical centers based on the symptoms type and severity when their test result is positive. Their condition is assessed at three levels: camps, specialized hospitals, and general hospitals. Patient transfer between the levels is possible when the symptoms of patients admitted to the lower-level medical centers may worsen later, and they need to take more specialized medical services. Finally, improved populations are transferred to the available quarantine stations for the recovery plan. This study aims to analyze the conditions under which the transfer of infected people with coronavirus all over the network is at the lowest cost, distance, and de-resiliency so that the rate of spread decreases. To this end, the suspected cases are referred to the nearest screening center and then assigned to medical centers based on the shortest distance and resiliency measures.

Therefore, all in all, identifying the infected people, providing complete medical treatment services for them, and maintaining the social distance between them and healthy people are the most important known factors in preventing the outbreak of such diseases as COVID-19. This study addresses the following research questions with the essential motivation of designing an efficient and resilient health system to implement the above policies.

• Which factors have a significant role in establishing a resilient health service network for infected people with COVID-19?

• What is the effective strategy for decreasing the possibility of virus transmission to healthy people when infected people commute in society?

• How many screening centers, camps, and quarantine stations must be set up, and what are the best places for these facilities to provide complete medical treatment services for the sufferers?

• How do different types of infected people in the health services network transfer between camps, general hospitals, and specialized hospitals?

• How do the improved cases from all three levels (i.e., specialized hospitals, general hospitals, and camps) transfer to quarantine stations after completing medical treatment?

It is worth noting that many researchers have conducted studies on the spread of coronavirus in recent months to investigate this global phenomenon from various aspects. Although designing and managing a transit system for coronavirus-infected people and establishing a medical treatment procedure for them is of great importance, to our knowledge, no focused paper has been done on the subject so far. This study adopts Operations Research (OR) techniques and mathematical formulation to design and improve a management and transit system for the infected people of such infectious diseases as coronavirus; the identified research gaps and four substantial contributions of the current study, in this regard, are as follows:

First, modeling and optimization techniques develop a powerful tool for the design of an efficient network. On the other hand, the availability of an efficient service network in the event of global crises, such as the coronavirus outbreak, is the most necessary measure that needs to be taken by health systems. However, no previous research has exploited the considerable potential of OR techniques for designing a network to provide infected people with diseases with healthcare services. Thus, the study employs OR techniques to enhance the quality of health services so that the spread of such viruses as COVID-19 decreases.

Second, accurately identifying coronavirus-infected people is a significant issue in preventing its spread. Therefore, the study creates a new treatment network design where people with suspected COVID-19 symptoms undergo a screening test to be admitted to the medical centers when their test result is positive.

Third, the instability of prevalence in different periods and the stochastic number of patients with different disease severity increase the complexity of service management for infected people with COVID-19. However, with increasing complexity, any unpredictable event such as staff error and equipment failure (e.g., detection kit equipment) causes a misdiagnosis, more prevalence, and a significant mortality rate. Consequently, it necessitates considering the resiliency factor in establishing a health service network to be flexible in the face of any unexpected change. Accordingly, the present research determines three resiliency measures to enrich the designed network against potential threats.

Fourth, since the sufferers of infectious diseases experience various symptoms, they require medical care at different levels. It is one of the significant issues that must be considered in designing an efficient treatment network. Therefore, this study identifies symptom types and severity to provide infected people with effective treatment.

Fifth, the transit system for the infected people must largely avoid contact with healthy people. Thus, a mathematical model considering the lowest level of patients’ movement in society is the fifth contribution of the study.

The rest of the study is structured as follows. Section 2 reviews studies on using OR applications in designing a health system for infectious diseases. Section 3 states the problem and develops a mathematical model. Section 4 describes the evaluation procedure: a novel hybrid uncertainty programming method to cope with mixed uncertainty and an interactive fuzzy approach to address the multi-objective problem. Section 5 provides a real case study from Tehran city of Iran. Sections 6 and 7 present the computational results, sensitivity analyses, and management findings. At last, Sect. 8 concludes the study and develops future recommendations.

2 Related literature

The study of applications of quantitative techniques in health service networks has drawn more interest in recent years since the outbreak of the COVID-19 virus. A review paper by Ivanov and Dolgui (2021) indicated that the existing OR techniques could effectively overcome the lasting effects at five pandemic stages of COVID-19 (i.e., Anticipation, Early Detection, Containment, Control and Mitigation, and Elimination). Another review paper on decision-making strategies for the COVID-19 pandemic is provided by Moosavi et al. (2022), which conducted that resiliency and sustainability had relatively great attention in popular keywords of scholars. Overall, the main focus of the current section is to review the literature on the applications of OR in the design of medical service networks during the epidemic. Therefore, the related literature can be divided into two main categories: 2.1. Applications of OR in epidemic outbreaks and 2.2. Applications of OR in health service network design. Eventually, research gaps in the literature are presented in Sect. 2.3 to display the distinguishing characteristics of the present study.

2.1 Applications of OR in epidemic outbreaks of disease

OR, as a common standard of system thinking, appears to have gained increasing popularity among healthcare-related sectors. The established reputation of powerful techniques in addressing health issues makes it significant to conduct further research on their potential applications in infectious diseases. The following paragraphs briefly explain the few studies on adopting OR techniques in the outbreak of contagious diseases. Then, efforts are made to propose new ideas and bridge the knowledge gaps.

Johanis (2007) analyzed a pandemic response plan at the international airport of Toronto Pearson in 2002–2003 when the airline industry experienced the catastrophic effects of a SARS epidemic at a global level. Rachaniotis et al. (2012) presented a mathematical model according to the schedule developed for fighting the flu epidemic. The amount of the needed effort and time for control was considered an increasing function of the starting time for an effort to suppress. They used the model for the widespread vaccination against $A\left( {H1N1} \right)v$ influenza in the Attica region, Greece, as a case study. Büyüktahtakın et al. (2018) developed a decision-support framework when the Ebola outbreak had severely affected global logistics. The framework facilitated the estimation of epidemic proportions and the effects on supply chains by offering a choice of logistics policy measures during and after the disaster.

Considering the influential role of truck drivers in the outbreak of infectious diseases such as HIV in sub-Saharan Africa, a non-governmental organization, namely the North Star Alliance, constructed a network of health facilities along the longest truck routes in sub-Saharan Africa. Accordingly, de Vries et al. (2020) addressed the problem of the extra facilities' location and the type of health services. The goals of their study included an increase in admission rate per facility and the improvement of the efficiency of health services delivery. A multi-objective optimizing approach was adopted by Sun et al. (2014) to allocate resources during an influenza pandemic efficiently. It brought commuting distance to hospitals and non-ICU resources into focus, considering the total bed capacity of hospitals as a constraint. Also, there are a limited number of studies (such as Hackl and Dubernet (2019); Currie et al. (2020)) on the disturbances of simulation and transportation caused by epidemic outbreaks.

Following the global coronavirus outbreak, a growing body of published literature on the subject is to apply quantitative methods such as operations research in addressing the issue of epidemic proportions and the effects from various aspects. Ivanov (2020a) checked the profile of uncertainty types to analyze the impact of COVID-19 on supply chain networks at a global level. Long- and short-term effects were predicted and simulated through logic software applications. Govindan et al. (2020) adopted a fuzzy inference system to develop a practical method of decision support for minimizing the disturbances of the healthcare supply chain caused by the outbreak of the COVID-19 epidemic with help to demand management. According to the report of WHO on COVID-19, they assessed the efficiency of their method.

Yu et al. (2020) presented a multi-period multi-objective model supporting the design idea for a reverse logistics network to efficiently handle the medical waste produced from an infectious disease outbreak such as coronavirus. Their proposed model used a way to identify the most convenient location of temporary facilities and transportation policy to effectively manage the medical waste that exponentially increases in a brief period. El-Baz and Ruel (2021) examined the effect of risk management in diminishing the disruptive influences of the COVID-19 pandemic on supply chain resilience. Choi (2020) investigated the impact of coronavirus outbreaks on the behavioral pattern of both consumers and service providers in the service operation system of Hong Kong within an analytical framework. He has also proposed a "bring-service-near-young-home" strategy for handling disasters such as the coronavirus outbreak based on the commercial model of mobile service operations.

Ivanov (2020b) introduced viability as an underlying concept at three levels of agility, resiliency, and sustainability in supply chains to propose a model enabling companies to shape their decisions on the revival of their supply chains after long-term global problems such as the pandemic COVID -19. Yang and Wang (2020) found numerous transmission routes in the spread dynamics of coronavirus, with particular emphasis on the role of a natural reservoir in the disease outbreak. The numerical data showed that coronavirus would remain an endemic disease, necessitating long-term intervention programs to prevent its spread. Ivanov and Dolgui (2020) offered a new insight into the resistance of the supply chain to critical disturbances on a scale of viability. They gained a conceptual understanding of a new decision-making model for intertwined supply network (ISN) viability to assess the viability by a dynamic game-theoretic model of a biological system resemblance the ISN.

Due to the virus's novelty, prediction of the COVID-19 pandemic growth is essential to enable governments to put new measures to slow down the spread of the virus. Therefore, Khalilpourazari et al. (2021) suggested a gradient-based Grey wolf optimizer (GGWO) for predicting the COVID-19 pandemic in the US. To avoid getting trapped in local optima, they also used the Gaussian walk and L ́evy flight to improve the capabilities to explore and exploit in their proposed method. Their results predicted an upcoming peak in the number of infected and ICU-admitted cases in healthcare systems to help policymakers and avoid equipment shortages. Khalilpourazari and Hashemi-Doulabi (2021) proposed an efficient reinforcement learning-based algorithm to simulate the COVID-19 pandemic in France. As output, they derived the values of significant parameters, such as reproduction rate, that would help healthcare professionals plan for future measures limiting community transmission. In another study, Khalilpourazari and Hashemi-Doulabi (2021) developed a stochastic fractal search algorithm combined with a mathematical model to predict the number of symptomatic, asymptomatic, life-threatening, recovered, and death cases of COVID-19, in Canada. Their results showed that asymptomatic cases were the main factor in the transmission of the virus in society. They also concluded that as the frequency of diagnostic tests increased, the likelihood of detecting asymptomatic people increased, and preventing from spreading the virus occurred. Most recently, Khalilpourazari and Hashemi-Doulabi (2022) proposed a novel hybrid reinforcement learning-based algorithm to predict the COVID-19 outbreak based on the most recent data from Quebec, Canada. Also, they combined their proposed algorithm with the most recent mathematical model for COVID-19 pandemic prediction to accurately show the future trend of the pandemic with a logical mean square error.

In the latest review papers, Queiroz et al. (2020) offered a framework for supervising operations and monitoring supply chain performance during the outbreak of the COVID-19 pandemic from the aspects of sustainability, lasting effects, recovery, preparedness, digitalization, and adaptation. Chowdhury et al. (2021) examined available studies on the COVID-19 epidemic disease in supply chain fields, which have issued before September 28, 2020. Their examination disclosed the lack of studies with an experimental design and a theoretical ground in light of the COVID-19 pandemic. Also, their review revealed that most of them have concentrated on supply chains for essential products with a great demand level and healthcare goods, regardless of items with a lower demand level and SMEs. Sotoudeh-Anvari (2022) revealed the increasing popularity of the multiple criteria decision-making (MCDM) techniques in constructing a model of the COVID-19 pandemic problems due to its multi-dimensional nature and socioeconomic intricacy of the healthcare systems. They also disclosed that most recently conducted investigations integrated different fuzzy sets with MCDM approaches to cope with the issue of ambiguity and uncertainty during data analysis.

Ehsani et al. (2023) presented a new humanitarian location-allocation-inventory model concentrating on controlling an outbreak of the COVID-19 pandemic by IoT-based technology in the reaction stage of catastrophes. IoT-based technology-enabled systems in their investigation made corporates relating to health and first aid capable of monitoring patients remotely, detecting, supervising, and disinfecting the suspected individuals, and transporting relief materials. The model presented by this study had two phases. The first phase consisted of describing infected individuals, quickly moving patients to transient hospitals and housing individuals in evacuation hubs. The next one was to locate distribution hubs and evenly transfer relief materials to evacuation hubs and temporary hospitals, considering the minimization objective of shortage. They used the LP-metric approach to solve the model whose validity was confirmed in a real-world case study in Salas-e-Babajani, Kermanshah, Iran. Their findings indicated that using an IoT-based technology-enabled system in evacuation hubs and involved zones decreased the number of infected individuals and the shortage of relief materials. Goodarzian et al. (2021a) constructed a multi-objective multi-echelon multi-period multi-product linear mixed-integer programming model for novel flow, production, location, allocation, stock holding, and distribution problems to create a unique resilient-sustainable healthcare network for the COVID-19 epidemic disease under uncertainty. They utilized a simulation strategy to assess the significance of the existing demand for pharmaceutical products and stochastic chance constraint programming to deal with parameters with inherent uncertainty. They also suggested meta-heuristic Genetic Algorithm (GA), Multiple Objective Teaching–learning-based optimization (TLBO), and Particle Swarm Optimization (PSO) techniques to achieve Pareto solutions. They conducted a real-world case study in the US to confirm the validity of their model, which could be helpful for hospitals, distributors, drugstores, medical suppliers, and the Health Ministry. To warrant cost and time considerations for transportation, Li et al. (2023) regarded a network of hub-and-spoke multimodal transportation for crisis relief programs in the event of facing unplanned COVID-19 epidemic disease. As the first step, they constructed a mixed integer nonlinear programming (MINLP) model according to multimodal transportation and crisis relief of multiple types. Their presented model had two objectives of transportation time and cost minimization. Moreover, they redesigned Grey Wolf Optimizer (GWO) algorithm to resolve the NP-hardness of the considered problem.

Kargar et al. (2020) developed a linear programming model with three objective functions to minimize the amount of waste, the hazard of infectious waste, and the total cost in medical centers. Also, they presented a variety of function relations to measure the amount of produced waste in terms of COVID-19 parameters in Iran. Mosallanezhad et al. (2023) designed a supply chain network for COVID-19 Pandemic Wastes (CPWs) employing devices for optimization modeling. Furthermore, they developed an IoT platform to allow the presented model for real-time data retrieval from IoT tools as inputs for the model. Also, they incorporated sustainability factors into their model enabled by IoT-based technology, assuming its triplet pillars as objective functions. To confirm the validity of their model, they conducted a case study in Puebla city and several experiments using integrated metaheuristic algorithms to solve it. Mondal and Roy (2021) regarded multi-period multi-objective planning for an open-close loop sustainable supply chain with multiple products to support supply among hospitals and manufacturing centers during the COVID-19 epidemic disease. To construct a less infectious logistics network, they developed the problems of transport and routing of pick-up-delivery vehicles in two phases considering carry-out distribution. They presented a decision-making process with multiple attributes to define the preferences of involved zones based on entropy weights. Furthermore, they employed an uncertain mixed environment by specifying random-uncertain parameters in the presented model and used the augmented weighted Tchebycheff technique for problem-solving.

Babaee-Tirkolaee et al. (2022a) proposed a novel socio-economic bi-objective model to design a multi-echelon blood supply chain network (BSCN) during a pandemic such as COVID-19. They assumed uncertainty in parameters, such as demand, capacity, and blood disposal rates, and utilized interactive possibilistic programming to treat the problem optimally. To validate the developed methodology, they analyzed a real case study of a blood supply chain in Tehran, Iran, along with sensitivity analyses of the main parameters. Gilani and Sahebi (2022) presented a mathematical model for a dual-channel sustainable COVID-19 vaccine supply considering the economic, environmental, and social factors. They have also utilized a polyhedral uncertainty set to propose a robust data-driven model to cope with uncertainty in the unfair distribution of vaccines in the world. They implemented their proposed model in a real case in Iran, and their model output reported the construction of two domestic vaccine production centers and five foreign distributors strategically. Hosseini-Motlagh et al. (2021) designed a supply network to allocate various COVID-19 test kits to the suspected people to minimize the total network cost and decrease false results of COVID-19 tests. They proposed a multi-stage stochastic programming (MSSP) method with a combined scenario tree to cope with the uncertain parameters (such as potential demands for various test kits and the rate of prevalence of COVID-19) in a dynamic condition. Eventually, they used a real case in Iran to confirm the validity of their proposed methods. Goodarzian et al. (2021b) presented a multi-objective sustainable integrated model related to the medical supply chain network, considering the distribution of COVID-19 medicines to patients and medicine delivery and production periods according to the perishability of some of them. They suggested three hybrid meta-heuristic algorithms to solve the proposed model. Also, they investigated the dynamicity of the COVID-19 outbreak to estimate the number of required medicines using the simulation approach. Babaee-Tirkolaee et al. (2022b) developed a novel multi-objective model to design a sustainable multi-period multi-echelon multi-product mask closed-loop supply chain network during the COVID-19 outbreak. In their proposed model, they addressed the locational, supply, production, distribution, collection, quarantine, recycling, reuse, and disposal decisions to minimize the total cost, total pollution, and total human risks simultaneously. Also, they implemented Multi-Objective Grey Wolf Optimization (MOGWO) algorithm and Non-Dominated Sorting Genetic Algorithm II (NSGA-II) to solve the proposed model and find Pareto optimal solutions.

Liu et al. (2023) concentrated on locating the testing installations, such as test kits, to meet varying demands induced by epidemic diseases. They presented an optimization framework with two stages to determine the location of establishments and adapt potential over emergencies of a large size. Using a developed online convex optimization-based Lagrangian relaxation approach to solving the sample-average-approximation (SAA) method, prespecified fill-rate prerequisites were met by initial prepositioning techniques in the first stage. Then they adapted the potential to meet varying demands dynamically in the second stage. Furthermore, they accomplished an extensive case study on the hazard of the COVID-19 pandemic to assess their presented technique. Shiri et al. (2023) constructed a linear two-stage mixed-integer model with multiple objectives for a healthcare network at home over pandemic diseases, e.g., COVID-19. In the first stage, the productive healthcare centers were opened to perform scheduling and routing subject to social accountability and efficacy. They considered multiple objectives, including total cost and level of inefficiency minimization and social factors maximization. They integrated the presented optimization model and the augmented data envelopment analysis (DEA) approach to determine the efficiency level. Besides, they designed the TH method as an interactive technique to solve the presented multiple-objective model and a powerful fuzzy strategy to address social aspects, cost, and time of service as parameters with inherent uncertainty. Ultimately, they carried out a real-world case study in Kermanshah, Iran.

Using a two-stage stochastic mixed integer program, Zhang et al. (2023) proposed strategies with multiple mitigations in medical facilities to guarantee supply without interruption for hospitals and substantial rescues over pandemic diseases. They planned to generate an emergency reaction application integrating preparedness activity (contract provider choosing, reserve site, and stock level) with actions post-event (assigning medical items through different ways). Furthermore, they designed a branch-and-Benders-cut technique for their problem, outperforming considerably in the time of solution compared with other classical ones. As the final step, they employed data on the COVID-19 epidemic disease in Wuhan, China, to confirm the validity of the presented technique. Ardakani et al. (2023) constructed a location-allocation model with multiple objectives to boost healthcare systems resilience using alternative sources, such as trainee nurses and field and backup hospitals, aiming for system cost minimization and rate maximization of satisfaction among patients of COVID-19 and medical employees. They also developed a powerful method to encounter the uncertainty of data. To explore the usability of their model, they conducted a case study with an analysis of sensitivity in the real world. Their findings indicated that the number decrease in existing nurses increased the system costs and decreased the satisfaction rate of nurses and patients. Also, medical employees and field and backup hospitals upgraded the system's resilience. Ash et al. (2022) developed a robust multi-objective multi-period framework for distribution optimization to boost the supply chains' resiliency of personal protective equipment (PPE) against disturbances induced by pandemic diseases, inspired by challenges facing a healthcare supplier in a province of Canada over the COVID-19 epidemic disease. Specifying demand, cost, and supply as undetermined parameters, they produced effective solutions along a trade-off between maximizing service rank and minimizing cost by the $\varepsilon$-constraint strategy. Their investigation emphasized the significance of supervision and preliminary alert systems in enabling decision-makers in the supply chain to initiate probable programs such as closing contracts, strengthening logistical potentials, and taking advantage of emergency supplies.

Çetinkaya et al. (2023) presented a process with five stages for solving the problem of selecting mass vaccination locations. As the first step, they specified the criteria for location choosing and provided a map of the gathered spatial information utilizing the software of Geographical Information System (GIS). Then, using the entropy weighting method (EWM), they determined the proximate significance grades of criteria and ranked the possible mass vaccination locations using the multiple attribute utility theory (MAUT) methods. Finally, they utilized the GIS's network analyst device to analyze the ranked alternative places based on the population undercover. Furthermore, they accomplished a case study in Gaziantep City, Turkey, which was the 9th most populated and had an above-average number of COVID-19 patients. To resolve the inherent uncertainty in both problem sides of vaccine distribution, i.e., demand and supply, Dastgoshade et al. (2022) presented a new two-stage stochastic programming model with two objectives by the sample-average-approximation (SAA) technique. Also, they designed a lexicographic goal programming method where social fairness was a preferred objective. They supplied proof of the advantages of including social fairness in a decision-making process based on a model, employing data about COVID-19 in two significant provinces of Iran. Goodarzian et al. (2022) developed a novel responsive-green-cold vaccine supply chain network over the COVID-19 epidemic disease, based on which they created a renewed multiple objective multi-echelon multi-period mathematical model for the problems of location, allocation, and distribution simultaneously. They also applied Internet-of-Things (IoT) for the COVID-19 pandemic in their model to improve accuracy, pace, and fairness in injecting the vaccine with available preferences. They solved their model using LP-metric, Variable Neighborhood Search (VNS), and Gray Wolf Optimization (GWO) algorithms and confirmed its efficacy by conducting a real-world case study in Iran. Their findings demonstrated that compared to other mentioned algorithms, MGO delivered a higher level of quality and outperformed. Pointing to academies as one of the most congested metropolitan areas, Kamran et al. (2023) designed a novel stochastic multi-product multi-period multi-objective simulation optimization model for the COVID-19 vaccine's manufacturing, distribution, location, allocation, and stock management decisions. Their presented supply chain network comprised four echelons of suppliers, clinics, vaccination hubs, and students volunteering for vaccine injection. They also created a system with a dynamic design of the spread of the COVID-19 pandemic in academies to assess demand for the vaccine through simulation, where demand as a specified stochastic parameter entered the model. Accordingly, their model's objectives were to minimize costs associated with the supply chain, maximize the desirableness of vaccine injection among the students, and maximize fairness in vaccine distribution. They solved their model using the Whale Optimization Algorithm (WOA) and Variable Neighborhood Search (VNS) algorithms. They also confirmed its validity by conducting a real-world case study of the COVID-19 epidemic disease span in Tehran, Iran.

In a review of the literature on the potential application of OR in the outbreak of epidemic diseases, a considerable proportion of the research has worked on OR techniques to analyze social and economic conditions created by the outbreak of infectious diseases in the business sector. OR methods have the potential capability for the design of an efficient treatment network. However, no research has covered the issue of spreading diseases. To fill the gap, this study seeks to apply OR techniques in designing a network of specialist medical services for infected people with the COVID-19 virus.

2.2 Applications of OR in health service network design

This sub-section reviews the published articles on OR applications in the medical service network. Location-allocation models, as an example of OR models, have an increased role in the success of health service networks since they are capable of identifying the crucial factors of a healthcare network, including the number of healthcare facilities to be constructed, the allocated portion of patient zones to the facilities, the most convenient location of the facilities, and patterns of interaction among health service providers at the lowest cost or highest profit (Rais & Viana, 2011). Thus, the models have been widely utilized in health service networks such as organ transplant services (Zahiri et al., 2014a, 2014b), emergency medical service designs (Andersson et al., 2020; Baharmand et al., 2019; Beraldi & Bruni, 2009; Haeri et al., 2020a; Mohamadi & Yaghoubi, 2017), preventive healthcare facility network designs (Ershadi & Shemirani, 2021; Haeri et al., 2022; Zhang et al., 2009), home healthcare supply chain network design (Fathollahi-Fard et al., 2018, 2019; Khodaparasti et al., 2018), pharmaceutical supply chain network design (Akbarpour et al., 2020; Mousazadeh et al., 2015), and blood supply chain network design (Haeri et al., 2020b; Haghjoo et al., 2020; Samani & Hosseini-Motlagh, 2019; Samani et al., 2019, 2020; Yaghoubi et al., 2020; Zahiri et al., 2015).

In a review paper, Ahmadi-Javid et al. (2017) categorized research studies on the issue of location in healthcare networks based on case study inclusion, solution method, approach to the mathematical model, fundamental discrete location problem, constraints, decision variables, objective function, particular input/setting, multi-period setting, and uncertainty. Zarrinpoor et al. (2018) tailored a robust-scenario-based stochastic programming approach to develop a two-level reliable hierarchical location-allocation model with service referral by handling the design problem of the health service network in the real world. Also, they adopted the enhanced accelerating Benders decomposition methods to solve the proposed model in large-scale sizes. Mousazadeh et al. (2018a) addressed the redesign problem of a multi-period three-level health service network to establish a viable, stable, and efficient network in the real world. A robust mixed possibilistic-flexible programming approach and the augmented $\varepsilon$-constraint method were also used to cope with the uncertainty of model parameters and to show the Pareto front.

Shishebori and Babadi (2015) introduced a robust optimization technique with optimal performance for the design problem of a reliable location network in the medical service center that conducted a simultaneous assessment of investment budget limits, system disruptions, and uncertain parameters. A bi-objective model for a hierarchical three-level health service network design was presented by Mousazadeh et al. (2018b) in another research study to decrease the total cost of construction and shorten the total weighted distance from patient zones to health facilities.

Denoyel et al. (2017) developed an optimization model for payers as a combination of Reference Pricing and a Tiered Network to solve a difference of opinion over payment policies for the healthcare sector in quantitative research. The objective function was the specification of health service providers exempt from Reference Pricing that their patients incur no out-of-pocket costs. Their model made a trade-off between cost reduction for the payer and the quality of the provider's health services. Wang et al. (2019) used a dynamic model to design a reverse logistics network for urban medical waste at two-stage. They determined the quantity of medical waste by the prediction model of Grey n the first stage to minimize environmental impacts and operating costs by a multi-objective model in the second stage.

Iloglu and Albert (2018) represented a novel type of the P-median problem to simulate the interdependence of infrastructural facilities and health service providers, in which all emergency personnel offered the essential services and the recovery center repaired severe damage to the infrastructure network. The objective function was to minimize the weighted cumulative effect of a time lag between emergency personnel service calls. They used the Lagrangian relaxation algorithm to solve the model by sub-gradient optimization.

Acar and Kaya (2019) presented a two-stage stochastic programming model to design an efficient healthcare service in facing disasters. They investigated proper logistics models for catastrophes in mobile hospitals to use them for an expected earthquake in Istanbul. Nasrabadi et al. (2020) constructed a model of the public healthcare sector's problem in the real world by a combination of short- and long-term uncertainties. They developed an efficient solution method for identifying the location of healthcare facilities, determining the capacities of healthcare facilities, and allocating service units to healthcare facilities. Also, more recently, Hashemi-Doulabi and Khalilpourazari (2022) proposed a state-variable model to formulate the two-stage stochastic operating room planning problem considering an exponential number of scenarios. Their objective function was to minimize the sum of the fixed opening cost of operating rooms and the expected overtime costs. The main advantage of their proposed model was that it had a pseudo-polynomial number of variables and constraints significantly fewer than that of other stochastic models presented in the literature. They improved the strength of their proposed model by developing several valid inequalities. Their output stated that the proposed model could find optimal solutions for instances with 50 surgeries and 1.55E+40 scenarios.

With this respect to the above points, many studies have examined the issue of health network design from various aspects. Given that there has been no research on giving medical services to infected people with contagious diseases so far. Thus, the present study develops a mathematical model to design a network for providing infected people with infectious viruses such as COVID-19 with medical services.

3 Research gaps

Many researchers have conducted studies on applying OR techniques to spread infectious viruses and design health networks for infected people with the viruses. However, there is no research on developing a mathematical model for designing a proper network of medical services for infected people with viruses. Given that the outbreak of infectious diseases creates critical conditions for their sufferers, establishing an efficient network of medical services to the infected people is the most challenging work of vital importance that must be carried out to prevent the spread of the virus in the community as much as possible. Accordingly, the present study aims to bridge the specified gaps. The novelty value of the study can be demonstrated from various aspects as follows:

• Presenting a network model of medical services to the infected people with coronavirus;

• Allocating the medical centers to the infected people with this respect to the severity of symptoms;

• Developing new indicators of resiliency in the network and using them as optimizing tools for addressing the spread of coronavirus;

• Considering the potential of existing centers in the city (such as crisis management sheds, Red Crescent Centers, student dormitories, and sports halls) to provide fast and convenient service to COVID-19 patients;

• Introducing a new hybrid uncertainty programming approach to eliminating the mixed and inaccurate parameters;

• Considering the effect of social distance in preventing the spread of coronavirus;

• Using the proposed model for the real-world case study of the COVID-19 epidemic in Iran.

4 Problem description and mathematical programming formulation

In this section, a resilient health service network is designed to provide the sufferers of COVID-19 with medical services in a more convenient and specialized way to enjoy the availability of healthcare facilities, which consists of suspected people zone, screening centers, medical service providers (such as camp stations (CSs), general hospitals (GHs), and specialized hospitals (SHs)), and quarantine stations. As illustrated in Fig. 1, first, the suspected people come to screening centers from different residential areas. Then, the necessary viral tests, including swab and or polymerase chain reaction (PCR) testing, will be done to identify the level of infection. Based on the results of screening tests, people with positive test results are identified as patients (definitively affected). Afterward, the affected people are introduced to different medical centers for treatment. Considering the underlying disease and the severity of symptoms, each sufferer will take a different kind of medical treatment. Thus, in the network under investigation, three types of medical service providers, including camps, general hospitals, and specialized hospitals, are considered at the third level. At this level, the unilateral transfer of infected people from a medical center to a more advanced one is also feasible. In other words, this consideration makes it possible to transfer infected people who have come to the camps into general hospitals or between general and specialized hospitals as their symptoms worsen and the emergency arises. Eventually, the improved infected cases are transferred into quarantine stations for around a few days since they may be carriers of the virus, and a long distance away from society needs to be maintained after discharge. It is worth mentioning that in Fig. 1, patients' direct and unilateral transshipment flows are indicated by continuous and dashed lines, respectively.

Fig. 1

An overview of the proposed health service network design for patients with COVID-19

Since the number of COVID-19 patients exceeds the capacity of medical centers, the lack of medical necessities (e.g., space, beds, and staff) and social distancing put the health system infrastructure under considerable pressure, which has unpleasant consequences for patients' health. In these circumstances, the adaptation level of the health system to the rising referral rate with no disruption in the supply chain of medical services will show the resiliency of the health network and its importance. Multiple indicators of resiliency are considered instruments for design optimization in Sect. 3.2 to improve the network's reliability. Therefore, to reduce risks and enhance the resiliency of the investigated health network structure, the following indicators of resiliency are taken into account:

• Health facility criticality (congestion criteria) given that the commuting of sufferers in society increases the probability of virus spread, the congestion criterion calculates the total quantity of inflows and outflows in the health facility. Higher health facility congestion tends to create a less resilient network. Hence, health facility criticality is applied to assess the health service network resiliency. A health facility (including screening centers, camp stations, and quarantine stations) becomes critical as the summation of inflows and outflows of COVID-19 virus carriers in that facility exceeds a determined threshold.

• Patient dissatisfaction level (shortage criteria) timely decision about hospitalization and quarantine is one of the most crucial strategies for effective treatment and preventing the further outbreak of COVID-19 disease. The limited capacity of medical centers makes it impossible to provide all patients with medical services, especially at peak times. It puts COVID-19 patients’ lives at risk, leads to some delays in the treatment of emergency patients, increases the rate of spread caused by commuting in society, and disrupts the health system. Thus, the dissatisfaction criterion shows non-admission to medical centers, which is caused by their limited potential. On the other hand, it is an indicating factor of deficiencies in the centers. The higher the number of non-admissions, the more inefficient the healthcare system.

• Dispersion of suspicious people (de-concentration criteria) during the outbreak of COVID-19 disease, the more accurate identification of infected cases requires that the suspected patients take a test in screening centers introduced by the healthcare sector. Although all the centers offer the same services, some have a higher referral rate leading to an imbalance in the network. Therefore, the even distribution of the suspected patients among the centers is a good solution for using all the infrastructures and preventing the spread. The de-concentration criterion states that the visit-capacity ratio of a screening center should reach a uniform size and not be overcrowded. More precisely, the number of visits to each center must be the same as a predetermined constant ratio plus a tolerance.

According to the above explanations, the presented model tends to determine the optimal number and location of screening centers, camps, and quarantine stations, as well as the allocated portion of each medical center to the infected people with COVID-19, efficient assignment of patient zones to screening centers, and their transfer from screening centers to camps or different kinds of hospitals, and efficient allocation of improved cases to quarantine stations to reduce the commuting time of infected people in the society and subsequently the rate of virus spread, to make a tradeoff relationship between the network resiliency, mileage of sufferers, and network costs.

4.1 Assumptions

The fundamental assumptions below are used in the suggested model.

• According to symptoms severity and underlying disease, coronavirus patients must receive various medical services (Helmy et al., 2020). Thus, this study divides infected people into three categories: mild symptoms and severe ones with and without underlying disease.

• Since making a treatment plan for each patient is impossible, infected people are grouped in several patient zones based on residential areas for the planning process.

• The central point of each patient zone is regarded as an indicator for calculating commuting distance.

• Since the COVID-19 pandemic causes considerable fluctuations with unpredictable effects, the number of infected cases per period and scenario is an uncertain parameter.

• Little time and the need for medium-term planning make it impossible to construct new hospital buildings during the COVID-19 outbreak. Thus, several existing general and specialized hospitals offer medical services to the sufferers. However, several camps are established to serve outpatients due to the limited capacity of existing hospitals.

• Screening centers, medical centers, and quarantine stations contain limited test kits and beds. Thus, they own a limited capacity, a small part of which is assigned to COVID-19 patients.

• Since hospitalized patients’ conditions may become acute over time, and there may be a need for more advanced medical services, unilateral transfer between medical centers (camps and hospitals) is allowed.

• Since the improved patients need to stay away from the community for a period to prevent the transmission of the virus, they must be in quarantine stations for a specified time regardless of their symptom severity.

4.2 Mathematical model

As mentioned before, the model is aimed at minimizing the de-resiliency of the health service network, travel distance of all sufferers, and total network costs subject to the most intelligent decision on the number and location of health providers such as camps or quarantine stations, the distribution of infected people in the different kinds of medical centers and camps, the distribution of improved patients in quarantine stations, and the distribution of infected people in each of the medical centers. The structure of the model is demonstrated in the following equations, and its notations are provided in Appendix A. Also, the structural properties of the coming model are provided in Appendix B.

4.2.1 First objective function (resiliency measure)

$$ \begin{aligned} Min\,\, obj1 & = \mathop \sum \limits_{g} \vartheta \times y_{g} + \mathop \sum \limits_{j} \vartheta^{\prime } \times y_{j}^{\prime CS} + \mathop \sum \limits_{q} \vartheta^{\prime \prime } \times y_{q}^{\prime \prime } \\ & \quad + \mathop \sum \limits_{t} \mathop \sum \limits_{s} \left( {pe^{GH} \times \mathop \sum \limits_{j} u_{j}^{tsGH} + pe^{SH} \times \mathop \sum \limits_{j} u_{j}^{tsSH} + pe^{CS} } \right. \\ & \quad \left. { \times \mathop \sum \limits_{j} u_{j}^{tsCS} + pe^{\prime } \times \mathop \sum \limits_{q} u_{q}^{\prime ts} } \right) + \mathop \sum \limits_{g} \mathop \sum \limits_{t} \mathop \sum \limits_{s} \left( {\theta \times \varepsilon_{g}^{ - ts} + \theta^{\prime } \times \varepsilon_{g}^{ + ts} } \right) \\ \end{aligned} $$

(1)

The resiliency of a health service network is demonstrated by calculating the penalty coefficient for each of the mentioned resiliency measures. The above objective function is served to minimize the de-resiliency of the network in terms of the indicators. In this objective function, the first to third terms calculate the fines for critical screening centers, camp stations, and quarantine stations. Also, the fourth term calculates the penalty for shortages in medical centers and quarantine stations. Finally, the last one shows the penalty for negative and positive deviation from the congestion threshold value in screening centers.

4.2.2 Second objective function (distance measure)

$$ Min\,\, obj2 = \mathop \sum \limits_{t} \left( {\mathop \sum \limits_{i} \mathop \sum \limits_{g} z_{ig}^{ts} \times d_{ig} + \mathop \sum \limits_{g} \mathop \sum \limits_{j} z_{gj}^{\prime ts} \times d_{gj}^{\prime } + \mathop \sum \limits_{j} \mathop \sum \limits_{{j^{\prime}}} z_{{jj^{\prime}}}^{\prime \prime ts} \times d_{jj\prime }^{\prime \prime } + \mathop \sum \limits_{j} \mathop \sum \limits_{q} z_{jq}^{\prime \prime \prime ts} \times d_{jq}^{\prime \prime \prime } } \right) $$

(2)

The second aim is to minimize and limit the total distance of all suspected and infected people in society, as shown in Eq. (2). The first and second terms of this objective function express the distance between suspected people zones and screening centers and the distance between screening centers and medical centers (such as camp stations, general hospitals, and specialized hospitals), respectively. Also, the third and fourth terms show the distance between medical centers and the one between medical centers and quarantine stations, respectively.

4.2.3 Third objective function (cost measure)

$$ \begin{aligned} Min\,\, obj3 & = \mathop \sum \limits_{g} f_{g} \times x_{g} + \mathop \sum \limits_{j} f_{j}^{\prime } \times x_{j}^{\prime CS} + \mathop \sum \limits_{q} f_{q}^{\prime \prime } \times x_{q}^{\prime \prime } + \mathop \sum \limits_{i} \mathop \sum \limits_{g} \mathop \sum \limits_{t} \mathop \sum \limits_{s} o_{g}^{ts} \times b_{ig}^{ts} \\ & \quad + \mathop \sum \limits_{j} \mathop \sum \limits_{t} \mathop \sum \limits_{s} o_{j}^{\prime tsGH} \times l_{j}^{tsGH} + o_{j}^{\prime tsSH} \times l_{j}^{tsSH} + o_{j}^{\prime tsCS} \left. { \times l_{j}^{tsCS} } \right) + \mathop \sum \limits_{q} \mathop \sum \limits_{t} \mathop \sum \limits_{s} o_{q}^{\prime \prime ts} \times l_{q}^{\prime ts} \\ \end{aligned} $$

(3)

Equation (3) minimizes the total accumulative cost for establishing screening centers, camps, and quarantine stations, plus operational costs in the screening centers, medical centers (general hospitals, specialized hospitals, camp stations), and quarantine stations, respectively.

4.2.4 Capacity constraints

$$ \mathop \sum \limits_{i} b_{ig}^{ts} \le x_{g} \times c_{g} \quad \forall g,t,s $$

(4)

Equation (4) is a capacity constraint that limits incoming flows to screening centers from people zones in each period t if the screening center is located.

$$ \varpi_{j}^{tsGH} \le n_{j}^{GH} \quad \forall j \left( {general\;hospital} \right),t,s $$

(5)

$$ \varpi_{j}^{tsSH} \le n_{j}^{SH} \quad \forall j \left( {specialized\;hospital} \right),t,s $$

(6)

Equations (5) and (6) show that the allocated beds for infected cases of COVID-19 in each general and specialized hospital in each period could not exceed the maximum number of beds in each kind of hospital, respectively.

$$ l_{j}^{tsGH} - \varpi_{j}^{tsGH} = u_{j}^{tsGH} \quad \forall j \left( {general\;hospital} \right),t,s $$

(7)

$$ l_{j}^{tsSH} - \varpi_{j}^{tsSH} = u_{j}^{tsSH} \quad \forall j \left( {specialized\;hospital} \right),t,s $$

(8)

$$ l_{j}^{tsCS} - x_{j}^{\prime } \times c_{j}^{\prime CS} = u_{j}^{tsCS} \quad \forall j \left( {camp\;station} \right),t,s $$

(9)

$$ l_{q}^{\prime \prime ts} - x_{q}^{\prime \prime } \times c_{q}^{\prime \prime } = u_{q}^{\prime ts} \quad \forall q,t,s $$

(10)

Equations (7)–(10) shows the demand satisfaction in general hospitals, specialized hospitals, camps, and quarantine stations, respectively, by considering the lack of empty beds that may occur in them.

4.2.5 Allocation constraints

$$ \mathop \sum \limits_{g} z_{ig}^{ts} = 1\quad \forall i,t,s $$

(11)

$$ b_{ig}^{ts} \le e_{i}^{ts} a_{i} \times z_{ig}^{ts} \quad \forall i,g,t,s $$

(12)

Equation (11) guarantees the assignment of each patient zone to one screening center in each period. Equation (12) assures that the suspended people can be referred from a people zone to the screening center if the people zone is allocated to the screening center.

$$ \mathop \sum \limits_{j } z_{gj}^{\prime tstoCS} = 1\quad \forall g,t,s $$

(13)

$$ r_{gj}^{tstoCS} \le \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \times z_{gj}^{\prime tstoCS} \quad \forall g,j \left( {camp\;station} \right),t,s $$

(14)

$$ \mathop \sum \limits_{j} z_{gj}^{\prime tstoGH} = 1\quad \forall gt,s $$

(15)

$$ r_{gj}^{tsto\;GH} \le \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \times z_{gj}^{\prime tsto\;GH} \quad \forall g,j \left( {general\;hospital} \right),t,s $$

(16)

$$ \mathop \sum \limits_{j} z_{gj}^{\prime tsto\;SH} = 1\quad \forall g,t,s $$

(17)

$$ r_{gj}^{tsto\;SH} \le \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \times z_{gj}^{\prime tsto\;SH} \quad \forall g,j \left( {specialized\;hospital} \right),t,s $$

(18)

Equations (13), (15), and (17) guarantee the assignment of each screening center to one camp station, general, and specialized hospital in each period, respectively. Equations (14), (16), and (18) assure that the infected people can be referred from a screening center to one camp station, general and specialized hospital, if the screening center is allocated to them, respectively.

$$ \mathop \sum \limits_{{j^{\prime}}} z_{{jj^{\prime}}}^{\prime \prime tsfrom GH to SH} = 1,\quad \forall j \left( {general\;hospital} \right),t,s $$

(19)

$$ \begin{aligned} &w_{{jj^{\prime}}}^{{ts\;from\;GH\;to\;SH}{}} \le \omega_{t}^{s} \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \\ & \quad \times z_{{jj^{\prime}}}^{\prime \prime ts\;from\;GH\;to\;SH} \quad \forall j \left( {general\;hospital} \right),j^{\prime } \left( {specialized\;hospital} \right),t,s \end{aligned}$$

(20)

$$ \mathop \sum \limits_{{j^{\prime}}} z_{{jj^{\prime}}}^{\prime \prime ts\;from\;CS\;to\;GH} = 1\quad \forall j \left( {camp\;station} \right),t,s $$

(21)

$$ \begin{aligned} & w_{{jj^{\prime}}}^{ts\;from\;CS\;to\;GH} \le \omega_{t}^{\prime s} \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \\ & \quad \times z_{{jj^{\prime}}}^{\prime \prime ts\;from\;CS\;to\;GH} \quad \forall j \left( {camp\;station} \right),j^{\prime } \left( {general\;hospital} \right),t,s \end{aligned}$$

(22)

Equations (19) and (21) guarantee that each general hospital and each camp station should be assigned to one specialized hospital and one general hospital, respectively. Equations (20) and (22) assure that the infected people can be referred from a general hospital to a specialized one or from a camp station to a general hospital if the general hospital is allocated to a specialized hospital or the camp station is allocated to a general hospital, respectively.

$$ \mathop \sum \limits_{q} z_{jq}^{\prime \prime \prime ts} = 1\quad \forall j,{\text{t}},{\text{s}} $$

(23)

$$ v_{jq}^{ts} \le \tau_{t}^{s} \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \times z_{jq}^{\prime \prime \prime ts} \quad \forall j,q,{\text{t}},{\text{s}} $$

(24)

Equation (23) guarantees that each medical center (general hospital, specialized hospital, and camp station) should be assigned to one quarantine station in each period. Equation (24) assures that the improved patients can be referred from a medical center (general hospital, specialized hospital, and camp station) to a quarantine station if previously it is allocated to a quarantine station.

4.2.6 Non-criticality constraints

$$ \left( {\psi_{g} - \left( {\mathop \sum \limits_{b} b_{ig}^{ts} + \mathop \sum \limits_{j} r_{gj}^{ts} } \right)} \right)\left( {1 - y_{g} } \right) \ge \iota \left( {\left( {1 - y_{g} } \right)} \right)\quad \forall g,t,s $$

(25)

$$ \left( {\psi_{j}^{\prime CS} - \left( {\mathop \sum \limits_{g} r_{gj}^{ts} + \mathop \sum \limits_{{j^{\prime}}} w_{{j^{\prime}j}}^{ts} + \mathop \sum \limits_{q} v_{jq}^{ts} } \right)} \right)\left( {1 - y_{j}^{\prime CS} } \right) \ge \iota \left( {\left( {1 - y_{j}^{\prime CS} } \right)} \right)\quad \forall j \left( {camp\;station} \right),t,s $$

(26)

$$ \left( {\psi_{q}^{\prime \prime } - \mathop \sum \limits_{j} v_{jq}^{ts} } \right)\left( {1 - y_{q}^{\prime \prime } } \right) \ge \iota \left( {\left( {1 - y_{q}^{\prime \prime } } \right)} \right)\quad \forall q,t,s $$

(27)

Equations (25)–(27) respectively guarantee that the screening centers, camps, and quarantine stations be non-critical. These centers become critical if the number of total inflows and outflows in them exceeds a threshold. The above equations are calculated based on Eqs. (28)–(30), respectively.

$$ y_{g} = 1\;{\text{if}} \mathop \sum \limits_{b} b_{ig}^{ts} + \mathop \sum \limits_{j} r_{gj}^{ts} \ge \psi_{g} \quad \forall g,t,s $$

(28)

$$ y_{j}^{\prime CS} = 1\;{\text{if}} \mathop \sum \limits_{g} r_{gj}^{ts} + \mathop \sum \limits_{{j^{\prime\prime}}} w_{{j^{\prime}j}}^{ts} + \mathop \sum \limits_{q} v_{jq}^{ts} \ge \psi_{j}^{\prime CS} \quad \forall j \left( {camp\;station} \right),t,s $$

(29)

$$ y_{q}^{\prime \prime } = 1\;{\text{if }}\mathop \sum \limits_{j} v_{jq}^{ts} \ge \psi_{q}^{\prime \prime } \quad \forall q, t,s $$

(30)

4.2.7 Suspicious people dispersion constraint

$$ \frac{{\mathop \sum \nolimits_{i} b_{ig}^{ts} }}{{C_{g} }} = {\Gamma } + \varepsilon_{g}^{ - ts} - \varepsilon_{g}^{ + ts} \quad \forall g,t,s $$

(31)

Equation (31) calculated the tolerance of the congestion ratio from a predetermined constant for each screening center. It states that the number of visits/capacities of the screening center ratio should reach a uniform size not to be overcrowded. The number of visits to each center must be the same as a predetermined constant ratio plus a tolerance. The higher the tolerance, the worse the ratio.

4.2.8 Balance constraints

$$\begin{aligned} &l_{j}^{t - 1,sGH} + \mathop \sum \limits_{g} r_{gj}^{ts} + \mathop \sum \limits_{{j^{\prime}}} w_{{j^{\prime}j}}^{ts\;from\;CSs} - \mathop \sum \limits_{q} v_{jq}^{t - 1,s} - \mathop \sum \limits_{{j^{\prime}}} w_{{jj^{\prime}}}^{ts\;to\;SHs} - \left( {\rho_{t}^{sGH} \times l_{j}^{t - 1,sGH} } \right) \\ & \quad = l_{j}^{tsGH} \quad \forall j \left( {general\;hospital} \right),t,s \end{aligned}$$

(32)

$$\begin{aligned} &l_{j}^{t - 1,sSH} + \mathop \sum \limits_{g} r_{gj}^{ts} + \mathop \sum \limits_{{j^{\prime}}} w_{{j^{\prime}j}}^{ts\;from\; GH} - \mathop \sum \limits_{q} v_{jq}^{t - 1,s} - \left( {\rho_{t}^{sSH} \times l_{j}^{t - 1,sSH} } \right) \\ & \quad = l_{k}^{tsSH} \quad \forall j \left( {specialized\;hospital} \right),t,s\end{aligned} $$

(33)

$$\begin{aligned} &l_{j}^{t - 1,sCS} + \mathop \sum \limits_{g} r_{gj}^{ts} - \mathop \sum \limits_{q} v_{jq}^{t - 1,s} - \mathop \sum \limits_{{j^{\prime}}} w_{{jj^{\prime}}}^{ts\;to\;GHs} - \left( {\rho_{t}^{sCS} \times l_{j}^{t - 1,sCS} } \right) \\ &\quad = l_{j}^{tscCS} \quad \forall j \left( {camp\; station} \right),t,s\end{aligned} $$

(34)

$$ l_{q}^{\prime t - 1,s} + \mathop \sum \limits_{j} v_{jq}^{ts} - \left( {\pi_{t} \times l_{q}^{\prime t - 1,s} } \right) = l_{q}^{\prime ts} \quad \forall q,t,s $$

(35)

Equation (32) states an inflow and outflow conservation constraint (flow balance equation) for a general hospital. This constraint indicated the total number of hospitalized infected cases in this hospital is equal to the total number of hospitalized infected ones in the last period, plus the total amount of infected people with crucial symptoms and no underlying disease that transferred from the screening center in the current period, plus the number of infected people with worsening symptoms transferred from camp stations to the general hospital in the current period, minus the amount of improved and died infected people in the previous period, and also transferred infected people to a specialized hospital in the current period. Similarly, the flow balance for the specialized hospital, camp, and quarantine station is represented in Eqs. (33)–(35), respectively.

4.2.9 Logical constraints

$$ \mathop \sum \limits_{g} b_{ig}^{ts} \le a_{i} \times e_{i}^{ts} \quad \forall i,{\text{t}},{\text{s}} $$

(36)

Equation (36) implies that the total number of suspected people referred to screening centers in each zone and period should be less than the maximum population of that zone.

$$ \mathop \sum \limits_{i} b_{ig}^{ts} \times \Delta_{t}^{s} \times \beta_{t}^{s} \ge \mathop \sum \limits_{j} r_{gj}^{tsGH} \quad \forall g,{\text{t}},{\text{s}} $$

(37)

$$ \mathop \sum \limits_{i} b_{ig}^{t} \times \Delta_{t}^{s} \times \gamma_{t}^{s} \ge \mathop \sum \limits_{j} r_{gj}^{tsSH} \quad \forall g,{\text{t}},{\text{s}} $$

(38)

$$ \mathop \sum \limits_{i} b_{ig}^{t} \times \Delta_{t}^{s} \times \alpha_{t}^{s} \ge \mathop \sum \limits_{j} r_{gj}^{tsCS} \quad \forall g,{\text{t}},{\text{s}} $$

(39)

Equations (37)–(39) calculated the number of suspected people whose test is positive and are classified into one of the categories of infected people with mild symptoms, serious symptoms, and severe symptoms along with the underlying disease that should be transferred from screening centers to one of the medical centers of general, specialized hospital or camp station, respectively.

$$ \omega_{t}^{s} \times l_{j}^{tsGH} \ge \mathop \sum \limits_{{j^{\prime}}} w_{{jj^{\prime}}}^{ts\;to\;SH} \quad \forall j \left( {general\;hospital} \right),t,s $$

(40)

$$ \omega_{t}^{\prime s} \times l_{j}^{tsCS} \ge \mathop \sum \limits_{{j^{\prime}}} w_{{jj^{\prime}}}^{ts\;to\;GH} \quad \forall j \left( {camp\;station} \right),t,s $$

(41)

Equations (40) and (41) calculated the number of infected people whose condition was worse and transferred from a general to a specialized hospital or camp station to the general hospital in each period, and scenario, respectively.

$$ \tau_{t}^{sGH} \times l_{j}^{tsGH} \ge \mathop \sum \limits_{q} v_{jq}^{ts} \quad \forall j \left( {general\;hospital} \right),t,s $$

(42)

$$ \tau_{t}^{sSH} \times l_{j}^{tsSH} \ge \mathop \sum \limits_{q} v_{jq}^{ts} \quad \forall j \left( {specialized\;hospital} \right),t,s $$

(43)

$$ \tau_{t}^{sCS} \times l_{j}^{tCS} \ge \mathop \sum \limits_{q} v_{jq}^{ts} \quad \forall j \left( {camp\;station} \right),t,s $$

(44)

Equations (42)–(44) calculated the number of improved infected people that transferred from the general hospital, specialized hospital, and camp station to quarantine station in each period and scenario, respectively.

$$ l_{j}^{tsGH} \ge \varpi_{j}^{tsGH} \quad \forall j \left( {general\;hospital} \right),t,s $$

(45)

$$ l_{j}^{tsSH} \ge \varpi_{j}^{tsSH} \quad \forall j \left( {specialized\;hospital} \right),t,s $$

(46)

$$ l_{j}^{tsCS} \ge x_{j}^{\prime } \times c_{j}^{\prime } \quad \forall j \left( {camp\;station} \right),t,s $$

(47)

$$ l_{q}^{\prime ts} \ge x_{q}^{\prime \prime } \times c_{q}^{\prime \prime } \quad \forall q,t,s $$

(48)

Equations (45)–(48) display a higher number of people seeking hospitalization in medical centers (hospitals, camp stations, and quarantine stations) than their capacities. The number of beds assigned to patients with coronavirus is lower than the need for hospitalization in all medical centers, and a more likely possibility that the patients are affected by a shortage of beds.

4.2.10 Domain of the decision variables constraints

$$ \begin{gathered} x_{g} ,x_{j}^{\prime } ,x_{q}^{\prime \prime } ,y_{g} ,y_{j}^{\prime } ,y_{q}^{\prime \prime } \in \left\{ {0,1} \right\}\quad \forall g,j \left( {camp\;station} \right),q \hfill \\ z_{ig}^{ts} ,z_{gj}^{\prime ts} ,z_{{jj^{\prime}}}^{\prime \prime ts} ,z_{jq}^{\prime \prime \prime ts} \in \left\{ {0,1} \right\}\quad \forall i,g,j,q,t,s \hfill \\ \end{gathered} $$

(49)

$$ b_{ig}^{ts} ,r_{gj}^{ts} ,w_{{jj^{\prime}}}^{ts} ,v_{jq}^{ts} ,l_{j}^{ts} ,l_{q}^{\prime ts} \ge 0\quad \forall i,g,j,q,t,s $$

(50)

Equations (49) and (50) place the binary and non-negativity constraints upon the decision variables, respectively.

4.3 Model linearization

In the above model, constraints (25)–(27) are nonlinear and can be linearized by a binary variable $k$ and by replacing it with the multiplication of integer $x$ and binary $\epsilon$ variables $\left( {k = \epsilon \times x} \right)$. Accordingly, the value of variable $k$ is equal to that of the positive variable as the value of the binary variable is equal to 1; otherwise, it is 0. The three terms used for converting it to the linear form are the following:

$$ k \le x $$

(51)

$$ k \le r \times \epsilon $$

(52)

$$ k \ge x - r\left( {1 - \epsilon } \right) $$

(53)

$$ k \ge 0 $$

(54)

5 Solution methodology

In the proposed model, several parameters, such as the number of suspected people and operating and installation costs, are considered scenario-based and fuzzy imprecise parameters, respectively. This study provides a novel hybrid method of robust stochastic and possibilistic programming (RSPP) to solve the presented mathematical model with mixed uncertainty. Then, it addresses the proposed multi-objective mathematical model by an efficient solution approach called TH (Torabi-Hassini) (Torabi & Hassini, 2008).

5.1 Robust stochastic-possibilistic programming (RSPP)

Uncertainties are highly significant in network design and are caused by various reasons such as unavailable or inaccurate data, environmental factors, and the erroneous estimate of non-measurable parameters. A low degree of uncertainty can significantly affect the performance of networks. Therefore, a proper technique must be applied to resolve them and avoid their effects on supply chains. Considering the available data sets, uncertainties can be divided into three categories: random, epistemic, and inherent. Robust optimization, fuzzy programming, and stochastic programming of unique features, as the three main approaches for resolving any uncertainty available in mathematical programming, are employed based on the context and structure of the problem, the incompleteness level of model parameters, and the type of uncertainty. After analyzing the uncertainty type, the most appropriate approach(es) is(are) adopted to resolve it. Random ones are caused by adequate historical information for input parameters with the patterns of future situations. When randomness is the essential source of uncertainty in input data, it can be resolved by stochastic programming techniques. Superficial knowledge produces non-accurate parameters causing epistemic ones, which are specified by experts’ viewpoints. Fuzzy mathematical programming techniques can appropriately deal with both epistemic uncertainties in data and flexibility in goals and elasticity in constraints and are adopted to resolve them (Mousazadeh et al., 2014). Inherent uncertainties caused by unavailable data are the reason for specifying only the interval of input parameters.

Historical data are insufficient for modeling uncertain parameters as random data. It necessitates estimating uncertain data reasonably with the reliance on the viewpoints of the decision-makers in real-life situations. Thus, each non-accurate data set can be represented by a trapezoidal or triangular fuzzy numbers probability distribution. A possibilistic programming (PP) approach is employed to achieve a solution to mathematical programming models with possibilistic data (Mousazadeh et al., 2018a), among which Chance constrained programming (CCP) is most popular and guarantees an optimal confidence level (α) for possibilistic constraints, including non-accurate parameters. Necessity (Nec), Possibility (Pos), and credibility (Cr) are three commonly used fuzzy measures in possibilistic chance-constrained formulations. As a significant advantage, they assign a degree of occurrence to any fuzzy event in the interval [0, 1] with varying optimistic-pessimistic attitudes. Nec and Pos measures represent decision-makers extremely pessimistic and optimistic attitudes, respectively. The Cr measure represents an uncertain event occurrence with a degree of certainty. Xu and Zhou (2013) introduced the Me as a novel fuzzy measure, which is more flexible than Cr and proper for the decision-making process in real-world fuzzy situations. In this approach, the decision-maker can choose any point of extreme attitude by a convex combination of pessimistic and optimistic extremes. For this reason, this study uses the Me measure to convert possibilistic chance constraints into crisp ones in the formulation.

Accordingly, the RSPP method is employed to resolve the randomness and epistemic uncertainties since hybrid uncertainties exist in the presented model, including two groups of scenario- and fuzzy-based parameters. It integrates three $Me$ measure-based approaches to specifying the fuzzy (Possibilistic Programming) and scenario (Stochastic Programming) based parameters and to make the adjustments in the conservatism level of the output data (Robust Optimization) in terms of the uncertainty in parameters. Accordingly, a brief explanation of possibilistic chance-constrained programming (PCCP) and the Basic Stochastic- Possibilistic Programming (BSPP) approaches with an emphasis on the $Me$ measure is provided in Appendix C.

As discussed in Appendix C, the BPCCP model showed insensitivity to any deviation from the RHS of chance constraints (feasibility robustness) and the optimal value of the objective function (optimality robustness). Thus, the RSPP approach was proposed by Dehghan et al. (2018) to improve the robust performance of models in the simultaneous randomness and epistemic uncertainty of parameters in terms of $Me$ measure. It is implemented according to the definition below.

$$ \begin{aligned} & Min E\left[ z \right] + \eta \left( {z_{max} - z_{min} } \right) + \omega \mathop \sum \limits_{s} p_{s} \left| {E\left[ z \right] - E\left[ {z_{s} } \right]} \right| \\ & + \delta_{1} \mathop \sum \limits_{s} p_{s} \left[ {\frac{{\left( {\alpha_{s} - \lambda } \right)d_{1s} + \left( {1 - \alpha_{s} } \right)d_{2s} }}{1 - \lambda } - d_{1s} } \right] \\ & Subject\;to \\ & Ax_{s} \le \frac{{\left( {\alpha_{s} - \lambda } \right)d_{1s} + \left( {1 - \alpha_{s} } \right)d_{2s} }}{1 - \lambda } \\ & Bx_{s} \ge b \\ & Ex_{s} \le Ny \\ & Fx_{s} \le g_{s} \\ & y \in \left[ {0,1} \right], x \ge 0 \\ \end{aligned} $$

(55)

In the objective function, the first term refers to the same estimated value $\left( z \right)$ as the BSPP model. The optimality robustness under fuzzy parameters is described in the second term and is controlled by a reduction in the maximum ($z_{max}$) and minimum ($z_{min}$) possible values. The second term denotes a fuzzy-based deviation (possibilistic deviation) from the optimal value, and it has been shown by Eqs. (56) and (57). Also, $\eta$ indicates the weighted importance of the possibilistic deviation. It reduces the maximum deviation from the minimum one. (Pishvaee et al. (2012a), Farokh et al. (2018)).

$$ z_{max} = f_{4} y + \mathop \sum \limits_{s} p_{s} c_{4s} y_{s} $$

(56)

$$ z_{min} = f_{1} y + \mathop \sum \limits_{s} p_{s} c_{1s} y_{s} $$

(57)

The third term also denotes a scenario-based deviation (stochastic deviation) from the optimal value. It shows the deviation of the estimated value ($E\left[ z \right]$) from the estimated value of each scenario ($E\left[ {z_{s} } \right]$), and it has been expressed by Eq. (58). The third term denotes the difference in optimality robustness between fuzzy and scenario parameters. Also, $\omega$ indicates the weighted importance of the stochastic deviation.

$$ E\left[ z \right] = \left[ {\frac{{1 - {\uplambda }}}{2}\left( {f_{1} + f_{2} } \right) + \frac{\lambda }{2}\left( {f_{3} + f_{4} } \right)} \right]y + \left[ {\frac{{1 - {\uplambda }}}{2}\left( {c_{1s} + c_{2s} } \right) + \frac{\lambda }{2}\left( {c_{3s} + c_{4s} } \right)} \right]x_{s} $$

(58)

Additionally, the fourth term serves as an indicating factor of the feasibility robustness in which $\delta_{1}$ determines the penalty rate. The third term of Eq. (59) has an absolute value that can become linear by the approach developed by Yu (2000), who considered the additional variable $\theta_{s}$ within a constraint.

$$ \begin{aligned} & Min E\left[ z \right] + \eta \left( {z_{max} - z_{min} } \right) + \omega \mathop \sum \limits_{s} p_{s} \left\{ {\left( {E\left[ z \right] - E\left[ {z_{s} } \right]} \right) + 2\theta_{s} } \right\} + \delta_{1} \mathop \sum \limits_{s} p_{s}\\ & \quad \times \left[ {\frac{{\left( {\alpha_{s} - \lambda } \right)d_{1s} + \left( {1 - \alpha_{s} } \right)d_{2s} }}{1 - \lambda } - d_{1s} } \right] \\ & Subject\;to \\ & Ax_{s} \le \frac{{\left( {\alpha_{s} - \lambda } \right)d_{1s} + \left( {1 - \alpha_{s} } \right)d_{2s} }}{1 - \lambda } \\ & Bx_{s} \ge b \\ & Ex_{s} \le Ny \\ & Fx_{s} \le g_{s} \\ & y \in \left[ {0,1} \right], x \ge 0 \\ \end{aligned} $$

(59)

In the following, we provide details of the RSPP model for the considered problem regarding the updated model after dealing with uncertainty.

$$ \begin{aligned} Min obj1 & = \mathop \sum \limits_{g} \vartheta \times y_{g} + \mathop \sum \limits_{j} \vartheta^{\prime } \times y_{j}^{\prime CS} + \mathop \sum \limits_{q} \vartheta^{\prime \prime } \times y_{q}^{\prime \prime } 0+ \mathop \sum \limits_{t} \mathop \sum \limits_{s} \\ & \quad \times \left( {pe^{GH} \times \mathop \sum \limits_{j} u_{j}^{tsGH} + pe^{SH} \times \mathop \sum \limits_{j} u_{j}^{tsSH} + pe^{CS} } \right.\left. { \times \mathop \sum \limits_{j} u_{j}^{tsCS} + pe^{\prime } \times \mathop \sum \limits_{q} u_{q}^{\prime ts} } \right) \\ & \quad + \mathop \sum \limits_{g} \mathop \sum \limits_{t} \mathop \sum \limits_{s} \left( {\theta \times \varepsilon_{g}^{ - ts} + \theta^{\prime } \times \varepsilon_{g}^{ + ts} } \right) \\ \end{aligned} $$

(60)

$$ Min obj2 = \mathop \sum \limits_{t} \left( {\mathop \sum \limits_{i} \mathop \sum \limits_{g} z_{ig}^{ts} \times d_{ig} + \mathop \sum \limits_{g} \mathop \sum \limits_{j} z_{gj}^{\prime ts} \times d_{gj}^{\prime } + \mathop \sum \limits_{j} \mathop \sum \limits_{{j^{\prime}}} z_{{jj^{\prime}}}^{\prime \prime ts} \times d_{jj\prime }^{\prime \prime } + \mathop \sum \limits_{j} \mathop \sum \limits_{q} z_{jq}^{\prime \prime \prime ts} \times d_{jq}^{\prime \prime \prime } } \right) $$

(61)

$$ \begin{aligned} Min obj3 & = Min \mathop \sum \limits_{g} \left[ {\left[ {\frac{1 - \lambda }{2}\left( {f_{g}^{1} + f_{g}^{2} } \right) + \frac{\lambda }{2}\left( {f_{g}^{3} + f_{g}^{4} } \right)} \right]x_{g} } \right] \\ &\quad + \mathop \sum \limits_{j} \left[ {\left[ {\frac{1 - \lambda }{2}\left( {f_{j}^{\prime 1} + f_{j}^{\prime 2} } \right) + \frac{\lambda }{2}\left( {f_{j}^{\prime 3} + f_{j}^{\prime 4} } \right)} \right]x_{j}^{\prime CS} } \right] \\ & \quad + \mathop \sum \limits_{q} \left[ {\left[ {\frac{1 - \lambda }{2}\left( {f_{q}^{\prime \prime 1} + f_{q}^{\prime \prime 2} } \right) + \frac{\lambda }{2}\left( {f_{q}^{\prime \prime 3} + f_{q}^{\prime \prime 4} } \right)} \right]x_{q}^{\prime \prime } } \right] \\ & \quad + \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \left[ {\left[ {\frac{1 - \lambda }{2}\left( {o_{g}^{ts1} + o_{g}^{ts2} } \right) + \frac{\lambda }{2}\left( {o_{g}^{ts3} + o_{g}^{ts4} } \right)} \right]b_{ig}^{ts} } \right] \\ & \quad + \mathop \sum \limits_{j} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \left[ {\left[ {\left[ {\frac{1 - \lambda }{2}\left( {o_{j}^{\prime tsGH1} + o_{j}^{\prime tsGH2} } \right) + \frac{\lambda }{2}\left( {o_{j}^{\prime tsGH3} + o_{j}^{\prime tsGH4} } \right)} \right]l_{j}^{tsGH} } \right]} \right. \\ & \quad + \left[ {\left[ {\frac{1 - \lambda }{2}\left( {o_{j}^{\prime tsSH1} + o_{j}^{\prime tsSH2} } \right) + \frac{\lambda }{2}\left( {o_{j}^{\prime tsSH3} + o_{j}^{\prime tsSH4} } \right)} \right]l_{j}^{tsSH} } \right] \\ & \quad + \left. {\left[ {\left[ {\frac{1 - \lambda }{2}\left( {o_{j}^{\prime tsCS1} + o_{j}^{\prime tsCS2} } \right) + \frac{\lambda }{2}\left( {o_{j}^{\prime tsCS3} + o_{j}^{\prime tsCS4} } \right)} \right]l_{j}^{tsCS} } \right]} \right] \\ & \quad + \mathop \sum \limits_{q} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \left[ {\left[ {\frac{1 - \lambda }{2}\left( {o_{q}^{\prime \prime ts1} + o_{q}^{\prime \prime ts2} } \right) + \frac{\lambda }{2}\left( {o_{q}^{\prime \prime ts3} + o_{q}^{\prime \prime ts4} } \right)} \right]l_{\prime q}^{ts} } \right] \\ & \quad + \eta \left( {\left[ {\mathop \sum \limits_{g} f_{g}^{4} x_{g} + \mathop \sum \limits_{j} f_{j}^{^{\prime}4} x_{j}^{\prime CS} + \mathop \sum \limits_{q} f_{q}^{\prime \prime 4} x_{q}^{\prime \prime } + \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \left( {o_{g}^{ts4} b_{ig}^{ts} } \right)} \right.} \right. \\ & \quad + \mathop \sum \limits_{j} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \left( {\left( {o_{j}^{\prime tsGH4} l_{j}^{tsGH} } \right) + \left( {o_{j}^{\prime tsSH4} l_{j}^{tsSH} } \right) + \left( {o_{j}^{\prime tsCS4} l_{j}^{tsCS} } \right)} \right) \\ & \quad \left. { + \mathop \sum \limits_{q} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \left( {o_{q}^{\prime \prime ts4} l_{q}^{\prime ts} } \right)} \right] \\ & \quad - \left[ {\mathop \sum \limits_{g} f_{g}^{1} x_{g} + \mathop \sum \limits_{j} f_{j}^{\prime 1} x_{j}^{\prime CS} + \mathop \sum \limits_{q} f_{q}^{\prime \prime 1} x_{q}^{\prime \prime } \mathop \sum \limits_{i} \mathop \sum \limits_{j} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \left( {o_{g}^{ts1} b_{ig}^{ts} } \right)} \right. \\ & \quad + \mathop \sum \limits_{j} \mathop \sum \limits_{t} \mathop \sum \limits_{s} p_{s} \left( {\left( {o_{j}^{\prime tsGH1} l_{j}^{tsGH} } \right) + \left( {o_{j}^{\prime tsSH1} l_{j}^{tsSH} } \right) + \left( {o_{j}^{\prime tsCS1} l_{j}^{tsCS} } \right)} \right) \\ & \quad \left. {\left. { + \mathop \sum \limits_{q} \mathop \sum \limits_{t} \mathop \sum \limits_{s} o_{q}^{\prime \prime ts1} l_{q}^{\prime ts} } \right]} \right) + \delta_{1} \mathop \sum \limits_{s} p_{s} \left[ {a_{i} \frac{{\left( {\alpha_{s} - \lambda } \right)e_{1i}^{ts} + \left( {1 - \alpha_{s} } \right)e_{2i}^{ts} }}{1 - \lambda } - a_{i} e_{1i}^{ts} } \right] \\ \end{aligned} $$

(62)

S.t:

$$ \mathop \sum \limits_{i} b_{ig}^{ts} \le x_{g} \times c_{g} \quad \forall g,t,s $$

(63)

$$ \varpi_{j}^{tsGH} \le n_{j}^{GH} \quad \forall j \left( {general\;hospital} \right),t,s $$

(64)

$$ \varpi_{j}^{tsSH} \le n_{j}^{SH} \quad \forall j \left( {specialized\;hospital} \right),t,s $$

(65)

$$ l_{j}^{tsGH} - \varpi_{j}^{tsGH} = u_{j}^{tsGH} \quad \forall j \left( {general\;hospital} \right),t,s $$

(66)

$$ l_{j}^{tsSH} - \varpi_{j}^{tsSH} = u_{j}^{tsSH} \quad \forall j \left( {specialized\;hospital} \right),t,s $$

(67)

$$ l_{j}^{tsCS} - x_{j}^{\prime } \times c_{j}^{\prime CS} = u_{j}^{tsCS} \quad \forall j \left( {camp\;station} \right),t,s $$

(68)

$$ l_{q}^{\prime \prime ts} - x_{q}^{\prime \prime } \times c_{q}^{\prime \prime } = u_{q}^{\prime ts} \quad \forall q,t,s $$

(69)

$$ \mathop \sum \limits_{g} z_{ig}^{ts} = 1\quad \forall i,t,s $$

(70)

$$ b_{ig}^{ts} \le e_{i}^{ts} a_{i} \times z_{ig}^{ts} ,\quad \forall i,g,ts, $$

(71)

$$ \mathop \sum \limits_{j } z_{gj}^{\prime ts\;to\;CS} = 1\quad \forall g,t,s $$

(72)

$$ r_{gj}^{ts\;to\;CS} \le \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \times z_{gj}^{\prime ts\;to\;CS} \quad \forall g,j \left( {camp\;station} \right),t,s $$

(73)

$$ \mathop \sum \limits_{j} z_{gj}^{\prime tsto\;GH} = 1,\quad \forall g,t,s $$

(74)

$$ r_{gj}^{ts\;to\;GH} \le \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \times z_{gj}^{\prime ts\;to\;GH} \quad \forall g,j \left( {general\;hospital} \right),t,s $$

(75)

$$ \mathop \sum \limits_{j} z_{gj}^{\prime tsto\;SH} = 1\quad \forall g,t,s $$

(76)

$$ r_{gj}^{ts\;to\;SH} \le \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \times z_{gj}^{\prime tsto\;SH} \quad \forall g,j \left( {specialized\;hospital} \right),t,s $$

(77)

$$ \mathop \sum \limits_{{j^{\prime}}} z_{{jj^{\prime}}}^{\prime \prime ts\;from\;GH\;to\;SH} = 1\quad \forall j \left( {general\;hospital} \right),t,s $$

(78)

$$ \begin{aligned} & w_{{jj^{\prime}}}^{ts\;from\;GH\;to\;SH} \le \omega_{t}^{s} \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \\ & \quad \times z_{{jj^{\prime}}}^{\prime \prime ts\;from\;GH\;to\;SH} \quad \forall j \left( {general\;hospital} \right),j^{\prime } \left( {specialized\;hospital} \right),t,s \end{aligned}$$

(79)

$$ \mathop \sum \limits_{{j^{\prime}}} z_{{jj^{\prime}}}^{\prime \prime tsfrom\;CS\;to\;GH} = 1\quad \forall j \left( {camp\;station} \right),t,s $$

(80)

$$ \begin{aligned} & w_{{jj^{\prime}}}^{ts\;from\;CS\;to\;GH} \le \omega_{t}^{\prime s} \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \\ & \quad \times z_{{jj^{\prime}}}^{\prime \prime ts\;from\;CS\;to\;GH} ,\quad \forall j \left( {camp\;station} \right),j^{\prime } \left( {general\;hospital} \right),t,s\end{aligned} $$

(81)

$$ \mathop \sum \limits_{q} z_{jq}^{\prime \prime \prime ts} = 1\quad \forall j,t,s $$

(82)

$$ v_{jq}^{ts} \le \tau_{t}^{s} \Delta_{t}^{s} \left( {\mathop \sum \limits_{i} e_{i}^{ts} a_{i} } \right) \times z_{jq}^{\prime \prime \prime ts} \quad \forall j,q,{\text{t}},{\text{s}} $$

(83)

$$ \left( {\psi_{g} - \left( {\mathop \sum \limits_{b} b_{ig}^{ts} + \mathop \sum \limits_{j} r_{gj}^{ts} } \right)} \right)\left( {1 - y_{g} } \right) \ge \iota \left( {\left( {1 - y_{g} } \right)} \right)\quad \forall g,t,s $$

(84)

$$ \left( {\psi_{j}^{\prime CS} - \left( {\mathop \sum \limits_{g} r_{gj}^{ts} + \mathop \sum \limits_{{j^{\prime}}} w_{{j^{\prime}j}}^{ts} + \mathop \sum \limits_{q} v_{jq}^{ts} } \right)} \right)\left( {1 - y_{j}^{\prime CS} } \right) \ge \iota \left( {\left( {1 - y_{j}^{\prime CS} } \right)} \right)\quad \forall j \left( {camp\;station} \right),t,s $$

(85)

$$ \left( {\psi_{q}^{\prime \prime } - \mathop \sum \limits_{j} v_{jq}^{ts} } \right)\left( {1 - y_{q}^{\prime \prime } } \right) \ge \iota \left( {\left( {1 - y_{q}^{\prime \prime } } \right)} \right)\quad \forall q,t,s $$

(86)

$$ \frac{{\mathop \sum \nolimits_{i} b_{ig}^{ts} }}{{C_{g} }} = {\Gamma } + \varepsilon_{g}^{ - ts} - \varepsilon_{g}^{ + ts} \quad \forall g,t,s $$

(87)

$$ l_{j}^{t - 1,sGH} + \mathop \sum \limits_{g} r_{gj}^{ts} + \mathop \sum \limits_{{j^{\prime}}} w_{{j^{\prime}j}}^{ts\;from\;CSs} - \mathop \sum \limits_{q} v_{jq}^{t - 1,s} - \mathop \sum \limits_{{j^{\prime}}} w_{{jj^{\prime}}}^{ts\;to\;SHs} - \left( {\rho_{t}^{sGH} \times l_{j}^{t - 1,sGH} } \right) = l_{j}^{tsGH} \quad \forall j \left( {general \;hospital} \right),t,s $$

(88)

$$ l_{j}^{t - 1,sSH} + \mathop \sum \limits_{g} r_{gj}^{ts} + \mathop \sum \limits_{{j^{\prime}}} w_{{j^{\prime}j}}^{ts\;from \;H} - \mathop \sum \limits_{q} v_{jq}^{t - 1,s} - (\rho_{t}^{sSH} \times l_{j}^{t - 1,sSH} ) = l_{k}^{tsSH} \quad \forall j \left( {specialized\;hospital} \right),t,s $$

(89)

$$ l_{j}^{t - 1,sCS} + \mathop \sum \limits_{g} r_{gj}^{ts} - \mathop \sum \limits_{q} v_{jq}^{t - 1,s} - \mathop \sum \limits_{{j^{\prime}}} w_{{jj^{\prime}}}^{ts\;to\;GHs} - \left( {\rho_{t}^{sCS} \times l_{j}^{t - 1,sCS} } \right) = l_{j}^{tscCS} \quad \forall j \left( {camp\;station} \right),t,s $$

(90)

$$ l_{q}^{\prime t - 1,s} + \mathop \sum \limits_{j} v_{jq}^{ts} - \left( {\pi_{t} \times l_{q}^{\prime t - 1,s} } \right) = l_{q}^{\prime ts} \quad \forall q,t,s $$

(91)

$$ \mathop \sum \limits_{g} b_{ig}^{ts} \le a_{i} \frac{{\left( {\alpha_{s} - \lambda } \right)e_{1i}^{ts} + \left( {1 - \alpha_{s} } \right)e_{2i}^{ts} }}{1 - \lambda }\quad \forall i,{\text{t}},{\text{s}} $$

(92)

$$ \mathop \sum \limits_{i} b_{ig}^{ts} \times \Delta_{t}^{s} \times \beta_{t}^{s} \ge \mathop \sum \limits_{j} r_{gj}^{tsGH} \quad \forall g,{\text{t}},{\text{s}} $$

(93)

$$ \mathop \sum \limits_{i} b_{ig}^{t} \times \Delta_{t}^{s} \times \gamma_{t}^{s} \ge \mathop \sum \limits_{j} r_{gj}^{tsSH} \quad \forall g,{\text{t}},{\text{s}} $$

(94)

$$ \mathop \sum \limits_{i} b_{ig}^{t} \times \Delta_{t}^{s} \times \alpha_{t}^{s} \ge \mathop \sum \limits_{j} r_{gj}^{ts\;CS} \quad \forall g,{\text{t}},{\text{s}} $$

(95)

$$ \omega_{t}^{s} \times l_{j}^{tsGH} \ge \mathop \sum \limits_{{j^{\prime}}} w_{{jj^{\prime}}}^{ts\;to\;SH} \quad \forall j \left( {general\;hospital} \right),t,s $$

(96)

$$ \omega_{t}^{\prime s} \times l_{j}^{ts\;CS} \ge \mathop \sum \limits_{{j^{\prime}}} w_{{jj^{\prime}}}^{ts\;to\;GH} \quad \forall j \left( {camp \;station} \right),t,s $$

(97)

$$ \tau_{t}^{sGH} \times l_{j}^{tsGH} \ge \mathop \sum \limits_{q} v_{jq}^{ts} \quad \forall j \left( {general\;hospital} \right),t,s $$

(98)

$$ \tau_{t}^{sSH} \times l_{j}^{tsSH} \ge \mathop \sum \limits_{q} v_{jq}^{ts} \quad \forall j \left( {specialized\; hospital} \right),t,s $$

(99)

$$ \tau_{t}^{sCS} \times l_{j}^{tCS} \ge \mathop \sum \limits_{q} v_{jq}^{ts} \quad \forall j \left( {camp\; station} \right),t,s $$

(100)

$$ l_{j}^{tsGH} \ge \varpi_{j}^{tsGH} \quad \forall j \left( {general\; hospital} \right),t,s $$

(101)

$$ l_{j}^{tsSH} \ge \varpi_{j}^{tsSH} \quad \forall j \left( {specialized \;hospital} \right),t,s $$

(102)

$$ l_{j}^{tsCS} \ge x_{j}^{\prime } \times c_{j}^{\prime } \quad \forall j \left( {camp \;station} \right),t,s $$

(103)

$$ l_{q}^{\prime ts} \ge x_{q}^{\prime \prime } \times c_{q}^{\prime \prime } \quad \forall q,t,s $$

(104)

$$ x_{g} ,x_{j}^{\prime } ,x_{q}^{\prime \prime } ,y_{g} ,y_{j}^{\prime } ,y_{q}^{\prime \prime } \in \left\{ {0,1} \right\}\quad \forall g,j \left( {camp\; station} \right),q $$

(105)

$$ z_{ig}^{ts} ,z_{gj}^{\prime ts} ,z_{{jj^{\prime}}}^{\prime \prime ts} ,z_{jq}^{\prime \prime \prime ts} \in \left\{ {0,1} \right\}\quad \forall i,g,j,q,t,s $$

(106 )

5.2 Interactive fuzzy programming solution (TH) approach

Several methods have been applied to solve the multi-objective models in the research literature (To review the multi-objective models presented in the literature, interested readers can refer to the following papers: (Alinezhad et al., 2022; Tirkolaee et al., 2020a, 2020b, 2022b, 2023)), among which the fuzzy programming approaches (Lai & Hwang, 1993; Li et al., 2006; Selim & Ozkarahan, 2008; Werners, 1988; Zimmermann, 1978) have an increasing use with the capability of determining the satisfaction level of each objective function in an explicit statement as the main advantage that enables decision-makers to make the final decision by finding the most effective solution based on the satisfaction level and relative importance of each objective function. This study uses TH as an interactive single-phase method proposed by Torabi and Hassini (2008). It achieves an efficient solution, especially in the multi-objective mixed integer linear models. The proposed approach involves the following steps:

Step 1 Positive and negative ideal solutions $(PIS$ and $NIS)$ are provided for each objective function. In this regard, those solutions with $\alpha$-positive values of ($z_{1}^{\alpha - Pis}$,$x_{1}^{\alpha - Pis}$),($z_{2}^{\alpha - Pis}$,$x_{2}^{\alpha - Pis}$), and ($z_{3}^{\alpha - Pis}$,$x_{3}^{\alpha - Pis}$) are reached by solving the crisp multi-objective programming model separately for each objective function. Then, the $\alpha$-negative solutions are achieved as follows:

$$ z_{1}^{\alpha - Nis} = Max\left\{ {Z_{1} \left( {x_{2}^{\alpha - Pis} } \right),Z_{1} \left( {x_{3}^{\alpha - Pis} } \right)} \right\}, $$

(107)

$$ z_{2}^{\alpha - Nis} = Max\left\{ {Z_{2} \left( {x_{1}^{\alpha - Pis} } \right),Z_{2} \left( {x_{3}^{\alpha - Pis} } \right)} \right\}, $$

(108)

$$ z_{3}^{\alpha - Nis} = Max\left\{ {Z_{3} \left( {x_{1}^{\alpha - Pis} } \right),Z_{3} \left( {x_{2}^{\alpha - Pis} } \right)} \right\}, $$

(109)

Step 2 A linear membership function is specified for each objective function as follows:

$$ \mu_{1} \left( x \right) = \left\{ {\begin{array}{*{20}l} 1 \hfill & { if\; z_{1} \le z_{1}^{\alpha - Pis} } \hfill \\ {\frac{{z_{1}^{\alpha - Nis} - z_{1} }}{{z_{1}^{\alpha - Nis} - z_{1}^{\alpha - Pis} }}} \hfill & { if\; z_{1}^{\alpha - Pis} \le z_{1} \le z_{1}^{\alpha - Pis} } \hfill \\ 0 \hfill & {if\; z_{1} \ge z_{1}^{\alpha - Pis} } \hfill \\ \end{array} } \right. $$

(110)

$$ \mu_{2} \left( x \right) = = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\; z_{2} \le z_{2}^{\alpha - Pis} } \hfill \\ {\frac{{z_{2}^{\alpha - Nis} - z_{2} }}{{z_{2}^{\alpha - Nis} - z_{2}^{\alpha - Pis} }}} \hfill & {if\; z_{2}^{\alpha - Pis} \le z_{2} \le z_{2}^{\alpha - Pis} } \hfill \\ 0 \hfill & {if\; z_{2} \ge z_{2}^{\alpha - Pis} } \hfill \\ \end{array} } \right. $$

(111)

$$ \mu_{3} \left( x \right) = = \left\{ {\begin{array}{*{20}l} 1 \hfill & {if\; z_{3} \le z_{3}^{\alpha - Pis} } \hfill \\ {\frac{{z_{3}^{\alpha - Nis} - z_{3} }}{{z_{3}^{\alpha - Nis} - z_{3}^{\alpha - Pis} }}} \hfill & {if\; z_{3}^{\alpha - Pis} \le z_{3} \le z_{3}^{\alpha - Pis} } \hfill \\ 0 \hfill & {if\; z_{3} \ge z_{3}^{\alpha - Pis} } \hfill \\ \end{array} } \right. $$

(112)

where $\mu_{h} \left( x \right)$ indicates the satisfaction level of objective function h for the given solution vector x.

Step 3 The TH aggregation function below is chosen to convert the multi-objective model into the single-objective one.

$$ \begin{aligned} & \max \lambda \left( x \right) = \gamma \lambda_{0} + \left( {1 - \gamma } \right)\mathop \sum \limits_{h} \theta_{h} \mu_{h} \left( x \right) \\ & Subject\;to \\ & \lambda_{0} \le \mu_{h} \left( x \right) \\ & \forall h = 1,2,3 \\ \end{aligned} $$

(113)

$$ x \in F\left( x \right) $$

(114)

$$ \lambda_{0} \;{\text{and}}\;\lambda \in \left[ {0,1} \right] $$

(115)

where $F\left( x \right)$ represents the constraint of the equivalent crisp model as the feasible area, and the importance of objective function h and the coefficient of compensation are indicated by $\theta_{h}$ and $\gamma$, respectively.

Step 4 Solve the resulting single-objective RSPP model using the TH approach.

6 Case study

Due to the increasing trend in the number of patients with COVID-19, reports from Tehran city indicate that medical centers lack the capacity and medical services for non-coronary patients in need of treatment have been cut and that there is no necessary infrastructure to provide new cases with medication. According to the Ministry of Health in Iran, Tehran hospitals have the potential to accommodate only a quarter of patients with COVID-19. On the other hand, its high population density has caused main difficulties in controlling the disease. It has created a completely red state in Tehran. The lack of a system for patient referral and prioritization in the Iranian health system is one of the underlying problems in the prevention and treatment phases. It disrupts the active monitoring of the population to identify patients with definite diagnoses quickly for efficient medical services.

According to information published by the Ministry of Health of Iran, in September 2020, over 80% of outpatients needed hospitalization. On the other hand, the ratio of hospitalized people to definite cases has been one to three. Meanwhile, 500 daily definitive cases have been detected in Tehran, which has the highest number of victims in Iran. Thus, the Corona National Headquarters is trying to design a medical service network by establishing new medical centers such as camps and quarantine stations, isolating and allocating patients with different symptoms to medical centers, the optimum use of hospitals’ capacity, and the uniform distribution among medical centers. Thus, in a successful collaboration with Iranian experts of the national healthcare network in MHME, a health service system for the infected cases of COVID-19 is designed to demonstrate the effectiveness of the proposed model and improve the current health network in Tehran by more efficiently designed. It is worth noting that the reliable reports from the expert panel of Tehran University Medical Science (TUMS), local surveys, Corona National Headquarters, and the municipality of Tehran are considered the essential data sources for the presented method.

As a case study, Tehran is located in the center portion of Iran, in which the population density is very high. This city, as the capital of Iran, has a population of 8,693,706. As shown in Fig. 2, it has been divided into 22 residential areas with different areas as patient zones. The study aims to design an efficient and resilient health service system for the infected people with COVID-19 in Tehran to reduce the rate of spread. As mentioned before, the population density is assumed in the central part of each patient zone. Table 1 shows the estimated population density and the geographical position for each patient zone, based on which the number of admissions to the camps, general and specialized hospitals, and quarantine stations are determined.

Fig. 2

Geographical dispersion of 22 municipal districts of Tehran (segmentation of the patient zones)

Table 1 The characteristics of each district of Tehran

The specifications of general and specialized hospitals located in different Districts of Tehran city are presented in Tables 2 and 3. Also, Fig. 3. represents the geographic dispersion of them, respectively. It is worth noting that all the general and specialized hospitals are subject to availability.

Table 2 Characteristics of the general hospitals in Districts of Tehran

Table 3 Characteristics of the specialized hospitals in Districts of Tehran

Fig. 3

Geographic dispersion of hospitals in Districts of Tehran

Concerning the experts of the University of Medical Sciences and the National Corona Headquarters viewpoint, several health centers in Tehran have been considered candidate locations for selecting screening centers based on geographical position and population density as a primary selection criterion. The geographic coordinates of candidate locations for screening centers are presented in Table 4. Also, in cooperation and consultation with the Municipality of Tehran, some candidate locations, including crisis management sheds, red Crescent Centers, student dormitories, and sports halls, were determined for the construction of the camps and quarantine stations. Tables 5 and 6 represent the geographic coordinates of each candidate location for camps and quarantine stations, respectively, based on the field experts’ opinions. In addition, Fig. 4. illustrates the candidate locations for establishing screening centers, camps, and quarantine stations.

Table 4 Characteristics of the candidate locations for screening centers in Districts of Tehran

Table 5 Characteristics of the candidate locations for camp stations in Districts of Tehran

Table 6 Characteristics of the candidate locations for quarantine stations in Districts of Tehran

Fig. 4

Geographic dispersion of candidate locations for screening centers, camps, and quarantine stations

Also, the equation below can be utilized to calculate the distance between two points.

$$ \begin{aligned} & Distance \left( {i,j} \right) \\ & = 6371.1 \times arccos\Bigg[ \sin \left( {LAT_{i} } \right) \times \sin \left( {LAT_{j} } \right) + \cos \left( {LAT_{i} } \right) \times \cos \left( {LAT_{j} } \right) \\ & \quad \quad \times cos\left( {LONG_{j} - LONG_{i} } \right) \Bigg] \\ \end{aligned} $$

(116)

7 Implementation and evaluation

The performance and applicability of the proposed model for improving the quality of service to infected people with COVID-19, the prevention of virus spread, and the effect of various variables on the results are investigated. The formulated model in Sect. 3.2 has been implemented by GAMS 24.1.2 using CPLEX 12.6 solver, and the tests run on an Intel R core (TM) i7 CPU and 4.00 GB RAM. Also, all computational results with no gap are worth mentioning. Thus, the related computational results, sensitivity analysis, and managerial findings are reported in Sects. 6.1, 6.2 and 6.3, respectively.

7.1 Computational results

Real data sets from districts of Tehran city are used to solve the proposed model, in which the suggested locations for establishing screening centers, camp stations, and quarantine stations are depicted in Fig. 4. As stated before, according to Fig. 4, around the districts of Tehran city, 16 general hospitals, and 12 specialized hospitals have been selected to serve infected people with COVID-19. Due to the limited space, some fundamental input data of the case study are listed in Appendix D. It is worth noting that the value of some parameters, such as capacity, percentage of patients with different symptoms, mortality rate, etc., has been determined by a panel of experts and direct referral to the medical centers. Additionally, the DMs define the same as the relative weight of objective functions. This study has considered six periods and three scenarios (mild outbreak, moderate outbreak, and a severe outbreak of the virus).

As seen from Fig. 5, the optimal solution assigns screening centers to all the potential locations except locations No. 3 and 4. Also, three camp stations (Al-Mahdi crisis management shed, Mahdieh Tehran, and Red Crescent Center 17) are assigned to Districts 5, 11, and 17. Also, four quarantine stations (Shohadaye Tarasht Sports Complex, Jahan Ara Sports Complex, Shohadaye Afsariyeh Sports Complex, and Ghaem Sports Complex) are assigned to Districts 2, 5, 14, and 18.

Fig. 5

The opened screening centers, camp stations, and quarantine stations

Moreover, the assignment of suspected people zones to screening centers for all periods and the first scenario are depicted in Fig. 6. As shown in the following figure, in total periods, the lowest number of referrals to opened screening centers occurred in Districts 2 (Saadat Abad Community Health Center), 7 (Zahra Homayoun Health Center), 8 (Dokmechi Comprehensive Health Center), and 20 (Shahid Nik Nezhad Health Center). Also, the highest number of referrals to opened screening centers occurred in Districts 6 (Fazel Health Center) and 21 (Tehransar Community health center).

Fig. 6

Assignment of suspected people zones to screening centers for all periods and the first scenario

Also, the assignment of screening centers to medical centers (general hospitals, specialized hospitals, and camp stations) for all periods and the first scenario is shown in Fig. 7. As it turns out in this figure, the most referrals from screening centers to medical centers are done in Firoozgar general hospital, Madaen specialist hospital, and camp station 4 (Al-Mahdi crisis management shed), and camp station 9 (Mahdieh Tehran). It is worth noting that under the first scenario, no referrals occurs to Shahid Chamran, Atieh, Alghadir, and Shariat Razavi general hospitals, as well as Milad and Imam Khomeini specialized hospitals. Also, there are fewer referrals to Camp 12 (Red Crescent Center 17) than to other camp stations.

Fig. 7

Assignment of screening centers to medical centers for all periods and the first scenarios

The assignment of camp stations to general hospitals and general hospitals to specialized hospitals and the assignment of camp stations and general and specialized hospitals to quarantine stations are shown in Figs. 8 and 9, respectively. Figure 8 indicates that general hospitals, such as Shahid Chamran, Alghadir, and Shahid Lavasani, and general hospitals, such as Atieh and Shahid Modarres, have been allocated to the Masih Daneshvari and Milad specialized hospitals, respectively. Also, the general hospitals of Firoozgar and Sina have been assigned to the Madaen specialized hospital, and the general hospitals of Azadi and Shahid Fahmideh have been allocated to the Lolagar specialized hospital. In addition, the general hospitals of Shariat Razavi and Shahid Fayaz Bakhsh have been assigned to the Yaftabad specialized hospital, and Ayatollah Kashani and Firooz-Abadi general hospitals have been allocated to the Amir Alam specialized hospital. Finally, the general hospitals of Shohadaye Tajrish, Sarem, and Imam Hossein are assigned to the Khatam-Al-Anbia, Payambaran, and Imam Khomeini specialized hospitals, respectively. It is worth noting that no general hospital has been allocated to the specialized hospitals Baqiyatallah, Labbafinezhad, and Ziaeian. Also, opened camps, including Camp No. 4 (Al-Mahdi crisis management shed), Camp No. 9 (Mahdieh Tehran), and Camp No. 12 (Red Crescent Center 17), have been allocated to the Shahid Chamran, Sina, and Shahid Fayaz Bakhsh general hospitals, respectively. Also, according to Fig. 9, most medical centers are assigned to quarantine station No. 5 (Jahan Ara Sports Complex), located in the most central part. As a result, the allocation process has occurred to the nearest centers as much as possible.

Fig. 8

Assignment of medical centers to each other

Fig. 9

Assignment of medical centers to quarantine stations

Figures 10 and 11 present the number of allocated beds for infected people with COVID-19 in general and specialized hospitals under different periods and scenarios, respectively. As shown in the figures, the number of patients admitted to the general is more than the specialized in the first, third, and fifth periods, with a decreased incidence. While the number of patients admitted to specialized hospitals experiences a marked increase in the periods with a peak incidence (i.e., in the second, fourth, and sixth periods). The number of patients admitted to general and specialized hospitals rises with the increasing severity of the disease under scenarios 1 to 3.

Fig. 10

The allocated beds for infected people with COVID-19 in the general hospitals

Fig. 11

The allocated beds for infected people with COVID-19 in the specialized hospitals

Also, the shortage level of beds under different periods and scenarios in medical centers is shown in Table 7. Thus, this table indicates that a few medical centers have been affected by bed shortages during all periods and scenarios. is worth mentioning that Alghadir and Shariat Razavi hospitals have the highest rate of bed shortage among the general hospitals in the third period and under Scenario 3. In comparison, other general hospitals have rarely suffered from bed shortages. On the other hand, Lolagar Hospital has the highest rate of bed shortage among the specialized hospitals. Also, the Al-Mahdi crisis management shed is facing a high rate of bed shortage among the camp stations. It is worth noting that with the increase in the prevalence rate in the second, fourth, and fifth scenarios, general and specialized hospitals are facing more shortages.

Table 7 The shortage level in medical centers in period t under scenarios

Finally, the values of negative and positive deviations from the predetermined congestion ratio of screening centers under different periods and scenarios are listed in Tables 8 and 9, respectively. These tables reflect that the referral rate to screening centers deviates slightly from the threshold value of 0.2. Also, the suspected cases evenly distribute within the screening stations, and the input flow is quite balanced. These suspected cases show an even distribution among the screening centers, and the referral rate to each center never exceeds the threshold value. Thus, the proposed model avoids the increasing congestion in the centers efficiently allocating patients to screening centers and the optimum use of the centers’ potential.

Table 8 The value of negative deviation from the predetermined congestion ratio in the opened screening centers

Table 9 The value of positive deviation from the predetermined congestion ratio in the opened screening centers

7.2 Sensitivity analysis

The sensitivity of the significant variables is analyzed in the proposed model to study their effect on the model.

7.2.1 Analyzing the impacts of camp stations capacity on unilateral transfer rate to the general hospital

This sub-section has examined the relationship between the capacity of the established camps and the unilateral transfer rate between these centers and general hospitals. As shown in Fig. 12, an increase and a decrease in the capacity of camps make a decrease and a significant increase in the referral rate from them to general hospitals, respectively. It shows that establishing temporary camps with more capacity in the event of crises such as the COVID-19 pandemic affects the transmission rate of disease and the transfer rate between medical centers. It is worth noting that an increase in capacity makes no decrease from a given limit to zero in the reduction slope of transfer rate to general hospitals since some infected people with the worsened condition need to receive more advanced services in each period.

Fig. 12

The relationship between the capacity of the camp stations and the unilateral transfer rate

7.2.2 Analyzing the relationship between the critical penalty coefficient and the number of critical screening centers

The effect of the critical penalty coefficient on the number of critical screening centers is examined in Fig. 13. As the penalty coefficient increases concerning the threshold of each screening center, the number of critical screening centers gradually reduces, and the total number of opened screening centers increases. With the lowest level of the penalty coefficient, seven screening centers have been opened, six of which are critical. Then, with an increase in penalty coefficient, critical screening centers gradually reduce in number, and more centers are opened, which leads to the activation of all 14 potential screening centers. It shows that the optimal threshold and penalty coefficient are significant factors for screening centers to which health decision-makers should devote serious attention by balancing the costs of activating centers and becoming critical.

Fig. 13

The effect of the critical penalty coefficient on the number of opened and critical screening centers

7.2.3 The performance of the objective functions in various situations

The performance sensitivity of objective functions is analyzed in the sub-section. Table 10 gives an analysis of the values of de-resiliency (Z₁), distance (Z₂), and total network cost (Z₃) as objective functions under different statuses. As can be seen from the table, status 4 with total network cost as the only objective function, represents the best value of Z₃ and the worst values of Z₁ and Z₂. The best value of Z₂ and the worst values of Z₁ (2.98643E+10) and Z₃ (1.56254E+10) are represented by status 3 with distance as only the objective function. Status 2 with de-resiliency as the only objective function, reflects the best value of the Z₁ compared to the other values. It can be concluded that the simultaneous use of Z₁, Z₂, and Z₃ as the objective functions (status 1) generates better results than the other statuses.

Table 10 Values of objective functions in various situations

Figure 14 shows the best places for screening centers, camps, and quarantine stations and their efficient allocations under different statuses. It has a message that a tradeoff between values of the above objective functions (i.e., de-resiliency, distance, and total network cost) enables decision-makers (DMs) to decide on the best candidate for screening centers, camps, and quarantine stations. Given the cost considerations, for example, status 4 satisfies the selection criterion for the best candidate for medical centers and camps. Thus, the importance of objectives can be weighted based on the decision-makers' priorities. It is worth noting that the values of the total cost, shortage, and distance have shown in the following statuses.

Fig. 14

The best locations for Screening centers, camps, and quarantine stations and their allocations under different statuses

7.2.4 Analyzing the effect of resiliency measures on the cost and de-resiliency

In this sub-section, we intend to discuss the importance and impact of resiliency measures on objective functions. Specifying the best indicators of resiliency to improve the network's reliability in unforeseen situations based on the total network cost is under attention while establishing the health service network in an outbreak of the infectious disease. In this regard, in this section, the effect of different resiliency measures on the cost and de-resiliency objective functions is evaluated, separately. Generally, considering the effect of resiliency measures, the values of de-resiliency and cost objective functions are 4.936511E+9 and 4.07836E+10, respectively. However, according to Fig. 15, the neglect of the congestion criterion effect offers values ​​of 8.033397E+9 and 3.86150E+10 for these objective functions, respectively.

Fig. 15

Total costs and de-resiliency with and without considering node critically measure

As shown in Fig. 16, the neglect of dissatisfaction criterion effect creates a worsening situation in which the values of de-resiliency and cost measures are equal to 5.744491E+9 and 5.43568E+9, respectively; however, a decrease is observed in the value of the distance objective function. In other words, neglect of the dissatisfaction criterion places the de-resiliency objective function in a worsening situation, increases the total cost, and decreases the entire distance between the medical centers of a network with new centers and allocations.

Fig. 16

Total costs and de-resiliency with and without considering dissatisfaction measure

Also, Fig. 17 shows that neglect of the dispersion criterion effect makes a decrease of 3.4442E+8 and an increase of 1.902415E+9 in the values of cost and de-resiliency, respectively, and that the neglect of the de-concentration produces the values of 3.73394E+10 and 7.506074E+9 for cost and de-resiliency objective functions, respectively.

Fig. 17

Total costs and de-resiliency with and without considering dispersion measure

Table 11 compares the importance and effect of different resiliency measures. It shows that dissatisfaction is the most significant measure, neglect of which increases the de-resiliency and cost objective functions by 178% and 33%, respectively, since the network is seeking to shorten the distance by reallocation. However, dispersion is the least significant measure that causes a lower increase than other measures in the objective functions of de-resiliency and cost, respectively.

Table 11 Comparison between resiliency measures

7.2.5 Analyzing the effects of γ and θ

Compared to the original multi-objective model, the TH model achieves an optimal solution over which no solution has priority. The optimal solution is developed by changing the values of parameters γ (i.e., compensation coefficient) and $\theta$ (i.e., the importance of objective functions) based on DM’s preference for each objective function until arriving at the final preferred solution. Accordingly, an analysis of model sensitivity to various values of γ (Table 12) and θ (Fig. 18) is conducted. Table 12 shows the effect of compensation coefficient on the terms of the TH model $\left( {\max \lambda \left( x \right) = \gamma \lambda_{0} + \left( {1 - \gamma } \right)\mathop \sum \limits_{h} \theta_{h} \mu_{h} \left( x \right)} \right)$ considering $\theta = 0.33$, while γ is in the range of 0 to 1. The first term seeks a balance between the membership function values of objective functions and increases them as much as possible. The second term brings the weights of objective functions into focus and sorts out them in order of priority. As DM prefers to produce acceptable solutions with a balance between objective functions and their membership function values, more weight is placed on the first term (i.e., the increased value of γ). As DM prefers to produce acceptable solutions with the great importance of objective functions, a decrease is made in the value of γ so that the second term becomes more important.

Table 12 The performance of the model subject to different ${\Gamma }$

Fig. 18

Values ​​of objective functions subject to different θ

Figure 18 shows the effect of θ₁, θ₂, and θ₃ on the terms of the TH model $\left( {\max \lambda \left( x \right) = \gamma \lambda_{0} + \left( {1 - \gamma } \right)\mathop \sum \limits_{h} \theta_{h} \mu_{h} \left( x \right)} \right)$, considering $\gamma = 0.5$. Based on the assumption made in previous sections, the network is designed by three objective functions of the same value and importance. It is not satisfied in the real world, and one of them is more significant from the experts’ point of view. The probability of moving towards a better solution for the objective function of greater importance exists to resolve this issue. For this purpose, different cases are considered based on the significance of objective functions in which $\theta_{h}$ is in the range of 0.1 to 0.9. Since the third objective function has been a high priority for the experts in Case 5, it has been assigned more weight (θ₃ = 0.7) than other functions. Also, since experts have given the de-resiliency objective function a higher priority than others in Case 10, it carries more weight (θ₁ = 0.7).

8 Managerial findings

This section offers some insights to give healthcare managers a clear understanding of the proposed model that is advantageous for controlling the spread of contagious diseases, such as coronavirus. Important managerial insights from the results of the proposed model are as follows.

First, including different resiliency measures in the proposed model and specifying the best one based on cost considerations must be devoted to further attention, as the significant issues in designing the health service network for the infected people with COVID-19. It makes the network more reliable towards any unexpected design change with the aim of improvement in health centers. Besides, the results obtained from the present study show that a trade-off between resiliency, cost, and distance as objective functions is an important point. It enables decision-makers to design the network concerning their preferences. Moreover, the limited capacity of current medical centers for providing COVID-19 patients and other patients with adequate services makes it necessary to establish and evenly distribute camps and quarantine stations within the community and design an efficient network for patients with different symptoms. It results in the optimum use of the potential capacity of medical centers and the low rate of bed shortage in hospitals. Also, the construction of temporary treatment centers (camp stations) with ample potential eliminates the need for transferring patients with mild symptoms to general hospitals due to the limited capacity, preventing the further outbreak of the disease. Given the importance of keeping social distance and avoiding the increasing congestion in medical centers, the proposed model can balance admittance to and discharge from the medical centers. Also, healthcare decision-makers have determined the optimal threshold and penalty coefficient for screening centers, activating sufficient screening centers with as much possible resilience to criticality. Finally, another insight drawn is that an efficient allocation of the suspect and definite cases to the nearest screening and care centers makes it possible to prevent the disease carriers from commuting within the community and increasing the transmission rate of coronavirus.

9 Conclusions

The key finding of the study, practical implications, the limitations of the research, and future research avenues are provided in this section.

10 Summary of this paper

Given that COVID-19 is a novel type of disease with a severe outbreak around the world and a high risk of transmission, there is no specific policy on getting it under control. However, maintenance of social distance, early diagnosis of disease, and extra attention to patients with acute underlying disease are limiting factors in an outbreak of disease and its fatality rate. Designing an effective strategy for managing the problem can help control the spread of disease. Thus, it necessitates developing a resilient health service network to supervise medical services provision to infected people with COVID-19. This study proposes a multi-objective mathematical model to minimize the de-resiliency, distance, and total cost. It determines the number and location of screening centers, camps, and quarantine stations, the allocated portion of each medical center to the infected people with COVID-19, the efficient allocation of patient zones to screening centers, and from screening centers to camps or different kinds of hospitals, and the efficient assignment of improved infected people to quarantine stations to reduce the commuting time of infected people in the society and subsequently the rate of virus spread. A hybrid robust stochastic-possibilistic programming approach is adopted to resolve inherent stochastic and epistemic uncertainty regarding input parameters. The model seems compatible with the defining characteristics of the COVID-19 pandemic.

The real data derived from districts of Tehran is used to make the case study more practical and applicable. An analysis of the proposed model is conducted based on different parameters, and some findings offer insightful observations to management systems. The results state that the simultaneous use of resiliency, distance, and cost as objective functions and the trade-off between them can facilitate the work process in the health service network for the infected people with COVID-19. Thus, DMs have required a balance between three objective functions considering personal preferences to decrease the risk of virus transmission in the community. Also, the managerial insights show that establishing camps and quarantine stations within the community results in the optimum use of the potential capacity of medical centers and the low rate of shortage in the hospitals.

10.1 Limitations

This study, however, is subject to several limitations; no consideration is given to infrastructural requirements for the laboratory equipment of screening tests such as PCR, how to identify the suspected patients in the screening centers, the best decision on the location of screening centers, camps, and quarantine stations through the multi-attribute decision making approaches (based on criteria such as ample open space, efficient ventilation system, availability, spatial proximity to pharmacies and hospitals in each patient zone), and the lack of hospitals facilities sharing (especially ventilators) in times of the increased incidence. They are some limitations in addressing the research, which could be promoted.

10.2 Future remarks

To our knowledge, designing a health service network for the infected people with coronavirus is pioneering work. Thus, there is a belief that the proposed model can bring considerable advantages. The following suggestions are offered for future research. The proposed model can be highly developed by considering other resiliency factors. Ambiguous parameters can be addressed by other uncertainty methods with a more qualitative degree, e.g., Multivariate Adaptive Regression Spline (MARS), Gray Systems, etc. Since an outbreak of the disease necessitates disposing of the infectious medical waste (IMW) of an increasing level, the proposed model can be extended to a sustainable health network by a group of environmental and social factors. The dangers caused by going suspected elders and vulnerable people to medical centers at the outbreak peak make it possible to develop the model by providing home health care such as identification of suspects, nursing services delivery to sufferers, and drug administration. As an essential point, other researchers can first use SIDARTHE or SIR methods to accurately predict the values of pandemic parameters to increase the capability of their model. And finally, the development of decomposition algorithms or metaheuristics can be used as a guide in problems of larger size for which commercial solvers have no solution at a reasonable processing time.

Appendices

Appendix A: Notations of the proposed model

The sets, parameters, and decision variables below are applied to formulate the mathematical model.

Sets and indices

I :

Suspected people zones $\left( {i = 1, 2, \ldots , I} \right)$.

G :

Screening centers $\left( {g = 1, 2, \ldots , G} \right)$.

J :

Medical centers (CSs, GHs, and SHs) $\left( {j = 1,2, \ldots , J} \right)$.

Q :

Quarantine stations $\left( {q = 1,2, \ldots , Q} \right)$.

T :

Periods $\left( {t = 1,2, \ldots , T} \right)$.

S :

Scenarios $\left( {s = 1,2, \ldots , S} \right)$.

Parameters

Demand parameters

$a_{i}$:

The population of the people zone i

$e_{i}^{ts}$ :

The percentage of the suspected people in zone i in period t under scenario s

Capacity parameters

$C_{g}$:

The capacity of potential screening center at node g.

$C_{j}^{^{\prime}}$ :

The capacity of the potential camp station at node j.

$C_{q}^{^{\prime\prime}}$ :

The capacity of potential quarantine station at node q.

$n_{j}$ :

Maximum number of beds in the medical centers (general hospitals or specialized hospitals) j

Distance parameters

$d_{ig}$:

Distance between patient zone i and screening center is located in node g

$d_{gj}^{^{\prime}}$ :

Distance between screening center is located in node g and medical centers j

$d_{jj\prime }^{\prime \prime }$ :

Distance between medical centers j and medical centers $j^{\prime}$

$d_{jq}^{\prime \prime \prime }$ :

Distance between medical centers j and quarantine station q

Cost parameters

Fixed cost parameters

$f_{g}$:

Fixed installation cost to established screening center in node g

$f_{j}^{^{\prime}}$ :

Fixed installation cost to an established temporary medical center (camp station) in node j

$f_{q}^{^{\prime\prime}}$ :

Fixed installation cost to established quarantine station in node q

Operation cost parameters

$o_{g}^{ts}$:

Operating cost of the screening center g in period t under scenario s

$o_{j}^{\prime ts}$ :

Operating cost of the medical centers (camp station, general and specialized hospital) in period t under scenario s

$o_{q}^{\prime ts}$ :

Operating cost of the quarantine station q in period t under scenario s

Penalty cost parameters

$pe$:

The penalty coefficient cost of shortage in medical centers (camp stations, general hospitals, specialized hospitals)

$pe^{^{\prime}}$ :

The penalty coefficient cost of shortage in quarantine stations

COVID-19 disease parameters

${\Delta }_{t}^{s}$:

The average percentage of suspected people with positive screening test results in period t under scenario s.

$\alpha_{t}^{s}$ :

Percentage of infected people with mild symptoms in period t under scenario s.

$\beta_{t}^{s}$ :

Percentage of infected people with severe symptoms and no underlying disease in period t under scenario s.

$\gamma_{t}^{s}$ :

Percentage of infected people with severe symptoms and underlying disease in period t under scenario s.

$\omega_{t}^{s}$ :

Percentage of infected people with worsening symptoms admitted to general hospitals in period t under scenario s.

$\omega_{t}^{\prime s}$ :

Percentage of infected people with worsening symptoms admitted to camp stations in period t under scenario s.

$\pi_{t}$ :

The complete recovery rate of infected people admitted to quarantine stations in period t.

$\rho_{t}^{s}$ :

The mortality rate in medical centers in period t under scenario s.

$\tau_{t}^{s}$ :

The improved rate in medical centers in period t under scenario s.

Resiliency parameters

$\vartheta$:

The penalty for critical screening centers.

$\vartheta^{\prime}$ :

The penalty for critical temporary medical centers (camp stations).

$\vartheta^{\prime\prime}$ :

The penalty for critical quarantine stations.

${\Gamma }$ :

The predetermined constant ratio of congestion (visits/capacity) in screening centers.

$\theta$ :

The penalty of negative deviation from the predetermined constant ratio of congestion in the screening centers.

$\theta^{\prime}$ :

The penalty of positive deviation from the predetermined constant ratio of congestion in the screening centers.

$\psi_{g}$ :

The threshold value of total inflows and outflows in screening center g.

$\psi_{j}^{\prime CS}$ :

The threshold value of total inflows and outflows in temporary medical center (camp station) j.

$\psi_{q}^{^{\prime\prime}}$ :

The threshold value of total inflows and outflows in quarantine station q.

Other parameters

$p_{s}$:

Probability of the occurrence of scenario s

$\iota$ :

A very small number.

$M$ :

A very large number.

Decision variables

Location variables

$x_{g}$:

It is equal to 1, if a potential screening center is located at node g, 0 otherwise.

$x_{j}^{\prime CS}$ :

It is equal to 1, if a temporary medical center (camp station) is located at node j, 0 otherwise.

$x_{q}^{\prime \prime }$ :

It is equal to 1, if a quarantine station is located at node q, 0 otherwise.

Allocation variables

$z_{ig}^{ts}$:

It is equal to 1 if patient zone i is allocated to screening center located in node g in period t under scenario s

$z_{gj}^{\prime ts}$ :

It is equal to 1 if the screening center is located in node g allocated to medical center (general hospital, specialized hospital, and camp station) j in period t under scenario s

$z_{{jj^{\prime}}}^{\prime \prime ts}$ :

It is equal to 1 if medical center (camp station, or general hospital) j is allocated to the more advanced medical center (general hospital, or specialized hospital) $j^{\prime}$ in period t under scenario s

$z_{jq}^{\prime \prime \prime ts}$ :

It is equal to 1 if medical center j is allocated to quarantine station q in period t under scenario s

Flow variables

$b_{ig}^{ts}$:

The number of suspicious people in zone i that refer to screening center g in period t under scenario s

$r_{gj}^{ts}$ :

The number of infected people with different conditions that transferred from the screening center is located in node g to medical center j in period t under scenario s

$w_{{jj^{\prime}}}^{ts}$ :

The number of infected people with worsening symptoms admitted to medical center j, transferred to the more advanced medical center $j^{\prime}$ in period t under scenario s

$v_{jq}^{ts}$ :

The number of improved infected people that transferred from general hospital h to quarantine station q in period t under scenario s

Shortage variables

$u_{h}^{ts}$:

Shortage level of beds in medical center (general hospital, specialized hospital, and camp station) j in period t under scenario s

$u_{q}^{\prime ts}$ :

Shortage level of beds in quarantine station q in period t under scenario s

Resiliency variables

$y_{g}$:

It is equal to 1 if a potential screening center is located at node g be critical, 0 otherwise.

$y_{j}^{\prime CS}$ :

It is equal to 1 if a medical center (camp station) is located at node j be critical, 0 otherwise.

$y_{q}^{^{\prime\prime}}$ :

It is equal to 1 if a quarantine station is located at node q be critical, 0 otherwise.

$\varepsilon_{g}^{ - ts}$ :

The amount of negative deviation from the predetermined constant visits/capacity of screening center ratio in the screening center g under scenario s.

$\varepsilon_{g}^{ + ts}$ :

The amount of positive deviation from the predetermined constant visits/capacity of screening center ratio in the screening center g under scenario s.

Capacity variables

$\varpi_{j}^{ts}$ :

Number of beds in medical center (general or specialized hospital) j that allocated to infected people with COVID-19 in period t under scenario s.

State variables

$l_{h}^{ts}$:

The number of infected people admitted to general hospital $h$ in period $t$ under scenario s

$l_{q}^{\prime ts}$ :

The number of improved infected people in quarantine station $q$ in period $t$ under scenario s

Appendix B: Structural properties of the proposed model

In this study, a mixed-integer linear programming model is developed to design a network of health services for people with coronavirus at the time of the outbreak of COVID-19 disease. The proposed network comprises suspicious people, screening centers, health centers (camp stations, general hospitals, and specialized hospitals), and quarantine stations. The first objective function aims to minimize the de-resiliency of the health service network during the outbreak of COVID-19 disease by calculating the penalty coefficient for each of the resiliency measures comprises of congestion criteria for screening centers ($\mathop \sum \limits_{g} \vartheta \times y_{g}$), camp stations ($\mathop \sum \limits_{j } \vartheta^{\prime} \times y_{j}^{\prime \;camp\;station}$), and quarantine stations ($\mathop \sum \limits_{q} \vartheta^{\prime\prime} \times y_{q}^{^{\prime\prime}}$), shortage criteria for general hospitals ($\mathop \sum \limits_{t} \mathop \sum \limits_{s} \mathop \sum \limits_{j} pe^{general\; hospital} \times u_{j}^{ts\;general \;hospital}$), specialized hospitals ($\mathop \sum \limits_{t} \mathop \sum \limits_{s} \mathop \sum \limits_{j} pe^{specialized\; hospital} \times u_{j}^{ts\;specialized\; hospital}$), camp stations ($\mathop \sum \limits_{t} \mathop \sum \limits_{s} \mathop \sum \limits_{j} pe^{camp \;station} \times u_{j}^{ts\;camp \;station}$), and quarantine stations ($pe^{\prime } \times \mathop \sum \limits_{q} u_{q}^{\prime ts}$), and de-concentration criteria for screening centers ($\mathop \sum \limits_{g} \mathop \sum \limits_{t} \mathop \sum \limits_{s} \left( {\theta \times \varepsilon_{g}^{ - ts} + \theta^{\prime} \times \varepsilon_{g}^{ + ts} } \right)$). Also, the second objective function aims to minimize the total distance of all suspected and infected people in society comprises of the distance of assigning suspicious people to screening centers ($\mathop \sum \limits_{t} \mathop \sum \limits_{i} \mathop \sum \limits_{g} z_{ig}^{ts} \times d_{ig}$), distance of assigning infected people with different symptoms from screening centers to medical centers(such as camp stations, general hospitals, and specialized hospitals) ($\mathop \sum \limits_{t} \mathop \sum \limits_{g} \mathop \sum \limits_{j} z_{gj}^{\prime ts} \times d_{gj}^{\prime }$), distance of assigning infected people with worsening symptoms from a medical center (camp stations or general hospitals) to more advanced medical centers (general hospitals or specialized hospitals) ($\mathop \sum \limits_{t} \mathop \sum \limits_{j} \mathop \sum \limits_{{j^{\prime}}} z_{{jj^{\prime}}}^{\prime \prime ts} \times d_{jj\prime }^{\prime \prime }$), distance of improved infected people from medical centers (such as camp stations, general hospitals, and specialized hospitals) to quarantine stations ($\mathop \sum \limits_{t} \mathop \sum \limits_{j} \mathop \sum \limits_{q} z_{jq}^{\prime \prime \prime ts} \times d_{jq}^{\prime \prime \prime }$). Eventually, the third objective function aims to minimize the costs of the network comprised of the cost of opening screening centers ($\mathop \sum \limits_{g} x_{g} \times f_{g}$), cost of opening camp stations ($\mathop \sum \limits_{j } x_{j}^{\prime \;camp\; station} \times f_{j}^{\prime }$), cost of opening quarantine stations ($\mathop \sum \limits_{q} x_{q}^{\prime \prime } \times f_{q}^{\prime \prime }$), cost of provided test kits in screening centers ($\mathop \sum \limits_{i} \mathop \sum \limits_{g} \mathop \sum \limits_{t} \mathop \sum \limits_{s} o_{g}^{ts} \times b_{ig}^{ts}$), cost of operating in camp stations ($\mathop \sum \limits_{j} \mathop \sum \limits_{t} \mathop \sum \limits_{s} o_{j}^{\prime ts\;camp\; station} \times l_{j}^{ts\;camp\; station}$), cost of operating in general hospitals ($\mathop \sum \limits_{j} \mathop \sum \limits_{t} \mathop \sum \limits_{s} o_{j}^{\prime ts\;general \;hospital} \times l_{j}^{ts\;general\; hospital}$), cost of operating in specialized hospitals ($\mathop \sum \limits_{j} \mathop \sum \limits_{t} \mathop \sum \limits_{s} o_{j}^{\prime ts\;specialized\; hospital} \times l_{j}^{ts\;specialized \;hospital}$), and cost of operating in quarantine stations ($\mathop \sum \limits_{q} \mathop \sum \limits_{t} \mathop \sum \limits_{s} o_{q}^{\prime \prime ts} \times l_{q}^{\prime ts}$).

In the presented model, we considered different screening centers in the determined area to get the necessary tests from people with suspicious symptoms from different zones. Because the equipment is limited, such as test kits, selected screening centers have limited capacity to provide services to people with suspicious symptoms. Therefore, the total number of suspects referring to each screening center from different areas should not exceed the maximum capacity of that center, which is shown by constraint (4). Also, existing medical centers such as general and specialized hospitals have a limited number of beds for hospitalization. On the other hand, in this research, we assume that only part of the capacity (number of beds) of each general and specialized hospital should be allocated to coronavirus patients. Therefore, the number of cases assigned to patients with COVID-19 should be less than the maximum capacity (total number of beds) of each general and specialized hospital, which are shown by constraints (5) and (6), respectively. During the outbreak of pandemic diseases such as COVID-19, the number of people infected with the virus who need medical care should increase daily. However, medical centers and quarantine stations dedicated to patients and recovered people have limited capacity, and those referred to these centers may face a shortage of empty beds for hospitalization. However, the lack of hospitalization of patients in medical centers leads to an increase in the prevalence of the virus in the community and the inefficiency of the health system. Therefore, constraints (7)–(10), calculate the shortage of empty beds in medical centers (camp stations, general hospitals, and specialized hospitals) and quarantine stations, respectively.

As mentioned before, in the designed network, several centers should be established among the candidate points as screening centers, camps, and quarantine stations. In addition, it is assumed that each center, in each period, should be allocated to only one other center, which is called a single allocation. These limitations are shown in the constraints (11), (13), (15), (17), (19), (21), and (23). On the other hand, the flow of suspects and patients will refer to these centers if these centers are established. Therefore, these restrictions have been stated by constraints (12), (14), (16), (18), (20), (22), and (24).

Since the centers that are built as temporary screening centers, camps, and quarantine centers (such as municipal health care centers, crisis management sheds, red crescent centers, university dormitories, and sports centers) are very limited in terms of infrastructure and capacity compared to existing centers such as hospitals, increasing the number of referrals is more likely to cause congestion and the prevalence of the disease in these centers is also increasing and eventually they are considered as critical centers. Therefore, a threshold is defined for the number of referrals for each center, and if that value is exceeded, that center becomes critical, which these facts and their calculation are shown by constraints (25) and (28) for screening centers, constraints (26) and (29) for camp stations, and constraints (27) and (30) for quarantine stations, respectively.

In addition to the above criteria, since in all screening centers, only the testing process is performed from suspects and the same service is provided, for various reasons, the number of referrals to a specific center may be very high and at the same time do not refer to another selected center, which will also increase the prevalence in busy laboratory centers. Therefore, it is better to plan in such a way that the number of referrals to different centers has the same and uniform distribution. Therefore, a fixed value is considered for the number of referrals to each screening center and the amount of positive and negative deviations from that value is calculated, which is shown by constraint (31) for each screening center.

In general, the number of patients admitted to medical centers in each period is calculated by the sum of the total number of patients admitted to the previous period, plus newly identified patients and the number of patients transferred from other medical centers at the beginning of the current period, minus the number of patients who died, the number of patients transferred to other medical centers as well as the number of recovered patients referred to quarantine centers at the end of the previous period, which are expressed by constraints (32)–(34) for general hospitals, specialized hospitals, and camp stations, respectively. Also, the number of recovered people accommodated in quarantine stations in each period is calculated by the total number of people recovering in the previous period, plus the number of newly improved patients at the beginning of the current period, minus the number of released recovering patients at the end of the previous period, which is mentioned in constraint (35).

The number of suspect people referred to screening centers in each period is calculated as a percentage of the population in each zone, is calculated by constraint (36). Also, the number of patients referred to general hospitals, specialized hospitals, and camp stations, are calculated as a percentage of the number of suspected people with positive coronavirus tests at screening centers, which are shown by constraints (37)–(39), respectively.

In medical centers such as camp stations and general hospitals, some hospitalized patients may be in poor condition and need to receive services from more advanced medical centers in each period. Hence, the number of people transferred from general hospitals to specialized hospitals, as well as from camp stations to general hospitals, are calculated by constraints (40) and (41), respectively.

According to the WHO reports, since the cured people with coronavirus may continue to carry the virus for a while, it is best to stay out of the community after completing the treatment. Therefore, improved patients are referred from medical centers to quarantine stations in the designed network. For this purpose, the number of patients referred from general hospitals, specialist hospitals, and camp stations to quarantine stations is calculated by constraints (42)–(44), respectively.

During the outbreak of diseases such as coronavirus, the number of referrals to medical centers certainly increases significantly, and, as a result, the demand for hospitalization usually exceeds the capacity of medical centers facing a shortage of empty beds, related equations for general hospitals, specialist hospitals, camp stations, and quarantine stations are shown in the constraints (45)–(48), respectively.

Appendix C: Preliminaries of the RSPP method

• a. Possibilistic chance-constrained programming (PCCP)

PCCP is considered one of the most popular Possibilistic Programming methods for specifying epistemic parameters. It is subject to the condition that a determined confidence level $\left( \alpha \right)$ achieved by each chance constraint (Pishvaee et al. (2012b)). Two basic fuzzy possibility $\left( {Pos} \right)$ and necessity $\left( {Nec} \right)$ measures were introduced by Dubois and Prade (1987) to satisfy the condition in PCCP models. $Pos$ and $Nec$ measures have extremely optimistic and pessimistic views on chance constraints, respectively. Liu and Liu (2002) introduced the credibility $\left( {Cr} \right)$ measure as the average of $Pos$ and $Nec$ measures to moderate the extreme views. $Me$ measure has been recently suggested by Xu and Zhou (2013). As an extended version of the $Cr$ measure, it is an indicator of the weighted average of $Pos$ and $Nec$ measures. To define $Me$ measure (the relation below), an optimistic–pessimistic parameter (i.e., $\lambda$ (0 ≤ $\lambda$ ≤ 1)) is specified as the weight of $Pos$ measure.

$$ Me\left\{ A \right\} = Nec\left\{ A \right\} + \lambda \left( {Pos\left\{ A \right\} - Nec\left\{ A \right\}} \right) = \lambda Pos\left\{ A \right\} + \left( {1 - \lambda } \right)Nec\left\{ A \right\} $$

(C.1)

Consider a trapezoidal fuzzy variable $\tilde{\xi } = \left( {r_{1} ,r_{2} ,r_{3} ,r_{4} } \right),r_{1} \le r_{2} \le r_{3} \le r_{4}$ whose membership function is as Eq. (C.2):

$$ \mu_{3} \left( x \right) = \left\{ {\begin{array}{*{20}l} {\frac{{x - r_{1} }}{{r_{2} - r_{1} }}} \hfill & {r_{1} \le x \le r_{2} } \hfill \\ 1 \hfill & {r_{2} \le x \le r_{3} } \hfill \\ {\frac{{r_{x} - x}}{{r_{4} - r_{3} }}} \hfill & {r_{3} \le x \le r_{4} } \hfill \\ 0 \hfill & {Otherwise} \hfill \\ \end{array} } \right. $$

(C.2)

The fuzzy measures of the events $\tilde{\xi } \le x$ and $\tilde{\xi } \ge x$ are presented as Eqs. (C.3) and (C.4) (Xu and Zhou 2013).

$$ Me\left\{ {\tilde{\xi } \le x} \right\} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {x \le r_{1} } \hfill \\ {\lambda \frac{{x - r_{1} }}{{r_{2} - r_{1} }}} \hfill & {r_{1} \le x \le r_{2} } \hfill \\ \lambda \hfill & {r_{2} \le x \le r_{3} } \hfill \\ {\lambda + \left( {1 - \lambda } \right) \frac{{x - r_{1} }}{{r_{2} - r_{1} }}} \hfill & {r_{3} \le x \le r_{4} } \hfill \\ 1 \hfill & {x \ge r_{4} } \hfill \\ \end{array} } \right. $$

(C.3)

$$ Me\left\{ {\tilde{\xi } \ge x} \right\} = \left\{ {\begin{array}{*{20}l} 1 \hfill & {x \le r_{1} } \hfill \\ {\lambda + \left( {1 - \lambda } \right) \frac{{x - r_{1} }}{{r_{2} - r_{1} }}} \hfill & {r_{1} \le x \le r_{2} } \hfill \\ \lambda \hfill & {r_{2} \le x \le r_{3} } \hfill \\ {\lambda \frac{{x - r_{1} }}{{r_{2} - r_{1} }}} \hfill & {r_{3} \le x \le r_{4} } \hfill \\ 0 \hfill & {x \ge r_{4} } \hfill \\ \end{array} } \right. $$

(C.4)

Eq. (C.5) shows the expected value of the fuzzy variable $\tilde{\xi }$ based on the Me measure (Xu and Zhou 2013).

$$ E^{Me} \left[ \xi \right] = \mathop \int \limits_{0}^{ + \infty } Me\left\{ {\tilde{\xi } \ge x} \right\}dx + \mathop \int \limits_{ - \infty }^{0} Me\left\{ {\tilde{\xi } \le x} \right\}dx = \frac{1 - 2\lambda }{2}\left( {r_{1} - r_{2} } \right) + \frac{\lambda }{2}\left( {r_{3} + r_{4} } \right) $$

(C.5)

• b. Basic PCCP (BPCCP) model

For simplicity, the compact version of the model is developed, where $x$, and $y$ represent continuous and binary decision variables, respectively. $A$, $B$, $N$, $E$, $F,$ and $b$ indicate coefficient matrices, and parameters of the model are represented by $f$, $c$, $d,$ and $g$. The vectors $c$ and $d$ are equivalent to operating cost and the level of demand (number of the suspected people), respectively, that specify the scenario and fuzzy-based parameters. Also, the vectors $f$ and $g$ determine the only fuzzy-based and scenario-based parameters, which are associated with installation cost and the rate of suspected people with the positive screening test result, respectively.

$$ \begin{aligned} & \min Z = \tilde{f}y + \tilde{c}_{s} x_{s} \\ & {\text{s}}.{\text{t}}. \\ & Ax_{s} \le \tilde{d}_{s} \\ & Bx_{s} \ge b \\ & Ex_{s} \le Ny \\ & Fx_{s} \le g_{s} \\ & y \in \left[ {0,1} \right], x \ge 0 \\ \end{aligned} $$

(C.6)

According to Pishvaee et al. (2012b) and Xu and Zhu (2013), the definition of the Basic Stochastic- Possibilistic Programming (BSPP) model is proposed below.

$$ \begin{aligned} & \min \left[ Z \right] = E\widetilde{\left[ f \right]}y + E\left[ {\tilde{c}_{s} } \right]x_{s} \\ & Subject to \\ & Me \left\{ {Ax_{s} \le \tilde{d}_{s} } \right\} \ge \alpha_{s} \\ & Bx_{s} \ge b \\ & Ex_{s} \le Ny \\ & Fx_{s} \le g_{s} \\ & y \in \left[ {0,1} \right], x \ge 0 \\ \end{aligned} $$

(C.7)

The Upper Approximation Model $(UAM)$ and the Lower Approximation Model $(LAM)$ have been proposed by Xu and Zhou (2013) as two approximation models that are defined as follows:

$$ UAM\left\{ {\begin{array}{*{20}l} {\min \left[ Z \right] = E\widetilde{\left[ f \right]}y + E\left[ {\tilde{c}_{s} } \right]x_{s} } \hfill \\ {Subject \;to} \hfill \\ {Pos \left\{ {Ax_{s} \le \tilde{d}_{s} } \right\} \ge \alpha_{s} } \hfill \\ {Bx_{s} \ge b} \hfill \\ {Ex_{s} \le Ny} \hfill \\ {Fx_{s} \le g_{s} } \hfill \\ {y \in \left[ {0,1} \right], x \ge 0} \hfill \\ \end{array} } \right.\& LAM\left\{ {\begin{array}{*{20}l} {\min \left[ Z \right] = E\widetilde{\left[ f \right]}y + E\left[ {\tilde{c}_{s} } \right]x_{s} } \hfill \\ {Subject\; to} \hfill \\ {Nec \left\{ {Ax_{s} \le \tilde{d}_{s} } \right\} \ge \alpha_{s} } \hfill \\ {Bx_{s} \ge b} \hfill \\ {Ex_{s} \le Ny} \hfill \\ {Fx_{s} \le g_{s} } \hfill \\ {y \in \left[ {0,1} \right], x \ge 0 } \hfill \\ \end{array} } \right. $$

(C.8)

As shown in Eq. (C.8), the model proposed by Xu and Zhu (2013) goes through a two-phase solution process to solve $UAM$ and $LAM$ problems (So that, firstly, $UAM$ problem must be solved and then $LAM$ is solved). Also, it can be proven in the same way as the credibility measure that if $\tilde{\xi }$ is a trapezoidal fuzzy number and two confidence levels $\alpha \ge 0.5$, then: (Refer to Dehghan et al. (2018) to see the proof.)

$$ \begin{aligned} Me\left\{ {\xi \ge x} \right\} & \ge \alpha \leftrightarrow x \le \frac{{\left( {\alpha - \lambda } \right)r_{1} + \left( {1 - \alpha } \right)r_{2} }}{1 - \lambda } \\ Me\left\{ {\xi \le x} \right\} & \ge \alpha \leftrightarrow x \ge \frac{{\left( {\alpha - \lambda } \right)r_{4} + \left( {1 - \alpha } \right)r_{3} }}{1 - \lambda } \\ \end{aligned} $$

(C.9)

Eq. (C.7) specifies the hybrid uncertain parameters of objective function and constraints in the presented model whose, crisp equivalent is defined as follows:

$$ \begin{aligned} & Min E\left[ z \right] = \left[ {\frac{{1 - {\uplambda }}}{2}\left( {f_{1} + f_{2} } \right) + \frac{\lambda }{2}\left( {f_{3} + f_{4} } \right)} \right]y + \mathop \sum \limits_{s} p_{s} \left[ {\frac{{1 - {\uplambda }}}{2}\left( {f_{1} + f_{2} } \right) + \frac{\lambda }{2}\left( {f_{3} + f_{4} } \right)} \right]x_{s} \\ & Subject\; \, to \\ & Ax_{s} \le \frac{{\left( {\alpha_{s} - \lambda } \right)d_{1s} + \left( {1 - \alpha_{s} } \right)d_{2s} }}{1 - \lambda } \\ & Bx_{s} \ge b \\ & Ex_{s} \le Ny \\ & Fx_{s} \le g_{s} \\ & y \in \left[ {0,1} \right], x \ge 0 \\ \end{aligned} $$

(C.10)

where $\alpha_{s}$ indicates the minimum confidence level of chance constraints in every scenario, which is determined by DMs ($\alpha_{s} > 0.5$).

Appendix D: Supplementary data

In this appendix, we provide supplementary data from the case study for the proposed model. It is worth noting that the value of some parameters, such as the population of each distinct, distances, and the maximum capacity of general and specialized hospitals, are reported in the main body of the paper. Also, it is notable that fixed installation costs, fixed operating costs, and the rate of suspected people are uncertain, and we used the fuzzy approach to capture this uncertainty. The varying quality of these parameters in the long term necessitates considering them in solving the problem. To convert the definitive data to the trapezoidal fuzzy numbers as $\left( {r_{1} ,r_{2} ,r_{3} ,r_{4} } \right)$, the experts have suggested $\left( {r_{1} ,r_{3} } \right)$ values for these parameters, and $\left( {r_{2} ,r_{4} } \right)$ are computed as an increase of 10% in the values ​​of $\left( {r_{1} ,r_{3} } \right)$. Rial (i.e., Iran’s currency) is used as the monetary value.

The average percentage of the suspected people in each district of Tehran is provided in Table

Table 13 The average percentage of the suspected people in distinct i (${\text{e}}_{i}$)

13. Based on the Corona National Headquarters in Tehran, District 4 has the highest rate of coronavirus outbreaks in this city. Also, Districts 2, 5, and 14 have the highest incidence rates after District 4. Meanwhile, Districts 21 and 22 also have the lowest infection rates. Therefore, according to the above reports, the average percentage of the suspected people in each distinct of Tehran is as follows:

Also, in collaboration with the Tehran Municipality, the Ministry of Science, and the Ministry of Health, the capacity of potential centers for screening centers, camp stations, and quarantine stations has been estimated, as shown in Tables

Table 14 The capacity of the potential screening center at node g $\left( {c_{g} } \right)$

14,

Table 15 The capacity of the potential camp station at node j $\left( {c_{j}^{\prime Cs} } \right)$

15 and

Table 16 The capacity of potential quarantine station at node q $\left( {c_{q}^{\prime \prime } } \right)$

16, respectively.

In addition, according to the Ministry of Health, physicians, and medical professionals, the fixed costs of providing infrastructure, equipment, and requirements related to the establishment of screening centers, camp stations, and quarantine stations have been determined and reported in Tables

Table 17 Fixed installation cost to the potential screening center in node g $\left( {f_{g} } \right)$ [Million Rial]

17,

Table 18 Fixed installation cost to the potential camp station in node j $\left( {f_{j}^{\prime Cs} } \right)$[Million Rial]

18 and

Table 19 Fixed installation cost to the potential quarantine station in node q $\left( {f_{q}^{\prime \prime } } \right)$[Million Rial]

19, respectively.

According to the Iranian Ministry of Health and Medical Education, in Tehran, on average, 45% of people who had a coronavirus test such as PCR have a positive result. Therefore, in consultation with the Ministry of Health consultants, tolerance of this number as a percentage of people who have tested positive for coronavirus under different periods and scenarios is presented in Table

Table 20 Percentage of suspected people with positive screening test results in period t under scenario s ($\Delta_{t}^{s} )$

20.

Based on the collected information from the historical data in National Corona Headquarters in Tehran, the average percentage of infected people with mild symptoms, infected people with severe symptoms and no underlying disease, and infected people with severe symptoms and underlying disease have been estimated under mild, moderate, and severe outbreaks of coronavirus in Tehran. Then, according to the experts and consultants in the treatment field, the values ​​of these parameters have been developed for the intended periods and scenarios, which are provided in Tables

Table 21 Percentage of infected people with mild symptoms in period t under scenario s ($\alpha_{t}^{s} )$

21,

Table 22 Percentage of infected people with severe symptoms and no underlying disease in period t under scenario s ($\beta_{t}^{s} )$

22 and

Table 23 Percentage of infected people with severe symptoms and underlying disease in period t under scenario s ($\gamma_{t}^{s} )$

23, respectively.

The values ​​suggested by medical professionals and consultants presented in Tables

Table 24 Percentage of infected people with worsening symptoms admitted to general hospitals in period t under scenario s ($\omega_{t}^{s} )$

24 and

Table 25 Percentage of infected people with worsening symptoms admitted to camp stations in period t under scenario s ($\omega_{t}^{\prime s} )$

25 have been used to determine the percentage of transfer rate between medical centers (i.e., from camp stations to public hospitals or from public hospitals to specialized hospitals).

Based on the collected information from the historical data in National Corona Headquarters in Tehran, the average mortality rate of infected people with mild symptoms, infected people with severe symptoms and no underlying disease, and infected people with severe symptoms and underlying disease have been estimated under mild, moderate, and severe outbreaks of coronavirus in Tehran. Then, according to the experts and consultants in the field of treatment, the values ​​of mortality rate in different medical centers have been suggested for the camp stations, general hospitals, and specialized hospitals under periods and scenarios, which are provided in Tables

Table 26 The mortality rate in camp stations in period t under scenario s ($\rho_{t}^{s\;camp \;station} )$

26,

Table 27 The mortality rate in general hospitals in period t under scenario s ($\rho_{t}^{s\;general\;hospital} )$

27 and

Table 28 The mortality rate in specialized hospitals in period t under scenario s ($\tau_{t}^{s\;specialized \;hospital} )$

28, respectively.

Also, based on the collected information from the historical data in National Corona Headquarters in Tehran, the average improved rate of infected people with mild symptoms, infected people with severe symptoms and no underlying disease, and infected people with severe symptoms and underlying disease have been estimated under mild, moderate and severe outbreaks of coronavirus in Tehran. Then, according to the experts and consultants in the field of treatment, the values ​​of improved rates in different medical centers have been suggested for the camp stations, general hospitals, and specialized hospitals under periods and scenarios, which are provided in Tables

Table 29 The improved rate in camp stations in period t under scenario s ($\tau_{t}^{s\;camp\;station} )$

29,

Table 30 The improved rate in general hospitals in period t under scenario s ($\tau_{t}^{s\;general\; hospital} )$

30 and

Table 31 The improved rate in specialized hospitals in period t under scenario s ($\tau_{t}^{s\;specialized hospital} )$

31, respectively.

Also, based on the opinion of infectious disease specialists, the values of the complete recovery rate of infected people admitted to quarantine stations ​​in different periods are estimated as shown in Table

Table 32 The complete recovery rate of infected people admitted to quarantine stations in period t ($\pi_{t} )$

32.

According to consultants from the Ministry of Health and the National Corona Midwifery Headquarters in Iran, the critical threshold values ​​for potential locations of screening centers, camp stations, and quarantine stations are set as shown in Tables

Table 33 The threshold value of total inflows and outflows in screening center g $\left( {\psi_{g} } \right)$

33,

Table 34 The threshold value of total inflows and outflows in camp station j $\left( {\psi_{j}^{\prime Cs} } \right)$

34 and

Table 35 The threshold value of total inflows and outflows in quarantine station q $\left( {\psi^{\prime\prime}_{q} } \right)$

35, respectively.

Finally, the values of other parameters such as the penalty for critical screening centers (ϑ), camp stations ($\vartheta$), and quarantine stations $(\vartheta^{\prime\prime}$), the predetermined constant ratio of congestion in screening centers (${\Gamma }$), the penalty for negative and positive deviation from the predetermined constant ratio of congestion in screening centers ($\theta ,\theta^{\prime}$, and the penalty coefficient cost of shortage in medical centers (camp stations ($pe^{CS}$), general hospitals ($pe^{GH}$), and specialized hospitals ($pe^{SH}$)) and quarantine stations($pe^{^{\prime}}$) are suggested based on the opinion of experts and consultants of the Ministry of Health in Iran, as shown in Table

Table 36 The value of the other parameters

36.