Disentangling the sources of bank inefficiency: a two-stage network multi-directional efficiency analysis approach

Abstract

To disentangle the sources of bank inefficiency, this paper presents an extended two-stage network multi-directional efficiency analysis (NMEA) approach by taking the internal structure of the banking system into account. The proposed two-stage NMEA approach extends the conventional “black-box” MEA approach, providing a unique efficiency decomposition and identifying which variables drive the inefficiency for banking systems with a two-stage network structure. An empirical application of Chinese listed banks from 2016 to 2020 during the 13th Five-year Plan reveals that the overall inefficiency of sample banks is primarily sourced from the deposit-generating subsystem. Additionally, different types of banks display differentiated evolution modes over different dimensions, confirming the importance of applying the proposed two-stage NMEA approach.

1 Introduction

The banking industry is an essential part of the financial system, which has been played an irreplaceable role in supporting the development of economic growth (An et al. , 2015; Caprio et al. , 2007). Over the past four decades, China has achieved tremendous growth in gross domestic product (GDP). This is partly due to the development of financial systems including the banking industry. However, since China jointed the World Trade Organization (WTO) in 2001, the elevated level of competition level has made it necessary for bank managers to analyze and assess the internal aspects of bank operations, especially given the current landscape of intense competition. This emphasizes the urgency of improving bank performance from both policy and operational perspectives (Yu et al. , 2019). First, as illustrated by various empirical studies, the superior performance is important to promote competitive advantage (Asmild & Matthews , 2012). As such, bank managers have to resort to portfolio management practices which potentially contribute to superior performance. Second, poor performance might directly lead to bankruptcy and sometimes suffer from serious consequences such as economic crisis. Therefore, it is both necessary and urgent to conduct an accurate and appropriate estimation of bank’s performance so that further actions may be taken to improve bank performance and can be implemented methodically.

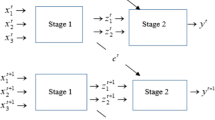
However, evaluating bank performance presents a notable challenge, in that one must be able to disentangle the contributions of different sources of bank inefficiency. First, those aggregated measures that used for characterizing bank performance could produce distorted results. For example, if two factors have a positive and a negative impact respectively on bank performance, then their net effect could be either positive, negative or neutral. As such, a “one size fits all” approach is likely to lead to misleading results when the contributions of these factors are not appropriately disentangled. Second, conventional wisdom relying on aggregated measures can overlook the fact that the negative (positive) effect of some factors can be offset by the positive (negative) effects of some other factors. Therefore, one may implement misguided policy initiatives such that the factors that do not need to be improved are improved, while those that need to be improved are not improved. To illustrate, consider a two-stage network production system as shown in Fig. 1. If one implements the performance improvement initiative based solely on the results of conventional “black-box” data envelopment analysis (DEA) models, then resources may be incorrectly allocated for those “inefficient” decision making units (DMUs) identified by those “black-box” DEA models. For example, one may conduct resource reallocation practices for the whole system, even though it is efficient from the perspective of one sub-stage (e.g., either stage one or stage two). Analogously, for those DMUs whose efficiency in stage one (two) has large room for improvement, one might neglect the importance of reallocating resources for these DMUs, as their overall efficiencies may not exhibit as poor as their corresponding efficiencies associated with subsystems.

In this paper, we propose a two-stage network multi-directional efficiency analysis (NMEA) approach to estimate bank performance. The novel approach extends the standard “black-box” MEA to identify specific sources of inefficiency by taking into account the inner structure of DMUs (banks). In view of the complexity of actual bank operations highlighted by a number of studies (Avkiran , 2009), the proposed two-stage NMEA approach has the advantage of identifying variable-specific inefficiencies within a two-stage banking system, enabling insights into the sources of bank (in)efficiency. In a recent work, Boubaker et al. (2020a) develop a fuzzy multi-objective two-stage DEA model to analyze the performance of banks affiliated with single- and multi-bank holding companies, and then conduct a series of empirical studies to investigate the role of bank affiliation in bank efficiency. However, the measure of bank efficiency used therein is still an aggregate term, which fails to capture the dimension-specific inefficiency identified by the proposed two-stage NMEA approach.

In general, the contribution of the paper can be summarized as follows: First, it contributes to the existing literature by introducing a new two-stage NMEA approach. Compared with conventional single-stage MEA formulation, the proposed approach can identify specific sources of inefficiency by opening the “black-box” of efficiency analysis. Importantly, such a two-stage framework relies on a set of endogenously determined directional vectors, which avoid possible inconsistent estimates arisen from arbitrary directions. Moreover, it differs significantly from many existing network DEA studies (Kao & Liu, 2019; Shi et al., 2021) that may suffer from non-unique decomposition results. In this respect, one can always guarantee unique efficiency decomposition given predetermined stage weights. Interestingly, it also enables to select benchmarks for variable optimization that are proportional to potential improvements associated with each discretionary variable separately (Kapelko & Lansink , 2017), which generally ensures the characteristic of technological monotonicity (Bogetoft & Hougaard , 1999) and provides the decision maker with a useful technique to access to the diagnostic information that might beyond management’s reach (Avkiran, 2009).

Second, it is also potentially contributed to the literature on DEA in finance. Boubaker et al. (2018, 2020b) and Boubaker et al. (2021) adopt DEA to examine firm’s investment and productive efficiencies, and then conduct regression analysis to examine the determinants of these efficiency scores that used to proxy for firm performance. Similarly, Vidal-García et al. (2018) apply DEA to explore the efficiency of mutual funds, and then utilize parametric techniques to explore the relation between expenses and risk-adjusted performance after controlling various control variables. However, these studies pertain to conventional single-stage evaluation process that follows directly from the “black-box” paradigm. By contrast, the present study aims to disentangle the sources of bank inefficiency. In this respect, the proposed technique will be useful for future studies that intend to examine the determinants of dimension-specific bank efficiency, which is of great importance to have more insights into relations between bank efficiency and those key variables of interest.

Finally, we also contribute to the empirical study on identifying the sources of inefficiency of Chinese commercial banks during 13th Five-Year Plan. Specifically, the following results can be concluded. Firstly, there is relatively large room for improvement of Chinese banks in terms of the system efficiency, and the majority of banks are inefficient at least for one year during 13th Five-Year Plan. Secondly, there are significant differences between efficiencies of each bank type across different dimensions, which further confirms the necessity of employing the proposed two-stage NMEA approach. Last but not least, sensitivity analysis results indicate the robustness of the proposed approach. Interestingly, compared with prior studies (Wang et al., 2014; Boubaker et al., 2020a), the present study determines variable-specific efficiencies of each discretionary variable separately. This directly facilitates us to identify the sources of inefficiency in a two-stage banking system, which can also provide alternative banks with an efficient way to explore paths to improve their efficiencies.

The reminder of the paper can be summarized as follows: In Sect. 2, we present the related literature associated with the present paper. Then, we will introduce the development of the proposed two-stage NMEA approach in Sect. 3. The application of our approach in evaluating the (in)efficiency of Chinese commercial banks during 2016–2020 is presented in Sect. 4. The last section summarizes our findings and suggests several directions for further research.

2 Related literature

Since it is first introduced by Charnes et al. (1978), DEA has become one of the most popular approaches to assess the efficiency of financial institutions. Sherman and Gold (1985) is the first to employ DEA to evaluate bank performance. Subsequently, a number of DEA-based studies have been applied to assess the performance of banks from different perspectives. Specifically, the extant DEA-based studies on bank performance can be roughly classified into two classes. The first class tends to evaluate bank efficiency at the branch level. For example, Das et al. (2009) evaluate the labor-use efficiency of individual branches of a large public sector bank by using the DEA approach. Yang (2009) apply the DEA approach to explore the performance of 758 branches of a Canadian bank. Eskelinen et al. (2014) utilize a DEA-based value efficiency analysis approach to examine the sales performance of bank branches of a Finnish bank. LaPlante and Paradi (2015) apply the DEA approach to assess the growth potential of individual branches within one of Canada’s top five banks. Aggelopoulos & Georgopoulos (2017) apply a bootstrap input-oriented profit DEA model to evaluate efficiency change of bank branches of a Greek systemic bank. Paradi and Zhu (2013) provide an excellent survey focusing on the use of DEA in branch analysis.

The second class focuses on evaluating bank performance at an institutional level. Specifically, one may find that most of the existing DEA-based banking studies typically fall into this class partly due to differences in data availability (LaPlante & Paradi, 2015). Early attempts in this class try to regard the banking system as a “black-box”, which does not consider the internal structure of banking operations (Liu et al., 2020; Yu et al., 2016). For example, Epure et al. (2011) explore the productivity and efficiency of Spanish private and savings banks by using DEA-based Malmquist productivity indices and the Luenberger productivity indicator. Juo et al. (2012) develop a non-oriented slacks-based measure (SBM) model to investigate changes in the operating profit of the banking sector; specifically, they also decompose the activity effect into a product mix efficient, a resource mix effect and a scale effect. Yang (2014) develop an enhanced DEA model to evaluate the efficiency of commercial banks. Specifically, their model enables to decompose the technical efficiency into operating efficiency and risk management efficiency. Given possible technological heterogeneity of bank operation, Fu et al. (2016) develop the associated risk-based measures of the meta Nerlovian profit efficiency to investigate the bank performance. Moreover, they also decompose the meta profit efficiency into technology and allocative efficiencies. Kevork et al. (2017) develop a Malmquist productivity index to examine the productivity levels of 28 European countries by adopting the probabilistic characterization of directional distance functions. Toloo and Mensah (2019) propose a robust DEA model to evaluate the performance of 250 European banks. Their model can efficiently reduce the computational burden arising from nonnegative variables. Recently, Zhu et al. (2020) innovatively evaluate the performance of Chinese commercial banks by using an alternative way of ranking banks based on the expected marginal impact on structural efficiency.

The prior studies have made significant contributions to understanding bank efficiency from various perspectives. However, as noted previously, these studies generally inherit the conventional DEA paradigm which regards the banking system as a “black box” without considering the operational procedures taking place inside banks (Kourtzidis et al., 2021). To the best of our knowledge, Wang et al. (1997) and Seiford and Zhu (1999) were the most earliest studies that evaluate bank performance by taking the internal structure of bank operations into account (Kourtzidis et al., 2021). Avkiran (2009) utilize a non-oriented network slacks-based measure (SBM) to evaluate the domestic commercial banks in the United Arab Emirates. Specifically, the sub-DMUs of the production process is composed of three profit centres. An et al. (2015) develop an alternative two-stage DEA approach to evaluate the slacks-based efficiency of Chinese commercial banks; specifically, their model simultaneously considers the increase of desirable outputs and the decrease of undesirable outputs. Liu et al. (2015) estimate the efficiencies of Chinese listed banks by using a novel two-stage DEA model with undesirable intermediate variables. Zha et al. (2016) develop a dynamic two-stage SBM model to assess the efficiencies of Chinese banks. Yu et al. (2019) develop an inverse-like two-stage DEA model to evaluate operational efficiencies and potential income gains by taking the credit risk into account. Zhao et al. (2021) develop two SBM-based models to evaluate the efficiencies of Chinese banks under the natural disposability and managerial disposability strategies, respectively. Specifically, their findings confirm the existence of disparities in inefficiencies between these two strategies. Recently, Li et al. (2021) introduce a new two-stage DEA approach to evaluate the performance of Chinese listed banks over the period from 2014 to 2018; specifically, they consider deposits as a flexible measure to investigate the possibility of identifying a potential Pareto-improvement for individual banks. Other similar studies can be found in Fukuyama and Matousek (2017), Liu et al. (2020), among others.

In general, most of the aforementioned studies tend to apply the network-like DEA models to evaluate the overall and stage efficiencies of various banking entities. However, many of these studies assess and decompose efficiencies based on their current observed production mixes [see e.g., (Fukuyama & Matousek, 2017; Zhao et al., 2021)]. While this practice is easy to implement, it is subjective, making the final estimates susceptible to the subjective choice of directional vectors. Moreover, from a policy perspective, instead of focusing on production mixes occurred in the past, it seems reasonable to design future development planning from identifying endogenous directions based on real banking operations. To mitigate the arbitrariness arising from the selection of alternative directional vectors, Bogetoft and Hougaard (1999) and Asmild et al. (2003) develop and operationalize the MEA to provide an alternative efficiency estimation approach based on the potential improvement. The advantages of MEA can be summarized in several aspects: (1) it is not restricted to radial contractions of inputs or radial expansions of outputs; instead, the efficiency is identified by specifying input reduction and output expansion benchmarks in proportional to the improvement potentials of each discretionary variable (Asmild & Matthews, 2012; Kapelko & Lansink, 2017; Wang et al., 2015; 2) it can identify efficiency improvement potentials of each discretionary variable separately, and the efficiency level and efficiency pattern can be identified for each DMU simultaneously (Asmild & Matthews, 2012; Wang et al., 2015); and (3) compared with other measures such as the SBM, the MEA approach also ensures the characteristic of technological monotonicity (Bogetoft & Hougaard, 1999; Kapelko & Lansink, 2017).

Several authors have conducted efficiency estimation based on the MEA approach. From an application perspective, Asmild and Matthews (2012) utilize the MEA approach to detect differences in efficiency patterns across different types of banks. Their empirical tests validate the ability of MEA in identifying differences both in levels and in patterns of inefficiencies between two types of banks. Wang et al. (2015) employ the MEA approach to evaluate the environmental efficiency of industrial sectors of Chinese major cities, and find that different cities should have different pollutant reduction priorities. Zhu et al. (2019) apply their improved MEA approach to assess regional energy efficiencies of China during the period of 2005–2016. Their empirical application finds that the spatial distribution of energy efficiency in China is unbalance and generally decreases from east to west, and that the comprehensive MEA efficiency of most provinces varies in adjacent state types. From a methodological perspective, Asmild and Pastor (2010) develop the associated slack-free MEA and Range Directional Model (RDM) to account for any types of technical inefficiency, and show that their novel estimates are units invariant and translation invariant. Asmild et al. (2016b) build a statistical model for distinguishing the inefficiency contributions between different subgroups based on the MEA approach. Kapelko and Lansink (2016a) extend the MEA approach to conduct variable-specific analysis of productivity change, and demonstrate that the conventional DEA-based Malmquist index might overlook important differences in variable-specific performance of farms. Kapelko & Lansink (2017) extend the MEA approach to account for dynamics of firms’ production decisions, and introduce a dynamic multi-directional inefficiency analysis approach to identify variable input- and investment-specific inefficiency.

However, to our knowledge, there is no research aims to examine the variable-specific (in)efficiency by taking the internal structure of the production system into account. This may fail to provide sufficient information for managers to identify specific sources of inefficiency embedded in various variables. Importantly, compared with those practices with arbitrary direction vectors (Fukuyama & Matousek, 2017; Zhao et al., 2021), the proposed two-stage NMEA approach formally provides the decision maker with alternative and well-defined efficiency estimates for a two-stage production system. This can also help to identify which variable the inefficiency is located on, potentially providing regulators with significant insights on the sources of the (in)efficiency of DMUs.

3 Methodology

3.1 Two-stage bank operational process

Without loss of generality, assume that there are n DMUs (individual banks) in the banking system, represented by $DMU_j (j=1,\ldots ,n)$. In practice, the actual production process of the banking system is complicated. Differing from some existing studies that consider the banking system as a “black-box”, following Boussemart et al. (2019), we regard the operational process of each bank as a two-stage process, which is illustrated in Fig. 1.

Fig. 1

Two-stage process of bank operations

In the first stage, banks use m inputs $\textrm{X}_j=\left( x_{1j},\ldots ,x_{mj}\right)$ to produce D intermediate products $\textrm{Z}_j=\left( z_{1j},\ldots ,z_{Dj}\right)$. Specifically, in order to differentiate between controllable and uncontrollable factors, we partition the input vector into a fixed (semi-fixed) and variable part. That is, $\textrm{X}_j=\left( \textrm{X}_j^f,\textrm{X}_j^v\right)$ with $\textrm{X}_j^f \in \mathbb {R}_+^{m_1}$ and $\textrm{X}_j^v \in \mathbb {R}_+^{m_2}$ such that $m_1+m_2=m$. In the second stage, banks utilize the intermediate products to produce s desirable outputs $\textrm{Y}_j=\left( y_{1j},\ldots ,y_{sj}\right)$ and L undesirable outputs $\textrm{B}_j=\left( b_{1j},\ldots ,b_{Lj}\right)$. The production technology corresponding to the first stage can be represented as follows:

$$\begin{aligned} \begin{aligned} T^1 = \left\{ \left( \textrm{X},\textrm{Z} \right) \in \mathbb {R}_{+}^{m}\times \mathbb {R}_{+}^{D}: \mathrm{X\,can\,produce\,Z} \right\} \end{aligned} \end{aligned}$$

(1)

Similarly, the production technology corresponding to the second stage can be characterized as follows:

$$\begin{aligned} \begin{aligned} T^2 = \left\{ (\textrm{Z},\textrm{Y},\textrm{B})\in \mathbb {R}_+^{D}\times \mathbb {R}_+^{s}\times \mathbb {R}_+^{L}: \textrm{Z}\ \mathrm{can\ produce}\ (\textrm{Y},\textrm{B}) \right\} \end{aligned} \end{aligned}$$

(2)

Following conventional assumptions such as strong disposability of inputs and desirable outputs, null-joint, and convexity [see, e.g., (Boussemart et al., 2019)], the production possibility set of technologies $T^1$ and $T^2$ under the assumption of variable returns to scale (VRS) can be defined as:

$$\begin{aligned} \begin{aligned} T^1 = \left\{ (\textrm{X},\textrm{Z})\in \mathbb {R}_+^{m}\times \mathbb {R}_+^{D}: \sum _{j=1}^n \lambda _j \mathrm{X_j} \le \textrm{X},\sum _{j=1}^n \lambda _j \textrm{Z}_j \ge \textrm{Z},\sum _{j=1}^n \lambda _j = 1.\right\} \end{aligned} \end{aligned}$$

(3)

and

$$\begin{aligned} T^2 = \left\{ \begin{array}{l} (\textrm{Z},\textrm{Y},\textrm{B})\in \mathbb {R}_+^{D}\times \mathbb {R}_+^{s}\times \mathbb {R}_+^{L}: \sum _{j=1}^n \gamma _j \textrm{Z}_j \le \textrm{Z},\\ \sum _{j=1}^n \gamma _j \textrm{Y}_j \ge \textrm{Y}, \sum _{j=1}^n \gamma _j \textrm{B}_j = \textrm{B}, \sum _{j=1}^n \gamma _j = 1.\\ \end{array} \right\} \end{aligned}$$

(4)

where $\lambda =\left( \lambda _1,\ldots ,\lambda _n\right)$ and $\gamma =\left( \gamma _1,\ldots ,\gamma _n\right)$ are two vectors of intensity variables associated with $T_1$ and $T_2$, respectively (Boussemart et al., 2019). To link the above two stages, the existing studies may regard the overall production technology as the intersection of two sub-technologies, i.e., $T= T_1 \cap T_2$ (Boussemart et al., 2019). However, it is worth noting that the intermediate products are generally common elements, as part of technology $T_1$ and technology $T_2$. To avoid possible wastes caused by the situation that the amount of target intermediate products acting as the outputs of the first stage can be greater than that acting as the inputs of the second stage, i.e., $\sum _{j=1}^n \lambda _j \textrm{Z}_j > \sum _{j=1}^n \gamma _j \textrm{Z}_j$, following Kao (2017), we require that the quantity of all intermediate products “produced” by $T_1$ must be equal to that “consumed” by $T_2$, that is $\sum _{j=1}^n \lambda _j \textrm{Z}_j = \sum _{j=1}^n \gamma _j \textrm{Z}_j$. This is also known as the “fixed-link” situation emphasized in Tone and Tsutsui (2009). Given above, our banking production possibility set can be formulated as follows:

$$\begin{aligned} T = \left\{ \begin{array}{l} (\textrm{X},\textrm{Z},\textrm{Y},\textrm{B})\in \mathbb {R}_+^{m} \times \mathbb {R}_+^{D}\times \mathbb {R}_+^{s}\times \mathbb {R}_+^{L}: \sum _{j=1}^n \lambda _j \textrm{X}_j \le \textrm{X},\\ \sum _{j=1}^n \lambda _j \textrm{Z}_j \ge \textrm{Z}, \sum _{j=1}^n \gamma _j \textrm{Y}_j \ge \textrm{Y}, \sum _{j=1}^n \gamma _j \textrm{Z}_j \le \textrm{Z},\\ \sum _{j=1}^n \gamma _j \textrm{B}_j = \textrm{B}, \sum _{j=1}^n \lambda _j \textrm{Z}_j = \sum _{j=1}^n \gamma _j \textrm{Z}_j,\\ \sum _{j=1}^n \lambda _j = 1, \sum _{j=1}^n \gamma _j = 1, \lambda _j,\gamma _j \ge 0, j=1,\ldots ,n. \end{array} \right\} \end{aligned}$$

(5)

Note that if we delete constraints $\sum _{j=1}^n \lambda _j = 1$ and $\sum _{j=1}^n \lambda _j = 1$ from technology T, then constant returns to scale (CRS) is assumed for this empirical non-parametric production technology. In other words, our following analysis can be easily extended to deal with problems exhibiting CRS. Table 1 provides notations used in the present study.

Table 1 Notations used in the present study

3.2 Estimation of bank performance with a two-stage multi-directional efficiency analysis approach

Based on technology T, one may estimate the performance of each bank through assessing the distance from observed position of each bank to its corresponding efficient frontier constructed from T (Boussemart et al., 2019). This can be done by using the well-konwn directional distance function models [see, e.g., (Chambers et al., 1996)]. Specifically, the MEA model and the Range Directional Model (RDM) are two famous directional distance function models that appear in the literature (Asmild & Pastor, 2010). The RDM model was developed in Portela and Thanassoulis (2010), which is inspired by, which was inspired by the well known directional distance model of Chambers et al. (1996). The MEA model was first suggested by Bogetoft and Hougaard (1999) and subsequently operationalised by Asmild et al. (2003).

Compared with RDM, the reason for choosing MEA is explained as follows: firstly, MEA selects a specific ideal point such that input reductions or output expansions are proportional to potential improvements for each unit and each variable separately (Asmild & Matthews, 2012), while RDM considers the same ideal point for all DMUs. Secondly, MEA can be employed under any returns to scale assumption while RDM specifically assumes that VRS assumption is required, as a CRS assumption might be inconsistent with the existence of negative data (Portela & Thanassoulis, 2010). And thirdly, MEA generally uses the DMU-specific directional vectors and can measure variable-specific efficiencies against various ideal points that are proportional to potential improvements, which is especially important for some specific industries such as the agricultural sector in which its input markets are regulated via the support policies (Baležentis & De Witte, 2015). Moreover, compared with those measures emphasized in Kapelko and Lansink (2017), the MEA also maintains the property of technological monotonicity (Bogetoft & Hougaard, 1999).

In the first step of two-stage NMEA, one needs to find the associated ideal points of each discretionary variable. Specifically, the following linear program can be used to identify the unit-specific ideal points for each variable input for the evaluated DMU k:

$$\begin{aligned} d_{i_1k}^* ={} & {} \, min\ d_{i_1k}\nonumber \\ s.t.{} & {} \sum _{j=1}^n \lambda _j x_{i_1j}^v \le d_{i_1k},\nonumber \\{} & {} \sum _{j=1}^n \lambda _j x_{i_1}^v \le x_{(-i_1)k}^v,-i_1=1,\ldots ,i_1-1,i_1+1,\ldots ,m_1,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j x_{i_2}^f \le x_{i_2k}^f,i_2=1,\ldots ,m_2,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j z_{lj} \ge z_{lk},l=1,\ldots ,D,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j = 1,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j y_{rj} \ge y_{rk}, r=1,\ldots ,s,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j b_{tj} \le b_{tk},t=1,\ldots ,L,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j z_{lj} \le z_{lk},l=1,\ldots ,D,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j z_{lj} = \sum _{j=1}^n \gamma _j z_{lj},l=1,\ldots ,D,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j = 1,l=1,\ldots ,D,\nonumber \\{} & {} \lambda _j, \gamma _j \ge 0,j=1,\ldots ,n. \end{aligned}$$

(6)

where $x_{-i_1}^v$ denotes the $(-i_1)$th variable input in which the $i_1$th input is excluded. Similarly, the unit-specific idea points for each desirable output and undesirable output can be determined by solving the following linear programs (7) and (8), respectively.

$$\begin{aligned} \phi _{rk}^* ={} & {} max\ \phi _{rk}\nonumber \\ s.t.{} & {} \sum _{j=1}^n \lambda _j x_{i_1}^v \le x_{i_1k}^v,i_1=1,\ldots ,m_1,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j x_{i_2}^f \le x_{i_2k}^f,i_2=1,\ldots ,m_2,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j z_{lj} \ge z_{lk},l=1,\ldots ,D,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j = 1,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j y_{rj} \ge \phi _{rk},\nonumber \\{} & {} \sum _{j=1}^n \gamma _j y_{rj} \ge y_{(-r)k}, -r=1,\ldots ,r-1,r+1,\ldots ,s,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j b_{tj} \le b_{tk},t=1,\ldots ,L,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j z_{lj} \le z_{lk},l=1,\ldots ,D,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j z_{lj} = \sum _{j=1}^n \gamma _j z_{lj},l=1,\ldots ,D,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j = 1,\nonumber \\{} & {} \lambda _j, \gamma _j \ge 0,j=1,\ldots ,n. \end{aligned}$$

(7)

and

$$\begin{aligned} \psi _{tk}^* ={} & {} min\ \psi _{tk}\nonumber \\ s.t.{} & {} \sum _{j=1}^n \lambda _j x_{i_1}^v \le x_{i_1k}^v,i_1=1,\ldots ,m_1,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j x_{i_2}^f \le x_{i_2k}^f,i_2=1,\ldots ,m_2,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j z_{lj} \ge z_{lk},l=1,\ldots ,D,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j = 1,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j y_{rj} \ge y_{rk}, r=1,\ldots ,s,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j b_{tj} \le \psi _{tk},\nonumber \\{} & {} \sum _{j=1}^n \gamma _j b_{tj} \le b_{(-t)k},-t=1,\ldots ,t-1,t+1,\ldots ,L,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j z_{lj} \le z_{lk},l=1,\ldots ,D,\nonumber \\{} & {} \sum _{j=1}^n \lambda _j z_{lj} = \sum _{j=1}^n \gamma _j z_{lj},l=1,\ldots ,D,\nonumber \\{} & {} \sum _{j=1}^n \gamma _j = 1,\nonumber \\{} & {} \lambda _j, \gamma _j \ge 0,j=1,\ldots ,n. \end{aligned}$$

(8)

In model (7), $y_{(-r)k}$ represents the $(-r)$th desirable output that the rth output is excluded. In model (8), $b_{(-t)k}$ represents the $(-t)$th undesirable output in which the tth desirable output is excluded. All the above models are assumed under the VRS, which can be easily extended to solve problems under the CRS by deleting the associated normalization constraints $\sum _{j=1}^n \lambda _j = 1$ and $\sum _{j=1}^n \gamma _j = 1$.

Note that, according to Färe and Grosskopf (2003, 2004), the treatment of undesirable outputs should comply with standard axioms of the production theory. In this respect, it seems that those constraints associated with undesirable outputs in models (6)–(8) should be equalities. However, it is important to emphasize that models (6)–(8) are only used for identifying unit-specific ideal points for each disposable measure. As such, if one assigns an equal sign to the undesirable output constraints, implying that the amount of the associated undesirable outputs should remain unchanged. This is nevertheless inconsistent with practical abatement activities such as introducing advanced disposing technologies. In fact, the effect of imposing equality to the undesirable output constraints in models (6)–(8) will be that it narrows the feasible region as tighter constraints are imposed. However, this practice may not comply with the definition of ideal points as mentioned previously. By contrast, the current study, which imposes relaxed constraints on the undesirable outputs, generally complies with the core idea of the original MEA approach. That is, those ideal points are determined under the most favorable scenario for each disposable measure. Importantly, as mentioned, these ideal points are only used for specifying the directions for improvement. In the following model (9), the undesirable output constraints are formulated in equalities, which is consistent with the practice of Färe and Grosskopf (2003; 2004).

With those unit-specific ideal points determined by models (6)–(8), the overall two-stage NMEA score can be determined by the following model:

$$\begin{aligned} D(x,z,y,b;w_1,w_2,\epsilon ) =&max\ w_1 \beta _1 + w_2 \beta _2 \end{aligned}$$

(9)

$$\begin{aligned} s.t.&\sum _{j=1}^n \lambda _j x_{i_1}^v \le x_{i_1k}^v - \beta _1\left( \epsilon + x_{i_1k}^v - d_{i_1k}^*\right) ,i_1=1,\ldots ,m_1, \end{aligned}$$

(9.1)

$$\begin{aligned}&\sum _{j=1}^n \lambda _j x_{i_2}^f \le x_{i_2k}^f,i_2=1,\ldots ,m_2, \end{aligned}$$

(9.2)

$$\begin{aligned}&\sum _{j=1}^n \lambda _j z_{lj} \ge z_{lk},l=1,\ldots ,D, \end{aligned}$$

(9.3)

$$\begin{aligned}&\sum _{j=1}^n \lambda _j = 1, \end{aligned}$$

(9.4)

$$\begin{aligned}&\sum _{j=1}^n \gamma _j y_{rj} \ge y_{rk} + \beta _2 \left( \epsilon + \phi _{rk}^* - y_{rk}\right) , r=1,\ldots ,s, \end{aligned}$$

(9.5)

$$\begin{aligned}&\sum _{j=1}^n \gamma _j b_{tj} = b_{tk} - \beta _2 \left( \epsilon + b_{tk} - \psi _{tk}^* \right) ,t=1,\ldots ,L, \end{aligned}$$

(9.6)

$$\begin{aligned}&\sum _{j=1}^n \gamma _j z_{lj} \le z_{lk},l=1,\ldots ,D, \end{aligned}$$

(9.7)

$$\begin{aligned}&\sum _{j=1}^n \lambda _j z_{lj} = \sum _{j=1}^n \gamma _j z_{lj},l=1,\ldots ,D, \end{aligned}$$

(9.8)

$$\begin{aligned}&\sum _{j=1}^n \gamma _j = 1, \end{aligned}$$

(9.9)

$$\begin{aligned}&\lambda _j , \gamma _j \ge 0,j=1,\ldots ,n. \end{aligned}$$

(9.10)

where $w_1$ and $w_2$ are weights attached to stage 1 and stage 2, respectively. Specifically, $w_1+w_2=1$ always holds. Constraint (9.1) seeks to simultaneous radial improvements in variable inputs along the direction $\left( \epsilon + x_{1k}^v - d_{1k}^*,\ldots ,\epsilon + x_{m_1k}^v - d_{m_1k}^*\right)$. Constraint (9.2) is the fixed input constraint, which is analogous to the practice of Syrjänen (2004) and Asmild and Matthews (2012). Constraints (9.3), (9.7), and (9.8) build the linkage of the intermediate measures associated with two subsystems. Constraint (9.4) leads to the assumption of VRS for stage one, while constraint (9.9) relates to the assumption of VRS for stage two. As mentioned previously, one can obtain the associated CRS version when these two constraints are omitted. Constraints (9.5) and (9.6) seek to simultaneous increase in desirable outputs and decrease in undesirable outputs given directions $\left( \epsilon + \phi _{1k}^* - y_{1k},\ldots ,\epsilon + \phi _{sk}^* - y_{sk}\right)$ and $\left( \epsilon + b_{1k} - \psi _{1k}^*,\ldots ,\epsilon + b_{Lk} - \psi _{Lk}^*\right)$, respectively.

Given model (9), several comments are worth investigating. First, the ideal point of each discretionary variable can be their current observed levels. Taking variable input $i_1$ as an example, $x_{i_1k}^v$ can actually be equal to $d_{i_1k}^*$. Under this circumstance, model (9) might be unbounded as the improvement direction $x_{i_1k}^v - d_{i_1k}^* = 0$. In fact, this might occur in almost all MEA formulations. To avoid such a case, we thus introduce an infinite small number $\epsilon$ associated with each discretionary variable. As can be seen in model (9), if there is one measure such that the ideal point of this measure is just its current observed value, then the decision variable associated with this measure in model (9) should be equal to zero. For example, if $x_{i_1k}^v - d_{i_1k}^* = 0$, then $\beta _1=0$ must hold. In this circumstance, one may concern that how the incorporation of $\epsilon$ affects which variable the inefficiency is located on for a concerned system. To illustrate it, we need to distinguish between two possible cases. In the first case, if there exists at least one measure (variable input or desirable/undesirable output) such that its ideal point is just its current observed value, then the incorporation of $\epsilon$ into other associated measures does not affect the optimal value associated with this measure. For example, if there exists at least one variable input such that its ideal point $d_{i_1k}^*$ is just its current observed value $x_{i_1k}^v$, then $\beta _1=0$ must hold. However, in the second case, if there is no measure such that its current observed value equal to the ideal point, then the introduction of parameter $\epsilon$ can actually have limited effects on the estimation results as long as it is small enough. For example, as shown in the following sensitivity analysis, the estimation results with different values of $\epsilon$ are highly correlated, which further imply limited impact of $\epsilon$ on the estimates determined by the proposed approach. To the best of our knowledge, the present study is the first to highlight this kind of issue and resolve it in a relatively reasonable way. Further, we can have the following proposition:

Proposition 1

$0 \le D(x,z,y,b;w_1,w_2,\epsilon ) \le 1$.

Proof

The proof of Proposition 1 can be summarized into two parts. On the one hand, it is easy to verify that $\beta _1=\beta _2=0$ is a feasible solution to variables $\beta _1$ and $\beta _2$, respectively. Consequently, $D(x,z,y,b;w_1,w_2,\epsilon )\ge 0$ always holds. On the other hand, we would like to prove $D(x,z,y,b;w_1,w_2,\epsilon ) \le 1$ by a contradiction. Suppose that the optimal solution to model (9) is $\left( \lambda _j^*,\gamma _j^*,\beta _1^*,\beta _2^*\right)$. Then, if the objective value of model (9) is strictly greater than one, implying that $D(x,z,y,b;w_1,w_2,\epsilon ) > 1$. As $w_1+w_2=1$ always holds. Thus, there is at least one of $\beta _1^*$ and $\beta _2^*$ is strictly greater than one. Without loss of generality, suppose that $\beta _1^*>1$ is a feasible solution to variable $\beta _1$ in model (9). Then, we can have that $x_{i_1k}^v - \beta _1^*\left( \epsilon + x_{i_1k}^v - d_{i_1k}^*\right) - d_{i_1k}^* = \left( \beta _1^*-1\right) \left( d_{i_1k}^* - x_{i_1k}^v\right) - \beta _1^*\epsilon <0$. This implies that a feasible solution with a smaller value of $d_{i_1k}^{'} = x_{i_1k}^v - \beta _1\left( \epsilon + x_{i_1k}^v - d_{i_1k}^*\right)$ exists. This contradicts the fact that $d_{i_1k}^*$ is the optimal objective function value of model (6). A similar logic can be applied to the case when $\beta _2^*>1$. This naturally completes the proof. $\square$

Proposition 2

The overall system is efficient if and only if two sub-systems are efficient simultaneously.

Proof

The proof of Proposition 2 is straightforward. $\square$

Proposition 3

The optimal solutions of model (9) corresponding to variables $\beta _1$ and $\beta _2$ are unique.

Proof

Without loss of generality, suppose that $\left( \lambda _j^*,\gamma _j^*,\beta _1^*,\beta _2^*\right)$ is an optimal solution to model (9). Then, we proceed to prove Proposition 3 by a contradiction. That is, $\beta _1^*$ and $\beta _2^*$ are not unique. In other words, we can find a different optimal solution $\left( \lambda _j^{*'},\gamma _j^{*'},\beta _1^{*'},\beta _2^{*'}\right)$ to model (9) such that $w_1\beta _1^* + w_2\beta _2^* = w_1\beta _1^{*'} + w_2\beta _2^{*'}$ and equalities $\beta _1^* = \beta _1^{*'}$ and $\beta _2^* =\beta _2^{*'}$ cannot be satisfied simultaneously. To guarantee these conditions, it is not hard to have that one and only one of the inequalities $\beta _1^{*'} > \beta _1^*$ and $\beta _2^{*'} > \beta _2^*$ must hold. Without loss of generality, suppose that $\beta _1^{*'} > \beta _1^*$ always holds. As $w_1\beta _1^* + w_2\beta _2^* = w_1\beta _1^{*'} + w_2\beta _2^{*'}$, we have that $\beta _2^{*'} < \beta _2^*$. Then, it is not hard to find that $\left( \lambda _j^{*'},\gamma _j^{*},\beta _1^{*'},\beta _2^{*}\right)$ is also a feasible solution to model (9). However, the objective function value of this solution is equal to $w_1 \beta _1^{*'} + w_2\beta _2^{*}$, which is greater than $w_1 \beta _1^{*} + w_2\beta _2^{*}$. In other words, there exists a feasible solution to model (9) such that its objective function value is greater than $w_1 \beta _1^{*} + w_2\beta _2^{*}$, which is an obvious contradiction that $w_1 \beta _1^{*} + w_2\beta _2^{*}$ is the optimal function value of model (9). Therefore, $\beta _1^*$ and $\beta _2^*$ must be unique. This naturally completes the proof. $\square$

Proposition 3 is important as it indicates that our proposed model (9) generally guarantees a unique efficiency decomposition. Interestingly, the reason why $\beta _1$ and $\beta _2$ are unique in model (9) lies in the fact that model (9) can be solved in two independent linear programs, which can be accomplished by separating the constraints associated with stage one and stage two, respectively. Moreover, this holds directly depending on the “fixed-link” constraint, i.e., $\sum _{j=1}^n \lambda _j z_{lj} = \sum _{j=1}^n \gamma _j z_{lj}$. Otherwise, the interaction effect between $\beta _1$ and $\beta _2$ might lead to possible multiple solutions. That is, constraints (9.3) and (9.7)-(9.8) together with the objective function of model (9) directly lead to the above interesting conclusion that the proposed two-stage NMEA approach is equivalent to two linear programs that can be solved independently. Compared with those two-phase approaches that employed in conventional multiplicative network DEA formulations, the proposed approach provides a simple but efficient technique for simultaneously identifying the potential of contracting inputs and expanding outputs in a two-stage production system uniquely.

For a given $DMU_k$ under examination, denote its optimal solution to model (9) as $\left( \lambda _j^{k*},\gamma _j^{k*},\beta _1^{k*},\beta _2^{k*}\right)$, then the overall efficiency for $DMU_k$ can be determined by its optimal objective function value of model (9), i.e., $E_k=w_1\beta _1^{k*} + w_2\beta _2^{k*}$, where $\beta _1^{k*}$ and $\beta _2^{k*}$ can be interpreted as stage efficiencies corresponding to stage one and stage two, respectively.

Finally, the vector of variable-specific multi-directional efficiency scores for DMU k can be formulated as follows:

$$\begin{aligned}{} & {} E_{i_1k}^x=\frac{x_{i_1k}^v - \beta _1^{k*} \left( \epsilon + x_{i_1k}^v - d_{i_1k}^*\right) }{x_{i_1k}^v} \end{aligned}$$

(10)

$$\begin{aligned}{} & {} E_{rk}^y=\frac{y_{rk}}{y_{rk} + \beta _2^{k*} \left( \epsilon + \phi _{rk}^* - y_{rk}\right) } \end{aligned}$$

(11)

$$\begin{aligned}{} & {} E_{tk}^b=\frac{b_{tk} - \beta _2^{k*} \left( \epsilon + b_{tk} - \psi _{tk}^*\right) }{b_{tk}} \end{aligned}$$

(12)

4 Empirical illustration

In this section, we illustrate and validate the proposed approach by applying it to Chinese banking industry.

4.1 Data and variables

We utilize a dataset of Chinese public listed banks available from the Wind Financial Database (WIND). This database has been employed by a variety of studies, including Poon and Chan (2008), Shan and Zhu (2013), Wang et al. (2020), and Xu et al. (2013), and provides comprehensive and structed financial data for listed Chinese firms. The Shanghai Stock Exchange and the Shenzhen Stock Exchange are two major exchanges in mainland China.¹ The WIND database contains all public listed financial and non-financial firms associated with these two exchanges.

According to China Security Regulatory Commission (CSRC) Industry Classification standard, we collected 43 banks that belong to the Monetary Financial Services industry. After removing those missing data, we finally employ 41 banks. As illustrated by various studies, there are institutional and operational differences across different types of Chinese banks. To gain more insights into these differences, following Zhao et al. (2021), we categorized these banks into four groups: 5 stated owned banks, 11 joint-stock commercial banks, 15 city commercial banks, and 10 rural commercial banks. The information of these banks are provided in Table 2.

Table 2 Classification of banks by ownership

We utilize annual consolidated financial data from 2016 to 2020, which covers the whole period in the 13th Five-Year Plan. The selection of this sample period is justified by two factors: firstly, the 13th Five-Year Plan is one of China’s most recent mid- and long-term socio-economic development plans, making it pertinent to grasp the evolution of bank performance over this pivotal period, which may have significant implications for policy formation and execution. Secondly, the advent of the COVID-19 pandemic in late 2019 has further heightened the urgency to investigate how the unexpected pandemic affects bank performance. By investigating this, we believe that it can bring about more insights into how banks can potentially enhance their performance and be better-prepared for unforeseen circumstances.

Regarding the selection of indicators, one can observe a variety of measures being used depending on the research objectives. Moreover, apart from deposits, there generally appears to be accord concerning the major categories of indicators for evaluating the performance of banking operations (Wang et al., 2014). With regard to the role of deposits, different perspectives are likely to emerge according to the approach taken. For instance, the production approach tends to consider the deposits as an output, while the intermediation approach opts to regard the deposits as an input. To tackle this dilemma of whether to view the deposits as an input or an output, Holod and Lewis (2011) develop a two-stage DEA model in which the role of the deposits is considered as an intermediate product. Subsequently, a number of studies have utilized this approach for appraising bank performance from different perspectives (Boussemart et al., 2019; Holod & Lewis, 2011; Wang et al., 2014; Zhao et al., 2021). Nevertheless, there is usually not much consensus when it comes to selecting the practical framework that should be implemented in assessing bank performance. As reviewed by Lozano (2016), it seems that the two-stage series framework is the most represented one. Following prior studies, we divide the Chinese banking system into two subsystems: the deposit-generating subsystem and the loan subsystem. For the deposit-generating stage, the inputs of this stage are (1) assets (FX), which regard to a fixed input and refer to the total assets of the associated bank; (2) employee (X1), which refers to the number of employees; and (3) expense (X2), which refers to operating expenses used for bank operations. For the loan subsystem, the outputs of this stage are as follows: (1) Bad loan (B), which is an undesirable output and represents the problem loans for which borrowers are unable to make repayment (Wang et al., 2014); and (2) Good loan (Y), which is calculated by the total loan minus the associated bad loan.² Bank deposit (Z) is considered as the intermediate product that can be both the output of the deposit-generating subsystem and the input of the loan subsystem. All data are deflated to constant price relative to 2016 using the consumer price index. Table 3 presents the summary statistics of concerned variables for original data. Specifically, except for X1, all the other variables are in billion yuan.

Table 3 Summary statistics

4.2 Results

Before presenting the results, we need to assign the stage weights appropriately. For illustration, following Zhao et al. (2021), both stages are assumed to contribute equally to the overall efficiency, this directly leads to the treatment that weights assigned to both stages are identical, i.e., $w_1=w_2=0.5$. Importantly, for completeness, in the following subsection, we conduct sensitivity analysis to examine how the choice of stage weights might affect the results. The results generally indicate the stage weights do have no significant impact on rankings of banks, and the impacts of stage weights on the estimation results, to certain extent, can be neglected. Also, we set $\epsilon =0.001$ for illustration, below we will further examine how this parameter affects the estimation results. On the other hand, as the CRS assumption often relates to the operation at an optimal scale, and we can hardly find banks to operate at such an ideal status due to imperfect competition and financial constraints (Kourtzidis et al., 2021). Thus, following Kourtzidis et al. (2021), Li et al. (2021), and Wang et al. (2014), we adopt the VRS assumption.

4.2.1 The overall and stage efficiencies of Chinese banks

In Table 4, we present the results of overall efficiencies of each bank in detail. The last column shows the associated rankings of the average overall efficiency of each bank. As shown in Table 4, we can draw the following conclusions. First, the average overall efficiency of concerned banks is 0.5182, indicating that there is large room for improvement. Second, there are few efficient banks (3 out of 41) identified by the proposed two-stage NMEA model during 2016–2020. This indicates that most banks are inefficient at least for one year. For example, bank of China (BOC) is evaluated as inefficient in 2016, while it is evaluated as efficient during 2017–2020. Similarly ZRCB, WRCB, BABJ, BASH, BCM, RRCB, BOC, SZRCB also possess an overall efficiency score of unity in at least one year. Third, we have an interesting finding that the average overall efficiency of Chinese banks one year before and after the outbreak of COVID-19 increases from 0.4962 to 0.5325, indicating that Chinese banks in general can utilize less inputs to produce more outputs after the outbreak of the sudden pandemic.

Table 4 Estimates of overall efficiencies

Table 5 reports stage efficiencies of 41 selected banks. It can be seen from Tables 4 and 5 that if a bank is estimated as efficient in overall efficiency in one year, it would also be evaluated as efficient in terms of stage efficiencies. For example, ICBC is evaluated as overall efficient during 2016–2020, and its stage efficiencies are both evaluated as efficient over this sample period. This is consistent with the prediction of Proposition 2.

Table 5 Efficiency results of stage efficiencies

In addition, we also provide the evolution of overall and stage efficiencies in Fig. 2. As shown in this figure, the average efficiency of the loan subsystem is much higher than that of the deposit-generating subsystem under the proposed approach. This confirms that the inefficiency is mainly due to inefficiencies of the deposit-generating subsystem Zhao et al. (2021). Hence, more attention should be paid to enhance the performance of the deposit-generating stage, i.e., the input resources should be utilized more efficiently. However, as emphasized previously, we do not have any ideas of which variable should be enhanced through the above traditional efficiency decomposition procedure. For this aim, in the following, we would like to conduct the multi-directional efficiency analysis within such a two-stage banking system so that more details can be derived through uncovering the sources of the inefficiency of banking operations.

Fig. 2

Average efficiencies of selected banks during 2016–2020

4.2.2 Multi-directional efficiency analysis with two-stage systems

In the previous subsection, we provide the efficiency analysis from the perspective of overall and stage efficiencies. This is consistent with the practice of employing traditional two-stage DEA models. However, as noted previously, one cannot identify the sources of inefficiency from the perspective individual variable. For this aim, Table 6 below presents the summary statistics for four concerned discretionary variables across four bank types. In addition, Table 6 also presents the summary statistics of variable-specific inefficiencies for the whole sample.

Table 6 Summary statistics for the multi-directional efficiency by bank type

The results in Table 6 show that the average Employee-specific, Expense-specific, Good loan-specific and Bad loan-specific inefficiency in the whole sample are 0.8115, 0.8284, 0.9419 and 0.9068, respectively. This indicates potentials for reducing the use of Employee (18.85%) and Expense (17.16%) and for increasing Good loan (5.81%) and for decreasing Bad loan (9.32%). Moreover, we can also identify substantial variations in variable-specific efficiency across different bank types. For example, the variable-specific efficiencies for SOB are greater than 0.9 across all five discretionary variables. However, other three bank types have relative vulnerable performance for specific variables. Taking R-CB as an example, the potential for reducing the use of Employee (22.64%) is significantly greater than that for increasing good loan (5.16%). In addition, the difference between the minimum and the maximum efficiencies demonstrate that the highest dispersion was found for R-CB. For this type of bank, the minimum efficiency had an average efficiency of 0.2671, while for the maximum level this efficiency estimate was as high as 1.0000.

4.2.3 Evolution of two-stage multi-directional efficiency scores of four types of banks

In this subsection, we proceed to investigate the evolution of variable-specific efficiencies of four types of Chinese commercial banks as presented in Fig. 3. Specifically, as the previous section have already illustrated that there is considerable dispersion in efficiency estimates for banks in the sample, the development of average efficiency might not be a good representations for the data utilized in the present study (Kapelko & Lansink, 2017). As a result, following Kapelko and Lansink (2017), we depict the evolution of median NMEA values for each discretionary variables, which provides the decision maker with a better understanding of the central tendency rather than averages.

From Fig. 3, we can have the following observations. First, we observe that there are clear differences between efficiencies of each bank type across different dimensions. Specifically, the SOB generally being consistently more efficient than other three types of banks. However, the evolution mode differs from different variable-specific efficiencies. For example, as shown in Fig. 3a the median NMEA scores of Employee for R-CB exhibited an inverse-U shape, while generally exhibited a “U” shape for JS-CB and C-CB. Similarly, as presented in Fig. 3c, the evolution of median NMEA scores of Good loan for JS-CB presented a relatively stable increasing trend, while for C-CB’s median NMEA scores first decreased and then increased until 2019 and eventually presented an obvious declining trend after 2019.

Fig. 3

Evolution of median NMEA scores for discretionary variables

Second, we can obtain mixed results for the MEA efficiency comparisons over other three types of banks. For example, with regard to NMEA scores for Expense, R-CB consistently performs better than JS-CB and C-CB over the sample period. However, the median NMEA scores for Good loan is less than that of JS-CB during 2017–2020. In terms of C-CB, this type of banks has the worst median NMEA scores for Employee during 2016–2020 while has higher median NMEA scores for Expense than JS-CB during 2018–2020. This demonstrates that different types of banks generally have different evolution modes over different dimensions. This generally provides the decision maker with a detailed picture of the dynamics of bank performance. However, this cannot be observed by traditional network DEA models, demonstrating the importance of employing the proposed approach.

Third, as the outbreak of the unexpected COVID-19 generally occurred in late 2019, it is therefore meaningful to compare the bank performance between 2019 and 2020. In doing so, we believe that one may have a more thorough understanding of determinants which might guide banks out of the crisis. Focusing on these two years, we can find obvious changes in terms of efficiency scores corresponding to some discretionary variables. For example, in terms of NMEA scores for Employee, the median score for C-CB seems to decrease from a trend perspective, however an opposite direction showing a marked increase in 2020. Interestingly, the trends for different types of banks exhibit different patterns for different discretionary variables. To illustrate, it is obvious that, the median NMEA scores of Expense for all types of banks, except for the SOB, exhibit an increasing trend in 2020 compared to 2019. However, the median NMEA scores of both good and bad loans for JS-CB generally increased in 2020 compared with 2019, while an opposite trend can be observed for C-CB and R-CB. This result might indicate that small banks appear to be more fragile over the post-pandemic period. However, they have differentiated ability in respond to the pandemic. For instance, the median NMEA scores for R-CB experienced an increase for variable Expense. This nevertheless cannot be observed in traditional efficiency results such as the Fig. 2, because the aggregated efficiency scores might neglect those information hidden in specific variables.

Finally, we demonstrate whether the efficiency scores are statistically different among the four types of groups. Following Zhao et al. (2021), we apply the Kruskal-Wallis H test for examining the efficiency differences across four types of banks. In addition, as the Mann–Whitney U text is suitable for comparing two independent samples, we further apply the Mann–Whitney U text to investigate differences between two groups in the four types of banks. Table 7 reports the detailed results. Based on this table, it is shown that we can reject the null hypothesis of equal efficiency scores among these four bank groups. This implies that there are significant differences between the four types of banks in the five discretionary variables.

However, from the results derived from the Mann–Whitney test, we can generally identify varied differences across different groups. Specifically, the MEA score difference for Employee is the result of differences between SOB and JS-CB, SOB and C-CB, SOB and R-CB, and JS-CB and C-CB. The NMEA score difference for Expense is the result of differences between SOB and JS-CB, SOB and C-CB, SOB and R-CB, JS-CB and R-CB, and C-CB and R-CB. Similar conclusions can be found in the final outputs. For example, the MEA score difference for good loan is the result of differences between SOB and JS-CB, SOB and C-CB, SOB and R-CB, JS-CB and C-CB, and C-CB and R-CB, while the difference for bad loan is the result of differences between SOB and JS-CB, SOB and C-CB, SOB and R-CB, and JS-CB and C-CB. Overall, the results shown in Table 7 generally conveys an important result that there are significant differences across different variable-specific efficiencies for different types of banks. This further confirms the importance of the proposed approach, as it is able to uncover efficiency differences in a more comprehensive way.

Table 7 Rank-sum test results of the efficiency differences of four types of banks

4.3 Sensitivity analysis

In this section, we would like to examine the impacts of stage weights on the efficiency results and then investigate how parameter $\epsilon$ affect the results.

4.3.1 Impact of stage weights on the two-stage NMEA results

In the proceeding analysis, we give the same priority to both the deposit-generating and loan subsystems, i.e., $w_1=w_2=0.5$. To better understand how these weights affect the estimation results, we further consider the following four cases to recalculate the overall and stage efficiencies of the concerned banks: (1) $w_1=0.1$ and $w_2=0.9$; (2) $w_1=0.3$ and $w_2=0.7$; (3) $w_1=0.7$ and $w_2=0.3$; (4) $w_1=0.9$ and $w_2=0.1$. Figure 4 shows the graph of rankings associated with the overall efficiencies in 2020. In the Appendix B, we also provide similar graphs for other years.

Fig. 4

Rankings of average overall efficiencies under different cases of stage weights

As shown in Fig. 4 we can find subtle changes in the estimation results of overall efficiencies. As noted in Zhao et al. (2021), if efficiency rankings determined by different scenarios are totally different, one may conclude that we have different estimation results. The similar results under these five cases imply that the impact of stage weights on the estimation results is limited. To further confirm this finding, following Zhao et al. (2021), we conduct the Friedman testing of the results in 2020. Details can be found in Table 8. The Friedman test results suggest that there are no significant ranking differences between the five cases both in terms of the overall efficiencies as well as in terms of two stage efficiencies. Further, we also conduct the Friedman test for other four years in the Appendix B. The results further confirm the above conclusions. In other words, the stage weights do have no significant impact on the rankings of banks both based on the overall efficiency and the stage efficiencies. Given these, the impacts of stage weights on the estimation results can be neglected in our concerned study. However, the manner in which $w_1$ and $w_2$ are determined may have an effect - even if it is limited - on the measurement of efficiency, which in turn affect the improvement strategies that DMUs should adopt. Thus, it is advisable to reach a consensus prior to assigning these weights.

4.3.2 Impact of parameter $\epsilon$ on the NMEA results

Before conducting sensitivity analysis associated with $\epsilon$, we would like to empirically illustrate the necessity of adopting parameter $\epsilon$. For example, if we set $\epsilon =0$, and then apply the data in 2020 to model (9). Table 9 presents the gaps between original values and those ideal values determined by models (6)–(8). As shown in the table, it is obvious that the ideal values associated with variables X1, X2, and Y for many banks are equal to their corresponding current observed values, i.e., obtain zero gap between original value and ideal value. For all these banks, model (9) obtains an unbounded solution. However, one can always guarantee a feasible solution by employing the proposed approach by introducing a strictly positive constant $\epsilon$.

Table 8 Friedman test results with different stage weights

To further investigate the impact of $\epsilon$ on the results of overall and stage efficiencies, we test the sensitivity of our baseline results to changes in values of $\epsilon$. Table 10 provides the detailed Pearson and Spearman correlation coefficients across different scenarios in terms of the overall and stage efficiencies in 2020. The tests for other years are provided in the Appendix C. For the overall and stage efficiencies, Tables 10 and 15 in Appendix C indicate that the effect of $\epsilon$ on efficiency results is limited, as the estimation results with different values of $\epsilon$ are highly correlated.

Table 9 Gaps between original values and ideal values in 2020

Table 10 Correlation tests between different values of $\epsilon$ in 2020

5 Conclusions

This paper proposes a novel two-stage NMEA approach to evaluate the performance of Chinese banks. Compared with existing studies, the proposed approach can not only guarantee a unique efficiency decomposition under a relatively mild condition, but also allow for efficiency analysis in each discretionary variable. Through this approach, one may be able togain insights into the complex banking system and make informed performance improvement initiatives.

The empirical results validate the usefulness of the proposed approach. Moreover, the paper also grasps several interesting conclusions. First, the average overall efficiency of Chinese listed banks is less than 0.6, suggesting that there is large room for improvement and that it might generate potential gains by improving the performance of Chinese listed banks. Second, the inefficiency is mainly sourced from the deposit-generating subsystem, which indicates that more attention should be paid to this stage so as to enhance the efficiency of Chinese listed banks as a whole. Third, different types of banks generally have different evolution modes over different dimensions. This cannot be observed in the analysis of traditional two-stage DEA models, which further emphasizes the importance of employing the proposed two-stage NMEA approach. Finally, the sensitivity analysis in terms of the weights attached to each stage and the changes in values of $\epsilon$ confirms the robustness of the proposed approach.

Future works can be extended in the following ways. First, it should be noted that the empirical study is conducted for the listed commercial banks operated in China. In fact, the proposed approach can also be applied to assess bank performance across different countries. We believe that this may convey more fruitful information on efficiency differences over different institutional environments.

Second, in our proposed model, we assume a basic two-stage network framework. In practice, we recognize that there may exist other structures which generally present more complex structure [See e.g., (Kao , 2014)]. Fortunately, the proposed approach can be easily adapted to these cases. As such, future works can potentially investigate how to extend the proposed approach to accounting for bank performance with other alternative network frameworks. Similarly, it is also interesting to apply the proposed approach to have more insights into the variable-specific (in)efficiency of other production systems.

Finally, the present study also has broad applicability. For example, it is of interests to extend the proposed approach to adopt advanced DEA methods such as additive/slack-based measures DEA (Wang et al., 2014), common set of weights DEA (Hammami et al., 2020), inverse DEA (Boubaker et al., 2022), Malmquist DEA (Asmild et al., 2016a), among others.

Appendix

1.1 Appendix A: Comparison to the case when the interest income is considered

In the main analysis, we focus on the loan procurement process. In theory, when all necessary data is available to characterize the real banking operational process, we can assess bank performance in a more accurate way. However, the practical situation often constrained by data availability. To isolate the impact of other potential factors, we thus focus primarily on the loan procurement process. Interestingly, as illustrated in the main context, one may also consider other potential outputs generated by the deposits. Specifically, the interest income can be as an alternative output that represents the ability of banks to generate income (Wang et al., 2014; Zhao et al., 2021). Though this indicator is composed of various incomes such as deposit income, loan interest, bond interest, arrears interest and other income, it can be proxy for the ability of banks who employ the deposits to generate income. So, one may concern that whether the incorporation of the interest income will significantly affect the estimation results or not.

Table 11 The overall efficiency results when the interest income is considered during 2016–2020

Following the same procedure as in the main analysis, we recalculate efficiencies of each bank during 2016–2020 based on models (6)–(9). Table 11 presents the results associated with the overall when the interest income is considered.

To illustrate differences between different practices of whether taking the interest income into account or not, we denote the case of the main analysis as Scenario A, while the case when the interest income is considered as Scenario B. Figure 5 shows the ranking comparison of average overall efficiency between scenarios A and B. The figure clearly demonstrates that most banks exhibit similar rankings, which implies that, though with slightly fluctuations, the practice of focusing on the loan process can exactly capture the relative position of overall NMEA scores of most banks by using the proposed approach.

Fig. 5

Ranking comparison of average overall efficiency between scenario A and scenario B

Table 12 contains the results of stage efficiency scores when the interest income is considered. We can also confirm similar conclusions the same as those obtained from the overall NMEA efficiency.

To further confirm the relevance of both scenarios, we also conduct the correlation tests of the overall efficiency results from 2016 to 2020. Table 13 provides the detailed Pearson and Spearman correlation coefficients in terms of the overall NMEA efficiency over the sample period. Table 13 indicates that the overall NMEA scores obtained from scenario A and scenario B have a closer association with the relative measure of bank performance.

Table 12 The stage efficiency results when the interest income is considered during 2016–2020

Table 13 Correlation tests between scenario A and scenario B during 2016–2020

1.2 Appendix B: Sensitivity analysis of stage weights on the two-stage NMEA results during 2016–2019

In the main analysis, we provide rankings of overall NMEA scores in 2020 under different cases of stage weights. In this appendix, we further provide ranking comparisons of overall NMEA scores for other four years. Figures 6,  7, 8 and 9 depict rankings of overall efficiency scores under different cases of stage weights in 2016, 2017, 2018, and 2019, respectively.

As can be seen from Figs. 6, 7, 8 and 9, we also find subtle changes in the estimation results with respect to the overall NMEA scores. Further, we also conduct Friedman tests for the remaining four years. Table 14 clearly indicates that there are no significant ranking differences between the five cases in terms of both overall NMEA scores and stage NMEA scores during 2016–2019. Given these, we can conclude that the stage weights do have no significant impact on the rankings of banks and can be neglected in our concerned study.

Fig. 6

Rankings of overall efficiency scores in 2016 under different cases of stage weights

Fig. 7

Rankings of overall efficiency scores in 2017 under different cases of stage weights

Fig. 8

Rankings of overall efficiency scores in 2018 under different cases of stage weights

Fig. 9

Rankings of overall efficiency scores in 2019 under different cases of stage weights

1.3 Appendix C: Impact of parameter $\epsilon$ on the two-stage NMEA results during 2016–2019

Table 15 provides the correlation tests between different values of $\epsilon$ during 2016–2019. From this table, we can clearly obtain similar conclusions as those in the main analysis. That is, the ranking results under different values of $\epsilon$ are distinctly correlated. That is, the choice of different values of $\epsilon$ generally has limited impact on the NMEA ranking results.

Table 14 Friedman test results with different stage weights

Table 15 Correlation tests between different values of $\epsilon$