1 Introduction

COVID-19 was first diagnosed in Wuhan, China, in December 2019 and then quickly spread throughout the world. The subsequent unique and unprecedented COVID-19 pandemic has inflicted devastating damage on the world economy, people’s health, jobs, and lives, and put the entire globe on hold for almost a year. According to official statistics, by April 2022, over 484 million COVID-19 cases and 6,152,000 deaths had been reported to World Health Organisation (WHO). Furthermore, the COVID-19 pandemic outbreak has negatively affected global economic growth. Estimations show that it could have reduced growth of the world’s economy by 6.0% in 2020, despite partial improvement in 2021 and 2022, presuming no waves of reinfection. Due to the pandemic, the risks of a global economic slump are rising dramatically and unemployment has been rising at an unprecedented rate since the Great Depression of the 1930s. The human and economic costs such as death, poverty, and social unrest are only some examples of the devastation wrought by the COVID-19 pandemic.

One particularly affected area by the COVID-19 pandemic is supply chains (SCs). SCs are experiencing unparalleled vulnerabilities and disruptions (Zahedi et al., 2021). This type of pandemic can cause many parts of an SC to be inoperable and inefficient for an uncertain period (Govindan et al., 2020). The spread of the COVID-19 pandemic around the globe shows the importance and essential role of resilient SCs in supplying products and providing services to the world. The pandemic is testing the features of resilient SCs such as flexibility, robustness, and recovery (Elluru et al., 2019; Sharmin et al., 2021). Moreover, many organisations use the opportunity of this unprecedented crisis to adopt global SCs strategies and address sustainability in order to mitigate future challenges (Karmaker et al., 2020). Integrating sustainable and resilient concepts into SCs—including those of healthcare—is critical for organisations. Even so, the literature has not adequately addressed these concepts in healthcare SCs.

Efficiency assessment of healthcare SCs in the face of pandemic outbreaks, particularly COVID-19, can support healthcare systems to identify the existing inefficiencies. Disruptions in healthcare SCs, due to the surge of demand, can severely affect the performance of healthcare systems, leading to a substantial increase in the number of infected people and death. To mitigate the destructive impacts of COVID-19, different stages of healthcare SC such as suppliers, hospitals, and pharmacies need to act efficiently and resiliently. To benefit from an efficient healthcare system, each stage of healthcare SCs should use the available resources, reduce waste, provide timely services, and control process costs (Göleç & Karadeniz, 2020; Min et al., 2021). It should be noted that developing state-of-the-art performance evaluation approaches can assist healthcare managers to enhance the performance of healthcare systems in disaster management such as the COVID-19 epidemic (Md Hamzah et al., 2021).

Operating under uncertainty, resource scarcity, and demands surge are major issues for SCs in face of pandemic outbreaks. In this regard, Operations Research (OR) approaches and models are of huge importance (Besiou et al., 2018). Data envelopment analysis (DEA) derived from OR is a rigorous nonparametric approach to measure efficiency in many areas such as healthcare and humanitarian supply chains (Jola-Sanchez et al., 2016). DEA is the most accepted method to evaluate efficiency (Emrouznejad & Yang, 2018). Since the outbreak of COVID-19 in December 2019, the performance of healthcare SCs has been adversely affected. Under such turbulent circumstances, it is essential to develop and apply OR advanced methods such as network DEA to identify inefficiency sources and performance improvement in healthcare systems.

In this paper we deal with some research questions as follows: (1) how sustainability and resilience of healthcare supply chains can be evaluated in response to the COVID-19 pandemic outbreak? (2) how dissimilar types of data can be modeled in network structures? (3) to what extent sustainability and resilience of healthcare supply chains are changed under different conditions?

The main objective of this paper is to measure the sustainability and resilience of healthcare SCs in the face of the COVID-19 pandemic. Our proposed approach is built based on the range directional measure (RDM) model in the network DEA context. Furthermore, the developed model can deal with ratio data, integer data, stochastic data, negative data, undesirable data, and zero data. In sum, and to the best of our knowledge, this study makes the following contributions:

  • To assess the sustainability and resilience of healthcare SCs, we propose a novel non-radial RDM network model.

  • Our proposed approach can address different types of data such as ratio, integer, undesirable, stochastic, negative, and zero, simultaneously.

  • Our proposed approach recommends how to improve the efficiency of healthcare SCs.

  • We have validated this approach using a case study.

The rest of this paper is organised as follows. In Sect. 2, we provide the literature review. In Sect. 3, we present our approach, followed by the case study in Sect. 4. Finally, we conclude and propose possible future research in Sect. 5.

2 Literature review

2.1 Pandemic outbreaks and healthcare supply chains (SCs)

Healthcare SCs play a key role in providing required medical devices and services to people (Leite et al., 2020). After a pandemic disease, medical assistance is needed instantaneously (Verma & Gustafsson, 2020). The COVID-19 pandemic has adversely affected healthcare SCs. Pandemic diseases including COVID-19 and SARS are considered a specific type of risk to SCs. In epidemic outbreaks, efficient healthcare SCs can supply not only medical equipment but also mitigate disruptions (Rainisch et al., 2020). The outbreak of a pandemic disease quickly increases the demand for medical assistance (Dolinskaya et al., 2018). Healthcare SCs cannot be efficient when there is high uncertainty in demand (Hoyos et al., 2015). Moreover, due to the complexity of the structures of healthcare SCs, any unexpected event results in considerable changes to the services provided to patients (Md Hamzah et al., 2021). For example, inaccurate evaluations of needs can lead to shortages in crucial medical devices and services. However, efficient transportation systems in healthcare SCs improve inventory and capacity (Ruan, et al., 2014).

2.2 Efficiency measurement in healthcare SCs

The literature does address efficiency measurement somewhat in healthcare SCs. Chen et al. (2013) examined the effect of hospital–supplier incorporation on SC efficiency. Their study showed the effect of knowledge exchange, trust, and information technology (IT) integration on hospital SCs. Al-Saa'da et al. (2013) evaluated different aspects of SCs such as compatibility, relationship with suppliers, standards, requirements, and delivery of quality healthcare services. They demonstrated the important impact of these aspects on the quality of healthcare services. They also showed that there are no differences between SCM and the quality of health services owing to different factors. Nyaga et al. (2015) investigated the influence of internal and external factors on the performance of healthcare SCs. They used the data for more than 200 hospitals in the US over several consecutive years to estimate regression models. They demonstrated that employing physicians and managing contracts improved the efficiency of healthcare SCs.

Supeekit et al. (2016) used the analytic network process (ANP) for evaluating the efficiency of hospital SCs. They examined the interdependencies between efficiency groups. They demonstrated that the completeness of treatment and processing times of clinical care is the most significant dimension of hospital SCs. Chorfi et al. (2019) presented a DEA model to measure the efficiency of healthcare SCs in the presence of interval data. To do so, first, they used the Latin hypercube sampling by replacement (LHSR) method for identifying a set of deterministic data from interval data; then they used DEA models to evaluate the efficiency of healthcare SCs. To evaluate the performance of sustainable healthcare SCs, Leksono et al. (2019) integrated a balanced scorecard (BSC), a decision-making trial, an evaluation laboratory (DEMATEL), and ANP techniques. They showed that the customer perspective is the most significant factor in the performance evaluation of healthcare SCs. Göleç and Karadeniz (2020) presented a fuzzy model to analyse the efficiency of healthcare SCs concerning competency-based operation assessment. They took the hierarchical structure of healthcare SCs such as processes and sub-processes into account in their proposed method. They also used two levels for evaluating processes and sub-processes. Gerami et al. (2020) presented a network DEA-R model to assess the performance of healthcare SCs. They modelled relations between the different layers of healthcare SCs based on network DEA and free-link and fixed-link assumptions. Md Hamzah et al. (2021) examined the performance of healthcare systems in Malaysia in the face of the COVID-19 epidemic. To address this issue, they applied a network DEA model using a secondary data. Md Hamzah et al.’s (2021) proposed network structure for evaluating the performance of the healthcare systems consisted of three stages. Min et al. (2021) sought to detect the sources of the success and failure of COVID-19 control measures and to enhance public health policies aimed at decreasing COVID-19 spread. They assessed the efficiency of different combinations of COVID-19 control measures and public health polices in OECD countries by focusing on the country-specific factors of government COVID-19 preventive measures in OECD countries. In doing so, they detected influential cultural variables. Although the above studies investigated performance evaluation of healthcare SCs from different perspectives, none of them evaluated the sustainability or resilience of healthcare SCs in response to a pandemic outbreak such as SARS and COVID-19.

2.3 Data envelopment analysis (DEA)

DEA has been recognised as the most rigorous and accepted method for measuring the relative efficiency of a set of decision-making units (DMUs). DEA forms an efficient combination of inputs and outputs to make an efficient frontier (Ayanso & Mokaya, 2013; Troutt et al., 2000). A DMU is efficient if it lies on the efficiency frontier; otherwise, it is inefficient. Charnes et al. (1978) (CCR) and Banker et al. (1984) (BCC) are two basic DEA models. Because of the advantages of DEA, it has been used in many areas over the last decades (Emrouznejad & Yang, 2018). However, there are some issues with standard DEA models. Firstly, there might be ratio data in performance evaluations. To deal with the ratio data, some approaches have been developed by scholars (e.g., Emrouznejad & Amin, 2009; Hatami-Marbini & Toloo, 2019; Henriques et al., 2020; Hollingsworth & Smith, 2003). Furthermore, the traditional DEA models assume that all the values are real numbers. Nevertheless, in many real-world applications, there might be integer inputs and outputs. To address this issue, Lozano and Villa (2006) were the first to propose integer-valued DEA. Matin and Kuosmanen (2009) improved the model proposed by Lozano and Villa (2006). Over the last few years, there has been some research in the field of DEA and integer data (Azadi & Farzipoor Saen, 2014; Chen et al., 2012; Khoveyni et al., 2019; Kordrostami et al., 2019; Wu & Zhou, 2015). Moreover, the conventional DEA models assume that the inputs and outputs are positive, while there might be negative and zero data. Our literature survey shows that over the last few years, some scholars have endeavoured to tackle this issue (e.g., Allahyar & Rostamy-Malkhalifeh, 2015; Charnes et al., 1985; Chen & Liang, 2011; Cheng et al., 2013; Emrouznejad et al., 2010; Izadikhah & Farzipoor Saen, 2016; Khoveyni et al., 2017; Lee & Zhu, 2012; Lin & Chen, 2018; Portela et al., 2004; Tavana et al., 2018; Tavassoli et al., 2015). Indeed, a weakness of standard DEA models is their inability to address uncertainty in data. To deal with stochastic data, some research has been conducted by Land et al. (1993), Olesen and Petersen (1995), Azadi and Farzipoor Saen (2011), and Izadikhah et al. (2020).

On the other hand, traditional DEA models deal with black box DMUs and ignore the internal components of DMUs. It is argued that ignoring the internal structure of DMUs may lead to misleading results (Mirhedayatian et al., 2014). For the first time, Färe and Grosskopf (1996) developed the network DEA. Since then, network DEA has been used in many areas (e.g., Azadi et al., 2014; Izadikhah et al., 2019; Kao & Hwang, 2010; Lewis & Sexton, 2004; Matin et al., 2022; Samavati et al., 2020). Recently, network DEA has been applied successfully to measure sustainable, resilient SCs (see Izadikhah et al., 2019; Matin et al., 2022; Goodarzian et al., 2021).

2.4 Research gaps

Despite the importance of evaluating healthcare SCs, our literature review shows that little research has been done, particularly in the face of a pandemic outbreak. On the other hand, the current approaches do not take both the sustainability and resilience aspects into account in the efficiency assessment of healthcare SCs. This is while addressing sustainability and resilience aspects in performance evaluation of SCs in other areas has been a hot topic for scholars and managers. In addition, many current approaches are not suitable for uncertain situations such as epidemic outbreaks in which there are unexpected and extreme disruptions in SCs. It should be noted that uncertainty in SCs is a specific type of risk management. Moreover, none of the existing approaches can deal with different types of data, including ratio, integer, stochastic, negative, and zero in efficiency measurement of DMUs. To address these gaps in the literature we propose a new network DEA for evaluating the sustainability and resilience of healthcare SCs in response to the COVID-19 pandemic outbreak.

3 Proposed method

In this section, we develop our new model to evaluate the sustainability and resilience of healthcare SCs in response to the COVID-19 pandemic outbreak. Table 1 depicts the used notation.

Table 1 The notations
Full size table

Izadikhah and Farzipoor Saen (2016) developed a network RDM model in the presence of negative data. They dealt with negative data as absolute values. Tavana et al. (2018) proposed a dynamic network RDM model in the presence of desirable and undesirable carry-overs as well as negative data. In this paper, given the models proposed by Izadikhah and Farzipoor Saen (2016) and Tavana et al. (2018), a novel network RDM model based on the non-radial directional distance function is developed. Moreover, the novel model takes into account the non-radial changes by which all the inefficiencies in inputs, outputs, and intermediate measures are considered. Furthermore, the intermediate measures as outputs of the first stage and inputs of the second stage are discussed from different aspects. More importantly, our proposed model can simultaneously deal with stochastic data, integer data, zero data, negative data, ratio data, and undesirable outputs.

Assume that the stochastic factors are normally distributed. In the classical DEA approaches, the ratio data are converted to the fractions, and the numerator is considered as output and the denominator is considered as input. Despite the classical DEA approaches, here, the ratio data are dealt with directly. For the ratio inputs, the reduced inputs should be less than or equal to 100%. However, since the inputs should be reduced, no need to add a constraint to ensure that the reduced inputs should be less than or equal to 100%.

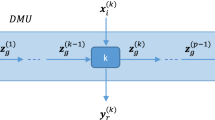
To deal with the negative data, one of the very first models mathematically formulated in DEA is the RDM model developed by Portela et al. (2004). There exist other papers that extended the basic RDM model. Here, the models of Portela et al. (2004) and Tavana et al. (2018) are extended. To consider all the factors’ inefficiencies in the stages, the non-radial changes of factors are taken into account. Note that the intermediate measures as inputs of stage 2 are considered less than or equal to the outputs of stage 1. Also, the ranges are determined for the undesirable outputs. Finally, the integer data and the stochastic data are dealt with. Figure 1 shows a network with two stages.

Fig. 1
figure 1

A two-stage network

Full size image

As is seen in Fig. 1, the intermediate measure \(z_{f}\) is the output of stage 1 and the input of stage 2. In the intermediate measures, there might be stochastic elements as denoted by \(\tilde{z}_{f} , \forall f \in F_{2}\). The other intermediate measures are integer \(z_{f} , \forall f \in F_{1} .\) The \(x_{i}^{1} , i \in I_{1}\) is a deterministic input of stage 1. The \(x_{i}^{2} , i \in I_{2}\) is a deterministic input of stage 2. The \(x_{i}^{2} , i \in I_{3}\) is an integer input of stage 2. Consider that \(I_{1} \cup I_{2} \cup I_{3} = I\). Also, some outputs of stage 2 might be undesirable \(y_{r}^{2} , r \in R_{1}\) and some might be an integer \(y_{r}^{2} , r \in R_{2}\). The rest can be deterministic and desirable outputs \(y_{r}^{2} , r \in R_{3}\). Note that \(R_{1} \cup R_{2} \cup R_{3} = R\) and \(F_{1} \cup F_{2} = F\).

Given Expression (1), in model (4), the ranges of inputs and outputs of stage 1 are incorporated. All the ranges are non-negative. The outputs of stage 1 \((f \in F_{2} )\), the intermediate measures, are stochastic and have a normal distribution.

$$ \begin{gathered} R_{io}^{1x} = x_{io}^{1} - \min \{ x_{ij}^{1} |\forall j\} ,\quad \forall i \in I_{1} ; \hfill \\ Q_{fo}^{1z} = \max \left\{ {z_{fo} |\forall j} \right\} - z_{fo} ,\quad \forall f \in F_{1} ;\quad \tilde{R}_{fo}^{1z} = \max \left\{ {\tilde{z}_{fo} |\forall j} \right\} - \tilde{z}_{fo} , \quad \forall f \in F_{2} ; \hfill \\ \end{gathered} $$
(1)

Given Expression (2), in model (5), the ranges of inputs and outps of stage 2 are incorporated.

$$ \begin{gathered} {\text{R}}_{io}^{2x} = x_{io}^{2} - \min \{ x_{ij}^{2} |\forall j\} ,\quad \forall i \in I_{2} \cup I_{3} ;\quad Q_{fo}^{2z} = z_{fo} - \min \left\{ {z_{fj} |\forall j} \right\},\quad \forall f \in F_{1} \hfill \\ {\tilde{\text{R}}}_{fo}^{2z} = \tilde{z}_{fo}^{{}} - \min \left\{ {\tilde{z}_{fj}^{{}} |\forall j} \right\},\quad \forall f \in F_{2} ;\quad R_{ro}^{2y} = \max \left\{ {y_{rj}^{2} |\forall j} \right\} - y_{ro}^{2} ,\quad \forall r \in R_{2} \cup R_{3} ; \hfill \\ {\text{G}}_{ro}^{2y} = y_{ro}^{2} - \min \left\{ {y_{rj}^{2} |\forall j} \right\},\quad \forall r \in R_{1} \hfill \\ \end{gathered} $$
(2)

Note that the range of ith input of DMUo in Expressions (1) and (2) equals the deduction of the smallest ith input of all DMUs from the ith input of DMUo. Since consuming less input is better, the smallest ith input is considered in Expressions (1) and (2). Also, the range of rth output of DMUo in Expressions (1) and (2) equals the deduction of the biggest rth output of all DMUs from the rth output of DMUo. Since more output is better, the biggest rth output is considered in Expressions (1) and (2). Thus, there is no improvement room for the inputs and outputs that their ranges are zero. Note that since \({y}_{r}^{2}, r\in {R}_{1}\) is an undesirable output, its range is defined as input.

The intermediate measures can be outputs of stage 1 and inputs of stage 2. If the intermediate measures are inputs, then Expression (2) is used. If the intermediate measures are outputs, then Expression (1) is used.

Expression (3) is the modified objective function of the RDM model. Despite the classical RDM model, Expression (3) deals with the non-radial changes of inputs, outputs, and intermediate measures. Thus, it can incorporate all the factors' inefficiencies into the model.

$$ Max\;\rho = \sum\limits_{{i \in I_{1} }} {\beta_{i}^{1x} } + \sum\limits_{{f \in F_{1} }} {\gamma_{f}^{1z} } + \sum\limits_{{f \in F_{2} }} {\dot{\gamma }_{f}^{1z} } + \sum\limits_{{i \in I_{2} \cup I_{3} }} {\beta_{i}^{2x} } + \sum\limits_{{f \in F_{2} }} {\dot{\tau }_{f}^{2z} } + \sum\limits_{{f \in F_{1} }} {\tau_{f}^{2z} } + \sum\limits_{{r \in R_{2} \cup R_{3} }} {\delta_{r}^{2y} } + \sum\limits_{{r \in R_{1} }} {\dot{\delta }_{r}^{2y} } $$
(3)

Model (4) is developed for stage 1. Constraint (b) corresponds with the non-radial reduction of ratio inputs. To deal with ratio inputs, we set the corresponding reductions in a way that its reduced input remains between 0 and 100%. Thus, \(0 \le {\text{x}}_{io}^{1} - \beta_{i}^{1x} {\text{R}}_{io}^{1x} \le 100\) should be added to the model. However, since the inputs are supposed to be decreased, the constraint is redundant and can be omitted. Constraints (c) are related to the integer outputs of stage 1. In constraints (c), the corresponding improved factor gets integer values. Thus, \(l_{f}^{1} = z_{fo} + \gamma_{f}^{1z} {\text{Q}}_{fo}^{1z}\) is considered in the model where \(l_{f}^{1} \in Z\). Constraint (d) is associated with the stochastic outputs of stage 1. Constraints (e) imply the variable returns to scale (VRS) assumption and the non-negativity of the variables. Note that the objective function of model (4) is similar to (3). The only difference is that the objective function of model (4) deals with stage 1.

$$ \begin{array}{*{20}l} {Max\;\rho = \sum\limits_{{i \in I_{1} }} {\beta_{i}^{1x} } + \sum\limits_{{f \in F_{1} }} {\gamma_{f}^{1z} } + \sum\limits_{{f \in F_{2} }} {\dot{\gamma }_{f}^{1z} } } \hfill & {} \hfill & {(a)} \hfill \\ {s.t.} \hfill & {} \hfill & {} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} x_{ij}^{1} \le x_{io}^{1} - \beta_{i}^{1x} R_{io}^{1x} ,} \hfill & {\forall i \in I_{1} } \hfill & {(b)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} z_{fj} \ge l_{f}^{1} \;l_{f}^{1} = z_{fo} + \gamma_{f}^{1z} Q_{fo}^{1z} ,} \hfill & {\forall f \in F_{1} } \hfill & {(c)} \hfill \\ {P\left( {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} \ge \tilde{z}_{fo} + \dot{\gamma }_{f}^{1z} \tilde{R}_{fo}^{1z} } \right) \ge 1 - \alpha ,} \hfill & {\forall i \in F_{2} } \hfill & {(d)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} = 1, \lambda_{j}^{1} \ge 0,\beta_{i}^{1x} \ge 0,\dot{\gamma }_{f}^{1z} \ge 0,\gamma_{f}^{1z} \ge 0,l_{f}^{1} \in Z} \hfill & {\forall j,\forall i,\forall f} \hfill & {(e)} \hfill \\ \end{array} $$
(4)

Now, model (5) is developed for stage 2. The objective function of model (5) deals with stage 2. Constraint (f) is associated with the external inputs (\(i \in I_{2}\)) of stage 2, which are reduced non-radially. Constraints (g) are related to the integer external inputs (\(i \in I_{3}\)) of stage 2. In Constraints (g), the corresponding improved factor gets integer values. Thus, \(a_{i}^{2} = x_{io}^{2} - \beta_{i}^{2x} R_{io}^{2x}\), where \(a_{i}^{2} \in Z\) is added to the model. Constraints (h) correspond to integer intermediate measures (\(F \in F_{1}\)). For this constraint, the corresponding improved factor gets integer values. Thus, \(l_{f}^{2} = z_{fo}^{{}} - \dot{\tau }_{f}^{2z} Q_{fo}^{2z}\), where \(l_{f}^{2} \in Z\) is added to the model. Constraint (l) is associated with the stochastic intermediate measure. Constraints (p) are related to the integer and undesirable outputs of stage 2, which are considered inputs of stage 2. Note that according to the definition of ranges in (2), the range of undesirable outputs is similar to the range of inputs. Constraints (q) are associated with the integer outputs of stage 2. The corresponding improved factor gets integer values. Thus, \(s_{r}^{2} = y_{ro}^{2} + \delta_{r}^{y} R_{ro}^{y} \in Z, r \in R_{2}\) is added to the model. Constraint (t) is related to the outputs of stage 2, which can be positive, zero, and negative. Constraints (u) and (w) imply the VRS and the non-negativity of the variables.

$$ \begin{array}{*{20}l} {Max\; \rho = \sum\limits_{{i \in I_{2} \cup I_{3} }} {\beta_{i}^{2x} } + \mathop \sum \limits_{{f \in F_{2} }} \dot{\tau }_{f}^{2z} + \mathop \sum \limits_{{f \in F_{1} }} \tau_{f}^{2z} + \sum\limits_{{r \in R_{2} \cup R_{3} }} {\delta_{r}^{2y} } + \sum\limits_{{r \in R_{1} }} {\dot{\delta }_{r}^{2y} } } \hfill & {} \hfill & {} \hfill \\ {s.t.} \hfill & {} \hfill & {} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} x_{ij}^{2} \le x_{ij}^{2} - \beta_{i}^{2x} R_{io}^{2x} ,} \hfill & {\forall i \in I_{2} } \hfill & {(f)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} x_{ij}^{2} \le a_{i}^{2} ,\; a_{i}^{2} = x_{io}^{2} - \beta_{i}^{2x} R_{io}^{2x} ,} \hfill & {\forall i \in I_{3} ,} \hfill & {(g)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} z_{fj} \le l_{f}^{2} ,\; l_{f}^{2} = z_{fo} - \dot{\tau }_{f}^{2z} Q_{fo}^{2z} } \hfill & {\forall f \in F_{2} ,} \hfill & {(h)} \hfill \\ {P \left( {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} \tilde{z}_{fj} \le \tilde{z}_{fo} - \tau_{f}^{2z} \tilde{R}_{fo}^{2z} } \right) \ge 1 - \alpha ,} \hfill & {\forall f \in F_{1} ,} \hfill & {(l)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \le t_{r}^{2} ,\;t_{r}^{2} = y_{ro}^{2} - \dot{\delta }_{r}^{y} G_{ro}^{y} ,} \hfill & {\forall r \in R_{1} ,} \hfill & {(p)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \ge s_{r}^{2} ,\; s_{r}^{2} = y_{ro}^{2} + \delta_{r}^{y} R_{ro}^{y} ,} \hfill & {\forall r \in R_{2} ,} \hfill & {(q)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \ge y_{ro}^{2} + \delta_{r}^{2y} R_{ro}^{2y} , } \hfill & {\forall r \in R_{3} ,} \hfill & {(t)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} = \lambda_{j}^{2} \ge 0,\;\beta_{i}^{2x} \ge 0,\delta_{r}^{2y} \ge 0,l_{f}^{2} , t_{r}^{2} ,s_{r}^{2} , a_{i}^{2} \in Z} \hfill & {\forall j,i,r,} \hfill & {(u)} \hfill \\ {\tau_{f}^{2z} \ge 0,\;\dot{\tau }_{f}^{2z} \ge 0, \;\dot{\delta }_{r}^{2y} \ge 0} \hfill & {\forall f,r,} \hfill & {(w)} \hfill \\ \end{array} $$
(5)

If the range of inputs and outputs, for each stage, is zero, then there is no room for improvement as these already include the smallest and the largest outputs. Thus, it is clear that there is no room for reducing the inputs and increasing the outputs. Therefore, their associated variables \(\beta_{i}^{1x} ,\dot{\gamma }_{f}^{1z} ,\gamma_{f}^{1z}\), \(\beta_{i}^{2x} ,\tau_{f}^{2z} ,\dot{\tau }_{f}^{2z} , \dot{\delta }_{r}^{2y} ,\) and \(\delta_{r}^{2y}\) are zero. To deal with stochastic data, chance-constrained programming is one of the main methods in DEA (Cooper et al., 2002).

Lemma 1

Constraint (d) of model (4) is converted to the deterministic constraint as follows:

$$ P\left( {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} \ge \tilde{z}_{fo} + \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right) \ge 1 - \alpha ,\quad \forall f \in F_{2} , $$
(6)

where \(\alpha\) shows the risk level, which is between 0 and 1. The \(\tilde{z}\) and \({\tilde{\text{R}}} \) random variables.

Constraint (d) can be written as follows:

$$ P\left( {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \tilde{R}_{fo}^{1z} \ge 0} \right) \ge 1 - \alpha ,\quad \forall f \in F_{2} , $$
(7)

Assume that S is a random variable and d, a, e, and c are constants. If \(P\left( {S \ge d} \right) = c\) and \(e > d\), then the numbers like \(a < c\) can be found where \(P\left( {S \ge e} \right) = a\) (Hosseinzadeh Lotfi et al., 2011). Thus, for each f, constraint (7) can be written as follows:

$$ P\left( {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \tilde{R}_{fo}^{1z} \ge 0} \right) = 1 - \alpha + \varepsilon_{f} ,\quad \forall f \in F_{2} , $$
(8)
$$ P\left( {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;{\tilde{\text{R}}}_{fo}^{1z} \ge {\text{S}}_{f} } \right) = 1 - \alpha ,\quad \forall f \in F_{2} , $$
(9)

Assuming \(\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \tilde{R}_{fo}^{1z} = h_{f}\), we have

$$ P\left( {\frac{{h_{f} - E\left( {\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right) }}{{\sqrt {Var\left( {\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right)} }} \le \frac{{S_{f} - E\left( {\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right) }}{{\sqrt {Var\left( {\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right)} }}} \right) = \alpha, \forall f \in F_{2},$$
(10)

Assume that \({D}_{f}\) is defined as follows:

$$ D_{f} = \frac{{h_{f} - E\left( {\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \tilde{R}_{fo}^{1z} } \right)}}{{\sqrt {Var\left( {\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \tilde{R}_{fo}^{1z} } \right)} }},\quad \forall f \in F_{2} , $$
(11)

Expression (10) can be rewritten as follows:

$$ P\left( {D_{f} \le \frac{{S_{f} - E\left( {\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right)}}{{\sqrt {Var\left( {\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right)} }}} \right) = \alpha , \quad \forall f \in F_{2} , $$
(12)

The \(\varphi\) is the cumulative function of normal distribution and \(\overline{z}\) is the average of \(\tilde{z}\). The \(\sigma\) is the standard deviation. As discussed by Cooper et al. (2002), Expression (12) can be written as follows:

$$ \varphi \left( {\frac{{S_{f} - \mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} + \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \;\overline{R}_{fo}^{1z} }}{{\sqrt {Var\left( {\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right)} }}} \right) = \alpha ,\quad \forall f \in F_{2} , $$
(13)

Given \(\alpha \), the inverse of the cumulative distribution function \((\varphi )\) is as follows:

$$ \varphi^{ - 1} \left( \alpha \right) = \frac{{S_{f} - \mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} + \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \;\overline{R}_{fo}^{1z} }}{{\sqrt {Var\left( {\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right)} }} = \frac{{S_{f} - \mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} + \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \;\overline{R}_{fo}^{1z} }}{{\sigma_{f} \left( {\lambda^{1} ,\dot{\gamma }} \right)}},\quad \forall f \in F_{2} , $$
(14)

where

$$ \sqrt {Var\left( {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right)} = \sigma_{f} \left( {\lambda^{1} ,\dot{\gamma }} \right),\quad \forall f \in F_{2} , $$
(15)

Thus, we have

$$ S_{f} + \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \overline{R}_{fo}^{1z} = \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} + \varphi^{ - 1} \left( \alpha \right)\sigma_{f} \left( {\lambda^{1} ,\dot{\gamma }} \right),\quad \forall f \in F_{2} , $$
(16)

Note that, in the optimisation models, the stochastic relations are replaced by Expression (16). Given the \(\sigma_{f} \left( {\lambda^{1} ,\dot{\gamma }} \right)\), it is clear that Expression (16) is quadratic. Using the following expression, Expression (16) can be simplified as follows:

$$ S_{f} + \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \overline{R}_{fo}^{1z} \ge 0,\;S_{f} \ge 0,\quad \forall f \in F_{2} , $$
(17)

As a result, constraint (d) in model (4) can be written as follows:

$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} + \varphi^{ - 1} \left( \alpha \right)\sigma_{f} \left( {\lambda^{1} ,\dot{\gamma }} \right) \ge \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \;\overline{R}_{fo}^{1z} ,\quad \forall f \in F_{2} , $$
(18)

To calculate the variance of the outputs we have

$$ \begin{aligned} \sigma_{f}^{2} \left( {\lambda^{1},\dot{\gamma }} \right) &= Var\left( {\mathop \sum \limits_{j =1}^{n} \lambda_{j}^{1} \tilde{z}_{fj} - \tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right) = Var\left( {\mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne o} \\ \end{array}}}^{n} \lambda_{j}^{1} \tilde{z}_{fj} + (\lambda_{o}^{1} -1)\tilde{z}_{fo} - \dot{\gamma }_{f}^{1z} \tilde{R}_{fo}^{1z} }\right) \\&\quad \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\{j \ne o} \\ \end{array} }}^{n} \left( {\lambda_{j}^{1} }\right)^{2} Var\left( {\tilde{z}_{fj}^{{}} } \right) +(\lambda_{o}^{1} - 1)^{2} Var\left( {\tilde{z}_{fo}^{{}} } \right) +\left( {\dot{\gamma }_{f}^{1z} } \right)^{2} Var\left( {\tilde{R}_{fo}^{1z} } \right) \\&\quad + 2COV\left( {\mathop \sum \limits_{j = 1}^{n}\lambda_{j}^{1} \tilde{z}_{fj} ,(\lambda_{o}^{1} - 1)\tilde{z}_{fo}} \right) 2COV\left( {\mathop \sum \limits_{j = 1}^{n}\lambda_{j}^{1} \tilde{z}_{fj} ,\dot{\gamma }_{f}^{1z}\;,\tilde{R}_{fo}^{1z} } \right)\\&\quad - 2COV\left( {(\lambda_{o}^{1} - 1)\tilde{z}_{fo},\dot{\gamma }_{f}^{1z} \;\tilde{R}_{fo}^{1z} } \right),\quad \forall f \in F_{2},\end{aligned} $$
(19)

For simplicity, the covariance is assumed to be zero and the following expression is obtained:

$$ \sigma_{f}^{2} \left( {\lambda^{1} ,\dot{\gamma }} \right) = \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne o} \\ \end{array} }}^{n} (\lambda_{j}^{1} )^{2} Var\left( {\tilde{z}_{fj} } \right) + (\lambda_{o}^{1} - 1)^{2} Var\left( {\tilde{z}_{fo} } \right) + \left( {\dot{\gamma }_{f}^{1z} } \right)^{2} Var\left( {\tilde{R}_{fo}^{1z} } \right),\quad \forall f \in F_{2} $$
(20)

For the other stochastic constraints of stage 2, the final variance is as follows:

$$ \sigma_{f}^{2} \left( {\lambda^{2} ,\tau } \right) = \mathop \sum \limits_{{\begin{array}{*{20}c} {j = 1} \\ {j \ne o} \\ \end{array} }}^{n} (\lambda_{j}^{2} )^{2} Var\left( {\tilde{z}_{fj} } \right) + (\lambda_{o}^{2} - 1)^{2} Var\left( {\tilde{z}_{fo} } \right) + \left( {\tau_{f}^{2z} } \right)^{2} Var\left( {\tilde{R}_{fo}^{2z} } \right),\quad \forall f \in F_{2} $$
(21)

Using the chance-constrained programming approach, constraint (d) in model (4) and constraints (l) and (h) in model (5) can be written as follows:

$$ \begin{gathered} \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} + \varphi^{ - 1} \left( \alpha \right)\;\sigma_{f} \left( {\lambda^{1} ,\dot{\gamma }} \right) \ge \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \;\overline{R}_{fo}^{1z} ,\quad \forall f \in F_{2} \hfill \\ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} \overline{z}_{fj} - \varphi^{ - 1} \left( \alpha \right)\;\sigma_{f} \left( {\lambda^{2} ,\tau } \right) \le \overline{z}_{fo} - \tau_{f}^{2z} \;\overline{R}_{fo}^{2z} ,\quad \forall f \in F_{2} \hfill \\ \end{gathered} $$
(22)

Models (4) and (5) are quadratic programming problems, and their deterministic versions are presented in models (23) and (24).

$$ \begin{array}{*{20}l} {Max\;\rho = \sum\limits_{{i \in I_{1} }} {\beta_{i}^{1x} } + \sum\limits_{{f \in F_{1} }} {\gamma_{f}^{1z} } + \sum\limits_{{f \in F_{2} }} {\dot{\gamma }_{f}^{1z} } } \hfill & {} \hfill & {} \hfill \\ {s.t.} \hfill & {} \hfill & {} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} x_{ij}^{1} \le x_{io}^{1} - \beta_{i}^{1x} R_{io}^{1x} ,} \hfill & {\forall i \in I_{1} ,} \hfill & {(b)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} z_{fj} \ge l_{f}^{1} ,\quad l_{f}^{1} = z_{fo} + \gamma_{f}^{1z} Q_{fo}^{1z} ,} \hfill & {\forall f \in F_{1} ,} \hfill & {(c)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} + \varphi^{ - 1} \left( \alpha \right) \sigma_{f} \left( {\lambda^{1} ,\dot{\gamma }} \right) \ge \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \overline{R}_{fo}^{1z} ,} \hfill & { \forall f \in F_{2} ,} \hfill & {(d)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} = 1,\;\lambda_{j}^{1} \ge 0,\beta_{i}^{1x} \ge 0,\dot{\gamma }_{f}^{1z} \ge 0,\gamma_{f}^{1z} \ge 0,l_{f}^{1} \in Z} \hfill & {\forall j,i,f,} \hfill & {(e)} \hfill \\ \end{array} $$
(23)

Consider model (24) as follows:

$$ \begin{array}{*{20}l} {Max \;\rho = \mathop \sum \limits_{{i \in I_{2} \cup I_{3} }} \beta_{i}^{2x} + \mathop \sum \limits_{{f \in F_{1} }} \dot{\tau }_{f}^{2z} + \mathop \sum \limits_{{f \in F_{2} }} \tau_{f}^{2z} + \mathop \sum \limits_{{r \in R_{2} \cup R_{3} }} \delta_{r}^{2y} + \mathop \sum \limits_{{r \in R_{1} }} \dot{\delta }_{r}^{2y} } \hfill & {} \hfill & {} \hfill \\ {s.t.} \hfill & {} \hfill & {} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} x_{ij}^{2} \le x_{io}^{2} - \beta_{i}^{2x} R_{io}^{2x} , } \hfill & {\forall i \in I_{2} } \hfill & {(f)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} x_{ij}^{2} \le a_{i}^{2} ,\quad a_{i}^{2} = x_{io}^{2} - \beta_{i}^{2x} \;R_{io}^{2x} ,} \hfill & {\forall i \in I_{3} ,} \hfill & {(g)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} z_{fj} \le l_{f}^{2} ,\;l_{f}^{2} = z_{fo} - \dot{\tau }_{f}^{2z} \;Q_{fo}^{2z} ,} \hfill & {\forall f \in F_{1} ,} \hfill & {(h)} \hfill \\ { \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} \overline{z}_{fj} - \varphi^{ - 1} \left( \alpha \right) \sigma_{f} \left( {\lambda^{2} ,\tau } \right) \le \overline{z}_{fo} - \tau_{f}^{2z} \overline{R}_{fo}^{2z} ,} \hfill & {\forall f \in F_{2} ,} \hfill & {(l)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \le t_{r}^{2} ,\quad t_{r}^{2} = y_{ro}^{2} - \dot{\delta }_{r}^{2y} G_{ro}^{2y} ,} \hfill & {\forall r \in R_{1} ,} \hfill & {(p)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \ge s_{r}^{2} ,\quad s_{r}^{2} = y_{ro}^{2} + \delta_{r}^{2y} \;R_{ro}^{2y} ,} \hfill & {\forall r \in R_{2} ,} \hfill & {(q)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \ge y_{ro}^{2} + \delta_{r}^{2y} R_{ro}^{2y} } \hfill & {\forall r \in R_{3} ,} \hfill & {(t)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} = 1, \lambda_{j}^{2} \ge 0,\beta_{i}^{2x} \ge 0,\tau_{f}^{2z} \ge 0,\dot{\tau }_{f}^{2z} \ge 0,l_{f}^{2} , a_{i}^{2} , t_{r}^{2} ,s_{r}^{2} \in Z} \hfill & {\forall j,i,f,} \hfill & {(u)} \hfill \\ {\delta_{r}^{2y} \ge 0,\dot{\delta }_{r}^{2y} \ge 0,} \hfill & {\forall r,} \hfill & {(w)} \hfill \\ \end{array} $$
(24)

Model (25) assesses the overall efficiency of supply chains.

$$ \begin{array}{*{20}l} Max \;\rho = \mathop \sum \limits_{{i \in I_{1} }} \beta_{i}^{1x} + \mathop \sum \limits_{{f \in F_{1} }} \gamma_{f}^{1z} + \mathop \sum \limits_{{f \in F_{2} }} \dot{\gamma }_{f}^{1z} \hfill &\\ + \mathop \sum \limits_{{i \in I_{2} \cup I_{3} }} \beta_{i}^{2x} + \mathop \sum \limits_{{f \in F_{1} }} \dot{\tau }_{f}^{2z} + \mathop \sum \limits_{{f \in F_{2} }} \tau_{f}^{2z} + \mathop \sum \limits_{{r \in R_{2} \cup R_{3} }} \delta_{r}^{2y} + \mathop \sum \limits_{{r \in R_{1} }} \dot{\delta }_{r}^{2y} \hfill & {} \hfill & {} \hfill \\ {s.t.} \hfill & {} \hfill & {} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} x_{ij}^{1} \le x_{io}^{1} - \beta_{i}^{1x} R_{io}^{1x} ,} \hfill & { \forall i \in I_{1} ,} \hfill & {(a)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} z_{fj} \ge l_{f}^{1} ,\;l_{f}^{1} = z_{fo} + \gamma_{f}^{1z} Q_{fo}^{1z} , } \hfill & { \forall f \in F_{1} ,} \hfill & {(b)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} + \varphi^{ - 1} \left( \alpha \right) \sigma_{f} \left( {\lambda^{1} ,\dot{\gamma }} \right) \ge \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \overline{R}_{fo}^{1z} , } \hfill & { \forall f \in F_{2} , } \hfill & {(c)} \hfill \\ { \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} = 1,\lambda_{j}^{1} \ge 0,\beta_{i}^{1x} \ge 0,\dot{\gamma }_{f}^{1z} \ge 0,\gamma_{f}^{1z} \ge 0, l_{f}^{1} \in Z } \hfill & { \forall j,i,f,} \hfill & {(d)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} x_{ij}^{2} \le x_{io}^{2} - \beta_{i}^{2x} R_{io}^{2x} , } \hfill & { \forall i \in I_{2} ,} \hfill & {(e)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} x_{ij}^{2} \le a_{i}^{2} ,\quad a_{i}^{2} = x_{io}^{2} - \beta_{i}^{2x} R_{io}^{2x} , } \hfill & {\forall i \in I_{3} , } \hfill & {(f)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} z_{fj} \le l_{f}^{2} ,\; l_{f}^{2} = z_{fo} - \dot{\tau }_{f}^{2z} Q_{fo}^{2z} , } \hfill & {\forall f \in F_{1} ,} \hfill & {(g)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} \overline{z}_{fj} - \varphi^{ - 1} \left( \alpha \right) \sigma_{f} \left( {\lambda^{2} ,\tau } \right) \le \overline{z}_{fo} - \tau_{f}^{2z} \overline{R}_{fo}^{2z} } \hfill & { \forall f \in F_{2} ,} \hfill & {(h)} \hfill \\ { \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \le t_{r}^{2} ,\quad t_{r}^{2} = y_{ro}^{2} - \dot{\delta }_{r}^{2y} G_{ro}^{2y} ,} \hfill & {\forall r \in R_{1} ,} \hfill & {(p)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \ge s_{r}^{2} ,\quad s_{r}^{2} = y_{ro}^{2} + \delta_{r}^{2y} R_{ro}^{2y} } \hfill & { \forall r \in R_{2} ,} \hfill & {(q)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \ge y_{ro}^{2} + \delta_{r}^{2y} R_{ro}^{y} , } \hfill & {\forall r \in R_{3} ,} \hfill & {(t)} \hfill \\ {\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} = 1,\lambda_{j}^{2} \ge 0,\beta_{i}^{2x} \ge 0,\tau_{f}^{2z} \ge 0,\dot{\tau }_{f}^{2z} \ge 0,l_{f}^{2} ,a_{i}^{2} ,t_{r}^{2} ,s_{r}^{2} \in Z} \hfill & {\forall j,i,f,} \hfill & {(u)} \hfill \\ {\dot{\delta }_{r}^{*2y} \ge 0,\delta_{r}^{2y} \ge 0, } \hfill & {\forall r} \hfill & {} \hfill \\ \end{array} $$
(25)

Theorem 1

Models (23), (24), and (25) are always feasible and bounded.

Proof

Without loss of generality, assume that, except for o, for each j we have \({ }\lambda_{j}^{1} = 0\) and \(\lambda_{j}^{2} = 0\). If \(\lambda_{{o{ }}}^{1} = 1\), \(\lambda_{o}^{2} = 1\), and the rest of the variables are zero, a feasible solution is obtained for every level of \(\alpha\).

$$ \begin{gathered} \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} + \varphi^{ - 1} \left( \alpha \right)\sigma_{f} \left( {\lambda^{1} ,\gamma } \right) \ge \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} \ge \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \;\overline{R}_{fo}^{1z} , \hfill \\ \dot{\gamma }_{f}^{1z} \le \frac{{\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} \overline{z}_{fj} - \overline{z}_{fo} }}{{\overline{R}_{fo}^{1z} }},\;\forall f \in F_{2} \hfill \\ \end{gathered} $$
(26)

Similarly, the same approach applies to other inequalities. As a result, the solution is bounded. Note that if \(\alpha = 0.5\), then \(\varphi^{ - 1} \left( \alpha \right) = 0\), and the deterministic equivalent is obtained. Note that the data are assumed to have positive values with normal distribution. □

Theorem 2

In the optimal solution of models (23), (24), and (25), all the constraints are binding.

Proof

Assume that at least one constraint is strictly unequal (not binding). Thus, to change the inequality to equality, there exist fewer inputs for the input constraints and more outputs for the output constraints. As a result, the better solution violates the optimality, the assumption is invalidated, and the theorem is proven. □

We will now discuss the changes in each factor. Without loss of generality, one of the input’s constraints is as follows:

$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} x_{ij}^{1} \le x_{io}^{1} - \beta_{i}^{1x} R_{io}^{1x} ,\;\forall i \to \beta_{i}^{1x} \le \frac{{x_{io}^{1} - \mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1} x_{ij}^{1} }}{{R_{io}^{1x} }} $$
(27)

Since in the optimality, every constraint has an equal sign, we have

$$ \beta_{i}^{*1x} = \frac{{x_{io}^{1} - \mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1*} \;x_{ij}^{1} }}{{R_{io}^{1x} }},\quad \forall i \in I_{1} $$
(28)

Note that there is slack in the numerator as it is the difference between the input of the DMUo and the efficiency frontier. Also, the denominator shows the range. The same discussion applies to the rest of the inputs.

Since in the optimality the associated constraint has an equal sign, Expression (29) exists for the first constraint. Note that the numerator of Expression (29) plays the role of slack as it is the difference between the average output of DMUo and the stochastic efficiency frontier. Also, the denominator shows the range. As demonstrated, the numerator is less than the denominator. In Expression (29), for each r, the \({\gamma }_{r}^{*1y}\) indicates the associated inefficiency of the factors.

$$ \dot{\gamma }_{f}^{*1z} = \frac{{\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{*1} \overline{z}_{fj} + \varphi^{ - 1} \left( \alpha \right)\;\sigma_{f} \left( {\lambda^{1} ,\dot{\gamma }} \right) - \overline{z}_{fo} }}{{\overline{R}_{fo}^{1z} }} = \frac{{\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{*1} \overline{z}_{fj} + \varphi^{ - 1} \left( \alpha \right)\sigma_{f} \left( {\lambda^{1} ,\dot{\gamma }} \right) - \overline{z}_{fo} }}{{\max \left\{ {z_{fj} |\forall j} \right\} - z_{fo} }},\quad \forall f \in F_{2} $$
(29)

Definition 1

Without loss of generality, consider the input constraint of Model (23). The efficiency of the input is defined as follows:

$$ E_{i}^{1} = 1 - \beta_{i}^{*1x} ,\;\forall i $$
(30)

where

$$ \beta_{i}^{*x} = \frac{{x_{io}^{1} - \mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1*} \;x_{ij}^{1} }}{{R_{io}^{1x} }} $$
(31)
$$ 1 - \beta_{i}^{*x} = 1 - \frac{{x_{io}^{1} - \mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1*} \;x_{ij}^{1} }}{{R_{io}^{1x} }} = 1 - \frac{{x_{io}^{1} - \mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1*} \;x_{ij}^{1} }}{{x_{io}^{1} - \min \{ x_{ij}^{1} |\forall j\} }} = \frac{{x_{io}^{1} - \min \{ x_{ij}^{1} |\forall j\} - x_{io}^{1} + \mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1*} \;x_{ij}^{1} }}{{x_{io}^{1} - \min \{ x_{ij}^{1} |\forall j\} }},\;\forall i $$
(32)

Thus, we can write

$$ 1 - \beta_{i}^{*x} = \frac{{\mathop \sum \nolimits_{j = 1}^{n} \lambda_{j}^{1*} x_{ij}^{1} - \min \{ x_{ij}^{1} |\forall j\} }}{{x_{io}^{1} - \min \{ x_{ij}^{1} |\forall j\} }},\quad \forall i $$
(33)

Since \(\sum\nolimits_{j = 1}^{n} {\lambda_{j}^{1*} x_{ij}^{1} }\) is always less than or equal to \(x_{io}^{1}\), then

$$ 1 - \beta_{i}^{*x} \le 1, \quad \forall i \in I_{1} $$
(34)

Consider the output of stage 1. Since \(0 \le \gamma_{f}^{{{*}1z}} \le 1\), the output efficiency is defined as follows:

$$ 1 + \gamma_{f}^{*1z} \ge 1,\quad \forall f \in F_{1} $$
(35)

The same holds for the decision variables of inputs and outputs of stages 1 and 2.

Lemma 2

If the range of inputs, outputs, and intermediate measures of DMUo is zero, there is no room for their improvements.

Proof

The zero range implies that the associated factors have the smallest input and the biggest output. In this case, the associated constraint is considered with an equal sign. For instance, consider the input constraint with zero range.

$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{1} x_{ij}^{1} = x_{io}^{1} - \beta_{i}^{*1x} x_{io}^{1} = \left( {1 - \beta_{i}^{*1x} } \right)x_{io}^{1} \to \beta_{i}^{*1x} = 0 \quad \forall i \in I_{1} $$
(36)

The same reasoning applies to other constraints. □

Using the objective function of model (25), the total efficiency (TE) is calculated as follows:

$$ TE = \frac{1}{1 + \rho } = \frac{1}{{1 + \sum\limits_{{i \in I_{1} }} {\beta_{i}^{*1x} } + \sum\limits_{{f \in F_{1} }} {\gamma_{f}^{*1z} } + \sum\limits_{{f \in F_{2} }} {\dot{\gamma }_{f}^{*1z} } + \sum\limits_{{i \in I_{2} \cup I_{3} }} {\beta_{i}^{*2x} } + \sum\limits_{{f \in F_{1} }} {\dot{\tau }_{f}^{*2z} } + \sum\limits_{{f \in F_{2} }} {\tau_{f}^{*2z} } + \sum\limits_{{r \in R_{2} \cup R_{3} }} {\delta_{r}^{*2y} } + \sum\limits_{{r \in R_{1} }} {\dot{\delta }_{r}^{*2y} } }} $$
(37)

Using the objective function of model (23), the efficiency of stage 1 (ES1) is as follows:

$$ ES_{1} = \frac{1}{{1 + \mathop \sum \nolimits_{{i \in I_{1} }}^{{}} \beta_{i}^{*1x} + \mathop \sum \nolimits_{{f \in F_{1} }}^{{}} \gamma_{f}^{*1z} + \mathop \sum \nolimits_{{f \in F_{2} }} \dot{\gamma }_{f}^{*1z} }} $$
(38)

Using the objective function of model (24), the efficiency of stage 2 (ES2) is as follows:

$$ ES_{2} = \frac{1}{{1 + \mathop \sum \nolimits_{{i \in I_{2} \cup I_{3} }}^{{}} \beta_{i}^{*2x} + \mathop \sum \nolimits_{{f \in F_{2} }} \dot{\tau }_{f}^{*2z} + \mathop \sum \nolimits_{{f \in F_{1} }} \tau_{f}^{*2z} + \mathop \sum \nolimits_{{r \in R_{2} \cup R_{3} }}^{{}} \delta_{r}^{*2y} + \mathop \sum \nolimits_{{r \in R_{1} }}^{{}} \dot{\delta }_{r}^{*2y} }} $$
(39)

Theorem 3

The efficiency scores obtained from Expressions (37), (38), and (39) are as follows:

$$ TE \le 1, ES_{1} \le 1, ES_{2} \le 1 $$
(40)

Proof

Since the associated variables of inputs and outputs are non-negative, in optimality we have

$$ \beta_{i}^{*1x} \ge 0,\dot{\gamma }_{f}^{*1z} \ge 0,\gamma_{f}^{*1z} \ge 0,\beta_{i}^{*2x} \ge 0,\tau_{f}^{*2z} \ge 0,\dot{\tau }_{f}^{2z} \ge 0,\delta_{r}^{*2y} \ge 0,\dot{\delta }_{r}^{*2y} \ge 0 $$
(41)

Therefore, given Expressions (37), (38), (39), and (41), the efficiency scores are always less than or equal to one. □

Theorem 4

In models (23), (24), and (25), given the VRS technology, the DMUs with the smallest input and biggest output are efficient, and there is no room for improvement in the factors.

Proof

Given Expressions (1) and (2), if the DMUo has the smallest input and the biggest output, then its associated variable in models (23), (24), and (25) is considered zero, and there is no room for improvement. Otherwise, if the range is non-zero, then the DMUo can improve its performance.

$$ \min \{ x_{ij}^{1} |\forall j\} = x_{io}^{1} \to R_{io}^{1x} = x_{io}^{1} - \min \{ x_{ij}^{1} |\forall j\} = x_{io}^{1} - x_{io}^{1} = 0,\quad \forall i $$
(42)

The same holds for other ranges as defined in (1) and (2). If the DMUo has positive changes for inputs and outputs, then it is inefficient. The more changes, the less efficiency of DMUo. □

The improved factors of the first stage are determined as follows:

$$ \begin{gathered} \hat{z}_{fo}^{1z} = z_{fo} + \gamma_{f}^{1z} R_{fo}^{1z} ,\quad \forall f \in F_{1} \hfill \\ \hat{z}_{fo}^{1z} = \overline{z}_{fo} + \dot{\gamma }_{f}^{1z} \overline{R}_{fo}^{1z} ,\quad \forall f \in F_{2} \hfill \\ \hat{x}_{io}^{1x} = x_{io}^{1} - \beta_{i}^{1x} R_{io}^{1x} ,\quad \forall i \in I_{1} \hfill \\ \end{gathered} $$
(43)

The improved factors of the second stage are determined as follows:

$$ \begin{gathered} \hat{x}_{io}^{2x} = x_{io}^{2} - \beta_{i}^{2x} R_{io}^{2x} ,\quad \forall i \in I_{1} \cup I_{2} \hfill \\ \hat{z}_{fo}^{2z} = z_{fo} - \dot{\tau }_{f}^{2z} R_{fo}^{2z} ,\quad \forall f \in F_{2} ;\;\hat{z}_{fo}^{2z} = \overline{z}_{fo} - \tau_{f}^{2z} \overline{R}_{fo}^{2z} ,\quad \forall f \in F_{1} \hfill \\ \hat{y}_{ro}^{2y} = y_{ro}^{2} - \dot{\delta }_{r}^{2y} G_{ro}^{2y} ,\quad \forall r \in R_{1} ;\;\hat{y}_{ro}^{2y} = y_{ro}^{2} + \delta_{r}^{2y} R_{ro}^{2y} ,\quad \forall r \in R_{2} \cup R_{3} \hfill \\ \end{gathered} $$
(44)

Theorem 5

The obtained improved factors in (43) and (44) are Pareto efficient.

Proof

Assume that an improved factor does not lie on the Pareto efficiency frontier. Thus, the improved factor is dominated by the other dominant point. The dominant point has a better solution in the objective function. This violates the Pareto optimality and the theorem is proved. □

Theorem 6

The objective functions of models (23), (24), and (25) are not greater than the DDF model.

Proof

Without loss of generality, consider the input constraints in stage 1. The \(\beta_{i}^{1x}\) is the non-negative variable that changes the ith input. The \(R_{io}^{1x}\) is the range of the ith input of DMUo. Given Expression (1), the range of input is as follows:

$$ R_{io}^{1x} = x_{io}^{1} - \min \{ x_{ij}^{1} |\forall j\} ,\quad \forall i \in I_{1} $$
(45)

The improved inputs in the DDF model are as follows:

$$ \hat{x}_{io}^{1x} = x_{io}^{1} - \beta_{i}^{1x} x_{io}^{1} ,\quad \forall i \in I_{1} $$
(46)

To compare Expressions (45) and (46), we have

$$ x_{io}^{1} - \beta_{i}^{1x} R_{io}^{1x} \ge x_{io}^{1} - \beta_{i}^{1x} x_{io}^{1} ,\quad \forall i \in I_{1} $$
(47)

Given Expression (45), it is clear that \({\text{R}}_{io}^{1x} \le {\text{x}}_{io}^{1}\). Thus, the efficiency score of Expression (37) is less than or equal to the DDF model. □

Theorem 7

Constraints of models (23), (24), and (25) are unit invariant and translation invariant.

Proof

Without loss of generality, assume that \(h_{r}\) \(\forall r \in R_{1}\) is added to the output of stage 2. Thus, we have

$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} \left( {y_{rj}^{2} + h_{r} } \right) \ge \left( {y_{ro}^{2} + h_{r} } \right) + \dot{\gamma }_{r}^{2y} R_{ro}^{2y} ,\quad \forall r \in R_{3} $$
(48)

Since \(\sum\nolimits_{j = 1}^{n} {\lambda_{j}^{2} = 1}\), we have

$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} + \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} h_{r} = \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} + \left( {h_{r} } \right)\mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} = \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} + \left( {h_{r} } \right) \ge \left( {y_{ro}^{2} + h_{r} } \right) + \dot{\gamma }_{r}^{2y} R_{ro}^{2y} ,\;\forall r \in R_{3} $$
(49)

Given Expression (2), by adding \(h_{r}\), the ranges do not change. As a result,

$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \ge y_{ro}^{2} + \dot{\gamma }_{r}^{2y} R_{ro}^{2y} ,\quad \forall r \in R_{3} $$
(50)

This proves that the model is a translation invariant. Now, assume that \(h_{r}\) is multiplied by the output. Thus, it is multiplied by the ranges. Therefore, we have

$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} \left( {y_{rj}^{2} \times h_{r} } \right) \ge \left( {y_{ro}^{2} \times h_{r} } \right) + \dot{\gamma }_{r}^{2y} \left( {R_{ro}^{2y} \times h_{r} } \right)\quad \forall r \in R_{3} $$
(51)

Expression (51) can be written as follows:

$$ \mathop \sum \limits_{j = 1}^{n} \lambda_{j}^{2} y_{rj}^{2} \ge y_{ro}^{2} + \dot{\gamma }_{r}^{2y} \;R_{ro}^{2y} \quad \forall r \in R_{3} $$
(52)

Thus, constraint (t) of model (52) is unit invariant. This procedure can be performed for other constraints of inputs and outputs of stages 1 and 2. □

Figure 2 represents two stages of the network. Note that both outputs of stage 1 are positive and an output of stage 2 is negative. Figure 2 shows the non-radial changes in the negative output.

Fig. 2
figure 2

The efficiency frontiers of stages 1 and 2

Full size image

The red line in stage 1 shows the direction of improvement for DMU K. Given Expression (1), the outputs’ range of DMU K is (2, 4). Using model (23), DMU K is projected on K‴, which lies on the efficiency frontier. For the second stage, the first output of DMU H is negative. If DMU H is assessed by the classical directional distance function model, it should be projected on the efficiency frontier given the vector \(\overrightarrow {OH}\), marked by the blue colour. In this case, the first output becomes more negative, which is worse. However, using Expression (2), it is projected on the efficiency frontier (point \(\acute{B}\)) by \(\overrightarrow {{HI_{H} }}\), marked in red colour. Using Expression (2), it is clear that \({\text{I}}_{H} = \left( {4.5, 4.5} \right)\). Using the classic RDM model for stage 2, we have

$$ \lambda_{B}^{*} = 0.67,\;\lambda_{C}^{*} = 0.33 $$
(53)

Consider \(\beta\) as radial alterations. As a result, its radial change is \(\beta^{*} = 0.52\). Using model (24) the results are as follows:

$$ \lambda_{B}^{*} = 1,\;\beta_{1}^{{*y_{1} }} = 0.67,\;\beta_{2}^{{*y_{2} }} = 0.44 $$
(54)

The average non-radial changes of outputs are \(\rho^{*} = 0.55\). As is seen in Fig. 2 of stage 2, the radial projected point \(\acute{B}\) has a small difference with DMU B. However, due to the inclusion of all inefficiencies of outputs, the non-radial efficiency score is less than the radial efficiency score. By the non-radial change, DMU H is projected on DMU B, which is shown by the green vector. The point \(\acute{B}\) is obtained as follows.

$$ \begin{array}{*{20}c} {y_{1} = - 0.5 + 0.52 \times 4.5 = 1.8} \\ {y_{2} = 1.0 + 0.52 \times 4.5 = 3.3} \\ \end{array} \to \acute{B} = \left( {\begin{array}{*{20}c} {1.8} \\ {3.3} \\ \end{array} } \right) $$
(55)

By equal radial change, both outputs are changed with coefficient 4.5 and point \(\acute{B}\) is obtained. Now, consider the triangle \(H\acute{B} I_{H}\), which is marked in the red line. The non-radial changes of outputs are done separately, and the outputs of DMU H are increased. The \(HP\acute{B}\) in Fig. 2 shows the increase. Given Fig. 2 of stage 2, it is clear that HP and \(P\acute{B}\) have equal edges in the triangle. The non-radial changes in the outputs are as follows:

$$ \begin{array}{*{20}c} {y_{1} = - 0.5 + 0.67 \times 4.5 = 2.5} \\ {y_{2} = 1 + 0.44 \times 4.5 = 3} \\ \end{array} \to B = \left( {\begin{array}{*{20}c} {2.5} \\ 3 \\ \end{array} } \right) $$
(56)

As is seen in Fig. 2 of stage 2, by \(\beta_{1}^{{{*}y_{1} }} = 0.67{\text{ and }}\beta_{2}^{{{*}y_{2} }} = 0.44\), DMU H is projected on DMU B. Given Thales’s theorem (Heilberg and Fitzpatrick, 2007) and the triangles \(H\acute{B} I_{H}\) and \(HP\acute{B}\), we get \(\frac{HP}{{H\acute{P} }} = \frac{{\acute{B} P}}{{\acute{I}_{H} P}}\). The interpretation of Fig. 2 for stage 1 is straightforward.

4 Case study

Iran is one of the most affected countries by COVID-19 disease, with over 726,000 total cases and 40,000 deaths by November 2020. At the moment of writing this paper, the country was experiencing a considerable increase in the number of COVID-19 infections and deaths. The sustainability and resilience of the healthcare SCs have received much attention during the course of this unprecedented pandemic. However, the efficiency of healthcare SCs in disaster situations such as pandemics can be largely affected due to the uncertainties of some key indicators such as increased demand, numerous SC disruptions, and shortages of vital medical equipment (Dolinskaya et al., 2018).

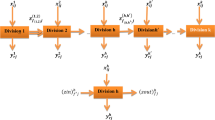
In this case study, we evaluate the sustainability and resilience of the healthcare SCs in Iran. In this study, healthcare SCs consist of suppliers (stage 1) and hospitals (stage 2). The suppliers manufacture COVID-19 testing kits. The kits detect new Coronavirus cases and are one of the most important medical devices. The inputs of stage 1 are raw material costs (\({x}_{1}^{1}\)), the rate of inferior raw material (\({x}_{2}^{1}\)), environmental costs (\({x}_{3}^{1}\)), and personnel costs (\({x}_{4}^{1}\)). The number of produced COVID-19 testing kits and the average inventory are intermediate measures, which exit from stage 1 and enter stage 2. The external inputs of stage 2 include employees’ health and safety costs (\({x}_{1}^{2}\)), the number of personnel (\({x}_{2}^{2}\)), personnel costs (\({x}_{3}^{2}\)), the number of patients (\({x}_{4}^{2}\)), and the number of beds (\({x}_{5}^{2}\)). The outputs of stage 2 are the number of errors in diagnosing COVID-19 disease (\({y}_{1}^{2}\)), the number of discharged patients (\({y}_{2}^{2}\)), and profit (\({y}_{3}^{2}\)). Figure 3 shows the structure of healthcare SC.

Fig. 3
figure 3

The two-stage supply chain

Full size image

Table (9 see Appendix) summarises the indicators. In this study, several meetings were held with managers and experts of suppliers and hospitals to identify the most important indicators for measuring the sustainability and resilience of healthcare SCs in response to the COVID-19 pandemic outbreak. Table (10 see Appendix) presents the dataset of 28 healthcare SCs. The dataset is related to March to June 2020, which is extracted by observing documents of suppliers and hospitals of healthcare SCs.Footnote 1

4.1 Results and discussions

Given different α values, Table 2 reports the suppliers’ efficiencies obtained from Expression (38). Considering Expression (38), the aim is to evaluate efficiency of the fist stage of the network. As is seen, the higher α, the higher efficiency of DMUs. As an example, consider DMU 1. This DMU has an efficiency value of 0.627759 for α = 0.02. As the value of error α increases, specifically considering α = 0.04, the efficiency value of this unit is increased and becomes 0.628231. This upward trend continued for unit number 1 until at α = 0.1 its efficiency value becomes 0.628949. DMUs 2, 5, 8, 9, 10, 15, 16, 20, 23, 25, and 26 have the same behavior as DMU 1, and their efficiencies are increased by increasing α. This means that by considering the variance of random data, different values of efficiency are obtained for each error level. This shows the effectiveness of the random nature of the data in this practical example. Now, consider DMU 3. This DMU has an efficiency value of 1 with all values of α = 0.02, α = 0.04, α = 0.06, α = 0.08, and α = 0.1. For DMUs 3, 4, 6, 7, 11, 12, 13, 14, 17, 18, 19, 21, 22, 23, 24, 27, and 28, the efficiency stability is clearly shown by the constant efficiency value of 1 due to the increase of the error level value. This means that by increasing the error level, these DMUs maintain their unity efficiency. Also, changes of random data and their variance have no effect on the efficiency value.

Table 2 The stochastic efficiency of suppliers given different α values
Full size table

Figure 4 summarises the results shown in Table 2.

Fig. 4
figure 4

Summary of the results

Full size image

Given different α values, Table 3 depicts the hospitals’ efficiencies using Expression (39). Taking into consideration Expression (39), the efficiency of the second stage is investigated. As is seen, the higher α, the higher the efficiency of DMUs. According to Table 3, the efficiency of DMUs are calculated considering different levels of α. As is shown in Table 3, DMUs 1, 3, 11, 13, 15, 16, 17, 18, 19, 21, 22, 23, 24, 26, and 27, in all error levels, are inefficient. The efficiency of these DMUs is increased by increase in the error level. Note that DMUs 8 and 28 are inefficient in α = 0.02 and α = 0.04. By increasing the error level to α = 0.06, α = 0.08, and α = 0.1, their efficiencies become 1. DMUs 2, 4, 5, 6, 7, 9, 10, 12, 14, 20, and 25 are efficient in all levels of errors. It means these DMUs have excellent performance in different error levels

Table 3 The stochastic efficiency of hospitals given different α values
Full size table

Given different α values, Table 4 shows the TE of supply chains using Expression (37). Taking into account Expression (37), the efficiency of the entire network is calculated. Note that in Expression (37), the network is not evaluated as a black box and interactions among stages are considered. As is seen, the higher α, the higher efficiency of DMUs. In Table 4, the whole network efficiency is reported. DMUs 4, 6, 7, 12, and 14 are evaluated as efficient. However, DMUs 1, 2, 3, 5, 8, 9, 10, 11, 13, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, and 27 are inefficient. The efficiency values are increased by considering different error levels. Note that DMU 28 is inefficient in α = 0.02 and α = 0.04 and is efficient in α = 0.06, α = 0.08, and α = 0.1.

Table 4 The stochastic TE of supply chains given different α values
Full size table

By comparing Tables 2, 3, and 4, we find out that DMUs 4, 6, 7, 12, and 14 are efficient in the two stages and entire network. As is seen in Table 4, the total efficient supply chains are those supply chains efficient in both stages. Now, improved factors are introduced. For the sake of brevity, the improved factors are introduced just for \(\alpha = 0.1\). To this end, Table 5 reports the optimal values of decision variables associated with the inputs and outputs of suppliers given \(\alpha =0.1\). Note that the optimal values for efficient DMUs are zero.

Table 5 The optimal values of the supplier decision variables
Full size table

Given \(\alpha = 0.1\), Table 6 depicts the improved supplier factors. For inefficient DMUs, the inputs are reduced and the outputs are increased.

Table 6 The improved supplier factors
Full size table

According to the initial inputs and outputs of the first stage in α = 0.1, and the improved data presented in Table 6, it can be said that the sum of inputs of DMUs is improved by an average of 0.94. Also, the total outputs of the first stage are improved by an average of 1.02. Given \(\alpha = 0.1\), Table 7 reports the optimal values of decision variables associated with the inputs and outputs of hospitals.

Table 7 The optimal values of hospital decision variables of
Full size table

Given \(\alpha = 0.1\), Table 8 depicts the improved hospital factors of. For inefficient DMUs, the inputs are reduced and the outputs are increased.

Table 8 The improved hospital factors of
Full size table

According to the initial inputs and outputs of the first stage in α = 0.1 and the improved data presented in Table 8, it can be said that the sum of inputs of DMUs is improved by an average of 0.93. It can also be said that according to the initial inputs and outputs of the first stage in α = 0.1, and the improved data presented in Table 8, the sum of absolute value of the outputs of DMUs is improved by an average of 1.83.

4.2 Managerial implications

The proposed method provides different implications for healthcare SC managers and decision makers. Healthcare SC efficiency in response to pandemics such as COVID-19 and SARS can be broken down into SC stages, and our use of the network RDM method can then enable managers to detect and trace inefficient resources. Thus, healthcare SC managers and decision makers can identify bottlenecks and take remedial measures. Another feature of our proposed approach is its consideration of sustainability and resilience in measuring healthcare SC efficiency. Due to the pressures of social media, high competition, and public awareness, managers should integrate sustainability and resilience into their decisions. The proposed approach provides managers with a tool to deal with the sustainability and resilience issues in the face of disasters.

The proposed approach also deals with different types of data. These can help managers avoid making wrong the decisions leading to potential losses. Uncertainty in decision-making is another key challenge for managers in the face of disasters. To mitigate the risks, managers should not only apply appropriate approaches, they should also consider stochastic changes. The proposed method in this paper is a suitable tool for dealing with uncertainty. The obtained results show how the efficiency of healthcare SCs changes according to different Alpha values. This, in turn, assists healthcare managers and decision makers with better planning and resource allocation.

5 Conclusions and future research

The recent outbreak of Coronavirus resulting in an unprecedented crisis has negatively affected countries all over the world. Healthcare systems play a key role in facing such crises. Assessing the efficiency of healthcare SCs in disasters such as COVID-19 is critical. However, doing so, particularly in the face of uncertainty, is a major challenge for managers.

Jomthanachai et al. (2021) and Matin et al. (2022) measured supply chain resilience using DEA. Similarly, Kalantary and Farzipoor Saen (2022), Fathi and Farzipoor Saen (2021), Mohtashami et al. (2021), Dey et al. (2021), Malesios et al. (2020), and Wang et al. (2020) used DEA to measure supply chain sustainability. In all the cited papers, they used resilience and sustainability factors in DEA. Then, the efficiency scores obtained from DEA were interpreted as sustainability and resilience. In this paper, we proposed a new network RDM model to measure the sustainability and resilience of healthcare SCs. The developed model can deal with different types of data such as ratio, integer, stochastic, zero, and undesirable, simultaneously. Furthermore, we used the CCP approach to deal with stochastic data. Finally, we provided a case study to validate the proposed models. In sum, the study makes the following contributions: (1) proposing a novel network non-radial RDM model to evaluate the sustainability and resilience of healthcare SCs, (2) addressing different types of data such as ratio, integer, undesirable, stochastic, negative, and zero, simultaneously, (3) recommending how to enhance the inefficiency of healthcare SCs, (4) presenting a case study.

The results demonstrated how well our proposed method can evaluate the sustainability and resilience of healthcare SCs in view of different types of data. In addition, the results showed that under different conditions, the efficiency of healthcare SCs changes. Another contribution of this study is that it can support healthcare managers and decision makers in identifying and tracing inefficient resources. This allows them to then concentrate on bottlenecks and take remedial measures to improve the performance of sustainable-resilient healthcare SCs.

Owing to limitations in gathering data in this study, we identified 14 indicators for evaluating sustainable-resilient healthcare SCs. Nevertheless, other indicators that could be applied to assess sustainable-resilient healthcare SCs. Using the proposed method, we suggest researchers study translation invariance property in network DEA and measure the performance of healthcare SCs.