Heuristics for a cash-collection routing problem with a cluster-first route-second approach

Abstract

Motivated by a routing problem faced by banks to enhance their encashment services in the city of Perm, Russia, we solve versions of the traveling salesman problem (TSP) with clustering. To minimize the risk of theft, suppliers seek to operate multiple vehicles and determine an efficient routing; and, a single vehicle serves a set of locations that forms a cluster. This need to form independent clusters—served by distinct vehicles—allows the use of the so-called cluster-first route-second approach. We are especially interested in the use of heuristics that are easily implementable and understandable by practitioners and require only the use of open-source solvers. To this end, we provide a short survey of 13 such heuristics for solving the TSP, five for clustering the set of locations, and three to determine an optimal number of clusters—all using data from Perm. To demonstrate the practicality and efficiency of the heuristics, we further compare our heuristic solutions against the optimal tours. We then provide statistical guarantees on the quality of our solution. All of our anonymized code is publicly available allowing extensions by practitioners, and serves as a decision-analytic framework for both clustering data and solving a TSP.

1 Introduction

We consider a problem of optimizing the collection of cash from different merchants or points of sales (POSs) and automated teller machines (ATMs) by multiple vehicles. This problem is increasingly faced by banks to enable effective encashment services (Dandekar and Ranade, 2015; Gubar et al., 2011). We are motivated by a similar problem faced by banks in the city of Perm, Russia, where several vehicles collect cash on a periodic basis from over two hundred POSs and ATMs. The particular problem we address in this work was initially proposed by Perm’s branch of Sberbank—Russia and Eastern Europe’s largest bank as of 2014. Earlier the bank’s routing was a manual exercise that became a bottleneck in its growing market of cash-collection and growth of its ATM-network.

Although cash-collection and cash-dispersion for ATMs are of relatively low risk due to the use special secured cassettes, major risks are associated with cash-collection from merchants and POSs where unsecured cash is transferred (Scott, 2001). Here, cash is transported as banknotes in safe boxes within vehicles (Kurdel and Sebestyénová, 2013). To minimize the risk of cash-in-transit robberies (Bozkaya et al., 2017; Gill, 2001), vehicles carrying cash seek to reduce the time spent on the road. Perm has an elongated landscape—the city spans 70 kms along the Kama River and has two major railroad crossings, which significantly limit the connectivity of the city’s districts; see Fig. 1. For a study of the history of crime in Perm, see Varese (2001). Thus, to enhance security, suppliers prefer multiple vehicles as opposed to a single vehicle.

There are a number of classical routing problems with close connections to our work. To describe the problem we consider in this work, we begin with a few subtle differences from the classical routing problems. Due to the use of multiple vehicles, our problem differs from a direct application of a classical traveling salesman problem (TSP). Instead, our problem is more related to the multiple traveling salesman problem (mTSP) with possibly multiple depots, where multiple vehicles complete their respective tours visiting locations only once and the overall sum of the tour lengths is minimized, see, e.g., Çetiner et al. (2010). A similar problem is studied by Svestka and Huckfeldt (Svestka and Huckfeldt, 1973). An optimal solution for the traditional mTSP fulfills the following conditions:

• (i) It finds a route for every vehicle that starts and ends at a depot (the depot may be a single central depot or different regional depots for different vehicles),

• (ii) It visits every location—apart from the depots—exactly once, and

• (iii) It minimizes the overall transportation cost.

For the case of a single vehicle, the mTSP reduces to the classical TSP. The mTSP is a relaxation of another classical problem, namely the vehicle routing problem (VRP), where the capacity restrictions on the vehicles are removed (Bektas, 2006; Laporte, 2010; Osman, 1993). Although classical variants of the VRP allow both a single depot or multiple depots (Bullnheimer et al., 1999), the VRP is unrelated to this work. This is because we do not include any capacity restrictions, time windows, or bounded tour lengths. To fulfill the needs of Perm’s suppliers, we allow the possibility of multiple depots as opposed to a single central depot and search for multiple independent tours. We do not consider a fixed set of locations that serve as depots, thus vehicles can start a valid tour at any location. This is because the vehicles used by Perm’s suppliers are also deployed in other businesses, and we do not know a vehicle’s location at the start of the day. This assumption further simplifies our problem. To this end, we partition our set of locations into different clusters, or partitions, that are served by independent vehicles. Then, within each cluster we derive the optimal routing by solving a standard TSP. This approach for solving a routing problem is known as the cluster-first route-second approach (Miranda-Bront et al., 2016; Raff, 1983). As we show later in this work, this approach provides two benefits over a direct solution of the mTSP: (i) it is computationally cheaper, and (ii) it allows the use of open-source solvers with only a slight loss in optimality.

Another related problem is the clustered traveling salesman problem (CTSP); in the CTSP certain locations and the associated partitions are visited contiguously and in a pre-specified order, respectively, see, e.g., Laporte and Osman (1995). Tours within the different clusters are connected by edges, thereby forming a single overall tour for all the locations. When all the clusters are singletons, the CTSP reduces to the classical TSP. Chisman solves this CTSP by inflating inter-partition distances, thereby discouraging their inclusion in the original tour (Chisman, 1975). Later, Guttmann-Beck et al. (2000) and  Ahmed (2012) study exact solution methods for this problem, and Baniasadi et al. (2020) provide an algorithm for its solution. In contrast, we treat clusters independently and do not reconnect them. In this sense, our work is similar to  Ding et al. (2007), where the authors find a Hamiltonian cycle within every partition, disconnect an edge, and then reconnect the partitions. The approach we follow in this work differs in the sense that we do not reconnect the edges and are flexible in the choice of our initial partitions. Further, as opposed to the classical single-depot VRP we do not consider a central depot. As we mention before, we are also flexible for depots within a partition; i.e., vehicles can start a valid tour from any location. Summarizing, closest to the existing literature our problem can be described as a mTSP that we solve using a cluster-first route-second approach.

To this end, the following are the key questions we consider in this work:

• Q.1 What is a “good” set of locations that form part of each of the clusters?

• Q.2 What is a “good” number of clusters?

• Q.3 What is an “efficient” routing within a cluster?

Since the mTSP is a relaxation of the VRP, Q.1–Q.3 are also answered by the VRP. In the first phase of our analysis, we answer questions Q.1 and Q.2 of the list above and quantify “good”. Multiple algorithms, without consensus, exist to determine good clustering, and the choice of the algorithm depends on the underlying application. We focus on centroid-based methods, that are popular within the last few decades (Kaufman and Rousseeuw, 1990; Schubert and Rousseeuw, 2019). In the second phase, we solve a TSP to determine the tours within the clusters that minimize the total distance. In general, finding an optimal tour is $\mathcal{NP}\mathcal{}$-hard (Garey and Johnson 1979), and we discuss a variety of heuristics exist for “efficiently” solving the TSP to answer question Q.3.

The main contributions of this article are the following:

• (i) We provide a comparison and review of several heuristic methods for both clustering and the TSP;

• (ii) We present extensive computational results on a real-world case study to guide practitioners facing similar problems, and statistically validate the quality of our results;

• (iii) We use only open-source software and demonstrate the competitiveness of existing implementations to the state-of-the art solution methods;

• (iv) We publicly and freely provide our code in R to serve as a modeling guide for future applications.

The structure of the rest of this article is as follows. In Sect. 2, we describe the dataset from Perm that we use as an example throughout the article. We present five heuristics for clustering and our computational experiments in Sect. 3 . We summarize three methods for determining the number of clusters, and explain our decision-making process, in Sect. 4. In Sect. 5, we focus on finding tours for the clusters; we present both heuristics and a method guaranteed to find the optimal tours. Finally, we present some limitations of our work and a summary in Sect. 6.

Fig. 1

Dataset of the considered 237 locations on the map of Perm. For details, see Sect. 2

2 Data sources and estimation

For our computational experiments, we use a list of 237 POSs and ATMs in Perm. Perm lies on the banks of the Kama River near the Ural Mountains; all locations are within the latitude range of (57$^{\circ }$57’05.8”N, 58$^{\circ }$09’43.0”N) and longitude range of (55$^{\circ }$55’09.5”E, 56$^{\circ }$26’36.0”E). Figure 1 visualizes our dataset, and we provide an anonymized dataset at: https://github.com/Oberfichtner/Clustering_and_TSP_with_R.git. Most of the locations are present in the center of the city, with the Kama river forming a natural boundary between the locations. We use the great-circle-distances between two locations to construct a matrix of distances, D, instead of the actual road distances. Let $D_{i,l}$ denote the distance between locations i and l. Then, the distance matrix is symmetric in our study; i.e., $D_{i,l}= D_{l,i}$.

Existing literature on routing problems often distinguish two classes—the asymmetric routing problem and the symmetric routing problem—and both classes have a rich history. Formally, an asymmetric distance function, f(x, y), between two locations x and y satisfies $f(x,y) = f(y,x)$ only if $x=y$. For other mathematical differences between these two functions that are beyond the scope of this work, see, e.g., Mennucci (2013). Although the asymmetric routing problem caters better to real-world problems, it is a significantly more challenging problem and heuristics towards it are less developed than its symmetric counterpart (Rodríguez and Ruiz, 2012). Rodríguez and Ruiz (Rodríguez and Ruiz, 2012) study the effect of asymmetry on heuristics of the TSP, and provide reasons in support of the use of both versions. The asymmetric routing problem also involves the use of a geographic information system (GIS) to compute road distances. GIS services could be expensive (Sutton et al., 2009)¹ and/or have privacy concerns (Blatt, 2012). For these reasons, and in a similar spirit to several classical works (Fischetti et al., 1995; Snyder and Daskin, 2006; Potvin, 1996), our work is on the symmetric TSP. For a detailed computational comparison between these two classes, we direct the interested reader to Cirasella et al. (2001).

3 Answering Q.1: clustering

In this section, we seek to answer question Q.1 from Sect. 1. As we mention in Sect. 2, we have a distance matrix D available. This allows a direct application of so-called centroid methods as opposed to hierarchical clustering methods. Within centroid based methods, k-means and k-medoids are two popular choices; however, the k-means method is more sensitive to outliers than k-medoids. To ensure robustness in our clustering, in this work we use the k-medoid method; for a survey of clustering methods, see, e.g., Leskovec et al. (2014); Rokach and Maimon (2005).

Fig. 2

a PAM b FPAM c FKM d RKM e IKM with $\alpha =1.1$ f IKM with $\alpha =1.5$. Clusters obtained using the five clustering methods, with two rows for the IKM method, shown on the map of Perm. The left, middle, and right panels display the clustering for $k=2,4,6$, respectively

Questions Q.1 and Q.2 go hand-in-hand. As we mention in Sect. 1, we serve each cluster independently with a single vehicle. If the number of vehicles is known apriori, then we simply partition our locations into that many clusters and this answers question Q.2. We then proceed to determine the set of locations that form these clusters (methods for which we describe below). If the number of vehicles is not known, we seek to determine both a good number of clusters from a range of practical values and the corresponding locations in each cluster. In Sect. 4, we describe three methods to determine a good number of clusters; we then conclude $k^*=4$ clusters provide a good fit to our data. However, to ensure generality of our observations, we describe clustering our dataset between $k=2$ and $k=20$ clusters. For values beyond 20, we get a significant number of clusters with just one location in them rendering them impractical.

The structure of the rest of this section is as follows. In Sects. 3.1–3.5, we study five heuristic methods for clustering. For each of the five methods, we first provide a review of the algorithm and a reference for the details. Then, we provide computational experiments on our dataset, using open-source packages implemented in R. We also provide guidelines on identifying good clustering. In Fig. 2 we visualize the clustering for the five methods for $k=2,4,6$; we present the other clusters in the Appendix. We begin with a notation and definitions that are general to all the five algorithms. The five methods divide the total set of n locations into k distinct clusters, $C_1, C_2, \ldots , C_k$, where k is known. Then, $\cup _j C_j = \{ 1,2,\ldots ,n\}$ and $C_j \cap C_{j'} = \phi , \forall j,j' \in \{1,2,\ldots k\}$. Our goal is to determine the set of locations that form $C_j, \forall j =1,\ldots ,k$. The methods proceed by iteratively determining a set of locations assigned to a set of medoids, m, to form clusters. The medoid is a location that forms part of the dataset. We denote the set of locations that are not yet assigned to a medoid as “non-selected”. We calculate the total distance, $TD_j$, within cluster j at each iteration as $\sum _{p\in C_j} D_{p, m_{j}}$, and the total overall distance, $\overline{TD}$, as $\sum _{j = 1}^k TD_j$. All methods are separated into two phases — build and swap. In the build phase we determine the initial medoids, and in the swap phase we exchange these medoids until a termination criteria is fulfilled.

3.1 Partitioning around medoids

3.1.1 Background

We first employ the Partitioning Around Medoids algorithm (PAM) of Kaufman and Rousseeuw (1990). By default, PAM starts by selecting k locations from the set of n locations in a manner that “locally” minimizes the average dissimilarities of objects, see Simovici (2019) for details. We then initialize PAM by using these k locations as the initial medoids $m_1,\ldots ,m_k$. This completes the build phase. After assigning every location to a medoid, and determining $\overline{TD}$ the build phase finishes, and we update the medoids. We exchange every selected medoid successively with all non-selected locations and recompute $\overline{TD}$ for the corresponding clustering. We find the minimum of these and compare it with the $\overline{TD}$ from the previous iteration. If the minimum is less than before, we update the set the medoids and repeat the process of exchanging every selected medoid. We stop when we either reach a maximum number of iterations or when $\overline{TD}$ does not decrease further. For details on PAM, see Kaufman and Rousseeuw (1990).

3.1.2 Computational experiments

We use the implementation of PAM in R from Maechler (2019). Figure 2a presents our results for $k=2,4,6$. Loosely speaking, the clustering partitions the locations into three regions—the city center, locations to the west of the river, and locations to the north of the river. Different values of k hone in on this observation further, see Fig. A1 in the Appendix for details. We revisit this method in Sect. 4, where we determine an optimal number of clusters.

3.2 Fast partitioning around Medoids

3.2.1 Background

The Fast Partitioning Around Medoids (FPAM) algorithm is an improvement of the PAM algorithm where both the build and swap phases are improved (Schubert and Rousseeuw, 2019). In the initialization of the build phase, we choose the first medoid as the one that is closest to all the other locations. The rest of the initial medoids are determined successively by relating the minimum overall $\overline{TD}$ with the already determined medoid. The swap phase is similar to PAM in the sense that both methods choose the new candidate as the one that minimizes $\overline{TD}$ from the existing k medoids, and that the methods terminate if the revised $\overline{TD}$ is not reduced. The difference is that FPAM saves all the best candidates that are swapped for each medoid, whereas PAM saves only the single-best. FPAM proceeds by choosing one of the following two choices determined by the user: (i) swapping any of the $k-1$ medoids to the new one if $\overline{TD}$ decreases further, or (ii) exchanging only if the swap still obtains at least the same decrease in $\overline{TD}$ as before. For details on FPAM, see Schubert and Rousseeuw (2019).

3.2.2 Computational experiments

FPAM is part of the same R package as PAM (Maechler, 2019). Although FPAM is theoretically faster than PAM and capable of handling larger datasets (Schubert and Rousseeuw, 2019), in our computational experiments we do not notice any significant difference. Figure 2b presents our results for $k=2,4,6$, and Fig. A2 in the Appendix presents results for the other clusters. Most of the clusters are similar to PAM, except $k=9$ and $k=12$ where the clusters differ on the west side of the center.

3.3 Simple and fast k-Medoid

3.3.1 Background

Next, we look at the Simple and Fast k-Medoid (FKM) algorithm of Park and Jun Park and Jun (2009). FKM initializes with the k most “centered” locations as the starting medoids. To this end, it computes a metric, $v_i$, as follows:

$$\begin{aligned} v_i=\sum _{l=1}^{n}\frac{D_{l,i}}{\sum _{p=1}^{n}D_{l,p}}, i \in \{1,2,\ldots ,n \}. \end{aligned}$$

Then, we set the k locations with the smallest $v_i$ values as our starting medoids. We assign all non-selected locations to their closest medoid. We update the medoids by searching for a new medoid at every assignment; for this, we only consider the locations within the assignment. Then, we recompute $\overline{TD}$. We repeat this update-step until $\overline{TD}$ does not decrease compared to the previous iteration, or we have accomplished a maximum number of iterations. FKM has two major differences from PAM: (i) FKM only updates the medoids within the chosen clusters, and (ii) FKM updates all the medoids while PAM updates just one. For details on FKM, see Park and Jun (2009).

3.3.2 Computational experiments

FKM is implemented in R in the package “kmed” (Budiaji, 2019). We use an iteration limit of 200, although we observe the algorithm terminates before this limit is reached. Figure 2c presents our results for $k=2,4,6$, For $k=2$, FKM splits the locations nearly in half, unlike PAM and FPAM. However, for $k=3$ (see Fig. A3 in the Appendix) the partitioning is again into the three zones of the center, north of the river, and west of the river. We also observe clusters with lesser variability in the number of points, as compared to the PAM and FPAM methods; we discuss this further in Sect. 3.6, see, also Fig. 3 and Table A1 in the Appendix.

3.4 Ranked k-Medoid

3.4.1 Background

Unlike the methods in Sects. 3.1–3.3, the Ranked k-Medoid (RKM) algorithm of Zadegan et al. is not directly focused on $\overline{TD}$ (Zadegan et al., 2013). Analogous to the D matrix, here we compute a matrix R, where an entry $R_{i,j}$ shows a rank of the similarity of locations i and j. Lower ranks indicate higher similarity, and $R_{i,i} =1$. In each iteration of the method, we select a set of w “closest” locations to a given medoid $m_j$; i.e., $G_j=\{i|R_{i,m_j}=1,\dots ,w\}, \forall i\in I, \forall j=1, \ldots , k$. Similar to the $v_i$ metric in Sect. 3.3, we compute a metric—the hostility value—for all locations in $G_j$ as follows:

$$\begin{aligned} h_{ik}=\sum _{l\in G_j}R_{i,l} , \forall i\in G_j, \forall j=1, \ldots , k. \end{aligned}$$

The hostility value, h, suggests a degree of dissimilarity of location i to the others within $G_j$. To update the medoids, we select the new medoid as the location with the highest hostility value; in the event of a tie, we pick one arbitrarily. We then assign each non-selected location to the medoid with the smallest R value. The choice of the parameter w influences the resulting clusters and the speed of the algorithm. For details on RKM, see Zadegan et al. (2013).

3.4.2 Computational experiments

RKM is available in R using the same package as FKM (Budiaji, 2019); here, it is suggested to keep the parameter w between 5 and 15. We choose $w=5$ for our computational experiments as the total number of our locations is less than that used in Zadegan et al. (2013). We use the same iteration limit of 50 as Zadegan et al. (2013). Unlike the methods in Sects. 3.1–3.3, the output of RKM is not deterministic; i.e., we do not get back the same clustering for every run. This is due to the fact that RKM starts with a set of random locations, and the search space is limited to the set $G_j$. An artifact of this randomness is that we tend to get outliers that are farther away from the other clusters. Figure 2d presents one example of a clustering obtained via RKM.

3.5 Improved k-Medoids

3.5.1 Background

The fifth clustering method we summarize is the Improved k-Medoids (IKM) algorithm of  Yu et al. (2018). The IKM algorithm is based on the FKM and primarily differs in the selection of the initial medoids. Yu et al. define the variance of a location i as (Definition 2 Yu et al. (2018)):

$$\begin{aligned} \sigma _i := \sqrt{\frac{1}{n-1} \sum _{l=1}^n D_{i,l}^2}\quad \forall i= \{1,\ldots ,n\}, \end{aligned}$$

and the variance of a dataset as

$$\begin{aligned} \sigma := \sqrt{\frac{1}{n-1} \sum _{i=1}^n D_{i,m^*}^2}, \end{aligned}$$

where $m^*$ is the mean of the dataset. Given a parameter $\alpha$, the candidate subset of medoids is defined as:

$$\begin{aligned} S_m = \{i| \sigma _i \le \alpha \sigma , i= 1, 2, \ldots , n \}. \end{aligned}$$

The set $S_m$ contains all locations that are possible choices for medoids. Outliers are avoided inclusion in the set $S_m$ using small values of $\alpha$. IKM initializes by choosing two medoids, and then sequentially adding one until all k medoids are chosen. The first medoid, $m_1$, is chosen as:

$$\begin{aligned} m_1= {{\,\mathrm{arg\,min}\,}}_{i\in S_m}{\sum _{l=1}^{n}D_{i,l}}. \end{aligned}$$

The second medoid, $m_2$, is chosen farthest away from $m_1$ to reduce the likelihood of both $m_1$ and $m_2$ being in the same cluster:

$$\begin{aligned} m_2={{\,\mathrm{arg\,max}\,}}_{i\in S_m} D_{i,m_1}. \end{aligned}$$

Then the method proceeds iteratively. We first select a candidate, $m_j'$, in each of the given $2 \le k' \le k$ medoids as $m_j'={{\,\mathrm{arg\,max}\,}}_{l\in C_j\cap S_m}D_{l,m_j}$ with $j \in \{1,\dots ,k'\}$. Then, we determine the next initial medoid as follows:

$$\begin{aligned} m_{k'+1}={{\,\mathrm{arg\,max}\,}}_{j \in \{1,2,\ldots ,k'\}} D_{m_j,m_j'} \end{aligned}$$

We repeat this process until $k'=k$. This finishes the build phase as all initial medoids are determined. The swap phase for our implementation of IKM is the same as that of the FKM method we describe in Sect. 3.3.1. For details on IKM, see Yu et al. (2018).

3.5.2 Computational experiments

IKM is also available in R in the same package as FKM and RKM (Budiaji, 2019). Although Yu et al. (2018) recommend a value of $\alpha$ between 1.5 and 2.5, the default value for $\alpha$ in the R package is 1 (Budiaji, 2019). However, the default value of $\alpha =1$ results in only a single value within the candidate set $S_m$, while $\alpha =1.1$ and $\alpha =1.5$ result in 75 and 172 values, respectively. In this sense, we find the recommendation of  Yu et al. (2018) more helpful than the default value of $\alpha$ in the R package. In Fig. 2e and f we present results for $\alpha = 1.1$ and $\alpha = 1.5$, respectively, for $k=2,4,6$.

Fig. 3

Comparison of the standard deviation (y-axis) of the number of locations in different clusters (x-axis) for the different clustering methods

3.6 Summary of computational experiments

In this section, we seek to compare the quality of the clustering by the five methods we describe above. In Sects. 3.1–3.5 we see that that the methods can lead to widely different clusters. One measure of the variability in the clustering is the dispersion of the number of locations in each cluster. Figure 3 plots the standard deviation of the number of locations in each cluster for PAM, FPAM, FKM, and two runs of IKM with $\alpha =1.1,1.5$; see also, Table A1 in the appendix. Since RKM returns a random output for each run, we do not include it in Fig. 3. For $k=2$, the methods result in contrasting clusters. PAM, FPAM, IKM with $\alpha =1.5$ split the locations to the west and east of the river, while FKM and IKM with $\alpha =1.1$ split the locations in the center to get two nearly similar sized clusters. This is reflected in the large and small standard deviations in Fig. 3 for $k=2$. For $k=3$, the distributions between the methods are again not similar. PAM, FPAM, IKM with $\alpha =1.5$ split the locations into the west of the river, the north of the river, and the center; while FKM splits the locations to the west and IKM with $\alpha =1.1$ the north section away from the center with the rest in half. For $k=4$, all methods separate the locations to the west of the river, north-east of the city center, and two clusters in the center. For $k>4$, the clusters do not differ widely. They have a similar structure and split the locations in the center into smaller clusters. The standard deviation of the locations in a cluster in Fig. 3 further suggests that PAM and FPAM are similar; we also discuss this in Sect. 3.2.2. For the two IKM methods, we notice little variation in the clustering from Fig. 3 when k is large; i.e., the $\alpha$ value ceases to create a significant effect.

We conclude this section with a summary of the five clustering methods we consider in Table 1.

Table 1 Summary of five clustering methods described in Sect. 3

4 Answering Q.2: number of clusters

In this section, we build on the results of Sect. 3 and seek to answer question Q.2 from Sect. 1. To this end, we describe three quantitative tests that determine an optimal number of clusters. The tests determine this optimal k—that we denote as $k^*$—based on a given clustering; thus, the answers to questions Q.1 and Q.2 depend on each other. Here, we employ each of the five the methods of Sect. 3 for $k=2,3,\ldots ,20$ and then for every method determine $k^*$ using the three tests. Unfortunately, in practice, these tests do not always lead to the same $k^*$. We thus provide guidance on selecting $k^*$ by summarizing our reasons for choosing $k^*=4$.

The structure of this section is similar to that of Sect. 3. We first provide a short review of the three tests for determining $k^*$ and references for the details. Then, we provide computational experiments on our dataset, and analyze the clustering provided by the five methods in Sect. 3. As we mention in Sect. 3.4, the RKM outputs a different clustering for each run. Thus, we run RKM a thousand times and compute the frequency of $k^*$. For the IKM, we compute $k^*$ for both $\alpha =1.1$ and $\alpha =1.5$. This provides us $k^*$ for each of the five methods for each of the three tests. Finally, we provide guidance on determining $k^*$ when the different tests provide conflicting results. Figure 5 summarizes our results of this section, and we explain this figure below.

4.1 Elbow method

4.1.1 Background

The Elbow Method (EM) serves as a simple visual guide to determine $k^*$ and relies on “statistical folklore” (Tibshirani et al., 2001). The method is remarkably simple in the sense that the only parameter required is $\overline{TD}_k$ — the total distance when the dataset is clustered into k clusters. Then, the EM compares the trade-off between k and $\overline{TD}_k$ by computing an “elbow”. To this end, we plot $\overline{TD}_k$ and identify the first k where the angle is larger than the one before and after; this point determines $k^*$. With this intuition, we formalize the concept of an elbow or a bend in Fig. 4. Then, the angle $\beta _k$ is $180^{\circ } + \tan ^{-1}( \frac{1}{\overline{TD}_{k-1} -\overline{TD}_k})- \tan ^{-1}( \frac{1}{\overline{TD}_k -\overline{TD}_{k+1}})$ for cluster k; here $\tan ^{-1}(\cdot )$ denotes the inverse tangent of its argument. The elbow method chooses $k^* = \min \{k: \beta _k< \beta _{k-1}, \beta _k < \beta _{k+1} \}$.

Fig. 4

An explanatory figure for the Elbow Method. For details, see Sect. 4.1

4.1.2 Computational results

First, for the thousand runs of RKM the EM suggests $k^*= 2,3,4,5,6$ in 163, 449, 303, 73, 12 of these runs, respectively. Thus, overall the EM suggests $k^*=3$ or $k^*=4$ for the RKM, with a preference towards $k^*=3$. Next, Fig. 5a presents our results for the EM for the other four methods. The circles provide the values of $k^*$. Here, the EM suggests $k^*=4$ for PAM, FPAM, FKM, and IKM with $\alpha =1.1$; however, the EM suggests $k^*=3$ for IKM with $\alpha =1.5$.

4.2 Average Silhouette method

4.2.1 Background

The Average Silhouette Method (ASM) provides a metric of the relative fit of a location in its own cluster versus its fit in other clusters. Given a clustering of locations into k clusters, consider the following two quantities: (i) $a_{ik} =\frac{1}{|C_j|} \sum _{l\in C_j }D_{i,l}, \forall i\in C_j, j=2,\ldots ,k$, and (ii) $b_{ik} =\min _{h \in \{1,2,\ldots ,k\}; h \ne j} \frac{1}{|C_h|} \sum _{l \in C_h} D_{i,h}, \forall i\in C_j, j=2,\ldots ,k$. Then, $a_{ik}$ denotes the average distance of location i to other locations within its own cluster, while $b_{ik}$ denotes the minimum average distance of location i to any cluster except its own. The silhouette coefficient for the ASM is defined as

$$\begin{aligned} s_{ik} = \frac{b_{ik}-a_{ik}}{\max \{ a_{ik},b_{ik} \} }, \forall k, \forall i =1,2,\ldots ,n. \end{aligned}$$

Then, $-1 \le s_{ik} \le 1$. A value of $s_{ik}$ close to one suggests a good clustering as the locations are relatively closer to their own cluster than others, while a value close to minus one suggests a poor clustering. To determine $k^*$, we choose the clustering that provides the maximum average silhouette value; i.e., $k^* = \frac{1}{n} {{\,\mathrm{arg\,max}\,}}_{k} \sum _i s_{ik}$. For details on the ASM, see Rousseeuw (1987).

4.2.2 Computational results

470 of the thousand runs of the RKM with the EM suggest $k^*= 2$, while 123 runs suggest $k^*=3$. The remaining runs do not have a clear consensus. Hence, the RKM suggests $k^*= 2$ with the ASM. For the other four methods, Fig. 5b presents a plot of the average value of $s_{ik}$ versus k. Again, the circles provide the values of $k^*$. Here, the ASM computes $k^*=3$ for PAM, FPAM, and IKM with $\alpha =1.5$, while the ASM computes $k^*=4$ for FKM and IKM with $\alpha =1.1$.

4.3 Gap statistic method

4.3.1 Background

The third method we study to determine $k^*$ is the Gap Statistic Method (GSM) of Tibshirani et al. (2001). Similar to the ASM, given a clustering of locations into k clusters, there are two quantities we consider in the GSM. First, let $W_k=\sum _{j=1}^{k}\frac{1}{2 |C_j|}\sum _{i,l\in C_j}D_{i,l}$ be the within-cluster sum of distances. Next, we seek to determine the deviation of $W_k$ from a reference. We do so by generating B reference datasets; let ${W_k^*}_b$ with $b=1,\ldots ,B$ be the within-cluster distances for the $b^\text {th}$ reference data set.

Next, we compute three key quantities:

• (i) $Gap_k =\frac{1}{B}\sum _{b=1}^{B}(\log {W_k^*}_b) - \log W_k$,

• (ii) $sd_k = \sqrt{\frac{1}{B}\sum _{b=1}^{B} \big ( \log {W_k^*}_b-\frac{1}{B}\sum _{b=1}^{B}\log {W_k^*}_b \big )^2}$,

• (iii) $se_k = \sqrt{1+\frac{1}{B}} sd_k$.

Then, $k^*$ is the smallest k such that ${Gap}_k \ge {Gap}_{k+1} - se_{k+1}$ is satisfied. For details on the GSM, see Tibshirani et al. (2001).

4.3.2 Computational results

We use $B=500$ for our computational experiments with the GSM. For the RKM, we use the same 500 reference datasets. In the thousand runs, the GSM computes $k^*=2,3,4,5$ in 858, 134, 7, 1 of the runs, respectively; i.e., we conclude $k^*=2$ for the RKM. For the other four methods ², Fig. 5c presents the values of ${Gap}_k$ with circles indicating $k^*$. Here, the GSM suggests $k^*=3$ for IKM with $\alpha =1.5$; however, the GSM computes $k^*=4$ for consistently for all the other methods.

Fig. 5

a Elbow Method. $k^*$= 3 for IKM with $\alpha =1.5$, while $k^*$= 4 for PAM, FPAM, FKM and IKM with $\alpha =1.1$. b Average Silhouette Method. $k^*$= 3 for PAM, FPAM, and IKM with $\alpha =1.5$, while $k^*$= 4 for FKM and IKM with $\alpha =1.1$. c Gap Statistic Method. $k^*$= 3 for IKM with $\alpha =1.5$, while $k^*$= 4 for PAM, FPAM, FKM and IKM with $\alpha =1.1$. Comparison of three methods to determine an optimal number of clusters, $k^*$. The x-axis denotes the number of clusters, while the y-axis denotes the corresponding metric. The circles indicate $k^*$. For details, see Sect. 4

4.4 Summary of computational results

The three methods in Sects. 4.1–4.3 suggest different choices of $k^*$; in this section, we summarize our key results and provide a reasoning for our final choice of $k^*$. Table 2 provides a summary; here, the suggested $k^*$ for the RKM is the one suggested in most of its thousand runs. Excluding the RKM—given its different outputs for every run—our choice of $k^*$ is then between $k^*=3$ or $k^*=4$. From the 18 instances in Table 2, 10 suggest $k^*=4$. Further, EM and GSM provide a strong suggestion indication for $k^*=4$ across all the methods except RKM and IKM with $\alpha =1.5$. Thus, we decide in the favor of $k^*=4$ and answer question Q.2.

Given $k^*=4$, we next seek to answer question Q.1—specifically, which method’s clustering with $k^*=4$ do we choose? We observe that FKM and IKM with $\alpha =1.1$ result in $k^*=4$ for all the three methods. Further, both the FKM and IKM have the same set of medoids. Thus, we use the clusters provided by the clustering methods FKM and IKM with $k^*=4$. Although we presented these clusters in Fig. 2, for the sake of clarity we present these again in Fig. 6a and denote them as $C_1$ (red), $C_2$ (green), $C_3$ (blue), $C_4$ (yellow), respectively. Clusters $C_1$ and $C_4$ are the larger clusters, and both are located in the center of the city; these include 77 and 113 locations, respectively. Clusters $C_2$ and $C_3$ are significantly smaller with 23 and 24 points, respectively; these are located in the west and northeast, respectively.

Table 2 Suggested optimal number of clusters for the different clustering methods of Sect. 4

Fig. 6

a The four optimal clusters. For details, see Sect. 4.4b The shortest tours for the four clusters. For details, see Sect. 5.5. The four optimal clusters of the 237 locations in Perm — $C_1$ (red), $C_2$ (blue), $C_3$ (green), and $C_4$ (yellow)

Some existing work on clustering algorithms within the routing literature also considers the notion of fairness. This is especially pervasive in works on wireless sensor networks, see, e.g., (Haseeb et al., 2017; Jiang et al., 2009; Zahedi et al., 2016). Nallusamy et al. (2010) study a problem with multiple traveling salesman where each salesman visits the same number of locations. Such concerns are beyond the scope of our work, but can be easily incorporated by using a so-called balanced k-means clustering method (Malinen and Fränti, 2014). Then, the clusters have an equal number of locations.

We conclude this section with a summary of the three methods we consider in Table 3.

Table 3 Summary of three methods described in Sect. 4 to determine an optimal number of clusters

5 Answering Q.3: routing within clusters

In Sects. 3 and 4, we distribute our data locations into four clusters with the idea that each cluster is served by a single vehicle. In this section, we determine the optimal tour for a vehicle within a cluster by solving a TSP. To assist practitioners, we restrict ourselves to open-source and pre-implemented solvers for the TSP that are available in R. We use five methods—Nearest Neighbor, Nearest Neighbor Repeat, Nearest Insertion, Farthest Insertion, Cheapest Insertion, Arbitrary Insertion, and Two-Opt—all of which are included in the “Traveling Salesperson Problem - R package” (Hahsler and Hornik, 2020) (henceforth, “TSP-Package”). Since all of these methods are heuristics without a guarantee of finding the optimal route, we next compare the respective tours with an optimal tour. To this end, we determine the optimal tour using the so-called subtour elimination method from  Miller et al. (1960), using an implementation in GAMS (Rosenthal (2007); GAMS (2020)).

We employ a similar structure for this section as that of Sects. 3 and 4. We first provide a short review of the heuristic methods tests for determining the routing, and then we provide computational experiments on our dataset. As the heuristics can return a different tour for each run, we repeat each of the heuristics 5000 times for our results to have a statistical relevance. Table 5 summarizes our results, and we discuss this in greater detail below. Next, in Sect. 5.5 we compare the quality of the heuristic tours against an optimal routing. In Sect. 5.6 we repeat our computational experiments, but without clustering and then compare our overall tour lengths.

5.1 Nearest neighbor

5.1.1 Background

The Nearest Neighbor (NN) heuristic starts with an arbitrarily chosen location. The method iterates by successively adding the nearest location, that is not yet included, to the last added location. The process repeats until all the locations are included, and a tour is formed. Despite the heuristic’s simplicity, a performance guarantee on the tour length is available, see Table 4. For details on NN, see Bellmore and Nemhauser (1968).

Table 4 Summary of some performance guarantees for heuristics discussed in Sect. 5

5.1.2 Computational experiments

Two versions of NN are available in the TSP-Package: (i) the plain NN that we describe in Sect. 5.1.1, and (ii) a version where every possible location is used as the initial starting point, we denote this version as “Nearest Neighbor Repeat” (NNR). In NNR, the minimum tour length over all initial locations is returned; thus, if the number of locations is small then NNR is advisable over NN. Also, NN can return tours within a wide range due to the arbitrary choice of the initial point. Since NNR returns the best possible tour available from NN at each run, there is no dispersion in its output. See the first two rows of Table 5 for details.

5.2 Nearest insertion, farthest insertion, cheapest insertion, and arbitrary insertion

5.2.1 Background

Insertion methods work on the principle of greedily “inserting” a location, p, to an existing edge connecting locations i and j such that the quantity $D_{i,p}+D_{p,j}-D_{i,j}$ is minimized. Thus, at each iteration, the size of an existing tour size is increased by one location and exactly one existing edge is updated. The second row of Table 4 provides a performance guarantee for any insertion method.

We use four insertion methods as heuristics for solving our TSP. In the Nearest Insertion (NI) heuristic, we choose the location closest to the existing location in the tour. In the Farthest Insertion (FI) heuristic, we choose the location farthest to the locations in the tour. In the Cheapest Insertion (CI) heuristic, we choose the location where the cost or gain of tour length is the minimum, while in the Arbitrary Insertion (AI) heuristic, we choose an arbitrary location that is not part of the existing tour. For more details on insertion methods, see, e.g., Bentley (1992); Rosenkrantz et al. (1977).

5.2.2 Computational experiments

The third to sixth rows of Table 5 provide results of our computational experiments for the four insertion methods. For cluster $C_2$ the four insertion methods provide nearly the same results; the dispersion between the maximum (24.59 kms) and minimum (23.80 kms) tour lengths is less than a kilometer. For the other three clusters, we observe NI performs worse than FI; the maximum tour length of FI is less than the minimum tour length of NI. Thus, we prefer FI over NI for these three clusters. FI also performs better in a comparison with CI—for $C_3$ the worst tour of FI is nearly half a kilometer better than the best tour of CI, and for $C_1$ the worst tour of FI is only 120 meters more than the best tour of CI. The average tour length for CI is over 4.5 kms more than that of FI. Although the minimum tour lengths of AI are the best of the four insertion methods, it has a high variance reflected in large ranges of tour lengths.

5.3 Two-Opt

5.3.1 Background

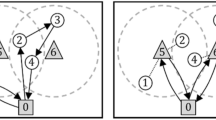
The Two-Opt (2O) method is based on Croes (1958). The method seeks to improve already existing tours by inverting edges; i.e., we remove two edges and reconnect them in the opposite order, thereby inverting the order for a part of the tour. We explain this with an example. Consider the tour $1,2,\dots 12,1$ in Fig. 7a. Assume that we remove the two edges between locations 3, 4 and 9, 10. Now, we reconnect the locations to have two new edges—3, 9 and 4, 10—and we invert the direction of the tour between 4 and 9. Thus, the new tour is 1, 2, 3, 9, 8, 7, 6, 5, 4, 10, 11, 12, 1, see Fig. 7b.

Fig. 7

a before b after. Example of one iteration for the 2O heuristic. The edges connecting the locations a, b, c, d are changed. For details, see Sect. 5.3.1

In general, we only switch the edges if there is a decrease in the length of a tour; i.e., $D_{a,b}+D_{d,c}>D_{a,d}+D_{b,c}$, with a, b, c, d defined as in Fig. 7. We improve until the result is “two-optimal”; i.e., the tour length can not decrease further with these two-edge inversions. For a so-called “metric” TSP, where the distances satisfy the triangle inequality, Table 4 provides a performance guarantee for 2O; i.e., the ratio of the length of a tour with n locations calculated by 2O to that of an optimal tour is no more than $\sqrt{\frac{n}{2}}$.

5.3.2 Computational experiments

In the TSP-Package, 2O heuristic is initialized with an arbitrary tour that is then improved until it is two-optimal. The seventh row in Table 5 presents our results. The 2O heuristic results in tour lengths of a wide range, e.g., $C_1$ has a range of almost 14 kms that is 30% of the minimum tour. This observation leads to the conclusion that 2O is strongly dependent on the initial tour.

Since we already have tours from six heuristics in Sects. 5.1–5.2, we now use them as the initial tours for the 2O method. We denote these new schemes as 2ONN, 2ONNR, 2ONI, 2OFI, 2OCI, 2OAI. The last six rows of Table 5 present these results. The cluster $C_2$ has short tour lengths already for all the heuristics with a dispersion of less than 5%. For the other methods, the mean and maximum tour length both decrease after implementing 2O; e.g., for $C_1$ the mean tour length drops from 56.21 with NN to 49.80 with 2ONN. As the 2O heuristic is guaranteed to improve a tour, we suggest additionally using the 2O heuristic after running any other heuristic method.

Table 5 Summary of the computational results of the 13 heuristic methods for TSP presented in Sects. 5.1–5.3 using 5000 runs

5.4 Choice of the best heuristic

In this section, we employ statistical tests to compare the optimal tours obtained from the various heuristics against each other. First, we determine if the tour lengths across the 13 heuristics indeed differ. We have 5000 runs for each of the four clusters for the 13 methods. To this end, we use the Friedman Rank Test with $n=5000$ samples and $k=13$ groups (Friedman, 1937). The null hypothesis for this test is that the heuristics produce identical tours; from Table 5 we do not expect this hypothesis to hold. Indeed, the null hypothesis is rejected for each of the four clusters with p-values of practically zero. Thus, there is statistically significant evidence to suggest that the choice of the heuristics affects the optimal tour lengths. The next question is if a single heuristic method can be declared as the one that provides the best tour. We seek to determine this in the current section.

From Table 5, we observe that 2OAI achieves the minimum tour length across all the 13 methods for $C_1$ and $C_4$. For $C_2$ and $C_3$, 2OAI again achieves the minimum tour length—this minimum tour length is also achieved by four and eight other heuristics for $C_2$ and $C_3$, respectively. To validate this good performance of 2OAI, we further employ a statistical test. To this end, let $\mu _X$ and $\mu _Y$ denote the mean length of a tour found by heuristic X and Y over 5000 runs. Then, consider the following null and alternative hypotheses:

$$\begin{aligned} H_0: \, \,&\mu _X =\mu _Y \\ H_A: \, \,&\mu _X \ne \mu _Y. \end{aligned}$$

For $Y= \texttt {2OAI}$, we test all four clusters and all the 13 heuristics, at a significance level of $\alpha =5\%$, and compute a z-score. For the large sample size of 5000, a normal distribution suffices instead of a Student-t distribution. Three cases exist:

• (i) $-1.96<z <1.96$; i.e., we have no statistical significant evidence to reject $H_0$.

• (ii) $z<-1.96$; i.e., we have statistically sufficient evidence to reject $H_0$, and conclude that method X performs better than Y,

• (iii) $z>1.96$; i.e., we have statistically sufficient evidence to reject $H_0$, and conclude that method X performs worse than Y.

For $C_1$, we are in the third case for all the heuristics except 2OFI. Thus, we next test the hypotheses with $Y=\texttt {2OFI}$. Then, we are always in the third case; thus, we conclude that the mean tour length obtained using 2OFI is statistically shorter than any other method for $C_1$. This trend repeats for $C_2$ as well. Analogously for $C_3$, for $Y=\texttt {2OAI}$ and $X= \texttt {NNR}, \texttt {FI}, \texttt {2ONNR}, \texttt {2OFI}, \texttt {2OCI}$ we are in the second case. Repeating the process with $Y= \texttt {2ONNR}$, we are always in the third case; i.e., we conclude the mean tour length obtained using 2ONNR is statistically shorter than any other method for $C_3$. Similarly, for $C_4$ we conclude the winner is 2OAI.

To summarize, we have statistically significant evidence to conclude that, on average, the shortest tours for clusters $C_1,C_2,C_3,C_4$ are determined by 2OFI, 2OFI, 2ONNR, and 2OAI, respectively. This is loosely reflected in Table 5 as well—the upper limit of 95% CI of the best-performing heuristic is lower than the lower limit of the competing methods. Had we not employed a statistical test we could have erroneously concluded 2OAI as the best performing heuristic.

5.5 Shortest tours

5.5.1 Background

As we describe above, the heuristics offer the advantage of simplicity and solutions can be obtained using open-source solvers. However these advantages come at the expense of a suboptimal tour. We now benchmark the tours computed by the heuristic methods by comparing them with the shortest possible tours. Finding an optimal tour of the TSP requires the so-called subtour elimination constraints (SECs) that eliminate any tours not involving the entire set of considered locations.

Let $x_{i,j}=1$ if location i is directly connected to location j in a tour, and 0 otherwise. And, let $u_i$ denote the position of node i in the tour, with $i>1$. Then, model 2 presents a formulation of the TSP (Miller et al., 1960).

(2a)

(2b)

(2c)

(2d)

(2e)

(2f)

(2g)

Constraints (2b)–(2c) ensure that each location is visited only once, while constraints (2d)–(2f) are the SEC from Miller et al. (1960). The objective function in (2a) minimizes the total tour length.

5.5.2 Computational experiments

We solve model 2 with $n=|C_j|, j=1,\ldots ,4$ for the clusters we present in Sect. 3. We use the pre-implemented TSP solver—“Traveling Salesman Problem - Five” (GAMS, 2020)—in the modeling language GAMS; this solver is again based on the formulation by Miller et al. (1960). Table 6 presents the lengths of optimal tours.

Table 6 Optimal tour lengths for the four clusters

From Tables 5 and 6 we observe that at least one of the heuristics manages to obtain the optimal tour for clusters $C_1$, $C_2$, and $C_3$. For cluster $C_4$—the largest cluster with 113 locations—none of the heuristics manage to determine the optimal tour for this cluster in any of their 5000 runs. Our preferred method 2OAI falls short by 0.5% from the optimal, however the mean tour length is significant larger by 5.6%. For cluster $C_1$—with 77 locations—2OAI finds the optimal tour. Our choice of the best performing heuristic, 2OFI, could not find the optimal tour and its shortest tour is 0.5% larger. However, the mean tour lengths for 2OAI and 2OFI are 4.2% and 3.3% away from the optimal, lending credence to our choice of 2OFI as a preferred method in Sect. 5.4. For cluster $C_2$—the smallest cluster with 23 locations—five of the 13 heuristic methods find the optimal tour. The mean of our preferred method, 2OFI, falls short by less than 0.01% from the optimal tour length. For cluster $C_3$—with 24 locations—ten of the thirteen methods find the optimal tour. 2ONNR, our preferred method, finds the optimal tour as well.

Summarizing the the total tour length over the four clusters by the use of the preferred heuristics from Sect. 5.4 is in the range (161.93,162.02). The optimal tour length over the four clusters is 157.67; i.e., the best heuristics are worse by at least 4.26 kms and at most 4.35 kms.

5.6 A tour without clustering

5.6.1 Background

In the preceding sections, to satisfy the needs of our particular problem’s application, we solve a TSP separately on our four clusters assuming a different vehicle serves each cluster. Next, we solve a single TSP over the entire set of locations to provide another benchmark for our four tours. Both versions of the problem have the same number of edges. If clusters are far away from each other, with few outliers close to other clusters, then the total tour length of the cluster-first route-second version is expected to be shorter than that of the benchmark version. However, if our clustering is poor and with locations closer to other clusters, we expect the benchmark version to provide a shorter tour length. This intuition serves to provide another indicator of the quality of clustering.

Table 7 Analogous results to Table 5 for the 13 heuristic methods without clustering

5.6.2 Computational experiments

We again use 5000 runs for the 13 heuristic methods. Table 7 presents results analogous to Table 5. In Table 7, the maximum tour lengths for 2ONNR and 2OFI are less than the minimum tour length for NN, NNR, NI, CI, and 2ONI, while the best tour—with a length of 155.42 kms—is determined by 2OAI. We further determine the optimal tour length using the method we present in Sect. 5.5.1 with a length of 153.48 kms; i.e., in this case our heuristics are at least 2 kms worse. Summarizing, the shortest total tour length by the use of heuristics for the cluster-first route-second version is 157.91 kms (optimal tour length = 157.67 kms), while that of the benchmark is 155.42 kms (optimal tour length = 153.48 kms). These numbers further signify that open-source and already implemented heuristics have the potential to quickly obtain near-optimal solutions in practical instances.

6 Conclusion

In this article, we present a review and a practical guide on the use of heuristics and open-source solvers for a problem of collecting and dispersing cash from POSs using a fleet of vehicles. We use data from the city of Perm, and empirically study the relationship of our problem to the standard TSP and VRP. Our analysis demonstrates that, despite the relatively small-sized problem we consider, a single heuristic does not uniformly perform the best. The ease of understanding of methods by a practitioner—as well as the application—guides our choice of the clustering; and, visual illustrations, such as the ones we present in this work, assist in the decision-making process. Heuristics can fail to be optimal especially when the number of data points is large. Yet, there are several grounds that encourage their use. First, heuristics present an easy way for a practitioner to understand both the clustering and the TSP. Second, heuristics have a direct and an open-source implementation available in many programming languages, such as R, thereby allowing a straightforward application.

Our study has several limitations. Since we optimize based on the estimated distances between the locations, we exclude several other aspects such as the amount of cash to restock or withdraw from the POSs, time windows of delivery, and limits of cash a vehicle is allowed to carry. Further, we ignore service hours of banks, shift length of the drivers, and service times at each stop. Finally, the use of the great circle distance instead of the actual road distance occasionally provides tours that cross the river over points that are not directly connected. Future work could incorporate such extensions.

All our codes are publicly available at: https://github.com/Oberfichtner/Clustering_and_TSP_with_R.git.