The nucleolus and inheritance of properties in communication situations

Abstract

This paper studies the nucleolus of graph-restricted games as an alternative for the Shapley value to evaluate communication situations. We focus on the inheritance of properties of cooperative games related to the nucleolus: strong compromise admissibility and compromise stability. These two properties allow for a direct, closed formula for the nucleolus. We characterize the families of graphs for which the graph-restricted games inherit these properties from the underlying games. Moreover, for each of these two properties, we characterize the family of graphs for which the nucleolus is invariant

1 Introduction

In a cooperative game with transferable utility, players can coordinate their actions and in particular obtain a joint monetary profit as a group. One of the main issues in cooperative game theory is the allocation of this joint profit among the players, taking into account the economic possibilities of all coalitions. Two distinguished solutions that solve this issue are the Shapley value (cf. Shapley , 1953) and the nucleolus (cf. Schmeidler , 1969).

Myerson (1977) extended cooperative games by introducing communication situations in which the communication restrictions of the players are modeled by a communication graph. The corresponding graph-restricted game is a modified cooperative game in which the communication restrictions are taken into account.

The Myerson value (cf. Myerson , 1977) of a communication situation is defined as the Shapley value of the corresponding graph-restricted game. This value is axiomatically characterized by Myerson (1980) and studied in several other contexts as well: hypergraphs (cf. van den Nouweland et al. , 1992), union stable structures (cf. Algaba et al. , 2001), antimatroids (cf. Algaba et al. , 2004), bipartite graphs (cf. van den Brink & Pintér, 2015), two-level communication structures (cf. van den Brink et al. , 2016) and communication situations in which the players have different bargaining abilities (cf. Manuel & Martín, 2021). Moreover, several studies are devoted to the inheritance of properties of cooperative games that are related to the Shapley value. In particular, Owen (1986) studied the inheritance of superadditivity, van den Nouweland and Borm (1991) studied convexity and Slikker (2000) studied, among others, average convexity. The inheritance of convexity is also studied in a unified approach by Algaba et al. (2001).

Also the nucleolus is studied in the context of communication situations. Potters and Reijnierse (1995) showed that the nucleolus is the unique element of the kernel if the communication graph is a tree. Reijnierse and Potters (1998) and Katsev and Yanovskaya (2013) studied the collection of coalitions that determine the nucleolus and prenucleolus, respectively. Khmelnitskaya and Sudhölter (2013) provided an axiomatic characterization of the prenucleolus for games with communication structures. Instead, we follow the lines initiated by Owen (1986) and focus on the inheritance of two properties of cooperative games that are related to the nucleolus. Moreover, we study the invariance of the nucleolus, that is, the feature that the nucleolus of the graph-restricted game equals the nucleolus of the underlying game of a communication situation.

For the inheritance, we concentrate on the properties strong compromise admissibility and compromise stability. In general, computing the nucleolus of a cooperative game is not straightforward. However, interestingly, for cooperative games satisfying strong compromise admissibility or compromise stability, there exists a direct, closed formula for the nucleolus, based on the Talmud rule for bankruptcy problems (cf. Quant et al. , 2005) and (cf. Driessen , 1988). In particular, when these properties are inherited, computation of the nucleolus can still be facilitated. For strongly compromise admissible games it holds that the nucleolus coincides with the compromise value (cf. Tijs , 1981), which can be directly computed using the utopia vector, as shown by Driessen (1988). Furthermore, Driessen (1988) also showed that strongly compromise admissible games are characterized by their core allocations. The class of strongly compromise admissible games contains for example the class of simple games with one veto-player, while the larger class of compromise stable games contains several interesting classes of economic games, like big boss games (cf. Muto et al. , 1988), clan games (cf. Potters et al. , 1989) and bankruptcy games (cf. O’Neill , 1982) and (cf. Curiel et al. , 1987).

With regard to strong compromise admissibility, we show that the graph-restricted game is strongly compromise admissible for every communication situation with an underlying strongly compromise admissible game, if the graph is biconnected. In fact, for every connected graph that is not biconnected, we explicitly construct a communication situation with an underlying strongly compromise admissible game such that the graph-restricted game is not strongly compromise admissible.

To ensure compromise stability for the graph-restricted game of a communication situation with an underlying strongly compromise admissible game, the connected graph needs to be biconnected or a star. Again, for every connected graph that is not biconnected and not a star, we explicitly construct a communication situation with an underlying strongly compromise admissible game such that the graph-restricted game is not compromise stable.

Finally, we show that the graph-restricted game is compromise stable for every communication situation with an underlying compromise stable game, if the graph is complete. For every connected graph that is not complete (and has at least four players), we explicitly construct a communication situation with an underlying compromise stable game such that the graph-restricted game is not compromise stable.

For the invariance of the nucleolus, we identify families of graphs for which it is guaranteed that the nucleolus of the graph-restricted game equals the nucleolus of the underlying game for communication situations with an underlying strongly compromise admissible or compromise stable game. We use the inheritance results to employ the direct formula for the nucleolus for both the graph-restricted game and the underlying game. We show that the nucleolus is invariant for all communication situations with an underlying strongly compromise admissible game, if the graph is biconnected. For every connected graph that is not biconnected, we construct a communication situation with an underlying strongly compromise admissible game such that the nucleolus of the graph-restricted game is not equal to the nucleolus of the underlying game. For communication situations with an underlying compromise stable game, we show that the connected graph needs to be complete in order to guarantee the invariance of the nucleolus. That is, we prove the invariance of the nucleolus if the graph is complete and for every connected graph that is not complete, we provide a communication situation with an underlying compromise stable game such that the nucleoli are different.

This paper is structured in the following way. Section 2 provides all relevant preliminaries on cooperative game theory and graph theory. Section 3 studies the inheritance of strong compromise admissibility and compromise stability. Section 4 studies the invariance of the nucleolus. Finally, Section 5 contains the concluding remarks.

2 Preliminaries

A (transferable utility) cooperative game is a pair (N, v) where N is a non-empty, finite set of players and $v:2^N\rightarrow \mathbb {R}$ is a characteristic function with $v(\emptyset )=0$. Here, $2^N$ is the collection of all subsets (called coalitions) of N and v(S) is the worth of coalition $S\in 2^N$, representing the joint monetary rewards this coalition can obtain on its own. The class of all cooperative games with player set N is denoted by $TU^N$, and a cooperative game (N, v) is also denoted by $v\in TU^N$.

For a cooperative game $v\in TU^N$, the imputation set is given by

$$\begin{aligned} I(v) = \left\{ x\in \mathbb {R}^N \ \Big |\ \sum _{i\in N} x_i = v(N) \text { and } x_i \ge v(\{i\} ) \text { for all } i\in N \right\} , \end{aligned}$$

the core (cf. Gillies , 1959) is given by

$$\begin{aligned} C(v) = \left\{ x\in \mathbb {R}^N \ \Big |\ \sum _{i\in N} x_i = v(N) \text { and } \sum _{i\in S} x_i \ge v(S) \text { for all } S\in 2^N \right\} , \end{aligned}$$

and the core cover (cf. Tijs & Lipperts, 1981) is given by

$$\begin{aligned} CC(v) = \left\{ x\in \mathbb {R}^N \ \Big |\ \sum _{i\in N} x_i=v(N) \text { and } m(v)\le x\le M(v) \right\} , \end{aligned}$$

where $M(v),m(v)\in \mathbb {R}^N$ are, for all $i\in N$, defined by

$$\begin{aligned} M_i(v) = v(N) - v(N\setminus \{i\} ), \end{aligned}$$

and

$$\begin{aligned} m_i(v)= \max _{S\in 2^N:i\in S}\left\{ v(S) - \sum _{j\in S,j\not =i} M_j(v)\right\} . \end{aligned}$$

A cooperative game $v\in TU^N$ is called

• imputation admissible if $I(v)\not =\emptyset$;

• superadditive if $v(S)+v(T) \le v(S\cup T)$ for all $S,T\in 2^N$ with $S\cap T=\emptyset$.

• balanced if $C(v)\not =\emptyset$;

• compromise stable if $CC(v)\not =\emptyset$ and $C(v)=CC(v)$, or equivalently if $CC(v)\not =\emptyset$ and $v(S) \le \max \left\{ \sum _{i\in S} m_i(v), v(N) - \sum _{j\in N\setminus S} M_j(v)\right\}$ for all $S\in 2^N\setminus \{\emptyset \}$ (cf. Quant et al. , 2005);

• strongly compromise admissible if $CC(v)\not =\emptyset$ and $v(S) \le v(N) - \sum _{j\in N\setminus S} M_j(v)$ for all $S\in 2^N\setminus \{\emptyset \}$ [formerly known as 1-convex, (cf. Driessen , 1988), but we adopt the terminology of Quant et al. (2005)].

Note that strong compromise admissibility implies compromise stability, compromise stability implies balancedness, and balancedness implies imputation admissibility. Moreover, for a cooperative game with two players, all notions are equivalent. For a three player game, only balancedness and compromise stability are equivalent, while all notions differ for games with more than three players.

Let $v\in TU^N$ be an imputation admissible game. The excess of a coalition $S\in 2^N$ with respect to an imputation $x\in I(v)$ is defined as $Exc(S,x,v)= v(S) - \sum _{i\in S} x_i$, while the excess vector $\theta (x)\in \mathbb {R}^{2^{\left| N\right| }}$ is defined as the vector consisting of the excesses in non-increasing order, i.e. $\theta (x)_k\ge \theta (x)_{k+1}$ for all $k\in \{1,\ldots ,2^{\left| N\right| }-1\}$. The nucleolus (cf. Schmeidler , 1969) $\text {nuc}(v)\in \mathbb {R}^N$ is the unique imputation for which $\theta (\text {nuc}(v)) \preceq \theta (x)$ for all $x\in I(v)$, where $\preceq$ denotes the lexicographical order. It is known that $\text {nuc}(v)\in C(v)$ for all balanced games $v\in TU^N$.

A collection $B\subseteq 2^N\setminus \{\emptyset \}$ is called balanced if there exists a function $\lambda :B \rightarrow \mathbb {R}_{++}$ such that $\sum _{S\in B: i\in S} \lambda (S) =1$ for all $i\in N$. According to the Kohlberg criterion (cf. Kohlberg , 1971), for a balanced game $v\in TU^N$ and an imputation $x\in I(v)$, it holds that $x=\text {nuc}(v)$ if and only if the collection $\bigcup _{k=1}^s B_k(x,v)$ is balanced for all $s\in \{1,\ldots ,t(x)\}$, where $B_k(x,v)$ is recursively defined by:

$$\begin{aligned} B_1(x,v) = \left\{ S\in 2^N\setminus \{\emptyset ,N\} \ \Big |\ Exc(S,x,v) \ge Exc(T,x,v) \text { for all } T\in 2^N\setminus \{\emptyset ,N\} \right\} , \end{aligned}$$

and for all $k\in \{2,\ldots ,t(x)\}$:

$$\begin{aligned} B_k(x,v)= \biggl \{ S\in 2^N\setminus \{\emptyset ,N\} \ \biggl | \ S\notin \bigcup _{r=1}^{k-1} B_r(x,v) \text { and } Exc(S,x,v)\ge Exc(T,x,v) \\ \text { for all } T\in 2^N\setminus \{\emptyset ,N\} \text { with } T\notin \bigcup _{r=1}^{k-1} B_r(x,v) \biggr \}. \end{aligned}$$

Here, $t(x)\in \mathbb {N}$ is the unique number such that $B_{k}(x,v)\not =\emptyset$ for all $k \in \{1,\ldots ,t(x)\}$ and $B_{t(x)+1}(x,v)=\emptyset$.

A bankruptcy problem (cf. O’Neill , 1982) is a triple (N, A, c) where N is a non-empty, finite set of players, $A\in \mathbb {R}_+$ and $c\in \mathbb {R}^N_+$ consists of the claims of the players on A such that $\sum _{i\in N} c_i \ge A$. For a bankruptcy problem (N, A, c), the constrained equal awards rule (CEA) allocates $\textit{CEA}_{i}\left( N,A,c\right) = \min \left\{ \alpha ,c_i\right\}$ for all $i\in N$, where $\alpha \in \mathbb {R}$ is such that $\sum _{i\in N} \min \left\{ \alpha ,c_i\right\} = A$, while the Talmud rule (TAL) (cf. Aumann & Maschler, 1985) allocates

$$\begin{aligned}\textit{TAL}\left( N,A,c\right) = {\left\{ \begin{array}{ll} \textit{CEA}\left( N,A,\frac{1}{2}c\right) , &{} \text{ if } \sum _{i\in N} c_i \ge 2A;\\ c-\textit{CEA}\left( N,\sum _{i\in N}c_i - A, \frac{1}{2}c\right) , &{} \text{ if } \sum _{i\in N} c_i < 2A. \end{array}\right. }\end{aligned}$$

For compromise stable games and strongly compromise admissible games, the nucleolus can be described by a direct, closed formula.

Proposition 2.1

(cf. Quant et al. , 2005) and (cf. Driessen , 1988) Let $v\in TU^N$.

• (i) If v is compromise stable, then, for all $i\in N$,

  $$\begin{aligned}\text {nuc}_{i}(v)= m_i(v) + \textit{TAL}_{i}\left( N,v(N)-\sum _{j\in N} m_j(v), M(v) - m(v)\right) ;\end{aligned}$$

• (ii) If v is strongly compromise admissible, then, for all $i\in N$,

  $$\begin{aligned}\text {nuc}_{i}(v)=M_i(v) - \frac{1}{\left| N\right| } \left( \sum _{j\in N} M_j(v) - v(N)\right) .\end{aligned}$$

A graph is a pair (N, E), where N is a non-empty, finite set of players, with $\left| N\right| \ge 3$ and $E\subseteq \left\{ \{i,j\} \ \Big |\ i,j\in N, i\not =j \right\}$ is a finite set of edges. For a graph (N, E) and a subset of players $S\in 2^N\setminus \{\emptyset \}$, the induced subgraph on S is defined as the graph $(S,E_S)$, where $E_S= \left\{ \{i,j\} \in E \ \Big |\ i,j\in S \right\}$. A path in a graph (N, E) is defined as a sequence of players $(i_0,\ldots ,i_m)$ such that $i_k\not =i_\ell$ for all $k,\ell \in \{0,1,\ldots ,m\} , k\not =\ell$ and $\{i_{k-1},i_k\} \in E$ for all $k\in \{1,\ldots ,m\}$.

A graph (N, E) is called

• connected if for all $i,j\in N$ with $i\not =j$, there is a path $(i,\ldots ,j)$;

• complete if $\{i,j\} \in E$ for all $i,j\in N$ with $i\not =j$;

• biconnected if for all $i\in N$ the induced subgraph $(N\setminus \{i\} , E_{N\setminus \{i\} })$ is connected;

• a star if there exists a player $i\in N$ such that $E=\left\{ \{i,j\} \ \Big |\ j\in N\setminus \{i\} \right\}$.

Note that every complete graph is biconnected and that every biconnected graph is connected. Also a star is connected. For a graph (N, E), a component $C\in 2^N\setminus \{\emptyset \}$ is defined as a maximal (inclusion-wise) subset of players such that the induced subgraph $(C,E_C)$ is connected. For a graph (N, E) and a subset of players $S\in 2^N\setminus \{\emptyset \}$, let S/E denote the set of all components in the induced subgraph $(S,E_S)$.

For a graph (N, E) and a cooperative game $v\in TU^N$, the graph-restricted game $v^E\in TU^N$ is (cf. Myerson , 1977), for all $S\in 2^N\setminus \{\emptyset \}$, defined by

$$\begin{aligned} v^E(S) = \sum _{C\in {S}/{E}} v(C). \end{aligned}$$

Note that for a connected graph (N, E) and a cooperative game $v\in TU^N$, it holds that $v^E(N) = v(N)$, since ${N}/{E} = \{N\}$. Next, we formally define a communication situation, using a slightly modified version of the definition as stated by Myerson (1977).

Definition 2.1

A communication situation is a triple (N, v, E) where $\left| N\right| \ge 3$, $v\in TU^N$ and (N, E) is a connected graph such that, for all $S\in 2^N$,

$$\begin{aligned} v^E(S) \le v(S). \end{aligned}$$

The set of all communication situations is denoted by $\mathcal {CS}^N$.

Note that, for any (connected) graph (N, E) and any cooperative game $v\in TU^N$ that is superadditive, it holds that $v^E(S)\le v(S)$ for all $S\in 2^N$. In other words, the (additional) inequality in Definition 2.1 is satisfied if the underlying game is superadditive.

3 Inheritance of properties

This section studies the inheritance of two properties: strong compromise admissibility and compromise stability. For each of these properties, we identify the family of graphs for which the inheritance of this property from the underlying game to the graph-restricted game is guaranteed. First, we want to remark that both balancedness and imputation admissibility are always inherited. That is, for every communication situation with an underlying balanced (imputation admissible) game it holds that the graph-restricted is balanced (imputation admissible) as well. This was first observed by van den Nouweland and Borm (1991).

For strong compromise admissibility, the graph needs to be biconnected in order to guarantee the inheritance. In Theorem 3.1, we show that for every communication situation with an underlying strongly compromise admissible game it holds that the graph-restricted game is strongly compromise admissible as well, if the graph is biconnected. Moreover, for every connected graph that is not biconnected, we construct a communication situation with an underlying strongly compromise admissible game such that the graph-restricted game is not strongly compromise admissible. Thus, we can conclude that the family of biconnected graphs guarantees the inheritance of strong compromise admissibility.

In the proof of Theorem 3.1, we use the following lemma.

Lemma 3.1

Let $\left( N,v,E\right) \in \mathcal {CS}^N$. Then, $M(v^E)\ge M(v)$ and $m(v^E)\le m(v)$. Consequently, $CC(v)\subseteq CC(v^E)$.

Proof

Let $\left( N,v,E\right) \in \mathcal {CS}^N$. Since $v^E(N)=v(N)$ and $v^E(S)\le v(S)$ for all $S\in 2^N$, we have

$$\begin{aligned} M_i(v^E) = v^E(N) - v^E(N\setminus \{i\} ) \ge v(N) - v(N\setminus \{i\} ) = M_i(v), \end{aligned}$$

for all $i\in N$. Using this, we have that

$$\begin{aligned} m_i(v^E)= & {} \max _{S\in 2^N:i\in S}\left\{ v^E(S) - \sum _{j\in S,j\not =i} M_j(v^E)\right\} \le \max _{S\in 2^N:i\in S}\left\{ v(S) - \sum _{j\in S,j\not =i} M_j(v)\right\} \\= & {} m_i(v), \end{aligned}$$

for all $i\in N$. Finally, for $x\in CC(v)$, we have

$$\begin{aligned} \sum _{i\in N} x_i = v(N)=v^E(N), \end{aligned}$$

and

$$\begin{aligned} m(v^E)\le m(v) \le x \le M(v) \le M(v^E). \end{aligned}$$

Consequently, $x\in CC(v^E)$.$\square$

Theorem 3.1

The following two statements hold:

• (i) Let $\left( N,v,E\right) \in \mathcal {CS}^N$ be a communication situation with (N, E) is biconnected and v is strongly compromise admissible. Then, $v^E$ is strongly compromise admissible;

• (ii) Let (N, E) be a connected graph that is not biconnected. Then, there exists a communication situation $\left( N,v,E\right) \in \mathcal {CS}^N$ where v is strongly compromise admissible such that $v^E$ is not strongly compromise admissible.

Proof

(i) Since v is strongly compromise admissible, we have that $CC(v)\not =\emptyset$. This implies that $CC(v^E)\not =\emptyset$, using Lemma 3.1. Moreover, since (N, E) is biconnected, $M_i(v^E)=M_i(v)$ for all $i\in N$ and hence, for all $S\in 2^N\setminus \{\emptyset \}$,

$$\begin{aligned} v^E(S) \le v(S) \le v(N) - \sum _{j\in N\setminus S} M_j(v) = v^E(N) -\sum _{j\in N\setminus S} M_j(v^E). \end{aligned}$$

Here, the second inequality is due to the fact that v is strongly compromise admissible. Consequently, $v^E$ is strongly compromise admissible.

(ii) Since (N, E) is not biconnected, we can set $N=\{1,2,\ldots ,n\}$ and assume w.l.o.g. that $\{1,2\} ,\{2,3\} \in E$, while the induced subgraph on $N\setminus \{2\}$ is not connected and that players 1 and 3 are in two different components in the induced subgraph on $N\setminus \{2\}$. Consider the communication situation $(N,v_1,E)\in \mathcal {CS}^N$ with, for all $S\in 2^N$,

$$\begin{aligned}v_1(S)={\left\{ \begin{array}{ll} 1, &{} \text{ if } \{1,2\} \subseteq S \text { or } \{1,3\} \subseteq S;\\ 0, &{} \text{ otherwise }. \end{array}\right. }\end{aligned}$$

Note that $CC(v_1)\not =\emptyset$, since it can be readily checked that $M(v_1)=m(v_1)=(1,0,0,\ldots ,0)$. Moreover, for $S\in 2^N$ for which $1\in S$, $v_1(S)\le 1= v_1(N)-\sum _{j\in N\setminus S} M_j(v_1)$. For $S\in 2^N$ for which $1\notin S$, $v_1(S)=0=v_1(N)-\sum _{j\in N\setminus S} M_j(v_1)$. Hence, $v_1$ is strongly compromise admissible.

We show that $v^E_1$ is not strongly compromise admissible, by showing that

$$\begin{aligned} v^E_1(\{3\} )> v^E_1(N)-\sum _{j\in N,j\not = 3} M_j(v^E_1). \end{aligned}$$

First, note that $v^E_1(\{3\} )=v_1(\{3\} )=0$. Secondly, since $v^E_1(N\setminus \{2\} )=0$ (due to the fact that players 1 and 3 are in two different components of the induced subgraph on $N\setminus \{2\}$), we have that $M_2(v^E_1)=1$. Using Lemma 3.1, $M(v^E_1)\ge M(v_1)\ge 0$ and in particular, $M_1(v^E_1)\ge 1$. Hence,

$$\begin{aligned} v^E_1(N)-\sum _{j\in N,j\not =3} M_j(v^E_1) \le v^E_1(N) - M_1(v^E_1) - M_2(v^E_1) \le -1. \end{aligned}$$

Consequently, $v^E_1$ is not strongly compromise admissible. This finishes the construction of the communication situation $(N,v_1,E)\in \mathcal {CS}^N$ where $v_1$ is strongly compromise admissible, while $v^E_1$ is not strongly compromise admissible.$\square$

Theorem 3.1 characterizes the family of graphs that guarantees the inheritance of strong compromise admissibility from the underlying game to the graph-restricted game. The next theorem characterizes the family of graphs that guarantees compromise stability for the graph-restricted game of any communication situation with an underlying strongly compromise admissible game. This family includes of course all biconnected graphs (cf. Theorem 3.1) and, in addition, it is seen that it contains all stars.

Theorem 3.2

The following two statements hold:

• (i) Let $\left( N,v,E\right) \in \mathcal {CS}^N$ be a communication situation with (N, E) is biconnected or a star and v is strongly compromise admissible. Then, $v^E$ is compromise stable;

• (ii) Let (N, E) be a connected graph that is not biconnected and not a star. Then, there exists a communication situation $\left( N,v,E\right) \in \mathcal {CS}^N$ where v is strongly compromise admissible such that $v^E$ is not compromise stable.$\square$

Proof

(i) If (N, E) is biconnected, then $v^E$ is strongly compromise admissible, according to part (i) of Theorem 3.1. Hence, $v^E$ is compromise stable.

If (N, E) is a star, then let $k\in N$ such that $E=\left\{ \{i,k\} \ \Big |\ i\in N\setminus \{k\} \right\}$. First, note that $CC(v^E)\not =\emptyset$, by using Lemma 3.1 and the fact that v is strongly compromise admissible. Secondly, it remains to prove that for all $S\in 2^N\setminus \{\emptyset \}$,

$$\begin{aligned} v^E(S)\le \max \left\{ \sum _{i\in S} m_i(v^E), v^E(N) - \sum _{j\in N\setminus S} M_j(v^E)\right\} . \end{aligned}$$

Let $S\in 2^N\setminus \{\emptyset \}$. If $k\notin S$, then

$$\begin{aligned} v^E(S) = \sum _{i\in S} v(\{i\} ) = \sum _{i\in S} v^E(\{i\} ) \le \sum _{i\in S} m_i(v^E). \end{aligned}$$

If $k\in S$, then $M_j(v^E)=M_j(v)$ for all $j\in N\setminus S$ and hence,

$$\begin{aligned} v^E(S) \le v(S) \le v(N) - \sum _{j\in N\setminus S} M_j(v)= v^E(N) - \sum _{j\in N\setminus S} M_j(v^E). \end{aligned}$$

Consequently, $v^E$ is compromise stable.

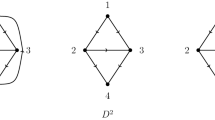
ii) Since (N, E) is neither biconnected, nor a star, it follows that $\left| N\right| \ge 4$. Set $N=\{1,2,3,4,\ldots ,n\}$ and since (N, E) is connected, we can assume w.l.o.g. that $\{1,2\} ,\{2,3\} ,\{3,4\} \in E$, that the induced subgraph on $N\setminus \{3\}$ is not connected, and that players 1 and 2 are in one component of the induced subgraph on $N\setminus \{3\}$ and player 4 is in another (Figure 1 provides a schematic representation). Consider the communication situation $(N,v_2,E)\in \mathcal {CS}^N$ with, for all $S\in 2^N$,

$$\begin{aligned}v_2(S)={\left\{ \begin{array}{ll} 8, &{} \text{ if } S=N;\\ 8, &{} \text{ if } S=N\setminus \{j\} \text { for } j\in N\setminus \{1,2,3,4\} ;\\ 6, &{} \text{ if } S\in \{N\setminus \{1\} , N\setminus \{2\} ,N\setminus \{3\} , N\setminus \{4\} \} ;\\ 3, &{} \text{ if } \left| S\right| \le n-2 \text { and } \{1,2\} \subseteq S;\\ 0, &{} \text{ otherwise }. \end{array}\right. }\end{aligned}$$

Fig. 1

Schematic representation of the graph (N, E)

It can be readily checked that $M(v_2)=m(v_2)=(2,2,2,2,0,\ldots ,0)$. Hence, $CC(v_2)\not =\emptyset$. Obviously, $v_2(S)\le v_2(N)-\sum _{j\in N\setminus S} M_j(v_2)$ holds for $S\in 2^N$ for which $\left| S\right| >n-2$. For $S\in 2^N$ for which $\left| S\right| \le n-2$ and $\{1,2\} \subseteq S$, we have $v_2(N)-\sum _{j\in N\setminus S} M_j(v_2) \ge 8-4>3=v_2(S)$. Finally, for $S\in 2^N$ for which $v_2(S)=0$, $v_2(N)-\sum _{j\in N\setminus S} M_j(v_2) \ge 8-8=0$. Hence, $v_2$ is strongly compromise admissible.

We show that $v^E_2$ is not compromise stable, by showing that

$$\begin{aligned} v^E_2(\{1,2\} )>\max \left\{ m_1(v^E_2)+m_2(v^E_2),v^E_2(N)-\sum _{j\in N,j\not =1,2} M_j(v^E_2)\right\} . \end{aligned}$$

First, note that $v^E_2(\{1,2\} )=v_2(\{1,2\} )=3$. Secondly, since $v^E_2(N\setminus \{3\} )=v_2(\{1,2\} )=3$ (due to the fact that the induced subgraph on $N\setminus \{3\}$ is not connected, but consists of at least one component with $\{1,2\} \in E$), we have that $M_3(v^E_2)=5$. Using Lemma 3.1, we have that $M(v^E_2)\ge M(v_2)\ge 0$ and in particular, $M_4(v^E_2)\ge M_4(v_2)=2$, such that it follows that

$$\begin{aligned} v^E_2(N)-\sum _{j\in N,j\not =1,2} M_j(v^E_2) \le v^E_2(N) - M_3(v^E_2) - M_4(v^E_2) \le 8-5-2=1. \end{aligned}$$

Moreover, we claim that $m_1(v^E_2)=\max _{S\in 2^N:1\in S}\left\{ v^E_2(S) - \sum _{j\in S,j\not =1} M_j(v^E_2)\right\} \le 1$: for $S=N$ and $S=N\setminus \{j\}$ for $j\in N\setminus \{1,2,3\}$, we see that $\{2,3\} \subseteq S$ and $v^E_2(S)\le 8$, and, consequently,

$$\begin{aligned} v^E_2(S) - \sum _{j\in S,j\not =1} M_j(v^E_2) \le v^E_2(S) - M_2(v^E_2)- M_3(v^E_2) \le 8-2-5=1. \end{aligned}$$

For $S=N\setminus \{3\}$, we have that $v^E_2(S)=3$ and $M_2(v^E_2)\ge 2$, and, consequently,

$$\begin{aligned} v^E_2(S) - \sum _{j\in S,j\not =1} M_j(v^E_2) \le v^E_2(S) - M_2(v^E_2) \le 3-2=1. \end{aligned}$$

For $S=N\setminus \{2\}$, we have that $\{3,4\} \subseteq S$ and $v^E_2(S)\le 6$, and, consequently,

$$\begin{aligned} v^E_2(S) - \sum _{j\in S,j\not =1} M_j(v^E_2) \le v^E_2(S) - M_3(v^E_2)- M_4(v^E_2) \le 6-5-2=-1. \end{aligned}$$

For all $S\in 2^N$ with $\left| S\right| \le n-2$ and $\{1,2\} \subseteq S$, we have that $v^E_2(S)\le v_2(S)=3$ and $2\in S$, and, consequently,

$$\begin{aligned} v^E_2(S) - \sum _{j\in S,j\not =1} M_j(v^E_2) \le v_2(S) - M_2(v^E_2)\le 3-2=1. \end{aligned}$$

Finally, for $S\in 2^N$ with $v_2(S)=0$ it clearly holds that $v^E_2(S)-\sum _{j\in S,j\not =1} M_j(v^E_2)\le 0$.

We may conclude that $m_1(v^E_2)\le 1$. Similarly, one can show that $m_2(v^E_2)\le 1$ and thus

$$\begin{aligned} m_1(v^E_2)+m_2(v^E_2)\le 2. \end{aligned}$$

Consequently, $v^E_2$ is not compromise stable. This finishes the construction of the communication situation $(N,v_2,E)\in \mathcal {CS}^N$ where $v_2$ is strongly compromise admissible, while $v^E_2$ is not compromise stable.$\square$

The next theorem provides a characterization of the family of graphs for which the inheritance of compromise stability is guaranteed. Note that for a three player game, balancedness and compromise stability are equivalent. Therefore, for every communication situation with an underlying compromise stable game with three players it holds that the graph-restricted is compromise stable as well, since balancedness is always inherited. For more than three players, the graph needs to be complete in order to guarantee compromise stability for the graph-restricted game, for every communication situation with an underlying compromise stable game.

Theorem 3.3

The following two statements hold:

• (i) Let $\left( N,v,E\right) \in \mathcal {CS}^N$ be a communication situation with $\left| N\right| =3$ or (N, E) is complete, and v is compromise stable. Then, $v^E$ is compromise stable;

• (ii) Let (N, E) be a connected graph that is not complete and $\left| N\right| >3$. Then, there exists a communication situation $\left( N,v,E\right) \in \mathcal {CS}^N$ where v is compromise stable such that $v^E$ is not compromise stable.

Proof

(i) It is left for the reader

ii) Since (N, E) is not complete and $\left| N\right| >3$, set $N=\{1,2,3,4,\ldots ,n\}$ with $n\ge 4$ and assume w.l.o.g. that $\{1,2\} \notin E$, while $\{1,3\} \in E$. Consider the communication situation $(N,v_3,E)\in \mathcal {CS}^N$ with, for all $S\in 2^N$,

$$\begin{aligned}v_3(S)={\left\{ \begin{array}{ll} 7, &{} \text{ if } S=N;\\ 6, &{} \text{ if } S=N\setminus \{1\} ;\\ 5, &{} \text{ if } S=N\setminus \{2\} ;\\ 4, &{} \text{ if } S=N\setminus \{4\} ;\\ 3, &{} \text{ if } S\notin \{N, N\setminus \{1\} , N\setminus \{2\} , N\setminus \{4\} \} , \text { and } \{1,2\} \subseteq S \text { or } \{1,3\} \subseteq S;\\ 0, &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

Note that $M(v_3) = (1,2,4,3,4,\ldots ,4)$ and $m(v_3)=(1,2,2,0,0,\ldots ,0)$, which means that $CC(v_3)\not =\emptyset$. Obviously, the inequality $v_3(S)\le \mathrm{max}\, \big \{\sum _{i\in S} m_i(v_3), v_3(N)-\sum _{j\in N\setminus S} M_j(v_3)\big \}$ is satisfied for $S\in \{N,N\setminus \{1\} ,N\setminus \{2\} ,N\setminus \{4\} \}$ and for all $S\in 2^N$ with $v_3(S)=0$. For $S\in 2^N, S\notin \{N, {N\setminus \{1\} }, N\setminus \{2\} , N\setminus \{4\} \}$, it holds that $v_3(S)\le m_1(v_3) + m_2(v_3)$ if $\{1,2\} \subseteq S$, and $v_3(S)\le m_1(v_3)+m_3(v_3)$ if $\{1,3\} \subseteq S$. Hence, $v_3$ is compromise stable.

We show that $v^E_3$ is not compromise stable, by showing that

$$\begin{aligned} v^E_3(\{1,3\} ) > \max \left\{ m_{1}(v^E_3) + m_{3}(v^E_3), v^E_3(N) - \sum _{j\in N, j\not =1,3} M_j(v^E_3)\right\} . \end{aligned}$$

First, note that $v^E_3(\{1,3\} )=v_3(\{1,3\} )=3$. Secondly, with regard to $m_1(v_3)$, we have that $v_3(S)-\sum _{j\in S,j\not =1} M_j(v_3)\le 0$ for all $S\in 2^N$ with $1\in S$ and $S\not =\{1,2\}$ and $v_3(\{1,2\} )-M_2(v_3)=1$. Using the fact that $v^E_3(S)\le v_3(S)$ for all $S\in 2^N$ and $M(v^E_3)\ge M(v_3)$ (according to Lemma 3.1), it can be seen that $v^E_3(S)-\sum _{j\in S,j\not =1} M_j(v^E_3)\le 0$ for all $S\in 2^N$ with $1\in S$ and $S\not =\{1,2\}$. Moreover, $v^E_3(\{1,2\} )=0$ (since $\{1,2\} \notin E$) and hence, $v^E_3(\{1,2\} )-M_2(v^E_3)\le 0$. Consequently, $m_1(v^E_3)=0$. Lemma 3.1 also implies that $m_3(v^E_3)\le m_3(v_3)=2$. Hence,

$$\begin{aligned} m_1(v^E_3)+m_3(v^E_3)\le 2. \end{aligned}$$

Finally, $v^E_3(N)=v_3(N)=7$, $M_2(v^E_3)\ge M_2(v_3)=2$, $M_4(v^E_3)\ge M_4(v_3)=3$ and $M_j(v^E_3)\ge M_j(v_3)\ge 0$ for all $j\in N$, imply that

$$\begin{aligned} v^E_3(N) - \sum _{\begin{array}{c} j\in N,\\ j\not =1,3 \end{array}} M_j(v^E_3) \le v^E_3(N) - M_{2}(v^E_3) - M_{4}(v^E_3) \le 7-2-3 =2. \end{aligned}$$

Subsequently, $v^E_3$ is not compromise stable. This finishes the construction of a communication situation $(N,v_3,E)\in \mathcal {CS}^N$ where $v_3$ is compromise stable, while $v^E_3$ is not compromise stable.$\square$

4 Invariance of the nucleolus

In this section, we study the invariance of the nucleolus. That is, we focus on necessary and sufficient conditions on a communication situation such that the nucleolus of the graph-restricted game equals the nucleolus of the game underlying the communication situation. In particular, we reconsider communication situations with an underlying strongly compromise admissible game and an underlying compromise stable game, respectively. We start out with the former. Recall from Theorem 3.1 that the family of biconnected graphs guarantees the inheritance of strong compromise admissibility from the underlying game to the graph-restricted game. For communication situations with an underlying strongly compromise admissible game, we show that this family of biconnected graphs also guarantees the invariance of the nucleolus. Moreover, for every connected graph that is not biconnected, we explicitly construct a communication situation with an underlying strongly compromise admissible game for which the nucleolus of the graph-restricted game is not equal to the nucleolus of the underlying game. For this, we benefit from the construction in the proof of Theorem 3.1.

Theorem 4.1

The following two statements hold:

• (i) Let $\left( N,v,E\right) \in \mathcal {CS}^N$ be a communication situation with (N, E) is biconnected and v is strongly compromise admissible. Then, $\text {nuc}(v^E)=\text {nuc}(v)$;

• (ii) Let (N, E) be a connected graph that is not biconnected. Then, there exists a communication situation $\left( N,v,E\right) \in \mathcal {CS}^N$ where v is strongly compromise admissible such that $\text {nuc}(v^E)\not =\text {nuc}(v)$.

Proof

(i) First, note that $v^E$ is strongly compromise admissible, according to part (i) of Theorem 3.1. Hence, by using Proposition 2.1, for all $i\in N$,

$$\begin{aligned} \text {nuc}_{i}(v^E)&= M_i(v^E) - \frac{1}{\left| N\right| }\left( \sum _{j\in N} M_j(v^E)- v^E(N) \right) \\&= M_i(v)-\frac{1}{\left| N\right| }\left( \sum _{j\in N} M_j(v)- v(N) \right) \\&=\text {nuc}_{i}(v), \end{aligned}$$

since $M(v^E)=M(v)$ for any biconnected graph (N, E).

(ii) Since (N, E) is not biconnected, set $N=\{1,2,\ldots ,n\}$ and assume w.l.o.g. that $\{1,2\} ,\{2,3\} \in E$, that the induced subgraph on $N\setminus \{2\}$ is not connected and that players 1 and 3 are in two different components in the induced subgraph on $N\setminus \{2\}$. Reconsider the communication situation $(N,v_1,E)\in \mathcal {CS}^N$ with, for all $S\in 2^N$,

$$\begin{aligned}v_1(S)={\left\{ \begin{array}{ll} 1, &{} \text{ if } \{1,2\} \subseteq S \text { or } \{1,3\} \subseteq S;\\ 0, &{} \text{ otherwise }. \end{array}\right. }\end{aligned}$$

Recall that $v_1$ is strongly compromise admissible and since $M(v_1)=(1,0,0,\ldots ,0)$, we have that, using Proposition 2.1,

$$\begin{aligned} \text {nuc}(v_1)=(1,0,0,\ldots ,0). \end{aligned}$$

Moreover, for all $S\in 2^N$,

$$\begin{aligned} v^E_1(S) = {\left\{ \begin{array}{ll} 1, &{} \text{ if } \{1,2\} \subseteq S; \\ 0, &{} \text{ otherwise }, \end{array}\right. }\end{aligned}$$

and consequently,

$$\begin{aligned} \text {nuc}(v^E_1)=(\frac{1}{2},\frac{1}{2},0,\ldots ,0). \end{aligned}$$

Hence, $\text {nuc}(v^E_1)\not =\text {nuc}(v_1)$. This concludes the construction of the communication situation $(N,v_1,E)\in \mathcal {CS}^N$ where $v_1$ is strongly compromise admissible such that $\text {nuc}(v^E_1)\not =\text {nuc}(v_1)$.$\square$

Next, we reconsider the class of communication situations with an underlying compromise stable game. We need a stronger condition than biconnectedness to guarantee the invariance of the nucleolus for this class, since this class of communication situations is larger than the class of communication situations with an underlying strongly compromise admissible game. It turns out that to guarantee invariance, we need the strongest condition possible, a complete graph. For every connected graph that is not complete, one can construct a communication situation with an underlying compromise stable game for which the nucleolus is not invariant. This construction, however, is quite intricate.

Theorem 4.2

The following two statements hold:

• (i) Let $\left( N,v,E\right) \in \mathcal {CS}^N$ be a communication situation with (N, E) is complete and v is compromise stable. Then, $\text {nuc}(v^E)=\text {nuc}(v)$;

• (ii) Let (N, E) be a connected graph that is not complete. Then, there exists a communication situation $\left( N,v,E\right) \in \mathcal {CS}^N$ where v is compromise stable such that $\text {nuc}(v^E)\not =\text {nuc}(v)$.

Proof

(i) It is left for the reader

(ii) We distinguish between two cases: either $\left| N\right| =3$ or $\left| N\right| \ge 4$. First, suppose that $\left| N\right| =3$ and set $N=\{1,2,3\}$. Assume w.l.o.g. that $\{1,3\} \notin E$. Then, $\{1,2\} ,\{2,3\} \in E$, since (N, E) is connected. Reconsider the communication situation $(N,v_1,E)\in \mathcal {CS}^N$ with, for all $S\in 2^N$,

$$\begin{aligned}v_1(S)={\left\{ \begin{array}{ll} 1, &{} \text{ if } \{1,2\} \subseteq S \text { or } \{1,3\} \subseteq S;\\ 0, &{} \text{ otherwise }. \end{array}\right. }\end{aligned}$$

For all $S\in 2^N\setminus \{\emptyset \}$,

$$\begin{aligned}v^E_1(S)={\left\{ \begin{array}{ll} 1, &{} \text{ if } \{1,2\} \subseteq S; \\ 0, &{} \text{ otherwise }. \end{array}\right. }\end{aligned}$$

Consequently, $\text {nuc}(v^E_1)=(\frac{1}{2},\frac{1}{2},0)\not =(1,0,0)=\text {nuc}(v_1)$.

Secondly, suppose that $\left| N\right| \ge 4$. Set $N=\{1,2,3,4,\ldots ,n\}$ and assume w.l.o.g. that $\{1,2\} \notin E$ and $\{1,3\} \in E$. Reconsider the communication situation $(N,v_3,E)\in \mathcal {CS}^N$ with, for all $S\in 2^N$,

$$\begin{aligned}v_3(S)={\left\{ \begin{array}{ll} 7, &{} \text{ if } S=N;\\ 6, &{} \text{ if } S=N\setminus \{1\} ;\\ 5, &{} \text{ if } S=N\setminus \{2\} ;\\ 4, &{} \text{ if } S=N\setminus \{4\} ;\\ 3, &{} \text{ if } S\notin \{N, N\setminus \{1\} , N\setminus \{2\} , N\setminus \{4\} \} , \text { and } \{1,2\} \subseteq S \text { or } \{1,3\} \subseteq S;\\ 0, &{} \text{ otherwise }. \end{array}\right. }\end{aligned}$$

Then, $M(v_3) = (1,2,4,3,4,\ldots ,4)$ and $m(v_3)=(1,2,2,0,0,\ldots ,0)$, and using Proposition 2.1,

$$\begin{aligned}\text {nuc}_{i}(v_3)={\left\{ \begin{array}{ll} 1, &{}\text{ if } i=1;\\ 2, &{}\text{ if } i=2;\\ 2+\frac{2}{n-2}, &{}\text{ if } i=3;\\ \frac{2}{n-2}, &{}\text{ otherwise }. \end{array}\right. }\end{aligned}$$

To show that $\text {nuc}(v^E_3)\not =\text {nuc}(v_3)$, we use the Kohlberg criterion and show that $B_1(\text {nuc}(v_3),v^E_3)$ is not balanced. For this, we need to identify the coalitions (non-empty and not the grand coalition) with the highest excess. To structure this identification process, for $S\in 2^N$ we distinguish between seven cases, in which players 1, 2 and 3 play an important role:

• (i) $\left| S\right| =1$ or $S\in \{ \{1,2\} ,\{1,3\} ,\{2,3\} \}$;

• (ii) $\left| S\right| =3$ with $\{1,2\} \subseteq S$ and $3\notin S$;

• (iii) $3<\left| S\right| <n-1$ with $\{1,2\} \subseteq S$ and $3\notin S$;

• (iv) $2<\left| S\right| <n-1$ with $\{1,3\} \subseteq S$;

• (v) $1<\left| S\right| <n-1$ with $\{1,2\} \not \subseteq S$, $\{1,3\} \not \subseteq S$ and $j\in S$ for $j\in N\setminus \{1,2,3\}$;

• (vi) $\left| S\right| =n-1$ with $S=N\setminus \{j\}$ for $j\in N\setminus \{1,2,3,4\}$;

• (vii) $S\in \{ N\setminus \{1\} ,N\setminus \{2\} ,N\setminus \{3\} ,N\setminus \{4\} \}$.

Case i), vi) and vii) deal with all coalitions with exactly 1 or $n-1$ players, respectively. Case i) also includes three 2-player coalitions. For the other coalitions, we distinguish whether $\{1,2\} \subseteq S$ (and $3\notin S$) or $\{1,3\} \subseteq S$ or neither of the two inclusions. In particular, case ii) deals with the 2-player coalitions that contains both players 1 and 2, but not 3 and case iii) deals with similar coalitions that contain at least 4 players. In case iv), $\{1,3\} \subseteq S$ and finally, case v) deals with all coalitions such that both $\{1,2\} \not \subseteq S$ and $\{1,3\} \not \subseteq S$.

Case (i) For this first case, we know that

$$\begin{aligned}v^E_3(S)={\left\{ \begin{array}{ll} 0, &{} \text{ if } S=\{j\} \text { for } j\in N; \\ 0, &{} \text{ if } S=\{1,2\} ; \\ 3, &{} \text{ if } S=\{1,3\} ; \\ 0, &{} \text{ if } S=\{2,3\} , \end{array}\right. }\end{aligned}$$

and hence, one readily checks that

$$\begin{aligned}Exc(S,\text {nuc}(v_3),v^E_3)={\left\{ \begin{array}{ll} -1, &{}\text{ if } S=\{1\} ;\\ -2, &{}\text{ if } S=\{2\} ;\\ \frac{-2}{n-2}-2, &{}\text{ if } S=\{3\} ;\\ \frac{-2}{n-2}, &{}\text{ if } S=\{j\} \text { for } j\in N\setminus \{1,2,3\} ;\\ -3, &{}\text{ if } S=\{1,2\} ;\\ \frac{-2}{n-2}, &{}\text{ if } S=\{1,3\} ;\\ \frac{-2}{n-2}-4, &{}\text{ if } S=\{2,3\} . \end{array}\right. } \end{aligned}$$

Case (ii) For all $S\in 2^N$ with $\left| S\right| =3$, $\{1,2\} \subseteq S$ and $3\notin S$, it holds that

$$\begin{aligned}v^E_3(S)={\left\{ \begin{array}{ll} 3, &{} \text{ if } \text{ the } \text{ induced } \text{ subgraph } \text{ on } S \text { is connected};\\ 0, &{} \text{ otherwise }, \end{array}\right. } \end{aligned}$$

and hence,

$$\begin{aligned} Exc(S,\text {nuc}(v_3),v^E_3)={\left\{ \begin{array}{ll} \frac{-2}{n-2}, &{}\text{ if } \text{ the } \text{ induced } \text{ subgraph } \text{ on } S \text { is connected};\\ \frac{-2}{n-2}-3, &{}\text{ otherwise }. \end{array}\right. }\end{aligned}$$

Note that the induced subgraph on S is connected if and only if $\{1,j\} ,\{2,j\} \in E$ for $j\in N\setminus \{1,2,3\}$.

Case (iii) For all $S\in 2^N$ with $3<\left| S\right| <n-1$, $\{1,2\} \subseteq S$ and $3\notin S$, it holds that

$$\begin{aligned}v^E_3(S)\le 3,\end{aligned}$$

and hence,

$$\begin{aligned}&Exc(S,\text {nuc}(v_3),v^E_3)<v^E_3(S)-\text {nuc}_{1}(v_3)-\text {nuc}_{2}(v_3)-\text {nuc}_{j}(v_3)\\&\quad \le 3-1-2-\frac{2}{n-2}=\frac{-2}{n-2}, \end{aligned}$$

since $\text {nuc}_{i}(v_3)> 0$ for all $i\in N$. Subsequently, these coalitions can not be coalitions with the highest excess.

Case (iv) For all $S\in 2^N$ with $2<\left| S\right| <n-1$ and $\{1,3\} \subseteq S$, it holds that $v^E_3(S)=3$ and hence,

$$\begin{aligned} Exc(S,\text {nuc}(v_3),v^E_3) < v^E_3(S)-\text {nuc}_{1}(v_3)-\text {nuc}_{3}(v_3) =3-1-2-\frac{2}{n-2}=\frac{-2}{n-2}. \end{aligned}$$

Case (v) For all $S\in 2^N$ with $1<\left| S\right| <n-1$, $\{1,2\} \not \subseteq S$, $\{1,3\} \not \subseteq S$ and $j\in S$ for $j\in N\setminus \{1,2,3\}$, it holds that $v^E_3(S)=0$ and hence,

$$\begin{aligned} Exc(S,\text {nuc}(v_3),v^E_3)<v^E_3(S)-\text {nuc}_{j}(v_3)=0-\frac{2}{n-2}=\frac{-2}{n-2}. \end{aligned}$$

Case (vi) For all $S\in 2^N$ with $\left| S\right| =n-1$ and $S=N\setminus \{j\}$ for $j\in N\setminus \{1,2,3,4\}$, it holds that $v^E_3(S)=3$, since $\{1,3\} \subseteq S$ and hence,

$$\begin{aligned} Exc(S,\text {nuc}(v_3),v^E_3)<v^E_3(S)-\text {nuc}_{1}(v_3)-\text {nuc}_{3}(v_3)=3-1-2-\frac{2}{n-2}=\frac{-2}{n-2}. \end{aligned}$$

Case (vii) Finally, for all $S\in 2^N$ with $S\in \{ N\setminus \{1\} ,N\setminus \{2\} ,N\setminus \{3\} ,N\setminus \{4\} \}$, the worth of the coalition S in the graph-restricted game depends on whether the induced subgraph is connected or not:

$$\begin{aligned} v^E_3(N\setminus \{4\} )&={\left\{ \begin{array}{ll} 4, &{}\text{ if } \text{ the } \text{ induced } \text{ subgraph } \text{ on } N\setminus \{4\} \text { is connected};\\ 3, &{} \text{ otherwise }, \end{array}\right. } \\ v^E_3(N\setminus \{3\} )&={\left\{ \begin{array}{ll} 3, &{}\text{ if } \text{ the } \text{ induced } \text{ subgraph } \text{ on } N\setminus \{3\} \text { is connected};\\ 0, &{} \text{ otherwise }, \end{array}\right. } \\ v^E_3(N\setminus \{2\} )&={\left\{ \begin{array}{ll} 5, &{}\text{ if } \text{ the } \text{ induced } \text{ subgraph } \text{ on } N\setminus \{2\} \text { is connected};\\ 3, &{} \text{ otherwise }, \end{array}\right. } \\ v^E_3(N\setminus \{1\} )&={\left\{ \begin{array}{ll} 6, &{}\text{ if } \text{ the } \text{ induced } \text{ subgraph } \text{ on } N\setminus \{1\} \text { is connected};\\ 0, &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

Consequently,

$$\begin{aligned} Exc(N\setminus \{4\} ,\text {nuc}(v_3),v^E_3)&={\left\{ \begin{array}{ll} \frac{2}{n-2}-3, &{}\text{ if } \text{ the } \text{ induced } \text{ subgraph } \text{ on } N\setminus \{4\} \text { is connected};\\ \frac{2}{n-2}-4, &{}\text{ otherwise }, \end{array}\right. }\\ Exc(N\setminus \{3\} ,\text {nuc}(v_3),v^E_3)&={\left\{ \begin{array}{ll} \frac{2}{n-2}-2, &{}\text{ if } \text{ the } \text{ induced } \text{ subgraph } \text{ on } N\setminus \{3\} \text { is connected};\\ \frac{2}{n-2}-5, &{}\text{ otherwise }, \end{array}\right. }\\ Exc(N\setminus \{2\} ,\text {nuc}(v_3),v^E_3)&={\left\{ \begin{array}{ll} 0, &{}\text{ if } \text{ the } \text{ induced } \text{ subgraph } \text{ on } N\setminus \{2\} \text { is connected};\\ -2, &{}\text{ otherwise }, \end{array}\right. }\\ Exc(N\setminus \{1\} ,\text {nuc}(v_3),v^E_3)&={\left\{ \begin{array}{ll} 0, &{}\text{ if } \text{ the } \text{ induced } \text{ subgraph } \text{ on } N\setminus \{1\} \text { is connected};\\ -6, &{}\text{ otherwise }. \end{array}\right. } \end{aligned}$$

In order to determine which of the above excesses is the highest, note that, if $n\ge 4$,

$$\begin{aligned} Exc(N\setminus \{4\} ,\text {nuc}(v_3),v^E_3)\le \frac{2}{n-2}-3\le -2<\frac{-2}{n-2}, \end{aligned}$$

and, if $n>4$,

$$\begin{aligned} Exc(N\setminus \{3\} ,\text {nuc}(v_3),v^E_3)\le \frac{2}{n-2}-2<-1<\frac{-2}{n-2}. \end{aligned}$$

We may conclude that, if the induced subgraph on $N\setminus \{1\}$ or the induced subgraph on $N\setminus \{2\}$ is connected, the highest excess equals 0 and

$$\begin{aligned} B_1(\text {nuc}(v_3),v^E_3)&=\{N\setminus \{1\} ,N\setminus \{2\} \} ,\\ B_1(\text {nuc}(v_3),v^E_3)&=\{N\setminus \{1\} \} , \text { or }\\ B_1(\text {nuc}(v_3),v^E_3)&=\{N\setminus \{2\} \} . \end{aligned}$$

Clearly, for these cases, $B_1(\text {nuc}(v_3),v^E_3)$ is not a balanced collection and $\text {nuc}(v^E_3)\not =\text {nuc}(v_3)$. Note that, if $n=4$, it holds that the induced subgraph on $N\setminus \{1\}$ or the induced subgraph on $N\setminus \{2\}$ is connected, due to the connectedness of the graph and the fact that $\{1,2\} \notin E$.

For the remaining case, we can assume that $n>4$ and that both induced subgraphs on $N\setminus \{1\}$ and $N\setminus \{2\}$ are not connected. Then, the highest excess equals $\frac{-2}{n-2}$ ($>-1$) and

$$\begin{aligned} B_1(\text {nuc}(v_3),v^E_3)=&\left\{ \{j\} \ \Big |\ j\in N\setminus \{1,2,3\} \right\} \\&\cup \{\{1,3\} \} \\&\cup \left\{ \{1,2,j\} \ \Big |\ j\in N\setminus \{1,2,3\} \text { and both } \{1,j\} \in E \text { and } \{2,j\} \in E \right\} . \end{aligned}$$

Note that if $B_1(\text {nuc}(v_3),v^E_3)=\left\{ \{j\} \ \Big |\ j\in N\setminus \{1,2,3\} \right\} \cup \{\{1,3\} \}$, then $B_1(\text {nuc}(v_3),v^E_3)$ is not balanced, since $2\notin S$ for all $S\in B_1(\text {nuc}(v_3),v^E_3)$. So let $j\in N\setminus \{1,2,3\}$ be such that $\{1,2,j\} \in B_1(\text {nuc}(v_3),v^E_3)$. Suppose $\lambda :B_1(\text {nuc}(v_3),v^E_3)\rightarrow \mathbb {R}_{++}$ is such that $\sum _{S\in B_1(\text {nuc}(v_3),v^E_3): i\in S} \lambda (S)=1$ for all $i\in N$. For $i=3$, this condition boils down to $\lambda (\{1,3\} )=1$. Then, however,

$$\begin{aligned}\sum _{S\in B_1(\text {nuc}(v_3),v^E_3): 1\in S} \lambda (S) \ge \lambda (\{1,3\} ) + \lambda (\{1,2,j\} ) > 1.\end{aligned}$$

Hence, also in this case, $\text {nuc}(v^E_3)\not =\text {nuc}(v_3)$. This concludes the construction of the communication situation $(N,v,E)\in \mathcal {CS}^N$ (with $v=v_1$ if $\left| N\right| =3$ and $v=v_3$ if $\left| N\right| \ge 4$) where v is compromise stable such that $\text {nuc}(v^E)\not =\text {nuc}(v)$.$\square$

5 Concluding remarks

In this paper, we studied both the inheritance of strong compromise admissibility and compromise stability and the invariance of the nucleolus. With regard to the inheritance, the results are summarized in Table 1. Loosely speaking, in Theorem 3.1, we showed that strong compromise admissibility is always inherited from the underlying game to the graph-restricted game if and only if the graph is biconnected. Moreover, to go from strong compromise admissibility for the underlying game to compromise stability for the graph-restricted game, the graph needs to be either biconnected or a star, as shown in Theorem 3.2. Finally, in Theorem 3.3, we showed that compromise stability is always inherited if and only if there are only three players or the graph is complete. To finalize Table 1, it remains to check whether we can obtain a strongly compromise admissible graph-restricted game if the underlying game is compromise stable. Example 5.1 shows that this is not possible. More precisely, for every connected graph there exists a communication situation with a compromise stable underlying game such that the graph-restricted game is not strongly compromise admissible.

Table 1 Survey of inheritance of properties

Example 5.1

Let (N, E) be a connected graph. We can set $N=\{1,2,\ldots ,n\}$ and assume w.l.o.g. that $\{1,2\} \in E$. Consider the communication situation $(N,v_4,E)\in \mathcal {CS}^N$ with, for all $S\in 2^N$,

$$\begin{aligned}v_4(S) ={\left\{ \begin{array}{ll} 1, &{} \text{ if } \{1,2\} \subseteq S;\\ 0, &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

Note that $M(v_4)=(1,1,0,\ldots ,0)$ and $m(v_4)=(0,0,0,\ldots ,0)$, and hence, $CC(v_4)\not =\emptyset$. Moreover, $v_4(S)\le v_4(N) - \sum _{j\in N\setminus S} M_j(v_4)$ for all $S\in 2^N$ for which $\{1,2\} \subseteq S$ and $v_4(S)\le \sum _{i\in S} m_i(v_4)$ for all other $S\in 2^N$. Hence, $v_4$ is compromise stable.

Furthermore, $v^E_4=v_4$, which is not strongly compromise admissible, because

$$\begin{aligned} v_4(\{3\} )=0> -1 = v_4(N) - \sum _{j\in N\setminus S} M_j(v_4). \end{aligned}$$

$\triangle$

Table 2 Survey of invariance of the nucleolus

With regard to the invariance of the nucleolus, Table 2 summarizes our results. For both properties, it identifies the weakest condition on the graph for which invariance of the nucleolus is guaranteed for all communication situations with an underlying game satisfying this property.

Interestingly, the condition on the graph with regard to compromise stability can be relaxed if we restrict attention to communication situations with an underlying simple game. A cooperative game $v\in TU^N$ is called simple if $v(S)\in \{0,1\}$ for all $S\in 2^N$, $v(N)=1$ and $v(S)\le v(T)$ for all $S,T\in 2^N$ with $S\subseteq T$. Moreover, for a simple game $v\in TU^N$, the set of veto-players is given by

$$\begin{aligned} \text {veto}(v) = \bigcap \left\{ S\in 2^N \ \Big |\ v(S)=1 \right\} . \end{aligned}$$

For simple games, having veto-players is equivalent to balancedness, which in turn is equivalent to compromise stability. Moreover, if a simple game has veto-players, then the nucleolus divides the worth of the grand coalition equally among these veto-players. Note that if the game underlying a communication situation is simple, then the graph-restricted game is simple too.

If, in addition to compromise stability, we also require that the underlying game is simple, it turns out that the nucleolus is invariant for all such communication situations if the graph is biconnected. Furthermore, for every connected graph that is not biconnected, we construct a communication situation with an underlying game that is both compromise stable and simple for which the nucleolus of the graph-restricted game is not equal to the nucleolus of the underlying game. Again, we benefit from the construction in the proof of Theorem 3.1 (and Theorem 4.1).

Proposition 5.1

The following two statements hold:

• (i) Let $\left( N,v,E\right) \in \mathcal {CS}^N$ be a communication situation with (N, E) is biconnected and v is both compromise stable and simple. Then, $\text {nuc}(v^E)=\text {nuc}(v)$;

• (ii) Let (N, E) be a connected graph that is not biconnected. Then, there exists a communication situation $\left( N,v,E\right) \in \mathcal {CS}^N$ where v is both compromise stable and simple such that $\text {nuc}(v^E)\not =\text {nuc}(v)$.

Proof

(i) It suffices to show that $\text {veto}(v)=\text {veto}(v^E)$. Since $v^E(S)=1$ implies that $v(S)=1$, it holds that $\text {veto}(v)\subseteq \text {veto}(v^E)$. Suppose there exists $i\in \text {veto}(v^E)$ with $i\notin \text {veto}(v)$. Clearly, $v(N\setminus \{i\} )=1$. Then, since the induced subgraph on $N\setminus \{i\}$ is connected, it holds that $v^E(N\setminus \{i\} )=v(N\setminus \{i\} )=1$. This contradicts the fact that $i\in \text {veto}(v^E)$.

(ii) As before, since (N, E) is not biconnected, set $N=\{1,2,\ldots ,n\}$ and assume w.l.o.g. that $\{1,2\} ,\{2,3\} \in E$, that the induced subgraph on $N\setminus \{2\}$ is not connected and that players 1 and 3 are in two different components in the induced subgraph on $N\setminus \{2\}$. Reconsider the communication situation $(N,v_1,E)\in \mathcal {CS}^N$ with, for all $S\in 2^N$,

$$\begin{aligned} v_1(S)={\left\{ \begin{array}{ll} 1, &{} \text{ if } \{1,2\} \subseteq S \text { or } \{1,3\} \subseteq S;\\ 0, &{} \text{ otherwise }. \end{array}\right. } \end{aligned}$$

Note that $v_1$ is simple. Recall that $v_1$ is strongly compromise admissible, and thus compromise stable. Moreover, as seen before, $\text {nuc}(v^E)=(\frac{1}{2},\frac{1}{2},0,\ldots ,0)\not =(1,0,0,\ldots ,0)=\text {nuc}(v)$, which concludes the proof.$\square$