1 Introduction

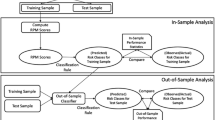
Nowadays, the use of analytical methods in extracting intelligence from data, in general, and business-related data, in particular, to support decision-making is increasing gaining popularity amongst practitioners. The popularity of descriptive analytics techniques, predictive analytics techniques, and prescriptive analytics techniques vary substantially from one industry to another. The financial industry is one amongst many first movers where predictive analytics techniques are widely used to predict risk and return amongst other variables that drive investment decision-making. The focus of this paper is on predictive analytics techniques for risk-class prediction. Analytics techniques for risk-class prediction fall into two main categories; namely, parametric methods and non-parametric methods, where non-parametric prediction methods have obvious advantages over parametric ones. In this paper, we extend the toolbox of non-parametric predictive methods by proposing a new integrated classifier that performs both in-sample and out-of-sample predictions, where in-sample predictions are devised with a first VIKOR-based classifier and out-of-sample predictions are devised with a CBR-based classifier trained on the risk class predictions provided by the proposed VIKOR-based classifier—see Fig. 1 for a snapshot of the design of the proposed prediction framework.

Fig. 1
figure 1

An integrated VIKOR-CBR prediction framework for in-sample and out-of-sample analyses

Full size image

VIKOR is a multi-criteria method originally designed for ranking a number of alternatives, say \( m \), under multiple non-commensurable (i.e., measured on different scales or in different units) and often conflicting criteria, say \( n \), where criteria are conflicting in the sense that improving a criterion is only achievable at the expense of at least another criterion; therefore, trade-offs between conflicting criteria is the way to reach an acceptable solution. VIKOR is grounded into compromise programming, as it is designed to devise a solution that is the closest to an ideal one. In sum, VIKOR benchmarks all alternatives against an ideal solution and makes use of the relative closeness, as measured by the \( L_{p} \) distance, from the ideal solution—typically virtual and infeasible—to construct an index for each alternative or entity \( i \), say \( Q_{i} \), which is a convex combination of the standardized distance between entity \( i \) and the alternative with the best (observed) average performance and the standardized distance between entity \( i \) and the entity with the least (observed) regret. Since the publication of seminal paper by Duckstein and Opricovic (1980), several hundreds of papers were published on VIKOR and its variants. Application papers apart, papers on methodological contributions on the crisp version of VIKOR could be divided into two main categories; namely, VIKOR and variants for multi-criteria decision problems where all alternatives are assessed based on a common set of criteria, and VIKOR and variants for multi-criteria decision problems where different alternatives are assessed based on different sets of criteria. Examples of contributions in the first category include the original VIKOR (Duckstein and Opricovic 1980); VIKOR enhanced with Weight Stability Analysis and Trade-offs Analysis (Opricovic and Tzeng 2007); VIKOR with Choiceless and Discontent Utilities (Huang et al. 2009); VIKOR with Logic Judgment (Chang 2010); and VIKOR for criteria with a Normal Reference Range (Zeng et al. 2013). On the other hand, examples of contributions in the second category include the modified VIKOR by Liou et al. (2011) and the modified VIKOR by Anvari et al. (2014). For reviews on VIKOR application areas, we refer the reader to Mardani et al. (2016), Gul et al. (2016), and Yazdani and Graeml (2014).

The remainder of this paper unfolds as follows. In Sect. 2, we provide a detailed description of the proposed integrated in-sample and out-of-sample framework for VIKOR-based classifiers and discuss implementation decisions. In Sect. 3, we empirically test the performance of the proposed framework in bankruptcy prediction of companies listed on the London Stock Exchange (LSE) and report on our findings. Finally, Sect. 4 concludes the paper.

2 An integrated framework for designing and implementing VIKOR-based classifiers

In this section, we shall describe our integrated VIKOR-based classification framework—see Fig. 1 for a graphical representation of the process. Without loss of generality, we shall customize the presentation of the proposed framework to a bankruptcy application as follows:

  • Input: A set of \( n \) entities (e.g., LSE listed firm-year observations) to be assessed on \( m \) pre-specified criteria (e.g., financial criteria) along with their measures (e.g., financial ratios), where the measure of each criterion could either be minimized or maximized. Thus, each entity, say \( i \) (\( i = 1, \ldots ,n \)), is represented by an \( m \)-dimensional vector of (observed) measures of the criteria under consideration, say \( x_{i} = \left( {x_{ij} } \right) \), where \( x_{ij} \) denote the observed measure of criterion \( j \) for entity \( i \) and the set of \( x_{i} \) s shall be denoted by \( X \). An observed risk-class membership, say \( Y \), is also available for all entities. The historical sample \( X \) is divided into a training sample, say \( X^{E} \), and a test sample, say \( X^{T} \).

2.1 Phase 1: VIKOR-based in-sample classifier

2.1.1 Step 1: Compute the best and worst virtual alternatives or benchmarks

Compute the best virtual alternative—also referred to as the ideal positive alternative, say \( r^{ + } \), as the best performer on each and every criterion \( j \) amongst all entities or alternatives \( i \) in the training sample \( X^{E} \); that is:

$$ r_{j}^{ + } = \left\{ {\begin{array}{*{20}c} {\mathop {\hbox{min} }\limits_{{i = 1, \ldots ,\# X^{E} }} x_{i,j}^{E} IF j \in M^{ - } } \\ {\mathop {\hbox{max} }\limits_{{i = 1, \ldots ,\# X^{E} }} x_{i,j}^{E} IF j \in M^{ + } } \\ \end{array} } \right.;\quad j = 1, \ldots ,m $$

and compute the worst virtual alternative—also referred to as the ideal negative alternative, say \( r^{ - } \), as the worst performer on each and every criterion \( j \) amongst all alternatives \( i \) in the training sample \( X^{E} \); that is:

$$ r_{j}^{ - } = \left\{ {\begin{array}{*{20}c} {\mathop {\hbox{max} }\limits_{{i = 1, \ldots ,\# X^{E} }} x_{i,j}^{E} IF j \in M^{ - } } \\ {\mathop {\hbox{min} }\limits_{{i = 1, \ldots ,\# X^{E} }} x_{i,j}^{E} IF j \in M^{ + } } \\ \end{array} } \right.;\quad j = 1, \ldots ,m $$

where \( M^{ - } \) (resp. \( M^{ + } \)) denote the set of features for which lower (resp. higher) values are better, \( x_{i,j}^{E} \) denote the observed performance of alternative \( i \in X^{E} \) on criterion \( j \) (\( j = 1, \ldots ,m \)), and \( \# X^{E} \) denote the cardinality of \( X^{E} \). Note that we refer to benchmarks \( r^{ + } \) and \( r^{ - } \) as virtual, because they are not observed as such; in fact, they are made up of the observed best (respectively, worst) performer on each criterion.

2.1.2 Step 2: Compute measures of the average performance behavior of alternatives

For each entity \( i \) in the training sample \( X^{E} \) (\( i = 1, \ldots ,\# X^{E} \)), compute a measure of its average performance behavior, say \( S_{i} \), which allows for full compensation between criteria, as follows:

$$ S_{i} = \left( {\mathop \sum \limits_{j = 1}^{m} \left( {w_{j} \frac{{\left( {r_{j}^{ + } - x_{i,j}^{E} } \right)}}{{\left( {r_{j}^{ + } - r_{j}^{ - } } \right)}}} \right)^{p} } \right)^{{\frac{1}{p}}} \,{\text{with}}\,p = 1;\,{\text{i}} . {\text{e}} .,\,S_{i} = \mathop \sum \limits_{j = 1}^{m} w_{j} \frac{{\left( {r_{j}^{ + } - x_{i,j}^{E} } \right)}}{{\left( {r_{j}^{ + } - r_{j}^{ - } } \right)}}. $$

Also, compute \( S^{ + } = \mathop {\hbox{min} }\limits_{i} S_{i} \) and \( S^{ - } = \mathop {\hbox{max} }\limits_{i} S_{i} \).

Note that \( S_{i} \) is an \( L_{p} \)-metric based aggregation function for \( p = 1 \) that quantifies how close entity \( i \) is from the positive ideal alternative and could be interpreted as a utility function of entity \( i \). Note also that an aggregating function is used here instead of a utility function, because in many multi-criteria decision problems it is not possible to obtain a mathematical representation of the decision maker’s utility function. Finally, notice that \( \left( {r_{j}^{ + } - x_{i,j}^{E} } \right)\bigg{/}\left( {r_{j}^{ + } - r_{j}^{ - } } \right) \) is the deviation from the best virtual alternative on criterion \( j \), \( \left( {r_{j}^{ + } - x_{i,j}^{E} } \right) \), standardized by the distance between the best and the worst virtual alternatives on criterion \( j \), \( \left( {r_{j}^{ + } - r_{j}^{ - } } \right) \); therefore, \( S_{i} \) is the weighted sum over all criteria of standardized deviations from the best virtual alternative, where \( w_{j} \) denote the weight assigned to criterion \( j \). In sum, \( S_{i} \) reflects the average performance behavior of entity \( i \), which allows for full compensation between criteria. Since \( S_{i} \) reflects the average performance behavior of entity \( i \), \( S^{ + } = \mathop {\hbox{min} }\limits_{i} S_{i} \) and \( S^{ - } = \mathop {\hbox{max} }\limits_{i} S_{i} \) are the best and worst observed average performance behavior across all entities in-sample, respectively. Note that \( S^{ + } \) is often interpreted as the maximum group utility of the “majority”. Let \( i^{ + } = argmin_{i} S_{i} \) and \( i^{ - } = argmax_{i} S_{i} \). Thus, \( \left( {S_{i} - S^{ + } } \right)/\left( {S^{ - } - S^{ + } } \right) \) is the distance between entity \( i \) and the best (on average) observed performer; i.e., entity \( i^{ + } \), standardized by the distance between the best and worst (on average) observed performers; i.e., entities \( i^{ + } \) and \( i^{ - } \), respectively.

2.1.3 Step 3: Compute measures of the worst performance behavior of alternatives

For each entity \( i \) in the training sample \( X^{E} \) (\( i = 1, \ldots ,\# X^{E} \)), compute a measure of its worst performance behavior, say \( R_{i} \), which does not allow for any compensation between criteria, as follows:

$$ R_{i} = \left( {\mathop \sum \limits_{j = 1}^{m} \left( {w_{j} \frac{{\left( {r_{j}^{ + } - x_{i,j}^{E} } \right)}}{{\left( {r_{j}^{ + } - r_{j}^{ - } } \right)}}} \right)^{p} } \right)^{{\frac{1}{p}}} \,{\text{with}}\,p = \infty ;{\text{ i}} . {\text{e}} .,\,R_{i} = \mathop {\hbox{max} }\limits_{j} \left\{ {w_{j} \frac{{\left( {r_{j}^{ + } - x_{i,j}^{E} } \right)}}{{\left( {r_{j}^{ + } - r_{j}^{ - } } \right)}}} \right\}. $$

Also, compute \( R^{ + } = \mathop {\hbox{min} }\limits_{i} R_{i} \) and \( R^{ - } = \mathop {\hbox{max} }\limits_{i} R_{i} \).

Note that \( R_{i} \) is also an \( L_{p} \)-metric based aggregation function with \( p = \infty \) that quantifies how far, in the extreme case, entity \( i \) is from the positive ideal alternative and could be interpreted as a regret function of entity \( i \). In fact, unlike \( S_{i} \), \( R_{i} \) is the maximum over all criteria of the weighted standardized deviations from the best virtual alternative and thus reflects the worst performance behavior of entity \( i \). Note also that \( R_{i} \) does not allow for any compensation between criteria. Since \( R_{i} \) reflects the worst performance behavior of entity \( i \), \( R^{ + } = \mathop {\hbox{min} }\limits_{i} R_{i} \) and \( R^{ - } = \mathop {\hbox{max} }\limits_{i} R_{i} \) represent the least and most observed individual regrets amongst all entities in-sample, respectively. Let \( i^{ + + } = argmin_{i} R_{i} \) and \( i^{ - - } = argmax_{i} R_{i} \). Thus, \( \left( {R_{i} - R^{ + } } \right)/\left( {R^{ - } - R^{ + } } \right) \) is the distance between entity \( i \) and the observed entity with the least regret; i.e., entity \( i^{ + + } \), standardized by the distance between the observed entities with the least and the most regrets; i.e., entities \( i^{ + + } \) and \( i^{ - - } \), respectively.

2.1.4 Step 4: Compute a VIKOR score for each alternative

For each entity \( i \) in the training sample \( X^{E} \) (\( i = 1, \ldots ,\# X^{E} \)), compute a performance score, say \( Q_{i} \), which represents a measure of closeness to the positive ideal solution, as a convex combination of the standardized distance between entity \( i \) and the alternative with the best (observed) average performance, \( i^{ + } \), and the standardized distance between entity \( i \) and the entity with the least (observed) regret, \( i^{ + + } \):

$$ Q_{i} = \left\{ {\begin{array}{*{20}l} {\alpha \left( {\frac{{S_{i} - S^{ + } }}{{S^{ - } - S^{ + } }}} \right) + \left( {1 - \alpha } \right)\left( {\frac{{R_{i} - R^{ + } }}{{R^{ - } - R^{ + } }}} \right) IF S^{ - } \ne S^{ + } and R^{ - } \ne R^{ + } ; 0 \le \alpha \le 1} \hfill \\ {\frac{{R_{i} - R^{ + } }}{{R^{ - } - R^{ + } }} IF S^{ - } = S^{ + } and R^{ - } \ne R^{ + } } \hfill \\ {\frac{{S_{i} - S^{ + } }}{{S^{ - } - S^{ + } }} IF S^{ - } \ne S^{ + } and R^{ - } = R^{ + } } \hfill \\ {constant IF S^{ - } = S^{ + } and R^{ - } = R^{ + } } \hfill \\ \end{array} } \right. $$

Notice that the definition of \( Q_{i} \) allows the user to measure the performance of entities using indexes that capture the extent to which the benchmarking emphasis is put on the best observed performer, \( i^{ + } \), the observed performer with the least regret, \( i^{ + + } \), or a combination between these two extreme behaviors, depending on the value chosen for \( \alpha \). Note that lower values of \( {\text{Q}} \), \( S \), and \( R \) respectively, indicate better performance. Finally, note that the weights assigned to criteria could be chosen in many different ways; we refer the reader to Table 1 for a sample of commonly used weighting schema in VIKOR implementations.

Table 1 Sample of commonly used weighting schema in VIKOR
Full size table

2.1.5 Step 5: Compute in-sample classification of alternatives

Use the performance scores, \( Q_{i} \) s, computed in the previous step to classify alternatives \( i \) in the training sample \( X^{E} \) according to a user-specified classification rule into, for example, risk (e.g., bankruptcy) classes, say \( \hat{Y}^{E} \). Then, compare the VIKOR based classification of alternatives in \( X^{E} \) into risk classes; that is, the predicted risk classes, \( \hat{Y}^{E} \), with the observed risk classes of alternatives in the training sample, \( Y^{E} \), and compute the relevant in-sample performance statistics. The choice of a decision rule for classification depends on the nature of the classification problem; that is, a two-class problem or a multi-class problem. In this paper, we are concerned with a two-class problem; therefore, we shall provide a solution that is suitable for these problems. In fact, we propose a VIKOR score-based cut-off point procedure to classify entities in \( X_{E} \). The proposed procedure involves solving an optimization problem whereby the VIKOR score-based cut-off point, say \( \kappa \), is determined so as to optimize a given classification performance measure, say \( \pi \) (e.g., Type I error, Type II error, Sensitivity, Specificity), over an interval with a lower bound, say \( \kappa_{LB} \), equal to the smallest VIKOR score of entities in \( X_{E} \) and an upper bound, say \( \kappa_{UB} \), equal to the largest VIKOR score of entities in \( X_{E} \). Any derivative-free unidimensional search procedure could be used to compute the optimal cut-off score, say \( \kappa^{*} \)—for details on derivative-free unidimensional search procedures, the reader is referred to Bazaraa et al. (2006). The optimal cut-off score \( \kappa^{*} \) is used to classify observations in \( X_{E} \) into two classes; namely, bankrupt and non-bankrupt firms. To be more specific, the predicted risk classes \( \hat{Y}^{E} \) are determined so that firms with VIKOR scores greater than \( \kappa^{*} \) are assigned to a bankruptcy class and those with VIKOR scores less than or equal to \( \kappa^{*} \) are assigned to a non-bankruptcy class. Note that an important feature of the design of our VIKOR score-based cut-off point procedure for classification lies in the determination of a cut-off score to optimise a specific performance measure of the classifier.

2.2 Phase 2: CBR-based out-of-sample classifier

2.2.1 Step 6: Compute out-of-sample classification of alternatives

Use an instance of case-based reasoning (CBR); namely, the k-nearest neighbour (k-NN) algorithm, to classify alternatives in \( X^{T} \) into risk classes (i.e., bankruptcy class, non-bankruptcy class), say \( \hat{Y}^{T} \). Then, compare the predicted risk classes \( \hat{Y}^{T} \) with the observed ones \( Y^{T} \) and compute the relevant out-of-sample performance statistics. A detailed description of k-NN is hereafter outlined:

figure a

We would like to stress out that, when the decision maker is not confident enough to provide a value for \( \alpha \) in step 5, one could automate the choice of \( \alpha \). In fact, an optimal value of \( \alpha \) with respect to a specific performance measure (e.g., Type 1 error, Type 2 error, Sensitivity, or specificity) to be optimized either in-sample only or both in-sample and out-of-sample could be obtained by using a derivative-free unidimensional search procedure, which calls either a procedure that consists of steps 4 and 5 to optimize in-sample performance, or a procedure that consists of steps 4 to 6 to optimize both in-sample and out-of-sample performances simultaneously.

Finally, note that VIKOR outcome depends on the choice of the ideal solution, whose calculation depends on the given set of alternatives \( X^{E} \). Therefore, inclusion or exclusion of one or several alternative; e.g., \( X^{T} \), would affect the VIKOR outcome unless the ideal solution is chosen or fixed at the outset by the decision maker independently from \( X^{E} \). This is the main reason for choosing a CBR framework for the out-of-sample classification instead of VIKOR.

In the next section, we shall report on our empirical evaluation of the proposed VIKOR-CBR integrated prediction framework.

3 Empirical results

In order to assess the performance of the proposed framework, we considered a sample of 6605 firm-year observations consisting of non-bankrupt and bankrupt UK firms listed on the London Stock Exchange (LSE) during 2010–2014 excluding financial firms and utilities as well as those firms with less than 5 months lag between the reporting date and the fiscal year. The source of our sample is DataStream. The list of bankrupt firms is however compiled from London Share Price Database (LSPD)—codes 16 (Receiver appointed/liquidation. Probably valueless, but not yet certain), 20 (In Administration/Administrative receivership) and 21 (Cancelled and assumed valueless). In other terms, a company is considered bankrupt if it is cancelled and assumed valueless, or it is under administration or receivership, or it is being liquidated. Recall that entities such as businesses are referred to as insolvent when they have insufficient assets to cover their debts or are unable to pay their debts when they are supposed to. There are mainly five categories of procedures to deal with insolvency; namely, administrations, company voluntary arrangements, administrative receiverships, compulsory liquidations, and creditor’s voluntary liquidations, where the first three options provide the potential for rescuing the company. For the benefit of the reader, hereafter we shall provide brief descriptions of the insolvency procedures relevant to this research. The purpose of putting a company under administration is to hold a business together while plans are being prepared either to put in place a financial restructuring to rescue the company, or to sell the business and assets to produce a better result for creditors than liquidation. The process starts with an application to court for an administration. Once the court has appointed an administrator, he or she takes over the day to day control and management of the company while devising proposals to be voted on by creditors. Possible exit routes of the administration process include the company goes into a scheme of arrangement such as company voluntary arrangement, and if unsuccessful, the company is liquidated and then dissolved; the company goes into a creditors’ voluntary liquidation and then dissolved; or the company goes into compulsory liquidation and then dissolved. Receivership is a procedure similar to administration, where the main difference lies into who appoints the administrator. In administration, the administrator is appointed by the court, whereas in receivership, the receiver is appointed by a lender or a consortium of lenders to whom he or she has the primary duty to collect a maximum debt for them. Finally, liquidation refers to turning a company’s assets into cash and then distributing it to creditors and could take the form of a Creditor’s voluntary liquidation—also known as solvent liquidation, or a compulsory liquidation—also known as insolvent liquidation. Information on our dataset composition is summarised in Table 2 broken down by industry. As to the selection of the training sample and the test sample, we have chosen the size of the training sample to be twice the size of the test sample. The selection of observations was done with random sampling without replacement to ensure that both the training sample and the test sample have the same proportions of bankrupt and non-bankrupt firms. A total of thirty pairs of training sample-test sample were generated.

Table 2 Dataset composition
Full size table

In our experiment, we reworked a standard and well known parametric model within the proposed VIKOR-CBR framework; namely, the multivariate discriminant analysis (MDA) model of Taffler (1984), to provide some empirical evidence on the merit of the proposed framework. Recall that Taffler’s model makes use of four explanatory variables or bankruptcy drivers which belong to the same category; namely, liquidity. These drivers are current liabilities to total assets, number of credit intervals, profit before tax to current liabilities, and current assets to total liabilities. Note that lower values are better than higher ones for Current Liabilities to Total Assets and Number of Credit Intervals, whereas higher values of Current Assets to Total Liabilities and Profit Before Tax to Current Liabilities are better than lower ones. We report on the performance of the proposed framework using four commonly used metrics; namely, Type I error (T1), Type II error (T2), Sensitivity (Sen) and Specificity (Spe), where T1 is the proportion of bankrupt firms predicted as non-bankrupt, T2 is the proportion of non-bankrupt firms predicted as bankrupt, Sen is the proportion of bankrupt firms predicted as bankrupt, and Spe is the proportion of non-bankrupt firms predicted as non-bankrupt.

Since both the VIKOR classifier and the k-NN classifier, trained on the in-sample classification obtained with VIKOR, require a number of decisions to be made for their implementation, we considered several combinations of decisions to find out about the extent to which the performance of the proposed framework is sensitive or robust to these decisions. Recall that, for the VIKOR classifier, the analyst must choose (1) a value for \( \alpha \), (2) a weighting scheme, and (3) the classification rule. On the other hand, for the k-NN classifier, the analyst must choose (1) the metric to use for computing distances between entities, \( d_{k - NN} \), (2) the classification criterion, and (3) the size \( k \) of the neighbourhood. Our choices for these decisions are summarised in Table 3.

Table 3 Implementation decisions for VIKOR and k-NN
Full size table

Hereafter, we shall provide a summary of our empirical results and findings. Tables 4, 5, 6, 7 and 8 provide summaries of In-sample statistics on the performance of the MDA model of Taffler (1984) reworked within the VIKOR-CBR framework, which is an integrated In-sample-Out-of-sample framework for VIKOR-based classifiers, for \( \alpha = 0, 0.25, 0.5, 0.75, 1 \) respectively. In sum; In-sample performance statistics are reported for different scenarios ranging from a non-compensating scheme (\( \alpha = 0 \)) to a fully compensating scheme \( (\alpha = 1 \)). Note that a non-compensating scheme does not allow for any compensation between criteria. These results show that the performance of the classifier In-sample is outstanding. In fact, none of the bankrupt firms is misclassified. As to non-bankrupt firms, the misclassification errors are almost zero. For example, 0.075% (i.e., 4) firms are misclassified by VIKOR as compared to 0.26% (i.e., 16) firms misclassified by MDA—see Tables 4 and 9. Notice that, as \( \alpha \) increases or equivalently compensation between criteria is increased, the misclassification errors tend to zero. This performance could be explained by the fact that the non-compensating scheme is benchmarking each alternative \( i \) against the entity with the least regret, whereas the compensating scheme is benchmarking against the best-observed performer.

Table 4 Summary statistics of the performance of the proposed framework for \( \alpha = 0 \) (non-compensating scheme)
Full size table
Table 5 Summary statistics of the performance of the proposed framework for \( \alpha = 0.25 \) (mixed scheme)
Full size table
Table 6 Summary statistics of the performance of the proposed framework for \( \alpha = 0.5 \) (mixed scheme)
Full size table
Table 7 Summary statistics of the performance of the proposed framework for \( \alpha = 0.75 \)(mixed scheme)
Full size table
Table 8 Summary Statistics of the Performance of the Proposed Framework for \( \alpha = 1 \)(compensating scheme)
Full size table
Table 9 Summary statistics of the performance of MDA
Full size table

On the other hand, the performance of the classifier out-of-sample is also outstanding—see Tables 4, 5, 6, 7 and 8. In fact, for all values of \( \alpha \) or compensation schema, all bankrupt and non-bankrupt firms are correctly classified. Note however that the performance of the out-of-sample classifier CBR trained on the in-sample classification provided by VIKOR seems to be marginally affected by the choice of the distance metric; to be more specific, the Mahalanobis distance seems to have slightly affected the performance – see Table 5, where the average type II error increased from 0 to 0.02% and the average specificity decreased from 100 to 99.98%. These differences in performance are however marginal to recommend that the Mahalanobis distance be avoided in implementing CBR. In sum, the performance of CBR trained on VIKOR classifier’s output is robust to the choice of the distance metric.

To conclude, our results suggest that the predictive performance of the proposed classification framework is by far superior to the predictive performance of multivariate discriminant analysis—see Table 8.

4 Conclusions

The analytics toolbox of risk management is crucial for the financial industry amongst others. In this paper, we extended such toolbox with a new non-parametric classifier for predicting risk class belonging. The proposed new integrated classifier has several appealing characteristics. First, it performs both in-sample and out-of-sample predictions, where in-sample predictions are devised with a first VIKOR-based classifier and out-of-sample predictions are devised with a CBR-based classifier. Both the newly proposed VIKOR-based classifier and CBR-based classifier are nonparametric and thus do not have the limitations of the usual statistical assumptions underlying the parametric classifiers. Second, the proposed VIKOR-based classifier delivers an outstanding empirical performance suggesting that VIKOR scores are highly informative, on one hand, and the computation of the thresholds for classification using a nonlinear programming algorithm are optimised, on the other hand. Third, the empirical performance of the CBR-based classifier is enhanced by training it on the high-quality risk class predictions provided by the VIKOR-based classifier. Fourth, the proposed VIKOR classifier is based on a benchmarking framework, which contributes to its design’s strength. In fact, VIKOR benchmarks alternatives against the positive ideal solution by measuring the average and the maximum deviations from it, respectively, standardized by the distance between the positive and negative ideals. These deviations or distances from the positive ideal are then used to compute the distance between the performance behavior of each alternative and the behavior of the best observed performer, standardized by the distance between the behaviors of the best and worst observed performers, and the distance between the regret behavior of each alternative and the behavior of the observed entity with the least regret, standardized by the distance between the observed entities with the least and the most regrets. A convex combination of these behavioral measures is then used as the VIKOR score. Last, but not least, the basic concepts behind both VIKOR and CBR are easy to explain to managers.

We assessed the performance of the proposed VIKOR-CBR framework using a UK dataset of bankrupt and non-bankrupt firms. Our results support its outstanding predictive performance. In addition, the outcome of the proposed framework is robust to a variety of implementation decisions; namely, the choice of the value of \( \alpha \), the choice of the weighting Scheme, and the choice of the classification rule for VIKOR, and the choice of the distance metric \( d_{k - NN} \), the choice of the classification criterion, and the choice of the size \( k \) of the neighbourhood for k-NN instance of CBR. Last, but not least, the proposed classification framework delivers a high performance similar to the DEA-based classifier proposed by Ouenniche and Tone (2017) and the MCDM classifiers proposed by Ouenniche et al. (2018a, b, c).

In sum, this research relates to both the field of MCDM and the field of AI. In fact, this paper proposes a hybrid design that integrates MCDM and artificial intelligence (AI) techniques, where a VIKOR-based classifier is proposed for the first time and the output of VIKOR is used to train a CBR out-of-sample classifier. Empirical evidence supports our claim that the hybridisation of MCDM and AI fields is promising.