Abstract
Given recent requirements for ensuring the robustness of algorithmic trading strategies laid out in the Markets in Financial Instruments Directive II, this paper proposes a novel agent-based simulation for exploring algorithmic trading strategies. Five different types of agents are present in the market. The statistical properties of the simulated market are compared with equity market depth data from the Chi-X exchange and found to be significantly similar. The model is able to reproduce a number of stylised market properties including: clustered volatility, autocorrelation of returns, long memory in order flow, concave price impact and the presence of extreme price events. The results are found to be insensitive to reasonable parameter variations.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Over the last three decades, there has been a significant change in the financial trading ecosystem. Markets have transformed from exclusively human-driven systems to predominantly computer driven. These machine driven markets have laid the foundations for a new breed to trader: the algorithm. According to Angel et al. (2010), algorithmically generated orders are now thought to account for over 80% of volume traded on US equity markets, with figures continuing to rise.
The rise of algorithmic trading has not been a smooth one. Since its introduction, recurring periods of high volatility and extreme stock price behaviour have plagued the markets. The SEC and CFTC (2010) report, among others, has linked such periods to trading algorithms, and their frequent occurrence has undermined investors confidence in the current market structure and regulation. Indeed, Johnson et al. (2013) reports that so called extreme price movement Flash Crashes are becoming ever more frequent with over 18,000 of them occurring between 2006 and 2011 in various stocks.
Thus, in this paper, we describe for the first time an agent-based simulation environment that is realistic and robust enough for the analysis of algorithmic trading strategies. In detail, we describe an agent-based market simulation that centres around a fully functioning limit order book (LOB) and populations of agents that represent common market behaviours and strategies: market makers, fundamental traders, high-frequency momentum traders, high-frequency mean reversion traders and noise traders.
The model described in this paper includes agents that operate on different timescales and whose strategic behaviours depend on other market participants. The decoupling of actions across timescales combined with dynamic behaviour of agents is lacking from previous models and is essential in dictating the more complex patterns seen in high-frequency order-driven markets. Consequently, this paper presents a model that represents a richer set of trading behaviours and is able to replicate more of the empirically observed empirical regularities than any other paper. Such abilities provide a crucial step towards a viable platform for the testing of trading algorithms as outlined in MiFID II.
We compare the output of our model to depth-of-book market data from the Chi-X equity exchange and find that our model accurately reproduces empirically observed values for: autocorrelation of price returns, volatility clustering, kurtosis, the variance of price return and order-sign time series and the price impact function of individual orders. Interestingly, we find that, in certain proportions, the presence of high-frequency trading agents gives rise to the occurrence of extreme price events. We asses the sensitivity of the model to parameter variation and find the proportion of high-frequency strategies in the market to have the largest influence on market dynamics.
This paper is structured as follows: Sect. 2 gives a background on the need for increased regulation and the rise of MiFID II. Section 3 gives an overview of the relevant literature while Sect. 4 provides a description of the model structure and agent behaviours in detail. In Sect. 5 the results are summarised while Sect. 6 gives concluding remarks and discusses potential future work.
2 The need for improved oversight and the scope of MiFID II
One of the more well known incidents of market turbulence is the extreme price spike of the 6th May 2010. At 14:32, began a trillion dollar stock market crash that lasted for a period of only 36 min (Kirilenko et al. 2014). Particularly shocking was not the large intra-day loss but the sudden rebound of most securities to near their original values. This breakdown resulted in the second-largest intraday point swing ever witnessed, at 1010.14 points. Only 2 weeks after the crash, the SEC and CFTC released a joint report that did little but quash rumours of terrorist involvement. During the months that followed, there was a great deal of speculation about the events on May 6th with the identification of a cause made particularly difficult by the increased number of exchanges, use of algorithmic trading systems and speed of trading. Finally, the SEC and CFTC released their report on September 30th concluding that the event was initiated by a single algorithmic order that executed a large sale of futures contracts in an extraordinarily short amount of time from fund management firm Waddell and Reed (W&R) (SEC 2010).
The report was met with mixed responses and a number of academics have expressed disagreement with the SEC report. Menkveld and Yueshen (2013) analysed W&Rs orderflow and identified an alternative narrative. They did not conclude that the crash was simply the price W&R were required to take for demanding immediacy in the S&P. Instead, they found that cross-market arbitrage, which provided e-mini sellers with increased liquidity from S&P buyers in other markets, broke down minutes before the crash. As a result of the breakdown, W&R were forced to find buyers only in E-mini and so they decelerated their selling. An extreme response (in terms of price and selling behaviour) then resulted in W&R paying a disproportionately high price for demanding liquidity.
Easley and Prado (2011) show that major liquidity issues were percolating over the days that preceded the price spike. They note that immediately prior to the large W&R trade, volume was high and liquidity was low. Using a technique developed in previous research (Easley et al. 2010), they suggest that, during the period in question, order flow was becoming increasingly toxic. They go on to demonstrate how, in a high-frequency world, such toxicity may cause market makers to exit - sowing the seeds for episodic liquidity. Of particular note, the authors express their concern that an anomaly like this is highly likely to occur, once again, in the future.
Another infamous crash occurred on the 23rd March 2012 during the IPO of a firm called BATS. The stock began trading at 11:14 a.m. with an initial price of $15.25. Within 900 ms of opening, the stock price had fallen to $0.28 and within 1.5 s, the price bottomed at $0.0007. Yet another technological incident was witnessed when, on the 1st August 2012, the new market-making system of Knight Capital was deployed. Knight Capital was a world leader in automated market making and a vocal advocate of automated trading. The error occurred when testing software was released alongside the final market-making software. According to the official statement of Knight Capital Group (2012):
Knight experienced a technology issue at the open of trading...this issue was related to Knights installation of trading software and resulted in Knight sending numerous erroneous orders in NYSE-listed securities...which has resulted in a realised pre-tax loss of approximately 440 million [dollars].
This 30 min of bogus trading brought an end to Knights 17 year existence, with the firm subsequently merging with a rival.
The all-too-common extreme price spikes are a dramatic consequence of the growing complexity of modern financial markets and have not gone unnoticed by the regulators. In November 2011, the European Union (2011) made proposals for a revision of the Markets in Financial Instruments Directive (MiFID). Although this directive only governs the European markets, according to the World Bank (2012) (in terms of market capitalisation), the EU represents a market around two thirds of the size of the US. In the face of declining investor confidence and rapidly changing markets, a draft of MiFID II was produced. After nearly three years of debate, on the 14th January 2014, the European Parliament and the Council reached an agreement on the updated rules for MiFID II, with a clear focus on transparency and the regulation of automated trading systems (European Union 2014).
MiFID II came to be as a result of increasing fears that algorithmic trading had the potential to cause market distortion over unprecedented timescales. Particularly, there were concerns over increased volatility, high cancellation rates and the ability of algorithmic systems to withdraw liquidity at any time. Thus, MiFID II introduces tighter regulation over algorithmic trading, imposing specific and detailed requirements over those that operate such strategies. This increased oversight requires clear definitions of the strategies under regulation.
MiFID II defines algorithmic trading as the use of computer algorithms to automatically determine the parameters of orders, including: trade initiation, timing, price and modification/cancellation of orders, with no human intervention. This definition specifically excludes any systems that only deal with order routing, order processing, or post trade processing where no determination of parameters is involved.
The level of automation of algorithmic trading strategies varies greatly. Brokers and large sell side institutions tend to focus on optimal execution, where the aim of the algorithmic trading is to minimise the market impact of orders. These algorithms focus on order slicing and timing. Other institutions, often quantitative buy-side firms, attempt to automate the entire trading process. These algorithms may have full discretion regarding their trading positions and encapsulate: price modelling and prediction to determine trade direction, initiation, closeout and monitoring of portfolio risk. This type of trading tends to occur via direct market access (DMA) or sponsored access.
Under MiFID II, HFT is considered as a subset of algorithmic trading. The European Commission defines HFT as any computerised technique that executes large numbers of transactions in fractions of a second using:
-
Infrastructure designed for minimising latencies, such as proximity hosting, collocation or DMA.
-
Systematic determination of trade initiation, closeout or routing with-out any human intervention for individual orders; and
-
High intra-day message rates due to volumes of orders, quotes or cancellations.
Specifically, MiFID II introduces rules on algorithmic trading in financial instruments. Any firm participating in algorithmic trading is required to ensure it has effective controls in place, such as circuit breakers to halt trading if price volatility becomes too high. Also, any algorithms used must be tested and authorised by regulators. We find the last requirement particularly interesting as MiFID II is not specific about how algorithmic trading strategies are to be tested.
Given the clear need for robust methods for testing these strategies in such a new, relatively ill-explored and data-rich complex system, an agent-oriented approach, with its emphasis on autonomous actions and interactions, is an ideal approach for addressing questions of stability and robustness.
3 Background and related work
This section begins by exploring the literature on the various universal statistical properties (or stylised facts) associated with financial markets. Next, modelling techniques from the market microstructure literature are explored before discussing the current state of the art in agent-based modelling of financial markets.
3.1 The statistical properties of limit order markets
The empirical literature on LOBs is very large and several non-trivial regularities, so-called stylised facts, have been observed across different asset classes, exchanges, levels of liquidity and markets. These stylised facts are particularly useful as indicators of the validity of a model (Buchanan 2012). For example, Lo and MacKinlay (2001) show the persistence of volatility clustering across markets and asset classes, which disappears with a simple random walk model for the evolution of price time series, as clustered volatility suggests that large variation in price are more like to follow other large variations.
3.1.1 Fat-tailed distribution of returns
Across all timescales, distributions of price returns have been found to have positive kurtosis, that is to say they are fat-tailed. An understanding of positively kurtotic distribution is paramount for trading and risk management as large price movements are more likely than in commonly assumed normal distributions.
Fat tails have been observed in the returns distributions of many markets including: the American Stock Exchange, Euronext, the LSE, NASDAQ, and the Shenzhen Stock Exchange (see Cont 2001; Plerou and Stanley 2008; Chakraborti et al. 2011) but the precise form of the distribution varies with the timescale used. Gu et al. (2008) found that across various markets, the tails of the distribution at very short timescales are well-approximated by a power law with exponent \(\alpha \approx 3\). Drozdz et al. (2007) found tails to be less heavy (\(\alpha > 3\)) in high-frequency data for various indices from 2004 to 2006, suggesting that the specific form of the stylised facts may have evolved over time with trading behaviours and technology. Both Gopikrishnan et al. (1998) and Cont (2001) have found that at longer timescales, returns distributions become increasingly similar to the standard normal distribution.
3.1.2 Volatility clustering
Volatility clustering refers to the long memory of absolute or square mid-price returns and means that large changes in price tend to follow other large price changes. Cont (2001), and Stanley et al. (2008) found this long memory phenomenon to exist on timescales of weeks and months while its existence has been documented across a number of markets, including: the NYSE, Paris Bourse, S&P 500 index futures and the USD/JPY currency pair (Cont 2005; Gu and Zhou 2009; Chakraborti et al. 2011). Lillo and Farmer (2004) formalise the concept as follows. Let \(X = X(t_1),X(t_2),\ldots ,X(t_k)\) denote a real-valued, wide-sense stationary time series. Then, we can characterise long memory using the diffusion properties of the integrated series Y:
A stationary process \(Y_t\) (with finite variance) is then said to have long range dependence if its autocorrelation function, \(C(l) = corr(Y_t,Y_{t+\tau })\), decays as a power of the lag:
for some \(H \in (0.5,1)\). The exponent H is known as the Hurst exponent.
In the empirical research studies outlined above, the values of the Hurst exponent varied from \(H \approx 0.58\) on the Shenzhen Stock Exchange to \(H \approx 0.815\) for the USD/JPY currency pair. There are a number of potential explanations for volatility clustering and Bouchaud et al. (2009) suggest the arrival of news and the splicing of large orders by traders.
3.1.3 Autocorrelation of returns
Stanley et al. (2008) and Chakraborti et al. (2011) observed that, across a number of markets, returns series lacked significant autocorrelation, except for weak, negative autocorrelation on very short timescales. This includes: Euronext, FX markets, the NYSE and the S&P500 index (Chakraborti et al. 2011; At-Sahalia et al. 2011). Cont (2001) explains the absence of strong autocorrelations by proposing that, if returns were correlated, traders would use simple strategies to exploit the autocorrelation and generate profit. Such actions would, in turn, reduce the autocorrelation such that the autocorrelation would no longer remain. Evidence suggests that the small but significant negative autocorrelation found on short time-scales has disappeared more quickly in recent years, perhaps an artefact of the new financial ecosystem. Bouchaud and Potters (2003) report that from 1991 to 1995, negative autocorrelation persisted on timescales of up to 20–30 min but no longer for the GBP/USD currency pair. Moreover, Cont et al. (2013), discovered no significant autocorrelation for timescales of over 20 s in the NYSE during 2010.
3.1.4 Long memory in order flow
The probability of observing a given type of order in the future is positively correlated with its empirical frequency in the past. In fact, analysis of the time series generated by assigning the value \(+\) 1 to incoming buy orders and − 1 to incoming sell orders has been shown to display long memory on the NYSE, the Paris Bourse and the Shenzhen stock Exchange (Gu and Zhou 2009). Study of the LSE has been particularly active, with a number of reports finding similar results for limit order arrivals, market order arrivals and order cancellations, while Axioglou and Skouras (2011) suggest that the long memory reported by Lillo and Farmer (2004) was simply an artefact caused by market participants changing trading strategies each day.
3.1.5 Long memory in returns
The long memory in order flow discussed above has lead some to expect long memory in return series, yet has not been found to be the case. Studies on the Deutsche Bourse, the LSE and on the Paris Bourse have all reported Hurst exponents of around 0.5, i.e. no long memory (Carbone et al. 2004; Lillo and Farmer 2004). Bouchaud et al. (2004) have suggested that this may be due to the long memory of market orders being negatively correlated with the long memory of price changes caused by the long memory of limit order arrival and cancellation.
3.1.6 Price impact
The changes in best quoted prices that occur as a result of a trader’s actions is termed the price impact. The importance of monitoring and minimising price impact precedes the extensive adoption of electronic order driven markets. This paper will specifically focus on the impact of single transactions in limit order markets (as opposed to the impact of a large parent order) with volume v.
A Great deal of research has investigated the impact of individual orders, and has conclusively found that impact follows a concave function of volume. That is, the impact increases more quickly with changes at small volumes and less quickly at larger volumes. However, the detailed functional form has been contested and varies across markets and market protocols (order priority, tick size, etc.).
Some of the earliest literature found strongly concave functions though did not attempt to identify a functional form (Hasbrouck 1991; Hausman et al. 1992). In a study of the NYSE, Lillo et al. (2003) analysed the stocks of 1000 companies and divided them into groups according to their market capitalisation. Fitting a price impact curve to each group, they found that the curves could be collapsed into a single function that followed a power law distribution of the following form:
where \(\Delta p\) is the change in the mid-price caused by a traders action, v is the volume of the trade, \(\eta \) takes the value 1 in the event of a sell and \(+\) 1 in the event of a buy and \(\lambda \) allows for adjustment for market capitalisation. They found the exponent \(\beta \) to be approximately 0.5 for small volumes and 0.2 for large volumes. After normalising for daily volumes, \(\lambda \) was found to vary significantly across stocks with a clear dependence on market capitalisation M approximated by \(M \approx \lambda ^\delta \), with \(\delta \) in the region of 0.4.
Good approximations of the value for the exponent \(\beta \) have also been found by Lillo and Farmer (2004) on the London Stock Exchange and Hopman (2007) on the Paris Bourse to fall in the range 0.3–0.4. Consequently, all explorations have identified strongly concave impact functions for individual orders but find slight variations in functional form owing to differences in market protocols.
3.1.7 Extreme price events
Though the fat-tailed distribution of returns and the high probability of large price movements has been observed across financial markets for many years (as documented in Sect. 3.1.1), the new technology-driven marketplace has introduced a particularly extreme kind of price event.
Since the introduction of automated and algorithmic trading, recurring periods of high volatility and extreme stock price behaviour have plagued the markets. Johnson et al. (2013) define these so called price spikes as an occurrence of a stock price ticking down [up] at least ten times before ticking up [down] and with a price change exceeding 0.8% of the initial price. Remarkably, they found 18,520 crashes and spikes with durations less than 1500 ms to have occurred between January 3rd 2006 and February 3rd 2011 in various stocks. One of the many aims of recent regulation such as MiFID II and the DoddFrank Wall Street Reform and Consumer Protection Act is to curtail such extreme price events.
3.2 Modelling limit order books
The financial community has expressed an active interest in developing models of LOB markets that are realistic, practical and tractable (see Predoiu et al. 2011; Obizhaeva and Wang 2013). The literature on this topic is divided into four main streams: theoretical equilibrium models from financial economics, statistical order book models from econophysics, stochastic models from the mathematical finance community, and agent-based models (ABMs) from complexity science. Each of these methodologies is described below with a detailed discussion of ABMs in Sect. 3.3.
Financial economics models tend to be built upon the idea of liquidity being consumed during a trade and then replenished as liquidity providers try to benefit. Foucault et al. (2005) and Goettler et al. (2005), for example, describe theoretical models of LOB markets with finite levels of resilience in equilibrium that depend mainly on the characteristics of the market participants. In these models, the level of resilience reflects the volume of hidden liquidity. Many models are partial equilibrium in nature. taking the dynamics of the limit order book as given. For example, Predoiu et al. (2011) provide a framework that allows discrete orders and more general dynamics, while Alfinsi et al. (2010) implement general but continuous limit order books. In order to operate in a full equilibrium setting, models have to heavily limit the set of possible order-placement strategies. Rosu (2009), for example, allows only orders of a given size, while Goettler et al. (2005) only explore single-shot strategies. Though these simplifications enable the models to more precisely describe the tradeoffs presented by market participants, it comes at the cost of unrealistic assumptions and simplified settings. It is rarely possible to estimate the parameters of these models from real data and their practical applicability is limited (Farmer and Foley 2009). Descriptive statistical models, on the other hand, tend to fit the data well but often lack economic rigour and typically involve the tuning of a number of free parameters (Cont et al. 2010). Consequently, their practicability is questioned.
Stochastic order book models attempt to balance descriptive power and analytical tractability. Such models are distinguished by their representation of aggregate order flows by a random process, commonly a Poisson process (as in Farmer et al. 2005; Cont et al. 2010). Unfortunately, the high level statistical description of participant behaviour inherent in stochastic order book models ignores important complex interactions between market participants and fails to explain many phenomena that arise (Johnson et al. 2013). As such, a richer bottom-up modelling approach is needed to enable the further exploration and understanding of limit order markets.
3.3 Agent-based models
Grimm et al. (2006) provides a simple yet adept definition of ABMs as models in which a number of heterogeneous agents interact with each other and their environment in a particular way. One of the key advantages of ABMs, compared to the aforementioned modelling methods, is their ability to model heterogeneity of agents. Moreover, ABMs can provide insight into not just the behaviour of individual agents but also the aggregate effects that emerge from the interactions of all agents. This type of modelling lends itself perfectly to capturing the complex phenomena often found in financial systems and, consequently, has led to a number of prominent models that have proven themselves incredibly useful in understanding, e.g. the interactions between trading algorithms and human traders (De Luca and Cliff 2011), empirical regularities in the inter-bank foreign exchange market Chakrabarti (2000), the links between leveraged investment and bubbles/crashes in financial markets (Thurner et al. 2012), and the complexities of systemic risk in the wider economy (Geanakoplos et al. 2012).
The effectiveness of ABMs has also been demonstrated with LOBs. The first ABMs of LOBs assume the sequential arrival of agents and the emptying of the LOB after each time step (see e.g. Foucault 1999). Unfortunately, Smith et al. (2003) notes that approaches such as this fail to appreciate the function of the LOB to store liquidity for future consumption. More recently, ABMs have begun to closely mimic true order books and successfully reproduce a number of the statistical features described in Sect. 3.
To this end, Cont and Bouchaud (2000) demonstrate that in a simplified market where trading agents imitate each other, the resultant returns series fits a fat-tailed distribution and exhibits clustered volatility. Furthermore, Chiarella and Iori (2002) describe a model in which agents share a common valuation for the asset traded in a LOB. They find that the volatility produced in their model is far lower than is found in the real world and there is no volatility clustering. They thus suggest that significant heterogeneity is required for the properties of volatility to emerge.
Additionally, Challet and Stinchcombe (2003) note that most LOB mod-els assume that trader parameters remain constant through time and explore how varying such parameters through time affected the price time series. They find that time dependence results in the emergence of autocorrelated mid-price returns, volatility clustering and the fat-tailed distribution of mid-price changes and they suggest that many empirical regularities might be a result of traders modifying their actions through time.
Correspondingly, Preis et al. (2006) reproduced the main findings of the state-of-the-art stochastic models using an ABM rather than and independent Poisson process, while Preis et al. (2007) digs deeper and explores the effects of individual agents in the model. They found that the Hurst expo-nent of the mid-price return series depends strongly on the relative numbers of agent types in the model.
In similar vein, Mastromatteo et al. (2014) use a dynamical-systems / agent-based approach to understand the non-additive, square-root dependence of the impact of meta-orders in financial markets. Their model finds that this function is independent of epoch, microstructure and execution style. Although their study lends strong support to the idea that the square-root impact function is both highly generic and robust, Johnson et al. (2013) notes that it is somewhat specialised and lacks some of the important agent-agent interactions that give rise to crashes that spikes and crashes in price that have been seen to regularly occur in LOB markets.
Similarly, Oesch (2014) describes an ABM that highlights the importance of the long memory of order flow and the selective liquidity behaviour of agents in replicating the concave price impact function of order sizes. Although the model is able to replicate the existence of temporary and permanent price impact, its use as an environment for developing and testing trade execution strategies is limited. In its current form, the model lacks agents whose strategic behaviours depend on other market participants.
Though each of the models described above are able to replicate or explain one or two of the stylised facts reported in Sect. 3.1, no one model exists that demonstrates all empirically observed regularities a clear requirement of a model intended for real-world validation. Also, no paper has yet presented agents that are operate on varying timescales. Against this background, we propose a novel modelling environment that includes a number of agents with strategic behaviours that act on differing timescales as it is these features, we believe, that are essential in dictating the more complex patterns seen in high-frequency order-driven markets.
4 The model
This paper describes a modelFootnote 1 that implements a fully functioning limit order book as used in most electronic financial markets. By following the principle of Occam’s razor, “the simplest explanation is more likely the correct one”, we consider a limited set of parameters that would show a possible path of the system dynamics. The main objective of the proposed agent based model is to identify the emerging patterns due to the complex/complicated interactions within the market. We consider five categories of traders (simplest explanation of the market ecology) which enables us to credibly mimic (including extreme price changes) price patterns in the market. The model is stated in pseudo-continuous time. That is, a simulated day is divided into \(T = 300{,}000\) periods (approximately the number of 10ths of a second in an 8.5 h trading day) and during each period there is a possibility for each agent to act a close approximation to reality. The model comprises of 5 agent types: Market makers, liquidity consumers, mean reversion traders, momentum traders and noise traders that are each presented in detail later in this section.
To replicate the mismatch in the timescales upon which market participants can act [as highlighted by Johnson et al. (2013)], during each period every agent is given the opportunity to act based on probability, \(\delta _{\tau }\), that is determined by their type, \(\tau \), (market maker, trend follower, etc.). In more detail, to represent a high-frequency trader’s ability to react more quickly to market events than, say, a long term fundamental investor, we assigned a higher delta providing a higher chance of being chosen to act. Importantly, when chosen, agents are not required to act. This facet allows agents to vary their activity through time and in response the market, as with real-world market participants. A more formal treatment of the simulation logic is presented in Algorithm 1:

The probability of a member of each agent group acting is denoted \(\delta _{mm}\) for market makers, \(\delta _{lc}\) for liquidity consumers, \(\delta _{mr}\) for mean reversion traders, \(\delta _{mt}\) for momentum traders and \(\delta _{nt}\) for noise traders. Upon being chosen to act, if an agent wishes to submit an order, it will communicate an order type, volume and price determined by that agent’s internal logic. The order is then submitted to the LOB where it is matched using price-time priority. If no match occurs then the order is stored in the book until it is later filled or canceled by the originating trader. Such a model conforms to the adaptive market hypothesis proposed by Lo (2004) as the market dynamics emerge from the interactions of a number of species of agents adapting to a changing environment using simple heuristics. Although the model contains a fair number of free parameters, those parameters are determined through experiment (see Sect. 5.1) and found to be relatively insensitive to reasonable variation. Below we define the 5 agent types.
As mentioned above, MiFID II characterises HFT as transactions executing in fractions of a second. Since the model considers that the minimum possible time for execution of transactions is approximately \(\frac{1}{10}\)th of a second, the artificial market with the agents represents HFT environment. The market ecology of traders is described by the participating agents types, with the trading speed of the individual agent being determined by that agent’s action probability \(\delta _{\tau }\). We set the parametric values for \(\delta _{\tau }\) such that the artificial market summary statistics most closely resembles those of the real market. For example, in Sect. 5, we identify the required action probabilities in order to calibrate the agent based models are \(\delta _{mm}=0.1, \delta _{lc}=0.1, \delta _{mr}=0.4, \delta _{mt}=0.4, \delta _{nt}=0.75\). One can see that the chances of participation of the noise traders at each and every tick of the market is high which means that noise traders are very high frequency traders. Similarly, the trading speed of the traders from the other categories can be verified. Lower action probabilities correspond to slower the trading speeds.
4.1 Market makers
Market makers represent market participants who attempt to earn the spread by supplying liquidity on both sides of the LOB. In traditional markets, market makers were appointed but in modern electronic exchanges any agent is able to follow such a strategy.Footnote 2 These agents simultaneously post an order on each side of the book, maintaining an approximately neutral position throughout the day. They make their income from the difference between their bids and oers. If one or both limit orders is executed, it will be replaced by a new one the next time the market maker is chosen to trade. In this paper we implement an intentionally simple market making strategy based on the liquidity provider strategy described by Oesch (2014). Each round, the market maker generates a prediction for the sign of the next period’s order using a simple w period rolling-mean estimate. When a market maker predicts that a buy order will arrive next, she will set her sell limit order volume to a uniformly distributed random number between \(v_{min}\) and \(v_{max}\) and her buy limit order volume to \(v^{-}\). An algorithm describing the market makers logic is given in Algorithm 2.

4.2 Liquidity consumers
Liquidity consumers represent large slower moving funds that make long term trading decisions based on the rebalancing of portfolios. In real world markets, these are likely to be large institutional investors. These agents are either buying or selling a large order of stock over the course of a day for which they hope to minimise price impact and trading costs. Whether these agents are buying or selling is assigned with equal probability. The initial volume \(h_0\) of a large order is drawn from a uniform distribution between \(h_{min}\) and \(h_{max}\). To execute the large order, a liquidity consumer agent looks at the current volume available at the opposite best price, \(\varPhi _t\). If the remaining volume of his large order, \(h_t\), is less than \(\varPhi _t\) the agent sets this periods volume to \(v_t = h_t\), otherwise he takes all available volume at the best price, \(v_t = \varPhi _t\). For simplicity liquidity consumers only utilise market orders. An algorithm describing the Liquidity Consumer’s logic is given in Algorithm 3.

4.3 Momentum traders
This group of agents represents the first of two high frequency traders. This set of agents invest based on the belief that price changes have inertia a strategy known to be widely used (Keim and Madhavan 1995). A momentum strategy involves taking a long position when prices have been recently rising, and a short position when they have recently been falling. Specifically, we implement simple momentum trading agents that rely on calculating a rate of change (ROC) to detect momentum, given by:
When \(\text {roc}_t\) is greater than some threshold \(\kappa \) the momentum trader enters buy market orders of a value proportional to the strength of the momentum. That is, the volume of the market order will be:
where \(W_{a,t}\) is the wealth of agent a at time t. A complete description of the momentum trader’s logic is given in Algorithm 4.

4.4 Mean reversion traders
The second group of high-frequency agents are the mean-reversion traders. Again, this is a well documented strategy (Serban 2010) in which traders believe that asset prices tend to revert towards their a historical average (though this may be a very short term average). They attempt to generate profit by taking long positions when the market price is below the historical average price, and short positions when it is above. Specifically, we define agents that, when chosen to trade, compare the current price to an exponential moving average of the asset price, ema\(_t\), at time t calculated as:
where \(p_t\) is the price at time t and \(\alpha \) is a discount factor that adjust the recency bias. If the current price, \(p_t\), is k standard deviations above \(ema_t\) the agent enters a sell limit order at a single tick size improvement of the best price offer, and if it is k standard deviations below then he enters a buy. The volume of a mean reversion trader’s order is denoted by \(v_{mr}\). An algorithm describing the mean reversion traders logic is given in Algorithm 5.

4.5 Noise traders
These agents are defined so as to capture all other market activity and are modelled very closely to Cui and Brabazon (2012). There parameters are fitted using empirical order probabilities. The noise traders are randomly assigned whether to submit a buy or sell order in each period with equal probability. Once assigned, they then randomly place either a market or limit order or cancel an existing order according to the probabilities \(\lambda _m\), \(\lambda _l\) and \(\lambda _c\) respectively.
When submitting an order, the size of that order, \(v_t\), is drawn from a log-normal distribution described by:
where \(\mu \) and \(\sigma \) represent the mean and standard deviation of the \(v_t\)s natural logarithm and \(u_v\) is a uniformly distributed random variable between 0 and 1. If a limit order is required the noise trader faces four further possibilities:
-
With probability \(\lambda _{\text {crs}}\) the agent crosses the spread and places a limit order at the opposing best ensuring immediate (but potentially partial) order fulfillment. If the order is not completely filled, it will remain in the order book.
-
With probability \(\lambda _{\text {inspr}}\) the agent places a limit order at a price within the bid and ask spread, \(p_{\text {inspr}}\), that is uniformly distributed between the best bid and ask.
-
With probability \(\lambda _{\text {spr}}\) the agent places a limit order at the best price available on their side of the book.
-
With probability \(\lambda _{\text {offspr}}\) the agent will place a limit order deeper in the book, at a price, \(p_{\text {offspr}}\), distributed with the power law:
$$\begin{aligned} \text {xmin}_{\text {offspr}} * (1-u_0)^{-\frac{1}{\beta - 1}} \end{aligned}$$(8)where \(u_0\) is a uniformly distributed random variable between 0 and 1 while \(\text {xmin}_{\text {offspr}}\) and \(\beta \) are parameters of the power law that are fitted to empirical data.
The sum of these probabilities must equal one \((\lambda _\text {crs}+\lambda _\text {inspr}+\lambda _\text {spr}+\lambda _\text {ospr} = 1)\). To prevent spurious price processes, noise traders market orders are limited in volume such that they cannot consume more than half of the total opposing side’s available volume. Another restriction is that noise traders will make sure that no side of the order book is empty and place limit orders appropriately. The full noise trader logic is described in Algorithm 6.

We believe that our range of 5 types of market participant reflects a more realistically diverse market ecology than is normally considered in models of financial markets. Some traders in our model are uninformed and their noise trades only ever contribute random perturbations to the price path. While other trader types are informed, it would be unrealistic to think that that these could monitor the market and exploit anomalies in an unperturbed way. In reality, there are always time lags between observation and consequent action between capturing market data, deducing an opportunity, and implementing a trade to exploit it. These time gaps may persist for only a few milliseconds but in todays most liquid assets, many quotes, cancellations and trades can occur in a few milliseconds. Even in such small time intervals, a sea of different informed and uninformed traders compete with each other. Among the informed traders, some perceived trading opportunities will be based on analysis of long-horizon returns, while others will come into focus only when looking at short-term return horizons. Traders will possess differing amounts of information, and some will make cognitive errors or omissions. The upshot of all this is that some traders perceive a buying opportunity where others will seek to sell. That conclusion should not be controversial. Buyers and sellers must exist in the same time interval for any trading to occur. Real financial markets are maelstroms of competing forces and perspectives, and the only way to model them with any degree of realism is by using some sort of random selection process.
Our analysis shows that the standard models of market microstructure are too Spartan to be used directly as the basis for agent-based simulations. However, by enriching these standard market microstructure model with insights from behavioural finance, we develop a usable agent based model for finance. OHara (1995) identifies three main market-microstructure agent types: market-makers, uninformed (noise) traders and informed traders. The first two agent-types are clearly identifiable in our framework. Our three remaining types of agent are different types of informed agent. While the market microstructure literature does not distinguish between different types of informed agent, behavioural finance researchers make precisely this distinction e.g. Using a multi-month return horizon, Jegadeesh and Titman (1993) showed that exploiting observed momentum (i.e. positive serial correlation) effects in empirical data by buying winners and selling losers was a robust profitable trading strategy. De Bondt and Thaler (1985) found the opposite effect at a different time horizon. They showed how persistent reversal (negative serial correlation) observed in multi-year stock returns can be profitably exploited by a similar, but opposite, buy-losers and sell-winners trading rule strategy. A re-examination of the market microstructure literature bearing these ideas in mind is revealing.
Almost all market microstructure models about informed trading, dating back to Bagehot (1971), assume that private information is exogenously derived. This is consistent with our liquidity consumer agent type and also with the view of information being based on fundamental information about intrinsic value but it is at odds with our momentum and mean reversion traders. However, an empirical market microstructure paper by Evans and Lyons (2002) opens the door to the idea that private information could be based on endogenous technical (i.e. price and volume) information, such as drives our momentum and mean-reversion agents. Evans and Lyons (2002) show that price behaviour in the foreign exchange markets is a function of cumulative order flow. Order flow is the difference between buyer-initiated trading volume and seller-initiated trading volume. It can be thought of as a measure of net buying (selling) pressure. Crucially, order flow does not require any fundamental model to be specified. Endogenous technical price behaviour is sufficient to generate it. The preceding enables us to conclude that while our 5 types of market participant initially seem at odds with the standard market microstructure model, closer scrutiny reveals that all 5 of our agent types have very firm roots in the market microstructure literature.
5 Results
In this section we begin by performing a global sensitivity analysis to explore the influence of the parameters on market dynamics and ensure the robustness of the model. Subsequently, we explore the existence of the following stylised facts in depth-of-book data from the Chi-X exchange compared with our model: fat tailed distribution of returns, volatility clustering, autocorrelation of returns, long memory in order flow, concave price impact function and the existence of extreme price events.
5.1 Sensitivity analysis
In this section, we asses the sensitivity of the agent-based model described above. To do so, we employ an established approach to global sensitivity analysis known as variance-based global sensitivity (Sobol 2001). In variance-based global sensitivity analysis, the inputs to an agent-based model are treated as random variables with probability density functions representing their associated uncertainty. The impact of the set of input variables on a model’s output measures may be independent or cooperative and so the output f(x) may be expressed as a finite hierarchical cooperative function expansion using an analysis of variance (ANOVA). Thus, the mapping between input variables \(x_1,\ldots ,x_n\) and output variables \(f(x) = f(x_1,\ldots ,x_n)\) may be expressed in the following functional form:
where \(f_0\) is the zeroth order mean effect, \(f_i(x_i)\) is a first order term that describes the effect of variable \(x_i\) on the output f(x), and \(f_{i,j}(x_i,x_j)\) is a second order term that describes the cooperative impact of variables \(x_i\) and \(x_j\) on the output. The final term, \(f_{1,2,\ldots ,n}(x_1,x_2,\ldots ,x_n)\) describe the residual nth order cooperative effect of all of the input variables. Consequently, the total variance is calculated as follows:
where \(\rho (x)\) is the probability distribution over input variables. Partial variances are then defined as:
Now, the total partial variances \(D_{i}^{tot}\) for each parameter \(x_i\), \(i = \overline{1,n}\), is computed as
where \(\langle i \rangle \) refers to the summations over all D that contains i. Once the above is computed, the total sensitivity indicies can be calculated as:
It follows that the total partial variance for each parameter \(x_i\) is
In this paper, twenty three input parameters and four output parameters are considered. The input parameters include: The probabilities of each of the five agent groups performing an action (\(\delta _{mm}, \delta _{lc}, \delta _{mr}, \delta _{mt}, \delta _{nt}\)), the market makers parameters (w, the period length of the rolling mean, and \(v_{max}\), the max order volume for limit order), the upper limit of the distribution from which liquidity consumers order volume is drawn (\(h_{max}\)), the momentum traders’ parameters (\(n_r\), the lag parameter of the ROC, and \(\kappa \), the trade entry point threshold), as well as the following noise trader parameters:
-
Probability of submitting a market order, \(\lambda _m\)
-
Probability of submitting a limit order, \(\lambda _l\)
-
Probability of canceling a limit order, \(\lambda _c\)
-
Probability of a crossing limit order, \(\lambda _{crs}\)
-
Probability of a inside-spread limit order, \(\lambda _{inspr}\)
-
Probability of a spread limit order, \(\lambda {spr}\)
-
Probability of a off-spread limit order, \(\lambda _{offspr}\)
-
Market order size distribution parameters, \(\mu _{mo}\) and \(\sigma _{mo}\)
-
Limit order size distribution parameters, \(\mu _{lo}\) and \(\sigma _{lo}\)
-
Off-spread relative price distribution parameters, \(xmin_{offspr}\) and \(\beta _{offspr}\)
The following output parameters are monitored: the Hurst exponent H of volatility [as calculated using the DFA method described by Peng et al. (1994)], the mean autocorrelation of mid-price returns R(m), the mean first lag autocorrelation term of the order-sign series R(o), and the best t exponent \(\beta \) of the price impact function as in Eq. 3.
As our model is stochastic (agents’ actions are defined over probability distributions), there is inherent uncertainty in the range of outputs, even for fixed input parameters. In the following, ten thousand samples from within the parameter space were generated with the input parameters distributed uniformly in the ranges displayed in Table 1.
For each sample of the parameters space, the model is run for 300, 000 trading periods to approximately simulate a trading day on a high-frequency timescale. The global variance sensitivity, as defined in Eq. 14 is presented in Fig. 1.
The global variance sensitivities clearly identify the upper limit of the distribution from which liquidity consumers order volume is drawn (\(h_{max}\)) and the probabilities of each of the agent groups acting (particularly those of the high-frequency traders, \(\delta _{mr}\) and \(\delta _{mt}\)) as the most important input parameters for all outputs. The biggest influence of each of these parameters was on the mean first lag autocorrelation term of the order-sign series R(o) followed by the exponent of the price impact function \(\beta \).
To find the set of parameters that produces outputs most similar to those reported in the literature and to further explore the influence of input parameters we perform a large scale grid search of the input space. This yields the optimal set of parameters displayed in Table 2. With this set of parameters we go on to explore the model’s ability to reproduce the various statistical properties that are outlined in Sect. 3.
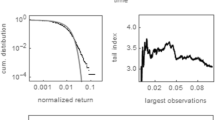
5.2 Fat tailed distribution of returns
Figure 2 displays a side-by-side comparison of how the kurtosis of the mid-price return series varies with lag length for our model and an average of the top 5 most actively traded stocks on the Chi-X exchange in a period of 100 days of trading from 12th February 2013 to 3rd July 2013. A value of 1000 on the x-axis mean that the return was taken as \(\log (p_{t+1000}) - \log (p_t)\). In our LOB model, only substantial cancellations, orders that fall inside the spread, and large orders that cross the spread are able to alter the mid price. This generates many periods with returns of 0 which significantly reduces the variance estimate and generates a leptokurtic distribution in the short run, as can be seen in Fig. 2a.
Kurtosis is found to be relatively high for short timescales but falls to match levels of the normal distribution at longer timescales. This not only closely matches the pattern of decay seen in the empirical data displayed in Fig. 2b but also agrees with the findings of Cont (2001) and Gu et al. (2008).
5.3 Volatility clustering
To test for volatility clustering, we compute the Hurst exponent of volatility using the DFA method described by Peng et al. (1994). Figure 3 details the percentage of simulations runs with significant volatility clustering defined as \(0.6< H < 1\). Once again, in the shortest time lags volatility clustering seems to be present at short timescales in all the simulations but rapidly disappears for longer lags in agreement with Lillo and Farmer (2004).
5.4 Autocorrelation of returns
Table 3 reports descriptive statistics for the first lag autocorrelation of the returns series for our agent based model and for the Chi-X data. In both instances, there is a very weak but significant autocorrelation in both the mid-price and trade price returns. The median autocorrelation of mid-price returns for the agent-based model and the Chi-X data were found to be − 0.0034 and − 0.0044, respectively. Using a non-parametric test, the distributions of the two groups were not found to differ significantly (Mann–Whitney \(U = 300,P > 0.1\) two-tailed).
This has been empirically observed in other studies (see Sect. 3.1.3) and is commonly thought to be due to the refilling effect of the order book after a trade that changes the best price. The result is similar for the trade price autocorrelation but as a trade price will always occur at the best bid or ask price a slight oscillation is to be expected and is observed.
5.5 Long memory in order flow
As presented in Table 4, we find the mean first lag autocorrelation term of the order-sign series for our model to be 0.2079 which is close to that calculated for the empirical data and those reported in the literature. Most studies find the order sign autocorrelation to be between 0.2 and 0.3 (see Lillo and Farmer 2004 for example). In Table 4, H order signs shows a mean Hurst exponent of the order signs time series for our model of \(\approx \) 0.7 which indicates a long-memory process and corresponds with the findings of previous studies and with our own empirical results [see Lillo and Farmer (2004) and Mike and Farmer (2008)].
5.6 Concave price impact
Figure 4a illustrates the price impact in the model as a function of order size on a log-log scale. The concavity of the function is clear. The shape of this curve is very similar t that of the empirical data from Chi-X shown in Fig. 4b. The price impact is for the model is found to be best fit by the relation \(\Delta p \propto v^{0.28}\), while the empirically measured impact was best fit by \(\Delta p \propto v^{0.35}\). Both of these estimates of the exponent of the impact function agree with the findings of Lillo et al. (2003), Lillo and Farmer (2004) and Hopman (2007) but the model is sensitive to the volume provided by the market makers. When the market order volume is reduced, the volume at the opposing best price reduces compared to the rest of the book. This allows smaller trades to eat further into the liquidity stretching the right-most side of the curve.
Figure 5 demonstrates the effects of varying consumers’ volume parameter \(h_{max}\) on the price impact curve. This parameter appears to have very little influence on the shape of the price impact function. However, it does appear to have an effect on the size of the impact. Although \(h_{max}\) is relatively insensitive to minor changes, when the volume traded by the liquidity consumers is reduced dramatically, the relative amount of available liquidity in the market increases to the point where price impact is reduced. Very similar results are seen as the market makers’ order size \((v_{max})\) is increased.
Figure 6 shows the effects on the price impact function of adjusting the relative probabilities of events from the high frequency traders. It is clear that strong concavity is retained across all parameter combinations but some subtle artefacts can be seen. Firstly, increasing the probability of both types of high frequency traders equally seems to have very little effect on the shape of the impact function. This is likely due to the strategies of the high frequency traders restraining one another. Although the momentum traders are more active—jumping on price movements and consuming liquidity at the top of the book—they are counterbalanced by the increased activity of the mean reversion traders who replenish top-of-book liquidity when substantial price movements occur. In the regime where the probability of momentum traders acting is high but the probability for mean reversion traders is low (the dotted line) we see an increase in price impact across the entire range of order sizes. In this scenario, when large price movements occur, the activity of the liquidity consuming trend followers outweighs that of the liquidity providing mean reverters, leading to less volume being available in the book and thus a greater impact for incoming orders.
5.7 Extreme price events
We follow the definition of Johnson et al. (2013) and define an extreme price event as an occurrence of a stock price ticking down [up] at least ten times before ticking up [down] and with a price change exceeding 0.8% of the initial price. Figure 7 shows a plot the mid-price time-series provides with an illustrative example of a flash occurring in the simulation. During this event, the number of sequential down ticks is 11, the price change is \(1.3\%\), and the event lasts for 12 simulation steps.
Table 5 shows statistics for the number of events for each day in the Chi-X data and per simulated day in our ABM. On average, in our model, there are 0.8286 events per day very close to the average average number observed in empirical data.
Upon inspection, we can see that such events occur when an agent makes a particularly large order that eats through the best price (and sometimes further price levels). This causes the momentum traders to submit particularly large orders on the same side, setting off a positive feedback chain that pushes the price further in the same direction. The price begins to revert when the momentum traders begin to run out of cash while the mean reversion traders become increasingly active.
Figure 8 illustrates the relative numbers of extreme price events as a function of their duration. The event duration is the time difference (in simulation time) between the first and last tick in the sequence of jumps in a particular direction. It is clear that these extreme price events are more likely to occur quickly than over a longer timescale. This is due to the higher probability of momentum traders acting during such events. It is very rare to see an event that lasts longer than 35 time steps.
Figure 9 shows the relative number of crash and spike events as a function of their duration for different schemes of high frequency activity. The solid line shows the result with the standard parameter setting from Table 2. The dashed line shows results from a scheme with an increased probability of both types of high frequency trader acting. Here, we see that there is an increased incidence of short duration flash events. It seems that the increased activity of the trend follows causes price jumps to be more common while the increased activity of the mean reverts ensures that the jump is short lived. In the scenario where the activity of the momentum followers is high but that of the mean reverts is low (the dotted line) we see an increase in the number of events cross all time scales. This follows from our previous analogy.
6 Conclusion
In light of the requirements of the forthcoming MiFID II laws, an interactive simulation environment for trading algorithms is an important endeavour. Not only would it allow regulators to understand the effects of algorithms on the market dynamics but it would also allow trading firms to optimise proprietary algorithms. The agent-based simulation proposed in this paper is designed for such a task and is able to replicate a number of well-known statistical characteristics of financial markets including: clustered volatility, autocorrelation of returns, long memory in order flow, concave price impact and the presence of extreme price events, with values that closely match those identified in depth-of-book equity data from the Chi-X exchange. This supports prevailing empirical findings from microstructure research.
On top of model validation, a number of interesting facets are explored. Firstly, we find that increasing the total number of high frequency participants has no discernible effect on the shape of the price impact function while increased numbers do lead to an increase in price spike events. We also find that the balance of trading strategies is important in determining the shape of the price impact function. Specifically, excess activity from aggressive liquidity-consuming strategies leads to a market that yields increased price impact.
The strategic interaction of the agents and the differing time-scales on which they act are, at present, unique to this model and crucial in dictating the complexities of high-frequency order-driven markets. As a result, this paper presents the first model capable of replicating all of the aforementioned stylised facts of limit order books, an important step towards an environment for testing automated trading algorithms. Such environment not only fulfills a requirement of MiFID II, more than that, it makes an important step towards increased transparency and improved resilience of the complex socio-technical system that is our brave new marketplace.
Our model offers regulators a lens through which they can scrutinise the risk of extreme prices for any given state of the market ecology. MiFID II requires that all the firms participating in algorithmic trading must get tested and authorised by the regulators for their trading algorithms. Our analysis demonstrates that there is a strong relationship between market ecology and the size/duration of price movements (see Fig. 9). Furthermore, our agent based model setting offers a means of testing any individual automated trading strategy or any combination of strategies for the systemic risk posed, which aims specifically to satisfy the MiFID II requirement . “ ..... that algorithms should undergo testing, and thus facilities will be required for such testing.” (p. 19, MiFID 2012). Moreover, insights from our model and the continuous monitoring of market ecology would enable regulators and policy makers to assess the evolving likelihood of extreme price swings. The proposed agent based model fulfils one of the main objectives of MiFID II that is testing the automated trading strategies and the associated risk.
While this model has been shown to accurately produce a number of order book dynamics, the intra-day volume profile has not been examined. Future work will involve the exploration of the relative volumes traded throughout a simulated day and extensions made so as to replicate the well known u-shaped volume profiles (see Jain and Joh 1988; McInish and Wood 1992).
Notes
Note that the financial markets evolved from concentrated markets to fragmented Multilateral Trading Facilities (MTFs). Recent studies by Upson and Ness (2017), Thierry and Albert (2014) and Félez-Viñas (2018) verify that the market fragmentation is not the root cause for market instability and moreover, fragmentation is associated with improved market liquidity. As there is no evidence that fragmentation is a likely cause of extreme price spikes and the complexity introduced by including market fragmentation would make it harder to find a stable viable agent based model, we consider only a concentrated single market in our model.
Although, at present, any player in a LOB may follow a market making strategy, MIFiD II is likely to require all participants that wish to operate such a strategy to register as a market maker. This will require them to continually provide liquidity at the best prices no matter what.
References
Alfinsi, A., Fruth, A., & Schied, A. (2010). Optimal execution strategies in limit order books with general shape functions. Quantitative Finance, 10, 143–157.
Angel, J. J., Harris, L. E., Katz, G., Levitt, A., Mathisson, D., Niederauer, D. L., et al. (2010). Current perspectives on modern equity markets: A collection of essays by financial industry experts. New York: Knight Capital Group, Inc.
At-Sahalia, Y., Mykland, P. A., & Zhang, L. (2011). Ultra high frequency volatility estimation with dependent microstructure noise. Journal of Econometrics, 160(1), 160–175.
Axioglou, C., & Skouras, S. (2011). Markets change every day: Evidence from the memory of trade direction. Journal of Empirical Finance, 18(3), 423–446.
Bagehot, W. (1971). The only game in town. Financial Analysts Journal, 27, 12–14.
Bouchaud, J. P., Farmer, J. D., & Lillo, F. (2009). How markets slowly digest changes in supply and demand. In T. Hens & K. R. Schenk-Hoppe (Eds.), Handbook of financial markets: Dynamics and evolution (pp. 57–160). North Holland: Elsevier.
Bouchaud, J. P., Gefen, Y., Potters, M., & Wyart, M. (2004). Fluctuations and response in financial markets: The subtle nature of ‘random’ price changes. Quantitative Finance, 4(2), 176–190.
Bouchaud, J. P., & Potters, M. (2003). Theory of financial risk and derivative pricing: From statistical physics to risk management. Cambridge: Cambridge University Press.
Buchanan, M. (2012). It’s a (stylized) fact!. Nature Physics, 8(1), 3.
Carbone, A., Castelli, G., & Stanley, H. E. (2004). Time-dependent Hurst exponent in financial time series. Physica A: Statistical Mechanics and its Applications, 344(1), 267–271.
Chakrabarti, R. (2000). Just another day in the inter-bank foreign exchange market. Journal of Financial Economics, 56, 2–32.
Chakraborti, A., Toke, I. M., Patriarca, M., & Abergel, F. (2011). Econophysics review: I. Empirical facts. Quantitative Finance, 11(7), 991–1012.
Challet, D., & Stinchcombe, R. (2003). Non-constant rates and over-diffusive prices in a simple model of limit order markets. Quantitative finance, 3(3), 155–162.
Chiarella, C., & Iori, G. (2002). A simulation analysis of the microstructure of double auction markets. Quantitative Finance, 2(5), 346–353.
Cont, R. (2001). Empirical properties of asset returns: Stylized facts and statistical issues. Quantitative Finance, 1(2), 223–236.
Cont, R. (2005). Long range dependence in financial markets. In J. Lévy-Véhel & E. Lutton (Eds.), Fractals in engineering (pp. 159–179). London: Springer.
Cont, R., & Bouchaud, J. P. (2000). Herd behavior and aggregate fluctuations in financial markets. Macroeconomic Dynamics, 4(2), 170–196.
Cont, R., Kukanov, A., & Stoikov, S. (2013). The price impact of order book events. Journal of Financial Econometrics, 12(1), 47–88.
Cont, R., Stoikov, S., & Talreja, R. (2010). A stochastic model for order book dynamics. Operations Research, 58(3), 549–563.
Cui, W., & Brabazon, A. (2012). An agent-based modeling approach to study price impact. In 2012 IEEE Conference on Computational Intelligence for Financial Engineering & Economics (CIFEr) (pp. 1–8). IEEE.
De Bondt, W., & Thaler, R. (1985). Does the stock market overreact? Journal of Finance, 40, 793–807.
De Luca, M., & Cliff, D. (2011). Human-agent auction interactions : Adaptive-aggressive agents dominate. In Twenty-second international joint conference on artificial intelligence (p. 178).
Drozdz, S., Forczek, M., Kwapien, J., Oswiecimka, P., & Rak, R. (2007). Stock market return distributions: From past to present. Physica A: Statistical Mechanics and its Applications, 383(1), 59–64.
Easley, D., De Prado, M., & O’Hara, M. (2010). The microstructure of the “flash crash”: flow toxicity, liquidity crashes, and the probability of informed trading. Technical Report. Unpublished Cornell University working paper.
Easley, D., & De Prado, M. M. Lopez. (2011). The microstructure of the “flash crash”: Flow toxicity, liquidity crashes, and the probability of informed trading. Journal of Portfolio Management, 37, 118–128.
European Union. (2011). Proposal for a directive of the European Parliment and of the council on markets in financial instruments repealing Directive 2004/39/EC of the European Parliament and of the Council (Recast). Official Journal of the European Union. http://eur-lex.europa.eu/legal-content/EN/TXT/?qid=1398344410276&uri=CELEX:52011PC0656.
European Union. (2014). Markets in Financial Instruments (MiFID): Commissioner Michel Barnier welcomes agreement in trilogue on revised European rules. Memo. http://europa.eu/rapid/press-release_MEMO-14-15_en.htm?locale=en.
Evans, M. D. D., & Lyons, R. K. (2002). Order flow and exchange rate dynamics. Journal of Political Economy, 110, 170–180.
Farmer, J. D., & Foley, D. (2009). The economy needs agent-based modelling. Nature, 460, 685–686.
Farmer, J. D., Patelli, P., & Zovko, I. I. (2005). The predictive power of zero intelligence in financial markets. Proceedings of the National Academy of Sciences of the United States of America, 102(6), 2254–9.
Félez-Viñas, E. (2018). Market fragmentation, mini flash crashes and liquidity. Working paper presented at the FMA European Conference, Kristiansand, Norway.
Foucault, T. (1999). Order flow composition and trading costs in a dynamic limit order market. Journal of Financial Markets, 2(2), 99–134.
Foucault, T., Kandan, O., & Kandel, E. (2005). Limit order book as a market for liquidity. The Review of Financial Studies, 18, 1171–1217.
Geanakoplos, J., Axtell, R., Farmer, J., Howitt, P., Conlee, B., Goldstein, J., et al. (2012). Getting at systemic risk via an agent-based model of the housing market. The American economic review, 102(3), 53–58.
Goettler, R. L., Parlour, C. A., & Rajan, U. (2005). Equilibrium in a dynamic limit order market. Journal of Finance, 60, 1–44.
Gopikrishnan, P., Meyer, M., Amaral, L. A. N., & Stanley, H. E. (1998). Inverse cubic law for the distribution of stock price variations. The European Physical Journal B-Condensed Matter and Complex Systems, 3(2), 139–140.
Grimm, V., Berger, U., Bastiansen, F., Eliassen, S., Ginot, V., Giske, J., et al. (2006). A standard protocol for describing individual-based and agent-based models. Ecological Modelling, 198(1–2), 115–126.
Gu, G. F., Chen, W., & Zhou, W. X. (2008). Empirical distributions of Chinese stock returns at different microscopic timescales. Physica A: Statistical Mechanics and its Applications, 387(2), 495–502.
Gu, G. F., & Zhou, W. X. (2009). Emergence of long memory in stock volatility from a modified Mike-Farmer model. EPL (Europhysics Letters), 86(4), 48,002.
Hasbrouck, J. (1991). Measuring the information content of stock trades. The Journal of Finance, 46, 179–207.
Hausman, J. A., Lo, A. W., & Mackinlay, A. C. (1992). An ordered probit analysis of transaction stock prices. Journal of Financial Economics, 31, 319–379.
Hopman, C. (2007). Do supply and demand drive stock prices? Quantitative Finance, 7(1), 37–53.
Jain, P. C., & Joh, G. H. (1988). The dependence between hourly prices and trading volume. The Journal of Financial and Quantitative Analysis, 23, 269–283.
Jegadeesh, N., & Titman, S. (1993). Returns to buying winners and selling losers: Implications for stock market efficiency. Journal of Finance, 48, 65–91.
Johnson, N., Zhao, G., Hunsader, E., Qi, H., Johnson, N., Meng, J., et al. (2013). Abrupt rise of new machine ecology beyond human response time. Scientific Reports, Nature Publishing Group, 3, 2627.
Keim, D. B., & Madhavan, A. (1995). Anatomy of the trading process empirical evidence on the behavior of institutional traders. Journal of Financial Economics, 37(3), 371–398.
Kirilenko, A., Kyle, A.S., Samadi, M., & Tuzun, T. (2014). The flash crash: The impact of high frequency trading on an electronic market. Available at SSRN 1686004.
Knight Capital Group. (2012). Knight capital group provides update regarding august 1st disruption to routing in NYSE-listed securities. Retrieved from http://www.knight.com/investorRelations/pressReleases.asp?compid=105070&releaseID=1721599.
Lillo, F., & Farmer, J. D. (2004). The long memory of the efficient market. Studies in Nonlinear Dynamics & Econometrics, 8(3), 1–33.
Lillo, F., Farmer, J. D., & Mantegna, R. N. (2003). Master curve for price impact function. Nature, 421(6919), 129–130.
Lo, A., & MacKinlay, A. (2001). A non-random walk down Wall Street. Princeton, NJ: Princeton University Press.
Lo, A. W. (2004). The adaptive markets hypothesis. The Journal of Portfolio Management, 30(5), 15–29.
Mastromatteo, I., Toth, B., & Bouchaud, J. P. (2014). Agent-based models for latent liquidity and concave price impact. Physical Review E, 89(4), 042,805.
McInish, T. H., & Wood, R. A. (1992). An analysis of intraday patterns in bid/ask spreads for NYSE stocks. The Journal of Finance, 47, 753–764.
Menkveld, A.J., & Yueshen, B.Z. (2013). Anatomy of the flash crash. SSRN Electronic Journal. Available at SSRN 2243520.
MiFID II Hand book, Thomson Reuters. (2012). Retrieved from http://online.thomsonreuters.com/edm/assets/BG636126646047157632e/MiFID%20II%20Handbook.pdf.
Mike, S., & Farmer, J. D. (2008). An empirical behavioral model of liquidity and volatility. Journal of Economic Dynamics and Control, 32(1), 200–234.
Obizhaeva, Aa, & Wang, J. (2013). Optimal trading strategy and supply/demand dynamics. Journal of Financial Markets, 16(1), 1–32.
Oesch, C. (2014). An agent-based model for market impact. In 2014 IEEE symposium on computational intelligence for financial engineering and economics (CIFEr).
OHara, M. (1995). Market microstructure. New York: Wiley.
Peng, C. K., Buldyrev, S. V., Havlin, S., Simons, M., Stanley, H. E., & Goldberger, A. L. (1994). Mosaic organization of DNA nucleotides. Physical Review E, 49, 1685–1689.
Plerou, V., & Stanley, H. E. (2008). Stock return distributions: Tests of scaling and universality from three distinct stock markets. Physical Review E—Statistical, Nonlinear, and Soft Matter Physics, 77(3), 037,101.
Predoiu, S., Shaikhet, G., & Shreve, S. (2011). Optimal execution in a general one-sided limit-order book. SIAM Journal on Financial Mathematics, 2(1), 183–212.
Preis, T., Golke, S., Paul, W., & Schneider, J. J. (2006). Multi-agent-based order book model of financial markets. Europhysics Letters (EPL), 75(3), 510–516.
Preis, T., Golke, S., Paul, W., & Schneider, J. J. (2007). Statistical analysis of financial returns for a multiagent order book model of asset trading. Physical Review E—Statistical, Nonlinear, and Soft Matter Physics, 76(1), 016,108.
Rosu, I. (2009). A dynamic model of the limit order book. Review of Financial Studies, 22, 4601–4641.
SEC, CFTC. (2010). Findings regarding the market events of May 6, 2010. Technical report, Report of the Staffs of the CFTC and SEC to the Joint Advisory Committee on Emerging Regulatory Issues.
Serban, A. F. (2010). Combining mean reversion and momentum trading strategies in foreign exchange markets. Journal of Banking and Finance, 34, 2720–2727.
Smith, E., Farmer, J., Gillemot, L., & Krishnamurthy, S. (2003). Statistical theory of the continuous double auction. Quantitative Finance, 3(6), 481–514.
Sobol, I. M. (2001). Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates. Mathematics and Computers in Simulation, 55, 271–280.
Stanley, H. E., Plerou, V., & Gabaix, X. (2008). A statistical physics view of financial fluctuations: Evidence for scaling and universality. Physica A: Statistical Mechanics and its Applications, 387(15), 3967–3981.
Thierry, F., & Albert, M. (2014). Competition for order flow and smart order routing systems. Journal of Finance, 63, 119–158.
Thurner, S., Farmer, J. D., & Geanakoplos, J. (2012). Leverage causes fat tails and clustered volatility. Quantitative Finance, 12(5), 695–707.
Upson, J., & Van Ness, R. A. (2017). Multiple markets, algorithmic trading, and market liquidity. Journal of Financial Markets, 32, 49–68.
World Bank. (2012). Data retrieved from http://data.worldbank.org/indicator/CM.MKT.LCAP.CD.
Acknowledgements
This work was supported by an EPSRC Doctoral Training Centre Grant (EP/G03690X/1).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
McGroarty, F., Booth, A., Gerding, E. et al. High frequency trading strategies, market fragility and price spikes: an agent based model perspective. Ann Oper Res 282, 217–244 (2019). https://doi.org/10.1007/s10479-018-3019-4
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-018-3019-4