Abstract
A key prediction of the Capital Asset Pricing Model (CAPM) is that idiosyncratic risk is not priced by investors because in the absence of frictions it can be fully diversified away. In the presence of constraints on diversification, refinements of the CAPM conclude that the part of idiosyncratic risk that is not diversified should be priced. Recent empirical studies yielded mixed evidence with some studies finding positive correlation between idiosyncratic risk and stock returns, while other studies reported none or even negative correlation. We examine whether idiosyncratic risk is priced by the stock market and what are the probable causes for the mixed evidence produced by other studies, using monthly data for the US market covering the period from 1980 until 2013. We find that one-period volatility forecasts are not significantly correlated with stock returns. The mean-reverting unconditional volatility, however, is a robust predictor of returns. Consistent with economic theory, the size of the premium depends on the degree of ‘knowledge’ of the security among market participants. In particular, the premium for Nasdaq-traded stocks is higher than that for NYSE and Amex stocks. We also find stronger correlation between idiosyncratic risk and returns during recessions, which may suggest interaction of risk premium with decreased risk tolerance or other investment considerations like flight to safety or liquidity requirements. We identify the difference between the correlations of the idiosyncratic volatility estimators used by other studies and the true risk metric the mean-reverting volatility as the likely cause for the mixed evidence produced by other studies. Our results are robust with respect to liquidity, momentum, return reversals, unadjusted price, liquidity, credit quality, omitted factors, and hold at daily frequency.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
There have been long debates whether idiosyncratic risk is a significant factor in explaining the cross-section of stock returns, and if so, what the direction of that influence is. The capital asset pricing model (CAPM) developed by Sharpe (1964) and Lintner (1965) proposes that in complete, frictionless markets the only factor that is priced by the market is the asset beta that measures the covariation of the assets’ returns with the return on the aggregate value-weighted portfolio comprising all the available assets in the economy. The assumptions under which the CAPM was derived are rather strict, and subsequent studies have sought to relax those assumptions, as well as to examine the implications of those relaxations on equilibrium prices. Levy (1978) developed a model that imposed a limit on the number of securities held by each investor, which resulted in investors holding underdiversified portfolios and bearing idiosyncratic risk. One of the most influential models explaining why idiosyncratic risk should be a priced factor was that of Merton (1987). The model assumes that investors are tracking only a subset of the asset universe and as a result of the incomplete diversification securities with higher idiosyncratic volatility in equilibrium should earn higher expected returns. Malkiel and Xu (2004) propose an extension of Merton’s model, which relax the assumption that idiosyncratic risk is uncorrelated across securities and demonstrate that the premium for idiosyncratic risk depends on the covariance of idiosyncratic risk with the market-wide undiversified idiosyncratic risk.
Clearly investors do not hold fractions of the entire market portfolio. Studies of portfolios of investors (e.g. Kelly 1995; Goetzmann and Kumar 2001) suggest that many individual investors hold quite undiversified portfolios. How many assets are necessary to achieve a ‘reasonable’ level of diversification also remains an open question, with estimates ranging between 20 and 50 randomly selected securities. However, the degree of diversification increases with wealth, and professional investors probably hold sufficiently diversified portfolios. Therefore it is important to examine the empirical evidence in order to understand whether under-diversification is a market-wide phenomenon or is limited only to investors holding an insignificant amount of assets.
Early tests of that hypothesis suggested that idiosyncratic risk is in fact a significant predictor of an asset’s expected return. Such tests estimate equity beta, i.e. the correlation between the return on a security and the excess return on the market, using time series regressions. Then, the estimated betas are used as predictor variables in order to examine whether equities with higher beta (correlation with the market) earn higher return, as they should if the CAPM is valid. However, that second step of the analysis uses estimated betas instead of the unobservable true betas. Subsequent studies offered significant methodological improvements by refining the portfolio formation methodology (Black et al. 1972) and the cross-sectional regressions methodology (Fama and MacBeth 1973). These studies alleviated the estimation problems in two ways: firstly, they pooled individual securities in portfolios in order to reduce the error of the estimation of beta; secondly, they separate in time the estimation of beta from the tests of the hypotheses. In particular, Fama and MacBeth (1973) use seven years of data to form twenty portfolios by betas and further five years to compute initial values of the independent variables for the cross-sectional regression; then, the risk-return cross-sectional regressions are fit month by month for the following four-year period, and the estimation window is rolled forward to the next testing period. In this way their study confirmed the significance of the correlation between returns and portfolio betas, and also rejected the hypothesis that idiosyncratic volatility predicted returns, at least not on a portfolio basis.
Recent studies into the significance of idiosyncratic risks produce conflicting evidence. These studies often use different proxies for the inherently unobservable idiosyncratic volatility, which contributes to the confusion and comparison of the results from different studies. Ang et al. (2006) find that, contrary to both CAPM and Merton (1987), monthly idiosyncratic returns were negatively correlated to past month’s idiosyncratic risk. Ang et al. (2009) provide further evidence from the G7 countries and other developed markets and find that the spread between high-volatility stocks and low-volatility stocks is again negative, standing at \(-1.31\)% per month after controlling for world market, and size and value factors. Various explanations have been proposed to this puzzle. Fu (2009) replicates and extends the study of Ang et al. (2006), focussing on the two-fifths of the stocks (the top-two quintiles) in terms of volatility; he finds that most of the negative abnormal return documented by Ang et al. (2006) is due to stocks that have scored a positive abnormal return in the previous month \((t-1)\), which is then followed by a negative abnormal return in following month (t).
Babenko et al. (2016) develop of a stochastic model where firm value is determined as the discounted future profit, which is dependent on a systematic factor and idiosyncratic demand shocks. In their model idiosyncratic shocks increase the value of the firm and decrease its beta, but also increase idiosyncratic volatility, and hence proposes an explanations of the negative correlation reported by Ang et al. (2006). They conduct simulations confirming the prediction of the model that idiosyncratic volatility is negatively correlated with returns (specification VI in their Table VI), although there is no information whether the result holds when beta, capitalisation and value ratios are included as controls. Aabo et al. (2017) explore a behavioural explanation of the link between idiosyncratic volatilities and returns that builds upon the noise trading approach, which assumes that the decisions of some traders (‘noise trades’) are not driven by the intrinsic value of the stocks but the costs of arbitrage limits the capacity of arbitrageurs to benefit from the resulting mispricing. They measure the prominence of noise trades in terms of four mispricing ratiosFootnote 1 and find that in all cases idiosyncratic volatility is positively and significantly correlated to the mispricing measures, as well as to the absolute value of abnormal returns (alphas) from three factor models. Similarly motivated, Cao and Han (2016) examine whether the direction of the mispricing determines the sign of the correlation of idiosyncratic volatility with the overall market. They use quintile portfolio sorts by book-to-market value of equity (as a measure of mispricing) and idiosyncratic volatility and find that the correlation between idiosyncratic risk and returns is positive for the quintile portfolio with greatest underpricing, but negative for the portfolio with greatest overpricing. Shi et al. (2016) match stock returns with information from a news database in order to explore whether the sentiment of the news impacts the idiosyncratic volatility and returns. They find that when measures of the count and sentiment of news are included in the estimation of the mean equation for the volatility model, the strength of the positive correlation between returns and volatility decreases by about 10%; however, when they use an index of negative news only, they find that the correlation is almost halved, which they interpret as evidence that the pricing of negative news confounds investors and blurs the correlation between volatility and risk.
The studies of Malkiel and Xu (2004), Spiegel and Wang (2005)), Fu (2009) and Cao and Xu (2010) reach quite the contrary conclusions, that there is significant positive correlation between idiosyncratic volatility and returns. Fu (2009) points out that it is the expected rather than historical idiosyncratic risk that matters for the cross-section of expected returns and uses EGARCH(p, q) model to estimate the expected volatility at the beginning of the period. He finds significant evidence that idiosyncratic risk is positively correlated with expected returns. Peterson and Smedema (2011) similarly distinguish between realised volatility and expected volatility. Cao and Xu (2010) distinguish between long-term and short term risk but use a Hodrick–Prescot filter to extract the cyclical component volatility without offering convincing justification for its parametrisation or comparison to the properties of the filters employed by the rest of the authors in the field.
The reports of positive correlation between volatility and returns are questioned by a number of authors. Bali and Cakici (2008) challenge the robustness of the link between idiosyncratic risk and the cross-section of stock returns and report that the results of previous studies are not robust with respect to weighting scheme, time frequency, portfolio formation, and screening for size, price, and liquidity. Huang et al. (2012) use volatility forecasts from an ARIMA model and note that in the presence of return reversal, estimation of the cross-sectional model that includes next period volatility but does not include last period volatility is biased downwards. Huang et al. (2012) test the hypothesis with four estimators of idiosyncratic volatility and find that introducing the lagged return as a control variable, which was omitted in other studies, renders idiosyncratic volatility (lagged or predicted by the ARIMA model) statistically insignificant. In contrast, they find significant positive correlation between predicted volatility from the EGARCH model and expected return, a result similar to Fu and Schutte (2010). The results of Fu (2009) are questioned by Fink et al. (2012) and Guo et al. (2014) who find that the significant positive correlation is due to look-ahead bias due to the inclusion of contemporaneous returns in the estimation of the EGARCH model. They find that there is no relation between risk and expected idiosyncratic volatility when present returns are not used in the procedure. Chabi-Yo (2011) find no significant relation between returns and idiosyncratic volatility once they introduce a control for non-systematic co-skewness. Khovansky and Zhylyevskyy (2013) propose a new GMM-type estimation procedure and employ it with data over the period 2000–2011 but find the sign of the premium depends on the frequency: for daily returns it is positive, but becomes negative for monthly, quarterly and annual data. Contrary to the findings of Spiegel and Wang (2005), Han et al. (2016) argue that idiosyncratic liquidity is the proper predictor of returns, and the previously reported correlations are due to prices bouncing between the bid and ask prices. Malagon et al. (2015) argue that the role of idiosyncratic volatility is due mainly to the omission of firm-specific characteristics (profitability and investment), which is not reflected in the factor loadings.
In our view there are three crucial and closely interrelated aspects of this debate that deserve careful attention when interpreting the results from different studies: firstly, the differences and similarities of the employed definitions; secondly, the estimators of the true unobserved volatility; thirdly: the investment horizon and the formulation of the portfolio construction problem.
The first problem is the difference in definitions from study to study. For example, Malkiel and Xu (2004) measure idiosyncratic volatility as the standard deviation of residuals from the one-factor CAPM model or the three-factor Fama–French model, i.e. \(IV^{OLS} = \sqrt{(1/N)\sum _{i}e_{-i}^2},\) where residuals from OLS regression by construction have a mean of 0. This is a long-standing measure of idiosyncratic risk, but it is important to observe that \(e_{-i}^2\) is an unbiased estimator of the unobserved idiosyncratic shocks, and so the above formula could be interpreted as a simple moving average filter. The moving average filter has the desired property of filtering white noise from the input signal while maintaining a sharp unit-step response. A downside of the filter is the significant share of higher-frequency signals that can pass through it. From the perspective of idiosyncratic volatility analysis we should observe that the filter (usually employed at rolling windows of 24 to 60 months, as available) effectively smooths out the variations of the true unobserved idiosyncratic volatility and the noise contained in the estimator (\(e_{-i}^2\)) to produce an estimate of the medium- to long-run monthly volatility.
At the opposite end of the measurement of idiosyncratic risk are Ang et al. (2006). They use the same approach described above but instead of applying it on a rolling window of monthly data, they use it to split the daily returns in each month into systematic and idiosyncratic components and to calculate the mean daily variance in that month (\(IV^{daily}\)). That approach is consistent with the results of Merton (1980) and Nelson (1992), who demonstrate that the variance of a diffusion process without drift can be estimated with arbitrary precision using an arbitrarily short period, provided that sufficiently high frequency data are used.
The remaining studies use measures that could be classified as closer to one of these two extremes. The approach of Cao and Xu (2010) relies on filtering high-frequency changes to volatilities and is thus similar to the OLS regression. Bali and Cakici (2008) employ two measures of idiosyncratic risk: the first, \(IV^{daily}\) is the same as that used by Ang et al. (2006), and \(IV^{monthly}\) calculated as a rolling average of \(IV^{daily}\) for the preceding 24 to 60 months; thus the latter measure is again similar to the OLS regressions except that they average a difference estimator of realised monthly volatility—\(IV^{daily}\) instead of \(e_{-i}^2\).
Fu (2009) emphasises the importance of using forward-looking models in order to obtain ex ante risk measures. To that end, Fu (2009) and Spiegel and Wang (2005) employ EGARCH(p,q) models fitted on monthly data using expanding windows of a minimum length of 60 months. Fu (2009) employs lags \(p, q=1\dots 3\) selected based on Akaike Information Criterion in order to achieve best possible forecasts, while Spiegel and Wang (2005) report that EGARCH accuracy can significantly reduce mean errors compared to \(IV^{OLS}\). This approach takes the middle ground between the extremes of Ang et al. (2006) and the OLS regressions. The simple GARCH model offers a transparent specification to see this point—in it the next-period forecast is formed as the sum of an intercept, the previous-month forecasts, and the squared return in the last month, which measures previous-month realised volatility.
Huang et al. (2012) take a similar approach using forecasts from an ARIMA model fitted using realised monthly volatilities. Conceptually this approach is similar to GARCH; in our context an important difference between the two is the employed measures of last-month realised volatility, which is used to update the volatility forecasts: in the case of GARCH this is the squared realised monthly idiosyncratic return, while in the ARIMA approach this is the monthly volatility estimated from daily idiosyncratic returns. Thus, differences between the two forecasts could be due to, firstly, the differences in the two specifications, and secondly, differences in the quality of the two measures of the unobserved realised volatility.
The second problem is the unobservability of the true idiosyncratic volatility; even after the end of the month we do not know what the true volatility was. Instead, ex-post estimators of volatility are used to judge out-of-sample performance. The choice of the estimator of the true volatility could predetermine the outcome of such tests. Spiegel and Wang (2005) employ loss functions to compare the performance of forecasts from EGARCH models compared to the OLS rolling average volatility. As an estimator of the true volatility they employ the squared idiosyncratic return in each month. Other studies evaluate the forecasting performance of competing models by filtering the true volatilities from some model (usually GARCH), in order to obtain the in-sample fitted values of volatilities and employ them as proxies of true volatility. However, that approach may affect the outcome: if the GARCH forecasts on monthly data smooth-out the true volatility, then the regressions will tend to favour the rolling average estimators. Such GARCH smoothing could result from the computational complexity of estimating the parameters of the model from the scarce monthly data as well as the noisy input signal fed to the model (squared returns) as a proxy of the realised volatility and likely result in a parameter uncertainty problem. For example, Hwang and Pereira (2006) report that in small samples (100 and 250 returns) GARCH with Bollerslev positivity constraint result in convergence errors in 55 and 25% of the cases, and GARCH persistence is systematically understated, resulting in faster reversal to the unconditional mean. They suggest estimating GARCH with at least 500 observations, which in the case of monthly returns would imply forty years of data.
The third problem concerns the horizon over which portfolios are constructed is another issue that remains unaddressed by those debates. The Merton (1987) model is worked out in a two-period setting and has limitations in providing insights about the dynamic effects that would occur under time-varying volatility. The CAPM model assumes a static, deterministic covariance structure. In that setting the horizon is not really important, and assuming the continuous readjustment of portfolios, it is dropped from the portfolio optimisation problem. In practice, however, horizon irrelevance may fail to hold. One reason might be the costs of continuous rebalancing and the stationarity of idiosyncrtic volatilities (Fu 2009). If volatility is stationary, a rational investor should be pricing the expected trajectory of volatility rather than myopically investing using one-period-ahead expected volatility.
In this paper we examine the correlation between idiosyncratic risk and the cross-section of returns using monthly data and individual securities as assets and we demonstrate that there is strong and statistically-significant positive correlation between idiosyncratic risk and return, and that the controversy in the literature is due to divergence in the estimation methods. We contribute to the debate by offering a new comparison of the predictive accuracy of the principal families of forecasting methods used in our field of study and answering the debate how these compare in terms of predictive accuracy. Then we demonstrate that idiosyncratic volatility is positively correlated to expected returns, and the pattern is consistent with the underlying economic models of Levy (1978), Merton (1987) and Malkiel and Xu (2004). We demonstrate that the divergence of previous studies is due to differences of the correlation of their estimators with the mean-reverting volatility; thus, the GARCH forecasts with monthly data are strongly correlated with the mean-reverting level of volatility, while the last-month return is less correlated to it and more correlated to short-term expected volatility, and therefore is no a robust predictor of the cross-section of returns. Our results would be particularly useful for practitioners in the field of finance and risk management by offering clear guidance on the use of volatility for portfolio construction and risk assessment.
The rest of the paper is organised as follows: in Sect. 2 we summarise the data sources and data transformations used to estimate idiosyncratic returns, volatility and the control variables. In Sect. 3 we compare how well the different volatility forecasts predict the true volatility, and what is the link between expected volatility and the cross-section of returns. Section 4 puts our results in perspective, ans 5 concludes the study.
2 Data and variables
2.1 Idiosyncratic returns
The primary data source for this study is the Thomson Reuters Datastream, and save for the Fama-French factors and market returns, all data items have been sourced from there. In order to ensure consistency of our results we implement the safeguards suggested in Ince and Porter (2006), and we have discarded returns over 300% and their reversals as possible data errors. Consecutive months or days with identical prices are excluded as indicating likely lack of trading. Securities with prices below USD 1 are also excluded. We do not include pre-1979 securities in our study either as that period is associated with poorer data coverage and presence of survivorship bias.
In our study we include only equities; all non-equity instruments like American depository receipts, non-equity investment instruments, real estate investment trusts, shares of beneficial interest, preferred shares, and other non-equity instrument types have been excluded. Our data set covers all shares with primary listing on the New York Stock Exchange (henceforth NYSE), the NASDAQ Stock Market (henceforth NASDAQ), or the NYSE MKT exchange (henceforth NYSE MKT, formerly known as NYSE AMEX LLC). We have included equities from all available sectors except financials, identified based on the Thomson Reuters business classification. Available price data start from the beginning of 1973. Values for some of the requisites (e.g., price-to-book value) are missing or start at a later date. Therefore, cross-sectional regressions cover the period from July 1980 until March 2013.
The estimation of expected idiosyncratic risk requires the choice of a particular mean equation. Different factor models in principle yield different residuals, and hence different residual volatility estimates. Therefore, in principle idiosyncratic risk is defined relative to the assumed factor model. In practice the link between the number of factors included in the mean equation and the estimates of idiosyncratic volatility does not appear to affect conclusions significantly because idiosyncratic variance is a second moment. Earlier studies like Black et al. (1972) and Fama and MacBeth (1973) consider idiosyncratic risk relative to the market model. Following the results of Fama and French (1992) and Fama and French (1993) much of the recent studies measure idiosyncratic risk relative to the three-factor Fama–French model, in which the market excess return is augmented with two more factors—the SMB (small-minus-big) and HML (high-minus-low) factors. A momentum factor can also be added to the Fama–French model in view of the empirical evidence for the existence of return momentum (Jegadeesh and Titman 1993; Carhart 1997) and the inclusion of momentum measures in empirical analyses. In this article we define idiosyncratic risk relative to the following four-factor Fama–French–Carhart (FFC) model:
where \((R_{it} - R_{ft})\) is the excess return on stock i over the risk-free rate, \((R_{Mt} - R_{ft})\) is the excess return on the market, and \(SMB_t\), \(HML_t\) and \(MOM_t\) are the innovations on the SMB, HML and the momentum factors at month t. All residuals used in this study are based on that mean model.
In this paper we use \(Ret_t\) to denote the raw month-on-month return for each security at month t, and \(XRet_t\) is the excess return for each security calculated as the difference between \(Ret_t\) and the risk-free rate for the respective month as retrieved from Kenneth French’s data library. \(IRet_t\) is the idiosyncratic return calculated as the residual corresponding to month t from the four-factor Carhart model (1) estimated with monthly data from \((t-60)\) to \((t-1)\).
2.2 Idiosyncratic volatility
The estimators of idiosyncratic volatility could differ from one another in a number of ways, e.g. in terms of mean equation, volatility model, or estimator of realised volatility. The count of permutations of possible choices would imply an immense number of competing models and for practical purposes we need to narrow down the list to a few cautiously selected alternatives that are sufficiently representative for the available options. Here we discuss four alternatives that we employ in our study, which we believe to represent the range of available options.
Early studies such as that of Fama and MacBeth (1973) identified idiosyncratic risk as the standard deviation of the residuals from the fitted market models. That framework essentially considers volatilities as stable across time, smoothing out low-volatility and high-volatility episodes. The resulting estimates are strongly autocorrelated as the estimates are obtained using nearly-identical data sets – in two consecutive months there would be one month leaving the sample and one month entering the sample (rolling window design), or one period added to the sample (expanding window design). In this study idiosyncratic volatility (standard deviation) is obtained from the residuals of the rolling regressions with data ending at period (t-1) and including 60 to 30 months of return (as available). These volatility estimates are denoted by \(IV_{t-1}^{OLS}\).
\(IV^{d}_{t-1}\) is the previous month idiosyncratic volatility, calculated as the standard deviation of daily returns in the previous calendar month. We require at least 15 non-zero returns in the preceding month, save for September 2001 where only 12 trading days were required. Zero-return days were discarded in order to reduce the impact of infrequent trading on the volatility measure. \(IV^{daily}_{t-1}\) has been scaled to monthly frequency by multiplying by square root of the number of trading days in the respective month in order to ease comparison of coefficients across volatility measures.
Modelling of volatilities was revolutionised by Engle (1982) who introduces the ARCH model, and Bollerslev (1986) who generalises Engle’s results to formulate the Generalised Autoregressive Conditional Heteroscedasticity (GARCH(p, q) model). The simplest but also remarkably successful version is the GARCH(1,1) model:
The model always yields positive predicted variance when the three parameters are positive (\(\omega \)) or non-negative (\(\alpha \), \(\beta \)), i.e. \(\omega > 0\), \(\alpha , \beta \ge 0\). When \(\alpha + \beta < 1\), the model is covariance stationary and its unconditional volatility is \(\sigma ^2 = \omega /(1 - \alpha - \beta )\). Since the introduction of the original GARCH(p, q), a number of alternative specifications have been proposed, but GARCH(1,1) specification has transpired to be difficult to outperform out of the sample for one-step-ahead forecasts (Hansen and Lunde 2001). GARCH(1,1) is the model of choice for our study because of its simplicity; other GARCH models are better in accounting for prominent features of volatility such as asymmetric response to shocks. On the other hand, such models introduce non-linear specifications involving parameters that are too numerous to allow reliable parameter estimation with monthly data. Furthermore, the specification of GARCH(1,1) is transparent in the sense that its properties are well understood and the parameter values are easy to interpret. Finally, Hansen and Lunde (2005) demonstrate that for one-step forecasts the specification is remarkably successful and difficult to improve upon. Therefore, we employ GARCH(1,1) but impose the constraint of covariance stationarity (\(\alpha +\beta <1\)), and we choose a flexible distribution-the Skewed Generalised Error Distribution (SGED) -as distribution of the error term in order to accommodate asymmetric innovations. \({\widehat{IV}}^{garch}_{t}\) is the expected volatility estimated using GARCH(1,1) with SGED innovations. We address the critique of Fink et al. (2012) and Guo et al. (2014) by fitting the GARCH model using an expanding window containing all available data up to the end of the previous month \((t-1)\); at least 60 months of data are required in order to estimate the model and yield a forecast for month-t idiosyncratic volatility.
The last volatility forecasting model explored here is a simple mean-reverting ARMA(1,1) model for the volatility of individual securities. Following Huang et al. (2012) we fit that model on the series of past volatilities calculated from daily idiosyncratic returns (i.e., \(IV^{d}_{t-1}\)). Our motivation to choose the simple ARMA(1,1) is twofold. Firstly, the scarcity of long series hinders the estimation of more complex if more versatile models. For example, as a rule of thumb at least 100 returns are usually required to estimate a GARCH model, and at least 1000 are often suggested for reasonable parameter accuracy. That benchmark is completely feasible with daily or intra-daily data, but in the realm of monthly returns one usually starts with five years of data, i.e. 60 returns. Therefore, we opt for a reasonably simple model of volatility dynamics. The second motivation is the significant noise contained in squared monthly returns as estimators of true monthly volatility. The ARMA (1,1) model has the form:
where m is the mean-revering level of volatility. Values of \(\phi , \theta \in \left( -1,1\right) \) ensure that the ARMA process is invertible. The expected value of the process is m, \(\mathrm {E}\left( \sigma _{i,t}\right) = m\), and \(\phi \) controls the speed of mean-reversion. An alternative parametrisation for the process uses \(\mu = m (1-\phi )\) instead of m, giving the alternative form \(\sigma _{i,t} = \mu + \phi \sigma _{i,t-1} + \theta \epsilon _{i,t-1} + \epsilon _{i,t}\). The ARMA model has many desirable properties. First, it bridges the gap between the historical measure used by Ang et al. (2006) (\(IV^{d}_{t-1}\)) and the expected volatility at various planning horizons, including the mean-reverting level m. Special cases accommodated by the specification are constant expected volatility (\(\phi =0, \theta =0\)) and random-walk volatility (\(\phi =1, \theta =0\)). Stationarity requires that the parameters \(\phi , \theta \) of ARMA(1,1) be in the interval \(\left( -1, +1\right) \). However, a negative value of \(\phi \) (the mean-reversion parameter) implies that the expected volatility oscillates around the mean-reverting level. Therefore we enforce a stricter limit for the mean-reversion parameter: \(\phi \in \left[ 0,1\right) \). A downside of the ARMA(1,1) approach is that the forecasted volatility may become negative. We discard from our sample those forecasts where volatility is non-positive (109 records) or exceeds \(200\%\) on a monthly basis (8 records), which is \(0.01\%\) of the sample total of 812, 920 forecasts.
Overall, the four measures of idiosyncratic risk that we consider in this sub-section are fairly representative of the prevailing practice. Thus \(IV^{OLS}\) represents the filter-based measures; other examples of this class are the Hodrick-Prescott filter used by Cao and Xu (2010), or the moving average of \(IV^{d}_{t-1}\), employed by Bali and Cakici (2008). GARCH(1,1) can be considered as representative of the GARCH-based models. \(IV^{d}_{t-1}\), the measure used by Ang et al. (2006) is a measure based on the assumption of random-walk volatility. Finally, \({\widehat{IV}}^{arma}\) is representative of the mean-reversion volatility hypothesis. We evaluate these four measures as forecasts for period-t idiosyncratic variance.
Table 1 summarises the descriptive statistics for the idiosyncratic volatility forecasts employed in this study.
2.3 Control variables
The CAPM proposes that the only factor explaining the cross-section of market returns is the market beta. The estimation of beta, however, is fraught with problems, not least of which are the measurement errors in betas. In this study we measure systemic risk (Beta) following the procedure proposed by Fama and French (1992) with minor modifications. In each month we calculate the betas using the previous 60 months (but no less than 30 months) of data, not including the current month. Stocks are then assigned to five quintile size portfolios. Within each quintile size portfolio, ten decile beta portfolios are formed. For calculation of the quintile breakpoints for size sorting and the decile breakpoints for beta sorting we have excluded the NASDAQ and NYSE MKT shares. The beta for each of the 50 size-beta portfolios is calculated running full-period regression of the equally-weighted average monthly excess returns on the current and previous period market excess returns. Then Beta is calculated as the sum of the slopes of the two market returns, which is intended to correct for non-synchronous trading, and that beta is assigned to all securities in those portfolios.
Fama and French (1992, 1993) identify two more factors that explain the cross-section of returns. Since the estimation of the loadings on these factors is hindered by the same hurdles as the estimation of betas, we follow the approach of Fama and French (1992) and Fu (2009) to use two characteristics—the market capitalisation (Size) and the log of book-to-market value ratio as proxies of the loadings on the two factors. Market capitalisation for each security has been calculated as the product of unadjusted price (UP Datastream series) and number of shares issued (NOSH series). \(\ln \left( B/M\right) \) is the natural logarithm of the ration of book value of equity to its market value at the end of the preceding month (B / M), and is calculated from the price-to-book value series from Datastream (PTBV) where book values of equity are taken at a lag of six months to ensure that they are known to investors.
Jegadeesh and Titman (1993) have reported that past returns are predictors of current performance (momentum effect), and following Fu (2009) we construct a return proxy equal to the cumulative gross return from months \(t-7\) till \(t-2\) inclusive, i.e. \(Ret(-2,-7) = \prod _{i=2}^{7}\left( 1 + R_{t-i}\right) \), where R is the gross return; thus a cumulative decline of 20% over the six-month period is recorded as \(Ret(-2,-7) = 0.8\). Return in \(t-1\) is not included in order to ensure that the variable significance is not due to return reversals.
Asset liquidity has often been discussed in the context of the cross-section of stock returns. Spiegel and Wang (2005) demonstrate that liquidity is inversely correlated with idiosyncratic risk, while Han et al. (2016) argue that liquidity overshadows idiosyncratic risk as a predictor of the cross-section. There is no single measure of volatility, and a number of measures are used in the literature. For example, Amihud and Mendelson (1986) proposed that liquidity measured in terms of bid-ask spread is desired by investors and therefore the less liquid shares should earn a premium. Fu (2009) measures idiosyncratic risk in terms of rolling average trading volume as well as the coefficient of variation of traded volume. Das and Hanouna (2010) introduces the concept of run length (the consecutive series of price moves without sign reversal) as a measure of liquidity and demonstrate that it is correlated with the bid-ask spread and is a significant predictor of the cross-section of stock returns. We estimate liquidity using the Roll (1984) model-based estimator (Roll) of the bid-ask spread since the spread between the buy and sell sides of the market might be a less ambiguous measure of liquidity compared to traded volume, where arguably the free float instead of total number of shares should be in the denominator. This approach is consistent with the findings of Han et al. (2016) that the significance of idiosyncratic risk in fact reflects prices bouncing between the bid and ask levels. In Roll (1984) the spread (Roll) is estimated from the auto-covariance of prices as they bounce back and forth between the sell side and the buy side of the market:
where \(Cov\left( .\right) \) is the first order return covariance. The estimator is biased when the sample size is small and the frequency is low (less frequent than daily); therefore we estimate the spread using the daily returns from the past year.
3 Results
3.1 Predictive accuracy
The first first problem that we address is how the alternative volatility forecasts compare in terms of predictive accuracy. Such an analysis requires two inputs: estimates of ex ante expected returns, and measurements of the ex post realised returns. Unlike expected volatility, where we have a range of alternative estimators, estimating the true (ex post, realised) volatility is more difficult because it is an unobservable quantity. Therefore some ex-post estimator of volatility should be used to judge performance. Spiegel and Wang (2005) employ a loss-function approach to compare the performance of forecasts from EGARCH models and the OLS rolling average volatility (\(IV^{OLS}\)). As an estimator of the true variance they employ the squared idiosyncratic return in each month (\(IRet_t\)). Bali and Cakici (2008) compare predictive accuracy from running Mincer and Zarnowitz (1969) regressions using the volatilities from GARCH(1,1) and EGARCH(1,1) models filtered from the full available history of monthly returns for each security. However, if the monthly (E)GARCH forecasts smooth out the true variability of volatility, then the regressions will tend to favour the rolling average estimator.Thus the choice of an estimator of the true volatility could predetermine the outcome of such tests.
Loss functions are not suitable for comparing forecasts based on daily data because a comparison would require accurate scaling of the mean daily volatilities to monthly horizons. Therefore, we use Mincer and Zarnowitz (1969) regressions of the form
where \(h_t\) is some estimator of the true variance, and \({\widehat{\sigma }}^2_{t}\) is the variance forecast from some model. The forecasting accuracy of different methods could then be judged based on the comparison of \(R^2\)’s from different regressions.Footnote 2
We consider two estimators of the true variance. The first is the traditional but noisy squared idiosyncratic return, i.e. \(h_t = IRet^2_{t}\). In order to obtain a more accurate estimate we also estimate an EGARCH(1,1) model using all available daily data. The in-sample estimates for idiosyncratic variance are averaged by months (we require estimated variances for at least 10 days in each month). Thus \(h_t = \frac{1}{\tau _t} \sum _{i=1}^{\tau _t}\sigma ^2_i\), where \(\tau _t\) is the number of days in month t. EGARCH(p, q) is defined by the following volatility equation:
The distribution of \(\epsilon _{t-1}/\sigma _{t-1}\) is assumed to be standard Gaussian and then \(\mathrm {E}\left( \epsilon _{t-1} / \sigma _{t-1}\right) = (2/\pi )^{1/2}\). The specification allows an asymmetric response of volatility, a phenomenon observed in equity index returns. When \(\gamma < 0\) in the above model, a negative shock \(\epsilon _{t-1}\) increases volatility more than a positive shock of equal magnitude would. The mean equation for the volatility model is again the Fama–French–Carhart four-factor model.
Table 2 reports the average cross-sectional Spearman rank correlations between the ex ante (expected) and ex post (realised) volatility estimators. The correlations demonstrate the importance of the choice of measure of realised volatility as the two measures of realised volatilities correlate more closely with some of the forecasts than with each other. The realised volatility estimated on the basis of daily returns from the EGARCH(1,1) model correlates more closely with the past volatility (0.83) used by Ang et al. (2006) and the forecasts from ARMA(1,1) (0.91) than with the other estimator of realised volatility (0.81). Conversely, realised volatility inferred from GARCH(1,1) with monthly returns correlates most closely with two of the forecasts—the historical OLS estimator (0.86) and forecasts from GARCH(1,1) (0.90). The correlation table confirms the importance of the choice of estimator of realised volatility, as well as the split of volatility forecasts into two broad groups—one including the static volatilities as measured in terms of variance of OLS residuals and forecasts from GARCH(1,1) model. The other groups includes historical volatilities of Ang et al. (2006) and forecasts from ARMA(1,1) model.
Bali and Cakici (2008) evaluate the forecasting performance of \(IV^{daily}_{t-1}\) and a rolling average of \(IV^{daily}_{t-1}\) in a similar method. Instead of running the regression above in variance they run it into volatilities (standard deviations).
The Mincer and Zarnowitz (1969) regressions are estimated individually for each security. We require at least 24 months of pairwise-complete data. The mean and median \(R^2\)’s are reported in Table 3. The results confirm that the conclusions depend crucially on the particular measure of realised volatility. When we filter daily volatilities from EGARCH(1,1) and then aggregate them to monthly volatilities, we find that the forecasts from ARMA(1,1) vastly outperform all other forecasting methods. Nonetheless, the historical measure of Ang et al. (2006) is not too far behind. Unlike those two forecasts, the forecasts from GARCH(1,1) are lagging far behind and are outperformed even by the mean-reverting level of volatility.
Conversely, when we estimate realised volatility from monthly returns using GARCH(1,1) model we find that forecasts from GARCH(1,1) significantly outperform all other forecasting methods, and in particular improve the goodness-of-fit (as measured in terms of \(R^2\)) 3.4 times compared to the historical volatilities of Ang et al. (2006). The forecasting performance of the other three estimators is very similar and results in similar \(R^2\)’s of about 0.30.
Nonetheless our analysis suggests that EGARCH with daily returns produces a more accurate estimate of the realised volatility. The first argument for this is based on the errors of the estimated parameters. Indeed, if we have 15 years of data for a given security, the error of the parameter estimates would be orders of magnitude lower when one uses EGARCH with daily returns (about 3750 trading days) compared with GARCH with monthly returns (180 months). Secondly, the GARCH model updates the forecasts from the previous period using the last return. That return, however, is a noisy estimator of the volatility in the last period, which introduces noise in the next-period forecast. When one estimates monthly volatility from daily returns, those random shocks would tend to cancel out and would allow reliable estimation of monthly volatility. The approach of estimating lower-frequency volatility from higher-frequency data is theoretically justified by Merton (1980) who demonstrates that volatility could be estimated with arbitrary precision using sufficiently high-frequency data. In order to evaluate those arguments, we also ran regression of squared idiosyncratic returns on each of the two estimators of realised idiosyncratic variance. In those regressions we find an average \(R^2\) of 11.77 when using monthly volatilities from EGARCH with daily returns compared to 3.07 when using GARCH with monthly returns. The \(R^2\) for the EGARCH approach exceeded the corresponding value for GARCH in 3819 securities out of a total of 4485 with pairwise-complete data.Footnote 3 The correlations reported in Table 2 provide further support to our claim that realised volatility inferred from the GARCH model with monthly returns smooths out the month-on-month changes of volatilities. Indeed, we find that the correlation between \(IV^{garch}_{t}\) and \(IV^{OLS}\) is 0.86—one of the highest coefficients in the correlation matrix.
Considering the previous observation, we find that EGARCH is a more reliable measure of realised volatility, and therefore that ARMA(1,1) produces the most accurate volatility forecasts. Furthermore, the parameters of the fitted ARMA(1,1) allow us to infer the mean-reverting level of volatility, which could proxy the more static volatility forecasts.
3.2 Idiosyncratic volatility and the cross-section of stock returns
We evaluate the significance of idiosyncratic volatility in explaining the cross-section of market returns using Fama–MacBeth cross-sectional regressions (Fama and MacBeth 1973). At each calendar date for which there is available information on capitalisation (Cap), CAPM beta (Beta), and positive book-to-market ratio (B / M) we estimate the following cross-sectional regressions
where \(\beta _{kit}\) is the loading of stock \(i = 1\ldots N\) on factor \(k=1\ldots K\) at time \(t=1\ldots T\), and \(\gamma _{kt}\) are the parameters to be estimated. In the approach of Fama and MacBeth (1973) the estimates \({\widehat{\gamma }}_{kt}\) are treated as random variables and the mean of the estimates from the individual cross-sectional regressions is used as an estimator of the true value (\({\widehat{\gamma }}_k\)), i.e. \({\widehat{\gamma }}_k = (1/T)\sum _{t=1}^{T}{\widehat{\gamma }}_{kt}.\) The standard error of the estimates is calculated using the the estimator of Newey and West (1987) with four lags.
The method of Fama–Macbeth can be employed using portfolios or individual securities as base assets in the test. Fama and French (1992) observe that grouping securities into similar portfolios is a good method to reduce the errors in variables when estimating betas but is inefficient with respect to other variables that can be calculated with high precision, e.g. capitalisation or book-to-market ratio. Ang et al. (2010) examine more closely the choice of base assets in asset pricing tests and demonstrate that the practice of aggregating stocks into portfolios shrinks the cross-sectional dispersion of betas, resulting in significant loss of efficiency in the calculation of factor risk premia, which ultimately offsets the gains from the reduced errors-in-variables problem. That critique also extends to the Fama and French (1992) methodology. We observe that apart from market betas, the explanatory factors in our sample, including capitalisation, B/M, idiosyncratic volatility (a second moment), and to a somewhat lesser extent, the liquidity spread based on auto-covariances can be estimated with reasonable accuracy. To mitigate the impact of extreme values of the explanatory factors on the cross-sectional regressions, each month the explanatory variables are censored at the 0.005 and 0.995 quantiles.
Securities with low prices tend to have greater noise in their returns, which is related to the minimum step by which prices move, causing abrupt discrete changes in share prices. To mitigate this concern, studies usually remove from the sample securities with an unadjusted price below a selected threshold value. We opt for a low threshold of $1 for most regressions. Some studies (e.g., Bali and Cakici 2008) choose a higher threshold of $10. The choice of threshold could affect conclusions. Brandt et al. (2010, p. 881) document that the level of institutional ownership and market capitalisation are significantly lower for low-priced stocks (defined as those in price deciles 1 through 3). The low-priced stocks typically have a price below $10, market capitalisation below $100 million, and institutional ownership below 10%. Therefore setting a threshold of $10 would discard proportionately more securities with high retail ownership, where investors are typically less diversified and thus more sensitive to idiosyncratic risk. Therefore, we employ a baseline threshold of $1 but key relationships are also tested against higher filters. The filter applied to each regression model is reported in the tables.
We examine how the forecasts from ARMA(1,1), \({\widehat{IV}}_{t}^{arma}\), explain the cross-section of returns. The results from Fama–Macbeth regressions reported in Appendix A, Table 8 demonstrate that beta is not a significant predictor of the cross-section. Nonetheless, in view of the strong theoretical arguments for its significance (the CAPM), we keep the variable in all specification in order to avoid omitted variable bias. Other control variables are also insignificant in some specifications, but we keep them nevertheless for the same motivation.
We test whether idiosyncratic volatility explains the cross-section of returns using the best volatility forecasts in our sample—those produced by ARMA(1,1) model. We find no support for the hypothesis that next-month expected volatility is correlated with returns. Specifications 1 through 8 suggest that it is not a significant predictor of the cross-section. Unlike most control variables, which preserve the sign and order of magnitude across different specifications, idiosyncratic volatility forecasts are both statistically insignificant and change sign and magnitude across specifications. To limit the effect of extreme volatility forecasts, we also employ the log of volatility as a predictor (specifications 5 through 8), but we reach the same conclusion. The coefficients for \({\widehat{IV}}^{arma}_t\) and \(\ln \left( {\widehat{IV}}_t^{arma}\right) \) are significant only in specifications 1 and 5, where essentially all control variables are omitted. We test the hypothesis using both the full available sample (marked ‘all’), as well as only those securities with unadjusted price above USD 10 (‘\(UP>10\)’), but we reach the same conclusions in both samples. Overall, ARMA(1,1) producing superior volatility forecasts, but we find that it is not a significant predictor of the cross-section of returns.
The theoretical framework of Merton (1987) assumes a two-period economy with conditionally homogeneous beliefs, in which transaction costs prevent investors from fully diversifying their exposure to idiosyncratic risk. In the presence of transaction costs next-month volatility may not be a good risk metric if those transaction costs prevent investors from rebalancing their portfolios. If the reason for the insignificance of \({\widehat{IV}}^{arma}_t\) as a predictor of the cross-section are transaction costs that limit the profitability of arbitrage trades, then investors would be constructing their portfolios using longer planning horizons (Gunthorpe and Levy 1994). Fu (2009) reports that idiosyncratic volatilities are overwhelmingly stationary. Therefore, as the investor planning horizon expands, the mean-reverting level of volatility would become an increasingly important reference for portfolio construction. We test this hypothesis in the remaining specification in Table 8.
Specifications 9 through 16 examine if the mean-reverting level of volatility (m) and its logarithm explain the cross-section of stock returns. In all specifications the mean-reverting level of volatility and its natural logarithm are significant predictors of the cross-section of stock returns. The magnitudes of the coefficients are very similar across specifications, and, with an interquartile distance of mean-reverting volatility of 8.65 per cent, the coefficients imply an economically significant spread of expected returns between highest quartile and lowest quartile stocks of about 0.25 % per month. The result is not driven by penny stocks and remains true when only securities with unadjusted price of more than $10 are used. Furthermore, in the presence of the mean-reverting level of idiosyncratic volatility both capitalisation and liquidity tend to be insignificant, suggesting that their significance in explaining the cross-section might be due to their correlation with idiosyncratic risk.
Specifications 17 through 20 test whether the mean-reverting level of volatility m is significant if \({\widehat{IV}}^{arma}_t\) is added as an explanatory variable, and we find that neither coefficient nor significance are affected. Nevertheless, those specifications are exposed to significant multicollinearity due to the correlation of the explanatory variables. Indeed, larger stocks tend to have lower idiosyncratic volatility, lower beta, higher liquidity and narrower bid-ask spreads. Moreover, in Table 2 we report that the average Spearman correlation between \({\widehat{IV}}^{arma}_t\) and m is 0.85. Therefore, in specifications 21 through 24 (marked as ’Ort. m’) for each month in our sample we first run a cross-sectional regression of m or \(\ln (m)\) on all other predictor variables and use the residuals from those regressions as explanatory variable in the Fama-Macbeth cross-sectional regression instead of m or \(\ln (m)\). The results demonstrate that the significance of the mean-reverting level of volatility is not due to its correlation with the other explanatory variables.
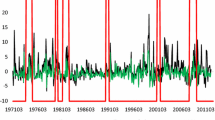
Some studies document differences in stock response in stress situations compared to unstressed periods (e.g. John and Harris 1990). We therefore compare the significance of idiosyncratic volatility in different market environments. We calculate the mean monthly volatility of the Thomson Reuters’ DataStream Total Market Return Index from daily data. Similarly to Fink et al. (2010) we classify the volatility regimes in the market using a Markov chain with three states, where volatility in each state is assumed to be normally distributed with unknown mean and variance. The transition matrix and the parameters of each volatility state are estimated using the Baum–Welch algorithm (Baum et al. 1970), and the sequence of states of the market (the Viterbi path) at any point in time is estimated using the Viterbi algorithm (Viterbi 1967). The model identifies three states with mean volatilities of 9.25 (the high-volatility state), 4.68 (the medium-volatility state), and 2.97 (the low-volatility state). The high-volatility state includes only 40 months, while the medium- and low-volatility states include 150 and 210 months, respectively (starting from January 1980).
We find that the mean-reverting level idiosyncratic volatility is a significant predictor of the cross-section in both medium- and low-volatility episodes (specifications 25–30). The coefficient of the mean-reverting volatility is very similar across the low-volatility and the medium-volatility state, albeit it is marginally significant in specification 26, which could be due to the correlation with other explanatory variables as well as the smaller sample of medium-volatility months. In contrast, during episodes of market turbulence idiosyncratic volatility makes little difference for expected returns. However, the number of high-volatility months (only forty) means that the results from that sub-sample should be interpreted with caution.
In order to examine whether idiosyncratic risk explains returns for all markets and not only for Nasdaq stocks, which are characterised with higher idiosyncratic risk and higher beta but also with smaller size and lower liquidity, we split our sample into two sub-samples based on their primary trading market as classified by the Datastream database: Nasdaq and non-Nasdaq (NYSE and AMEX); these results are reported in specifications 31–34. The Nasdaq sub-sample includes 3,375 securities, while the non-Nasdaq sub-sample includes 3,103 securities. We find that the mean-reverting volatility is significant in both specifications, however the magnitude of the coefficient for non-Nasdaq securities is between one-third and one-half that for Nasdaq shares, suggesting that the differences between the two sub-samples are economically significant. The direction of the result is consistent with the underlying economic model of Merton (1987) which predicts that the idiosyncratic risk premium would depend on the breadth of the investor base. Securities that are widely followed (e.g., the larger stocks) would earn a smaller premium than securities that are not well-known and consequently are not included in the investment opportunity frontier of most investors.
We also investigate whether the significance of idiosyncratic volatility in explaining the cross-section holds both in periods of economic growth and during recessions. We split our sample into two sub-samples using the business cycle breakpoints of the National Bureau of Economic Research (NBER). These breakpoints are determined informally by the NBER’s Business Cycle Dating Committee based on a broad set of economic indicators and served as a benchmark for the state of the US economy. The results are reported under specifications 35–42 in Table 8. During both expansion and recession episodes we find that idiosyncratic volatility is a significant predictor of the cross-section of stock returns, although in specification 36 the confidence level is lower. The differences in the point estimates for idiosyncratic risk between expansion and contraction are particularly striking—between four- and five-fold difference between contraction and expansion periods. In general, the direction of the difference is consistent with the economic intuition that in expansion episodes investors are less risk averse and would be willing to assume more risk (in this case – idiosyncratic risk) for premium compared to contraction episodes. Nonetheless, that explanation also has caveats: firstly, the magnitude of the difference does not match the magnitude of risk aversion changes; secondly, as a baseline case one would expect that a change of risk aversion would have a similar effect for the different types of risk, which is not reflected in the values of liquidity premium or beta. At any rate we note that this specification could also be affected by multicollinearity, as the contraction episodes show negative coefficients for beta and liquidity.
The prospect theory of investing suggests that the decisions could depend on whether the position has an accumulated loss or gain relative to some reference value. There is no definite guideline concerning the value used as reference by the investors. Bhootra and Hur (2014) employ the Capital Gains Overhang, where the reference price is measured as a weighted average of all prices in the preceding three years with weights depending on the traded volume. Benartzi and Thaler (1995) suggest that annual period is consistent with the tax return frequency, while Malkiel and Xu (2004) point out that some institutional investors are required to disclose individual loss-making positions on a quarterly basis. We investigate if differences in accumulated gains and losses affect decisions by splitting our sample into two sub-samples based on the accumulated gains over the six months preceding the previous month, i.e. our \(Ret(-7,-2)\) variable, with one sub-sample including all securities with cumulative net gain over that period (\(Ret(-7,-2)>1\)), while the other sub-sample including the remaining non-profit-making positions (\(Ret(-7,-2)\le 1\)). These results are reported in specifications 39–42. The mean-reverting level of idiosyncratic volatility remains a significant predictor of the cross-section, and its magnitude is unaffected by the six-month cumulative return.
We also investigate if idiosyncratic volatility serves as a proxy for default risk. (Damodaran (2004), 256–57) suggests that stocks which have lost substantial value over the previous year are often riskier than the remaining stocks. He points out that this is due both to the empirical regularity that low-priced stocks are more volatile, as well as to the increased leverage and financial risk when the market value of equity declines substantially. Therefore we also estimate the Fama–Macbeth regression on a sub-sample of securities with lower default probability. For that sample we exclude stocks with beta over 1.25, last-month volatility (\(IV_{t-1}\)) or expected volatility (\({\widehat{IV}}_t^{arma}\)) over 23.09% and price/earnings (P/E) ratio between 12.0 and 26.0, which corresponds to the first and the third quartile of the P/E data. The rationale for exclusion of low P/E securities is that the low values could signal low expected future growth or low quality of earning. The rationale for exclusion of high P/E stocks was that these may have very low earnings, which could be a signal of distress, e.g. the securities in the dot-com bubble. The cumulative application of these criteria results in a small subset of the original data set -only 269,685 rows remain, i.e. about 31.2% of the original data set. That subset is flagged as the low default subset in the table of results (specifications 47–48). We find that the significance and magnitude of the coefficients of the cross-sectional regression are unaffected by the restriction to the low-default-risk subsample. Therefore, we do not find evidence that the significance of idiosyncratic volatility is driven by possible correlation with probabilities of default.
3.3 Is there an omitted factor?
The evidence presented suggests that the mean-reverting level of idiosyncratic volatility is a significant predictor of the cross-section of returns. However, idiosyncratic risk is measured with respect to some specific factor model–in our case, the Fama-French-Carhart specification. It may happen that idiosyncratic volatility serves only as a proxy for the loading on some other, omitted factor. On the other hand, if the Merton model is correct, investors should dislike idiosyncratic risk purely because of under-diversification and not because high-volatility stocks have greater exposure to some systematic factor. We address that question by estimating the principal omitted factor and adding its loading as an explanatory variable in the cross-sectional regressions. If the principal factor is the reason for the significance of the idiosyncratic risk variable, then we expect that the addition of the new loading will make the slope of idiosyncratic risk insignificant. We use the heteroscedastic factor analysis of Jones (2001) in order to extract a set of K common factors underlying observed idiosyncratic returns (\(IRet_{i,t}\)). We then use the loadings of the individual securities on that factor in our cross-sectional regressions. The common factor is extracted from the full data set, comprising all available time series of idiosyncratic innovations for the studied period. Then, factor loadings are estimated as the coefficients of ordinary least squares (OLS) regressions of monthly returns on each stock on the set of factors identified at the preceding stage of the analysis. Let \(R^n\) denote the \(n\times {}T\) matrix of observed idiosyncratic returns, H—the matrix of (unobservable) factor realisations, \(B^n\)—the matrix of factor loading, and \(E^n\)—residual returns. These residual returns could be viewed as the remaining idiosyncratic innovations after accounting for the omitted factors of idiosyncratic returns. Then the model of idiosyncratic returns is assumed to be in the form \(R^n=B^n H+E^n.\) Let \(F \equiv M^{-1/2} H\) stand for the matrix of rotated factor realisations, introduced to simplify notation, and let D denote the diagonal matrix of average idiosyncratic variances. Jones (2001) proves that the average variance \((1/n){R^n}^\prime R^n\) converges to \(F^\prime F+D\) and could be estimated using Jöreskog’s procedure:
-
1.
Compute \(C=(1/n)R^n\prime R^n\);
-
2.
Guess an initial D, e.g. \(D = 0.5 C\);
-
3.
Obtain the K largest eigenvalues of \(D^{-1/2} C D^{-1/2}\) and create a diagonal matrix \(\Lambda \) having the largest eigenvalues along its main diagonal; then create a matrix V of their corresponding eigenvectors;
-
4.
Estimate the factor matrix as \(F=D^{1/2} V (\Lambda -I)^{1/2}\);
-
5.
Compute a new estimate of \(D=C-F'F\) and return to 3 until the algorithm converged;
-
6.
Estimate factor loading using OLS regression of observed excess returns on estimated factors and obtain residual idiosyncratic errors \(\varepsilon \).
An important issue in factor analysis is the choice of an appropriate number of factors. Remembering that we are analysing residuals (idiosyncratic returns) obtained from a factor model that already has three factors, we perform this test assuming only one omitted common factor. That factor would be the one with the highest contribution in explaining the common pattern of idiosyncratic residuals. The methodology could be readily expanded further with the inclusion of more than one factor.
Summary statistics for the recovered factor and the loading of idiosyncratic returns on the extracted factor (\(f_{hfa}\)) are given in Table 4. Factor loadings (\(\beta _{hfa}\)) are estimated using rolling regressions with monthly idiosyncratic returns (\(IRet_{i,t}\)) from the last 24 to 60 months preceding the current month, as available (i.e. from \((t-1)\) until \((t-k)\), \(k=24\ldots 60\)).
Table 5 reports the results from FamaMacbeth cross-sectional regressions involving the loading (\(\beta _{hfa}\)) on the statistical factor (\(f_{hfa}\)). We find that although the coefficient of the loading is always negative, it is not significant at conventional levels. On the contrary, the coefficients for both the mean-reverting level of volatility (m) and its natural logarithm (\(\ln (m)\)) are significant and positive, consistent with the results from the previous section. The results support the conclusion that the mean-reverting level of volatility is a significant predictor of the cross-section of returns and its significance is not attributable to correlation with the loading on some unknown factor that affects idiosyncratic returns but was omitted from the Fama French Carhart specification.
3.4 Evidence from daily data
The Capital Asset Pricing Model (CAPM) and its extension—Merton’s model—are not linked to any specific time frequency. Results that hold on daily data should also hold at lower frequencies, e.g. weekly, monthly, quarterly, or annually. The opposite is also true: if the mean-reverting level of volatility explains the cross-section of returns at monthly frequency, then a similar effect should be observed at daily frequency. The ARMA(1,1) model that we used firstly estimated monthly volatilities from daily returns, and then used the series of monthly volatilities to predict the next-month volatility. It should be possible to reproduce the same effect if we estimate the volatility model directly from daily returns. This is not a trivial task: models that are suited for monthly frequency by accommodating the shorter time-series and the higher noise in the observed proxies of the underlying, unobservable idiosyncratic volatility, could be unsuitable for higher frequencies. For example, the previously referenced study of Hansen and Lunde (2001) documents the strong empirical performance of the simple GARCH(1,1) for one-day forecasts. On the other hand, the simple model also has certain drawbacks, which invited the development of a host of GARCH extensions that accommodate phenomena observed in various financial time series. In our study we emphasise the role of the mean-reverting level of idiosyncratic volatility, which suggests that we should aim to employ a model that has long memory in volatility and which will not be unduly affected by short-term volatility outbursts. Such considerations could suggest the use of the Fractionally Integrated GARCH (Baillie et al. 1996) or Regime Switching (G)ARCH models (Hamilton and Susmel 1994), both of which offer interesting approaches for capturing the mean-reverting level of volatility. Structurally, however, we think that the Component GARCH (CGARCH) model of Lee and Engle (1999) offers a more direct and transparent route to capturing the mean-reverting volatility while allowing the mean-reverting level to evolve over time. Lee and Engle (1999) propose to model volatility as the sum of two components: a permanent one and a transitory one. The permanent component has persistence close to unity, whereas the transient component has an expected value of zero and decays more quickly. More specifically, we employ Component GARCH(1,1), which has the following specification:
where \(q_t\) is the permanent component of volatility, while (\(\sigma _t^2 - q_t)\) is the transitory component of volatility. The n-step expected values from the CGARCH(1,1) are found to be as follows:
and
and when \(n\rightarrow \infty \), the unconditional expected value becomes \({\mathbb {E}}_{t-1}(\sigma _{t+n}^2 ) = {\mathbb {E}}_{t-1} (q_{t+n} ) = \omega /(1-\rho )\).
These formulae allow us to test our results from the previous section. Firstly, we can calculate the forecasted volatility for one month ahead, which we can take to be 21 days, so that the one-month forecast would be \({\mathbb {E}}_{t-1} (\sigma _{t+21} )\), which would be an equivalent of the volatility forecasts from the previous section. We can also calculate the unconditional expectation of the permanent component, towards which volatility is expected to revert as \(n\rightarrow \infty \), i.e. \({\mathbb {E}}_{t-1} (q_{t+\infty } ) = \omega /(1-\rho )\). We could then use these two volatility forecasts to analyse the cross-section of monthly returns. Based on the results the preceding sections we expect that \({\mathbb {E}}_{t-1} (\sigma _{t+21} )\) would not be a significant predictor of the cross-section of returns, while \({\mathbb {E}}_{t-1} (q_{t+\infty } )\) would be significant. Due to the computational burden we proceed by drawing a random sample of 2100 securities from the full sample of available securities. For each security at the start of each month we calculate daily idiosyncratic returns from the Fama French Carhart model using the last five years of data, as available, but not less than 250 returns. We estimate the CGARCH(1,1) model using the available history from the rolling window, and forecast the expected volatility at the end of the month (\({\mathbb {E}}_{t-1} (\sigma _{t+21} )\)), as well as the unconditional expected value of the mean level (\({\mathbb {E}}_{t-1} (q_{t+\infty })\)). The summary statistics for these calculated variates are presented in Table 6.
Our results are presented in Table 7. Consistent with the results from the preceding sections, we find that expected volatility for the next month, \({\mathbb {E}}_{t-1} (\sigma _{t+21} )\), is not a significant predictor of the cross-section of returns. On the other hand, the unconditional volatility \({\mathbb {E}}_{t-1} (q_{t+\infty } )\) is a significant predictor. The slopes of \({\mathbb {E}}_{t-1} (q_{t+\infty } )\) and \(\ln ({\mathbb {E}}_{t-1} (q_{t+\infty }))\) are somewhat lower than those estimated from monthly ARMA(1,1), which were reported previously in this thesis. Part of the reason could be the scaling from daily to monthly frequency, which is evident in the higher average expected idiosyncratic volatilities reported in Table 1, compared with the summary statistics of the series obtained directly from daily data, reported in Table 6. Nevertheless, the magnitude of the difference cannot be explained solely by scaling. One plausible explanation could be the lower persistence of daily volatilities compared to monthly volatilities, which may somewhat dilute the predictive performance of the mean-reverting level estimated from daily data. The predictive performance of the mean-reverting volatility however remains robust in the alternative model specifications, which confirmed its relevance in explaining the cross-section of returns.
4 Discussion
In this study we demonstrate that the mean-reverting level of idiosyncratic risk is positively correlated with expected returns, while short-term volatilities are an insignificant predictor of the cross-section of stock returns. Why is there such a weak link between next-period volatility and expected returns? One assumption of factor models of asset returns is that investors adjust their portfolios continuously. In that setting, the time horizon does not enter into the pricing models, so that the CAPM, and factor models in general, should hold at any horizon. In practice, continuous portfolio adjustment is costly and investors invest on a certain target horizon and strive to avoid adjustment of their portfolios. An example of how horizon affects allocations is provided by Gunthorpe and Levy (1994). Such behaviour is consistent with rational asset allocation in the presence of transaction costs: if portfolio rebalancing is costly, arbitrageurs will be constrained from executing trading strategies that require significant trade turnover. If volatility quickly reverts to its mean, it would be costly for investors to benefit from brief episodes of high volatility. Instead, they would tend to analyse idiosyncratic volatilities over longer planning horizons, where volatilities would converge to the mean-reverting level. Thus, the mean-reverting level of volatility would dominate next-month volatility as an explanatory characteristic of the cross-section of stock returns.
Our approach highlights the consistency of the existing body of evidence, rather than its divergence. We see that studies which support the predictions of Levy (1978) and Merton (1987) use GARCH-based forecasts (Spiegel and Wang 2005; Fu 2009; Fu and Schutte 2010) or filtered volatilities (Cao 2010; Cao and Xu 2010), both of which would be correlated with the mean-reverting level of volatilities. We find (see Table 2) that forecasts from monthly GARCH(1,1) models correlate more closely with OLS residuals (0.92) than with the historical volatility employed by Ang et al. (2006) (0.65), which we find to be the second best predictor of true volatility. Likewise, its cross-sectional correlation with true volatility is 0.79, similar to the results for OLS residuals (0.78) and the mean-reverting level (0.81). In contrast, the correlation of true volatility with the forecast from ARMA is 0.91. Therefore, despite the forward-looking nature of the model per se, in practice GARCH forecasts with monthly data correlate better with OLS and the mean-reverting level, rather than future volatilities. For this reason the studies of Fu (2009), Fu and Schutte (2010), Cao (2010), Cao and Han (2016) and other studies employing (E)GARCH models with monthly returns find significant positive correlation between volatility and returns.
On the other hand, studies that relay on last-month volatility calculated from daily returns find nil or negative correlation. In the case of Ang et al. (2006) and Ang et al. (2009) that finding is driven mostly by securities with extreme volatilities. The cross-sectional distribution of volatilities is positively skewed (see Table 1); when we use the natural logarithm of volatility as an explanatory variable we find that last-month volatility is an insignificant predictor of returns. This is consistent with the findings of Fu (2009) that the negative correlation is due to a small part of the sample and is not a pervasive pattern.
Tests employing portfolios are reported to produce mixed results as well. Some tests are based only on the spread of returns between the extremes quintile portfolios in terms of idiosyncratic volatility, after controlling for some correlated variable (double sorts). (Bali and Cakici 2008) use that approach and find that last-month idiosyncratic volatility is not a robust predictor of the cross-section, as its significance depends on the choice of breakpoints. In their study they perform the sort based on the last-month volatility and on averaged volatility from the last 2 to 5 years. Our analysis suggests that only the latter is appropriate basis for testing the Merton (1987) model, as it correlates better with the mean-reverting volatility. Even then, the outcome would be dependent on the choice of breakpoints and value- or equal-weighting of the portfolios. Such findings are consistent with the underlying economic model of Merton (1987), which predicts that the idiosyncratic risk premium would depend on the breadth of the investor base (how widely ‘known’ is the security). Therefore, we should expect a lower or even non-existent premium for high-capitalisation and high-liquidity stocks, because these are presumably followed by many investors. NYSE stocks should yield lower idiosyncratic risk premium, and indeed our results find that they do. Similarly, excluding stocks that are preferred by the less-diversified investors, e.g. stocks with lower unadjusted prices, would also result in a weaker idiosyncratic risk premium.
The underlying economic models also provide useful perspective on investment strategies aimed to profit from ‘volatility anomalies’, most often—the negative correlation documented by Ang et al. (2006, 2009). Unlike short-term volatility anomalies, the mean-reverting level is result of equilibrium prices and as such would not earn arbitrage profit; however, designing strategies that are exposed to higher idiosyncratic risk could give a false impression of earning alpha when in fact they would be earning returns commensurate with the risk assumed when investing in less-followed, smaller, less liquid stocks. The recent study of McLean and Pontiff (2016) may be particularly relevant in that matter, as it uncovers that markets rapidly exploit abnormal returns, albeit not to the full extent. Since the return to idiosyncratic volatility is an equilibrium phenomenon rather than an anomaly, we should expect that it should continue to be a reliable predictor of the cross-section. The presence of perceived or actual mispricing is particularly important for investors. In a recent study, Nicolosi et al. (2017) explore how fund managers allocate resources under benchmark-related incentives when volatilities are mean-reverting. In such cases it could be optimal for under-performing fund manager to increase the exposure to idiosyncratic volatility in a bid to compensate the underperformance. Therefore, the resolving the volatility puzzle is of great importance not only for finance theory, but also for investors.
The significance of idiosyncratic risk is occasionally related to other characteristics like liquidity and size. These are valid concerns because higher idiosyncratic risk is often associated with a small investor base, wider bid-ask spreads and less active trading. In our view it is important to analyse further how investors form their portfolios. The economic theory is based on the assumption of investors maximising expected utilities, and the mean-variance approach in particular assumes that the utility function could be approximated quadratically. However, in practice there are other approaches to allocate portfolios. Kremer et al. (2017) analyse the empirical performance of eight state-of-the-art risk minimisation strategies and find that non of them results in superior allocation in all cases. Two of the other tested allocation strategies (the inverse volatility-based weights and the \(\ell _2\)-regularised equal correlation contribution) are directly exposed to the volatility of the individual security. Such portfolio construction strategies could shift allocations based on individual volatilities and result in volatility aversion.
Institutional investors may need to stand ready to convert their portfolios in cash to support any liquidity needs. Such considerations may result in investors excluding from their investment horizon securities with low liquidity. The liquidity preference could be incorporated directly in the portfolio-decision problem; one such approach was proposed by Lo et al. (2003), who used it in conjunction with five liquidity measures: the traded volume and its natural logarithm, turnover, percentage bid-ask spread, and Loeb price-impact function. They suggested three alternative formulations of the portfolio-selection problem. The first approach is the liquidity-filtered portfolio, which is identical to the standard portfolio-selection problem but with the added constraint that only securities with normalised liquidity exceeding some threshold value (specific for each investor) are allowable investments. The important consequence is that the set of liquidity-filtered securities in this case corresponds directly to the set of securities the investor ‘knows’ about in Merton’s model. Thus, the preference for liquidity in the formulation of Lo et al. (2003) would result in a risk premium for idiosyncratic risk of the less liquid securities. This means that if all (or many) investors select their portfolio allocations based on liquidity filters, the premia for idiosyncratic risk would be just another name of the premium for liquidity; illiquid securities would earn higher return in equilibrium because the few investors in them are exposed to the undiversified idiosyncratic risk, while heavily-traded securities would earn no or low excess return for idiosyncratic risk because most of that risk is diversified. In this setting there is no real distinction between the liquidity premium and the idiosyncratic risk premium: the former simply refers to the underlying preference for liquidity, while the latter refers to the mechanism of how the aversion to illiquidity translates to risk premium through the channel of undiversified idiosyncratic risk. However, liquidity need not be the only filtering criterion: some investors may be excluding securities on other grounds, e.g. ethical (tobacco, weapons, etc.), transaction costs or creditworthiness (e.g. avoiding penny stocks), asset indivisibility (avoiding high-priced stocks), etc. All such considerations could result in premia under the same mechanism as the premium for liquidity, which could be one reason why in this study idiosyncratic risk was found to be a more reliable predictor than liquidity. The two additional constraints proposed by Lo et al. (2003) could also have a similar impact on the equilibrium, although they do not map directly to the formulation of Merton.
One aspect of the problem that remained unexplored by this study is the link between idiosyncratic volatility and economic factors. Kim and Nelson (2014) find that only cyclical market volatility is priced, while market volatility that is not related to cyclical factors is not priced. It remains unclear if and how this would apply to individual securities, whether low-volatility and high-volatility stocks have a similar composition in terms of cyclical and non-cyclical volatility, and whether non-cyclical volatility is priced at individual securities. In our sample we find that the mean-reverting level of volatility is linked to stock returns. However, the magnitude of the correlation is materially higher in recession periods. This could reflect a higher price for assuming idiosyncratic risk in periods of market illiquidity, but the magnitude of the spread between the two economic regimes is high, leaving the door open of complementary explanations, related to economic variables or behavioural biases. Future studies could ameliorate the problem by employing variance decomposition in order to validate the findings, but also to clarify whether some of the spread in the slopes is due to industry volatility rather than pure idiosyncratic risk. In the latter case, other firm characteristics may account for the spread of the slopes between recession and expansion. For example, companies that have over-invested during expansion periods may suffer more from capacity overhang, and markets could require higher premium for such companies.
Our results invite further analysis of the significance of the idiosyncratic risk premium, as such studies would enhance investment management and portfolio construction practices, and would shed more light on current debates in finance, like behavioural and classical explanations of market anomalies, the interplay and the marginal contributions of size, liquidity, accounting ratios, planning horizons, transaction costs and idiosyncratic risk to equilibrium returns. Our study invites further research in the field, especially one on employing portfolios as assets and Generalised Method of Moments (GMM), as well as refined volatility forecasting methods that estimate the anticipated mean-reverting level of volatility directly from higher-frequency data.
Finally, future research could broaden the range of employed measures of idiosyncratic risk. This could include considering a five-factor pricing model, or alternative measure of idiosyncratic risk. For example, the divergence of analyst or investor forecasts could be interpreted as another measure of idiosyncratic risk. Combining different measures of idiosyncratic risk could plausibly result in superior return forecasting. Future research should also benefit from incorporating insights for asset pricing from stochastic volatility models. For example, Campbell et al (Forthcoming) propose an intertemporal asset pricing model with stochastic volatility and investor with Epstein–Zin preferences. They show that the logarithm of the stochastic discount factor could be represented as the sum of three terms: the market return, the revisions of expected future returns (news about discount rates), and revisions about the variance of future returns and discount factors. In that setting they estimate that after 1963, stocks with low book-to-market value of equity (growth stocks) have higher volatility betas and lower average returns, while the pattern is reversed for issuers with high book-to-market value (value stocks). These results highlight that volatility betas vary with stock characteristics, and successful models should aim to identify and exploit the link between volatility betas and issuer characteristics.
5 Conclusions
The significance of idiosyncratic volatility in explaining the cross-section of returns has been drawing significant interest ever since the CAPM was introduced and predicted that idiosyncratic risk is not a priced characteristic. Recent evidence yields conflicting results. While some studies find no significant evidence on the importance of idiosyncratic risk in explaining the cross-section, others report positive correlations, and yet other studies document puzzling significant negative correlation. In our study we compare the predictive performance of the main classes of estimators of idiosyncratic volatility, as well as their performance in predicting future returns. We use four estimators of returns: the historical volatility; the forward-looking ARMA(1,1) forecasts; the GARCH(1,1) forecasts; and the OLS estimator. We find that the latter two significantly underperform in forecasting next-period realised volatility, while forecasts from ARMA(1,1) and historical volatility are superior forecasting methods in the context of forecasting monthly idiosyncratic volatilities.
Using Fama–Macbeth regressions with monthly data and individual securities as assets we find that idiosyncratic risk and stock returns are robustly correlated, but returns correlate with the mean-reverting level of volatility, rather than next-month volatility. The former is a very robust predictor of the cross-section of stock returns that remains statistically and economically significant after controlling for beta, size, book/market, momentum, return reversals, liquidity, change of frequency (from monthly to daily data), omitted factors, unadjusted price, credit risk, and for primary exchange, on which shares are traded. We find that the strength of the correlation between mean-reverting volatility and returns is not constant, but depends on the primary market, on which the stock is traded, with a regression slope for Nasdaq-traded stocks almost trice that of NYSE and Amex stocks. This finding is consistent with observations that NYSE and Amex are preferred by larger investors, while stocks traded at Nasdaq are preferred by smaller and presumably-less diversified investors. Thus, differences in slopes between Nasdaq and NYSE-traded stocks are fully-consistent with the underlying economic models that predict lower premium per unit of idiosyncratic risk the better known the stock is. We also document significant spread between the correlation between idiosyncratic risk and returns in expansion and contraction periods.
Overall, our results reconcile the conflicting evidence produced by other studies and suggest that in the presence of transaction costs investors construct portfolios on longer planning horizons, which makes short-term volatility forecasts an unsuitable predictor of the cross-section of returns, while the correlation of returns with the mean-reverting level of volatility is significant and positive, consistent with economic models. We find that studies that report positive correlation between idiosyncratic risk and return use volatility forecasts that correlate highly with the mean-reverting level of volatility, while studies that report negative or nil correlation tend to use last-month volatility, which is a good predictor of next-month volatility but a poor predictor of the mean-reverting level. We find that unlike the mean-reverting level, the next-month volatility is not a reliable predictor of returns.
Notes
e.g, like the absolute value of market value to equity to the value derived from equity valuation models, or the ratio of book to market value and the market median ratio
This is very similar to the approach used by Bali and Cakici (2008) except that they run the predictive regressions in terms of standard deviations instead of variances.
The low value of \(R^2\) in Mincer and Zarnowitz (1969) regressions is well known. Andersen and Bollerslev (1998) point out that the reason for the low \(R^2\)s is not a failure of the GARCH models but rather the fact that squared returns are quite a noisy estimator of volatility. They show that the \(R^2\)s for GARCH(1,1) models are bounded above by \(1/\kappa \), where \(\kappa \) is the kurtosis of the underlying noise distribution; in particular, for normally-distributed noise, \(R^2 < 1/3\), and for heavy-tailed distributions the bound is even lower.
References
Aabo, T., Pantzalis, C., & Park, J. C. (2017). Idiosyncratic volatility: An indicator of noise trading? Journal of Banking and Finance, 75, 136–151. https://doi.org/10.1016/j.jbankfin.2016.11.003.
Amihud, Y., & Mendelson, H. (1986). Asset pricing and the bid-ask spread. Journal of Financial Economics, 17(2), 223–249.
Andersen, T. G., & Bollerslev, T. (1998). Answering the Skeptics: Yes, Standard Volatility Models Do Provide Accurate Forecasts. International Economic Review, 36(4), 885–905.
Ang, A., Hodrick, R. J., Xing, Y., & Zhang, X. (2006). The cross-section of volatility and expected returns. Journal of Finance, 61(1), 259–299.
Ang, A., Hodrick, R. J., Xing, Y., & Zhang, X. (2009). High idiosyncratic risk and low returns: International and further US evidence. Journal of Financial Economics, 91, 1–23.
Ang, A., Liu, J., & Schwarz, K. (2010). Using stocks or portfolios in tests of factor models. American Finance Association 2009 Meetings Paper http://hq.ssrn.com/Conference/Reports/conf_preliminary_program.cfm?conflink=AFA-2009-San-Francisco.
Babenko, I., Boguth, O., & Tserlukevich, Y. (2016). Idiosyncratic cash flows and systematic risk. Journal of Finance, 71(1), https://doi.org/10.1111/jofi.12280.
Baillie, R. T., Bollerslev, T., & Mikkelsen, H. O. (1996). Fractionally integrated generalized autoregressive conditional heteroskedasticity. Journal of Econometrics, 74, 3–30.
Bali, T. G., & Cakici, N. (2008). Idiosyncratic volatility and the cross section of expected returns. Journal of Financial and Quantitative Analysis, 43(1), 29–58.
Baum, L. E., Petrie, T., Soules, G., & Weiss, N. (1970). A maximization technique occurring in the statistical analysis of probabilistic functions of Markov chains. Annals of Mathematical Statistics, 41(1), 164–171.
Benartzi, S., & Thaler, R. H. (1995). Myopic loss aversion and the equity premium puzzle. Quarterly Journal of Economics, 110(1), 73–92.
Bhootra, A., & Hur, J. (2014). High idiosyncratic volatility and low returns: A prospect theory explanation. Financial Management (forthcoming).
Black, F., Jensen, M. C., & Scholes, M. (1972). The capital asset pricing model: Some empirical tests. Santa Barbara: Praeger Publishers Inc.
Bollerslev, T. (1986). Generalized autoregressive Conditional heteroscedasticity. Journal of Econometrics, 31, 307–327.
Brandt, M. W., Brav, A., Graham, J. R., & Kumar, A. (2010). The idiosyncratic volatility puzzle: Time trend or speculative episodes? Review of Financial Studies, 23(2), 863–899.
Campbell, J.Y., Giglio, S., & Polk, C., Turley, R. (Forthcoming) An intertemporal capm with stochastic volatility. Journal of Financial Economics
Cao, J., & Han, B. (2016). Idiosyncratic risk, costly arbitrage, and the cross-section of stock returns. Journal of Banking and Finance, 73, 1–15. https://doi.org/10.1016/j.jbankfin.2016.08.004.
Cao, X. (2010). Three essays on the puzzles in finance. Dissertation/thesis, The University of Texas at Dallas, http://search.proquest.com/docview/752066757.
Cao, X., & Xu, Y. (2010). Long-run idiosyncratic volatilities and cross-sectional stock returns. Available at SSRN 10.2139/ssrn.1569945 http://ssrn.com/abstract=1569945.
Carhart, M. M. (1997). On persistence of mutual fund performance. Journal of Finance, 52(1), 57–82.
Chabi-Yo, F. (2011). Explaining the idiosyncratic volatility puzzle using Stochastic discount factors. Journal of Banking and Finance, 35, 1971–1983. https://doi.org/10.1016/j.jbankfin.2011.01.002.
Damodaran, A. (2004). Investment Fables: Exposing the Myths of ”Can’t Miss” Investment Strategies. Financial Times Prentice Hall.
Das, S. R., & Hanouna, P. (2010). Run lengths and liquidity. Annals of Operations Research, 176(1), 127–152. https://doi.org/10.1007/s10479-008-0508-x.
Engle, R. F. (1982). Autoregressive conditional heteroscedasticity with estimates of variance of United Kingdom inflation. Econometrica, 50, 987–1008.
Fama, E. F., & French, K. R. (1992). The cross-section of expected stock returns. Journal of Finance, 47(2), 427–465.
Fama, E. F., & French, K. R. (1993). Common risk factors in the returns of stocks and bonds. Journal of Financial Economics, 33, 3–56.
Fama, E. F., & MacBeth, J. D. (1973). Risk, return, and equilibrium: Empirical tests. Journal of Political Economy, 81(3), 607–636.
Fink, J., Fink, K. E., Grullon, G., & Weston, J. P. (2010). What drove the increase in idiosyncratic volatility during the internet boom? Journal of Financial and Quantitative Analysis, 45(5), 1253–1278.
Fink, J. D., Fink, K. E., & He, H. (2012). Expected idiosyncratic volatility measures and expected returns. Financial Management, 41, 519–553. https://doi.org/10.1111/j.1755-053X.2012.01209.x.
Fu, F. (2009). Idiosyncratic risk and the cross-section of expected stock returns. Journal of Financial Economics, 91, 24–37.
Fu, F., & Schutte, M. G. (2010). Investor diversification and the pricing of idiosyncratic risk. In Financial Management Association Asian Conference, Financial Management Association, Research Collection Lee Kong Chian School Of Business.
Goetzmann, W. N., & Kumar, A. (2001). Equity portfolio diversification. NBER Working Papers.
Gunthorpe, D., & Levy, H. (1994). Portfolio composition and investment horizon. Financial Analysts Journal, 50(1), 51–56.
Guo, H., Kassa, H., & Ferguson, M. F. (2014). On the relation between EGARCH idiosyncratic volatility and expected stock returns. Journal of Financial and Quantitative Analysis, 49(1), 271–296.
Hamilton, J. D., & Susmel, R. (1994). Autoregressive conditional heteroskedasticity and changes in regime. Journal of Econometrics, 64, 307–333.
Han, Y., Hu, T., & Lesmond, D. A. (2016). Liquidity biases and the pricing of cross-sectional idiosyncratic volatility around the world. Journal of Financial and Quantitative Analysis, 50(6), https://doi.org/10.1017/S0022109015000605.
Hansen, P. R., & Lunde, A. (2001). A comparison of volatility models: Does anything beat a GARCH(1,1)? University of Aarhus, Centre for Analytical Finance Working Paper Series 84.
Hansen, P. R., & Lunde, A. (2005). A forecast comparison of volatility models: Does anything beat a GARCH(1,1)? Journal of Applied Econometrics, 20(7), 873–889.
Huang, W., Liu, Q., Rhee, S. G., & Zhang, L. (2012). Return reversals, idiosyncratic risk, and expected returns. Review of Financial Studies, 23, 147–168.
Hwang, S., & Pereira, P. L. V. (2006). Small sample properties of GARCH estimates and persistence. The European Journal of Finance, 12(6–7), 473–494.
Ince, O. S., & Porter, R. B. (2006). Individual equity return data from thomson datastream: Handle with care!. Journal of Financial Research, 19(4), 463–479.
Jegadeesh, N., & Titman, S. (1993). Returns to buying winners and selling losers: Implications for stock market efficiency. Journal of Finance, 48(1), 65–91.
John, M., & Harris, M. F. S. (1990). Systematic pricing during the stock crash: Assessing market efficiency. Journal of Business Research, 21(1), 59–68.
Jones, C. (2001). Extracting factors from heteroscedastic asset returns. Journal of Financial Economics, 62, 293–325.
Kelly, M. (1995). All their eggs in one basket: Portfolio diversification of US households. Journal of Economic Behavior and Organization, 27, 87–96.
Khovansky, S., & Zhylyevskyy, O. (2013). Impact of idiosyncratic volatility on stock returns: A cross-sectional study. Journal of Banking & Finance, 37, 3064–3075.
Kim, Y., & Nelson, C. N. (2014). Pricing Stock Market Volatility: Does it matter whether the volatility is related to the business cycle? Journal of Financial Econometrics, 12(2), 307–328.
Kremer, P. J., Talmaciu, A., & Paterlini, S. (2017). Risk minimization in multi-factor portfolios: What is the best strategy?. Annals of Operations Research, 1–37. https://doi.org/10.1007/s10479-017-2467-6.
Lee, G., & Engle, R. F. (1999). A permanent and transitory component model of stock return volatility. In R. F. Engle & H. White (Eds.), Cointegration Causality and Forecasting A Festschrift in Honor of Clive W. J. Granger (pp. 475–497). Oxford: Oxford University Press.
Levy, H. (1978). Equilibrium in an imperfect market: A constraint on the number of securities in the portfolio. American Economic Review, 68(4), 643–658.
Lintner, J. (1965). The valuation of risk assets and the selection of risky investments in stock portfolios and capital budgets. Review of Economics and Statistics, 47(1), 13–37.
Lo, A. W., Petrov, C., & Wierzbicki, M. (2003). It’s 11pm– Do you know where your liquidity is? The mean-variance liquidity frontier. Journal of Investment Management, 1(1), 55–93.
Malagon, J., Moreno, D., & Rodríguez, R. (2015). The idiosyncratic volatility anomaly: Corporate investment or investor mispricing? Journal of Banking and Finance, 60, 224–238. https://doi.org/10.1016/j.jbankfin.2015.08.014.
Malkiel, BG., & Xu, Y. (2004). Idiosyncratic Risk and security returns. AFA 2001 New Orleans Meetings. https://doi.org/10.2139/ssrn.255303, http://ssrn.com/abstract=255303.
McLean, R. D., & Pontiff, J. (2016). Does academic research destroy stock return predictability? Journal of Finance, 71(1), 5–32.
Merton, R. C. (1980). On estimating the expected return on the market. Journal of Financial Economics, 8, 323–361.
Merton, R. C. (1987). A simple model of capital market equilibrium with incomplete information. Journal of Finance, 42(3), 483–510.
Mincer, J., & Zarnowitz, V. (1969). The evaluation of economic forecasts. In J. A. Mincer (Ed.), Economic forecasts and expectations: Analysis of forecasting behavior and performance (pp. 3–46). Washington: NBER.
Nelson, D. B. (1992). Filtering and forecasting with misspecified ARCH models I: Getting the right variance with the wrong model. Journal of Econometrics, 52, 61–90.
Newey, W. K., & West, K. D. (1987). A simple, positive semi-definite, heteroscedasticity and autocorrelation consistent covariance matrix. Econometrica, 55(3), 703–708.
Nicolosi, M., Angelini, F., & Herzel, S. (2017). Portfolio management with benchmark related incentives under mean reverting processes. Annals of Operations Research, 1–22. https://doi.org/10.1007/s10479-017-2535-y.
Peterson, D. R., & Smedema, A. R. (2011). The return impact of realized and expected idiosyncratic volatility. Journal of Banking and Finance, 35, 2547–2558. https://doi.org/10.1016/j.jbankfin.2011.02.015.
Roll, R. (1984). A simple implicit measure of the effective bid-ask spread in an efficient market. Journal of Finance, 39, 1127–1139.
Sharpe, W. F. (1964). Capital asset prices: A theory of market equilibrium under conditions of risk. Journal of Finance, 19(3), 425–442.
Shi, Y., Liu, W. M., & Ho, K. Y. (2016). Public news arrival and the idiosyncratic volatility puzzle. Journal of Empirical Finance, 37, 159–172. https://doi.org/10.1016/j.jempfin.2016.03.001.
Spiegel, MI., & Wang, X. (2005). Cross-sectional variation in stock returns: Liquidity and idiosyncratic risk. Yale ICF Working Paper No 05-13; EFA 2005 Moscow Meetings Paper http://ssrn.com/abstract=709781.
Viterbi, AJ. (1967). Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Transactions on Information Theory, VOL IT-IS, NO 2, APRIL 1967 IT-13(2):260–269.
Acknowledgements
This study was partially supported by Korea National Research Foundation through Global Research Network Program (Project no. 2016S1A2A2912265). The authors are grateful to the anonymous referees for valuable ideas for improvement of this study and directions for future research.
Author information
Authors and Affiliations
Corresponding author
Results from Fama–MacBeth regressions
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bozhkov, S., Lee, H., Sivarajah, U. et al. Idiosyncratic risk and the cross-section of stock returns: the role of mean-reverting idiosyncratic volatility. Ann Oper Res 294, 419–452 (2020). https://doi.org/10.1007/s10479-018-2846-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10479-018-2846-7