Partial commitment in an endogenous timing duopoly

Abstract

A duopoly game with timing announcements endogenizes the sequence of commitments. In duopolistic price competition, endogenous moves lead to a coordination problem with two non-Pareto ranked subgame perfect equilibria (SPEs). In these SPEs both firms prefer followership to leadership. We suggest that a unique SPE can be found if firms use partial commitments to their timing announcements. Using partial commitments, the firms first announce the timing of moves but reserve the option to deviate from this announcement and pay a deviation cost. We show that given a sufficient asymmetry in stochastic production technologies, there exists a unique SPE with sequential moves if the deviation costs are sufficiently different or if a common deviation cost belongs to a suitable interval. We also discuss the information sharing implications of the results and find that information is not shared at the unique SPE.

1 Introduction

Commitment in oligopoly games has been an active research topic since Von Stackelberg (1934) proposed that a timing asymmetry in the Cournot duopoly model leads to an asymmetry in equilibrium payoffs even for firms that are symmetric in other ways, e.g. have equal costs and face the same (inverse) demand function. The Stackelberg solution concept, where the leader anticipates the follower’s reaction and optimizes own strategy against it, creating for itself a first mover advantage, has found applications in various areas within and outside the industrial organization literature. However, the applicability of the Stackelberg solution concept is limited to situations where the structure that sets the timing of decisions is exogenously given. Even in the case of asymmetric duopolists, the Stackelberg solution concept does not yield insight into timing and does not answer exactly which firm should move first and which second.

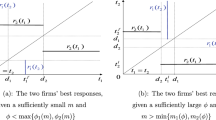
Relaxing the exogenous timing structure, Hamilton and Slutsky (1990) give the firms the possibility to announce when they commit to their strategies (the “extended game with observable delay”, henceforth the “HS game”). Timing announcements are made simultaneously at Stage 0 of the game. The leader decides at Stage 1 and the follower decides at Stage 2. The firms are committed to their announcements and the outcome of the game is decided upon the announcements. Hamilton and Slutsky’s (1990) important observation is the dependence of leader/follower preference on the sign of the reaction correspondences. With decreasing reactions, which are typical in quantity competition, there is simultaneous play where both announce leadership. With increasing reaction correspondences the players face a coordination dilemma where the two sequential-move outcomes are preferred over the simultaneous-move outcomes. The timing problem in the Stackelberg solution concept is thus partially solved by Hamilton and Slutsky (1990), in the case of quantity competition, suggesting that both firms should announce leadership.

The subsequent literature on endogenous timing games has presented conditions under which one sequential-move outcome would prevail over the other sequential-move outcome and the simultaneous-move outcomes. Some examples include differing convexity properties of the demand functions (Amir and Grilo 1999), informational asymmetries (Normann 2002), commitment riskiness (Van Damme and Hurkens 1999), and non-monotonicity of reactions (Hoffmann and Rota Graziosi 2010).

Price competition in duopoly with heterogenous goods forms a clear situation where the reaction correspondences are increasing and there are two sequential-move equilibria in nondominated strategies. The payoffs in this game are qualitatively as in the Battle of the Sexes, where a coordination failure leads to worse payoffs than coordinating on the least desirable equilibrium outcome. One way to look for a solution to this coordination dilemma—i.e. which firm should emerge as the leader and which as the follower—is to look at asymmetries in the technological capabilities of the firms. Amir and Stepanova (2006) show that when the firms compete in prices and they have sufficient unit production cost asymmetry, the high cost firm is selected as the follower and the low cost firm as the leader by a risk dominance argument. This is because the product of deviation losses is larger in the equilibrium where the high cost firm is the follower than in the other equilibrium. Firms that are interested in reducing the probability of a coordination failure will pick the risk dominant equilibrium.

Laboratory evidence enriches the implications of the HS game by suggesting that subjects play a coordination game even when the strategies are quantities, reaction correspondences are decreasing and theory predicts simultaneous play (Fonseca et al. 2006). Santos-Pinto (2008) argues that inequity aversion explains why a coordination game evolves in the game: an experimentally robust phenomenon, inequity aversion leads to nonmonotonic, rather than strictly decreasing, reaction correspondences, thus yielding multiple sequential-move equilibria on the intersections of the increasing parts of the reaction correspondences rather than a single simultaneous-move one.

In this paper we aim to resolve the coordination problem that arises when duopolists compete in prices in the HS game by introducing the idea that a duopolist may deviate from its announced commitment and pay a cost for doing so if it sees that as a better alternative than sticking to its commitment. This kind of a commitment is called partial commitment because it is an intermediary case between full commitment (pay an infinitely large cost from deviating) and no commitment (do not pay at all from deviating). We show that a unique equilibrium may be attained in such a situation if the firms have sufficient asymmetry in their stochastic production technologies.

As a motivating example, think of two market-leading restaurant chains that compete in prices and contemplate on opening new facilities in the same shopping mall. According to the HS model, if the firms post their prices on the opening day, they will not announce simultaneous opening; each prefers to see the other’s prices first and then enjoy their second-mover advantage. Given that the firms may freely choose when to open, a coordination problem ensues. In this paper we are interested to solve this problem by studying the conditions under which a unique equilibrium may be attained if one or both restaurant chains can renege on their announcements and delay their opening, and possibly incur themselves a deviation cost, for example, in the form of contractual fine or reputational damage in the local market.

The commitment concept that we consider here is that of partial commitments. The player who makes the partial commitment to leadership (followership) reserves the option to renege and opt for followership (leadership) instead by paying a finite deviation cost. In that case, the mere option of deviating from the announced strategy affects equilibrium behavior, because then the other firm can form rational expectations on the profitability of the competitor’s deviation and prepare an appropriate reaction. The level of commitment can be parameterized by the choice of the deviation cost: an expensive deviation cost implies a high level of commitment whereas a cheap deviation cost implies that the level of commitment is low. Specifying the game in this way makes it possible to inspect the whole continuum of commitment options, from full commitment (infinitely large deviation cost) to cheap talk (zero deviation cost), and find a level of commitment that yields unique solutions. In our main result, in the unique SPE the firm with higher expected marginal cost of production becomes the follower if the deviation cost is common to both firms and suitably chosen.

The idea of partial commitments in strategic decisions dates back to Schelling (1960). Partial commitments have received interest in the bargaining literature. Muthoo (1996) studies bargaining with partial commitments and finds that the level of commitment dictates the equilibrium share of the surplus, and Kambe (1999) extends the results for players who are patient vs. impatient. Signaling intentions by burning money, which as a concept is close to partial commitments, has been studied in coordination games e.g. by Ben-Porath and Dekel (1992).

The literature on partial commitments in duopoly games is narrower. Henkel (2002) and Weber (2014) consider games with exogenously given timing and find that it is sometimes profitable for the first mover to renege on its commitment to the leader’s strategy and pay a deviation cost. We extend the ideas of these papers to the endogenous timing literature. However, our results differ from Henkel (2002) and Weber (2014) in an important sense, namely in that the mere option of reneging on the commitment affects the existence of SPEs. Our paper is closest to Caruana and Einav (2008) who study a partial commitment model in an endogenous timing game where there are sequential opportunities to commit within the 0-Stage and each opportunity becomes costlier than the previous one. We discuss how our model relates to the models of Caruana and Einav (2008) as well as Henkel (2002) and Weber (2014) in the Discussion section.

In our model the firms have initially stochastic production technologies, represented by stochastic marginal costs, and leading to the analysis of Bayesian strategies. It is possible in some applications that this uncertainty is learned privately by each firm before decision making takes place. It is therefore relevant to also consider how information sharing affects our results. In the information sharing literature, it is known that the firms’ incentives to share their private cost information depend on whether they are leaders, followers or simultaneous movers. However, as the role differentiation is resolved only after the actual decision making about commitments has taken place, it is relevant to consider the ex-ante information revelation implications. We derive a result where it is always optimal for both firms to conceal their private marginal costs even for a high deviation cost that favors one firm (the high cost firm) to become the follower.

The paper proceeds as follows. In Sect. 2 we formulate the model without partial commitments and show that the coordination game in timing announcements exists. Then in Sect. 3 we show that this coordination game can be resolved, i.e. a unique equilibrium attained, with partial commitments if the firms have asymmetric marginal cost distributions. Section 4 considers the duopolists’ incentives to share their private cost information, and Sect. 5 links our results to existing literature on partial commitments and discusses applications.

2 The model without partial commitments

We first describe the model in the case when an endogenous timing game with observable delay (Hamilton and Slutsky 1990) is played with perfect commitments, i.e. without the possibility to renege on the announced strategy. Firms $i=1,2$ choose prices $p_i \in P_i \subset \mathbb {R}^+ \cup \{0\}$ in a market with heterogenous goods and constant marginal costs of production. The production technologies are stochastic and the marginal cost distributions are characterized by means and variances. The mean of Firm i is $\mathrm {E}\{c_i\}=\bar{c}_i$ and the variance is $\mathrm {Var}\{c_i\}=\sigma _i \ge 0$. We consider Firm 1 as a high cost producer and Firm 2 as a low cost producer, meaning that $\bar{c}_1 > \bar{c}_2$. To simplify the ensuing analytical expressions, in the rest of the paper we scale $\bar{c}_2=0$ without loss of generality, and assume $\bar{c}_1>0$. The prices are chosen before the firms learn each others’ marginal costs, but the cost distributions are common knowledge. For each ex-post level of marginal cost $c_i$ the profits for player i are

$$\begin{aligned} f_i(p_1,p_2;c_i)=(p_i-c_i) D_i(p_1,p_2) \end{aligned}$$

(1)

where the demand function is given by $D_i(p_1,p_2)=a-p_1+bp_2$, where $a \in A \subset \mathbb {R}^+$ and $b\in (0,1)\subset \mathbb {R}$. The parameter a describes market demand and b describes product heterogeneity.

The demand function is strictly log-supermodular and therefore the reaction functions are nondecreasing and at least one firm has a second-mover advantage in a game where prices $p_1,p_2$ are set and profits (1) follow (Amir and Stepanova 2006). We denote by game $G(\alpha )$ the endogenous timing duopoly game where the firms decide upon their timings by announcing $\alpha _1,\alpha _2 \in \{L,F\}$ at Stage 0, where L means moving at Stage 1 (leader) and F moving at Stage 2 (follower). Equilibrium prices depend on the ex-post values of the marginal costs and are denoted by $(p_i^{\alpha _i}(c_i),p_j^{\alpha _j}(c_j))$.

The fact that the marginal costs are realized only after the pricing decisions means that the solution concepts are Bayesian equilibria as in Albaek (1990). The timing announcements fully characterize the four possible market outcomes in game $G(\alpha )$; this means that we can denote the outcomes using the timing announcements. We denote an outcome by the 2-tuple $\alpha =(\alpha _1,\alpha _2)$, where for example (L, F) means that Firm 1 is the leader and Firm 2 is the follower and the equilibrium prices are $(p_1^L(c_1),p_2^F(c_2))$ and the ex-ante expected profits are those of the corresponding Stackelberg equilibrium. To further streamline notation we denote the ex-ante expected equilibrium profits in $G(\alpha )$ by

$$\begin{aligned} \varPi _i(\alpha ) \equiv E_{c_i}\{E_{c_j}\{f_i(p_1^{\alpha _1}(c_1),p_2^{\alpha _2}(c_2);c_i)\}\}, \quad i,j=1,2, \quad i \ne j, \end{aligned}$$

where $E_{c_i}\{\cdot \}$ is the expectation over $c_i$. In the remainder of the article these are just referred to as profits.

Amir and Stepanova (2006) show that with nonstochastic costs ($\sigma _i=0$ for $i=1,2$) and certain left-side restrictions on the demand parameter there are two sequential move equilibria that Pareto dominate the simultaneous move equilibria. In what follows we show that this also goes for the stochastic cost case under certain additional restrictions on the parameters of the marginal cost distributions. We restrict the demand parameter from below such that (i) only such sequential move equilibria that Pareto dominate the simultaneous move equilibria exist in game $G(\alpha )$ and that (ii) both firms have a second mover advantage in game $G(\alpha )$. These restrictions are necessary conditions for $G(\alpha )$ to be a coordination game with two non-Pareto ranked equilibria.

Before we formulate the equilibrium profits, we must restrict the interval A of feasible demand parameters such that the equilibrium prices are not smaller than the costs.

Assumption 1

$A \triangleq (-\frac{(b^2 - 2)}{b + 2} \bar{c}_1, \infty )$.

Proposition 1 in Amir and Stepanova (2006) together with our Assumption 1 guarantees that at least one of the firms prefers followership to any other outcome.

Lemma 1

Given that $a \in A$, the equilibrium prices in the simultaneous-move outcomes are

$$\begin{aligned} \begin{aligned}&(p_1^L(c_1),p_2^L(c_2)) = (p_1^F(c_1),p_2^F(c_2)) \\&\quad =\Bigg (\frac{2 a (b + 2) + 4 c_1 + b^2 (-c_1 + \bar{c}_1) }{- 2 b^2 + 8}, \frac{2 a (b + 2) + 4 c_2 + b (-b c_2 + 2 \bar{c}_1)}{- 2 b^2 + 8}\Bigg ) \end{aligned} \end{aligned}$$

(2)

and the corresponding profits,

$$\begin{aligned} \begin{aligned} \varPi _1(L,L)&=\varPi _1(F,F)=\frac{(a (b + 2) + (b^2 - 2) \bar{c}_1)^2}{(b^2 - 4)^2} + \frac{\sigma _1}{4},\\ \varPi _2(L,L)&=\varPi _2(F,F)=\frac{(a (b + 2)+ b \bar{c}_1)^2}{(b^2 - 4)^2} + \frac{\sigma _2}{4}. \end{aligned} \end{aligned}$$

(3)

The equilibrium prices in the Stackelberg outcome with Firm i as the leader are

$$\begin{aligned} \begin{aligned}&p_j^F(c_j,p_i^L) = \frac{1}{2}(a + bp_i^L + c_j),\\&p_i^L(c_i) = \frac{a (b + 2) + 2 c_i + b (-b c_i + \bar{c}_j)}{- 2 b^2 + 4}, \end{aligned} \end{aligned}$$

(4)

for $i,j=1,2$, $i \ne j$ and $\bar{c}_2=0$, and the corresponding profits with Firm 1 as the leader,

$$\begin{aligned} \begin{aligned} \varPi _1(L,F) =&\frac{(a (b + 2) + (b^2 - 2) \bar{c}_1)^2}{8 (- b^2 + 2)} -\frac{1}{8} (b^2 - 2) \sigma _1,\\ \varPi _2(L,F) =&\frac{(a ((b - 2) b - 4) + b (b^2 - 2) \bar{c}_1)^2}{16 (b^2 - 2)^2} + \frac{1}{16} (b^2 \sigma _1 + 4 \sigma _2), \end{aligned} \end{aligned}$$

(5)

and with Firm 1 as the follower

$$\begin{aligned} \begin{aligned} \varPi _1(F,L) =&\frac{(a ((b - 2) b - 4) + (- 3 b^2 + 4) \bar{c}_1)^2}{16 (b^2 - 2)^2} + \frac{1}{16} (b^2 \sigma _2 + 4 \sigma _1), \\ \varPi _2(F,L) =&\frac{(a (b + 2) + b \bar{c}_1)^2}{8 (- b^2 + 2)} - \frac{1}{8} (b^2 - 2) \sigma _2. \end{aligned} \end{aligned}$$

(6)

Proof

In this class of linear-quadratic models the unique Bertrand equilibrium prices are linear in the private cost information (Vives 1999), $\hat{p}_j(c_j) \equiv \beta _j+\gamma _j c_j$, $j\ne i$. The first-order condition for Firm i for a specific level of own cost $c_i$ and the conjectured Firm j’s price $\hat{p}_j(c_j)$ is

$$\begin{aligned} \frac{\partial }{\partial p_i} f_i(p_i,\hat{p}_j(c_j);c_i) = 0, \quad i\ne j, \end{aligned}$$

(7)

from which we solve the ex-ante expected price candidate

$$\begin{aligned} p_i(c_i) = \frac{1}{2} (a + c_i + b E_{c_j}\{\hat{p}_j(c_j)\}). \end{aligned}$$

(8)

Assuming that Firm j does the same calculation we can see that the conjectured coefficient $\gamma _i=\gamma _j=\frac{1}{2}$. The expected value of $\hat{p}_j(c_j)$ is therefore $E_{c_j}\{\hat{p}_j(c_j)\} = \beta _j+\frac{1}{2} \bar{c}_j$. This can be substituted to (8) to get two equations for $i=1,2$, $i \ne j$,

$$\begin{aligned} \beta _i+\frac{1}{2}c_i = \frac{1}{2} \left( a + c_i + b \left( \beta _j+\frac{1}{2} \bar{c}_j\right) \right) , \end{aligned}$$

from which we solve

$$\begin{aligned} \beta _i=\beta _j=\frac{4 a + 2 a b + b^2 \bar{c}_i + 2 b \bar{c}_j}{2 (- b^2 + 4)} \end{aligned}$$

for $i,j=1,2$, $i\ne j$ and $\bar{c}_2=0$. From these calculations (2) and (3) follow.

To compute the Stackelberg equilibria we first assume that Firm j is the follower and reacts with $\hat{p}_j(p_i;c_j)=\frac{1}{2} (a + c_j + b p_i)$. Firm i as the leader optimizes its price against this and the ex-ante expected prices are (4) and the corresponding ex-ante expected profits with Firm 1 as the leader are (5). (6) are obtained similarly. $\square$

Next we restrict the parameters of the marginal cost distributions so that each firm prefers the sequential move outcomes over the simultaneous move outcomes and that each firm prefers followership to leadership. This first calls for obtaining a suitable subinterval of A for the demand parameter a. From the profits given in (3), (5), and (6) we can see that they are upwards-opening quadratic functions in a and therefore above a certain point in A the outcomes are Pareto-ranked.

Corollary 1

There is a point in the interval A above which the profits are ordered $\varPi _1(F,L)>\varPi _1(L,F)>\varPi _1(L,L)=\varPi _1(F,F)$ and $\varPi _2(L,F)>\varPi _2(F,L)>\varPi _2(L,L)=\varPi _2(F,F)$.

Proof

Each profit expression in Lemma 1 is a second-degree polynomial in a. The second-degree coefficients of a of each of the Firm 1’s profits $\varPi _1(F,L)$, $\varPi _1(L,F)$, and $\varPi _1(F,F)$ (or $\varPi _1(L,L)$) are strictly positive and given and ordered by

$$\begin{aligned} \frac{((b - 2) b - 4)^2}{16 (b^2 - 2)^2}> \frac{(b + 2)^2}{8 (- b^2 + 2)} > \frac{1}{(b - 2)^2}, \end{aligned}$$

respectively for all feasible values of b. The comparison can be similarly conducted for Firm 2’s profits. This implies that the curvatures of the upwards-opening quadratics are ordered as such and there is the sought after point in the positive a-axis. $\square$

Corollary 1 shows that there is an open subinterval $A_1 \subset A$ where both firms’ follower profits exceed leader profits and leader profits exceed those from the simultaneous-move equilibria.¹ This is the subinterval to which we restrict a in the remainder of the article. Assumption 2 states the infimum of this subinterval.

Assumption 2

$a>\underline{a}=\max \{ a_1,a_2 \}$, where

$$\begin{aligned} \begin{aligned} a_1 =&\frac{(- 2 b^5 - b^4 + 2 b^3)\bar{c}_1}{b^3 (3 b + 4)} + \frac{(- b^2 + 2)}{b^3 (3 b + 4)} \\&\times \,\sqrt{\frac{b^5 \big (2 b (b + 1)^2 \bar{c}_1^2 + 2 (3 b + 4) (b^2 - 2) \sigma _1 + (3 b + 4) (b^2 - 2) \sigma _2\big )}{-b^2 + 2}},\\ a_2 =&-\frac{b\bar{c}_1}{b + 2} + \frac{b^2\sigma _2}{\sqrt{b^6\sigma _2/\big ((b - 2)^2(-b^2 + 2)\big )}}. \end{aligned} \end{aligned}$$

For $\sigma _2=0$, $a_2=-b\bar{c}_1/(b + 2)$.

The point $a_1$ in Assumption 2 is found by comparing Firm 1’s leader and simultaneous play profits and Firm 2’s follower and leader profits. The value of a where the latter profits are equal is always smaller than $a_0$. Thus, $a_1$ is the value of a where Firm 1’s leader profit equals its simultaneous play profit. The point $a_2$ is found by equating Firm 2’s follower and leader profits. Straightforward profit comparisons show that all the other possibilities lie below these values, including the point $a_0$.

Assumption 3

$\bar{c}_1$ must satisfy

$$\begin{aligned} \bar{c}_1 \ge \sqrt{\frac{(b + 2)^2 (- b^2 + 2) (\sigma _1 + 2 \sigma _2)}{2b^2(b + 1)^2}}. \end{aligned}$$

The restriction in Assumption 3 is found by calculating the range of $\bar{c}_1$ that satisfies the inequality $a_0 \le \max \{a_1,a_2\}$. It can also be shown that the same restriction forces the term inside the square-root in $a_1$ to be strictly positive. Assumption 3 implies that the lower limit of the mean of Firm 1’s marginal cost increases as the variances increase either separately or together. The effect of Firm 2’s variance on this is higher than Firm 1’s variance.

Lemma 2

Under Assumptions 1–3, the sequential-move equilibria of game $G(\alpha )$ Pareto dominate the simultaneous move equilibria:

$$\begin{aligned} \begin{aligned}&\varPi _i(L,F)> \varPi _i(L,L), \quad \varPi _i(L,F)> \varPi _i(F,F),\\&\varPi _i(F,L)> \varPi _i(L,L), \quad \varPi _i(F,L) > \varPi _i(F,F) \end{aligned} \end{aligned}$$

for $i=1,2$. Furthermore, under Assumptions 2 and 3, both firms have a second mover advantage in G:

$$\begin{aligned} \varPi _1(F,L)> \varPi _1(L,F), \quad \varPi _2(L,F) > \varPi _2(F,L). \end{aligned}$$

Proof

Trivially results from Lemma 1, Assumptions 1–3 and Corollary 1. $\square$

3 The model with partial commitments

We now relax the full commitments in game $G(\alpha )$ by formulating an “extended game” $\tilde{G}(\alpha ,t)$ in which a decision stage is added between stages 0 and 1. In this new stage, the firms can decide whether they wish to renege on the commitments $\alpha$ that they made on stage 0 by announcing their timings. Let this stage be called the “0.5th stage”, and let $t=(t_1,t_2)$ denote the 2-tuple that determines the firms’ timing decisions similarly as $\alpha$. The timing decisions are made simultaneously. Both firms as well as the demand side of the market observes the 0-Stage announcements perfectly before stage 0.5 is played. The outcomes in the actual duopoly game are then determined on the basis of the timing decisions. If Firm i reneges on its announcement, it has to pay a deviation cost $k_i \in \mathbb {R}^+$. The deviation cost is introduced to the profits in $\tilde{G}(\alpha ,t)$ such that for $i=1,2$ the profit is

$$\begin{aligned} \tilde{\varPi }_i(\alpha _i;t) = \varPi _i(t)-\kappa (\alpha _i,t_i) \end{aligned}$$

where

$$\begin{aligned} \kappa (\alpha _i,t_i) = \Bigg \{ \begin{array}{lr} 0, &{}\quad t_i = \alpha _i,\\ k_i, &{}\quad t_i \ne \alpha _i. \end{array} \end{aligned}$$

The conduct of $\tilde{G}(\alpha ,t)$ is as follows:

• Stage 0: The following events take place in the given order

  • Nature reveals $c_i$ to Firm i

  • The firms choose $\alpha$

• Stage 0.5: The firms choose t

• Stage 1: The leader moves

• Stage 2: The follower moves

Proposition 1

Assume that $\bar{c}_1$ is restricted below as in Assumption 3 and that at least one of the variances $\sigma _1$ or $\sigma _2$ is nonzero. Assume also that $k_i \ne 0$ for $i=1,2$. Then,

• if $k_1 > \underline{k}_1$ and $k_2 \le \underline{k}_2$, $\tilde{G}(\alpha ,t)$ has a unique SPE given by $\alpha =(F,L)$ and $t=(F,L)$;

• if $k_1 \le \underline{k}_1$ and $k_2 > \underline{k}_2$, $\tilde{G}(\alpha ,t)$ has a unique SPE given by $\alpha =(L,F)$ and $t=(L,F)$;

where

$$\begin{aligned} \begin{aligned}&\underline{k}_1 =\frac{b^4 (a (b + 2) + (b^2 - 2) \bar{c}_1)^2}{8 (b^2 - 4)^2 (- b^2 + 2)} - \frac{b^2 \sigma _1}{8}, \\&\underline{k}_2 =\frac{b^4 (a (b + 2) + b \bar{c}_1)^2}{8 (b^2 - 4)^2 (- b^2 + 2)} - \frac{b^2 \sigma _2}{8}.\\ \end{aligned} \end{aligned}$$

(9)

Proof

We shall first formulate two conditions for the existence of the two SPE’s. These are then shown to be the conditions that guarantee uniqueness.

3.1 Condition 1: $\tilde{\varPi }_1((F,\alpha _2),(L,F))<\tilde{\varPi }_1((F,\alpha _2),(F,F))$, $\alpha _2=L,F$

This means that

$$\begin{aligned} \varPi _1(L,F)-k_1<\varPi _1(F,F) \Rightarrow k_1 > \varPi _1(L,F)-\varPi _1(F,F). \end{aligned}$$

This gives $\underline{k}_1$.

3.2 Condition 2: $\tilde{\varPi }_2((\alpha _1,L),(F,F))<\tilde{\varPi }_2((\alpha _1,F),(F,F))$, $\alpha _1=L,F$

This means that

$$\begin{aligned} \varPi _2(F,L)-k_2 < \varPi _2(F,F) \Rightarrow k_2>\varPi _2(F,L)-\varPi _2(F,F). \end{aligned}$$

This gives $\underline{k}_2$.

$\tilde{G}(\alpha ,t)$ is presented below in normal form. Each quadrant (numbered I–IV) corresponds to a subgame that starts when both firms observe the announcements $\alpha$. If there is a unique SPE in the game, then iterated elimination of strictly dominated strategies leaves only one outcome in only one of the quadrants, and this is the unique NE of that subgame. To show that the SPE’s are unique when $k_i > \underline{k}_i$ but $k_j \le \underline{k}_j$, $i,j=1,2$, $i \ne j$, we shall inspect each case separately.

3.3 Case 1: $k_1 \le \underline{k}_1$, $k_2 \le \underline{k}_2$

In this case $\varPi _1(L,F)-k_1>\varPi _1(F,F)$ and $\varPi _2(F,L)-k_2>\varPi _2(F,F)$ and there are two Nash equilibria in nondominated strategies in each quadrant. In all of these NE’s the firms move sequentially. The cases $k_1=0$, $k_2=0$ and $k_1=k_2=0$ do not form exceptions.

3.4 Case 2: $k_1 > \underline{k}_1$, $k_2 \le \underline{k}_2$

In this case $\varPi _1(L,F)-k_1<\varPi _1(F,F)$ from which it follows that $t_1=F$ strictly dominates $t_1=L$ in quadrants III and IV but not in quadrants I and II. Because $\varPi _2(F,L)-k_2>\varPi _2(F,F)$, there is one NE in each quadrant III and IV, among which $\alpha _2=L$ strictly dominates $\alpha _2=F$ given that $k_2 \ne 0$. Therefore, the SPE with $(\alpha ,t)=((F,L),(F,L))$, guaranteed by Condition 1, is unique.

3.5 Case 3: $k_1 \le \underline{k}_1$, $k_2 > \underline{k}_2$

In this case $\varPi _2(F,L)-k_2<\varPi _2(F,F)$ from which it follows that $t_2=F$ strictly dominates $t_2=L$ in quadrants II and IV but not in quadrants I and III. Because $\varPi _1(L,F)-k_1>\varPi _1(F,F)$, there is one NE in each quadrant II and IV, among which $\alpha _1=L$ strictly dominates $\alpha _1=F$ given that $k_1 \ne 0$. Therefore, the SPE with $(\alpha ,t)=((L,F),(L,F))$, guaranteed by Condition 2, is unique.

3.6 Case 4: $k_1 > \underline{k}_1$, $k_2 > \underline{k}_2$

In this case $\varPi _1(L,F)-k_1<\varPi _1(F,F)$ and $\varPi _2(F,L)-k_2<\varPi _2(F,F)$ and again there are two Nash equilibria in nondominated strategies in each quadrant. Therefore, the SPE’s cannot be unique. $\square$

Proposition 1 thus gives two possibilities for the SPEs to be unique, depending on the relative size of the deviation costs. In each unique SPE either the low cost or the high cost firm enjoys the second mover advantage. It should be noted that the restrictions that Proposition 1 places on the deviation costs depend on the asymmetry in the stochastic costs. Uniqueness as laid out in either case of Proposition 1 is guaranteed if our initial assumption $\bar{c}_1>0$ holds, because then $\underline{k}_1 \ne \underline{k}_2$, forcing either case in Proposition 1 to hold.

To get a better idea of how a partial commitment might work in $\tilde{G}(\alpha ,t)$, we may look at the situation when a suitably chosen common deviation cost $k=k_1=k_2$ is in place. In this situation, the high cost Firm 1 can make a cheaper partial commitment than the low cost Firm 2 and become the follower, as Corollary 2 below shows.

Corollary 2

If the deviation cost is exogenously given and common to both firms, $k=k_1=k_2$, then there exists such a k for which $\underline{k}_1 < k \le \underline{k}_2$ that guarantees a unique SPE where Firm 1 is the follower and Firm 2 the leader.

Proof

We show that from the condition $\bar{c}_1>0$ it follows that $\underline{k}_1 < \underline{k}_2$. Note that for $\bar{c}_1=0$, $\underline{k}_2<\underline{k}_1$ if $\frac{1}{8} b^2 (\sigma _1 - \sigma _2)<0$ which is satisfied for $\sigma _2<\sigma _1$. Therefore, $\bar{c}_1=0$ cannot satisfy the Corollary. Then for $\bar{c}_1>0$ we see that

$$\begin{aligned} \underline{k}_2-\underline{k}_1 = \frac{a b^4 (b + 1)}{4 (b^4 - 6 b^2 + 8)}\bar{c}_1 + \frac{b^4 (b^2 - 1)}{8 (b^4 - 6 b^2 + 8)}\bar{c}_1^2 + \frac{b^2 \sigma _1}{8} - \frac{b^2 \sigma _2}{8} \end{aligned}$$

which is clearly above zero for all $\bar{c}_1$ that satisfy Assumption 3, i.e. for

$$\begin{aligned} \bar{c}_1 \ge \sqrt{\frac{(b + 2)^2 (- b^2 + 2) (\sigma _1 + 2 \sigma _2)}{2b^2(b + 1)^2}}. \end{aligned}$$

$\square$

We also find that in a situation where $k_j = 0 < \underline{k}_j$ and $k_i > \underline{k}_i$, there are “babbling” equilibria where Firm j’s announcement is not informative of its intentions on the equilibrium path. This is because if Firm j does not have to pay a deviation cost, it is indifferent about which announcement it makes.

4 Information sharing

Because our model has stochastic production technologies, a situation may occur where a firm learns its own marginal cost before it makes the timing decision. For example, a manufacturer may learn the exact marginal cost by conducting production test runs. Likewise there may be costs related to e.g. staff training with a novel business model that are privately learned before business is opened. Would the firm in such a situation have the incentive to share this private information with the competitor, in order to obtain a favorable outcome for itself in the game?

This “private values” problem has been previously analyzed in games with full commitment, see e.g. Vives (1984) and Raith (1996). Gal-Or (1986) shows that in simultaneous-move Bertrand markets with private marginal costs, firms conceal rather than share their private cost information. However, in our case the decision to share with the competitor the private cost does not trivially depend on the leader/follower role assignment, as this is decided endogenously via the announcements. The firms must also consider what implications information sharing has on the profitability of the timing sequence that ensues. Rather than having a direct effect on pricing behavior, information sharing has a direct effect on the (partial) commitments that the firms make at the 0th stage of the game.

In Sect. 3 we showed how the SPEs $(\alpha ,t){=}\big ((F,L),(F,L)\big )$ and $(\alpha ,t)=\big ((L,F),(L,F)\big )$ of game $\tilde{G}(\alpha ,t)$ depend on the values of the deviation costs $k_1$ and $k_2$. It was shown that if $k_i$ is greater than $\underline{k}_i$ but $k_j$ equal to or less than $\underline{k}_j$, then in the unique SPE Firm i is the follower and Firm j is the leader, $i,j=1,2$, $i \ne j$. However, as we assumed that no information was shared in Sect. 3, these results have to be reconsidered under the four different information sharing conditions, which are both conceal, one firm shares while the other conceals (and vice versa), and both share their private marginal costs. Lemma 3 establishes profits when information sharing is bilateral or unilateral, and these profits are then used in a reformulation of the results obtained in Sect. 3.

In this section we consider the implications of information sharing for the results obtained in the previous section. If the firms decide to share their private information, this happens before any decision making takes place and they are assumed to do so with perfect precision, e.g. via a trade association using industry-wide contracts (as in Vives 1984 and Shapiro 1986). Furthermore, firms make the decision to share before they learn their costs (as in Raith 1996). Therefore we abstain from building a model where information sharing is strategic, i.e. we do not consider a signaling model in the sense of the signaling literature such as Milgrom and Roberts (1982) where actions convey inferential impacts. The purpose of this section is to complement the literature on information sharing in oligopoly games (Raith 1996) with a consideration of partial commitments. A sizeable literature exists on signaling asymmetric information in endogenous timing games, see e.g. Daughety and Reinganum (1994), Normann (1997), and Brindisi et al. (2014).

To simplify the analyses, we first define the certainty equivalence profits that are profits of the game when the cost variances are zero. We then define the different outcomes that result when both firms share and when only one firm shares the private cost information.

Lemma 3

The “certainty equivalence profits”, i.e. the profit expressions with zero variances, are given by

$$\begin{aligned} \begin{aligned} \varPi _1^{CE}(L,F)&= \frac{(a (b + 2) + (b^2 - 2) \bar{c}_1)^2}{8 (- b^2 + 2)}, \\ \varPi _2^{CE}(L,F)&= \frac{(a ((b - 2) b - 4) + b (b^2 - 2) \bar{c}_1)^2}{16 ( b^2 - 2)^2}, \\ \varPi _1^{CE}(F,L)&= \frac{(a ((b - 2) b - 4) + (- 3 b^2 + 4) \bar{c}_1)^2}{16 ( b^2 - 2)^2}, \\ \varPi _2^{CE}(F,L)&= \frac{(a (b + 2) + b \bar{c}_1)^2}{8 (- b^2 + 2)}, \\ \varPi _1^{CE}(F,F)&= \frac{(a (b + 2) + (b^2 - 2) \bar{c}_1)^2}{(b^2 - 4)^2}, \\ \varPi _2^{CE}(F,F)&= \frac{(a (b + 2) + b \bar{c}_1)^2}{(b^2 - 4)^2}. \\ \end{aligned} \end{aligned}$$

When both firms share $c_1,c_2$, the profits are:

$$ \begin{aligned} \varPi _1^{1 \& 2,sh}(L,F)= & {} \varPi _1^{CE}(L,F) + \frac{(b^2 - 2)^2 \sigma _1 + b^2 \sigma _2}{8 (- b^2 + 2)}\\ \varPi _2^{1 \& 2,sh}(L,F)= & {} \varPi _2^{CE}(L,F) + \frac{1}{16} \bigg (b^2 \sigma _1 + \bigg (\frac{- 3 b^2 + 4}{b^2 - 2}\bigg )^2\sigma _2\bigg )\\ \varPi _1^{1 \& 2,sh}(F,L)= & {} \varPi _1^{CE}(F,L) + \frac{1}{16} \bigg (\bigg (\frac{- 3 b^2 + 4}{b^2 - 2}\bigg )^2\sigma _1 + b^2 \sigma _2\bigg ) \\ \varPi _2^{1 \& 2,sh}(F,L)= & {} \varPi _2^{CE}(F,L) + \frac{b^2 \sigma _1}{- 8 b^2 + 16} + \frac{1}{8} (- b^2 + 2) \sigma _2 \\ \varPi _1^{1 \& 2,sh}(F,F)= & {} \varPi _1^{CE}(F,F) + \frac{(b^2 - 2)^2 \sigma _1 + b^2 \sigma _2}{(b^2 - 4)^2}\\ \varPi _2^{1 \& 2,sh}(F,F)= & {} \varPi _2^{CE}(F,F) + \frac{b^2 \sigma _1 + (b^2 - 2)^2 \sigma _2}{(b^2 - 4)^2} \end{aligned}$$

When Firm 1 shares $c_1$ but Firm 2 conceals $c_2$, the profits are:

$$\begin{aligned} \begin{aligned} \varPi _1^{1,sh}(L,F)&= \varPi _1^{CE}(L,F) +\frac{1}{8} (- b^2 + 2) \sigma _1 \\ \varPi _2^{1,sh}(L,F)&= \varPi _2^{CE}(L,F) + \frac{b^2 \sigma _1}{16} + \frac{\sigma _2}{4} \\ \varPi _1^{1,sh}(F,L)&= \varPi _1^{CE}(F,L) + \frac{1}{16} \bigg (\bigg (\frac{- 3 b^2 + 4 }{b^2 - 2}\bigg )^2\sigma _1 + b^2 \sigma _2\bigg )\\ \varPi _2^{1,sh}(F,L)&= \varPi _2^{CE}(F,L) + \frac{b^2 \sigma _1}{8 (- b^2 + 2)} + \frac{1}{8} (- b^2 + 2) \sigma _2\\ \varPi _1^{1,sh}(F,F)&= \varPi _1^{CE}(F,F) + \bigg (\frac{b^2 - 2}{b^2 - 4}\bigg )^2 \sigma _1 \\ \varPi _2^{1,sh}(F,F)&= \varPi _2^{CE}(F,F) + \frac{b^2 \sigma _1}{(b^2 - 4)^2} + \frac{\sigma _2}{4} \end{aligned} \end{aligned}$$

When Firm 1 conceals $c_1$ but Firm 2 shares $c_2$, the profits are:

$$\begin{aligned} \begin{aligned} \varPi _1^{2,sh}(L,F)&= \varPi _1^{CE}(L,F) + \frac{1}{8} (- b^2 + 2) \sigma _1 + \frac{b^2 \sigma _2}{8 (- b^2 + 2)}\\ \varPi _2^{2,sh}(L,F)&= \varPi _2^{CE}(L,F) + \frac{1}{16} \bigg (b^2 \sigma _1 + \bigg (\frac{-3b^2 + 4}{b^2 - 2}\bigg )^2\sigma _2 \bigg )\\ \varPi _1^{2,sh}(F,L)&= \varPi _1^{CE}(F,L) + \frac{\sigma _1}{4} + \frac{b^2 \sigma _2}{16}\\ \varPi _2^{2,sh}(F,L)&= \varPi _2^{CE}(F,L) + \frac{1}{8} (- b^2 + 2) \sigma _2 \\ \varPi _1^{2,sh}(F,F)&= \varPi _1^{CE}(F,F) + \frac{\sigma _1}{4} + \frac{b^2 \sigma _2}{(b^2 - 4)^2}\\ \varPi _2^{2,sh}(F,F)&= \varPi _2^{CE}(F,F) + \bigg (\frac{b^2 - 2}{b^2 - 4}\bigg )^2\sigma _2 \end{aligned} \end{aligned}$$

The profits are ordered as follows:

$$ \begin{aligned} \begin{array}{ccccccc} \varPi _1^{1,sh}(F,F) &{}<&{} \varPi _1(F,F) &{}<&{} \varPi _1^{1 \& 2,sh}(F,F) &{}<&{} \varPi _1^{2,sh}(F,F),\\ \varPi _1^{1,sh}(L,F) &{}=&{} \varPi _1(L,F) &{}<&{} \varPi _1^{1 \& 2,sh}(L,F) &{}=&{} \varPi _1^{2,sh}(L,F),\\ \varPi _1^{1,sh}(F,L) &{}=&{} \varPi _1^{1 \& 2,sh}(F,L) &{}<&{} \varPi _1(F,L) &{}=&{} \varPi _1^{2,sh}(F,L),\\ \varPi _2^{2,sh}(F,F) &{}<&{} \varPi _2^{1 \& 2,sh}(F,F) &{}<&{} \varPi _2(F,F) &{}<&{} \varPi _2^{1,sh}(F,F),\\ \varPi _2^{2,sh}(F,L) &{}=&{} \varPi _2(F,L) &{}<&{} \varPi _2^{1 \& 2,sh}(F,L) &{}=&{} \varPi _2^{1,sh}(F,L),\\ \varPi _2^{2,sh}(L,F) &{}=&{} \varPi _2^{1 \& 2,sh}(L,F) &{}<&{} \varPi _2(L,F) &{}=&{} \varPi _2^{1,sh}(L,F). \end{array} \end{aligned}$$

(10)

Proof

When Firm i shares $c_i$ to Firm j, the latter does not act upon the expected price $E_{c_j}\{p_i(c_i)\}$ as in Lemma 1 but with the actual cost information. This fact is used to derive the payoffs in the different situations. $\square$

Corollary 3

Let $\underline{k}_i^{i,sh}$, $\underline{k}_i^{j,sh}$, and $\underline{k}_i^{i \& j,sh}$ denote the lower limits of the deviation cost sets (as in Proposition 1) in the different information sharing conditions (i shares unilaterally, j shares unilaterally, $i \& j$ share, respectively). The upper limits of these sets extend to infinity. Then the lower limits are ordered such that

$$ \begin{aligned} \underline{k}_1<\underline{k}_1^{2,sh}<\underline{k}_1^{1,sh}<\underline{k}_1^{1 \& 2,sh}<\underline{k}_2<\underline{k}_2^{1,sh}<\underline{k}_2^{2,sh}<\underline{k}_2^{1 \& 2,sh} \end{aligned}$$

(11)

where $\underline{k}_1,\underline{k}_2$ are as given in Proposition 1.

Proof

The lower limits of the deviation cost sets are calculated as in Conditions 1 and 2 of the Proof of Proposition 1. They are:

$$ \begin{aligned} \begin{aligned}&\underline{k}_1^{2,sh} = \frac{b^4 (a (b + 2) + (b^2 - 2) \bar{c}_1)^2}{8 (b^2 - 4)^2 (- b^2 + 2)} - \frac{b^2 \sigma _1}{8} + \frac{b^6 \sigma _2}{8 (b^2 - 4)^2 (- b^2 + 2)}, \\&\underline{k}_1^{1,sh} = \frac{b^4 (a (b + 2) + (b^2 - 2) \bar{c}_1)^2}{8 (b^2 - 4)^2 (- b^2 + 2)} + \frac{b^4 (- b^2 + 2) \sigma _1}{8 (b^2 - 4)^2}, \\&\underline{k}_1^{1 \& 2,sh} = \frac{b^4 (a (b + 2) + (b^2 - 2) \bar{c}_1)^2}{8 (b^2 - 4)^2 (- b^2 + 2)} +\frac{b^4 (- b^2 + 2) \sigma _1}{8 (b^2 - 4)^2} + \frac{b^6 \sigma _2}{8 (b^2 - 4)^2 (- b^2 + 2)}, \end{aligned} \end{aligned}$$

and

$$ \begin{aligned} \begin{aligned}&\underline{k}_2^{1,sh} = \frac{b^4 (a (b + 2) + b \bar{c}_1)^2}{8 (b^2 - 4)^2 (- b^2 + 2)} + \frac{b^6 \sigma _1}{8 (b^2 - 4)^2 (- b^2 + 2)} - \frac{b^2 \sigma _2}{8}\\&\underline{k}_2^{2,sh} = \frac{b^4 (a (b + 2) + b \bar{c}_1)^2}{8 (b^2 - 4)^2 (- b^2 + 2)} + \frac{b^4 (- b^2 + 2) \sigma _2}{8 (b^2 - 4)^2}\\&\underline{k}_2^{1 \& 2,sh} = \frac{b^4 (a (b + 2) + b \bar{c}_1)^2}{8 (b^2 - 4)^2 (- b^2 + 2)} + \frac{b^6 \sigma _1}{8 (b^2 - 4)^2 (- b^2 + 2)} + \frac{b^4 (- b^2 + 2) \sigma _2}{8 (b^2 - 4)^2}. \end{aligned} \end{aligned}$$

It is straightforward to check, by comparing the variance terms and taking into account Assumption 3, that the ordering (11) holds. $\square$

Corollary 3 suggests that information sharing places more stringent criteria for the deviation cost than information concealment: The firms will not consider information sharing if the deviation cost is close to the lower boundary of their deviation cost sets. Therefore, Proposition 1 does not sufficiently describe the conditions for the unique SPE when information is shared unilaterally or bilaterally.

Proposition 2

Let us assume that the deviation costs are common to both firms, $k=k_1=k_2$. If the firms can decide whether they share their private cost information or not before they make announcements in game $\tilde{G}(\alpha ,t)$, then the unique SPE where Firm 1 is the follower and Firm 2 is the leader exists for $\underline{k}_1 < k \le \underline{k}_2$. In this SPE neither firm shares its private cost information.

Proof

When information is not shared, a unique SPE in $\tilde{G}(\alpha ,t)$ exists if the common deviation cost $\underline{k}_1 < k \le \underline{k}_2$ (Proposition 1). However, given the various possibilities for information sharing conditions we should consider the deviation cost sets given in Corollary 3 that extend the interval $(\underline{k}_1,\underline{k}_2]$. Equations (10) in Lemma 3 show that Firm 1 prefers concealing information to own unilateral sharing or bilateral sharing. Therefore values $k\in (\underline{k}_2,\underline{k}_2^{1 \& 2,sh}]$ are not feasible because $\underline{k}_2^{1,sh}<\underline{k}_2^{2,sh}<\underline{k}_2^{1 \& 2,sh}$ (Corollary 3). $\square$

Proposition 2 states that if the firms have a common deviation cost, neither firm shares their private marginal cost information in the unique SPE if the deviation cost is above the lower limit of Firm 1’s deviation cost set but below that of Firm 2. Therefore, the equilibrium selection implications of Sect. 3 are preserved for the case where private cost information can be learned.

5 Discussion

The deviation cost $k_i$ can be thought of as a cost of a lost opportunity that is imposed if the move that is announced is reneged on. Such opportunities arise frequently as a result of advertising campaigns where firms aim to increase their brand value.²

Think of two price-setting firms who are about to open business at a new location, such as the restaurant chains in the motivating example of Sect. 1. They have fairly similar product portfolios and they face a coordination dilemma in the form of that described in Sect. 2, i.e. they prefer to open at different dates instead of opening at the same date. To inform customers, the firms advertise their opening date at the local media and face reputational damage or the loss of loyal customers if they renege on their announced date. Assume therefore that the deviation cost $k_i=\beta +\gamma _i$, where $\gamma _i$ is the cost that incurs from reputational loss and $\beta$ is a fine imposed by a third party from a contractual breach. Assume further that $\gamma _i=\gamma _i(y_i)$ is increasing in a campaign investment $y_i$. According to our analysis in Sect. 3, the low cost Firm 2 must make a higher campaign investment than Firm 1 to become the follower, i.e. $\gamma _2(y_2)+\beta >\gamma _1(y_1)+\beta$. However, Firm 2’s investment leads to its followership only if $\gamma _2(y_2)+\beta > \underline{k}_2$ but $\gamma _1(y_1)+\beta \le \underline{k}_1$. This problem can also be solved by the third party—e.g. a facility owner that stands on the other side of the contract—by adjusting $\beta$ such that the deviation cost is within the interval $(\underline{k}_1,\underline{k}_2]$. In this case only the timing structure where the high cost Firm 1 becomes the follower is viable.

5.1 Related literature

Caruana and Einav (2008) study a model of partial commitments that allows repeated and sequential adjustments of announcements at a switching cost that increases after every adjustment before the final commitments. Their model is generic and can explain a host of situations involving costly delays, such as sequential market entry. On the other hand, their model does not answer to the questions that we study, namely which of the asymmetric cost firms affords a more costly commitment and how cost uncertainty affects partial commitments. In principle our model could also allow for multiple rounds of timing announcements $\alpha _i$ before the final timings t are decided upon. This would require that Firm i at announcement round r observes Firm j’s announcement at the previous round $r-1$, denoted $\alpha _j^{r-1}$, before making its own announcement $\alpha _i^r$, assuming that $r \in \{2,3,\ldots \}$ and $i \ne j$. Because of the nature of the pricing game that we consider, we would have $\alpha _i^r \ne \alpha _j^{r-1}$ for each r (this is implied by Lemma 2). If we assume that the deviation cost increases from one round to the next and that the increase in the deviation cost between rounds is not larger than the interval $(\underline{k}_1,\underline{k}_2]$, i.e. $\underline{k}_2-\underline{k}_1>\kappa _r(\alpha _i,t_i)-\kappa _{r-1}(\alpha _i,t_i)>0$, we would observe essentially the same result as given in Proposition 1. This result would say that the high cost Firm 1 stops switching announcements when the deviation cost hits the lower bound $\underline{k}_1$. After this the low cost Firm 2 would also not have reason to switch from the announcement given that $\alpha _2^{r-1} \ne \alpha _1^r$. Therefore, such an assumption of sequential announcements would not be restrictive to our results.

Henkel (2002) and Weber (2014) consider partial commitments in duopoly with exogenous timing. In their models the leader deviates from its announced strategy after the follower has decided. With increasing reaction functions this gives the leader a partial commitment for moderate deviation cost levels. We should therefore compare our model to these models and ask: Does the partial commitment to price, rather than to timing as in Sect. 3, yield a unique SPE in $G(\alpha )$? The answer is no—this is because we do not consider deviations from followership or simultaneous play. As a result the coordination problem between multiple SPEs persists for any deviation cost level. The argument is as follows. First consider the subgame $\alpha =(L,F)$. In this case Firm 1 deviates from $p_1^L$ to $R(p_{2})$, where $R(p_2)$ is the argmax of its ex-ante expected profit function given Firm 2’s price $p_2$, and pays a deviation cost $l_i \in (0,\infty )$. Firm 2 takes this deviation into account and prices at $p_2=p_2^L$ and Firm 1 enjoys a profit that is maximal at zero deviation cost, which is then the follower payoff. Hence, for small deviation costs there are two Nash equilibria in nondominated strategies in this subgame and as the deviation cost $l_i$ increases, Firm 1’s deviation becomes dominated by non-deviation. Then repeat these arguments for the subgame $\alpha =(F,L)$ with the players’ roles reversed. Even if we consider all deviation cost levels from zero to infinity there are always two SPE’s in this game, one in each subgame.

Amir and Stepanova (2006) present a risk dominance argument in the pricing game with full commitments and nonstochastic costs. If the firms are interested in minimizing the risk of a coordination failure, they will naturally want coordinate on the equilibrium that has a larger product of deviation losses. It can be easily shown that, as in Amir and Stepanova (2006), in game $G(\alpha )$ presented in Sect. 2 of this article the equilibrium $\alpha =(F,L)$ risk dominates the equilibrium $\alpha =(L,F)$ regardless of the variance levels (as long as Assumptions 1–3 are satisfied). However, as Amir and Stepanova (2006) note, the concept of risk dominance is applicable only to the $2 \times 2$ game with announcements and not the actual duopoly game where firms decide upon the continuous price levels. It is therefore ambiguous how the firms would actually apply the risk dominance concept. We present one way to endogenize the selection of one of two possible sequential move equilibria in the HS game with observable delay that also complements the arguments offered by risk dominance considerations.

5.2 Related applications

Various applications in the oligopoly literature bear resemblance to partial commitments described in this article and in Henkel (2002) and Weber (2014). While constructing a unifying framework of the economic models of partial commitments is out of scope for this paper, it is illustrative to discuss selected examples. Cooper (1986) studies most-favored customer pricing and finds that a unilateral promise of rebates to current customers in case of a future price cut works as a commitment device to a price that is above a Nash equilibrium and thus facilitates collusion.

Side payments are used in economic contracting to reduce externalities and this in general is seen as enhancing efficiency. However, as Jackson and Wilkie (2005) find, strategic use of side payments may not always increase efficiency, because the player offering the side payment aims to alter the other’s behavior to its own advantage rather than to increase efficiency. In this sense strategy contingent side payments resemble partial commitments.

Sunk costs can be seen as commitment devices when market entry is considered, and not only as entry barriers that modify the pre-entry conditions as in the classical entry literature (e.g. Dixit, 1980). As in the side payments case, the sunk costs can alter both players’ behavior. Cabral and Ross (2008) present a model where the entrant’s sunk investment softens the incumbent who would otherwise resort to predatory behavior. The sunk investment commits the entrant by making its exit unattractive.

The Bertrand model with homogenous products can be applied to model procurement auctions with supply-side competition. Arozamena and Weinschelbaum (2009) note that sequential price competition arises in procurement auctions when one of the firms has a right of first refusal, i.e. the option to observe the other’s price before submitting own price. Our model could be extended to allow homogenous products and the possibility of bidding for this right—creating a partial commitment—could be explicitly modeled. The option value of partial commitments should provide avenues for future research.