A timing game in a mixed duopoly

Abstract

This paper investigates a timing game in a mixed duopoly, whereby a relatively inefficient state-owned firm maximizing the linear combination of its profit and social welfare competes against a relatively efficient, profit-maximizing private firm over the timing of entry. We find that the incentives for firms to enter the market depend on the degrees of privatization of a state-owned firm and of the cost asymmetry between the two firms. We also provide welfare analysis by comparing the equilibrium timing of entry with the socially optimal one. When the two firms’ products are perfect substitutes, the socially optimal timing of both firms entering the market can be achieved if the state-owned firm is fully public.

1 Introduction

Mixed oligopolies, where public and private firms co-exist in a market, are quite common in the telecommunications, banking, airplane, and automobile industries. The timing competition of entering a new market (adopting a new technology) in a mixed oligopoly often occurs, yet differences exist in the role distribution (leader or follower) among firms in the same industry and across industry sectors. This paper investigates the timing competition in a mixed duopoly, whereby a relatively inefficient state-owned firm maximizing the linear combination of its profit and social welfare competes against a relatively efficient, profit-maximizing private firm over the timing of entry.

Our aim is to provide answers to the following questions. How does the timing of entry vary between different market structures, and in particular between a pure duopoly and a mixed duopoly? How do the degrees of privatization and cost asymmetry influence the speed of entry? Is there market failure in the choices of timing of entry?

We observe in some circumstances that a state-owned firm may try to enter a new market segment and launch its product first, while a private firm subsequently enters the new market segment and behaves as a follower. NTT DoCoMo, which previously was a state-owned telecommunications company in Japan, is one example. It launched i-Mode mobile wireless Internet service in February 1999 before private telecommunications companies did, successfully opening up a new market.

We also note examples in other circumstances in which the private firm gives priority to bringing its new product to a market or the state-owned firm and the private firm nearly simultaneously enter a new market segment. For instance, in the hybrid gasoline-electric vehicle market in China the private manufacturer Toyota Motor Corporation (TMC) was the first to launch related products, including Prius in 2005, Lexus LS600h in 2007, and RX400h in 2009. In 2020, TMC licensed the core system of hybrid technology to Guangzhou Automobile, which is a state-owned follower. In Taiwan’s telecommunications industry, the major companies there, including state-owned and private firms, deployed the commercial scope of fifth-generation (5 G) mobile communications technology almost at the same time in 2019.

This study relates to the literature of timing games. From the viewpoint of firms’ information structure, the two classical timing games are: (1) precommitment game in which firms are able to commit to their timing of adoption at the beginning of the game; and (2) preemption game in which firms are not able to credibly commit to their timing of adoption and are flexible in altering their timing of adoption. In her seminal article, Reinganum (1981) investigates the precommitment game, showing that the model has a unique Nash equilibrium that involves sequential adoption and there is a first-mover advantage.¹ Fudenberg and Tirole (1985) first investigate the preemption game, noting that preemption motives force the first adoption to occur earlier in a preemption game compared to a precommitment game, until payoffs are the same for both firms.²

The equilibrium analysis of a timing game focuses on factors that affect the timing of adoption, such as government regulation (Hendricks 1992; Riordan 1992), market competition (Milliou and Petrakis 2011; Argenziano and Schmidt-Dengler 2013), location differentiations (Meza and Tombak 2009; Ebina et al. 2015), and information asymmetry (Hopenhayn and Squintani 2011; Bobtcheff and Mariotti 2012). The welfare analysis of a timing game explores whether firms adopt new technologies too early or too late from the viewpoint of social welfare, such as Argenziano and Schmidt-Dengler (2013) and Sun (2018). In particular, Argenziano and Schmidt-Dengler (2013) examine how the equilibrium entry times compare to those that would be socially optimal, showing in a preemption game that all entries, except the first one, occur earlier than socially optimal.

This paper also relates to the mixed oligopoly literature. Merrill and Schneider (1966) first investigate a mixed oligopoly with a state-owned firm seeking to maximize an industry’s total output and private firms seeking to maximize their profits. Ever since Merrill and Schneider (1966), related research on a mixed oligopoly presents quite rich and diversified development. Some studies compare between Bertrand and Cournot equilibria, variations of a state-owned firm’s objective function, and welfare analysis of privatization policies.

We also note that some papers offer an analysis of the endogenous timing of choosing actions in a mixed oligopoly, finding results that differ somewhat from those in Hamilton and Slutsky (1990) pure oligopoly. In particular, Pal (1998) extends the endogenous timing game to a mixed oligopoly, illustrating under Cournot competition that all firms choosing quantities simultaneously cannot be sustained as an equilibrium outcome. Bárcena-Ruiz (2007) investigates an endogenous timing game in a mixed oligopoly, finding under Bertrand competition that firms simultaneously choose prices in equilibrium.³ We document that the endogenous timing game helps analyze the timing of choosing prices or quantities in the product market, but our target is on the endogenous leader and follower competing over the timing of entry.

The timing game literature mostly assumes that all firms seek to maximize their respective own profit, which refers to a pure oligopoly. The mechanisms via which the objectives of firms affect the timing of entry remain unexplored. Based on a precommitment game, we analyze the timing of firms entering a new market segment (adopting a new technology) in a mixed oligopoly to fill the related gap in the literature.

Suppose the market has a state-owned firm (or, say, a partially-privatized firm), which is relatively inefficient in production, seeking to maximize the linear combination of its own profit and social welfare and a relatively efficient private firm seeking to maximize its own profit. A game with an infinite horizon is analyzed in which a new technology appears at the game’s beginning, and both firms decide when to adopt the new technology and enter the market. In every period thereafter, a firm chooses its output when it enters the market.

What follows runs central to our findings. We find for a given sufficiently small degree of cost asymmetry that when the degree of privatization of the state-owned firm is relatively small, the unique equilibrium outcome is the state-owned firm being a leader and the private firm being a follower. The reason is that each firm’s incentive to enter the market is increasing in its incremental payoff from entry and the state-owned firm’s incremental payoff from entry is decreasing in the degrees of cost asymmetry and privatization, while the private firm’s incremental payoff from entry is increasing in the degrees of cost asymmetry and privatization. As the degree of privatization decreases, the follower state-owned firm’s incentive to enter the market increases, implying that the private firm as the leader and the state-owned firm as the follower no longer remain as the equilibrium outcome.

In the unique equilibrium with an increase in the degree of privatization, the incentive for the leader state-owned firm to enter the market declines, and so it will enter the market later. As the degree of privatization increases, the incentive for the follower private firm to enter the market increases, and therefore it enters the market earlier. Subsequently, the time span between successive entries, meaning the timing differentiation between the two firms, decreases with the degree of privatization. This implies that the time span between successive entries in a mixed duopoly is longer than that in a pure duopoly.

For a given sufficiently large degree of privatization, when the degree of cost asymmetry is also relatively large, the unique equilibrium outcome is the private firm being a leader and the state-owned firm being a follower. The reason is that as the degree of cost asymmetry increases, the follower private firm’s incentive to enter the market also increases while the leader state-owned firm’s incentive to enter the market decreases, meaning that the state-owned firm as the leader and the private firm as the follower cannot be sustained as an equilibrium outcome. In the unique equilibrium, as the degree of cost asymmetry increases, the incentive for the leader private firm to enter the market also increases, while the incentive for the follower state-owned firm to enter the market decreases. It follows that the time span between successive entries is increasing along with the degree of cost asymmetry.

We find from the viewpoint of social welfare that the leader state-owned firm enters the market too late. When the two firms’ products are perfect substitutes, the follower private firm enters the market too early. However, the follower private firm enters the market too late if the state-owned firm is fully public. When the two firms’ products are perfect substitutes, the socially optimal timing of both firms entering the market can be achieved if the state-owned firm is fully public. The intuition is that the leader state-owned firm’s objective is to maximize social welfare and thus first entry is socially optimal. For the second entry, when the products are perfect substitutes, fully nationalizing the state-owned firm completely offsets the consumer surplus effect (i.e., a potential entrant takes into account its own profit from entry, but ignores the consumer surplus it generates), resulting in the follower’s timing of entry being socially optimal.

The rest of the paper runs as follows. Section 2 describes the model. Section 3 discusses the equilibrium outcomes. Section 4 conducts the welfare analysis. Section 5 concludes the paper.

2 The model

Suppose that firm 1 is a state-owned firm, which can be partially privatized, that seeks to maximize the linear combination of its profit and social welfare, and firm 2 is a private firm that aims to maximize its own profit. Time is continuous ($t\in [0,\infty ))$, and a new technology appears at the game’s beginning ($t=0)$. If a firm adopts this new technology, then it can launch a new product and enter a new market segment. At time t, if only one firm launches a new product, then it is the exclusive firm; if both firms launch new products, then the two firms’ products are horizontally differentiated. Following Singh and Vives (1984), we assume each firm’s inverse demand function at time t is $p_{i}=1-q_{i}-bq_{j}$, $i,j\in \{1,2\}$ and $i\ne j$, where $p_{i}$ and $q_{i}$ are correspondingly firm i’s price and output, and $b\in [0,1]$ represents product substitutability.

Suppose that the two firms use constant-returns-to-scale technology to produce differentiated products, so that their unit production costs are equal to $m_{1}=m\in [0,1/2]$ and $m_{2}=0$, respectively. Here, $0\le m=m_{1}-m_{2}\le 1/2$ represents the degree of cost asymmetry, implying that each firm’s profit flow is positive when both firms enter the market.⁴ The two firms’ objective functions (payoff functions) are given by:

$$\begin{aligned} {v_{1}}&={\phi \pi _{1}+(1-\phi )w,}\nonumber \\ {\pi _{2}}&= {p_{2}q_{2}=(1-q_{2}-bq_{1})q_{2},} \end{aligned}$$

(1)

where $\pi _{1}=(p_{1}-m)q_{1}$ and $\pi _{2}$ are their profits, $w=(\pi _{1}+\pi _{2})+cs$ is social welfare, and $cs=(q_{1}+q_{2})-{(q_{1}^{2} +2bq_{1}q_{2}+q_{2}^{2})}/2-p_{1}q_{1}-p_{2}q_{2}$ is consumer surplus. The degree of privatization, $\phi \in [0,1]$, denotes the weight of firm 1’s profit in its payoff function. If $\phi =0$, then firm 1 is a fully-public firm, and its goal is to maximize social welfare. As $\phi$ increases, firm 1 pays more attention to maximizing its own profit, and it is a fully-private firm seeking to pursue profit maximization for $\phi =1$.

Assuming that a firm enters the market at time t, it needs to pay the discounted entry cost, referring to the cost to obtain the new technology, $c(t)=\bar{c}\cdot e^{-t(\alpha +r)}$, where $r>0$ is the interest rate, $\alpha <r$ is the exponential decay parameter, and $\bar{c}>0$ is the entry cost at $t=0$. Following the related literature such as Fudenberg and Tirole (1985) and Argenziano and Schmidt-Dengler (2013), we assume the exponential decay parameter $\alpha >0$ in order to guarantee that the current adoption cost, $c(t)\cdot e^{rt}=\bar{c}\cdot e^{-\alpha t}$, falls over time at a decreasing rate. The drop in entry cost over time can be due to technological progress, economies of scale, or learning. We assume that $\bar{c}$ is sufficiently large, implying that no firm enters at the game’s beginning ($t=0)$.⁵

The game structure goes as follows. At the game’s beginning, each firm simultaneously decides when to enter the market, $t_{i}\in [0,\infty )$, which is a precommitment game. The precommitment game captures the idea that a firm, which would like to launch a new product and enter a new market segment, follows well-designed long-term plans. When a firm enters the market, it determines its quantity supplied $q_{i}\in [0,\infty )$ at each time $t\in [t_{i},\infty )$.

Following the related literature, we normalize the two firms’ payoffs to zero before entering the new market segment. If the two firms enter the market at $t_{i}$ and $t_{j}$, respectively, then firm i’s discounted sum of payoff is:

$$\begin{aligned} \Pi _{i}(t_{i},t_{j})=\left[ \begin{array}{l} {L_{i}(t_{i},t_{j})} \quad {\textrm{if}}\text { }{t_{i}\le t_{j}}\\ {F_{i}(t_{i},t_{j})} \quad {\textrm{if}}\text { }{t_{i}\ge t_{j}} \end{array} \right. , \end{aligned}$$

when $t_{1}\le t_{2}$:

$$\begin{aligned} {L_{1}(t_{1},t_{2})}&= {v_{1}^{l}(\phi ,m)\cdot \int _{t_{1}}^{t_{2}} e^{-rt}dt+v_{1}^{b}(\phi ,m)\cdot \int _{t_{2}}^{\infty }e^{-rt}dt-\bar{c}\cdot e^{-t_{1}(\alpha +r)},}\\ {F_{2}(t_{2},t_{1})}&= {\pi _{2}^{f}(\phi ,m)\cdot \int _{t_{1}}^{t_{2} }e^{-rt}dt+\pi _{2}^{b}(\phi ,m)\cdot \int _{t_{2}}^{\infty }e^{-rt}dt-\bar{c}\cdot e^{-t_{2}(\alpha +r)},} \end{aligned}$$

and when $t_{1}\ge t_{2}$:

$$\begin{aligned} {F_{1}(t_{1},t_{2})}&= {v_{1}^{f}(\phi ,m)\cdot \int _{t_{2}}^{t_{1}} e^{-rt}dt+v_{1}^{b}(\phi ,m)\cdot \int _{t_{1}}^{\infty }e^{-rt}dt-\bar{c}\cdot e^{-t_{1}(\alpha +r)},}\nonumber \\ {L_{2}(t_{2},t_{1})}&= {\pi _{2}^{l}(\phi ,m)\cdot \int _{t_{2}}^{t_{1} }e^{-rt}dt+\pi _{2}^{b}(\phi ,m)\cdot \int _{t_{1}}^{\infty }e^{-rt}dt-\bar{c}\cdot e^{-t_{2}(\alpha +r)}.} \end{aligned}$$

(2)

We define the first argument of firm i’s payoff function $\Pi _{i} (t_{i},t_{j})$ as its own timing of entry and the second argument as its opponent’s timing of entry. The leader’s payoff function, $L_{i}(t_{i},t_{j} )$, and the follower’s payoff function, $F_{i}(t_{i},t_{j})$, are twice continuously differentiable with respect to $t_{i}$ and $t_{j}$, and $L_{i}(t_{i},t_{j})=F_{i}(t_{i},t_{j})$ if $t_{i}=t_{j}$. If only firm i enters the market, then it obtains the leader’s payoff flow, $v_{1}^{l} (\phi ,m)$ for $i=1$, and $\pi _{2}^{l}(\phi ,m)$ for $i=2$, and firm j obtains the follower’s payoff flow, $\pi _{2}^{f}(\phi ,m)$ for $j=2$, and $v_{1} ^{f}(\phi ,m)$ for $j=1$. If both firms enter the market, then firm i obtains the payoff flow, $v_{1}^{b}(\phi ,m)$ for $i=1$, and $\pi _{2}^{b}(\phi ,m)$ for $i=2$.

3 Equilibrium analysis

We first discuss the product market competition. At time t, if only firm 1 enters the market, then its payoff flow is $v_{1}=\phi (1-q_{1}-m)q_{1} +(1-\phi )(q_{1}-{q_{1}^{2}}/2-mq_{1})$. Solving the first-order condition for firm 1’s payoff maximization, we obtain firm 1’s equilibrium quantity as $q_{1}^{l}={(1-m)/(1+\phi )}$, its payoff flow as $v_{1}^{l}(\phi ,m)={(1-m)^{2}}/[2(1+\phi )]$, and firm 2’s payoff flow as $\pi _{2}^{f} (\phi ,m)=0$. The social welfare flow when only firm 1 enters the market is $w_{1}^{1}(\phi ,m)={(1+2\phi )(1-m)^{2}}/[2(1+\phi )^{2}]$.

At time t, if only firm 2 enters the market, then its payoff flow is $\pi _{2}=(1-q_{2})q_{2}$. Firm 2’s equilibrium quantity is ${q_{2}^{l}=1}/2$. Its payoff flow is $\pi _{2}^{l}(\phi ,m)=1/4$, firm 1’s payoff flow is $v_{1}^{f}(\phi ,m)={(3-3\phi )}/8$, and the social welfare flow when only firm 2 enters the market is $w_{1}^{2}(\phi ,m)=3/8$.

At time t, if both firms enter the market, then the payoff flow of each firm is $v_{1}=\phi (1-q_{1}-bq_{2}-m)q_{1}+(1-\phi )[(q_{1}+q_{2})-{(q_{1} ^{2}+2bq_{1}q_{2}+q_{2}^{2})}/2-mq_{1}]$ and $\pi _{2}=(1-q_{2}-bq_{1})q_{2}$. Solving the two firms’ payoff maximization yields: $q_{1}^{b}={(2-b-2m)} /(2-b^{2}+2\phi )$ and $q_{2}^{b}={(1-b+\phi +bm)}/(2-b^{2}+2\phi )$. Here, $q_{1}^{b}$ is decreasing in $\phi$ and m, while $q_{2}^{b}$ is increasing in $\phi$ and m. Substituting $q_{1}^{b}$ and $q_{2}^{b}$ into the two firms’ payoffs and social welfare, we obtain $v_{1}^{b}(\phi ,m)$, $\pi _{2} ^{b}(\phi ,m)$, and $w_{2}(\phi ,m)$.

We now analyze the timing competition. If $t_{1}\le t_{2}$, then we calculate the two firms’ first-order conditions (${\partial L_{1}\left( {t_{1},t_{2} }\right) }/{\partial t_{1}}=0$ and ${\partial F_{2}(t_{2},t_{1})/\partial t_{2}}=0)$ for payoff maximization as⁶

$$\begin{aligned} {t_{1}^{l}(\phi ,m)}&= {\frac{1}{\alpha }\cdot \ln \left( \frac{\bar{c}(\alpha +r)}{v_{1}^{l}(\phi ,m)}\right) ,}\nonumber \\ {t_{2}^{f}(\phi ,m)}&= {\frac{1}{\alpha }\cdot \ln \left( \frac{\bar{c}(\alpha +r)}{\pi _{2}^{b}(\phi ,m)}\right) .} \end{aligned}$$

(3)

When no firm enters the market, firm 1’s payoff will rise from 0 to $v_{1}^{l}(\phi ,m)$ if it chooses to enter the market. We thus interpret $v_{1}^{l}(\phi ,m)$ as the incentive for the leader state-owned firm to enter the market, which is decreasing in $\phi$ and m:

$$\begin{aligned} {\frac{\partial v_{1}^{l}(\phi ,m)}{\partial \phi }}&= {-\frac{(1-m)^{2} }{2(1+\phi )^{2}}<0,}\nonumber \\ {\frac{\partial v_{1}^{l}(\phi ,m)}{\partial m}}&= {-\frac{1-m}{1+\phi }<0.} \end{aligned}$$

(4)

It follows that ${\partial t_{1}^{l}(\phi ,m)}/\partial \phi >0$ and ${\partial t_{1}^{l}(\phi ,m)}/\partial m>0$. Applying the Envelope Theorem, the increase in the degree of privatization $\phi$ directly reduces firm 1’s payoff by the consumer surplus $cs_{1}^{1}={q_{1}^{l}(\phi ,m)^{2}}/2$. Again applying the Envelope Theorem, the increase in the degree of cost asymmetry m directly raises firm 1’s production cost and reduces its payoff by $q_{1}^{l}({\phi },m)$.

When firm 1 has entered the market, firm 2’s payoff rises from $\pi _{2} ^{f}({\phi },m)=0$ to $\pi _{2}^{b}(\phi ,m)$ if it chooses to enter the market. Therefore, $\pi _{2}^{b}(\phi ,m)$ is interpreted as the incentive for the follower private firm to enter the market, which is increasing in $\phi$ and m:

$$\begin{aligned} {\frac{\partial \pi _{2}^{b}(\phi ,m)}{\partial \phi }}&= {\frac{2b(-2+b+2m)(1-b+bm+\phi )}{(-2+b^{2}-2\phi )^{3}}>0,}\nonumber \\ {\frac{\partial \pi _{2}^{b}(\phi ,m)}{\partial m}}&= {\frac{2b(1-b+bm+\phi )}{(2-b^{2}+2\phi )^{2}}>0.} \end{aligned}$$

(5)

It follows that ${\partial t_{2}^{f}(\phi ,m)}/\partial \phi <0$ and ${\partial t_{2}^{f}(\phi ,m)}/\partial m<0$. The explanation is that as the degree of privatization $\phi$ rises, the weight of firm 1’s profit in its payoff function increases, its output decreases, and firm 2’s output and payoff rise. On the other hand, as the degree of cost asymmetry m rises, firm 1’s unit production cost increases, its output decreases, and firm 2’s output and payoff rise. We summarize the results in the following Proposition 1.

Proposition 1

${\partial t_{1}^{l}(\phi ,m)}/\partial \phi >0$, ${\partial t_{1}^{l}(\phi ,m)}/\partial m>0$, ${\partial t_{2}^{f} (\phi ,m)}/\partial \phi <0$, and ${\partial t_{2}^{f}(\phi ,m)}/\partial m<0$.

If $t_{1}\ge t_{2}$, then we calculate the two firms’ first-order conditions (${\partial F_{1}(t_{1},t_{2})}/\partial {t_{1}}=0$ and ${\partial L_{2}\left( {t_{2},t_{1}}\right) }/\partial {t_{2}}=0)$ for payoff maximization as⁷

$$\begin{aligned} {t_{1}^{f}(\phi ,m)}&= {\frac{1}{\alpha }\cdot \ln \left( \frac{\bar{c}(\alpha +r)}{v_{1}^{b}(\phi ,m)-v_{1}^{f}(\phi ,m)}\right) ,}\nonumber \\ {t_{2}^{l}(\phi ,m)}&= {\frac{1}{\alpha }\cdot \ln \left( \frac{\bar{c}(\alpha +r)}{\pi _{2}^{l}(\phi ,m)}\right) .} \end{aligned}$$

(6)

When no firm enters the market, $\pi _{2}^{l}(\phi ,m)$ is explained as the incentive for the leader private firm to enter the market, which is independent of $\phi$ and m, implying ${\partial t_{2}^{l}(\phi ,m)} /\partial \phi =0$ and ${\partial t_{2}^{l}(\phi ,m)}/\partial m=0$. When firm 2 has entered the market, firm 1’s payoff will rise from $v_{1}^{f}(\phi ,m)$ to $v_{1}^{b}(\phi ,m)$ if it chooses to enter the market. We thus interpret $(v_{1}^{b}(\phi ,m)-v_{1}^{f}(\phi ,m))$ as the incentive for the follower state-owned firm to enter the market.

Appendix shows the following Proposition 2.

Proposition 2

(1) ${\partial t_{1}^{f}(\phi ,m)} /\partial \phi <0$ if and only if $b>0.348$ and $m>\hat{m}$. (2) ${\partial t_{1}^{f}(\phi ,m)}/\partial m<0$ if and only if $b>0.699$, $\phi <\bar{\phi }$, and $m>\bar{m}$. (3) ${\partial t_{2}^{l}(\phi ,m)}/\partial \phi =0$ and ${\partial t_{2}^{l}(\phi ,m)}/\partial m=0$.⁸

The intuition behind Proposition 2 (1) is that when the degree of cost asymmetry is large ($m>\hat{m})$, firm 1’s output is small, thus lowering the direct decline of $(v_{1}^{b}-v_{1}^{f})$ caused by the rise of ${\phi }$. When product substitutability is large ($b>0.348)$, the rise of firm 2’s output caused by the rise of ${\phi }$ is large, which in turn creates a large increase in $(v_{1}^{b}-v_{1}^{f})$. Consequently, ${\partial (v_{1}^{b} -v_{1}^{f})}/\partial \phi >0$ for $m>\hat{m}$ and $b>0.348$, and the follower firm 1 enters the market earlier as the degree of privatization increases. The intuition behind Proposition 2 (2) is that when the degree of cost asymmetry is large ($m>\bar{m})$, firm 1’s output is small, again lowering the direct decline of $(v_{1}^{b}-v_{1}^{f})$ caused by the rise of m. When product substitutability is large ($b>0.699)$ and the degree of privatization is small ($\phi <\bar{\phi })$, the rise of firm 2’s output caused by the rise of m is large, spurring a large increase in $(v_{1}^{b}-v_{1}^{f})$. Consequently, ${\partial (v_{1}^{b}-v_{1}^{f})}/\partial m>0$ for $m>\bar{m}$, $b>0.699,$ and $\phi <\bar{\phi }$, and the follower firm 1 enters the market earlier as the degree of cost asymmetry increases.

We define $r_{i}^{+} (t_{j} )\ge t_{j}$ ($r_{i}^{-} (t_{j} )\le t_{j}$, respectively) as firm i’s best response if it chooses to enter the market after $t_{j}$ (before $t_{j}$, respectively). The above analysis implies that for a given $t_{1} \le t_{2}^{f} (\phi ,m)$, if firm 2 chooses to enter the market after $t_{1}$, then its best response is $r_{2}^{+} (t_{1} )=t_{2}^{f} (\phi ,m)$. For a given $t_{2} \ge t_{1}^{l} (\phi ,m)$, if firm 1 chooses to enter the market before $t_{2}$, then its best response is $r_{1}^{-} (t_{2} )=t_{1}^{l} (\phi ,m)$.

We now discuss whether or not there is an incentive for firm 1 to deviate to $t_{1}>t_{2}$. Applying the Envelope Theorem, $F_{1}(r_{1}^{+}(t_{2} ),t_{2})-L_{1}(r_{1}^{-}(t_{2}),t_{2})$ is strictly decreasing in $t_{2}$. Since $F_{1}(r_{1}^{+}(t_{2}),t_{2})-L_{1}(r_{1}^{-}(t_{2}),t_{2})>0$ for $t_{2}=t_{1}^{l}(\phi ,m)$ and $F_{1}(r_{1}^{+}(t_{2}),t_{2})-L_{1}(r_{1} ^{-}(t_{2}),t_{2})<0$ for $t_{2}=t_{1}^{f}(\phi ,m)$, there is a single point $d_{1}(\phi ,m)$ solving for $F_{1}(r_{1}^{+}(t_{2}),t_{2})-L_{1}(r_{1} ^{-}(t_{2}),t_{2})=0$. By similar argument, there is a single point $d_{2}(\phi ,m)$ solving for $F_{2}(r_{2}^{+}(t_{1}),t_{1})-L_{2}(r_{2} ^{-}(t_{1}),t_{1})=0$.

Lemma 1

Firm i’s best response is:

$r_{i}(t_{j})=\left\{ \begin{array}{c} {t_{i}^{l}(\phi ,m)}\text { }{\textrm{if}}\text { }{t_{j}\ge d_{i} (\phi ,m)\mathrm {\;}}\\ {t_{i}^{f}(\phi ,m)}\text { }{\textrm{if}}\text { }{t_{j}\le d_{i} (\phi ,m)\mathrm {\;}} \end{array},\right.$ where $d_{i}(\phi ,m)\in (t_{i}^{l}(\phi ,m),t_{i}^{f}(\phi ,m))$.

When seeing an opponent’s relatively early entry ($t_{j}\le d_{i}(\phi ,m))$, firm i chooses a late entry and behaves as a follower ($t_{i}^{f}(\phi ,m))$. However, when seeing an opponent’s relatively late entry ($t_{j}\ge d_{i}(\phi ,m))$, firm i chooses an early entry and behaves as a leader ($t_{i}^{l}(\phi ,m))$. Lemma 1 means that each firm i’s best response is discontinuous, and there is a unique downward jump point, $d_{i}(\phi ,m)$.

The following Lemma is proven in the Appendix.

Lemma 2

Suppose that product substitutability b is relatively small. Then, (1) ${\partial d_{1}(\phi ,m)}/{\partial \phi }>0$, ${\partial d_{1}(\phi ,m)}/{\partial m}>0$, ${\partial d_{2}(\phi ,m)} /{\partial \phi }<0$, and ${\partial d_{2}(\phi ,m)}/{\partial m}<0$. (2) $t_{1}^{l}(1,1/2)>d_{2}(1,1/2)$ and $t_{2}^{f}(1,1/2)<d_{1}(1,1/2)$. (3) $t_{1}^{f}(0,0)<d_{2}(0,0)$ and $t_{2}^{l}(0,0)>d_{1}(0,0)$.

Lemmas 1 and 2 imply the following. Given a sufficiently small m, there is a unique $\phi _{1}(m)\in [0,1]$ satisfying $t_{1}^{f}(\phi _{1},m)=d_{2}(\phi _{1},m)$ and a unique $\phi _{2}(m)\in [0,1]$ satisfying $t_{2}^{l}(\phi _{2},m)=d_{1}(\phi _{2},m)$. When $\phi <\max \{\phi _{1} (m),\phi _{2}(m)\}$, Fig. 1a presents the two firms’ best responses.

Fig. 1

a The two firms’ best responses, given a sufficiently small m and $\phi <\max \{\phi _1(m),\phi _2(m)\}$. b The two firms’ best responses, given a sufficiently large $\phi$ and $m>\min \{m_1(\phi ),m_2(\phi )\}$

We note that the blue line represents firm 1’s best response and the black line represents firm 2’s best response. Given a sufficiently large $\phi$, there is a unique $m_{1}(\phi )\in [0,1/2]$ satisfying $t_{1}^{l} (\phi ,m_{1})=d_{2}(\phi ,m_{1})$ and a unique $m_{2}(\phi )\in [0,1/2]$ satisfying $t_{2}^{f}(\phi ,m_{2})=d_{1}(\phi ,m_{2})$. When $m>\min \{m_{1} (\phi ),m_{2}(\phi )\}$, Fig. 1b presents the two firms’ best responses. We thus obtain the following proposition.

Proposition 3

• (1) Given a sufficiently small degree of cost asymmetry m, when the degree of privatization is relatively small ($\phi <\max \{\phi _{1}(m),\phi _{2}(m)\})$, the unique equilibrium outcome is given by ($t_{1}^{l}(\phi ,m),t_{2}^{f}(\phi ,m))$.

• (2) Given a sufficiently large degree of privatization $\phi$, when the degree of cost asymmetry is relatively large ($m>\min \{m_{1}(\phi ),m_{2}(\phi )\})$, the unique equilibrium outcome is given by ($t_{1}^{f}(\phi ,m),t_{2}^{l} (\phi ,m))$.

• (3) Otherwise, $(t_{1}^{l}(\phi ,m),t_{2}^{f}(\phi ,m))$ and $(t_{1}^{f} (\phi ,m),t_{2}^{l}(\phi ,m))$ are both the equilibrium outcomes.

We note each firm’s incentive to enter the market is increasing in its incremental payoff from entry and that the state-owned firm’s incremental payoff from entry is decreasing in the degrees of cost asymmetry m and privatization $\phi$, while the private firm’s incremental payoff from entry is increasing in those parameters. Given a sufficiently small degree of cost asymmetry m, when the degree of privatization $\phi$ is small, the follower state-owned firm’s incentive to enter the market is large, meaning that the private firm as the leader and the state-owned firm as the follower $(t_{1}^{f}(\phi ,m),t_{2}^{l}(\phi ,m))$ no longer remain as the equilibrium outcome. We note a special case is that given the cost symmetry ($m=0)$, as the degree of privatization decreases from $\phi =1$, the follower state-owned firm’s incentive to enter the market increases. It follows that when the degree of privatization is relatively small ($\phi <\max \{\phi _{1}(0),\phi _{2}(0)\})$, the unique equilibrium outcome is given by ($t_{1}^{l} (\phi ,0),t_{2}^{f}(\phi ,0))$.

Under general $\phi \in [0,1]$ and $m\ge 0,$ the state-owned firm as the leader enters the market at $t_{1}^{l}(\phi ,m)$. Here, the marginal benefit from delaying entry, $-{c}^{\prime }(t_{1}^{l})$, which is the cost reduction, exactly equals the marginal cost from delaying entry, $v_{1}^{l}(\phi ,m)\cdot e^{-r\cdot t_{1}^{l}}$, which is the foregone discounted payoff flow from delaying entry. The private firm as the follower enters the market at $t_{2}^{f}(\phi ,m)$, where the marginal benefit from delaying entry, $-{c}^{\prime }(t_{2}^{f}),$ exactly equals the marginal cost from delaying entry, $\pi _{2}^{b}(\phi ,m)\cdot e^{-r\cdot t_{2}^{f}}$.

Given a sufficiently large degree of privatization $\phi$, when the degree of cost asymmetry m is large, the follower private firm’s incentive to enter the market is large, meaning that the state-owned firm as the leader and the private firm as the follower $(t_{1}^{l}(\phi ,m),t_{2}^{f}(\phi ,m))$ cannot be sustained as an equilibrium outcome. We note a special case is that given the stated-owned firm is fully private ($\phi =1)$, as the degree of cost asymmetry increases from $m=0$, the follower private firm’s incentive to enter the market increases and the leader state-owned firm’s incentive to enter the market decreases. In this case, when the degree of cost asymmetry is relatively large ($m>\min \{m_{1}(1),m_{2}(1)\})$, the unique equilibrium outcome is given by ($t_{1}^{f}(1,m),t_{2}^{l}(1,m))$.

Under general $\phi \in [0,1]$ and $m\ge 0,$ the private firm enters first at $t_{2}^{l}(\phi ,m)$, where the marginal benefit from delaying entry, $-{c}^{\prime }(t_{2}^{l})$, which is the cost reduction, equals the marginal cost from delaying entry, $\pi _{2}^{l}(\phi ,m)\cdot e^{-r\cdot t_{2}^{l}}$, which is the foregone discounted payoff flow from delaying entry. The state-owned firm enters second at $t_{1}^{f}(\phi ,m)$, where the cost reduction from delaying entry, $-{c}^{\prime }(t_{1}^{f})$, equals the foregone discounted payoff flow from delaying entry, $(v_{1}^{b}(\phi ,m)-v_{1}^{f} (\phi ,m))\cdot e^{-r\cdot t_{1}^{f}}$.

We observe in reality that NTT DoCoMo, which previously was a state-owned telecommunications company in Japan, launched mobile wireless Internet service and behaved as a leader, while private telecommunications companies subsequently entered the new market and behaved as followers. The findings in Proposition 3 (1) when the degree of privatization is relatively small may partly explain this phenomenon. On the other hand, when the degree of cost asymmetry is relatively large, the results in Proposition 3 (2) can explain the phenomenon that the private manufacturer Toyota Motor Corporation (TMC), which is relatively efficient in production with its technological advantage, and the state-owned Guangzhou Automobile sequentially unveiled their product launches in China in that order.⁹

We note $t_{2}^{f}(\phi ,m)$ is decreasing and $t_{1}^{l}(\phi ,m)$ is increasing in $\phi$. On the other hand, $t_{1}^{f}(\phi ,m)$ is increasing and $t_{2}^{l}(\phi ,m)$ is decreasing in m. We define the time span between successive entries as the timing differentiation between the two firms, $\left| {t_{2}-t_{1}}\right|$, and yield the following Proposition 4.

Proposition 4

• (1) Given a sufficiently small m, when $\phi <\max \{\phi _{1}(m),\phi _{2}(m)\}$, the time span between successive entries is decreasing in ${\phi }$ (${\partial (t_{2}^{f}(\phi ,m)-t_{1}^{l} (\phi ,m))}/{\partial \phi }<0)$.

• (2) Given a sufficiently large $\phi$, when $m>\min \{m_{1}(\phi ),m_{2} (\phi )\}$, the time span between successive entries is increasing in m (${\partial (t_{1}^{f}(\phi ,m)-t_{2}^{l}(\phi ,m))}/{\partial m}>0)$.

Given a sufficiently small m, when the degree of privatization is larger the follower firm 2 enters faster, and the leader firm 1 enters slower. Thus, the time span between successive entries is shorter as the degree of privatization is larger. This also implies the time span between successive entries in a mixed duopoly ($\phi <1)$ is longer than that in a pure duopoly ($\phi =1)$. Given a sufficiently large $\phi$, when the degree of cost asymmetry is larger the leader firm 2 enters faster, and the follower firm 1 enters slower. Thus, the time span between successive entries is longer as the degree of cost asymmetry is larger.

4 Welfare analysis

We now address social welfare and focus only on the case of cost symmetry ($m=0)$. Given the degree of privatization $\phi$, the social welfare flows when only firm 1 enters and when both firms enter the market are respectively $w_{1}^{1}(\phi ,0)$ and $w_{2}(\phi ,0)$. Since the social welfare flow when only firm 1 enters the market is larger than that when only firm 2 enters the market (i.e., $w_{1}^{1}(\phi ,0)>w_{1}^{2}(\phi ,0)$), the discounted sum of social welfare reaches its maximum only if firm 1 enters the market first. We hence analyze the second-best socially optimal levels of $t_{1}$ and $t_{2}$, conditional on the degree of privatization $\phi$:

$$\begin{aligned} \mathop {\max }\limits _{t_{1},\text { }t_{2}} W=w_{1}^{1}(\phi ,0)\cdot \int _{t_{1}}^{t_{2}}{e^{-rt}dt}+w_{2}(\phi ,0)\cdot \int _{t_{2}} ^{\infty }{e^{-rt}dt}-c(t_{1})-c(t_{2}). \end{aligned}$$

(7)

The socially optimal entry times are calculated as:

$$\begin{aligned} t_{1}^{w}&=\frac{1}{\alpha }\cdot \ln \left( {\frac{\bar{c}(\alpha +r)}{w_{1}^{1}(\phi ,0)}}\right) ,\\ t_{2}^{w}&=\frac{1}{\alpha }\cdot \ln \left( {\frac{\bar{c}(\alpha +r)}{w_{2}(\phi ,0)-w_{1}^{1}(\phi ,0)}}\right) , \end{aligned}$$

for:

$$\begin{aligned}&w_{1}^{1}(\phi ,0) =\frac{1+2\phi }{2\left( {1+}\phi \right) ^{2} },\nonumber \\&w_{2}(\phi ,0)-w_{1}^{1}(\phi ,0) =\frac{\left( {1-b+}\phi \right) \left( \begin{array}{c} {3-3b-10b\phi -7b\phi ^{2}-b^{2}-b^{2}\phi }\\ {+b^{3}+2b^{3}\phi +9\phi +9\phi ^{2}+3\phi ^{3}} \end{array} \right) }{2\left( {2-b^{2}+2}\phi \right) ^{2}\left( {1+}\phi \right) ^{2} }. \end{aligned}$$

(8)

From the welfare perspective, the socially optimal timing of entry $t_{i}^{w}$ meets the following condition: the marginal benefits from delaying entry, $-{c}^{\prime }(t_{i}^{w})$ for $i=1,2$, equal the marginal costs from delaying entry, $w_{1}^{1}(\phi ,0)\cdot e^{-rt_{1}^{w}}$ and $(w_{2}(\phi ,0)-w_{1} ^{1}(\phi ,0))\cdot e^{-rt_{2}^{w}}$.

Since $d_{1}(\phi ,0)\le t_{2}^{f}(\phi ,0)$ and $d_{2}(\phi ,0)\ge t_{1} ^{l}(\phi ,0)$, $\forall \phi \in [0,1]$, the state-owned firm as the leader and the private firm as the follower, $(t_{1}^{l}(\phi ,0),t_{2}^{f}(\phi ,0))$, are definitely the equilibrium outcome under cost symmetry and are the unique equilibrium outcome if $t_{1}^{f}(\phi ,0)<d_{2}(\phi ,0)$ or $t_{2}^{l} (\phi ,0)>d_{1}(\phi ,0)$.¹⁰ We compare the equilibrium timing of entry $(t_{1} ^{l}(\phi ,0),t_{2}^{f}(\phi ,0))$ to the socially optimal one ($t_{1}^{w},t_{2}^{w})$. Solving for $v_{1}^{l}(\phi ,0)-w_{1}^{1}(\phi ,0)$ yields:

$$\begin{aligned} v_{1}^{l}(\phi ,0)-w_{1}^{1}(\phi ,0)=-\frac{\phi }{2(1+\phi )^{2}}<0\text { for }\phi >0. \end{aligned}$$

(9)

The following Proposition is proven in the Appendix.

Proposition 5

• (1) The socially optimal timing of entry is given by $t_{1}^{w}$ and $t_{2}^{w}$.

• (2) When the two firms’ products are perfect substitutes ($b=1$), the socially optimal timing of both firms entering the market can be achieved if the state-owned firm is fully public ($\phi =0$).

The policy implication of the second part of Proposition 5 is that the socially optimal timing of both firms entering the market can be achieved if a social planner is able to fully nationalize the state-owned firm in a mixed duopoly (or fully nationalize either one firm in a pure duopoly). The intuition goes as follows. A firm entering the market cares about its own profits, but ignores its full impact on consumer surplus, denoted as the “consumer surplus effect”, as well as the full impact on its competitor’s profit, denoted as the “business stealing effect”. From the viewpoint of social welfare, the “consumer surplus effect” causes a firm to enter the market too late, while the “business stealing effect” causes a firm to enter the market too early.

The timing of first entry is socially optimal ($t_{1}^{l}(0,0)=t_{1}^{w}$) since the leader state-owned firm’s objective is to maximize social welfare and there is no consumer surplus effect. For the second entry, when the products are perfect substitutes, fully nationalizing the state-owned firm completely offsets the consumer surplus effect and the follower’s timing of entry is also optimal ($t_{2}^{f}(0,0)=t_{2}^{w}$).

Appendix shows the following Proposition 6.

Proposition 6

• (1) The leader state-owned firm enters the market too late ($t_{1}^{l}(\phi ,0)>t_{1}^{w},\forall \phi >0$) except when $\phi =0$.

• (2) When $\phi =0$, the follower private firm enters the market too late ($t_{2}^{f}(\phi ,0)>t_{2}^{w},\forall b<1$) except when $b=1$. When $b=1$, the follower private firm enters the market too early ($t_{2} ^{f}(\phi ,0)<t_{2}^{w},\forall \phi >0$) except when $\phi =0$.

• (3) For a given $\phi >0$, the follower private firm enters the market too early ($t_{2}^{f}(\phi ,0)<t_{2}^{w}$) if and only if b is relatively large.

We note the business stealing effect works if a firm entering the market reduces its competitor’s profit. For the first entry, given $\phi >0$, there is no business stealing effect and the consumer surplus effect makes the leader state-owned firm enter the market too late. Comparing the findings of the first part of Proposition 6 with those of Argenziano and Schmidt-Dengler (2013) shows in a precommitment game that first entry occurs too late, without depending on the condition of the interest rate.¹¹ The reason is that the preemption motives force the first adoption to occur earlier in a preemption game than that in a precommitment game.

When the degree of privatization is zero ($\phi =0$), the state-owned firm chooses marginal-cost pricing and this firm’s profit is zero, no matter whether it only enters the market or both firms enter the market. Therefore, there is also no business stealing effect for the second entry when the degree of privatization of the state-owned firm is zero. The consumer surplus effect thus makes the follower enter the market too late. On the other hand, when the two firms’ products are perfect substitutes ($b=1$), the business stealing effect dominates the consumer surplus effect, making the follower enter the market too early.

For a given $\phi >0$, the third part of Proposition 6 means that the business stealing effect tends to prevail over the consumer surplus effect as b increases. As a consequence, a higher b makes a too early entry by the follower private firm more likely to occur.

5 Conclusions

After the global wave of market liberalization and privatization of state-owned enterprises in the 1980s, mixed oligopolies arose in which a state-owned firm competes with private firms. It is commonly observed that there is timing competition of entering a new market segment (adopting a new technology) among firms in a mixed oligopoly.

This paper investigates a timing game in a mixed duopoly, whereby a relatively inefficient state-owned firm maximizing the linear combination of its profit and social welfare competes against a relatively efficient, profit-maximizing private firm. We investigate whether the state-owned and private firms enter the new market segment at the same time or in sequence under a mixed oligopoly. We explore the impacts of the degree of privatization and the degree of cost asymmetry on the timing of entry. We also provide welfare analysis by comparing the equilibrium timing of entry to the socially optimal one.

The results turn out for a given sufficiently small degree of cost asymmetry that the unique equilibrium outcome is the state-owned firm being a leader and the private firm being a follower when the degree of privatization is relatively small. The incentive for the leader state-owned firm to enter the market is decreasing in the degree of privatization and cost asymmetry. In contrast, the incentive for the follower private firm to enter the market is increasing in the degree of privatization and cost asymmetry.

For a given sufficiently large degree of privatization, the unique equilibrium outcome is the private firm being a leader and the state-owned firm being a follower when the degree of cost asymmetry is relatively large. Welfare analysis shows that the leader enters the market too late. When the two firms’ products are perfect substitutes, the follower enters the market too early. However, the follower enters the market too late if the state-owned firm is fully public.

Appendix

Proof of Proposition 2

Differentiating $(v_{1}^{b}(\phi ,m)-v_{1} ^{f}(\phi ,m))$ with respect to $\phi$ yields:

$$\begin{aligned} \frac{\partial (v_{1}^{b}(\phi ,m)-v_{1}^{f}(\phi ,m))}{\partial \phi } =\frac{\left( -2+b+2m\right) \left( \begin{array}{l} {-16+24b+24b\phi +4b^{2}+4b^{2}\phi m}\\ {-4b^{2}\phi -4b^{2}m-14b^{3}-2b^{3}\phi -2b^{4}}\\ {+2b^{4}m+3b^{5}-16\phi +16\phi m+16m} \end{array} \right) }{8\left( -2+b^{2}-2\phi \right) ^{3}}, \end{aligned}$$

(A1)

which is concave in m with two roots:

$$\begin{aligned} \hat{m}=\frac{16-24b-24b\phi -4b^{2}+4b^{2}\phi +14b^{3}+2b^{3}\phi +2b^{4}-3b^{5}+16\phi }{2(8-2b^{2}+2b^{2}\phi +b^{4}+8\phi )},\text { }\hat{\hat{m}}=\frac{2-b}{2}>\frac{1}{2}. \end{aligned}$$

(A2)

Since $0<\hat{m}<1/2,\forall \phi \in [0,1]$ if and only if $b>0.348$, we conclude ${\partial (v_{1}^{b}(\phi ,m)-v_{1}^{f}(\phi ,m))}/{\partial \phi }>0$ if and only if $b>0.348$ and $m>\hat{m}$, implying ${\partial t_{1}^{f}(\phi ,m)}/{\partial \phi }<0$.

Differentiating $(v_{1}^{b}(\phi ,m)-v_{1}^{f}(\phi ,m))$ with respect to m yields:

$$\begin{aligned}&{\frac{\partial (v_{1}^{b}(\phi ,m)-v_{1}^{f}(\phi ,m))}{\partial m}} = {\frac{\left( \begin{array}{c} -4+3b+2b\phi -b\phi ^{2}+b^{2}+b^{2}\phi m-b^{2}\phi \\ -b^{2}m-b^{3}+b^{3}\phi -4\phi +4m+4\phi m \end{array} \right) }{(2-b^{2}+2\phi )^{2}}>0,}\nonumber \\&\quad {\textrm{for}}\text { }{m} > {\frac{4-3b-2b\phi +b\phi ^{2}-b^{2}+b^{2} \phi +b^{3}-b^{3}\phi +4\phi }{4-b^{2}+b^{2}\phi +4\phi }\equiv \bar{m},} \end{aligned}$$

(A3)

where $\bar{m}<1/2$ if and only if:

$$\begin{aligned} b>0.699\,\textrm{and} \, \phi <\frac{-4+4b-b^{2} +2b^{3}+\sqrt{16-64b+72b^{2}-16b^{3}+b^{4}-4b^{5}+4b^{6}}}{4b}\equiv \bar{\phi }. \end{aligned}$$

(A4)

Therefore, ${\partial (v_{1}^{b}(\phi ,m)-v_{1}^{f}(\phi ,m))}/{\partial m}>0$ if and only if $b>0.699$, $\phi <\bar{\phi }$, and $m>\bar{m}$, implying ${\partial t_{1}^{f}(\phi ,m)}/{\partial m}<0$.$\square$

Proof of Lemma 2

Suppose that b is relatively small such that ${\partial (v_{1}^{b}(\phi ,m)-v_{1}^{f}}{(\phi ,m))}/{\partial \phi }<0$ and ${\partial (v_{1}^{b}(\phi ,m)-v_{1}^{f}}{(\phi ,m))}/{\partial m}<0$. Letting $f\equiv F_{1}(r_{1}^{+}(d_{1}),d_{1},{\phi },m)-L_{1}(r_{1}^{-}(d_{1} ),d_{1},{\phi },m)$, the implicit function theorem implies ${\partial d_{1}(\phi ,m)}/{\partial \phi }=-{\left( {{\partial f}}/{\partial \phi }\right) /\left( {{\partial f}}/{\partial d}_{1}\right) }>0$ and ${\partial d_{1}(\phi ,m)}/{\partial m}=-{\left( {{\partial f}}/{\partial m}\right) /\left( {{\partial f}}/{\partial d}_{1}\right) }>0$:

$$\begin{aligned} {\frac{\partial f}{\partial \phi }}&= {\frac{\partial (v_{1}^{b} (\phi ,m)-v_{1}^{f}(\phi ,m))}{\partial \phi }\frac{e^{-rt_{1}^{f}}-e^{-rd_{1}} }{r}-\frac{\partial v_{1}^{l}(\phi ,m)}{\partial \phi }\frac{e^{-rt_{1}^{l} }-e^{-rd_{1}}}{r}>0,}\nonumber \\ {\frac{\partial f}{\partial m}}&= {\frac{\partial v_{1}^{b}(\phi ,m)}{\partial m}\frac{e^{-rt_{1}^{f}}-e^{-rd_{1}}}{r}-\frac{\partial v_{1} ^{l}(\phi ,m)}{\partial m}\frac{e^{-rt_{1}^{l}}-e^{-rd_{1}}}{r}>0,}\nonumber \\ {\frac{\partial f}{\partial d_{1}}}&= {-(v_{1}^{l}(\phi ,m)-v_{1}^{b} (\phi ,m)+v_{1}^{f}(\phi ,m))e^{-rd_{1}}<0.} \end{aligned}$$

(A5)

Letting $g\equiv F_{2}(r_{2}^{+}(d_{2}),d_{2},{\phi },m)-L_{2}(r_{2}^{-} (d_{2}),d_{2},{\phi },m)$, the implicit function theorem implies ${\partial d_{2}(\phi ,m)}/{\partial \phi }=-{\left( {{\partial g}}/{\partial \phi }\right) /\left( {{\partial g}}/{\partial d}_{2}\right) }<0$ and ${\partial d_{2}(\phi ,m)}/{\partial m}=-{\left( {{\partial g}}/{\partial m}\right) /\left( {{\partial g}}/{\partial d}_{2}\right) }<0$:

$$\begin{aligned} \frac{\partial g}{\partial \phi }&=\frac{\partial \pi _{2}^{b}(\phi ,m)}{\partial \phi }\frac{e^{-rt_{2}^{f}}-e^{-rd_{2}}}{r}<0,\nonumber \\ {\frac{\partial g}{\partial m}}&= {\frac{\partial \pi _{2}^{b}(\phi ,m)}{\partial m}\frac{e^{-rt_{2}^{f}}-e^{-rd_{2}}}{r}<0,}\nonumber \\ {\frac{\partial g}{\partial d_{2}}}&= {-e^{-rd_{2}}(\pi _{2}^{l} (\phi ,m)-\pi _{2}^{b}(\phi ,m))<0.} \end{aligned}$$

(A6)

Solving for $\pi _{2}^{b}(1,1/2)-v_{1}^{l}(1,1/2)$ yields:

$$\begin{aligned} \pi _{2}^{b}(1,{1/2})-v_{1}^{l}(1,{1/2})=\frac{(12-2b-b^{2})(4-2b+b^{2} )}{16(2+b)^{2}(2-b)^{2}}>0,\forall b\in [0,1]. \end{aligned}$$

(A7)

Solving for $(v_{1}^{b}(0,0)-v_{1}^{f}(0,0))-\pi _{2}^{l}(0,0)$ yields:¹²

$$\begin{aligned} (v_{1}^{b}(0,0)-v_{1}^{f}(0,0))-\pi _{2}^{l}(0,0)=\frac{8-24b+12b^{2} +8b^{3}-5b^{4}}{8(2-b^{2})^{2}}>0,\quad \textrm{for}\,\, b<0.466. \end{aligned}$$

(A8)

$\square$

Proof of Proposition 5

Solving for $\pi _{2}^{b} (\phi ,0)-\mathrm {(}w_{2}(\phi ,0)-w_{1}^{1}(\phi ,0)\mathrm {)}$ yields:

$$\begin{aligned} \pi _{2}^{b}(\phi ,0)-(w_{2}(\phi ,0)-w_{1}^{1}(\phi ,0))=\frac{\left( {-1+b-}\phi \right) \left( \begin{array}{c} {1-b-6b\phi -5b\phi ^{2}-b^{2}-b^{2}\phi }\\ {+b^{3}+2b^{3}\phi +3\phi +3\phi ^{2}+\phi ^{3}} \end{array} \right) }{2\left( {2-b^{2}+2}\phi \right) ^{2}\left( {1+}\phi \right) ^{2} }. \end{aligned}$$

(A9)

Substituting $b=1$ and $\phi =0$ into Eq. (A9) yields $\pi _{2}^{b}(\phi ,0)-\mathrm {(}w_{2}(\phi ,0)-w_{1}^{1}(\phi ,0))=\textrm{0}.$ Since $v_{1}^{l}(\textrm{0},0)=w_{1}^{1}(\textrm{0},0)$ and $\pi _{2}^{b} (\textrm{0},0)=w_{2}(\textrm{0},0)-w_{1}^{1}(\textrm{0},0)$ for $b=1$ and $\phi =0$, we obtain the second part of Proposition 5.¹³$\square$

Proof of Proposition 6

Substituting $b=1$ into Eq. (A9) yields:

$$\begin{aligned} \pi _{2}^{b}(\phi ,0)-\mathrm {(}w_{2}(\phi ,0)-w_{1}^{1}(\phi ,0))=\frac{\phi ^{2}\left( 2+2\phi -\phi ^{2}\right) }{2\left( 1+2\phi \right) ^{2}\left( 1+\phi \right) ^{2}}>0\text { for }b=1\text { and }\phi >0. \end{aligned}$$

(A10)

When $b=1$, the follower private firm enters the market too early ($t_{2}^{f}(\phi ,0)<t_{2}^{w},\forall \phi >0$) except when $\phi =0$. Substituting $\phi =0$ into Eq. (A9) yields:

$$\begin{aligned} \pi _{2}^{b}(0,0)-(w_{2}(\textrm{0},0)-w_{1}^{1}(\textrm{0},0))=-\frac{\left( 1+b\right) \left( 1-b\right) ^{3}}{2\left( 2-b^{2}\right) ^{2}}<0 \quad \text { for }\phi =0 \,\, \text { and }b<1. \end{aligned}$$

(A11)

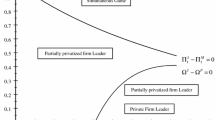
When $\phi =0$, the follower private firm enters the market too late ($t_{2}^{f}(\phi ,0)>t_{2}^{w},\forall b<1$) except when $b=1$. The frontier condition $t_{2}^{f}(b,\phi )=t_{2}^{w}(b,\phi )$ corresponds to the plotted curve in the $b-\phi$ plane in Fig. 2. $\square$

Fig. 2

The frontier condition $t_2^f(b,\phi )=t_2^w(b,\phi )$

When $\phi$ is relatively large, $\pi _{2}^{b}(b,\phi )-\mathrm {(} w_{2}(b,\phi )-w_{1}^{1}(b,\phi )\mathrm {)}$ increases with b; when $\phi$ is relatively small, $\pi _{2}^{b}(b,\phi )-\mathrm {(}w_{2}(b,\phi )-w_{1} ^{1}(b,\phi )\mathrm {)}$ first increases and then decreases with b and $\pi _{2}^{b}(b,\phi )-(w_{2}(b,\phi )-w_{1}^{1}(b,\phi ))>0$ for $b=1$. Therefore, given $\phi >0$, there is a critical threshold for b such that $t_{2}^{f}(0,\phi )<t_{2}^{w}(0,\phi )$ for any b above this threshold, corresponding to the region at the RHS of the curve in Fig. 2, and $t_{2}^{f}(0,\phi )>t_{2}^{w}(0,\phi )$ for any b below that threshold, corresponding to the region at the LHS of the curve in Fig. 2.