1 Introduction

Owing to tremendous development in technology, globalization of markets, and heightened customers’ expectations, today’s market competition has shifted from competitive independent firms to competitive SCs. E-business is another prominent factor that encourages different firms to compete as an integral part of SCs (Zhang 2006). Rice and Hoppe (2001) and Xiao and Yang (2008) highlighted that now the competition is SC versus SC instead of traditional company versus company. There are several instances of SC versus SC competition in different industries such as Microsoft-HTC and Nokia-Symbian SCs in the electronic industries (Xiao and Yang 2008), Amazon.com and barnesandonoble.com in the book market (Bernstein and Federgruen 2004), Dell’s competition against Apple in personal computer market (Rice and Hoppe 2001) etc.

Supply chain network (SCN) is a strategic level decision making problem that deals with various issues such as determination of size, number and location of facilities in a supply chain, tactical decision making such as distribution, transportation and inventory management policies, and also involves operational decisions such as fulfilment of customer demand, pricing and customer service level (Farahani et al. 2014). In today’s global competitive era, companies strive to minimize the relevant costs and maximize their opportunities in the market, and thereby they consistently focus on the improving partnerships and alliance relationships. According to Croom et al. (2000), any endeavour in managing the information and/or material flow is likely to be ineffective in absent of effective supply chain organizational relationship. Moreover, there is an increasing concern over environmental, health and safety regulations issues of workers involved in the production processes. For example, leading corporations like Apple, Liz Claiborne, Disney, Nike and Wal-Mart have faced damaging media reports, external pressure from activists, and internal pressure from investors demanding that companies acknowledge responsibility for labour rights’ abuses in factories (Cruz and Wakolbinger 2008, and references therein). Consequently, companies show their interest in tackling of social and environmental issues.

Motivated by these factors, we model a multi-objective multi-period (MOMP) integrated supply chain model that considers the effects of social relationship levels in presence of disruption risk and opportunism risk in a multi-tier SCN. The environmental issue is also incorporated in developing the proposed mathematical model of SCN. In this manner, this research primarily focuses on responding the following questions:

  1. (1)

    What are the effects of the evolving social relationships on price and demands, and finally on the objectives (profitability, risk and emission) of supply chain?

  2. (2)

    How do the upstream firms’ relationships affect the relationships of downstream firms, and how these relationships influence the objectives of the SC?

  3. (3)

    How does the supply disruption risk interact with the opportunism risk through supply chain relationships, and how these risks affect the objectives of the SC?

  4. (4)

    How do three conflicting objectives interact and trade-off with each other?

This research formulates a multi-objective problem (MOP) for supply chain network (SCN) design by incorporating the issues of social relationship, carbon emissions, and supply chain risks such as disruption and opportunism. The proposed MOP includes three conflicting objectives: maximization of total profit, minimization of supply disruption and opportunism risks, and minimization of carbon emission considering a number of supply chain constraints. Furthermore, this research analyses the effect of social relationship levels between different tiers of SCN on the profitability, risk, and emission over the time.

NSGA-II is an efficient algorithm to solve a MOP particularly when the number of objectives is more (Deb et al. 2002). It is a population based random search algorithm, in which solution quality is improved over iterations. The proposed MOMP integrated SCN has three conflicting objectives and therefore in order to obtain good near optimal solution, we employ NSGA-II to our mathematical model. Moreover, one of the main motivations to choose this approach is its successful and proven application in various other domains of multi-objective optimization (MOO). In order to find the better solution, this research chooses the algorithmic parameters of NSGA-II by using Taguchi method. It is well known that Taguchi method is based upon statistical experimental design that evaluate and implement improvement in products, process and equipment (Tiwari et al. 2010).

The rest of the paper is organized as follows: Sect. 2 provides brief literature review. Section 3 discusses the mathematical model followed by description of solution methodologies: MOEA and NSGA-II in Sect. 4. Section 5 presents computational studies. Section 6 discusses tuning of parameters of NSGA-II using Taguchi method. Results of numerical experiment and discussion are presented in Sect. 6 followed by conclusion and direction for future research in Sect. 8.

2 Literature review

This section reviews the relevant literature in specific domains of modelling of supply chain relationships, modelling of supply chain risks including opportunism and disruption and models which included carbon emission as an objective in supply chains. In addition, we also reviewed several multi-objective models used to solve these problems to make a case for the application of NSGA II.

Supply chain relationship issues in SCs have received a great research attention in the area of operations management, economics and marketing (Cruz and Liu 2011). A competitive advantage and efficiencies flexibility could be achieved by promoting the collaborative relationships amongst supply chain partners. Moreover, long-term collaborative relationship may result in creating unique value, which could only be possible when the partners make cooperative efforts rather than independent. Its an on-going process to lower acquisition and operating costs (Nyaga et al. 2010). Daugherty et al. (2006), suggested that the firms build multiple collaborative relationship to accomplish higher service level, increased flexibility, increased customers’ satisfaction, reduced cycle times and lower risks. Moreover, strong multiple relationships encourage firms to change the marketplaces and to create customer value and loyalty, finally leading to maximum profit margin (Cruz and Liu 2011). Dyer (2000) found that the collaborative behaviours of supply chain tend to be more accountable to reduce the supply chain-wide costs (costs associated with negotiating, monitoring, and enforcing contracts). According to Uzzi (1997) and Gadde and Snehota (2000), the negative effects related to dependency of supply chain partners can be mitigated through the strong multiple relationships. Krause et al. (2007) recognized that commitment and social capital accumulation among the stakeholders are important complementary conditions that establish performance goals and improve buying performance. However, most of these research focussed on establishing the benefits of having multiple relationships. Very negligible work has been done o demonstrate the effects of the evolving social relationships on price and demands. In addition, tvery limited work investigated the impact of these relationships on firms’ objectives such as profitability, risk mitigation and carbon emission in a supply chain.

Supply chain risks including disruption and its management have received a great attention in academic literature as well as in industrial applications. Supply chain disruption is an unanticipated event that spawns disturbance in normal flow of material within SCN (Craighead et al. 2007). Supply chain risk management (SCRM) has emerged due to various reasons including globalization, volatile market places, crisis and calamities etc., and substantially more susceptible than traditional integrated production planning (Hoffmann et al. 2013). An empirical study of around 800 instances of supply chain disruptions conducted by Hendricks and Singhal (2005) suggested that the companies that suffered with supply chain disruptions earned lower share prices return (33–40 % lesser) and higher share price volatility (13.5 % higher) compared to the general market benchmarks. In light of three dimensions of supply disruption risk namely magnitude, probability, and overall supply disruption risk, Ellis et al. (2010) empirically explored that both the probability and magnitude are important to overall perception of supply disruption risk. According to Cruz and Liu (2011), supply chain disruptions have worldwide impacts and therefore in order to capture the complex interactions among stakeholders, a holistic and system-wide SCN modelling and analysis is essential. Nonetheless, very limited researchers have examined SCRM considering supply chain relationship issues. An exhaustive latest review related to supply chain disruption is presented in Ellis et al. (2010).

In addition to supply disruption risk, opportunism risk is also studied in several SCN literatures (e.g., Tangpong et al. 2010; Vandenbosch and Stephen 2010). Opportunism is lack of candour/honesty in transaction and self-interest seeking with guile, which also includes falsification of expense reports, breach of distribution contracts, bait-and-switch tactics, quality shirking, and violation of promotion agreements (Cruz and Liu 2011; Handley and Benton 2012). Very little or negligible work has been done to combine social relationship, supply disruption and opportunism risks in designing SCN and therefore an identified research gaps to pursue the proposed research. In addition, environmental concerns have also been considered in this research.

Increasing awareness of the need of environmental protection and sustainability stimulate government, consumers, local communities, and stakeholders groups to exert pressure on companies to effectively incorporate sustainability issues into their supply chain management practices (Cruz 2013; Gold et al. 2010). Now a day, environmental performance at any stage of supply chain is one of the most crucial criteria to evaluate the reputation of a company. As an example of public awareness campaigns by advocacy group, many companies such as McDonalds, Mitsubishi, Monsanto, Nestle, Shell, and Texaco have suffered with damages of reputation and sales (Svendsen et al. 2001). In recent years, increasing environmental concerns enforced researchers to deal with environmental risks. The increased focus on environment highly influences the supply chain schemes. Consequently, stakeholders of an organization are forced to stretch their responsibility for their product beyond their sales and delivery locations (Bloemhof-Ruwaard et al. 1995). An exhaustive review concentrating about environmental issues is available in Cruz and Wakolbinger (2008), Cruz (2013) and Tseng and Hung (2014). However, social relationship is capable to lead the programs of collaborative waste reduction, cost-effective environmental solutions, environmental innovation at the interface, the rapid development and uptake of innovation in environmental technologies, and allows firms to better understand the environmental impact of their supply chains (Simpson and Power 2005).

Environmental issue in sustainable SC and closed-loop SC has been modelled by many researchers such as Wang and Gunasekaran (2015), De Giovanni (2014), Costa et al. (2014). Zakeri (2014) discussed the impact of carbon trading schemes and its impact on tactical supply chain planning decision. Similarly, Fahimnia et al. (2015a) discussed a tactical planning model to manage supply chains under two carbon regulatory schemes. They implemented their model using real data from an Australian furniture manufacturing company. Fahimnia et al. (2013) developed a SC model in which environmental issue is tackled by minimization of emission. Battini et al. (2014) proposed a sustainable SC focusing on \(\hbox {CO}_{2}\) emission due to transportation, in which an economic order quantity is derived for material purchasing. Zakeri et al. (2015) discussed the impact of carbon trading schemes and its impact on tactical supply chain planning decision. Rezaee et al. (2015) extended Fahimnia et al. (2015a, b) model by considering stochastic demand. Andriolo et al. (2015) proposed a bi-objective SC focusing on minimization of total cost including transportation, while second objective is to minimize the carbon emission. An exhaustive review of modelling of environmental issues in supply chain is conducted Fahimnia et al. (2015a, b).

The aforementioned discussion indicates that negligible research has been done in developing models which have simultaneously dealt with social relationship, supply disruption and opportunism risks, and emissions. Furthermore, most of the previous models have focussed on single-objective optimization process. However, real-life supply chain environment is very sophisticated and complex in nature, and involves optimization of several incommensurable objectives simultaneously. Therefore, there is need to consider the multi-objective nature of SCN problems. Researchers have shown a great interest in recent years to use multi-objective optimization techniques in supply chain modelling problems such as Liao et al. (2011), Soysal et al. (2014), Zhang et al. (2013), Govindan et al. (2014), Liang et al. (2013) and Devika et al. (2014) in various domains of supply chain. However, none of this research simultaneously considered social-relationship, risk, and emission in supply chain.

In recent years, researchers have shown their interest to use MOO techniques in SC modelling problems. The classical method of solving a MOP is to use weighted sum method that combines all the objective functions into one-objective function and treat it as a single objective with multiple constraints. Value fraction, \(\varepsilon \)-constraint, and weighted-matrix are some other classical methods to solve the MOPs. All these algorithms convert the MOP into single-objective problem (SOP). Other way to solve the MOP is to develop a Pareto-front for given objectives, and then select the Pareto-front using several methods. Liao et al. (2011) formulate an MOP for vendor managed inventory (VMI) setup, which integrates the effects of distribution, facility location, and inventory issues, then used a multi-objective evolutionary algorithm based on the non-dominated sorting genetic algorithm-II (NSGA-II) (see Deb et al. 2002) to solve the MOP. Similarly, Govindan et al. (2014) formulated a mathematical model of an MOP to solve environmental issues of food supply chain for perishable product. Furthermore, they employed multi-objective evolutionary algorithm NSGA-II to solve the problem.

Motivated by identified research gaps in literature and the complexity of real-life supply chain environment, we formulate a MOP for multi-tier, multi-period supply chain that simultaneously includes social relationship, supply disruption and opportunism risks, and emission. In this research, we present a model [an extension of Cruz and Liu (2011)] to integrate the concepts of social relationship, supply chain disruption and opportunism risks, and emissions. To obtain good near optimal solution, we employ famous and efficient multi-objective based meta-heuristic NSGA-II. One of the main motivations to choose this approach is its successful applicability in various other domains of multi-objective optimization. In addition, it is well known that Taguchi method is based upon statistical experimental design that evaluate and implement improvement in products, process and equipment (Tiwari et al. 2010). This research integrates Taguchi method to tune the algorithmic parameters of NSGA II to improve the quality of solutions obtained by NSGA-II.

3 The MOMP integrated SCN model

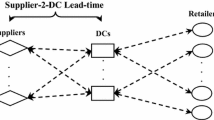
This section develops the proposed MOMP integrated SCN model by incorporating the emission and disruption risk. This model is based on the assumption that a centralized decision maker makes all decisions of the SCN including the size of shipments between the stakeholders, levels of social relationship, production quantities and inventories in each period. At this stage, our first objective is to maximize the profit of entire supply chain consisting of the profits of I suppliers, J manufacturers, and K retailers. The second objective is to minimize the risks including supply disruption and opportunism, while, third objective is to minimize the emission of entire supply chain. Furthermore, we assume that the planning horizon is finite and is discretized into T periods, as shown in Fig. 1. As we endeavour to extend the model proposed by Cruz and Liu (2011), the indices and decision variables used throughout the paper are adopted from Cruz and Liu (2011), and are described in Tables 1 and 2.

Fig. 1
figure 1

Time evolution of the SCN model (adopted from Cruz and Liu 2011)

Full size image

The SCN under consideration comprises of three tiers. The top tiers (i.e. suppliers) provides parts/raw-materials to the manufacturers, who convert them to finished goods, which are then sold to the retailers i.e. the bottom tier of the SCN. The retailers sell these products to the consumers. In our model, we have assumed that there are no constraints on the interaction between the tiers i.e. each manufacturer can procure materials from any of the suppliers, and each of the retailers can acquire products from any of the manufacturers. This would result in two variables (1) transaction quantity (q) and (2) social relationship level (\(\upeta \)) associated with any pair of supplier and manufacturer, manufacturer and retailer. We have also considered a fixed planning horizon with discretised time periods. The evolution of the SCN over the planning horizon is shown in Fig. 1.

The model consists of I number of suppliers, J number of manufacturers, K number of retailers, and a fixed planning horizon T which is discretized into periods: 1,...,t,...,T. A typical supplier in the top tier is denoted by i, a typical manufacturer in the middle tier is denoted by j, and a typical retailer in the bottom tier is denoted by k. As shown in Fig. 1, the nodes (i, t) denotes supplier i in time period t, node (j, t) represents the manufacturer j in time period t, and the node (k, t) denotes the retailer k in time period t. In summary, the suppliers (1,...,i,...,I), manufacturers (1,...,j,...,J), and retailers (1,...,k,... K) remain the same throughout the planning horizon, but the transaction quantities, and social relationship levels varies with time period. Therefore, the SCN at a time period t represents the level of transaction quantity and social relationship between the entities of the SC. The indices and decision variables used throughout the paper are adopted from Cruz and Liu (2011), and are described in Tables 1 and 2.

Table 1 Indices used throughout the paper
Full size table
Table 2 Description of decision variables
Full size table
Table 3 Description of cost functions
Full size table

The cost incurred on suppliers, manufacturers, and retailers are described in terms of transaction and social relationship level in Table 3. The production cost for each supplier or manufacturer at each time period t is a function of product out-turns. The transaction cost between stakeholders depends upon product quantity transacted between them. Suppliers, manufacturers and retailers may keep inventory to avoid supply disruption and to quickly deliver product. Thus, inventory cost depends upon quantities of product held for the periods. Furthermore, to mitigate risks associated with SCN, certain level of relationships to be achieved between the supplier and the manufacturer, the manufacturer and the retailer, and vice-versa. To achieve this objective, each stakeholder may spend money in the form of time, service, information sharing, assets or additional personnel. The relationship cost functions reflect the expenditure in order to maintain and/or improve the relationship level. However, relationship establishment and maintenance cost functions for each combination such as supplier–manufacturer or manufacturer–retailer may be distinct. The buyer–seller interaction and communication magnitude changes the relationship strength (Crosby and Stephens 1987), and vice-versa. The functional form of social relationship cost may be influenced by many factors such as the willingness of decision-maker to establish/maintain a level of social relationship and improvement in level of relationship (Cruz and Liu 2011). The level of relationship is a real number that lies between zero and one where zero indicates no social relationship and one indicates the strongest possible level of social relationship. The levels of social relationship and the material flows are endogenous and are determined by the decision maker.

Table 4 presents the description of the risk functions, which are often inherent in the supply chain. The risk functions considered in this model are functions of the transaction quantity and the relationship level. Juttner et al. (2003) highlighted that there are mainly three sources of supply chain-relevant risk: (1) environmental, e.g., fire, flood, or social-political actions, (2) organizational, e.g., supply disruption, production uncertainties or exchange rate risk, and (3) network-related risk. Furthermore, Johnson (2001) and Norrman and Jansson (2004) discussed that lack of cooperation and interaction between the stakeholders within the SC engender network-related risk. This model assumes that each stakeholder faces environmental and/or organizational engendered supply disruption risks, and opportunism risk engendered by insufficient cooperation and commitment between the partners of the SCN. In this research, our presented model considers organizational risk, environmental risk and network related risk of supply chain by defining risk as a function of transaction volume and level of social relationship.

Table 5 presents a description of the emission functions. The growing environmental concerns motivate to incorporate the environmental issues specifically carbon emission while modelling a SC problem (Qiu et al. 2001). The amount of emissions generated depends upon the volume of product produced and transacted as well as level of social relationship in current and previous periods (Cruz and Wakolbinger 2008). In this model, we assume that the decision maker seeks to minimize the total emissions generated by suppliers, manufacturers and retailers in the process of production as well as in the process of product delivery to the next tier of supply chain.

Table 4 Description of risk functions
Full size table
Table 5 Description of emission functions
Full size table

The inverse demand function associated with the retail market is presented in Table 6.

Table 6 Inverse demand function
Full size table

3.1 Profit maximization

The first objective of this MOP is to maximize the total profit of entire supply chain over the planning horizon T. Most of the decision variables considered in this model are adopted from Cruz and Liu (2011), and are described in Table 2. The associated cost functions are described in Table 3. The profit of entire supply chain is the sum of the profits earned by the suppliers, manufacturers, and retailers over the periods T. Hence, the profit maximization problem of entire supply chain can be expressed as follows:

$$\begin{aligned}&\max \mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{i=1}^I \left[ {\mathop {\sum }\limits _{j=1}^J \left[ {\rho _{1jt}^i q_{jt}^i -c_{jt}^i \left( q_{jt}^i\right) -b_{jt}^i \left( {\eta _{jt}^i} \right) -b_{jt}^{i+} \left( {\eta _{jt}^{i+}} \right) } \right] -f_{it} (y_{it})-h_{it} (\upsilon _{it})} \right] \nonumber \\&\quad +\mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{j=1}^J \left[ {\begin{array}{l} \mathop {\sum }\limits _{k=1}^K \left[ {\rho _{2kt}^j q_{kt}^j -c_{kt}^j \left( {q_{kt}^j} \right) -b_{kt}^j \left( {\eta _{kt}^j} \right) -b_{kt}^{j+} \left( {\eta _{kt}^{j+}} \right) } \right] -f_{jt} \left( {y_{jt}} \right) -h_{jt} \left( {\upsilon _{jt} } \right) \\ -\mathop {\sum }\limits _{i=1}^I \left[ {c_{it}^j \left( {q_{jt}^i} \right) +b_{it}^j \left( {\eta _{jt}^i} \right) +b_{it}^{j+} \left( {\eta _{jt}^{i+}} \right) +\rho _{1jt}^i q_{jt}^i} \right] \\ \end{array}} \right] \nonumber \\&\quad +\mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{k=1}^K \left[ {\rho _{3kt} q_{kt} -f_{kt} (q_{kt})-h_{kt} \left( {\upsilon _{kt}} \right) -\mathop {\sum }\limits _{j=1}^J [c_{jt}^k \left( q_{kt}^j\right) +b_{jt}^k \left( \eta _{jt}^k\right) +b_{jt}^{k+} \left( \eta _{jt}^{k+}\right) ]-\mathop {\sum }\limits _{j=1}^J \rho _{2kt}^j q_{kt}^j} \right] \nonumber \\ \end{aligned}$$
(1)

Equation (1) represents the cost function of entire SCN. The first summation represents cost functions of all suppliers, in which first term represents revenue and the next five terms represent transaction costs, costs of social relationship with manufacturers, costs of social relationship improvement, production costs and inventory costs respectively. The second summation of Eq. (1) represents cost function for all manufacturers, in which first term represents revenue and subsequent five terms represent transaction costs with retailers, costs of social relationship with retailers, costs of social relationship improvement with retailers, production costs and inventory costs respectively. Remaining four terms of the second summation represent transaction costs with suppliers, social relationship costs with suppliers, costs of social relationship improvement with suppliers and purchasing costs respectively. The last summation represents cost function for retailers, in which first term represents revenue, second term represents production cost, third term represents inventory cost, fourth term represents transaction costs with manufacturer, fifth term represents costs of social relationship with manufacturer, sixth term represents cost of social relationship improvement with manufacturer, and the last one represents purchasing costs. Equation (1) can be simplified and re-written in the following form:

$$\begin{aligned}&\max \mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{k=1}^K \left[ {\rho _{3kt} q_{kt} -f_{kt} \left( {q_{kt}} \right) -h_{kt} \left( {\upsilon _{kt}} \right) \!-\!\mathop {\sum }\limits _{j=1}^J \left[ {c_{jt}^k \left( {q_{kt}^j} \right) \!+\!b_{jt}^k \left( {\eta _{jt}^k} \right) +b_{jt}^{k+} \left( {\eta _{jt}^{k+}} \right) } \right] } \right] \nonumber \\&\quad -\mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{i=1}^I \left[ {\mathop {\sum }\limits _{j=1}^J \left[ {c_{jt}^i \left( {q_{jt}^i} \right) +b_{jt}^i \left( {\eta _{jt}^i} \right) +b_{jt}^{i+} \left( {\eta _{jt}^{i+}} \right) } \right] +f_{it} \left( {y_{it}} \right) +h_{it} (\upsilon _{it})} \right] \nonumber \\&\quad -\mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{j=1}^J \left[ {\begin{array}{l} \mathop {\sum }\limits _{k=1}^K \left[ {c_{kt}^j \left( {q_{kt}^j} \right) +b_{kt}^j \left( {\eta _{kt}^j} \right) +b_{kt}^{j+} \left( {\eta _{kt}^{j+}} \right) } \right] +f_{jt} \left( {y_{jt}} \right) +h_{jt} \left( {\upsilon _{jt}} \right) \\ +\mathop {\sum }\limits _{i=1}^I \left[ {c_{it}^j \left( {q_{jt}^i} \right) +b_{it}^j \left( {\eta _{jt}^i} \right) +b_{it}^{j+} \left( {\eta _{jt}^{i+}} \right) } \right] \\ \end{array}} \right] \end{aligned}$$
(2)

3.2 Risk minimization

The second objective of the proposed MOP is the minimization of risks. In this model, individual firms intend to minimize both supply disruption and opportunism risks while dealing with the adjacent echelon/echelons. The parameters related to the risks are described in Table 4. The risk minimization of the entire SC is mathematically expressed as:

$$\begin{aligned}&\min \mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{i=1}^I \mathop {\sum }\limits _{j=1}^J \left[ {\omega _j^{1i} r_{jt}^{1i} \left( {q_{jt}^i} \right) +\omega _j^{2i} r_{jt}^{2i} \left( q_{jt}^i ,\eta _{jt}^i\right) } \right] \nonumber \\&\quad +\mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{j=1}^J \left[ \mathop {\sum }\limits _{i=1}^I \left[ {\omega _i^{1j} r_{it}^{1j} \left( {q_{jt}^i} \right) +\omega _i^{2j} r_{it}^{2j} \left( q_{jt}^i ,\eta _{jt}^i\right) } \right] \right. \nonumber \\&\qquad \left. +\mathop {\sum }\limits _{k=1}^K \left[ {\omega _k^{1j} r_{kt}^{1j} \left( q_{kt}^j\right) +\omega _k^{2j} r_{kt}^{2j} \left( {q_{kt}^j ,\eta _{kt}^j} \right) } \right] \right] \nonumber \\&\quad +\mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{k=1}^K \mathop {\sum }\limits _{j=1}^J \left[ {\omega _j^{1k} r_{jt}^{1k} \left( q_{kt}^j\right) +\omega _j^{2k} r_{jt}^{2k} \left( {q_{kt}^j ,\eta _{kt}^j} \right) } \right] \end{aligned}$$
(3)

In Eq. 3, \(\omega _j^{1i}, \omega _i^{1j}, \omega _k^{1j} \) and \(\omega _j^{1k} \) are non-negative weights assigned for supply disruption risk, and \(\omega _j^{2i}, \omega _i^{2j}, \omega _k^{2j}\) and \(\omega _j^{2k} \) are non-negative weights assigned for opportunism risk. The non-negative weights quantify importance of risks, in addition it also transform these values into monetary units. In general, supply disruption and opportunism risks are uncertain in nature. As Cruz and Liu (2011) suggested, statistical uncertainty is included in these two types of risk. In particular, \(r_{jt}^{1i} \left( {q_{jt}^i}\right) , r_{it}^{1j} \left( {q_{jt}^i}\right) , r_{kt}^{1j} \left( {q_{kt}^j}\right) \) and \(r_{jt}^{1k} \left( {q_{kt}^j}\right) \) are defined as expected material quantities subject to the supply disruption risk, and \(r_{jt}^{2i} \left( {q_{jt}^i , \eta _{jt}^i}\right) , r_{it}^{2j} \left( {q_{jt}^i , \eta _{jt}^i}\right) , r_{kt}^{2j} \left( {q_{kt}^j , \eta _{jt}^j}\right) \) and \(r_{jt}^{2k} \left( {q_{kt}^j , \eta _{kt}^j}\right) \) are expected material quantities subject to opportunism risk, and these are defined as follows in Eqs. (4)–(11).

$$\begin{aligned} r_{jt}^{1i} \left( {q_{jt}^i}\right)= & {} \mathop {\int }\limits _0^{q_{jt}^i} \left( {q_{jt}^i -u}\right) p_j^i (u)du \end{aligned}$$
(4)
$$\begin{aligned} r_{it}^{1j} \left( {q_{jt}^i}\right)= & {} \mathop {\int }\limits _0^{q_{jt}^i} \left( {q_{jt}^i -u}\right) p_i^j (u)du \end{aligned}$$
(5)
$$\begin{aligned} r_{kt}^{1j} \left( q_{kt}^j\right)= & {} \int _0^{q_{kt}^j} {\left( q_{kt}^j -u\right) p_k^j (u)du} \end{aligned}$$
(6)
$$\begin{aligned} r_{jt}^{1k} \left( q_{kt}^j\right)= & {} \mathop {\int }\limits _0^{q_{kt}^j} \left( {q_{kt}^j -u}\right) p_j^k (u)du \end{aligned}$$
(7)
$$\begin{aligned} r_{jt}^{2i} \left( {q_{jt}^i, \eta _{jt}^i}\right)= & {} \phi _{jt}^i \left( {1-\eta _{jt}^i}\right) q_{jt}^i \end{aligned}$$
(8)
$$\begin{aligned} r_{it}^{2j} \left( {q_{jt}^i, \eta _{jt}^i}\right)= & {} \phi _{it}^j \left( {1-\eta _{jt}^i}\right) q_{jt}^i \end{aligned}$$
(9)
$$\begin{aligned} r_{kt}^{2j} \left( {q_{kt}^j, \eta _{kt}^j}\right)= & {} \phi _{kt}^j \left( {1-\eta _{kt}^j}\right) q_{kt}^j \end{aligned}$$
(10)
$$\begin{aligned} r_{jt}^{2k} \left( {q_{kt}^j, \eta _{kt}^j}\right)= & {} \phi _{jt}^k \left( {1-\eta _{kt}^j}\right) q_{kt}^j \end{aligned}$$
(11)

where \(p_j^i (u)\) is probability distribution function indicating that supplier i is able to deliver u units of the material/parts to manufacturer j without any disruption and delay. \(\phi _{jt}^i \) is the probability that manufacturer j conduct opportunism behaviours such as cancellation of order, failure or delay of payments, etc., in the transactions with supplier i, when relationship level between the two parties is 0. \(p_i^j (u), p_k^j (u)\) and \(p_j^k (u)\), and \(\phi _{it}^j, \phi _{kt}^j \) and \(\phi _{jt}^k \) can be defined in the similar way.

3.3 Emission minimization

The third objective of the MOMP supply chain is the minimization of the total emissions engendered during production and transactions among SC partners, over the planning horizon T. Hence, total emissions of entire SC can be expressed mathematically as:

$$\begin{aligned}&\min \mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{i=1}^I \mathop {\sum }\limits _{j=1}^J \omega _j^{3i} e_{jt}^i \left( q_{jt}^i, \eta _{jt}^i\right) \nonumber \\&\quad +\mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{j=1}^J \left[ {\mathop {\sum }\limits _{i=1}^I \omega _i^{3j} e_{it}^j \left( q_{jt}^i ,\eta _{jt}^i\right) +\mathop {\sum }\limits _{k=1}^K \omega _k^{3j} e_{kt}^j \left( {q_{kt}^j ,\eta _{kt}^j} \right) } \right] \nonumber \\&\quad +\mathop {\sum }\limits _{t=1}^T \mathop {\sum }\limits _{k=1}^K \mathop {\sum }\limits _{j=1}^J \omega _j^{3k} e_{jt}^k \left( {q_{kt}^j, \eta _{kt}^j}\right) \end{aligned}$$
(12)

In emission minimization as mentioned in Eq. (12), \(\omega _j^{3i} \) is a non-negative weight assigned by supplier i to total emission engendered by production process and transaction with manufacturer j. \(\omega _i^{3j} \) and \(\omega _k^{3j} \) are non-negative weights assigned by manufacturer to total emission engendered by production activities and transaction with supplier i and retailer k, respectively. Non-negative weight \(\omega _j^{3k}\) is assigned by retailer k to total emission generated by production process and transaction with manufacturer j. The non-negative weights quantify the importance of emissions, and, in addition transform these values into monetary units. In particular, \(e_{jt}^i ,e_{it}^j ,e_{kt}^j \) and \(e_{jt}^k \) are defined as follows in Eqs. (13)–(16).

$$\begin{aligned} e_{jt}^i \left( {q_{jt}^i, \eta _{jt}^i}\right)= & {} \left( {1-a_j^i \mathop {\sum }\limits _{s=1}^t \eta _{js}^i}\right) q_{jt}^i \end{aligned}$$
(13)
$$\begin{aligned} e_{it}^j \left( {q_{jt}^i, \eta _{jt}^i}\right)= & {} \left( {1-a_i^j \mathop {\sum }\limits _{s=1}^t \eta _{js}^i} \right) q_{jt}^i \end{aligned}$$
(14)
$$\begin{aligned} e_{kt}^j \left( {q_{kt}^j, \eta _{kt}^j}\right)= & {} \left( {1-a_k^j \mathop {\sum }\limits _{s=1}^t \eta _{ks}^j} \right) q_{kt}^j \end{aligned}$$
(15)
$$\begin{aligned} e_{jt}^k \left( {q_{kt}^j, \eta _{kt}^j}\right)= & {} \left( {1-a_j^k \mathop {\sum }\limits _{s=1}^t \eta _{ks}^j} \right) q_{kt}^j \end{aligned}$$
(16)

where \(a_j^i ,a_i^j ,a_k^j \) and \(a_j^k \) are positive real numbers. Most of these functions are adopted from Cruz and Liu (2011).

3.4 Constraints

The constraints imposed on the suppliers, manufacturers, and retailers are discussed as follows in Eqs. (17)–(31).

$$\begin{aligned}&y_{it} \le CAP_{it} ,\forall t \end{aligned}$$
(17)
$$\begin{aligned}&y_{i1} \ge \mathop {\sum }\limits _{j=1}^J q_{j1}^i +\upsilon _{i1} \end{aligned}$$
(18)
$$\begin{aligned}&y_{it} +\upsilon _{it-1} \ge \mathop {\sum }\limits _{j=1}^J q_{j1}^i +\upsilon _{it} ,t=2,\ldots ,T \end{aligned}$$
(19)
$$\begin{aligned}&y_{jt} \le CAP_{jt} ,\forall t \end{aligned}$$
(20)
$$\begin{aligned}&y_{jt} \le \mathop {\sum }\limits _{i=1}^I q_{jt}^i ,\forall t \end{aligned}$$
(21)
$$\begin{aligned}&y_{j1} \ge \mathop {\sum }\limits _{k=1}^K q_{k1}^j +\upsilon _{j1} \end{aligned}$$
(22)
$$\begin{aligned}&y_{jt} +\upsilon _{jt-1} \ge \mathop {\sum }\limits _{k=1}^K q_{kj}^j +\upsilon _{jt} ,t=2,\ldots ,T \end{aligned}$$
(23)
$$\begin{aligned}&\mathop {\sum }\limits _{j=1}^J q_{k1}^j \ge q_{k1} +\upsilon _{k1} \end{aligned}$$
(24)
$$\begin{aligned}&\mathop {\sum }\limits _{j=1}^J q_{kt}^j +\upsilon _{kt-1} \ge q_{kt} +\upsilon _{kt} ,t=2,\ldots ,T \end{aligned}$$
(25)
$$\begin{aligned}&\eta _{j1}^i =\dot{\eta }_j^i \end{aligned}$$
(26)
$$\begin{aligned}&\eta _{jt}^i +\eta _{jt}^{i+} -\eta _{jt}^{i-} =\eta _{jt+1}^i, t=1,2,\ldots ,T-1 \end{aligned}$$
(27)
$$\begin{aligned}&\eta _{k1}^j =\dot{\eta }_k^j \end{aligned}$$
(28)
$$\begin{aligned}&\eta _{kt}^j +\eta _{kt}^{j+} -\eta _{kt}^{j-} =\eta _{kt+1}^j, t=1,2,\ldots ,T-1 \end{aligned}$$
(29)
$$\begin{aligned}&\mathop {\sum }\limits _{k=1}^K q_{kt} =d_t ,\forall t \end{aligned}$$
(30)
$$\begin{aligned}&q_{jt}^i \ge 0,q_{kt}^j \ge 0,q_{kt} \ge 0,0\le \eta _{jt}^i \le 1,0\le \eta _{jt}^{i+} \le 1,0\le \eta _{jt}^{i-} \le 1,0\le \eta _{kt}^j \le 1,0\nonumber \\&\quad \le \eta _{kt}^{j+} \le 1,0\le \eta _{kt}^{j-} \le 1, \nonumber \\&0\le \eta _{jt}^k \le 1,0\le \eta _{jt}^{k+} \le 1,0\le \eta _{jt}^{k-} \le 1,y_{it} \ge 0,y_{jt} \ge 0,\upsilon _{it} \ge 0,\upsilon _{jt} \nonumber \\&\quad \ge 0,\upsilon _{kt} \ge 0,\rho _{3kt} \ge 0,\forall i,j,k,t \end{aligned}$$
(31)

Constraint (17) restricts the produced quantity of material/part by supplier i in each time period t less than or equal to production capacity. Constraints (18) and (19) provide a balanced relationship among production, inventory and material for manufacturers in each time period t. Constraint (20) restricts the produced quantity of material/part by manufacturer j in each time period t be always less than or equal to production capacity. Constraint (21) ensures the material requirement for production by manufacturers. Constraints (22) and (23) provide the balance relationship among production, inventory and material flow for retailers in each time period t. Constraints (24) and (25) provide the balanced relationship between inventory and material flow for customers. Constraints (26) and (27) identify the relationship levels between suppliers and manufacturers, and constraints (28) and (29) identify the relationship levels between manufacturers and retailers where \(\dot{\eta }_j^i \) and \(\dot{\eta }_k^j \) denote initial relationship levels. Constraints in Eq. (31) are non-negativity constraints related to transaction quantities, social relationship levels, production quantities and inventories.

The following section discusses the method used for solving the multi-objective mathematical model developed in this section.

4 Solution methodology

4.1 Multi-objective optimization approach

A MOO technique deals with simultaneous optimization of several conflicting objective functions. One of the major difficulties is to find the best or the global solution with respect to all the objectives. The classical MOO techniques focussed on combining the multiple objective functions into a single composite objective, and then optimize it by using traditional mathematical methods. In this process, a precedence or utility function needs to be identified according to the preference of a decision-maker. The other method, which is frequently used, is Pareto optimal. This method is based on the non-dominance solution concept, and prohibits converting the multi-objective functions into a single objective function (Govindan et al. 2014). In Pareto optimal solutions, the improvement of each objective component of any solution along with the Pareto front is based on the degradation of at least one of its other objective component. In the non-dominated set, no solution is absolutely better than any other, thus any one of them is an acceptable solution. As it is difficult to choose a particular solution as a unique global optimal solution without iterative interaction with the decision maker, the general approach is to choose entire set of the Pareto optimal solutions. There are many algorithms that can be used to generate the non-dominant Pareto optimal solutions such as ant-Q algorithm, tabu search, Simulated Annealing (SA), fuzzy logic, neural networks, genetic algorithm and other evolutionary strategies etc. (Luh et al. 2003). A detailed description of these meta-heuristics is discussed in Osman (1993), Shukla et al. (2009), Shukla et al. (2013a, b). A population search based multi-objective evolutionary algorithm (MOEA) can present a set of Pareto optimal solution of a MOP. MOEA randomly generates an initial set of solutions called a population and thereafter performs a set of genetic operations namely selection, crossover and mutation, to generate a new set of solutions for next iteration called a generation (for detail see Deb 2001). After a certain number of iterations, the final set of solutions is obtained based on defined criteria. The following presents some definitions that are useful for further discussion.

A solution x of multi-objective minimization problem, \(f(x)=[f_1 (x),f_2 (x),\ldots ,f_m (x)]\) subject to constraints \(g_j (x)\le 0(j=1,\ldots ,k)\), dominates a solution \(y (x\prec y)\) if \(\forall i,f_i (x)\le f_i (y)\) and there exists at least one l such that \(f_l (x)<f_l (y)\). If x does not dominate y and vice-versa, the two are called to be non-dominated solutions. A set of non-dominated solutions is called a non-dominated front.

The non-dominated front obtained for a given population can be ranked on domination criterion. Each front is represented by a unique number k, and is denoted by \(F_k \), where \(k(k\ge 1)\) is the front number. The smaller value of k represents a higher rank and is a better solution. For example, \(F_1 \) ranks higher than \(F_2 \), and \(F_2 \) ranks higher than \(F_3 \). The non-dominated fronts have the properties: (1) every solution in \(F_{k+1} \) must be dominated by at least solution of \(F_k \) and (2) a solution in \(F_k \) may or may not dominate solutions in \(F_{k+1} \). Hence, high-ranked solutions front have higher fitness value (preference), and are preferred for selection in comparison to low-ranked fronts.

4.2 Non-dominated sorting genetic algorithm-II (NSGA-II)

The concept of non-dominated sorting genetic algorithm (NSGA) is introduced by Goldberg (1989), and is first time implemented by Srinivas and Deb (1995) in the context of MOO problem. The working of selection operator in NSGA is the only criterion that differentiates it from the well-established genetic algorithm (GA). Although, NSGA has been widely used to solve a variety of MOPs, yet it has some drawbacks such as: (1) high computational complexity of non-dominated sorting, (2) lack of elitism and (3) the need for specifying the tuning parameters. Deb et al. (2002) developed a robust algorithm called non-dominated sorting genetic algorithm-II (NSGA-II) to overcome these drawbacks associated with NSGA.

NSGA-II maintains a population of random individuals, which are improved over iterations. The improvement over iterations is represented in terms of the fitness value of the individual with respect to all the objectives of the problem. Each individual in a population is called as a chromosome and it represents an individual solution of the problem. Chromosomes may be coded as binary or real value strings. The population is updated over iterations through a process of genetic operations of selection, cross-over and mutation. In crossover operation, two individuals or chromosomes exchange digits to form two new individuals or new chromosomes. In mutation, an individual is modified through string modification operations. In NSGA-II, we first create an offspring population \(Q_t \) (of size N) from the parent population \(P_t \). Offspring population thus obtained is combined with parent population to form an intermediate population of size 2N. The new population is obtained after updating the existing population. In each iteration, the fitness of the individual is evaluated in terms of all the objectives. After evaluation of individuals in each generation, multiple individuals are selected through different selection mechanism. The detailed steps involved in NSGA-II are schematically presented in Fig. 2.

Fig. 2
figure 2

Flow-chart of NSGA-II algorithm

Full size image
Fig. 3
figure 3

Chromosome representation

Full size image

4.3 Implementation of NSGA-II

The detailed implementation of the algorithm to solve the current multi-objective model is discussed as follows.

4.3.1 Chromosome representation

Each bit of the chromosome represents a decision variable described in Table 2. The model consists of I suppliers, J retailers, K retailers, and T time periods. For a particular time period, there would be a total of \(I\times J\) transaction quantity variables between the suppliers and the manufacturers, \(J\times K\) transaction quantity variables between the manufacturers and the retailers, and K transaction variables representing the quantity sold by the retailers. These transaction quantity variables are represented by the first \(I\times J+J\times K+K\) bits of the chromosome. The next \(I+J\) bits of the chromosome represent the production quantity variables of I suppliers and J manufacturers. Similarly the next \(I+J+K\) bits of the chromosome represents the inventory variables of I suppliers, J manufacturers, and K retailers. There would be a total of \(I\times J\) social relationship level variables between the suppliers and manufacturers, and \(J\times K\) social relationship level variables between the manufacturers and retailers. These transaction quantity variables are represented by the next \(I\times J+J\times K\) bits of the chromosome. The next \(I\times J+J\times K\) bits of the chromosome represent the increment in the value of the social relationship level at a particular time period. Similarly the last \(I\times J+J\times K\) bits of the chromosome represent the increment in the value of the social relationship level at a particular time period.

Hence, a total of

\((I\times J+J\times K+K+I+J+I+J+K+I\times J+J\times K+I\times J +J\times K+I\times J+J\times K)\) bits are used to represent the variables of one time period. Representing variables of all the time periods would require a chromosome of length

\((I\times J+J\times K+K+I+J+I+J+K+I\times J+J\times K+I\times J +J\times K+I\times J+J\times K)\times T\) bits. Such a representation of chromosome is shown in Fig. 3. It should be noted that the order of bits representing different variables in the chromosomes is not important. But an assumed fixed order is to be maintained throughout the population of chromosomes generated, so that when an optimal solution is generated in the form of a chromosome, it would be convenient to map the values of the bits of the chromosome to the variables. A sample representation of chromosome is presented in Fig. 3.

Initially a set of random chromosomes (Initial Population Count – IPC) are generated. The algorithm is run for a specified number of generations (GEN), considering it as the termination criterion.

4.3.2 Crossover operation

Since the encoded chromosomes consist of real values, in the current problem simulated binary crossover (SBX) has been used. The number of chromosomes participating in crossover is controlled by crossover probability (CP). A detailed study on SBX can be found in Deb (2001).

4.3.3 Mutation operation

A polynomial mutation is used to perform the mutation operation in NSGA II to solve the problem under consideration. The number of bits participating in mutation is controlled by mutation probability (MP), which is a tuning parameter. A detailed study on polynomial mutation can be found in Deb (2001).

There are four controllable parameters in NSGA-II: (1) IPC, (2) GEN, (3) CP, and (4) MP. The quality of solution obtained depends largely on these four parameters. User defined these parameters and therefore there is a need to choose the optimal values for these parameters that yield better solutions. This can be achieved by tuning of parameters. Many parameter tuning approaches have been studied in literature, among them Taguchi method is vastly used for the analysis of robust design. In this research, Taguchi method of fractional factorial design has been implemented to obtain the optimal NSGA-II parameters. This method has been discussed in the Sect. 6.

5 An illustrative example and computational studies

An illustrative example is presented and analysed using the above mentioned NSGA-II algorithm. Most of the functions and parameters considered in this study are collected from Cruz and Liu (2011) and Cruz and Wakolbinger (2008), and are presented in Table 7. This numerical problem considers two suppliers \((I=2)\), two manufacturers \((J=2)\), and two retailers \((K=2)\), who trade for a term of five periods \((T=5)\).

Suppliers primarily incur production costs and inventory holding costs for the given supply chain problem. Manufacturers incur costs related to transaction, supply disruption, opportunism risks, and relationship maintenance and improvement in addition to production and inventory costs. Since, there is no production involved at the retailers, they mainly incur handling costs, inventory costs, costs related to transaction, supply disruption, opportunism risks, and relationship maintenance and improvement.

Table 7 Functions and parameters used for computational study
Full size table

In this research, handling and fixed production costs are not considered and are assumed as sunk costs. Linear terms used for handling and production costs reflect the unit costs. The fact of increasing marginal production as the production quantity approaches the maximum capacity is reflected by the quadratic terms.

Analysis of this study has been carried out by solving four different variants of the problem: (1) profit versus risk, (2) profit versus emission, (3) emission versus risk, and (4) profit versus risk versus emission. These analysis are presented in Sect. 7 followed by parameter setting and Taguchi application in the next section.

6 Parameter tuning and application of Taguchi method

This section discusses Taguchi method implementation (Sadeghi et al. 2014) for NSGA-II parameters setting in order to obtain the better quality solutions (with respect to objectives’ values) of the proposed SCN model. Fisher introduced factorial designs to investigate the effect of various factors on the mean response. In our context, factors are the parameters of algorithmic solution and response is the fitness value of the solution. In order to reduce large number of experiments in full factorial designs, Taguchi designed fractional factorial experiments. In Taguchi method the parameters affecting the solution are divided into two parts: controllable (signal) factors S and noise factors N. In experiments only S factors can be directly controlled. In order to reduce the variation around the target, Taguchi developed a procedure to control the N factors. Analysis of results is performed in two ways: (1) employing analysis of variance of experiments with a single replicate; (2) using signal to noise ratio (S/N) in experiments with multiple replications. Owing to the better performance of the second way (the one with multiple replications), solution in the current problem is analysed using S/N ratio. This method aims to minimize the effect of noise factors, in other words the parameter setting at which the S/N ratio is maximum [effect of Signal (S) is much greater than effect of Noise (N)] is considered as the optimal.

6.1 Implementation of Taguchi method

Four tuning parameters namely, IPC, GEN, CP, and MP of NSGA-II are considered as the affecting parameters in Taguchi method. Three different levels of these parameters employed for fractional factorial design are shown in Table 8. These levels of the parameters have been obtained using trial and error procedure. Tuning of parameters is carried out utilizing the Taguchi \(\hbox {L}^{9}\) orthogonal array shown in Table 9.

Table 8 Three different levels of parameters considered for parameter tuning
Full size table
Table 9 Nine different sets of parameter setting
Full size table

Three different responses: (1) Pareto solution count (PSC), (2) spacing (Sp), and (3) best solution (Bsol) (Deb 2001), each representing a specific quality of a solution obtained using NSGA-II are considered as response variables for the experiments. To obtain the Bsol in a replication, the fitness values of the solution are first normalized employing the linear dimensionless approach of a multi-attribute decision making processes. Then they are summed together with a weight of 1/3 each. Since it is a minimization problem the solution with the lowest combined value of the normalized objective function values is considered as the best. In case of a minimization problem, lower value of Sp and higher values of PSC and Bsol explain better efficiency of NSGA-II.

Three replications have been carried out for analysis. The results obtained for nine different parameter settings (\(\hbox {L}^{9}\) orthogonal array) in the first replication are displayed in Table 10. Table 11 shows the normalized values of responses, and the sum for each parameter setting. These normalized values are obtained as follows.

For PSC, normalized value of a parameter setting i is given by :

$$\begin{aligned} \frac{PSC_i}{\max (PSC_1 ,PSC_2 ,\ldots ,PSC_9)} \end{aligned}$$
(32)

For Sp, normalized value of a parameter setting i is given by :

$$\begin{aligned} \frac{\min (Sp_1, Sp_2, \ldots , Sp_9)}{Sp_i} \end{aligned}$$
(33)

For Bsol, normalized value of a parameter setting i is given by :

$$\begin{aligned} \frac{\min (\hbox {Bsol}_1, \hbox {Bsol}_2, \ldots , \hbox {Bsol}_9)}{Bsol_i} \end{aligned}$$
(34)
Table 10 Metrics obtained in the first replication
Full size table
Table 11 Normalized metrics obtained in case of first replication
Full size table

Sum values of all three replications are displayed in Table 12. Since a solution with the highest sum is desired, the aim is to find the maximum S/N calculated by

$$\begin{aligned} S/N=-Log_{10} \left( {\frac{1}{n}\sum \nolimits _{i=1}^n {\frac{1}{sum_i^{2}}}} \right) \end{aligned}$$
(35)

where \(n =3\) represents the number of replications, and \(sum_i\) represents the sum in the ith replication.

Table 12 Experimental results of three replications
Full size table
Fig. 4
figure 4

Mean S/N plot for different levels of IPC

Full size image
Fig. 5
figure 5

Mean S/N plot for different levels of GEN

Full size image
Fig. 6
figure 6

Mean S/N plot for different levels of CP

Full size image
Fig. 7
figure 7

Mean S/N plot for different levels MP

Full size image

Figures 4, 5, 6 and 7 display the graph of mean S/N against the three levels of IPC, GEN, CP, and MP. The mean value of S/N for a level j of the various parameters is calculated as follows:

$$\begin{aligned} mean(S/N)_j =\frac{1}{3}\left[ {\sum _{i\in IPC_j} {(S/N)_i}} \right] \end{aligned}$$
(36)

where \(IPC_{j}\) represents the set of parameter combinations in which the level of IPC is j.

$$\begin{aligned} mean(S/N)_j =\frac{1}{3}\left[ {\sum _{i\in GEN_j} {(S/N)_i}} \right] \end{aligned}$$
(37)

where \(GEN_{j}\) represents the set of parameter combinations in which the level of GEN is j.

$$\begin{aligned} mean(S/N)_j =\frac{1}{3}\left[ {\sum _{i\in CP_j} {(S/N)_i}} \right] \end{aligned}$$
(38)

where \(CP_{j}\) represents the set of parameter combinations in which the level of CP is j.

$$\begin{aligned} mean(S/N)_j =\frac{1}{3}\left[ {\sum _{i\in CM_j} {(S/N)_i}} \right] \end{aligned}$$
(39)

where \(CM_{j}\) represents the set of parameter combinations in which the level of CM is j.

Based on the highest mean values of S/N, optimal NSGA-II parameters are obtained after tuning as: \(IPC=600,GEN=7000,CP=0.6,\hbox { and }MP=0.0095\).

7 Results and discussion

In this section, illustrative example presented in Sect. 4 is solved by NSGA-II, where optimal algorithmic parameters (IPC = 600, GEN = 7000, CP = 0.6, and MP = 0.0095) derived by Taguchi method application in the above section, has been used. Next, we discuss the results obtained for four problem variants.

7.1 Problem 1: profit versus risk

We solve the proposed model considering three different cases with a view to examine the effectiveness of the parameters of relationship maintaining cost and risks on the decision policies. It is also aimed to answer the first three questions mentioned in the introduction section.

Case 1: the functions and parameters mentioned in Table 7 are used in this case. It can be observed that all the transaction costs and relationship costs are same between any pair of stakeholders of different tiers (i.e., between suppler and manufacturer; between manufacturer and retailer). Since profit maximization and risk minimization are conflicting objectives, our natural conscience would be to expect a Pareto-optimal relation between profit and risk. Figure 8 shows a graph displaying the relationship between the risk and profit of the SCN. It is evident from the graph that as risk decreases profit also decreases. This can be justified by arguing that an increase in the level of social relationship requires investment in the form of time, additional personnel, money, etc. leading to decreased profit. This improvement in relationship level curtails the opportunism risks due to improved co-operation and communication between the tiers of supply chain. A firm chooses one solution among the Pareto-optimal front based on its profit preference and risk standards. One solution from the set of Pareto solutions, displaying data related to product flows, relationship level, demand and inventories is shown in Table 13.

Fig. 8
figure 8

Pareto optimal front obtained for profit versus risk

Full size image
Table 13 Computational results for profit versus risk (Case 1)
Full size table

It can be observed from Table 13 that social relationship level between each pair of adjacent echelon firm increases from 0 in period 1 to 0.429 in period 5, which means that social relationships become stronger over the periods. The increasing relationships curtail opportunism risks leading to a decrease in overall risk in supply chain. The following observations can also be made from Table 13: product flow consistently increase from 2.909 to 3.865 over the period, demand increases from 11.636 in period 1 to 15.460 in period 5, and price decreases from 38.364 in period 1 to 34.540 in period 5. From these observations it can be concluded that the evolving relationships have significant effects on the product flows, supply, price, and demand.

Case 2: in this case, we attempt to answer the second question, how do the upstream firms’ relationships affect the relationships with downstream firms, and how these relationships influence the objectives of the SCN? An assumption is made that manufacturer 1 has lower cost parameter associated with maintaining the relationships with suppliers than manufacturer 2, while remaining parameters are same as in Case 1. In particular, we let \(b_{it}^1 =6({\eta _{it}^1})^{2}\) and \(b_{it}^2 =14({\eta _{it}^2})^{2}\). Since the objective functions are the same as in Case 1, we again obtain a Pareto optimal front as in Case 1. One result from the set of Pareto solutions displaying data related to product flows, relationship level, demand and inventories is shown in Table 14.

The following observations can be made from Table 14. Firstly, it can be observed that the relationship levels evolution between manufacturer 1 and suppliers, \(\eta _{1t}^i\) s are faster compared to relationship levels evolution between manufacturer 2 and the suppliers, \(\eta _{2t}^i\) s. As for example, increment in \(\eta _{1t}^i\) s are from 0 in period 1 to 0.794 in period 5, while at the same period, increment in \(\eta _{2t}^i\) s are from 0 to 0.228. Moreover it can be observed that the product flows between suppliers and manufacturer 1 rapidly increase from 2.909 in period 1 to 4.334 in period 5, while the product flows between suppliers and manufacturer 2 increases from 2.909 in period 1 to 3.283 in period 2, thereafter consistently decrease to 3.042 in period 5. Such observations are not astonishing since manufacturer 1 has lower cost parameter in relationship maintaining cost functions compared to manufacturer 2, thus by encouraging the suppliers to maintain stronger relationships with manufacturer 1 preferred to manufacturer 2. Moreover, though the relationship maintaining cost functions are identical between the manufacturers and the retailers, the relationship levels of the retailers with manufacturer 1 still evolve rapidly than those with manufacturer 2. As for example, \(\eta _{kt}^1\) s increase from 0 to 0.441 over the periods, while increments in \(\eta _{kt}^2\) s during the same are 0–0.321. These outcomes manifest that if the upstream firms maintain better relationship in the SCN, then downstream firms will be eager to improve the relationship with the company. The reason behind phenomena is that better relationships of upstream firms generate lower total risks. Such an advantage makes the manufacturer more competitive compared to other manufacturers, so that the retailers are interested to develop strong relationship, and purchase more product from this manufacturer.

Table 14 Computational results for profit versus risk (Case 2)
Full size table

Above mentioned discussion also indicates that if a manufacturer is more cost effective in better managing relationships with upstream supply chain partners, then the firm will achieve lower supply risk, and will gain competitive advantage over other manufacturers. Such competitive edge will significantly encourage the downstream supply chain partners to establish stronger relationships with the manufacturer. In brief, better relationships with upstream supply chain partners encourage downstream partners to improve the relationship with supply chain partners.

Case 3: in this case focus is on the third research question: “how through supply chain relationship, the supply disruption risk interacts with the opportunism risks, and affects the objectives of the SC?” For this, we consider that manufacturer 2 is less reliable, and hence it has more chance of supply disruption. The remaining functions parameters are same as those in Case 1. In particular, we let \(p_k^j (u)=e^{-u/15}/15\hbox { for } j=2, k=1,2\). Note that the expected value 15 of probability density function implies that 15 quantities can be supplied without any disruption. Similar to the above two cases we obtain a set of Pareto solutions in this case. For our analysis, one solution among Pareto solutions considered is displayed in Table 15.

Table 15 Computational results for profit versus risk (Case 3)
Full size table

It can be observed from Table 15 that the transaction quantities from manufacturer 1 to the retailers are higher than those from manufacturer 2, because manufacturer 1 is more reliable than manufacturer 2. For instance, \(q_{kt}^1\) s increases from 2.672 to 3.090 and \(q_{kt}^2\) s decreases from 2.671 to 2.508 over the periods. Due to higher product flows with manufacturer 1, the retailers are interested to develop stronger relationships with manufacturer 1 compared to manufacturer 2. For example, the relationship levels \(\eta _{kt}^1\) s between retailers and manufacturer 1 increases to 0.776 in period 5 from 0 in period 1 compared to lower increase of \(\eta _{kt}^2\) s (relationship levels between retailers and manufacturer 2) to 0.624 in period 5 from 0 in period 1.

In summary, supply disruption has significant influence on relationship level and product flows. Stakeholders with more reliable productions (as manufacturer 1) have better relationships with supply chain partners, and maintain higher product flows.

7.2 Problem 2: profit versus emission

In this problem, profit and emission of the SC are considered and solved employing NSGA-II. The parameters displayed in Table 7 are used to obtain the computational results. Since it is a multi-objective scenario involving conflicting objectives, we could expect a Pareto optimal front. The result obtained is displayed in Fig. 9. From the graph it can be observed that as emission decreases, profit also decreases. This can be justified by arguing that, the stakeholders invest in innovative technologies, build stronger relationships to reduce their emissions below the environmental standards. Such investment in novel technologies and stronger relationships leads to an increase in the cost thereby reducing the profit of the supply chain. In summary, it can be said that lower emissions lead to lower profits, and vice versa.

Fig. 9
figure 9

Pareto optimal front obtained for profit versus emission

Full size image

7.3 Problem 3: risk versus emission

In this problem, risk and emission of the SC are considered and solved for the data mentioned in Table 7 employing NSGA-II. The result obtained is displayed in Fig. 10. It can be observed that there is only one optimal solution rather than multiple solutions as obtained in the above mentioned problems. Justification for such a result is discussed below.

Fig. 10
figure 10

Pareto optimal front obtained for risk versus emission

Full size image

Consider the risk function displayed in Eq. (3). It is basically a sum of supply disruption and opportunism risks. It can be observed from supply disruption risk functions displayed in Eqs. (4)–(7) that supply disruption risk increases with increase in transaction quantity. Now, let consider the opportunism risk functions displayed in Eqs. (8)–(11), it can be observed that opportunism risk increases with an increase in transaction quantity and decreases with an increase in the relationship level. In summary, it can be said that:

  • Total risk of SC increases with increase in transaction quantities.

  • Total risk of SC decreases with decrease in relationship levels.

Now considering the emission functions displayed in Eqs. (13)–(16), it can be said that

  • Emission of SC increases with increase in transaction quantities.

  • Emission of SC decreases with increase in relationship levels.

It can be said from the above arguments that both risk and emission functions are increasing with respect to transaction quantities and decreasing with respect to relationship levels. Since our objective is to decrease risk and emissions, the optimal choice would be lowest possible value for transaction quantities, and highest possible value for relationship levels. The lowest possible value for transaction quantities is zero, but since demand constraints are present, the lowest possible value for transaction quantities cannot be zero. The highest possible value for relationship level would be 1. The result obtained is displayed in Table 16. It can be observed that relationship levels take highest possible value i.e., 1.

Table 16 Computational results for profit versus emission
Full size table

7.4 Problem 4: profit versus risk versus emission

In this problem, all the three objectives profit maximization, risks minimization, and emission minimization is considered. The result obtained is displayed in Fig. 11. It can be concluded from Fig. 11 that as risk decreases profit also decreases, which is in tune with the conclusion of Sect. 7.1. It can be observed from the figure that as emission decreases profit also decreases, which is also in tune with the conclusion derived in Sect. 7.2.

Fig. 11
figure 11

3-D graph displaying the result for profit versus risk versus emission

Full size image

In the above discussion, we observed that social relationship levels between stakeholders increase over the periods starting with 0 from first period. In case of long term planning horizon the solution of the model reaches a converging point at which the social relationship levels between the stakeholders reaches the value 1. The solution of the model after this converging point results in constant transaction quantities and social relationship levels. In summary, after a certain time period all the variables of the model attain saturation values which remain constant in further time periods.

8 Conclusion

In this paper, we have proposed a MOMP integrated supply chain network consisting of suppliers, manufacturers and retailers, who work in collaborative environment to mitigate the risks including supply disruption and opportunism. To achieve this, each stakeholder maintains a level of social relationship with unlike tier’s stakeholders. We have evaluated the level of social relationship over time and described its effects. The collaborative approach is also aimed to maximize the profitability of entire supply chain as well as to minimize the emission. Owing to the complexity of the problem, to generate near optimal solution for multiple objectives more effectively and efficiently, population based random search algorithm NSGA-II have been used to find the Pareto efficient solution. Furthermore, in order to ameliorate the quality of solutions, tuning parameters of the NSGA-II are modulated by using the Taguchi method.

We have examined the proposed model through numerical experiment. The numerical experiment determined the trade-off of the profit, risks and emissions that have been considered in the objective and also provided the insights that assist the decision making process. Furthermore, we have determined the trade-offs of the profit and risks, the profit and emission, and risks and emission. We have also discussed how the relationship level changes over a period of time, and how it affects the profitability, risks, and emission.

This model aims at SC versus SC competition, i.e., optimizing supply chain as a whole. Hence, in a real setting, this would require the stakeholders of a SC to work collaboratively to optimize the objectives of entire SC. In this aspect, each stakeholder of the network would require the knowledge of the other potential stakeholders. Stakeholders working in such collaboration would strive to reduce the risk and emission associated with the flow of transaction quantities. This would ultimately lead to establishment of social relationships between the stakeholders and would result in optimal profits of all the stake holders, therefore giving way to a robust and optimized SCN.

This model is limited in a way due to our assumption that each stakeholder of upstream SC transacts with all the stakeholders of downstream supply chains without considering the issue of geographical location. Thus, incorporation of geographical location of stakeholders, and accordingly minimization of transportation cost is a potential future scope of this study. The other primary limitation of the model is the determination of parameters associated with the risk and emission. Determining these parameters would require incorporating a number of factors which vary drastically with domain. For example the risk factors associated with an aviation supply network would differ largely with the risk factors in a pharmaceutical industry. Furthermore, this model does not consider any level of association between the stake holders of the same tier, which could be a potential future research area. This model can further be extended to incorporate additional factors besides the price to determine the customer demand. All received quantity may not be passable to the next tiers because during the operation, product volume may decrease. Hence, conversion factor of received quantity to passable quantity can be considered in this model. This model can be extended for perishable food supply chain, wherein preventing technology reduces the perishing rate. Thus, minimization of perish product can be considered as an objective.