Skip to main content
SpringerLink
Log in

Irregular packing: MILP model based on a polygonal enclosure

  • Published:
Annals of Operations Research Aims and scope Submit manuscript

Abstract

This paper addresses the two-dimensional irregular packing problem, also known as the nesting problem. This is a subset of cutting and packing problems of renowned practical and theoretical relevance. A mixed integer-linear programming formulation is proposed to optimize the packing of particular polygonal shapes, convex forms with 3–8 sides, since their opposite sides are parallel. The model can be used to pack enclosures of general irregular shapes, generating upper bounds to the optimal solutions. The model was tested with 270 mass generated instances of small dimensions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  • Alvarez-Valdes, R., Martinez, A., & Tamarit, J. M. (2013). A branch & bound algorithm for cutting and packing irregularly shaped pieces. International Journal of Production Economics, 145(2), 463–477.

    Article  Google Scholar 

  • Art, R. C. (1966). An approach to the two-dimensional irregular cutting stock problem. Tech. Report 36.Y08, IBM Cambridge Scientific Centre.

  • Babu, A. R., & Babu, N. R. (2001). A generic approach for nesting of 2-D parts in 2-D sheets using genetic and heuristic algorithms. Computer-Aided Design, 33(12), 879–891.

    Article  Google Scholar 

  • Bennell, J. A., & Dowsland, K. A. (1999). A tabu thresholding implementation for the irregular stock cutting problem. International Journal of Production Research, 37(18), 4259–4275.

    Article  Google Scholar 

  • Bennell, J. A., & Dowsland, K. A. (2001). Hybridising tabu search with optimisation techniques for irregular stock cutting. Management Science, 47(8), 1160–1172.

    Article  Google Scholar 

  • Bennell, J. A., & Oliveira, J. F. (2008). The geometry of nesting problems: A tutorial. European Journal of Operational Research, 184(2), 397–415.

    Article  Google Scholar 

  • Bennell, J. A., Scheithauer, G., & Stoyan, Y. (2010). Tools of mathematical modeling of arbitrary object packing problems. Annals of Operations Research, 179(1), 343–368.

    Article  Google Scholar 

  • Bennell, J. A., & Song, X. (2008). A comprehensive and robust procedure for obtaining the nofit polygon using Minkowski sums. Computers & Operations Research, 35(1), 267–281.

    Article  Google Scholar 

  • Bennell, J. A., & Song, X. (2010). A beam search implementation for the irregular shape packing problem. Journal of Heuristics, 16(2), 167–188.

    Article  Google Scholar 

  • Bichoff, E. E., & Wäscher, G. (1995). Cutting and packing. European Journal of Operational Research, 84, 503–505.

    Article  Google Scholar 

  • Burke, E., Hellier, R., & Kendall, G. (2006). A new bottom-left-fill heuristic algorithm for the two-dimensional irregular packing problem. Operations Research, 54(3), 587–601.

    Article  Google Scholar 

  • Burke, E., Hellier, R., & Kendall, G. (2007). Complete and robust no-fit polygon generation for the irregular stock cutting problem. European Journal of Operational Research, 179(1), 27–49.

    Article  Google Scholar 

  • Chernov, N., Stoyan, Y., & Romanova, T. (2009). Mathematical model and efficient algorithms for object packing problem. Computational Geometry, 43, 535–553.

    Article  Google Scholar 

  • Dowsland, K. A., & Dowsland, W. B. (1995). Solution approaches to irregular nesting problems. European Journal of Operational Research, 84, 506–521.

    Article  Google Scholar 

  • Egeblad, J., Nielsen, B. K., & Odgaard, A. (2007). Fast neighborhood search for two- and three-dimensional nesting problems. European Journal of Operational Research, 183, 1249–1266.

    Article  Google Scholar 

  • Fischetti, M., & Luzzi, I. (2009). Mixed-integer programming models for nesting problems. Journal of Heuristics, 15(3), 201–226.

    Article  Google Scholar 

  • Gomes, A. M., & Oliveira, J. F. (2002). A 2-exchange heuristic for nesting problems. European Journal of Operational Research, 141, 359–370.

    Article  Google Scholar 

  • Gomes, A. M., & Oliveira, J. F. (2006). Solving irregular strip packing problems by hybridising simulated annealing and linear programming. European Journal of Operational Research, 171, 811–829.

    Article  Google Scholar 

  • Imamichi, T., Mutsunori, Y., & Hiroshi, N. (2009). An iterated local search algorithm based on nonlinear programming for the irregular strip packing problem. Discrete Optimization, 6(4), 345–361.

    Article  Google Scholar 

  • Jakobs, S. (1996). On genetic algorithms for the packing of polygons. European Journal of Operational Research, 88(1), 165–181.

    Article  Google Scholar 

  • Kenmochi, M., Imamichi, T., Nonobe, K., Yagiura, M., & Nagamochi, H. (2009). Exact algorithms for the two-dimensional strip packing problem with and without rotations. European Journal of Operational Research, 198, 73–83.

    Article  Google Scholar 

  • Lamousin, H., & Waggenspack, W. N, Jr. (1997). Nesting of two-dimensional irregular parts using a shape reasoning heuristic. Computer-Aided Design, 29(3), 221–238.

    Article  Google Scholar 

  • Lee, W. C., Ma, H., & Cheng, B. W. (2008). A heuristic for nesting problems of irregular shapes. Computer-Aided Design, 40, 625–633.

    Article  Google Scholar 

  • Leung, S. C. H., Lin, Y., & Zhang, D. (2012). Extended local search algorithm based on nonlinear programming for two-dimensional irregular strip packing problem. Computers & Operations Research, 39, 678–686.

    Article  Google Scholar 

  • Li, Z., & Milenkovic, V. (1995). Compaction and separation algorithms for non-convex polygons and their applications. European Journal of Operational Research, 84, 539–561.

    Article  Google Scholar 

  • Licari, R., & Lo Valvo, E. (2011). Optimal positioning of irregular shapes in stamping die strip. International Journal of Advanced Manufacturing Technology, 52(5–8), 497–505.

    Article  Google Scholar 

  • Ma, H., & Liu, C. C. (2007). Fast nesting of 2-D sheet parts with arbitrary shapes using a greedy method and semi-discrete representations. IEEE Transactions on Automation Science and Engineering, 4(2), 273–282.

    Article  Google Scholar 

  • Martins, T. C., & Tsuzuki, M. S. G. (2010). Simulated annealing applied to the irregular rotational placement of shapes over containers with fixed dimensions. Expert Systems with Applications, 37(3), 1955–1972.

    Article  Google Scholar 

  • Nielsen, B. K., & Odgaard, A. (2003). Fast neighborhood search for the nesting problem. Tech. Rep. 03/03, DIKU, Department of Computer Science, University of Copenhagen.

  • Peng, W., Tong, R. F., & Tang. M. (2005). A parallel algorithm of polygons packing based on ant colony. In Proceedings of the 9th international conference on computer supported cooperative work in design, Coventry, England (pp. 846–851).

  • Sawaya, N. W., & Grossmann, I. E. (2005). A cutting plane method for solving linear generalized disjunctive programming problems. Computers and Chemical Engineering, 29, 1891–1913.

    Article  Google Scholar 

  • Stoyan, Y. G., Novozhilova, M. V., & Kartashov, A. V. (1996). Mathematical model and method of searching for a local extremum for the non-convex oriented polygons allocation problem. European Journal of Operational Research, 92, 193–210.

    Article  Google Scholar 

  • Terashima-Marín, H., Ross, P., Farías-Zárate, C. J., López-Camacho, E., & Valenzuela-Rendón, M. (2010). Generalized hyper-heuristics for solving 2D regular and irregular packing problems. Annals of Operations Research, 179, 369–392.

    Article  Google Scholar 

  • Wäscher, G., Haußner, H., & Schumann, H. (2007). An improved typology of cutting and packing problems. European Journal of Operational Research, 183, 1109–1130.

    Article  Google Scholar 

  • Wong, W. K., & Guo, Z. X. (2010). A hybrid approach for packing irregular patterns using evolutionary strategies and neural network. International Journal of Production Research, 48(20), 6061–6084.

    Article  Google Scholar 

  • Wong, W. K., & Leung, S. Y. S. (2008). Genetic optimization of fabric utilization in apparel manufacturing. International Journal of Production Economics, 114, 376–387.

    Article  Google Scholar 

  • Wong, W. K., Wang, X. X., & Mok, P. Y. (2009). Solving the two-dimensional irregular objects allocation problems by using a two-stage packing approach. Expert Systems with Applications, 36(2), 3489–3496.

    Article  Google Scholar 

  • Yang, H. H., & Lin, C. L. (2009). On genetic algorithms for show making nesting—A Taiwan case. Experts Systems with Applications, 36, 1134–1141.

    Article  Google Scholar 

  • Yu, M. T., Lin, T. Y., & Hung, C. (2009). Active-set sequential quadratic programming method with compact neighborhood algorithm for the multi-polygon mass production cutting-stock problem with rotatable polygons. International Journal of Production Economics, 121(1), 148–161.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Escola Politécnica/Universidade de São Paulo, Av. Prof. Almeida Prado, Travessa 2, No 128, Cidade Universitária, São Paulo, SP, Brazil

    Miguel Cezar Santoro & Felipe Kesrouani Lemos

Authors
  1. Miguel Cezar Santoro
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Felipe Kesrouani Lemos
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Felipe Kesrouani Lemos.

Appendix: Details of instances

Appendix: Details of instances

The instances run in Sect. 4 (“computational results”) are described in detail. In Table 5 the characteristics of instances are shown. In Table 6, we present the data about each item.

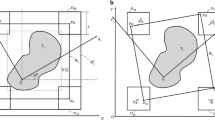
It is important to stress that \(\hbox {k}_{\mathrm{a}}\) and \(\hbox {k}_{\mathrm{b}}\) are parameters of each instance, since the model requires parallel edges among all items. A consequence of this fact is that \(\hbox {m}_{\mathrm{pi}}\), \(\hbox {k}_{\mathrm{a}}\) and \(\hbox {k}_{\mathrm{b}}, \hbox {n}_{\mathrm{pi}}\) are given.

Table 5 Characteristics of the instances
Full size table
Table 6 Characteristics of the items
Full size table

Finally, Table 7 shows the results obtained for each instance of the mass generated set, for further comparison as benchmark.

Table 7 Results obtained for mass generated instances
Full size table

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Santoro, M.C., Lemos, F.K. Irregular packing: MILP model based on a polygonal enclosure. Ann Oper Res 235, 693–707 (2015). https://doi.org/10.1007/s10479-015-1971-9

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10479-015-1971-9

Keywords

Search

Navigation