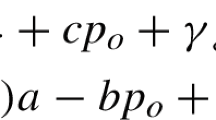1 Introduction

In facility location competition, the main instrument is the choice of location. Since the first model of Hotelling (1929), many extensions have been studied in competitive location science where firms basically decide on locating one or more facilities at location(s) \(x\) trying to attract market share. We focus on the situation where the choice of location can be complemented by investment into the quality of the facility. One of the first models describing market capture using location and quality (also called location-design) is the original Huff model (Huff 1964). In this model, the market capture is represented by so-called demand points with a fixed (inelastic) demand called purchase power. Although the model describes the supplier choice of a customer as so-called probabilistic, i.e. the customer can fulfil her demand partly by various suppliers, the supplier choice can also be deterministic, i.e. the customer chooses one of the suppliers to supply her demand.

Besides the customer behavior, one can distinguish several ways of how suppliers in the market compete with each other. One question deals with studying the existence of stable market situations using the concept of Nash equilibria. Another consideration is to study a market situation where a so-called leader player is knowing how a so-called follower supplier is going to react. In location literature Hakimi (1983) baptized the latter decision problem as an \((r|p)\)-centroid problem, where a leader intends to locate \(r\) facilities taking into account the reaction of a competitor (follower) in locating \(p\) facilities. In this classification, the problem under study can be classified as a continuous \((1|1)\)-centroid location-design problem with deterministic supplier choice, i.e. both competitors locate one facility in the plane and have a continuous choice in quality, whereas the customer chooses one of the competitors to fulfil her demand. We first define mathematically what this means and then have a look at what has already been found in literature with respect to the problem to be investigated before formulating new research questions.

Consider a location-design problem where the objective \(\varPi (x,a)\) is to capture market share by attracting customers choosing location \(x\) and setting a quality \(a\). As far as known to the author, Eiselt and Laporte (1989) were the first to include a quality parameter (called weight) in an optimization attraction problem based on the maximum capture model of Revelle (1986). Plastria (1997) describes the first competitive location-design problem in the plane involving both the choice of the location and a continuous quality choice as variables of the model. Now consider two competitor supplier firms that plan to locate one facility and choose a quality for it. Define the decision vector \((x,y,a,b)\) with locations \(x\) and \(y\) of the two competing firms and \(a\) and \(b\) their quality. The payoff of firm \(i\) is given by \(\varPi _i(x,y,a,b)\). Then we define \((x^*,y^*,a^*,b^*)\) as Nash equilibrium if

$$\begin{aligned} x^*,a^* \in \arg \max _{x,a} \varPi _1(x,y^*,a,b^*) \ \ ; \ \ y^*,b^* \in \arg \max _{y,b} \varPi _2(x^*,y,a^*,b). \end{aligned}$$
(1)

In a Stackelberg situation, one of the suppliers (let say firm 1) knows how the other is going to react. This is also called a leader-follower situation and the solution is called a Stackelberg equilibrium. For the location-design problem, solution \((x^*,y^*,a^*,b^*)\) is a Stackelberg equilibrium if

$$\begin{aligned}&x^*,a^* \in \arg \max _{x,a} \varPi _1(x,y^*(x,a),a,b^*(x,a)) \ \ \mathrm{where } \end{aligned}$$
(2)
$$\begin{aligned}&y^*(x,a),b^*(x,a) \in \arg \max _{y,b} \varPi _2(x,y,a,b). \end{aligned}$$
(3)

We consider fist what has already been found before in literature with respect to this problem. For a general overview on competitive location, we refer to the overview papers (Eiselt et al. 1993; Plastria 2001; Kress and Pesch 2012). Now let us focus on the \((1|1)\)-centroid location-design problem in the plane with deterministic supplier choice.

Fernández et al. (2007) analyse first the second level optimisation of \(\varPi (x,a)\) over a continuous quality parameter \(a\) when location \(x\) is fixed. They show that for the classical Huff model with convex investment cost this implies a concave problem. Therefore the optimum quality level \(a^*(x)\) is relatively easy to find. Substitution of the second level decision provides a first level problem \(\max _x \varPi (x,a^*(x))\) in location space. The latter problem is typically a Global optimization problem, classified by Hakimi (1983) as a medianoid problem.

Focusing on the situation of two competing firms in a location-design environment, Fernández and Hendrix (2013) in a recent overview discuss the different situations considered in the papers of Kücükaydin et al. (2011), Sáiz et al. (2011), Saidani et al. (2012), that all use the Huff model with several cost functions on quality to analyse different settings of a firm entering the market. In a two competitor case, one can consider a Nash equilibrium or a Stackelberg situation, as defined before.

For a situation where two competing firms enter a new market without active suppliers in continuous location-design, Sáiz et al. (2011) derive Nash equilibria. The Huff model facilitates the derivation of explicit analytical expressions for the optimal (Nash) values of the quality to be set by the two competitors. This facilitates studying the existence of location Nash equilibria on the first level. However, if customers choose for one of the suppliers only, i.e. deterministic behavior, the analytical study is hindered as the market capture depends in a discontinuous way on the location and quality decision.

For cases where the quality design \(a,b\) is fixed, several analyses can be found in literature for the leader-follower situation. Sáiz et al. (2009) provide for a Huff-like continuous problem, Global Optimization (GO) solution \(y^*(x)\) to be substituted into GO problem \(\max _{x} \varPi _1(x,y^*(x))\). The elegance of the approach described in that paper is that it provides a guarantee to find the global optimum solution for both leader and follower. More recently Roboredo and Pessoa (2013) find the optimum with a guarantee for location on a network where both competitors decide on the location of several facilities, i.e. an \((r|p)\)-centroid problem. If we now focus on the location-design \((1|1)\)-centroid problem, one can find a Huff-like description in Redondo et al. (2010). That paper states that this is a “hard to solve global optimization problem” and does not follow the earlier analytical approach. Instead it approximates the solution of this six-dimensional problem by heuristics that basically generate millions of trial points of which the best one is selected.

To the knowledge of the author, no analysis was done on a \((1|1)\)-centroid problem in the plane with deterministic customer behavior. The research questions of this paper is, whether a Stackelberg equilibrium exists for deterministic customer behavior and what are its characteristics. Insight in the characteristics of this model facilitates predicting the behavior in the corresponding market situation. Two companies enter a new market and try to win as many customers with their demand (purchase power) as possible by deciding on their location \(x\) and \(y\), but also on their quality \(a\) and \(b\). The research question is to predict the behavior of both actors. For instance, whether co-location is a natural tendency in this market situation and under which circumstances one of the firms decides not to enter the market. Sáiz et al. (2011) found that in probabilistic supplier choice the optimal (Nash) locations for each firm is found at a demand point. Is it natural in deterministic supplier choice that firms locate at a customer?

To investigate these questions, first a game theoretic model is defined in Sect. 2 describing the market situation. Section 3 then analyses the decision on the level of the quality. Section 4 investigates several properties of the location behavior. Section 5 summarizes the findings on the research questions.

2 Model of a Stackelberg location-design market situation

To depict the situation, one can think of two competing news vendors or street bars located at \(x\) and \(y\) in a new neighbourhood that attract customers located in points \(p_i\) to come over every morning and to buy their desired newspaper or coffee. Customers may have a different purchase power \(w_i\) although this does not have an important influence on the problem characteristics. The analysis becomes more cumbersome when already several suppliers exist. To keep notation as simple as possible, we leave this aspect out at the moment, although tendencies may be similar. The two competitors can also invest in their attractiveness by deciding on their quality. The situation under investigation is that in the decision process, the leader supplier (firm 1), knows what the follower supplier (firm 2) is going to do. The question is what is the corresponding behavior of the two players. The following notation describes the situation formally:

Indices

\(i\) :

index of demand points, \(i=1,\ldots ,n\), index set \(I=\{1,\ldots ,n\}\)

Variables

\(x=(x_{1},x_{2})\) :

location of firm 1,

\(y=(y_{1},y_{2})\) :

location of firm 2

\(a\) :

quality facility firm 1,

\(b\) :

quality facility firm 2

All variables are continuous variables.

Data

\(p_i\) :

location of the \(i\)-th demand point (customer), \(P=\{p_i, i=1,\ldots ,n\}\)

\(w_i\) :

demand (purchase power) of customer \(i\), \(w_i>0\)

\(\alpha ,\beta \) :

cost parameters for firm 1 and 2 respectively, \(\alpha ,\beta >0\)

\(S\) :

location space, in fact the convex hull of the set of demand points

Miscellaneous

\(W=\sum _i w_i\) :

total demand

\(d_{i}(z)\) :

Euclidean distance between \(p_i\) and \(z=x\) or \(z=y\)

\(c_1()\), \(c_2()\) :

cost functions for firm 1 and firm 2 with respect to quality expressed in demand

\(J(x,y,a,b)\) :

Subset of clients captured by firm 2, \(J(x,y,a,b)\subset I\)

We consider the linear relation \(c_1(a)=\alpha a\), \(c_2(b)=\beta b\), where the coefficients are expressed in the same units as the demand. The supplier choice of the customers is to choose for one of the suppliers according to an attractiveness \(\frac{a}{d_i(x)}\) for firm 1 and \(\frac{b}{d_i(y)}\) for firm 2. In our study we assume that there is the so-called ’novelty seeking’ behaviour where the customer prefers the follower (firm 2) in case the values are the same. Notice that in case the two suppliers co-locate on a demand point, the customer prefers the one with the best quality. To describe the market capture \(M(x,y,a,b)\) of the follower, we use an index set \(J(x,y,a,b)\) of the customers attracted by the follower:

$$\begin{aligned} J(x,y,a,b)&= \{i\in I| b\ge a \,\mathrm{if}\, d_i(x)=d_i(y)=0, \,\mathrm{else}\,bd_i(x) \ge ad_i(y)\}\end{aligned}$$
(4)
$$\begin{aligned} M(x,y,a,b)&= \sum _{i\in J(x,y,a,b)} w_i \end{aligned}$$
(5)

and \(W-M(x,y,a,b)\) demand goes to the leader (firm 1). The resulting objective functions are well defined. The profit function of firm 1 is given by

$$\begin{aligned} \varPi _1(x,y,a,b) = W-M(x,y,a,b) - c_1(a) \end{aligned}$$
(6)

and for firm 2

$$\begin{aligned} \varPi _2(x,y,a,b) = M(x,y,a,b) - c_2(b) . \end{aligned}$$
(7)

We assume nonnegativeness of profit, i.e. a firm does not enter the market if it cannot obtain nonnegative profit. Another assumption of the market situation is that if one of the firms manages to capture total demand against a nonnegative profit, it will follow this strategy to take the competitor out of the market.

On the location decision level \((x,y)\), both firms have to take the optimal decision on the quality decision level \((a,b)\) into account. Moreover, the leader knows what the follower is going to do on the quality level, \(b^*(x,y,a)\) as well as on the location level: \(y^*(x,a,b^*(x,y,a))\). This situation makes the supplier behavior hard to analyse. Thinking in more than one level helps to consider the situation.

We first focus on the question of possible Nash and Stackelberg equilibria with respect to the choice of the quality of the facilities \((a,b)\) given the facility locations \((x,y)\). Then in Sect. 4, we study properties of location equilibria given the optimum levels on quality choice.

3 Equilibria on the level of the quality choice

First the behavior of a firm 2 is studied in Sect. 3.1. The follower reacts on the decision of the other firm, but cannot anticipate on its behavior. Given the behavior, we can focus on the Nash equilibrium definition and study its existence. Then in Sect.  3.2, we focus on the behavior of the leader and study possible Stackelberg equilibria.

3.1 Firm 1 quality choice and Nash equilibrium

Firm 2 is choosing its quality level \(b\) given the position of both competitors \((x,y)\) and the quality \(a\) set by firm 1. It is convenient to order the location advantage of the firm 1 expressed by the ratios \(\frac{d_i(y)}{d_i(x)}\). The order of these ratios provides the order in which firm 2 is going to attract the customers with increasing value for quality \(b\). A complication is that the relative distance \(\frac{d_i(y)}{d_i(x)}\) of two or more customers \(i\) and \(j\) can be the same. Actually, analysing forward, it is in the interest of firm 2 that this takes place; increasing his quality he captures several customers at the same time. In the case of co-location, only one ratio exists with a value of 1.

Definition 1

Let \(r_j(x,y), j=1,..,t\) be the ordered values of \(\frac{d_i(y)}{d_i(x)}\) from small to big using the valuation \(\frac{d_i(y)}{d_i(x)}=1\) for the case where \(d_i(x)=d_i(y)=0\).

Customers \(i\) with the same relative distance are included in the same ratio value \(j\), such that \(t \le n\). Notice that \(r_t(x,y)\) can take the value \(\infty \) if firm 1 is located at a demand point and firm 2 is not. We can write the total demand \(m_j\) going to firm 2 after capturing the customers corresponding to the first \(j\) relative distances using an index set \(I_j(x,y)\) of captured customers:

$$\begin{aligned} I_j(x,y)&= \{i\in I|\frac{d_i(y)}{d_i(x)}\le r_j(x,y)\}\end{aligned}$$
(8)
$$\begin{aligned} m_j&= \sum _{i\in I_j(x,y)} w_i . \end{aligned}$$
(9)

Notice that the series \(m_j\) is strictly increasing and in case of co-location \(m_1=W\). Now we can rewrite the profit of firm 2 given the locations \(x,y\) and quality \(a\) as

$$\begin{aligned} \varPi _2(x,y,a,b) = m_k - \beta b , k=\max \{j| b \ge a r_j(x,y)\}. \end{aligned}$$
(10)

Example 1

An instance consists of ten customers located at \(P= \{(1,4), (4,2), (5,8), (1,9)\), \((8,5), (7,4), (6,3), (3,7), (8,8), (2,2)\}\) who each spend \(w_i=1\) unit each morning at their most attractive supplier. Firm 1 is located at \(x=(3,3)\) and firm 2 at \(y=(7,7)\). The instance is designed such that two pairs of customers are at equal relative distance to the two suppliers, i.e. \(t=8\). Investing in quality costs firm 2 \(\beta =1\) units. Firm 1 already invested \(a=4\) units in its quality. Figure 1 gives the development of \(\varPi _2\) in (10) as function of \(b\) according to the model. The circles correspond to the attracted customers. The firm is not entering the market if it cannot make nonnegative profit, as demarcated by the dotted line. Notice that following an increasing value of \(b\), the figure reveals \(t=8\) peaks that correspond to the increasing values of \(r_j\). The values of \(b\) for which \(\varPi _2\) is discontinuous do not depend on \(\beta \), the value of the function \(\varPi _2\) itself does. Firm 2 obtains the maximum profit investing \(b=4\).

The figure illustrates several characteristics. Notice that \(\varPi _2\) is discontinuous and its local maxima are not necessarily first increasing in \(b\) and then decreasing. Second, depending on the quality set by firm 1 and the locations, firm 2 will decide to stay out of the market if the cost of investing in quality is higher than the gain in market capture: \(\beta a r_k(x,y) >m_k, k=1,\ldots ,t\). Notice that in case of co-location, firm 2 will stay out of the market if \(\beta >\frac{W}{a}\).

Fig. 1
figure 1

Profit of the firm 2 with increasing quality \(b\)

Full size image

Given the introduced notation, one can write now the optimal behaviour of firm 2 with respect to quality in an exact way.

Lemma 1

Given the described game with \(r_j(x,y)\) as described by definition 1, let \(r_0(x,y)=0\), \(m_j\) defined by (8) and \(m_0=0\). Let locations \(x,y\) and quality \(a\) be given. The optimum quality investment for firm 2 is \(b^*=a r_k(x,y)\) with \(k={\mathrm {argmax}}_{j=0,\ldots ,t} \{m_j-\beta a r_j(x,y) \}\). The corresponding profit is \(\varPi _2(x,y,a,b^*)=m_k-\beta a r_k(x,y)\) and market capture is \(M(x,y,a,b^*)=m_k\).

Notice that in case of co-location, we have an all or nothing game, where firm 2 captures \(m_1=W\) setting \(a=b\) or stays out of the market with \(m_0=0\) if \(a=0\).

The former analysis helps us to proof that there is no Nash equilibrium on the quality level if both firms have no information on the reaction behavior of the other.

Proposition 1

Given the described game and locations \(x,y\). No Nash equilibrium \(a,b>0\) exists on the quality level.

Proof

By contradiction, let \(a,b>0\) be a Nash equilibrium with the firms located at \(x,y\). This means \(a\) is optimal for firm 1 and \(b\) is optimal for firm 2. According to lemma 1 for firm 2, \(\exists k,\ b=a r_k(x,y)\). Now firm 1 by increasing its quality to \(a+\epsilon \) for a value \(0<\epsilon <\frac{m_k-m_{k-1}}{\alpha }\) increases its profit with \(m_k-m_{k-1} -\alpha \epsilon >0\). This proofs that \(a\) is not an optimal quality for firm 1 and contradicts \(a,b\) to be a Nash equilibrium. \(\square \)

The proposition shows that according to this model, both suppliers cannot exist at the same time in the market in a Nash situation. The proof also shows that this is not necessarily true if a maximum on the quality \(a\) is included into the model that is smaller than \(\frac{W}{\alpha }\), which is the natural upper bound. Other location-design models like Kücükaydin et al. (2011) and Saidani et al. (2012) include such limits in order to obtain numerical results.

3.2 Leader behavior and Stackelberg equilibrium

For a Stackelberg equilibrium, the line of the proof already shows what the leader (firm 1) should look for: an \(\epsilon \) optimal solution. So, what is the optimal quality \(a^*(x,y)={\mathrm {argmax}}_a \varPi _1(x,y,a,b^*(x,y,a))\) in a leader-follower situation? Let us first consider the co-location case.

Proposition 2

Given the described game. Let \(x=y\). No solution \(a, b>0\) exists where both firms stay in the market, i.e. co-location does not take place.

Proof

In the co-location situation, \(x=y\), all distances are the same for the two firms. This means that the follower gets all according to (4), if \(b\ge a\) and nothing if \(a>b\). The follower at most wants to invest \(b=\frac{W}{\beta }\) to have a nonnegative profit. For \(\alpha <\beta \) the leader can set his investment \(a=\frac{2W}{\alpha +\beta }>\frac{W}{\beta }\) generating the positive profit \(\varPi _1=W-\alpha \frac{2W}{\alpha +\beta }=\frac{\beta -\alpha }{\alpha +\beta } W>0\) taking the follower out of the market. For \(\beta \le \alpha \) the follower can invest \(b=\frac{W}{\beta }\) generating nonnegative profit \(\varPi _2=0\) taking the leader out of the market. \(\square \)

If both suppliers are not located at the same position, the leader has to maximize \(W-M(x,y,a,b)-\alpha a\), where \(M(x,y,a,b)\) is defined in Lemma 1. This typically has the character of minimizing the damage caused by the follower:

$$\begin{aligned} \min _a \left( M(x,y,a,b)+\alpha a \right) = \min _a \left( \max _j \{m_j-\beta r_j(x,y) a\} + \alpha a\right) . \end{aligned}$$
(11)

Example 2

We consider the same instance as that of Example 1 with ten customers, where the leader has an investment cost coefficient of \(\alpha =1.2 > \beta =1\). Figure 2 sketches the development of \(\varPi _1\) as function of \(a\), where the follower continuously adapts its quality \(b^*(x,y,a)\). The figure illustrates the multi-modal and discontinuous character of the profit function. Starting at \(a=0\), the leader does not have any market capture and increasing quality \(a\) leads to negative profit up to the moment that the follower loses three customers near \(a=0.83\). We will see where this approximate number comes from. Typically, if the leader increases its quality, then for certain values of quality \(a\) the follower loses one or several customers. This provides a higher market share for the leader against a higher cost of investment in quality.

Fig. 2
figure 2

Profit of the leader with increasing quality \(a\); the follower adapts its quality \(b^*(x,y,a)\)

Full size image

To study the optimal quality choice for the leader, one should first observe that with increasing quality \(a\) of the leader, the follower will never have more customers. He will also increase the quality up to a certain level where he should let the customer go to the competitor. That ”certain level”, is exactly the candidate solution for the leader we are interested in.

Starting at \(a=0\) where the leader does not attract any customer and where \(M(x,y,a,b)=m_t=W\), we study when the follower will give up customers with a relative distance higher than \(r_{t-k}\). The loss in market share is \(m_t-m_{t-k}\), but the gain in cost reduction is \(\beta (r_t-r_{(t-k)})a\). This means that the follower will let these customers go to firm 1 and reduce investments if \(a>\frac{m_t-m_{t-k}}{\beta (r_t-r_{t-k})}\). For increasing \(a\), in the example this happens for \(k=3\), where the ratio is \(.827\). So, starting with a follower having \(q=n\) customers, the first candidate optimal choice for the leader should be an epsilon solution:

$$\begin{aligned} a=\min _{k= 1,..,q} \frac{m_p-m_{q-k}}{\beta (r_q-r_{(q-k)})} +\epsilon , \end{aligned}$$
(12)

where \(\epsilon \) is an arbitrary small positive number. After finding the number of dropped customers \(k\), one can find more candidates by repeating (12) iteratively setting \(q:=q-k\) up to the follower has no more customers left over, \(q=0\). The latter is the most interesting option for the leader as long as it provides a positive profit; he can take the follower out of the market. After generating the candidates for \(a\) via (12), one has to evaluate \(\varPi _1\) for them to find the best quality level for the leader. This procedure is described in Algorithm 1.

figure a

Example 3

We consider the Algorithm 1 for same instance as that of Example 1 with ten customers and investment cost coefficients \(\alpha =1.1, \beta =1\), locations \(x=(3,3)\) and \(y=(7,7)\). The algorithm generates the threshold values that can be recognized in Fig. 2 being \(a\in \{0.8275, 2.6712, 5.1302, 7.2250\}\). Notice that the threshold values derived by (12) do not depend on the value of \(\alpha \), but of course the profit does. Although the highest profit of \(2.0\) is found at \(a=0.8275\), the leader has the alternative to take the follower out of the market at \(a=7.22\) against a positive profit. According to the rules of the game, he will do so. In the complete game of the market situation, the follower does not necessarily enter the market. This example specifically shows that the location \(y=(7,7)\) is not optimal if firm 1 is located at \(x=(3,3)\).

The analysis does not yield closed analytical expressions due to the typical discrete character of the problem. Are the results easily extendible? What happens if already several suppliers exist in the market? The follower simply has to focus on the most attractive competitor for customer \(i\), who is not necessarily the leader. For the leader, expression (11) becomes less straightforward, as the other competitors also have to be taken into account.

Concluding, Stackelberg equilibria for the described market situation may occur in contrast to Nash equilibria as shown by Proposition 1 and 2. The latter result on co-location suggests that the follower can take the leader out of the market if \(\beta \le \alpha \). As the leader knows the follower is going to locate at the same place, he can never beat the follower and practically has to leave the market. The follower gets all.

4 Stackelberg location equilibrium for the case \(\alpha <\beta \)

In the former section, we already analysed the situation \(\beta \le \alpha \), i..e. a strong follower firm (easy access to financing an increase in quality) can prevent a leader to enter into the market according to the model assumptions. This leaves us with the analysis of the case \(\alpha <\beta \), i.e. the leader can increase quality at lower cost. Under which circumstances does a Stackelberg equilibrium exist where both firms are in the market and where do the firms prefer to locate?

First, as discussed in Proposition 2, co-location (choosing \(y=x\),) is not of interest to the follower as the leader can take the follower out of the market by increasing quality in a cheaper way. Second, the follower is always going to participate in the market. Firm 2 can at least locate at a customer with the largest demand, if firm 1 is not there. Otherwise, it can locate at the second largest demand point. To formalise this behaviour it is convenient to introduce the second largest weight.

Definition 2

Let \(\{w_i, i=1,\ldots ,n\}\) be a set of weights. The second largest weight \(w_{(2)}\) is \(w_{(2)}=\max _i w_i\) if \(|{\mathrm {argmax}}_i w_i|>1\) else it is \(w_{(2)}=\max (\{w_i, i=1,\ldots ,n\}\setminus \{\max w_i\})\).

Proposition 3

Given the described game with \(\alpha <\beta \). The follower is always going to participate in the market and his optimal profit is at least \(\varPi _2(x,y^*,a,b^*)\ge w_{(2)}\).

Proof

Given a location \(x\) and quality choice \(a\) of the leader, a feasible solution of the follower is locating at \(y=p_k\) where \(k\in {\mathrm {argmax}}_i{w_i}\) and \(b=0\). However, if \(x=p_k\), the follower should locate at a demand point with weight \(w_{(2)}\). The corresponding profit is \(\varPi _2= w_{(2)}\), as he attracts the customer without any investment cost. So the follower has no reason to stay out of the market and will at least gain a value of \(w_{(2)}\). \(\square \)

Consider the profit of the follower \(\varPi _2(x,y,a^*(x,y),b^*(x,y,a^*(x,y)))\) varying his location \(y\) when \(x\) is given. In most of the area, the leader can take the follower out of the market setting its quality and knowing the reaction of the follower; profit is 0. However, at the demand points \(p_i\), function \(\varPi _2\) has at least a local maximum of \(w_i\) as long as the leader is not located there.

Example 4

Consider firm 1 located at \(x=(3,3)\) and \(\beta =1\), the ten customers located at \(P= \{(1,4), (4,2), (5,8), (1,9), (8,5), (7,4), (6,3), (3,7), (8,8), (2,2)\}\), \(w_i=1\ \forall i\). For \(\alpha >\beta \), the profit of firm 2 has clearly a peak of \(\varPi _2=10\) for \(y=x\) and also local optima at the customers. These local optima are better visible for the case where the leader has easier access to investing capital, \(\alpha <\beta \). For \(\alpha =0.9\), Figure 3 outlines the profit with a maximum of \(\varPi _2=1.52\) attained near \(y=(6.34,3.96)\). At most of the surface, the follower is not able to capture demand against a low enough quality (profit is zero) and at the customer locations he attracts at least the purchase power of one customer \(w_i\) without any additional cost.

Fig. 3
figure 3

Profit of the follower as function of location \(y\) given \(x=(3,3)\) and the optimal quality \((a^*,b^*)\) as function of \(x,y\), \(\alpha =0.9, \beta =1\)

Full size image

The example illustrates that the optimum location of the follower is not necessarily at a demand point in contrast to what was found as a property of the equivalent probabilistic Huff variant of the model in Sáiz et al. (2011). In most of the area, gradient information, i.e. in which direction does the objective improve, is lacking. Finding the best location can be done by a heuristic based on a finite number of function evaluations, like a grid search. Notice that given the solution of the quality level, we are dealing with a problem in only two-dimensional space. Following a grid search procedure as is done to generate Fig. 3, we can also get an impression of the location decision for the leader, substituting the level of the follower decision.

An interesting consequence of Proposition 3 is the following bound on the profit of the leader.

Corollary 1

Given the described game. If \(\alpha <\beta \) the optimal profit of the leader is bounded by \(0\le \varPi _1(x,y,a,b)\le W-w_{(2)}\). For \(\alpha \ge \beta \), the leader stays out of the market.

Example 5

Consider the case of Example 4. For each location of the leader over a grid of 10,000 points, the follower decision is evaluated by solving the quantity level and the best location is taken as an approximation of \(y^*(x)\). The resulting profit function for the leader is depicted in Fig. 4. One can observe very well, that outside the convex hull of the demand points the leader loses profit, as the follower can locate at a more profitable place. The optimum profit value is \(\varPi _1=6.57\) at a location near \(x=(3.66,4.31)\) if the follower chooses as demand point \(y=P_7=(1,9)\) gaining a profit of 1. The figure illustrates the discontinuous character of the objective function.

Fig. 4
figure 4

Profit of the leader as function of location \(x\), the optimum follower location \(y^ *\) and the optimal quality \((a^*,b^*)\) as function of \(x,y^ *\), \(\alpha =0.9, \beta =1\)

Full size image

5 Conclusions and discussion

We analysed a market situation of two firms, firm 1 and firm 2, entering a new market where customers reveal a deterministic supplier choice being attracted by low distance and high quality with a game theoretic model. In case of breaking tie, i.e. both firms are as attractive, the customer chooses firm 2 as the supplier. We investigated the behavior of the supplying firms with respect to Nash equilibrium, co-location tendency, tendency to locate at customer locations and strength to take the competitor out of the market.

We found the following results. No Nash equilibria exist for the described situation. Co-location does not occur, as one of the firms has the ability to take the other out of the market. If the second firm (firm 2) behaves as a follower, it will always enter the market with more tendency to locate at a customer location (supplying only that customer) if its abilities to invest in quality is less strong. When its ability is stronger than that of the leader, it will take the leader (firm 1) out of the market. The leader (firm 1) does not have the tendency to locate at a customer.

A specific algorithm has been developed to determine the optimal quality of both firms for the case the investment cost coefficient of the leader is lower than that of the follower. The algorithm is based on systematically following the order in which customers are taken from the competitor depending on the relative distance to both competitors.

The mathematical location problem when substituting the optimal quality levels is discontinuous and derivative information is lacking in most of the area. A heuristic procedure can be used to generate a good, but not necessarily optimal location for the leader and the follower.

Natural research questions following from this study is whether the tendency extends to situations where other suppliers are already in the market. A more mathematical question is what happens if the investment costs are not taken as linear, but as strictly convex, such that a firm has less tendency to take a high quality cost to take the competitor out of the market. The properties found are also less strong if the investment in quality is limited by a bound that is less than the natural bound that is implicit in the model. The proof of not having a Nash equilibrium loses its validity for that case.