Analysis of strong-arm comparator with auxiliary pair for offset calibration

Abstract

This paper analyzes the principle of the input-referred off calibration using the auxiliary pair for Strong-Arm comparator as well as its impact from the additional common-mode current and parasitic capacitance on the input-referred noise, offset, and decision time in detail. The comparison with the simulation results demonstrates the accurate prediction with the proposed analysis. This paper also discusses the design guideline to optimize the Strong-Arm comparator with the auxiliary pair for offset calibration.

1 Introduction

The latched comparator is one of the key building blocks of analog-to-digital converters (ADCs). For example, with the requirement of ADC being highly accurate and operating faster with improved power efficiency, the embedded comparator is required to be low power, less delay, higher precision, lower noise, and so on. As the Strong-Arm comparator can achieve fast speed and low power consumption with a simple structure, it is widely used in recent studies. The offset of the comparator in a single-channel SAR ADC mainly due to the process variation will simply cause a shift in the ADC transfer function. In the ADC with multiple comparators embedded in, on the other hand, the offset can impact the effective resolution as it degrades the DNL of the ADC. There are several methods to minimize the effect of the comparator offset.

A conventional method is to design redundancy [1]: a bank of comparators based on different reference levels is designed. One of them with the minimum offset after the fabrication will be activated and used in ADC. In [2, 3], combinational redundancy exploits inherent random variables to satisfy the requirement of the matching of transistors to increase the yield of the comparator. A similar idea from [4] is to digitally control the selection of the input transistor pair based on the detection of offsets due to different input transistor pairs applied. The weakness of these techniques is that the rest non-ideal comparators cost too much area. Thus the built-in calibration capability is almost always employed. By adjusting the load capacitance of the comparator, an offset generated by the adjustable capacitance is tuned to have the same amount but opposite polarity with the offset caused by process error [5]. This calibration requires many capacitor arrays to cover a sufficient range, thus requires a large chip area and increases energy consumption per comparison [6]. These large capacitors will significantly reduce the comparator operating speed. The unbalanced clock is introduced to compensate for the input-referred offset voltage caused by the process error by adjusting the clock signal [7,8,9]. Several clock signals (i.e., three clocks in [7, 8]) greatly increase the complexity of chip design. The body voltage of the input transistor pair is controlled to tune the current to compensate for input-referred offset [10]. However, it requires a special process to have enough calibration range and resolution.

The Strong-Arm comparator with offset calibration using auxiliary pair is often used in practical designs [11,12,13]. It has the advantages of simple circuit structure, tiny additional load capacitance, zero static power consumption, etc. To the best of the authors’ knowledge, there is no paper systematically analyzing this design at present. Hence, in this paper, we mathematically model the Strong-Arm comparator’s operating principle and reveal how the auxiliary pair calibrates the input-referred offset as well as affects input-referred noise and decision time. We introduce a guideline to help designers size the auxiliary pair and predict the comparator’s performance based on the analysis. Then a practical example is given to facilitate the guideline for the optimized design.

2 Performance analysis of strong-arm comparator

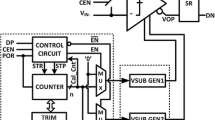
Figure 1 shows the structure of a Strong-Arm comparator with auxiliary pair. The operating principle of a Strong-Arm comparator is divided into four phases according to the working states of the transistors, which are resetting, sampling, propagation, and regeneration phases  [5].

2.1 Without auxiliary pair

A performance of the Strong-Arm comparator without the auxiliary pair is analyzed in detial in  [5]. We first outline the analysis in  [5], in order to extend it to the circuit with the auxiliary pair. Figures 2 and 3 show the common-mode and differential-mode currents flowing in the Strong-Arm comparator with auxiliary pair for offset calibration during the sampling and propagation phases, respectively. The capacitor pair $C_C$ is the parasitic capacitance at the drains of M1 and M2, and capacitor pair $C_L$ is the parasitic capacitance at the output ends. The voltages on $C_{C1}$ and $C_{C2}$ are denoted as $V_{cn}$ and $V_{cp}$, and the voltages on $C_{L1}$ and $C_{L2}$ are $V_{outn}$ and $V_{outp}$, respectively.

During the resetting phase, CLK is low to precharge the capacitor pair $C_C$ and $C_L$ to the supply voltage $V_{DD}$. When CLK goes high, the comparator starts its decision process. The rest three phases are detailed in the following subsections.

Fig. 1

Structure of strong-arm comparator with auxiliary pair

Fig. 2

Operation diagram of strong-arm comparator with auxiliary pair during the sampling phase

Fig. 3

Operation diagram of strong-arm comparator with auxiliary pair during the propagation phase

The blue lines and the red lines in Fig. 2 represent the common-mode currents ($I_{ic}$, $I_{calc}$) and the differential-mode currents ($i_{id}$, $i_{cald}$) through M1,2 and M7,8 during the sampling phase, respectively. Referring to  [5], when there is no auxiliary pair, M7,8 disconnected, the common-mode and differential-mode currents, $I_{ic}$ and $i_{id}$, are given by

$$\begin{aligned} I_{ic}= & {} \frac{1}{2}\cdot g_{m1,2}\cdot (V_{cm}-V_{S1}-V_{tN}) , \end{aligned}$$

(1)

$$\begin{aligned} i_{id}= & {} \frac{1}{2}\cdot g_{m1,2}\cdot v_{id} , \end{aligned}$$

(2)

where $g_{m1,2}$ is the transconductance of M1,2, $V_{cm}$ and $v_{id}$ are the common-mode and differential-mode input voltages, respectively. The tail switch S1 is assumed to operate in the triode region so that $V_{S1}\approx 0$V. $V_{tN}$ is the threshold voltage of NMOS transistor. During the sampling and propagation phases, M1 and M2 are supposed to operate in the saturation region.

2.1.1 Decision speed

Fig. 4

Signal waveforms in the decision process

As shown in Fig. 4, $V_{cp}$ and $V_{cn}$ drop from $V_{DD}$ to $V_{DD}-V_{tN}$ during the sampling phase, and then drop to $V_{DD}-V_{tN}-|V_{tP}|$ during the propagation phase. $V_{outp}$ and $V_{outn}$ remain at the same value during the sampling phase, and then drop from $V_{DD}$ to $V_{DD}-|V_{tP}|$ during the propagation phase.

During the sampling phase, the common-mode current discharges load capacitance $C_C$. The time window of the sampling phase is given by

$$\begin{aligned} T_s=\frac{C_C\cdot V_{tN}}{I_{ic}}. \end{aligned}$$

(3)

Then, in the propagation phase, the common-mode current discharges load capacitance $C_C$ and $C_L$, the time window of the propagation phase is given by

$$\begin{aligned} T_p=\frac{(C_C+C_L)\cdot |V_{tP}|}{I_{ic}}, \end{aligned}$$

(4)

where $V_{tP}$ is the threshold voltage of PMOS transistor.

In the regeneration phase, the differential-mode output voltage integrated during the sampling and propagation phases exponentially increases to $V_{DD}$, the time window is given by

$$\begin{aligned} T_{reg}= & {} {\tau }_{reg}\cdot {\mathrm {ln} \left( \frac{V_{DD}}{2\cdot V_{OD}}\right) }={\tau _{reg}}\cdot {\mathrm {ln}\left( \frac{V_{DD}}{2\cdot A_v \cdot v_{id}}\right) }, \end{aligned}$$

(5)

where ${\tau }_{reg}\approx C_L/g_{m5,6}$, $A_v$ is the differential-mode input-to-half-output gain of the comparator without the auxiliary pair  [14], which is given by

$$\begin{aligned} A_v= & {} \left\{ \begin{array}{l} \frac{1}{2}\cdot g_{m1,2}\cdot \frac{T_s+T_p}{C_{L}-C_C} \frac{C_C}{C_{L}}\ll \frac{1}{2} \\ \frac{1}{2}\cdot g_{m1,2}\cdot \frac{T_s+\frac{1}{2}\cdot T_p}{C_{L}-C_C}\cdot \frac{T_p}{{\tau }_p} \frac{C_C}{C_{L}}\approx 1 \\ \frac{1}{2}\cdot g_{m1,2}\cdot \frac{{\tau }_p-T_s}{C_{L}-C_C}\cdot e^{-\frac{T_p}{\tau _p}} \frac{C_C}{C_{L}}\gg 2 \end{array}\right. \nonumber \\\approx & {} \left\{ \begin{array}{l} \frac{1}{2}\cdot g_{m1,2}\cdot \frac{T_p}{C_{L}} \frac{C_C}{C_{L}}\ll \frac{1}{2} \\ \frac{1}{2}\cdot g_{m1,2}\cdot \frac{T_s+\frac{1}{2}\cdot T_p}{C_{L}\cdot C_C}\cdot {T_p}\cdot g_{m3,4} \frac{C_C}{C_{L}}\approx 1 \\ \frac{1}{2}\cdot g_{m1,2}\cdot \frac{\frac{C_L}{g_{m3,4}}+ T_s}{C_C}\cdot e^{-\frac{T_s}{\tau _p}} \frac{C_C}{C_{L}}\gg 2 , \end{array}\right. \end{aligned}$$

(6)

where $\tau _p$ is the time constant in the propagation phase, which is given by

$$\begin{aligned} \tau _p=\frac{C_{L}\cdot C_C}{g_{m3,4}\cdot (C_{L}-C_C)} . \end{aligned}$$

(7)

The total decision time is given by the sum of time windows of three phases:

$$\begin{aligned} T_{total}=T_{s}+T_{p}+T_{reg}. \end{aligned}$$

(8)

2.1.2 Input-referred noise

In the Strong-Arm comparator, based on the analysis in  [5], the power of output noise at the end of the propagation phase is composed of two parts: the integration of thermal noise PSD across $C_L$ pair in the propagation phase, and the noise across $C_C$ pair integrated during the sampling phase transmitted to $C_L$ pair. Then, the input-referred noise $v^2_{n,in}$ is given by

$$\begin{aligned} v^2_{n,in}= & {} {{v}^2_{n,out}}/{(A_v)^2} \nonumber \\\approx & {} \frac{4\cdot S_{in}}{g_{m1,2}^2}\cdot \left\{ \begin{array}{l} \frac{1}{T_s+T_p} \frac{C_C}{C_{L}}\ll \frac{1}{2} \\ \frac{T_s+\frac{1}{3}\cdot T_p}{(T_s+\frac{1}{2}\cdot T_p)^2} \frac{C_C}{C_{L}}\approx 1 \\ \frac{1}{T_s-\tau _p} \frac{C_C}{C_{L}}\gg 2, \end{array} \right. \end{aligned}$$

(9)

where $S_{in}=S_{in1}+S_{in2}=8kT\gamma g_{m1,2}$ is the total noise current PSD from the differential input pair, where $S_{in1}$ and $S_{in2}$ are the noise current PSD in M1 and M2 respectively. k is the Boltzmann constant and $\gamma$ is a process-dependent parameter.

2.2 Introduction of auxiliary pair

In practice, due to the process variation, a differential-mode current through M1 and M2 will be generated during the sampling and propagation phases even with two equal input voltages. Hence, after a while, the voltage drops on the load capacitor pairs are not equal. The unequal load capacitor pairs $C_C$ and $C_L$ will also unbalance the comparator. The positive feedback loop of the regeneration phase will enlarge the differential-mode output, and then the comparator will generate the wrongly latched output. This undesired output can be regarded as from that the input-referred offset produces a differential-mode current $i_{os}$ to unbalance the ideal Strong-Arm comparator. The auxiliary pair M7 and M8 can be introduced to ensure that the differential-mode output after pre-amplification keeps zero when there is no differential-mode input. It introduces the additional common-mode discharging current $I_{calc}$ as shown in Figs. 2 and 3 with the blue line through M7,8. Besides, it also brings the additional parasitic capacitance. For the convenience of analysis, we have two assumptions:

• (a) The voltage drops on switches S1, S2, and S3 as shown in Fig. 1 are equal, i.e. $V_{S1}=V_{S2}=V_{S3}$, and small enough. In other words, these switches are operating in the deep triode region.

• (b) The common-mode input voltages on M7,8 and M1,2 are equal, i.e. $V_{calc}=V_{cm}=V_{DD}/2$.

2.2.1 Additional common-mode current

As stated above, the auxiliary pair will introduce an additional common-mode discharging current $I_{calc}$ during the sampling and propagation phases. The increased discharging current will reduce the time windows of the sampling and propagation phases. Based on the assumptions (a) and (b), the operating statuses of M1,2 and M7,8 are the same. Similar to $I_{ic}$, the additional common-mode current $I_{calc}$ from the auxiliary pair M7,8 is given by

$$\begin{aligned} I_{calc}= & {} \frac{1}{2}\cdot g_{m7,8}\cdot (V_{calc}-V_{S2,3}-V_{tN}) . \end{aligned}$$

(10)

$I_{calc}$ and $I_{ic}$ jointly affect the key performance of the comparator. Since M7 and M8 are supposed to operate in the saturation region in the pre-amplification phase, the increment ratio of the common-mode current r is given by

$$\begin{aligned} r= & {} \frac{I_{ic}+I_{calc}}{I_{ic}}\approx \frac{g_{m1,2}+g_{m7,8}}{g_{m1,2}}\approx \frac{\beta _{1,2}+\beta _{7,8}}{\beta _{1,2}}, \end{aligned}$$

(11)

where $\beta _{1,2}=\mu \cdot C_{ox} \cdot W_{1,2}/L_{1,2}$ and $\beta _{7,8}=\mu \cdot C_{ox} \cdot W_{7,8}/L_{7,8}$. $C_{ox}$ and $\mu$ are the oxide capacitance per unit area and surface mobility of the carrier.

2.2.2 Additional differential-mode current

The auxiliary pair generates an additional differential-mode current to compensate for the contribution from the offset current to the output. Similar to the $i_{id}$ derivation, the differential-mode current $i_{cald}$ through M7,8 is given by

$$\begin{aligned} i_{cald}= & {} \frac{1}{2}\cdot g_{m7,8}\cdot v_{cald} . \end{aligned}$$

(12)

Therefore, when a comparison starts, the total differential-mode current unbalancing the circuit becomes $i_{id}+i_{os}+i_{cald}$.

2.2.3 Additional load capacitance

As explained in the previous sections, the capacitance $C_C$ and $C_L$ are the key parameters that determine the performance of the Strong-Arm comparator. Here we first analyze $C_C$ and $C_L$ in the different phases for the Strong-Arm comparator without auxiliary pair. During the sampling phase, M3 and M4 are off. For the left half circuit of the comparator, the capacitance $C_{C1}$ is composed of the parasitic capacitance from M1, M3, and S6.

All the parasitic capacitance is related to the width but can be assumed to be independent of the length of the transistors. Hence, the total capacitance from M1 is approximately expressed as $c_{pc}\cdot W_{M1}$, where $c_{pc}$ represents parasitic capacitance per unit width, which is fixed by the process technology. Similarly, the total parasitic capacitance from M3 and S6 is given by $c_{pc}\cdot W_{M3}$ and $c_{pc}\cdot W_{S6}$ respectively, where $W_{S6}$ is the width of switch S6. Thus, during the sampling phase, $C_{L1}$ is isolated by M3, $C_{C1}$ of the comparator without the auxiliary pair is given by

$$\begin{aligned} C_{C1}= c_{pc}\cdot (W_{M1}+W_{M3}+W_{S6}). \end{aligned}$$

(13)

During the propagation phase, M3 and M1 operate in the saturation region. Thus, $C_{C1}$ of the comparator without the auxiliary pair still approximates $c_{pc}\cdot (W_{M1}+W_{M3}+W_{S6})$. Since the output of the comparator is always followed by an inverter, $C_{L1}$ of the comparator without the auxiliary pair is composed of the drain-gate parasitic capacitance of S4, M3, M6 and a following CMOS (inverter), which is given by

$$\begin{aligned} C_{L1}=c_{pc}\cdot (W_{inv,p}+W_{inv,n}+W_{S6}+W_{M6}+W_{M3}), \end{aligned}$$

(14)

where $W_{inv,p}$ and $W_{inv,n}$ are the channel widths of the PMOS and NMOS of the inverter. $C_L$ remains at the same value in the regeneration phase, while $C_C$ does not affect regeneration.

The introduction of the auxiliary pair will add additional load capacitance to $C_C$, which is from the parasitic capacitance of the additional transistors M7 and M8. It is again given by $c_{pc}\cdot W_{M7}$. Hence, the updated capacitor pair $C'_{C1,2}$ with the introduction of the auxiliary pair is given by

$$\begin{aligned} C'_{C1,2}=c_{pc}\cdot (W_{M1,2}+W_{M3,4}+W_{S6,7}+W_{M7,8}) , \end{aligned}$$

(15)

which is increased by $1+\frac{W_{M7,8}}{W_{M1,2}+W_{M3,4}+W_{S6,7}}$ times compared with the original one. We define the increase ratio as $\eta$, which is given by

$$\begin{aligned} \eta = \frac{C'_C}{C_C}\approx 1+\frac{W_{M7,8}}{W_{M1,2}+W_{M3,4}+W_{S6,7}} . \end{aligned}$$

(16)

On estimating $C_{L}$, it is evident that the auxiliary pair does not affect $C_{L}$. Hence, $C_{L}$ keeps constant with the introduction of an auxiliary pair.

2.3 Decision speed with auxiliary pair

The time window of the sampling phase of the comparator with auxiliary pair is the period that the capacitor $C_C$ being discharged by the common-mode current through the input differential pair $I_{ic}$ as well as the common-mode current through the auxiliary pair $I_{calc}$ until the voltage on $C_C$ drops by a $V_{tN}$. Then the time window in  [5] is rewritten as:

$$\begin{aligned} T'_s=\frac{\eta \cdot C_C\cdot V_{tN}}{I_{ic}+I_{calc}}=\frac{\eta \cdot C_C\cdot V_{tN}}{I_{ic}+\frac{g_{m7,8}}{g_{m1,2}}\cdot I_{ic}}=\frac{\eta }{r} \cdot T_s . \end{aligned}$$

(17)

The sampling phase time window of the comparator with auxiliary pair compared with the case without an auxiliary pair is changed by $\eta /r$ times due to the additional common-mode current and capacitance.

Similarly, the time window of the propagation phase of the comparator with auxiliary pair $T'_p$ is the period of that the capacitors $C'_C$ and $C'_{L}$ being simultaneously discharged by $I_{ic}$ and $I_{calc}$ until the voltage on $C'_{L}$ drops by a $|V_{tP}|$. The auxiliary pair has no impact on $C_L$, thus $C'_L=C_L$. Supposing that M1,2 and M7,8 operate in the saturation region, the time window for the comparator with auxiliary pair, $T'_p$, is rewritten as:

$$\begin{aligned} T'_p=\frac{(C'_C+C'_{L})\cdot |V_{tP}|}{I_{ic}+\frac{g_{m7,8}}{g_{m1,2}}\cdot I_{ic}}=\frac{\eta \cdot C_C+C_L}{r\cdot (C_C+C_L)} \cdot T_p . \end{aligned}$$

(18)

During the regeneration phase, the differential-mode output voltage of the comparator with auxiliary pair at the end of the propagation phase, $2V'_{OD}$, exponentially increases to $V_{DD}$, similarly as given by (5). The updated time window of the regeneration phase is given by

$$\begin{aligned} \begin{array}{c} T'_{reg}={\tau }'_{reg}\cdot {\mathrm {ln}\left( \frac{V_{DD}}{2\cdot V'_{OD}}\right) }={\tau }_{reg}\cdot \mathrm {ln}\left( \frac{V_{DD}}{2\cdot A'_v \cdot v_{id}}\right) , \end{array} \end{aligned}$$

(19)

where $\tau '_{reg}=\tau _{reg}$ since $C_L$ is unchanged. By replacing the time windows and the load capacitance in (6) with the values for the Strong-Arm comparator with the auxiliary pair, the updated input-output voltage gain $A'_v$ is given

$$\begin{aligned} A'_v= & {} \left\{ \begin{array}{l} \frac{1}{2}\cdot g_{m1,2}\cdot \frac{T'_s+T'_p}{C'_{L}-C'_C} \frac{C'_C}{C'_{L}}\ll \frac{1}{2} \\ \frac{1}{2}\cdot g_{m1,2}\cdot \frac{T'_s+\frac{1}{2}\cdot T'_p}{C'_{L}-C'_C}\cdot \frac{T'_p}{{\tau }'_p} \frac{C'_C}{C'_{L}}\approx 1 \\ \frac{1}{2}\cdot g_{m1,2}\cdot \frac{{\tau }'_p-T'_s}{C'_{L}-C'_C}\cdot e^{-\frac{T'_p}{\tau '_p}} \frac{C'_C}{C'_{L}}\gg 2 \end{array}\right. \nonumber \\\approx & {} \left\{ \begin{array}{l} \frac{g_{m1,2}}{2}\cdot \frac{T_p}{r\cdot C_{L}} \frac{C_C}{C_{L}}\ll \frac{1}{2} \\ \frac{g_{m1,2}}{2}\cdot \frac{\frac{\eta }{r}\cdot T_s +\frac{1+\eta }{4\cdot r}\cdot T_p}{\eta \cdot C_{L}\cdot C_C}\cdot \frac{(1+\eta )\cdot {T_p}\cdot g_{m3,4}}{2\cdot r} \frac{C_C}{C_{L}}\approx 1 \nonumber \\ \frac{g_{m1,2}}{2}\cdot \frac{\frac{C_L}{g_{m3,4}}+ \frac{\eta }{r}T_s}{\eta \cdot C_C}\cdot e^{-\frac{\eta \cdot T_p}{r \cdot \tau _p}} \frac{C_C}{C_{L}}\gg 2 \end{array}\right. \nonumber \\\approx & {} \left\{ \begin{array}{l} \frac{A_v}{r} \frac{C'_C}{C'_{L}}\ll \frac{1}{2} \\ \frac{3+\eta }{4\cdot r^2}\cdot A_v \frac{C'_C}{C'_{L}}\approx 1 \\ \frac{(A_v)^{\frac{\eta }{r}}}{r} \frac{C'_C}{C'_{L}}\gg 2 . \end{array}\right. \end{aligned}$$

(20)

By deriving this differential input-output gain $A'_v$, we can quickly obtain the differential-mode output of the comparator with the auxiliary pair at the end of the propagation phase $2V'_{OD}$ and the time window of the regeneration phase $T'_{reg}$ given by (19).

The total decision time is the sum of time windows of three phases:

$$\begin{aligned} \begin{array}{c} T'_{total} = T'_s+T'_p+T'_{reg} \end{array} . \end{aligned}$$

(21)

According to (17), (18) and (19), the change in the total decision time due to the introduction of the auxiliary pair is given by

$$\begin{aligned} \Delta T_{total}= & {} T'_{total}-T_{total}\nonumber \\= & {} \left( \frac{\eta }{r} -1\right) \cdot T_s + \left( \frac{\eta \cdot C_C+C_L}{r\cdot (C_C+C_L)}-1\right) \cdot T_p \nonumber \\&+ \tau _{reg}\cdot \mathrm {ln}\left( \frac{A_v}{A'_v}\right) . \end{aligned}$$

(22)

With the auxiliary pair, the time windows of the sampling and propagation phases usually decrease. In contrast, the time window of the regeneration phase increases since $V'_{OD}$ is reduced from $V_{OD}$ with the introduction of the auxiliary pair as explained in the next subsection. Since $g_{m7,8}$ is normally small enough compared with $g_{m1,2}$ ($r \approx 1$), the reduction of time windows of the sampling and propagation phases dominates the change in the total decision time. When $g_{m7,8}$ becomes larger (r increases), the increment in the time window of the regeneration phase starts to dominate the change of the total decision time. In practice, however, we do not see the increment since $T_s+T_p$ is often multiples of $\tau _p$. The decision time starts to increase when r is larger than 2. This means that the $g_m$ of the auxiliary pair is larger than that of the main differential pair according to (11), which is not reasonable for our purpose to calibrate the offset caused by M1 and M2.

2.4 Calibration sensitivity and range with auxiliary pair

The total differential-mode current unbalancing capacitor pairs is updated to $i_{id}+i_{os}+i_{cald}$. The calibration guarantee the sum of the different-mode output voltages integrated by $i_{os}$ and $i_{cald}$ to be zero. Based on the assumptions (a) and (b) given at the beginning of this section, the process is approximated to make $i_{os}+i_{cald}=0$. According to $i_{cald}=\frac{1}{2}\cdot g_{m1,2}\cdot v_{os,cal}$, we refer the differential-current $i_{cald}$ to the differential input pair to give the offset calibrated by the auxiliary pair, which is $v_{os,cal}$. We define the ratio between the calibrated offset and the differential-mode input voltage to auxiliary pair as the calibration sensitivity, which is given by

$$\begin{aligned} \alpha= & {} \frac{v_{os,cal} }{v_{cald}} \approx \frac{g_{m7,8}}{g_{m1,2}} \approx \frac{\beta _{7,8}}{\beta _{1,2}} . \end{aligned}$$

(23)

The calibration range determines the maximum input-referred offset that the auxiliary pair can compensate. According to the calibration sensitivity $\alpha$ given by (23), the calibration range can be determined if we determine the input range for the auxiliary pair. All the analysis above is based on the assumption that M1,2 and M7,8 operate in the saturation region during the pre-amplification phase. The allowable input range for M7 and M8 is $V_{tN}+V_{S2,3}<V_{calp,n}<V_{DD}-|V_{tP}|$. Supposing that the common-mode input voltage is $V_{cm}=V_{DD}/2$, the allowable input range for M7 and M8 is limited to $V_{tN}+V_{S2,3}<V_{calp,n}<V_{DD}-V_{tN}-V_{S2,3}$ when we assume $|V_{tP}|=V_{tN}$. Then the calibration range is derived as:

$$\begin{aligned} \pm v_{os,cal,max} =\pm 2\cdot \alpha \cdot \left( V_{cm}-(V_{tN}+V_{S2,3}))\right. . \end{aligned}$$

(24)

The change in $C_C$ and $C_{L}$ leads to the change in the integration time window, which has the same impact on the auxiliary pair and the main input transistor pair. Thus, the calibration sensitivity is independent of the load capacitance $C_C$ and $C_{L}$. As a result, the change of the parasitic capacitance does not change the calibration sensitivity. The calibration range $\pm v_{os,cal,max}$ is determined by $\alpha$, as well as the input range to the auxiliary pair $V_{cm}-(V_{tN}+V_{S2,3})$ which is also independent of $C_C$ and $C_{L}$, as given by (24). Thus, the change in the parasitic capacitance does not change the calibration range, either.

The input voltage to the auxiliary pair is usually generated from a digital-analog-converter (DAC). The calibration resolution equals the product of the calibration sensitivity and the DAC resolution. Since $\alpha$ is usually small, there is no strict requirement for the DAC resolution. Though the auxiliary pair itself has an additional offset, this offset can also be referred to the differential input pair by sensitivity $\alpha$, and then calibrated by the auxiliary pair itself.

2.5 Input-referred noise derivation with auxiliary pair

With the introduction of the auxiliary pair, by replacing the noise current PSD and time windows in (9) with the values for the Strong-Arm with the auxiliary pair, the input-referred noise voltage is given by

$$\begin{aligned} v'^2_{n,in}\approx & {} \frac{4\cdot (S_{in}+S_{in,cal})}{g_{m1,2}^2}\cdot \left\{ \begin{array}{l} \frac{1}{T'_s+T'_p} \frac{C_C}{C_{L}}\ll \frac{1}{2} \\ \frac{T'_s+\frac{1}{3}\cdot T'_p}{(r \cdot T'_s+\frac{1}{2}\cdot T'_p)^2} \frac{C_C}{C_{L}}\approx 1 \\ \frac{1}{T'_s-\tau '_p} \frac{C_C}{C_{L}}\gg 2\\ \end{array} \right. \nonumber \\\approx & {} \frac{4\cdot r \cdot S_{in}}{g_{m1,2}^2}\cdot \left\{ \begin{array}{l} \frac{1}{\frac{\eta }{r}\cdot T_s+\frac{1}{r} \cdot T_p} \frac{C_C}{C_{L}}\ll \frac{1}{2} \\ \frac{\frac{\eta }{r}\cdot T_s+\frac{1}{3}\cdot \frac{1+\eta }{2\cdot r}\cdot T_p}{(\frac{\eta }{r}\cdot T_s+\frac{1}{2}\cdot \frac{1+\eta }{2\cdot r}\cdot T_p)^2} \frac{C_C}{C_{L}}\approx 1\\ \frac{1}{\frac{\eta }{r}\cdot T_s-\frac{1}{r}\cdot \tau _p} \frac{C_C}{C_{L}} \gg 2 \\ \end{array} \right. \nonumber \\\approx & {} \left\{ \begin{array}{l} {r^2} \cdot {v^2_{n,in}} \frac{C_C}{C_{L}}\ll \frac{1}{2} \\ \frac{4\cdot {r^2} }{3\cdot \eta +1} \cdot {v^2_{n,in}} \frac{C_C}{C_{L}}\approx 1\\ \frac{{r^2} }{\eta } \cdot {v^2_{n,in}} \frac{C_C}{C_{L}} \gg 2 , \\ \end{array} \right. \end{aligned}$$

(25)

From (25), we can see the following:

• (a) When ${C_C}/{C_{L}} \ll {1}/{2}$, $T_s \ll T_p$. Then the additional parasitic capacitance almost has no effect on the input-referred noise voltage.

• (b) When ${C_C}/{C_{L}}\approx 1$, $2T_s \approx T_p$. Then the additional parasitic capacitance reduces the input-referred noise voltage by $\sqrt{{4}/({3\cdot \eta +1})}$ times.

• (c) When ${C_C}/{C_{L}}\gg 2$, $T_s \approx T_p \gg \tau _p$. Then the additional parasitic capacitance reduces the input-referred noise voltage by $\sqrt{{1}/{\eta }}$ times.

3 Simulation results

Table 1 Transistors size setting

To demonstrate the feasibility of the analysis, the prototype Strong-Arm comparator circuit is designed in 28nm FD-SOI technology, whose nominal supply is 1V. W and L of each transistor in the circuit are summarized in Table. 1.

3.1 Decision time

3.1.1 Decision time dependence on input voltage

Fig. 5

Decision time dependence on a the common-mode voltage and b the differential-mode voltage

Figure 5(a) shows the decision time dependence on the common-mode input voltage $V_{cm}$ applied on M1,2 and M7,8 while $v_{id}$ and $v_{cald}$ are fixed to 0.5mV and 0mV, respectively. The increment of the common-mode input voltage leads to a larger discharging current that speeds up the comparator decision. The time windows of the sampling and propagation phases decrease with the trend of the function $1/V_{cm}$, which is given by (8).

We then fix the common-mode input voltage $V_{cm}$ to $V_{DD}/2=0.5V$ and sweep $v_{id}$ from 0.5mV to 4mV while $v_{cald}$ is kept 0mV as shown in Fig. 5(b). Even with the increased differential-mode input voltage $v_{id}$, the time windows of the sampling and propagation phases stay almost constant, while the time window of the regeneration phase decreases due to the increment of differential-mode output at the end of the propagation phase. The downward trend corresponds to $-\mathrm {ln}({v_{id}})$, which agrees with (19).

Fig. 6

Decision time versus $\alpha$

3.1.2 Decision time dependence on size of auxiliary pair

Figure 6 shows the decision time dependence on $\alpha$, representing how the size of M7,8 affects the decision time of the comparator with auxiliary pair. We change $W_{M7,8}$ from 120nm to $1.2\mu$m while $L_{M7,8}$ is fixed to 90nm. $v_{id}$ and $v_{cald}$ are 0.5mV and 0mV respectively. Analysis considers both additional current and parasitic capacitance based on (21). When we take the additional capacitance into account, with the increment in $W_{M7,8}$, increasing $\eta$ and $r={1+\alpha }$ jointly determine the decision time according to (17) and (18), then the curve becomes flatter to have better agreement with simulation, as shown in Fig. 6.

3.2 Calibration sensitivity

Fig. 7

Calibration sensitivity versus size change of transistors

Fig. 8

Input-referred offset voltage dependent

Figure 7 shows the sensitivity $\alpha$ dependent on $\beta _{7,8}/\beta _{1,2}$. Circles show the simulation results when $W_{M7,8}/L_{M7,8}$ is fixed to $240\mathrm {nm}/90\mathrm {nm}$, while $W_{M1,2}/L_{M1,2}$ is fixed $9\mu \mathrm {m}/45\mathrm {nm}$ in triangle case. Our analysis in (23) gives a good prediction of the sensitivity. The discrepancy when $\alpha$ becomes larger is explained by two reasons:

• (a) The unequal voltage drops between S1 and S2,3 will change the sensitivity.

• (b) The auxiliary pair can not generate sufficient compensating current as expected since M7 and M8 can go into the triode region before the regeneration starts.

When the input transistors operate in the triode region after the regeneration starts, the voltage difference between $V_{S1}$ and $V_{S2,3}$ can not be ignored if $V_{S2,3}$ is larger than $V_{S1}$. Thus, the auxiliary pair is not able to generate enough compensating current, which means that the calibrated integrated differential-mode output voltage, in reality, will be slightly smaller than the simplified calculation result. Besides, if $\beta _{7,8}$ increases, it will lead to a larger common-mode current $i_{calc}$ resulting in a larger $V_{S2,3}$. The calibrated integrated differential-mode output voltage, in reality, will increase slower along with the increment of $\beta _{7,8}$.

Figure 8 shows the input-referred offset voltage dependent on $v_{cald}$ when transistor sizes are fixed as summarized in Table. 1. The calibrated offset changes linearly with the increment of $v_{cald}$. When $v_{cald}$ is small, the analysis results precisely agree with the simulation. As $|v_{cald}|$ increases, the slope of the simulation results becomes flatter leading to a discrepancy with analysis results. This is because M7 or M8 starts to operate in the triode region at the boundaries of the allowable input range.

3.3 Input-referred noise

Fig. 9

Input-referred noise dependence on a transistor size of the comparator and b relative size of auxiliary and main circuits

Fig. 9(a) shows the input-referred noise simulation result when we keep W/L ratio of the transistors in the circuit constant and scale all transistors simultaneously in the same proportion, which is defined as $\xi$. Since increasing sizes of transistors give larger parasitic capacitance considered as load capacitor pairs while keeping the current through the comparator, it leads to larger $T_s$ and $T_p$ according to (3) and (4). Thus, the input-referred thermal noise voltage decreases with the trend of $1/\sqrt{\xi }$ according to (9).

Fig. 9(b) shows the input-referred noise dependence on $\alpha$. Firstly, $W_{M7,8}$ is fixed to 240nm, then $L_{M7,8}$ is swept from 360nm to 90nm. Secondly, $L_{M7,8}$ is fixed to 90nm, and $W_{M7,8}$ is swept from 240nm to 960nm. There are two slopes of the input-referred noise increment along with $\alpha$. The slope, while decreasing $L_{M7,8}$, is larger than the that while increasing $W_{M7,8}$. This result is due to the additional capacitance of the auxiliary pair at $C_C$. When we change the length $L_{M7,8}$ and fix the width $W_{M7,8}$, $\beta _{7,8}$ changes, but the parasitic capacitance from the auxiliary pair does not increase, which means $\eta$ is fixed. Regardless of the ratio of $C_C$ to $C_{L}$, the input noise increases by ${r}=1+\alpha$ times according to (9). When we fix the length $L_{M7,8}$ and change the width $W_{M7,8}$, on the other hand, $\beta _{7,8}$ increases while the additional parasitic capacitance from the auxiliary pair also increases. The increment in capacitance leads to a narrower bandwidth limiting thermal noise PSD integration, thereby reducing the input-referred noise. Hence, the increment of the additional capacitance suppresses the increment of input-referred noise caused by r. The complete change of input-referred noise voltage is related to the ratio between $C_C$ and $C_{L}$ as given by (25).

4 Design guideline

The analysis given in this paper can help to design a Strong-Arm comparator with auxiliary pair by intuitively predicting its performance and calibration ability with simple mathematical equations.

Suppose that we will add an auxiliary pair to calibrate the input-referred offset of the Strong-Arm comparator. The introduction of the auxiliary pair adds the input-referred noise. Besides, depending on the $\alpha$ and $\eta$, the decision time of the comparator may change. There are trade-off relationships among the calibration range, decision time, and input-referred noise to determine the size of the auxiliary pair. For instance, if we need a wider calibration range, a larger $g_{m7,8}$ is needed according to (23) and (24). It leads to more input-referred noise according to (25). Also, the additional parasitic capacitance increases the power consumption but reduces the decision time by reducing $T_s$ and $T_p$. To insert a suitable auxiliary pair to calibrate the Strong-Arm comparator, we need to optimize its size by determining the values of $\alpha$ and $\eta$. We first need to know the desired calibration resolution and the minimum voltage step from the digital-to-analog converter (DAC) to the auxiliary pair to determine the maximum calibration sensitivity $\alpha$. Then, we can determine the minimum $\alpha$ with the required calibration range. Based on the requirements of decision time and input-referred noise, we can decide $\eta$. Finally, $W_{M7,8}$ and $L_{M7,8}$ are determined.

Table 2 Transistors size setting of the strong-arm comparator without the auxiliary pair

4.1 Parameter setting process

As one of the practical examples, we start with a Strong-Arm comparator without the auxiliary pair whose transistor sizes are summarized in Table. 1 except M7, M8, S2 and S3. Its input-referred noise voltage, decision time (while $v_{id}=0.5$mV) and input-referred offset are 0.475mV, 44ps and $\sigma =0.5$mV, respectively. $|V_{tP}|=V_{tN}=0.2V$ is used for the threshold voltage. Then we are required to add an auxiliary pair by finding the optimum size of M7,8 to satisfy the metrics listed in Table. 2. Here we suppose that the voltage applied to the auxiliary input is ideal and noiseless. Although the variation and noise on the auxiliary input affect the performance of the comparator by introducing the fluctuations on both the differential- and common-mode currents, according to (11) and (23) the impact on the decision time, the input-referred noise and the offset is suppressed by the factor of $g_{m7,8}/g_{m1,2}$, which is usually $\ll$1. As it is common to supply the auxiliary input voltage from an on-chip DAC or regulator, we can safely assume that the variation and noise on the voltage are originally small. Thus, in total, its impact on the comparator performance can be negligible.

• (a) Suppose that we need to calibrate $\pm 3\sigma =\pm 1.5$mV offset, so that the calibration success rate can reach $99.7\%$. Since the input range to the auxiliary pair is limited to $\pm v_{os,cal,max}=\pm 2\cdot (V_{cm}-(V_{tN}+V_{S2,3}))=\pm 0.6$V according to (24) in Sect. 2.4, we can determine the minimum $\alpha$ that meets the calibration requirements, which is $\alpha \ge {3\sigma }/{v_{os,cal,max}} \approx {1}/{400}$. Hence, we are able to get the allowable minimum of $\beta _{7,8}$ from $\alpha = {\beta _{7,8}}/{\beta _{1,2}}$ in (23) while $\beta _{1,2}$ is given. In practice, we need to leave a certain margin since the auxiliary pair itself is also affected by the process variation.

  A larger $\alpha$ is always accompanied by lower calibration resolution when the input voltage to the auxiliary pair comes from the embedded DAC whose minimum voltage step is limited. When the required calibration resolution is ${\sigma }/{16}=0.03125$mV supposing that the minimum step voltage of the embedded DAC is 1mV, $\alpha \le {0.03125}={1}/{32}$.

• (b) When introducing the auxiliary pair, we need to accept a certain amount of additional noise as given by (25). With a fixed $\alpha$, a larger $\eta$ can suppress the increase of the input-referred noise but slow down the decision. If the input-referred noise voltage is allowed to increase $\chi$ times compared with the original one, according to (25), when $C_C \approx C_{L}$ for instance, $\sqrt{{(2\cdot (1+\alpha ))^2}/{(3\cdot \eta +1)}} \le \chi$. Then, $\eta \ge \left( \left( {2\cdot (1+\alpha )}/{\chi }\right) ^2-1\right) /3$.

• (c) Regarding the decision time, we know that the change in the decision time is dominated by the change of the time window of the pre-amplification phase, as explained in Sect. 2.3 . According to (17) and (18), whether the time window of the pre-amplification phase increases or decreases depends on whether $r\eta$ is greater or smaller than 1. We prefer not to increase the decision time of the comparator which means $r \eta = {\eta }/{(1+\alpha )}\le 1$. Hence, $\eta \le (1+\alpha )$.

Then, when we are allowed to increase the input-referred noise $1\%$, i.e., $\chi =1.01$, we are able to obtain $\alpha \le {1}/{62}$ from $\left( \left( {2\cdot (1+\alpha )}/{\chi }\right) ^2-1\right) /3 \le \eta \le 1+\alpha$.

When we choose $\alpha ={1}/{75}$, $\left( \left( {2\cdot (1+\alpha )}/{\chi }\right) ^2-1\right) /3 = 1.0088\le \eta \le 1+\alpha = 1.0133$, which means from $\eta = 1+{W_{M7,8}}/{(W_{M1,2}+W_{M3,4}+W_{S6,7})}$ in (16), $211\mathrm {nm} \le W_{M7,8} \le 319 \mathrm {nm}$. When we choose 240nm for $W_{M7,8}$, from $\alpha = {\beta _{7,8}}/{\beta _{1,2}} = ({W_{M7,8}/L_{M7,8}})/({W_{M1,2}/L_{M1,2}}) = {1}/{75}$, we can determine $L_{M7,8}=90 \mathrm {nm}$.

4.2 Performance prediction

From ${W_{M7,8}}/{L_{M7,8}}={240\mathrm {nm}}/{90\mathrm {nm}}$, we can use $\alpha ={1}/{75}$, $r={75}/{76}$ and $\eta ={101}/{100}$. Since in this example $C_C/C_{L} < 1$ but $C_C$ is not much smaller than $C_{L}$, we can predict the key performances of the comparator compared with the original one through two models: $C_C/C_{L}\ll 1/2$ and $C_C \approx C_{L}$.

• (a) The time window of the pre-amplification phase is reduced by $0.1\mathrm {ps}\sim 0.3 \mathrm {ps}$, while the time window of the regeneration phase keeps almost constant. From the simulation results in Fig. 6, the decision time drop is 0.2ps when $\alpha =1/75$.

• (b) The input-referred noise is predicted to increase to $0.481\mathrm {mV} \sim 0.487\mathrm {mV}$. From the simulation results in Fig. 9(a), the input referred noise is 0.482mV.

• (c) The calibration range can reach $\pm 8$mV without considering the margin. From the simulation results in Fig. 8, when $v_{cald}$ reaches $V_{calp}-V_{valn}=0.6$V, the calibrated offset reaches 6.9mV. The discrepancy is 1.1mV compared with the expected value 8mV. It is because the actual $V_{tN}$ and $|V_{tP}|$ are slightly larger than 0.2V.

• (d) The calibration resolution can reach ${1}/{75}\mathrm {mV}={2\sigma }/{75}$ which agrees with the simulation results shown in Fig. 8.

Sometimes we may not find an intersection region based on decision time and input-referred noise voltage requirements. Then, we need to relax the specifications. For instance, we may need to allow the comparator more decision time to increase the maximum limitation of $\eta$. Or we may need to allow more input-referred noise, while increasing $\chi$ will reduce the minimum limitation of $\eta$. By following the above design procedure, we have the optimum $W_{M7,8}$ and $L_{M7,8}$ with a minimized performance penalty.

5 Conclusion

This paper systematically analyzes the operating principle of the Strong-Arm comparator with offset calibration using the auxiliary pair. Through simplified equations, the calibration principle and ability of the auxiliary pair are accurately predicted. The impact of the auxiliary pair, including additional current and parasitic capacitance, on the decision speed and input-referred noise is analyzed with these equations. The designers can find the optimum size of the auxiliary pair in the Strong-Arm comparator by determining the values of $\alpha$ and $\eta$ defined in the analysis, which can be efficiently derived according to their design requirements. A practical example is given to facilitate the guideline for the optimized design.