Abstract
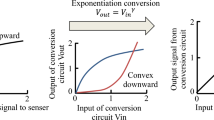
We proposed an exponentiation conversion circuit which can change its power exponent to any value to compensate the nonlinearity of electronic devices. The proposed circuit is a small scale circuit utilizing the exponential characteristic in the subthreshold operation of MOSFET. In the proposed circuit, the new exponential conversion circuit converts signal multiplied logarithmically transformed input signal by the power exponent value, thereby obtaining the exponential power raised power function characteristic. The proposed circuit is suitable to integrate on a microcomputer chip used for IoT. The performance of the circuit was evaluated by a prototype IC made by 0.6 μm CMOS process. In measured results, the exponential conversion characteristics as set were obtained, the exponent value was set to 0.50, 1.00 and 2.00. By using the cascode exponential conversion circuit, the signal dynamic range was expanded by 5.2 dB when the exponent value was set to 2.00.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many input devices for electronic circuits such as temperature sensors and pressure sensors have nonlinear input/output characteristics [1]. Likewise, many output devices such as various actuators and light emitting devices also have nonlinear characteristics. Cost reductions have been advancing in these devices, and they are used in various electronic equipment. Especially recently, opportunities for these devices to be mounted on a microcomputer board used for Internet of things (IoT) etc. are increasing. In the interface circuits of sensors and actuators, linear correction has been performed on small-scale circuits by line approximation, but the correction accuracy has deteriorated [2].
On the other hand, image input/output devices are equipped with gamma correction circuits that have a signal conversion characteristic as an exponentiation function to the power of gamma value in order to correct device-specific nonlinearity [3]. For gamma correction circuits used for computer monitor displays or high definition televisions which have been developed for high-performance and are mass-produced, large-scale digital circuits with LSIs are used with implemented large signal processing programs. The gamma correction circuits can realize nonlinearity corrections while processing much data at high speed, although these are not inexpensive.
However, general corrections for the nonlinearity of input/output devices in various applications from business use to consumer use, needs to be realized at lower costs using a small scale circuit. These nonlinearity corrections are generally accomplished by having device interface circuits which have nonlinear characteristics that are inverse to the device characteristics. However, the conventional inverse nonlinear characteristics have been realized with low cost circuits in which errors are reduced by polygonal line approximation [4].
In this paper, we propose an exponentiation conversion circuit which can change its power exponent to any value. The proposed circuit is a small scale circuit utilizing the exponential characteristic appearing in the voltage/current characteristic at the subthreshold operation of MOSFET [5]. In the proposed circuit, exponential conversion is performed after multiplying the logarithmically transformed input signal by the power exponent value, thereby obtaining the exponentiation function characteristic. The power exponent can be set to a value matched for the device by electronic control. Because the proposed circuit is composed of integrated MOSFETs, it is suitable to integrate it on a microcomputer chip used for IoT and the like as an interface circuit for sensor input and device output. The performance of the proposed circuit was evaluated by a prototype IC.
2 Principle of exponentiation conversion
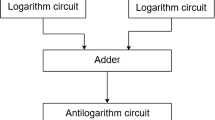
A block diagram of the proposed exponentiation conversion circuit is shown in Fig. 1. In this circuit, a logarithmically transformed input signal ln(Iin) is multiplied by power exponent γ and then an exponential conversion is performed. By electronically arbitrarily changing the power exponent to any value used for multiplication, it is possible to compensate nonlinearity in input signals from various electronic devices.
3 Design of circuit
In the exponentiation conversion circuit, it is necessary to logarithmically/exponentially convert the signal, so the exponential transfer characteristic in the subthreshold operation of MOSFET is utilized. The subthreshold operation is obtained in the weak inverting region where the gate-source voltage Vgs is less than the threshold voltage Vt. The drain current Ids can be expressed by the Eq. (1) and shows the exponential characteristic with respect to Vgs [6].
where \({\mu }_{\mathrm{eff}}\): Effective mobility, \({C}_{\mathrm{ox}}\): Gate oxide capacitance, \(W\): Channel width, L: Channel length,
\({C}_{\mathrm{dm}}\): Maximum depletion capacitance,
\({V}_{\mathrm{ds}}\): Drain-source voltage,\(m=1+({C}_{\mathrm{dm}}/{C}_{\mathrm{ox}})\)
Figure 2 shows all the circuit schematic of the exponentiation conversion IC. The bias currents of Irin and Irout are both 0.5 \(\mathrm{\mu A}\). The MOSFETs operating in subthreshold are M1–M8 and M14–M17. The logarithmic converting part of the exponentiation conversion circuit is shown in Fig. 3. A differential voltage obtained by logarithmically converting the input signal current Iin flowing through M1 is input to the gates of M9 and M10 in the multiplying circuit. At that time, because the refference current IRin is flowing through M2, the input signal Vg109 to the multiplier circuit is expressed by the Eq. (2).
Here, S is called a subthreshold swing value, which is equal to the increase amount of the gate-source voltage Vgs when the drain current Id is increased ten times in the subthreshold region range, and is represented by the expression (3).
Also, subthreshold swing values of Pch and Nch MOSFETs are defined as S(p) and S(n), respectively.
The output voltage Vg1614 of the multiplying circuit can be expressed by the Eq. (4).
Further, the voltage Vg1614 is expressed by the following equation using the current IRout and the output signal current.
Iout of the exponential conversion circuit composed of M14 to M17.
Here, in order to obtain the output signal current Iout proportional to the γ power of the input signal current Iin, it is necessary to satisfy the expression (6), so that the power exponent γ can be represented by expression (7).
Therefore, the power exponent γ can be controlled by changing at least one of IMni and IMi from the Eq. (7). Figure 4 shows the simulation results at γ: 0.5, 1.0, 2.0. In each gamma, the slope of the characteristic in the log–log graph is a straight line, and we can obtain the characteristic of exponentiation function.
4 Exponential conversion circuit
In the original circuit, there was an effect of voltage fluctuation on M17 due to the output resistance. In addition, by applying cascade connection to output, the dynamic range of the output signal was expanded by suppressing both of the influence of channel length modulation and substrate effect with the MOSFET. The cascode exponential conversion circuit is shown in Fig. 5. The improved points for the original circuit are the following two [7, 8].
-
1.
To suppress change in the drain voltage of M17, the gate-grounded MOSFET M18 was connected in cascode.
-
2.
The substrates of Pch MOSFET M15, M17, and M18 were connected to their sources, and the increase in the gate-source voltages due to the substrate effect were suppressed.
The simulated dynamic range in input/output signal characteristics as shown in Fig. 6. The range, in that slope of characteristics curve is within ± 5%, was improved 5.2 dB at the γ of 2.00. As shown in Table 1, the largest expansion in the dynamic range was obtained at the γ of 2.00. As Vdg of M15 increased from 0 V to Vgs by M18, the Vgs of M15 dropped to a small voltage and the error in small signal current is reduced. At γ: 1.0 and γ: 2.0, the dynamic range has been expanded compared to previous works.
The power consumption was 249 \(\mathrm{\mu W}\), and the upper cut-off frequency of the entire circuit was 398 kHz. Since our circuit operates with a differential signal, it is possible to reduce the effects of external common-mode noise and substrate bias effects in MOSFETs.
5 Layout design of the IC
A layout diagram designed using a 0.6 \(\mathrm{\mu m}\) CMOS process is shown in Fig. 7. In order to keep the current density for the subthreshold operation, largest blocks consist of 44 MOSFETs in parallel. The circuit area was 5.4 mm × 6.1 mm, and the multiplying circuit, which has high resistors, occupies 90% of the layout area. It is considered that similar signal dynamic range can be obtained even in use of a finer IC process, if attention to mismatch of pair devices in both of the multiplication circuit and the exponential conversion circuit is paid.
6 Measured results
Figures 8 and 9 show the measured results of the input/output characteristics when the exponent value γ is set to 0.50, 1.00 and 2.00. Although little error occurred in measuring, the three characteristic lines crossover at one point in Fig. 8. While the operating points meet, the output current does not coincide with its theoretical value, even though it was correct at the time of simulation. The slopes of the three curves are the same as the power exponent values in Fig. 9.
7 Conclusion
We proposed an exponentiation conversion circuit which can change its power exponent to any value to compensate nonlinearity of electronic devices. In measured results, the exponential conversion characteristics as set were obtained, in the exponent value set to 0.50, 1.00 and 2.00. Therefore, the signal dynamic range in which non-linear input or output device can be used has been expanded.
Future tasks are required for further expansion of the dynamic range and the analysis of error factors.
References
Toyoaki, O. (1986). Sensor technology popular. Fuji Techno System.
Popa, C. (2008). Improved accuracy pseudo-exponential function generator with applications in analog signal processing. IEEE Transactions on VLSI Systems, 16(3), 318–321
Shomo, C. (2012). Digital color engineering. Kyoritsu Shuppan.
The Institute of Image Information and Television Engineers. (2001). Information display handbook, baifukan
Wang, A., Calhoun, B. H., & Chandrakasan, A. P. (2006). Sub-threshold design for ultra low-power systems. Springer.
Taur, Y., & Ning, T. H. (1998). Fundamentals of modern VLSI devices. (2nd ed., pp. 128–129). Berlin: Springer.
Arai, M., Sano, Y., Miyamoto, Y. (2019).Development of universal gamma collection IC composed of MOSFET operating in subthreshold region. In IEEJ electronics, information and systems, PS1–5, 2018 (in Japanese).
Arai, M., & Sano, Y. (2020). Exponentiation conversion circuit capable of changing the power exponent to any value. IEEJ Transactions on Electronics, Information and Systems, 140(1), 24–31 (in Japanese).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Arai, M., Sano, Y. Exponentiation conversion circuit capable of changing the power exponent to any value. Analog Integr Circ Sig Process 108, 651–655 (2021). https://doi.org/10.1007/s10470-021-01873-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10470-021-01873-4