1 Introduction

Many new wireless standards have emerged in recent years as a result of strong consumer demand in wireless applications. The abundance of these wireless applications, increasing demand and crowding of the spectrum pose challenges for designers. These emerging wireless standards have to be backward compatible with the existing standards. Hence, very strong interferers can coexist in the nearby channels whereas the desired signal in the channel of interest might be very weak. This is particularly the case for mobile-TV applications, where 46-dB stronger analog interferers can exist in the close vicinity of desired channel [1]. As a result, the classical noise-linearity-power-area tradeoff becomes an even more pronounced challenge in wireless receiver design. Battery life concerns require low power compact solutions for portable devices must allow a low-power operation. To reduce system size designs should be reconfigurable for different frequency bands and applications.

Recently, many high performance direct conversion receiver (DCR) and low-IF receiver circuits have been reported [2–11]. Most of these designs tailor the technology and the classical circuit techniques to achieve good performance for a given application. As the supply voltages decrease, this approach does not remain competitive. Lower supply voltage requires lower noise levels to be able to maintain comparable dynamic range (DR) performance. In most integrated receivers a channel select filter is employed to attenuate the near by blockers and hence relax the DR requirement of the ADC. Design of low-noise classical filter circuits involves the use of large on-chip capacitors, which translates into large die area. Hence, in order to alleviate the area tradeoff in a high cost deep-sub-micron process, new circuit topologies are investigated. The work in this paper introduces noise shaping circuit techniques to enable the transition to a lower supply voltage without incurring the cost of extra area. The noise shaping blocker filtering baseband architecture is described in Sect. 2. Detailed circuit designs of various blocks are discussed in Sect. 3. Experimental results from a 65-nm CMOS test-chip are presented in Sect. 4 and we present our conclusions in Sect. 5.

2 Baseband architecture

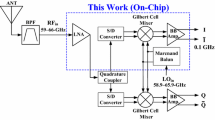
The block diagram of the wide-band direct conversion receiver including the proposed baseband architecture is shown in Fig. 1. In most of radio front-ends, the mixers are followed by a highly linear low-noise post-mixer amplifier (PMA) [2–4]. The main reason designers choose such an architecture is that it allows the desired signal level after the mixers to be low and relaxes the linearity requirements on the LNA and mixer. The cost related to this choice however is high. First, the lower mixer and the preceding low-noise amplifier gains needed increase the linearity required in the higher gain PMA. This means that the noise of the baseband circuitry should be kept even lower since it experiences a lower gain ahead of it (implying more area and power in the baseband). Second, the design of the PMA in the presence of unfiltered strong blockers poses a challenge regarding the linearity requirement of this amplifier (more power). Thus, if one can somehow introduce a small area low-noise blocker filtering following the mixers, one can obtain two-fold benefit; a relaxed baseband noise specification, requiring less power and area, and a relaxed PMA linearity specification, also leading to less power. If this filtering can also protect the mixer outputs from large blockers, then the benefit becomes even more substantial by allowing more gain in the front-end and allowing a less stringent noise requirement for the following PMA and the other baseband circuits. In the proposed baseband architecture, we utilize a unique post-mixer noise-shaping high-order blocker pre-filter to achieve the benefits mentioned above. Unlike existing filter topologies, the proposed circuit achieves filtering at the mixer outputs and helps the mixer linearity [5].

Fig. 1
figure 1

The receiver chain including the proposed baseband architecture

Full size image

The same basic noise-shaping high-order filtering idea is also utilized in the following PMA stage. This time, an instrumentation type PMA stage is introduced, providing gain only in the band of interest and at the same time a relative third-order elliptic filtering for the out-of-band signals. The approach here is to amplify only the signal of interest rather than amplifying the blockers as well and then trying to filter them out in subsequent filtering stages. Eliminating any such redundancies in the system results in additional power and area savings. Moreover, because of the noise shaping characteristics of the proposed technique, the mentioned relative third-order filtering is obtained without any significant noise penalty. Gain of this stage is programmable for gains of 20-, 15-, 8-, or 0-dB.

The PMA is followed by a two-stage voltage-ramp-based rail-to-rail input and output swing variable gain amplifier (VGA) with linear-in-dB gain characteristics [6]. Many CMOS VGA designs proposed in the literature report very linear operation by controlling the VGA gain in steps [7, 12]. This gain switching however may not be acceptable for orthogonal frequency-division multiplexing (OFDM) based systems, such as mobile-TV. There is however linearity and noise degradation associated with continuous gain control, noise is contributed by the gain-tuning MOS switches when they not be fully on or off. The novel VGA circuit of the baseband chain achieves a continuous highly linear 65-dB gain range with two additional passive poles (a pole per stage). A voltage-ramp circuit generates 10 differential ramp control voltages which control the VGA stages in both the I and Q branches. AC coupling using 50 pF MIM capacitors after the mixers eliminates any signal dependent DC offset resulting from the front-end amplification and mixing. Because the DC offsets from the PMA and the VGA stages can be estimated accurately, a simple DC offset calibration circuit is employed inside each of the VGA stages rather than area consuming servo loops. Since the design intends to eliminate the offset inherent to the amplifier, the cancellation is gain and temperature independent to first order.

The output buffer driving the off-chip load is a class-AB amplifier in a third-order Sallen–Key configuration. This buffer configuration is preferred for two main reasons. First, the additional third-order filtering serves as the anti-aliasing filter for the following data converter stage, and prevents the SNR degradation due to aliasing. Second, because of the two-path feedback used in that stage, the compensation requirement is relaxed providing a wider bandwidth without extra power. Slight peaking is allowed in this stage to provide compensation for the droop caused by the passive VGA poles.

A bandwidth calibration circuit calculates a 6-bit calibration code during the power-up calibration sequence for the filtering blocks. This circuit can be clocked from any crystal reference frequency in the range 10–40 MHz. A 7-bit resistor DAC in this block is used to choose the crystal frequency and the desired bandwidth in the range 700-KHz to 5.2 MHz.

The signal and blocker profiles along the baseband chain are shown in Fig. 2 for a DVB-H channel. Interleaving the gain and third-order noise shaping filtering along the chain eliminates the need for a stand alone high order filter. Most of the filtering elements mentioned serve a dual purpose, gain and filtering. This approach results in significant power and area savings.

Fig. 2
figure 2

The signal and blocker profiles along the baseband chain

Full size image

3 Circuit design

3.1 Pre-filter and PMA with blocker suppression

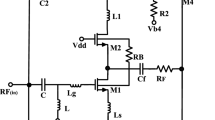
The schematic of the post-mixer blocker pre-filter and a PMA is shown in Fig. 3. The pre-filter section is a frequency dependent negative resistance (FDNR) based circuit that reutilizes the mixer load resistor R f, to create a third-order elliptic response at the mixer output and PMA input. In early 1970s, FDNRs were used extensively to realize high order filter functions [13–17]. However, drawbacks associated in the filter implementations, such as the total number of opamps required, have limited their use as a filter section. Also the FDNR circuit satisfies the negative resistance function only in reference to the circuit ground. Hence the total number of opamps employed in an FDNR based differential filter is greater than that of an integrator based implementation of the same transfer function. Due largely to these disadvantages, these FDNR based topologies have long been abandoned. The circuit of the proposed third-order section, however, offers some useful features with regard to noise that can be utilized to design a very low noise, blocker-aware radio receiver. Such a configuration is unique in that it does not allow blocker voltage swing at the mixer outputs and hence relaxes the mixer linearity specification, allowing a low power mixer design. Moreover, since the mixer gain can now be increased, the following PMA and the baseband chain can be noisier; providing another opportunity for power savings. In order to quantify the savings in just the following PMA stage, we present a simple noise-power tradeoff for this stage. The total differential opamp noise contribution in the PMA stage shown in Fig. 3 can be approximated as follows:

Fig. 3
figure 3

Noise shaping pre-filter and blocker-reject PMA schematic

Full size image
$$ V_{{n_{\text{OPA}} }}^{2} \cong {\frac{16\;kT\gamma }{{g_{\text{m}} }}} $$
(1)

where g m is the transconductance of input differential pair devices, k is Boltzman constant and γ is the bias dependent noise parameter. The resistor noise contributions are:

$$ V_{{n_{\text{R}} }}^{2} = 8\;kTR_{\text{in}} . $$
(2)

Assuming γ of unity for the minimum channel length device (higher than 2/3 in deep-sub-micron processes) and combining (1) and (2), the total PMA noise is approximated as:

$$ V_{{n_{\text{T}} }}^{2} = 2 \cdot \left[ {4\;kTR_{\text{in}} + 4\;kTR_{\text{eq}} } \right] $$
(3)

where R eq = 2/g m. In order not to be dominated by the resistor noise contribution, we choose R in = R eq/2 = 1/g m. The noise equation in (3) can now be rewritten as:

$$ V_{{n_{\text{T}} }}^{2} = 6 \cdot 4\;kTR_{\text{in}} . $$
(4)

The current level that the opamp output stage needs to be able to deliver can be written in terms of input resistance as follows:

$$ I_{\text{out}} = {\frac{{nV_{{{\text{in}}\;p}} }}{{R_{\text{in}} }}} $$
(5)

where n is the extra current margin factor at the output devices and can be chosen to be 1.5 in a conservative design. Using (4) and (5), the output current can be summarized in terms of noise voltage and the peak input voltage swing as follows:

$$ I_{\text{out}} = {\frac{{36 \cdot kT \cdot V_{{{\text{in}}\;p}} }}{{V_{{n_{\text{T}} }}^{2} }}}. $$
(6)

Input differential-pair device transconductance is written down in terms of tail current as:

$$ g_{\text{m}} = \sqrt {2KI_{\text{tail}} /2} = \sqrt {KI_{\text{tail}} } . $$
(7)

where K = μC ox (W/L).

Since R in = R eq/2 = 1/g m was the design choice, using (4) the minimum tail current using the maximum K value K max, can be written down in terms of noise voltage as:

$$ I_{\text{tail}} = {\frac{{576\;\left( {kT} \right)^{2} }}{{K_{\max } V_{{n_{\text{T}} }}^{4} }}} $$
(8)

Combining (6) and (8), the total current consumption for a desired noise voltage level can be approximated as:

$$ I_{\text{total}} = I_{\text{out}} + I_{\text{tail}} = {\frac{{36\;kT \cdot V_{{{\text{in}}\;p}} }}{{V_{{n_{\text{T}} }}^{2} }}} + {\frac{{576\;\left( {kT} \right)^{2} }}{{K_{\max } V_{{n_{\text{T}} }}^{4} }}} . $$
(9)

Based on Eq. 9, a plot of the current consumption corresponding to various noise levels in the PMA is shown in Fig. 4. This allows us to quantify the effect of a reduced noise requirement on the overall power and so manage this tradeoff. Reducing the noise requirement of the PMA by employing such pre-filtering can result in substantial power saving in this baseband stage.

Fig. 4
figure 4

PMA noise density versus required current consumption

Full size image

An interesting property of this pre-filtering circuit is its noise shaping characteristic. It uses only one noisy resistor in the signal path, the load resistor of the mixer (R f), to realize the desired filter transfer function. The noise contribution of this particular resistor is already accounted for in the mixer noise budget and the noise of all the FDNR resistors R 1, R 2, R 3, and R z is shaped [5]. Since the opamps are not in the signal path, their flicker noise contributions are also shaped reducing their contribution to the overall filter noise as well. Moreover, as opposed to classic filter topologies, the opamps of the proposed third-order section are not in the signal path and hence do not contribute any IQ mismatch or DC offset, a much desired property in a receiver chain. The signal transfer function of this circuit from input to output can be written down as follows:

$$ {\frac{{V_{\text{out}} \;\left( s \right)}}{{I_{\text{in}} \;\left( s \right)}}} = {\frac{{R_{f} \left( {s^{2} DR_{z} + 1} \right)}}{{s^{3} DR_{z} R_{f} C_{f} + s^{2} \left( {DR_{z} + DR_{f} } \right) + s\left( {R_{f} C_{f} } \right) + 1}}} $$
(10)
$$ D = {\raise0.7ex\hbox{${C_{1} C_{2} R_{1} R_{3} }$} \!\mathord{\left/ {\vphantom {{C_{1} C_{2} R_{1} R_{3} } {R_{2} }}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${R_{2} }$}}. $$
(11)

This signal transfer function provides a notch at a frequency, \( \omega_{\text{notch}} = 1/\sqrt {DR_{z} } \) and the notch frequency depends on the value of D and R z . Figure 5 shows the plots for the magnitude of noise transfer functions of the various noise sources as well as the signal transfer function. Since the noise generated by the FDNR resistors is shaped, the designer can use larger resistors (noisier) and hence can reduce the capacitor size. This again results in a significant area saving. The total integrated in-band noise voltage can be calculated as [5]:

Fig. 5
figure 5

Noise transfer functions showing the noise-shaping in the FDNR-based pre-filter

Full size image
$$ V_{{n_{\text{T}} }} = \left[ {f_{c} \cdot 2\pi R_{f} C_{1} /\sqrt 3 } \right] \cdot \sqrt {\left( {3\;V_{{n_{R} }}^{2} + 2V_{\text{namp}}^{2} } \right)f_{c} } = \alpha \cdot V_{{{\text{nthermal}}\_{\text{tot}}}} $$
(12)

Thus, one can see that the total noise generated by the filter components is reduced by the factor \( \alpha = [f_{c} \cdot 2\pi R_{f} C_{1} /\sqrt 3 ]. \) The value of R f is determined by the pass-band gain of the mixer, while f c is the filter 1-dB cutoff frequency. Therefore, the only design parameter available for noise shaping is the value of the capacitor C1. Clearly, C1 should be minimized to obtain better noise performance. The minimum value for C1 is limited by the maximum op-amp output swing at the internal FDNR nodes.

This noise shaped filtering idea is also utilized in the following high input impedance instrumentation type PMA stage (Fig. 3). An asymmetric floating frequency dependent negative resistance (AFFDNR) feedback structure is introduced, to simultaneously provide both gain and filtering. Avoiding the amplification of the blockers both relaxes the linearity requirement of the amplifier and relieves the filtering requirements of the following stages. This time the feedback gain resistor R fb is reutilized, and the noise of the AFFDNR circuit elements in the feedback path is shaped, and hence, once more, the desired third-order elliptic filtering is obtained without any significant noise degradation. It should be noted that the proposed AFFDNR is not a reciprocal circuit and that the mentioned filtering action can only be obtained provided that the polarity is as shown in Fig. 3. Specifically as shown in the inset in Fig. 3, the impedance looking into the node A, Z A, is negative with node B grounded, whereas, the impedance looking into the node B, Z B, is inductive when node A is at ground. Depending on the signal strength in the band of interest, the gain of the PMA stage can be adjusted and is 2-bit programmable to be 20-, 15-, 8-, or 0-dB. R in is used to set the gain without affecting the cut-off and notch response of the circuit. In the 0-dB gain mode, the AFFDNR circuit is powered down to save power.

The input referred noise density of this combination is 10 and 14 nV/sqrtHz in DVB-H and ISDB-T modes respectively. This section consumes a die area of 0.28 mm2. In ISDB-T full-gain mode, 2.4- and 4.4-MHz blockers (3.5 dBm each) result in −59.6-dBm IM3 product which corresponds to an out-of-band IIP3 of 44.5 dBm. In-band IIP3 for this case is 18 dBm. In DVB-H mode, 5- and 8-MHz blockers (3.5 dBm each) result in −55-dBm IM3 which corresponds to an out-of-band IIP3 of 42.6 dBm. In-band IIP3 for DVB-H case is 15.5 dBm. The pre-filter consumes 2.6 mA from a 1.2-V supply, while the PMA needs 3.9 mA in full-gain mode from the same 1.2-V supply.

The figure of merit (FOM) defined in [18] and performance metrics from which the FOM is calculated are summarized in Table 1. This FOM however neglects the die area as a performance factor. Hence we define and also show in Table 1 a simple figure of merit (FOM) that compares the performance of this pre-filter-PMA section with the other filters in the literature that incorporates the area tradeoff. The FOM proposed in this work is as follows:

Table 1 Performances summary for various filters in literature
Full size table
$$ {\text{FOM}} = {\frac{{(DR \cdot BW)/V_{DD} }}{{\left( {\left( {BW \cdot C_{\text{tot}} } \right)/N} \right) \cdot \left( {\left( {Pwr} \right)/\left( {N \cdot BW} \right)} \right)}}} $$
(13)

where DR is dynamic range, BW is the filter bandwidth, C tot is the total amount of capacitance used, Pwr is the power consumption and N is the number of poles. This FOM includes dynamic range as well as the required power consumption and total capacitance, scaling them with respect to the filter bandwidth and number of poles.

3.2 Continuous linear-in-dB VGA and Sallen–Key output buffer

The circuit schematic of the two-stage VGA and the third-order Sallen–Key buffer is shown in Fig. 6. The target gain of each VGA stage was in the range −9 to 24 dB. The total measured gain of this two-stage VGA varies from −18 to 47 dB, which was 1 dB off the design target due to the layout related secondary effects such as proximity effect. Each stage has a passive pole to provide additional filtering. These two poles as well as the following three poles in the Sallen–Key output buffer can be tuned from 700 kHz to 5 MHz to cover multiple applications.

Fig. 6
figure 6

Schematic of the back-end chain including the two-stage VGA and the third-order Sallen–Key buffer

Full size image

The VGA topology introduced in this work is based on the classical technique that achieves the desired gain variation by altering the feedback network around an amplifier. Unlike the g m based VGA techniques, this eliminates the linearity degradation caused by large signal swing at the inputs of the diff-pair by providing fully differential operation. However, in most of the continuous-tuning CMOS implementations, MOS devices in triode region are used in the feedback network as the gain tuning elements and this is itself a significant source of nonlinearity. To achieve an approximately exponential gain characteristic, the input resistance and the feedback resistance are varied in opposite directions, one rising as the other falls. The gain per stage that can be obtained without exceeding the exponential approximation boundary is 24 dB per stage (e2x = (1 + x)/(1 − x) is a close approximation for ~x ≪ 1). Another disadvantage of the usual use of MOS devices as resistive feedback tuning elements is that the desired gain range corresponds to a very limited control voltage range. Hence, the two drawbacks of the technique are limited control range and the non-linearity of the MOS resistors.

The technique used here provides a unique solution to these drawbacks, making it an attractive choice for the target 1.2-V baseband receiver application. This is done by introducing a multiple-ramp controlled, gradually changing feedback network. The cost is an additional differential voltage ramp circuit which leads to only a slight increase in area and power. The schematic of one of these stages with complementary control ramps is shown in Fig. 7. With increasing AGC control voltage, the control voltages of the input resistors rise, while the control voltages on the feedback resistors decrease, increasing the closed loop amplifier gain approximately exponentially. For a particular gain setting, most of the switches are completely on or off causing no linearity degradation. Only a few of these switches are in their mid-range and so with careful design the non-linearity contribution of these can be insignificant. The question then becomes: how many unit elements are needed to attain the desired linearity?

Fig. 7
figure 7

a Schematic of the proposed fully differential ramp-based VGA stage. b Differential ramp control voltages versus AGC control voltage

Full size image

The differential ramp voltage generation circuit is shown in Fig. 8. The input AGC control voltage is compared with a reference voltage V ref and the difference current running through R 1 causes the current in one of the diode connected devices to increase and the current through the other one to decrease. By mirroring this current into a resistor, a control voltage proportional to the input voltage difference can be obtained. Multiple control voltages with the desired amount of offset are obtained by simply pulling fixed amount of offset current from each of these mirrored branches. The ramp voltage V cpN, for example, can be written down as follows:

Fig. 8
figure 8

Schematic of the differential ramp voltage circuit

Full size image
$$ V_{\text{cpN}} = \left( {Vctr_{\text{AGC}} - V_{\text{ref}} } \right){\frac{{R_{2} }}{{R_{1} }}} - \left( {(N - 1)I_{b} } \right) \cdot R_{2} . $$
(14)

The resistor ratio in the first term, (R 2/R 1), defines the slope of the characteristics, whereas the second term is the fixed offset. In order to have flexibility in the design, R 1 is trimmable with two-bit slope control word enabling adjustment of the slope of the control ramps and hence the VGA characteristics.

The fully differential class-A VGA amplifier with DC offset calibration (DCOC) is shown in Fig. 9. When the chip is powered up, the inputs to the first gain stage in the baseband chain are shorted and then starting with this stage every gain stage is subsequently calibrated to remove any DC offset. To ensure the smallest residual DC offset each amplifier is set to its maximum gain during this procedure. Once the calibration of all the blocks is complete, the design switches into the normal mode of operation. The VGA amplifier is a two stage, fully differential Miller-compensated opamp with a unity gain bandwidth greater than 250-MHz. A phase margin of 70° is allocated for both common-mode and differential-mode loops. The PMOS devices, M22 and M23, compare the common-mode level with the desired reference level, and to set the output common-mode voltage this feedback loop injects the proper amount of current into the differential output nodes of the first stage. During the start-up, to eliminate the possibility of the inputs and outputs of the amplifier latching-up to VDD, a small bleed current is applied through M15, causing the very weak NMOS devices M7 and M8 turn-on and pull down the amplifier inputs. After the amplifier turns on and common mode levels are reached, these devices turn off.

Fig. 9
figure 9

a Schematic of the class-A VGA amplifier with dc-offset control (DCOC). b DCOC correction circuit

Full size image

The DCOC circuits are also included in the amplifier schematic (Fig. 9(a)). During the calibration sequence, a comparator detects any DC offset at the differential outputs. Depending of the polarity of the offset, a successive approximation engine updates the six-bit trim code reducing the amount of offset error in every cycle. At the end of six cycles, the resultant six-bit trim code is latched and the “calibration done” signal is flagged. The DCOC correction circuit is shown in Fig. 9(b). Depending on the polarity of the offset, the circuit injects a differential current into the output nodes of the first stage, balancing the offset. The input referred offset correction range is 20 mV per VGA. The maximum level of offset that can occur at any point along the chain is limited by comparator accuracy to 2–3 mV.

The output buffer which drives the off-chip load is a class-AB amplifier in a third-order Sallen–Key (SK) configuration. This buffer configuration is preferred for two main reasons. First, the additional third-order filtering serves as the anti-aliasing filter for the following data converter stage, and prevents the SNR degradation due to aliasing. Second, because of the two-path feedback, the amount of compensation required for this buffer is relaxed allowing a wider bandwidth with no additional power. Slight peaking is allowed in this stage to compensate for the droop caused by the passive VGA poles. The class-AB amplifier of the PMA is reused in this buffer stage with only a slight change in the compensation network.

The measured VGA gain characteristics and the gain error curve are shown in Fig. 10. In maximum gain configuration, the measured in-band OIP3 corresponding to 3- and 4-MHz −48 dBm input tones is 22 dBm, whereas, 5- and 8-MHz N + 1 blockers at a −50 dBm input level results in a 34 dBm OIP3. The input referred in-band noise density is 11 nV/sqrtHz for the VGA-SK combination. The total die area of this section is 0.17 mm2. The block consumes 2.65 mA of current from a 1.2-V supply and 200 μA current from a 2.5-V supply for the switch control ramp circuit.

Fig. 10
figure 10

a The measured gain characteristics for the nominal slope setting. b The gain error curve for the same nominal slope setting

Full size image

3.3 Bandwidth calibration circuit

The bandwidth calibration circuit and its timing diagram are shown in Fig. 11. During the initial calibration a 7-bit bandwidth calibration code sets the resistive DAC targeting the desired filter bandwidth for a given crystal clock frequency. The trim range of this resistor is large enough to cover whole filter bandwidth as well as any reference crystal frequency in the range of 10–40 MHz. Following this, successive approximation logic computes a calibration code with the help of a comparator as illustrated in Fig. 11. Note that, since the resistor in this configuration is used as a trim element determining the bandwidth and crystal frequency, the capacitor is used as the calibration element with 6-bit resolution.

Fig. 11
figure 11

The bandwidth calibration circuit and its timing diagram

Full size image

The first baseband stages (FDNR pre-filter and PMA) require a different calibration code than the backend circuits. There are multiple ways to generate the two sets of codes corresponding to different trim element ratios in the different circuit blocks. One solution is to use two different calibration circuits. Because of the extra die area required, this solution is not an attractive one. A second solution is to generate a code for one of the blocks and then use a digital fractional multiplier to scale this code to generate the trim codes required by the other block. Although, the area penalty in this solution is much less, it still adds to the total die area. Another solution, which is used in this design, eliminates the area penalty completely. The idea is to run the calibration sequence twice. After the first sequence the first calibration code is latched into a register (FDNR code). Following this, the capacitor ratios in the calibration engine are reconfigured to generate another set of calibration codes for the backend blocks. A new set of resistor trim codes is also switched into be able to set the poles of the backend blocks independently. In this way, the overall cut-off, notch and stop-band response of the whole chain can be adjusted independently, offering a universal widely tunable solution.

On the filter side, in addition to the 6-bit resolution capacitor bank, there is a resistor trim to switch between the high-end and the low-end of the bands. The tuning resolution at the low-band mode is around 20 kHz while it is 80 kHz in the high-band mode.

4 Experimental results

The proposed baseband architecture was implemented in a 65-nm CMOS process and tested. The die photo is shown in Fig. 12. The inputs and outputs of various sub-blocks were connected to pins to enable measurement of each section separately. The parameters of various sections used in the design are useful in illustrating the limitations of each block. Table 2 summarizes the performance parameters of the individual blocks and the whole baseband chain. The frequency response of the analog baseband chain in ISDB-T and DVB-T/H modes is shown in Fig. 13. 85-dB blocker-aware continuous gain range combined with low-noise operation results in 87.2 and 82.5 dB dynamic range in ISDB-T and DVB-T/H modes, respectively. The two-tone linearity measurements for N + 1 blockers are conducted at a gain of 56 dB. In ISDB-T mode, 2.4- and 4.4-MHz blockers (−10 dBm each at the output) result in a −22-dBm IM3 which corresponds to an out-of-band IIP3 of 24.2 dBm (Fig. 14(a)). In DVB-H mode, 7- and 12-MHz blockers (−15 dBm each at the output) result in a −38-dBm IM3 which corresponds to an out-of-band IIP3 of 24 dBm (Fig. 14(b)). Figure 15 shows the measured IIP3 interpolation data for the target bands. The chain achieves an input referred noise level of 10.5 nV/sqrtHz. The measured input referred noise plot is shown in Fig. 16. The entire receiver baseband occupies a total die area of 0.45 mm2. The design consumes total of 9 mA of current from a 1.2-V supply, as well as, an additional 0.2 mA VGA ramp-control current from a 2.5-V supply. Total power consumption is 11.5 mW.

Fig. 12
figure 12

Die photo of the complete receiver baseband

Full size image
Table 2 Performance summary of various baseband blocks
Full size table
Fig. 13
figure 13

The measured baseband frequency response in: a ISDB-T mode and b DVB-H mode

Full size image
Fig. 14
figure 14

a Two-tone test in ISDB-T mode. b Two-tone test in DVB-H mode

Full size image
Fig. 15
figure 15

Measured IIP3: a in ISDB-T mode and b in DVB-H mode

Full size image
Fig. 16
figure 16

Total input referred noise

Full size image

5 Conclusion

A unique analog baseband chain approach is introduced to mitigate the disadvantages incurred with the supply voltage scaling required in a deep-sub-micron process. The performance metrics of this design as well as other baseband receivers in the literature are summarized in Table 3. This approach provides comparable or superior performance for certain metrics, relative to higher voltage alternatives, without requiring the additional area needed for large capacitors. The new techniques introduced, noise-shaped blocker filtering and linear VGA operation with continuous gain tuning, maximize the dynamic range of the radio. This baseband receiver circuit when placed at the mixer output allows a higher front-end gain, thus relaxing its noise requirement. Measurements have been conducted for two mobile-TV applications, ISDB-T and DVB-T/H but the receiver can be tuned to suit any application in a frequency band from 700 kHz to 5.2 MHz. The frequency response can be configured to accommodate the blocker profile appropriate for the desired application. The multiple calibration sequences during the power-up provide multiple trim codes for various blocks along the chain. Thus, independent characteristics along the chain can be combined to yield the best response for the desired application.

Table 3 Performance comparison of various receiver baseband in the literature
Full size table