Abstract
In order to conduct an in-depth study of Zhan’s methodology pertaining to the covering of multigranulation fuzzy rough sets (\(\hbox {C}_{{MG}}\)FRSs), we build two families: the family of fuzzy \(\beta \)-minimum descriptions and the family of \(\beta \)-maximum descriptions. Subsequently, utilizing these notions, we proceed to develop two variations of covering via optimistic (pessimistic) multigranuation rough set samples (\(\hbox {CO(P)}_{{MG}}\)FRS). The axiomatic properties are examined. In this study, we examine four models of covering using variable precision multigranulation fuzzy rough sets (\(\hbox {CVP}_{{MG}}\)FRSs). We proceed with analyzing the features of these models. Interconnections between these planned plans are also elucidated. This study explores algorithms that aim to identify innovative strategies for addressing multiattribute group decision-making problems (MAGDM) and multicriteria group decision-making problems (MCGDM). The test examples have been elucidated to provide an inclusive grasp of the efficacy of the offered samples. Ultimately, the distinctions between our methodologies and the preexisting research have been demonstrated.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
This article studies new models of covering via multigranulation fuzzy rough sets by introducing the notions of family fuzzy \(\beta \)-minimal and \(\beta \)-maximal descriptions.
1.1 Background
Pawlak (1982) invented rough set theory as a strategy that scholars can use to address the conflicts and complexity in information systems as well as data processing.
Therefore, in recent years, several improvements have been distinguished, in which the partitioning part has been replaced with different structures, namely binary relations (Herawan et al. 2010) and (Jensen and Shen 2004), neighborhood systems (Atef et al. 2020) and (Yao 1998), Boolean algebras (Liu and Zhu 2008) and (Wu and Zhang 2002), and covering techniques (Bonikowski et al. 1998) and (Pomykala 1987, 1988).
Many academics have worked on covering rough sets. Two couple mixed approximation operators were created by Pomykala (1987, 1988) and then analyzed through the concept of neighborhood by Yao (1998). Couso and Dubois (2011) explored new models of insufficient input, and Bonikowski et al. (1998) discovered a CRS framework using minimum description. Zhu (2007); Zhu and Wang (2003, 2007) and Zhu and Wang (2012) defined different covering methods and examined their relations. Additionally, there were various templates presented by Tsang et al. (2008) and Xu and Zhang (2007) and at the same time (Liu and Sai 2009) provided us with the differences among Zhu’s schemes and structures given by Xu and Zhang (2007). Ma (2012) generated new CRS models via a complementary neighborhood, while (Yao and Yao 2012) identified four neighborhoods and derived six covering models from them. To widen the range of the study, multigranulation rough sets (MGRS) were demonstrated by Qian et al. (2010) using multiple binary relations. The MGRS was generated with variable precision by Xu et al. (2011). Yang et al. (2011) introduced MGRS according to a fuzzy relation. Furthermore, Liu et al. (2014) observed multigranulation covering rough sets (MGCRS), and (Lin et al. 2013) showed a covering through multigranulation rough set (CMGRS). Further information regarding the (MGRS) and its various uses can be obtained from numerous sources. For instance, Yang et al. (2012), Huang et al. (2014), Sun and Ma (2015), Xue et al. (2023), Zhan and Xu (2020) and Chen and Zhu (2023).
RS techniques are incompetent at working real-valued features successfully because RS fundamentally handles qualitative data (Jensen and Shen 2004). So, Zadeh (1975) introduced fuzzy set theory (FS) to treat this problem effectively using a membership function. After that, by combining RS and FS, the views of rough fuzzy sets (RFS) and fuzzy rough sets (FRS) appear by Dubois and Prade (1990). Many investigators have worked on this definition and tried to use distinct samples to develop FRS. A well-thought-out structure is designed utilizing fuzzy relations and fuzzy sets rather than crisp ones.
De Cock et al. (2024) developed FRS through R-foresets of every object in the universe in relation to a fuzzy relation. Li et al. (2008) and Feng et al. (2012) initiated the definition of a fuzzy covering (FC). Then, Ma (2016) worked to determine the barriers of FC and process them by offering a fuzzy \(\beta \) covering (\(\hbox {F}_{\beta }\)CRS). She introduced it by substituting 1 with an undetermined variable \(\beta \) that takes values between 0 and 1. This indicates that if \(\beta =1\), FC is a particular instance from Ma\('\)s manner. After that several scientists extended Ma\('\)s method in different ways such as Yang and Hu (2017, 2019) proposed new kinds of \(\hbox {F}_{\beta }\)CRS and examined their properties utilizing the complementary fuzzy \(\beta \)-neighborhood, fuzzy \(\beta \)-minimum and \(\beta \)-maximum descriptions, D’eer et al. (2017, 2016) debates neighborhoods through CRS and fuzzy neighborhoods via FC, Jiang et al. (2020) and Atef and Azzam (2021) established covering fuzzy rough sets through variable precision, Garg and Atef (2022) created new approaches to a covering using Pythagorean fuzzy sets and q-ROF sets; new extensions via two different global groups are demonstrated by Yang (2022) and Yang and Atef (2023), Atef et al. (2023) examined the topological properties of covering soft rough and used them to solve MGDM problems and the latest models are explored through fermatean and interval-valued fermatean fuzzy sets by Qi et al. (2024). Multigranulation in fuzzy variations of rough sets has been linked to three-way multi-attribute group decision-making Zhang et al. (2021a, b, 2022) recently. Thus, Zhan et al. (2023) presented a survey for three-way behavioral decision-making with a hesitant fuzzy environment. As well as, Zhan et al. (2024) presented a hybrid multivariate time series prediction framework based on fuzzy C-means clustering coupled with feature selection.
1.2 Motivation and contribution of this article
Numerous propositions have been put out to investigate the domain of fuzzification of MGRS. The meaning of multigranulation fuzzy rough sets (MGFRS) was proposed by Xu et al. (2011, 2014) through the utilization of an equivalence relation, drawing inspiration from the ideas put out by Dubois and Prade (1990). Here, let us further emphasize this research to be able to proceed with a larger volume of data, Liu and Wang (2011) and Liu and Miao (2011) discovered coverage fuzzy rough methods through MGRS, Liu and Pedrycz (2016) put forward new covering models by MGFRSs, Zhan et al. (2019) proposed the covering based multigranulation (I, T) fuzzy rough sets with practical tests, Ma et al. (2020) discussed certain kinds of covering samples in the view of multigranulation (I, T) fuzzy rough sets, Zhan et al. (2020) demonstrated \(\hbox {C}_{{MG}}\)FRS models via the collection of fuzzy \(\beta \)-neighborhoods and Atef and El-Atik (2021) constructed four types of approximations according to the notion of the collection of fuzzy complementary \(\beta \)-neighborhoods, a novel model of fuzzy \(\beta \)-covering through MGRS was presented and applied for attribute picking to reduce the impact of noisy data by Zhang and Dai (2022) explored new types of FRS models in \(\hbox {F}_{\beta }\)CAS to eliminate some of the noise data, Ye et al. (2021) proposed the \((\mathscr {I},\mathscr {T})\)-FRS templates to address MCDM problems, Huang and Li (2022) suggested a new scale of discrimination using fuzzy \(\beta \)-neighborhood and evaluated its effectiveness through the attribute reduction algorithm, Atef and Liu (2024) discovered the grey \(\beta \) coverings and examined their properties. Consequently, Zhang et al. (2021a, b) and Ma et al. (2021) defined the fuzzy \(\alpha \) covering with reflexivity to solve the classical concept issues. Based on this idea, Huang and Li (2024a) presented fuzzy \(\gamma \) neighborhoods with reflexivity and utilized them to investigate a noise-tolerant variable precision discrimination index (VPDI), Huang et al. (2022) established fuzzy \(\beta \) covering based multigranulation rough sets, Huang et al. (2024) improved noise-tolerant ability through introduced multigranulation variable precision via fuzzy \(\beta \) covering and Huang and Li (2024b) proposed fuzzy \(\beta \) covering via multigranulation rough fuzzy sets and used it in a feature selection process.
The study conducted by Sun et al. (2017) focused on examining the procedure of three-way group decision-making utilizing a multigranulation fuzzy decision approach. Group Decision Making (GDM) has been widely recognized as a highly successful approach for addressing intricate challenges encountered in real-world contexts. The utilization of multi-criteria in (GDM) was investigated by Hwang and Lin (1987) in their study. Multi-criteria group decision-making (MCGDM) pertains to the process of evaluating and prioritizing many feasible alternatives based on competing and interactive criteria. Numerous scholars are actively involved in this field through the utilization of MCGDM. For instance, notable studies conducted by Chen et al. (2012), Hong and Choi (2000), and Zhang et al. (2014) exemplify this trend. In their study, Mardani et al. (2015) conducted a comprehensive evaluation of Multiple Criteria Group Decision Making (MCGDM) methods that are grounded in FS. The review specifically focused on the period between 1994 and 2014. Numerous scholars have proposed novel procedures and strategies pertaining to decision-making methods such as Zhu et al. (2023a) constructed MADM with probabilistic linguistic three-way decision method according to the regret theory (RT), Han and Zhan (2023) discovered MAGDM problems in the environment of probabilistic linguistic term sets (PLTSs), Zhu et al. (2023b) investigated three-way consensus model based on RT over the PLTSs to fix MAGDM, Han et al. (2024a) introduced a three-way group consensus methodology grounded in probabilistic linguistic preference relations (PLPRs), Han et al. (2024b) and Ma et al. (2024) use PLPRs to solve complex problems, Xiao et al. (2023) proposed a new method, namely, prospect theory through intuitionistic fuzzy numbers within generalized three way decision framework (PT-IF-G3WD), Guo et al. (2023) established a large scale group decision making through fuzzy preference relations (FPRs) and Xiao et al. (2024) defined novel way to solve real problems under multi-scale decision information systems. Subsequently, Sivaprakasam and Angamuthu (2023) presented the concept of a generalized Z-fuzzy soft-covering-based rough matrices to address MAGDM issues, Pamucar et al. (2022) explored a novel way in the modification of the CRiteria Importance Through Intercriteria Correlation (CRITIC) sample using fuzzy rough numbers, Shen (2024) demonstrated a rough set based bipolar method, Kakati et al. (2024) constructed fermatean fuzzy archimedean heronian mean-based method to fix transport issues, Donbosco and Ganesan (2022) discovered the energy of rough neutrosophic matrix to treat the MCDM problem and Zhang et al. (2024) defined a multi-scale neighborhood for feature selection. Upon reviewing the extant literature, it becomes evident that there is a dearth of research pertaining to the exploration of \(\hbox {C}_{{MG}}\)FRSs, with a specific focus on their applications in the domain of multi-attribute decision-making. Therefore, to widen the range of studying of the given approaches, we present novel \(\hbox {C}_{{MG}}\)FRS models utilizing the definition of the family of fuzzy \(\beta \)-minimum and \(\beta \)-maximum descriptions. According to the literature reviewed above, it is evident that there are restricted studies on \(\hbox {C}_{{MG}}\)FRSs. So, we have the following list that outlines the main works:
-
1.
We introduce the meaning of the family of fuzzy \(\beta \)-minimum and maximum descriptions over the universe.
-
2.
According to these definitions, we investigate two new models of \(\hbox {CO(P)}_{MG}\)FRS (optimistic and pessimistic) and studied their pr.
-
3.
Four samples of \(\hbox {CVP}_{{MG}}\)FRSs are established and their relevant characteristics are informed.
-
4.
Relations and comparisons between these models and the existing models (i.e., Zhan et al. 2019, 2020; Atef and El-Atik 2021 and Ma et al. 2021) are clarified.
-
5.
Numerical examples are presented to show their efficacy in supporting physicians’ decision-making through practical issues in MAGDM and MCGDM
The major goal of this article can be explained in the next Fig. 1.
Where white boxes describe existing work and blue boxes shows our research direction in this article.
1.3 Structure of the present paper
The outline of this article is the following. Section 2 gives the principle information about the previous work. Sections 3 and 4 present two new \(\hbox {CO(P)}_{MG}\hbox {FRS}\) methods using the notions of fuzzy \(\beta \)-minimal and maximal descriptions. We propose distinct \(\hbox {CVP}_{MG}\hbox {FRS}\) models and discuss their properties. Section 6 establishes relations among these covering models. Section 7 presents procedures for fixing MAGDM and MCGDM issues that take advantage of our theoretical framework along with some algorithms that facilitate the use of these methods. The main findings and future vision are explained in Sect. 8.
2 Preliminaries
Throughout this section, several fundamental notions will be mentioned for covering models and their generalizations.
Definition 1
(Zhu 2007) Let \(\mathscr {F}\) be a collection of subsets of the common set \(\Omega \) and \(\Omega =\bigcup _{\mathbb {F} \in \mathscr {F}}\mathbb {F}\). Then \(\mathscr {F}\) is a covering of \(\Omega \). The \((\Omega ,\mathscr {F})\) is said to be a (\(\textbf{CAS}\)).
Definition 2
(Feng et al. 2012) Let \((\Omega ,\mathscr {F})\) be a \(\textbf{CAS}\) and \(\mathscr {F}=\{\mathbb {F}_{1}, \mathbb {F}_{2},\ldots , \mathbb {F}_{n}\}\), where \(\mathbb {F}_{j}\in \mathcal {F}(\Omega )(j=1, 2, \ldots , n)\). If \((\bigcup _{i=1}^{n} \mathbb {F}_{j})(a) =1\), \(\forall a \in \Omega \), then \((\Omega ,\mathscr {F})\) is said to be a \(\textbf{FCAS}\).
After that (Ma 2016) developed \(\textbf{FCAS}\) using the parameter \(\beta \) that accepts values (0, 1] as \((\bigcup _{i=1}^{m} \mathbb {F}_{j})(a) \ge \beta \). Thus, \((\Omega ,\mathscr {F})\) is a \({\textbf {F}}_{\beta }\)CAS.
Definition 3
(Ma 2016; Yang and Hu 2017, 2019) Let \((\Omega ,\mathscr {F})\) be a \({\textbf {F}}_{\beta }\)CAS. For all \(a \in \Omega \), we have the following neighborhoods.
-
1.
\(\mathbb {N}^{\beta }_{a}= \cap \{\mathbb {F}_{j} \in \mathscr {F}:\mathbb {F}_{j} \ge \beta \}\).
-
2.
\(\mathbb {M}^{\beta }_{a}(y)= \mathbb {N}^{\beta }_{y}(a)\).
-
3.
\(\mathbb {M}d^{\beta }_{a}=\{\mathbb {F}\in \mathscr {F}: (\mathbb {F}(a)\ge \beta ) \wedge (\forall \mathbb {D}\in \mathscr {F} \wedge \mathbb {D}(a) \ge \beta \wedge \mathbb {D} \subseteq \mathbb {F} \rightarrow \mathbb {D}=\mathbb {F})\}\).
-
4.
\(\mathbb {M}D^{\beta }_{a}= \{\mathbb {F}\in \mathscr {F}: (\mathbb {F}(a)\ge \beta ) \wedge (\forall \mathbb {D}\in \mathscr {F} \wedge \mathbb {D}(a) \ge \beta \wedge \mathbb {D} \supseteq \mathbb {F} \rightarrow \mathbb {D}=\mathbb {F})\}\).
Zhan et al. (2020) gave the \(\hbox {C}_{{MG}}\)FRSs utilizing the concepts of CRS, MGFRS and \({\textbf {F}}_{\beta }\)CAS.
Let \((\Omega ,{\kappa })\) be a \({\textbf {F}}_{\beta }\)CAS and \({\kappa }= \{\mathbb {F}_{1}, \mathbb {F}_{2},\ldots ,\mathbb {F}_{n}\}\) be n fuzzy \(\beta \) coverings of \(\Omega \), where \(\mathbb {F}_{j}= \{\mathbb {F}_{j1}, \mathbb {F}_{j2},\ldots ,\mathbb {F}_{jr}\}\), for all \(j=1,2,\ldots ,n\). Then, we can call \((\Omega ,{\kappa })\) by \({\textbf {MGF}}_{\beta }\)CAS for short.
Definition 4
(Zhan et al. 2020) Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G} \in {\mathcal {F}}(\Omega ),\) define the i-OLA, i-OUA, i-PLA, and the i-PUA, respectively, as follows:
Atef and El-Atik (2021) extended the studies of Zhan et al. (2020) using the family of fuzzy complementary \(\beta \) neighborhoods and examined their properties.
Definition 5
(Atef and El-Atik 2021) Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G} \in {\mathcal {F}}(\Omega ),\) define the ii(resp. iii and iv)-OLA, ii(resp. iii and iv)-OUA, ii(resp. iii and iv)-PLA, and the ii(resp. iii and iv)-PUA, respectively, as follows:
and
for all \(a \in \Omega \).
3 The first \(\hbox {CO(P)}_{MG}\)FRS model via the fuzzy \(\beta \)-minimal description
This section presents the \(\hbox {CO}_{{MG}}\)FRS and \(\hbox {CP}_{{MG}}\)FRS models, which are based on a set of fuzzy \(\beta \)-minimal descriptions and examine some of their characteristics.
Definition 6
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For all \(a \in \Omega \),
is called the family of fuzzy \(\beta \)-minimal descriptions of a for any \(j=1,\ldots ,n\) and \(i,r=1,\ldots ,m\).
Example 1
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and \(\kappa = \{\mathbb {F}_{1}, \mathbb {F}_{2}\}\) be a family of \(\hbox {F}_{\beta }\)Cs of \(\Omega \), where \(\Omega =\{a_1,a_2,a_3,a_4,a_5,a_6\}\), \(\beta =0.5\) and \(\mathbb {F}_{1}=\) \(\{\mathbb {F}_{11}, \mathbb {F}_{12},\ldots ,\mathbb {F}_{15}\}\) and \(\mathbb {F}_{2}= \{\mathbb {F}_{21}, \mathbb {F}_{22},\ldots ,\mathbb {F}_{25}\}\) as shown in Tables 1 and 2.
The fuzzy beta-minimal description \(\tilde{\mathbb {M}d}_{\mathbb {F}_{j}}^{\beta }(a)\) \((j=1,2)\) can subsequently be computed. See Tables 3 and 4.
3.1 \(\hbox {CO}_{{MG}}\)FRSs
Definition 7
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For every \(\mathscr {G} \in {\mathcal {F}}(\Omega ),\) the 1-OLA and 1-OUA are defined as follows:
If \({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\ne {_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\), then \(({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}), {_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}))\) is called a 1-\(\hbox {CO}_{{MG}}\)FRS, otherwise it is definable.
Example 2
Consider Example 1, and when \(\mathscr {G}= \frac{0.6}{a_1}+ \frac{0.3}{a_2}+\) \(\frac{0.7}{a_3}+ \frac{0.1}{a_4}+ \frac{0.5}{a_5}+ \frac{0.8}{a_6}\). Then we compute the \(\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y)\) for \(\kappa = \{\mathbb {F}_{1},\mathbb {F}_{2}\}\) as next in Tables 5 and 6.
So,
Theorem 1
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G} \in {\mathcal {F}}(\Omega ),\) the below items for 1-LAO and 1-UAO hold.
-
(1)
\({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^{c}) \bigg )^c\) and \({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^{c}) \bigg )^c\).
-
(2)
\({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\Omega )=\Omega \) and \({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\emptyset )=\emptyset \).
-
(3)
If \(\mathscr {G} \subseteq \mathscr {Y}\), then \({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) \(\subseteq {_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(4)
\({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})={_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})\subseteq {_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(5)
\({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y}) \supseteq {_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y})={_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(6)
If \(1-\mathbb {N}_{\mathbb {F}_{j}(x)}^{\beta }\le \mathscr {G}(a) \le \mathbb {N}_{\mathbb {F}_{j}(a)}^{\beta }\), \(\forall a \in \Omega \), then \({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\).
Proof
-
(1)
$$\begin{aligned} ({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^{c}))^c(a)&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y)\wedge \mathscr {G}^{c}(y)\bigg \}^{c}\\&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y)\wedge (1-\mathscr {G}(y))\bigg \}^{c}\\&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y))\vee \mathscr {G}(y)\bigg \}\\&={_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})(a). \end{aligned}$$
-
(2)
Since \(\Omega (a)= 1\), for any \(a \in \Omega \),
\({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\Omega )(a)=\) \(\bigwedge \limits _{i=1}^{n}\bigvee \limits _{y\in \Omega }\bigg \{(1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y))\vee \Omega (a)\bigg \}=1=\Omega (a).\)
-
(3)
Let \(\mathscr {G}, \mathscr {Y} \in \mathcal {F}(\Omega )\) such that \(\mathscr {G} \subseteq \mathscr {Y}\) and \(a \in \Omega \). Then
$$\begin{aligned} {_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})(a)&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1- \vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y))\vee \mathscr {G}(y)\bigg \}\\&\le \bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y))\vee \mathscr {Y}(y)\bigg \}\\&={_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})(a). \end{aligned}$$ -
(4)
When \(a \in \Omega \), then
$$\begin{aligned} {_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})(a)&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y))\vee (\mathscr {G}\cap \mathscr {Y})(y)\bigg \}\\&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y))\vee \mathscr {G}(y)\bigg \}\\&\cap \bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y))\vee \mathscr {Y}(y)\bigg \}\\&={_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})(a)\cap {_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})(a). \end{aligned}$$ -
(5)
Similar to (4).
-
(6)
If \(1-{\mathbb {N}}_{\mathbb {F}_{j}(a)}^{\beta }\le \mathscr {G}(a) \le {\mathbb {N}}_{\mathbb {F}_{j}(a)}^{\beta }\), \(\forall a \in \Omega \), then
$$\begin{aligned} \mathscr {G}(a)&=\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(a) \wedge \mathscr {G}(a)\le \bigvee \limits _{y\in \Omega }\bigg (\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y) \wedge \mathscr {G}(y)\bigg )\\&\implies \mathscr {G}(a)\le \bigwedge \limits _{i=1}^{n}\bigvee \limits _{y\in \Omega }\bigg \{\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y)\wedge \mathscr {G}(y)\bigg \}={_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})(a)\\&\implies \bigwedge \limits _{y\in \Omega }\bigg \{(1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y))\vee \mathscr {G}(y)\bigg \}\le (1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(a))\vee \mathscr {G}(a)\le \mathscr {G}(a) \\&\implies \bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }(y))\vee \mathscr {G}(y)\bigg \}\le \mathscr {G}(a)\\&\implies {_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})(a)\le \mathscr {G}(a)\\&\implies {_{-1}\mathscr {R}}^{o}_{\sum _{i=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq \mathscr {G} \subseteq {_{+1}\mathscr {R}}^{o}_{\sum _{i=1}^{n}\mathbb {F}_{j}}(\mathscr {G}). \end{aligned}$$
\(\square \)
Definition 8
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and for any \(a,y \in \Omega \). A MGFMD \(^{1}\mathscr {D}^{\beta }_{\mathbb {F}_{j}(a_i)}(a,y)\), where \(a_i \in \Omega \) and \(i=1,\ldots ,m\) is shown by
Example 3
(Continued from Examples 1 and 2) If \(\beta =0.5\), then we have the following in \(\mathbb {F}_{1}\):
-
(1)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_1)=1, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_2)=0.47, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_3)=0.7, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_4)=0.64, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_5)=0.66,\)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_6)=0.82\).
-
(2)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_1)=0.47, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_2)=1, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_3)=0.4, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_4)=0.49, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_5)=0.66,\)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_6)=0.42\).
-
(3)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_1)=0.7, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_2)=0.4, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_3)=1, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_4)=0.78, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_5)=0.66,\)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_6)=0.86\).
-
(4)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_1)=0.64, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_2)=0.49, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_3)=0.78, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_4)=1, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_5)=0.74, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_6)=0.73\).
-
(5)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_1)=0.66, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_2)=0.66, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_3)=0.66, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_4)=0.74, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_5)=1, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_6)=0.62\).
-
(6)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_1)=0.82, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_2)=0.42, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_3)=0.86, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_4)=0.73, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_5)=0.62, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_6)=1\).
And in \(\mathbb {F}_{2}\):
-
(i)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_1)=1, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_2)=0.49, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_3)=0.87, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_4)=0.85, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_5)=0.7, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_6)=0.88\).
-
(ii)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_1)=0.49, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_2)=1, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_3)=0.49, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_4)=0.54, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_5)=0.63, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_6)=0.54\).
-
(iii)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_1)=0.87, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_2)=0.49, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_3)=1, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_4)=0.78, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_5)=0.7, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_6)=0.88\).
-
(iv)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_1)=0.85, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_2)=0.54, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_3)=0.78, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_4)=1, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_5)=0.76, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_6)=0.75\).
-
(v)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_1)=0.7, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_2)=0.63, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_3)=0.7, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_4)=0.76, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_5)=1, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_6)=0.74\).
-
(vi)
\(^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_1)=0.88, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_2)=0.54, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_3)=0.88, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_4)=0.75, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_5)=0.74, ^{1}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_6)=1\).
Definition 9
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and \(^{1}\mathscr {D}^{\beta }_{\mathbb {F}_{j}}\) be a MGFMD of \(\Omega \). For every \(\mathscr {G} \in {\mathcal {F}}(\Omega )\) and \(\alpha \in [0,1)\), the 1-O\(\alpha \)LA and the 1-O\(\alpha \)UA are given by
Example 4
(Continued from Example 3) When \(\alpha =0.65\),
Theorem 2
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For every \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), the below items for 1-O\(\alpha \)LA and 1-O\(\alpha \)UA hold.
-
(1)
\({_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c)\bigg )^c\) and \({_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c)\bigg )^c\).
-
(3)
\({_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\Omega )=\) \(\Omega \) and \({_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\emptyset )=\) \(\emptyset \)
-
(4)
If \(\mathscr {G} \subseteq \mathscr {Y}\), then \({_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) \(\subseteq {_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) \(\subseteq {_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(5)
\({_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})=\) \({_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})\subseteq \) \({_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\)
-
(6)
\({_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y})\supseteq {_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y})= {_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(7)
If \(1-\mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\le \mathscr {G}(a) \le \mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\), \(\forall a \in \Omega \), then \({_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}) \subseteq \mathscr {G} \subseteq {_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\).
Proof
Similarly, by Theorem 1. \(\square \)
Now, we give another MGFRC form by \(^{1}\mathscr {D}^{\beta }_{\mathbb {F}_{j}}\).
Definition 10
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and \(^{1}\mathscr {D}^{\beta }_{\mathbb {F}_{j}}\) be a MGFMD of \(\Omega \). For every \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), the 1-O\(\mathscr {D}\)LA and 1-O\(\mathscr {D}\)UA are given by
Example 5
(Continued from Example 3) We have,
Theorem 3
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For every \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), the below items for 1-O\(\mathscr {D}\)LA and 1-O\(\mathscr {D}\)UA hold.
-
(1)
\({_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c)\bigg )^c\) and \({_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c)\bigg )^c\).
-
(2)
\({_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\Omega )=\) \(\Omega \) and \({_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\emptyset )=\) \(\emptyset \)
-
(3)
If \(\mathscr {G} \subseteq \mathscr {Y}\), then \({_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) \(\subseteq {_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) \(\subseteq {_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(4)
\({_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})=\) \({_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})\subseteq \) \({_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\)
-
(5)
\({_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y})\supseteq {_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y})= {_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(6)
If \(1-\mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\le \mathscr {G}(a) \le \mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\), \(\forall a \in \Omega \), then \({_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}) \subseteq \mathscr {G} \subseteq {_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\).
Proof
The proof is obvious by Theorem 1. \(\square \)
3.2 \(\hbox {CP}_{{MG}}\)FRSs
Definition 11
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G} \in {\mathcal {F}}(\Omega ),\) the 1-PLA and the 1-PUA are introduced respectively as next.
If \({_{-1}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\ne {_{+1}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\), then \(\mathscr {G}\) is called a 1-\(\hbox {CP}_{{MG}}\)FRS, otherwise it is definable.
Definition 12
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and \(^{1}\mathscr {D}^{\beta }_{\mathbb {F}_{j}}\) be an MGFMD of \(\Omega \). For any \(\mathscr {G} \in {\mathcal {F}}(\Omega )\) and \(\alpha \in [0,1)\), the 1-P\(\alpha \)LA and the 1-P\(\alpha \)UA are given by
Definition 13
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and \(^{1}\mathscr {D}^{\beta }_{\mathbb {F}_{j}}\) be an MGFMD of \(\Omega \). For every \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), the 1-P\(\mathscr {D}\)LA and 1-P\(\mathscr {D}\)UA, where \(a_i \in \Omega \) and \(i=1,..,m\) are given by
Example 6
(Continued from Examples 1 and 2) Let \(\mathscr {G}=\frac{0.6}{a_1}+\frac{0.3}{a_2}+\frac{0.7}{a_3}+\) \(\frac{0.1}{a_4}+\frac{0.5}{a_5}+\frac{0.8}{a_6}\) and \(\alpha =0.65\). Then we have
-
(1)
\({_{-1}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.4}{a_1}+\frac{0.2}{a_2}+\frac{0.3}{a_3}+\frac{0.1}{a_4}+\) \(\frac{0.1}{a_5}+\frac{0.1}{a_6}\) and
\({_{+1}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.7}{a_1}+\frac{0.5}{a_2}+\frac{0.7}{a_3}+\frac{0.7}{a_4}+\) \(\frac{0.7}{a_5}+\frac{0.7}{a_6}\).
-
(2)
\({_{-1}\mathscr {R}}^{p,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.5}{a_1}+\frac{0.3}{a_2}+\frac{0.1}{a_3}+\frac{0.1}{a_4}+\) \(\frac{0.1}{a_5}+\frac{0.1}{a_6},\) and
\({_{+1}\mathscr {R}}^{p,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.8}{a_1}+\frac{0.5}{a_2}+\frac{0.8}{a_3}+\frac{0.8}{a_4}+\) \(\frac{0.8}{a_5}+\frac{0.8}{a_6}.\)
-
(3)
\({_{-1}\mathscr {R}}^{p,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.15}{a_1}+\frac{0.3}{a_2}+\frac{0.22}{a_3}+\) \(\frac{0.1}{a_4}+\frac{0.24}{a_5}+\frac{0.25}{a_6},\) and
\({_{+1}\mathscr {R}}^{p,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.8}{a_1}+\frac{0.52}{a_2}+\frac{0.8}{a_3}+\frac{0.75}{a_4}+\) \(\frac{0.74}{a_5}+\frac{0.8}{a_6}.\)
4 The second \(\hbox {CO(P)}_{MG}\)FRS model via the fuzzy \(\beta \)-maximal description
This section aims to construct \(\hbox {CO}_{{MG}}\)FRS and \(\hbox {CP}_{{MG}}\)FRS models by using a family of a fuzzy \(\beta \)-maximal description, and their relations are investigated.
Definition 14
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For every \(a \in \Omega \),
is called the family of fuzzy \(\beta \)-maximal description of a for every \(j=1,\ldots ,n\) and \(j,r=1,\ldots ,m\).
Example 7
(Continued from Example 2) Then we can calculate the \(\tilde{\mathbb {M}D}_{\mathbb {F}_{j}(a_i)}^{\beta }\) \((i=1,2,3,4,5,6)\) for \(\kappa \). See Tables 7 and 8.
4.1 \(\hbox {CO}_{{MG}}\)FRSs
Definition 15
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For every \(a \in \Omega \), the 2-OLA and the 2-OUA are defined as follows.
If \({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\ne {_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\), then \(({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}), {_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}))\) is called a 2-\(\hbox {CO}_{{MG}}\)FRS, otherwise it is definable.
Example 8
(Continued from Example 7) The below results hold, if \(\mathscr {G}= \frac{0.6}{a_1}+ \frac{0.3}{a_2}+\) \(\frac{0.7}{a_3}+ \frac{0.1}{a_4}+ \frac{0.5}{a_5}+ \frac{0.8}{a_6}\). Then we calculate the \(\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}(a)}^{\beta }\) for \(\kappa = \{\mathbb {F}_{1}, \mathbb {F}_{2}\}\) as below in Tables 9 and 10.
So,
Theorem 4
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G}\in \mathscr {F}(\Omega )\), the below properties hold for 2-OLA and 2-OUA.
-
(1)
\({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c) \bigg )^c\) and \({_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c) \bigg )^c\).
-
(2)
\({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\Omega )=\Omega \) and \({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\emptyset )=\emptyset \).
-
(3)
If \(\mathscr {G} \subseteq \mathscr {Y}\), then \({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(4)
\({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})={_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y})={_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(5)
\({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y}) \supseteq {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y}) \subseteq {_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(6)
If \(1-\mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\le \mathscr {G}(a) \le \mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\), \(\forall a \in \Omega \), then \({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\).
Proof
-
(1)
$$\begin{aligned} ({_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c))^c(a)&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y)\wedge \mathscr {G}^{c}(y)\bigg \}^{c}\\ {}&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y)\wedge (1-\mathscr {G}(y))\bigg \}^{c}\\ {}&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y))\vee \mathscr {G}(y)\bigg \}\\ {}&={_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})(a). \end{aligned}$$
-
(2)
Since \(\Omega (a)= 1\), \(\forall a \in \Omega \),
\({_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\Omega )=\) \(\bigwedge \limits _{i=1}^{n}\bigvee \limits _{y\in \Omega }\bigg \{(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y))\vee \Omega (a)\bigg \}=1=\Omega (a).\)
-
(3)
Let \(\mathscr {G}, \mathscr {Y} \in \mathcal {F}(\Omega )\) such that \(\mathscr {G} \subseteq \mathscr {Y}\) and \(a \in \Omega \). Then
$$\begin{aligned} {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})(a)&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y))\vee \mathscr {G}(y)\bigg \}\\&\le \bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y))\vee \mathscr {Y}(y)\bigg \}\\&={_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})(a). \end{aligned}$$ -
(4)
If \(a \in \Omega \), then we have
$$\begin{aligned} {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})(a)&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y))\vee (\mathscr {G}\cap \mathscr {Y})(y)\bigg \}\\&=\bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y))\vee \mathscr {G}(y)\bigg \}\\&\cap \bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y))\vee \mathscr {Y}(y)\bigg \}\\&={_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})(a)\cap {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})(a). \end{aligned}$$ -
(5)
Similar to (4).
-
(6)
If \(1-\mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\le \mathscr {G}(a) \le \mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\), for all \(a \in \Omega \), then
$$\begin{aligned} \mathscr {G}(a)&=\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(a) \wedge \mathscr {G}(a)\le \bigvee \limits _{y\in \Omega }\bigg (\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y) \wedge \mathscr {G}(y)\bigg )\\&\implies \mathscr {G}(a)\le \bigwedge \limits _{i=1}^{n}\bigvee \limits _{y\in \Omega }\bigg \{\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y)\wedge \mathscr {G}(y)\bigg \}={_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})(a)\\&\implies \bigwedge \limits _{y\in \Omega }\bigg \{(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y))\vee \mathscr {G}(y)\bigg \}\le (1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(a))\vee \mathscr {G}(a)\le \mathscr {G}(a) \\&\implies \bigvee \limits _{i=1}^{n}\bigwedge \limits _{y\in \Omega }\bigg \{(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(y))\vee \mathscr {G}(y)\bigg \}\le \mathscr {G}(a)\\&\implies {_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})(a)\le \mathscr {G}(a)\\&\implies {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq \mathscr {G} \subseteq {_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}). \end{aligned}$$
\(\square \)
Definition 16
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and \(a,y \in \Omega \). A MGFMD \(^{2}\mathscr {D}^{\beta }_{\mathbb {F}_{j}(a_i)}(a,y)\), where \(a_i \in \Omega \) and \(i=1,\ldots ,m\) is shown by
Example 9
(Continued from Example 7) If \(\beta =0.5\), then the below outcomes hold for \(\mathbb {F}_{1}\):
-
(1)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_1)=1, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_2)=0.37, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_3)=0.54, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_4)=0.61, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_5)=0.8, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_1,a_6)=0.85\).
-
(2)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_1)=0.37, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_2)=1, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_3)=0.5, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_4)=0.34, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_5)=0.41,\)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_2,a_6)=0.32\).
-
(3)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_1)=0.54, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_2)=0.5, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_3)=1, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_4)=0.58, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_5)=0.63,\)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_3,a_6)=0.57\).
-
(4)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_1)=0.61, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_2)=0.34, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_3)=0.58, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_4)=1, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_5)=0.64, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_4,a_6)=0.63\).
-
(5)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_1)=0.8, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_2)=0.41, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_3)=0.63, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_4)=0.64, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_5)=1, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_5,a_6)=0.69\).
-
(6)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_1)=0.85, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_2)=0.32, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_3)=0.57, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_4)=0.63, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_5)=0.69, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{1}}(a_6,a_6)=1\).
And for \(\mathbb {F}_{2}\):
-
(i)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_1)=1, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_2)=0.34, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_3)=0.81, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_4)=0.71, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_5)=0.81, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_1,a_6)=0.86\).
-
(ii)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_1)=0.34, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_2)=1, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_3)=0.29, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_4)=0.29, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_5)=0.36, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_2,a_6)=0.28\).
-
(iii)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_1)=0.81, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_2)=0.29, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_3)=1, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_4)=0.74, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_5)=0.67, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_3,a_6)=0.71\).
-
(iv)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_1)=0.71, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_2)=0.29, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_3)=0.74, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_4)=1, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_5)=0.69, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_4,a_6)=0.77\).
-
(v)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_1)=0.81, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_2)=0.36, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_3)=0.67, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_4)=0.69, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_5)=1, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_5,a_6)=0.7\).
-
(vi)
\(^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_1)=0.86, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_2)=0.28, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_3)=0.71, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_4)=0.77, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_5)=0.7, ^{2}\mathscr {D}^{0.5}_{\mathbb {F}_{2}}(a_6,a_6)=1\).
Definition 17
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and \(^{2}\mathscr {D}^{\beta }_{\mathbb {F}_{j}}\) be an MGFMD of \(\Omega \). For any \(\mathscr {G} \in {\mathcal {F}}(\Omega )\) and \(\alpha \in [0,1)\), the 2-O\(\alpha \)LA and the 2-O\(\alpha \)UA are given by
Example 10
(Continued from Example 9) If \(\alpha =0.65\), then we have
Theorem 5
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), the next properties hold for 2-O\(\alpha \)LA and 2-O\(\alpha \)UA.
-
(1)
\({_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c)\bigg )^c\) and \({_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c)\bigg )^c\).
-
(2)
\({_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\Omega )=\) \(\Omega \) and \({_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\emptyset )=\) \(\emptyset \)
-
(3)
If \(\mathscr {G} \subseteq \mathscr {Y}\), then \({_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) \(\subseteq {_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) \(\subseteq {_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(4)
\({_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})=\) \({_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})\subseteq \) \({_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\)
-
(5)
\({_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y})\supseteq {_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y})= {_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(6)
If \(1-\mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\le \mathscr {G}(a) \le \mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\), \(\forall a \in \Omega \), then \({_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}) \subseteq \mathscr {G} \subseteq {_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\).
Proof
Similarly, follows from Theorem 4. \(\square \)
Now, we give another MGFRC form by \(^{2}\mathscr {D}^{\beta }_{\mathbb {F}_{j}}\).
Definition 18
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and \(^{2}\mathscr {D}^{\beta }_{\mathbb {F}_{j}}\) be an MGFMD of \(\Omega \). For any \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), the 2-O\(\mathscr {D}\)LA and 2-O\(\mathscr {D}\)UA are given by
Example 11
(Continued from Examples 1 and 9) We have,
Theorem 6
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), the below properties hold for 2-O\(\mathscr {D}\)LA and 2-O\(\mathscr {D}\)UA.
-
(1)
\({_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c)\bigg )^c\) and \({_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\bigg ({_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}^c)\bigg )^c\).
-
(2)
\({_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\Omega )=\) \(\Omega \) and \({_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\emptyset )=\) \(\emptyset \)
-
(3)
If \(\mathscr {G} \subseteq \mathscr {Y}\), then \({_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) \(\subseteq {_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) \(\subseteq {_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(4)
\({_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})=\) \({_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cap \mathscr {Y})\subseteq \) \({_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cap {_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\)
-
(5)
\({_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y})\supseteq {_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\) and \({_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}\cup \mathscr {Y})= {_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\cup {_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {Y})\).
-
(6)
If \(1-\mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\le \mathscr {G}(a) \le \mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\), \(\forall a \in \Omega \), then \({_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}) \subseteq \mathscr {G} \subseteq {_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\).
Proof
The evidence is comparable to Theorem 4. \(\square \)
4.2 \(\hbox {CP}_{{MG}}\)FRSs
Definition 19
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G} \in {\mathcal {F}}(\Omega ),\) the 2-PLA and the 2-PUA are established as indicated below.
If \({_{-2}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\ne {_{+2}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\), then \(({_{-2}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}), {_{+2}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}))\) is called a 2-\(\hbox {CP}_{{MG}}\)FRS, otherwise it is definable.
Definition 20
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and \(^{2}\mathscr {D}^{\beta }_{\mathbb {F}_{j}}\) be a MGFMD of \(\Omega \). For any \(\mathscr {G} \in {\mathcal {F}}(\Omega )\) and \(\alpha \in [0,1)\), the 2-P\(\alpha \)LA and 2-P\(\alpha \)UA are given by
Definition 21
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS and \(^{2}\mathscr {D}^{\beta }_{\mathbb {F}_{j}}\) be a MGFMD of \(\Omega \). For every \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), the 2-P\(\mathscr {D}\)LA and 2-P\(\mathscr {D}\)UA are given by
Example 12
(Continued from Examples 7 and 8) Let \(\mathscr {G}=\frac{0.6}{a_1}+\frac{0.3}{a_2}+\frac{0.7}{a_3}+\) \(\frac{0.1}{a_4}+\frac{0.5}{a_5}+\frac{0.8}{a_6}\) and \(\alpha =0.65\). Then we have
-
(1)
\({_{-2}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.4}{a_1}+\frac{0.4}{a_2}+\frac{0.1}{a_3}+\frac{0.4}{a_4}+\) \(\frac{0.2}{a_5}+\frac{0.4}{a_6}\) and
\({_{+2}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.7}{a_1}+\frac{0.3}{a_2}+\frac{0.7}{a_3}+\frac{0.4}{a_4}+\) \(\frac{0.5}{a_5}+\frac{0.7}{a_6}\).
-
(2)
\({_{-2}\mathscr {R}}^{p,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.1}{a_1}+\frac{0.3}{a_2}+\frac{0.1}{a_3}+\frac{0.1}{a_4}+\) \(\frac{0.1}{a_5}+\frac{0.1}{a_6},\) and
\({_{+2}\mathscr {R}}^{p,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.8}{a_1}+\frac{0.3}{a_2}+\frac{0.8}{a_3}+\frac{0.8}{a_4}+\) \(\frac{0.8}{a_5}+\frac{0.8}{a_6}.\)
-
(3)
\({_{-2}\mathscr {R}}^{p,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.29}{a_1}+\frac{0.3}{a_2}+\frac{0.26}{a_3}+\) \(\frac{0.1}{a_4}+\frac{0.31}{a_5}+\frac{0.23}{a_6},\) and
\({_{+2}\mathscr {R}}^{p,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})=\) \(\frac{0.8}{a_1}+\frac{0.41}{a_2}+\frac{0.71}{a_3}+\frac{0.77}{a_4}+\) \(\frac{0.7}{a_5}+\frac{0.8}{a_6}.\)
5 Four kinds of \(\hbox {CVP}_{{MG}}\)FRS models
In this section, we investigate four novel forms of \(\hbox {CVP}_{{MG}}\)FRSs samples and their relevant characteristics are obvious from the above sections, so we introduce the definitions only.
Definition 22
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For every \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), and a variable precision attribute \(\gamma \in [0,1]\).
-
1.
The 1-VPLA and 1-VPUA are given as next
$$\begin{aligned} _{-1}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})(a)= \bigvee \limits _{j=1}^{n}\bigg (\bigwedge \limits _{\mathscr {G}(y)\le \gamma }((1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta })\vee \gamma )\wedge \bigwedge \limits _{\mathscr {G}(y)> \gamma }(1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta })\vee \mathscr {G}(y)\bigg ), \end{aligned}$$and
$$\begin{aligned} _{+1}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})(a)= \bigwedge \limits _{j=1}^{n}\bigg (\bigvee \limits _{\mathscr {G}(y)\le \gamma }(\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }\wedge (1-\gamma ))\vee \bigvee \limits _{\mathscr {G}(y)> \gamma }(\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }\wedge \mathscr {G}(y))\bigg ). \end{aligned}$$ -
2.
The 2-VPLA and 2-VPUA are defined as next
$$\begin{aligned} _{-2}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})(a)= \bigwedge \limits _{j=1}^{n}\bigg (\bigwedge \limits _{\mathscr {G}(y)\le \gamma }((1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta })\vee \gamma )\wedge \bigwedge \limits _{\mathscr {G}(y)> \gamma }(1-\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta })\vee \mathscr {G}(y)\bigg ), \end{aligned}$$and
$$\begin{aligned} _{+2}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})(a)= \bigvee \limits _{j=1}^{n}\bigg (\bigvee \limits _{\mathscr {G}(y)\le \gamma }(\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }\wedge (1-\gamma ))\vee \bigvee \limits _{\mathscr {G}(y)> \gamma }(\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}(a)}^{\beta }\wedge \mathscr {G}(y))\bigg ). \end{aligned}$$ -
3.
The 3-VPLA and 3-VPUA are established as next
$$\begin{aligned} _{-3}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})(a)= \bigvee \limits _{j=1}^{n}\bigg (\bigwedge \limits _{\mathscr {G}(y)\le \gamma }((1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}(a)}^{\beta })\vee \gamma )\wedge \bigwedge \limits _{\mathscr {G}(y)> \gamma }(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}(a)}^{\beta })\vee \mathscr {G}(y)\bigg ), \end{aligned}$$and
$$\begin{aligned} _{+3}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})(a)= \bigwedge \limits _{j=1}^{n}\bigg (\bigvee \limits _{\mathscr {G}(y)\le \gamma }(\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}(a)}^{\beta }\wedge (1-\gamma ))\vee \bigvee \limits _{\mathscr {G}(y)> \gamma }(\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}(a)}^{\beta }\wedge \mathscr {G}(y))\bigg ). \end{aligned}$$ -
4.
The 4-VPLA and 4-VPUA are shown as next
$$\begin{aligned} _{-4}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})(a)= \bigwedge \limits _{j=1}^{n}\bigg (\bigwedge \limits _{\mathscr {G}(y)\le \gamma }((1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}(a)}^{\beta })\vee \gamma )\wedge \bigwedge \limits _{\mathscr {G}(y)> \gamma }(1-\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}(a)}^{\beta })\vee \mathscr {G}(y)\bigg ), \end{aligned}$$and
$$\begin{aligned} _{+4}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})(a)=\bigvee \limits _{j=1}^{n}\bigg (\bigvee \limits _{\mathscr {G}(y)\le \gamma }(\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}(a)}^{\beta }\wedge (1-\gamma ))\vee \bigvee \limits _{\mathscr {G}(y)> \gamma }(\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}(a)}^{\beta }\wedge \mathscr {G}(y))\bigg ). \end{aligned}$$For all \(a \in \Omega \) and if \(_{-H}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})\ne _{+H}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})\), then \((\ _{-H}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G}),\ _{+H}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G}))\) is called a H-\(\hbox {VP}_{{MG}}\)FRS, otherwise it is definable, where \(H \in \{1,2,3,4\}\).
Example 13
(Continued from Examples 1 and 7). If \(\gamma =0.5\), then we have,
-
(1)
$$\begin{aligned}{} & {} _{-1}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})=\frac{0.5}{a_1}+ \frac{0.5}{a_2}+ \frac{0.5}{a_3}+ \frac{0.5}{a_4}+ \frac{0.5}{a_5}+ \frac{0.5}{a_6},\hbox { and } \\{} & {} _{+1}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})=\frac{0.5}{a_1}+ \frac{0.5}{a_2}+ \frac{0.5}{a_3}+ \frac{0.5}{a_4}+ \frac{0.5}{a_5}+ \frac{0.5}{a_6}. \end{aligned}$$
-
(2)
$$\begin{aligned}{} & {} _{-2}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})=\frac{0.5}{a_1}+ \frac{0.5}{a_2}+ \frac{0.5}{a_3}+ \frac{0.5}{a_4}+ \frac{0.5}{a_5}+ \frac{0.5}{a_6},\hbox { and } \\{} & {} _{+2}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})=\frac{0.5}{a_1}+ \frac{0.5}{a_2}+ \frac{0.5}{a_3}+ \frac{0.5}{a_4}+ \frac{0.5}{a_5}+ \frac{0.5}{a_6}. \end{aligned}$$
-
(3)
$$\begin{aligned}{} & {} _{-3}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})=\frac{0.5}{a_1}+ \frac{0.5}{a_2}+ \frac{0.5}{a_3}+ \frac{0.5}{a_4}+ \frac{0.5}{a_5}+ \frac{0.5}{a_6},\hbox { and } \\{} & {} _{+3}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})=\frac{0.5}{a_1}+ \frac{0.2}{a_2}+ \frac{0.5}{a_3}+ \frac{0.3}{a_4}+ \frac{0.5}{a_5}+ \frac{0.5}{a_6}. \end{aligned}$$
-
(4)
$$\begin{aligned}{} & {} _{-4}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})=\frac{0.5}{a_1}+ \frac{0.5}{a_2}+ \frac{0.5}{a_3}+ \frac{0.5}{a_4}+ \frac{0.5}{a_5}+ \frac{0.5}{a_6},\hbox { and } \\{} & {} _{+4}\mathscr {R}_{\sum _{j=1}^{n}\mathbb {F}_{j}}^\gamma (\mathscr {G})=\frac{0.5}{a_1}+ \frac{0.3}{a_2}+ \frac{0.5}{a_3}+ \frac{0.4}{a_4}+ \frac{0.5}{a_5}+ \frac{0.5}{a_6}. \end{aligned}$$
6 Connections between the \(\hbox {CO}_{{MG}}\)FRS and \(\hbox {CP}_{{MG}}\)FRS models
Now, the relationships among presented models are given. From the above study, we have the next outcomes.
Proposition 1
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), we have
-
(1)
\({_{-1}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
-
(2)
\({_{-2}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
-
(3)
\({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+1}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
-
(4)
\({_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+2}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
Proof
Follows from Definitions 7, 11, 15 and 19. \(\square \)
Proposition 2
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), if \(1-\mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\le \mathscr {G}(a) \le \mathbb {N}_{\mathbb {F}_{j}}^{\beta }(a)\), \(\forall a \in \Omega \),
-
(1)
\({_{-1}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq \mathscr {G} \subseteq {_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+1}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
-
(2)
\({_{-2}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq \mathscr {G} \subseteq {_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+2}\mathscr {R}}^{p}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
Proof
Directly from Theorems 1 and 4. \(\square \)
Proposition 3
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For every \(\mathscr {G} \in {\mathcal {F}}(\Omega )\),
-
(1)
\({_{-1}\mathscr {R}}^{p,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{-1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq \mathscr {G} \subseteq {_{+1}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+1}\mathscr {R}}^{p,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
-
(2)
\({_{-2}\mathscr {R}}^{p,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{-2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq \mathscr {G}\subseteq {_{+2}\mathscr {R}}^{o,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+2}\mathscr {R}}^{p,\alpha }_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
Proof
Directly from Theorems 2 and 5. \(\square \)
Proposition 4
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For every \(\mathscr {G} \in {\mathcal {F}}(\Omega )\),
-
(1)
\({_{-1}\mathscr {R}}^{p,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{-1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq \mathscr {G} \subseteq {_{+1}\mathscr {R}}^{o,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+1}\mathscr {R}}^{p,^{1}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
-
(2)
\({_{-2}\mathscr {R}}^{p,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}) \subseteq {_{-2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}) \subseteq \mathscr {G} \subseteq {_{+2}\mathscr {R}}^{o,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+2}\mathscr {R}}^{p,^{2}\mathscr {D}}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
Proof
Follows from Theorems 3 and 6. \(\square \)
Proposition 5
Let \((\Omega ,{\kappa })\) be a \({\textbf {MGF}}_{\beta }\)CAS. For any \(\mathscr {G} \in {\mathcal {F}}(\Omega )\), we have
-
(1)
\({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{-2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
-
(2)
\({_{+2}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\subseteq {_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G}).\)
Proof
Its obvious. \(\square \)
The correlations can be depicted in Figs. 2 and 3.
The relationships between 1-\(\hbox {CO}_{{MG}}\)FRLA and 1-\(\hbox {CP}_{{MG}}\)FRLA models as in Sect. 3
The relationships between 2-\(\hbox {CO}_{{MG}}\)FRLA and 2-\(\hbox {CP}_{{MG}}\)FRLA models as in Sect. 4
7 Approaches to MCGDM and MAGDM based on the presented methods
In this section, using the concepts presented in Sects. 3 and 4, we apply the mentioned methods to decide on real-life problems. Next, we construct novel approaches to MCGDM and MAGDM based on \(\hbox {C}_{{MG}}\)FRS. Further, we demonstrate the main characterization of the MCGDM problem in Sect. 7.1 and MAGDM problem in Sect. 7.2.
7.1 MCGDM problem
7.1.1 Description and process
Let \(\Omega =\{a_r: r=1, 2, \ldots , n\}\) be the group of n patients, \(S=\{y_i: i= 1, 2, \ldots , m\}\) be m significant indicators and manifestations (fever, cough, sore throat, headache, and a chill) of \(\mathscr {A}\) sickness, and \(\kappa =\{\mathbb {F}_{j}(a_r)\}\) specify the effectiveness value of \(a_r\) for \(y_i\) signs, for some \(\beta \in (0,1]\), \((\Omega ,\kappa )\) is a \({\textbf {MGF}}_{\beta }\)CAS.
We provide a decision-making algorithm according to the proposed approaches to reach the outcome by the following phases.
Step 1: The on-call physician \(\mathcal {P}\) calls n specialists \(\mathcal {E}_i (i = 1, 2,\ldots , n)\) to estimate each sick \(a_k (k = 1, 2,\ldots , l)\) and every decision maker \(\mathcal {E}_i\) deemed valid each patient \(a_k \in \Omega \) has a clear sign impact denote by \(\mathbb {F}_{ij}(a_k)\).
Step 2: Experts evaluates each \(a_k \in \Omega \) with respect to their symptoms by the following formula \(\{y_i:\mathbb {F}_{ij}(a)\ge \beta \}\).
Step 3: According to the decision maker (physician \(\mathcal {D}\)), consider a FS \(\mathscr {G}\) represents the potential of the drugs in \(\Omega \) to treat the \(\mathcal {A}\) sickness. This assists the decision maker in determining whether or not those suffering \(a_k \in \Omega \) have the disease \(\mathcal {A}\).
Step 4: Evaluate the OLA and the OUA by the proposed models.
Step 5: Compute the MCGDM of \(\mathscr {G}\) by
, and hence make a decision.
We provide an algorithm to answer decision-making issues depending on the Definitions 7 and 15 based on these stages. Algorithm 1 summarizes the stages that relate to it.
Algorithm 1. Algorithm for MCGDM approach. | |
|---|---|
Input: Information systems. | |
Output: Decision Making. | |
1: Enter \(\mathscr {G}\), \(\beta \), \(\kappa \) and \(\Omega \). | |
2: From Definition 3, compute the \(\vee \tilde{\mathbb {M}d}_{\mathbb {F}_{j}}^{\beta }(a_i)\) ( \(\wedge \tilde{\mathbb {M}D}_{\mathbb {F}_{j}}^{\beta }(a_i)\)), \(\forall a \in \Omega , i=1,..,n\). | |
3: From Step 2, calculate \({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) and \({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\). | |
4: Enter the value of \(\psi \in [0,1]\). | |
5: Calculate the MCGDM of \(\mathscr {G}\) by \(\sum _{i=1}^{n}\Re _i(\mathscr {G})\). | |
6: Obtain the decision. |
7.1.2 An illustrative example
The preceding steps are built numerically in the below example.
Example 14
To treat a condition, various types of medications are generally mixed. Let \(\Omega =\{a_j: j=1, 2, \ldots , 6\}\) be the group of 6 illness, \(S=\{y_i: i= 1, 2, \ldots , 5\}\) be 5 the primary signs (e.g., fever, cough, sore, headache, and chill) of \(\mathcal {A}\) ailments, and \(\mathbb {F}_{j}(a_i)\) represent the therapeutic associated with \(a_i\) for \(y_i\) disorders. Let \(\beta =0.6\) be the crucial value. If the physician \(\mathcal {D}\) asks the two specialists \(\mathcal {E}_i (i=1,2)\) to examine patients \(a_j (j=1,2,\ldots ,6)\) as shown in Tables 1 and 2.
The phases of the specified algorithm are carried out next.
Step 1. As shown in Example 1, the physician \(\mathcal {D}\) calculates the probable value \(\mathscr {G}\) of a sickness \(\mathcal {A}\) for each patient.
.
Step 2. Compute \(\vee \tilde{\mathbb {M}d}^{\beta }_{\mathbb {F}_{j}}(a_i)\) as listed on Tables 5 and 6.
Step 3. Compute the 1-OLA and the 1-OUA as the following
Step 4. Based on these approximations, compute the MCGDM of \(\mathscr {G}\) by the following method
So, if \(\psi =0.6\), then we have
and hence the order of the degree of susceptible to infection is obtained as the next.
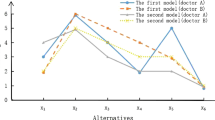
\(a_1\approx a_3 \approx a_6\ge a_4 \ge a_2 \ge a_5.\)
From the computation, the doctor \(\mathcal {D}\) determines that the patients \(a_1, a_3\), and \(a_6\) are more vulnerable to contamination for the condition \(\mathcal {A}\).
Remark 1
The value of \(\psi \) represents the decision-makers perspectives on the dangers of deciding difficulties. When the decision-maker prefers risk, the higher the value of \(\psi \). When an administrator is risk-averse, the outcome of \(\psi \) tends to be lower. Consequently, the professional can ascertain the conclusion of \(\psi \) by considering the objective. We also have the next conditions.
-
1.
\(\sum _{i=1}^{n}\Re _i(\mathscr {G})={_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\), when \(\psi =1\).
-
2.
\(\sum _{i=1}^{n}\Re _i(\mathscr {G})={_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\), when \(\psi =0\).
In a word, we face a slew of complex concerns fraught with uncertainty. As a result, the expert can change the result of \(\psi \) to fix specific problems in the actual world.
7.2 MAGDM problem
7.2.1 Description and process
Let \(\Omega =\{a_1,a_2,\ldots ,a_n\}\) be n candidates and \(\mathcal {X}=\{t_1,t_2,\ldots ,t_r\}\) be r decision makers. Assume that for each \(\varPsi _i\) is a vector correspondingly to \(t_i\), with \(\varPsi _i\ge 0\) for \(r=1,\ldots ,i\) and \(\sum _{i=1}^{r}\varPsi _i=1\). Hence, \(\mathbb {F}_{j}= \{\mathbb {F}_{j1}, \mathbb {F}_{j2},\ldots ,\mathbb {F}_{jm}\}\), for any \(j=1,2,\ldots ,n\) is the attribute set. A collection of functions \(\mathcal {H}=\{h_r: \Omega \times \mathbb {F}_{j} \rightarrow [0,1]\}\). Thus, we establish the MAGDM through the mentioned schemes to obtain the suitable decision is such problems \((\Omega ,\mathbb {F}_{j},\mathcal {X},\mathcal {H}).\)
Step 1: Create the decision-making entity with fuzzy information. We have the following formulas using the TOPSIS method.
and
where \(\bigvee \) and \(\bigwedge \) denotes to "max" and "min", respectively.
Step 2: Calculate the distances \(\overline{\mathscr {S}}\) and \(\underline{\mathscr {S}}\) as below:
and
where \(\mathscr {S}(\hat{L},\hat{P})=\sqrt{\frac{1}{m}\sum _{j=1}^{m}(\hat{L}(a_i)-\hat{P}(a_i))^{2}}\).
Step 3: Achieve the presented method of approximation using Definition 7, to get the values of the OLA and OUA.
Step 4: Calculate the closeness coefficient degree by \(\mathscr {C}_{r}(a_i)=\frac{\underline{\mathcal {V}_{r}}(a_i)}{\underline{\mathcal {V}_{r}}(a_i)+\overline{\mathcal {V}_{r}}(a_i)}.\)
Where \(\underline{\mathcal {V}_{r}}(a_i)=\mathcal {S}_{{p}}\bigg ({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\underline{\mathscr {S}}_{r}(a_i)),{_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\underline{\mathscr {S}}_{r}(a_i))\bigg ),\) and
\(\overline{\mathcal {V}_{r}}(a_i)=\mathcal {S}_{{p}}\bigg ({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\overline{\mathscr {S}}_{r}(a_i)),{_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\overline{\mathscr {S}}_{r}(a_i))\bigg )\),
and \(0\le \underline{\mathcal {V}_{r}}(a_i),\overline{\mathcal {V}_{r}}(a_i)\le 1\) with \(\mathcal {S}_{{p}}(a,b)=a+b-a*b.\)
Step 5: Compute the arranging function \(\mathscr {C}(a_i)=\sum _{r=1}^{t}\varpi _{r}\mathscr {C}_{r}(a_i),\) and then rank the candidates.
By following the aforementioned stages, we develop an algorithm to address the problems associated with decision making, based on the suggested template outlined in Algorithm 2.
Algorithm 2. Algorithm for MAGDM approach. | |
|---|---|
Input: Fuzzy information systems \((\Omega ,\kappa , {\mathcal {X}},{\mathcal {H}})\). | |
Output: Decision Making. | |
1: Enter \(\mathscr {G}\), \(\beta \), \(\kappa =\{\mathbb {F}_{j}:j=1,\ldots ,n\}\) and \(\Omega =\{a_i:i=1,\ldots ,m\}\). | |
2: From Definition 3, compute \(\mathbb {N}^{\beta }_{\mathbb {F}_{j}}(a)\) and \(\mathbb {M}^{\beta }_{\mathbb {F}_{j}}(a)\). | |
3: From Steps 2, compute \(\tilde{\mathbb {M}d}_{\mathbb {F}_{j}}^{\beta }(a).\) | |
4: Get \(\overline{\mathscr {G}}_{r}\) and \(\underline{\mathscr {G}}_{r}\). | |
5: Compute the distances \(\overline{\mathscr {S}}_{r}\) and \(\underline{\mathscr {S}}_{r}\). | |
6: From Definition 7, compute the 1-OLA \({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\) and the 1-OUA \({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}(\mathscr {G})\). | |
7: Calculate the least well and greatest decision-making factors \(\overline{\mathcal {V}_{r}}\) and \(\underline{\mathcal {V}_{r}}\). | |
8: Compute the ordering mapping \(\mathcal {C}_{r}\). | |
9: Compute the set sorting mapping \(\mathcal {C}\). | |
10: Obtain the decision. |
7.2.2 Numerical example
Now, we give an illustrative example to explain the above steps in Algorithm 2.
Example 15
Let \(\Omega =\{a_1,a_2,\ldots ,a_6\}\) be six engineers and \(\kappa =\{\) steadiness (\(\mathbb {F}_{1}\)), skills (\(\mathbb {F}_{2}\)), personality (\(\mathbb {F}_{3}\)), experience (\(\mathbb {F}_{4}\)), aplomb (\(\mathbb {F}_{5}\)) \(\}\) be the description of the candidates’ attribute set. Assume that three specialists \(t_1, t_2\) and \(t_3\) are called to estimate the alternatives based on their information. Every expert’s ratings are: \(\varpi _1=0.4, \varpi _2 = 0.1\) and \(\varpi _3 = 0.5\).
Step 1: Experts estimate each alternative as summarized in Tables 11, 12 and 13.
Step 2: Based on the significant of these parameters, we have the next outcomes for each decision maker.
and
and
and
Step 3: If \(\beta = 0.5\), then \(\mathbb {N}^{\beta }_{\mathbb {F}_{j}}, \mathbb {M}^{\beta }_{\mathbb {F}_{j}},\) and \(\tilde{\mathbb {M}d}_{\mathbb {F}_{j}}^{\beta }\) as put in Tables 14, 15, 16, 17, 18 and 19 below.
Step 4: Determine the distances \(\overline{\mathscr {S}}_{r}\) and \(\underline{\mathscr {S}}_{r}\) as next.
Step 5: Compute the 1-OLA \({_{-1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}\) and the 1-OUA \({_{+1}\mathscr {R}}^{o}_{\sum _{j=1}^{n}\mathbb {F}_{j}}\) as follows.
When \(t=t_1\), we have
When \(t=t_2,\) we have
When \(t=t_3,\) we have
Step 6: The following are the most destructive and finest decision-making belongings.
Then, as seen below, we calculate the nearby factor.
Step 7: SO, we compute \(\mathscr {C}\) as follows.
and thus get the order as
\(a_4\ge a_1 \approx a_3 \ge a_6 \approx a_2 \approx a_5.\)
As a consequence, we employ our methods based MAGDM with a fuzzy information template to carry out the decision-making for the best possible choice. We can attain the ultimate optimal solution of the fourth engineer by considering the previous phases.
7.3 Comparative analysis
This study presents a new approach for MAGDM by utilizing the \(\hbox {C}_{{MG}}\)FRSs with the aid of fuzzy \(\beta \)-minimum and maximum descriptions. This framework presents novel mathematical structures that are seen as an extension of the works by Zhan et al. (2020), Atef and El-Atik (2021), Zhan et al. (2019), and Ma et al. (2020). Here, we provide an explanation of the comparisons between the given methods and the previous one (i.e., Zhan et al. 2020; Atef and El-Atik 2021; Zhan et al. 2019 and Ma et al. 2020) to show the efficiency and the performance of these studies. We divide it into two items, that is, MCGDM and MAGDM, respectively.
-
1.
We explain the differences between MCGDM approach and the last ones (i.e., Zhan et al. 2020 as in Definition 4 and Atef and El-Atik (2021) as in Definition 5) as in Table 20.
From Table 20, in Zhan et al. (2020) and Atef and El-Atik (2021), the patients \(a_3\) and \(a_6\) are susceptible to infection for the disease \(\mathcal {A}\) and here the patients \(a_3\), \(a_6\) and \(a_1\) are susceptible to infection for the disease \(\mathcal {A}\). There is slight difference in the ranking of the other alternatives. So, our approach is effective and reliable.
-
2.
Here, we clarify the comparisons between MAGDM approach and the previous studies such as the Zhan et al. (2019) scheme and Ma et al. (2020) model. The ordering of the alternatives by these different models and ours are established in Table 21.
The above Table 21 provides us with the sorting of these different approaches and it is clear that the \(a_4\) engineer is the optimal candidate for all methods (i.e., Zhan et al. 2019 model, Ma et al. (2020) template and our approach). This leads that our presented work is effective.
-
3.
Additionally, the ranking of candidates among several approaches is elucidated in Fig. 4. These methods include our proposed methods, the samples presented by Zhan et al. (2019) and (2020), Atef and El-Atik (2021) and the template proposed by Ma et al. (2020). Based on the visual representation provided, it is evident that choice \(a_3\) exhibits superior qualities compared to the other alternatives under consideration for the first technique and \(a_4\) for the second strategy.
-
4.
Hence, to further explain the differences in the selection of optimal candidates with the difference value of the risk parameter \(\psi \), you can see Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15 which shows comparisons among alternatives in various methods (i.e., 1-\(\hbox {CO}_{{MG}}\)FRS, 2-\(\hbox {CO}_{{MG}}\)FRS, i-\(\hbox {CO}_{{MG}}\)FRS, ii-\(\hbox {CO}_{{MG}}\)FRS, iii-\(\hbox {CO}_{{MG}}\)FRS and iv-\(\hbox {CO}_{{MG}}\)FRS) with different outcomes of \(\psi \). Subsequently, Table 22 explains the variations of ordering the global set using the 1-\(\hbox {CO}_{{MG}}\)FRS model, because this is the better one according to maximum the lower approximation and minimum the upper approximation that helps us to decrease the boundary area and increase the accuracy via several results of \(\psi \).
-
5.
As is generally known, aggregation algorithms are mostly used in conventional MAGDM situations. This means that the choices of various decision-makers can be predicted by employing the selected aggregation operators. The fundamental issues of conventional MAGDM difficulties then focus on selecting effective aggregation operators. In this paper, we investigate an alternate technique for MAGDM models using CMGFRS. This article attempts to address the issue. The decision-making concept and procedure of the CMGFRS-based MAGDM model and approach differ from those of the aggregation operator strategy for MAGDM problems.
The downside of the suggested approach is that it is more sophisticated than traditional MAGDM issues, but we can solve it using computer tools (Matlab and Excel).
8 Conclusion and future work
In this research, we set the definitions of the family of fuzzy \(\beta \)-minimum and maximum descriptions and then construct novel covering strategies called \({\textbf {MGF}}_{\beta }\)CAS with respect to the (O,P,VP) FRSs. According to these concepts, we extend a new structure for a multigranulation fuzzy measure degree and utilize it to construct two models of optimistic (pessimistic) \(\alpha \) lower and upper approximations. By these approximations, we introduce two methods of optimistic (pessimistic) \(\mathscr {D}\) lower and upper approximations and discuss their features. Relationships between these models are also examined. Then, using MCGDM and MAGDM methodologies, we demonstrate the dependability of our methods. Finally, we provide numerical comparisons between the presented models and the previous research to demonstrate their effectiveness as shown in Tables 20 and 21, and Fig. 4. Consequently, we examine the sensitivity analysis of our presented models through Table 22 and Figs. 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 and 15 that analyze the outcomes over different values of \(\psi \). Another advantage for this article is to introduce the minimal set of attributes and this will allow us to examine the reduction for this approach in further research. Furthermore, we aim to investigate the algebraic and topological aspects of \(\hbox {C}_{{MG}}\)FRS models.
Data availability
No datasets were generated or analysed during the current study.
Abbreviations
- CRS:
-
Covering rough sets
- CAS :
-
Covering approximation space
- FCAS :
-
Fuzzy covering approximation space
- \({\textbf {F}}_{\beta }\) CAS :
-
Fuzzy \(\beta \) covering approximation space
- FRS:
-
Fuzzy rough sets
- MGFRS:
-
Multigranulation fuzzy rough set
- \({\textbf {MGF}}_{\beta }\) CAS :
-
Multigranulation fuzzy \(\beta \) covering approximation space
- \(\hbox {O}_{{MG}}\)FRS:
-
Optimistic multigranulation fuzzy rough set
- \(\hbox {P}_{{MG}}\)FRS:
-
Pessimistic multigranulation fuzzy rough set
- \(\hbox {CO}_{{MG}}\)FRS:
-
Covering optimistic multigranulation fuzzy rough set
- \(\hbox {CP}_{{MG}}\)FRS:
-
Covering pessimistic multigranulation fuzzy rough set
- \(\hbox {CVP}_{{MG}}\)FRS:
-
Covering variable precision multigranulation fuzzy rough set
- OLA:
-
Optimistic lower approximation
- OUA:
-
Optimistic upper approximation
- PLA:
-
Pessimistic lower approximation
- PUA:
-
Pessimistic upper approximation
- MGFMD:
-
Multigranulation fuzzy measure degree
- O\(\alpha \)LA:
-
Optimistic \(\alpha \)-lower approximation
- O\(\alpha \)UA:
-
Optimistic \(\alpha \)-upper approximation
- P\(\alpha \)LA:
-
Pessimistic \(\alpha \)-lower approximation
- P\(\alpha \)UA:
-
Pessimistic \(\alpha \)-upper approximation
- O\(\mathscr {D}\)LA:
-
Optimistic \(\mathscr {D}\)-lower approximation
- O\(\mathscr {D}\)UA:
-
Optimistic \(\mathscr {D}\)-upper approximation
- P\(\mathscr {D}\)LA:
-
Pessimistic \(\mathscr {D}\)-lower approximation
- P\(\mathscr {D}\)UA:
-
Pessimistic \(\mathscr {D}\)-upper approximation
- MAGDM:
-
Multi-attribute group decision making
- MCGDM:
-
Multi-criteria group decision making
References
Atef M, Azzam AA (2021) Covering fuzzy rough sets via variable precision. J Math 2021(5525766):10. https://doi.org/10.1155/2021/5525766
Atef M, El-Atik AA (2021) Some extensions of covering-based multigranulation fuzzy rough sets from new perspectives. Soft Comput 25(8):6633–6651
Atef M, Liu S (2024) Four types of grey \(\beta \) covering models and their applications. Math Comput Simul 223:108–129
Atef M, Khalil AM, Li SG, Azzam A, El Atik AA (2020) Comparison of six types of rough approximations based on j-neighborhood space and j-adhesion neighborhood space. J Intell Fuzzy Syst 39(3):4515–4531
Atef M, Nada S, Nawar A (2023) Covering soft rough sets and its topological properties with application. Soft Comput 27(8):4451–4461
Bonikowski Z, Bryniarski E, Wybraniec-Skardowska U (1998) Extensions and intentions in the rough set theory. Inf Sci 107(1–4):149–167
Chen J, Zhu P (2023) A variable precision multigranulation rough set model and attribute reduction. Soft Comput 27(1):85–106
Chen Y, Kilgour D, Hipel K (2012) A decision rule aggregation approach to multiple criteria-multiple participant sorting. Group Decis Negot 21:727–745
Couso I, Dubois D (2011) Rough sets, coverings and incomplete information. Fund Inform 108(3–4):223–247
De Cock M, Cornelis C, Kerre EE (2004) Fuzzy rough sets: beyond the obvious. In: Proceedings of the 2004 IEEE international conference on fuzzy systems, vol 1, pp 103–108
D’eer L, Restrepo M, Cornelis C, Gómez J (2016) Neighborhood operators for covering-based rough sets. Inf Sci 336:21–44
D’eer L, Cornelis C, Godo L (2017) Fuzzy neighborhood operators based on fuzzy coverings. Fuzzy Sets Syst 312:17–35
Donbosco JSM, Ganesan D (2022) The Energy of rough neutrosophic matrix and its application to MCDM problem for selecting the best building construction site. Decis Making 5(2):30–45. https://doi.org/10.31181/dmame0305102022d
Dubois D, Prade H (1990) Rough fuzzy sets and fuzzy rough sets. Int J Gen Syst 17:191–201
Feng T, Zhang S, Mi J (2012) The reduction and fusion of fuzzy covering systems based on the evidence theory. Int J Approx Reason 53:87–103
Garg H, Atef M (2022) Cq-ROFRS: covering q-rung orthopair fuzzy rough sets and its application to multi-attribute decision-making process. Complex Intell Syst 8:2349–2370
Guo L, Zhan J, Zhang C, Xu Z (2023) A large-scale group decision-making method fusing three-way clustering and regret theory under fuzzy preference relations. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2023.3335965
Han X, Zhan J (2023) A sequential three-way decision-based group consensus method under probabilistic linguistic term sets. Inf Sci 624:567–589
Han X, Zhan J, Bao Y, Sun B (2024a) Three-way group consensus method based on probabilistic linguistic preference relations with acceptable inconsistency. Inf Fusion 103:102100
Han X, Zhan J, Xu Z, Martinez L (2024b) Trust risk test-based group consensus with probabilistic linguistic preference relations under social networks. IEEE Trans Fuzzy Syst 32(6):3508–3520. https://doi.org/10.1109/TFUZZ.2024.3377126
Herawan T, Deris MM, Abawajy JH (2010) A rough set approach for selecting clustering attribute. Knowl-Based Syst 23(3):220–231
Hong D, Choi C (2000) Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst 114:103–113
Huang Z, Li J (2022) Discernibility measures for fuzzy \(\beta \)-covering and their application. IEEE Trans Cybern 52(9):9722–9735
Huang Z, Li J (2024a) Noise-tolerant discrimination indexes for fuzzy \(\gamma \) covering and feature subset selection. IEEE Trans Neural Netw Learn Syst 35(1):609–623
Huang Z, Li J (2024b) Covering based multi-granulation rough fuzzy sets with applications to feature selection. Expert Syst Appl 238:121908
Huang B, Guo C, Zhang Y, Li H, Zhou X (2014) Intuitionistic fuzzy multigranulation rough sets. Inf Sci 277:299–320
Huang Z, Li J, Qian Y (2022) Noise-tolerant fuzzy \(\beta \)-covering-based multigranulation rough sets and feature subset selection. IEEE Trans Fuzzy Syst 30(7):2721–2735
Huang Z, Li J, Wang C (2024) Robust feature selection using multigranulation variable-precision distinguishing indicators for fuzzy covering decision systems. IEEE Trans Syst Man Cybern 54(2):903–914
Hwang C, Lin M (1987) Group decision making under multiple criteria. Lecture Notes in Economics and Mathematical Systems, Springer, Berlin
Jensen R, Shen Q (2004) Semantics-preserving dimensionality reduction: rough and fuzzy-rough-based approaches. IEEE Trans Knowl Data Eng 16(12):1457–1471
Jiang H, Zhan J, Sun B, Alcantud JCR (2020) An MADM approach to covering-based variable precision fuzzy rough sets: an application to medical diagnosis. Int J Mach Learn Cybern 11:2181–2207
Kakati P, Senapati T, Moslem S, Pilla F (2024) Fermatean fuzzy Archimedean Heronian mean-based model for estimating sustainable urban transport solutions. Eng Appl Artif Intell 127:107349
Li TJ, Leung Y, Zhang WX (2008) Generalized fuzzy rough approximation operators based on fuzzy covering. Int J Approx Reason 48:836–856
Lin G, Liang J, Qian Y (2013) Multigranulation rough sets: from partition to covering. Inf Sci 241:101–118
Liu CH, Miao DQ (2011) Covering rough set model based on multigranulations. In: Rough sets, fuzzy sets, data mining and granular computing: 13th international conference, RSFDGrC 2011. Russia, Moscow, pp 87–90
Liu C, Pedrycz W (2016) Covering-based multi-granulation fuzzy rough sets. J Intell Fuzzy Syst 30(1):303–318
Liu G, Sai Y (2009) A comparison of two types of rough sets induced by coverings. Int J Approx Reason 50(3):521–528
Liu CH, Wang MZ (2011) Covering fuzzy rough set based on multi-granulations. In: International conference on uncertainty reasoning and knowledge engineering, pp 146–149
Liu G, Zhu W (2008) The algebraic structures of generalized rough set theory. Inf Sci 178(21):4105–4113
Liu C, Miao D, Qian J (2014) On multi-granulation covering rough sets. Int J Approx Reason 55(6):1404–1418
Ma L (2012) On some types of neighborhood-related covering rough sets. Int J Approx Reason 53(6):901–911
Ma L (2016) Two fuzzy covering rough set models and their generalizations over fuzzy lattices. Fuzzy Sets Syst 294:1–17
Ma J, Atef M, Nada S, Nawar A (2020) Certain types of covering-based multigranulation \((I, T)\)-fuzzy rough sets with application to decision-making. Complexity 2020(6661782):20. https://doi.org/10.1155/2020/6661782
Ma J, Atef M, Khalil AM, Hassan N, Chen GX (2021) Novel models of fuzzy rough coverings based on fuzzy \(\alpha \)-neighborhood and its application to decision-making. IEEE Access 8:224354–224364
Ma X, Zhu J, Kou G, Zhan J (2024) Consistency improvement and local consensus adjustment for probabilistic linguistic preference relations considering personalized individual semantics. Inf Sci 662:120233
Mardani A, Jusoh A, Zavadskas EK (2015) Fuzzy multiple criteria decision-making techniques and applications-two decades review from 1994 to 2014. Expert Syst Appl 42(8):4126–4148
Pamucar D, Žižović M, Đuričić D (2022) Modification of the CRITIC method using fuzzy rough numbers. Decis Making 5(2):362–371. https://doi.org/10.31181/dmame0316102022p
Pawlak Z (1982) Rough sets. Int J Comput Inf Sci 11(5):341–356
Pomykala JA (1987) Approximation operations in approximation space. Bull Acad Pol Sci 35(9–10):653–662
Pomykala JA (1988) On definability in the nondeterministic information system. Bull Acad Pol Sci 36(3–4):193–210
Qi G, Atef M, Yang B (2024) Fermatean fuzzy covering-based rough sets and their applications in multi-attribute decision-making. Eng Appl Artif Intell 127:107181
Qian YH, Liang JY, Yao YY, Dang CY (2010) MGRS: a multi-granulation rough set. Inf Sci 180:949–970
Shen KY (2024) The exploring the relationship between financial performance indicators, ESG, and stock price returns: a rough set-based bipolar approach. Decis Making Adv 2(1):186–198. https://doi.org/10.31181/dma21202434
Sivaprakasam P, Angamuthu M (2023) Generalized Z-fuzzy soft \(\beta \)-covering based rough matrices and its application to MAGDM problem based on AHP method. Decis Making 6(1):134–152. https://doi.org/10.31181/dmame04012023p
Sun BZ, Ma W (2015) Multigranulation rough set theory over two universes. J Intell Fuzzy Syst 28:1251–1269
Sun BZ, Ma W, Xiao X (2017) Three-way group decision making based on multigranulation fuzzy decision theoretic rough set over two universes. Int J Approx Reason 81:87–102
Tsang EC, Degang C, Yeung DS (2008) Approximations and reducts with covering generalized rough sets. Comput Math Appl 56(1):279–289
Wu W, Zhang W (2002) Neighborhood operator systems and approximations. Inf Sci 144:263–282
Xiao Y, Zhan J, Zhang C, Wu WZ (2023) Three-way decision method within prospect theory via intuitionistic fuzzy numbers in multi-scale decision information systems. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2023.3329486
Xiao Y, Zhan J, Zhang C, Liu P (2024) A sequential three-way decision-based group consensus method with regret theory under interval multi-scale decision information systems. IEEE Trans Emerg Topics Comput Intell 8(2):1670–1686
Xu WH, Zhang WX (2007) Measuring roughness of generalized rough sets induced by a covering. Fuzzy Sets Syst 158(22):2443–2455
Xu WH, Wang QR, Zhang XT (2011) Multi-granulation fuzzy rough sets in a fuzzy tolerance approximation space. Int J Fuzzy Syst 13(4):246–259
Xu WH, Wang Q, Luo S (2014) Multi-granulation fuzzy rough sets. J Intell Fuzzy Syst 26(3):1323–1340
Xue ZA, Jing MM, Li YX, Zheng Y (2023) Variable precision multi-granulation covering rough intuitionistic fuzzy sets. Granul Comput 8(3):577–596
Yang B (2022) Fuzzy covering-based rough set on two different universes and its application. Artif Intell Rev 55(6):4717–4753
Yang B, Atef M (2023) Novel classes of fuzzy \(\beta \)-covering-based rough set over two distinct universes. Fuzzy Sets Syst 461:108350
Yang B, Hu BQ (2017) On some types of fuzzy covering-based rough sets. Fuzzy Sets Syst 312:36–65
Yang B, Hu BQ (2019) Fuzzy neighborhood operators and derived fuzzy coverings. Fuzzy Sets Syst 370:1–33
Yang XB, Song XN, Dou HL (2011) Multi-granulation rough set: from crisp to fuzzy case. Ann Fuzzy Math Inform 1(1):55–70
Yang X, Song X, Chen Z, Yang J (2012) On multigranulation rough sets in incomplete information system. Int J Mach Learn Cybern 3:223–232
Yao YY (1998) Relational interpretations of neighborhood operators and rough set approximation operators. Inf Sci 111(1–4):239–259
Yao Y, Yao B (2012) Covering based rough set approximations. Inf Sci 200:91–107
Ye J, Zhan J, Ding W, Fujita H (2021) A novel fuzzy rough set model with fuzzy neighborhood operators. Inf Sci 544:266–297
Zadeh LA (1975) The concept of a linguistic variable and its application to approximate reasoning. Inf Sci 8:199–249
Zhan J, Xu W (2020) Two types of coverings based multigranulation rough fuzzy sets and applications to decision making. Artif Intell Rev 53(1):167–198
Zhan J, Sun B, Alcantud JCR (2019) Covering based multigranulation (I, T)-fuzzy rough set models and applications in multi-attribute group decision-making. Inf Sci 476:290–318
Zhan J, Zhang X, Yao Y (2020) Covering based multigranulation fuzzy rough sets and corresponding applications. Artif Intell Rev 53(2):1093–1126
Zhan J, Wang J, Ding W, Yao Y (2023) Three-way behavioral decision making with hesitant fuzzy information systems: survey and challenges. IEEE/CAA J Autom Sin 10(2):330–350
Zhan J, Huang X, Qian Y, Ding W (2024) A fuzzy C-means clustering-based hybrid multivariate time series prediction framework with feature selection. IEEE Trans Fuzzy Syst. https://doi.org/10.1109/TFUZZ.2024.3393622
Zhang K, Dai J (2022) Redefined fuzzy rough set models in fuzzy \(\beta \)-covering group approximation spaces. Fuzzy Sets Syst 442:109–154
Zhang B, Dong YY, Xu Y (2014) Multiple attribute consensus rules with minimum adjustments to support consensus reaching. Knowl-Based Syst 67:35–48
Zhang K, Zhan J, Wu WZ (2021a) On multicriteria decision-making method based on a fuzzy rough set model with fuzzy \(\alpha \)-neighborhoods. IEEE Trans Fuzzy Syst 29(9):2491–2505
Zhang C, Ding J, Li D, Zhan J (2021b) A novel multi-granularity three-way decision-making approach in q-rung orthopair fuzzy information systems. Int J Approx Reason 138:161–187
Zhang C, Ding J, Zhan J, Li D (2022) Incomplete three-way multi-attribute group decision making based on adjustable multigranulation Pythagorean fuzzy probabilistic rough sets. Int J Approx Reason 147:40–59
Zhang L, Lin G, Wei L, Kou Y (2024) Feature subset selection for multi-scale neighborhood decision information system via mutual information. Artif Intell Rev 57(1):1–30
Zhu J, Ma X, Martínez L, Zhan J (2023a) A probabilistic linguistic three-way decision method with regret theory via fuzzy c-means clustering algorithm. IEEE Trans Fuzzy Syst 31(8):2821–2835
Zhu J, Ma X, Kou G, Herrera-Viedma E, Zhan J (2023b) A three-way consensus model with regret theory under the framework of probabilistic linguistic term sets. Inf Fusion 95:250–274
Zhu W (2007) Topological approaches to covering rough sets. Inf Sci 177(6):1499–1508
Zhu W, Wang FY (2003) Reduction and axiomization of covering generalized rough sets. Inf Sci 152:217–230
Zhu W, Wang FY (2007) On three types of covering-based rough sets. IEEE Trans Knowl Data Eng 19(8):1131–1144
Zhu W, Wang FY (2012) The fourth type of covering-based rough sets. Inf Sci 201:80–92
Funding
Open Access funding provided by the IReL Consortium.
Author information
Authors and Affiliations
Contributions
Mohammed Atef: Conceptualization, Methodology, Formal Analysis, Writing—original draft Sifeng Liu: Conceptualization, Methodology ,Validation, Writing—original draft Sarbast Moslem: Conceptualization, Supervision, Writing—review & editing Dragan Pamucar: Supervision, Visualization, Writing—review & editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Atef, M., Liu, S., Moslem, S. et al. New covering techniques and applications utilizing multigranulation fuzzy rough sets. Artif Intell Rev 57, 283 (2024). https://doi.org/10.1007/s10462-024-10860-w
Accepted:
Published:
DOI: https://doi.org/10.1007/s10462-024-10860-w