1 Introduction

In the case of static loads on foundations, geotechnical researchers have widely studied bearing capacity theories in different situations. The original works were conducted by Prandtl (1920) and Terzaghi (1943); subsequently, Meyerhof (1951) and (1974), Hansen (1961) and (1970) and Vesic (1973) made great efforts on the static bearing capacity, considering various effective factors such as groundwater table, foundation geometry, slope, depth, eccentricity, and load inclination. In parallel, the bearing capacity for seismic conditions has been studied using some techniques such as equivalent pseudo-static and reduction coefficients (Tiznado and Paillao 2014). The equivalent pseudo-static technique was used to express the bearing capacity factors as the dynamic internal friction angle (Puri and Prakash 2007). Additionally, Meyerhof (1951) and Shinohara et al. (1963) used a pseudo-static attitude based on acceleration in different directions, such as vertical and horizontal, as gravity applied to the structure's center so that this problem was modified to the static case with an eccentrically inclined load (Soubra 1999). Foundation seismic bearing capacity in cohesive soil has not been fully discovered by geotechnical researchers even after the Northridge earthquakes in 1994, Kocaeli in 1999, and Chi-Chi in 1999 (Martin et al. 2004; Bray and Sancio 2006). In the earlier investigations (Kishida 1970; Shibata et al. 1972; Mulilis et al. 1977), only the dynamic bearing capacity was studied in granular soils under liquefaction. For example, Marcuson (1978) found this phenomenon to be the transformation of granular soil from a solid mode to a liquefied approach based on the increased pore water pressure, which absolutely reduces effective stress.

One of the most popular foundations is the ring type because of the less-used material compared to other foundation types (e.g., rectangular). The ring foundation may be designed and constructed in different structures, such as water storage tanks, silos, bridge piers, transmission towers, chimneys, and TV antennas. However, there is a limited range of studies investigating the behavior and bearing capacities of ring foundations. Some small-scale models on sandy soils were planned and tested to obtain the bearing capacity for ring footing (Saha 1978; Boushehrian and Hataf 2003). In another study, Kumar and Ghosh (2005) investigated the bearing capacity factor (Nɣ) for smooth and rough ring foundations using the stress characteristic method (SCM), but they did not simulate the stress at the inner and outer edges of the foundation. Zhao and Wang (2008) carried out some analyses using FlAC to obtain Nɣ for smooth and rough ring foundations in sand under different flue rules, i.e., associative and non-associative. Several studies have been done to figure out how well ring foundations can hold up. This has been done by using the plastic stress field approach constructed by some methods, such as the method of characteristics (Kumar and Ghosh 2005), limit equilibrium theory (Karaulov 2005, 2006), finite difference method (Zhao and Wang 2008; Benmebarek et al. 2012), and the finite element method (Choobbasti et al. 2010; Lee et al. 2016). The ring plate on the sands model has also been used in some tests in the laboratory (Ohri et al. 1997). Besides, some efforts have been made to analyze the geotechnical stability of ring foundations on reinforced soil. El Sawwaf and Nazir (2012) also looked at how well the ring foundation could hold up under loads that were not straight.

Apart from theoretical and numerical approaches available for calculating bearing capacities of foundations, probabilistic and machine learning techniques have been widely used for the same purposes (Shahin 2010; Armaghani et al. 2017b, 2020; Hajihassani et al. 2018; Momeni et al. 2018, 2020; Khari et al. 2019; Pham et al. 2020; Ghanizadeh et al. 2022). It is important to mention that these techniques have been successfully used with an excellent degree of accuracy in other areas of mining and geotechnical engineering such as underground space (Armaghani et al. 2017a; Yang et al. 2020, 2022; Shan et al. 2022; He et al. 2023), slope stability (Gelisli et al. 2015; Asteris et al. 2022), blasting environmental issues (Hasanipanah et al. 2015; Zhou et al. 2020; Hosseini et al. 2021, 2022a, b, c; Armaghani et al. 2022), and geomaterial strength prediction (Asteris et al. 2021; Bhatawdekar et al. 2021; Indraratna et al. 2022; Liu et al. 2022; Skentou et al. 2022).

The existing literature has also witnessed limited studies on the behavior and bearing capacities of ring foundations, a popular choice in construction due to material efficiency. However, the available analyses often lack comprehensive simulations and stress assessments at the inner and outer edges of the foundation. Recognizing the gaps in current understanding, this paper introduces a Fuzzy Inference System (FIS) integrated with Z-number theory to predict the bearing capacity of circular foundations. This novel approach aims to overcome the uncertainty associated with expert views in determining fuzzy rules, enhancing the accuracy of models and reducing computational times. By addressing these research gaps, our work contributes to the advancement of bearing capacity prediction models for circular foundations in civil engineering applications.

In light of the above discussion, in this paper, a Fuzzy inference system (FIS) is developed to predict the bearing capacity of ring foundations. The main novelty of this study is that it uses Z-number reliability to overcome uncertainty in the expert view when determining fuzzy rules. The proposed approach can successfully increase the accuracy level of models and decrease computational times. The calculation of the ultimate bearing capacity is mostly based on the academic method. In the case of soil complexity, the uncertainty of the boundary assumption and the restriction of the calculation means that the use of the theoretical technique to solve the problem or achieve calculation accuracy is often problematic.

2 Research significance

It is important to estimate the bearing capacity values of foundations under both static and seismic conditions accurately or close to their real capacity. The relevant principal theories can fundamentally be used if the effective parameters in these theories are available for the same purposes. Numerical approaches are good alternatives most of the time; however, their settings and implementation can be time-consuming. In addition, to apply them, there is a need to be an expert with acceptable knowledge of numerical analysis. Therefore, if some real soil and foundation properties are available, the said theories can always be used with enough confidence in design. The bearing capacity values obtained from these theories, along with some real test results, can help create a comprehensive database in this regard. The same database can be applied to machine learning techniques to propose an alternative approach with acceptable performance to predict the bearing capacity of foundations.

3 Methodology

This study focuses on developing an accurate system for modeling bearing capacity. In this regard, a new perspective of FIS is presented. The Z-number concept was employed to overcome the uncertainty of FIS rules determined by expert opinions. Therefore, the conversion rules were first determined. Based on the conversion rules of Z-number theory, FIS technique was improved and a reliability-based system was presented to predict and model bearing capacity.

Fuzzy set theory is employed to model uncertainties in linguistic variables, representing imprecise information commonly encountered in engineering systems. In this context, fuzzy numbers play a crucial role in quantifying the degrees of membership and non-membership associated with linguistic terms. Linguistic variables, expressed in terms like "high" or "low," allow for the representation of qualitative information in a fuzzy logic system. Building upon these concepts, Z numbers are introduced to handle the uncertainty inherent in fuzzy rules, providing a more robust framework for capturing imprecision in expert knowledge.

The proposed FIS, enhanced with Z-number theory, utilizes these foundational concepts to predict the bearing capacity of circular foundations. While the detailed intricacies of fuzzy set theory, fuzzy numbers, linguistic variables, and Z numbers are fundamental to the development of the model, the subsequent sections will focus on their specific application within the context of our research methodology. This streamlined approach aims to maintain clarity and relevance, ensuring that readers can grasp the essential components of our novel methodology without unnecessary complexity.

3.1 Z-numer concept

The initial idea of Z-numbers for modeling uncertain information was first proposed by Zadeh in 2011 (Zadeh 2011). Mahler (1968) also proposed the notion of Z-numbers in 1968, which is different from Z-numbers introduced by Zadeh. Z-numbers are ordered pairs of fuzzy numbers [\(Z=(\widetilde{A},\widetilde{B})\)], which are defined as an uncertain variable Z-values by Zadeh. \(\widetilde{A}\) as the first component of Z indicates restriction on a real variable X. Nevertheless, \(\widetilde{B}\) as the second component of Z denotes the reliability of the first component. Zadeh (2011) defined Z-numbers as follows inherent meaning:

$$Z = \left( {A,B} \right) = Z^{ + } \left( {A,\mu_{A} \cdot p_{{X_{A} }} \,is\,B} \right)$$
(1)

3.2 Fuzzy Inference System

As aforementioned, fuzzy set theory was first introduced by Zadeh (1965). This theory satisfied approximately a mathematical solution to solve complicated judgment problems with intuitive, imperfect, and inaccurate knowledge, which classical methods are not able efficiently to explain them. This theory can process all types of information varying from interval-valued numerical data to linguistics terms (Dubois and Prade 2012; Talpur et al. 2022). Obtaining fuzzy models from observed or estimated information has recently gained increasing attention. Fuzzy sets theory considers an uncertainty of human decisions and reflects the overview of real world; therefore, these sets have more applications compared to the classic sets (Shams et al. 2015). The fuzzification is a process to define membership functions related to fuzzy variables, which knowlege of experts is used to determine membership function. Then, all inputs are transformed into degree of a memberships according to relevant appropriate membership function (Yagiz and Gokceoglu 2010).

4 Laboratory tests and database preparation

The datasets achieved in the laboratory were used to develop the models in this study. The device for conducting a direct shear test is shown in Fig. 1. This device is used to identify soil resistance parameters such as cohesion and internal angle of friction. The database used for developing models in this study is tabulated in Table 1. The descriptive statistics of effective parameters and bearing capacity for 968 data are summarized in this table. Figure 2 represents correlations between the parameters used for the development models. As can be found from Fig. 2, the correlation between depth (D), density of soil (DS), internal angle of friction (IAF) and the bearing capacity (BC) are approximately good with correlations of 0.57, 0.648, and 0.709, respectively, while the correlation between the foundation radius (FR) and cohesion of soil (CS) with the BC are very low with the correlations of -0.807, and 0.281, respectively. Furthermore, the correlation between the FR and other parameters is very weak. The correlation between CS with DS and IAF, D with IAF, and CS with BC was negative.

Fig. 1
figure 1

Apparatus of direct shear test

Full size image
Table 1 Descriptive statistics of parameters
Full size table
Fig. 2
figure 2

The correlations between inputs and output

Full size image

The frequency histogram of the BC is presented in Fig. 3. As can be seen, 303 data are accompanied by a BC in the interval (645.06,1056.10] kg/cm2; nevertheless, a BC in the interval (3933.39,4344.43] kg/cm2 is observed in 3 BC data.

Fig. 3
figure 3

Frequency histogram of the BC

Full size image

5 Results and analysis

The prediction of bearing capacity for circular foundations holds paramount importance in civil engineering, influencing the design and construction processes. Accurate predictions are crucial for ensuring the structural integrity and stability of foundations under varying soil conditions. Traditional methods often face challenges in handling uncertainties inherent in soil properties, leading to the exploration of advanced techniques, such as FIS and Z-number theory. This study focuses on comparing the performance of traditional regression models, conventional FIS, and a Z-number-based FIS in predicting the bearing capacity of circular foundations. The incorporation of Z-number theory is motivated by its ability to address the uncertainty inherent in fuzzy rules, providing a more reliable and precise prediction model. This comparative analysis aims to demonstrate the superiority of the proposed Z-FIS model over traditional FIS and regression models in accurately estimating bearing capacity.

5.1 Statistical model for bearing capacity

The multivariate regression (MR) method was used to construct a statistical model. The multivariate regression analysis is a statistical technique used to examine the relationship between multiple independent variables and a dependent variable. The general form of the multivariate regression model used in this study can be expressed as:

$$y = \beta_{0} + \beta_{1} x_{1} + \beta_{2} x_{2} + ... + \beta_{n} x_{n} + \varepsilon$$
(2)

y represents the predicted bearing capacity, β0 is the intercept, β1, β2, …, βn are the regression coefficients for the respective independent variables, x1, x2, …,xn are the independent variables (depth, density of soil, internal angle of friction, cohesion of soil, and foundation radius), ε is the error term accounting for unobserved factors affecting bearing capacity. The coefficients β1, β2, …, βn​ were estimated using the least squares method to minimize the sum of squared differences between the predicted and observed bearing capacity values.

The relationships between effective parameters and output parameters as respectively independent and dependent parameters are established. This statistical technique has been used effectively to solve engineering problems (Recep 2022; Akan et al. 2015; Akan and Keskin 2019). In this study, BC is determined by using product of the five independent parameters, i.e., D, DS, IAF, CS, and FR. The Statistical Package for Social Sciences (SPSS) software version 25 is employed to obtain a predictive regression model for the forecast of BC (Eq. (3)). The statistical information concerning the constituted predictive model is presented in Table 2. As can be seen, the velues of t-stat and p-value are presented for each parameter. The t-stat and p-value columns refer to the hypothesis test of the coefficients. The t-test is used to determine the significant difference between the average of a group with a default value or the average of two groups. The larger the value of t, the weaker the hypothesis that the coefficient is zero and the greater the import of that variable in modeling. This largeness is also determined by the value of p-value or Sig that reveals the significance of coefficients. If the p-value is smaller than 0.05 (5%), the null hypothesis, which indicates that the variable is ineffective in the model, is rejected. Therefore, all coefficients are statistically significant according to Table 2 and should be included in the regression model. The formulated regression model is as follows:

$$\begin{gathered} BC = - 4449.441 + \left( {107.843 \times D} \right) + \left( {618.219 \times \, DS} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, + \left( {131.078 \times IAF} \right) + \left( {CS \times \left( { - 85.430} \right)} \right) + \left( {14.579 \times FR} \right) \hfill \\ \end{gathered}$$
(3)

where D is Depth (m), DS is Density of soil (gr/cm3), IAF is Internal angle of friction (degree), CS is Cohesion of Soil (kg/cm2), FR is Foundation Radius (m), and BC is Bearing Capacity (kg/cm2).

Table 2 MR results for prediction of BC
Full size table

5.2 Fuzzy model for bearing capacity

Building upon the statistical model, a FIS model is introduced to account for the inherent uncertainties in soil properties. This section delves into the intricacies of the FIS model, discussing the role of depth, soil density, internal angle of friction, cohesion of soil, and foundation radius as input parameters. The limitations and uncertainties associated with the conventional FIS approach are acknowledged, setting the stage for the introduction of the Z-number-based fuzzy model.

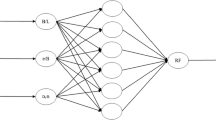
The Mamdani structure was used to establish fuzzy model and develop BC predictive model. The parameters of depth, density of soil, internal angle of friction, cohesion of soil, and foundation radius were imported as inputs of the fuzzy model to estimate bearing capacity as model output. The fuzzy structure with the imported input and output parameters in the model is shown in Fig. 4. In the first step of FIS modeling, the input parameters are fuzzified using most the fitting membership functions. For this aim, gaussian (gaussmf) and gaussian combination (gauss2mf) membership functions as the most usable membership functions were applied to fuzzification parameters.

Fig. 4
figure 4

Schematic illustration of the fuzzy inference model

Full size image

Here, the linguistic terms with nine categories were defined as “extremely low (EL)“, “very low (VL)“, “Low (L)“, “medium low (ML)“, “medium (M)“, “medium high (MH)“, “high (H)“, “very high (VH)“, and “extremely high (EH)“. Notably, the degrees of membership for parameters are selected according to experts' knowledge and experiences. In addition, the number of membership functions was widely obtained based on the trial and error procedure. The “underfitting” (requisite accuracy occurs) and “overfitting” (mendacious accuracy occurs) problems are the consequences that are respectively accrued due to the insufficient and excessive number of rules.

The membership functions of input parameters and output parameters were specified as shown in Fig. 5. In the FIS modeling, a total number of 1,125 rules were applied to develop the Mamdani-based model. It should be mentioned that this number of rules has been finalized after removing overlapped rules. Finally, the Mamdani aggregation algorithm as the widest method in FIS was used considering the problem's complexity. Table 3 summarizes some of the fuzzy rules employed in the FIS modeling.

Fig. 5
figure 5

Membership functions of parameters

Full size image
Table 3 Several examples of if–then fuzzy rules
Full size table

In the last step of FIS modeling, the defuzzification process is performed, in which the fuzzy values are converted into crisp values using the COA technique. The rule viewer and fuzzy reasoning engine of the MATLAB environment are depicted in Fig. 6. As can be found, when input parameters are D = 7.75 m, DS = 1.81 gr/cm3, IAF = 22.3 degree, CS = 0.0649 kg/cm2, and FR = 12.7 m, then BC would be 851 kg/cm2, which is very close to measured BC with the value of 843.

Fig. 6
figure 6

An example calculation for the FIS model

Full size image

5.3 Z-number-based Fuzzy model for bearing capacity

The Z-number concept was introduced to address the uncertainty inherent in expert opinions when determining fuzzy rules for the Mamdani-based FIS model. The fuzzy rules are specified based on expert knowledge. Nevertheless, expert opinions to determine fuzzy rules have uncertainty. Therefore, the membership functions identified for the output variable deal with very insufficient reliability. Therefore, this study focused on implementing the Z-number concept to overcome the uncertainty of expert views. Therefore, the reliability level of the Z-number is applied in the analysis process, and the range of 0–100% confidence is specified for expert use. In other words, a particular scale was defined as tabulated in Table 4 to express the judgments reliability level of experts. The membership degrees of Z-number linguistic terms are displayed in Fig. 7. The confidence of 0 and 100% are applied for strong reliability and unreliability, respectively. This reliability level can significantly improve the results.

Table 4 The rules of transformation concerned with linguistic variables of possibilities
Full size table
Fig. 7
figure 7

Membership degree of Z-numbers of transformation rules

Full size image

In the first phase, the experts first determined 1125 fuzzy rules to develop the Mamdani-based FIS model. In the second phase, they also expressed their reliability level of opinions based on 21 linguistic terms. For this aim, the scale presented in Table 5 was identified to evaluate the first component of Z-number, Z = (A, B). The Membership degree of TrFNs for A component is depicted in Fig. 8. It should be mentioned that the scale shown in Table 4 is used for determining B component of Z.

Table 5 The rules of transformation concerned with linguistic variables of restrictions
Full size table
Fig. 8
figure 8

Membership degree of TrFNs identified for A component

Full size image

Therefore, each member of Tables 4 and 5 is transformed into a regular number by repeating the procedure presented in "Converting Z-numbers to crisp numbers" section. To further clarify the application of Z-numbers, we have included a detailed explanation of the transformation process from linguistic terms to Z-numbers and subsequently to crisp numbers. This is exemplified in Table 6, which illustrates the judgment of experts with reliability information and the conversion of Z-numbers to crisp numbers. Table 6 presents a sample of Z-calculation for the same rules summarized in Table 3. Combining translation terms (Table 5) and reliabilities related to constraints (Table 4) results in the conversion rules of linguistic variables of experts of Z-numbers. A fuzzy rating is then created based on these results. Suppose n criteria are met by the object of research for the restriction. Accordingly, the number of membership functions of output parameters is modified based on the new Z-rules. The 59 Z-based membership functions were defined for BC as shown in Fig. 9. In this step, the new Z-based FIS is developed for predicting BC.

Table 6 Judgment of expert with reliability information
Full size table
Fig. 9
figure 9

Z-based Membership functions of BC

Full size image

The bearing capacity predictions are crucial for civil engineering applications, impacting the safety and stability of structures. The improved accuracy and efficiency demonstrated by the Z-FIS model have direct implications for optimizing foundation design and construction practices.

5.4 Sensitivity analysis

The sensitivity analysis is performed to determine the most influential input parameters on output parameter(s). In this study, the impact of each input parameter on BC was specified using the cosine amplitude method. The sensitivity is evaluated through a factor, namely 'r' can be calculated as follows (Hosseini et al. 2022c, b):

$$r_{ij} = \frac{{\sum\limits_{k = 1}^{m} {\left( {x_{ik} \times x_{jk} } \right)} }}{{\sqrt {\left( {\sum\limits_{k = 1}^{m} {x_{ik}^{2} } \times \sum\limits_{k = 1}^{m} {x_{jk}^{2} } } \right)} }}$$
(4)

In which, xi stands input parameters, xj indicates output parameter(s), and n is the number of data. The impact value of each inputs on BC is illustrated in Fig. 10. As can be seen, IAF, D, and DS have the most impact on BC.

Fig. 10
figure 10

Sensitivity alaysis of input parameters

Full size image

6 Discussions

In this study, 968 data for BC were estimated through Z-FIS, FIS, and MR Methods. Based on the suggestion of literature and previous studies, the dataset is first split into two categories: training (80% of data) and testing (20% of data). Next, the three statistical indicators-coefficient of determination (R2), root-mean-squared error (RMSE), and value account for (VAF)-were calculated to compare the developed models with FIS and MR. The indicators are calculated as follows:

$$R^{2} = 1 - \left( {\frac{{\sum\limits_{i = 1}^{n} {(O_{i} - P_{i} )^{2} } }}{{\sum\limits_{i = 1}^{n} {(P_{i} - \overline{P}_{i} )^{2} } }}} \right)$$
(5)
$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {(O_{i} - P_{i} )^{2} } }$$
(6)
$$VAF = 100 \cdot \left( {1 - \frac{{var(O_{i} - P_{i} )}}{{var(O_{i} )}}} \right)$$
(7)

where Oi and Pi are real values and estimated amounts, respectively; \(\overline{P}_{i}\) is the average of the estimated values, and n is the number of all data. The most accurate model yields respectively 1, 0, and 100 for R2, RMSE, and VAF. The R2 measures the proportion of the variance in the dependent variable that is predictable from the independent variable(s). It ranges from 0 to 1, with 1 indicating a perfect fit. Furthermore, The RMSE quantifies the average magnitude of the residuals between the predicted and actual values. VAF assesses the proportion of the total variance in the data that is captured by the model. Notably, a higher R2 indicates better goodness-of-fit, while lower values of RMSE and higher values of VAF signify improved accuracy in the estimation of BC.

The selection of hyperparameters and tuning of the models was performed as follows: the gaussmf and gauss2mf membership functions were used for fuzzification of the parameters. Notably, extremely low (EL)“, “very low (VL)“, “Low (L)“, “medium low (ML)“, “medium (M)“, “medium high (MH)“, “high (H)“, “very high (VH)“, and “extremely high (EH)“ were identified as the most suitable linguistic terms of memberships. It is noteworthy that membership degrees were determined based on experts' knowledge and experiences. Finally, the last step is defuzzification, which was conducted according to COA technique and the crisp values were obtained.

The estimated BC using Z-FIS and FIS compared to the measured one for training and testing parts is displayed in Figs. 11 and 12, respectively. Furthermore, correlation between measured and obtained BC by statistical model (Eq. 3) is depicted in Fig. 13. As shown, the proposed Z-FIS model presents the highest accuracy for estimating BC as compared to the FIS. The R2 values of 0.977 and 0.971 show the superiority of the Z-FIS model in estimating the BC. Whilst, the value of 0.912 and 0.904 are achieved for FIS method, and R2 of 0.795 and 0.715 was obtained for training and testing set of statistical model. Furthermore, the values of other indicators are tabulated in Table 7. The values of RMSE and VAF for training and testing Z-FIS is better than the FIS model. In Table 7, the computational time of these models is also specified. The models were developed in the MATLAB environment and a PC (Intel Core (TM) i3-5010U CPU -2.10 GHz, with 6 GB of RAM, Windows 10).

Fig. 11
figure 11

Correlation between measured and predicted BC in (a) training and (b) testing FIS model

Full size image
Fig. 12
figure 12

Correlation between measured and predicted BC in (a) training and (b) testing Z-FIS model

Full size image
Fig. 13
figure 13

Correlation between measured and predicted BC in (a) training and (b) testing statistical model

Full size image
Table 7 Performance indices of the predictive models for all datasets
Full size table

As shown in Table 7, the computational time for Z-FIS was 18.65 s; while, this value for FIS model was 159.98 s. Therefore, the proposed approach not only decreased the computational time (89.28%) but also increased accuracy. It can be concluded that the proposed model outperforms the FIS method in estimating the BC. A part of used dataset for testing MLR, FIS, Z-FIS models and their predicted values are summarized in Table 8. Furthermore, the illustration of camparision of measured and presicted values are depicted in Fig. 14. Based on presented results, it is obvious that the proposed Z-FIS model is superior to other models, which reveals the minimum error compared to MLR and FIS model.

Table 8 Sample of 16 testing data and predicted values by MLR, FIS, and Z-FIS models
Full size table
Fig. 14
figure 14

Comparison of measured predicted data

Full size image

The Z-FIS model incorporates zero-order Sugeno fuzzy inference systems, which extend the capabilities of traditional FIS. The enhanced accuracy observed in the Z-FIS model can be attributed to the following key factors:

  • Membership Function Selection: The Z-FIS model utilizes gaussmf and gauss2mf membership functions for fuzzification, enabling a more precise representation of linguistic terms. The careful selection of linguistic terms such as "extremely low," "very low," etc., based on expert knowledge and experiences, contributes to the model's ability to capture complex relationships in the dataset.

  • Hyperparameter Tuning: The hyperparameters of the Z-FIS model are tuned to optimize its performance. The use of the COA technique for defuzzification ensures that crisp values are obtained, further refining the accuracy of the model.

  • Computational Efficiency: The Z-FIS model demonstrates significantly improved computational efficiency compared to the FIS model. This is attributed to the efficient handling of fuzzy inference systems with zero-order rules, resulting in a reduction in computational time by 89.28%. The specific advantages of the Z-FIS approach in terms of algorithmic efficiency contribute to its superiority.

Table 9 summarises the outcomes that we have achieved regarding the effectiveness metrics of the proposed Z-FIS technique. The R2 value recorded in Table 9 reveals a comparison between the estimation precision and performance degree of our proposed model and that of a number of the most recent studies. Based on the collected information, the Z-FIS model presents a higher accuracy ability in the modeling and estimation of bearing capacity than the other techniques.

Table 9 Comparative analysis of the performance of our developed model with literature
Full size table

7 Conclusions

Uncertainty always poses problems to engineering projects. Artificial intelligence methods that involve expert opinions have been associated with reliability. The fuzzy inference system (FIS) is one of the methods in which the fuzzy rules used are determined based on expert opinions. Therefore, it is obvious that there is uncertainty in it. This paper presents a reliability-based FIS model to predict bearing capacity (BC) based on Z-number concept in civil projects by accounting for uncertainties. In this regard, 968 BC data points were measured, and the most effective independent parameters of estimations were identified. These parameters are depth, density of soil, internal angle of friction, cohesion of soil, and foundation radius. A multiple regression model was constructed to establish relationships between such parameters and the BC values. The obtained results of the proposed model were compared to conventional FIS. The predictive models were constituted by utilizing five input parameters (i.e., depth, density of soil, internal angle of friction, cohesion of soil, and foundation radius) to predict BC. It is shown that the Z-FIS model performance is significantly better than the FIS model with the R2 of 0.977 and 0.971 for training and testing parts, respectively. A sensitivity analysis showed that the angle of friction has the most effect on the BC estimations.