1 Introduction

Linear and nonlinear equations are fundamental mathematical tools that play essential roles in several industrial applications, such as robot path planning, image recognition, and signal processing (Zhao 2013; Tsiligianni et al. 2015; Zhang and Jin 2017; Li et al. 2019). Extensive work has been conducted on solving linear and nonlinear equations, typically using numerical algorithms (Sharma 2005; Neta et al. 2014; Abdelmalek 1977; Donoho et al. 2012; Zeng et al. 2014; Spedicato et al. 2000; Morigi and Sgallari 2001) and neurodynamic methods (Kumar 2022a, b; Kumar 2023; Cichocki et al. 1992; Xia et al. 1999; Liang and Tso 2002). Among the numerical algorithms, direct methods and iterative methods are mainly used. In Abdelmalek (1977), the minimum \(L_{\infty }\) solution of the linear equation was first proposed. In Donoho et al. (2012), the sparse approximate solution of the linear equation was obtained by using the stagewise orthogonal matching pursuit algorithm. Many iterative algorithms have also been developed to bring solutions to the linear equation, such as adaptive iterative thresholding algorithms (Zeng et al. 2014), abstraction algorithms (Spedicato et al. 2000), and regularizing Lanczos iterative algorithms (Morigi and Sgallari 2001). However, these numerical algorithms may encounter challenges such as the accumulation of numerical errors, slow convergence rates, and low stability (Zhang et al. 2013).

In recent years, neural network models have garnered widespread attention for addressing modeling and control problems in both linear and nonlinear dynamic systems (Zhang et al. 2018; Li et al. 2019; Xiao et al. 2020; Liao et al. 2024; Kumar 2022a, b; Kumar 2023). Particularly, the introduction of novel neural network models such as the Lyapunov-stability-based context-layered recurrent pi-sigma neural network (CLRPSNN) (Kumar 2022a), the memory recurrent Elman neural network (MRENN) (Kumar 2022b), and the higher-order recurrent neural network (HORNN) (Kumar 2023) have provided new approaches for solving the identification and control problems of nonlinear dynamic systems. The CLRPSNN model effectively addresses the issue of nonlinear system identification by introducing an additional layer of context nodes, demonstrating significant performance advantages in simulation results. However, stability has always been a crucial consideration in the design of neural network models. The MRENN and HORNN models innovate in stability design, ensuring stability and convergence of the models by combining Lyapunov stability criteria and recursive learning rate schemes. This emphasis on stability makes these models more reliable and practical when dealing with nonlinear dynamic systems.

Similar to numerical algorithms, neurodynamic methods also significantly improve the efficiency of solving the linear equation. Cichocki et al. (1992) proposed different recurrent neural networks (RNNs) to address the linear equation with an inequality constraint. Xia et al. (1999) designed an RNN model that can converge faster and provide more accurate solutions to the linear equation with an inequality constraint. The discrete-time form of such an RNN model was further deduced by Liang and Tso (2002). It is worth noting that these studies are based on the assumption of time-invariant when solving linear equations. However, many systems in practical engineering applications are always time-varying. Therefore, directly applying these methods to solve time-varying linear equations may yield poor results. Moreover, the mathematical domain of the variables involved in a linear equation must be set during the solution process (Zhang et al. 2018; Park et al. 1998). For example, it is assumed that many robotic arms can lead to task failure or even damage if the physical constraints of the joints are exceeded. Thus, appropriate methods must be investigated to ensure that joint angle, velocity, and/or acceleration are within the proper mathematical intervals (Guo et al. 2018; Zhang et al. 2013). In other words, solving time-varying underdetermined linear equations with boundary constraint is of importance in practical engineering applications.

In many industrial applications, there is a high demand for the real-time performance of linear equation, making them time-dependent. Existing studies are less concerned with methods for solving time-dependent linear equation (TDLE) with boundary constraint. To solve a given time-dependent problem, a representative RNN was presented and refined by Zhang and Guo (2015); Zhang and Yi (2011); Zhang et al. (2012, 2015). The main idea of this model was to define the error control equation and then derive the RNN (depicted in an ordinary equation) so that the computational error can converge globally and eventually become 0, hence the name zeroing neural network (ZNN). Focusing on solving the bound-constrained TDLE (BCTDLE), Xu et al. (2019a) developed the continuous-time ZNN (CTZNN) model, which they successfully employed to solve time-varying linear equations and inequality systems (Xu et al. 2019b). Sun and Liu (2020) designed a novel noise-resistant CTZNN model for solving time-varying Lyapunov equations. However, directly implementing the CTZNN model into hardware in practical engineering applications is challenging.

Therefore, for the purpose of possible hardware implementation, researchers discretize the CTZNN model using difference equations. The traditional numerical differentiation algorithm for discretizing continuous systems is typically implemented using the Euler difference formula. Specifically, in Guo and Zhang (2012), a one-step iteration description of the DTZNN model is proposed for dynamic matrix inversion. The simulation results show that this model has an error mode of \(O({{\varepsilon }^{2}})\), that is, when the sampling interval \(\varepsilon\) decreases by a factor of 10, the steady-state calculation error (SSCE) decreases by a factor of 100. Unlike the traditional Euler difference formula, in Guo et al. (2017), a new Taylor-type difference rule is constructed. For the approximation of first-order derivatives, this rule has been proven to have a smaller SSCE than the Euler difference rule and possesses an error mode of \(O({{\varepsilon }^{3}})\), that is, when the sampling interval \(\varepsilon\) decreases by a factor of 10, the SSCE decreases by a factor of 1000. Using the new Taylor difference rule, researchers have successively developed Taylor difference formulas with the error modes \(O({{\varepsilon }^{4}})\) and \(O({{\varepsilon }^{5}})\). Specifically, Huang et al. (2022) developed a Taylor difference formula with an error mode of \(O({{\varepsilon }^{4}})\) to solve time-variant underdetermined nonlinear systems under bound constraint. Different from the proposed DTZNN model in this paper, their model focuses on solving nonlinear systems and may not necessarily be applicable to linear equations, whereas DTZNN model proposed in this paper exhibits superior accuracy. Cai et al. (2021) also discretized the CTZNN model based on Taylor series expansion. However, their model mainly focuses on solving a time-varying system of linear equation and inequality, and does not consider boundary constraint. A recent study (Ma and Guo 2021) showed that the DTZNN model can effectively solve the BCTDLE with an SSCE of the order \(O(\varepsilon ^{4})\), where \(\varepsilon\) is the sampling distance.

Following but differing from the previous work (Ma and Guo 2021), this paper establishes a new DTZNN model that can effectively solve the TDLE with boundary constraint. The validity of such a model is supported by both theoretical and numerical results. Considering the importance of robotic arms in industrial applications (Xu et al. 2019a; Ma and Guo 2021; Zhang et al. 2019), this paper further applies the proposed DTZNN model to the PUMA560 robotic arm to demonstrate the applicability of the model. The primary contributions of this paper can be summarized as follows:

  1. (1)

    The new DTZNN model, which has not been previously reported, is studied to solve the TDLE with boundary constraint. Notably, the proposed model is clearly different from the previous DTZNN model (Ma and Guo 2021), and achieves better performance on computing and solving the BCTDLE.

  2. (2)

    Theoretical analysis denotes the computational characteristic of the proposed DTZNN model, and numerical results verify its validity. More importantly, these results show that the DTZNN calculation error at steady state is of order \(O(\varepsilon ^{5})\). This is the first time that a computing model with \(O(\varepsilon ^{5})\) mode is presented to solve the BCTDLE.

  3. (3)

    The proposed DTZNN model is utilized for robotic arms by solving the linear kinematic equation that involves joint physical constraint. Simulation results using the PUMA560 robotic arm with different examples demonstrate the effectiveness and practicality of the proposed DTZNN model.

The upcoming sections of this paper are structured as follows. Section 2 presents the problem statement and the ZNN models for the TDLE with boundary constraint. Section 3 describes the proposed DTZNN composition and theoretical analysis. Section 4 provides numerical validation experiments with the proposed DTZNN model. Section 5 shows the applicability of the DTZNN model to robotic arms with joint constraints. Section 6 concludes this paper.

2 Preliminary

This section outlines the problem to address the TDLE with boundary constraint. To probe the matter further, the continuous- and discrete-time models of ZNN are shown as basis.

2.1 Problem statement

The TDLE with boundary constraint considered in this paper is formulated as follows (Lu et al. 2019; Xu et al. 2019a):

$$\begin{aligned} {\left\{ \begin{array}{ll} G(t)x(t)=h(t),\\ x^{-}\leqslant x(t)\leqslant x^{+}, \end{array}\right. } \end{aligned}$$
(1)

where matrix \(G(t)\in R^{m\times n}\) (with \(m<n\)) is time-dependent and full-rank, vector \(h(t)\in R^{m}\) is time-dependent and smooth, vector \(x(t)\in R^n\) is unknown and must be obtained by solving (1), and \(x^\pm\) is the bounds of x(t). This paper aims to find a viable x(t) that satisfies both the linear equation and the boundary constraint outlined in (1).

As shown in Xu et al. (2019b), solving the BCTDLE (1) can be transformed into finding the solution of the system as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} G(t)x(t)-h(t)=0,\\ Ux(t)-\vartheta +V(t)y(t)=0, \end{array}\right. } \end{aligned}$$
(2)

with \(U=[-I;I]\in R^{2n\times n}\), \(\vartheta =[-x^{-};x^{+}]\in R^{2n}\), and \(V(t)=\text {diag}\{y_{1}(t),\cdots ,y_{2n}(t)\}\in R^{2n\times 2n}\). \(I\in R^{n\times n}\) is the identity matrix, and y(t) is an unknown vector that must still be determined when solving (2). The matrix–vector form of (2) is then expressed as follows:

$$\begin{aligned} Q(t)w(t)-r(t)=0, \end{aligned}$$
(3)

with \(Q(t)\in R^{(m+2n)\times (3n)}\), \(w\left( t\right) \in R^{(3n)}\), and \(r(t)\in R^{(m+2n)}\) being

$$\begin{aligned}&Q\left( t \right) =\left[ \begin{matrix} G(t) &{} 0 \\ U &{} V(t) \\ \end{matrix} \right] , \\&w\left( t \right) =\left[ \begin{matrix} x(t) \\ y(t) \\ \end{matrix} \right] , \\&r\left( t \right) =\left[ \begin{matrix} h(t) \\ \vartheta \\ \end{matrix} \right] . \end{aligned}$$

In this way, solving the BCTDLE (1) is equivalent to solving the matrix–vector equation presented in (3) for \(t\geqslant 0\).

2.2 CTZNN model

In this subsection, to solve the BCTDLE (1), following the ZNN design principle (Xu et al. 2019b), the error equation \(e(t)\in R^{(m+2n)}\) is defined by

$$\begin{aligned} e(t)=Q(t)w(t)-r(t). \end{aligned}$$
(4)

Then, a decay exponent formula is introduced to achieve the convergence of e(t) to 0 (Xu et al. 2019b), and the resultant CTZNN model is derived and formulated as follows (Lu et al. 2019):

$$\begin{aligned} \dot{w}(t)=-P^+(t)(\lambda (Q(t)w(t)-r(t))+M(t)w(t)-\dot{r}(t)), \end{aligned}$$
(5)

where vectors \(\dot{w}(t)\) and \(\dot{r}(t)\) denote the time derivatives of \(w\left( t\right)\) and \(r\left( t\right)\), respectively, and matrices \(P(t)\in R^{(m+2n)\times (3n)}\) and \(M(t)\in R^{(m+2n)\times (3n)}\) are

$$\begin{aligned} P(t)=\begin{bmatrix} G(t)&{}0\\ U&{}2V(t)\\ \end{bmatrix},~\text {and}~ M(t)=\begin{bmatrix} \dot{G}(t)&{}0\\ 0&{}0\\ \end{bmatrix}, \end{aligned}$$

with \(P^+(t)\in R^{(3n)\times (m+2n)}\) being the right pseudoinverse matrix of P(t). The following theoretical conclusion regarding the CTZNN model (5) is given and proved in Xu et al. (2019b).

Lemma 1

When considering a solvable BCTDLE (1), the CTZNN model (5) can produce an exact time-dependent solution of (1).

2.3 DTZNN model

The study of discrete-time models of ZNN is of practical interest because of hardware implementation and development of numerical algorithms (Guo et al. 2017; Mathews and Fink 2004). The widely-used method for deriving a discrete-time model is by using the Euler difference formula (Mathews and Fink 2004), which is given by

$$\begin{aligned} {\dot{w}}_k=\dot{w}(t_k=k\varepsilon )=\frac{w_{k+1}-w_k}{\varepsilon }+O(\varepsilon ), \end{aligned}$$
(6)

where \({w}_k={w}(t_k=k\varepsilon )\), \(\varepsilon =t_{k+1}-t_k\) represents the sampling interval, \(k=0,1,2,\ldots\) is the number of iterations, and \(O(\varepsilon )\) is the truncation error.

Evidently, the discretization of the CTZNN model (5) via Euler difference formula (6) yields the following expression:

$$\begin{aligned} w_{k+1}=w_k-\mu P_k^+(Q_kw_k-r_k)-\varepsilon P_k^+(M_kw_k-{\dot{r}}_k)+O(\varepsilon ^2), \end{aligned}$$
(7)

where \(P_k^+=P^+(t_k=k\varepsilon )\), \(Q_k=Q(t_k=k\varepsilon )\), \(M_k=M(t_k=k\varepsilon )\), \({\dot{r}}_k={\dot{r}}(t_k=k\varepsilon )\), \(r_k=r(t_k=k\varepsilon )\), and \(\mu =\lambda \varepsilon >0\) is the step size.

By eliminating \(O(\varepsilon ^2)\) from (7), the following DTZNN model to solve the BCTDLE (1) is derived below:

$$\begin{aligned} w_{k+1}=w_k-uP_k^+(Q_kw_k-r_k)-\varepsilon P_k^+(M_kw_k-{\dot{r}}_k). \end{aligned}$$
(8)

In relation to the DTZNN model (7), it is a variation law with an \(O(\varepsilon ^2)\) error form. That is, when the sampling interval \(\varepsilon\) is reduced by a factor of 10, the stationary error is reduced by a factor of 100. Such a DTZNN model may not satisfy the high-precision requirement in practice. Thus, a new DTZNN model with better performance on computing and solving the BCTDLE (1) is proposed in this paper.

3 New DTZNN model

In this section, on the basis of the Taylor difference formula (Cai et al. 2021), the new DTZNN model is developed to solve the BCTDLE (1). Theoretical analysis is also provided to denote the computational characteristic of the proposed DTZNN model.

3.1 Model formulation

The approximation of a first order derivative via Taylor series expansion has been the subject of numerous studies (Zhang et al. 2019). In the previous study (Cai et al. 2021), the Taylor difference formula that has higher accuracy and lower steady-state error than the conventional Euler difference formula (6) has been constructed.

Lemma 2

The following Taylor difference formula (Cai et al. 2021) is shown to approximate the first order derivative:

$$\begin{aligned} \begin{aligned} \dot{f}(t_{k})=&(54 f(t_{k+1})-5 f(t_{k})-10 f(t_{k-1})-55f(t_{k-2})+10f(t_{k-3})\\&+f(t_{k-4})+10 f(t_{k-5}) -5 f(t_{k-6}))/(120 \varepsilon )+O(\varepsilon ^{4}), \end{aligned} \end{aligned}$$
(9)

with \(k=6,7,8,\cdots\) and \(f(\cdot )\) being the objective function.

To discretize the CTZNN model (5) using the above Taylor difference formula (9), the following vector form of (9) is presented for the approximation of \(\dot{w}_{k}\):

$$\begin{aligned} \begin{aligned} \dot{w}_{k}=&(54 w_{k+1}-5 w_{k}-10 w_{k-1}-55 w_{k-2}+10 w_{k-3}\\&+w_{k-4}+10 w_{k-5}-5 w_{k-6}) /(120 \varepsilon ) +O(\varepsilon ^{4}). \end{aligned} \end{aligned}$$
(10)

By applying the Taylor difference formula (10) to the discretization of the CTZNN model (5), the discrete-time expression is given by

$$\begin{aligned} \begin{aligned} w_{k+1}=&\frac{5}{54} w_{k}+\frac{5}{27} w_{k-1}+\frac{55}{54} w_{k-2}-\frac{5}{27} w_{k-3}-\frac{1}{54} w_{k-4}-\frac{5}{27} w_{k-5} \\&+\frac{5}{54} w_{k-6}-\frac{20}{9} P_{k}^{+}(\mu (Q_{k} w_{k}-r_{k})+\varepsilon M_{k} w_{k}-\varepsilon \dot{r}_{k})+O(\varepsilon ^{5}). \end{aligned} \end{aligned}$$
(11)

By eliminating \(O(\varepsilon ^5)\) from (11), the DTZNN model proposed in this paper to solve the BCTDLE (1) is expressed as follows:

$$\begin{aligned} \begin{aligned} w_{k+1}=&\frac{5}{54}w_k+\frac{5}{27}w_{k-1}+\frac{55}{54}w_{k-2}-\frac{5}{27}w_{k-3}-\frac{1}{54}w_{k-4}-\frac{5}{27}w_{k-5}\\&+\frac{5}{54}w_{k-6}-\frac{20}{9} P_k^+(\mu (Q_kw_k-r_k)+\varepsilon M_kw_k-\varepsilon {\dot{r}}_k). \end{aligned} \end{aligned}$$
(12)

Regarding the proposed DTZNN model (12), it requires seven initial states (i.e., \(w_0\), \(w_1\), \(w_2\), \(w_3\), \(w_4\), \(w_5\) and \(w_6\)) to activate the iterative computation. Thus, given an initial value \(w_0\), the rest are found by the DTZNN model (8) and are computed as follows:

$$\begin{aligned} \left\{ \begin{array}{l} w_{1}=w_{0}-\mu P_{0}^{+}\left( Q_{0} w_{0}-r_{0}\right) -\varepsilon P_{0}^{+}\left( M_{0} w_{0}-\dot{r}_{0}\right) , \\ w_{2}=w_{1}-\mu P_{0}^{+}\left( Q_{1} w_{1}-r_{1}\right) -\varepsilon P_{0}^{+}\left( M_{1} w_{1}-\dot{r}_{1}\right) , \\ w_{3}=w_{2}-\mu P_{0}^{+}\left( Q_{2} w_{2}-r_{2}\right) -\varepsilon P_{0}^{+}\left( M_{2} w_{2}-\dot{r}_{2}\right) , \\ w_{4}=w_{3}-\mu P_{0}^{+}\left( Q_{3} w_{3}-r_{3}\right) -\varepsilon P_{0}^{+}\left( M_{3} w_{3}-\dot{r}_{3}\right) , \\ w_{5}=w_{4}-\mu P_{0}^{+}\left( Q_{4} w_{4}-r_{4}\right) -\varepsilon P_{0}^{+}\left( M_{4} w_{4}-\dot{r}_{4}\right) , \\ w_{6}=w_{5}-\mu P_{0}^{+}\left( Q_{5} w_{5}-r_{5}\right) -\varepsilon P_{0}^{+}\left( M_{5} w_{5}-\dot{r}_{5}\right) . \end{array}\right. \end{aligned}$$

The procedure of the proposed DTZNN model (12) to solve the BCTDLE problem (1) is as follows:

  1. (i)

    Initialization: Given the time duration T, sampling gap \(\varepsilon\), step size \(\mu\), constraint boundary \(\left[ -{{x}^{-}},{{x}^{+}} \right]\). Initialize \({{t}_{0}}\), \({{w}_{0}}\), \({{G}_{0}}\), \({{\dot{G}}_{0}}\), \({{h}_{0}}\), and \({{\dot{h}}_{0}}\). Receive \(P_{0}^{+}\), \({{r}_{0}}\), \({{\dot{r}}_{0}}\), \({{Q}_{0}}\) and \({{M}_{0}}\). Compute \({{\left\| {{e}_{0}} \right\| }_{2}}={{\left\| {{Q}_{0}}{{w}_{0}}-{{r}_{0}} \right\| }_{2}}\).

  2. (ii)

    First Loop (with \(k = 0, 1, 2, 3, 4, 5\)): Compute \({{w}_{k+1}}\) through (8). Receive \(P_{_{k+1}}^{+}\), \({{r}_{_{k+1}}}\), \({{\dot{r}}_{_{k+1}}}\), \({{Q}_{_{k+1}}}\) and \({{M}_{_{k+1}}}\). Compute \({{\left\| {{e}_{_{k+1}}} \right\| }_{2}}={{\left\| {{Q}_{_{k+1}}}{{w}_{_{k+1}}}-{{r}_{_{k+1}}} \right\| }_{2}}\).

  3. (iii)

    Second Loop (with \(k = 6, \ldots {}\), int\((T) / \varepsilon )\)): Compute \({{w}_{k+1}}\) through (12). Receive \(P_{_{k+1}}^{+}\), \({{r}_{_{k+1}}}\), \({{\dot{r}}_{_{k+1}}}\), \({{Q}_{_{k+1}}}\) and \({{M}_{_{k+1}}}\). Compute \({{\left\| {{e}_{_{k+1}}} \right\| }_{2}}={{\left\| {{Q}_{_{k+1}}}{{w}_{_{k+1}}}-{{r}_{_{k+1}}} \right\| }_{2}}\).

  4. (iv)

    Output: Save \({{w}_{k}}\) and \({{\left\| {{e}_{_{k}}} \right\| }_{2}}={{\left\| {{Q}_{_{k}}}{{w}_{_{k}}}-{{r}_{_{k}}} \right\| }_{2}}\), and plot figures.

An important criterion for measuring the performance of numerical algorithms is computational complexity. For (12), the overall computational complexity is \(O((m+2n)\times (3n))\) (with \(m<n\in R\)). Thus, the proposed DTZNN model (12) has low computational complexity, i.e., \(O(n^2)\).

3.2 Theoretical analysis

In this subsection, the computational characteristic of the proposed DTZNN model (12) is analyzed and proved theoretically.

Lemma 3

The proposed DTZNN model (12) is characterized by zero stability and consistency, and thus has convergence property.

Proof

By analyzing the characteristic polynomial, it has been determined that the proposed DTZNN model in Equation (12) exhibits zero stability (Guo et al. 2018). Then, from the derivation of (12), its truncation error is \(O({\varepsilon }^5)\), reflecting its consistency. Referring to the findings of Griffiths and Higham (2010), the zero stability and consistency are essential for the convergence of the proposed DTZNN model (12). With that, the proof is now fully established. \(\square\)

Lemma 4

The proposed DTZNN model (12) can produce a precise time-dependent solution of the solvable BCTDLE (1).

Proof

By following Lemma 3, the solution \(w_k\) computed by the proposed DTZNN model (12) can converge to a theoretical solution \(w_k^*=w^*(t_k=k\varepsilon )\) of (3). Mathematically, \(w_k\rightarrow w_k^*\) if k is large enough (Huang et al. 2022). By virtue of \(Q_kw_k-r_k=0\) and the given definitions of \(Q_k\) and \(r_k\), the following equation can be deduced:

$$\begin{aligned} \lim _{k \rightarrow \infty }\left( \left[ \begin{array}{c} G_{k} x_{k}-h_{k} \\ U x_{k}-\vartheta \end{array}\right] \right) =\lim _{k \rightarrow \infty }\left( -\left[ \begin{array}{c} 0 \\ V_{k} y_{k} \end{array}\right] \right) . \end{aligned}$$
(13)

\(\square\)

Knowing that \(V_{k} y_{k} \ge 0, U=[-I; I] \in R^{2 n \times n}, \text{ and } \vartheta =\left[ -x^{-}; x^{+}\right] \in R^{n \times n}\), (13) is reformulated as stated below:

$$\begin{aligned} \left\{ \begin{array}{l} \lim _{k \rightarrow \infty }\left( G_{k} x_{k}-h_{k}\right) =0, \\ x^{-} \le \lim _{k \rightarrow \infty }\left( x_{k}\right) \le x^{+}. \end{array}\right. \end{aligned}$$
(14)

(14) indicates that, when k is large enough, the DTZNN model (12) has \(x_k\rightarrow x_k^*(t_k=k\varepsilon )\) for the BCTDLE (1) to hold. This statement further shows that the proposed DTZNN model (12) can offer a precise time-dependent solution of the solvable BCTDLE (1). With that, the proof is now fully established. \(\square\)

Lemma 5

Considering the BCTDLE (1) is solved by the proposed DTZNN model (12), the SSCE varies in the mode of \(O({\varepsilon }^5)\).

Proof

Based on the error function (4), the SSCE of (12) is given by

$$\begin{aligned} \lim _{k \rightarrow \infty }||e_{k}||_{2}=\lim _{k \rightarrow \infty }\left\| Q_{k} w_{k}-r_{k}\right\| _{2}. \end{aligned}$$

According to Lemmas 3 and 4, \(w_k=w_k^*+O({\varepsilon }^{5})\) with a large enough k. Then, the following result on the SSCE of (12) is obtained:

$$\begin{aligned} \begin{aligned} \lim _{k \rightarrow \infty }\left\| e_{k}\right\| _{2}&=\lim _{k \rightarrow \infty }\left\| Q_{k} w_{k}-r_{k}\right\| _{2} \\&=\lim _{k \rightarrow \infty }\left\| Q_{k}(w_{k}^{*}+O(\varepsilon ^{5}))-r_{k}\right\| _{2} \\&=\lim _{k \rightarrow \infty }\left\| Q_{k} O(\varepsilon ^{5})\right\| _{2} \\&=O(\varepsilon ^{5}). \end{aligned} \end{aligned}$$
(15)

\(\square\)which means that the DTZNN calculation error at steady state is of order \(O(\varepsilon ^{5})\). Therefore, considering the BCTDLE (1) is solved by the proposed DTZNN model (12), the SSCE varies in the mode of \(O({\varepsilon }^5)\). With that, the proof is now fully established. \(\square\)

To summarize, Lemmas 3–5 provide theoretical guarantees that the proposed DTZNN model (12) can effectively solve the BCTDLE (1).

Fig. 1
figure 1

Numerical results for the previous DTZNN model (16) with \(\varepsilon =0.01\) and \(\mu =0.1\) to solve the BCTDLE (1)

Full size image
Fig. 2
figure 2

Numerical results for the proposed DTZNN model (12) with \(\varepsilon =0.01\) and \(\mu =0.1\) to solve the BCTDLE (1)

Full size image

4 Numerical verification and comparison

This section showcases numerical simulations to verify the superiority and effectiveness of the proposed DTZNN model (12) in solving the BCTDLE (1). Notably, the recent research (Guo et al. 2017) indicates that the DTZNN model via Taylor difference formula can outperform the DTZNN model (8) via Euler difference formula. Thus, this section only offers the comparative numerical results of using the proposed DTZNN model (12) and the previous DTZNN model in Guo et al. (2017). For convenience, the previous DTZNN model in Guo et al. (2017) is expressed as follows:

$$\begin{aligned} \begin{aligned} w_{k+1}=&\frac{5}{24} w_{k}+\frac{1}{2} w_{k-1}+\frac{1}{4} w_{k-2}+\frac{1}{6} w_{k-3}-\frac{1}{8} w_{k-4} \\&-P_{k}^{+}\left( \mu \left( Q_{k} w_{k}-r_{k}\right) +2\varepsilon \left( M_{k} w_{k}-\dot{r}_{k}\right) \right) . \end{aligned} \end{aligned}$$
(16)

These simulations are also performed via MATLAB R2021b on a digital computer equipped with an AMD Ryzen 7 5800 H processor with Radeon Graphics @3.20 GHz, 32 GB of memory, and Windows 10 OS.

4.1 Model comparison

In this subsection, numerical simulation comparative experiments are conducted using the following example to demonstrate the effectiveness and superiority of the proposed DTZNN model (12) in solving BCTDLE (1). In the ensuing numerical experiments, the DTZNN models (12) and (16) are used to solve the BCTDLE (1) with the following coefficients:

$$\begin{aligned} \begin{array}{l} G(t)=[1+\sin t, 2+\cos (2 t), 5-\sin t], \\ h(t)=\sin (0.5 t)-\cos (2 t), \\ -x^{+}=x^{-}=[-0.3,-0.3,-0.3]. \end{array} \end{aligned}$$

The relevant numerical results are provided in Figs. 1, 2, 3, 4 and Table 1.

Fig. 3
figure 3

Numerical results for the previous DTZNN model (16) with \(\varepsilon =0.001\) and \(\mu =0.1\) to solve the BCTDLE (1)

Full size image
Fig. 4
figure 4

Numerical results for the proposed DTZNN model (12) with \(\varepsilon =0.001\) and \(\mu =0.1\) to solve the BCTDLE (1)

Full size image

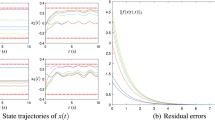
Figure 1 presents the simulation results of the previous DTZNN model (16) using \(\varepsilon =0.01\) and \(\mu =0.1\) and four different initial values to solve the BCTDLE (1), where \(x_k^{(i)}(i=1,2,3)\) indicates the ith element of the feasible solution vector \(x_k\) of (1). In Fig. 1a, the trajectories of \(x_k\) are time-dependent, and the changing values are within the constraint boundary \([x^-,x^+]\). These results mean that the exact solution of (1) can be obtained by applying the previous DTZNN model (16). In Fig. 1b, the calculation errors \(\Vert e_{k}\Vert _{2}\) of (16) converge, and the SSCEs are in the order of \({10}^{-6}\). According to these results, the previous DTZNN model (16) can effectively solve the BCTDLE (1).

Figure 2 presents the simulation results of the proposed DTZNN model (12) using \(\varepsilon =0.01\) and \(\mu =0.1\) and four different initial values to solve the BCTDLE (1). In Fig. 2a, the trajectories of \(x_k\) are time-dependent as well and numerically bounded (or say, they satisfy \(x_k\in [x^-,x^+]\)). In Fig. 2b, the calculation errors of (12) demonstrate convergence, with the SSCE values reaching the order of \({10}^{-8}\). These findings provide strong evidence for the validity of (12) in solving (1). More importantly, comparing the results in Figs. 1b and 2b, the SSCE of the proposed model (12) is 100 times smaller than that of the previous model (16). This comparison indicates that (12) has smaller errors and higher accuracy than (16). Therefore, the proposed DTZNN model (12) offers greater advantages than the previous DTZNN model (16) in solving the TDLE with boundary constraint, i.e., (1).

Table 1 SSNEs of the proposed DTZNN model (12) and the previous DTZNN model (16) using different \(\varepsilon\) and \(\mu\) to solve the BCTDLE (1)
Full size table

By reducing the sampling interval \(\varepsilon\) by a factor of 10 and repeating the above numerical experiments, the corresponding results of using the DTZNN models (16) and (12) are shown in Figs. 3 and 4, respectively. In such two figures, as computed by (16) or (12), the trajectories of \(x_k\) are time-dependent and satisfy \(x_k\in [x^-,x^+]\). The related computational errors converge with the SSCE being small enough. These simulation results verify again the effectiveness of the DTZNN models (16) and (12) in solving the BCTDLE (1). In particular, comparing Figs. 3b and 4b, the SSCEs of (16) and (12) for solving (1) are \({10}^{-{10}}\) and \({10}^{-{13}}\) orders of magnitude, respectively. The latter is about 1000 times smaller than the former. Therefore, the proposed DTZNN model (12) can be more advantageous than the previous DTZNN model (16) in solving the BCTDLE (1).

For further investigation, the SSCEs of the DTZNN models (16) and (12) are compared and validated using different values of \(\varepsilon\) and \(\mu\), with a fixed initial state of \(w_0=0.2\) and the same sampling time. The detailed data are provided in Table 1, which demonstrates that the proposed model (12) is computationally better than the previous model (16). These results also verify that the calculation error variation mode of (12) is \(O(\varepsilon ^5)\). Specifically, when \(\varepsilon =0.001\), the SSCE can reach the order of \({10}^{-14}\). In addition to this, the performance of the proposed DTZNN model (12) on computing and solving (1) can be improved by decreasing the sampling interval \(\varepsilon\) or increasing \(\mu\) in the appropriate range.

Overall, the simulation results presented in Figs. 1, 2, 3, 4 and Table 1 confirm the superiority and efficacy of the proposed DTZNN model (12) in solving the BCTDLE (1) in comparison with the previous DTZNN model (16).

Fig. 5
figure 5

Numerical results for the proposed DTZNN model (12) with \(\varepsilon =0.01\) and \(\mu =0.1\) to solve the BCTDLE (1)

Full size image
Fig. 6
figure 6

Numerical results for the proposed DTZNN model (12) with \(\varepsilon =0.001\) and \(\mu =0.1\) to solve the BCTDLE (1)

Full size image
Fig. 7
figure 7

Calculation errors for the proposed DTZNN model (12) with different \(\varepsilon\) and \(\mu\) to solve the BCTDLE (1)

Full size image

4.2 Influence of \(\varepsilon\) and \(\mu\)

In the previous section, the effectiveness and superiority of the proposed DTZNN model (12) in solving the BCTDLE problem are demonstrated through simulation comparisons. The proposed DTZNN model (12), it has two adjustable parameters (i.e., \(\varepsilon\) and \(\mu\)). Since different values of \(\varepsilon\) and \(\mu\) can have an effect on the solution effectiveness, this section delves into the influence of these two adjustable parameters on the proposed DTZNN model (12) using a new example. The time period for the simulation is set to \(T = 10\) s. The coefficient matrix and the constraint boundary of the BCTDLE (1) to be solved are given as follows:

$$\begin{aligned} \begin{array}{l} G(t)=[3+cos(3t), 1+sin(t),6-cos(t)-sin(t)], \\ h(t)=[sin(t)-cos(t)], \\ -x^{+}=x^{-}=[-0.4,-0.4,-0.4]. \end{array} \end{aligned}$$

To better demonstrate the effectiveness of the proposed DTZNN model (12) in solving BCTDLE (1), two additional computational errors are introduced: the equation error \({{\bar{e}}_{k}}=G(t)x(t)-h(t)\) and the constraint boundary error \({{\hat{e}}_{k}}=Ux(t)-\vartheta\).

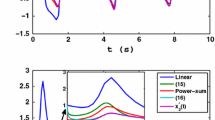
Figure 5a clearly illustrates that the feasible solution of the BCTDLE (1) under the influence of the proposed DTZNN (12) model, undergoes rapid convergence from an initially out-of-boundary state and reaches the boundary constraint range. This result clearly validates the effectiveness and convergence properties of the proposed DTZNN model (12). Figure 5b indicates that when the iteration count k is sufficiently large, the SSCE \({\left\| {{e}_{k}} \right\| }_{2}\) converges, and the maximum value is in the smaller order of magnitude of \({{10}^{-8}}\) after stabilization. This outcome suggests that the proposed DTZNN model (12) can effectively solve BCTDLE (1). From Fig. 5c, it can be seen that with increasing iteration count k and after reaching stability, the equation error \({{\bar{e}}_{k}}\) converges to 0. The trend of the variation in \({\hat{e}}_{k}\) in Fig. 5d and e also illustrates that under the influence of the proposed DTZNN model (12), \({x}_{k}\) transitions from initially exceeding the boundary to returning within the boundary constraint range. Therefore, in Fig. 5a, \({x}_{k}\) is the exact solution of BCTDLE (1), confirming that the proposed DTZNN model (12) can effectively solve BCTDLE (1).

The above simulation results are obtained with the sampling interval \(\varepsilon = 0.01\). To showcase the high precision characteristics of the proposed DTZNN model (12) and highlight the impact of the sampling interval on the solution effectiveness, the sampling interval is further reduced to \(\varepsilon = 0.001\), while keeping other parameters constant. The relevant simulation results for solving BCTDLE (1) are presented below.

Figures 6a, d, and e reveal that even with four different initial values exceeding the boundary constraints, \({x}_{^{k}}\) can rapidly converge within the boundary constraint range under the influence of the proposed DTZNN model (12). Comparing Fig. 5b with Fig. 6b, it is also noticeable that as the sampling interval \(\varepsilon\) decreases, the computational performance improves. Specifically, \((9.35241\times {{10}^{-13}})/(7.03878\times {{10}^{-8}})\approx 1.32870\times {{10}^{-5}}\), indicating that the proposed DTZNN model (12) follows an \(O({{\varepsilon }^{5}})\) error model, that is, as the sampling interval \(\varepsilon\) is reduced by a factor of 10, the SSCE can be reduced by a factor of 100000. Therefore, it is possible to appropriately decrease the value of \(\varepsilon\) based on practical requirements to enhance computational accuracy and obtain more precise time-varying solutions.

In addition to the sampling interval \(\varepsilon\), the proposed DTZNN model (12) has another adjustable parameter, \(\mu\). To further explore the influnce of the two parameters on the proposed DTZNN model (12), six sets of simulation experiments are conducted. From Fig. 7a, c, and e, it can be observed that with the sampling interval \(\varepsilon = 0.01\), the SSCEs of the proposed DTZNN model (12) for solving BCTDLE (1) decreases as the step size \(\mu\) increases. This similar conclusion can be obtained from Fig. 7b, d, and f. While the impact of increasing \(\mu\) on the SSCE is not as pronounced as decreasing \(\varepsilon\), in practical situations, the sampling interval cannot be made arbitrarily small owing to some constraints. Therefore, when adjusting the sampling interval to the minimum achievable under practical conditions, increasing \(\mu\) can be employed to further reduce the SSCE and enhance precision.

By comparing the simulation results between the left and right of Fig. 7, it can be observed that, with the step size \(\mu\) held constant, as the sampling interval \(\varepsilon\) decreases from 0.01 to 0.001, the SSCEs reduce from the order of \({10}^{-8}\) to \({10}^{-13}\). This magnitude reduction once again confirms that the proposed DTZNN model (12) exhibits an error model of \(O({{\varepsilon }^{5}})\). Therefore, the numerical simulation results above strongly demonstrate the effectiveness and superiority of the proposed DTZNN model (12) in solving BCTDLE (1).

It is worth noting that the main difference in this section compared to the previous one lies in the fact that the initial values exceed the boundary constraint. Therefore, the comparison of simulation results show that while keeping the sampling interval \(\varepsilon\) and the step size \(\mu\) constant, the SSCE in this section is reduced by a factor of 10 compared to the previous section. However, both sections still keep an \(O({{\varepsilon }^{5}})\) error model. Such a phenomenon occurs not only in the proposed DTZNN model (12) but also in the previous DTZNN model (16), where model accuracy is sacrificed to ensure regression to within the boundary constraint. However, the proposed DTZNN model has smaller calculation errors and demonstrates greater fault tolerance, thus making it more widely applicable in practical engineering scenarios.

5 DTZNN application to robotics

This section presents the application of the proposed DTZNN model (12) to the robotic arms with joint physical constraints to demonstrate the applicability of the model.

5.1 Motion planning of robotic arms

The motion planning of a robotic arm involves generating the joint trajectory \(\theta (t)\in R^n\) in real-time to accurately follow the desired Cartesian path \(r(t)\in R^m\) of the end-effector (Li et al. 2019).

In particular, taking into consideration the feedback and joint limits, the motion planning of robotic arms is achieved by efficiently solving the TDLE with boundary constraints as follows (Xu et al. 2019b):

$$\begin{aligned} \left\{ \begin{array}{c} J(\theta (t)) \dot{\theta }(t)=\dot{r}(t)-k(\phi (\theta (t))-r(t)), \\ \dot{\theta }^{-} \le \dot{\theta }(t) \le \dot{\theta }^{+},\\ \theta ^{-} \le \theta (t) \le \theta ^{+}, \end{array}\right. \end{aligned}$$
(17)

The above equation involves several key variables, including Jacobian matrix \(J(\theta (t))\in R^{m\times n}\), joint velocity \(\dot{\theta }(t)\in R^n\), time derivative of r(t) denoted as \(\dot{r}(t)\in R^m\), the feedback parameter \(k>0\in R\), and the differentiable nonlinear mapping function \(\phi (\cdot )\). In addition, \(\theta ^\pm\) and \({\dot{\theta }}^\pm\) represent the limits of \(\theta (t)\) and \(\dot{\theta }(t)\), respectively.

Fig. 8
figure 8

Simulation results of the motion planning scheme (19) with \(\varepsilon =0.01\) and \(\mu =0.1\) for PUMA560 robotic arm tracking the tricuspid path

Full size image

It follows from (Zhang et al. 2004) that the boundary constraints in (17) are unified as

$$\begin{aligned} \max \left\{ \rho (\theta ^{-}-\theta ), \dot{\theta }^{-}\right\} \le \dot{\theta } \le \min \left\{ \rho (\theta ^{+}-\theta ), \dot{\theta }^{+}\right\} , \end{aligned}$$

with \(\rho >0\in R\). Then, the following reformulation of (17) is further obtained:

$$\begin{aligned} \left\{ \begin{array}{c} J(\theta (t)) \dot{\theta }(t)=\dot{r}(t)-k(\phi (\theta (t))-r(t)), \\ \delta ^{-} \le \dot{\theta }(t) \le \delta ^{+}, \end{array}\right. \end{aligned}$$
(18)

with \(\delta ^{-}=\max \{\rho (\theta ^{-}-\theta ), \dot{\theta }^{-}\}\) and \(\delta ^{+}=\min \{\rho (\theta ^{+}-\theta ), \dot{\theta }^{+}\}\). At this point, solving (18) is the same as solving the BCTDLE (1), with the correlation coefficients as follows:

$$\begin{aligned}&G(t)=J(\theta (t)), \\&h(t)=\dot{r}(t)-k(\phi (\theta (t))-r(t)), \\&x(t)=\dot{\theta }(t). \end{aligned}$$

Moreover, the following augmented coefficient matrices and vectors are presented:

$$\begin{aligned} U= & {} \left[ \begin{array}{cc} -I \\ I\end{array}\right] , \quad \vartheta =\left[ \begin{array}{cc} -\delta ^{-} \\ \delta ^{+} \end{array}\right] , \\ P(t)= & {} \left[ \begin{array}{cc} G(t) &{} 0 \\ U &{} 2 V(t) \end{array}\right] =\left[ \begin{array}{cc} J(\theta (t)) &{} 0 \\ U &{} 2 V(t) \end{array}\right] , \\ r(t)= & {} \left[ \begin{array}{c} h(t) \\ \vartheta \end{array}\right] =\left[ \begin{array}{cc} \dot{r}(t)-k(\phi (\theta (t))-r(t)) \\ \vartheta \end{array}\right] , \\ Q(t)= & {} \left[ \begin{array}{cc} G(t) &{} 0 \\ U &{} V(t) \end{array}\right] =\left[ \begin{array}{cc} J(\theta (t)) &{} 0 \\ U &{} V(t) \end{array}\right] , \\ M(t)= & {} \left[ \begin{array}{cc} \dot{G}(t) &{} 0 \\ 0 &{} 0 \end{array}\right] =\left[ \begin{array}{cc} \dot{J}(\theta (t)) &{} 0 \\ 0 &{} 0 \end{array}\right] , \\ w(t)= & {} \left[ \begin{array}{c} x(t) \\ y(t) \end{array}\right] =\left[ \begin{array}{l} \dot{\theta }(t) \\ y(t) \end{array}\right] . \end{aligned}$$

Therefore, the proposed DTZNN model (12) for the BCTDLE (1) can be introduced to solve (18) and (17), where \(w_k=[{\dot{\theta }}_k;y_k] \in R^{3n}\). Notably, the Taylor difference formula (10) is also employed to calculate the joint angle \(\theta _k=\theta \left( t_k=k\varepsilon \right)\) at every instance. On the basis of (12), the following detailed formulation for realizing the motion planning of robotic arms with joint physical constraints is provided:

$$\begin{aligned} \left\{ \begin{array}{c} \begin{aligned} &{}\begin{aligned} \theta _{k+1}=&{}\frac{5}{54} \theta _{k}+\frac{5}{27} \theta _{k-1}+\frac{55}{54} \theta _{k-2}-\frac{5}{27} \theta _{k-3}-\\ &{}\frac{1}{54} \theta _{k-4}-\frac{5}{27} \theta _{k-5}+\frac{5}{54} \theta _{k-6}-\frac{20}{9} \varepsilon \dot{\theta }_{k},\\ \end{aligned}\\ &{}\begin{aligned} w_{k+1}=&{}\frac{5}{54} w_{k}+\frac{5}{27} w_{k-1}+\frac{55}{54} w_{k-2}-\frac{5}{27} w_{k-3}\\ &{}-\frac{1}{54} w_{k-4}-\frac{5}{27} w_{k-5}+\frac{5}{54} w_{k-6}-\\ &{}\frac{20}{9} P_{k}^{+}\left( \mu \left( Q_{k} w_{k}-r_{k}\right) + \varepsilon M_{k} w_{k}- \varepsilon \dot{r}_{k}\right) . \end{aligned} \end{aligned} \end{array}\right. \end{aligned}$$
(19)

Hereafter, (19) is called the new motion planing scheme for physically-constrained robotic arms. With regard to such a motion planning scheme (19), seven initial values must still be determined to start the iterative computation. Similarly, given the initial joint angle \(\theta _{0}\) and \(w_{0}\), the rest is obtained via the following iterative computation:

$$\begin{aligned} \left\{ \begin{array}{c} \begin{aligned} &{}\theta _{i+1}=\theta _{i}+\varepsilon \dot{\theta }_{i}, \\ &{}w_{i+1}=w_{i}-u P_{i}^{+}\left( Q_{i} w_{i}-r_{i}\right) -\varepsilon P_{i}^{+}\left( M_{i} w_{i}-\dot{r}_{i}\right) , \end{aligned} \end{array}\right. \end{aligned}$$

where \(i=0,1,\ldots ,6\).

Fig. 9
figure 9

Simulation results of the motion planning scheme (19) with \(\varepsilon =0.001\) and \(\mu =0.1\) for PUMA560 robotic arm tracking the tricuspid path

Full size image
Fig. 10
figure 10

Simulation results of the motion planning scheme (19) with \(\varepsilon =0.01\) and \(\mu =0.1\) for PUMA560 robotic arm tracking the circular path

Full size image
Fig. 11
figure 11

Simulation results of the motion planning scheme (19) with \(\varepsilon =0.01\) and \(\mu =0.1\) for PUMA560 robotic arm tracking the Rhodonea path

Full size image

5.2 Simulation verification

To demonstrate the effectiveness of the new motion planning scheme (19), simulations are conducted using the PUMA560 robotic arm for a set desired path [i.e., the tricuspid path (20), circular path (21), and Rhodonea path (22)]. In this way, the validity and practicality of the proposed DTZNN model (12) is thus confirmed.

In these simulations, the limits of the PUMA560 robotic arm are defined as

$$\begin{aligned} \begin{aligned}&-{\dot{\theta }}^+={\dot{\theta }}^-=[-0.8;-0.8;-0.8;-0.8;-0.8;-0.8] \text { rad/s},\\&\theta ^+=[2.7754;0.7506;3.9274;2.9674;1.7455;4.6256] \text { rad},\\&\theta ^-=-[2.7754;3.8925;0.7855;1.9201;1.7455;4.6256] \text { rad}. \end{aligned} \end{aligned}$$

The desired end-effector position vectors for the tricuspid path, circular path, and Rhodonea path are respectively designed as

$$\begin{aligned}{} & {} {{r}_{p}}=\left[ \begin{matrix} {{r}_{x}} \\ {{r}_{y}} \\ {{r}_{z}} \\ \end{matrix} \right] =\left[ \begin{matrix} r(2\cos (\phi )+\cos (2\phi ))-3r+{{i}_{{{x}_{0}}}} \\ r(2\sin (\phi )-\sin (2\phi ))\cos (\alpha )+{{i}_{{{y}_{0}}}} \\ r(2\sin (\phi )-\sin (2\phi ))\sin (\alpha )+{{i}_{{{z}_{0}}}} \\ \end{matrix} \right] , \end{aligned}$$
(20)
$$\begin{aligned}{} & {} {{r}_{p}}=\left[ \begin{matrix} {{r}_{x}} \\ {{r}_{y}} \\ {{r}_{z}} \\ \end{matrix} \right] =\left[ \begin{matrix} r\cos (\phi )-r+{{i}_{{{x}_{0}}}} \\ r\sin (\phi )\cos (\alpha )+{{i}_{{{y}_{0}}}} \\ r\sin (\phi )\sin (\alpha )+{{i}_{{{z}_{0}}}} \\ \end{matrix} \right] , \end{aligned}$$
(21)
$$\begin{aligned}{} & {} {{r}_{p}}=\left[ \begin{matrix} {{r}_{x}} \\ {{r}_{y}} \\ {{r}_{z}} \\ \end{matrix} \right] =\left[ \begin{matrix} r\cos (2\phi )\cos (\phi )-r+{{i}_{{{x}_{0}}}} \\ r\cos (2\phi )\sin (\phi )\cos (\alpha )+{{i}_{{{y}_{0}}}} \\ r\cos (2\phi )\sin (\phi )\sin (\alpha )+{{i}_{{{z}_{0}}}} \\ \end{matrix} \right] , \end{aligned}$$
(22)

where \(\phi =2\pi {{\sin }^{2}}({\pi t}/{2T})\), time \(t\in [0,T]\), the parameter \(\alpha\) is constant, and r is the radius of the desired path. In addition, \(i_{x_0}\), \(i_{y_0}\) and \(i_{z_0}\) respectively denote the X-axis, Y-axis and Z-axis components of the initial position vector of the end-effector.

To better show the simulation effect, the PUMA560 end-effector path tracking periods are all set to \(T=10s\), and the initial joint configuration is set to \(\theta _0=[0;0;0;0;0;0]\) rad. The related simulation results are depicted in Figs. 8, 9, 10, 11, where \(t\in \left\{ 0,\varepsilon ,2\varepsilon ,\ldots ,10\right\}\), \(e=\phi (\theta \left( t\right) )-r\left( t\right) \in R^3\), and \({\dot{\theta }}^{(i)}\) and \(\theta ^{(i)} (i=1,2,\cdots ,6)\) represent the ith element of \(\dot{\theta }(t)\) and \(\theta (t)\).

Figure 8 presents the results of the new motion planning scheme (19) with \(\varepsilon =0.01\) and \(\mu =0.1\) for the PUMA560 robotic arm tracking the tricuspid path. In Figs. 8a and b, it can be observed that the PUMA560 end-effector trajectory closely follows the desired tricuspid path, and the maximum positioning error is \({6.11775\times 10}^{-7}\) m. In particular, Fig. 8c denotes that the value of joint angle \(\theta\) calculated by (19) remains within its limits. In Fig. 8d, the joint velocity \(\dot{\theta }\) stays within the limits even after the lower limit is reached. That is, \({\dot{\theta }}^-\le \dot{\theta }(t)\le {\dot{\theta }}^+\) and \(\theta ^-\le \theta (t)\le \theta ^+\) are satisfied. These simulation results demonstrate that the new scheme (19) can effectively implement the motion planning of the PUMA560 robotic arm in the presence of joint physical constraints and further verify the practical application of the proposed DTZNN model (12).

To further present the high accuracy characteristics of the new motion planning scheme (19), the simulation is repeated with the sampling interval \(\varepsilon\) reduced by a factor of 10 (i.e., from \(\varepsilon =0.01\) to \(\varepsilon =0.001\)) and the rest of the condition parameters unchanged. The first two subfigures of Fig. 8 show that the PUMA560 end-effector successfully tracks the desired path again, with the maximum error is \({1.34149\times 10}^{-11}\) m. The rest of the subfigures of Figs. 8c and d denote that joint angle \(\theta\) and joint velocity \(\dot{\theta }\) also satisfy \({\dot{\theta }}^-\le \dot{\theta }(t)\le {\dot{\theta }}^+\) and \(\theta ^-\le \theta (t)\le \theta ^+\), respectively, thus demonstrating the effectiveness of the new motion planning scheme (19). Notably, the PUMA560 end-effector positioning error decreases by a factor of 10,000 as the sampling interval \(\varepsilon\) decreases, that is, \({(1.34149\times 10}^{-11})/{(6.11775\times 10}^{-7})\approx 2.19278\times {10}^{-5}\). This finding underscores the importance of the sampling interval \(\varepsilon\) for the new motion planning scheme (19) and reflects an \(O(\varepsilon ^5)\) error variation pattern. Therefore, in practical applications, \(\varepsilon\) in the new motion planning scheme (19) should be set small enough to ensure the high planning accuracy required for robotic arms.

For further investigation, the tracking path of the PUMA560 end-effector is set to a circular path and a Rhodonea path for the new motion planning scheme (19) with \(\varepsilon =0.001\) and \(\mu =0.1\). Figures 10 and 11 show the corresponding simulation results, which fully demonstrate the validity of the new motion planning scheme (19). In particular, the end-effector tracking trajectory closely follows the desired path, and the corresponding maximum error is of the order of \({10}^{-10}\) m or \({10}^{-11}\) m. Joint velocity \(\dot{\theta }\) and the joint angle \(\theta\) obtained through the new scheme (19) also remain within their respective limits, ensuring that they satisfy the conditions \({\dot{\theta }}^-\le \dot{\theta }(t)\le {\dot{\theta }}^+\) and \(\theta ^-\le \theta (t)\le \theta ^+\), respectively.

In summary, the simulation results provided in Figs. 8, 9, 10, 11 confirm the validity of the new motion planning scheme (19) for the PUMA560 robotic arm. Furthermore, these results underscore the effectiveness and practicality of the proposed DTZNN model (12).

6 Conclusion

In this paper, utilizing the Taylor difference formula (9) to discretize the CTZNN model (5), the new DTZNN model (12) is proposed and studied to address the BCTDLE (1). Theoretical analysis demonstrates that the proposed DTZNN model (12) has convergence property and can generate the exact time-dependent solution of (1). Numerical results indicate the validity and superiority of the proposed DTZNN model (12) and further point to the SSCE variation being of the \(O(\varepsilon ^5)\) mode. Such a DTZNN model is finally applied to robotic arms, and the related new motion planning scheme (19) is derived. Simulation results obtained from the PUMA560 robotic arm denote the validity and reliability of the new motion planning scheme (19) for different desired path tracking examples. The applicability of the proposed DTZNN model (12) is confirmed as well.

One future research directions involves utilizing the proposed DTZNN model (12) to solve the BCTDLE (1) in a noisy environment. Another direction is to explore the application of the proposed DTZNN model (12) in other tasks of redundant robot manipulators, such as repetitive motions and obstacle avoidance. As a continuation of this paper, further efforts will focus on designing and selecting different activation functions to enhance the robustness of the proposed DTZNN model (12).