An evidential linguistic ELECTRE method for selection of emergency shelter sites

Abstract

In many circumstances, decisions are based on subjective experience. However, some views can be vague, meaning that policymakers do not know exactly how they should express their opinions. Therefore, it is necessary for researchers to provide scientific decision frameworks, among which the multi-criteria decision making (MCDM) method in the linguistic environment is gradually favored by scholars. A large body of literature reports relevant approaches with regard to linguistic term sets, but existing approaches are insufficient to express the subjective thoughts of policymakers in a complex and uncertain environment. In this paper, we address this problem by introducing the concept of evidential linguistic term set (ELTS). ELTS generalizes many other uncertainty representations under linguistic context, such as fuzzy sets, probabilities, or possibility distributions. Measures on ELTS, such as uncertainty measure, dissimilarity measure and expectation function, provide general frameworks to handle uncertain information. Modeling and reasoning of information expressed by ELTSs are realized by the proposed aggregation operators. Subsequently, this paper presents a novel MCDM approach called evidential linguistic ELECTRE method, and applies it to the case of selection of emergency shelter sites. The findings demonstrate the effectiveness of the proposed method for MCDM problems under linguistic context and highlight the significance of the developed ELTS.

1 Introduction

In recent years, the rapid development of global urbanization and the economy has led to gradually increasing losses caused by natural disasters (Kılcı et al. 2015; Fei and Wang 2022). This is particularly true in densely populated and disaster-prone areas, where natural disasters deplete and destroy the material resources essential for human survival, thereby hindering societal development Şenik and Uzun (2021). A series of emergencies have highlighted that urban public spaces, especially crowd gathering places, are fraught with various risks and significant hidden dangers. In the event of an accident, if the safe evacuation of people cannot be guaranteed, the consequences can be even more catastrophic Wei et al. (2020). Therefore, in the context of disaster prevention and mitigation, ensuring safe evacuation is of paramount importance, with emergency shelters playing a crucial role Hosseini et al. (2022); Liu (2022). An emergency shelter is a pre-designated site equipped with specific functional facilities, enabling people to avoid direct or indirect harm from disasters and ensuring their basic needs are met for a period post-disaster Aydin and Cetinkale (2023). For effective disaster risk reduction, emergency shelters must possess certain characteristics, such as safety, accessibility, and effectiveness. This underscores the significance of their site selection, a key aspect of emergency management Zou et al. (2023).

As an important facility for post-disaster evacuation and resettlement of people, the location of emergency shelters is related to the efficiency of disaster relief and the level of evacuation services. Numerous scholars have extensively researched this area. Commonly used methods are single-objective model Kocatepe et al. (2018); Horner et al. (2018), multiobjective model Xu et al. (2018); Zhao et al. (2017) and hierarchical model Li et al. (2017). The literature focuses on the study of emergency shelter siting models throughout the analysis of goals, constraints, hazard types, and solutions Ma et al. (2019). Studies on location problems have offered us enlightenment. For instance, Mohammadi and his colleagues Arabahmadi et al. (2023) proposed strategies for optimizing facility locations under uncertain circumstances, while Rabbani Hirbod et al. (2023) explored the multi-treatment location arc routing problem with vehicle capacity constraints and considerations for waste separation. Furthermore, they established a hybrid integer nonlinear programming model for routing and location selection Moghaddasi et al. (2023). These contributions have provided valuable insights and inspired our approach to the location problem addressed in this study.

Another significant perspective involves studying emergency shelter site selection using multi-criteria decision-making (MCDM) methods. Liu Liu (2022) proposed a comprehensive framework to guide the site selection of post-earthquake medical service points, using the TOPSIS method to evaluate the suitability of alternative sites and rank them according to the evaluation results. Failures are given precedence through the application of Multi-Objective Optimization using Ratio Analysis, which is rooted in the Z-number theory outlined in Ghoushchi et al. (2021). This serves as a valuable reference for addressing the site selection issues discussed in this article. The literature Mishra et al. (2023) introduced a decision-making framework designed to assess sustainable wastewater treatment technology in an environment characterized by interval-valued intuitionistic fuzzy sets. This innovative approach has provided valuable insights and served as a source of inspiration for the present study. In Junian and Azizifar’s study Junian and Azizifar (2018), AHP was used as a MCDM method, considering principles such as vulnerable areas, access roads, fire centers, densely populated areas, and medical centers to determine the optimal site of temporary shelters in disaster-prone areas in northern Iran. Geng et al. Geng et al. (2021) employed Fuzzy-VIKOR to evaluate the performance of emergency shelters, determined the most ideal site of the shelter through multiple criteria. Taking Chengdu, Sichuan Province, China as an example, they provided a series of reliable solutions for the government. Song et al. Song et al. (2019) provided a rough QUALIFLEX method that combines the advantages of the QUALIFLEX method in manipulating multiple evaluation criteria with heterogeneity and the advantages of interval-rough numbers in fuzzy environments to solve the location problem of emergency shelters.

From the above analysis, it can be seen that the current emergency shelter site selection based on the MCDM method often involves a combination of specific technologies, such as AHP or TOPSIS, while overlooking the expression of evaluation information. To model the objective world from a mathematical point of view, a multitude of methodologies that conform to human cognition have been proposed. Fuzzy set theory Zadeh (1965) was put forward by Zadeh in 1965. It is an effective methodology that can quantitatively study and deal with inaccuracy, inconsonant and incomplete data and knowledge. As extensions, intuitionistic fuzzy sets Atanassov (1986); Hezam et al. (2023), Pythagorean fuzzy sets Yager (2013); Rani et al. (2023), and their related interval methods Pan et al. (2023); Zeng and Xiao (2023) were subsequently developed. However, these theories only work in the context of finite sets, considering a scenario in which decision makers are forced to choose between multiple possible values to accommodate existing approaches, often with unsatisfactory results. Hesitant fuzzy set was proposed by Torra Torra (2010) to model thus situation using multisets. However, it seems that humans are more accustomed to employing linguistic sets to give evaluations than to provide quantitative information. Inspired by this, Rodriguez et al. Rodriguez et al. (2011) extended HFS to linguistic contexts, which is widely concerned because it allows decision makers (DMs) to show the opinions in multiple linguistic terms. For example, the quietness of an engine is evaluated as “very poor” and “poor” and the safety of a car is described as “at least not low”. However, the hesitant fuzzy linguistic term set assigns equal weight or importance to each linguistic term, which is not in accordance with the reality Liu et al. (2023); Fei and Wang (2022). Consequently, probabilistic linguistic term set (PLTS) Pang et al. (2016) was developed to express the importance degrees of linguistic terms by probability distribution in a more general form. Going back to the example above, when a decision maker is $50\%$ sure that the quietness is “bad” and $50\%$ sure that it is “good”, his evaluation can be expressed as $\{bad(0.5),good(0.5)\}$ by the PLTS. In addition, one hundred buyers expressed their feelings about the comfortable degree of the vehicle, of which 50 consider it is “low”, 30 state it is “fair”, and 20 express it is “high”. This information could be expressed as $\{low(0.5)$,fair(0.3),$high(0.2)\}$ with PLTS.

The PLTS, which has received extensive attention in the field of MCDM Liu et al. (2023); Li et al. (2023, 2022), is flexible enough to represent information containing all possible values with an importance weight. However, information from the real world is affected by plenty of sources of uncertainty. Quite a few cases are found where PLTS cannot be used, such as

• (1) The information is incomplete. Taking the evaluation of vehicle comfort as an example, suppose 40 out of 100 consumers consider it is “low”, 30 state it is “fair”, and 20 express it is “high”. PLTS fails in this case because the sum of all possibilities is less than 1, i.e., $0.4+0.3+0.2<1$, where the information is identified to be incomplete. A suitable rule or mechanism is required to addresses the problem robustly.

• (2) When decision makers vacillate between two or more possible values. Continuing with the car comfort evaluation example, if 50 consumers state it is “low”, 40 express it is “fair”, and others hesitate between “fair” and “high” and cannot make a decision. If decision makers are forced to choose one by a hard assignment, unsatisfactory results might be obtained. Again, a new solution is required, and

• (3) A complete multi-criteria decision making problem involves numerous aspects, such as the expression of evaluation information [would be solved in 1) & 2)], calculation of criteria weight, aggregation of multiple opinions, ranking among alternatives, and so forth. The appropriate aggregation operator, comparison method, and several measures, such as uncertain measure and dissimilarity measure, are needed in applications.

Accordingly, the concept of evidential linguistic term set is developed, in this study, which would be capable of dealing with various types of uncertainties. An indispensable part of an outstanding MCDM approach is the ranking technique Wu et al. (2018), especially in the problem of emergency shelter site selection. The original outranking method called ELECTRE I was developed by Roy Roy (1968), followed by other methods of the ELECTRE family Roy (1978); Paelinck (1978); Roy and Hugonnard (1982). A distinctive aspect of ELECTRE techniques is their consideration of ordinal scales, which are transformed into abstract ranges while preserving their original verbal significance Jagtap and Karande (2023a). Additionally, ELECTRE methods excel at incorporating preference and indifference relations when modeling incomplete information, an advantage not found in other MCDM methodologies Jagtap and Karande (2023b); Jagtap et al. (2022). Nevertheless, despite the demonstrated utility of outranking methods in handling linguistic terms, there has been limited research exploring their application in this context Jagtap and Karande (2022).

This study focuses on employing outranking methods to address MCDM issues (primarily for emergency shelter site selection) in the evidential linguistic context. The main contributions are summarized below.

• (1) We define a new linguistic term set (LTS) that extends the traditional LTS to the power set. We assign unit degree of belief to elements in the new LTS to express the subjective opinion of the DMs. The proposed LTS and its belief distribution constitute the novel concept of evidential linguistic term set (ELTS). ELTS is a generalized uncertain LTS, which degrades to the PLTS when all degree of belief is assigned to single sets, and further, to the hesitant fuzzy LTS if the probability values are equal.

• (2) In conjunction with ELTS, some measures are developed, including uncertainty measure, dissimilarity measure and expectation function. Some properties related to them have been studied and proved. The aggregation operators between ELTSs are put forward, further, the weighted aggregation operators are developed considering the reliability of ELTSs. The reliability of ELTS is measured from two perspectives, i.e. inner and outer, where inner reliability measures the certainty of ELTSs and outer reliability measures the compatibility between ELTSs.

• (3) In this paper, a new approach to MCDM is introduced, which integrates ELTSs with the ELECTRE methodology. When dealing with decisions amidst uncertainty, the suggested technique not only innovates in how information is conveyed but also leverages the ELECTRE method’s strength in assessing the dominance relationships among various options.

• (4) The proposed method of evidence language MCDM is applied to the problem of emergency shelter location selection, the application of the proposed method is demonstrated, and the effectiveness of the method is demonstrated through sensitivity analysis and comparative experiments.

We arrange the rest of this paper in the following way: In Sect. 2, we introduce PLTS, the theory of belief function, and the concept of evidential linguistic term set. In Sect. 3, we give some measures of ELTSs, including uncertainty measure and dissimilarity measure. In Sect. 4, we present several aggregation operators of ELTSs. In Sect. 5, the expectation function of ELTSs is defined to enhance the computational power. In Sect. 6, we propose an MCDM method based on evidential linguistic term sets. In Sect. 7, a case study is conducted about selecting an emergency shelter site. Finally, in Sect. 8, some conclusions and future research focuses are given.

2 Evidential linguistic term set

We first review the basic concepts of PLTS Pang et al. (2016). We then provide an overview of belief function theory (BFT) Dempster (1967); Shafer (1976). Accordingly, the concept of evidential linguistic term set is presented.

2.1 Probabilistic linguistic term set

The basic definition of probabilistic linguistic term set is described below.

Definition 1

Pang et al. (2016) Let $S=\{s_\alpha \vert \alpha =0,1,...,\tau \}$ be a linguistic term set, a PLTS is formulated as

$$L\;(p) = \left\{ {L^{{(k)}} (p^{{(k)}} )|L^{{(k)}} \in S,p^{{(k)}} \ge 0,k = 1,2,...,\# L(p),\sum\limits_{{k = 1}}^{{\# L(p)}} {p^{{(k)}} } \le 1} \right\} $$

(1)

in which $L^{(k)}(p^{(k)})$ is the linguistic term $L^{(k)}$ with the probability $p^{(k)}$, and $\#L(p)$ is the number of linguistic terms in L(p).

The theory of PLTS is highly useful in addressing MCDM issues, allowing DMs to express their opinions using linguistic terms. However, it does have some shortcomings in information expression. For example, while it permits the existence of partial ignorance, it upholds certain probabilistic properties at the expense of normalization. Additionally, it is only effective when probabilities are assigned to a single set of linguistic terms, but it becomes inadequate when experts express hesitation over multiple sets of linguistic terms.

2.2 Theory of belief function

The theory of belief function gives a remarkable framework for addressing issues involving uncertainty and/or ambiguity Shafer (1976); Dempster (1967). As an effective tool for uncertainty modeling, BFT has attracted the attention of scholars in divers fields including information fusion Zhou and Deng (2023), multicriteria decision analysis Qi et al. (2023), etc. Recently, some scholars combined BFT with linguistic terms Liu et al. (2023, 2023); Xue et al. (2024), which makes significant contributions to coping with MCDM issues under uncertain linguistic environment. The basics of BFT are introduced briefly as follows.

The frame of discernment (FoD) in BFT is defined as a finite discrete set $\Theta = \{\theta _1,\theta _2,\ldots ,\theta _n\}$, which includes n mutually exclusive and exhaustive hypotheses. All the propositions of interest are contained in the power set of $\Theta$, expressed as $2^{\Theta } = \{\phi , \theta _1,\theta _2,\ldots ,\theta _n,\theta _1\cup \theta _2,\theta _1\cup \theta _3,\ldots ,\Theta \}$. The mapping $m: 2^\Theta \rightarrow [0,1]$ is defined as a belief function or basic probability assignment for $\Theta$ if it satisfies $m(\phi ) = 0$, $\sum _{A\in 2^\Theta }m(A)=1$. For $A\subseteq \Theta$, its belief function is defined as $Bel(A) = \sum _{B\subseteq A}m(B)$, and its plausibility function is defined as $Pl(A) = \sum _{B\cap A\ne \phi }m(B)$. From these concepts we can conclude that, for $A\subseteq \Theta$, its degree of support is represented by m(A), the degree of support of its all subsets is measured by Bel(A), and the degree to which A is credible is identified by Pl(A).

Another significant application of BFT is to obtain more reliable decision basis through information fusion. This process can be realized based on Dempster’s rule Dempster (1967). Two belief functions $m_1$ and $m_2$ can be combined as $(m_1\oplus m_2)(A)=\frac{1}{1-\kappa }\sum _{B\cap C=A}m_1(B)m_2(C)$, $\forall A \subseteq \Theta$, in which $\kappa = \sum _{B\cap C=\phi }m_1(B)m_2(C)$ is considered the degree of conflict between $m_1$ and $m_2$.

2.3 The concept of evidential linguistic term set

This study deals with limitations of PLTS listed above based upon the major ideological that derives from belief functions Shafer (1976). The philosophical contribution of BFT lies in the proposal of a multivalued mapping from one space S to another space $2^S$ Dempster (1967), which allows the extension of the basic event space in probability theory to its power set. This points of view is significant for applying the concept of multivalued mapping to linguistic context, where the basic event space in probability theory is replaced by linguistic term sets (shown in Fig. 1), and propositions are of the form $L^{(k)}(e^{(k)})$ meaning that the mass of belief of $L^{(k)}$ is $e^{(k)}$.

Fig. 1

Illustration of the mapping from linguistic term sets S to $2^S$

Consequently, the concept of evidential linguistic term set (ELTS) can be introduced by the following definition:

Definition 2

Fei and Wang (2022); Fei and Feng (2021) Let $S =\{s_\alpha \vert \alpha =-\tau ,...,-1,0,1,...,\tau \}$ be a LTS, an ELTS is represented by the form

$$ L(e) = \left\{ {L^{{(k)}} (e^{{(k)}} )|L^{{(k)}} \in 2^{S} ,e^{{(k)}} \ge 0,k = 1,2,...,\# 2^{S} ,\sum\limits_{{k = 1}}^{{\# 2^{S} }} {e^{{(k)}} } = 1} \right\} $$

(2)

where $L^{(k)}(e^{(k)})$ is the linguistic term $L^{(k)}$ associated with the mass of belief $e^{(k)}$, and $\#2^{S}$ is the number of elements in $2^{S}$. Note that $e^{(k)} = 0$ if $L^{(k)} = \phi$. For convenience, in this paper, L(e) is called the evidential linguistic element (ELE).

The relevant remark can be found in Remark 1 of Appendix E.

3 Some measures of the ELTSs

In this section, we propose two measures for ELTSs, which are the uncertainty measure and the dissimilarity measure.

3.1 Uncertainty measure of ELEs

No matter the type of decision environment, introducing some level of uncertainty in the process of information expression is inevitable. Effectively capturing and quantifying this uncertainty is crucial to enhancing the reliability of decision making. We define an entropy function for ELEs to measure their uncertainty.

Definition 3

Let L(e) be an ELE on LTS S, the entropy function of L(e) is defined as:

$$ H(L(e)) = H_{s} (Pl\_P_{{L(e)}} ) + H_{d} (L(e)) = \sum\limits_{{L^{{(A)}} \subseteq S}} P l\_P_{{L(e)}} (L^{{(A)}} )log\left( {\frac{1}{{Pl\_P_{{L(e)}} (L^{{(A)}} )}}} \right) + \sum\limits_{{A \subseteq S}} {L(e)} (L(e))log(|L^{{(A)}} |) $$

(3)

where $Pl\_P_{L(e)}$ indicates plausibility transform given by the following equations

$$\begin{aligned} Pl\_P_{L(e)}(L^{(A)}) = K^{-1} Pl_{L(e)}(L^{(A)}) \end{aligned}$$

(4)

where $K = \sum _{L^{(A)}\subseteq S}Pl_{L(e)}(L^{(A)})$ and $Pl_{L(e)}$ is the plausibility function of L(e) defined as:

$$\begin{aligned} Pl_{L(e)}(L^{(A)}) = \sum \{e^{(B)}\vert L^{(B)} \cap L^{(A)}\ne \phi \} \end{aligned}$$

(5)

The properties and proofs of the entropy of ELTS can be found in Appendix B.

3.2 Dissimilarity measure between ELEs

Dissimilarity or distance assessment is a crucial issue in BFT, therefore, the difference in information content between ELEs should be measured for further study.

Definition 4

Let $L_1(e)$ and $L_2(e)$ be two ELEs on LTS S, the dissimilarity between them can be calculated as:

$$\begin{aligned} \small d(L_1(e),L_2(e)) = \sqrt{\frac{1}{2}{{[{\overrightarrow{L_1(e)}} - {\overrightarrow{L_2(e)}}]}^T}{\underline{\underline{D}}}{\hspace{1.0pt}} {\hspace{1.0pt}} {\hspace{1.0pt}} {\hspace{1.0pt}} [{\overrightarrow{L_1(e)}} - {\overrightarrow{L_2(e)}}]} \end{aligned}$$

(6)

where $\overrightarrow{L_1(e)}=e_1^{(k)}$ and $\overrightarrow{L_2(e)}=e_2^{(k)}$ $(k = 1,2,..., \#2^{S})$ are the vector representations of ELEs $L_1(e)$ and $L_2(e)$, and ${\underline{\underline{D}}}$ is a $2^S \times 2^S$-dimensional matrix with elements

$$\begin{aligned} {\underline{\underline{D}}}(L^{(A)},L^{(B)}) = \frac{{\vert L^{(A)} \cap L^{(B)}\vert }}{{\vert L^{(A)} \cup L^{(B)}\vert }} \end{aligned}$$

(7)

where $L^{(A)}$, $L^{(B)}$ $\in$ $2^S$.

The properties and proofs of dissimilarity measure can be found in Appendix C.

4 Aggregation operators of ELTSs

To maximize the advantages of ELTSs in decision-making, a novel aggregation operator for ELTSs is developed firstly, followed by a weighted aggregation operator considering the importance of ELTSs.

4.1 Aggregation operators

In this section, a novel aggregation operator for ELTSs is developed by utilizing the Dempster’s rule, a couple of whose prominent characteristic are provided.

Definition 5

Let $L_1(e)$ and $L_2(e)$ be two ELEs on LTS S, the aggregation operator denoted by L(e) = $L_1(e) \oplus L_2(e)$ is defined as:

$$\begin{aligned} e^{(A)} = \frac{\sum _{L_1^{(B)}\cap L_2^{(C)}=L^{(A)}}e_1^{(B)}e_2^{(C)}}{1-\Lambda } \end{aligned}$$

(8)

with

$$\begin{aligned} \Lambda =\sum _{L_1^{(B)}\cap L_2^{(C)} = \phi }e_1^{(B)}e_2^{(C)} \end{aligned}$$

(9)

where $L^{(A)}$, $L_1^{(B)}$, and $L_2^{(C)}$ $\in$ $2^S$. Note that $e^{(k)} = 0$ if $L^{(k)} = \phi$.

Definition 6

Let $L_1(e)$, $L_2(e)$,..., $L_n(e)$ be n ELEs on LTS S, the aggregation operator denoted by L(e) = $L_1(e) \oplus L_2(e) \oplus \cdots \oplus L_n(e)$ is defined as:

$$\begin{aligned} e^{(A)} = \frac{\sum _{L_1^{(A_i)}\cap L_2^{(A_j)}\cap \ldots \cap L_n^{(A_k)}=L^{(A)}}e_1^{(A_i)}e_2^{(A_j)}...e_n^{(A_k)}}{1-\Lambda } \end{aligned}$$

(10)

with

$$\begin{aligned} \Lambda =\sum _{L_1^{(A_i)}\cap L_2^{(A_j)}\cap \ldots \cap L_n^{(A_k)}=\phi }e_1^{(A_i)}e_2^{(A_j)}...e_n^{(A_k)} \end{aligned}$$

(11)

where $L^{(A)}$, $L_1^{(A_i)}$, $L_2^{(A_j)}$, and $L_n^{(A_k)}$ $\in$ $2^S$. Note that $e^{(k)} = 0$ if $L^{(k)} = \phi$.

Based on literature Shafer (1976), it is easy to obtain the two properties of the proposed aggregation operator, namely, the commutative law and the associative law, which are expressed as $L_1(e)\oplus L_2(e) = L_2(e)\oplus L_1(e)$ and $(L_1(e)\oplus L_2(e))\oplus L_3(e) = L_1(e)\oplus (L_2(e)\oplus L_3(e))$. In addition, specifically, when ELTSs degenerates to PLTSs, according to Defs. 5 and 6, we can get the following definitions.

Definition 7

If two given ELEs $L_1(e)$ and $L_2(e)$ on LTS S degrade to PLEs $L_1(p)$ and $L_2(p)$, the aggregation operator denoted by L(p) = $L_1(p) \oplus L_2(p)$ is defined as:

$$\begin{aligned} p^{(A)} = \frac{p_1^{(A)}\times p_2^{(A)}}{1-\sum _{L_1^{(B)}\cap L_2^{(C)} = \phi }p_1^{(B)}p_2^{(C)}} \end{aligned}$$

(12)

where $L_1^{(B)}$ and $L_2^{(C)}$ $\in$ S.

Definition 8

If n given ELEs $L_1(e)$, $L_2(e)$,..., $L_n(e)$ on LTS S degrade to PLEs $L_1(p)$, $L_2(p)$,..., $L_n(p)$, the aggregation operator denoted by L(p) = $L_1(p) \oplus L_2(p) \oplus \cdots \oplus L_n(p)$ is defined as:

$$\begin{aligned} p^{(A)} = \frac{\prod _{i=1}^np_i^{(A)}}{1-\sum _{L_1^{(A_i)}\cap L_2^{(A_j)}\cap \ldots \cap L_n^{(A_k)}=\phi }p_1^{(A_i)}p_2^{(A_j)}...p_n^{(A_k)}} \end{aligned}$$

(13)

where $L_1^{(A_i)}$, $L_2^{(A_j)}$, and $L_n^{(A_k)}$ $\in$ S.

4.2 Weighted aggregation operators considering reliability

Due to the limited nature of cognition and experience, subjective judgments derived from human beings are often inaccurate, incomplete and unreliable. In what follows, we first define the reliability measure of ELEs and propose the weighted aggregation operators based on it.

4.2.1 The reliability of ELEs

Two aspects are taken into account in the definition of reliability of ELEs, i.e., certainty degree and compatibility that are called inner and outer reliability, respectively, in this paper.

In our previous related studies Xia et al. (2018); Fei and Wang (2022), the evidential reliability indicator (ERI) were defined to measure the reliability of the belief functions. In this work, based on which, the reliability of ELEs will be introduced. The inner reliability of ELEs will be proposed firstly based on the defined entropy function of ELEs in Sect. 3.1 as follows.

Definition 9

(Positive ideal ELE) Let $S =\{s_\alpha \vert \alpha =-\tau ,...,-1,0,1,...,\tau \}$ be a LTS, the positive ideal ELE $L^*(e)$ is one of ELEs on S that satisfies:

$$\begin{aligned} L^*(e) = \mathop {\mathrm {arg\,min}}\limits _{L}(H(L(e))) \end{aligned}$$

(14)

where $H(\cdot )$ is the entropy function of ELEs, and min means $L^*(e)$ is the ELE with minimum entropy on S. Following, the definition of negative ideal ELE $L_*(e)$ can be given below.

Definition 10

(Negative ideal ELE) Suppose a LTS $S =\{s_\alpha \vert \alpha =-\tau ,...,-1,0,1,...,\tau \}$, the negative ideal ELE $L_*(e)$ is one of ELEs on S that satisfies:

$$\begin{aligned} L_*(e) = \mathop {\mathrm {arg\,max}}\limits _{L}(H(L(e))) \end{aligned}$$

(15)

where max denotes $L_*(e)$ is one of ELEs on S with the maximum entropy.

Motivated by TOPSIS method Hwang and Yoon (1981), the inner reliability of ELEs, i.e., closeness index, is given by the following definition.

Definition 11

Suppose an ELE L(e) on LTS S, the inner reliability of ELE L(e) can be calculated as

$$\begin{aligned} \begin{aligned} \mathcal {I}(L(e)) = \frac{D^-(L(e))}{D^-(L(e)) + D^+(L(e))} = \frac{d(L(e),L_*(e))}{d(L(e),L_*(e)) + d(L(e),L^*(e))} \end{aligned} \end{aligned}$$

(16)

where $D^-(L(e))$ ($D^+(L(e))$) is the dissimilarity measure between L(e) and the negative ideal ELE $L_*(e)$ (positive ideal ELE $L^*(e)$), which is defined in Sect. 3.2. It is obvious that for a given ELE, the smaller the similarity $D^+(L(e))$, the closer it is to $L^*(e)$, which means the higher the reliability. And the smaller the dissimilarity $D^-(L(e))$, the closer it is to $L_*(e)$, which means the lower the reliability.

Note that $\mathcal {I}(L(e)) = 0$ iff $L(e) = L_*(e)$, and $\mathcal {I}(L(e)) = 1$ iff $L(e) = L^*(e)$, so we have $\mathcal {I}(\cdot ) \in [0,1]$ for all ELEs.

The inner reliability of ELEs has been defined above, then an interesting issue should be discussed, that is, how to get the positive and negative ideal ELEs. By Def. 9, the positive ideal ELE on LTS S is the one with minimum entropy. Based on Def. 3, the entropy of ELE L(e) would be the minimum when it satisfies $L(e)=\{s_\varpi (1)\}$, where $s_\varpi \in S$. Now we are interested in how to determine the special $s_\varpi$. The following definition is presented to obtain $s_\varpi$ that allows L(e) to achieve the minimum entropy.

Definition 12

Let L(e) be an ELE on LTS S, the single element $s_\varpi$ that generates the positive ideal ELE $L^*(e)$ is defined as

$$\begin{aligned} s_\varpi = \mathop {\mathrm {arg\,max}}\limits _{L^{(A)}}(ELE\_P(L^{(A)})), \forall L^{(A)}\subseteq S \end{aligned}$$

(17)

where $ELE\_P(\cdot )$ is the pignistic probability transform (PPT) function defined in Def. 16. Note that if there are two or multiple elements in S with the same pignistic probability, then $s_\varpi$ could be any of them.

According to Def. 10, the negative ideal ELE on LTS S is the one with maximum entropy. Based on the maximum entropy property proved in Def. 3, for ELE L(e) on S, the maximum entropy could be achieved when all the mass of belief is assigned to LTS S, i.e., $L(e)=\{S(1)\}$, so the negative ideal ELE can be determined as $L_*(e) = \{S(1)\}$.

With regard to a given ELE, the outer reliability of it takes into account its compatibility with other ELEs. In other words, the outer reliability of an ELE is denoted by the conflict between distinct ELEs to be aggregated, which is formalized as follows.

Definition 13

Let $L_1(e)$, $L_2(e)$,..., $L_n(e)$ be n ELEs on LTS S, the support degree of ELE $L_i(e)$ can be calculated as

$$\begin{aligned} Sup(L_i(e)) = \sum _{j=1,j\ne i}Sim(L_i(e),L_j(e)) \end{aligned}$$

(18)

where $Sim(L_i(e),L_j(e)) = 1- d(L_i(e),L_j(e))$, and d is the dissimilarity measure defined in Sec. 3.2. Following, the credibility degree of ELE $L_i(e)$ can be obtained as

$$\begin{aligned} Crd(L_i(e)) = \frac{Sup(L_i(e))}{\sum _{i=1}^nSup(L_i(e))} \end{aligned}$$

(19)

based on which, the outer reliability of ELE $L_i(e)$ can be calculated as

$$\begin{aligned} \mathcal {O}(L_i(e)) = \frac{Crd(L_i(e))- \min \limits _{1\le j\le n}Crd(L_j(e))}{\max \limits _{1\le j\le n}Crd(L_j(e))-\min \limits _{1\le j\le n}Crd(L_j(e))} \end{aligned}$$

(20)

Consequently, the comprehensive reliability of ELEs is defined by using the following equation

Definition 14

Let $L_1(e)$, $L_2(e)$,..., $L_n(e)$ be n ELEs on LTS S, the reliability of ELE $L_i(e)$ can be obtained as

$$\begin{aligned} \mathcal {R}(L_i(e)) = \beta \mathcal {I}(L_i(e)) + (1 - \beta ) \mathcal {O}(L_i(e)) \end{aligned}$$

(21)

in which $\beta$ is taken as a tuning parameter.

4.2.2 Weighted aggregation operation

In the last section, we developed the definition of ELE’s reliability from two aspects: the uncertainty of ELE itself and the compatibility among ELEs. The obtained reliability index can be regarded as the weight of ELE, based on which the weighted aggregation operation is defined as follows.

Definition 15

Let $L_1(e)$, $L_2(e)$,..., $L_n(e)$ be n ELEs on LTS S, the weighted aggregation operator considering reliability can be defined as:

$$\begin{aligned} L(e) = L_1(e) \widetilde{\oplus } L_2(e) \widetilde{\oplus } \cdots \widetilde{\oplus } L_n(e) = \underbrace{\widetilde{L}(e)\oplus \cdots \oplus \widetilde{L}(e)}_{n} \end{aligned}$$

(22)

where $\oplus$ is the aggregation operation defined in Def. 6, and $\widetilde{L}(e)$ is the arithmetic mean value of $L_1(e)$, $L_2(e)$,..., $L_n(e)$ that can be calculated as:

$$ L(e) = \left\{ {L^{{(A)}} \left( {\sum\limits_{{l = 1}}^{{\# 2^{S} }} {w_{l} } e_{l}^{{(A)}} } \right)} \right\},\forall L^{{(A)}} \subseteq S $$

(23)

where $w_l$ is the weight of $L_l(e)$, which can be calculated by $w_l = \mathcal {R}(L_l(e))/\sum _{l=1}^n\mathcal {R}(L_l(e))$.

An example is given in Example 1 of Appendix A.

5 Expectation function of ELTSs

In the context of linguistic terms, it is important enhance the computational power and scope among ELTSs Wu et al. (2018), so we define the expected function of ELTSs, which can map the ELEs to the unit interval [0, 1].

Definition 16

Let $L(e) = \{L^{(k)},(e^{(k)})\vert L^{(k)} \in 2^{S}, k = 1,2,..., \#2^{S}\}$ be an ELE on LTS $S =\{s_\alpha \vert \alpha = -\tau ,...,-1,0,1,...,\tau \}$, the PPT function of L(e) is given as

$$\begin{aligned} ELE\_P(L^{(A)}) = \sum _{L^{(B)}\subseteq S}\frac{\vert L^{(A)}\cap L^{(B)}\vert }{\vert L^{(B)}\vert }\frac{e^{(B)}}{1-e^{(\phi )}}, \forall L^{(A)} \in S \end{aligned}$$

(24)

where $\vert L^{(A)}\vert$ is the cardinality of element $L^{(A)}$.

Consequently, the expected value function of L(e) is defined as

$$ E(L(e)) = \sum\limits_{{l = 1}}^{{\# S}} {\left( {\frac{{\alpha ^{{(l)}} + \tau }}{{2\tau }}ELE\_P(L^{{(l)}} )} \right)} $$

(25)

where $\alpha ^{(l)}$ means the subscript of $L^{(l)}$. For instance, $\alpha ^{(1)} = -\tau$ corresponds to the linguistic term $L^{(1)} = s_{-\tau }$.

The relevant remark can be found in Remark 2 of Appendix E. A few properties can be found in Appendix D.

The presented expectation function could be employed as a scoring function to compare different ELEs. With regard to two ELEs $L_1(e)$ and $L_2(e)$, if $E(L_1(e)) > E(L_2(e))$, then $L_1(e)$ is superior to $L_2(e)$, denoted by $L_1(e) \succ L_2(e)$; if $E(L_1(e)) < E(L_2(e))$, then $L_1(e)$ is inferior to $L_2(e)$, denoted by $L_1(e) \prec L_2(e)$; However, if $E(L_1(e)) = E(L_2(e))$, then in which case, they cannot be distinguished. To address this issue, the deviation degree of an ELE is defined as follows.

Definition 17

Let $L(e) = \{L^{(k)},(e^{(k)})\vert L^{(k)} \in 2^{S}, k = 1,2,..., \#2^{S}\}$ be an ELE on LTS S, the variance value function of L(e) can be calculated as

$$\begin{aligned} \sigma (L(e)) = \sqrt{\sum _{l=1}^{\#S}[\frac{\alpha ^{(l)}+\tau }{2\tau }-E(L(e))]^2ELE\_P(L^{(l)})} \end{aligned}$$

(26)

where $\alpha ^{(l)}$ represents the subscript of $L^{(l)}$, $E(\cdot )$ is L(e)’s expectation function. $ELE\_P(\cdot )$ is the pignistic probability function of L(e).

The relevant remark can be found in Remark 3 of Appendix E.

For two ELEs $L_1(e)$ and $L_2(e)$ with $E(L_1(e)) = E(L_2(e))$, if $\sigma (L_1(e)) > \sigma (L_2(e))$, then $L_1(e) \prec L_2(e)$; if $\sigma (L_1(e)) < \sigma (L_2(e))$, then $L_1(e) \succ L_2(e)$; and if $\sigma (L_1(e)) = \sigma (L_2(e))$, then $L_1(e)$ is identical with $L_2(e)$, denoted by $L_1(e) \sim L_2(e)$;

An example is given in Example 3 of Appendix A.

6 An evidential linguistic ELECTRE method

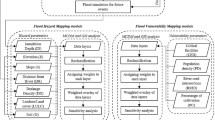
The proposed methodology employs ELTS in conjunction with the ELECTRE method to select the optimal alternative under multiple criteria. Firstly, we describe the MCDM problem in an evidential linguistic context, then put forward the approach to determine the decision matrix, followed by the method to obtain the criteria weight. Finally, we provide the concrete steps of the evidential linguistic ELECTRE method. The flowchart is shown in Fig. 2.

Fig. 2

The flowchart of the evidential linguistic ELECTRE method

6.1 Introduction of the evidential linguistic ELECTRE issue

An MCDM issue can be described as containing m alternative $A=\{a_1,a_2,...,a_m\}$, n criteria $C=\{c_1,c_2,...,c_n\}$ with the weight vector $W=(w_1,w_2,...,w_n)^T$, and q experts can be represented as $\mathcal {E}=\{\epsilon _1,\varepsilon _2,...,\epsilon _q\}$ in a group decision issue. The evaluation of expert $\epsilon _\kappa$ of alternative $a_i$ under criterion $c_j$ is expressed as $x_{ij}^\kappa$ that could also be denoted as ELE $L_{ij}^\kappa (e)$ in evidential linguistic environment. Therefore, the evaluation values provided by DMs can be expressed by evidential linguistic decision matrices as $E^\kappa = (L_{ij}^\kappa (e))_{m\times n}$, $\{i=1,2,...,m;j=1,2,...,n;\kappa =1,2,...,q\}$. Further, a group evidential linguistic individual decision matrix of DM $\epsilon _\kappa$ can be determined as

$$\begin{aligned} \textbf{E}^\kappa = [L_{ij}^\kappa (e)]_{m\times n} = \left[ \begin{array}{cccc} L_{11}^\kappa (e)&{} L_{12}^\kappa (e) &{} \cdots &{} L_{1n}^\kappa (e)\\ L_{21}^\kappa (e)&{} L_{22}^\kappa (e) &{} \cdots &{} L_{2n}^\kappa (e)\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ L_{m1}^\kappa (e)&{} L_{m2}^\kappa (e) &{} \cdots &{} L_{mn}^\kappa (e)\\ \end{array}\right] \end{aligned}$$

(27)

where $L_{ij}^\kappa (e)=\{L_{ij}^{\kappa (k)}(e_{ij}^{\kappa (k)})\vert L_{ij}^{\kappa (k)}\in 2^S\}$, and S is the specified LTS.

6.2 Determination of the aggregated decision matrix

The evaluation information from expert panel has been prepared. For each alternative, evaluations from diverse DMs should be combined to reflect his overall performance. To achieve it, the weighted aggregation operation proposed in Def. 15 is employed to combine evidential linguistic evaluations of multiple experts.

The evaluation values of alternative $a_i$ with regard to criterion $c_j$ from DMs $\{\epsilon _1,\epsilon _2,...,\epsilon _p\}$ can be aggregated by Eq. (22) as $L_{ij}(e) = L_{ij}^1(e) \widetilde{\oplus } L_{ij}^2(e) \widetilde{\oplus } \cdots \widetilde{\oplus } L_{ij}^p(e)$ (see Sect. 4.2.2 for details). So the aggregated evidential linguistic decision matrix of different experts can be calculated as

$$\begin{aligned} \textbf{E} = [L_{ij}(e)]_{m\times n} = \left[ \begin{array}{cccc} L_{11}(e)&{} L_{12}(e) &{} \cdots &{} L_{1n}(e)\\ L_{21}(e)&{} L_{22}(e) &{} \cdots &{} L_{2n}(e)\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ L_{m1}(e)&{} L_{m2}(e) &{} \cdots &{} L_{mn}(e)\\ \end{array}\right] \end{aligned}$$

(28)

where $L_{ij}(e)=\{L_{ij}^{(k)}(e_{ij}^{(k)})\vert L_{ij}^{(k)}\in 2^S\}$ on LTS S.

The obtained aggregated evidential linguistic decision matrix will be converted to numerical form to get the final decision matrix. The expectation values of evidential linguistic evaluations $L_{ij}(e)$, $\{i=1,2,...,m;j=1,2,...,n\}$ will be got using Def. 16 as $\mathbb {E}_{ij}=E(L_{ij}(e))$. Therefore, the numerical decision matrix of evaluations from expert panel can be determined as

$$\begin{aligned} D = [\mathbb {E}_{ij}]_{m\times n} = \left[ \begin{array}{cccc} \mathbb {E}_{11}&{} \mathbb {E}_{12} &{} \cdots &{} \mathbb {E}_{1n}\\ \mathbb {E}_{21}&{} \mathbb {E}_{22} &{} \cdots &{} \mathbb {E}_{2n}\\ \vdots &{}\vdots &{}\ddots &{}\vdots \\ \mathbb {E}_{m1}&{}\mathbb {E}_{m2} &{} \cdots &{} \mathbb {E}_{mn}\\ \end{array}\right] \end{aligned}$$

(29)

where $\mathbb {E}_{ij}$ is the expectation value of ELE $L_{ij}(e)$ associated with alternative $a_i$ under criterion $c_j$.

6.3 Obtainment of the criteria weight

The criteria weight will be obtained, in this paper, considering two aspects: objectivity and subjectivity. To determine objective weights, the Shannon entropy weight method is employed in conjunction with the obtained matrix D. First, standardize matrix $\mathbb {E}_{ij}$ as

$$\begin{aligned} {\widetilde{\mathbb {E}}}_{ij} = \frac{\mathbb {E}_{ij}}{\sqrt{\sum _{i=1}^m\mathbb {E}_{ij}^2}}, i = 1,2,\ldots ,m, j= 1,2,\ldots , n \end{aligned}$$

(30)

in which ${\widetilde{\mathbb {E}}}_{ij}$ is the standard matrix that needs to be further normalized to apply entropy weight method as

$$\begin{aligned} \xi _{ij} = \frac{ {\widetilde{\mathbb {E}}}_{ij}}{{\sum _{i=1}^m {\widetilde{\mathbb {E}}}_{ij}}}, i = 1,2,\ldots ,m, j= 1,2,\ldots , n \end{aligned}$$

(31)

then the entropy value of each criterion can be calculated as

$$\begin{aligned} \vartheta _j = -\rho \sum _{i=1}^m\xi _{ij}ln(\xi _{ij}) = -\frac{1}{ln(m)}\sum _{i=1}^m\xi _{ij}ln(\xi _{ij}) \end{aligned}$$

(32)

then, the divergence of the intrinsic information associated with $c_j (j = 1, 2,\ldots ,n)$ can be determined as

$$\begin{aligned} \zeta _j = 1 - \vartheta _j \end{aligned}$$

(33)

where $\zeta _j$ indicates the inherent contrast intensity of $c_j$. We have that the larger this value is, the more crucial $c_j$ is. Finally, the objective weight of $c_j$ can be calculated as

$$\begin{aligned} w_j^o = \frac{\zeta _j}{\sum _{j=1}^n\zeta _j} \end{aligned}$$

(34)

From the subjective perspective, the importance weights of different criteria would be provided by DMs in the form of evidential linguistic elements. As a consequence, the subjective weight matrix is expressed by

$$\begin{aligned} W^s = [\underline{L}_{\kappa j}(e)]_{p\times n} = \begin{array}{cccc} \left[ \begin{array}{cccc} \underline{L}_{11}(e)&{} \underline{L}_{12}(e) &{}\cdots &{} \underline{L}_{1n}(e)\\ \underline{L}_{21}(e)&{} \underline{L}_{22}(e) &{}\cdots &{} \underline{L}_{2n}(e)\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \underline{L}_{p1}(e)&{} \underline{L}_{p2}(e) &{}\cdots &{} \underline{L}_{pn}(e)\\ \end{array}\right] \end{array} \end{aligned}$$

(35)

where $\underline{L}_{\kappa j}(e)=\{L_{\kappa j}^{(k)}(e_{\kappa j}^{(k)})\vert L_{\kappa j}^{(k)}\in 2^S\}$ on LTS S.

For a given criterion $c_j$, the evaluation values of p DMs should be combined by Def. 15 as

$$\begin{aligned} \underline{L}_{j}(e) = \widetilde{\oplus }_{\kappa =1}^q\underline{L}_{\kappa j}(e) \end{aligned}$$

(36)

where $\underline{L}_{j}(e)$ is the evidential linguistic representation of $c_j$.

Further, the expectation values of criteria weights represented by ELEs will be calculated based on Def. 16 as

$$\begin{aligned} \underline{\mathbb {E}}_j = E(\underline{L}_{j}(e)) \end{aligned}$$

(37)

The subjective weights of criteria can be determined by normalization as

$$\begin{aligned} w_j^s = \frac{\underline{\mathbb {E}}_j}{\sum _{j=1}^n\underline{\mathbb {E}}_j} \end{aligned}$$

(38)

To describe the subjective preference of DMs and consider the objective characteristics of crtieria, the subjective weight and objective weight are combined to obtain the comprehensive weight of $c_j$ as

$$\begin{aligned} w_j = \frac{\sqrt{w_j^sw_j^o}}{\sum _{j=1}^n\sqrt{w_j^sw_j^o}} \end{aligned}$$

(39)

6.4 Evidential linguistic ELECTRE method

The ELECTRE method is known for the using of “outranking relations” to sort a large body of actions with MCDM problems. Several crucial definitions of ELECTRE I are summarized below Fei et al. (2019).

Definition 18

The preference relation of ELECTRE method is represented by a binary relation $\lhd$, which indicates “not inferior to”. Given two variables $\varphi$ and $\psi$, their relation might be

• (1) $\varphi$ $\lhd$ $\psi$ & $\lnot$($\psi$ $\lhd$ $\varphi$), which means $\varphi$ is completely superior to $\psi$.

• (2) $\psi$ $\lhd$ $\varphi$ & $\lnot$($\varphi$ $\lhd$ $\psi$), which means $\psi$ is completely superior to $\varphi$.

• (3) $\varphi$ $\lhd$ $\psi$ & $\psi$ $\lhd$ $\varphi$, which means $\varphi$ is not different from $\psi$.

• (4) $\lnot$($\varphi$ $\lhd$ $\psi$) & $\lnot$($\psi$ $\lhd$ $\varphi$), which means $\varphi$ and $\psi$ are incompatible.

Definition 19

In ELECTRE method, The relation between $\varphi$ and $\psi$ is mainly reflected by two concepts, namely concordance and discordance, and their interpretation is given below.

• (1) Concordance: if enough criteria support this assertion, $\varphi$ $\lhd$ $\psi$ can be verified.

• (2) Discordance: when (1) is true, none of the few criteria can strongly disagree with $\varphi$ $\lhd$ $\psi$.

In view of the advantages of ELECTRE method in dealing with MCDM problems, in this paper, we extend it to the linguistic context, and the specific steps are manifested below.

Step 1. Normalize the decision matrix $({\widetilde{\mathbb {E}}}_{ij})_{m\times n}$.

Matrix $({\widetilde{\mathbb {E}}}_{ij})_{m\times n}$ has been obtained by Eq. (30).

Step 2. Determine the weighted normalized matrix $({\widetilde{\mathbb {E}}}^w_{ij})_{m\times n}$.

The weighted normalized decision matrix is calculated based on the weights of criteria

$$\begin{aligned} {\widetilde{\mathbb {E}}}^w_{ij} = w_j{\widetilde{\mathbb {E}}}_{ij}, i = 1,2,...,m; j = 1,2,...,n. \end{aligned}$$

(40)

Step 3. Construct concordance and discordance sets.

For alternative pairs $(a_{\mu },a_{\nu })$, the subscript set $J = \{1,2,\ldots ,n\}$ of criteria $\{c_1,c_2,\ldots ,c_n\}$ can be divided into two unintersected subsets $\mathcal {Q}_{\mu \nu }$ and $\mathcal {T}_{\mu \nu }$. $\mathcal {Q}_{\mu \nu }$ is made up of criteria where $a_\mu$ is superior than or equal to $a_\nu$ (i.e., $a_\mu$ S $a_\nu$), which is called concordance set. $\mathcal {T}_{\mu \nu }$ consists of criteria where $a_\mu$ is inferior to $a_\nu$, which is called discordance set. The concordance and discordance sets can be determined as

$$\begin{aligned} \mathcal {Q}_{\mu \nu } = \{j \vert {\widetilde{\mathbb {E}}}^w_{\mu j}\ge {\widetilde{\mathbb {E}}}^w_{\nu j}\} \end{aligned}$$

(41)

$$\begin{aligned} \mathcal {T}_{\mu \nu } = \{j \vert {\widetilde{\mathbb {E}}}^w_{\mu j} < {\widetilde{\mathbb {E}}}^w_{\nu j}\} = J - \mathcal {Q}_{\mu \nu }, \end{aligned}$$

(42)

Step 4. Get concordance and discordance matrices.

Employing the weights of different criteria and constructed concordance set $\mathcal {Q}$, the concordance index can be calculated as $\texttt {c}_{\mu \nu } = \sum _{j\in Q_{\mu \nu }}w_j$ that indicates the importance of $a_\mu$ over $a_\nu$. It is obvious that $\texttt {c}_{\mu \nu }\in [0,1]$, and the larger the $\texttt {c}_{\mu \nu }$, the greater the degree to which $a_\mu$ is superior to $a_\nu$. Consequently, the concordance matrix is determined as

$$\begin{aligned} \mathcal {C} = \begin{array}{cccc} &{} \left[ \begin{array}{cccc} -&{} \texttt {c}_{12} &{}\cdots &{} \texttt {c}_{1m}\\ \texttt {c}_{21}&{} - &{}\cdots &{} \texttt {c}_{2m}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \texttt {c}_{m1}&{} \texttt {c}_{m2} &{}\cdots &{} -\\ \end{array}\right] \end{array} \end{aligned}$$

(43)

Using the weighted normalized matrix ${\widetilde{\mathbb {E}}}^w_{ij}$ and constructed discordance set $\mathcal {T}$, the discordance index can be calculated as $\texttt {d}_{\mu \nu } = \frac{max_{j\in \mathcal {T}_{\mu \nu }}\vert {\widetilde{\mathbb {E}}}_{\mu j}-{\widetilde{\mathbb {E}}}_{\nu j}\vert }{max_{j\in J}\vert {\widetilde{\mathbb {E}}}_{\mu j}-{\widetilde{\mathbb {E}}}_{\nu j}\vert }$ that indicates the degree to which $a_\mu$ is inferior to $a_\nu$. We can easily get $\texttt {d}_{\mu \nu }\in [0,1]$, and the greater $\texttt {d}_{\mu \nu }$ is, the larger the degree to which alternative $a_\mu$ is inferior to $a_\nu$. Therefore, the discordance matrix is determined as

$$\begin{aligned} \mathcal {D} = \begin{array}{cccc} &{} \left[ \begin{array}{cccc} -&{} \texttt {d}_{12} &{}\cdots &{} \texttt {d}_{1m}\\ \texttt {d}_{21}&{} - &{}\cdots &{} \texttt {d}_{2m}\\ \vdots &{} \vdots &{} \ddots &{} \vdots \\ \texttt {d}_{m1}&{} \texttt {d}_{m2} &{}\cdots &{} -\\ \end{array}\right] \end{array} \end{aligned}$$

(44)

The conclusion can be drawn that information is complementary between $\mathcal {C}$ and $\mathcal {D}$. Specifically, the comparison between the criteria is denoted by $\mathcal {C}$, and the comparison between evaluation values is manifested by $\mathcal {D}$.

Step 5. Construct the concordance and discordance dominance matrices.

We use $\mathcal {C}^{d}$ to represent the concordance dominance matrix that is defined as a Boolean matrix. The dominance of alternative $a_\mu$ over $a_\nu$ can be denoted by $\mathcal {C}^{d}_{\mu \nu }$ and calculated as

$$\begin{aligned} \mathcal {C}^{d}_{\mu \nu } = {\left\{ \begin{array}{ll} 0&{} {\texttt {c}_{\mu \nu }<\alpha }\\ 1&{} {\texttt {c}_{\mu \nu }\ge \alpha } \end{array}\right. } \end{aligned}$$

(45)

in which $\alpha$ is a threshold defined as $\alpha = \sum _{\mu =1}^n\sum _{\nu =1}^n\texttt {c}_{\mu \nu }/n(n-1)$. $\mathcal {C}^{d}_{\mu \nu } = 1$ indicates alternative $a_\mu$ dominating $a_{\nu }$.

The discordance dominance matrix $\mathcal {D}^{d}$ is also a Boolean matrix, which is calculated as

$$\begin{aligned} \mathcal {D}^{d}_{\mu \nu } = {\left\{ \begin{array}{ll} 0&{} {\texttt {d}_{\mu \nu }>\beta }\\ 1&{} {\texttt {d}_{\mu \nu }\le \beta } \end{array}\right. } \end{aligned}$$

(46)

in which $\beta$ is a threshold that indicates the discordance level, which is calculated by $\beta = \sum _{\mu =1}^n\sum _{\nu =1}^n\texttt {d}_{\mu \nu }/n(n-1)$. $\mathcal {D}^{d}_{\mu \nu } = 1$ demonstrates alternative $a_\mu$ dominating $a_{\nu }$.

Step 6. Obtain the comprehensive dominance matrix.

The comprehensive dominance matrix $\Phi$ could be calculated by peer to peer multiplication of the elements in matrices $\mathcal {C}^{d}$ and $\mathcal {D}^{d}$ as

$$\begin{aligned} \Phi = \mathcal {C}^{d} * \mathcal {D}^{d} \end{aligned}$$

(47)

in $\Phi$, element $\Phi _{\mu \nu }$ can be computed as $\Phi _{\mu \nu } = \mathcal {C}^{d}_{\mu \nu } \mathcal {D}^{d}_{\mu \nu }$.

Step 7. Identify the optimal compromise alternative.

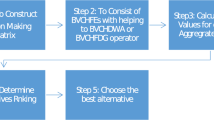
The outranking relation would be used to determined as small as possible a subset of alternatives as the optimal solutions. An illustrative graph $G = (V, E)$ could be constructed to manifest the outranking relation among alternatives, in which V stands for the collection of alternatives and E is the collection of their relation. There is an arc between $v_\mu$ and $v_\nu$ if either $a_\mu$ is superior to $a_{\nu }$ or $a_\mu$ is indifferent to $a_\nu$. Alternative $a_\mu$ is identified as preferred to $a_{\nu }$ if an arc exists between $v_\mu$ and $v_\nu$ and the arrow goes from $v_\mu$ to $v_\nu$ (i.e., $\Phi _{\mu \nu } = 1$). The relation is incomparable between $a_\mu$ and $a_\nu$ if no arc exists between $a_\mu$ outranks $a_{\nu }$ (i.e., $\Phi _{\mu \nu } = 0$). $a_\mu$ and $a_\nu$ are indifferent if an arc exists between $v_\mu$ and $v_\nu$ and two arrows exist in both directions (i.e., $\Phi _{\mu \nu } = 1$ and $\Phi _{\mu \nu } = 1$). The outranking relation could be expressed illustratively by a graph, where the binary relations $(i.e.,>, >^{-1}, \approx , ?)$ is shown in Fig. 3Fei et al. (2019),[58].

Fig. 3

The graphical expression of the binary relations (>,$>^{-1}$,$\approx$,?)

7 Emergency shelter site selection using the evidential linguistic ELECTRE method

An emergency shelter is a facility that provides various services, such as medical assistance and food supply, to people affected by natural disasters. This can effectively alleviate the casualties caused by such events Ma et al. (2019). In this section, the proposed evidential linguistic ELECTRE method is further demonstrated by addressing an emergency shelter site selection problem. In what follows, both sensitivity analysis and comparative analysis are conducted to emphasize the validity of the evidential linguistic ELECTRE approach.

7.1 Case description

The site selection of emergency shelters is an important part of emergency management Kılcı et al. (2015). A reasonable decision regarding the site selection of emergency shelters contributes to efficiently dealing with emergencies, and it helps in reducing losses and hazards caused by secondary disasters Wei et al. (2020). In recent years, with the continuous attention of the national government to emergency management, scholars have proposed new theoretical methods Ma et al. (2019). However, in the context of practical application, more complexity and uncertainty are inevitably involved Wu et al. (2018). In the case of inaccurate and fuzzy information, people tend to use linguistic evaluation rather than precise numerical methods Pang et al. (2016). Therefore, emergency shelter site selection can be subdivided into the MCDM domain Liu (2022).

In this part, the evidential linguistic approach is employed to the problem of emergency shelter site selection. The five main elements are extracted and processed to measure the performance of the emergency shelter, which constitute the criteria set $C=\{c_1, c_2, c_3, c_4, c_5\}$ of the decision. The meaning of each element is explained as follows. Safety $(c_1)$ is the most basic and important principle in the selection of the emergency shelter, which is to ensure the safety of the shelter, so as to avoid secondary harm to the refugees Wei et al. (2020); Liu (2022). Accessibility $(c_2)$ reflects the efficiency of emergency shelters to communicate with the outside world, including the distance to the main road, the distance to the transportation hub, the distance to the potential landing point and so on Liu (2022). Equilibrium $(c_3)$ means that the shelters should be distributed evenly, that is, the spatial distribution of the shelters should match the population density Hosseini et al. (2022). Effectiveness $(c_4)$ requires that the shelter needs to be of a certain size, and the number of refugees cannot exceed the capacity of the shelter Liu et al. (2022); Zhang et al. (2019). Environment $(c_5)$ directly affects the health of refugees, so necessary supplies such as clean air, water, and medical resources should be guaranteed Çetinkaya et al. (2021); Şenik and Uzun (2021).

Five emergency shelter sites ($A = \{a_1,a_2,a_3,a_4,a_5\}$) will participate in the evaluation according to the above criteria. To assess the sites’ performance effectively, the opinions of experts from different emergency departments are collected. The expert group is expressed as $\mathcal {E}=\{\epsilon _1,\varepsilon _2,\varepsilon _3,\varepsilon _4,\varepsilon _5\}$. The evaluation information of sites from experts is represented by means of ELEs based on the LTS S = $\{s_{-3}$ = very bad, $s_{-2}$ = bad, $s_{-1}$ = somewhat bad, $s_0$ = medium, $s_1$ = somewhat good, $s_2$ = good, $s_3$ = very good$\}$. The evaluation results of sites are shown in Table 1.

Table 1 Evaluation results of sites from experts based on ELEs

7.2 Evidential linguistic ELECTRE method for the case

In this section, we will demonstrate the decision-making process step by step. Step 1. For each site, evaluations from different experts are shown in Table 1. Step 2. The proposed weighted aggregation operations is used to combine the evaluations of each expert on the same site with regard to different criteria. Based on the definitions in Sect. 4.2, the aggregated evaluations from different experts can be calculated, and are shown in Table 2. Step 3. Based on the obtained aggregated decision matrix, the expectation values of evidential linguistic evaluations will be calculated using Def. 16 to determine the numerical decision matrix of evaluations.

$$\begin{aligned} D = \begin{array}{cccc} \left[ \begin{array}{ccccc} 0.5640&{} 0.5653 &{}0.7964&{} 0.5324&{} 0.8385\\ 0.3333&{} 0.8322&{} 0.3472&{} 0.6667 &{}0.9166\\ 0.5000&{} 0.8333 &{} 0.7551&{} 0.1690 &{}0.1708\\ 0.0012&{} 0.1752&{} 0.4759 &{} 0.0876 &{} 0.2691\\ 0.8266&{} 0.8825&{} 0.9635 &{} 0.9951&{} 0.9373\\ \end{array}\right] \end{array} \end{aligned}$$

(48)

Table 2 Aggregated evaluation results of sites with regard to different criteria

Step 4. The weights of criteria will be computed based on the definitions in Sect. 6.3 from two aspects, i.e., objective and subjective. To determine objective weights, the Shannon entropy weight method is employed based on Eqs. (30–34), and the objective weights of criteria $\{c_1\ldots c_5\}$ are $w_1^o = 0.3166$, $w_2^o = 0.1196$, $w_3^o = 0.0699$, $w_4^o = 0.2984$, and $w_5^o = 0.1955$. To determine subjective weights, the subjective weight matrix $W^s$ is provided by DMs in Eq. (49). Based on Eqs. (36–38), the subjective weights of criteria can be obtained as $w_1^j = 0.2521$, $w_2^j = 0.2076$, $w_3^j = 0.1854$, $w_4^j = 0.1650$, and $w_5^j = 0.1899$. The comprehensive weight is got using Eq. (39) as $w_1 = 0.2917$, $w_2 = 0.1627$, $w_3 = 0.1175$, $w_4 = 0.2291$, and $w_5 = 0.1989$.

$$\begin{aligned} W^s = \begin{array}{cccc} \left[ \begin{array}{lllll} {\{s_1s_2(1)\}}&{} {\{s_1s_2(1)\}} &{}{\{s_0(1)\}}&{} {\{s_0s_1s_2(1)\}}&{} {\{s_1(1)\}}\\ \{\begin{array}{l}s_1(0.9),s_2(0.1)\end{array}\}&\{\begin{array}{l}s_{0}(0.1), s_{1} (0.2), s_{0}s_{1} (0.7)\end{array}\}&{} \{\begin{array}{l}s_{-1} (0.2), s_{0} (0.1), s_{-1}s_{0} (0.7) \end{array}\}&{} {\{s_0(1)\}} &{}{\{s_0s_1(1)\}}\\ \{\begin{array}{l}s_1 (0.4), s_2 (0.6)\end{array}\}&\{\begin{array}{l}s_{0} (0.8), s_{1} (0.2)\end{array}\} &{} \{\begin{array}{l}s_{-1} (0.4), s_0 (0.6) \end{array}\}&{} \{s_{-1}s_{0}(1)\} &{}\{s_0s_1(1)\}\\ \{s_{1}(1)\}&{} \{s_{0}(1)\}&{} \{\begin{array}{l}s_{-1}(0.8),s_{0}(0.2)\end{array}\} &{} \{s_{-1}s_{0}(1)\} &{} \{\begin{array}{l}s_{0} (0.8), s_{1} (0.2)\end{array}\}\\ \{s_{0}(1)\}&{}\{s_{1}(1)\}&{} \{\begin{array}{l}s_{-1} (0.2), s_{0} (0.8)\end{array}\} &{} \{s_{-2}s_{-1}(1)\}&{} \{\begin{array}{l} s_{-1} (0.4), s_{0} (0.6)\end{array}\}\\ \end{array}\right] \end{array} \end{aligned}$$

(49)

Step 5. The evidential linguistic ELECTRE method can be employed to determine the ranking of the alternatives. First, the normalized decision matrix should be calculated by matrix D by Eq. (30) as

$$\begin{aligned} {\widetilde{\mathbb {E}}} = \begin{array}{cccc} \left[ \begin{array}{ccccc} 0.4832 &{} 0.3564 &{} 0.5057 &{} 0.4020 &{} 0.5279\\ 0.2855 &{} 0.5247 &{} 0.2205 &{} 0.5033 &{} 0.5770\\ 0.4284 &{} 0.5253 &{} 0.4795 &{} 0.1276 &{} 0.1075\\ 0.0010 &{} 0.1105 &{} 0.3022 &{} 0.0661 &{} 0.1694\\ 0.7082 &{} 0.5564 &{} 0.6118 &{} 0.7513 &{} 0.5901\\ \end{array}\right] \end{array} \end{aligned}$$

(50)

Second, the weighted normalized matrix can be determined by Eq. (40) as

$$\begin{aligned} {\widetilde{\mathbb {E}}_w} = \begin{array}{cccc} \left[ \begin{array}{ccccc} 0.1409 &{} 0.0580 &{} 0.0594 &{} 0.0921 &{} 0.1050\\ 0.0833 &{} 0.0854 &{} 0.0259 &{} 0.1153 &{} 0.1148\\ 0.1250 &{} 0.0855 &{} 0.0563 &{} 0.0292 &{} 0.0214\\ 0.0003 &{} 0.0180 &{} 0.0355 &{} 0.0151 &{} 0.0337\\ 0.2066 &{} 0.0905 &{} 0.0719 &{} 0.1721 &{} 0.1174\\ \end{array}\right] \end{array} \end{aligned}$$

(51)

Third, the concordance and discordance sets is got by means of Eqs. (41 and 42), and the outputs are manifested in Tables 3 and 4.

Table 3 The concordance set

Table 4 The discordance set

Fourth, the concordance and discordance matrices is got by means of Eqs. (43 and 44), and the outputs are manifested in Tables 5 and 6.

Table 5 The concordance matrix

Table 6 The discordance matrix

Fifth, the concordance and discordance dominance matrices can be constructed based on Eqs. (45 and 46). Assume that the threshold $\alpha$ and $\beta$ of concordance and discordance indexes are 0.5 and 0.5, respectively (sensitivity analysis of the threshold will be given below). The results are manifested in Tables 7 and 8.

Table 7 Boolean matrix B based on the minimum concordance level

Table 8 Boolean matrix H based on the minimum discordance level

Sixth, the comprehensive dominance matrix can be determined by Eq. (47) as manifested in Table 9.

Table 9 The global matrix Z

Finally, in Fig. 4 we give the decision graph, and based on which the alternatives are ranked. Some conclusions about the relationship between $\{a_1, \ldots ,a_5\}$ can be obtained according to Fig. 4. $a_5$ is preferred to other alternatives, so $a_5$ is identified as the emergency shelter best site. $a_4$ is worse than all the sites, so it is identified as the worst. $a_1$ is preferred to $a_3$. $a_1$ is incompatible with $a_2$. $a_2$ is incompatible with $a_3$.

Fig. 4

The decision graph for the case study of emergency shelter site selection

7.3 Sensitivity analysis

In this section, the sensitivity analysis of the proposed method is performed using two experiments.

To demonstrate the sensitivity of parameters $\alpha$ (threshold of concordance index) and $\beta$ (threshold of discordance index) to the selection result, a few tests are conducted on the above performance selection problem of emergency shelter sites. In the experiment, we take all possible values of parameters $\alpha$ and $\beta$ (step size 0.2) to observe the change of the selection result. The output consists of three items: the best site, the worst site, and other relations (Preference only), which are given in Table 10.

Table 10 Results of the first experiment in the sensitivity analysis

Some conclusions and analysis from Table 10 are as follows:

• (1) During the whole experiment, regardless of the values of $\alpha$ and $\beta$, the optimal alternative is always $a_5$.

• (2) Except when $\alpha$ reaches the maximum value of 1, the worst alternative is $a_4$.

• (3) Except in a few cases where the relation cannot be determined, $a_3$ is always better than $a_2$ and $a_1$.

• (4) In several cases where the relation can be determined, $a_2$ is superior to $a_3$.

From the above findings, it can be concluded that for different parameters $\alpha$ and $\beta$, the overall ranking result is relatively stable, but there are some fluctuations simultaneously. ELECTRE is a flexible ranking method by using outranking relations, where thresholds $\alpha$ and $\beta$ can be considered as parameters to reflect the attitude of DMs. For threshold of concordance index $\alpha$, the smaller $\alpha$ is, the lower the requirement of the DM for concordance is, that is, the more optimistic the DM is, and vice versa. For threshold of discordance index $\beta$, the larger $\beta$ is, the lower the requirement of the DM for concordance is, that is, the more optimistic the DM is, and vice versa.

Additionally, it is crucial to analyze how changes in attribute weights impact decision outcomes Ghorui et al. (2023); Bitarafan et al. (2023); Puška et al. (2023). For this purpose, we design six scenarios, each corresponding to six different configurations of attribute weights, to observe their effects on decision results. As shown in Table 11, under different weight distributions, the final decision outcomes exhibit similarities. Specifically, the results of Scenarios 1, 2, 4, and 6 are consistent with the conclusions of our study. Notably, Scenario 3, besides validating our conclusions, further reveals that when the weight of accessibility is higher, $a_1$ has a higher priority compared to $a_2$. Similarly, Scenario 5, while confirming the research conclusions, also indicates that when the weight of effectiveness increases, $a_2$ becomes more preferred than $a_3$. Through this series of sensitivity analyses, we can clearly see that the impact of changes in attribute weights on the ranking of options is minimal.

Table 11 Results of the second experiment in the sensitivity analysis

7.4 Comparison and discussion

In this section, we will compare the method proposed in this paper with the existing methods from two aspects, namely information expression and decision-making process, respectively. With regard to decision/assessment information representation in a linguistic context, various extended forms of LTS Rodriguez et al. (2011); Wang et al. (2014); Chen et al. (2016); Pang et al. (2016); Gou et al. (2017) have been developed. These extensions each have their own unique characteristics. By examining the sequence of their development, we can discern a gradual process of improvement. To compare these methods, we conduct an analysis from the perspectives of syntactic form, semantic comprehension, strengths, and weaknesses. The comparison results are presented in Table 12.

Table 12 Comparison of different LTS expansion forms to emergency shelter site selection

As shown in Table 12, HFLTS was proposed to solve MCDM problems in uncertain linguistic environment based on hesitant fuzzy sets Rodriguez et al. (2011). As a direct extension, IVHFLTS was developed by Wang et al. Wang et al. (2014). However, the methods on account of hesitant fuzzy sets treats the weight of criteria in the decision as equal, which is obviously inconsistent with the reality. To address the above issue, probabilistic linguistic sets have been proposed, starting with PHFLTS Chen et al. (2016), which includes the proportional information of each generalized linguistic term. Followed by PLTS Pang et al. (2016) and DHHFLTS Gou et al. (2017), which can express complex linguistic terms more accurately, but their common shortcomings are that they cannot express multi-subset linguistic information, which is extremely important in uncertain MCDM problems. To overcome such limitations, the concept of ELTS is introduced in this paper, and then an evidential linguistic ELECTRE approach is proposed.

For decision methods, we compare ELECTRE method used in this paper with TOPSIS method Hwang and Yoon (1981) and VIKOR method Shen and Wang (2018), which are well-known in MCDM field. Because they are utility value-based ranking methods, the normalized decision matrix in Eq. (50) and comprehensive weight w serve as the basis for subsequent decisions. The ranking results from diverse approaches are provided in Table 13. We can discover that TOPSIS and VIKOR methods get the same ranking result, which is somewhat distinguish from our method. The main difference lies in the ranking of $a_2$, which led to the three possible ranking results. However, for the determination of the best and worst alternatives, the conclusions of the three methods are consistent.

We further emphasize the advantage of the approach proposed in this paper, in that it is not limited to giving a simple ranking of alternatives, but rather reveals the outranking relation between them, i.e., preference, indifference, or incomparability. This can provide more valuable information, which is critical for analyzing the interrelationships between alternatives.

Table 13 Results from different ranking methods

8 Conclusions and future work

This study is dedicated to the proposing and developing of an innovative methodology: evidential linguistic term sets. The application of LTSs to MCDM problems has gone through a process from considering simplicity to including complexity, for example, from HFLTS to PHFLTS to PLTS. Although a large number of excellent works have been presented to handle the uncertainty of the decision-making environment, they are far from being sufficient conditions for the objective decision of DMs. For example, HFLTS considers that the criteria weights are equal, and PLTS assigns unit belief to each LTS. Even PHFLTS can only partially express the uncertainty of DMs. In this paper, by introducing the concept of evidential LTS, the opinion of DMs is characterized by the power set of LTS, which is a philosophical advance of uncertain MCDM in the linguistic environment. We axiomatize several measures of ELTSs, such as uncertainty measure, dissimilarity measure, and expectation function. The aggregation operations for ELTSs are also developed and strengthened by taking into account the reliability.

On account of the above theoretical basis, we propose a MCDM approach in an evidential linguistic environment with the ELECTRE method. The advantages of this method can be summarized as follows: (1) the opinions of the DMs can be more easily expressed correctly, as it is compatible with greater uncertainty, (2) the (weighted) aggregation operators among ELEs are put forward based on Dempster’s rule, which implies its function as an uncertain inference tool, (3) the ELECTRE method is well known for analyzing the outranking relation between alternatives so that more valuable information can be revealed. A case study applied to the selection of an emergency shelter site fully confirms the above discussion through comparisons and analyses. These findings in this study have significant implications for modeling uncertainty in the field of emergency management and decision analysis.

While this study has made strides in formally proposing and establishing the concept and usage framework of the ELTS, and in expanding the application of the ELECTRE decision-making method, it is not without its limitations and potential directions for future research. Currently, a comprehensive linguistic decision framework underpinned by the theory of belief function has yet to be fully developed. Moreover, the exploration of MCDM in this study, based solely on ELTS within the ELECTRE context, remains limited. Future research should more broadly focus on various MCDM methods to fully leverage the potential of ELTS in decision-making. Additionally, the application of this study to the selection of emergency shelters is only a numerical case study and has not yet been validated in real-world scenarios, leaving room for future practical applications. Given these considerations, we put forward several perspectives to track the current work: improve the theoretical framework of ELTS, and carry out research from the perspectives of upper and lower probability intervals, namely, belief function and plausibility function; apply current theories and properties in other interesting MCDM methods, such as MOORA, SMART, and MULTIMOORA; Dedicated to theoretical contributions in more applications, such as emergency capability evaluation, emergency plan selection, etc.

Appendices

Appendix A

1.1 Examples

Example 1

Let $L_1(e)$ $=$ $\{s_{1}(1)\}$, $L_2(e)$ $=$ $\{s_1(0.3),s_2(0.5),\{s_1,s_2\}(0.2)\}$ and $L_3(e)$ $=$ $\{s_0(0.45),s_1(0.1),s_2(0.45)\}$ be three ELEs on LTS $S =\{s_\alpha \vert \alpha = -2,-1,0,1,2\}$. By Eq. (15), the negative ideal ELE of $L_{1,2,3}(e)$ is $L_*(e)$ $=$ $\{S(1)\}$ $=$ $\{\{s_{-2},s_{-1},s_{0},s_1,s_2\}(1)\}$. By Eq. (14), the positive ideal ELE of $L_{1}(e)$, $L_{2}(e)$ and $L_{3}(e)$ are $L_1^*(e)=$ $\{s_{1}(1)\}$, $L_2^*(e)=$ $\{s_{2}(1)\}$ and $L_3^*(e)=$ $\{s_{0}(1)\}$, respectively. Then the dissimilarity measures can be obtained by Eq. (6) as $D^-(L_1(e))=0.8944$, $D^-(L_2(e))=0.7280$, $D^-(L_3(e))=0.7124$ and $D^+(L_1(e))=0$, $D^+(L_2(e))=0.4123$, $D^+(L_3(e))=0.5074$. By Eq. (16), the inner reliability of $L_{1}(e)$, $L_{2}(e)$, and $L_{3}(e)$ are $\mathcal {I}(L_1(e))=1$, $\mathcal {I}(L_2(e))=0.6384$, and $\mathcal {I}(L_3(e))=0.5840$. The outer reliability of $L_{1}(e)$, $L_{2}(e)$, and $L_{3}(e)$ are calculated as follows. First, the similarity matrix is obtained by dissimilarity measure (Eq. (6)) as

$$\begin{aligned} Sim = \begin{array}{*{3}c} {} &{} {\begin{array}{*{3}c} L_1(e) &{} L_2(e) &{} L_3(e) \\ \end{array}} \\ {\begin{array}{*{3}c} L_1(e)\\ L_2(e) \\ L_3(e) \end{array}} &{} { \left[ \begin{array}{ccc} 1&{} 0.3917 &{} 0.2206\\ 0.3917 &{}1&{}0.5907\\ 0.2206 &{}0.5907&{}1\\ \end{array}\right] } \\ \end{array} \end{aligned}$$

(52)

Second, the support degree of each ELE is calculated by Eq. (18) as $Sup(L_1(e)) = 1.6123$, $Sup(L_2(e)) = 1.9824$, and $Sup(L_3(e)) = 1.8113$. Third, the credibility degree of each ELE is obtained by Eq. (19) as $Crd(L_1(e)) = 0.2982$, $Crd(L_2(e)) = 0.3667$, and $Crd(L_3(e)) = 0.3351$. Finally, the outer reliability of each ELE is determined by Eq. (20) as $\mathcal {O}(L_1(e)) = 0$, $\mathcal {O}(L_2(e)) = 1$, and $\mathcal {O}(L_3(e)) = 0.2945$. In this case, we let $\beta = 0.5$, then the comprehensive reliability of ELEs $L_1(e)$, $L_2(e)$ and $L_3(e)$ can be determined as $\mathcal {R}(L_1(e)) = 0.5$, $\mathcal {R}(L_2(e)) = 0.8192$ and $\mathcal {R}(L_3(e)) = 0.392$. The weighted aggregation operator will be employed to combine the three ELES. The arithmetic mean value of $L_1(e)$, $L_2(e)$ and $L_3(e)$ can be obtained by Eq. (23) as $\widetilde{L}(e) = \{s_0(0.103),s_1(0.459),s_2(0.096),\{s_1,s_2\}(0.342)\}$. The aggregated ELE $L(e) = L_1(e) \widetilde{\oplus } L_2(e) \widetilde{\oplus } L_3(e) = \widetilde{L}(e) \oplus \widetilde{L}(e) \oplus \widetilde{L}(e) = \{s_0(0.002),s_1(0.8477),s_2(0.0788),\{s_1,s_2\}(0.0715)\}$.

Example 2

(Continued to Example 1) Based on Def. 16, the expected values of $L_1(e)$, $L_2(e)$ and $L_3(e)$ in Example 1 can be calculated as $E(L_1(e)) = 0.75$, $E(L_2(e)) = 0.9$, and $E(L_3(e)) = 0.75$.

Example 3

(Continued to Example 2) Since $E(L_1(e)) = E(L_3(e)) = 0.75$, their variance value can be calculated by Def. 17 as $\sigma (L_1(e)) = 0$ and $\sigma (L_3(e)) = 0.24$. So the ranking of these three ELEs is $L_2(e) \succ L_1(e) \succ L_3(e)$.

Appendix B

1.1 The properties of the entropy of ELTSs

According to $Jirou\check{s}ek$ and ShenoyJiroušek and Shenoy (2018), the entropy function of ELEs consists of two components, the conflict in L(e) is measured by the first one, and the non-specificity in L(e) is measured by the second one. The entropy H(L(e)) for ELE L(e) on S defined in Eq. (3) satisfies several outstanding properties, such as nonnegativity, maximum entropy, monotonicity, and probability consistency.

(I) Nonnegativity: $H(L(e))\ge 0$, and $H(L(e))=0$ iff there is a $s\in S$ such that $L(e) = \{s(1)\}$.

(II) Maximum entropy: H(L(e)) gets the maximum $H_\uparrow (L(e))$ iff $L(e) = \{S(1)\}$.

(III) Monotonicity: for two ELEs $L_1(e)$ and $L_2(e)$ on distinct LTSs $S_1$ and $S_2$, if $\vert S_1\vert < \vert S_2\vert$, $H_\uparrow (L_1(e))<H_\uparrow (L_2(e))$.

(IV) Probability consistency: if an ELE L(e) degrades to a PLE L(p), then $H(L(e)) = H(L(p))$.

Proof

Let L(e), $L_1(e)$ and $L_2(e)$ be three ELEs on S, $S_1$, and $S_2$, respectively.

(I) based on Eqs. (3), (4), and (5), for L(e) on S, it is easy to have $H_s(Pl\_P_{L(e)})\ge 0$ and $H_d(L(e))\ge 0$, so $H(L(e))\ge 0$. When $L(e) = \{s(1)\}$, $H_s(Pl\_P_{L(e)})=0$ and $H_d(L(e))=0$, so $H(L(e))=0$. Thus, $H(\cdot )$ satisfies the nonnegativity property.

(II) let $\vert S\vert = \#S$, then $Pl\_P_{L(e)}(L^{(A)}) = \frac{1}{\#S}$ for all $L^{(A)}\in S$, and therefore $H_s(Pl\_P_{L(e)})=log(\#S)$, which is the maximum of all PLEs defined on S. We also have $H_d(L(e))=log(\#S)$. Thus, $H(\cdot )$ satisfies the maximum entropy property.

(III) based on the proof (II), we have $H_\uparrow (L(e)) = 2log(\#S)$. Thus, since it is monotonic in $\vert S\vert$, $H_\uparrow (\cdot )$ satisfies the monotonicity property.

(IV) when ELE L(e) degrades to PLE L(p), it can be easily obtained that $H_d(L(e))=0$, then $H(L(e))=H(L(p))$, Thus, $H(\cdot )$ satisfies the probability consistency property.

$\square$

Appendix C

1.1 The properties of dissimilarity measure of ELTSs

Theorem 1

Nonnegativity: $d(L_1(e),L_2(e)) \ge 0$.

Proof

Since ${\underline{\underline{D}}}_{ij}>0$, ${{[{\overrightarrow{L_1(e)}} - {\overrightarrow{L_2(e)}}]}^T}=[e_1^{(k)}-e_2^{(k)}]^T\ge 0$, and $[{\overrightarrow{L_1(e)}} - {\overrightarrow{L_2(e)}}]$ $=$ $[e_1^{(k)}-e_2^{(k)}] \ge 0$, based on Eq. (6), it is easy to have $d(L_1(e),L_2(e))\ge 0$. $\square$

Theorem 2

Nondegeneracy: $L_1(e) = L_2(e) \Longleftrightarrow d(L_1(e),L_2(e)) = 0$.

Theorem 3

Symmetry: $d(L_1(e),L_2(e)) = d(L_2(e),L_1(e))$.

The proof of Theorems 2 and 3 is obvious and has been omitted here.

Note that when $L_1(e)$ and $L_2(e)$ degrades to two PLEs denoted as $P_1(e)$ and $P_2(e)$, that is, ${\underline{\underline{D}}}(L^{(A)},L^{(B)}) = \frac{{\vert L^{(A)} \cap L^{(B)}\vert }}{{\vert L^{(A)} \cup L^{(B)}\vert }}={\textbf {1}}_{\#S}$, so the dissimilarity measure can be represented as

$$\begin{aligned} \begin{aligned} d(P_1(e),P_2(e)) = \sqrt{\frac{1}{2}{{[{\overrightarrow{L_1(e)}} - {\overrightarrow{L_2(e)}}]}^T}[{\overrightarrow{L_1(e)}} - {\overrightarrow{L_2(e)}}]} = \sqrt{\sum _{l=1}^{\#{S}}(e_1^{(l)}-e_2^{(l)})^2} \end{aligned} \end{aligned}$$

(53)

Appendix D

1.1 The properties of expectation function of ELTSs

Property 1: For a given ELE $L^{\vee }(e) = \{s_{-\tau }(1)\}$, we have $E(L^{\vee }(e)) = 0$.

Proof

By Def. 16, $E(L^{\vee }(e)) = \frac{-\tau +\tau }{2\tau }\times 1=0$. $\square$

In this case, $L^{\vee }(e)$ is called minimum ELE.

Property 2: For a given ELE $L^{\wedge }(e) = \{s_{\tau }(1)\}$, we have $E(L^{\wedge }(e)) = 0$.

Proof

By Def. 16, $E(L^{\wedge }(e)) = \frac{\tau +\tau }{2\tau }\times 1=1$. $\square$

In this case, $L^{\wedge }(e)$ is called maximum ELE.

Property 3: For a given ELE L(e), we have $E(L(e)) \in [L^{\vee }(e),L^{\wedge }(e)] = [0,1]$.

Proof

Since $\alpha ^{(l)}\in [-\tau ,\tau ]$, we have $\frac{\alpha ^{(l)}+\tau }{2\tau }\in [\frac{-\tau +\tau }{2\tau },\frac{\tau +\tau }{2\tau }]=[0,1]$. And since $ELE\_P(L^{(l)})\ge 0$ and $\sum _{l=1}^{\#S}ELE\_P(L^{(l)})=1$, we have $\sum _{l=1}^{\#S}(\frac{\alpha ^{(l)}+\tau }{2\tau }ELE\_P(L^{(l)}))$ $\in [\sum _{l=1}^{\#S}(0\times ELE\_P(L^{(l)})),\sum _{l=1}^{\#S}(1\times ELE\_P(L^{(l)}))]$ $=[0,1]$. $\square$

An example is given in Example 2 of Appendix A.

Appendix E

1.1 Remarks

Remark 1

Various versions of LTS are used by scholars, such as $\tilde{S} =\{\tilde{s}_\alpha \vert \alpha = 0,1,...,\tau \}$ and $\tilde{\tilde{S}} =\{\tilde{s}_\alpha \vert \alpha = 1,...,\tau \}$. In this paper, we refer to LTS $S =\{s_\alpha \vert \alpha =-\tau ,...,-1,0,1,...,\tau \}$ without any special instructions.

Remark 2

When LTSs $\tilde{S} =\{\tilde{s}_\alpha \vert \alpha = 0,1,...,\tau \}$ and $\tilde{\tilde{S}} =\{\tilde{\tilde{s}}_\alpha \vert \alpha = 1,...,\tau \}$ associated to the ELTS is concerned, in which cases, the expected values functions of $\tilde{L}(e)$ and $\tilde{\tilde{L}}(e)$ could be defined as $E(\tilde{L}(e))=\sum _{l=1}^{\#\tilde{S}}(\frac{\alpha ^{(l)}}{\tau }ELE\_P(\tilde{L}^{(l)}))$ and $E(\tilde{\tilde{L}}(e))=\sum _{l=1}^{\#\tilde{\tilde{S}}}(\frac{\alpha ^{(l)}}{\tau }ELE\_P(\tilde{\tilde{L}}^{(l)}))$. In this paper, if not specified, we refer to LTS S. If the ELE degrades to PLE, the expectation function would be consistent with the one in literature Wu et al. (2018).

Remark 3

With regard to LTS $\tilde{S} =\{\tilde{s}_\alpha \vert \alpha = 0,1,...,\tau \}$, the variance value function of $\tilde{L}(e)$ could be defined as

$$\begin{aligned} \sigma (\tilde{L}(e)) = \sqrt{\sum _{l=1}^{\#\tilde{S}}[\frac{\alpha ^{(l)}}{\tau }-E(\tilde{L}(e))]^2ELE\_P(\tilde{L}^{(l)})} \end{aligned}$$

(54)

Note that if the mass of belief is entirely assigned to the singleton set, i.e. ELE degrades to PLE, the variance value function would be consistent with the form in literature Wu et al. (2018).