Solution to the n-bubble problem on $\mathbb {R}^1$ with log-concave density

Abstract

We study the n-bubble problem on $\mathbb {R}^1$ with a prescribed density function f that is even, radially increasing, and satisfies a log-concavity requirement. Under these conditions, we find that isoperimetric solutions can be identified for an arbitrary number of regions, and that these solutions have a well-understood and regular structure. This generalizes recent work done on the density function $|x |^p$ and stands in contrast to log-convex density functions which are known to have no such regular structure.

1 Introduction

The isoperimetric problem examines all simple closed curves $\gamma \subset \mathbb {R}^2$ with a fixed perimeter and seeks to find the curve that maximizes its enclosed area. The solution to the isoperimetric problem is a circle and has been assumed knowledge for centuries. A modern approach to this problem was first developed by Steiner in the 1830s [13], and a rigorous proof was introduced by Schmidt [11]. For a brief history and overview of this classic problem, we refer to [2].

The isoperimetric problem has many generalizations, and we introduce several below. Perhaps the most immediate generalization is to higher dimensional spaces, where we examine hypersurfaces $\gamma ^n \subset \mathbb {R}^{n+1}$ or $\gamma ^n \subset \Omega ^{n+1}$ (with $\Omega ^{n+1} \subseteq \mathbb {R}^{n+1}$ a subset of Euclidean space, and with boundary $\partial \Omega$ that might intersect $\gamma$). Here, solutions take on the familiar name of “bubbles” because soap bubbles and soap film naturally model the isoperimetric problem in $\mathbb {R}^3$.

Another generalization introduces two or more regions. In this problem, we use (unions of pieces of) hypersurfaces to enclose m fixed volume measurements and seek to minimize total surface area. A (modern classic) result in this direction is the solution to the double-bubble conjecture $(m=2)$ in $\mathbb {R}^3$, solved by Hutchings et al. [6]. Lawlor has found a solution to the triple-bubble problem in the plane and in $\mathbb {S}^2$ in the case of equal enclosed volume [7], and recently announced a proof to the solution to the triple bubble in $\mathbb {R}^3$ under the same assumptions. A full solution to the triple-bubble problem has been proven in the case of the plane by Wichiramala  [14]. In very recent work, Milman and Neeman announced the solutions of the double bubble in $\mathbb {R}^n$ and $\mathbb {S}^n$ for $n \ge 2$; the triple bubble for $n \ge 3$, and the quadruple bubble for $n \ge 4$, among other results [8].

A third generalization is to work with a density function. In this problem, a non-negative function f is introduced on the ambient space ($\Omega ^{n+1} \subseteq \mathbb {R}^{n+1}$) so that, when a hypersurface $\gamma ^{n}$ encloses an $(n+1)$-dimensional solid $\Gamma$ ($\partial \Gamma = \gamma$), the density-weighted volume $V_f$ and density-weighted surface area $A_f$ are defined to be

$$\begin{aligned} V_f(\Gamma )&= \int _\Gamma f\, \textrm{d}\mathcal {H}^{n+1}\\ A_f(\gamma )&= \int _\gamma f\, \textrm{d}\mathcal {H}^{n} \end{aligned}$$

where the integrals are taken with respect to the usual Hausdorff measures.

This work will focus on multi-bubble isoperimetric problems with a density, and with the ambient space being $\mathbb {R}^1$. Such problems have been studied under a variety of densities. By an argument in [9], it is known that a perimeter-minimizing 1-bubble will exist on $\mathbb {R}^m$ when using a density function that radially increases to infinity. On $\mathbb {R}^1$, some early results for a single bubble under a large class of density functions were first identified in [10]. For n-bubbles on $\mathbb {R}^1$, one can prove the following:

Proposition 1

Let f be a density function on $\mathbb {R}^1$. Assume that f is continuous, goes to infinity in both directions, and is non-negative with isolated points of zero density. Then, for any n finite, positive volumes, an isoperimetric n-bubble exists that consists of finitely many intervals.

A proof for this proposition for positive density function f can be found in [3, Prop. 3.1]. The positivity can be relaxed by taking an appropriate sequence density functions $f - \epsilon$, with $\epsilon \nearrow \min (f)$.

On $\mathbb {R}^1$, two families of density functions that have been studied recently are the $|x |^p$ functions and the log-convex functions. An initial exploration on density functions of the form $\vert x |^p$ was done by a research team under the mentorship of Frank Morgan [5]. This team identified solutions for the single and double bubble on these densities. In the case of $p=1$, these results were extended to the 3-bubble and the 4-bubble [1]. Of note in these results is that any isoperimetric solution maintains a predictable structure, regardless of the relative size (weighted volume) of the regions.

A very different family of density functions on $\mathbb {R}^1$ was studied by Bongiovanni et al. [3], who looked at single- and double-bubble solutions under log-convex density functions. They found that a double-bubble solution under a log-convex density function did not have a standard structure. Instead, the solution could either be made up of two intervals (one per region) or three intervals (with one region placed between two components of the other region), depending on the sizes of the two masses in question. This approach was motivated by Gregory Chamber’s proof [4] of the single-bubble isoperimetric solution in general $\mathbb {R}^n$ with log-convex density. In more recent work, these results were extended to possible triple bubbles [12].

1.1 Statement of our problem and result

This paper focuses on even, radially increasing density functions that satisfy an additional property of log-concavity, which we define as follows:

Definition 1

A positive density function f is said to be a log-concave function if, for all values a, b satisfying $a<b \le 0$ or $0\le a<b$, the line segment joining $(a, \log (f(a)))$ and $(b, \log (f(b)))$ lies below the graph of $\log (f)$.

This definition of log-concavity naturally extends to functions f for which $f(0) = 0$ and f is positive away from the origin. The statement of our main problem, and our main result, are below.

Problem 1

Let f be a density on $\mathbb {R}^1$ that is even, radially increasing, and log-concave. Let $0 < M_1 \le \dots \le M_n$ be a set of n positive masses. Is it possible to find a configuration of n regions with the prescribed weighted masses and with minimal weighted perimeter?

Theorem 2

A solution to Problem 1 can be found by arranging regions $R_i$ of mass $M_i$ along the real line as follows: Each $R_i$ consists of a single interval, and as i increases these intervals are placed on opposite sides of the origin according to the parity of i (so that $R_i$ with i odd appear on one side of the origin, while $R_i$ with i even appear on the other side). Additionally, if i, j have the same parity with $i < j$, then $R_i$ is closer to the origin than $R_j$. Such a configuration of regions is the unique isoperimetric solution up to reflection across the origin.

This study extends the work of [5] and [1], as $|x|^p$ is a log-concave function under this definition. An example of an isoperimetric solution with $n=5$ is given in Fig. 1.

Fig. 1

An example isoperimetric solution with $n=5$, using the log-concave density function $f(x) = |x|$

Remark 1

We find that the structure described in Theorem 2 perimeter is minimizing for all choices of n masses. We call this n-bubble structure the “standard configuration,” or sometimes the “standard position,” for n masses to be arranged. It is formally defined in Sect. 3.3.

1.2 Overview of the argument

Our argument follows a proof by induction on the number of regions. For a general log-concave density function, the base case is easily checked (and will be given as an immediate consequence of Corollary 6). For the inductive step, we assume that the standard configuration is the only perimeter-minimizing solution for bubbles of n or fewer regions. For contradiction, we assume there exists a specific set of $n+1$ masses for which a solution other than standard configuration exists. Due to specific results about the structure of any perimeter-minimizing configuration (the most important of which is Corollary 6), the standard and nonstandard configurations can be differentiated by identifying an “outermost interval that breaks the standard pattern.” The contradiction will be found by swapping the position of this interval with another interval, decreasing total perimeter. This strategy (swapping intervals appropriately) is based on previous ideas from [3] and [10], among possibly others: to make the comparison work in our case, we first carefully adjust the size of certain masses to create two isoperimetric solutions (one standard, one nonstandard) that can be easily compared. The mass adjustments are described in Sect. 4, and a fundamental result that allows us to adjust these masses is Proposition 7.

This paper is organized as follows. Section 2 includes definitions and other preliminary work. Section 3 explores variation formulas for mass and perimeter, using these formulas to show that any isoperimetric n-bubble must have exactly n intervals. Section 4 explores how careful adjustment of region sizes (achieved by inflating or deflating specific masses) will change the isoperimetric configurations. Finally, Sect. 5 uses these tools to prove the n-bubble theorem via the contradiction described above.

1.3 A quick remark on images in this paper

Throughout, we include images of the real line with a density function. The density function shown is typically $f(x) = |x |$. However, this is simply done to standardize the images: any even, log-concave density function would work. The exception is Fig. 2, which gives a basic example specifically for $f(x) = |x|$.

2 Preliminaries

In this section, we include some basic definitions and early results.

2.1 Basic definitions

Definition 2

A density is a function $f: \mathbb {R}^1 \rightarrow [0, \infty )$. Given an interval [a, b] and a density f, the weighted mass of the interval with respect to the density is $\int _a^b f$. The weighted perimeter with respect to the density is defined to be $f(a) + f(b)$.

In this paper, by abuse of notation, weighted mass is sometimes called mass, area, or volume, and weighted perimeter is sometimes called perimeter.

Definition 3

A region on $\mathbb {R}^1$ is a collection of disjoint intervals $[a_i, b_i]$ with mass M and perimeter P

$$\begin{aligned} M&= \displaystyle \sum _i \int _{a_i}^{b_i} f\\ P&= \displaystyle \sum _i f(a_i) + f(b_i). \end{aligned}$$

A region R with mass M and perimeter P is isoperimetric (also referred to as a bubble or a 1-bubble) if, out of all possible regions with mass M, R has the least perimeter.

Fig. 2

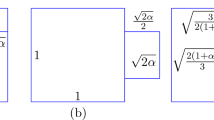
Above, we see an example with density function $f(x) = |x |$, and regions of weighted mass 10 arranged in two different configurations. The first configuration, defined on the interval $[-2,4]$, has weighted perimeter of 6. The second configuration, defined on the interval $[0,\sqrt{20}]$, has weighted perimeter of $\sqrt{20} \approx 4.47$. This second configuration is the isoperimetric 1-bubble, as shown in [5]. Note that in each picture, the “region” is an interval, while the weighted volume is calculated as (and displayed as) area under the density function

We also consider multiple regions on the real line. Each region consists of (possibly multiple, disjoint) intervals. Two intervals, each from a different region, are either completely disjoint or meet at a single endpoint. In addition to the mass and perimeter of each region, one can measure the total (weighted) perimeter by summing the perimeter of each of the regions, provided that endpoints shared by two intervals are only counted once.

Definition 4

A configuration of n regions $R_1, \dots , R_n$ with masses $M_1, \dots , M_n$ is said to be isoperimetric (and is referred to as an n-bubble) if, out of all possible configurations with the same masses, this configuration has the least total perimeter.

2.2 Initial condensing of configurations

A priori, an isoperimetric set of regions might look very wild, even in the one-dimensional case. A single region might consist of multiple intervals, and there might be empty space between intervals that does not correspond to any particular region. However, such configurations will never be isoperimetric: Proposition 3 shows that lower perimeter can be achieved by consolidating regions into adjacent intervals near the origin.

Proposition 3

Let f be an increasing density on the positive real line $(x \ge 0)$. Consider a configuration of n regions $R_i$ contained in $x\ge 0$. Then a new configuration of n regions can be created with the same masses and decreased total perimeter, such that each region consists of a single interval and there are no empty intervals.

Proof

Take an arbitrary configuration on n regions, with each region consisting of (possibly multiple) intervals on the non-negative real line $x \ge 0$, and let $P_0$ denote the total perimeter of the configuration. Without loss of generality (WLOG), identify $R_1$ to have a maximum value (and rightmost endpoint) of $b_1$, $R_2$ to have a maximum value of $b_2$, and so on, named so that $b_1< b_2< \dots < b_n$. Then a new configuration can be created in which regions (also named $R_i$) are adjacent, each consisting of a single interval, and are ordered so that $R_i$ sits to the left of $R_j$ if $i < j$. As seen in Fig. 3, this can clearly be done in such a manner that the mass $M_i$ of each region $R_i$ is the same as in our original configuration. Let $P_1$ be the perimeter of this new configuration. By construction, the new rightmost endpoint $b_j'$ of region $R_j$ satisfies $0 < b_j' \le b_j$ for $j = 1,..., n$. Therefore, $f(b_j') \le f(b_j)$, and one concludes $P_1 = \displaystyle \sum _{1\le j \le n} f(b_j') \le \displaystyle \sum _{1 \le j \le n} f(b_j) \le P_0$. $\square$

Fig. 3

We see how an arbitrary arrangement (on the left) can be consolidated (on the right) in a manner that lowers perimeter

Corollary 2

Let f be a density function on $\mathbb {R}^1$ that is even and is monotonically increasing (resp. decreasing) for $x \ge 0$ (resp. $x \le 0$). If a configuration of n regions is isoperimetric with density f, then the configuration consists of at most 2n intervals, all adjacent and with the origin contained in at least one of the intervals (being an interior point or an endpoint).

Proof

Applying Proposition 3 twice shows that there are, at most, n intervals on each side (positive and negative) of the origin. As part of this process, it is clear that the origin will either be between two different regions (in which case it serves an endpoint of each), or in a single region. $\square$

Next, we have a proposition for rearranging adjacent intervals according to their masses.

Proposition 4

Let f be an increasing density function on $x \ge 0$. Consider a configuration of regions in which two regions ($R_i$, $i = 1,2$) are adjacent intervals on the positive axis $x > 0$. Suppose each $R_i$ has mass $M_i$, and suppose $M_1 < M_2$. Then total perimeter is reduced when the interval for $R_1$ lies to the left of the interval for $R_2$.

Proof

Keeping the leftmost and rightmost endpoints fixed, and transposing the two intervals if necessary, the perimeter is lowered when the interval with less mass is placed to the left, as it moves the internal endpoint to the left. $\square$

Iterating Proposition 4 guarantees that, on one side of the origin, regions will be ordered (according to weighted mass) from smallest to largest as they are placed further from the origin.

Definition 5

A configuration of n regions is said to be in a condensed configuration if it satisfies the following conditions:

• The configuration consists of at most 2n adjacent intervals, with each region contributing at most one interval on each side of the origin.

• The origin is contained in at least one of the intervals, possibly as an endpoint.

• If two intervals $I_1$ and $I_2$ are on the same side of the origin, with $I_1$ closer to the origin than $I_2$, then the enclosed mass of $I_1$ will be less than or equal to the enclosed mass of $I_2$.

Due to Propositions 3 and 4, a perimeter-minimizing configuration is necessarily condensed.

Proposition 5

On the positive real line with a strictly increasing density f, consider two intervals $[a_1, b_1]$, $[a_2, b_2]$. Suppose that each of these intervals contains the same mass ($M_1 = M_2$), and suppose that $a_1 < a_2$. Then the following inequalities hold:

$$\begin{aligned} b_1 < b_2 \qquad \text {and} \qquad b_1 - a_1 > b_2 - a_2. \end{aligned}$$

Proof

The first inequality is an immediate consequence of the two intervals enclosing the same mass. To prove the second inequality, consider two cases. If $a_2\ge b_1$, then $(b_1-a_1)f(b_1)> \int _{a_1}^{b_1} f = \int _{a_2}^{b_2} f > (b_2-a_2)f(a_2) \ge (b_2-a_2)f(b_1)$, and so $b_1-a_1 > b_2-a_2$. If $a_2 < b_1$, then $M_1=M_2$ implies that $[a_1,a_2]$ and $[b_1,b_2]$ enclose the same weighted area, and by applying the preceding case, the statement holds immediately. $\square$

Note that, although the previous proposition was stated for the positive real line, when f is an even density there is a clear corresponding statement on the negative real line.

Corollary 3

The first inequality from Proposition 5 is still true when $M_2 \ge M_1$. The second inequality from Proposition 5 also holds when $M_2 \le M_1$.

3 Variations of mass and perimeter

In this section, we introduce the first variation formula for mass and perimeter and show how continuous variations can further reduce the number of intervals we expect each region to have in a perimeter-minimizing solution.

3.1 The first variation formulas

Suppose f is a $C^1$ density function. Consider an interval [a, x]. Letting $x = x(t)$ move at a rate of $x'(t) = 1/f(x(t)))$, the first variation of mass and perimeter are given by

$$\begin{aligned} \frac{\textrm{d}M}{\textrm{d}t}&= 1 \end{aligned}$$

(1)

$$\begin{aligned} \frac{\textrm{d}P}{\textrm{d}t}&= f'(x(t)) / f(x(t)) = \frac{\textrm{d}}{\textrm{d}x}\left[ \log (f(x(t))) \right] . \end{aligned}$$

(2)

Remark 2

(The first variation formula) Let f be a $C^1$ density function, and take an interval [a(t), b(t)]. If endpoints a(t), b(t) move to the right at rates 1/f(a(t)), 1/f(b(t)), respectively, then the weighted mass of the interval will not change, while the perimeter’s instantaneous rate of change will be $(\log (f))'(a(t)) + (\log (f))'(b(t))$.

Corollary 4

Let f be a $C^1$ density function, and consider a perimeter-minimizing n-bubble with interval endpoints listed as $x_1, x_2, \dots , x_m$. Then

$$\begin{aligned} \sum _{i=1}^m \log (f)'(x_i) = 0. \end{aligned}$$

Proof

If the configuration is isoperimetric, it has minimal perimeter out of all other configurations with the same prescribed masses. A variation that moves every endpoint to right at speed 1/f will preserve the mass of each region, and therefore the first variation of the perimeter will equal 0. $\square$

Remark 3

In general, a log-concave density function need not be $C^1$. In the case considered for Problem 1, f is even, radially increasing, and log-concave. In such cases, $(\log (f))'$ will be a decreasing function exhibiting odd symmetry wherever it is defined. Furthermore, $(\log (f))'$ will be negative when $x < 0$, and positive when $x > 0$, with $(\log (f))'(0)$ undefined. Where necessary, the first variation formula can be replaced with one-sided derivative formulas. These one-sided derivatives exist at every point, except possibly at 0 (where they could approach $+\infty$ as a right-handed limit, or $-\infty$ as a left-handed limit). The above corollary can be modified to state that an isoperimetric n-bubble will have endpoints which give us a non-negative sum for the left-sided derivatives, and a non-positive sum for the right-sided derivatives.

3.2 Consolidating regions using the first variation

Corollary 2 states that an n-bubble will be condensed, and therefore consist of at most 2n intervals. This number can be further reduced using the first variation formulas, especially in the case that our density function is log-concave.

Proposition 6

On the real line with a log-concave density function f, suppose we have n regions in a condensed form. Additionally, suppose that one region R can be written as the union of two intervals $R^-$, $R^+$, one on each side of the origin. Then there exists a configuration of n regions with the same masses, but with lower perimeter, in which R consists of a single interval on one side of the origin.

Proof

Identify region $R = R^- \cup R^+ = [r_1, r_2] \cup [r_3, r_4]$ with $r_2 \le 0 \le r_3$. Let A be the collection of interval endpoints $a_i$ that satisfy $a_i < r_2$ or $a_i > r_3$. (Note, in particular, that $r_1, r_4 \in A$ while $r_2, r_3 \not \in A$.) We consider two different variations on the points of A. In the first (Variation 1), these points are shifted to the right with rate 1/f. In the second (Variation 2), these points are shifted to the left with rate 1/f. The first variation formula guarantees that both variations keep the mass of each region constant. If f has well-defined second derivatives at each point of A, then Variation 1 will have total perimeter P satisfy

$$\begin{aligned} \frac{\textrm{d}P}{\textrm{d}t}&= \sum f'(x(t)) / f(x(t))\\ \frac{\textrm{d}^2P}{\textrm{d}t^2}&= \sum \frac{f(x(t)) f''(x(t)) - \left[ f'(x(t))\right] ^2}{\left[ f(x(t))\right] ^3} \end{aligned}$$

where the summation is taken over all points in A. By the chain rule, Variation 2 will have the same second derivative, but will have a sign change for $\frac{\textrm{d}P}{\textrm{d}t}$. P(t) is concave if f is log-concave and $C^2$ under either variation. There are two possibilities:

• Variation 1 has $\frac{\textrm{d}P}{\textrm{d}t} \le 0$ initially, in which case this variation locally decreases perimeter. The concavity of P guarantees that P will continue to decrease under this variation until the endpoint $r_1$ has been moved to collide with endpoint $r_2$, eliminating $R^-$.

• Variation 1 has $\frac{\textrm{d}P}{\textrm{d}t} > 0$ initially, in which case Variation 2 will locally decrease perimeter. The concavity of P guarantees that P will continue to decrease under this variation until the endpoint $r_4$ has been moved to collide with endpoint $r_3$, eliminating $R^+$.

If f fails to be sufficiently smooth, one can use appropriate left- or right-derivatives. We know the right-sided derivative, $\sum (\log f)'_R$, is a locally decreasing quantity. Thus, if Variation 1 initially lowers perimeter, it will continue to lower perimeter until $r_1$ collides with $r_2$. Alternatively, if $\sum (\log f)'_R > 0$, then Variation 1 locally increases perimeter, and consequently Variation 2 will locally decrease perimeter. Since $\log (f)$ is concave on each side of the origin, our right- and left-sided derivatives satisfy $(\log (f))'_R \le (\log (f))'_L$ at each non-zero point, and the one-sided derivative for perimeter under Variation 2 looks like $\sum (-1) (\log f)'_L \le (-1) (\log f)'_R < 0$. Therefore, one of these variations will result in lowering perimeter, and may be applied until either $R^-$ or $R^+$ disappears. $\square$

Corollary 5

Let f be a log-concave density on the real line. Consider a condensed configuration of n regions, with the origin contained in the interior of one region. Then the configuration is not isoperimetric, and perimeter can be lowered by varying in a manner that moves this region entirely to one side of the origin.

Proof

This is the same argument as in Proposition 6, but in the specific case where $r_2 = r_3 = 0$. Note that every interval endpoint in the whole configuration (except the origin) will move to the right or the left under the appropriate variation. $\square$

Corollary 6

Let f be a log-concave density on the real line. Suppose a configuration of n regions is perimeter-minimizing. Then each region in the configuration will consist of exactly one interval, and the origin will not sit as an interior point of a region.

We conclude this section with an important comparison inequality for intervals that contain the same mass. The result, due to the log-concavity of the density function, should be viewed as similar to the results of Proposition 5, and (as in that proposition) it is stated for the positive real line, with an equivalent statement about negative real line being readily available.

Proposition 7

Let f be a log-concave density defined on the positive real line. Suppose two intervals $[a_0, b_0]$ and $[a_1, b_1]$ contain the same mass. Additionally, suppose $a_0 < a_1$. Then $f(b_0) - f(a_0) > f(b_1) - f(a_1)$.

Proof

Let a(t), b(t) be variations so that $a(0) = a_0$, $b(0) = b_0$, and a(t), b(t) increase at a rate of 1/f. This variation preserves the mass of the interval [a(t), b(t)], and therefore there must exist a time $t = t_1$ for which $a(t_1) = a_1$ and $b(t_1) = b_1$. Define $Q(t) = f(b(t)) - f(a(t))$, and let $Q'_R$ represent the right-sided derivative of Q. Then

$$\begin{aligned} Q'_R (t) = (\log f)'_R (b(t)) - (\log f)'_R (a(t)). \end{aligned}$$

Since f is log-concave, $(\log f)'_R$ is a decreasing quantity. Thus, $Q'_R (t)$ is negative, and we conclude that $Q(0) > Q(t_1)$. $\square$

3.3 A standard n-bubble configuration

We now identify our “standard” n-bubble configuration. Corollary 6 has shown that every n-bubble must have exactly n intervals positioned along the real line; that the intervals must be arranged in a condensed manner (in the sense of Definition 5); and that the origin will not appear as an interior point of an interval. What remains is to discern is the perimeter-minimizing way to order the intervals.

Definition 6

Suppose we have a set of n fixed masses $\{ M_1, \dots , M_n \}$ that satisfy $0 < M_1 \le M_2 \le \dots \le M_n$. Then the standard configuration of these masses will be a condensed configuration of n regions (indexed so region $R_i$ contains mass $M_i$), organized so each region is an individual interval placed to the left or the right of the origin depending solely on the parity of its index.

In other words, for the standard configuration, odd-indexed regions appear on one side of the origin while even-indexed regions appear on the opposite side. Following Definition 5 and Proposition 4, it is known that placing smaller intervals closer to the origin reduces perimeter. This, along with the even/odd index split across the origin, completely determines the positions of the intervals for the standard configuration. That the standard configuration is perimeter-minimizing for Problem 1 is our main result, and is stated in the next theorem and corollary (formerly Theorem 2).

Theorem 8

Let f be a density function that is even, log-concave, radially increasing, and satisfies $f(0) = 0$. Then for any $n \in \mathbb {N}$, and any collection of n masses, the standard configuration is an isoperimetric n-bubble with these masses, and is the unique solution up to reflection across the origin.

A proof for this theorem will be presented in Sect. 5, following some necessary results developed in Sect. 4.

Corollary 7

In Theorem 8, $f(0) = 0$ can be relaxed.

Proof

Theorem 8 states that the standard configuration will be the unique isoperimetric solution for a density function f for which $f(0) = 0$. But it will also be a (non-unique) isoperimetric solution for constant density function c, $c \ge 0$. Thus, one needs to simply consider $f+c$. $\square$

4 Manipulating volumes of regions

In this section, we explore how changing the weighted volumes of the regions will affect the isoperimetric configuration. Throughout this section, we let our density function f be a log-concave, even, increasing density with $f(0) = 0$.

4.1 Adding a region of small size $\epsilon$

The following proposition shows that adding a new region of very small volume to a standard configuration known to be perimeter-minimizing is best done by maintaining the standard configuration, inserting the new region directly adjacent to the origin.

Proposition 9

Suppose there exists a set of n masses $M_i$, $1 \le i \le n$, for which the standard configuration is the unique perimeter-minimizing solution. Then there exists an $\epsilon _0 < M_1$, depending on n, f, and the $M_i$, such that the following is true: when adding an $(n+1)$th region to the configuration, if the mass $\epsilon$ of the new region satisfies $\epsilon \le \epsilon _0$, then the perimeter-minimizing configuration for masses $\epsilon$, $M_1, \dots , M_n$ is the corresponding standard configuration.

Proof

Consider the standard configuration of n regions with masses $M_i$. There are a total of n interval endpoints other than the origin, and each region can be identified by its endpoint furthest from the origin. Call these endpoints $b_i$, and note that the total perimeter of this configuration is $\sum _{i} f(b_i)$.

Other than the standard configuration, there are a finite number of condensed configurations (with one interval per region) that we can consider. Let $\hat{P} = \min \{P\}$, where the minimum is taken over all total perimeters of these nonstandard, condensed configurations. Since we assume the standard configuration is uniquely perimeter-minimizing, $\hat{P} - \sum _{i} f(b_i) > 0$.

Consider a standard configuration of $(n+1)$ regions, with masses $\{\epsilon , M_1, \dots , M_n \}$. Since $\epsilon$ is small, there exists a $b_*$ such that the region with mass $\epsilon$ will consist of an interval $(0, b_*)$ or $(b_*, 0)$ depending on whether $b_*$ is positive or negative. Note that $f(b_*) \searrow 0$ as $\epsilon \searrow 0$, since $f(0) = 0$. Choose $\epsilon _0$ so that its corresponding $b_*$ value satisfies $(n+1)f(b_*) < \frac{1}{2}(\hat{P} - \sum _{i} f(b_i))$, and note that this inequality will be true for every $\epsilon \le \epsilon _0$.

Compare the standard configurations with n masses $\{ M_i \}$ and with $n+1$ masses (including $\epsilon$). The new region will introduce a new perimeter value $f(b_*)$. Furthermore, all endpoints on the same side of the origin as the new region will shift. Due to Proposition 7, each endpoint’s shift will result in a perimeter increase less than $f(b_*)$. So as a (very rough) estimate, inserting this new mass adjacent to the origin will increase total perimeter less than $(n+1)f(b_*)$. By our choice of $\epsilon$, this perimeter increase will be less than $\frac{1}{2}(\hat{P} - \sum _{i} f(b_i))$, which is an underestimate for any other condensed configuration that involves the original n masses and $\epsilon$. Therefore, out of all condensed configurations on these $(n+1)$ regions, this standard configuration has minimal perimeter. $\square$

Corollary 8

Suppose that the standard configuration is perimeter minimizing for any set of n masses. Then given $n+1$ masses, where one of the masses is suitably small, the perimeter-minimizing configuration will be the standard position.

One concern is that there might exist a set of set of $n+1$ masses for which there are two distinct isoperimetric configurations. (Here, “distinct” means that the two configurations do not simply differ by reflection). One could imagine that varying the size (of one or more) of the masses in such a set could result in diverging isoperimetric configurations.

Definition 7

A set of masses $\{M_i \}$ for which two distinct configurations of regions are simultaneously isoperimetric will be called a bifurcating set of masses.

Corollary 9

Suppose, for n regions, a standard configuration minimizes perimeter. However, suppose there is a specific set of $n+1$ masses whose perimeter-minimizing configuration is nonstandard. Then, by shrinking the mass of the smallest region, one can find a bifurcating set of $n+1$ masses. Among the perimeter-minimizing configurations, one will be in standard position.

Proof

Assume there exists a set of $n+1$ regions (call the regions $R_i$, each of mass $M_i$, with $M_1 \le \dots \le M_{n+1}$) whose isoperimetric configuration is nonstandard. $M_1$ cannot be too small (or else the configuration would be standard due to Proposition 9). A mass $x > 0$ will be below the bifurcation threshold if the perimeter-minimizing configuration for masses $y, M_2, \dots , M_{n+1}$ is standard for all $y \le x$. Let $\epsilon$ be defined as $\epsilon = \sup \{ x: x\; \text {is below the bifurcation threshold} \}$. Then by continuity, the $n+1$ masses $\{ \epsilon , M_2, \dots , M_{n+1} \}$ form a bifurcating set: there are at least two configurations that minimize perimeter, one of which is standard. $\square$

4.2 Inflating a large mass in a bifurcating set

Here we explore in detail an argument that will be generalized later. Suppose we have a bifurcating set of masses $M_1 \le M_2 \le \dots \le M_{n+1}$. Work in Sects. 2 and 3 guarantees that both isoperimetric configurations contain exactly $n+1$ intervals, with intervals of larger mass placed further away from the origin. WLOG, we assume the region of mass $M_{n+1}$ appears on the positive side of the x-axis in both configurations. Let the $n+1$ endpoints (other than the origin) in the standard configuration be denoted as $a_{i}$, and let the endpoints in the nonstandard configuration be denoted as $b_i$. Since both configurations are isoperimetric, we have

$$\begin{aligned} \sum _{i=1}^{n+1} f(a_i) = \sum _{i=1}^{n+1} f(b_i). \end{aligned}$$

Let us assume for a moment that any configuration of n regions is perimeter-minimizing if and only if it is in standard position. Since the standard configuration of $n+1$ regions becomes the standard configuration of n regions when the largest region is deleted, we know

$$\begin{aligned} \sum _{i=1}^{n} f(a_i) < \sum _{i=1}^{n} f(b_i). \end{aligned}$$

This tells us that $a_{n+1} > b_{n+1}$. An immediate consequence of this follows:

Corollary 10

Suppose the unique isoperimetric solution with n regions is the standard configuration. Furthermore, suppose we have a bifurcating set of masses $\{M_i\}_{i=1}^{n+1}$. WLOG, assume the largest region appears on the positive side in both the standard and nonstandard isoperimetric configurations. Call the leftmost endpoint of the leftmost region $a_*$ (for the standard configuration) and $b_*$ (for the nonstandard). Then $a_* > b_*$.

Proof

Comparing the rightmost endpoint from both the standard and nonstandard configurations, we see that the standard configuration’s will sit further to the right. Since both configurations have the same total mass between the leftmost and rightmost endpoints (namely, $\sum M_i$), we must have $a_* > b_*$ as well. $\square$

Definition 8

Given a bifurcating set of masses $\{M_1 \le \dots \le M_{n+1} \}$, with $a_i$, $b_i$ and $a_*$, $b_*$ defined as above (for the standard and nonstandard solution, respectively), we say the nonstandard solution is shifted to the left of the standard solution if $b_*< a_* \le 0< b_{n+1} < a_{n+1}$.

If the standard configuration is perimeter minimizing for any set of n masses, Corollary 10 shows that a bifurcating set of $n+1$ masses will have a nonstandard solution that is shifted to the left of the standard solution.

Proposition 10

Consider a bifurcating set of masses with two isoperimetric solutions. Assume, for both solutions, that the largest region is on the positive side of the origin and the second-largest region (with mass $M_\star$) is on the negative side of the origin. Finally, assume the nonstandard solution is shifted to the left of the standard solution. Then, by increasing the value of $M_*$ (and thus inflating the leftmost region of each configuration), one creates a new set of masses in which the standard configuration fails to be isoperimetric.

Proof

Take the two isoperimetric configurations, one standard (with endpoints $a_i$) and one nonstandard (with endpoints $b_i$). Enlarging the second-largest mass, $M_*$ will shift $a_*$ and $b_*$ to new values, $a'_*$ and $b'_*$. However, since the nonstandard configuration is shifted to the left, Proposition 7 guarantees that $f(a'_*) - f(a_*) > f(b'_*) - f(b_*)$. Calculating the perimeter of configurations with this mass adjustment, we see that the nonstandard configuration has less perimeter than the standard. $\square$

5 Proof of the n-bubble theorem

We proceed by induction. The base case ($n=2$) follows immediately from Corollary 6. For the inductive argument: Suppose every set of n positive masses has the standard configuration as the unique perimeter-minimizing solution. For contradiction, assume this is not true for $n+1$. Then there exists at least one set of masses $M_1 \le \dots \le M_{n+1}$ for which there is a nonstandard isoperimetric solution. Using the fact that every minimizing configuration is necessarily condensed, as well as Corollary 6, we conclude that each region in this nonstandard configuration consists of a single interval, that each interval is entirely on one side of the origin, and that (on its respective side of the origin) the intervals are ordered according to mass size, with the smaller masses closer to the origin.

First, WLOG, one can assume (shrinking $M_1$ if necessary) that set of $n+1$ masses are bifurcating, with both a standard and nonstandard isoperimetric solution. Identify the unique outer endpoints for the interval region associated with mass $M_i$, and name this endpoint $a_i$ (in the case of the standard solution) and $b_i$ (in the case of the nonstandard solution). Orient the solutions so that the largest region (associated with $M_{n+1}$) appears on the positive side of the origin in both configurations.

The standard solution will have regions (and endpoints $a_i$) that alternate from the positive to the negative side as i increases. The nonstandard solution will not follow this pattern. Thus, there is a largest pair of consecutive indices j, $j+1$ for which $b_j$ and $b_{j+1}$ both land on the same side of the origin. The intervals associated with $M_j$ and $M_{j+1}$ will be used to construct a contradiction.

Assume $M_{n}$ is strictly smaller than $M_{n+1}$. Additionally, assume that $b_n$ and $b_{n+1}$ have opposite signs. (If they have the same sign, then we set $j=n$.) Corollary 10 shows that the nonstandard configuration is shifted to the left of the standard configuration, so that $b_n< a_n < 0$. Add mass to $M_n$ until it reaches the size of $M_{n+1}$. Per Proposition 10, adding any amount of mass to $M_n$ will result in new configurations for which the standard configuration fails to be isoperimetric: thus, this new set of masses $\{M_1, \dots , M_{n-1}, M_{n+1}, M_{n+1} \}$ (so identified because the two largest masses are of equal size) has a nonstandard configuration as a perimeter-minimizing solution.

Without renaming, we can shrink $M_1$ until our set of masses is once again a bifurcating set. Reflecting the nonstandard configuration across the origin if necessary, one can ensure third largest region, $M_{n-1}$, is on the positive side of the origin (this will already be true for the standard configuration). By Corollary 10 again, the nonstandard configuration is still shifted to the left of the standard configuration.

This process can be repeated until index j is reached. At each step, begin with a bifurcation in which the outermost intervals, in pairs, have the same enclosed mass. The following actions are taken:

• Flip the nonstandard configuration (if necessary) to put the region with the next-largest mass, $M_k$, on the positive side.

• Observe that the nonstandard configuration is shifted to the left of the standard one.

• If the interval with $M_{k-1}$ is on the negative side, “inflate” $M_{k-1}$ until it is the same size as $M_k$. Due to the left shift and an argument based on Proposition 7, the nonstandard configuration will have total perimeter no more than the standard configuration, meaning that the standard configuration is not the unique isoperimetric solution.

• Shrink $M_1$, if necessary, until the set of masses is once again bifurcating (only now with $M_{k-1}$ set equal to $M_k$) as well.

Iterate until consecutive indices j, $j+1$ are reached such that $b_j$, $b_{j+1}$ fall on the same (positive) side of the origin in the nonstandard configuration. Let $\ell$ be the largest index, smaller than j, on the negative side of the origin in the nonstandard configuration. Note that the outer regions are grouped into pairs of equal weighted volume. At this point, the nonstandard configuration looks like Fig. 4.

Fig. 4

The $n+1$ regions are alternating for large indices, and these large indices are grouped in consecutive pairs with equal volume ($M_{n+1} = M_n$, etc). The largest index that fails this pattern in $j+1$, so that $M_j$ and $M_{j+1}$ are on the same side of the origin. The largest index, smaller than j, that appears on the other side of the origin is $\ell$

Let c be the outer endpoint of the interval associated with region $M_\ell$, and let d be the endpoint separating $M_j$ from $M_{j+1}$, in the nonstandard configuration. Let $c'$ and $d'$ be the outer endpoints associated with $M_j$ and $M_{j-1}$, respectively, in the standard configuration. (The endpoints c, d, $c'$, $d'$ have been identified in Figs. 4 and 5.) We first want to show that $|d |< |c |$. This uses the fact, highlighted in Fig. 5, that our nonstandard configuration is still shifted to the left when compared to our standard configuration.

Fig. 5

A nonstandard and a standard configuration lined up for comparison. The nonstandard configuration is shifted to the left

Due to this shift to the left, and because both configurations have the same alternating pattern for the largest regions (i.e., those greater than j), one observes that $d' > d$ and that $c' > c$. Furthermore, because of the alternating nature of the standard configuration, $|c' |> |d' |$. Taken together, we get $|c |> |c' |> |d'|> |d |$ as desired.

Additionally recognize that $M_\ell < M_j$ (it is known that $M_\ell \le M_j$, and if $M_\ell = M_j$ we can simply change their index names so that $M_j$, $M_{j+1}$ appear on opposite sides of the origin). Then, as highlighted in Fig. 6, transposing the regions associated with $M_\ell$ and $M_j$ will result in lower total perimeter, yielding the desired contradiction. Let us see the precise argument.

Fig. 6

Transposing the locations of the jth and $\ell$th regions will result in a decreasing of perimeter. Endpoint c and those to the left of c will increase, but this increase in perimeter will be offset by the decrease in perimeter by d and points to the left of d

First, swapping the regions $M_j$ and $M_\ell$ will result in a shifting endpoints that are less than or equal to c (which will shift to the left, resulting in an increased contribution to perimeter), as well as endpoints that are greater than or equal to d (these will shift to the left, but will result in a decrease in perimeter). By counting regions, one sees that there is one more endpoint, d, moving on the right. All other shifting endpoints can be paired with a partner across the origin. Because $|c |> |d |$, and using Proposition 7, one can see that the decrease in perimeter from each endpoint on the right outweighs the increase in perimeter from its corresponding endpoint on the left. Taken together, total perimeter decreases after the transposition of $M_j$ and $M_\ell$. Thus, the original nonstandard configuration could not have been isoperimetric, a contradiction.