On certain classes of $\mathbf{Sp}(4,\mathbb{R})$ symmetric $G_2$ structures

Abstract

We find two different families of $\mathbf{Sp}(4,\mathbb{R})$ symmetric $G_2$ structures in seven dimensions. These are $G_2$ structures with $G_2$ being the split real form of the simple exceptional complex Lie group $G_2$. The first family has $\tau _2\equiv 0$, while the second family has $\tau _1\equiv \tau _2\equiv 0$, where $\tau _1$, $\tau _2$ are the celebrated $G_2$-invariant parts of the intrinsic torsion of the $G_2$ structure. The families are different in the sense that the first one lives on a homogeneous space $\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_l$, and the second one lives on a homogeneous space $\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_s$. Here $\mathbf{SL}(2,\mathbb{R})_l$ is an $\mathbf{SL}(2,\mathbb{R})$ corresponding to the $\mathfrak{sl}(2,\mathbb{R})$ related to the long roots in the root diagram of $\mathfrak{sp}(4,\mathbb{R})$, and $\mathbf{SL}(2,\mathbb{R})_s$ is an $\mathbf{SL}(2,\mathbb{R})$ corresponding to the $\mathfrak{sl}(2,\mathbb{R})$ related to the short roots in the root diagram of $\mathfrak{sp}(4,\mathbb{R})$.

1 Introduction: a question of Maciej Dunajski

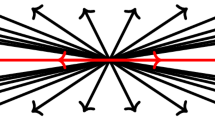
Recently, together with Hill [5], we uncovered an $\mathbf{Sp}(4,\mathbb{R})$ symmetry of the nonholonomic kinematics of a car. I talked about this at the Abel Symposium in Ålesund, Norway, in June 2019. After my talk Maciej Dunajski, intrigued by the root diagram of $\mathfrak{sp}(4,\mathbb{R})$ which appeared in the talk, asked me if using it I can see a $G_2$ structure on a 7-dimensional homogeneous space M = $\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})$.

My immediate answer was: ‘I can think about it, but I have to know which of the $\mathbf{SL}(2,\mathbb{R})$ subgroups of $\mathbf{Sp}(4,\mathbb{R})$ I shall use to built M.’ The reason for the ‘but’ word in my answer was that there are at least two $\mathbf{SL}(2,\mathbb{R})$ subgroups of $\mathbf{Sp}(4,\mathbb{R})$, which lie quite differently in there. One can see them in the root diagram above: the first $\mathbf{SL}(2,\mathbb{R})$ corresponds to the long roots, as, for example, $E_1$ and $E_{10}$, whereas the second one corresponds to the short roots, as, for example, $E_2$ and $E_9$. Since Maciej never told me which $\mathbf{SL}(2,\mathbb{R})$ he wants, I decided to consider both of them and to determine what kind of $G_2$ structures one can associate with the respective choice of a subgroup.

I emphasize that in the below considerations I will use the split real form of the simple exceptional Lie group $G_2$. Therefore, the corresponding $G_2$ structure metrics will not be Riemannian.¹ They will have signature (3, 4).

2 The Lie algebra $\mathfrak{sp}(4,\mathbb{R})$

The Lie algebra $\mathfrak{sp}(4,\mathbb{R})$ is given by the $4\times 4$ matrices

$$\begin{aligned} E=(E^\alpha {}_\beta )= \begin{pmatrix}{a_5}&{}{a_7}&{}{a_9}&{}{2a_{10}}\\ {-a_4}&{}{a_6}&{}{a_8}&{}{a_9}\\ {a_2}&{}{a_3}&{}{-a_6}&{}{-a_7}\\ {-2a_1}&{}{a_2}&{}{a_4}&{}{-a_5} \end{pmatrix}, \end{aligned}$$

where the coefficients $a_I$, $I=1,2,\dots 10$, are real constants. The Lie bracket in $\mathfrak{sp}(4,\mathbb{R})$ is the usual commutator $[E,E']=E\cdot E'-E'\cdot E$ of two matrices E and $E'$. We start with the following basis $(E_I)$,

$$\begin{aligned} E_I=\frac{\partial E}{\partial a_I},\quad I=1,2,\dots 10, \end{aligned}$$

in $\mathfrak{sp}(4,\mathbb{R})$.

In this basis, modulo the antisymmetry, we have the following nonvanishing commutators: $[{E_1},{E_5}]=2{E_1}$, $[{E_1},{E_7}]={-2E_2}$, $[{E_1},{E_9}]={-2E_4}$, $[{E_1},{E_{10}}]={4E_5}$, $[{E_2},{E_4}]={E_1}$, $[{E_2},{E_5}]={E_2}$, $[{E_2},{E_6}]={E_2}$, $[{E_2},{E_7}]={2E_3}$, $[{E_2},{E_8}]={E_4}$, $[{E_2},{E_9}]={-E_5-E_6}$, $[{E_2},{E_{10}}]={-2E_7}$, $[{E_3},{E_4}]={-E_2}$, $[{E_3},{E_6}]={2E_3}$, $[{E_3},{E_8}]={-E_6}$, $[{E_3},{E_9}]={-E_7}$, $[{E_4},{E_5}]={E_4}$, $[{E_4},{E_6}]={-E_4}$, $[{E_4},{E_7}]={E_5-E_6}$, $[{E_4},{E_9}]={-2E_8}$, $[{E_4},{E_{10}}]={-2E_9}$, $[{E_5},{E_7}]={E_7}$, $[{E_5},{E_9}]={E_9}$, $[{E_5},{E_{10}}]={2E_{10}}$, $[{E_6},{E_7}]={-E_7}$, $[{E_6},{E_8}]={2E_8}$, $[{E_6},{E_9}]={E_9}$, $[{E_7},{E_8}]={E_9}$, $[{E_7},{E_9}]={E_{10}}$.

We see that there are at least two $\mathfrak{sl}(2,\mathbb{R})$ Lie algebras here. The first one is

$$\begin{aligned} \mathfrak{sl}(2,\mathbb{R})_l=\mathrm{Span}_\mathbb{R}(E_1,E_5,E_{10}), \end{aligned}$$

and the second is

$$\begin{aligned} \mathfrak{sl}(2,\mathbb{R})_s=\mathrm{Span}_\mathbb{R}(E_2,E_5+E_6,E_9). \end{aligned}$$

The reason for distinguishing these two is as follows:

The eight 1-dimensional vector subspaces $\mathfrak{g}_I=\mathrm{Span}(E_I)$, $I=1,2,3,4,7,8,9,10$, of $\mathfrak{sp}(4,\mathbb{R})$ are the root spaces of this Lie algebra. They correspond to the Cartan subalgebra of $\mathfrak{sp}(4,\mathbb{R})$ given by $\mathfrak{h}=\mathrm{Span}(E_5,E_6)$. It follows that the pairs $(E_I,E_J)$ of the root vectors, such that $I+J=11$, $I,J\ne 5,6$, correspond to the opposite roots of $\mathfrak{sl}(2,\mathbb{R})$. Knowing the Killing form for $\mathfrak{sl}(2,\mathbb{R})$, which in the basis $(E_I)$, and its dual basis $(E^I)$, , is

$$\begin{aligned} K&= {} \tfrac{1}{12}K_{IJ}E^I\odot E^J=-4{E^1} \odot {E^{10}}+2 {E^2}\odot {E^9}+{E^3}\odot {E^8}\\&\quad-2 {E^4}\odot {E^7}+{E^5}\odot {E^5}+{E^6}\odot {E^6}, \end{aligned}$$

one can see that the roots corresponding to the root vectors $(E_1,E_{10})$ and $(E_3,E_8)$ are long, and the roots corresponding to the root vectors $(E_2,E_9)$ and $(E_4,E_7)$ are short; compare the Euclidian lengths of these roots as drawn on the $G_2$ root diagram presented at the beginning of this article.² Thus, the Lie algebra $\mathfrak{sl}(2,\mathbb{R})_l$ containing root vectors $(E_1,E_{10})$ corresponding to the long roots lies quite different in $\mathfrak{sp}(4,\mathbb{R})$ than the Lie algebra $\mathfrak{sl}(2,\mathbb{R})_s$ containing the root vectors $(E_2,E_9)$ corresponding to the short roots.

3 $G_2$ structures on $\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_l$

3.1 Compatible pairs $(g,\phi )$ on $M_l$

To consider the homogeneous space $M_l=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_l$, it is convenient to change the basis $(E_I)$ in $\mathfrak{sp}(4,\mathbb{R})$ to a new one, $(e_I)$, in which the last three vectors span $\mathfrak{sl}(2,\mathbb{R})_l$. Thus, we take:

$$\begin{aligned} e_1=E_2,\,\,e_2=E_3,\,\,e_3=E_4,\,\,e_4=E_6,\,\,e_5=E_7,\,\,e_6=E_8,\,\,e_7=E_9,\,\,e_8=E_1,\,\,e_9=E_5,\,\,e_{10}=E_{10}. \end{aligned}$$

If now, one considers $(e_I)$ as the basis of the Lie algebra of left invariant vector fields on the Lie group $\mathbf{Sp}(4,\mathbb{R})$ then the dual basis $(e^I)$, , of the left invariant forms on $\mathbf{Sp}(4,\mathbb{R})$ satisfies:

$$\begin{aligned} \begin{aligned} \mathrm{d}e^1&=-e^1\wedge (e^4+e^9)+e^2\wedge e^3-2e^5\wedge e^8\\ \mathrm{d}e^2&=-2e^1\wedge e^5-2e^2\wedge e^4\\ \mathrm{d}e^3&=-e^1\wedge e^6+e^3\wedge (e^4-e^9)-2e^7\wedge e^8\\ \mathrm{d}e^4&=e^1\wedge e^7+e^2\wedge e^6+e^3\wedge e^5\\ \mathrm{d}e^5&=2e^1\wedge e^{10}+e^2\wedge e^7+e^5\wedge (e^9-e^4)\\ \mathrm{d}e^6&=2e^3\wedge e^7-2e^4\wedge e^6\\ \mathrm{d}e^7&=2e^3\wedge e^{10}-e^5\wedge e^6+e^7\wedge (e^4+e^9)\\ \mathrm{d}e^8&=-e^1\wedge e^3-2e^8\wedge e^9\\ \mathrm{d}e^9&=e^1\wedge e^7-e^3\wedge e^5-4e^8\wedge e^{10}\\ \mathrm{d}e^{10}&=-e^5\wedge e^7-2e^9\wedge e^{10}. \end{aligned}\end{aligned}$$

(3.1)

Here we used the usual formula relating the structure constants $c^I{}_{JK}$, from $[e_J,e_K]=c^I{}_{JK}e_I$, to the differentials of the Maurer–Cartan forms $(e^I)$, $\mathrm{d}e^I=-\tfrac{1}{2} c^I{}_{JK}e^J\wedge e^K$.

In this basis, the Killing form on $\mathbf{Sp}(4,\mathbb{R})$ is

$$\begin{aligned} K=\tfrac{1}{12}c^I{}_{JK}c^K{}_{LI}e^J\odot e^L=(e^4)^2-2e^3\odot e^5+e^2\odot e^6+2e^1\odot e^7+(e^9)^2-4e^8\odot e^{10}. \end{aligned}$$

Here, we have used the notation $e^I\odot e^J=\tfrac{1}{2}(e^I\otimes e^J+e^J\otimes e^I)$, $(e^I)^2=e^I\odot e^I$.

One can now use equations (3.1) to see that the homogeneous space $M_l=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_l$ is the leaf space of a certain integrable rank 3 distribution $D_l$ on $\mathbf{Sp}(4,\mathbb{R})$, establishing explicitly that $\mathbf{Sp}(4,\mathbb{R})$ has, in particular, the structure of the principal $\mathbf{SL}(2,\mathbb{R})$ fiber bundle $\mathbf{SL}(2,\mathbb{R})_l\rightarrow \mathbf{Sp}(4,\mathbb{R})\rightarrow M_l=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_l$.

Indeed, the 3-dimensional distribution $D_l$, generated by the vector fields X on $\mathbf{Sp}(4,\mathbb{R})$ annihilating the span of the 1-forms $(e^1,e^2,\dots ,e^7)$, is integrable, $\mathrm{d}e^\mu \wedge e^1\wedge e^2\dots \wedge e^7\equiv 0$, $\mu =1,2\dots ,7$, so that we have a well-defined 7-dimensional leaf space $M_l$ of the corresponding foliation. Moreover, the Maurer–Cartan equations (3.1), restricted to a leaf defined by $(e^1,e^2,\dots ,e^7)\equiv 0$, reduce to $\mathrm{d}e^8=-2e^8\wedge e^9$, $\mathrm{d}e^9=-4e^8\wedge e^{10}$, $\mathrm{d}e^{10}=-2e^9\wedge e^{10}$, showing that each leaf can be identified with the Lie group $\mathbf{SL}(2,\mathbb{R})_l$. Thus, the projection $\mathbf{Sp}(4,\mathbb{R})\rightarrow M_l$ from the Lie group $\mathbf{Sp}(4,\mathbb{R})$ to the leaf space $M_l$ is the projection to the homogeneous space $M_l=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_l$.

In this section, I will use from now on Greek indices $\mu ,\nu$, etc., to run from 1 to 7. They number the first seven basis elements in the bases $(e_I)$ and $(e^I)$.

Now, I look for all bilinear symmetric forms $g=g_{\mu \nu }e^\mu \odot e^\nu$ on $\mathbf{Sp}(4,\mathbb{R})$, with constant coefficients $g_{\mu \nu }=g_{\nu \mu }$, which are constant along the leaves of the foliation defined by $D_l$. Technically, I search for those g whose Lie derivative with respect to any vector field X from $D_l$ vanishes,

$$\begin{aligned} {{\mathcal {L}}}_Xg=0\,\, \mathrm{for\,\, all}\,\, X\,\, \mathrm{in}\,\, D_l. \end{aligned}$$

(3.2)

I have the following proposition:

Proposition 3.1

The most general $g=g_{\mu \nu }e^\mu \odot e^\nu$ satisfying condition (3.2) is

$$\begin{aligned} g&= {} g_{22}(e^2)^2+2g_{24}e^2\odot e^4+g_{44}(e^4)^2+2g_{35}(e^3\odot e^5-e^1\odot e^7)\\&\quad+2g_{26}e^2\odot e^6+2g_{46}e^4 \odot e^6+g_{66}(e^6)^2. \end{aligned}$$

Thus, I have a 7-parameter family of bilinear forms on $\mathbf{Sp}(4,\mathbb{R})$ that descend to well-defined pseudo-Riemannian metrics on the leaf space $M_l$. Note that the restriction of the Killing form K to the space where $(e^8,e^9,e^{10})\equiv 0$ is in this family. This corresponds to $g_{22}=g_{24}=g_{46}=0$ and $g_{44}=2g_{26}=-g_{35}=1$.

Since the aim of my note is not to be exhaustive, but rather to show how to produce $G_2$ structures on $\mathbf{Sp}(4,\mathbb{R})$ homogeneous spaces, from now on I will restrict myself to only one $\mathbf{SL}(2,\mathbb{R})_l$ invariant bilinear form g on $\mathbf{Sp}(4,\mathbb{R})$, namely to

$$\begin{aligned} g_K=(e^4)^2-2e^3\odot e^5+e^2\odot e^6+2e^1\odot e^7, \end{aligned}$$

(3.3)

coming from the restriction of the Killing form. It follows from Proposition 3.1 that this form is a well-defined (3, 4) signature metric on the quotient space $M_l=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_l$.

I now look for the 3-forms $\phi =\tfrac{1}{6}\phi _{\mu \nu \rho }e^\mu \wedge e^\nu \wedge e^\rho$ on $\mathbf{Sp}(4,\mathbb{R})$ that are constant along the leaves of the distribution $D_l$, i.e., such that

$$\begin{aligned} {{\mathcal {L}}}_X\phi =0\,\, \mathrm{for\,\, all}\,\, X\,\, \mathrm{in}\,\, D_l. \end{aligned}$$

(3.4)

Then, I have the following proposition.

Proposition 3.2

There is a 10-parameter family of 3-forms $\phi =\tfrac{1}{6}\phi _{\mu \nu \rho }e^\mu \wedge e^\nu \wedge e^\rho$ on $\mathbf{Sp}(4,\mathbb{R})$ which satisfy condition (3.4). The general formula for them is:

$$\begin{aligned} \phi&= {} f e^{125}+a(e^{235}-e^{127})+pe^{145}+q(e^{147}+e^{345})\\&\quad+se^{156}+t(e^{356}-e^{167})+he^{237}+be^{246}+re^{347}+ue^{367}. \end{aligned}$$

Here $e^{\mu \nu \rho }=e^\mu \wedge e^\nu \wedge e^\rho$, and a, b, f, h, p, q, r, s, t and u are real constants.

Thus there is a 10-parameter family of 3-forms $\phi$ that descends from $\mathbf{Sp}(4,\mathbb{R})$ to the $\mathbf{Sp}(4,\mathbb{R})$ homogeneous space $M_l=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_l$.

Now, I introduce an important notion of compatibility of a pair $(g,\phi )$ where g is a metric and $\phi$ is a 3-form on a 7-dimensional oriented manifold M. The pair $(g,\phi )$ on M is compatible if and only if

Here $\mathrm{vol}(g)$ is a volume form on M related to the metric g.

Restricting, as I did, to the $\mathbf{Sp}(4,\mathbb{R})$ invariant metric $g_K$ on $M_l$ as in (3.3), I now ask which of the 3-forms $\phi$ from Proposition 3.2 are compatible with the metric (3.3). In other words, I now look for the constants a, b, f, h, p, q, r, s, t and u such that

(3.5)

for $g=g_K$ given in (3.3).

I have the following proposition.

Proposition 3.3

The general solution to the Eq. (3.5) is given by

$$\begin{aligned} b&= {} \tfrac{1}{2},\,\,f=\frac{ap}{1-q},\,\,h=\frac{a(q-1)}{p},\,\,r=\frac{q^2-1}{p},\,\,s=\frac{p(1-q)}{4a},\,\,t\\&= {} \frac{1-q^2}{4a},\,\,u=\frac{(q^2-1)(q+1)}{4ap}. \end{aligned}$$

This leads to the following corollary.

Corollary 3.4

The most general pair $(g_K,\phi )$ on $M_l$ compatible with the $\mathbf{Sp}(4,\mathbb{R})$ invariant metric

$$\begin{aligned} g_K=(e^4)^2-2e^3\odot e^5+e^2\odot e^6+2e^1\odot e^7, \end{aligned}$$

coming from the Killing form in $\mathbf{Sp}(4,\mathbb{R})$, is a 3-parameter family with $\phi$ given by:

$$\begin{aligned} \begin{aligned}\phi &=\frac{ap}{1-q} e^{125}+a(e^{235}-e^{127})+pe^{145}+q(e^{147}+e^{345})+\frac{p(1-q)}{4a}e^{156}\\ {}&+\frac{1-q^2}{4a}(e^{356}-e^{167})+\frac{a(q-1)}{p}e^{237}+\tfrac{1}{2}e^{246}+\frac{q^2-1}{p}e^{347}+\frac{(q^2-1)(q+1)}{4ap}e^{367}. \end{aligned} \end{aligned}$$

Here $a\ne 0$, $p\ne 0$, $q\ne 1$ are free parameters, and $e^{\mu \nu \rho }=e^\mu \wedge e^\nu \wedge e^\rho$ as before.

3.2 $G_2$ structures in general

Compatible pairs $(g,\phi )$ on 7-dimensional manifolds are interesting since they give examples of $G_2$ structures [2]. In general, a $G_2$ structure consists of a compatible pair $(g,\phi )$ of a metric g and a 3-form $\phi$ on a 7-dimensional manifold M, and it is in addition assumed that the 3-form $\phi$ is generic, meaning that at every point of M it lies in one of the two open orbits of the natural action of $\mathbf{GL}(7,\mathbb{R})$ on 3-forms in $\mathbb{R}^7$. The simple exceptional Lie group $G_2$ appears here as the common stabilizer in $\mathbf{GL}(7,\mathbb{R})$ of both g and $\phi$.

It follows (from compatibility) that the $G_2$ structures can have metrics g of only two signatures: the Riemannian ones and (3, 4) signature ones. If the signature of g is Riemannian, the corresponding $G_2$ structure is related to the compact real form of the simple exceptional complex Lie group $G_2$, and in the (3, 4) signature case the corresponding $G_2$ structure is related to the noncompact (split) real form of the complex group $G_2$. In this sense, our Corollary 3.4 provides a 3-parameter family of split real form $G_2$ structures on $M_l$.

$G_2$ structures can be classified according to the properties of their intrinsic torsion [1, 2]. Making a long story short, this torsion is totally determined by finding four p-forms $\tau _p$ on M, $p=0,1,2,3$, each belonging to one of four different irreducible representations of $G_2$. Before telling on how to find these forms given a $G_2$ structure $(g,\phi )$, we need some preparation.

We recall that the group $G_2$ acts in $\mathbb{R}^7$, and this induces its action on spaces $\bigwedge ^p$ of p-forms in $\mathbb{R}^7$. Of course the 1-dimensional space $\bigwedge ^0$ is $G_2$ irreducible, as well as is the space of 1-forms $\bigwedge ^1=\bigwedge ^1_7$. The $G_2$ irreducible decompositions of the spaces of 2- and 3-forms look like $\bigwedge ^2=\bigwedge ^2_7\oplus \bigwedge ^2_{14}$ and $\bigwedge ^3=\bigwedge ^3_1\oplus \bigwedge ^3_7\oplus \bigwedge ^3_{27}$. Here we use the convention that the lower index i in $\bigwedge ^p_i$ denotes the dimension of the corresponding representation. It is further convenient to introduce the Hodge dual, $*$, which is defined on p-forms $\lambda$ by

By the Hodge duality, the decomposition of $\bigwedge ^4$ into $G_2$ irreducible components is similar to this for $\bigwedge ^3$. We further mention that the 7-dimensional representations $\bigwedge ^1_7$, $\bigwedge ^2_7$ and $\bigwedge ^3_7$ are all $G_2$ equivalent. Also, one can see that, e.g., $\textstyle {\bigwedge ^3_{27}}=\{\alpha \in \bigwedge ^3\,\,\,\mathrm{s.t.}\,\,\,\alpha \wedge \phi =0\,\, \& \,\,\alpha \wedge *\phi =0\}$.

The intrinsic torsion components $\tau _0$, $\tau _1$, $\tau _2$ and $\tau _3$ have values in the following $G_2$ irreducible modules: the 3-form $\tau _3$ has values in the 27-dimensional irreducible representation $\bigwedge ^3_{27}$, the 2-form $\tau _2$ has values in the 14-dimensional irreducible representation $\bigwedge ^2_{14}$, the 1-form $\tau _1$ has values in the 7-dimensional irreducible representation $\bigwedge ^1_{7}$, and the 0-form $\tau _0$ has values in the trivial representation $\bigwedge ^0_1$.

The result of Bryant [1, 2] states that for every $G_2$ structure $(g,\phi )$ on M there exist unique forms $\tau _0$, $\tau _1$, $\tau _2$ and $\tau _3$ on M, with values in the above-mentioned representations, such that

$$\begin{aligned} \begin{aligned}&\mathrm{d}\phi =\tau _0 *\phi +3 \tau _1\wedge \phi +*\tau _3\\&\mathrm{d}*\phi =4\tau _1\wedge *\phi +\tau _2\wedge \phi . \end{aligned} \end{aligned}$$

(3.6)

Thus, Eq. (3.6) enable to determine all the intrinsic torsion components $\tau _0$, $\tau _1$, $\tau _2$ and $\tau _3$ of a given $G_2$ structure $(g,\phi )$. They are called Bryant’s [1, 2] equations. It follows that vanishing or not of each of the forms $\tau _p$ is a $G_2$ invariant property of a $G_2$ structure.

3.3 All $\mathbf{Sp}(4,\mathbb{R})$ symmetric $G_2$ structures on $M_l$ with the metric coming from the Killing form

The below theorem characterizes the $G_2$ structures corresponding to compatible pairs $(g_K,\phi )$ from Corollary 3.4; it summarizes the already obtained results and, in addition, provides formulas for the intrinsic torsion which are needed for the characterization.

Theorem 3.5

Let $g_K$ be the (3, 4) signature metric on $M_l=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_l$ arising as the restriction of the Killing form K from $\mathbf{Sp}(4,\mathbb{R})$ to $M_l$,

$$\begin{aligned} g_K=(e^4)^2-2e^3\odot e^5+e^2\odot e^6+2e^1\odot e^7. \end{aligned}$$

Then the most general $G_2$ structure associated with such $g_K$ is a 3-parameter family $(g_K,\phi )$ with the 3-form

$$\begin{aligned} \begin{aligned} \phi &=\frac{ap}{1-q} e^{125}+a(e^{235}-e^{127})+pe^{145}+q(e^{147}+e^{345})+\frac{p(1-q)}{4a}e^{156}\\ {}&\quad +\frac{1-q^2}{4a}(e^{356}-e^{167})+\frac{a(q-1)}{p}e^{237}+\tfrac{1}{2}e^{246}+\frac{q^2-1}{p}e^{347}+\frac{(q^2-1)(q+1)}{4ap}e^{367}. \end{aligned} \end{aligned}$$

For this structure, the torsions $\tau _\mu$ solving the Bryant’s equations (3.6) are:

$$\begin{aligned} \begin{aligned} \tau _0&=\,\frac{6}{7}\,\frac{(2a-p)^2q-(2a+p)^2}{ap},\\ \tau _1&=\frac{1}{4}\,(2a-p)\,\Big (\,-\,e^2\,+\,\frac{1}{2}\,\frac{(2a+p)(q-1)}{ap}\,e^4\,+\,\frac{1}{2}\,\frac{q^2-1}{ap}\,e^6\,\Big ),\\ \tau _2&=\,0 ,\\ \tau _3&=\,\Big (\tfrac{3}{28}(2a-p)^2 +\frac{8ap}{7(q-1)}\Big )e^{125}+\frac{11p^2+16ap-12a^2+3q(2a-p)^2}{28p}e^{127}\\&\quad - \frac{44a^2+16ap-3p^2+3q(2a-p)^2}{28a}e^{145}\\&\quad +\frac{(7-4q)(2a+p)^2-3q^2(2a-p)^2}{28ap}e^{147}\\&\quad +\frac{3p^2(q-1)^2-12ap(q^2-1)+4a^2(31+22q+3q^2)}{112a^2}e^{156}\\&\quad -\frac{(q^2-1)(44a^2+16ap-3p^2+3q(2a-p)^2)}{112a^2p}e^{167}\\&\quad +\frac{12a^2-16ap-11p^2-3q(2a-p)^2}{28p}e^{235}\\&\quad -\frac{12a^2(q-1)^2-12ap(q^2-1)+p^2(31+22q+3q^2)}{28p^2}e^{237}\\&\quad +\frac{4ap(6-q)+(4a^2+p^2)(q-1)}{14ap}e^{246}\\&\quad +\frac{(7-4q)(2a+p)^2-3q^2(2a-p)^2}{28ap}e^{345}\\&\quad + \frac{(q^2-1)(12a^2-16ap-11p^2-3q(2a-p)^2)}{28ap^2}e^{347}\\&\quad +\frac{(q^2-1)(44a^2+16ap-3p^2+3q(2a-p)^2)}{112a^2p}e^{356}\\&\quad +\frac{(q^2-1)(q+1)(12a^2-44ap+3p^2-3q(2a-p)^2)}{112a^2p^2}e^{367}, \end{aligned} \end{aligned}$$

where as usual $e^{\mu \nu }=e^\mu \wedge e^\nu$ and $e^{\mu \nu \rho }=e^\mu \wedge e^\nu \wedge e^\rho$.

Thus, the 3-parameter family of $G_2$ structures on $M_l$ described in this theorem have the entire 14-dimensional torsion $\tau _2=0$. This means that all these $G_2$ structures are integrable in the terminology of [3, 4], or what is the same, this means that they all have the totally skew symmetric torsion.

4 $G_2$ structures on $\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_s$

Now we consider the homogeneous space $M_s=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_s$. Since $\mathfrak{sl}(2,\mathbb{R})$ is spanned by $E_2,E_5+E_6,E_9$, it is convenient to put these vectors at the end of the new basis of the Lie algebra $\mathfrak{sp}(4,\mathbb{R})$. We choose this new basis $(f_I)$ in $\mathfrak{sp}(4,\mathbb{R})$ as:

$$\begin{aligned} f_1&= {} E_1,\,\,f_2=E_3,\,\,f_3=E_4,\,\,f_4=E_6-E_5,\,\,f_5=E_7,\,\,f_6=E_8,\,\,\\ f_7&= {} E_{10},\,\,f_8=E_2,\,\,f_9=E_5+E_6,\,\,f_{10}=E_{9}. \end{aligned}$$

If now, one considers $(f_I)$ as the basis of the Lie algebra of invariant vector fields on the Lie group $\mathbf{Sp}(4,\mathbb{R})$, then the dual basis $(f^I)$, , of the left invariant forms on $\mathbf{Sp}(4,\mathbb{R})$, satisfies:

$$\begin{aligned} \begin{aligned} \mathrm{d}f^1&=2f^1\wedge (f^4-f^9)+f^3\wedge f^8\\ \mathrm{d}f^2&=-2f^2\wedge (f^4+f^9)+2f^5\wedge f^8\\ \mathrm{d}f^3&=2f^1\wedge f^{10}+2f^3\wedge f^4+f^6\wedge f^8\\ \mathrm{d}f^4&=2f^1\wedge f^7+\tfrac{1}{2}f^2\wedge f^6+f^3\wedge f^5\\ \mathrm{d}f^5&=f^2\wedge f^{10}+2f^4\wedge f^5-2f^7\wedge f^8\\ \mathrm{d}f^6&=2f^3\wedge f^{10}-2(f^4+f^9)\wedge f^6\\ \mathrm{d}f^7&=2(f^4-f^9)\wedge f^{7}-f^5\wedge f^{10}\\ \mathrm{d}f^8&=2f^1\wedge f^5+f^2\wedge f^3-2f^8\wedge f^9\\ \mathrm{d}f^9&=-2f^1\wedge f^7+\tfrac{1}{2}f^2\wedge f^6+f^8\wedge f^{10}\\ \mathrm{d}f^{10}&=2f^3\wedge f^7-f^5\wedge f^6-2f^9\wedge f^{10}. \end{aligned} \end{aligned}$$

(4.1)

In this basis, the Killing form on $\mathbf{Sp}(4,\mathbb{R})$ is

$$\begin{aligned}&K=\tfrac{1}{12}c^I{}_{JK}c^K{}_{LI}f^J\odot \\&f^L=2(f^4)^2-2f^3\odot f^5+f^2\odot f^6-4f^1\odot f^7+2(f^9)^2+2f^8\odot f^{10}, \end{aligned}$$

where as usual the structure constants $c^I{}_{JK}$ are defined by $[f_I,f_J]=c^K{}_{IJ}f_K$.

Using the same arguments, as in the case of $M_l$, we again see that $\mathbf{Sp}(4,\mathbb{R})$ has the structure of the principal $\mathbf{SL}(2,\mathbb{R})$ fiber bundle $\mathbf{SL}(2,\mathbb{R})_s\rightarrow \mathbf{Sp}(4,\mathbb{R})\rightarrow M_s=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_s$ over the homogeneous space $M_s=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_s$. In particular, we have a foliation of $\mathbf{Sp}(4,\mathbb{R})$ by integral leaves of an integrable distribution $D_s$ spanned by the annihilator of the forms $(f^1,f^2,\dots ,f^7)$. As before, also in this section, we will use Greek indices $\mu ,\nu$, etc., to run from 1 to 7. They now number the first seven basis elements in the bases $(f_I)$ and $(f^I)$.

Repeating the procedure from the previous sections, I now search for all bilinear symmetric forms $g=g_{\mu \nu }f^\mu \odot f^\nu$ on $\mathbf{Sp}(4,\mathbb{R})$, with constant coefficients $g_{\mu \nu }=g_{\nu \mu }$, whose Lie derivative with respect to any vector field X from $D_l$ vanishes,

$$\begin{aligned} {{\mathcal {L}}}_Xg=0\,\, \mathrm{for\,\, all}\,\, X\,\, \mathrm{in}\,\, D_s. \end{aligned}$$

(4.2)

I have the following proposition.

Proposition 4.1

The most general $g=g_{\mu \nu }f^\mu \odot f^\nu$ satisfying condition (4.2) is

$$\begin{aligned} g&= {} g_{33}\big ((f^3)^2-2f^1\odot f^6\big )+g_{44}(f^4)^2+g_{55}\big ((f^5)^2+2f^2\odot f^7\big )\\&\quad+2g_{26}\big (-2f^3\odot f^5+f^2\odot f^6-4 f^1\odot f^7\big ). \end{aligned}$$

Thus, this time, I only have a 4-parameter family of bilinear forms on $\mathbf{Sp}(4,\mathbb{R})$ that descend to well-defined pseudo-Riemannian metrics on the leaf space $M_s$. Note that the restriction of the Killing form K to the space where $(f^8,f^9,f^{10})\equiv 0$ is in this family. This corresponds to $g_{33}=g_{55}=0$ and $g_{44}=2$, $g_{26}=1/2$.

Again for simplicity reasons, I will solve the problem of finding $\mathbf{Sp}(4,\mathbb{R})$ invariant $G_2$ structures on $M_s$ restricting to only those pairs $(g,\phi )$ for which $g=g_K$, where

$$\begin{aligned} g_K=2(f^4)^2-2f^3\odot f^5+f^2\odot f^6-4f^1\odot f^7, \end{aligned}$$

(4.3)

which again means that I only will consider one metric, the one coming from the restriction of the Killing form of $\mathbf{Sp}(4,\mathbb{R})$ to $M_s$. It is a well-defined (3, 4) signature metric on the quotient space $M_s=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_s$.

I now look for the 3-forms $\phi =\tfrac{1}{6}\phi _{\mu \nu \rho }f^\mu \wedge f^\nu \wedge f^\rho$ on $\mathbf{Sp}(4,\mathbb{R})$ which are such that

$$\begin{aligned} {{\mathcal {L}}}_X\phi =0\,\, \mathrm{for\,\, all}\,\, X\,\, \mathrm{in}\,\, D_s. \end{aligned}$$

(4.4)

I have the following proposition.

Proposition 4.2

There is precisely a 5-parameter family of 3-forms $\phi =\tfrac{1}{6}\phi _{\mu \nu \rho }f^\mu \wedge f^\nu \wedge f^\rho$ on $\mathbf{Sp}(4,\mathbb{R})$ which satisfies condition (4.4). The general formula for $\phi$ is:

$$\begin{aligned} \phi&= {} a(4f^{147}+f^{246}+2f^{345})+b(2f^{156}+f^{236}-4f^{137})+qf^{136}\\&\quad+h(f^{256}-4f^{157}-2f^{237})+pf^{257}. \end{aligned}$$

Here $f^{\mu \nu \rho }=f^\mu \wedge f^\nu \wedge f^\rho$, and a, b, q, h and p are real constants.

Solving for all 3-forms $\phi$ from this 5-parameter family that are compatible, as in (3.5), with the metric $g_K$ from (4.3), I arrive at the following proposition.

Proposition 4.3

The general solution to the equations (3.5) is given by

$$\begin{aligned} a=\tfrac{1}{2},\,\,b=h=0,\,\,p=\frac{1}{q}. \end{aligned}$$

This leads to the following corollary.

Corollary 4.4

The most general pair $(g_K,\phi )$ on $M_s$ compatible with the $\mathbf{Sp}(4,\mathbb{R})$ invariant metric

$$\begin{aligned} g_K=2(f^4)^2-2f^3\odot f^5+f^2\odot f^6-4f^1\odot f^7, \end{aligned}$$

coming from the Killing form in $\mathbf{Sp}(4,\mathbb{R})$, is a 1-parameter family with $\phi$ given by:

$$\begin{aligned} \begin{aligned}\phi &=2f^{147}+\tfrac{1}{2}f^{246}+f^{345}+qf^{136}+\frac{1}{q}f^{257} .\end{aligned} \end{aligned}$$

Here $q\ne 0$ is a free parameter, and $f^{\mu \nu \rho }=f^\mu \wedge f^\nu \wedge f^\rho$ as before.

4.1 All $\mathbf{Sp}(4,\mathbb{R})$ symmetric $G_2$ structures on $M_s$ with the metric coming from the Killing form

Similarly as in Sect. 3.3 we now summarize the already obtained results about the considered $Sp(2,\mathbb{R})$ symmetric $G_2$ structures on $M_s$ in a theorem; it is given below and has also a new part consisting of the formulas for the intrinsic torsion.

Theorem 4.5

Let $g_K$ be the (3, 4) signature metric on $M_s=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_s$ arising as the restriction of the Killing form K from $\mathbf{Sp}(4,\mathbb{R})$ to $M_s$,

$$\begin{aligned} g_K=2(f^4)^2-2f^3\odot f^5+f^2\odot f^6-4f^1\odot f^7. \end{aligned}$$

Then, the most general $G_2$ structure associated with such $g_K$ is a 1-parameter family $(g_K,\phi )$ with the 3-form

$$\begin{aligned} \phi = 2f^{147}+\tfrac{1}{2}f^{246}+f^{345}+qf^{136}+\frac{1}{q}f^{257}. \end{aligned}$$

For this structure

$$\begin{aligned} \mathrm{d}*\phi =0, \end{aligned}$$

i.e., the torsions

$$\begin{aligned} \tau _1=\tau _2=0. \end{aligned}$$

The rest of the torsions solving Bryant’s equations (3.6) are:

$$\begin{aligned} \begin{aligned} \tau _0&=\,-\frac{18}{7},\\ \tau _3&=\,\tfrac{2}{7}\,\big (\,4f^{147}+f^{246}+2f^{345}\,\big )\,-\,\tfrac{3}{7}\,\big (\,q\,f^{136}+\frac{1}{q}\,f^{257}\,\big ). \end{aligned} \end{aligned}$$

where, as usual $f^{\mu \nu \rho }=f^\mu \wedge f^\nu \wedge f^\rho$; $q\ne 0$.

So on $M_s=\mathbf{Sp}(4,\mathbb{R})/\mathbf{SL}(2,\mathbb{R})_s$ there exists a 1-parameter family of the above $G_2$ structures which is coclosed. Therefore, in particular, it is integrable

I note that formally I can also obtain coclosed $G_2$ structures on $M_l$, using Theorem 3.5. It is enough to take $p=2a$ in the solutions of this Theorem. The question if in the resulting 2-parameter family of the coclosed $G_2$ structures there is a 1-parameter subfamily equivalent to the structures I have on $M_s$ via Theorem 4.5 needs further investigation. However, I doubt that the answer to this question is positive, since it is visible from the root diagram for $\mathbf{Sp}(4,\mathbb{R})$ that the spaces $M_l$ and $M_s$ are geometrically quite different. Indeed, apart from the $\mathbf{Sp}(4,\mathbb{R})$ invariant $G_2$ structures, which I have just introduced in this note, the spaces $M_l$ and $M_s$ have quite different additional $\mathbf{Sp}(4,\mathbb{R})$ invariant structures. A short look at the root diagram on page 1 of this note shows that $M_l$ has two well-defined $\mathbf{Sp}(4,\mathbb{R})$ invariant rank 3-distributions, corresponding to the pushforwards from $\mathbf{Sp}(4,\mathbb{R})$ to $M_l$ of the vector spaces $D_{l1}=\mathrm{Span}_\mathbb{R}(E_2,E_3,E_7)$ and $D_{l2}=\mathrm{Span}_\mathbb{R}(E_4,E_8,E_9)$. Likewise $M_s$, in addition to the discussed $G_2$ structures, has also a well defined pair of $\mathbf{Sp}(4,\mathbb{R})$ invariant rank 3-distributions, corresponding to the pushforwards from $\mathbf{Sp}(4,\mathbb{R})$ to $M_s$ of the vector spaces $D_{s1}=\mathrm{Span}_\mathbb{R}(E_1,E_4,E_8)$ and $D_{s2}=\mathrm{Span}_\mathbb{R}(E_3,E_7,E_{10})$. The problem is that these two sets of pairs of $\mathbf{Sp}(4,\mathbb{R})$ invariant distributions are quite different. The distributions on $M_l$ have constant growth vector (2, 3), while the distributions on $M_s$ are integrable. These pairs of distributions constitute an immanent ingredient of the geometry on the corresponding spaces $M_l$ and $M_s$ and, since they are diffeomorphically nonequivalent and they make the $G_2$ geometries there quite different. I believe that this fact makes the $G_2$ structures obtained on $M_l$ and $M_s$ really nonequivalent.