Solid angles and Seifert hypersurfaces

Abstract

Given a smooth closed oriented manifold M of dimension n embedded in ${\mathbb {R}}^{n+2}$, we study properties of the ‘solid angle’ function $\varPhi :{\mathbb {R}}^{n+2}{{\setminus }} M\rightarrow S^1$. It turns out that a non-critical level set of $\varPhi$ is an explicit Seifert hypersurface for M. This gives an explicit analytic construction of a Seifert surface in higher dimensions.

1 Introduction

It has been known since Seifert [13] that every oriented link $L=\coprod S^1\subset {\mathbb {R}}^3$ possesses a Seifert surface, that is, a compact oriented surface $\varSigma \subset {\mathbb {R}}^3$ such that $\partial \varSigma =L$. Seifert gave an explicit algorithm for finding a Seifert surface from a link diagram.

In 1969 Erle [7] proved that any embedding $M^n\subset {\mathbb {R}}^{n+2}$ of codimension two of a closed oriented connected manifold M has a trivial normal bundle and admits a Seifert hypersurface $\varSigma ^{n+1} \subset {\mathbb {R}}^{n+2}$ with $\partial \varSigma = M \subset {\mathbb {R}}^{n+2}$. The proof of the existence of the latter fact is not constructive; it relies on the Pontryagin–Thom construction applied to any smooth map $f:{\mathrm{cl.}}({\mathbb {R}}^{n+2} \backslash M\times D^2) \rightarrow S^1$ representing the generator

$$\begin{aligned} 1 \in \left[{\mathrm{cl.}}\left({\mathbb {R}}^{n+2}\backslash M\times D^2\right),S^1\right]=H^1\left({\mathbb {R}}^{n+2}\backslash M\right)=H_n(M)={\mathbb {Z}}\end{aligned}$$

with $\varSigma =f^{-1}(t)$ for a regular value $t \in S^1$. An easy adjustment has to be made, because f is defined outside the tubular neighborhood of M; we refer to [7] for details.

Fig. 1

Scalar magnetic potential as a solid angle. The scalar magnetic potential is calculated at point O

In this paper, we use intuitions from physics to construct a concrete smooth map $\varPhi :{\mathbb {R}}^{n+2}{\setminus } M\rightarrow {\mathbb {R}}/{\mathbb {Z}}=S^1$. Namely, suppose $M\subset {\mathbb {R}}^3$ is a loop with constant electric current. The scalar magnetic potential $\widetilde{\varPhi }$ of M at a point $x\notin M$ is the solid angle subtended by M, that is, the signed area of a spherical surface bounded by the image of M under the radial projection, as seen from x (Fig. 1); see [10, Chapter III] or [9, Section 8.3]. As the complement ${\mathbb {R}}^3{\setminus } M$ is not simply connected, the potential $\widetilde{\varPhi }$ is defined only modulo a constant, which we normalize to be 1. The potential induces a well-defined function $\varPhi :{\mathbb {R}}^3{\setminus } M\rightarrow {\mathbb {R}}/{\mathbb {Z}}$. This physical interpretation suggests that there exists an open neighborhood N of M such that $\varPhi |_{N{\setminus } M}$ is a locally trivial fibration. In particular, a level set $\varPhi ^{-1}(t)$ should be a (possibly disconnected) Seifert surface for M. In [4, Chapter VII] the second author proved that this is indeed the case, although the proof is rather involved. Even for a circle, the exact formula for $\varPhi$ is complicated; it was given by Maxwell in [10, Chapter XIV] in terms of power series and also by Paxton in [11]. The formulae for $\varPhi$ for the circle show that the analytic behavior of $\varPhi$ near M is quite intricate, although we can show that $\varPhi$ is a locally trivial fibration in $U{\setminus } M$ for some small neighborhood U of M; see Sect. 5.3.

The construction can be generalized to higher dimensions, even though the physical interpretation seems to be a little less clear. For any closed oriented submanifold $M^n\subset {\mathbb {R}}^{n+2}$, by the result of Erle [7] there exists a Seifert hypersurface. For any such hypersurface $\varSigma$ and a point $x\notin \varSigma$, we define $\widetilde{\varPhi }(x)$ to be the high-dimensional solid angle of M, that is, the signed area of the image of the radial projection of $\varSigma$ to the $(n+1)$-sphere of radius 1 and center x. The value of $\widetilde{\varPhi }(x)$ depends on the choice of the hypersurface $\varSigma$, but it turns out that under a suitable normalization, $\varPhi (x):=\widetilde{\varPhi }(x)\bmod 1$ is independent of the choice of the Seifert hypersurface. Moreover, there is a formula for $\varPhi (x)$ in terms of integrals of some concrete differential forms over M, so the existence of $\varSigma$ is needed only to show that $\varPhi$ is well defined.

As long as $t\ne 0\in {\mathbb {R}}/{\mathbb {Z}}$, the preimage $\varPhi ^{-1}(t)$ is a bounded hypersurface in ${\mathbb {R}}^{n+2}{\setminus } M$. If, additionally, t is a non-critical value, $\varPhi ^{-1}(t)$ is smooth. To prove that $\varPhi ^{-1}(t)$ is actually a Seifert hypersurface for M, we need to study the local behavior of $\varPhi$ near M. It turns out that the closure of $\varPhi ^{-1}(t)$ is smooth except possibly at the boundary. We obtain the following result, which we can state as follows.

Theorem 1.1

Let $M\subset {\mathbb {R}}^{n+2}$ be a smooth codimension 2 embedding. Let $\varPhi :{\mathbb {R}}^{n+2}{\setminus } M\rightarrow {\mathbb {R}}/{\mathbb {Z}}$ be the solid angle map (or the scalar magnetic potential map).

• On the set of points$\{x\in {\mathbb {R}}^{n+2}{\setminus } M:(0,0,\ldots ,0,1)\not \in {{\,{\mathrm{Sec}}\,}}_x(M)\}$, the map$\varPhi$is given by

  $$\begin{aligned} \varPhi (x)=\int _M\frac{1}{\Vert y-x\Vert ^{n+1}} \lambda \left( \frac{x_{n+2}-y_{n+2}}{\Vert x-y\Vert }\right) \cdot \\ \sum _{i=1}^{n+1} (-1)^{i+1} (y_i-x_i) \hbox{d}y_1\wedge \cdots \widehat{\hbox{d}y_i}\cdots \wedge \hbox{d}y_{n+1}, \end{aligned}$$

  where${{\,{\mathrm{Sec}}\,}}_x$is the secant map${{\,{\mathrm{Sec}}\,}}_x(y)=\dfrac{y-x}{\Vert y-x\Vert }$and$\lambda$is an explicit function depending on the dimensionndescribed in (2.18).

• Let$t\ne 0$be a non-critical value of$\varPhi$. Then$\varPhi ^{-1}(t)$is a smooth (open) hypersurface whose closure is$\varPhi ^{-1}(t)\cup M$. The closure of$\varPhi ^{-1}(t)$is a possibly disconnected Seifert hypersurface forM(in the sense of Definition 2.1), which is a topological submanifold of${\mathbb {R}}^{n+2}$, smooth up to boundary.

• For$t\ne 0$, the preimage$\varPhi ^{-1}(t)$has finite$(n+1)$-dimensional volume.

To the best of our knowledge, up until now, there has been no known high-dimensional analogue of Seifert’s algorithm for constructing Seifert hypersurfaces for general links. Our method of constructing a Seifert hypersurface is by a mixture of differential geometry and analysis, so is not strictly speaking algorithmic. Nevertheless, it is the first explicit construction for general links.

The fact that the hypersurface $\varPhi ^{-1}(t)$ is a level set of the scalar magnetic potential function $\varPhi$ leads to the following question. We have, however, not been able to answer it so far.

Question 1

Does the physical interpretation of $\varPhi ^{-1}(t)$ imply some specific geometric or topological properties, like being a local minimizer for some energy function?

The structure of the paper is the following. Section 1 defines rigorously the solid angle map $\varPhi$. Then a formula for $\varPhi$ in terms of an integral of an n–form over M is given. In Sect. 3 we prove that for $t\ne 0$ the inverse images of $\varPhi ^{-1}(t)\subset {\mathbb {R}}^{n+1}$ are bounded. It is also proved that $\varPhi$ extends to a smooth map $S^{n+2}{\setminus } M\rightarrow {\mathbb {R}}/{\mathbb {Z}}$. In Sect. 4 we calculate explicitly $\varPhi$ for a linear subspace. The resulting simple formula is used later in the proof of the local behavior of $\varPhi$ for general M. In Sect. 5 we derive the Maxwell–Paxton formula for $\varPhi$ if M is a circle. These explicit calculations allow us to study the local behavior of $\varPhi$ in detail and give insight for the general case. In Sects. 6 and 7 we study the local behavior of $\varPhi$ for general M. This is the most technical part of the paper. We prove Theorem 1.1 in Sect. 8.

2 Definition of the map $\varPhi$

Consider a point $x\in {\mathbb {R}}^{n+2}$ and define the map ${{\,{\mathrm{Sec}}\,}}_x:{\mathbb {R}}^{n+2}{\setminus }\{x\}\rightarrow S^{n+1}$ given by

$$\begin{aligned} {{\,{\mathrm{Sec}}\,}}_x(y)=\frac{y-x}{\Vert y-x\Vert }. \end{aligned}$$

The map ${{\,{\mathrm{Sec}}\,}}_x$ can be defined geometrically as the radial projection from x onto the sphere: for a point $y\ne x$ take a half-line $l_{xy}$ going out from x and passing through y. We define ${{\,{\mathrm{Sec}}\,}}_x(y)$ as the unique point of intersection of $l_{xy}$ and $S_x$, where $S_x$ is the unit sphere with center x.

Let $\omega _{n+1}$ be the $(n+1)$-form

$$\begin{aligned} \omega _{n+1}=\sum _{j=1}^{n+2}(-1)^{j+1}u_j\hbox{d}u_1\wedge \cdots \wedge \widehat{\hbox{d}u_j}\wedge \cdots \wedge \hbox{d}u_{n+2} \end{aligned}$$

on $S^{n+1}$. Define also

$$\begin{aligned} \sigma _{n+1}=\int _{S^{n+1}} \omega _{n+1}, \end{aligned}$$

that is, the volume of the unit $(n+1)$-dimensional sphere; for instance, ${\sigma _1=2\pi }$, $\sigma _2=4\pi$.

Let M be a closed oriented connected and smooth manifold in ${\mathbb {R}}^{n+2}$ with $\dim M=n$.

Definition 2.1

A compact oriented $(n+1)$-dimensional submanifold $\varSigma$ of ${\mathbb {R}}^{n+2}$ such that $\partial \varSigma =M$, $\varSigma$ is smooth except possibly at the boundary and $\varSigma$ has finite $(n+1)$-dimensional volume, is called a Seifert hypersurface for M.

Remark 2.2

Unlike in many places in low-dimensional knot theory, we do not assume that $\varSigma$ is connected.

By Erle [7] any closed oriented submanifold $M\subset {\mathbb {R}}^{n+2}$ admits a Seifert hypersurface, which is smooth. Given such a hypersurface $\varSigma$, consider $x\in {\mathbb {R}}^{n+2}{\setminus }\varSigma$. The map ${{\,{\mathrm{Sec}}\,}}_x$ restricts to a map from $\varSigma$ to $S^{n+1}$, which we shall still denote by ${{\,{\mathrm{Sec}}\,}}_x$.

Definition 2.3

The solid angle of $\varSigma$ viewed from x is defined as

$$\begin{aligned} \widetilde{\varPhi }(x)=\frac{1}{\sigma _{n+1}}\int _{\varSigma }{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}. \end{aligned}$$

(2.4)

The map $\widetilde{\varPhi }(x)$ is a signed area of a spherical surface spanned by ${{\,{\mathrm{Sec}}\,}}_x(M)$, that is, the radial projection of M from the point x.

We have the following fact.

Lemma 2.5

The value$\widetilde{\varPhi }(x)\bmod 1$does not depend on the choice of$\varSigma$. In particular,$\widetilde{\varPhi }$induces a well-defined function

$$\begin{aligned} \varPhi :{\mathbb {R}}^{n+2}{\setminus } M\rightarrow {\mathbb {R}}/{\mathbb {Z}}\cong S^1. \end{aligned}$$

Proof

Take another hypersurface $\varSigma^{\prime}$. Let X and $X'$ be abstract models of $\varSigma$ and $\varSigma^{\prime}$, that is, X and $X^{\prime}$ are smooth compact $(n+2)$-dimensional manifolds and $\phi :X\rightarrow \varSigma$, $\phi ^{\prime}:X^{\prime}\rightarrow \varSigma^{\prime}$ are embeddings. Define $\varXi$ to be the closed $(n+2)$-dimensional manifold obtained by gluing X with $X^{\prime}$ along $\phi ^{-1}(M)$ and ${\phi ^{\prime}}^{-1}(M)$. Let $\phi _\varXi :\varXi \rightarrow {\mathbb {R}}^{n+2}$ be the map equal to $\phi$ on X and to $\phi ^{\prime}$ on $X^{\prime}$.

By functoriality of the integral, we have

$$\begin{aligned} \int _{X}\phi ^*{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}=\int _{\varSigma }{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1},\ \int _{X^{\prime}}{\phi ^{\prime}}^*{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}=\int _{\varSigma^{\prime}}{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}. \end{aligned}$$

Therefore,

$$\begin{aligned} \frac{1}{\sigma _{n+1}}\int _{\varSigma }{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}-\frac{1}{\sigma _{n+1}} \int _{\varSigma^{\prime}}{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}=\int _{\varXi }\phi ^*_\varXi {{\,{\mathrm{Sec}}\,}}^*_x \frac{1}{\sigma _{n+1}}\omega _{n+1}. \end{aligned}$$

The integral on the right-hand side is the evaluation of an $(n+1)$-form $\phi ^*_\varXi {{\,{\mathrm{Sec}}\,}}^*_x\frac{1}{\sigma _{n+1}}\omega _{n+1}$ on the fundamental cycle of $\varXi$. The form $\frac{1}{\sigma _{n+1}}\omega _{n+1}$ represents an integral cohomology class in $H^{n+1}(S^{n+1})$; hence, $\phi _\varXi ^*{{\,{\mathrm{Sec}}\,}}_x^*\frac{1}{\sigma _{n+1}}\omega _{n+1}$ represents an integral cohomology class on $\varXi$. Therefore,

$$\begin{aligned} \frac{1}{\sigma _{n+1}}\int _{\varXi }\phi ^*_\varXi {{\,{\mathrm{Sec}}\,}}^*_x\omega _{n+1} \end{aligned}$$

is an integer. This means that

$$\begin{aligned} \frac{1}{\sigma _{n+1}}\int _{\varSigma }{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1} -\frac{1}{\sigma _{n+1}}\int _{\varSigma^{\prime}}{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}\in {\mathbb {Z}}. \end{aligned}$$

$\square$

Remark 2.6

One should not confuse the solid angle with the cone angle studied extensively by many authors, like [2, 3, 5]. To begin with, the cone angle is unsigned and takes values in ${\mathbb {R}}_{\geqslant 0}$, whereas the solid angle is an element in ${\mathbb {R}}/{\mathbb {Z}}$. This indicates that there exist fundamental differences between the two notions.

From the definition of $\varPhi$, we recover its first important property.

Proposition 2.7

The map$\varPhi$is smooth away from the complement of${M\subset {\mathbb {R}}^{n+2}}$.

Proof

Take a point $y\notin M$. There exists a smooth compact surface $\varSigma$ such that $\partial \varSigma =M$ and $y\notin \varSigma$. Then, a small neighborhood U of y is disjoint from $\varSigma$. Thus, the map ${{\,{\mathrm{Sec}}\,}}_x$ depends smoothly on the parameter x. This means that ${{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}$ depends smoothly on x. Integrating over a finite measure hypersurface $\varSigma$ preserves smooth dependence of a parameter. It follows that $\widetilde{\varPhi }$ is smooth in U. $\square$

2.1 $\varPhi$ via integrals over M

The fact that the definition of $\varPhi (x)$ involves a choice of a Seifert hypersurface $\varSigma$ is quite embarrassing. In fact, it might be hard to find estimates for $\varPhi$ because we have little control over $\varSigma$. We want to define $\varPhi$ via integrals over M itself. The key tool will be the Stokes’ formula. We use the fact that while the volume form $\omega _{n+1}$ on $S^{n+1}$ itself is not exact, its restriction $\omega ^{\prime}$ to the punctured sphere $S^{n+1}{\setminus } \{z\}$ is.

We need the following result.

Proposition 2.8

Let$x\in {\mathbb {R}}^{n+2}{\setminus } M$and let$z\in S^{n+1}$be such that$z\notin {{\,{\mathrm{Sec}}\,}}_x(M)$. Then, there exists a Seifert hypersurface$\varSigma$forMsuch that${{\,{\mathrm{Sec}}\,}}_x(\varSigma )$missesz.

Remark 2.9

The result is non-trivial in the sense that one can construct a Seifert surface $\varSigma$ even for an unknot in ${\mathbb {R}}^3$ such that the restriction ${{\,{\mathrm{Sec}}\,}}_x|_\varSigma$ is onto. However, notice that since M is smooth, ${{\,{\mathrm{Sec}}\,}}_x|_M$ is never onto $S^{n+1}$ because $\dim M<\dim S^{n+1}$.

Proof

Let H be the half-line $\{x+tz,\,t > 0\}$. In other words $H={{\,{\mathrm{Sec}}\,}}_x^{-1}(z)$. Choose any Seifert hypersurface $\varSigma$. We might assume that H is transverse to $\varSigma$. The set of intersection points of H and $\varSigma$ is bounded and discrete, hence finite. Let $\{w_1,\ldots ,w_m\}=H\cap \varSigma$ and assume these points are ordered in such a way that on H the point $w_1$ appears first (with the smallest value of t), then $w_2,$ and so on (Fig. 2).

Fig. 2

Proof of Proposition 2.8. Reducing the intersection points of H with $\varSigma$. The disk D is replaced by the tube T and a large sphere

Choose the last point w_m of this intersection and a small disk $D\subset \varSigma$ with center w_m. We can make D small enough so that for any $w^{\prime}\in D$ the intersection

$$\begin{aligned} \{x+tw^{\prime},t>1\}\cap \varSigma \end{aligned}$$

is empty. Set now

$$\begin{aligned} T=\{x+tw^{\prime},t\geqslant 1,w^{\prime}\in D\}\,\hbox { and }\,\partial _v T=\{x+tw^{\prime},t\geqslant 1,w^{\prime}\in \partial D\}. \end{aligned}$$

Consider a sphere $S=S(x,r)$, where r is large. Set $S^{\prime}=S{\setminus } (S\cap T)$. Increasing r if necessary, we may and shall assume that $S^{\prime}$ is disjoint from $\varSigma$. The new Seifert hypersurface is defined as

$$\begin{aligned} \varSigma^{\prime}=(\varSigma {\setminus } D)\cup [(\partial _v T)\cap B(x,r)]\cup S^{\prime}. \end{aligned}$$

With this construction, we have $H\cap \varSigma^{\prime}=\{w_1,\ldots ,w_{m-1}\}$. Repeating this construction finitely many times, we obtain a Seifert hypersurface disjoint from H. $\square$

Let $\eta _z$ be an n–form on $S^{n+1}{\setminus }\{z\}$ such that $d\eta _z=\omega _{n+1}$, and suppose $\varSigma$ is a Seifert hypersurface for M such that $z\notin {{\,{\mathrm{Sec}}\,}}_x(\varSigma )$. By Stokes’ formula

$$\begin{aligned} \int _{\varSigma }{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}=\int _{M}{{\,{\mathrm{Sec}}\,}}_x^*\eta _z. \end{aligned}$$

Therefore, we obtain the following formula for $\varPhi$:

$$\begin{aligned} \varPhi (x)=\frac{1}{\sigma _{n+1}}\int _M{{\,{\mathrm{Sec}}\,}}_x^*\eta _z\bmod 1. \end{aligned}$$

(2.10)

The necessity of making the map modulo 1 comes now from different choices of the point $z\in S^{n+1}{\setminus } M$.

We shall need an explicit formula for $\eta _z$. For simplicity, we consider the case when $z=(0,0,\ldots ,1) \in S^{n+1}\subset {\mathbb {R}}^{n+2}$ and define $\eta := \eta _z$; the general case can be obtained by rotating the coordinate system. We start with the following proposition.

Proposition 2.11

Set$z=\{0,\ldots ,0,1\}$. Let$\lambda : S^{n+1} {\setminus } \{z\} \subset {\mathbb {R}}^{n+2} \rightarrow {\mathbb {R}}$be a smooth function with variables$u=(u_1,u_2,\ldots ,u_{n+2})$. If$\lambda$involves only$u_{n+2}$(write$\lambda (u) = \lambda (u_{n+2})$for convenience) and satisfies

$$\begin{aligned} (1-u^2_{n+2}) \lambda ^{\prime}(u_{n+2}) - (n+1) u_{n+2}\lambda (u_{n+2}) = (-1)^n, \end{aligned}$$

(2.12)

then on$S^{n+1}{\setminus }\{z\}$we have

$$\begin{aligned} d\left( \lambda (u_{n+2}) \omega _n\right) = \omega _{n+1}. \end{aligned}$$

Proof

Note that

$$\begin{aligned} u_1^2 + \cdots + u_{n+2}^2 = 1 \quad implies \quad u_1\hbox{d}u_1 + \cdots + u_{n+2}\hbox{d}u_{n+2} = 0, \end{aligned}$$

and hence

$$\begin{aligned} u_i \hbox{d}u_1\wedge \cdots \wedge \hbox{d}u_{n+1}=(-1)^{n+i}u_{n+2}\hbox{d}u_1\wedge \cdots \wedge \widehat{\hbox{d}u_i}\wedge \cdots \wedge \hbox{d}u_{n+2} \end{aligned}$$

for all $i\in \{1,2,\ldots ,n+1\}$. Therefore, by (2.12),

$$\begin{aligned}&\hbox{d}\left( \lambda (u_{n+2}) \omega _n\right) - \omega _{n+1} =\lambda ^{\prime}(u_{n+2})\hbox{d}u_{n+2}\wedge \omega _n+\lambda (u_{n+2})d\omega _n-\omega _{n+1}=\\&\quad = \frac{(-1)^n + (n+1)u_{n+2}\lambda (u_{n+2}) - \lambda ^{\prime}(u_{n+2})(1-u^2_{n+2})}{u_{n+2}}\hbox{d}u_1\wedge \cdots \wedge \hbox{d}u_{n+1} \end{aligned}$$

is the zero $(n+1)$-form. $\square$

To obtain a formula for $\eta$, it remains to solve (2.12). Rewriting it, we have

$$\begin{aligned} \lambda ^{\prime}(u_{n+2}) - \frac{(n+1) u_{n+2}}{\left( 1-u^2_{n+2}\right) }\lambda (u_{n+2}) = \frac{(-1)^n}{\left( 1-u^2_{n+2}\right) }. \end{aligned}$$

The integrating factor of this ordinary differential equation is $(1-u^2_{n+2})^{\frac{n+1}{2}}$, so the general solution of (2.12) can be written as

$$\begin{aligned} \left( 1-u^2_{n+2}\right) ^{\frac{n+1}{2}} \lambda (u_{n+2}) = (-1)^n \int \left( 1-u^2_{n+2}\right) ^{\frac{n-1}{2}} \mathrm{d}u_{n+2}. \end{aligned}$$

(2.13)

The requirement that the solution be smooth at $u_{n+2}=-1$ translates into the following formula

$$\begin{aligned} \lambda (u_{n+2})=(-1)^n{\left( 1-u_{n+2}^2\right) }^{-\frac{n+1}{2}}\int _{-1}^{u_{n+2}} {(1-s^2)}^{\frac{n-1}{2}}\mathrm{d}s. \end{aligned}$$

(2.14)

The integral in (2.14) can be explicitly calculated. If n is odd, the result is a polynomial. If n is even, successive integration by parts eventually reduces the integral to $\int \sqrt{1-s^2}\,\hbox{d}s$. For small values of n, the function $\lambda$ is as follows.

$$\begin{aligned} n&=1;\quad \lambda (u_3)=(u_3-1)^{-1}\\ n&=2;\quad \lambda (u_4)=-\frac{1}{4}\left( \pi +2u_4\sqrt{1-u_4^2}+2\arcsin u_4\right) \left( u_4^2-1\right) ^{-3/2}\\ n&=3;\quad \lambda (u_5)=\frac{1}{3}(u_5-2)(u_5-1)^{-1}. \end{aligned}$$

Definition 2.15

From now on, we shall assume that $\eta =\lambda (u_{n+2})\omega _n$, where $\lambda$ is as in (2.14).

We see that $\lambda$ is smooth for $u_{n+2}\in [-1,1)$ and has a pole at $u_{n+2}=1$. We shall work mostly in regions, where $u_{n+2}$ is bounded away from 1, so that $\lambda$ and its derivatives will be bounded.

2.2 The pullback of the form $\eta$

We shall gather some formulae for evaluating the pullback ${{\,{\mathrm{Sec}}\,}}_x^*\eta$. This will allow us to estimate the derivative of $\varPhi$.

First, notice that

$$\begin{aligned} d_y\frac{y_i-x_i}{\Vert y-x\Vert }=\frac{\hbox{d}y_i}{\Vert y-x\Vert }+(y_i-x_i)d_y\Vert y-x\Vert ^{-1}, \end{aligned}$$

(2.16)

where $d_y$ means that we take the exterior derivative with respect to the y variable (we treat x as a constant). Consider the expression

$$\begin{aligned} {{\,{\mathrm{Sec}}\,}}_x^* \hbox{d}u_1\wedge \cdots \wedge \widehat{\hbox{d}u_i}\wedge \cdots \wedge \hbox{d}u_{n+1}. \end{aligned}$$

To calculate the pullback, we replace $\hbox{d}u_i$ by $d_y\frac{y_i-x_i}{\Vert y-x\Vert }$. Notice that if in the wedge product the term $(y_i-x_i)d_y\Vert y-x\Vert ^{-1}$ from (2.16) appears twice or more, this term will be zero. Therefore, the pullback takes the form

$$\begin{aligned}&{{\,{\mathrm{Sec}}\,}}_x^* \hbox{d}u_1\wedge \cdots \wedge \widehat{\hbox{d}u_i}\wedge \cdots \wedge \hbox{d}u_{n+1}=\frac{1}{\Vert y-x\Vert ^n}\hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i}\wedge \cdots \hbox{d}y_{n+1}\\&\quad +\,\frac{1}{\Vert y-x\Vert ^{n-1}}\sum _{j\ne i} (-1)^{\theta (i,j)}(y_j-x_j) d_y\Vert y-x\Vert ^{-1}\wedge \hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i,\hbox{d}y_j}\wedge \cdots \wedge \hbox{d}y_{n+1}, \end{aligned}$$

where $\theta (i,j)$ is equal to $j-1$ if $j<i$ and $j-2$ if $j>i$. Using the above expression together with

$$\begin{aligned} d_y\Vert y-x\Vert ^{-1} = \frac{-1}{\Vert y-x\Vert ^3} \left( (y_1 - x_1)\hbox{d}y_1 + \cdots + (y_{n+1} - x_{n+1}) \hbox{d}y_{n+1}\right) , \end{aligned}$$

we can calculate the pullback of the form

$$\begin{aligned} \omega _{n}=\sum _{i=1}^{n+1} (-1)^{i+1}u_i\hbox{d}u_1\wedge \cdots \wedge \widehat{\hbox{d}u_i}\wedge \cdots \wedge \hbox{d}u_{n+1}. \end{aligned}$$

We calculate

$$\begin{aligned}&{{\,{\mathrm{Sec}}\,}}_x^*\omega _{n}=\frac{1}{\Vert y-x\Vert ^{n+1}}\sum _{i=1}^{n+1}(-1)^{i+1}(y_i-x_i)\hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i}\wedge \cdots \wedge \hbox{d}y_{n+1}\\&\quad +\frac{1}{\Vert y-x\Vert ^{n+3}}\sum _{i=1}^{n+1}\sum _{j\ne i} (-1)^{i+\theta (i,j)} (y_i-x_i)^2(y_j-x_j)\hbox{d}y_i\wedge \hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i,\hbox{d}y_j}\wedge \cdots \wedge \hbox{d}y_{n+1}\\&\quad +\frac{1}{\Vert y-x\Vert ^{n+3}}\sum _{i=1}^{n+1}\sum _{j\ne i} (-1)^{i+\theta (i,j)} (y_i-x_i)(y_j-x_j)^2 \hbox{d}y_j \wedge y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i,\hbox{d}y_j}\wedge \cdots \wedge \hbox{d}y_{n+1}. \end{aligned}$$

Notice that we can change the order of the sums in the last term of the above expression to be $\sum _{j=1}^{n+1}\sum _{i\ne j}$. Since $i+\theta (i,j) = j+\theta (j,i) \pm 1$, the last two sums cancel out. Hence, we obtain

$$\begin{aligned} {{\,{\mathrm{Sec}}\,}}_x^*\omega _{n}=\frac{1}{\Vert y-x\Vert ^{n+1}}\sum _{i=1}^{n+1}(-1)^{i+1} (y_i-x_i)\hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i}\wedge \cdots \wedge \hbox{d}y_{n+1}. \end{aligned}$$

(2.17)

In particular, using Definition 2.15 we get a proof of the first part of Theorem 1.1.

$$\begin{aligned} \begin{aligned} {{\,{\mathrm{Sec}}\,}}_x^*\eta&=\frac{1}{\Vert y-x\Vert ^{n+1}}\lambda \left( \frac{y_{n+2}-x_{n+2}}{\Vert y-x\Vert }\right) \\&\quad \cdot \sum _{i=1}^{n+1}(-1)^{i+1}(y_i-x_i)\hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i}\wedge \cdots \wedge \hbox{d}y_{n+1}. \end{aligned} \end{aligned}$$

(2.18)

If $n=1$ we obtain the following explicit formula, used in [4].

$$\begin{aligned} \varPhi (x_1,x_2,x_3)=\frac{1}{4\pi }\int _M \dfrac{(y_2-x_2)\hbox{d}y_1-(y_1-x_1)\hbox{d}y_2}{\Vert y-x\Vert ^2\left(1-\dfrac{y_3-x_3}{\Vert y-x\Vert }\right)}. \end{aligned}$$

(2.19)

It is worth mentioning the formula for $n=1$ and a general z (not necessarily (0, 0, 1)), which was given in [4, Theorem 5.3.7].

$$\begin{aligned} \varPhi (x_1,x_2,x_3)=\frac{1}{4\pi }\int _M\frac{\left( \dfrac{y-x}{\Vert y-x\Vert }\times z\right) \cdot \hbox{D}y}{\Vert y-x\Vert \left( 1-\dfrac{y-x}{\Vert y-x\Vert }\cdot z\right) }, \end{aligned}$$

where $Dy=(\hbox{d}y_1,\hbox{d}y_2,\hbox{d}y_3)$.

We conclude by remarking that if

$$\begin{aligned} \omega _{n+1}=\sum _{i=1}^{n+2} (-1)^{i+1} u_i \hbox{d}u_1\wedge \cdots \wedge \widehat{\hbox{d}u_i}\wedge \cdots \wedge \hbox{d}u_{n+2}, \end{aligned}$$

then analogous arguments as those that led to formula (2.17) imply that

$$\begin{aligned} {{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}=\frac{1}{\Vert y-x\Vert ^{n+2}}\sum _{i=1}^{n+2} (-1)^{i+1} (y_i-x_i)\hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i}\wedge \cdots \wedge \hbox{d}y_{n+2}. \end{aligned}$$

(2.20)

2.3 Estimates for derivatives of ${{\,{\mathrm{Sec}}\,}}_x^*\eta$

The following results are direct consequences of the pullback formula for $\eta$, (2.18). We record them for future use in Sects. 3 and 6 . Recall from Sect. 2.2 that $\eta$ was defined as a form on $S^{n+1}{\setminus }(0,\ldots ,0,1)$. The form $\eta _z$ for general $z\in S^{n+1}$ is obtained by rotation of the coordinate system.

Lemma 2.21

For any$m\geqslant 0$, there exists a constant$C^{\#}_{m,n}$such that for each nonnegative integers$k_1,\ldots ,k_{n+2}$such that$\sum k_i=m$, the (higher) differential of the pullback${{\,{\mathrm{Sec}}\,}}_x^*\eta$has the form

$$\begin{aligned} \frac{\partial ^m}{\partial x_1^{k_1}\cdots \partial x_{n+2}^{k_{n+2}}}{{\,{\mathrm{Sec}}\,}}_x^*\eta =\sum _{i=1}^{n+1}H_i\hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i}\wedge \cdots \wedge \hbox{d}y_{n+1}, \end{aligned}$$

where

$$\begin{aligned} H_i=\sum _{j=0}^m \lambda ^{(j)}\left( \frac{y_{n+2}-x_{n+2}}{\Vert y-x\Vert }\right) H_{i}^j, \end{aligned}$$

(2.22)

and$H_i^j$are smooth functions satisfying$|H_i^j|\leqslant C^{\#}_{m,n}\Vert y-x\Vert ^{-(n+m-j)}$.

Proof

If $m=0$, the proof is a direct consequence of (2.18). The general case follows by an easy induction. $\square$

As a consequence of Lemma 2.21, we prove the following fact.

Lemma 2.23

For any$D<1$and for any integer$m>0$, there is a constant$C^{D}_{n,m}$such that if$z\in S^{n+1}$, y, xsatisfy$\langle \frac{y-x}{\Vert y-x\Vert },z\rangle <D$and$\sum k_i=m$, then the derivative$\dfrac{\partial ^m}{\partial x_1^{k_1}\cdots \partial x_{n+2}^{k_{n+2}}}{{\,{\mathrm{Sec}}\,}}_x^*\eta _z$is a sum of forms of type$H_{i_1,\ldots , i_n} \hbox{d}y_{i_1}\wedge \cdots \wedge \hbox{d}y_{i_n}$, where all the coefficients$H_{i_1,\ldots ,i_n}$are bounded by$C^D_{n,m}\Vert y-x\Vert ^{-n-m}$.

Proof

Apply a linear orthogonal map of ${\mathbb {R}}^{n+2}$ that takes z to $(0,0,\ldots ,0,1)$. Let $x^{\prime}$ and $y^{\prime}$ be the images of x and y, respectively, under this map. We have $\Vert y^{\prime}-x^{\prime}\Vert =\Vert y-x\Vert$ and the condition $\langle \frac{y-x}{\Vert y-x\Vert },z\rangle <D$ becomes $\frac{y_{n+2}^{\prime}-x_{n+2}^{\prime}}{\Vert y-x\Vert }<D$. We shall use (2.22). As $D<1$, on the interval $[-1,D]$ the function $\lambda$ and its derivatives up to m-th inclusive are bounded above by some constant $C_{D,m}$ depending on D and m. The constant $C^D_{n,m}$ can be chosen as $C^D_{n,m}=(m+1)C^{\lambda }_{D,m}C^{\#}_{n,m}$. $\square$

3 Properness of $\varPhi$

Theorem 3.1

For any$t\in (0,1)$there exists$R_t$such that$\varPhi ^{-1}(t)\subset B(0,R_t)$. In other words, all fibers of$\varPhi$except$\varPhi ^{-1}(0)$are bounded.

Proof

Choose a Seifert hypersurface $\varSigma$ for M. We may assume that it is contained in a ball B(0, r) for some $r>0$. As $\varSigma$ is compact and smooth, there exists a constant $C_\varSigma$ such that if an $(n+1)$–form $\omega _{n+1}$ on ${\mathbb {R}}^{n+2}$ has all the coefficients bounded from above by T, then $|\int _\varSigma \omega _{n+1}|<C_\varSigma T$.

Now take $R\gg 0$ and suppose $x\notin B(0,R+r)$. Then the distance of x to any point $y\in \varSigma$ is at least R. Then ${{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}$ has all the coefficients bounded by $R^{-n-1}$, see (2.20), and therefore, $|\int _\varSigma {{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}|\leqslant C_\varSigma R^{-1-n}$. This means that

$$\begin{aligned} \varPhi ({\mathbb {R}}^{n+2}{\setminus } B(0,R+r))\subset (-C_\varSigma R^{-1-n},C_\varSigma R^{-1-n}), \end{aligned}$$

or equivalently, that if $t\notin (-C_\varSigma R^{-1-n},C_\varSigma R^{-1-n})$, then ${\varPhi ^{-1}(t)\subset B(0,R+r)}$. $\square$

Corollary 3.2

The map $\varPhi :{\mathbb {R}}^{n+2}{\setminus } M\rightarrow S^1$ extends to a $C^{n+1}$ smooth map from $S^{n+2}{\setminus } M$ to $S^1.$

Sketch of proof

Smoothness of $\varPhi$ at infinity is equivalent to the smoothness of $w\mapsto \varPhi (\frac{w}{\Vert w\Vert ^2})$ at $w=0$. The proof of Theorem 3.1 generalizes to show that for any $m>0$ there exists $C_m$ with a property that $|D^\alpha \varPhi (x)|\leqslant C_m\cdot \Vert x\Vert ^{-n-1-|\alpha |}$, and $\Vert D^\alpha \frac{w}{\Vert w\Vert ^2}\Vert \leqslant C_m\Vert w\Vert ^{-|\alpha |-1}$ whenever $|\alpha |\leqslant m$. Here $\alpha$ is a multi-index.

Now by the di Bruno’s formula for higher derivatives of the composite function, we infer that $|D^\alpha \varPhi (\frac{w}{\Vert w\Vert ^2})|\leqslant C\Vert w\Vert ^{n+2-|\alpha |}.$ (The worst case occurs when $\varPhi$ is differentiated only once, while $\dfrac{w}{\Vert w\Vert ^2}$ is differentiated $|\alpha |$ times.) Hence, the limit at $w\rightarrow 0$ of all derivatives of $w\mapsto \varPhi\left (\dfrac{w}{\Vert w\Vert ^2}\right)$ of order up to $n+1$ is zero. $\square$

We can also strengthen the argument of Theorem 3.1 to obtain more detailed information about the behavior of $\varPhi$ at a large scale.

Theorem 3.3

Suppose$\varSigma$is a Seifert hypersurface andris such that${\varSigma \subset B(0,r)}$. For any$R>r$, if$\Vert x\Vert >R$we have

$$\begin{aligned} \left| \sum _{i=1}^{n+2}x_i\frac{\partial \varPhi }{\partial x_i}+(n+1)\varPhi \right| \leqslant C_\varSigma (n+2)\frac{rR^{n+2}}{(R-r)^{n+2}}\Vert x\Vert ^{-(n+2)}, \end{aligned}$$

where$C_\varSigma$depends solely on$\varSigma$and not onRandr.

Proof

Using (2.20) write

$$\begin{aligned}&\frac{\partial {{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}}{\partial x_i}=\frac{-1}{\Vert y-x\Vert ^{n+2}} (-1)^{i+1} \hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i}\wedge \cdots \wedge \hbox{d}y_{n+2}+\\&\quad +(n+2)\frac{y_i-x_i}{\Vert y-x\Vert ^{n+4}}\sum _{j=1}^{n+2} (-1)^{j+1}(y_j-x_j)\hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_j}\wedge \cdots \wedge \hbox{d}y_{n+2}. \end{aligned}$$

This implies that

$$\begin{aligned} \sum _{i=1}^{n+2}x_i\frac{\partial {{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}}{\partial x_i}=-\xi _1+(n+2)\xi _2, \end{aligned}$$

where

$$\begin{aligned} \xi _1&=\frac{1}{\Vert y-x\Vert ^{n+2}}\sum _{i=1}^{n+2} (-1)^{i+1}x_i\hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i}\wedge \cdots \wedge \hbox{d}y_{n+2}\\ \end{aligned}$$

and

$$\begin{aligned} \xi _2&=\frac{1}{\Vert y-x\Vert ^{n+4}}\sum _{i=1}^{n+2}\sum _{j=1}^{n+2} (-1)^{j+1} (y_i-x_i)(y_j-x_j)x_i \hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_j}\wedge \cdots \wedge \hbox{d}y_{n+2}. \end{aligned}$$

Write also

$$\begin{aligned} \xi _3&=\frac{1}{\Vert y-x\Vert ^{n+2}}\sum _{i=1}^{n+2}(-1)^{i+1} (y_i-x_i)\hbox{d}y_1\wedge \cdots \wedge \widehat{\hbox{d}y_i}\wedge \cdots \wedge \hbox{d}y_{n+2}. \end{aligned}$$

Now suppose $\Vert x\Vert >R$ and $\Vert y\Vert <r$. Then $-\xi _1-\xi _3$ has all the coefficients bounded by $\frac{rR^{n+2}}{(R-r)^{n+2}}\Vert x\Vert ^{-n-2}$. Likewise, notice that

$$\begin{aligned} \left| \sum _{i=1}^{n+2}(y_i-x_i)x_i+\Vert y-x\Vert ^2\right| =\left| \sum _{i=1}^{n+2}(y_i-x_i)y_i\right| \leqslant \Vert y\Vert \Vert y-x\Vert , \end{aligned}$$

where we used Schwarz’ inequality in the last estimate. Therefore, $-\xi _2-\xi _3$ has all the coefficients bounded by $\frac{\Vert y\Vert }{\Vert y-x\Vert ^{n+2}}$, and by assumptions on $\Vert x\Vert$ and $\Vert y\Vert$ we have that

$$\begin{aligned} \frac{\Vert y\Vert }{\Vert y-x\Vert ^{n+2}}\leqslant \frac{rR^{n+2}}{(R-r)^{n+2}}\Vert x\Vert ^{-n-2}. \end{aligned}$$

We conclude that

$$\begin{aligned} \left| \int _\varSigma -\xi _1+(n+2)\xi _2+(n+1)\xi _3\right| \leqslant C_\varSigma (n+2)\frac{rR^{n+2}}{(R-r)^{n+2}} \Vert x\Vert ^{-(n+2)}. \end{aligned}$$

(3.4)

As $\varPhi (x)=\int _\varSigma \xi _3$, we obtain the statement. $\square$

The statement of Theorem 3.3, in theory, can be used to obtain information about $C_\varSigma$ from the behavior of $\varPhi$ at infinity. The left-hand side of (3.4) is equal to $\left| \sum \nolimits _{i=1}^{n+2} x_i\frac{\partial \varPhi }{\partial x_i}+(n+1)\varPhi \right|$ and does not depend on $\varSigma$. Therefore, if we know $\varPhi$ and its derivatives, we can find a lower bound for $C_\varSigma$, which roughly tells, how complicated $\varSigma$ might be. Unfortunately, we do not know of any examples where this can be used effectively.

4 $\varPhi$ for an n-dimensional linear surface

4.1 Calculations

The analysis of $\varPhi$ near M will rely on replacing M by its tangent space and estimate the error. Therefore, we shall now define M for an n-dimensional surface. Define

$$\begin{aligned} H=\left\{ w\in {\mathbb {R}}^{n+2}:w_1=0,w_2=0\right\} . \end{aligned}$$

The first technical problem arises because H is not compact; therefore, the map $\varPhi$ does not even have to be defined. In what follows, we shall define $\varPhi _H$ for H as above. We need to choose an analogue of the ‘Seifert hypersurface’, and our choice will be a half-hyperplane. As H is not compact, we cannot apply the argument of Lemma 2.5 to conclude that $\varPhi _H$ does not depend on the choice of a half-hyperplane. And indeed, $\varPhi _H$ will depend on this choice. In fact, $\varPhi _H$ will be well defined up to an overall constant. In particular, the derivatives of $\varPhi _H$ are well defined. This dependence is considered as a feature. Calculations for $\frac{\partial \varPhi }{\partial x_j}$ will be important in Sect. 6.

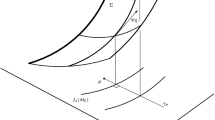
Set $\varSigma =\{w:w_1\leqslant 0,\ w_2=0\} \subset {\mathbb {R}}^{n+2}$. For any point $x\notin \varSigma$, the value of the map $\varPhi (x)$ is (up to a sign) the area of the image ${{\,{\mathrm{Sec}}\,}}_x(\varSigma )$. This image can be calculated explicitly.

Choose a point $y=(y_1,\ldots ,y_{n+2})\in S^{n+1}$. The half-line from $x\notin \varSigma$ through $x+y$ is given by $t\mapsto x+ty$, $t\geqslant 0$; see Fig. 3. By definition, $y\in {{\,{\mathrm{Sec}}\,}}_x(\varSigma )$ if and only if this half-line intersects $\varSigma$, that is, for some $t_0>0$ we have

$$\begin{aligned} x_2+t_0y_2=0\,\,{\text{and}}\,\,x_1+t_0y_1\leqslant 0. \end{aligned}$$

(4.1)

Fig. 3

The half-line from $(x_1,x_2)$ through $(x_1+y_1,x_2+y_2)$ hitting the Seifert hypersurface $\varSigma$

Note that if $x_2= 0$, then the half-line through x and any point in $\varSigma$ will meet H, which results in an n-dimensional image ${{\,{\mathrm{Sec}}\,}}_x(\varSigma )$ in $S^{n+1}$. Suppose $x_2\ne 0$. The condition $t_0>0$ together with (4.1) implies that the signs of $x_2$ and $y_2$ must be opposite. Plugging $t_0$ from the first equation of (4.1) into the second one, we obtain

$$\begin{aligned} x_1-\frac{x_2y_1}{y_2}\leqslant 0. \end{aligned}$$

(4.2)

The calculation of $\varPhi$ boils down to the study of the set of $x_1,x_2$ satisfying (4.2). Write $x_1=r\cos 2\pi \beta$ and $x_2=r\sin 2\pi \beta$. Multiply (4.2) by $\frac{y_2}{x_2}$ (which is negative) to obtain the inequality

$$\begin{aligned} y_1\leqslant y_2/\tan 2\pi \beta . \end{aligned}$$

There are four cases depending on in which quadrant of the plane contains $(x_1,x_2)$; see Fig. 4.

Fig. 4

The four cases of possible position of points $(x_1,x_2)$ and the image of the projection. Instead of drawing the preimage in the boundary on a circle, we draw a circular sector in a disk for better readability

We next calculate the area of the image ${{\,{\mathrm{Sec}}\,}}_x(\varSigma )$ of each of those four cases. To do so, we first deal with the calculations and then discuss the choice of the sign. For the moment, we choose a sign for the area as $\epsilon \in \{-1,+1\}$; refer to Sect. 4.2 for the discussion of the sign convention.

Notice that the area of the two-dimensional circular sector in Fig. 4 is (up to normalization) equal to the $(n+1)$-dimensional area of the image ${{\,{\mathrm{Sec}}\,}}_x(\varSigma )$. This is because the defining equations are homogeneous, and other variables $y_3,\ldots ,y_{n+2}$ do not enter in the definition of the region.

Case 1:

$x_1\geqslant 0$ and $x_2>0$. The region ${{\,{\mathrm{Sec}}\,}}_x(\varSigma )$ is given by $y_2 < 0$ (because the sign of $y_2$ is opposite to the sign of $x_2$), $y_1\leqslant y_2/\tan 2\pi \beta$ and $\tan 2\pi \beta \in (0,\infty )$. The area of the sector corresponding to Case 1 is equal to $\pi \beta$, and hence, $\varPhi (x)=\epsilon \beta$, where $\epsilon$ is a sign.

Case 2:

$x_1\leqslant 0$ and $x_2 > 0$. The region ${{\,{\mathrm{Sec}}\,}}_x(\varSigma )$ is given by $y_2 < 0$, $y_1\leqslant y_2/\tan 2\pi \beta$, where $\tan 2\pi \beta \in (-\infty ,0)$. The area of the sector is equal to $\pi \beta$ and so $\varPhi (x)=\epsilon \beta$.

Case 3:

$x_1\leqslant 0$ and $x_2 < 0$. Then $y_2 > 0$ and $\tan 2\pi \beta \in (0,\infty )$. The area of the sector is $\pi -\pi \beta$, but now the hypersurface $\varSigma$ is seen from the other side; hence, the signed area is $\epsilon (\pi \beta -\pi )$. After normalizing and taking modulo 1, we obtain that $\varPhi (x)=\epsilon \beta$.

Case 4:

$x_1\geqslant 0$, $x_2 < 0$. Then $y_2 > 0$ and $\tan 2\pi \beta \in (-\infty ,0)$. As in Case 3, we deduce that the area is $\pi -\pi \beta$ and we obtain $\varPhi (x)=\epsilon \beta$.

Putting all the cases together, we see that $\varPhi (x)=\epsilon \beta$.

Suppose we take another ‘Seifert surface’ for H, denoted $\varSigma^{\prime}$, given by $u_1=0$, $u_2\leqslant 0$. Let $\varPhi ^{\prime}$ be the map $\varPhi$ defined relatively to $\varSigma^{\prime}$. To calculate $\varPhi ^{\prime}$, we could repeat the above procedure, yet we present a quicker argument. A counterclockwise rotation A in the $(u_1,u_2)$-plane by angle $\frac{\pi }{2}$ fixes H and takes $\varSigma$ to $\varSigma^{\prime}$. In particular, $\varPhi ^{\prime}(x)=\varPhi (Ax)$. Hence, $\varPhi ^{\prime}(x)=\epsilon (\beta -\frac{1}{4})$ We notice that $\varPhi ^{\prime}\ne \varPhi$, but on the other hand $\varPhi ^{\prime}-\varPhi$ is a constant. This approach shows that if we take a linear hypersurface (a half-space) for the ‘Seifert surface’ of $\varPhi$, then it is well defined up to a constant, and so the derivatives are well defined.

4.2 The sign convention

Given that $\varPhi$ is defined as an integral of a differential form, changing the orientation of H induces a reversal of the sign of $\varPhi$. We use the example of a linear surface to show how the sign is computed.

Choose the orientation of H in such a way that $\frac{\partial }{\partial u_3},\ldots ,\frac{\partial }{\partial u_{n+2}}$ is a positive basis of TH. Stokes’ theorem is applicable if $\varSigma$ is oriented by the rule “normal outwards first”, see [14, Chapter 5], so that $\frac{\partial }{\partial u_1},\frac{\partial }{\partial u_3},\ldots ,\frac{\partial }{\partial u_{n+2}}$ is an oriented basis of $T\varSigma$.

The way of seeing the sign is by calculating $\int _\varSigma {{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}$. By (2.20) we know that

$$\begin{aligned} \widetilde{\varPhi }(x_1,\ldots ,x_{n+2})=\int _\varSigma {{\,{\mathrm{Sec}}\,}}_x^*\omega _{n+1}=\int _{\begin{array}{c} y_1\leqslant 0\\ y_2=0 \end{array}}\frac{x_2}{\Vert y-x\Vert ^{n+2}} \hbox{d}y_1\wedge \hbox{d}y_3\wedge \cdots \wedge \hbox{d}y_{n+2}. \end{aligned}$$

Given the orientation of $\varSigma$, we have

$$\begin{aligned} \begin{aligned}&\int _{y_1\leqslant 0,y_2=0}\frac{x_2}{\Vert y-x\Vert ^{n+2}} \hbox{d}y_1\wedge \hbox{d}y_3\wedge \cdots \wedge \hbox{d}y_{n+2}\\&\quad =x_2\int _{-\infty }^0\left( \int \frac{1}{\Vert y-x\Vert ^{n+2}} \hbox{d}y_3\ldots \hbox{d}y_{n+2}\right) \hbox{d}y_1. \end{aligned} \end{aligned}$$

(4.3)

Notice that on the left-hand side we have an integral of a differential form, whereas on the right-hand side the integral is with respect to the $(n+1)$-dimensional Lebesgue measure on a subset of ${\mathbb {R}}^{n+1}$.

The function $\int \frac{1}{\Vert y-x\Vert ^2} \hbox{d}y_3\ldots \hbox{d}y_{n+2}$ is positive; therefore, $\widetilde{\varPhi }$ is positive for $x_2>0$, negative for $x_2<0$ and 0 for $x_2=0,x_1>0$ (notice that (4.3) is not defined if $x_2=0$ and $x_1\leqslant 0$: if this holds, the point $(x_1,x_2,\ldots ,x_{n+2})$ lies on $\varSigma$ and the integral diverges). Therefore, $\frac{\partial }{\partial x_2}\widetilde{\varPhi }|_{x_2=0,x_1>0}$ is nonnegative. This is possible only if the choice of sign is $\epsilon =+1$.

5 $\varPhi$ for a circle

In Sect. 5 the manifold M is the round unit circle, that is $M=\{(x_1,x_2,x_3)\in {\mathbb {R}}^3:x_1^2+x_2^2=1,\ x_3=0\}$. We now use the formula for $\varPhi$ via the integrals of the pullback of $\eta$, see (2.18), to give an explicit formula for $\varPhi$. The output is given in terms of elliptic integrals. Detailed calculations can be found, e.g., in [4]; therefore, we omit some tedious computations. We focus on the analysis of the behavior of $\varPhi$ near the circle.

5.1 Elliptic integrals

For the reader’s convenience, we give a quick review of elliptic integrals and their properties. We shall use these definitions in future calculations. This section is based on [1].

Definition 5.1

Let $\varphi \in [0,\pi /2]$. For any $k\in [0,1]$, the complementary modulus$k^{\prime}$ of k is defined by $k^{\prime}=\sqrt{1-k^2}$.

• 1. The integral

  $$\begin{aligned} {\mathbf {F}}(\varphi ,k) = \int _0^{\varphi } \dfrac{dt}{\sqrt{1-k^2\sin ^2 t}} \end{aligned}$$

  (5.2)

  is called an elliptic integral of the first kind. If $\varphi = \pi /2$, it is called a complete elliptic integral of the first kind, denoted by ${\mathbf {K}}(k):= {\mathbf {F}}(\pi /2,k)$.

• 2. The integral

  $$\begin{aligned} {\mathbf {E}}(\varphi ,k) = \int _0^{\varphi } \sqrt{1-k^2\sin ^2 t}~dt \end{aligned}$$

  is called an elliptic integral of the second kind. If $\varphi = \pi /2$, it is called a complete elliptic integral of the second kind, denoted by ${{\mathbf {E}}(k):= {\mathbf {E}}(\pi /2,k)}$.

• 3. The integral

  $$\begin{aligned} {\varvec{{\Pi }}}(\varphi ,\alpha ^2,k) = \int _0^{\varphi } \dfrac{dt}{(1-\alpha ^2\sin ^2 t)\sqrt{1-k^2\sin ^2 t}} \end{aligned}$$

  is called an elliptic integral of the third kind. If $\varphi = \pi /2$, it is called a complete elliptic integral of the third kind, denoted by ${\varvec{{\Pi }}}(\alpha ^2,k):= {\varvec{{\Pi }}}(\pi /2,\alpha ^2,k)$.

• 4. Heuman’s Lambda function ${\varvec{{\Lambda }}}_0 (\beta ,k)$ can be defined by the formula

  $$\begin{aligned} {\varvec{{\Lambda }}}_0 (\beta ,k) = \dfrac{2}{\pi }\left( {\mathbf {E}}(k){\mathbf {F}}(\beta ,k^{\prime}) + {\mathbf {K}}(k){\mathbf {E}}(\beta ,k^{\prime}) - {\mathbf {K}}(k){\mathbf {F}}(\beta ,k^{\prime})\right) . \end{aligned}$$

Although ${\mathbf {K}}(k)$ blows up at $k=1$, we know how fast it goes to infinity as k approaches 1 from below.

Proposition 5.3

(see [6, formula (10) on page 318]) We have

$$\begin{aligned} {\mathbf {K}}(k) = \ln \dfrac{4}{\sqrt{1-k^2}} + O\left( (1-k^2)\ln \sqrt{1-k^2}\right) \quad as \quad k\rightarrow 1^-. \end{aligned}$$

In particular,

$$\begin{aligned} \lim _{k \rightarrow 1^-} \left( {\mathbf {K}}(k) - \ln \dfrac{4}{\sqrt{1-k^2}}\right) = 0. \end{aligned}$$

(5.4)

The differentials of ${\mathbf {K}}(k)$ and ${\mathbf {E}}(k)$ are calculated, e.g., in [1, page 282].

$$\begin{aligned} \dfrac{\hbox{d}}{\hbox{d}k}{\mathbf {K}}(k) = \dfrac{{\mathbf {E}}(k) - (k^{\prime})^2 {\mathbf {K}}(k)}{k(k^{\prime})^2} \end{aligned}$$

(5.5)

and

$$\begin{aligned} \dfrac{\hbox{d}}{\hbox{d}k}{\mathbf {E}}(k) = \dfrac{{\mathbf {E}}(k) - {\mathbf {K}}(k)}{k} \end{aligned}$$

(5.6)

where $k^{\prime} = \sqrt{1-k^2}$. The derivative of the Heuman’s Lambda function ${\varvec{{\Lambda }}}_0(\beta ,k)$ is given by the following formula; see [1, formulae 710.11 and 730.04].

$$\begin{aligned} \dfrac{\partial }{\partial k}{\varvec{{\Lambda }}}_0(\beta ,k)&= \dfrac{2({\mathbf {E}}(k)-{\mathbf {K}}(k))\sin \beta \cos \beta }{\pi k\sqrt{1-k^{\prime 2}\sin ^2 \beta }} \end{aligned}$$

(5.7)

and

$$\begin{aligned} \dfrac{\partial }{\partial \beta }{\varvec{{\Lambda }}}_0(\beta ,k)&= \dfrac{2({\mathbf {E}}(k)-k^{\prime 2}\sin ^2 \beta \, {\mathbf {K}}(k))}{\pi \sqrt{1-k^{\prime 2}\sin ^2 \beta }}. \end{aligned}$$

(5.8)

5.2 Computation of $\varPhi$ for the circle

In this section, we follow closely [4, Sections 6.2 and 6.3]. The circle U has the parameterization $\gamma :[-\pi ,\pi ] \rightarrow {\mathbb {R}}^3$ given by

$$\begin{aligned} \gamma (t) = (\cos t , \sin t, 0). \end{aligned}$$

Suppose $x\in {\mathbb {R}}^3$ is such that $x\notin \{u_1^2+u_2^2=1,\ u_3\leqslant 0\}$. Then ${{\,{\mathrm{Sec}}\,}}_x(U)$ does not contain (0, 0, 1) and (2.19) implies:

$$\begin{aligned} \varPhi (x_1,x_2,x_3)=\frac{1}{4\pi }\int _{-\pi }^{\pi } \frac{(x_1\cos t + x_2 \sin t - 1)\hbox{d}t}{Q+x_3\sqrt{Q}}, \end{aligned}$$

(5.9)

where

$$\begin{aligned} Q=1+\Vert x\Vert ^2 - 2x_1\cos t - 2x_2\sin t. \end{aligned}$$

Write $x_1=r\cos \theta$, $x_2=r\sin \theta$ for $r\geqslant 0$. Substituting this into (5.9), we observe that $\varPhi$ does not depend on $\theta$; hence, we can write $\varPhi =\varPhi (r,x_3)$, that is,

$$\begin{aligned} \varPhi (r,x_3) = \frac{1}{4\pi }\int _{-\pi }^{\pi } \dfrac{(r\cos t - 1)\hbox{d}t}{1+r^2+x_3^2 - 2r\cos t + x_3\sqrt{1+r^2+x_3^2 - 2r\cos t}}. \end{aligned}$$

(5.10)

We have some special cases where we can compute the integral explicitly. If $x_3 = 0$, we use the identity

$$\begin{aligned} \cos t = \dfrac{1-\tan ^2 (t/2)}{1+\tan ^2(t/2)} \end{aligned}$$

and deal with improper integrals; there are two situations:

• $r <1$: we have

  $$\begin{aligned} \varPhi (r,0) = \frac{1}{4\pi }\left[ -\dfrac{t}{2} - \arctan \left( \dfrac{1+r}{1-r} \tan \dfrac{t}{2}\right) \right] _{-\pi }^{\pi } = -\frac{1}{2}; \end{aligned}$$

• $r >1$: we have

  $$\begin{aligned} \varPhi (r,0) = \frac{1}{4\pi }\left[ -\dfrac{t}{2} + \arctan \left( \dfrac{r+1}{r-1} \tan \dfrac{t}{2}\right) \right] _{-\pi }^{\pi } = 0.\end{aligned}$$

This agrees with the geometric interpretation. If we choose the disk $D=\{r\leqslant 1,\ x_3=0\}$ as a Seifert surface for U, then for $x=(r\cos \theta ,r\sin \theta ,0)$ with $r>1$, the image ${{\,{\mathrm{Sec}}\,}}_x(D)$ is one-dimensional, so $\varPhi (x)=0$. Conversely, for $x=(r\cos \theta ,r\sin \theta ,0)$ with $r<1$ we choose a Seifert surface $\varSigma$ to be the disk D with a smaller disk centered at x replaced by a hemisphere with center at x. In this way, the image ${{\,{\mathrm{Sec}}\,}}_x(\varSigma )$ is a hemisphere; see Fig. 5.

Remark 5.11

The inverse image $\varPhi ^{-1}(0)$ contains (and actually it is equal) to the set $\{x_1^2+x_2^2>1,\ x_3=0\}$. This shows that the assumption that $t\ne 0$ in Theorem 3.1 is necessary.

Fig. 5

A Seifert surface for the circle with the property that its image under ${{\,{\mathrm{Sec}}\,}}_x$ is a hemisphere

We now express $\varPhi (r,x_3)$ in terms of elliptic integrals. We use the following simplification, which follows by explicit computations.

$$\begin{aligned}&\frac{r\cos t-1}{1+r^2+x_3^2-2r\cos t+x_3\sqrt{1+r^2+x_3^2-2r\cos t}}\nonumber \\&\quad =\frac{-x_3(r\cos t-1)}{(1+r^2-2r\cos t)\sqrt{1+r^2+x_3^2-2r\cos t}}+\frac{r\cos t-1}{1+r^2-2r\cos t}. \end{aligned}$$

(5.12)

Define

$$\begin{aligned} C(r)=\int _{-\pi }^{\pi }\frac{r\cos t-1}{1+r^2-2r\cos t}\hbox{d}t. \end{aligned}$$

Then

$$\begin{aligned} C(r):={\left\{ \begin{array}{ll}0&\quad {\text {if}}\quad r>1\\ -\pi &\quad {\text {if}}\quad r= 1 \\ -2\pi &\quad {\text {if}}\quad r<1 \end{array}\right. }. \end{aligned}$$

Using (5.12) and $\cos 2\theta = 1 - 2\sin ^2 \theta$, we write

$$\begin{aligned} 4\pi \varPhi (r,x_3)&=C(r)+ \dfrac{2x_3}{\sqrt{(1+r)^2 + x_3^2}} \int _{0}^{\pi /2} \dfrac{\hbox{d}t}{\sqrt{1 - \dfrac{4r}{{(1+r)^2 + x_3^2}}\sin ^2 t}} \\&\quad - \dfrac{2x_3 (r^2 -1)}{(1+r^2)^2\sqrt{(1+r)^2 + x_3^2}} \int _{0}^{\pi /2} \dfrac{\hbox{d}t}{\left( 1 - \dfrac{4r}{(1+r^2)}\sin ^2 t\right) \sqrt{1 - \dfrac{4r}{{(1+r)^2 + x_3^2}}\sin ^2 t}} \\&=\dfrac{2x_3}{\sqrt{(1+r)^2 + x_3^2}} {\mathbf {K}}\left( \sqrt{\dfrac{4 r}{(1+r)^2 + x_3^2}}\right) \\&\quad +\dfrac{2x_3 (1-r)}{(1+r)\sqrt{(1+r)^2 + x_3^2}} {\varvec{{\Pi }}}\left( \dfrac{4r}{(1+r)^2},\sqrt{\dfrac{4 r}{(1+r)^2 + x_3^2}}\right) + C(r). \end{aligned}$$

We may write the formula in terms of Heuman’s Lambda function ${\varvec{{\Lambda }}}_0$ using the formula relating ${\varvec{{\Pi }}}$ and ${\varvec{{\Lambda }}}_0$; see [1, page 228] or [11]. After straightforward but tedious calculations, we obtain the following explicit formula.

Proposition 5.13

(see [4, Proposition 6.3.1]) Let$x=(x_1,x_2,x_3)\in {\mathbb {R}}^3$.

• If$x\notin \{x_1^2 + x_2^2 = 1, x_3\leqslant 0\}$    and    $x_3 \ne 0$. Then

  $$\begin{aligned} 4\pi \varPhi (r,x_3)&= C(r) + \dfrac{2x_3}{\sqrt{(1+r)^2 + x_3^2}} {\mathbf {K}}(k)\\&\quad + \pi {\varvec{{\Lambda }}}_0 \left( \arcsin \dfrac{|x_3|}{\sqrt{(1-r)^2 + x_3^2}},k\right) \dfrac{x_3(1-r)}{|x_3\Vert 1-r|}, \end{aligned}$$

  where

  $$\begin{aligned} k=\sqrt{\frac{4r}{(1+r)^2+x_3^2}}. \end{aligned}$$

  (5.14)

• If$x_3=0$    but    $x_1^2+x_2^2\ne 1$, then

  $$\begin{aligned} \varPhi (r,0) = \frac{C(r)}{4\pi }. \end{aligned}$$

• If$x_1^2 + x_2^2 = 1 \quad { and} \quad x_3 < 0$, then

  $$\begin{aligned} \varPhi (1,x_3) = - \varPhi (1,-x_3) = \frac{1}{4} + \frac{1}{4\pi }\dfrac{2x_3}{\sqrt{4 + x_3^2}} {\mathbf {K}}\left( \sqrt{\dfrac{4}{4 + x_3^2}}\right) . \end{aligned}$$

Another approach in computing the solid angle for an unknot was given by F. Paxton; see [11]. He showed that the solid angle subtended at a point P with height L from the unknot and with distance $r_0$ from the axis of the unknot is equal to

$$\begin{aligned}\varPhi = {\left\{ \begin{array}{ll} \frac{1}{2} - \frac{1}{4\pi }\frac{2L}{R_{\max }}{\mathbf {K}}(k) - \frac{1}{4} {\varvec{{\Lambda }}}_0(\xi ,k) &\quad {\text {if}} \quad r_0 < 1 \\ \frac{1}{4} - \frac{1}{4\pi }\frac{2L}{R_{\max }}{\mathbf {K}}(k) &\quad {\text {if}} \quad r_0 = 1 \\ - \frac{1}{4\pi }\frac{2L}{R_{\max }}{\mathbf {K}}(k) + \frac{1}{4}{\varvec{{\Lambda }}}_0(\xi ,k) &\quad {\text {if}} \quad r_0 > 1 \end{array}\right. } \end{aligned}$$

where $R_{\max } = \sqrt{(1+r_0)^2 + L^2}$, $\xi = \arctan \frac{L}{|1-r_0|}$ and k is given by (5.14). It can be shown that the Paxton formula agrees with the result of Proposition 5.13.

Finally, we remark that the computation of the solid angle of the unknot was already studied by Maxwell. He gave the formulae in terms of infinite series; see [10, Chapter XIV].

5.3 Behavior of $\varPhi$ near U

We shall now investigate the behavior of $\varPhi$ and its partial derivatives near U. Let us write

$$\begin{aligned} x_1 = 1+\varepsilon \cos 2\pi \lambda ,\quad x_2 = 0 \quad and \quad x_3 = \varepsilon \sin 2\pi \lambda \end{aligned}$$

where $\varepsilon >0$ is small and $\lambda \in [0,1]$. We have the following result.

Proposition 5.15

(see [4, Proposition 6.4.2]) The limit as$\varepsilon \rightarrow 0^+$is given by

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0^+} \varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda ) = -\lambda \quad \in {\mathbb {R}}/Z. \end{aligned}$$

Sketch of proof

Use $r = 1 + \varepsilon \cos 2\pi \lambda$, $x_3 = \varepsilon \sin 2\pi \lambda$ and apply Proposition 5.13 together with a fact that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0^+}\dfrac{2\varepsilon \sin 2\pi \lambda }{\sqrt{4+4\varepsilon \cos 2\pi \lambda +\varepsilon ^2}} {\mathbf {K}}\left( \sqrt{\dfrac{4+4\varepsilon \cos 2\pi \lambda }{4+4\varepsilon \cos 2\pi \lambda +\varepsilon ^2}}\right) = 0. \end{aligned}$$

$\square$

Remark 5.16

The sign of the limit is $-\lambda$ and not $+\lambda$. It is not hard to see that the orientation convention for the circle, that is, such that $t\mapsto (\cos t,\sin t,0)$ is an oriented parameterization of U is opposite to the convention adopted in Sect. 4.2.

Next we compute the derivatives of $\varPhi$ near U. It is clear that the map $\varPhi$ for the circle is invariant with respect to the rotational symmetry around the z–axis. Hence, if $\alpha$ is the longitudinal coordinate near U, then $\dfrac{\partial }{\partial \alpha }\varPhi = 0$. The two coordinates we have to deal with are the meridional and radial coordinates $\lambda$ and $\varepsilon$. The first result is the following.

Proposition 5.17

(see [4, Proposition 6.4.3]) We have

$$\begin{aligned} \dfrac{\partial }{\partial \varepsilon } \varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda ) = \frac{1}{4\pi }\dfrac{2\sin 2\pi \lambda ( {\mathbf {K}}(k)-{\mathbf {E}}(k))}{(1+\varepsilon \cos 2\pi \lambda )\sqrt{4+4\varepsilon \cos 2\pi \lambda +\varepsilon ^2}}. \end{aligned}$$

We observe that as $\varepsilon \rightarrow 0^+$, we have $k\rightarrow 1^-$ by (5.14). The numerator ${\mathbf {K}}(k)-{\mathbf {E}}(k)$ blows up, so the right-hand side of the formula in Proposition 5.17 is divergent as $\varepsilon \rightarrow 0$. For future use, we remark that by (5.4) and Proposition 5.17 we have

$$\begin{aligned} \left| \dfrac{\partial }{\partial \varepsilon } \varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda )\right| \leqslant C_{lin}(-\ln \varepsilon ) \end{aligned}$$

(5.18)

for some constant $C_{\rm lin}$, which can be explicitly calculated.

By Proposition 5.17 the sign of $\dfrac{\partial }{\partial \varepsilon } \varPhi$ depends on $\sin 2\pi \lambda$. Hence, $\varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda )$ is non-decreasing with respect to $\varepsilon$ when $\lambda \in [0,\frac{1}{2}]$ and it is non-increasing when $\lambda \in [\frac{1}{2},1]$. Since we know that

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0^+} \varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda ) = -\lambda , \end{aligned}$$

Dini’s theorem, see, e.g., [12, Theorem 7.13], yields that as $\varepsilon \rightarrow 0^+$, $\varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda )$ converges uniformly to $-\lambda$ on [0, 1]. With this, the map $(\varepsilon ,\lambda )\mapsto \varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda )$ extends to the set $\{\varepsilon =0\}$ even though $\varPhi$ itself is not defined at (1, 0, 0).

Remark 5.19

This extension of $\varPhi$ through $\{\varepsilon =0\}$ will be generalized in the Continuous Extension Lemma 7.10.

We now estimate the derivative of $\varPhi$ with respect to $\lambda$.

Proposition 5.20

(see [4, Proposition 6.4.4])

$$\begin{aligned} \dfrac{\partial }{\partial \lambda } \varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda ) < 0 \end{aligned}$$

and

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0^+}\dfrac{\partial }{\partial \lambda } \varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda )= -1. \end{aligned}$$

Proof

Set

$$\begin{aligned} k&= \sqrt{\dfrac{4+4\varepsilon \cos 2\pi \lambda }{4+4\varepsilon \cos 2\pi \lambda + \varepsilon ^2}}\\ k^{\prime}&= \sqrt{1-k^2} = \dfrac{\varepsilon }{\sqrt{4+4\varepsilon \cos 2\pi \lambda + \varepsilon ^2}}. \end{aligned}$$

Note that

$$\begin{aligned} \dfrac{\partial k}{\partial \lambda }&= 2\pi \dfrac{-k^{\prime 3}\sin 2\pi \lambda }{\sqrt{1+\varepsilon \cos 2\pi \lambda }} \end{aligned}$$

and

$$\begin{aligned} \dfrac{\partial k^{\prime}}{\partial \lambda }&= \frac{-k}{\sqrt{1-k^2}} \frac{\partial k}{\partial \lambda } = -\frac{k}{k^{\prime}} \frac{\partial k}{\partial \lambda }. \end{aligned}$$

Using (5.7) and (5.8), we have

$$\begin{aligned}&\dfrac{\partial }{\partial \lambda } \varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda ) \\&\quad = \frac{1}{4\pi } \dfrac{\partial }{\partial \lambda } (2\sin 2\pi \lambda k^{\prime} {\mathbf {K}}(k) \pm \pi {\varvec{{\Lambda }}}_0 (\arcsin |\sin 2\pi \lambda |,k))\\&\quad = \frac{1}{2\pi }\sin 2\pi \lambda \left( {\mathbf {K}}(k)\frac{\partial k^{\prime}}{\partial \lambda } + k^{\prime}\frac{\partial {\mathbf {K}}(k)}{\partial \lambda }\right) + k^{\prime}{\mathbf {K}}(k)\cos 2\pi \lambda \\&\quad \pm \frac{1}{4}\left( \frac{\partial }{\partial (\arcsin |\sin 2\pi \lambda |)}{\varvec{{\Lambda }}}_0 (\arcsin |\sin 2\pi \lambda |,k))\right) \frac{\partial (\arcsin |\sin 2\pi \lambda |)}{\partial \lambda }\\&\quad \pm \frac{1}{4}\left( \frac{\partial }{\partial k}{\varvec{{\Lambda }}}_0 (\arcsin |\sin 2\pi \lambda |,k))\right) \frac{\partial k}{\partial \lambda }\\&\quad = \frac{1}{2\pi }\sin 2\pi \lambda \dfrac{\partial k}{\partial \lambda }\left( \dfrac{{\mathbf {E}}(k)- {\mathbf {K}}(k)}{kk^{\prime}}\right) + k^{\prime} {\mathbf {K}}(k)\cos 2\pi \lambda \\&\quad \quad - \left( \dfrac{{\mathbf {E}}(k) - k^{\prime 2}\sin ^2 2\pi \lambda {\mathbf {K}}(k))}{\sqrt{1-k^{\prime 2}\sin ^2 2\pi \lambda }}\right) - \frac{1}{2\pi }\left( \dfrac{({\mathbf {E}}(k)- {\mathbf {K}}(k))\sin 2\pi \lambda \cos 2\pi \lambda }{k \sqrt{1-k^{\prime 2}\sin ^2 2\pi \lambda }}\right) \dfrac{\partial k}{\partial \lambda }. \end{aligned}$$

See also [4, Equation (6.11) and Proposition 6.4.3]. As $\varepsilon \rightarrow 0^+$, we have $k\rightarrow 1$, $k^{\prime}\rightarrow 0$. Since $k^{\prime} {\mathbf {K}}(k)\rightarrow 0$ and $k^{\prime}{\mathbf {E}}(k)\rightarrow 0$ as $\varepsilon \rightarrow 0^+$, the only significant term in the above expression is $-\dfrac{{\mathbf {E}}(k)}{\sqrt{1-k^{\prime 2}\sin ^2 2\pi \lambda }}$, and hence,

$$\begin{aligned} \lim _{\varepsilon \rightarrow 0^+}\dfrac{\partial }{\partial \lambda } \varPhi (1+\varepsilon \cos 2\pi \lambda ,0,\varepsilon \sin 2\pi \lambda ) = -{\mathbf {E}}(1) = -1. \end{aligned}$$

$\square$

We have estimated the derivatives of $\varPhi$ with respect to $\varepsilon$ and $\lambda$. We can now give the following corollary, which is a straightforward consequence of (5.18).

Corollary 5.21

The derivatives$\frac{\partial }{\partial x_j}\varPhi (x_1,x_2,x_3)$, $j=1,2,3$have at most a logarithmic pole at points$(x_1,x_2,x_3)$close toU. More precisely, there exists a constant$C_{circ}$such that

$$\begin{aligned} \left| \frac{\partial }{\partial x_j}\varPhi (x_1,x_2,x_3)\right| \leqslant C_{circ}(-\ln {\text {dist}}((x_1,x_2,x_3),U)). \end{aligned}$$

We remark that from (2.18), we get much weaker estimates on the derivative. We do not know whether these weaker estimates can be improved for general manifolds M.

To conclude, we show level sets of the function $(r,x_3)\mapsto \varPhi (r,x_3)$ for the circle in Fig. 6. Notice that in the figure the half-lines stemming from point (1, 0) (and not parallel to the $x_3=0$ line) intersect infinitely many level sets near the point (1, 0). This suggests that the radial derivative $\frac{\partial }{\partial \varepsilon }\varPhi (1+\varepsilon \cos 2\pi \lambda , \varepsilon \sin 2\pi \lambda )$ is unbounded as $\varepsilon \rightarrow 0^+$. We proved this fact rigorously in Proposition 5.17.

Fig. 6

Level sets of the function $(r,x_3)\mapsto \varPhi (r,x_3)$ for the circle

6 Derivatives of $\varPhi$ near M

We begin by recalling a well-known fact in differential geometry.

Proposition 6.1

Let$X\subset {\mathbb {R}}^{n+2}$be ak-dimensional, smooth, compact submanifold with smooth boundary. Then, there exists a constant$C_X$such that for every$x\in {\mathbb {R}}^{n+2}$and for any$r>0$we have

$$\begin{aligned} {{\,{\mathrm{vol}}\,}}_k(X\cap B(x,r))\leqslant C_X r^k. \end{aligned}$$

Moreover, increasing$C_X$if necessary, we may assume that if$\omega$is ak–form on${\mathbb {R}}^{n+2}$whose coefficients are bounded byT, then$|\int _{X\cap B(x,r)}\omega |\leqslant C_X T r^k$.

The result is well known to the experts; therefore, we present only a sketchy proof.

Sketch of proof

Let $\delta _k$ be the volume of unit k-dimensional ball. By smoothness of X, we infer that $\lim _{r\rightarrow 0}\displaystyle \frac{{{\,{\mathrm{vol}}\,}}_k(X\cap B(x,r))}{r^k}$ is 0, $\frac{1}{2}\delta _k$ or $\delta _k$ depending on whether $x\notin X$, $x\in \partial X$ or $x\in X{\setminus }\partial X$. Using Vitali’s covering theorem, see, e.g., [8, Section 1.5], one shows that there exists $r_0$ independent of x such that $\displaystyle \frac{{{\,{\mathrm{vol}}\,}}_k(X\cap B(x,r))}{r^k}\leqslant 2\delta _k$ for all $r<r_0$. We take $C_X$ to be the maximum of $2\delta _k$ and ${{\,{\mathrm{vol}}\,}}_k(X)/r_0^k$.

The second part is standard and left to the reader. $\square$

6.1 The Separation Lemma

The form $\eta _z$ used in Sect. 2.2 has a pole at $z\in S^{n+1}$. In the applications for given $x\in {\mathbb {R}}^{n+2}{\setminus } M$, we choose a point z such that $z\notin {{\,{\mathrm{Sec}}\,}}_x(M)$. Such a point exists; see Remark 2.9. However, in order to obtain a meaningful bound for ${{\,{\mathrm{Sec}}\,}}_x^*\eta _z$, we need to know that z is separated from ${{\,{\mathrm{Sec}}\,}}_x(M)$, in the sense that there exists a constant D such that $\langle y,z\rangle \leqslant D$ for any $y\in {{\,{\mathrm{Sec}}\,}}_x(M)$. In this section, we show that the constant $D<1$ can be chosen independently of x.

Lemma 6.2

(Separation lemma) There exist$\varepsilon _0>0$and$D<1$such that the set$N_0$of points at distance less than$\varepsilon _0$fromMand not lying inM(using algebraic sums this set can be written as$N_0=(M+B(0,\varepsilon _0)){\setminus } M$) can be covered by a finite number of open sets$U_1,\ldots , U_l$with the following property: for eachithere exists a point$z_i\in S^{n+1}$such that for any$x\in U_i$we have${{\,{\mathrm{Sec}}\,}}_x(M)\subset \{u\in S^{n+1}:\langle u,z_i\rangle \leqslant D\}$.

Remark 6.3

In general, it is impossible for a given point $x\in M$ to find an element $z\in S^{n+1}$ and a neighborhood $U\subset {\mathbb {R}}^{n+2}$ of x, such that for every $x^{\prime}\in U$ we have $z\notin {{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M)$. In fact, the opposite holds. For any $z\in S^{n+1}$ the sequence $x_n=x-\frac{z}{n}$ has the property that $z\in {{\,{\mathrm{Sec}}\,}}_{x_n}(M)$ and $x_n\rightarrow x$. This is the main reason why the proof of an apparently obvious lemma is not trivial.

Put differently, the subtlety of the proof of Lemma 6.2 lies in the fact that the image ${{\,{\mathrm{Sec}}\,}}_x(M)$ can be defined for $x\in M$ as a closure of ${{\,{\mathrm{Sec}}\,}}_x(M{\setminus }\{x\})$, but we cannot argue that ${{\,{\mathrm{Sec}}\,}}_x(M)$ depends continuously on x, if $x\in M$.

Proof of Lemma 6.2

Take a point $x\in M$. Let V be the affine subspace tangent to M at x, that is, $V=x+T_xM$. The image ${{\,{\mathrm{Sec}}\,}}_x(V{\setminus } \{x\})$ is the intersection

$$\begin{aligned} S_x:=T_xM\cap S^{n+1}. \end{aligned}$$

Lemma 6.4

For any open subset$U\subset S^{n+1}$containing$S_x$, there exists$r>0$such that${{\,{\mathrm{Sec}}\,}}_x(M\cap B(x,r){\setminus }\{x\})$is contained inU.

Proof

Suppose the contrary, that is, for any n there exists a point $y_n\in M$ such that $\Vert x-y_n\Vert <\frac{1}{n}$ and ${{\,{\mathrm{Sec}}\,}}_x(y_n)\notin U$. In particular, $y_n\rightarrow x$. As M is a smooth submanifold of ${\mathbb {R}}^{n+2}$, the tangent space $T_xM$ is the linear space of limits of secant lines through x. This means that if $y_n\rightarrow x$ and $y_n\in M$, then, up to passing to a subsequence, ${{\,{\mathrm{Sec}}\,}}_x(y_n)$ converges to a point in $S_x$. But then, starting with some $n_0>0$, we must have ${{\,{\mathrm{Sec}}\,}}_x(y_n)\in U$ for all $n>n_0$. Contradiction. $\square$

Choose now a neighborhood U of $S_x$ and r from Lemma 6.4. As $S_x$ is invariant with respect to the symmetry $y\mapsto -y$, we may and shall assume that U also is. We assume that U is small neighborhood of $S_x$, but in fact we shall only need that U is not dense in $S^{n+1}$. We shall need the following technical result.

Lemma 6.5

Suppose$v\in S^{n+1}{\setminus } U$. Then there exists an open neighborhood$W_v\subset {\mathbb {R}}^{n+2}$ofx, such that if$x^{\prime}\in W_v$, then either$v\notin {{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M\cap \overline{B(x,r)})$or$-v\notin {{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M\cap \overline{B(x,r)})$.

Proof of Lemma 6.5

We argue by contradiction. Assume the statement of the lemma does not hold. That is, there is a sequence $x_n$ converging to x such that both v and $-v$ belong to ${{\,{\mathrm{Sec}}\,}}_{x_n}(M\cap \overline{B(x,r)})$. This means that for any n the line $l_{x_n}:=\{x_n+tv,t\in {\mathbb {R}}\}$ intersects $M\cap \overline{B(x,r)}$ in at least one point for $t>0$ and at least one point for $t<0$. For each n, choose a point $y_{n}^+$ in $M\cap \overline{B(x,r)}\cap l_{x_n}\cap \{t>0\}$ and a point $y_n^-$ in $M\cap \overline{B(x,r)}\cap l_{x_n}\cap \{t<0\}$. In particular, ${{\,{\mathrm{Sec}}\,}}_{x_n}(y_n^+)=v$ and ${{\,{\mathrm{Sec}}\,}}_{x_n}(y_n^-)=-v$.

By taking subsequences of $\{y^+_n\}$ and $\{y^-_n\}$ we can assume that $y_n^+\rightarrow y^+$ and $y_n^-\rightarrow y^-$ for some $y^+,y^-\in M\cap \overline{B(x,r)}$; compare Fig. 7.

Fig. 7

Proof of Lemma 6.5. To the left: a sequence of lines $l_{x_1},l_{x_2}$ converges to a line that is tangent to M at x, so that $v\in T_xM$. To the right: a sequence of lines $l_{x_1},l_{x_2}$ converges to a line that passes through x and intersects M at some point. Then $v\in {{\,{\mathrm{Sec}}\,}}_x(M)$

If $y^+\ne x$, then the line $l_x=\{x+tv\}$ passes through $y^+$, but this means that $v\in {{\,{\mathrm{Sec}}\,}}_x(M\cap \overline{B(x,r)})$, but the assumption was that $v\notin U$, so we obtain a contradiction. So $y^+=x$. Analogously we prove that $y^-=x$.

Finally, suppose $y^+=y^-=x$. The line $l_x=\{x+tv\}$ is the limit of secant lines passing through $y_n^+$ and $y_n^-$; therefore, $l_x$ is tangent to M at x. But then $v\in S_x\subset U$. Contradiction. $\square$

We extend the argument of Lemma 6.5 in the following way.

Lemma 6.6

Suppose$v\in S^{n+1}{\setminus } U$. Then there exist an open set$V_{\mathrm{\rm loc}}\subset S^{n+1}$containingvand an open ball$B_{\mathrm{\rm loc}}\subset B(x,r)$containingxsuch that if$x^{\prime}\in B_{\mathrm{\rm loc}}$then there exists a choice of sign$\eta \in \{\pm 1\}$possibly depending onxsuch that$\eta V_{\mathrm{\rm loc}}$is disjoint from the image${{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M\cap \overline{B(x,r)})$.

Proof

The proof is a modification of the proof of Lemma 6.5. We leave the details for the reader. $\square$

Resuming the proof of Lemma 6.2, define the sets $B_{\mathrm{\rm loc}+}$ and $B_{\mathrm{\rm loc}-}$ by

$$\begin{aligned} B_{\mathrm{\rm loc}\pm }=\{x^{\prime}\in B_{\mathrm{\rm loc}}:{\text{for every }}\,\,v^{\prime}\in V_{\mathrm{\rm loc}} {\text{we have}}\,\,\pm v^{\prime}\notin {{\,{\mathrm{Sec}}\,}}_{x^{\prime}} (M\cap \overline{B(x,r)}) \}. \end{aligned}$$

Then clearly $B_{\mathrm{\rm loc}+}\cup B_{\mathrm{\rm loc}-}=B_{\mathrm{\rm loc}}$.

Lemma 6.7

The subsets$B_{\mathrm{\rm loc}+}{\setminus } M$and$B_{\mathrm{\rm loc}-}{\setminus } M$are open subsets of$B_{\mathrm{\rm loc}}{\setminus } M$.

Proof

The lemma follows from the fact that $M\cap \overline{B(x,r)}$ is closed and ${{\,{\mathrm{Sec}}\,}}_{x^{\prime}}$ is continuous with respect to $x^{\prime}$ as long as $x^{\prime}\notin M$. $\square$

The next step in the proof of the Separation Lemma 6.2 is the following.

Lemma 6.8

There exists an open set$B_x\subset {\mathbb {R}}^{n+2}$containingx, a point$v_x\in S^{n+1}$and an open set$V_x\subset S^{n+1}$containing$v_x$such that if$x^{\prime}\in B_x$and$v^{\prime}\in V_x$then either$v^{\prime}$or$-v^{\prime}$does not belong to${{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M)$.

Moreover, there are two subsets$B_x^{\pm }$of$B_x$such that$B_x^+\cup B_x^-=B_x$, $B_x^\pm$are open in$B_x{\setminus } M$and if$x^{\prime}\in B_x^\pm$ and $v^{\prime}\in V_x$, then${{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M)$does not contain$\pm v^{\prime}$.

Proof

Let U and $r>0$ be as in the statement of Lemma 6.4. The set ${{\,{\mathrm{Sec}}\,}}_x(M{\setminus } B(x,r))$ is the image of the compact manifold $M{\setminus } B(x,r)$ of dimension n under a smooth map; hence, its interior is empty. Therefore, there exists a point $v\in S^{n+1}$ such that neither v nor $-v$ is in the image ${{\,{\mathrm{Sec}}\,}}_x(M{\setminus } B(x,r))$ and also neither v nor $-v$ is in U. By the continuity of ${{\,{\mathrm{Sec}}\,}}_x$, there exist a small ball $B_{gl}\subset B(x,r)$ with center x and a small ball $V_{gl}\subset S^{n+1}$ containing v such that if $v^{\prime}\in V_{gl}$ and $x^{\prime}\in B_{gl}$, then neither $v^{\prime}$ nor $-v^{\prime}$ belongs to ${{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M{\setminus } B(x,r))$. Let $V_{\mathrm{\rm loc}}$ and $B_{\mathrm{\rm loc}}$ be from Lemma 6.6. Define $V_x=V_{\mathrm{\rm loc}}\cap V_{gl}$ and $B_x=B_{\mathrm{\rm loc}}\cap B_{gl}$. Then for any $x^{\prime}\in B_x$ and $v^{\prime}\in V_x$ we have that either $v^{\prime}\notin {{\,{\mathrm{Sec}}\,}}_{x^{\prime}}M$ or $-v\notin {{\,{\mathrm{Sec}}\,}}_{x^{\prime}}$.

We define $B_x^\pm$ as intersections of $B_{\mathrm{\rm loc}\pm }$ with $B_x$, where $B_{\mathrm{\rm loc}\pm }$ are as in Lemma 6.7. $\square$

We resume the proof of the Separation Lemma 6.2. Define

$$\begin{aligned} \delta _x=\sup _{y\in S^{n+2}{\setminus } V_x} \langle v_x,y\rangle . \end{aligned}$$

As $V_x$ is an open set containing $v_x$, we have $\delta _x<1$. This means that if $x^{\prime}\in B_x$ and $y\in {{\,{\mathrm{Sec}}\,}}_x(M)$, then either $\langle y,v_x\rangle \leqslant \delta _x$ or $\langle y,-v_x\rangle \leqslant \delta _x$.

Cover now M by open sets $B_x$ for $x\in M$. As M is compact, there exists a finite set $x_1,\ldots ,x_n$ such that $M\subset B_{x_1}\cup \dots \cup B_{x_n}$. The compactness of M implies also that there exists $\varepsilon _0>0$ such that the set $M+B(0,\varepsilon _0)$, that is, the set of points at distance less than $\varepsilon _0$ from M, is contained in $B_{x_1}\cup \dots \cup B_{x_n}$. Define $D=\max (\delta _{x_1},\ldots ,\delta _{x_n})$ and let $N_0=(M+B(0,\varepsilon _0)){\setminus } M$. For $i=1,\ldots ,n$ define $v_i=v_{x_i}$ and $B_i^\pm =B_{x_i}^\pm \cap N_0$. Then $B_i^\pm$ cover $N_0$ and for any i, if $x^{\prime}\in B_i^\pm$ and $y\in {{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M)$, then $\langle y,\pm v_i\rangle \leqslant D$ as desired. $\square$

For points x that are at distance greater than $\varepsilon _0$ from M, the statement of the Separation Lemma 6.2 holds as well.

Theorem 6.9

(Separation Theorem) There exists a constant$D<1$such that for any$x\in {\mathbb {R}}^{n+2}{\setminus } M$there exists an open neighborhood$U_x\subset {\mathbb {R}}^{n+2}$ofxand a point$z\in S^{n+2}$, such that for any$x^{\prime}\in U_x$and$y\in {{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M)$we have$\langle y,z\rangle <D$.

Proof

Denote by $D_{close}$ the constant D from the Separation Lemma 6.2. The constant $D_{close}$ works for points at distance less than $\varepsilon _0$ from M.

We work with points far from M. Choose $R>0$ large enough so that $M\subset B(0,R)$. For any $x\notin B(0,R)$ we can take the point $\frac{x}{\Vert x\Vert }$ for z and then if $y\in {{\,{\mathrm{Sec}}\,}}_x(M)$, then $\langle y,z\rangle \leqslant 0$. By the continuity of $x\mapsto {{\,{\mathrm{Sec}}\,}}_x$, we may choose a neighborhood $W_x$ of x such that if $x^{\prime}\in W_x$ and $y_n\in {{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M)$, then $\langle y,z\rangle$ is bounded from above by a small positive number, say $\frac{1}{10}$. This takes care of the exterior of the ball B(0, R). We define $D_{far}=\frac{1}{10}$. The constant $D_{far}$ works for points outside the ball B(0, R).

Let $P=\{x\in \overline{{B}(0,R)}:{{\,\mathrm{dist}\,}}(x,M)\geqslant \varepsilon _0\}$. For any point $x\in P$, ${{\,{\mathrm{Sec}}\,}}_x(M)$ is the image of an n-dimensional compact manifold under a smooth map, so it is a closed nowhere dense subset of $S^{n+1}$. Thus, there exist a point $z_x\in S^{n+1}$ and a neighborhood of $U_x$ of $z_x$ such that $U_x\cap {{\,{\mathrm{Sec}}\,}}_x(M)=\emptyset$. Shrinking $U_x$ if necessary, we may guarantee that there exists a neighborhood $W_x\subset {\mathbb {R}}^{n+2}$ of x such that if $x^{\prime}\in W_x$ and $y\in {{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(M)$, then $y\notin U_x$. We define again

$$\begin{aligned} \delta _x=\sup _{y\in S^{n+2}{\setminus } V_x}\langle z_x,y\rangle <1. \end{aligned}$$

The sets $W_x$ cover P, and we take a finite subcover $W_{x_1},\ldots ,W_{x_M}$. We define $D_{\rm mid}$ as the maximum of $\delta _{x_1},\ldots ,\delta _{x_M}$. The constant $D_{\rm mid}$ works for points that are at distance between at least $\varepsilon _0$ from M, but stay inside B(0, R).

It is enough to take $D=\max (D_{\rm close},D_{\rm mid},D_{\rm far})$. $\square$

From now on, we assume that $D<1$ is fixed.

6.2 The Drilled Ball Lemma

We begin to bound the value of $\frac{\partial }{\partial x_i}\varPhi (x)$. To this end, we shall differentiate the coefficients of ${{\,{\mathrm{Sec}}\,}}_x^*\eta _z$. The point z will always be chosen in such a way that $\langle {{\,{\mathrm{Sec}}\,}}_{x^{\prime}}(y),z\rangle <D$ for all $y\in M$ and for all $x^{\prime}$ sufficiently close to x.

The next result estimates the contribution to $\frac{\partial \varPhi }{\partial x_j}$ from integrating ${{\,{\mathrm{Sec}}\,}}_x^*\eta$ on a drilled ball.

Lemma 6.10

Suppose$\alpha ,\beta \in (0,1)$and$x\in {\mathbb {R}}^{n+2}$. Fix$\varepsilon >0$and define

$$\begin{aligned} M_{\alpha \beta \varepsilon } := M\cap (B(x,\varepsilon ^\beta ){\setminus } B(x,\varepsilon ^\alpha )). \end{aligned}$$

Then, for any$i=1,\ldots ,n+2$

$$\begin{aligned} \left| \frac{\partial }{\partial x_i}\int _{M_{\alpha \beta \varepsilon }} {{\,{\mathrm{Sec}}\,}}_x^*\eta \right| <C_{\rm drill}\varepsilon ^\gamma , \end{aligned}$$

where$\gamma =n\beta -(n+1)\alpha$and$C_{\rm drill}=C_MC^D_{n,1}$is independent of$\alpha$, $\beta$andx.

Proof

By Lemma 2.23 and the Separation Lemma 6.2, the derivative of the pullback $\frac{\partial }{\partial x_i}{{\,{\mathrm{Sec}}\,}}_x^*\eta$ is an n–form whose coefficients are bounded from above by $\frac{C^D_{n,1}}{\Vert y-x\Vert ^{n+1}}$. If $y\in M_{\alpha \beta \varepsilon }$, then $\Vert y-x\Vert \geqslant \varepsilon ^{\alpha }$. The form $\frac{\partial }{\partial x_i}{{\,{\mathrm{Sec}}\,}}_x^*\eta$ is integrated over $M_{\alpha \beta \varepsilon }$. We use Proposition 6.1 twice: first to conclude that the volume of $M_{\alpha \beta \varepsilon }$ is bounded from above by $C_M\varepsilon ^{n\beta }$ and second to conclude that the integral is bounded by $C^D_{n,1}C_M\varepsilon ^{n\beta -(n+1)\alpha }$. $\square$

The next result shows that if M is locally parameterized by some $\varPsi$, then if we take a first-order approximation, the contribution to the derivative of $\varPhi (x)$ from the local piece does not change much. We need to set up some assumptions.

Choose $\varepsilon >0$ and $\alpha \in (\frac{1}{2},1)$. For a fixed point x at distance $\varepsilon$ from M, we set $M_{\alpha \varepsilon }=M\cap \overline{B(x,\varepsilon ^\alpha )}$. We assume that $\varepsilon ,\alpha$ are such that $M_{\alpha \varepsilon }$ can parameterized by

$$\begin{aligned} \varPsi :B^{\prime} \rightarrow M_{\alpha \varepsilon }, \end{aligned}$$

where $B^{\prime}$ is some bounded open subset in ${\mathbb {R}}^n$ and $\varPsi (0)$ is the point on $M_{\alpha \varepsilon }$ that is nearest to x. We also assume that $B^{\prime}$ is a star-shaped, that is, if $w\in B^{\prime}$, then tw is also in $B^{\prime}$ for $t\in [0,1]$. For simplicity of the formulae, we may transform $B^{\prime}$ in such a way that

$$\begin{aligned} D\varPsi (0)=\begin{pmatrix} 1&\quad 0&\quad \ldots &\quad 0\\ 0&\quad 1&\quad \ldots &\quad 0\\ \vdots &\quad \vdots &\quad \ddots &\quad \vdots \\ 0&\quad 0&\quad \ldots &\quad 1\\ 0&\quad 0&\quad \ldots &\quad 0\\ 0&\quad 0&\quad \ldots &\quad 0 \end{pmatrix}.\end{aligned}$$

(6.11)

Choose $\sigma >0$ in such a way that $B^{\prime}$ is a subset of an n-dimensional ball $B(0,\sigma )$ and $B^{\prime}$ is not a subset of $B(0,\sigma /2)$. Let $\varPsi _1$ be the first-order approximation of $\varPsi$, that is $\varPsi _1(w)=\varPsi (0)+D\varPsi (0)w$. Let $M_1$ be the image of $B^{\prime}$ under $\varPsi _1$. Write $C_1$ and $C_2$ for the supremum of the first and second derivatives of $\varPsi$ on $B^{\prime}$.

Lemma 6.12

(Approximation Lemma) Suppose

$$\begin{aligned} \varepsilon <\min \left( (4C_2)^{-1/\alpha }, 2^{-1/(\alpha -1)},(32C_2)^{-1/(2\alpha -1)}\right) \end{aligned}$$

(6.13)

and$\alpha \geqslant \frac{1}{2}$. There exists a constant$C_{\rm app}$depending on$\varPsi$such that

$$\begin{aligned} \left| \frac{\partial }{\partial x_j}\int _{M_{\alpha \varepsilon }}{{\,{\mathrm{Sec}}\,}}_{x}^*\eta - \frac{\partial }{\partial x_j}\int _{M_1}{{\,{\mathrm{Sec}}\,}}_{x}^*\eta \right| \leqslant C_{\rm app}\varepsilon ^{\delta }, \end{aligned}$$

where$\delta =\alpha (n+3)-(n+2)$.

Proof

As our first step, we relate $\sigma$ with $\varepsilon$ and $\alpha$. $\square$

Lemma 6.14

We have$\sigma \leqslant 4\varepsilon ^\alpha$.

Proof of Lemma 6.14

Suppose $w\in B(0,\sigma )$, $w\ne 0$. Write $\widetilde{w}$ for the vector in ${\mathbb {R}}^{n+2}$ given by $\frac{1}{\Vert w\Vert }(w,0,0)$. Define a function $\varPsi _w:{\mathbb {R}}\rightarrow {\mathbb {R}}$ by the formula $\varPsi _w(t)=\langle \varPsi (t\frac{w}{\Vert w\Vert }),\widetilde{w}\rangle$. By the definition, we have $\varPsi _w(0)=0$. From (6.11) we calculate that $\frac{\hbox{d}}{\hbox{d}t}\varPsi _w(0)=1$. Furthermore, as the second derivative of $\varPsi$ is bounded by $C_2$ we have that $|\frac{\hbox{d}^2}{\hbox{d}t^2}\varPsi _w(t)|<C_2$. It follows that $\varPsi _w(t)\geqslant t-\frac{C_2}{2}t^2$. Set $t_0=2\varepsilon ^\alpha$. As $\varepsilon ^\alpha <\frac{1}{4C_2}$ by the assumptions, we have $\varPsi _w(t_0)\geqslant 2\varepsilon ^\alpha -2C_2\varepsilon ^{2\alpha }\geqslant \frac{3}{2}\varepsilon ^\alpha$. Clearly, $\varPsi _w(t_0)\leqslant \Vert \varPsi (t_0\frac{w}{\Vert w\Vert })\Vert$; hence, $\Vert \varPsi (t_0\frac{w}{\Vert w\Vert })\Vert \geqslant \frac{3}{2}\varepsilon ^\alpha$.

The condition $\varepsilon <2^{-1/(\alpha -1)}$ implies that $\frac{1}{2}\varepsilon ^\alpha >\varepsilon$. By the triangle inequality,

$$\begin{aligned} \Vert \varPsi (t_0\frac{w}{\Vert w\Vert })-x\Vert \geqslant \Vert \varPsi (t_0\frac{w}{\Vert w\Vert })\Vert -\Vert x\Vert >\varepsilon +\varepsilon ^\alpha -\varepsilon =\varepsilon ^\alpha . \end{aligned}$$

This means that $\varPsi (t_0\frac{w}{\Vert w\Vert })$ cannot possibly belong to $B(x,\varepsilon ^\alpha )$; hence, it is not in the image $\varPsi (B^{\prime})=M\cap B(x,\varepsilon ^\alpha )$. This shows that $t_0\frac{w}{\Vert w\Vert }$ cannot belong to $B^{\prime}$. As w was an arbitrary point in $B^{\prime}$, this implies that no element in $B^{\prime}$ can have norm $2\varepsilon ^\alpha$. As $B^{\prime}$ is connected, this implies that $B^{\prime}$ must be contained in $B(0,2\varepsilon ^\alpha )$. By the definition of $\sigma$, we immediately recover that $\sigma \leqslant 4\varepsilon ^\alpha$. $\square$

We resume the proof of Lemma 6.12. Choose $w\in B(0,\sigma )$. Write $y_0=\varPsi (w)$, $y_1=\varPsi _1(w)$. By the Taylor formula, we have

$$\begin{aligned} \Vert y_0-y_1\Vert =\Vert \varPsi _1(w)-\varPsi (w)\Vert \leqslant C_2\Vert w\Vert ^2. \end{aligned}$$

(6.15)

We have $\Vert w\Vert <4\varepsilon ^\alpha$ and $2\alpha >1$. Using the assumption that $\varepsilon <(32C_2)^{-1/(2\alpha -1)}$ we infer that $C_2(4\varepsilon ^\alpha )^2\leqslant \frac{1}{2}\varepsilon$ so that $\Vert \varPsi _1(w)-\varPsi (w)\Vert \leqslant \frac{1}{2}\varepsilon$. Therefore, as ${{\,\mathrm{dist}\,}}(x,M_{\alpha \varepsilon })=\varepsilon$, we infer that for each point $y^{\prime}$ in the interval connecting $y_0$ and $y_1$ we have $\Vert x-y^{\prime}\Vert \geqslant \frac{1}{2}\varepsilon$; see Fig. 8.

Fig. 8

Notation of the proof of Approximation Lemma 6.12

Write now for $i=1,\ldots ,n+1$:

$$\begin{aligned} \frac{\partial {{\,{\mathrm{Sec}}\,}}_x^*\eta }{\partial x_i}=\sum _{i\ne j} F_{ij}(x,y)\hbox{d}y_1\wedge \cdots \widehat{\hbox{d}y_i,\hbox{d}y_j}\ldots \wedge \hbox{d}y_{n+2}. \end{aligned}$$

(6.16)

By the mean value theorem, for any i, j there exists a point $y^{\prime}$ in the interval connecting $y_0$ and $y_1$ such that

$$\begin{aligned} F_{ij}(x,y_0)-F_{ij}(x,y_1)=\Vert y_0-y_1\Vert \partial _vF_{ij}(x,y^{\prime}), \end{aligned}$$

(6.17)

where $\partial _v$ is the directional derivative in the direction of the vector $\frac{y_0-y_1}{\Vert y_0-y_1\Vert }$. Now $\Vert x-y^{\prime}\Vert \geqslant \frac{1}{2}\varepsilon$; hence, by Lemma 2.21:

$$\begin{aligned} \left| \partial _vF_{ij}(x,y^{\prime})\right| \leqslant C^D_{n,2}\left( \frac{1}{2}\varepsilon \right) ^{-n-2}. \end{aligned}$$

(6.18)

From (6.15) we deduce that

$$\begin{aligned} \left| F_{ij}(x,\varPsi (w))-F_{ij}(x,\varPsi _1(w))\right| \leqslant C\Vert w\Vert ^2\varepsilon ^{-n-2} \end{aligned}$$

(6.19)

for some constant C depending on $C_2$.

Set $G_{ij}(w)$ and $H_{ij}(w)$ to be defined by

$$\begin{aligned} \varPsi ^*\hbox{d}y_1\wedge \cdots \widehat{\hbox{d}y_i,\hbox{d}y_j}\ldots \wedge \hbox{d}y_{n+2}&=G_{ij}\hbox{d}w_1\wedge \cdots \wedge \hbox{d}w_n\\ \varPsi _1^*\hbox{d}y_1\wedge \cdots \widehat{\hbox{d}y_i,\hbox{d}y_j}\ldots \wedge \hbox{d}y_{n+2}&=H_{ij}\hbox{d}w_1\wedge \cdots \wedge \hbox{d}w_n.\\ \end{aligned}$$

The values of $G_{ij}$ and $H_{ij}$ are bounded by a constant depending on $C_1$. Moreover, the expression $D\varPsi (w)-D\varPsi _1(w)$ has all entries bounded from above by $\Vert w\Vert$ times a constant; hence, an exercise in linear algebra shows that

$$\begin{aligned} |G_{ij}(w)-H_{ij}(w)|\leqslant C_G\Vert w\Vert \end{aligned}$$

(6.20)

for some constant $C_G$ depending on $C_1$. Now write

$$\begin{aligned}&\varPsi ^*F_{ij}(x,y)\hbox{d}y_1\wedge \cdots \widehat{\hbox{d}y_i,\hbox{d}y_j}\ldots \wedge \hbox{d}y_{n+2}-\varPsi _1^*F_{ij}(x,y)\hbox{d}y_1\wedge \cdots \widehat{\hbox{d}y_i,\hbox{d}y_j}\ldots \wedge \hbox{d}y_{n+2} \\&\quad =\left( F_{ij}(x,\varPsi (w))G_{ij}(w)-F_{ij}(x,\varPsi _1)(w)H_{ij}(w)\right) \hbox{d}w_1\wedge \cdots \wedge \hbox{d}w_n. \end{aligned}$$

We estimate using (6.19):

$$\begin{aligned}&|F_{ij}(x,\varPsi (w))G_{ij}-F_{ij}(x,\varPsi _1)H_{ij}|\leqslant \\&\quad |F_{ij}(x,\varPsi (w))-F_{ij}(x,\varPsi _1(w))|\cdot |H_{ij}(w)|+|F_{ij}(x,\varPsi (w)|\cdot |G_{ij}(w)-H_{ij}(w)|. \end{aligned}$$

Combining this with (6.19), we infer that

$$\begin{aligned} |F_{ij}(x,\varPsi (w))G_{ij}-F_{ij}(x,\varPsi _1)H_{ij}|\leqslant C(\Vert w\Vert ^2\varepsilon ^{-n-2}+\Vert w\Vert \varepsilon ^{-n-1}), \end{aligned}$$

(6.21)

where the factor $\varepsilon ^{-n-1}$ comes from the estimate of $F_{ij}(x,\varPsi (w))$ and the constant C depends on previous constants, that is, C depends on $C_1$, $C_2$.

We use now (6.21) together with (6.16) and the definitions of $G_{ij}$, $H_{ij}$. After straightforward calculations, we obtain for some constant C:

$$\begin{aligned}\left| \int _{B^{\prime}}\frac{\partial }{\partial x_j}\left( \varPsi ^*{{\,{\mathrm{Sec}}\,}}_x(y)-\varPsi _1^*{{\,{\mathrm{Sec}}\,}}_x(y)\right) \right| \leqslant \int _{B(0,\sigma )} C(\Vert w\Vert ^2\varepsilon ^{-n-2}+\Vert w\Vert \varepsilon ^{-n-1}).\end{aligned}$$

The last expression is bounded by $C_{\rm app}(\varepsilon ^{(n+3)\alpha -(n+2)}+\varepsilon ^{(n+2)\alpha -(n+1)})$, where $C_{\rm app}$ is a new constant. As $\alpha <1$ and $\varepsilon \ll 1$, the term $\varepsilon ^{(n+3)\alpha -(n+2)}$ is dominating. $\square$

In the following result, we show that the constants in the Approximation Lemma 6.12 can be made universal, that is, depending only on M and $\alpha$ and not on x and $\varepsilon$.

Proposition 6.22

For any$\alpha \in (\frac{1}{2},1)$there exist constants$C_\alpha$and$\varepsilon _1>0$such that for any$x\notin M$such that${{\,\mathrm{dist}\,}}(x,M)<\varepsilon _1$we have

$$\begin{aligned} \left| \frac{\partial \varPhi }{\partial x_i}(x)-\frac{\partial \varPhi _V}{\partial x_i}(x)\right| \leqslant C_{\alpha }\varepsilon ^{(n+2)\alpha -(n+1)}. \end{aligned}$$

Here$\varPhi _V$is a map$\varPhi$defined relatively to the planeVthat is tangent toMat a pointysuch that${{\,\mathrm{dist}\,}}(x,M)=\Vert x-y\Vert$.

Proof

Cover M by a finite number of subsets $U_i$ such that each of these subsets can be parameterized by a map $\varPsi _i:V_i\rightarrow U_i$, where $V_i$ is a bounded subset of ${\mathbb {R}}^n$. By the compactness of M, there exists $\varepsilon _1>0$ such that if $U\subset M$ has diameter less than $\varepsilon _1$, then U is contained in one of the $U_i$. Shrinking $\varepsilon _1$ if necessary, we may and shall assume that if ${{\,\mathrm{dist}\,}}(x,M)<\varepsilon _1$, then there is a unique point $y\in M$ such that ${{\,\mathrm{dist}\,}}(x,M)=\Vert x-y\Vert$.

Set $C_1$ and $C_2$ to be the upper bound on the first and the second derivatives of all of the $\varPsi _i$. The derivative $D\varPsi _i(w)$ is injective for all $w\in V_i$. We assume that $C_0>0$ is such that $\Vert D\varPsi _i(w)v\Vert \geqslant C_0\Vert v\Vert$ for all $v\in {\mathbb {R}}^n$, $i=1,\ldots ,n$ and $w\in V_i$.

Choose a point x at distance $\varepsilon >0$ to M such that $2\varepsilon ^\alpha <\varepsilon _1$ and $\varepsilon <\varepsilon _1$. Let $M_{\alpha \varepsilon }=B(x,\varepsilon ^\alpha )\cap M$. As this set has diameter less than $\varepsilon _1$, we infer that $M_{\alpha \varepsilon }\subset U_i$ for some i. Let $B=\varPsi _i^{-1}(M_{\alpha \varepsilon })\subset V_i$. Let $y\in M$ be the unique point realizing ${{\,\mathrm{dist}\,}}(x,M)=\Vert x-y\Vert$. We translate the set B in such a way that $\varPsi _i(0)=y$. Next, we rotate the coordinate system in ${\mathbb {R}}^{n+2}$ in such a way that the image of $D\varPsi (0)$ has a block structure $A\oplus \left( {\begin{matrix} 0 & 0\\ 0& 0\end{matrix}}\right)$ for some invertible matrix A. We know that $A^{-1}$ is a matrix with coefficients bounded by a universal constant depending on $c_1$ and $C_1$. Define now $B_0=A^{-1}(B)$ and $\varPsi _x=\varPsi _i\circ A$. Then $\varPsi$ has first and second derivatives bounded by a constant depending on $C_1,C_2$ and $c_1$. Denote these constants by $C_1(x),C_2(x)$. Let also be $C_0(x)>0$ be such that if $w,w^{\prime}\in B$, then $\Vert \varPsi _x(w)-\varPsi _x(w^{\prime})\Vert \geqslant C_0(x)\Vert w-w^{\prime}\Vert$. Such constant exists because $D\varPsi (w)$ is injective and we use the mean value theorem. Moreover, $C_0(x)$ is bounded below by a constant depending on $C_1$, $C_2$ and $C_0$.

It remains to ensure that the following two conditions are satisfied. First, the set $B=\varPsi _x^{-1}(M_{\alpha \varepsilon })$ has to be star-shaped, second the inequality (6.13) is satisfied. The second condition is obviously guaranteed by taking $\varepsilon _1$ sufficiently small. We claim that the first condition can also be guaranteed by taking small $\varepsilon _1$. To see this, we first notice that if $\varepsilon _1$ is sufficiently small, then $M_{\alpha \varepsilon }$ is connected for all $\varepsilon <\varepsilon _1$. Next, we take a closer look at the definition of $B\subset V_i$. Namely, we can think of B as the set of points $w\in V_i$ satisfying the inequality $R(w)\leqslant \varepsilon ^\alpha$, where

$$\begin{aligned} R(w)=\Vert \varPsi _x(w)-x\Vert ^2=\langle \varPsi _x(w)-x,\varPsi _x(w)-x\rangle . \end{aligned}$$

For $v\in {\mathbb {R}}^{n}$ we have

$$\begin{aligned} D^2R(0)(v,v)=2\langle D\varPsi _x(0)(v,v),\varPsi _x(0)-x\rangle +\langle D\varPsi _x(0)v,D\varPsi _x(0)v\rangle . \end{aligned}$$

By the construction of $\varPsi _x,$ we have that $\langle D\varPsi _x(0)v,D\varPsi _x(0)v\rangle =\Vert v\Vert ^2;$ hence,

$$\begin{aligned} D^2R(0)(v,v)\geqslant (1-2\varepsilon C_2(x))\Vert v\Vert ^2. \end{aligned}$$

Generalizing this for $w\in B$ and $v\in {\mathbb {R}}^n,$ we have

$$\begin{aligned} D^2R(w)(v,v)= \Vert DR(w)v\Vert ^2+2\langle D^2\varPsi _x(w)(v,v),\varPsi _x(w)-x\rangle . \end{aligned}$$

Now $\Vert D^2\varPsi _x(w)(v)\Vert \leqslant C_2(x)\Vert v\Vert ^2$ and by the mean value theorem also $\Vert DR(w)-DR(0)\Vert \leqslant C_2(x)\Vert w\Vert$. Suppose $\Vert x-\varPsi _x(w)\Vert \leqslant \varepsilon ^\alpha$. Then $\Vert \varPsi _x(w)-\varPsi _x(0)\Vert \leqslant 2\varepsilon ^\alpha$ and so $\Vert w\Vert \leqslant 2C_0(x)\varepsilon ^\alpha$. Hence,

$$\begin{aligned} D^2R(w)(v,v)\geqslant (1-2\varepsilon ^\alpha C_0(x)C_2(x)-2\varepsilon ^\alpha C_2(x))\Vert v\Vert ^2. \end{aligned}$$

This shows that R is a convex function if $\varepsilon$ is sufficiently small. Hence, B is a convex subset, in particular, it is also star-shaped. Therefore, all the assumptions of the Approximation Lemma 6.12 are satisfied; the statement follows. $\square$

6.3 Approximation Theorem

Combining the Drilled Ball Lemma 6.10 and Proposition 6.22, we obtain a result which is the main technical estimate.

Theorem 6.23

(Approximation Theorem) For any$\theta \in (\frac{n+2}{n+4},1)$there exists a constant$C_\theta$such that ifxis at distance$\varepsilon >0$toMand$\varepsilon <\varepsilon _1$, $y_0\in M$is a point realizing the minimum ofdist(x, M) andVis the tangent space toMpassing through$y_0$, then for any$j=1,\ldots ,n+2$

$$\begin{aligned} \left| \frac{\partial }{\partial x_j}\varPhi (x)-\frac{\partial }{\partial x_j}\varPhi _V(x)\right| \leqslant C_\theta \varepsilon ^{-\theta }. \end{aligned}$$

Here,$\varPhi _V$is the map$\varPhi$defined relatively to the hyperplaneV.

Remark 6.24

In Sect. 4, we have shown that $\varPhi _V$ is not well defined, but if we restrict to ‘Seifert hypersurfaces’ for V which are half-spaces (and that is what we in fact do), then $\varPhi _V$ is defined up to an overall constant. In particular, its derivatives do not depend on the choice of the half-space.

Proof

Let $\xi =\frac{\partial }{\partial x_j}{{\,{\mathrm{Sec}}\,}}_x^*\eta$. Set also $\alpha _0=\frac{n+2}{n+3}-\frac{\theta }{n+3}$. We have $(n+3)\alpha _0-(n+2)= -\theta$; hence, by Proposition 6.22 we obtain.

$$\begin{aligned} \left| \int _{M\cap B(x,\varepsilon ^{\alpha _0})}\xi -\int _{V\cap B(x,\varepsilon ^{\alpha _0})}\xi \right| \leqslant C_{\rm app}\varepsilon ^{-\theta }. \end{aligned}$$

(6.25)

Set $\alpha _{k+1}=\alpha _k+\frac{1}{n}(\alpha _k-\theta )$. By the assumptions, we have $\alpha _0<\theta$, so $\alpha _{k+1}<\alpha _k$ and the sequence $\alpha _k$ diverges to $-\infty$. Suppose $k_0<\infty$ is the first index, when $\alpha _{k_0}\leqslant 0$. Set $\alpha _{k_0}=0$ in this case. We use repeatedly the Drilled Ball Lemma 6.10 for $\beta =\alpha _{k+1}$ and $\alpha =\alpha _k$, $k=0,\ldots ,k_0-1$. We are allowed to do that because for $k<k_0-1$ we have

$$\begin{aligned} n\alpha _{k+1}-(n+1)\alpha _k=n\left( \frac{n+1}{n}\alpha _k -\frac{1}{n}\theta \right) -(n+1)\alpha _k=-\theta \end{aligned}$$

and $n\alpha _{k_0}-(n+1)\alpha _{k_0-1}\geqslant -\theta$. Summing the inequality from the Drilled Ball Lemma 6.10 for k from 0 to $k_0-1$, we arrive at

$$\begin{aligned} \left| \int _{M\cap B(x,\varepsilon ^{\alpha _{k_0}}){\setminus } B(x,\varepsilon ^{\alpha _0})}\xi \right| \leqslant k_0\cdot C_{\rm drill}\varepsilon ^{-\theta }. \end{aligned}$$

(6.26)

Recall that $\alpha _{k_0}=0$. Equation (6.26) does not cover the part of M outside of B(x, 1). However, on $M{\setminus } B(x,1)$, the form $\xi$ is easily seen to have coefficients bounded above by a constant independent of $\varepsilon$ and x; hence,

$$\begin{aligned} \left| \int _{M{\setminus } B(x,1)}\xi \right| \leqslant C_{\rm ext}, \end{aligned}$$

(6.27)

for some constant $C_{\rm ext}$ depending on M but not on x and $\varepsilon$. It remains to show

$$\begin{aligned} \left| \int _{V\cap B(x,\varepsilon ^{\alpha _0})}\xi -\int _{V}\xi \right| \leqslant C_{\rm flat}\varepsilon ^{-\theta }. \end{aligned}$$

(6.28)

We cannot use the Drilled Ball Lemma 6.10 directly, because V is unbounded. However, we shall use similar ideas as in the proof of the Drilled Ball Lemma 6.10. The form $\xi$ is an n-form whose coefficients on V are bounded by ${C^{D^{\prime}}_{n,1}\Vert y-x\Vert ^{-(n+1)},}$ where $D^{\prime}$ is such that $\pi _x^{-1}(V)\subset \{u_{n+2}<D^{\prime}\}$. Its restriction to V is equal to some function $F_x(y)$ times the volume form on V, where $|F_x(y)|\leqslant C_VC^{D^{\prime}}_{n,1}\Vert y-x\Vert ^{-(n+1)}$ (it is easy to see that as V is a half-plane, $C_V$ exists). Therefore, we need to bound

$$\begin{aligned} \int _{V{\setminus } B(x,\varepsilon ^{\alpha _0})} \Vert y-x\Vert ^{-(n+1)}. \end{aligned}$$

(6.29)

The method is standard. Introduce radial coordinates on V centered at $y_0$, and notice that $\Vert y-x\Vert \leqslant 2\Vert y_0-y\Vert$ as long as $y\in V{\setminus } B(x,\varepsilon ^{\alpha _0})$. Perform first the integral (6.29) over radial coordinates obtaining the integral over the radius only, that is

$$\begin{aligned} \int _{V{\setminus } B(x,\varepsilon ^{\alpha _0})} \Vert y-x\Vert ^{-(n+1)}\leqslant \int _{\varepsilon ^{0}}^\infty 2^{n-1}\sigma _{n-1}r^{n-1}\cdot r^{-n-1}dr=\\ =2^{n-1}\varepsilon ^{-\alpha _0}\sigma _{n-1}\leqslant 2^{n-1}\sigma _{n-1}\varepsilon ^{-\theta }, \end{aligned}$$

where $\sigma _{n-1}$ is the volume of a unit sphere of dimension $n-1$. This proves (6.28) with $C_{\rm flat}=2^{n-1}\sigma _{n-1}C_V C^{D^{\prime}}_{n,1}$.

Combining (6.25), (6.26),(6.27) and (6.28), we obtain the desired statement. $\square$

6.4 The main estimate for the derivative

This section extends the intuitions given in Sect. 5.3.

The normal bundle of $M \subset {\mathbb {R}}^{n+2}$ is trivial, see [7], but there might be many different trivializations, one class for each element of $[M,SO(2)]=[M,S^1]=H^1(M)$. Choose a pair of two normal vectors $v_1,v_2$ on M such that at each point $y\in M$, $v_1(y)$ and $v_2(y)$ form an oriented orthonormal basis of the normal space $N_yM$. Choose $\varepsilon _0<\varepsilon _1$ and let N be the tubular neighborhood of M of radius $\varepsilon _0$. By taking $\varepsilon _0>0$ sufficiently small, we may and shall assume that each $y^{\prime}\in N$ can be uniquely written as $y+t_1v_1+t_2v_2$ for $y\in M$ and $t_1,t_2\in {\mathbb {R}}$.

Let $y\in M$. Choose a local coordinate system $w_1,\ldots ,w_n$ in a neighborhood of y such that $\left| \frac{\partial w_j}{\partial x_i}\right| \leqslant C_w$ for some constant $C_w$. The local coordinate system $w_1,\ldots ,w_n$ on M induces a local coordinate system on N given by $w_1,\ldots ,w_n,t_1,t_2$. Let $r,\phi$ be such that $t_1=r\cos (2\pi \phi )$, $t_2=r\sin (2\pi \phi )$.

Theorem 6.30

(Main Estimate Theorem) For$\theta \in \left( \frac{n+2}{n+4},1\right)$, we have $\left| \frac{\partial \varPhi }{\partial w_j}\right| \leqslant C_wC_\theta r^{-\theta }$ and $\left| \frac{\partial \varPhi }{\partial r}\right| \leqslant C_\theta r^{-\theta }$. Moreover,$\left| \frac{\partial \varPhi }{\partial \phi }-\epsilon \right| \leqslant C_{\theta }r^{1-\theta }$, where$\epsilon \in \{\pm 1\}$depending on the orientation ofM.

Proof

Choose a point $x=(w_1,\ldots ,w_n,t_1,t_2)$. Let $y_0=(w_1,\ldots ,w_n,0,0)$ be the point minimizing the distance from x to M. We shall use the Approximation Theorem 6.23. So let V be the n-dimensional plane tangent to M at $y_0$. The map $\varPhi _V$ is the map $\varPhi$ relative to V. By the explicit calculations in Sect. 4, we infer that $\frac{\partial \varPhi _V}{\partial w_j}(x)=\frac{\partial \varPhi _V}{\partial r}(x)=0$ for $j=1,\ldots ,n$ and $\frac{\partial \varPhi _V}{\partial \phi }=\epsilon$. Now $\frac{\partial \varPhi }{\partial w_j}$ differs from the derivatives of $\varPhi _V$ by at most $C_\theta r^{-\theta }$ by the Approximation Theorem 6.23.

On the other hand, by the chain rule $\frac{\partial \varPhi }{\partial \phi }=-r\sin \phi \frac{\partial \varPhi }{\partial t_1}+r\cos \phi \frac{\partial \varPhi }{\partial t_2}$. Applying Theorem 6.23, we infer that $\left| \frac{\partial \varPhi }{\partial \phi }(x)-\frac{\partial \varPhi _V}{\partial \phi }(x)\right| \leqslant C_\theta r^{1-\theta }$. The same argument shows that $\left| \frac{\partial \varPhi }{\partial r}(x)\right| \leqslant C_\theta r^{-\theta }$. Notice that the derivatives with respect to r and $\theta$ do not depend on $C_w$: this is so because the length of the framing vectors $v_1$ and $v_2$ is 1. $\square$

7 Behavior of $\varPhi$ near M

Throughout the section, we choose $\theta \in \left( \frac{n+2}{n+4},1\right)$. The constant $\varepsilon _0$ is as defined in Sect. 6.4. We decrease further $\varepsilon _0$ to ensure that

$$\begin{aligned} C_\theta \varepsilon _0^{1-\theta }<\frac{1}{2} \end{aligned}$$

(7.1)

so that, by Theorem 6.30

$$\begin{aligned} \left| \frac{\partial \varPhi }{\partial \phi }-\epsilon \right| <\frac{1}{2}. \end{aligned}$$

(7.2)

7.1 Local triviality of $\varPhi$ near M

Let now $X=(0,\varepsilon _0]\times S^1\times M$. Let $\varPi :X\rightarrow N{\setminus } M$ be a parameterization given by

$$\begin{aligned} \varPi :(r,\phi ,x)\mapsto x+v_1r\cos \phi +v_2r\sin \phi . \end{aligned}$$

The composition $\varPhi \circ \varPi :X\rightarrow S^1$ will still be denoted by $\varPhi$. We are going to show that this map is a locally trivial fibration whose fibers have bounded $(n+1)$-dimensional volume.

Lemma 7.3

(Fibration Lemma) The map$\varPhi :X\rightarrow S^1$is a smooth, locally trivial fibration, whose fiber is$(0,\varepsilon _0]\times M$.

Proof

Choose $r\in (0,\varepsilon _0]$ and $x\in M$. Consider the map $\varPhi _{r,x}:S^1\rightarrow S^1$ given by $\varPhi _{r,x}=\varPhi |_{\{r\}\times S^1\times \{x\}}$. The derivative of $\varPhi _{r,x}$ is equal to $\frac{\partial \varPhi }{\partial \phi }$; by (7.2) it belongs either to the interval $(-\frac{3}{2},-\frac{1}{2})$ or to $(\frac{1}{2},\frac{3}{2})$ depending on the $\epsilon$. By the mean value theorem, a map from $S^1$ to $S^1$ with derivative in $(\frac{1}{2},\frac{3}{2})$ or in $(-\frac{3}{2},-\frac{1}{2})$ is a diffeomorphism. It follows that $\varPhi _{r,x}$ is a diffeomorphism. In particular, given $r\in (0,\varepsilon _0]$ and $x\in M$, for any $t\in S^1$, there exists a unique point $\varTheta _t(r,x)$ such that $\varPhi (r,\varTheta _t(r,x),x)=t$. In this way, we get a bijection $\varTheta _t(r,x):(0,\varepsilon _0]\times M\rightarrow \varPhi ^{-1}(t)$.

Again by (7.2) $|\frac{\partial \varPhi }{\partial \phi }|>\frac{1}{2}>0$, so by the implicit function theorem we infer that $\varTheta _t$ is in fact a smooth map. Then $\varTheta _t$ is a smooth parameterization of the fiber of $\varPhi$. It remains to show that $\varPhi$ is locally trivial.

To this end, we choose a point $t\in S^1$ and let $U\subset S^1$ be a neighborhood of t. Define the map $\widetilde{\varTheta }:(0,\varepsilon _0]\times U\times M\rightarrow \varPhi ^{-1}(U)$ by the formula

$$\begin{aligned} \widetilde{\varTheta }(r,t,x)=(r,\varTheta _t(r,x),x). \end{aligned}$$

Clearly, $\widetilde{\varTheta }$ is a bijection. As $\varTheta _t$ depends smoothly on the parameter t, we infer that $\widetilde{\varTheta }$ is a smooth map and the map $\varPhi ^{-1}(U)\rightarrow (0,\varepsilon _0]\times U\times M$ given by $(r,\phi ,x)\mapsto (r,\varPhi (r,\phi ,x),x)$ is its inverse. Therefore, $\widetilde{\varTheta }$ is a local trivialization. $\square$

Remark 7.4

Define the map $\varPhi _M:X\rightarrow S^1\times M$ by $\varPhi _M(r,\phi ,x)=(\varPhi (r,\phi ,x),x)$. The same argument as in the proof of Fibration Lemma 7.3 shows that $\varPhi _M$ is a locally trivial fibration with fiber $(0,\varepsilon _0]$. For given $(t,x)\in S^1\times M,$ the map $r\mapsto (r,\varTheta _t(r,x),x)$ parameterizes the fiber over (t, x).

As a consequence of Fibration Lemma 7.3, we show that $\varPhi :{\mathbb {R}}^{n+2}{\setminus } M\rightarrow S^1$ does not have too many critical points. This is a consequence of Sard’s theorem and the control of $\varPhi$ near M provided by Lemma 7.3.

Proposition 7.5

The set of critical values of $\varPhi :{\mathbb {R}}^{n+2}{\setminus } M\rightarrow S^1$ is a closed nowhere dense set of measure zero.

Proof

Extend $\varPhi$ to a map from $S^{n+2}{\setminus } M\rightarrow S^1$ as in Corollary 3.2. We split the $S^{n+2}{\setminus } M$ as a union of $S^{n+2}{\setminus } N$ and $N{\setminus } M$, where, recall, N is the set of points at distance less than or equal to $\varepsilon _0$. By Sard’s theorem, the map $\varPhi$ restricted to $\overline{S^{n+2}{\setminus } N}$ has a set of critical points which is closed boundary and of measure zero. On the other hand, on $N{\setminus } M$ the map has no critical points at all, because by the Fibration Lemma 7.3 the map $\varPhi$ restricted to $N{\setminus } M\cong X$ is a locally trivial fibration. $\square$

We conclude by showing the following control of the fibers of $\varPhi :X\rightarrow S^1$:

Lemma 7.6

(Bounded Volume Lemma) There exists a constant$A>0$such that for any$t\in S^1$the$(n+1)$-dimensional volume of$\varPhi ^{-1}(t)\cap X$is bounded from above byA.

Proof

Parameterize $\varPhi ^{-1}(t)\cap X$ by $\varTheta _t:(0,\varepsilon _0]\times M\rightarrow X$ as in the proof of the Fibration Lemma 7.3. Choose local coordinate system on an open subset $Y\subset M$, and let $X_r^{\rm loc}=[r,\varepsilon _0]\times S^1\times Y$. We aim to show that

$$\begin{aligned} {{\,{\mathrm{vol}}\,}}_{n+1}(\varPhi ^{-1}(t)\cap X_r^{\rm loc}) \end{aligned}$$

is bounded by a constant independent of r. Write

$$\begin{aligned} {{\,{{\mathrm{vol}}}\,}}_{n+1}\varPhi ^{-1}(t)\cap X_r^{\rm loc}=\int _{[r,\varepsilon _0]\times Y}\sqrt{1+{\varTheta ^{\prime}}_{w_1}^2+\cdots +{\varTheta ^{\prime}}_{w_n}^2+{\varTheta ^{\prime}}_{r}^2}\, dl_{n+1}, \end{aligned}$$

(7.7)

where $dl_{n+1}$ is the $(n+1)$-dimensional Lebesgue measure on $[r,\varepsilon _0]\times Y$, we write $\varTheta$ for $\varTheta _t$ and $\varTheta ^{\prime}_z$ is a shorthand for $\frac{\partial \varTheta }{\partial z}$, and z is any variable of $\{r,w_1,\ldots ,w_n\}$. By the implicit function theorem $\varTheta ^{\prime}_z=-\frac{\partial \varPhi }{\partial z}\left( \frac{\partial \varPhi }{\partial \phi }\right) ^{-1}$. Equation (7.2) implies that $\left| \frac{\partial \varPhi }{\partial \phi }\right| \geqslant \frac{1}{2}$, then

$$\begin{aligned} \begin{aligned} |\varTheta ^{\prime}_{w_j}|&\leqslant 2C_\theta C_w r^{-\theta },\ \ j=1,\ldots ,n\\ |\varTheta ^{\prime}_{r}|&\leqslant 2C_\theta r^{-\theta }. \end{aligned} \end{aligned}$$

(7.8)

Hence,

$$\begin{aligned} \sqrt{1+{\varTheta ^{\prime}}_{w_1}^2+\cdots +{\varTheta ^{\prime}}_{w_n}^2+{\varTheta ^{\prime}}_{r}^2}\leqslant \sqrt{1+4C^2_\theta +4(n+1)C^2_wC^2_\theta }r^{-\theta }\leqslant C_\varTheta r^{-\theta }, \end{aligned}$$

where $C_\varTheta$ is a constant. Thus,

$$\begin{aligned} {{\,{\mathrm{vol}}\,}}_{n+1}\varPhi ^{-1}(t)\cap X_r^{\rm loc}\leqslant C_\varTheta (\varepsilon _0^{1-\theta }-r^{1-\theta }){{\,{\mathrm{vol}}\,}}_n Y\leqslant C_\varTheta \varepsilon _0^{1-\theta }{{\,{\mathrm{vol}}\,}}_nY. \end{aligned}$$

Now M being compact can be covered by a finite number of coordinate neighborhoods, we sum up all the contributions to get

$$\begin{aligned} {{\,{\mathrm{vol}}\,}}_{n+1}\varPhi ^{-1}(t)\cap X\leqslant C_\varTheta \varepsilon _0^{1-\theta }{{\,{\mathrm{vol}}\,}}_nM. \end{aligned}$$

$\square$

Remark 7.9

Bounded Volume Lemma 7.6 shows that the volume of the fibers $\varPhi ^{-1}(t)$ is bounded near M by a constant that does not depend on t. This does not generalize to bounding a global volume of $\varPhi ^{-1}(t)$: one can show that the volume of $\varPhi ^{-1}(0)$ is infinite using Corollary 3.2.

7.2 Extension to of $\varPhi$ through $r=0$

We pass to study the closure of the fibers $\varPhi ^{-1}(t)\cap X$. This is done by extending the map $\varPhi$. Set

$$\begin{aligned} \overline{X}=[0,\varepsilon _0]\times S^1\times M. \end{aligned}$$

The manifold $\overline{X}$ can be regarded as an analytic blowup of the neighborhood $N{\setminus } M$.

Lemma 7.10

(Continuous Extension Lemma) The map$\varPhi :X\rightarrow S^1$extends to a continuous map$\overline{\varPhi }:\overline{X}\rightarrow S^1$.

Proof

Let $f_r:S^1\times M\rightarrow S^1$ be given by $f_r(\phi ,x)=\varPhi (r,\phi ,x)$. We shall show that as $r\rightarrow 0$ the functions $f_r$ converge uniformly. The limit, $f_0$, will be the desired extension.

We use Proposition 6.30. In fact, choose $r_0,r_1\in (0,\varepsilon _0]$. Then for $(\phi ,x)\in S^1\times M$ we have

$$\begin{aligned} |f_{r_0}(\phi ,x)-f_{r_1}(\phi ,x)|\leqslant \int _{r_0}^{r_1} \left| \frac{\partial }{\partial r}f_r(\phi ,x)\right| dr\leqslant \int _{r_0}^{r_1} C_\theta r^{-\theta }dr=\frac{C_{\theta }}{1-\theta } (r_0^{1-\theta }-r_1^{1-\theta }). \end{aligned}$$

As $r\mapsto r^{1-\theta }$ is a uniformly continuous function taking value 0 at 0, we obtain that $f_r$ uniformly converge to some limit, which we call $f_0$. This amounts to saying that $\varPhi$ extends to a continuous function on $\overline{X}$. $\square$

Remark 7.11

Consider the map $\varPhi _M$ defined in Remark 7.4. Then the proof of the Continuous Extension Lemma 7.10 generalizes to showing that the map $\varPhi _M$ extends to the continuous map $\overline{\varPhi }_M:\overline{X}\rightarrow S^1\times M$.

We can also calculate the function $\varPhi$ for $r=0$.

Proposition 7.12

There exists a continuous function$\rho :M\rightarrow S^1$such that$\overline{\varPhi }(0,\phi ,x)=\epsilon \phi +\rho (x)\bmod 1$.

Proof

By Main Estimate Theorem 6.30 we have that for any $c>0$ there exists $r_c>0$ such that if $r\in (0,r_c)$, then for $\phi ,\phi ^{\prime}\in S^1$ and $x\in M$:

$$\begin{aligned} (1-c)|\phi -\phi ^{\prime}|\leqslant |\varPhi (r,\phi ,x)-\varPhi (r,\phi ^{\prime},x)|\leqslant (1+c)|\phi -\phi ^{\prime}|. \end{aligned}$$

(7.13)

As $\varPhi (r,\phi ,x)$ converges uniformly to $\varPhi (0,\phi ,x)$, we infer that (7.13) holds for $r=0$ and arbitrary $c>0$. This means that actually

$$\begin{aligned} |\overline{\varPhi }(0,\phi ,x)-\overline{\varPhi }(0,\phi ^{\prime},x)|=|\phi -\phi ^{\prime}|. \end{aligned}$$

This is possible only if $\overline{\varPhi }(0,\phi ,x)=\overline{\varPhi }(0,0,x)\pm \phi \bmod 1$, where the sign is equal to $\epsilon$. We set $\rho (x)=\overline{\varPhi }(0,0,x)$. $\square$

Recall from the Fibration Lemma 7.3 that

$$\begin{aligned} \varTheta _t:(0,\varepsilon _0]\times M\rightarrow \varPhi ^{-1}(t) \end{aligned}$$

is a diffeomorphism.

Theorem 7.14

For any$t\in S^1$, the maps$\varTheta _t:(0,\varepsilon _0]\times M\rightarrow \varPhi ^{-1}(t)$extend to a continuous map$\overline{\varTheta }_t:[0,\varepsilon _0]\times M\rightarrow \overline{\varPhi }^{-1}(t)\subset \overline{X}$. The map$\overline{\varTheta }_t$is injective.

Proof

By (7.8) $\frac{\partial \varTheta _t}{\partial r}$ is bounded by $2C_\theta r^{-\theta }$, so we the same argument as in the proof of Lemma 7.10 shows that $\varTheta _{t}(r,x)$ converges as $r\rightarrow 0$ uniformly with respect to x. Therefore, $\overline{\varTheta }_{t}$ is well defined.

The composition $\varPhi _M\circ \varTheta _t:(0,\varepsilon _0]\times M\rightarrow (0,\varepsilon _0]\times M$ is an identity. Hence, $\overline{\varPhi }_M\circ \overline{\varTheta _t}:[0,\varepsilon _0]\times M\rightarrow [0,\varepsilon _0]\times M$ is also an identity. In particular, $\overline{\varTheta }_t$ is injective. $\square$

We next prove the surjectivity of $\overline{\varTheta }_t$. Before we state the proof, we indicate a possible problem in Fig. 9.

Fig. 9

The picture indicates the necessity of proving the surjectivity of $\overline{\varTheta }_t$; the map $\overline{\varTheta }_t$ is not onto. In Theorem 7.15 we show that the situation as on the picture cannot happen

Theorem 7.15

The map$\overline{\varTheta }_t$is onto$\overline{\varPhi }^{-1}(t)$.

Proof

By the Fibration Lemma 7.3, the map $\varTheta _t$ is onto $\varPhi ^{-1}(t)\subset X$. Hence, it is enough to show that $\overline{\varTheta _t}|_{\{0\}\times M}$ is onto $\overline{\varPhi }^{-1}(t)\cap (\overline{X}{\setminus } X)$.

Observe that by Proposition 7.12 the intersection $\overline{\varPhi }^{-1}(t)\cap \{0\}\times S^1\times \{x\}$ consist of one point for any $x\in M$ and t.

On the other hand, since $\overline{\varPhi }^{-1}(t)\cap (\{0\}\times S^1\times \{x\})$ is a single point, this point has to be equal to $\varTheta _t(0,x)$. Therefore, $\varTheta _t(0,x)$ is onto $\overline{\varPhi }^{-1}(t)\cap \{r=0\}$ so $\varTheta _t(r,x)$ is onto $\overline{\varPhi }^{-1}(t)$. $\square$

As a corollary, we shall show the following result.

Theorem 7.16

(Continuous Fibration Theorem) The map$\overline{\varPhi }:\overline{X}\rightarrow S^1$is a continuous, locally trivial fibration.

Proof

We show that for any closed interval $I\subset S^1$, the preimage $\overline{X}_I:=\overline{\varPhi }^{-1}(I)$ is homeomorphic to the product $Y_I:= I\times [0,\varepsilon _0]\times M$ by a homeomorphism that preserves the fibers. Consider the map $\overline{\varTheta }_I:Y_I\rightarrow X_I$ given by $\overline{\varTheta }_I(t,x)=\overline{\varTheta }_t(x)$ for $x\in [0,\varepsilon _0]\times M$. By Theorems 7.14 and 7.15, this map is a bijection. Moreover, its inverse is $\overline{\varPhi }$, which is continuous by the Continuous Extension Lemma 7.10. A continuous bijection between compact sets is a homeomorphism. It is clear that $\overline{\varTheta }_I$ preserves the fibers. $\square$

8 Constructing Seifert hypersurfaces based on $\varPhi$

Theorem 8.1

Let$t\in S^1$be a non-critical value of the map$\varPhi$and$t\ne 0$. Then the closure of$\varPhi ^{-1}(t)$is a Seifert hypersurface forMwhich is smooth up to boundary. Moreover, the$(n+1)$-dimensional volume of$\varPhi ^{-1}(t)$is finite.

Proof

Let $\varSigma =\varPhi ^{-1}(t)$. Recall that N is the closure of a tubular neighborhood of $\varSigma$. By the implicit function theorem, $\varSigma$ is a smooth open submanifold of ${\mathbb {R}}^{n+2}{\setminus } M$. By Theorem 3.1 we infer that $\varSigma$ is contained in some ball B(0, R) for large R. This implies that $\varSigma {\setminus } {\text {int}} N$ is compact (here ${\text {int}}$ denotes the interior of N).

The main problem is to show that boundary of the closure of $\varSigma$ is M. To this end we study the intersection $\varSigma _0:=\varSigma \cap (N{\setminus } M)$. Notice that we have a diffeomorphism $\varSigma _0\cong \varPhi ^{-1}(t)\cap X$ via the map $X{\mathop {\rightarrow }\limits ^{\simeq }} (N{\setminus } M)$.

Now $\varSigma _0$ is a smooth submanifold diffeomorphic to $(0,\varepsilon _0]\times M$. By Theorem 7.14 the closure $\overline{\varSigma }_0$ of $\varSigma _0$ in $\overline{X}$ is homeomorphic to the product $[0,\varepsilon _0]\times M$. Under the map $\overline{X}\rightarrow N$ the closure $\overline{\varSigma }_0$ is mapped to the closure of $\varSigma$ in N. It follows that the boundary of the closure of $\varSigma \cap N$ is M itself.

To show the finiteness of the volume of $\varSigma$, notice that the area of $\varSigma {\setminus } N$ is finite, because $\varSigma {\setminus } N$ is smooth and compact. The finiteness of the volume of $\varSigma \cap N$ follows from the Bounded Volume Lemma 7.6. $\square$

In numerical applications, calculating the map $\varPhi$ in N can be challenging due to the lack of a good bound for derivatives of $\varPhi$ in N. Therefore, the following corollary should be useful.

Proposition 8.2

Choose$t\in S^1$, $t\ne 0$to be a non-critical value of$\varPhi$. Define$M^{\prime}=\varPhi ^{-1}(t)\cap \partial N$. Let$\varSigma^{\prime}=\varPhi ^{-1}(t){\setminus } N$. Then$M^{\prime}$is diffeomorphic toM, isotopic toMas knots in$S^{n+2}$and$\varSigma^{\prime}$is a smooth surface for$M^{\prime}$.

Proof

The fact that $M^{\prime}$ is diffeomorphic to M follows from the Fibration Lemma 7.3. The isotopy is given by $M_r=\pi \circ \overline{\varPhi }_t(\{r\}\times M)$, where $\overline{\varPhi }$ is as in Theorem 7.14 and $\pi :X\rightarrow N$ is the projection. By definition $\partial \varSigma^{\prime}=M^{\prime}$ and as $\varSigma^{\prime}$ is closed and bounded, it is also compact. $\square$