Abstract
A large number and wide variety of lake ecosystem models have been developed and published during the past four decades. We identify two challenges for making further progress in this field. One such challenge is to avoid developing more models largely following the concept of others (‘reinventing the wheel’). The other challenge is to avoid focusing on only one type of model, while ignoring new and diverse approaches that have become available (‘having tunnel vision’). In this paper, we aim at improving the awareness of existing models and knowledge of concurrent approaches in lake ecosystem modelling, without covering all possible model tools and avenues. First, we present a broad variety of modelling approaches. To illustrate these approaches, we give brief descriptions of rather arbitrarily selected sets of specific models. We deal with static models (steady state and regression models), complex dynamic models (CAEDYM, CE-QUAL-W2, Delft 3D-ECO, LakeMab, LakeWeb, MyLake, PCLake, PROTECH, SALMO), structurally dynamic models and minimal dynamic models. We also discuss a group of approaches that could all be classified as individual based: super-individual models (Piscator, Charisma), physiologically structured models, stage-structured models and trait-based models. We briefly mention genetic algorithms, neural networks, Kalman filters and fuzzy logic. Thereafter, we zoom in, as an in-depth example, on the multi-decadal development and application of the lake ecosystem model PCLake and related models (PCLake Metamodel, Lake Shira Model, IPH-TRIM3D-PCLake). In the discussion, we argue that while the historical development of each approach and model is understandable given its ‘leading principle’, there are many opportunities for combining approaches. We take the point of view that a single ‘right’ approach does not exist and should not be strived for. Instead, multiple modelling approaches, applied concurrently to a given problem, can help develop an integrative view on the functioning of lake ecosystems. We end with a set of specific recommendations that may be of help in the further development of lake ecosystem models.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
A large number and wide variety of lake ecosystem models have been developed and published during the past four decades, indicating the strong interest in capturing in a model the essential processes in lake ecosystems (e.g., Jørgensen 2010). The scientific interest in understanding fundamental processes in lake ecosystems can be traced back to the seminal paper by Forbes (1887) on the lake as a microcosm. Another major purpose has been to develop predictive tools supporting inter-disciplinary ecosystem management (Carpenter et al. 1999), acknowledging the great importance of lake ecosystems for society (MEA 2005). The ecological quality of lakes is threatened by a large number of anthropogenic stress factors, in particular eutrophication, pollution of various types, overexploitation and invasive species, changes in land use and hydrology in the catchment and climate change (e.g., Gulati and Van Donk 2002; MEA 2005; Mooij et al. 2005; Revenga et al. 2005; Jeppesen et al. 2009; MacKay et al. 2009).
But there is also a downside to the large number and variety of models that have been published. We identify two challenges: one related to the number of models and the other to the variety of models. With respect to the number of models, newly developed models often bear similarities to existing models (‘reinventing the wheel’) (e.g., Fitz et al. 1996). In such cases, it would most likely be more efficient to apply or adopt an existing model instead of creating a new one. With respect to the variety of models, we identify the risk that the approach taken in any specific model is too narrow and ignores other approaches that could be useful or even essential for gaining understanding and making predictions (‘having tunnel vision’) (e.g., Scheffer 1998, p308).
Before starting a lake ecosystem modelling project, it is essential to be aware of existing models and concurrent approaches and to properly conceptualize the issues, the variables, the time and space scales and the desired outcomes for the model simulations (Robson et al. 2008). We observe that publications that deal with a wide range of concurrent approaches in lake ecosystem modelling are scarce, although some attempts have been made (Van Nes and Scheffer 2005; Mooij et al. 2009; Jørgensen 2010), and several overviews concerning complex dynamic lake ecosystem models have been provided (e.g., Schauser and Strube 2007; Reichert and Mieleitner 2008). In this paper, we wish to proceed further in the direction of integrating lake ecosystem modelling approaches, without claiming to be comprehensive.
The ideas published here were stimulated by a collaborative research effort by Dutch and Russian scientists funded by a stimulus programme of the Netherlands Organization for Scientific Research and the Russian Foundation for Basic Research. The aim of this research programme was to combine the extensive knowledge of modelling temperate shallow lake ecosystems of the Dutch team (e.g., Janse 2005; Janse et al. 2008) with the skilled mathematical knowledge of modelling hydro-dynamic processes of the Russian team (e.g., Belolipetsky et al. 2010; Genova et al. 2010). The integrated model that resulted from this collaborative research project is documented elsewhere (Prokopkin et al. 2010). The aim of the current paper is to compare different modelling approaches and to focus on the potential for combining them either conceptually or technically.
In the first part of the paper, a wide range of modelling approaches is presented, each exemplified by rather arbitrarily selected existing models. The purpose of this first section is to provide the reader with ideas for potential approaches in lake ecosystem modelling, some of which, we believe, might otherwise be overlooked. In the second part of this paper, we focus on the multi-decadal development and application of a specific lake ecosystem model, PCLake. The aim of this section is to show the potential for expanding and redirecting the approach taken in an existing model. In the final section, the challenges and opportunities for integrating lake ecosystem modelling approaches are discussed. We end this section with a set of specific recommendations that may be of help in the further development of lake ecosystem models.
Lake ecosystem modelling approaches
The modelling of lake eutrophication started with empirical models relating total phosphorus (TP) and chlorophyll concentrations and input–output models relating TP loading and TP concentration (see e.g., Reckhow and Chapra (1983) and Harper (1992) for overviews). Because of the limitations of static equilibrium models, for instance to predict response times to management measures and to account for the role of sediments and, later, also food web effects, dynamic models for TP and chlorophyll were developed (see overviews by Chapra and Reckhow (1983); Jørgensen et al. (1995); Jørgensen and Bendoricchio (2001), among others). These differ widely in both functional (what compartments are included) and hydrodynamic and spatial aspects (such as 0-, 1-, 2- or 3-D). The inclusion of food web components was also triggered by experiences gained from biomanipulation studies (Gulati et al. 1990; Benndorf 1995; Hansson et al. 1998; Drenner and Hambright 1999; Søndergaard et al. 2008). All these models were developed for phytoplankton-dominated lakes; thus, macrophytes were lacking in many of the models, although the importance of macrophytes to water transparency had been acknowledged by some (e.g., Spence 1982; Chambers and Kalff 1985) and simple empirical models to quantify their effects exist (Hamilton and Mitchell 1996, 1997). In the 1990s, increasing knowledge of the crucial role of submerged macrophytes and the resulting non-linear behaviour and bistability in the response of transparency to nutrient loading became available, especially in countries with many shallow eutrophic lakes, such as the Netherlands and Denmark (e.g., Scheffer 1998; Jeppesen et al. 1998). These phenomena were studied extensively by means of ‘minimal dynamic models’ (Scheffer 1998).
Other workers included structural flexibility in dynamic models using optimization criteria (e.g., Jørgensen 1995, 1999; Zhang et al. 2010). Another modelling line that developed separately was that of physiologically structured models (Metz and Diekmann 1992; De Roos et al. 1992; De Roos and Persson 2001) with applications to zooplankton (e.g., Hülsmann et al. 2005) and fish (e.g., Claessen et al. 2000), and super-individual models, especially for zooplankton (Mooij et al. 2003), fish (Van Nes et al. 2002) and macrophytes (Van Nes et al. 2003). Yet another development is the use of evolutionary algorithms and neural network models (Cao et al. 2006; Chan et al. 2007; Recknagel et al. 2006) and of fuzzy logic in lake ecosystem models (Ibelings et al. 2003).
Many of the different modelling approaches in the literature are mentioned in two recent overviews by Jørgensen (2008, 2010). Our study, however, points to an even wider modelling perspective for lake ecosystems and reveals the opportunities for applying and combining different approaches. Below, we discuss each of the following approaches in some detail: static models, complex dynamic models, structurally dynamic models, minimal dynamic models and various individual-based models (see also Tables 1 and 2).
Static models
The classical models of lake eutrophication are the empirical models relating TP and chlorophyll (Sakamoto 1966 and Dillon and Rigler 1974 being the pioneers), and the input–output models relating TP loading and TP concentration first derived by Vollenweider (1968, 1975) and Vollenweider and Kerekes (1982). These steady-state models were the first to use the mass balance approach to lakes (Chapra 1975). Several modifications were made to these initial models, and the parameters were estimated by regression on multi-lake datasets (e.g., Dillon and Rigler 1974; Kirchner and Dillon 1975; Jones and Bachmann 1976; Larsen and Mercier 1976; Reckhow 1979; Canfield and Bachmann 1981; and others; see e.g., Reckhow and Chapra (1983) and Harper (1992) for overviews). These models allow the calculations of average nutrient and chlorophyll concentrations (and sometimes transparency) given P and N loading and some basic lake features, of which mean depth, and retention time have proven to be the most important. Nutrient loading criteria, together with uncertainty bounds (Reckhow and Chapra 1983), were derived for the classification of lakes in different trophic states (ultra-oligotrophic, oligotrophic, mesotrophic, eutrophic or hypertrophic). These states could be defined both in terms of TP, total nitrogen (TN), chlorophyll concentrations or transparency and also in terms of characteristic species composition. This type of model is still useful—and is being used—for giving a first estimate of the effects of eutrophication on lakes.
Other simple regression models include relationships between TP, TN and/or lake depth versus, respectively, bird numbers and richness (Hoyer and Canfield 1994), fish biomass and/or production (Hanson and Leggett 1982; Downing et al. 1990; Randall et al. 1995; Bachmann et al. 1996), zoobenthos biomass (Hanson and Peters 1984), macrophyte coverage and plant volume present (Bachmann et al. 2002; Søndergaard et al. 2010), zooplankton biomass (Hanson and Peters 1984; Jeppesen et al. 1997, 2005), zooplankton:phytoplankton biomass ratio (Jeppesen et al. 2005), phytoplankton biovolume at the class level (Downing et al. 2001; Jeppesen et al. 2005; Håkanson et al. 2007) and bacterioplankton biomass and production (Hardy et al. 1986; Roland et al. 2010). Some empirical models have linked measures of biodiversity (e.g., species richness or richness of native species) in lakes to external factors (e.g., Leibold 1999; Jeppesen et al. 2000; Alkemade et al. 2010).
The advantages of these static models are that they are simple and easy-to-use, they provide general relationships, they are based on a large amount of data from lakes with different trophic states and they implicitly account for the net effect of structural changes along the nutrient gradient, which are often difficult to include in more complex dynamic models. These simple regression models have, therefore, been extensively used by water quality managers worldwide for setting targets for acceptable nutrients concentrations and nutrient loadings. Their disadvantage is that the coefficient of variation in the predictions is generally high, and individual lakes may follow trajectories deviating from the general pattern.
Complex dynamic models (examples given in alphabetical order)
CAEDYM
The computational aquatic ecosystem dynamics model (CAEDYM) is a process-based library of water quality, biological and geochemical sub-models that is driven by either the DYnamic REServoir simulation Model (DYRESM: 1D Lagrangian vertical stratification model) or the Estuary and Lake COMputer model (ELCOM: 3-D-structured grid hydrodynamics model) to account for transport and mixing. Both DYRESM and ELCOM have been applied widely to investigate the stratification in lakes and drinking water reservoirs and inflow/outflow dynamics of waterbodies (Robson and Hamilton 2003; Hamilton 1999). The most recent version of CAEDYM (v3.3, Hipsey and Hamilton 2008) can also model suspended solids, oxygen and organic and inorganic nutrients (C, N, P and Si), multiple phytoplankton functional groups, zooplankton and fish, benthic biological communities (macroalgae, macrophytes and benthic invertebrates), pathogens, geochemistry (including ions, pH, redox and metals), and sediment oxygen, nutrient and metal fluxes. These are represented by a long series of mass-conservative coupled differential equations, but the ecosystem representation is configurable and can be varied by the user depending on the purpose of the model and the availability of data. For long-term simulations, DYRESM-CAEDYM has been widely used (e.g., Bruce et al. 2006; Burger et al. 2007; Trolle et al. 2008a, b; Gal et al. 2009), but when higher spatial resolution is required due to the importance of more complex horizontal circulation and transport processes, ELCOM-CAEDYM is more suitable (Hipsey et al. 2008; Chung et al. 2009; Leon et al. 2010). CAEDYM has been used widely for studying nutrient cycling, the effects of increased nutrient loading on algal blooms and changes to phytoplankton succession, as well as for identifying conditions that favour cyanobacteria (Wallace and Hamilton 2000; Lewis et al. 2004). CAEDYM is also able to resolve bacteria as a discrete ecosystem component, and this has been shown to be important to represent the dynamics of micro-grazers and the ‘microbial loop’ (Gal et al. 2009).
CE-QUAL-W2
CE-QUAL-W2 is a 2-D laterally averaged hydrodynamic and water quality model that simulates vertical stratification and longitudinal variability in key ecosystem properties. The current model (v3.6, Cole and Wells 2008) can simulate suspended solids, nutrient and organic matter groups, residence time, derived variables such as TN, TKN, TOC, chlorophyll-a, as well as pH, total dissolved gases and optional biotic groups, including multiple periphyton, multiple phytoplankton, multiple zooplankton and multiple macrophyte groups interacting with hydrodynamics (Berger and Wells 2008). The model includes various vertical turbulence closure, weirs/spillways, gates, pipes and pumps and re-aeration schemes for engineered systems, which can be simulated depending on the nature of the water body. The model is an open-source code written in FORTRAN. It has been used extensively throughout the United States (e.g., Deliman and Gerald 2002; Bowen and Hieronymous 2003; Debele et al. 2006) and elsewhere in the world (e.g., Chung and Oh 2006; Kuo et al. 2006, 2007) as a management and research tool, particularly for studying the nutrient and sediment dynamics of reservoirs and river impoundments. The model has also been used to drive models of food web dynamics (Saito et al. 2001) and to support the studies of fish habitat (Sullivan et al. 2003). Despite the model’s complexity, it has also been subject to advanced calibration procedures (Ostfeld and Salomons 2005).
Delft 3D-ECO
Delft3D is a 2-D/3-D modular modelling system to investigate hydrodynamics, sediment transport, morphology and water quality for lake, fluvial, estuarine and coastal environments. The FLOW module is the heart of Delft3D and is a multi-dimensional (2-D or 3-D) hydrodynamic model that calculates non-steady flows and transports resulting from tidal and meteorological forcing on a curvilinear, boundary-fitted grid. This allows one to align the grids with curving boundaries and channels and to concentrate the higher resolution in areas of interest. The sediment module Delft3D-SED simulates the inorganic sediment behaviour in the water and at the bed (transport, sedimentation and resuspension) as a function of discharges, sediment characteristics and waves and is widely applied to simulate suspended matter in shallow lakes. The ecological module (Delft3D-ECO) is always applied in conjunction with the water quality module (Delft3D-WAQ). Included in Delft3D-ECO are physical, biological and/or chemical reactions. These processes are related to algae growth and mortality, mineralization of organic matter, nutrient uptake and release and oxygen production and consumption. The Delft3D-ECO modelling instrument considers three nutrient cycles: nitrogen, phosphorus and silicon. The carbon cycle is partially modelled, with a mass balance of all components containing organic carbon. Phytoplankton kinetics are simulated by the model BLOOM, which is based on a competition principle using the ratio between the actual growth rates and the resource requirements (Los 2009). The model maximizes the net production of the phytoplankton community in a certain time period consistent with the environmental conditions and existing biomass levels by the use of an optimization technique called linear programming. Algal diversity in freshwater applications is represented in three species groups: diatoms, flagellates and green algae and three genera of cyanobacteria: Microcystis, Aphanizomenon and Planktothrix. To model variable stoichiometry, each group is represented by three types defined by the physiological state of the phytoplankton: phosphorus-, nitrogen- or light limitated. The model can easily be extended to extra groups/species of phytoplankton of freshwater or marine macro algae using characteristics stored in a large data base. Different formulations are available for the characterization of grazers, microphytobenthos, bottom sediment and sediment–water exchange. The most comprehensive description of the model and notes on the historical development of Delft 3D-ECO and some of its forerunners can be found in Los (2009, chapter 7).
ECOPATH with ECOSIM
ECOPATH (Christensen and Pauly 1993) is an ecosystem mass balance model for creating static snapshots of food webs, where functional groups are represented as biomasses, linked through their trophic interactions. The model establishes mass balances by solving sets of linear equations that describe the production and consumption of each group. ECOPATH has reasonably low data requirements, and single mass balances give valuable insights into how energy is transferred through the food web. Multiple balances are used for temporal or spatial comparisons of system functioning. The time-dynamic module ECOSIM (e.g., Li et al. 2010) applies differential equations to describe temporal variations of the flows identified by ECOPATH mass balances and is mostly used to study the effects of fisheries’ management policies in both marine and freshwater systems. ECOPATH is especially useful during the initial stages of investigations on a specific lake ecosystem because setting up and balancing models can unveil inconsistencies in source-data and inspire the development of hypotheses for further research.
LakeMab
Process-based models like LakeMab quantify fundamental transport processes in lakes, such as inflow, outflow, sedimentation, resuspension, diffusion, bio uptake and retention in different types of biota, mixing and substrate decomposition. The basic aim of this modelling is to find general functions for these transport processes that may be applied for all or, at least, most types of lakes, coastal systems and for most types of substances with a particulate phase. LakeMab has been tested for phosphorus, suspended particulate matter (Håkanson 2006), radionuclides and metals (see Håkanson 2000).
LakeWeb
Lake Web is a general model to quantify lake food web interactions, including biotic/abiotic feedbacks (Håkanson and Boulion 2002). The model has been tested against empirical datasets, mainly from Europe. It includes the following functional groups of organisms: phytoplankton, bacterioplankton, benthic algae, macrophytes, zoobenthos, herbivorous and predatory zooplankton, prey fish and predatory fish. It uses ordinary differential equations and gives weekly variations in production and biomass for nine groups of organisms. Fundamental concepts include consumption rates, metabolic efficiency ratios, distribution coefficients, migration of fish and predation pressure. An important feature of LakeWeb is that it can be run by just a few driving variables readily accessible from standard maps and monitoring programs. Several scenarios for management issues such as the consequences of biomanipulation, changes in land use, eutrophication, acidification and global temperature changes are available. LakeWeb can simulate such measures and predict the positive and negative consequences of remedial measures. The present version of LakeWeb has been tested for lakes smaller than 300 km2, but many of the structural components should be valid also for larger systems, e.g., for coastal areas or the large lakes of the world.
MyLake
MyLake (MultiYear Lake) is a 1-D lake model code that simulates daily changes in physical and chemical dynamics over the depth gradient, including surface radiation balance, vertical light attenuation, vertical temperature and density profiles, ice and snow cover, and phosphorus exchange between suspended particles and water, as well as between water and sediment (Saloranta and Andersen 2007). The modelling principle is mostly based on MINLAKE (Riley and Stefan 1988) with some adjustments and additions. In particular, incorporation of ice and snow dynamics based on physical processes (Leppäranta 1993; Saloranta 2000; Salonen et al. 2009) gives the model code additional utility for boreal lakes. MyLake has been applied to lakes in Norway (Lydersen et al. 2003; Saloranta 2006) and Finland (Kankaala et al. 2006; Saloranta et al. 2009).
PCLake
PCLake is an integrated ecological model of shallow non-stratifying lakes, describing phytoplankton, macrophytes and a simplified food web, within the framework of closed nutrient cycles. Its aim is to analyse the probability of a transition from the vegetation-dominated clear-water state to the phytoplankton-dominated turbid state, or vice versa, as a function of the external nutrient loading and other factors. Both bottom–up, top–down and indirect effects are included. PCLake has been designed to simulate the main nutrient and food web dynamics of a non-stratifying lake in response to eutrophication and related restoration measures (Janse et al. 1992, 1995, 2008, 2010; Janse and Van Liere 1995; Janse 1997, 2005). The model describes a completely mixed water body and comprises both the water column and the sediment top layer (10 cm), with the most important biotic and abiotic components (Fig. 1). The upper sediment layer is included to take into account sediment–water exchange and deposition history. Optionally, a wetland zone with helophytes can be added (Fig. 2). No further horizontal (like depth variations) or vertical distinction within the lake is taken into account. Mathematically, the model is composed of a number of coupled ordinary differential equations, one for each state variable. All biota are modelled as functional groups. The main groups in the water phase are three groups of phytoplankton (diatoms, greens and cyanobacteria), zooplankton, planktivorous, benthivorous and piscivorous fish. Submerged macrophytes are included, consisting of a shoot and a root fraction. Further groups in the top layer of the sediment are the settled fractions of the three types of phytoplankton, as well as zoobenthos. Closed mass balances throughout the model system were attained by modelling each compartment in three components, namely, dry weight as a surrogate for carbon, nitrogen and phosphorus. Additionally, diatoms and detritus are described in silicon. Inorganic carbon (CO2) is not explicitly modelled. Oxygen in the water column is modelled dynamically, while sediment oxygen is described by a simpler approach that still accounts for oxygen influence on nutrient release. By modelling dry weight, phosphorus and nitrogen explicitly, the nutrient-to-dry weight ratios are variable. Because the stoichiometry of organisms changes with trophic level, mechanisms are included to allow for those differences, such as a higher assimilation efficiency for nitrogen and phosphorus than for carbon. Apart from mass fluxes, the model also contains some empirical relationships to represent indirect effects between two groups of organisms, such as the impacts of fish and macrophytes on resuspension. For a detailed description of all processes, see Janse (2005). The model has been used to estimate the critical nutrient loading levels for both forward and backward switches between the ‘clear’ and the ‘turbid’ state of shallow lakes to identify the key processes determining the switch and the way critical loading levels depend on lake features and management factors (Janse et al. 2008). In the second part of this paper, we will look at PCLake in more detail.
Overview of the main biotic and abiotic components in the open water module of PCLake. Compartments are modelled in multiple components (dry weight as a surrogate for carbon, phosphorus, nitrogen, diatoms and detritus also in silicon). The group Algae is split into three functional groups: cyanobacteria, diatoms and other small edible algae. The group Plantivorous/Benthivorous Fish consists of a juvenile, zooplanktivorous and an adult, benthivorous subgroup. Solid arrows represent transfer of matter, dashed arrows represent functional relationships that do not involve transport of matter
PROTECH
PROTECH (Phytoplankton RespOnses To Environmental CHange) simulates the dynamic responses of up to 10 species of phytoplankton (from a library of over 100) to environmental variability in lakes and reservoirs. The model calculates exponents describing growth and loss processes (mortality, sedimentation, consumption by grazing zooplankton), on the basis of the maximum growth rates of algal species in culture. These maximum growth rates are derived from relationships established between the alga’s morphology and its growth rate subject to defined thresholds of light, temperature and nutrients. The model has been extensively applied as evident from over 30 peer-reviewed publications (see Elliott et al. 2010 for a review). Its formulation and equations are presented in Reynolds et al. (2001).
SALMO
SALMO (Simulation of an Analytical Lake MOdel, Benndorf and Recknagel 1982) simulates the most important planktonic food web compartments of lakes and reservoirs. The original version and the ‘basic version’ SALMO-II consist of two layers (epilimnion and hypolimnion) with variable mixing depth. In comparison with other models, the equations and parameters of SALMO are intended to be rather general, so that site-specific calibration can be avoided or at least limited to few site-specific parameters only (e.g., light extinction, sediment P-release and fish stock). If horizontal exchange rates are available (e.g., from a hydrodynamic 3-D model), multiple horizontal compartments can be combined. The recent version SALMO-HR is a vertically resolved 1-D hydrophysical–ecological coupled model that consists of the ecological sub-model SALMO-1D (Rolinski et al. 2005; Petzoldt et al. 2005; Baumert et al. 2005) and the hydrophysical k-ε-model LAKE (Baumert et al. 2005). It simulates the seasonal development of temperature, stratification and turbulence as well as the concentrations of phosphorus, nitrogen, phytoplankton (three or more functional groups), zooplankton, oxygen, DOC (with a focus on humic substances) and suspended matter (four particle classes). The model is used for scenario analysis (e.g., Petzoldt and Uhlmann 2006), in decision-making and as a research tool.
Structurally dynamic models
As stated in Zhang et al. (2010): “In structurally dynamic models, the parameters are constantly varied to account for adaptations and shifts in the species composition. Changes in the parameters are based on either expert knowledge or optimization of a goal function that can describe the fitness under changing environmental conditions. This approach attempts to overcome the weaknesses associated with traditionally used models: (1) Fixed and rigid parameter sets are used in such models, which can hardly reflect the changes of species properties and compositions according to the prevailing conditions of the ecosystem and (2) calibration is often difficult, because we have to deal with a number of uncertain parameters simultaneously and test them within a wide range of possible values.” A comparable approach using ‘dimensionless moderators’ was proposed by Håkanson and Peters (1995).
Minimal dynamic models
Like static models, minimal dynamic models are very simple. The difference with static models is that they describe changes through time and consist of a few differential or difference equations that focus on a single aspect of a system, based on clear assumptions (Van Nes and Scheffer 2005). These kinds of models are also called ‘strategic’ (Levins 1966) or sometimes ‘conceptual’ (Grimm 1994).
Minimal dynamic models often generate a hypothesis about a possible cause of a phenomenon that would not easily be arrived at intuitively (Scheffer and Beets 1994). These models are more popular in fundamental science than in applied science, as they aim at development of theory and understanding of complex lake systems rather than making realistic predictions. Even if the results are unrealistic, we can still learn from these models, as they may point to other mechanisms that are essential, but lacking in the minimal dynamic model that is analysed.
These models have the advantage that their behaviour can usually be explored completely with well-tested software tools for bifurcation analysis (Kuznetsov 1995). A subset of the simplest minimal dynamic models can even be analysed mathematically. The main disadvantage is that minimal models obviously focus on only one aspect of the ecosystem, while in reality the underlying causation may be much more complex (Scheffer and Beets 1994). Furthermore, the approach of minimal dynamic models may set artificial constraints to the level of abstraction, not dictated by nature but by the availability of tools for mathematical analysis. Minimal dynamic models have been developed to study non-linear dynamics between predator and prey (e.g., Scheffer et al. 1997) but also to study spatial pattern formation in predator–prey interactions (e.g., De Roos et al. 1991).
While being a conceptual instead of a dynamic model, the Plankton Ecology Group (PEG) model of seasonal planktonic succession in temperate lakes (Sommer et al. 1986) can be considered to be a minimal model. The strong impact of this model (measured by the numerous times it is cited) shows the potential of minimal models to provide conceptual insights into lake ecosystem dynamics. Subsequently, minimal dynamic models of seasonal succession have been developed (Scheffer et al. 1997), and these now also have been used for evaluating the impact of climate change on lake ecosystems (e.g., Scheffer et al. 2001a; Van Donk et al. 2003; De Senerpont Domis et al. 2007). It is important to notice that these models, due to being simple, can only give conceptual answers and should be used with great caution, e.g., when predicting the effects of climate change (Jeppesen et al. 2003).
Individual-based models
In many ecological systems, knowledge concerning the variation in sizes of individuals is essential (Huston et al. 1988). This is the case in fish populations, for instance, where size is a factor in survival (Mooij 1996), and also for macrophyte populations, which compete for light based on their height relative to other macrophytes in the water column. To model such populations accurately, we need to consider individual traits or even individuals separately. This individual-based approach (DeAngelis and Mooij 2005) has become popular among ecologists, as it may produce realistic patterns (for instance length distributions of fish) that can be checked against field data (Grimm et al. 2005). Individual-based models usually focus on a few ecological groups.
For modelling large populations in lakes, it is generally too computationally demanding to model all individuals separately (individual-based models sensu stricto). Three computationally more efficient approaches are presented below: models based on super-individuals (Scheffer et al. 1995), physiologically structured population models (De Roos et al. 1992) and stage-structured biomass models (De Roos et al. 2008). The latter approach could equally well be categorized as a minimal dynamic model and provides a nice bridge between individual-based approaches and simple, unstructured models of consumer-resource interactions in aquatic systems.
Trait-based models may be regarded as a subset of individual-based models. Here, the average value of traits vital to the functioning of the food web (e.g., body size, edibility, selectivity or carbon to nutrient ratios) is modelled dynamically, using either ordinary or partial differential equations.
Super-individual models
The super-individual approach starts with developing an individual-based model, in which individuals are modelled separately. These individuals differ in their characteristics (e.g., size, weight, age). In the super-individual approach, each individual has an extra property, namely the number of individuals that it represents. Mortality can modelled as drawing from binomial distributions and acts on this number. This type of model can easily be used in combination with a discrete event queue, which is sometimes used in individual-based models (Scheffer et al. 1995). This approach is closely related to that of physiologically structured models, but the implementation differs, and it is easier to scale down to a truly individual-based approach when modelling small populations (Scheffer et al. 1995).
The approach has been applied in the macrophyte model Charisma (Van Nes et al. 2003) and the fish model Piscator (Van Nes et al. 2002). In both models, competition between many species can be modelled. Charisma describes the seasonal cycle of macrophytes in temperate regions. Optionally, it is spatially explicit. It is especially detailed in the description of photosynthesis and can model self-shading and shading among different species. The model can show alternative stable states for different reasons (Van Nes et al. 2003). A truly individual-based version has been employed to describe in detail clonal growth of Potamogeton perfoliatus (Wolfer et al. 2006).
Piscator has, as a default, eight interacting fish species, three types of fishery (fykes, seine and gill nets), piscivorous birds and a simple representation of the fish food (zooplankton, benthos), but many user-defined species can be added, as required. The model can include size differences among year-classes by defining different super-individuals with slightly different growth rates. Feeding is modelled in an especially detailed way. Special attention has been paid to controlling complexity in the model. This is done by zooming in or out on different processes, by removing species without changing the computer code. Furthermore, an option has been implemented to shut down feedback mechanisms between predators and prey. This way the complexity can be increased gradually, which makes calibration easier (Van Nes et al. 2002), though caution should still be exercised in the knowledge that parameter values may change with the inclusion of different state variables.
Physiologically structured models
As stated in De Roos and Persson (2001): “Physiologically structured population models offer a concise framework to explicitly and mechanistically relate population-level phenomena to individual-level processes, in cases where the former are significantly influenced by physiological (e.g., size) differences among individuals. Central to physiologically structured population models is the clear distinction between the individual and its environment and the strict separation of the individual and population level. The model formulation process consists of the derivation of a mathematical description of how individual performance (growth, survival and reproduction) relates to the physiological characteristics of the individual and the condition of its environment. Hence, all assumptions about and parametrization of these functional relationships in response to its current environment take place exclusively at the level of a single individual organism. The derivation of the population model is subsequently only a matter of book-keeping without making any further assumptions.” While accounting for age or size, both known to be of paramount importance for physiological processes, the fact that dynamic energy budgets (Kooijman 2000; Baird and Suthers 2007) are obeyed in physiologically structured models implies that all traits are linked. Thus, all individuals of the same size or age are assumed to be identical. On the one hand, this keeps the model simple and allows, e.g., the quantification of trade-offs (Rinke et al. 2008), while on the other hand this linkage of traits makes these models less suited for including genotypic or phenotypic plasticity as in truly individual-based approaches.
Stage-structured models
As stated in De Roos et al. (2008) “the model, which we refer to as the stage-structured biomass model, is formulated in terms of a set of ordinary differential equations. Nonetheless, under equilibrium conditions the model predictions are identical to those of a physiologically structured population models accounting for a continuous size-distribution, from which the stage-structured biomass model is derived. Under these conditions, the model therefore consistently translates individual life history processes, in particular food-dependent growth in body size, to the population level.” An advantage of stage-structured biomass models over physiologically structured models is their mathematical tractability.
Trait-based models
The high diversity encountered at different hierarchical scales enables ecological systems to adapt to the prevailing conditions (e.g., by shifts in functional types, species, clones and genotypes), which often also buffers their responses to perturbations (Gunderson 2000). Allowing for such potential to adapt strongly alters the dynamic behaviour of laboratory food webs and their model representations (Yoshida et al. 2007). Hence, neglecting the naturally existing functional diversity and potential to adapt in lake models may strongly reduce their realism and predictive power. One approach to include this potential for adaptation in dynamic models is to split up one or more functional groups into several subunits which differ in their parameterization (e.g., Vos et al. 2004; Tirok and Gaedke 2010). The choice of parameters may follow trade-offs between the different functional traits, the importance of which becomes increasingly recognized (Litchman et al. 2007). This reduces, but does not altogether avoids, the increase in the number of free parameters.
Alternatively, the number of functional groups and free parameters can be kept small when traits are allowed to vary in time depending on ambient conditions. Such trait-based modelling approaches depict species (or functional groups, clones, genotypes, etc.) by their functional traits and the corresponding trait values (e.g., Wirtz and Eckhardt 1996; Norberg 2004; Savage et al. 2007; Harris 1994; Baird and Suthers 2007). A continuous trait value distribution describes the relative importance of the functionally different units, where the mean trait value reflects the strategy of the most abundant units and the variance the functional diversity. The trait value distribution may continuously change when growth conditions are altered, which reflects an increase in the share of species better suited for the current environment (Wirtz and Eckhardt 1996; Merico et al. 2009). Adaptive dynamics have been employed to study predator–prey coevolution (e.g., Abrams and Matsuda 1997) and increasingly also community dynamics and their potential to adapt to environmental changes (Norberg 2004; Savage et al. 2007). The multi-species and dynamic trait approach gives similar results when based on comparable assumptions (Merico et al. 2009).
So far, models describing the ability of community dynamics to adapt have been restricted to one trophic level (mostly primary producers, e.g., Wirtz and Eckhardt 1996; Norberg 2004) or at most two trophic levels (Abrams and Matsuda 1997; Tirok and Gaedke 2010). An extension to complex multi-trophic level food webs represents a future challenge, given the rise in model complexity and the uncertainties in the trade-off functions. A coarse, non-mechanistic but simple approach potentially suitable for complex food web models may be to extend the functional response using a term for predator interference which might mimic, e.g., increasing prey defence at high predator densities.
Use of hybrid evolutionary algorithms and neural networks
The hybrid evolutionary algorithm (Cao et al. 2006) was designed to uncover predictive rules in ecological time-series data. It combines genetic programming to generate and optimize the structure of rules and genetic algorithms to optimize parameters of rules (e.g., Recknagel et al. 2006). Resulting rules are subsequently evaluated by means of fitness criteria, where fitter rules are selected for recombination to create the next generation using genetic operators such as crossover and mutation. These steps are iterated over consecutive generations until the termination criterion of the run has been satisfied and the fittest rule has been determined. A detailed description of the design and functioning of hybrid evolutionary algorithms, including a demo software version, is provided by Cao et al. (2006). To determine generic rule-based agents for each lake category, hybrid evolutionary algorithms are imbedded in a k-fold cross-validation framework (Kohavi 1995) based on k-fold data partitioning and the consecutive use of each part of the data for both training and validation. This method has, for example, been used for a number of lakes, resulting in rule-based agents for forecasting 5- to 7-days ahead abundances of Microcystis in shallow polymictic and hypertrophic lakes in Japan, in warm monomictic and hypertrophic lakes in South Africa and abundances of Oscillatoria in two temperate shallow lakes in the Netherlands (Recknagel et al. 2006).
Use of Kalman filters and fuzzy logic
Most of the models described here were mainly designed for applications covering one or more seasons. From a management point of view, there is also a demand for (near) real-time forecasting of, for example, cyanobacterial blooms in lakes used for recreation. The accuracy of traditional models in predicting this type of event is usually not very high, however. An improvement may be obtained by a combination of different modelling approaches as was already described in the previous section. As an alternative, Kalman filters and fuzzy logic can also applied in real-time forecasting systems of phytoplankton blooms. Kalman filters are applied in conjunction with deterministic equations to improve the accuracy of predictions based on systematic discrepancies between modelled and observed conditions. They have been widely applied in predicting storm surges, high water events or weather forecasts that are often difficult to predict by models that are basically designed for simulating average conditions. Examples of existing applications for phytoplankton predictions in marine systems are given in Allen et al. (2003) and Mao and Lee (2009).
Fuzzy logic provides another technique to improve the predictive power of deterministic models. In this case certain processes, which cannot be easily described by deterministic equations, are modelled using knowledge rules. As an example consider ‘if the average wind speed is less than 4 m s−1 and the irradiance is high, then there is a high probability that a surface bloom of cyanobacteria is formed’. Fuzzy rule-based models are often employed to capture the approximate mode of reasoning that plays an essential role in dealing with uncertain and imprecise data. The fuzzy logic theory is based on an extension of the classical meaning of the term ‘set’ and formulates specific logical and arithmetical operations for processing imprecise and uncertain information (Zadeh 1965). The main application areas of the fuzzy set theory in ecological research are data analysis, knowledge-based modelling and decision-making (Salski and Holsten 2006). A combined application of fuzzy logic with the deterministic Delft3D-ECO model to describe the formation and horizontal distribution of surface water blooms of toxic cyanobacteria is given by Ibelings et al. (2003). Laanemets et al. (2006) use fuzzy logic to predict cyanobacteria blooms of Nodularia in the Baltic, Blauw et al. (2010) use fuzzy logic to predict foam on beaches.
PCLake as an in-depth example
In this section, we describe, as an in-depth example, the multi-decadal development of the model PCLake and the way it has been applied and linked to different modelling approaches. We chose this model, because several of the authors are familiar with it and were engaged in its development, and because it nicely illustrates the challenges met and the choices to be made when developing a model over several decades in response to changing management questions. Other models could have served as an example equally well.
First, we describe the model’s development and applications, including uncertainty analysis and some comparisons with other models. Secondly, we describe a metamodel derived from the dynamic model, and thirdly, the links that have been made with other approaches, namely coupling with hydrodynamic models and with empirical biodiversity relations. We conclude with apparent limitations of the model and ways to cope with these.
Model development and applications
As stated before, PCLake has been designed to simulate the nutrient, phytoplankton, macrophyte and food web dynamics of a non-stratifying temperate lake in response to eutrophication and restoration measures (Janse 1997, 2005). The first version (then called PCLoos) was developed within the Lake Loosdrecht Water Quality Project (WQL) for a shallow peat lake in the Netherlands (Van Liere and Janse 1992; Janse et al. 1992). This project aimed at elucidating the mechanisms causing the algal blooms in the lake and to estimate the effects of reduction in phosphorus loading and other restoration measures such as dredging, P fixation and biomanipulation. The model focused on phosphorus as a nutrient, the three main algal groups present, the upper sediment layer because of the intensive exchange between water and sediment in the lake and top–down effects on the algae via zooplankton and fish.
The choice was made to develop a model of ‘intermediate’ complexity, covering the broad ecological structure of the system, with limited chemical and hydrodynamical details compared to the existing models of the time. Variable P/C stoichiometry throughout the system was included from the start, based on field and experimental data from this and other lakes. The model correctly simulated that the proposed phosphorus reduction measure did not stop the algal bloom and indicated the causes of the failure such as a decrease in the P/C ratio (Gulati et al. 1991; Van Liere and Janse 1992). Scientific and management interests in alternative stable states in shallow lakes triggered an extension of the model, now called PCLake, with macrophytes, predatory fish and a nitrogen cycle in order to cover both states of the system: the current turbid and the desired clear state. Indeed, the model proved to be able to produce switches between clear and turbid states to mimic hysteresis in the response of the system (Janse 1997; Janse et al. 2008) and the effects of biomanipulation (Janse et al. 1995). Management interests also triggered the development of a wetland module to simulate the impacts of helophytes zones for lake restoration (Janse et al. 2001; Sollie et al. 2009). The model was originally implemented in the simulation package ACSL/Math (Aegis 2001), including a MATLAB-like user interface apt for batch calculations. Later, a freely distributed OSIRIS (Mooij and Boersma 1996) version was constructed, consisting of a C++ executable called from a Microsoft Excel shell.
The model has been tested by means of a sensitivity analysis by methods suited for non-linear models and a Bayesian parameter estimation and uncertainty analysis comparable to GLUE (Janse et al. 2010). After identifying the key sensitive parameters, these were calibrated on the combined data on total phosphorus, chlorophyll-a, macrophyte cover and Secchi depth in over 40 temperate shallow lakes. This was done by a Bayesian procedure, giving a weight to each parameter setting based on its likelihood (Aldenberg et al. 1995). This procedure hence aimed at an overall best fit for the whole sample of lakes, rather than an optimal fit for one lake at the expense of others. The weights were used for an uncertainty analysis, applied to the ‘critical phosphorus loading levels’ calculated by the model. These are the threshold loadings where a shallow lake will switch from the phytoplankton-dominated turbid state to the macrophytes-dominated clear-water state or vice versa. Apart from lake dimensions and loading, the model was most sensitive to zooplankton growth rate, settling rates and maximum growth rates of phytoplankton and macrophytes as process parameters. The results for the best run showed an acceptable agreement between model and data, i.e., that a regression of the predicted on the observed values did not deviate significantly from the 1:1 line and that nearly all lakes to which the model was applied were classified well as either clear or turbid (Janse et al. 2008). The critical loading levels for a chosen standard lake showed about a factor two uncertainty due to the variation in the posterior parameter distribution (Janse et al. 2010). Using the tested model, Janse et al. (2008) calculated how the critical loading levels depend on water depth, lake size, retention time, proportional marsh area and type of sediment.
PCLake has been used in several other case studies, both in static and dynamical ways, allowing water managers to evaluate both benefits and drawbacks of proposed restoration measures beforehand. The dynamical case studies, with detailed water and nutrient budgets as input, include management options for the Reeuwijk Lakes (Janse et al. 1993); different scenarios for water level fluctuations for Lake Oldambt (Witteveen+Bos 2009) and Lake Loenderveen and Terra Nova (Witteveen+Bos 2010a); the impact of a sediment trap on water quality in Lake Loosdrecht (Witteveen+Bos 2008a), the impact of fish and sediment removal in Bergse Plassen, the impact of different water storage scenarios in Lake Oldambt (Witteveen+Bos 2009) and Nieuwe Driemanspolder (Witteveen+Bos 2010b), and the impact of water flushing in Wieringen Borderlake (Witteveen+Bos 2008b).
The static applications of the model concern the estimation of the critical P-loading of lakes, i.e., the switch points between the usually undesired turbid state and the usually desired clear state. Estimation of the critical loadings of a lake is important for lake managers and is part of the diagnostic framework for shallow lakes recently developed in The Netherlands (STOWA 2008). Depending on the difference between actual P-loading and critical P-loading, measures can be taken to reduce the actual nutrient loading, increase the critical loadings of water systems by adjusting lake characteristics or change the ecological status directly by, for instance, fish removal (Meijer 2000). Janse (2005) and Janse et al. (2008) calculated critical loadings for some 50 European lakes. Critical loadings were calculated for both existing (e.g., Lake Zuidlaren, Lake Breukeleveen) and new water systems (e.g., Eendragtspolder, Nieuwe Driemanspolder) to be used in management projects, giving insight into the robustness of the system to eutrophication. While ignoring horizontal exchanges, PCLake has been run on a horizontal grid. In the design of new water systems (e.g., Wieringen Borderlake, Lake Oldambt), this method gives a first identification of parts of the lake that deserve closer inspection.
Although this was not intended from the beginning, the fact that temperature dependencies of all processes are included allows preliminary simulations of the effects of temperature rise in studies on climate change, the results being mainly in agreement with observations that warming will decrease the critical loading levels ( Schep et al. 2007; Mooij et al. 2007). Mooij et al. (2009) showed that the PCLake results were qualitatively comparable with those of a minimal dynamic model.
A metamodel of PCLake
In order to provide water managers with an easy-to-use method to estimate the critical P-loading of their lakes, a metamodel of PCLake has been developed. This generates static lake-specific critical P-loadings without the need to dynamically run PCLake itself. The first version can be accessed on the Internet (Janse et al. 2006); an improved version was published recently by Witteveen+Bos (2010c). Input variables are initial state, water depth, fetch, marsh area, residence time, soil type and background extinction. The range and distribution of each variable were derived from an analysis of Dutch lake characteristics, resulting in a dataset with 41492 different sets of input variables. Within a range of 0 and 10 mg·P m−2·day−1, the critical nutrient loading is determined much more accurately than previously through 18 iterations, revealing approximately 105 possible model outcomes per set of variables. The factor ‘Secchi depth/water depth’ was used as criterion for the ecological state of the lake (clear or turbid), as it was very sensitive for small changes in P-loading around the switch point. The results of all model runs were stored and analysed by different mathematical techniques to derive the metamodel: multiple regression, regression trees, black box neural network and the new technique white box neural network. Each method was applied separately for three soil types and two initial states, resulting in six different models for each method. The dataset was divided into two parts, in which 83% is used for calibration and 17% for validation. The neural network methods gave the best results, but the white box neural network was used for the metamodel because of a better interpretability. In any case, the average relative errors of the neural networks were smaller than the model uncertainty, assuming an average relative error of 0.4 in PCLake. Simplification (pruning) of the neural networks provided only little added value.
A general remark on metamodels is that their results are closely linked to the full-scale dynamic model they are derived from, implying the need for recalculating the metamodel in case of future changes in the latter.
Links with other model approaches
Interest from water managers triggered a parallel implementation of PCLake as a quality module in the 1-D or 2-D-horizontal water transport model DUFLOW (STOWA 1999, 2000). Fragoso et al. (2009) coupled PCLake (partly adapted for subtropical conditions) with a 3-D hydrodynamic model. Prokopkin et al. (2010) applied relevant parts of PCLake in a 1-D vertical model of the stratified saline Lake Shira in southern Siberia. Furthermore, PCLake has been coupled with empirical relations for species richness within functional groups, derived from a multi-lake dataset (De Meester et al. 2006). Links with static models (metamodel) and minimal dynamic models (climate studies) were mentioned above. The links with the IPH and Shira models are described here in some more detail.
IPH-TRIM3D-PCLAKE
The IPH-TRIM3D-PCLake model is a complex ecosystem model (available to download at http://www.peld.ufrgs.br). A detailed description of the model can be found in Fragoso et al. (2009). This model consists of a 3-D hydrodynamic module coupled with an ecosystem module. Together, these models describe the most important hydrodynamic, biotic and abiotic components of an aquatic ecosystem. The hydrodynamic model is based on the Navier–Stokes equations that describe dynamically the 3-D transport and mixing of water. An efficient numerical semi-implicit Eulerian–Lagrangian finite difference scheme was used in order to assure stability, convergence and accuracy (Casulli and Cheng 1992; Casulli and Cattani 1994). The chemical and biological dynamics in the open water and in the sediment are based on PCLake, with an adaptation to subtropical lakes by including omnivorous fish. The IPH-TRIM3D-PCLake ecosystem model further differs from PCLake, as it takes into account the horizontal spatial heterogeneity in the aquatic system at the cell level and stratification over the water column for several state variables (e.g., temperature, water density, nutrients, phytoplankton and zooplankton). In order to solve the advection–diffusion transport equation for each component in the water numerically, a flux limiting scheme was implemented that uses Roe’s superbee limiter (Roe 1985) with a second-order Lax–Wendroff scheme (Hirsch 1990). Water temperature is modelled through a heat budget algorithm (Chapra 1997). The main inputs of the model are water inflow, infiltration or seepage rate (if any), nutrient loading, particulate loading, temperature, light, wind, rainfall and evaporation, spatial maps (including waterbody bathymetry, bottom and surface stress coefficient), sediment features and initial conditions.
One-dimensional vertical model of Lake Shira
A one-dimensional vertical model of Lake Shira (Prokopkin et al. 2010) was developed by applying ideas and formulations in PCLake concerning ecosystem dynamics to a relatively rare type of natural waterbody, namely brackish lakes. For these lakes, strong stratification of physical–chemical and biological components is typical, together with low species diversity. These features provide special conditions for ecosystem functioning and nutrient cycling. In this model, a 1-D algorithm describing the hydrodynamic and thermal structure of Lake Shira has been used (Belolipetsky et al. 2010). As the temperature stratification of Lake Shira is pronounced in summer, it is important to describe this phenomenon correctly and take its effect into account everywhere in the model. The temperature regime is affected by wind-induced mixing, solar heating and heat exchange with the atmosphere. With regard to ecosystem processes, the impact of temperature was introduced when considered essential and where data were available. Processes such as phyto- and zooplankton growth, respiration, sedimentation and mineralization use functions mainly derived from PCLake. The resulting patterns of phytoplankton, nutrients and other dynamics show qualitative and quantitative agreement with the field observations during the summer season (Prokopkin et al. 2010).
Limitations of PCLake
The main advantage of a complex model like PCLake, its integrated nature, of course also constitutes its main problem: the large number of process parameters, of which the ranges can hardly be assessed together from one dataset. Seen from this perspective, the model analysis carried out by Janse et al. (2010) gives only incomplete estimates of the parameters. Nevertheless, some parameters can, and have been, reasonably well estimated from experimental data. Some simplifications and/or lumping of process formulations might be a promising direction. On the other hand, some factors are missing, such as the impact of sulphate, iron and nitrate on processes that lead to internal nutrient cycling and eutrophication.
A major limitation in PCLake is the assumption of a uniform water depth, leading to an ‘all or nothing’ response in lakes, which should show a more gradual response in reality because of depth variations. This limitation can sometimes be overcome by a grid set-up that ignores horizontal transport (e.g., Witteveen+Bos 2008b, 2009, 2010b), but this is not generally applicable. A complete 2-D or even 3-D implementation is possible (see Fragoso et al. 2009) but creates, among other problems, excessive computational time. A (pseudo-) 1- or 2-D version in the horizontal would, however, increase the applicability of the model. A 2-D implementation in the x–z plane would also allow accounting for the movement of animal populations between different habitats (e.g., Vos et al. 2002; Winder et al. 2004).
To address some management questions, a further splitting of some model components in more detailed groups, e.g., macrophytes and/or fish species, would be necessary. Some model versions have been created with this in mind (e.g., Janse et al. 1995), such as in the related ditch model PCDitch that includes several groups of macrophytes (Janse and Van Puijenbroek 1998; Janse 2005). Regarding fish, an oversimplification of the fish module currently appears to produce incorrect results for the effects of biomanipulation. For macrophytes, the potential impact of species like Elodea and Ceratophyllum on internal eutrophication is underestimated. Finally, results obtained with use of the marsh module are not always consistent with experiences in the field because of oversimplified relations between marsh size and water level. Further weaknesses, following from the model’s initial aim and set-up, are that it focuses on shallow non-stratified lakes and is restricted to lakes in the temperate zone (but see the studies by Fragoso et al. (2009)).
While the model has a closed balance for phosphorus and nitrogen, dynamics of inorganic carbon are not modelled. This limits the linkage of PCLake with models that focus on the effect of atmospheric CO2 elevation on freshwater ecosystems (e.g., Schippers et al. 2004).
Regarding the technical aspects, an easy-to-use, freely available user interface, allowing both easy ‘hands-on’ simulation and visualization for individual lakes, spatial (network) simulations, batch simulations for sensitivity studies and calibration runs and flexibility in model structure, has not yet been produced. Batch analyses would benefit from a procedure to renew the initial conditions.
Future perspectives for PCLake
There are four types of questions that may influence the future development of PCLake. First, to address demands for a more easy-to-use and more flexible version of the model, the applicability for lake managers will be improved by a closer relation with management options (including additional testing) and improvement in the user interface. The planning of this extension of the model will be done in cooperation with Dutch water managers, with the limitations mentioned above in mind, and may imply adding detail or, alternatively, making simplifications. The spatial structure of the model (vertically and/or horizontally) will be made adaptable to specific needs.
Secondly, policy makers ask for a lake model that can be used for projections on a global scale, i.e., covering a wider range of lake characteristics, including size and morphology, climate zones and hydrological features, to be embedded in an existing global catchment and land use model for anthropogenic pressures (PBL 2009; Alkemade et al. 2009, 2010). PCLake may be helpful, besides other model approaches, in the set-up of such a model.
Thirdly, the link with biodiversity modelling will be strengthened, which deserves much attention both on global (MEA 2005) and on regional scales. We refer to the discussion section for possible directions.
Finally, the PCLake model, or specific submodules or cut-outs from it, will be continuously available for use in other projects, such as the application for stratified saline lakes presented in this volume (Prokopkin et al. 2010; Degermendzhi et al. 2010).
Closing remarks on PCLake
The long exposition of PCLake in this paper might suggest that the model and its development did not suffer from the two wasteful trends of model development (‘reinventing the wheel’ and ‘having tunnel vision’) that are central to our message. It is not our intention to create this impression. In the Dutch setting, PCLake was developed independently from the other major Dutch lake ecosystem model, DELFT3D-ECO (and its forerunners). Moreover, in the development of PCLake the focus has always been on food web dynamics, with a more limited attention for spatial dynamics. One the positive side, and as documented above, PCLake has now been embedded in models focussing on spatial dynamics and has also been linked with minimal dynamic models and static models. The discussion that follows, concerning ‘leading principles’, might shed some more light on the choices made during the development of PCLake and the other models mentioned in this paper.
Discussion
Leading principles
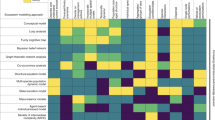
The rather arbitrarily chosen sample of lake models presented above indeed shows the diversity of approaches to lake ecosystem modelling. Because these approaches differ in many respects and overlap to various degrees, there is no single axis along which they can be adequately categorized. In an attempt to classify them, we scored each model or approach using multiple criteria concerning model components (Table 1) and model characteristics (Table 2). But perhaps the simplest way to get an overview of the whole range of approaches, and an appreciation of their advantages and disadvantages, is to look at the leading principle that led to the development of each approach.
Static models are developed from an empirical perspective with no or limited attention given to the underlying mechanisms. With their strong backing by data, they have successfully convinced scientists, water quality managers and politicians from the 1970 s onwards that eutrophication had a strong negative impact on aquatic ecosystems, and they still provide useful rules of thumb for water quality management.
Another important approach is that of complex dynamic lake ecosystem models based on differential equations. Two leading principles prevail here: a focus on spatial complexity and hydrology in 1-, 2- or 3-D or, alternatively, a focus on food web structure and complexity. The fact that in many models, one of these two important aspects of aquatic ecosystems is better developed than the other, suggesting a trade-off between spatial complexity and food web complexity in model development.
Within the category of complex dynamic models, more detailed knowledge on the leading principles that shaped each particular model could be identified, giving a better understanding of the choices and assumptions that were made during model development. This knowledge would enable model developers to better take advantage of the already existing principles and models and also to modify and combine the strengths of these principles and models. We stress, at the same time, the importance of breaking with the undesirable fragmentation in the development of complex dynamic lake ecosystem models, which currently exists within the modelling community.
While complex ecosystem models were considered very promising in the early 1980 s, when powerful computers became widely available (Rigler and Peters 1995), they were heavily criticized in the 1990s for being data hungry, overly complex and not leading to scientific insight or predictive power. For a critical discussion on complex dynamic models, see also Håkanson and Peters (1995).
Often the underlying model algorithms employ a simple ‘engineering-based’ paradigm, where small-scale ecosystem processes (e.g., algal growth, bacterial mineralization of nutrients, etc.) are ‘scaled-up’ (Flynn 2005). For example, fluxes of nutrients between simulated pools are approximated using semi-empirical algorithms determined in laboratory microcosms and applied within lake-scale models with little regard of organism adaptability or more complex ecological interactions (Arhonditsis and Brett 2004). Where attempts are made to resolve the higher ecological interactions such as fish and benthic communities within a spatially resolved hydrodynamic model, a lack of suitable validation data and excessive model complexity in the absence of guidance by sound empirical data hinders progress and often means that trophic levels above phytoplankton grazers are ignored. Furthermore, while the approach of using a coupled hydrodynamic-ecological model can improve our understanding of the physical, chemical and biological processes influencing water quality dynamics, it generally remains unclear whether all important ecosystem feedback mechanisms are represented. These fundamental limitations can have a profound impact on their ability to predict responses to change, and whether ‘emergent’ ecosystem behaviours—patterns that emerge due to complex system dynamics—such as those observed in nature can be resolved.
The above-mentioned points of criticism concerning complex dynamic models stimulated the development of minimal dynamic models. These models build on the seminal work on predator–prey interactions by Rosenzweig and MacArthur (1963) and Rosenzweig (1971) and aim at understanding non-linear processes and alternative stable states in lake ecosystems (and many other dynamic systems) (e.g., Scheffer 1990; Scheffer et al. 1993, 2001b, 2007). Even though they are highly abstract and do not produce quantitative output that is of direct use to water quality management, they fully accomplished their goal of generating general insight into large-scale mechanisms and had a surprisingly strong impact on management strategies for mitigating anthropogenic stress factors such as eutrophication.
The notion that the dynamics of higher trophic levels with their complex life-histories, ontogenetic shifts and behaviour cannot be captured in a single-state variable representing their carbon, phosphorus or nitrogen content alone led to the development of individual-based approaches (see DeAngelis and Mooij (2005) for a review of individual-based models of ecological and evolutionary processes). Various ‘schools’ exist within this broader approach, each with their own leading principles and levels of detail at which individual variation is captured in the model. Models based on super-individuals can include more empirical realism in individual and spatial variation, compared with physiologically structured population models and stage-structured biomass models. Both allow for taking into account the intricate and sometimes non-intuitive effects of ontogenetic development on food web dynamics (e.g., Claessen et al. 2000). Also trait-based models can be classified as individual-based. Here, the focus is on adaptation at various levels of integration and its consequences for food web dynamics (e.g., Abrams and Matsuda 1997).
Challenges and opportunities: Ecological aspects
Modelling the impact of climate change with eutrophication models
One of the aims with documenting in detail the multi-decadal development of PCLake was to show how a model that was developed for eutrophication studies is now also applied to climate studies. On the positive side, the results obtained so far show that, qualitatively, model output for climate scenarios (Mooij et al. 2007) coincides with what we know from empirical studies (Mooij et al. 2005) and with general patterns obtained with minimal dynamic models (Mooij et al. 2009). Importantly, the impacts of eutrophication and climate change are tightly linked (Mooij et al. 2005) and, therefore, require a model that simultaneously deals with both aspects. On the negative side, however, these predictions have not yet been verified in a formal comparison of model output with the scarce field data that we have on the interplay between eutrophication and climate change (in particular climate warming, e.g., Moss et al. 2003; Van De Bund et al. 2004; Jeppesen et al. 2009, 2010).
Cross-latitude studies that indicate major changes in the trophic structure in lakes may challenge model performance. The composition of fish stocks is expected to change towards higher dominance of zooplanktivorous and omnivorous fish, implying increased predation on zooplankton and, consequently, less grazing on phytoplankton (less top–down control), and a higher chlorophyll:TP ratio (higher yield). Moreover, in warmer lakes, fish are smaller, grow faster, mature earlier and have shorter lifespans, allocate more energy to reproduction and have a higher degree of omnivory than populations at higher latitudes, both between and within species (Blanck and Lammouroux 2007; Jeppesen et al. 2010). While several models include fish dynamically, most of the changes described above are not included, which may lead to too conservative predictions of the effect of climate change. The direction of the cross-latitude changes from cold to warm lakes, which in part might reflect also biogeographical differences and differences in lake age, are largely confirmed in time series from northern temperate lakes (e.g., Jeppesen et al. 2009, 2010).
In addition, the effects of plants on water clarity seem weaker in subtropical lakes than in north temperate lakes (Jeppesen et al. 2007). Hence, Bachmann et al. (2002) found no differences in chlorophyll:TP or Secchi depth:TP relationships in subtropical lakes with low, medium–high or high plant coverage or the amount of plant volume present (% PVI). This suggests that the refuge for zooplankton is poor in warm lakes, which is confirmed by comparative experimental studies conducted in temperate Denmark and subtropical Uruguay (Meerhoff et al. 2007). Moreover, a cross-system analysis of data from lakes from the temperate zone to the tropics gave evidence for a lower probability of macrophyte dominance in warm lakes and lower nutrient thresholds for loss of these plants (Kosten et al. 2009). No complex models have included such effects, which apparently play an important role for changes in the function of shallow lakes ecosystems and their water clarity as they get warmer, although preliminary PCLake results are in agreement with this direction (Mooij et al. 2008).
Another main challenge for predicting effects of climate change is the difficulty in accurately predicting regional wind speed and precipitation (and thus the boundary condition data that feed into the lake ecosystem models). While air temperature predictions from the global climate models are considered relatively reliable, regional wind speed and precipitation (and thus runoff) predictions are still unreliable, and certain variables, such as radiation, are rarely entered as input to the models. However, considerable progress is currently being made in this field (IPCC 2007; Sipkay et al. 2009). Similarly, it is highly uncertain which effects global change will have at the catchment scale, where increasing temperatures, changing land use and frequency of extreme events will lead to changing nutrient fluxes into the surface waters. A study on the influence of altered hydrological regimes brought about by shifting precipitation patterns in eastern Australia, using ELCOM-CAEDYM, has highlighted the potential significance of this on water quality processes (Vilhena et al. 2010).
A final point that we would like to make here is that climate studies have shown that in the temperate zone, changing conditions in winter may be as important as, or even more important, than changing conditions in summer. For instance, warm winters may lead to larger inocula of cyanobacteria and higher winter fish survival, leading to blooms and deteriorated water quality in the following summer. Also many invasive species benefit from warmer winters. In addition, increasing winter temperatures in boreal regions would impact lake surface freezing dynamics. We feel that the issue of ‘winter limnology’ has not yet gained the attention it needs in the light of climate change (but see e.g., Salonen et al. 2009).
Both from scientific and policy-oriented sides, there is a great need for lake models able to grasp the impact of combined anthropogenic factors (land use, climate change, fisheries and others) on ecosystem structure and function for a broad range of lake types. The combination of two approaches discussed in this paper, dynamical models with empirical relations, might be one approach to addresses these needs.
Modelling biodiversity
A certain level of biodiversity is included in models like CAEDYM, CE-QUAL-W2, Delft-3D ECO and PCLake, but the level of detail is still far from the biodiversity that we observe in lakes. Several studies have related species richness in natural lakes with global factors such as latitude, altitude, lake size and water chemistry (e.g., Amarasinghe and Welcomme 2002) and productivity (e.g., Leibold 1999; Jeppesen et al. 2000; Declerck et al. 2007). Many models rather deal with functional diversity by defining, for example, functional phytoplankton groups instead of using single species definitions and, therefore, do not allow projections for species richness. Probably, one of the main obstacles to including more details on biodiversity in models of aquatic ecosystems is that we still lack a good understanding of the mechanisms maintaining biodiversity. Currently, there is an ongoing debate about the role of niche-based versus neutral processes in maintaining biodiversity and potential links between the two theories. One line of research is to include variations within functional groups and to study the effects of these variations on ecosystem functioning. Another line of research focuses on deterministic chaos as an explanation for the maintenance of planktonic biodiversity (Huisman and Weissing 1999) through ‘super-saturated coexistence’ (Schippers et al. 2001). PROTECH fits in the niche-based approach and seems to indicate that considerable progress can be made along this line. Structurally dynamic and trait-based models also aim at capturing shifts in species composition, though they are still in a pre-mature stage.
An alternative approach is to calculate species diversity, functional diversity and size diversity from empirically based relationships using output variables (e.g., TP) from the complex ecological models. An example is the combination of empirical relations with PCLake output for total P, chlorophyll-a and other variables for a dataset of European lakes (De Meester et al. 2006). Another, more policy- or conservation-driven indicator of biodiversity, as used in the GLOBIO model (PBL 2009; Alkemade et al. 2010), is ‘biodiversity intactness’ (Scholes and Biggs 2005), or the remaining mean abundance of the species that are native to the specific type of ecosystem. These parameters have been linked to lake environmental factors such as nutrients (e.g., Alkemade et al. 2010). Yet another possible link is to add a functional-ecological index comparable to the ‘depletion index’ or ‘marine trophic index’ as used in marine ECOSIM models.
Modelling of sediment diagenesis and coupling of diagenetic processes to water column dynamics
It is well known that the amount and availability of nutrient pools in lake sediments can strongly influence the ecological dynamics of the overlying water column (Søndergaard et al. 2003) and can even prevent or delay the response of lake water quality to changes in external forcing, such as changes in nutrient loading or climate (Jeppesen et al. 2005, 2007). However, sediment nutrient cycling is often not dynamically accounted for, or only included through very simplistic representations, by lake ecosystem models. It will be a great challenge to improve this element of the models, thus being able to dynamically simulate the response (and resilience) of lake ecosystems to changes in nutrient loading and/or climate.
Both relatively simple two-layer oxic/anoxic sediment diagenesis models (e.g., Wang et al. 2003a, b) and multi-layer, 1-D, complex diagenesis models have been available for decades (e.g., Jørgensen et al. 1982; Boudreau 1996). Therefore, the most challenging aspect of improving representations of sediment dynamics in lake ecosystem models is not to develop new sediment diagenesis models but rather to obtain sediment nutrient data for testing, modification, calibration and validation of already existing models, as these data are rarely—or never—available at appropriate spatial scales over sufficiently long time periods (extending one or several decades) (e.g.Trolle et al. 2010).
Modelling fisheries in an ecosystem context
There is an increasing trend towards modelling fisheries in an ecosystem context in both marine (Hall and Mainprize 2004) and freshwater systems (Kitchell et al. 2000; Lammens et al. 2002). In both systems, studies on the impact of bottom-up processes through the food web on fisheries have been stimulated by effective management leading to re-oligotrophication of systems that had become eutrophied. In such cases, it has been questioned whether minimum levels of carrying capacity of the system for stocks of fish should be maintained. These stocks can be of interest for a commercial fishery, for sport fishing, or as food for bird species that have a protected status and hence there is a demand for embedding fisheries in lake ecosystem models.
Ecosystem Based Fishery Management (EBFM; EPAP 1999) is a significant departure from traditional fisheries management. EBFM considers the impact that fishing has on all aspects of the ecosystem, not just the target species (Pikitch et al. 2004). Starting from a different perspective, Makler-Pick (2010), has demonstrated the utility of linking an individual-based fish population model with a complex hydrodynamic-food web model (DYRESM-CAEDYM) to explore the impact of fishery management on the water quality of Lake Kinneret (Israel). The model allows the study of the role of the fish in a lake ecosystem and has to potential to serve as an EBFM tool, since it also includes fishery mortality.
Challenges and opportunities: conceptual and technical aspects
Model complexity
We take the point of view that a single ‘right’ approach or level of complexity does not exist. Instead, multiple modelling approaches, applied concurrently to a given problem, can help in developing an integrative view on the functioning of lake ecosystems (Scheffer 1998, p308; Van Nes and Scheffer 2005; Mooij et al. 2009). This is a shift in paradigms away from the hopes in the seventies and eighties of the past century that with increasing computational power, a full reductionist approach to ecosystem dynamics would yield both insight and predictive power. In the new view, we acknowledge that each modelling approach has fundamental shortcomings that cannot be overcome purely through enhanced computational power and increased model complexity.
Multiple-model paradigm
A plain approach is to accept all the virtues and shortcomings of each model and respect their identities. This is analogous to approaches and themes taken by the Intergovernmental Panel on Climate Change for their assessment of atmospheric climate models (global circulation models), where, for example, 23 climate models were applied individually, and their simulations for outgoing radiation were collated to produce a range of simulations (Randall et al. 2007). It was found that the simple arithmetic mean ‘model’ of all model simulations, which in itself has no ecological meaning, was the most accurate in predicting outgoing radiation. Such a multiple-model study will not just provide a quick overview of equally valid model alternatives to potential users or lake managers but will also give insights into selection of essential model features to a particular problem for the model developers. Whereas its benefits are obvious, adoption of this paradigm into lake ecosystem modelling may of course not be straightforward, as many lakes have highly variable natural conditions and anthropogenic impacts, and different models may have different scopes. Also the recently formed Intergovernmental Panel on Biodiversity and Ecosystem Services (IPBES, Larigauderie and Mooney 2010) advocates multi-model studies as a basis for future biodiversity assessments. Such models for freshwater biodiversity, coupled to global change and other drivers, are urgently needed to support policies at different geographical levels.
Directly linking approaches
In specific cases, however, different approaches can be linked directly. A good example is the derivation of static models from complex dynamic models in so-called metamodels. As documented above, such a link between dynamic and static applications has been realized for PClake. In this particular example, the purpose of the static application is to derive a system-dependent critical nutrient loading without having to run the dynamic model. The purpose of the dynamic model is to better understand the relative importance of different characteristics to the ecological functioning of lakes, through which key factors other than nutrient loading alone can be identified and to make specific predictions of the impact of management measures on ecological aspects of water quality.
Other possibilities for a direct link between modelling approaches are the inclusion of super-individual, physiologically structured or stage-structured modules for fish and zooplankton in complex ecosystem models. The usefulness of making this link was recently shown in the DYCD-FISH model for simulating fish populations in aquatic systems (Makler-Pick 2010) that was mentioned earlier.
Cyber-infrastructure
The recent advance in water-related cyber-infrastructure, defined as the system of hardware and software components that monitor, manage and model aquatic ecosystems (Shade et al. 2009), has created challenges and opportunities for lake modelling. For example, assimilation of observations from real-time lake sensors to reduce error in model parameterizations is emerging as a promising method to manage the uncertainty of complex models. For water quality or ecological applications, such methodologies are in their infancy; however, signal processing techniques that estimate lake metabolism from real-time oxygen and temperature measurements (Hanson et al. 2008) and similar approaches will ultimately support the validation of complex hydrodynamic-ecological models.
Calibration, uncertainty and error propagation
While the topics of model calibration, uncertainty and error propagation are of overwhelming importance in many of the more complex modelling approaches, we will be brief here, especially in the light of the many publications on this topic (see citations in Arhonditsis and Brett 2004; Arhonditsis et al. 2007; Janse et al. 2010). In the view of our discussion on complex versus more minimal models, the common notion is that a disadvantage of complex models is that they are both difficult to calibrate and ‘data hungry’. In this respect, it is important to make a clear separation between parameters that are chosen a priori versus those chosen a posteriori. In a study on error propagation in spatially explicit individual-based models, Mooij and DeAngelis (1999, 2003) showed that in a strict statistical sense complex models of which only a few parameters are estimated a posteriori (calibrated) have even narrower log-likelihood profiles for the estimated parameters than minimal models with an equal number of parameters. This gives rise to the counterintuitive notion that complex, more realistic models of which only a few parameters are calibrated may be less ‘data hungry’ than their minimal counterparts. Further, the procedure of determining sensitivity and uncertainty in complex models, if designed appropriately, can in fact be used to help extract important information about key processes (Makler-Pick et al. 2010).
Using optimization principles
There has been quite some controversy whether it is acceptable to employ some form of optimization principle in ecological lake models. A widely applied phytoplankton model that employs such principle is BLOOM II (Los 2009). The model is based upon a competition principle for individual ecotypes, which is translated into an equivalent optimization principle at the community level. First, the different possible states at which one of the nutrients, or light, limits the growth of one of the ecotypes are defined. Subsequently, the general linear programming algorithm selects from those states, the one at which the potential growth rate of all ecotypes is maximal and the requirement for the resources is minimal. It can be shown analytically that this method effectively gives equal weight to a high potential growth capacity, as well as to a low requirement for nutrients and light in determining the algal composition of the system in steady state. To prevent unrealistically fast jumps towards such steady-state solutions when BLOOM is embedded in a dynamic model, the realized growth rate of each species is limited to that which is feasible, given temperature and light conditions. Similarly, the model imposes a limit on mortality to prevent unrealistically rapid declines.
Optimization is also at the heart of the approach of structurally dynamic models (Håkanson and Peters 1995; Zhang et al. 2010). From a neo-Darwinian point of view, optimizing principles, such as maximization of exergy in structurally dynamic models, could be questioned, because these principles act at a high integration level and it is not always obvious how to link these principles with individual fitness. An opportunistic argument in favour of optimization would be that in practice these models do better in their confrontation with data than models that lack optimization. Whether this argument remains intact when major changes in environmental pressures occur (e.g., climate change) needs to be tested.
Reusing existing code in other or new models
The majority of models mentioned in this manuscript consists of differential equations. Insofar as these are ordinary differential equations, it is relatively simple to keep the algorithms in which they are coded separate from other model code. The only slight complication arises when the model contains (nested) if–then-else blocks, resulting in multiple definitions of the same variable under different conditions. While this facilitates the readability of the model code, it may spread the right-hand terms for a given variable throughout the code. Therefore, from a perspective of reusability of code the use of conditional statements that combine all assignments for given variable in one line of code might be preferred.
For models built on ordinary differential equations, many standard and reliable integration routines are available (e.g., Press et al. 1992). However, note that complex dynamic models often contain processes that can have very different time scales. The models may hence be rather ‘stiff’, which makes integration not a trivial task. If, in addition, the ordinary differential equations contain discontinuities (if–then statements) standard methods may rather easily generate numerical artefacts that are not obvious.
Insofar as partial differential equations relate to spatial grids, different mathematical integration routines are available, each with their advantages and disadvantages. Moreover, the complexity of these routines usually transcends the mathematical knowledge and skills of ecological modellers and demands involvement of mathematicians. While partial differential equations also are at the heart of physiologically structured models, they demand completely different implementations. Public well-documented libraries for implementing such models are now available (De Roos 2010; Soetaert et al. 2010). Such libraries facilitate the reusability of model code.
Individual-based models are often not well founded in mathematical theory and, in particular, deal with time in a very informal way. By this we mean that the clear separation between the state of the system and the processes that act on these states (a separation that is central to the numerical integration of differential equations) is lacking in individual-based models. This carries the risk that the order in which the model formulations are evaluated has an unknown impact on the model outcome. A more formal embedding in mathematics should be possible because most individual-based models are in fact a very complicated sets of difference equations (i.e., they consist of long lists of stepwise changes in model states). The mostly complicated code structure of individual-based models in practice prohibits the reuse of their code. Recent progress in formalizing the individual-based model approach has been made, however (Grimm et al. 2006).
The model experimentalist
Comparing different model approaches in a systematic and scientific way constitutes an almost unachievable task, as usually more than a single difference exists between two models. It is therefore difficult to attribute emerging differences in model behaviour to specific differences in model structure. However, the standard methodology of an experimental ecologist is to never change more than one factor at the same time, and the same philosophy should hold true for complex models. More scientific insight can be gained when several, competing approaches for specific processes/submodels (e.g., photosynthesis-light model, complexity of higher trophic levels) are implemented in the same model. For example, as Tian (2006) notes, thirteen functions exist for light forcing on phytoplankton growth, five for nutrient limitation, with similar diversity of other key types of processes. The model experimentalist can evaluate these submodels systematically while keeping the remaining model conserved and investigate their effects on the model performance (e.g., Tominaga et al. 2009).
Use of object-oriented programming
Object-oriented programming is increasingly used in many major software development projects, and some object-oriented programming frameworks can be useful in facilitating modular model design and reusability of code. Yet, its use in lake ecosystem modelling is still limited.
The 1-D hydrodynamic model DYRESM has been written following object-oriented programming principles, although care had to be taken for selecting an appropriate object structure for 2- or 3-D hydrodynamic versions of the model because of the computationally demanding nature of the numerical solutions. Moreover, PCLake has been implemented in the object-oriented framework OSIRIS (Mooij and Boersma 1996), but this implementation still does not take full advantage of the potential of the OSIRIS framework.
In contrast to modelling the structure of an ecosystem, Petzoldt and Rinke (2007) proposed a rather general object-oriented model using a state-space formulation of a dynamic system. Here, the object-oriented programming interface represents the model together with its data while preserving full freedom for the core functions. The approach was designed for a convenient implementation of minimal dynamic models in the R language (R Development Core Team 2009), and it allows to establish direct communication between model and solver codes written in compiled languages (Soetaert et al. 2010) to avoid communication overhead. Another development worth mentioning here is the work of Recknagel et al. (2008) and Cao et al. (2008).
The use of object-oriented programming within ecosystem modelling codes will ultimately support the portability and wider integration of them with physical models of different dimensionality. As exemplified within this paper, depending on site geography and the scientific basis for the modelling study, a number of hydrodynamic solvers are relevant even though the underlying biogeochemical and ecological parameterizations are common. Standards for model coupling and communication (e.g., OpenMI, http://www.openmi.org) and object-oriented programming code standards will allow transferability of model components to a wider range of applications.
Integrating individual-based models with models based on differential equations
It is now widely acknowledged that individual variation and behaviour cannot be ignored when looking in detail at higher trophic levels (DeAngelis and Mooij 2005). Fish populations are highly size structured, while birds often perform seasonal migration. These aspects are easily incorporated in individual-based models. While there are no major technical obstacles that prohibit the integration of stage-structured biomass models or physiologically structured population models of fish in complex ecosystem models, we are not aware of successful attempts to do so yet. Such developments would also be desirable for zooplankton, where size-structured interactions are known to be critically important for the dynamics of the system (Hülsmann et al. 2010).
For models based on super-individuals, the situation is conceptually more complex because, as outlined above, these employ a fundamentally different mathematical approach which is less suitable for integration in models that are based on differential equations and focus on the conservation of mass. The Lake Kinneret example by Makler-Pick (2010), however, does suggest that this approach is possible and can be further developed where field data are available. Another example is found in modelling approaches that link individual-based models of fish larvae with nutrient-phytoplankton-zooplankton chains (e.g., Hermann et al. 2001).
Model documentation and copyrights on source code
We take the point of view that for the progress of science it is essential that the source code in which the mathematical formulations of the model are turned into a working model is free of copyrights and fully documented to the level where the model can be re-implemented on the basis of the documentation, of course accompanied by a proper citation. We can understand some level of copyright protection, for example, related to the shell in which the model runs and the user interface through which it is operated. Full openness in the code, however, will ultimately allow scientists to interrogate the nuances of the numerical algorithms adopted to solve the differential equations in which the model is formulated. This openness serves two purposes. First, it allows for a completely transparent and ongoing evaluation of the correctness of the model. Second, and more importantly, it allows for an easy reimplementation of parts of the model into new models, and this will ultimately facilitate more rapid advance in model developments and associated applications. These new models can be of the same type, or of hybrid types (e.g., a complex dynamic model with a stage/physiologically structured fish or zooplankton module). Openness of source code thus can provide essential technical support to avoid both ‘reinventing the wheel’ and ‘having tunnel vision’.
Challenges and opportunities: recommendations
We would like to finish this paper with a list of practical and hopefully unpresumptuous recommendations that—we believe—may be of help in the further development of lake ecosystem models.
General
-
While acknowledging ongoing initiatives like the Register of Ecological Models (REM, http://www.ecobas.org, Benz et al. 2001), we feel that there is a need for more common venues for the lake ecosystem modelling community (e.g., workshops, conferences and/or a community website) to generate exposure to the scientific world, policy makers, water quality managers and funding agencies, to enhance awareness of models and model approaches and to transcend individual differences that keep us apart.
-
Once a model and its results have been published and can be properly cited, the code describing the process formulations should not be protected by copyrights and should be easily accessible in order to allow easier exchange and integration of different models, to facilitate comparison of different model approaches for the same problem and to allow for an ongoing assessment of the validity of the models.
-
Improved availability of global and regional datasets is important, but a better collaboration between data collectors and data users is equally important to warrant correct interpretation of the data in meta-analysis and further model development and validation.
Ecological
-
The importance of top–down control by fish and as a determinant of the state of aquatic ecosystems is greater than it is generally assumed, and there is a need to incorporate these impacts in lake ecosystem models.
-
When incorporating fish, but also with respect to zooplankton, attempts should be made when observation data allow this to represent them in a size- or stage-structured manner since size- or stage-structured interactions may be fundamental to the dynamics of the system.
-
The process of sediment diagenesis as a determinant of the state of aquatic ecosystems is generally overly simplified or neglected altogether, and there is a need to improve this aspect of lake ecosystem models.
-
There is an urgent need to focus more on biodiversity in lake ecosystem models. One of the ways to achieve this is by linking empirically based relationships to output from the dynamic models, such as total phosphorous and chlorophyll-a.
Conceptual and technical
-
Reuse of eutrophication models for studying climate change is a logical step but should be done with great care, because the validity of the outcomes has generally not yet been properly tested against empirical data, and field studies show clear synergistic effects that are not well covered by existing models.
-
Ongoing change in natural systems demands the inclusion of adaptive processes in lake ecosystem models.
-
There is an urgent need to find ways to integrate models focussing on spatial dynamics, hydrology and lower trophic levels with models that focus on the whole food web.
-
Sensitivity analysis, calibration and uncertainty analysis is not a one-time exercise but should rather be an ongoing effort within a modelling programme.
-
During model calibration and validation, we should focus not only on state variables but also on process rates.
-
Metamodels provide a powerful tool to bridge the gap between state-of-the-art dynamic models and easy-to-use static models.
-
In general, we believe that it will be fruitful to combine current dynamic and static model approaches.
-
In addition to detailed analyses, it is important to study the general non-linear behaviour of complex models using high level input and output parameters (e.g., P-loading and chlorophyll-a concentration).
-
IBM approaches to lake ecosystems should give more attention to a proper handling of time and mass balances.
-
We promote the modularity of source code through object-oriented programming on an adequate level while preserving efficiency, readability and portability of code.
Concluding remarks
In this paper, we identify two challenges for making further progress in lake ecosystem modelling: to avoid in future work ‘reinventing the wheel’ and ‘having tunnel vision’. While this may sound trivial and has been stated before, the continuing repetition in published models and the fragmentation of the field of lake ecosystem modelling as a whole brings us to restating them and stressing their importance as we did in this paper. We do not think that the main solution is in technically linking all kinds of models. Instead, we believe that applying multiple modelling approaches concurrently, using existing models and model components, can help to develop an integrative scientific view on the functioning of lake ecosystems and to provide managers with essential ecological information for water quality management.
References
Abrams PA, Matsuda H (1997) Fitness minimization and dynamic instability as a consequence of predator-prey coevolution. Evol Ecol 11:1–20
Aegis (2001) ACSL Reference manual, v. 1.1; ACSL/MATH User manual, v. 2.5; ACSL/MATH Reference manual, v. 2.5; ACSL/MATH Installation guide, v. 2.5
Aldenberg T, Janse JH, Kramer PRG (1995) Fitting the dynamic model PCLake to a multi-lake survey through Bayesian Statistics. Ecol Modell 78:83–99
Alkemade R, Van Oorschot M, Miles L, Nellemann C, Bakkenes M, Ten Brink B (2009) GLOBIO3: a framework to investigate options for reducing global terrestrial biodiversity loss. Ecosystems 12:374–390
Alkemade R, Janse JH, Van Rooij W, Trisurat Y (2010) Applying GLOBIO at different geographical levels. In: Trisurat Y, Shrestha RP, Alkemade R (eds) Global land use, climate change and biodiversity modelling: perspectives and applications. IGI (in press)
Allen JI, Eknes M, Evensen G (2003) An ensemble Kalman Filter with a complex marine ecosystem model: hind casting phytoplankton in the Cretan Sea. Ann Geophys 21:399–411
Amarasinghe US, Welcomme RL (2002) An analysis of fish species richness in natural lakes. Environ Biol Fish 65:327–339
Arhonditsis GB, Brett MT (2004) Evaluation of the current state of mechanistic aquatic biogeochemical modelling. Mar Ecol Prog Ser 271:13–26
Arhonditsis GB, Qian SS, Stow CA, Lamon EC, Reckhow KH (2007) Eutrophication risk assessment using Bayesian calibration of process-based models: application to a mesotropic lake. Ecol Modell 208:215–229
Bachmann RW, Jones BL, Fox DD, Hoyer M, Bull LA, Canfield DE (1996) Relationship between trophic state indicators and fish biomass in Florida (USA) lakes. Can J Fish Aquat Sci 53:842–855
Bachmann RW, Horsburgh CA, Hoyer MV, Mataraza LK, Canfield DE (2002) Relations between trophic state indicators and plant biomass in Florida lakes. Hydrobiologia 470:219–234
Baird ME, Suthers IM (2007) A size-resolved pelagic ecosystem model. Ecol Modell 203:185–203
Baumert HZ, Benndorf J, Bigalke K, Goldmann D, Nöhren I, Petzoldt Y, Post J, Rolinski S (2005) Das hydrophysikalisch ökologische Talsperren- und Seenmodel SALMO-HR–Modelldokumentation und Leitfaden für den Anwender. Dresden, www.baufachinformation.de/literatur.jsp?bu=2007029013557
Belolipetsky PV, Belolipetskii VM, Genova SN, Mooij WM (2010) Numerical modelling of vertical stratification of Shira Lake in summer. Aquat Ecol (this issue). doi:10.1007/s10452-010-9330-z
Benndorf J (1995) Possibilities and limits for controlling eutrophication by biomanipulation. Int Rev Gesamten Hydrobiol 80:519–534
Benndorf J, Recknagel F (1982) Problems of application of the ecological model SALMO to lakes and reservoirs having various trophic states. Ecol Modell 17:129–145
Benz J, Hoch R, Legovic T (2001) ECOBAS–modelling and documentation. Ecol Modell 138:3–15
Berger C, Wells S (2008) Modeling the effects of macrophytes on hydrodynamics. J Environ Eng 134:778–788
Blanck A, Lammouroux N (2007) Large-scale intraspecific variation in life-history traits of European freshwater fish. J Biogeogr 34:862–875
Blauw AN, Los FJ, Huisman J, Peperzak L (2010). Nuisance foam events and Phaeocystis globosa blooms in Dutch coastal waters analyzed with fuzzy logic. J Mar Syst. doi: 10.1016/j.jmarsys.2010.05.003
Boudreau BP (1996) A method-of-lines code for carbon and nutrient diagenesis in aquatic sediments. Comput Geosci 22:479–496
Bowen JD, Hieronymous JW (2003) A CE-QUAL-W2 model of neuse estuary for total maximum daily load development. J Water Resour Plann Manage 129:283–294
Bruce LC, Hamilton D, Imberger J, Gal G, Gophen M, Zohary T, Hambright KD (2006) A numerical simulation of the role of zooplankton in C, N and P cycling in Lake Kinneret, Israel. Ecol Modell 193:412–436
Burger DF, Hamilton DP, Pilditch CA (2007) Modelling the relative importance of internal and external nutrient loads on water column nutrient concentrations and phytoplankton biomass in a shallow polymictic lake. Ecol Modell 211:411–423
Canfield DE, Bachmann RW (1981) Prediction of total phosphorus concentrations, chlorophyll a, and Secchi depths in natural and artificial lakes. Can J Fish Aquat Sci 38:414–423
Cao HQ, Recknagel F, Joo GJ, Kim DK (2006) Discovery of predictive rule sets for chlorophyll-a dynamics in the Nakdong River (Korea) by means of the hybrid evolutionary algorithm HEA. Ecol Informatics 1:43–53
Cao HQ, Recknagel F, Cetin L, Zhang B (2008) Process-based simulation library SALMO-OO for lake ecosystems. Part 2: multi-objective parameter optimization by evolutionary algorithms. Ecol Informatics 3:181–190
Carpenter SR, Ludwig D, Brock WA (1999) Management of eutrophication for lakes subject to potentially irreversible change. Ecol Appl 9:751–771
Casulli V, Cattani E (1994) Stability, accuracy and efficiency of a semi-implicit method for three-dimensional shallow water flow. Comput Math Appl 27:99–112
Casulli V, Cheng RT (1992) Semi-implicit finite difference methods for three-dimensional shallow water flow. Int J Numer Methods Fluids 15:629–648
Chambers PA, Kalff J (1985) Depth distribution and biomass of submersed aquatic macrophyte communities in relation to Secchi depth. Can J Fish Aquat Sci 42:701–709
Chan WS, Recknagel F, Cao HQ, Park HD (2007) Elucidation and short-term forecasting of microcystin concentrations in Lake Suwa (Japan) by means of artificial neural networks and evolutionary algorithms. Water Res 41:2247–2255
Chapra SC (1975) Comment on ‘An empirical method of estimating the retention of phosphorus in lakes’ by W. B. Kirchner and P. J. Dillon. Water Resour Res 11:1033–1034
Chapra SC (1997) Surface water-quality modeling. McGraw-Hill Series in Water Resources and Environmental Engineering. 844 pp
Chapra SC, Reckhow KH (1983) Engineering approaches for lake management, vol 2. Mechanistic modeling. Butterworth Publishers, Stoneham
Christensen V, Pauly D (1993) Trophic models of aquatic ecosystems. ICLARM Conf. Proc. Int. Center for Living Resources Management, Manila
Chung SW, Oh JK (2006) Calibration of CE-QUAL-W2 for a monomictic reservoir in a monsoon climate area. Water Sci Technol 54:29–37
Chung SW, Hipsey MR, Imberger J (2009) Modelling the propagation of turbid density inflows into a stratified lake: Daecheong Reservoir, Korea. Environ Modell Softw 24:1467–1482
Claessen D, De Roos AM, Persson L (2000) Dwarfs and giants: cannibalism and competition in size-structured populations. Am Nat 155:219–237
Cole TM, Wells SA (2008) CE-QUAL-W2: s two-dimensional, laterally averaged, hydrodynamic and water quality model, version 3.6. Department of Civil and Environmental Engineering, Portland State University, Portland
De Meester L, Declerck S, Janse JH, Dagevos JJ, Portielje R, Lammens EHRR, Jeppesen E, Lauridsen T, Schwenk K, Muylaert K, Van Der Gucht K, Vyverman W, Zwart G, Van Hannen E, Van Puijenbroek PJTM, Conde-Porcuna JM, Sánchez-Castillo P, Vandekerkhove J, Brendonck L (2006) Biodiversity in European shallow lakes: a multilevel–multifactorial field study. In: Bobbink R, Verhoeven JTA (eds) Wetlands as a natural resource, vol. 2. Wetlands: functioning, biodiversity conservation and restoration, Ecological Studies 191. Springer, Berlin, pp 149–167
De Roos (2010) EBT software. http://staff.science.uva.nl/~aroos/EBTsoftware.htm
De Roos AM, Persson L (2001) Physiologically structured models–from versatile technique to ecological theory. Oikos 94:51–71
De Roos AM, McCauley E, Wilson WG (1991) Mobility versus density-limited predator-prey dynamics on different spatial scales. Proc R Soc Lond B 246:117–122
De Roos AM, Diekmann O, Metz JAJ (1992) Studying the dynamics of structured population models: a versatile technique and its application to Daphnia. Am Nat 139:123–147
De Roos AM, Schellekens T, Van Kooten T, Van De Wolfshaar K, Claessen D, Persson L (2008) Simplifying a physiologically structured population model to a stage-structured biomass model. Theor Popul Biol 73:47–62
De Senerpont Domis LN, Mooij WM, Hülsmann S, Van Nes EH, Scheffer M (2007) Can overwintering vs diapausing strategy in Daphnia determine match-mismatch events in zooplankton-algae interactions? Oecologia 150:682–698
DeAngelis DL, Mooij WM (2005) Individual-based models of ecological and evolutionary processes. Annu Rev Ecol Evol Syst 36:147–168
Debele B, Srinivasan R, Parlange J-Y (2006) Coupling upland watershed and downstream waterbody hydrodynamic and water quality models (SWAT and CE-QUAL-W2) for better water resources management in complex river basins. Environ Modell Assess 13:135–153
Declerck S, Vanderstukken M, Pals A, Muylaert K, De Meester L (2007) Plankton biodiversity along a gradient of productivity and its mediation by macrophytes. Ecology 88:2199–2210
Degermendzhi AG, Zadereev ES, Rogozin DYu, Prokopkin IG, Barkhatov YV, Tolomeyev AP, Khromechek EB, Janse JH, Mooij WM, Gulati RD (2010) Vertical stratification of physical, chemical and biological components in two saline lakes Shira and Shunet (South Siberia, Russia). Aquat Ecol (this issue). doi:10.1007/s10452-010-9336-6
Deliman PN, Gerald JA (2002) Application of the two-dimensional hydrothermal and water quality model, CE-QUAL-W2, to the Chesapeake Bay–Conowingo Reservoir. Lake Reservoir Manage 18:10–19
Dillon PJ, Rigler FH (1974) The phosphorus-chlorophyll relationships in lakes. Limnol Oceanogr 19:767–773
Downing JA, Plante C, Lalonde S (1990) Fish production correlated with primary production, not the mophoedaphic index. Can J Fish Aquat Sci 47:1929–1936
Downing JA, Watson SB, McCauley E (2001) Predicting cyanobacteria dominance in lakes. Can J Fish Aquat Sci 58:1905–1908
Drenner RW, Hambright KD (1999) Biomanipulation of fish assemblages as a lake restoration technique. Archiv für Hydrobiologie 146:129–165
EPAP, Ecosystem Principles Advisory Panel (1999) Ecosystem based fishery management. NOAA National Marine Fisheries Service, Silver Spring, MD. http://www.nmfs.noaa.gov/sfa/EPAPrpt.pdf
Elliott JA, Irish AE, Reynolds CS (2010) Modelling phytoplankton dynamics in fresh waters: affirmation of the PROTECH approach to simulation. Freshw Rev 3:75–96
Fitz HC, DeBellevue EB, Costanza R, Boumans R, Maxwell T, Wainger L, Sklar FH (1996) Development of a general ecosystem model for a range of scales and ecosystems. Ecol Modell 88:263–295
Flynn KJ (2005) Castles built on sand: dysfunctionality in plankton models and the inadequacy of dialogue between biologists and modellers. J Plankton Res 27:1205–1210
Forbes SA (1887) The lake as a microcosm. Bull Sci Assoc, Peoria, Illinois, pp 77–87. Reprinted in Illinois Natural History Survey Bulletin 15:537–550
Fragoso CR Jr, Van Nes EH, Janse JH, Da Motta Marques D (2009) IPH-TRIM3D-PCLake: a three-dimensional complex dynamic model for subtropical aquatic ecosystems. Environ Modell Softw 24:1347–1348
Gal G, Hipsey MR, Parparov A, Wagner U, Makler V, Zohary T (2009) Implementation of ecological modelling as an effective management and investigation tool: Lake Kinneret as a case study. Ecol Modell 220:1697–1718
Genova SN, Belolipetskii VM, Rogozin DY, Degermendzhy AG, Mooij WM (2010) A one-dimensional model of vertical stratification of Lake Shira focussed on winter conditions and ice cover. Aquat Ecol (this issue). doi:10.1007/s10452-010-9327-7
Grimm V (1994) Mathematical models and understanding in ecology. Ecol Modell 75(76):641–651
Grimm V, Revilla E, Berger U, Jeltsch F, Mooij WM, Railsback SF, Thulke J-H, Weiner J, Wiegand T, DeAngelis DL (2005) Pattern-oriented modelling of agent-based complex systems: lessons from ecology. Science 310:987–991
Grimm V, Berger U, Bastiansen F, Eliassen S, Ginot V, Giske J, Goss-Custard J, Grand T, Heinz S, Huse G, Huth A, Jepsen JU, Jørgensen C, Mooij WM, Müller B, Pe’er G, Piou C, Railsback SF, Robbins AM, Robbins MM, Rossmanith E, Rüger N, Strand E, Souissi S, Stillmann R, Vabø R, Visser U, DeAngelis DL (2006) A standard protocol for describing individual-based and agent-based models. Ecol Modell 198:115–126
Gulati RD, Van Donk E (2002) Lakes in the Netherlands, their origin, eutrophication and restoration: state-of-the-art review. Hydrobiologia 478:73–106
Gulati RD, Lammens EHHR, Meijer M-L, Van Donk E (1990) Biomanipulation, tool for water management. Hydrobiologia 200(201):1–628
Gulati RD, Siewertsen K, Van Liere L (1991) Carbon and phosphorus relationship of zooplankton and its seston food in Loosdrecht lakes. Memorie dell’Istituto Italiano di Idrobiologia 48:279–298
Gunderson LH (2000) Ecological resilience–in theory and application. Annu Rev Ecol Syst 31:425–439
Håkanson L (2000) Modelling radiocesium in lakes and coastal areas–new approaches for ecosystem modellers. A textbook with Internet support. Kluwer, Dordrecht, p 215
Håkanson L (2006) Suspended particulate matter in lakes, rivers and marine systems. The Blackburn Press, New Jersey, p 331
Håkanson L, Boulion V (2002) The Lake Foodweb–modelling predation and abiotic/biotic interactions. Backhuys Publishers, Leiden, p 344
Håkanson L, Peters RH (1995) Predictive limnology–methods for predictive modelling. SPB Academic Publishers, Amsterdam, p 464
Håkanson L, Bryhn AC, Hytteborn JK (2007) On the issue of limiting nutrient and predictions of cyanobacteria in aquatic systems. Sci Total Environ 379:89–108
Hall SJ, Mainprize B (2004) Towards ecosystem-based fisheries management. Fish Fish 5:1–20
Hamilton DP (1999) Numerical modelling and lake management: applications of the DYRESM model. In: Tundisi JG, Straskraba M (eds) Theoretical reservoir ecology and its applications. Backhuys Publishers, The Netherlands, pp 153–174
Hamilton DP, Mitchell SF (1996) An empirical model for sediment resuspension in shallow lakes. Hydrobiologia 317:209–220
Hamilton DP, Mitchell SF (1997) Wave-induced shear stresses, plant nutrients and chlorophyll in seven shallow lakes. Freshw Biol 38:159–168
Hanson JM, Leggett WC (1982) Empirical prediction of fish biomass and weight. Can J Fish Aquat Sci 39:257–263
Hanson JM, Peters RH (1984) Empirical prediction of crustacean zooplankton biomass and profundal macrobenthos biomass in lakes. Can J Fish Aquat Sci 41:439–445
Hanson PC, Carpenter SR, Kimura N, Wu C, Cornelius SP, Kratz TK (2008) Evaluation of metabolism models for free-water dissolved oxygen methods in lakes. Limnol Oceanogr Methods 6:454–465
Hansson L-A, Annadotter H, Bergman E, Hamrin SF, Jeppesen E, Kairesalo T, Luokkanen E, Nilsson P-Å, Søndergaard M, Strand J (1998) Biomanipulation as an application of food-chain theory: constraints, synthesis, and recommendations for temperate lakes. Ecosystems 1:558–574
Hardy FJ, Shortreed KS, Stockner JG (1986) Bacterioplankton, phytoplankton and zooplankton communities in a British Columbia Coastal lake before and after nutrient reduction. Can J Fish Aquat Sci 43:1504–1514
Harper D (1992) Eutrophication of freshwaters: principles, problems and restoration. Chapman & Hall, London
Harris GP (1994) Pattern, process and prediction in aquatic ecology–a limnological view of some general ecological problems. Freshw Biol 32:143–160
Hermann AJ, Hinckley S, Megrey BA, Napp JM (2001) Applied and theoretical considerations for constructing spatially explicit individual-based models of marine larval fish that include multiple trophic levels. ICES J Mar Sci 58:1030–1041
Hipsey MR, Hamilton DP (2008) Computational aquatic ecosystem dynamic model: CAEDYM v3 science manual. Centre for Water Research Report, University of Western Australia, Nedlands
Hipsey MR, Antenucci JP, Brookes JD (2008) A generic, process-based model of microbial pollution in aquatic systems. Water Resour Res, 44: W07408, 26 pp
Hirsch C (1990) Numerical computation of internal and external flows, vol 2. Computational methods for inviscid and viscous flows, 1st edn. Wiley, Chichester
Hoyer MV, Canfield DE (1994) Bird abundance and species richness on Florida lakes: influence of trophic status, lake morphology, and aquatic macrophytes. Hydrobiologia 279/280:107–119
Huisman J, Weissing FJ (1999) Biodiversity of plankton by species oscillations and chaos. Nature 402:407–410
Hülsmann S, Rinke K, Mooij WM (2005) A quantitative test of the size efficiency hypothesis by means of a physiologically structured model. Oikos 100:43–54
Hülsmann S, Rinke K, Mooij WM (2010) Size-selective predation and predator-induced life history shifts alter the outcome of competition between planktonic grazers. Funct Ecol. doi: 10.1111/j.1365-2435.2010.01768.x
Huston M, DeAngelis D, Post W (1988) New computer models unify ecological theory. Bioscience 38:682–691
Ibelings BW, Vonk M, Los FJ, Van Der Molen DT, Mooij WM (2003) Fuzzy modeling of cyanobacterial surface waterblooms, validation with NOAA-AVHRR satellite images. Ecol Appl 13:1456–1472
IPCC (2007) Climate change 2007: impacts, adaptation and vulnerability. In: Parry ML et al (eds) Contribution of working group II to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Janse JH (1997) A model of nutrient dynamics in shallow lakes in relation to multiple stable states. Hydrobiologia 342:1–8
Janse JH (2005) Model studies on the eutrophication of shallow lakes and ditches. PhD thesis, Wageningen University, Wageningen. (Available at http://edepot.wur.nl/121663)
Janse JH, Van Liere L (1995) PCLake–a modeling tool for the evaluation of lake restoration scenarios. Water Sci Technol 31:371–374
Janse JH, Van Puijenbroek PJTM (1998) Effects of eutrophication in drainage ditches. Environ Pollut 102(S1):547–552
Janse JH, Aldenberg T, Kramer PRG (1992) A mathematical-model of the phosphorus cycle in Lake Loosdrecht and simulation of additional measures. Hydrobiologia 233:119–136
Janse JH, Van der Does J, Van der Vlugt JC (1993) PCLake: modelling eutrophication and its control measures in Reeuwijk Lakes. In: G Giussani and C Callieri (eds.), Proceedings 5th International Conference on the Conservation and Management of Lakes, Stresa (Italy) pp 117–120
Janse JH, Van Donk E, Gulati RD (1995) Modelling nutrient cycles in relation to food-web structure in a biomanipulated shallow lake. Netherlands J Aquat Ecol 29:67–79
Janse JH, Ligtvoet W, Van Tol S, Bresser AHM (2001) A model study on the role of wetland zones in lake eutrophication and restoration. TheScientificWorldJournal [electronic resource] 1(S2):605–614
Janse JH, Schep S, Klinge M, Witmer MCH (2006) Metamodel PCLake, http://www.pbl.nl/nl/dossiers/water/modellen/WerkingModelPCLake.html
Janse JH, De Senerpont Domis LN, Scheffer M, Lijklema L, Van Liere L, Klinge M, Mooij WM (2008) Critical phosphorous loading of different types of shallow lakes and the consequences for management estimated with the ecosystem model PCLake. Limnologica 38:203–219
Janse JH, Scheffer M, Lijklema L, Van Liere L, Sloot JS, Mooij WM (2010) Estimating the critical phosphorus loading of shallow lakes with the ecosystem model PCLake: sensitivity, calibration and uncertainty. Ecol Modell 221:654–665
Jeppesen E, Jensen JP, Søndergaard M, Lauridsen TL, Pedersen LJ, Jensen L (1997) Top-down control in freshwater lakes: the role of nutrient state, submerged macrophytes and water depth. Hydrobiologia 342/343:151–164
Jeppesen E, Søndergaard M, Christoffersen K (eds) (1998) The structuring role of submerged macrophytes in lakes. Springer, New York, p 452
Jeppesen E, Jensen JP, Søndergaard M, Lauridsen T, Landkildehus F (2000) Trophic structure, species richness and biodiversity in Danish lakes: changes along a phosphorus gradient. Freshw Biol 45:201–218
Jeppesen E, Søndergaard M, Jensen JP (2003) Climatic warming and regime shifts in lake food webs–some comments. Limnol Oceanogr 48:1346–1349
Jeppesen E, Søndergaard M, Jensen JP, Havens KE, Anneville O, Carvalho L, Coveney MF, Deneke R, Dokulil MT, Foy B, Gerdeaux D, Hampton SE, Hilt S, Kangur K, Köhler J, Lammens EHRR, Lauridsen TL, Manca M, Miracle MR, Moss B, Nõges P, Persson G, Phillips G, Portielje R, Romo S, Schelske CL, Straile D, Tatrai I, Willén E, Winder M (2005) Lake responses to reduced nutrient loading- an analysis of contemporary long-term data from 35 case studies. Freshw Biol 50:1747–1771
Jeppesen E, Meerhoff M, Jacobsen BA, Hansen RS, Søndergaard M, Jensen JP, Lauridsen TL, Mazzeo N, Branco CWC (2007) Restoration of shallow lakes by nutrient control and biomanipulation–the successful strategy varies with lake size and climate. Hydrobiologia 581:269–285
Jeppesen E, Kronvang B, Meerhoff M, Søndergaard M, Hansen KM, Andersen HE, Lauridsen TL, Beklioglu M, Ozen A, Olesen JE (2009) Climate change effects on runoff, catchment phosphorus loading and lake ecological state, and potential adaptations. J Environ Qual 38:1930–1941
Jeppesen E, Meerhoff M, Holmgren K, González-Bergonzoni I, Teixeira-De Mello F, Declerck SAJ, De Meester L, Søndergaard M, Lauridsen TL, Bjerring R, Conde-Porcuna JM, Mazzeo N, Iglesias C, Reizenstein M, Malmquist HJ, Liu ZW, Balayla D, Lazzaro X (2010) Impacts of climate warming on lake fish community structure and potential effects on ecosystem function. Hydrobiologia 646:73–90
Jones JR, Bachmann RW (1976) Prediction of phosphorus and chlorophyll levels in lakes. J Water Pollut Control Fed 48:2176–2182
Jørgensen SE (1995) State-of-the-art of ecological modelling in limnology. Ecol Modell 78:101–115
Jørgensen SE (1999) State-of-the-art of ecological modelling with emphasis on development of structural dynamic models. Ecol Modell 120:75–96
Jørgensen SE (2008) Overview of the model types available for development of ecological models. Ecol Modell 215:3–9
Jørgensen SE (2010) A review of recent developments in lake modelling. Ecol Modell 221:689–692
Jørgensen SE, Bendoricchio G (2001) Fundamentals of ecological modelling, 3rd edn. Elsevier, Amsterdam
Jørgensen SE, Kamp-Nielsen L, Mejer HF (1982) Comparison of a simple and a complex sediment phosphorus model. Ecol Modell 16:99–124
Jørgensen SE, Halling-Sørensen B, Nielsen SN (1995) Handbook of environmental and ecological modeling. CRS Lewis Publishers, Boca Raton
Kankaala P, Huotari J, Peltomaa E, Saloranta T, Ojala A (2006) Methanotrophic activity in relation to methane efflux and total heterotrophic bacterial production in a stratified, humic, boreal lake. Limnol Oceanogr 51:1195–1204
Kirchner WB, Dillon PJ (1975) An empirical method of estimating the retention of phosphorus in lakes. Water Resour Res 11:182–183
Kitchell JF, Cox SP, Harvey CJ, Johnson TB, Mason DM, Schoen KK, Aydin K, Bronte C, Ebener M, Hansen M, Hoff M, Schram S, Schreiner D, Walters CJ (2000) Sustainability of the Lake Superior fish community: Interactions in a food web context. Ecosystems 3:545–560
Kohavi R. (1995) A study of cross-validation and bootstrap for accuracy estimation and model selection. In: Proceedings of the Fourteenth International Joint Conference on Artificial Intelligence. Morgan Kaufmann, San Mateo, California pp 1137–1143
Kooijman SALM (2000) Dynamic energy and mass budgets in biological systems, 2nd edn. Cambridge University Press, Cambridge
Kosten S, Kamarainen A, Jeppesen E, Van Nes EH, Peeters ETHM, Mazzeo N, Sass L, Hauxwell J, Hansel-Welch N, Lauridsen TL, Søndergaard M, Bachmann RW, Lacerot G, Scheffer M (2009) Likelihood of abundant submerged vegetation growth in shallow lakes differs across climate zones. Glob Chang Biol 15:2503–2517
Kuo J-T, Lung W-S, Yang C-P, Liu W-C, Yang M-D, Tang T-S (2006) Eutrophication modelling of reservoirs in Taiwan. Environ Modell Softw 21:829–844
Kuo J-T, Liu W-C, Lin R-T, Lung W-S, Yang M-D, Yang C-P, Chu S-C (2007) Water quality modeling for the Feitsui reservoir in northern Taiwan. J Am Water Resour Assoc 39:671–687
Kuznetsov YA (1995) Elements of applied bifurcation theory. Springer, New York, p 591
Laanemets J, Lilover MJ, Raudsepp U, Autio R, Vahtera E, Lips I, Lips U (2006) A fuzzy logic model to describe the cyanobacteria Nodularia spumigena blooms in the Gulf of Finland, Baltic Sea. Hydrobiologia 554:31–45
Lammens EHRR, Van Nes EH, Mooij WM (2002) Differences in the exploitation of bream in three shallow lake systems and their relation to water quality. Freshw Biol 47:2435–2442
Larigauderie A, Mooney HA (2010) The Intergovernmental science-policy Platform on Biodiversity and Ecosystem Services: moving a step closer to an IPCC-like mechanism for biodiversity. Curr Opin Environ Sustainability 2:9–14
Larsen DP, Mercier HT (1976) Phosphorus retention capacity of lakes. J Fish Res Board Can 33:1742–1750
Leibold MA (1999) Biodiversity and nutrient enrichment in pond plankton communities. Evol Ecol Res 1:73–95
Leon LF, Smith REH, Hipsey MR, Bocaniov SN, Higgins SN, Hecky RE, Antenucci JP, Guildford SJ (2010) Application of a 3D hydrodynamic-biological model for seasonal and spatial dynamics of water quality and phytoplankton in Lake Erie. J Great Lakes Res (in press)
Leppäranta M (1993) A review of analytical models of sea-ice growth. Atmosphere-Ocean 31:123–138
Levins R (1966) The strategy of model building in population biology. Am Sci 54:421–431
Lewis DM, Brookes JD, Lambert MF (2004) Numerical models for management of Anabaena circinalis. J Appl Phycol 16:457–468
Li YK, Song B, Chen Y, Chen LQ, Yu N, Olson D (2010) Changes in the trophic interactions and the community structure of Lake Taihu (China) ecosystem from the 1960s to 1990s. Aquat Ecol 44:337–348
Litchman E, Klausmeier CA, Schofield OM, Falkowski PG (2007) The role of functional traits and trade-offs in structuring phytoplankton communities: scaling from cellular to ecosystem level. Ecol Lett 10:1170–1181
Los FJ (2009) Eco-hydrodynamic modelling of primary production in coastal waters and lakes using BLOOM. PhD thesis, Wageningen University, Wageningen. (Available at http://edepot.wur.nl/1249)
Lydersen E, Aanes KJ, Andersen S, Andersen T, Brettum P, Bækken T, Lien L, Lindstrøm EA, Løvik JE, Mjelde M, Oredalen TJ, Lyche AS, Ropmstad R, Rørslett B, Saloranta T (2003) THERMOS-projektet: Fagrapport 1998-2002. NIVA rapport 4720-2003. Norwegian Institute for Water Research, Oslo, Norway 119 pp. (in Norwegian)
MacKay MD, Neale PJ, Arp CD, De Senerpont Domis LN, Fang X, Gal G, Jöhnk K, Kirillin G, Lenters JD, Litchman E, MacIntyre S, Marsh P, Melack J, Mooij WM, Peeters F, Quesada A, Schladow SG, Schmid M, Spence C, Stokes SL (2009) Modelling lakes and reservoirs in the climate system. Limnol Oceanogr 54:2315–2329
Makler-Pick V (2010) A computer ecosystem model applied to studying the food web and water quality of Lake Kinneret, with emphasis on topdown control. PhD thesis, Faculty of Civil and Environmental Engineering, Technion, Haifa, Israel
Makler-Pick V, Gal G, Gorfine M, Hipsey MR, Carmel Y (2010) Sensitivity analysis for complex ecological models–a new approach. Environ Modell Softw doi: 10.1016/j.envsoft.2010.06.010
Mao JQ, Lee JHW (2009) The extended Kalman filter for forecast of algal bloom dynamics. Water Res 43:4214–4224
MEA (2005) Inland Water Systems. In: Millennium ecosystem assessment, ecosystems and human well-being: current state and trends, vol 1, Chap 20:551–584
Meerhoff MM, Clemente FTM, Iglesias C, Pedersen AR, Jeppesen E (2007) Can warm climate-related structure of littoral predator assemblages weaken the clear water state in shallow lakes? Glob Chang Biol 13:1888–1897
Meijer M-L (2000) Biomanipulation in the Netherlands: 15 years of experience. PhD thesis, Wageningen University, Wageningen
Merico A, Bruggeman J, Wirtz K (2009) A trait-based approach for downscaling complexity in plankton ecosystem models. Ecol Modell 220:3001–3010
Metz JAJ, Diekmann O (1986) The dynamics of physiologically structured populations. Springer, New York
Mooij WM (1996) Variation in abundance and survival of larval fish in shallow eutrophic lake Tjeukemeer. Environ Biol Fish 46:265–279
Mooij WM, Boersma M (1996) An object-oriented simulation framework for individual-based simulations (OSIRIS): Daphnia population dynamics as an example. Ecol Modell 93:139–153
Mooij WM, DeAngelis DL (1999) Error propagation in spatially explicit population models: a reassessment. Conserv Biol 13:930–933
Mooij WM, DeAngelis DL (2003) Uncertainty in spatially explicit animal dispersal models. Ecol Appl 13:794–805
Mooij WM, Hülsmann S, Vijverberg J, Veen A, Lammens EHRR (2003) Modeling Daphnia population dynamics and demography under natural conditions. Hydrobiologia 491:19–34
Mooij WM, Hülsmann S, De Senerpont Domis LN, Nolet BA, Bodelier PLE, Boers PCM, Dionisio Pires LM, Gons HJ, Ibelings BW, Noordhuis R, Portielje R, Wolfstein K, Lammens EHRR (2005) The impact of climate change on lakes in the Netherlands: a review. Aquat Ecol 39:381–400
Mooij WM, Janse JH, De Senerpont Domis LN, Hülsmann S, Ibelings BW (2007) Predicting the effect of climate change on temperate shallow lakes with the ecosystem model PCLake. Hydrobiologia 584:443–454
Mooij WM, De Senerpont Domis LN, Hülsmann S (2008) The impact of climate warming on water temperature, timing of hatching and young-of-the-year growth of fish in shallow lakes in the Netherlands. J Sea Res 60:32–43
Mooij WM, De Senerpont Domis LN, Janse JH (2009) Linking species- and ecosystem-level impacts of climate change in lakes with a complex and a minimal model. Ecol Modell 220:3011–3020
Moss B, Mckee D, Atkinson D, Collings SE, Eaton JW, Gill AB, Harvey I, Hatton K, Heyes T, Wilson D (2003) How important is climate? Effects of warming, nutrient addition and fish on phytoplankton in shallow lake microcosms. J Appl Ecol 40:782–792
Norberg J (2004) Biodiversity and ecosystem functioning: a complex adaptive systems approach. Limnol Oceanogr 49:1269–1277
Ostfeld A, Salomons S (2005) A hybrid genetic-instance based learning algorithm for CE-QUAL-W2 calibration. J Hydrol 310:122–142
PBL (2009) GLOBIO-aquatic, http://www.globio.info
Petzoldt T, Rinke K (2007) Simecol: an object-oriented framework for ecological modeling in R. J Stat Softw 22:1–31
Petzoldt T, Uhlmann D (2006) Nitrogen emissions into freshwater ecosystems: Is there a need for nitrate elimination in all wastewater treatment plants? Acta Hydrochimica et Hydrobiologica 34:305–324
Petzoldt T, Rolinski S, Rinke K, König M, Baumert HZ, Benndorf J (2005) SALMO: Die ökologische Komponente des gekoppelten Modells. Wasserwirtschaft 95:28–33 (in German)
Pikitch EK, Santora C, Babcock EA, Bakun A, Bonfil R, Conover DO, Dayton P, Doukakis P, Fluharty D, Heneman B, Houde ED, Link J, Livingston PA, Mangel M, McAllister MK, Pope J, Sainsbury KJ (2004) Ecosystem based fishery management. Science 305:346–347
Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1992) Numerical recipes in C: the art of scientific computing, 2nd edn. Cambridge University Press, Cambridge, p 994
Prokopkin IG, Mooij WM, Janse JH, Degermendzhy AG (2010) A general one-dimensional vertical ecosystem model of Lake Shira (Russia, Khakasia): description, parametrization and analysis. Aquat Ecol (this issue). doi:10.1007/s10452-010-9326-8
R Development Core Team (2009) R: A language and environment for statistical computing. R Foundation for Statistical Computing, Vienna, Austria. http://www.R-project.org
Randall RG, Minns CK, Kelso JRM (1995) Fish production in freshwaters: are rivers more productive than lakes? Can J Fish Aquat Sci 52:631–643
Randall DA, Wood RA, Bony S, Colman R, Fichefet T, Fyfe J, Kattsov V, Pitman A, Shukla J, Srinivasan J, Stouffer RJ, Sumi A, Taylor KE (2007) Cilmate models and their evaluation. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL (eds) Climate change 2007: the physical science basis. Contribution of working Group I to the fourth assessment report of the intergovernmental panel on climate change. Cambridge University Press, Cambridge
Reckhow KH (1979) Empirical lake models for phosphorus: development, applications, uncertainty. In: Scavia D, Robertson A (eds) Perspectives on lake ecosystem modelling. Ann Arbor Science, Ann Arbor, pp 193–222
Reckhow KH, Chapra SC (1983) Data analysis and empirical modelling. Butterworth Publishers, Boston, p 340
Recknagel F, Cao H, Kim B, Takamura N, Welk A (2006) Unravelling and forecasting algal population dynamics in two lakes different in morphometry and eutrophication by neural and evolutionary computation. Ecol Informatics 1:133–151
Recknagel F, Cetin L, Zhang B (2008) Process-based simulation library SALMO-OO for lake ecosystems. Part 1: Object-oriented implementation and validation. Ecol Informatics 3:170–180
Reichert P, Mieleitner J (2008) Lake Models. In: Jørgensen SE, Fath BD (eds) Ecological models, vol 3 of Encyclopedia of ecology. Elsevier, Oxford, pp 2068–2080
Revenga C, Campbell I, Abell R, De Villiers P, Bryer M (2005) Prospects for monitoring freshwater ecosystems towards the 2010 targets. Philos Trans R Soc B Biol Sci 360:397–413
Reynolds CS, Irish AE, Elliott JA (2001) The ecological basis for simulating phytoplankton responses to environmental change (PROTECH). Ecol Modell 140:271–291
Rigler FH, Peters RH (1995) Science and limnology. Excellence in ecology no. 6. xxvi. Ecology Institute Oldendorf/Luhe, Germany 239
Riley MJ, Stefan HG (1988) MINLAKE: a dynamic lake water quality simulation model. Ecol Modell 43:155–182
Rinke K, Hülsmann S, Mooij WM (2008) Energetic costs, underlying resource allocation patterns, and adaptive value of predator-induced life-history shifts. Oikos 117:273–285
Robson BJ, Hamilton DP (2003) Three-dimensional modelling of a Microcystis bloom event in the Swan River estuary, Western Australia. Ecol Modell 174:203–222
Robson BJ, Hamilton DP, Webster IT, Chan T (2008) Ten steps applied to development and evaluation of process-based biogeochemical models of estuaries. Environ Modell Softw 23:369–384
Roe PL (1985) Some contributions to the modelling of discontinuous flows. Lect Appl Math 22:163–193
Roland F, Lobão L, Vidal LO, Jeppesen E, Paranhos R, Huszar VM (2010) Relationships between pelagic bacteria and phytoplankton abundances in contrasting tropical freshwaters. Aquat Microb Ecol 60:261–272
Rolinski S, Petzoldt T, Baumert HZ, Bigalke K, Horn H, Benndorf J (2005) Das physikalisch-ökologisch gekoppelte Talsperrenmodell. Wasserwirtschaft 95:34–38 (in German)
Rosenzweig ML (1971) Paradox of enrichment: destabilization of exploitation ecosystems in ecological time. Science 171:385–387
Rosenzweig ML, MacArthur RH (1963) Graphical representation and stability conditions of predator prey interactions. Am Nat 97:209–223
Saito L, Johnson BM, Bartholow J, Hanna RB (2001) Assessing ecosystem effects of reservoir operations using food web-energy transfer and water quality models. Ecosystems 4:105–125
Sakamoto M (1966) Primary production by the phytoplankton community in some Japanese lakes and its dependence upon lake depth. Archiv für Hydrobiologie 62:1–28
Salonen K, Leppäranta M, Viljanen M, Gulati RD (2009) Perspectives in winter limnology: closing the annual cycle of freezing lakes. Aquat Ecol 43:609–616
Saloranta TM (2000) Modeling the evolution of snow, snow ice and ice in the Baltic Sea. Tellus 52A:93–108
Saloranta TM (2006) Highlighting the model code sselection and application process in policy-relevant water quality modelling. Ecol Modell 194:316–327
Saloranta TM, Andersen T (2007) MyLake—A multi-year lake simulation model code suitable for uncertainty and sensitivity analysis simulations. Ecol Modell 207:45–60
Saloranta TM, Forsius M, Järvinen M, Arvola L (2009) Impacts of projected climate change on the thermodynamics of a shallow and deep lake in Finland: model simulations and Bayesian uncertainty analysis. Hydrol Res 40:234–248
Salski A, Holsten B (2006) A fuzzy and neuro-fuzzy approach to modelling cattle grazing on pastures with low stocking rates in Middle Europe. Ecol Informatics 1:269–276
Savage VM, Webb CT, Norberg J (2007) A general multi-trait-based framework for studying the effects of biodiversity on ecosystem functioning. J Theor Biol 247:213–229
Schauser I, Strube T (2007) Perspectives of lake modelling towards predicting reaction to trophic change. Kompetenzzentrum Wasser Berlin Publication Series, vol 9
Scheffer M (1990) Multiplicity of stable states in fresh water systems. Hydrobiologia 200:475–486
Scheffer M (1998) Ecology of shallow lakes. Chapman & Hall, London, p 357
Scheffer M, Beets J (1994) Ecological models and the pitfalls of causality. Hydrobiologia 275:115–124
Scheffer M, Van Nes EH (2007) Shallow lakes theory revisited: various alternative regimes driven by climate, nutrients, depth and lake size. Hydrobiologia 584:455–466
Scheffer M, Hosper SH, Meijer M-L, Moss B, Jeppesen E (1993) Alternative equilibria in shallow lakes. Trends Ecol Evol 8:275–279
Scheffer M, Baveco JM, DeAngelis DL, Rose KA, Van Nes EH (1995) Super-individuals a simple solution for modelling large populations on an individual basis. Ecol Modell 80:161–170
Scheffer M, Rinaldi S, Kuznetsov YA, Van Nes EH (1997) Seasonal dynamics of Daphnia and algae explained as a periodically forced predator-prey system. Oikos 80:519–532
Scheffer M, Straile D, Van Nes EH, Hosper SH (2001a) Climatic warming causes regime shifts in lake food webs. Limnol Oceanogr 46:1780–1783
Scheffer M, Carpenter S, Foley JS, Folke C, Walker B (2001b) Catastrophics shifts in ecosystems. Nature 413:591–596
Schep SA, Ter Heerdt, GNJ, Janse JH, Ouboter M (2007) Possible effects of climate change on ecological functioning of shallow lakes, Lake Loenderveen as a case study. Annals of Warsaw University of Life Sciences–SGGW. Land Reclamation, vol 38
Schippers P, Verschoor AM, Vos M, Mooij WM (2001) Does “supersaturated coexistence” resolve the “paradox of the plankton”? Ecol Lett 4:404–407
Schippers P, Vermaat JE, De Klein J, Mooij WM (2004) The effect of atmospheric CO2 elevation on plant growth in freshwater ecosystems. Ecosystems 7:63–74
Scholes RJ, Biggs R (2005) A biodiversity intactness index. Nature 434:45–49
Shade A, Carey CC, Kara E, Bertilsson S, McMahon KD, Smith MC (2009) Can the black box be cracked? The augmentation of microbial ecology by high-resolution, automated sensing technologies. ISME J 3:881–888
Sipkay Cs, Kiss KT, Vadadi-Fülöp Cs, Hufnagel L (2009) Trends in research on the possible effects of climate change concerning aquatic ecosystems with special emphasis on the modelling approach. Appl Ecol Environ Res 7:171–198
Soetaert K, Petzoldt T, Setzer RW (2010) Solving differential equations in R: package deSolve. J Stat Softw 33:1–25
Sollie S, Janse JH, Mooij WM, Coops H, Verhoeven JTA (2008) The contribution of the marsh zones to water quality in Dutch shallow lakes: a modelling study. Environ Manage 42:1002–1016
Sommer U, Gliwicz ZM, Lampert W, Duncan A (1986) The PEG-model of seasonal succession of planktonic events in fresh waters. Archiv für Hydrobiologie 106:433–471
Søndergaard M, Jensen JP, Jeppesen E (2003) Role of sediment and internal loading of phosphorus in shallow lakes. Hydrobiologia 506:135–145
Søndergaard M, Liboriussen L, Pedersen AR, Jeppesen E (2008) Lake restoration by fish removal: short and long-term effects in 36 Danish lakes. Ecosystems 11:1291–1305
Søndergaard M, Johansson LS, Lauridsen TL, Jørgensen TB, Liboriussen L, Jeppesen E (2010) Submerged macrophytes as indicators of the ecological quality of lakes. Freshw Biol 55:893–908
Spence DHN (1982) The Zonation of plants in fresh-water lakes. Adv Ecol Res 12:37–125
STOWA (1999) Procesbeschrijvingen DUFLOW, versie 3. (Process models in DUFLOW, version 3.) STOWA, Utrecht, Report nr. 99–21 (In Dutch)
STOWA (2000) DUFLOW for Windows v.3.3; User’s Guide, Reference Guide. STOWA, Utrecht, Report nr. 2000-27
STOWA (2008) Van helder naar troebel… en weer terug (From clear to turbid… and back again), STOWA, Utrecht. Report nr. 2008–04 (In Dutch)
Sullivan AB, Jager HI, Myers R (2003) Modeling white sturgeon movement in a reservoir: the effect of water quality and sturgeon density. Ecol Modell 167:97–114
Tian RC (2006) Toward standard parameterizations in marine biological modeling. Ecol Modell 193:363–386
Tirok K, Gaedke U (2010) Internally driven alternation of functional traits in a multispecies predator-prey system. Ecology 91:1748–1762
Tominaga K, Aherne J, Watmough SA, Alveteg M, Cosby BJ, Drilscoll CT, Posch M (2009) Voyage without constellation: evaluating the performance of three uncalibrated process-oriented models. Hydrol Res 40:261–272
Trolle D, Skovgaard H, Jeppesen E (2008a) The water framework directive: setting the phosphorus loading target for a deep lake in Denmark using the 1D lake ecosystem model DYRESM-CAEDYM. Ecol Modell 219:138–152
Trolle D, Jørgensen TB, Jeppesen E (2008b) Predicting the effects of reduced external nitrogen loading on the nitrogen dynamics and ecological state of deep Lake Ravn, Denmark, using the DYRESM-CAEDYM model. Limnologica 38:220–232
Trolle D, Hamilton DP, Pilditch CA (2010) Evaluating the influence of lake morphology, trophic status and diagenesis on geochemical profiles in lake sediments. Appl Geochem 25:621–632
Van De Bund WJ, Romo S, Villena MJ, Valentín M, Van Donk E, Vicente E, Vakkilainen K, Svensson M, Stephen D, Ståhl-Delbanco A, Rueda J, Moss B, Miracle MR, Kairesalo T, Hansson L-A, Hietala J, Gyllström M, Goma J, García P, Fernández-Aláez M, Fernández-Aláez C, Ferriol C, Collings SE, Bécares E, Balayla DM, Alfonso T (2004) Responses of phytoplankton to fish predation and nutrient loading in shallow lakes: a pan-European mesocosm experiment. Freshw Biol 49:1608–1618
Van Donk E, Santamaria L, Mooij WM (2003) Climate warming causes regime shifts in lake food webs: a reassessment. Limnol Oceanogr 48:1350–1353
Van Liere L, Janse JH (1992) Restoration and resilience to recovery of the Lake Loosdrecht ecosystem in relation to its phosphorus flow. Hydrobiologia 233:95–104
Van Nes EH, Scheffer M (2005) A strategy to improve the contribution of complex simulation models to ecological theory. Ecol Modell 185:153–164
Van Nes EH, Lammens EHRR, Scheffer M (2002) PISCATOR, an individual-based model to analyze the dynamics of lake fish communities. Ecol Modell 152:261–278
Van Nes EH, Scheffer M, Van den Berg MS, Coops H (2003) Charisma: a spatial explicit simulation model of submerged macrophytes. Ecol Modell 159:103–116
Vilhena LC, Hillmer I, Imberger J (2010) The role of climate change in the occurrence of algal blooms; Lake Burragorang, Australia. Limnol Oceanogr 55:1188–1200
Vollenweider RA (1968) Scientific fundamentals of the eutrophication of lakes and flowing waters, with particular reference to nitrogen and phosphorus as factors in eutrophication. OECD, Paris. Tech. Rpt. DA 5/SCI/68.27. 250 pp
Vollenweider RA (1975) Input-output models with special reference to the phosphorus loading concept. Aquat Sci 37:53–84
Vollenweider RA, Kerekes J (1982) Eutrophication of waters. Monitoring, assessment and control. OECD Cooperative programme on monitoring of inland waters (Eutrophication control), Environment Directorate, OECD, Paris. 154 pp
Vos M, Flik BJG, Vijverberg J, Ringelberg J, Mooij WM (2002) From inducible defences to population dynamics: modelling refuge use and life-history changes in Daphnia. Oikos 99:386–396
Vos M, Kooi BW, DeAngelis DL, Mooij WM (2004) Inducible defenses and the paradox of enrichment. Oikos 105:471–480
Wallace BB, Hamilton DP (2000) Simulation of water-bloom formation in the cyanobacterium Microcystis aeruginosa. J Plankton Res 22:1127–1138
Wang H, Appan A, Gulliver JS (2003a) Modeling of phosphorus dynamics in aquatic sediments: I–model development. Water Res 37:3928–3938
Wang H, Appan A, Gulliver JS (2003b) Modeling of phosphorus dynamics in aquatic sediments: II–examination of model performance. Water Res 37:3939–3953
Winder M, Spaak P, Mooij WM (2004) Trade-offs in Daphnia habitat selection. Ecology 85:2027–2036
Wirtz KW, Eckhardt B (1996) Effective variables in ecosystem models with an application to phytoplankton succession. Ecol Modell 92:33–53
Witteveen + Bos (2008a) Watersysteemanalyse Loosdrechtse Plassen. Report nr. LOOS20-1-1 (In Dutch)
Witteveen + Bos (2008b) Nadere uitwerking waterkwaliteit en ecologische kwaliteit Wieringerrandmeer. Report nr. WRW5-32 (In Dutch)
Witteveen + Bos (2009) Effecten peilbeheer en waterberging Oldambtmeer. Report nr. VDM53-1-1 (In Dutch)
Witteveen + Bos (2010a) Ecologische modellering Loenderveense Plas en Terra Nova. Report nr. LN4-1-1 (In Dutch)
Witteveen + Bos (2010b) Waterkwaliteit herinrichting Nieuwe Driemanspolder. Report nr. ZTM99-1-1 (In Dutch)
Witteveen + Bos (2010c) Neuraal netwerk PCLake ten behoeve van KRW-verkenner. Report nr. UT565-2-1 (In Dutch)
Wolfer SR, Van Nes EH, Straile D (2006) Modelling the clonal growth of the rhizomatous macrophyte Potamogeton perfoliatus. Ecol Modell 192:67–82
Yoshida T, Ellner SP, Jones LE, Bohannan BJM, Lenski RE, Hairston NG Jr (2007) Cryptic population dynamics: rapid evolution masks trophic interactions. PLoS Biol 5:1868–1879
Zadeh LA (1965) Fuzzy Sets, Information and Control 8:338–353
Zhang J, Gurkan Z, Jørgensen SE (2010) Application of eco-exergy for assessment of ecosystem health and development of structurally dynamic models. Ecol Modell 221:693–702
Acknowledgments
WM, RG, IP, SG, PV and AD were supported by grant 047.017.012 of the Netherlands Organization for Scientific Research (NWO) and the Russian Foundation for Basic Research (RFBR). LDSD was supported by NWO grant 817.01.007. DT and EJ were supported by EU-REFRESH, EU-WISER, CLEAR (a Villum Kann Rasmussen Centre of Excellence Project on lake restoration) and CRES. We thank Prof. André De Roos for his insightful comments and Dr. Tom Andersen for his contribution to the text. JJ wishes to thank Drs. T. Aldenberg, Dr. L. Van Liere, Mr. M.J. ‘t Hart, Ir. M.H.J.L Jeuken, Ing. S. van Tol, Ir. J.S. Sloot and many others including the many people who provided lake data, for their contributions to PCLake. This is publication 4838 of the Netherlands Institute of Ecology (NIOO-KNAW).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Handling Editor: R. D. Gulati.
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Mooij, W.M., Trolle, D., Jeppesen, E. et al. Challenges and opportunities for integrating lake ecosystem modelling approaches. Aquat Ecol 44, 633–667 (2010). https://doi.org/10.1007/s10452-010-9339-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10452-010-9339-3