Integrated uncertainty quantification and sensitivity analysis of single-component dynamic column breakthrough experiments

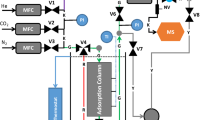
Abstract

We have carried out the traditional analysis of a set of dynamic breakthrough experiments on the $\hbox {CO}_2$/He system adsorbing onto activated carbon by fitting a 1D dynamic column breakthrough model to the transient experimental profiles. We have quantified the uncertainties in the fitted model parameters using the techniques of Bayesian inference, and have propagated these parametric uncertainties through the dynamic model to assess the robustness of the modelling. We have found significant uncertainties in the outlet mole fraction profile, internal temperature profile and internal adsorption profiles of approximately $\pm 15\%$. To assess routes to reduce these uncertainties we have applied a global variance-based sensitivity analysis to the dynamic model using the Sobol method. We have found that approximately $70\%$ of the observed variability in the modelling outputs can be attributed to uncertainties in the adsorption isotherm parameters that describe its temperature dependence. We also make various recommendations for practitioners, using the developed Bayesian statistical tools, regarding the choice of the isotherm model, the choice of the fitting data for the extraction of system specific parameters and the simplification of the wall energy balance.

1 Introduction

Gas-phase separations by adsorption underpin many important industrial processes, including oxygen purification, hydrogen production and carbon capture [1,2,3]. The model-based design and optimisation of adsorption separations depends on the validation of detailed numerical models against results obtained in the laboratory from dynamic column breakthrough (DCB) experiments. In a DCB experiment, a small column packed with pellets of an adsorbent material is used to adsorb a feed gas. During the dynamic adsorption process, the outlet gas composition and volumetric gas flow rate, the internal temperature (at one or more locations) and the internal adsorption profiles can all be measured as functions of time [4,5,6]. The dynamic adsorption process can be modelled by application of a DCB model, in which material and energy balances are solved, with respect to time, as a coupled system of partial differential equations using a finite-volumes numerical scheme [7]. The experimental measurements can be used to validate the implementation of the DCB model as well as to obtain system specific parameters such as the gas-phase longitudinal dispersion coefficient, the adsorption rate constant and the overall heat transfer coefficients [8].

The process of obtaining these parameters from the data generated in DCB experiments inevitably carries a degree of uncertainty. This uncertainty can owe to several factors, including uncertainties in measurements of the experimental data points themselves, any inadequacy of the available experimental conditions in parametrising the physical processes described by the model, and any inadequacy of the model itself in describing the physical processes taking place in the experiments. Due to the uncertainty present in obtaining the model parameters, there will also be uncertainty present in the subsequent model predictions. To enable using experimental data to validate the numerical model, one must be quite certain of the robustness of the modelling in the presence of experimental uncertainties. Further to this, in the case where the robustness of the model is found to be insufficient for the chosen application, an indication of how to improve the experimental procedure to effectively reduce the experimental uncertainties would prove very useful. These techniques would allow more confident validation of complex numerical models and more effective translation of lab-scale results into industrial process design.

The task of analyzing experimental uncertainties to assess the robustness of a model can be broken down into two key steps. Firstly, there is uncertainty quantification, where the uncertainties associated with each of the model parameters are extracted based on the relationship between the numerical model and the experimental data sets. These uncertainties can then be propagated through the model to gain understanding of the robustness of the model by observing the resulting variability in the model outputs. Secondly, a sensitivity analysis can be used to assess the contribution of each individual parametric uncertainty to the overall modelling uncertainty. In the scientific literature, there are examples of applications of a well-established and sophisticated suite of techniques for uncertainty quantification and sensitivity analysis, across a broad range of subject areas [9,10,11]. Bayesian inference has been relatively widely studied for the quantification of uncertainties in the prediction of adsorption equilibrium from isotherm models [12,13,14]. This technique has also been demonstrated to be effective in the context of prediction of adsorption process dynamics [15]. There have been attempts in the literature to analyse the sensitivity of adsorption process dynamics to various modelling parameters [16]. However, to the best of our knowledge, a rigorous global sensitivity analysis of the DCB model in the context of experimental uncertainties, for a particular laboratory-scale system, is not available in the literature. In other fields the application of variance-based sensitivity methods for the evaluation of the Sobol indices of a system is a popular technique [17, 18].

In this study, we demonstrate a methodology for integrating uncertainty quantification and sensitivity analysis of the DCB model. We consider the case of single-component DCB experiments and use Bayesian inference to quantify the amount of uncertainty in each of the fitted model parameters. Then, the approach of Sobol sensitivity indices (variance-based method) is applied in the context of the experimental uncertainties calculated in the previous step. These indices are used to recommend routes to reduce the presence of experimental uncertainties in the modelling results.

In the following, we will briefly discuss the experimental protocol and modelling of a DCB system used in one of our previous studies [5], which provides the context within which we demonstrate our methodological advancement.

2 Experiments

The DCB experiments referenced in this study were conducted by [5] in a previous study. All data associated with this study was available in-house, but a detailed description of the procedures, materials, methods and results can be found in [5]. In this study, we will analyse the uncertainties associated with the methodology presented in the prior study to demonstrate the general framework of uncertainty quantification and sensitivity analysis which can be applied to any given DCB system.

The experiments concerned the $\hbox {CO}_2$/He system adsorbing onto a packed bed of activated carbon rods, with $\hbox {CO}_2$ being the adsorbable component. A total of three dynamic experiments were conducted. In each experiment, an initially regenerated packed bed was exposed to a specified volumetric flow of pure $\hbox {CO}_2$. Upon reaching saturation of the packed bed, the flow was increased and switched to pure helium, to regenerate the bed. Therefore, in each experiment we observed the dynamic adsorption process, as well as the corresponding dynamic desorption process. This gives a total of 6 data sets with which we can analyse the associated modelling uncertainty. In each experiment, the transient profiles of outlet composition, outlet flow rate, internal temperature and internal adsorption were all measured. A full summary of the experimental conditions and parameters can be found in Table 1.

Table 1 Physical parameters describing the experimental system of [5]

3 Modelling

3.1 Adsorption equilibrium

The experiments of [5] were accompanied by a set of static volumetry measurements of the adsorption equilibrium for $\hbox {CO}_2$ adsorbing onto the activated carbon pellets used in the dynamic experiments. To describe the adsorption equilibrium of the system, we have applied a dual-site Langmuir (DSL) isotherm model:

$$\begin{aligned} q_1^* = \frac{q_{\mathrm {s,}1} b_{1}c}{1 + b_{1}c} + \frac{q_{\mathrm {s,}2} b_{2}c}{1 + b_{2}c} \end{aligned}$$

(1)

where $q_1^*$ is the equilibrium amount adsorbed (mol/kg) of component 1 ($\hbox {CO}_2$). The parameters $q_{\mathrm {s,}1}$ and $q_{\mathrm {s,}2}$ are the temperature independent saturation capacities of site 1 and site 2, respectively. The parameters $b_i$ are the adsorption equilibrium constants for each of the sites and are expressed as a function of the system temperature, T, using the van’t Hoff equation:

$$\begin{aligned} b_{i} = b_{0,i}\exp {(-\Delta U_i/RT)} \end{aligned}$$

(2)

where $b_{0,i}$ and $\Delta U_i$ are the reference equilibrium constant and change in internal energy due to adsorption, respectively, for site i. The molar concentration of the gas-phase in Eq. 1 is calculated using the ideal gas law:

$$\begin{aligned} c = \frac{p}{RT} \end{aligned}$$

(3)

The six parameters of the DSL model $(q_{\mathrm {s,}i}, b_{0,i} \, \mathrm {and} \, \Delta U_i, \forall i \in \{1, 2\})$ have been obtained by fitting Eq. 1 to the available volumetry data ($p = 0 - 1$ bar, $T = 293 - 313$ K) using the lsqcurvefit routine in MATLAB by solving the following optimization problem:

$$\begin{aligned} \min _{\varvec{\theta _{\mathrm {DSL}}}} J_\mathrm {q} = \sum _{i=1}^{N_{\mathrm {p,q}}} \left( q_1^* (p_i, T_i) - q_{i,\mathrm {exp}}^* \right) ^2 \end{aligned}$$

where $q_{i,\mathrm {exp}}^*$ is the equilibrium amount adsorbed at conditions $(p_i, T_i)$, $N_{\mathrm {p,q}}$ is the number of experimental data points and $\varvec{\theta _{\mathrm {DSL}}}$ is the vector of DSL isotherm parameters. The resulting isotherm parameters can be found in Table 2 and the fit of the DSL isotherm to the experimental data can be seen in Fig. 1. We can see that the DSL model provides an excellent description of the experimental data across the full range of available temperatures and pressures. In Sect. 4, we will describe the approach to quantify the uncertainty associated with the isotherm parameters reported in Table 2.

Table 2 Parameters of the DSL model for describing the equilibrium adsorption of $\hbox {CO}_2$ onto activated carbon

Fig. 1

Equilibrium adsorption capacity of activated carbon adsorbing $\hbox {CO}_2$ at three temperatures for pressures between 0-1bar. The open circles correspond to experimental measurements from volumetry [5] and the solid lines correspond to the fitted DSL isotherm model

3.2 Adsorption dynamics

The transient profiles measured in the experiments of [5] have been described using a 1D DCB model [5]. The model accounts for the compressible, non-isothermal flow of an ideal gas mixture containing two components (where one component is an inert non-adsorbing gas). The overall and component material balances account for the advection and longitudinal dispersion of the gas-phase. These balances are coupled with a solid-phase material balance, which expresses the sorption kinetics using the linear driving force (LDF) model. The pressure drop in the system is expressed using Darcy’s law. The material balances are solved simultaneously with a set of energy balances for both the gas-phase and the column wall. They account for several mechanisms of heat transfer, including conduction, convection, heat released by exothermic adsorption and the transfer of heat between the gas-phase, column wall and ambient surroundings. The material and energy balances are a coupled system of partial differential equations, and can be found in Table 3. The associated set of boundary conditions can be found in Table 4. The equations are written in a non-dimensional form to enhance computational efficiency. Definitions of the non-dimensional variables and dimensionless groups can be found in Appendix 1. The system has been discretised in space using the semi-implicit finite-volumes scheme with a weighted essentially non-oscillatory (WENO) flux-limiter function [7]. The discretised material and energy balances have been solved in MATLAB using the ode15s solver with the mass-matrix approach. A summary of the numerical discretization parameters can be found in Table 5.

Table 3 The system of non-dimensional partial differential equations representing the material and energy balances of the 1D DCB model

Table 4 Boundary conditions used to solve the material and energy balances of the 1D DCB model

Table 5 Parameters used in the numerical solution of the 1D DCB model

Several parameters of the model are obtained from correlations available in the literature. The longitudinal dispersion coefficient, $D_{\mathrm {L}}$, is evaluated using the following correlation [19]:

$$\begin{aligned} D_{\mathrm {L}} = 0.7D_{\mathrm {m}} + v_{\mathrm {F}}r_{\mathrm {p}} \end{aligned}$$

(4)

where $D_{\mathrm {m}}$ is the molecular diffusion coefficient, $v_{\mathrm {F}}$ is the interstitial velocity of the feed gas and $r_{\mathrm {p}}$ is the average pellet radius. It was found that an optimal match to the experimental outlet composition profiles was obtained when multiplying the dispersion coefficient values predicted in Eq. 4 by a factor of 4. The outside heat transfer coefficient, $h_{\mathrm {out}}$, has been evaluated using the correlation of [20]:

$$\begin{aligned} Nu = 0.027Re^{0.8}Pr^{1/3} \end{aligned}$$

(5)

where $Nu = (2h_\mathrm {out}r_\mathrm {out}/k_\mathrm {air})$ is the Nusselt number, $r_\mathrm {out}$ is the outside column radius and $k_\mathrm {air}$ is the thermal conductivity of air. $Re = (2r_\mathrm {out}u\rho _\mathrm {air}/\mu _\mathrm {air})$ is the Reynolds number of the ambient surroundings, where $\rho _\mathrm {air}$ and $\mu _\mathrm {air}$ are the density and dynamic viscosity of air, respectively. The density is evaluated using the ideal gas law, $\rho = p\omega /RT$, where $\omega$ is the molecular weight. A value of $u = 0.5 \mathrm {\,m\,s}^{-1}$ is used for airflow in a laboratory environment. $Pr = (C_\mathrm {p,air} \mu _\mathrm {air}/k_\mathrm {air})$ is the Prandtl number of the ambient surroundings, where $C_\mathrm {p,air}$ is the isobaric heat capacity of air. The adsorption rate constant, $k_{1}$, for the LDF adsorption kinetics model, has been evaluated using the relationship by [21]:

$$\begin{aligned} \frac{1}{k_1} = \frac{r_{\mathrm {p}}}{3k_{\mathrm {f}}} + \frac{\tau _{\mathrm {p}}r_{\mathrm {p}}^2}{15\epsilon _{\mathrm {p}}D_{\mathrm {m}}} \end{aligned}$$

(6)

where $k_{\mathrm {f}}$ is the film mass transfer coefficient for the diffusion of gas molecules through the laminar boundary layer surrounding adsorbent pellets, $\tau _{\mathrm {p}}$ is the pellet tortuosity factor and $\epsilon _{\mathrm {p}}$ is the pellet voidage. The film mass transfer coefficient is given by the correlation of [22]:

$$\begin{aligned} Sh = 2 + 1.1Sc^{1/3}Re_{\mathrm {p}}^{0.6} \end{aligned}$$

(7)

where $Sh = (2k_\mathrm {f}r_\mathrm {p}/D_\mathrm {m})$ is the Sherwood number, $Sc = (\mu /D_\mathrm {m}\rho )$ is the Schmidt number and $Re_\mathrm {p} = (2r_\mathrm {p}\epsilon v_\mathrm {F} \rho /\mu )$ is the particle Reynolds number inside the bed. The effective thermal conductivity of the bed, $K_{\mathrm {z}}$, is evaluated using the correlation of [23]:

$$\begin{aligned} K_{\mathrm {z}} = K_{\mathrm {z}}^0 + 0.75 k_{\mathrm {g}} Pr Re_{\mathrm {p}} \end{aligned}$$

(8)

where $K_{\mathrm {z}}^0$ is the effective thermal conductivity of the bed at $Re_p = 0$, given by:

$$\begin{aligned} K_{\mathrm {z}}^0 = k_\mathrm {g}\left( \frac{k_\mathrm {s}}{k_\mathrm {g}} \right) ^n \end{aligned}$$

(9)

where:

$$\begin{aligned} n = 0.28 - 0.757\log _{10}(\epsilon ) - 0.057\log _{10}\left( \frac{k_\mathrm {s}}{k_\mathrm {g}} \right) \end{aligned}$$

(10)

here, $k_{\mathrm {g}}$ and $k_{\mathrm {s}}$ are the thermal conductivity of the gas and adsorbent, respectively, and $Pr = (C_\mathrm {p,g} \mu /k_\mathrm {g})$ is the Prandtl number evaluated inside the column. Following the correlation of the model parameters, the model was then calibrated to the dynamic experimental measurements by fitting the internal temperature profile to that measured using the thermo-couple (located at $z = L/4$) by specifying the value of the inside heat transfer coefficient, $h_{\mathrm {in}}$. It should be noted that the value of $h_\mathrm {out}$ used in the modelling is predicted using Eq. 5. Although it is standard practice in the literature to fit the outside heat transfer coefficient, we do not do this in this case because, as will be discussed in Sect. 5, the DCB model has an extremely low sensitivity to this parameter under the presented experimental conditions. In later Sections, the role of the outside heat transfer coefficient is explored more thoroughly by including it in the set of uncertain model parameters. The fitting was carried out in MATLAB using the genetic algorithm routine. The inside heat transfer coefficient corresponding to each experiment was found by the solution of the following optimisation problem:

$$\begin{aligned} \min _{h_{\mathrm {in}}(f_{\mathrm {in}})} J_{\mathrm {T}} = \sum _{i=1}^{N_{\mathrm {p,T}}} \left( T_{\mathrm {tc}}^{\mathrm {sim}}(\tau _i, f_{\mathrm {in}}) - T_{\mathrm {tc}}^{\mathrm {exp}}(\tau _i, f_{\mathrm {in}}) \right) ^2 \end{aligned}$$

where $N_{\mathrm {p,T}}$ is the number of measurements made by the thermo-couple, $T_{\mathrm {tc}}^{\mathrm {exp}}$ is the temperature measured by the thermo-couple at reduced time $\tau _i$ and $T_{\mathrm {tc}}^{\mathrm {sim}}$ is the corresponding simulated temperature. A table of the fitted inside heat transfer coefficient values can be found in Table 6, and plots of the calibrated conventional model outputs, as compared to experimental measurements, can be found in Fig. 2. As can be seen, by following the procedure set out in this Section, the agreement between the model and the experiments is excellent.

Table 6 Fitted values of the inside heat transfer coefficient, $h_\mathrm {in}$, for each dynamic experiment

Fig. 2

Transient profiles of the outlet mole fraction, internal temperature at the thermo-couple and outlet flow rate from the dynamic breakthrough experiments. The results correspond to three flow rates: 50ccm (black), 100ccm (blue) and 200ccm (red) for adsorption, and 100ccm (black), 150ccm (blue) and 250ccm (red) for desorption. The open circles correspond to experimental measurements [5] and the solid lines correspond to predictions by the fitted 1D DCB model

4 Methods

The modelling work flow presented in Sects. 2, 3 represents a quite typical analysis of a set of DCB experiments. We have shown that by using the standard approach of calibrating the 1D DCB model to experimental measurements, it is possible to extract the value of the inside heat transfer coefficient for the system in each experiment. In the following, we will discuss the working principles of two tools; Bayesian inference for uncertainty quantification and Sobol indices for sensitivity analysis. In Sect. 5, we will present the results of the application of these tools to the dynamic breakthrough system presented in Sects. 2, 3. Finally, in Sect. 6, we will discuss some implications of the results and make recommendations for the experimental procedure and associated numerical analysis.

4.1 Bayesian inference

Bayesian inference [15, 24] is a widely applied tool across academic literature for the quantification of uncertainties in model parameters, given a set of measurements. In a traditional parameter extraction exercise, like that presented in Sect. 3, the model and data are used together to extract a point estimate for each of the unknown model parameters. Whereas, when using the Bayesian inference technique, the model and data are used together to extract probability distributions for each of the unknown parameters. The mean value of the parametric distribution will correspond to the point estimate of the parameter which would be obtained from a traditional parameter extraction exercise. However, there is also significant additional information which can be obtained from the distributions. The cumulative distribution function (CDF) corresponding to the parametric distribution can be used to quantify the uncertainty in each of the unknown parameters, to within some specified confidence level, by taking the appropriate quantile on the CDF.

Bayesian inference is derived from Baye’s Theorem, which is stated as follows:

$$\begin{aligned} P(\varvec{\theta } \vert \mathcal {D}) = \frac{P(\mathcal {D} \vert \varvec{\theta })P(\varvec{\theta })}{P(\mathcal {D})} \end{aligned}$$

(11)

where $P(\varvec{\theta } \vert \mathcal {D})$ is the posterior distribution, which is the probability distribution of the model parameters, $\varvec{\theta } = (\theta _1, ..., \theta _{\mathrm {n_p}})$, given the set of experimental data, $\mathcal {D}$. The term $P(\mathcal {D} \vert \varvec{\theta })$ is the probability of the data given a set of model parameters. This term is commonly called the likelihood, derived from traditional (frequentest) parametric analysis. The term $P(\varvec{\theta })$ is called the prior distribution, which represents our existing knowledge of the probability distribution of the model parameters before starting the Bayesian inference analysis. Finally, the term $P(\mathcal {D})$ is a normalizing constant which ensures that the posterior distribution has a cumulative area of unity across the full domain of the model parameters. We can see that Eq. 11 expresses a quite intuitive idea, which is that if we take our existing understanding of the model parameters, we can in some sense “update” this understanding to incorporate additional information which is present in the experimental data that we have measured.

For expression of the likelihood function, it is common to assume that the errors between the measured data and the model predictions (with a given set of parameters) are normally distributed. The following expression of the likelihood follows from this assumption:

$$\begin{aligned} P(\mathcal {D} \vert \varvec{\theta }) = \frac{1}{\left( \sqrt{2\pi } \sigma \right) ^{N_\mathrm {p}}} \exp \left[ -\frac{\sum _{j=1}^{N_\mathrm {p}} \left( Q_j^{\mathrm {exp}} - Q_j^{\mathrm {sim}} \right) ^2}{2\sigma ^2} \right] \end{aligned}$$

(12)

where $N_\mathrm {p}$ is the number of measurements in the data, $\mathcal {D}$. The term $Q_j^{\mathrm {exp}}$ is the value of the $j^{\mathrm {th}}$ measurement of quantity Q and $Q_j^{\mathrm {sim}}$ is the corresponding model prediction, given parameters $\varvec{\theta }$. The term $\sigma$ is the standard deviation of the distribution of residual errors between the model and the data. This term is not easy to estimate directly and is therefore taken as a hyper-parameter of the numerical model by including $\sigma$ within the vector of parameters $\varvec{\theta }$. This means that we effectively obtain $\sigma$ from the experimental data itself during the inference process. In this study, we obtain a first-approximation of $\sigma$ from the standard deviation of the distribution of the residual errors between the experimental measurements and the predictions of the model in the nominal case.

For expression of the normalising constant of Eq. 11, we can marginalise the joint distribution of the data and the parameters to obtain the following:

$$\begin{aligned} P(\mathcal {D}) = \int _{\varvec{\theta }} P(\mathcal {D} \vert \varvec{\theta }) P(\varvec{\theta }) \, d\varvec{\theta } \end{aligned}$$

(13)

where the integral is multi-dimensional and is taken over all of the model parameters. We can see, as in Eq. 11, that the likelihood and parametric prior distribution both appear in Eq. 13.

The expression of the parametric prior distribution is more ambiguous than the other terms of Eq. 11. Broadly, the prior distribution simply represents our existing knowledge of the probability distribution of the model parameters, prior to starting the Bayesian inference analysis. A popular approach for determining the prior distribution, particularly among practitioners in the fields of engineering, is to apply the so-called maximum entropy principle [25]. In the case of this study, the maximum entropy principle leads to an expression of the marginal prior distribution for parameter $\theta _j$ with the following form:

$$\begin{aligned} P(\theta _j) = \frac{1}{\theta _j^{\mathrm {nom}}}\exp \left( -\theta _j/\theta _j^{\mathrm {nom}} \right) \end{aligned}$$

(14)

which is an exponential distribution with a mean of $\theta _j^{\mathrm {nom}}$, which is the nominal (fitted) value of $\theta _j$. A thorough derivation of this result can be found in Appendix 1, but has been excluded from the main text for brevity. Assuming that the model parameters are independent of one another, we can then obtain the full prior distribution as the product of the marginal prior distributions:

$$\begin{aligned} P(\varvec{\theta }) = \prod _{j=1}^{n_\mathrm {p}} P(\theta _j) \end{aligned}$$

(15)

Given the above, we have expressions for each of the terms in Eq. 11 which allows us to calculate the (joint) posterior distribution, $P(\varvec{\theta } \vert \mathcal {D})$. We can then break this down into an individual probability distribution for each model parameter, given the experimental data, by marginalising Eq. 11:

$$\begin{aligned} P(\theta _j \vert \mathcal {D}) = \int _{\varvec{\theta }_{\sim j}} \frac{P(\mathcal {D} \vert \varvec{\theta })P(\varvec{\theta })}{P(\mathcal {D})} \, d\varvec{\theta }_{\sim j} \end{aligned}$$

(16)

where the integral is multi-dimensional and is taken for all parameters except $\theta _j$. Therefore, the evaluation of the parametric posterior distribution for each of the model parameters, $P(\theta _j \vert \mathcal {D})$, requires the evaluation of two multi-dimensional integrals, given by Eqs. 13 and 16. In this study, the integrals have been evaluated using the quasi-Monte Carlo technique [26]. The parameters, $\varvec{\theta }$, are sampled at N points in the parameter space using the $n_\mathrm {p}$-dimensional Halton sequence [27]. The integral terms are then approximated using their Monte Carlo estimators as:

$$\begin{aligned}&P(\mathcal {D}) \approx \frac{1}{N} \sum _{i=1}^{N} P(\mathcal {D} \vert \varvec{\theta }^{(i)}) P(\varvec{\theta }^{(i)}) \end{aligned}$$

(17)

$$\begin{aligned}&P(\theta _j \vert \mathcal {D}) \approx \frac{1}{N} \sum _{i = 1}^{N} \frac{P(\mathcal {D} \vert \varvec{\theta }_{\sim j}^{(i)}, \theta _j)P(\varvec{\theta }_{\sim j}^{(i)}, \theta _j)}{P(\mathcal {D})} \end{aligned}$$

(18)

where $\varvec{\theta }^{(i)}$ is the parameter combination sampled in the $i^{\mathrm {th}}$ Monte Carlo trial. Note that Eq. 18 must be applied individually at all points $\theta _j$ where the desired posterior distribution is required to be known. Therefore, to reduce the computational burden of the calculations, the posterior distribution for each model parameter is evaluated using Eq. 18 at a fixed number of values of the parameter, $\theta _j$, and the discrete probability distribution points generated by this process are then fit with a continuous skewed normal distribution, the probability density function of which is [28]:

$$\begin{aligned}&f(\theta _j) =\nonumber \\&\frac{1}{\omega \sqrt{2\pi }}\exp \left( -\frac{(\theta _j - \xi )^2}{2\omega ^2} \right) \cdot \left[ 1 + \mathrm {erf}\left( \frac{\alpha (\theta _j - \xi )}{\omega \sqrt{2}} \right) \right] \end{aligned}$$

(19)

where $\xi$ is the location parameter, $\omega$ is the scale parameter and $\alpha$ is the shape parameter. The skew normal distribution is fit to the numerically determined probability distribution points from Eq. 18 using the lsqcurvefit routine in MATLAB to find the values of $\xi$, $\omega$ and $\alpha$ corresponding to the parametric posterior distribution of each uncertain model parameter.

Given an expression for the posterior distribution of each parameter, $P(\theta _j \vert \mathcal {D}) = f(\theta _j)$, the point estimate of the parameter from Bayesian inference is evaluated by taking the mean of the distribution, $\mu$. In the case of the skew normal distribution, the mean is given by:

$$\begin{aligned} \mu = \xi + \omega \delta \sqrt{\frac{2}{\pi }} \end{aligned}$$

(20)

where $\delta = \alpha /\sqrt{1 + \alpha ^2}$. We can also use the parametric posterior distribution, $f(\theta _j)$, to quantify the uncertainty in the model parameter, $\theta _j$, given the experimental data, $\mathcal {D}$. Within a Bayesian framework, the uncertainty in parameter $\theta _j$ is quantified by the bounds of a “credibility interval” (analogous to a confidence interval in frequentist analysis). In this study, the 95% credibility interval for $\theta _j$ has been evaluated using the equal-tailed method according to the following expression:

$$\begin{aligned} \theta _j \in [\theta _j^{(-)} \vert F(\theta _j^{(-)}) = 0.025, \theta _j^{(+)} \vert F(\theta _j^{(+)}) = 0.975] \end{aligned}$$

(21)

where $F(\theta _j)$ is the cumulative distribution function corresponding to the probability density function $f(\theta _j)$. In the case of a skew normal distribution, the cumulative distribution function is given by:

$$\begin{aligned} F(\theta _j) = \frac{1}{2}\left[ 1 + \mathrm {erf}\left( \frac{\theta _j - \xi }{\omega \sqrt{2}} \right) \right] - 2\mathcal {T}\left( \frac{\theta _j - \xi }{\omega }, \alpha \right) \end{aligned}$$

(22)

where $\mathcal {T}$ is Owen’s T-function, given by [29]:

$$\begin{aligned} \mathcal {T}(h, a) = \frac{1}{2\pi }\int _{0}^{a} \frac{\exp \left( -\frac{1}{2}h^2(1 + x^2) \right) }{(1 + x^2)} \, dx \end{aligned}$$

(23)

Bayesian inference has been used in this study to obtain parametric distributions, and quantify uncertainty, for all of the fitted model parameters from the analysis presented in Sect. 3. This includes the parameters of the DSL isotherm model $(q_{\mathrm {s},i}, b_{0,i}, \Delta U_i)$ and the overall heat transfer coefficients on the inside and outside of the column wall from the 1D DCB model $(h_\mathrm {in}, h_\mathrm {out})$ for each dynamic experiment. We note that although the outside heat transfer coefficient was obtained using Eq. 5 in Sect. 3.2, for the remainder of this study we treat this parameter as part of the set of fitted parameters to allow us to thoroughly explore the role that this parameter plays in the DCB model. The quantified uncertainties in the model parameters have been propagated through the model to generate predictive distributions of process performance indicators for the dynamic experiments (Sect. 5.2) as well as being used as an input to the integrated global variance-based sensitivity analysis (Sect. 5.4).

4.2 Sobol sensitivity indices

The method of Sobol sensitivity indices [30] has been used in this study to carry out a global variance-based sensitivity analysis of the dynamic breakthrough system. The Sobol indices method is a global method, meaning that it considers the sensitivity of the numerical model to all of the uncertain parameters simultaneously. Sobol indices is also a variance-based method, meaning that these sensitivities are used to attribute a proportion (%) of the observed model variability to each of the model parameters. The first-order Sobol index, neglecting interactions between the parameters, for the 1D DCB model for parameter $\theta _j$ is:

$$\begin{aligned} {S_{1,j} = \frac{V_j}{\sum _{\forall i} V_i}} \end{aligned}$$

(24)

where $V_j$ is the variance in the DCB model outputs which is attributed to variability in parameter $\theta _j$, averaged over variations in each of the parameters. Therefore, the value of $S_{1,j}$ can be directly interpreted as the proportion of the model variability which is caused by variations in parameter $\theta _j$. This is not necessarily an intrinsically useful metric, however, it becomes very powerful when coupled with the idea of uncertainty quantification. By considering variations in the sensitivity step according to the quantified uncertainties in each of the model parameters from the Bayesian inference step, the Sobol indices of the breakthrough system directly rank the parameters of the model by their influence over the precision in the model outputs - in the context of the experiments. This allows us to easily identify the largest sources of experimental uncertainty ($S_{1,j} \gg 0$), and therefore potential routes for improving the robustness of the model. It also allows us to identify physical effects in the model which are irrelevant at the conditions of the system under consideration ($S_{1,j} \approx 0$). Model simplification may allow for both easier forward modelling procedures and a smaller computational burden when carrying out parameter fitting exercises.

In this study, we have evaluated the variance in the model outputs attributable to each of the model parameters using the method presented by [31]. Their method is a quasi-Monte Carlo method based on quasi-random sampling using the Sobol sequence. The d-dimensional Sobol sequence generates a set of quasi-random numbers on the interval $r \in [0, 1]^d$, such that as the number of points sampled in the d-dimensional space is increased, the set of sampled points distributes very evenly over the entire region $[0, 1]^d$. We may scale the points generated by the Sobol sequence using lower and upper bounds specified by the 95% credibility intervals for each of our uncertain model parameters. Therefore, the scaled Sobol sequence will represent a quasi-random sample of uncertain parameter realisations for our experimental system. The use of the Sobol sequence in this approach means that the full uncertainty space of the experimental system is explored evenly, and crucially, by using a small number of parameter points as compared to alternative sampling methods.

For the approach used in this study, we generate three sets of points for the evaluation of the variance attributable to each of the uncertain model parameters, $V_j$. These sets of points are specified by three matrices, $\varvec{A}, \varvec{B}$ and $\varvec{A_B^{(j)}}$. Each of these matrices has a number of columns equal to the number of uncertain model parameters, $n_\mathrm {p}$, and a number of rows equal to the number of Monte Carlo trials which are to be conducted, N. The columns of the matrices each correspond to one of the uncertain model parameters. Therefore, each row of each matrix specifies one combination of parameters at which the DCB model is evaluated. The specific parameter combinations are generated as follows. The $2n_\mathrm {p}$-dimensional Sobol sequence is generated for N points. The Sobol sequence is then scaled according to the credibility intervals for each of the model parameters. The matrix $\varvec{A}$ is then taken as the left-hand side of the scaled sequence (the first $n_\mathrm {p}$ columns) and the matrix $\varvec{B}$ is taken as the right-hand side (the second $n_\mathrm {p}$ columns). The matrix $\varvec{A_B^{(j)}}$ is then formed by taking $\varvec{A}$, and replacing the $j^{\mathrm {th}}$ column with that of $\varvec{B}$. Noting that we have a unique matrix $\varvec{A_B^{(j)}}$ for each of the model parameters, $\theta _j$, the model is run at a total of $N(n_\mathrm {p} + 2)$ points in the parameter uncertainty space. The following Monte Carlo estimator is then used to evaluate the model variance, $V_j$, which is attributable to uncertainties in parameter $\theta _j$:

$$\begin{aligned} V_j(N) \approx \frac{1}{N}\sum _{i=1}^{N} Y_Q(\varvec{B})_i \left[ Y_Q(\varvec{A_B^{(j)}})_i - Y_Q(\varvec{A})_i \right] \end{aligned}$$

(25)

where $Y_Q(\cdot )$ is a measure of the model variability, in prediction of quantity Q, as determined when the model is run at the parameter combination specified by $(\cdot )$. In this study, we have expressed the model variability using the sum of squared residuals between the nominal simulated profile, $Q_\mathrm {sim}^\mathrm {nom}(\tau )$, for quantity Q, and the simulated profile for Q as evaluated at the uncertain parameter combination $(\cdot )$, $Q_\mathrm {sim}^{\Delta }(\tau )$ :

$$\begin{aligned} Y_Q(\cdot ) = \sum _{\forall i} \left( Q_\mathrm {sim}^\mathrm {nom}(\cdot , \tau _i) - Q_\mathrm {sim}^{\Delta }(\cdot , \tau _i) \right) ^2 \end{aligned}$$

(26)

We have evaluated the Sobol indices for the three important 1D DCB model outputs separately, namely the outlet mole fraction profile, the internal temperature profile ($Z = 1/4$) and the internal adsorption profiles.

There are two challenges present in the evaluation of the Sobol indices which require addressing. The first is that the quasi-Monte Carlo scheme used here has a significant burn-in phase. This means that for many of the initial samples, the variance attributable to each parameter, $V_j$, as calculated using Eq. 25, is far from its true value. Therefore, these evaluations of the variance should be ignored. Secondly, there is a form of sampling bias present as the number of Monte Carlo trials increases, which arises from the fact that as more parameter samples are added to the total pool of trials, they are not added totally uniformly across the parameter uncertainty space. This means that even once the variance approaches the neighbourhood of the true value, there are still some small oscillations around this value. Therefore, we take the average value of the evaluated variance, $V_j^{\mathrm {avg}}$, after the burn-in phase, as the “true” value of the variance. This is given by:

$$\begin{aligned} V_j^{\mathrm {avg}} = \frac{1}{N_{\mathrm {tot}} - N_{\mathrm {burn}}} \sum _{\forall N > N_{\mathrm {burn}}} V_j(N) \end{aligned}$$

(27)

where $N_{\mathrm {tot}} = 1000$ is the total number of Monte Carlo trials and $N_\mathrm {burn} = 500$ is the number of trials considered to be within the burn-in phase. These values were set empirically according to the response of our specific numerical model to the techniques described in this section.

5 Results

5.1 Equilibrium model uncertainty quantification

We have applied the Bayesian inference workflow described in Sect. 4 to the isotherm modelling described in Sect. 3. Fig. 3 shows the posterior distributions for each of the model parameters. The corresponding mean parameter values (Eq. 20) and 95% credibility intervals (Eq. 21) are given in Table 7. By comparison of Table 7 with Table 2, we can see that there is agreement between the point value estimates of the isotherm parameters from traditional model fitting and from Bayesian inference. This serves to assure us that the numerical implementation of the Bayesian inference work flow is sound, because this key information is not lost during the inference process. Looking at Fig. 3, we can see that the process of Bayesian inference has been able to update the parametric prior distributions for all isotherm parameters, except $b_{0,1}$, with new information from the equilibrium data. This can be seen from the skew normal shape of the parametric distributions for these parameters - which represents a significant departure from the exponential prior distributions. This indicates that the equilibrium data contains significant information about these parameters and correspondingly they are given by relatively narrow 95% credibility intervals (Table 7). However, for the parameter $b_{0,1}$ the process of Bayesian inference has not been able to update the prior distribution with any new information from the equilibrium data. This can be seen in the exponential shape of the posterior distribution, $P(b_{0,1} \vert \mathcal {D})$, in Fig. 3. As a result of this, $b_{0,1}$ also has a very broad 95% credibility interval (large uncertainty).

Fig. 3

Parametric posterior distributions for each of the DSL isotherm parameters. Y-axis ticks are excluded for brevity (curves are normalised to have a shaded area of unity). Discrete points indicate the fitted parameter values from Sect. 3

Table 7 Parameter point estimates and 95% credibility intervals (CI) on the DSL isotherm parameters

The posterior distributions for the model parameters have been propagated through the dual-site Langmuir isotherm model. As shown in Fig. 4, this generates the 95% credibility interval for the fitted isotherm model as a function of the pressure. We can see across all three experimental temperatures ($T = 293$-313K) that there is a moderately large uncertainty in the amount of $\hbox {CO}_2$ adsorbed at equilibrium. The uncertainty in the equilibrium state grows as a function of the pressure and is highest, within the relevant pressure range, at atmospheric pressure. At the operating conditions of the column in the DCB experiments, the equilibrium amount adsorbed has a 95% credibility interval of $q_1^*$(1 bar, 293 K) $\in [2.24, 3.03]$ mol/kg. We can anticipate, based on this credibility interval, that we can expect quite significant uncertainties in predictions of the DCB model because there is significant uncertainty in the adsorbed amount at equilibrium at the conditions in the column.

Fig. 4

95% credibility intervals for the isotherm model predictions. Solid lines correspond to the nominal isotherm predictions and the shaded regions correspond to the 95% credibility intervals. Each panel corresponds to a different experimental temperature, as indicated on the plot

5.2 Dynamic model uncertainty quantification

We have also applied the Bayesian inference technique to the extraction of the overall heat transfer coefficients from the dynamic breakthrough experiments. Figs. 5 and 6 show the posterior distributions of the inside and outside heat transfer coefficients as determined by Bayesian inference from adsorption and desorption dynamic experiments, respectively. The 95% credibility intervals associated with these posterior distributions can be found in Table 8 for the adsorption and desorption experiments, respectively. The posterior distributions have been extracted using only the internal temperature profile for each experiment. Firstly, we can see that the inside heat transfer coefficient has been inferred successfully from the experimental data due to the significant change between the parametric prior and posterior distributions. On the contrary, the outside heat transfer coefficient has not been inferred successfully in any of the experimental scenarios. We see that there is only a small discrepancy between the prior and posterior distributions for this parameter, which is not significant and likely owes to an insufficient sampling range in the integration of Eqs. 13 and 16. The inability for the tools used in this study to infer the outside heat transfer coefficient could imply that either information about this parameter is not contained within the experimental temperature profiles, or that the model is not utilising this mechanism of heat transfer within the wall energy balance. This will be discussed in more detail in Sect. 6.3.

Fig. 5

Parametric posterior distributions for the dynamic column breakthrough model overall heat transfer coefficients in each adsorption experiment. Y-axis ticks are excluded for brevity (curves are normalised to have a shaded area of unity). Discrete points indicate the fitted parameter values from Sect. 3

Fig. 6

Parametric posterior distributions for the dynamic column breakthrough model overall heat transfer coefficients in each desorption experiment. Y-axis ticks are excluded for brevity (curves are normalised to have a shaded area of unity). Discrete points indicate the fitted parameter values from Sect. 3

Table 8 Parameter point estimates and 95% credibility intervals (CI) for the overall heat transfer coefficients from adsorption and desorption experiments

By comparison of the inside heat transfer coefficients obtained from the adsorption and desorption experiments, we can see that generally the heat transfer coefficients obtained from the desorption experiments take a higher value than those from the adsorption experiments as a function of the inlet gas flow rate. This is unexpected, as we would anticipate that the inside heat transfer coefficient is predominantly a function of the flow rate and should be invariant between adsorption and desorption experiments.

By reference to the nominal fits of the dynamic model shown in Fig 2, we can see that in the adsorption experiments the model provides a much more accurate description of the transient temperature profile than in the corresponding desorption experiments. Therefore, the discrepancy between the two sets of data in obtaining the heat transfer coefficients from the experimental data may be resolved by defaulting to the values obtained from adsorption experiments. This result highlights an important message for practitioners, which is that experimental data should only be used to extract system specific parameters in the case where the model offers a high quality of fit to the experimental data.

5.3 Predictive distributions of process performance indicators

The posterior distributions of the overall heat transfer coefficients have been propagated through the dynamic column breakthrough model to obtain predictive distributions for the experimental system. We have evaluated predictive distributions for a selection of process performance indicators, as shown in Fig. 7. The performance indicators for the system are evaluated as per the definitions provided in Table 9. The 95% credibility intervals associated with the predictive distributions in Fig. 7 are shown in Table 10. The 95% credibility intervals have been used to evaluate an approximate percentage uncertainty for each of the process indicators. We can see for the adsorption experiments that the equilibrium capacity of the bed ($q_\mathrm {br}^*$) does not vary significantly with flow rate. This is to be expected, as this indicator is a property of the system itself rather than of any quantities which vary between the experimental runs. The minor variability with flow rate can be attributed to a decrease in the sharpness of the adsorption front as the flow rate of the experiment decreases. Although there are not significant variations with the flow rate, the equilibrium capacity does show a relatively high uncertainty of approximately $\pm 15.6\%$, on average. We can see in Fig. 7 that the absolute uncertainty in the breakthrough time ($t_\mathrm {br}$) decreases as the flow rate of the experiment increases and that for the temperature rise ($\Delta T_\mathrm {ads}$), the absolute uncertainty increases as the flow rate increases. For the breakthrough time we observe a quasi-constant relative uncertainty of approximately $\pm 16.1\%$ at all flow rates. For the temperature rise we observe a relative uncertainty ranging from $\pm 12.8\%$, at the lowest flow rate, to $\pm 15.3\%$, at the highest flow rate. It is clear that uncertainties of this magnitude are intolerable and do not indicate that the numerical modelling work flow presented in Sect. 3 is robust enough to experimental uncertainties for confident extraction of system specific parameters.

Fig. 7

Predictive distributions for the process performance indicators defined in Table 9, as predicted by the 1D dynamic column breakthrough model. Panels on the left correspond to the adsorption process indicators and panels on the right correspond to the desorption process indicators. Each colour corresponds to a given flow rate, as indicated on the plots

Table 9 Definitions of the process performance indicators used to quantify the uncertainty in the predictions of the dynamic breakthrough model

Table 10 95% credibility intervals (CI) for the predictive distributions of the process performance indicators shown in Fig. 7

Observing the desorption process indicator distributions in Fig. 7 reveals a similar pattern to the corresponding adsorption experiments. We can see that the regeneration time ($t_\mathrm {regen}$) and temperature drop ($\Delta T_\mathrm {des}$) show the same flow rate dependence as the breakthrough time and temperature rise from the adsorption experiments, respectively. The regeneration time has a relative uncertainty which varies with flow rate, ranging from $\pm 21.4\%$ to $\pm 36.4\%$. The temperature drop has a constant relative uncertainty of $\pm 10.1\%$ across flow rates. The heat of regeneration ($Q_\mathrm {regen}$) shows no flow rate dependence, but does display a significant uncertainty of $\pm 17.3 \%$. Again, similarly to the adsorption experiments, we can notice that these uncertainties are generally quite large and are likely to be intolerable in real world applications.

5.4 Dynamic model sensitivity analysis

It is evident from the uncertainty quantification exercise on the dynamic breakthrough model that there are significant uncertainties on the process performance predictions of our experimental breakthrough system. To this end, we are further motivated to pursue the global variance-based sensitivity analysis to seek out routes to improve the robustness of the model. The sensitivity analysis has been conducted for our system using the methodology set out in Sect. 4.2, by varying the fitted model parameters in the uncertainty space defined by the 95% credibility intervals from the uncertainty quantification exercise.

In Fig. 8, we can see the 95% credibility intervals on the dynamic model outputs for the adsorption experiments. For each experiment, we show the outlet mole fraction profile, the internal temperature profile and the internal adsorption profile (at four specified times). We can see that the credibility intervals shown in these plots broadly agree with the assertions which come from the predictive distributions in the previous Sections. Particularly, there is significant uncertainty in the internal profiles, which grows as a function of time, owing to the large uncertainty in the equilibrium state of the system. Figure 9 shows the Sobol indices of this system for each model output at each experimental flow rate. We can see from these plots that there is essentially no significant flow rate dependence of the Sobol indices. The Sobol indices indicate that a very large proportion of the total model variability ($\sim 70\%$) can be attributed to the parameters of the isotherm model which describe its temperature dependence ($b_{0,i}, \Delta U_i$). This serves as a strong indication that there is an inadequacy in the parametrisation of the temperature dependent parameters from the available equilibrium data set. It would be strongly recommended in this case to include equilibrium data at a larger number of temperatures and over a larger range of temperatures to mitigate the significant uncertainties that this inadequacy propagates into the dynamic modelling results.

Fig. 8

95% credibility intervals of the dynamic model outputs for the adsorption experiments. Shown are the outlet mole fraction profiles, internal temperature profiles and the internal adsorption profiles (at several specified times). Each profile is shown at each experimental flow rate, as indicated on the plot. The solid lines correspond to the nominal profiles and the shaded regions correspond to the 95% credibility interval

Fig. 9

Bar charts of the Sobol sensitivity indices for adsorption experiments on the dynamic breakthrough system

The Sobol indices from the adsorption experiments also indicate that the outside heat transfer coefficient has essentially zero effect on the dynamic model outputs. This presents a clear opportunity for model simplification of the wall energy balance, which will be explored further in Sect. 6.3. This outcome also provides an explanation for the inability of Bayesian inference to update the outside heat transfer coefficient prior distribution with any additional information from the experimental temperature profile data. Therefore, it is not possible in this case to conclude whether or not the internal temperature profile contains sufficient information for fitting of the outside heat transfer coefficient. It is only possible to conclude that the model is insensitive to this parameter under the specified experimental conditions and that the model can not, therefore, be used to extract this parameters value.

Figures 10 and 11 show the 95% credibility intervals on the dynamic model outputs, and Sobol indices, respectively, for the desorption experiments. We can see that as anticipated by the predictive distributions of the process performance indicators that the uncertainties in the mole fraction and temperature profile are slightly smaller than those from the corresponding adsorption experiments. For the outlet mole fraction profile and internal adsorption profiles, the Sobol indices follow the same pattern as for the corresponding adsorption experiments. The temperature dependent parameters of the isotherm model largely contribute to the variability in these model outputs. This serves to reinforce the case for the use of additional equilibrium data at a more thorough spectrum of temperatures to reduce the observed uncertainties in the dynamic model. For the internal temperature profile, we can see that the Sobol index of the inside heat transfer coefficient is uncharacteristically large. This follows from the large quantified uncertainty in this model parameter when it is determined based on the temperature profile measured during the desorption experiment. The inadequacy of the energy balances in describing the transient temperature profile during desorption causes a very large parametric uncertainty in $h_\mathrm {in}$, meaning that the corresponding Sobol index is large - given that the indices are calculated from an uncertainty space determined from the actual parametric uncertainty of each model parameter. This serves to demonstrate further that temperature data from desorption experiments should not be used for model fitting, unless the model provides a stronger description of the experimental data than it did during the modelling presented in this study (Sect. 3.2).

Fig. 10

95% credibility intervals of the dynamic model outputs for the desorption experiments. Shown are the outlet mole fraction profiles, internal temperature profiles and the internal adsorption profiles (at several specified times). Each profile is shown at each experimental flow rate, as indicated on the plot. The solid lines correspond to the nominal profiles and the shaded regions correspond to the 95% credibility interval

Fig. 11

Bar charts of the Sobol sensitivity indices for desorption experiments on the dynamic breakthrough system

6 Discussion

6.1 Choice of isotherm model

In this study, we chose rather arbitrarily to apply a dual-site Langmuir (DSL) isotherm model for the description of the equilibrium state of our system (Sect. 3.1). This choice was made based on the DSL model providing an excellent fit to the experimental data which was available to us. However, it would be valid to question this choice and propose the use of a simpler single-site Langmuir (SSL) model instead. Classical model selection exercises are based around the comparison of two or more models by their quality of fit to the experimental data and their number of parameters (in comparison to the number of experimental measurements which have been made). One such approach is the evaluation of the Bayesian information criterion (BIC) [32]. The definition of the BIC is derived from a negative logarithm transform of the probability of observing the set of experimental measurements, provided with a given model, $\mathcal {M}$. Therefore, the model which provides the lowest BIC value is favoured. In the case where we assume that the residuals between the models and the experimental measurements are normally distributed, the BIC is evaluated as [33]:

$$\begin{aligned} \mathrm {BIC}\left( \mathcal {M}_{k_i} \right) = n \ln \left( \frac{\mathrm {RSS}_i}{n} \right) + k_i \ln (n) \end{aligned}$$

(28)

where $\mathcal {M}_{k_i}$ is model i under consideration which has $k_i$ parameters and there are n experimental measurements. The residual sum of squares between isotherm model $\mathcal {M}_{k_i}$ and the experimental equilibrium data, $\mathrm {RSS}_i$, is evaluated as:

$$\begin{aligned} \mathrm {RSS}_i = \sum _{j=1}^{n} \left( q^*_{j,\mathrm {exp}} - q_{i,j}^* \right) ^2 \end{aligned}$$

(29)

where $q^*_{j,\mathrm {exp}}$ is the experimental equilibrium amount adsorbed in measurement j and $q_{i,j}^*$ is the corresponding prediction by model $\mathcal {M}_{k_i}$. The BIC has been evaluated for both the SSL and DSL isotherm models using the available equilibrium data for the adsorption of $\hbox {CO}_2$ onto activated carbon. This resulted in values of $\mathrm {BIC(SSL)} = -570$ and $\mathrm {BIC(DSL)} = -785$. Based on the difference between these two values, [34] suggest that there is very strong evidence to choose the DSL model over the SSL model in this case. However, we contend that naive decision making based only on the residual against the equilibrium data is insufficient.

In Fig. 12, we show the predictive distributions for the equilibrium amount adsorbed at ambient conditions for both the SSL and DSL model. The corresponding 95% credibility intervals for the equilibrium amount adsorbed are [2.24, 3.03] mol/kg for the DSL model and [1.87, 3.15] mol/kg for the SSL model. Although the DSL model does indeed have a narrower credibility interval than the SSL model, the difference is not sufficient to prefer one model over the other, and one should not simply discard the SSL model at this stage.

Fig. 12

Predictive distributions for the equilibrium amount adsorbed at ambient conditions for the single-site Langmuir (left) and dual-site Langmuir (right) isotherm models

Figure 13 shows a series of box plots representing the dynamic process performance indicators for both the adsorption and desorption experiments when using either an SSL or DSL equilibrium model embedded within the dynamic column breakthrough model. The central black line represents the mean of the predictive distribution for each performance indicator and the span of the shaded area represents the 95% credibility interval. Firstly, we can see that both isotherm models lead to quite similar mean values of the performance indicators across all metrics apart from the temperature drop. As it has been discussed above, the desorption temperature profile is poorly described in any case, and it is therefore not concerning that the two approaches do not agree over the metric which corresponds to this model output. The agreement between the two cases on the other mean indicator values shows that, in fact, either model would be sufficient for the description of this experimental system in the nominal case. In terms of uncertainties, we can see that the magnitude of the 95% credibility interval is very comparable across the full set of performance indicators for both the SSL and DSL models. We can see that generally the uncertainty in the process indicators is lower when using the DSL model, but that the magnitude of the improvement by using DSL over SSL is not as significant as one might expect. These results paint a rather complex picture for the choice of the isotherm model. One may wish to make the decision based on the narrowness of the credibility interval for the performance metric associated with the model output which will be used for parameter fitting, where a more narrow credibility interval would be favourable. We have shown that the choice of isotherm model is not as trivial as the comparison of the squared residual against the equilibrium data and also depends upon the final application in which the isotherm will be embedded. Ultimately, either the SSL or DSL isotherm would have been sufficient in this case, despite a classical model selection exercise expressing a high level of preference for the DSL model.

Fig. 13

Box plots of the predictive distributions for the process performance indicators (defined in Table 9) using either the DSL or SSL model embedded within the 1D dynamic column breakthrough model. For each indicator, the solid black line represents the mean of the predictive distribution and the span of the shaded area represents the corresponding 95% credibility interval

6.2 Choice of fitting data for dynamic model

It is standard practice in the adsorption literature to fit the 1D DCB model to both the internal temperature profile (measured using a thermo-couple) and the outlet mole fraction profile (measured using a mass spectrometer) simultaneously [5, 8, 35, 36]. This choice of fitting data is justified by the desire for the dynamic model to capture both transient profiles accurately. However, we would suggest that this is not the optimal approach for extracting accurate values of system specific parameters from the available data. It may be the case that different measurements made during dynamic experiments contain distinctly different information about the system and cannot necessarily be used simultaneously for the extraction of a given set of model parameters. In the modelling presented in Sect. 3, we fit the dynamic column breakthrough model to the internal temperature profile using the overall inside heat transfer coefficient as the sole fitting parameter (while predicting the outside heat transfer coefficient using Eq. 5). Now, we wish to explore the relationship between the heat transfer coefficient and the outlet mole fraction profile. Before using measurements of multiple different quantities as fitting data to extract parameter values, we must first answer some important questions. Firstly, we need to determine if the outlet mole fraction profile contains any information about the inside heat transfer coefficient. Secondly, if the outlet mole fraction profile does contain information about the inside heat transfer coefficient, we need to determine if this information is consistent with that provided by the measurement of the internal temperature profile.

To this end, we have carried out the Bayesian inference of the inside heat transfer coefficient using the 1D DCB model against either the internal temperature profile measurements, or the outlet mole fraction profile measurements, for each of the experimental adsorption scenarios. Figure 14 shows the results of this exercise. The central black line represents the mean of the parametric posterior distribution for the inside heat transfer coefficient and the span of the shaded area represents the corresponding 95% credibility interval. We can see that there is significant disagreement between the heat transfer coefficient values extracted from each set of data. As can be anticipated from physical reasoning, the heat transfer coefficient as extracted from the internal temperature profile shows a strong dependence on the inlet flow rate of the experiment. We can see that the heat transfer coefficient values as extracted from the outlet mole fraction profile do not show a strong, if any, flow rate dependence. We can also see that the credibility intervals for the heat transfer coefficients are more narrow when extracting the parameter from the internal temperature profile than the outlet mole fraction profile. This suggests that the internal temperature profile contains a higher quality of information about the heat transfer coefficient than the outlet mole fraction profile.

Fig. 14

Box plots of the predictive distributions for the inside heat transfer coefficients obtained using either the internal temperature profile ($T_\mathrm {tc}(\tau )$) or the outlet mole fraction profile ($y_{1,\mathrm {out}}(\tau )$) as experimental data. For each distribution, the solid black line represents the mean of the predictive distribution and the span of the shaded area represents the corresponding 95% credibility interval

We can also see, with reference to the solid black lines in Fig. 14, that the value of the heat transfer coefficient from each set of data is in relative agreement at the highest experimental flow rate. However, this agreement drifts away as the flow rate decreases. By observing the quality of fit in the nominal case to the outlet mole fraction profile (Fig. 2) we can notice that the outlet mole fraction profile is most accurately described at the highest flow rate, but is over dispersed at the lower flow rates. This indicates that the modelling of the longitudinal dispersion coefficient by the correlation given in Eq. 4 is not sufficient for our system. Difficulties with modelling longitudinal dispersion are well known within the adsorption field [37], particularly when the adsorbent pellets in the packed bed are non-spherical (as in our case). However, by using fitting parameters, such as the heat transfer coefficient, to force the model to describe the outlet mole fraction profile well, we create two potential issues. Firstly, we invalidate the value of the heat transfer coefficient, as it will become skewed from its true value to allow an accurate description of the outlet mole fraction profile. This compromises the subsequent predictive capabilities of the developed model. Secondly, we fail to address the inadequacies of our modelling work flow in describing the longitudinal dispersion coefficient. By using Bayesian statistical tools, we are able to assess the quantity and quality of information contained within each individual series of experimental measurements to allow for a more critical analysis of the fitting procedures we routinely apply. We would recommend that this should be an important step in further work in this area to ensure that we report accurate parametrisations of physical processes occurring within our adsorption systems. It is particularly important in the context of model-based design and optimization of adsorption systems that we report accurate parametrisations of processes such as dispersion, adsorption kinetics and heat transfer, such that our modelling can be reliable beyond the scope of only analysing conditions described by available experimental data.

6.3 Simplification of wall energy balance

We have seen in Sect. 5.4 that the outside heat transfer coefficient appears to have no influence over the outputs of the 1D DCB model at the conditions analysed in this study, as indicated by a Sobol index of zero for this parameter in all of the simulated scenarios. This presents an opportunity for model simplification of the wall energy balance equation. To this end, we have proposed three alternative energy balance formulations to test which mechanisms of heat transfer are necessary within this system to accurately describe the flow of heat. Firstly, we may use the “full model” for the wall energy balance, as specified in Table 3. Secondly, we may use a “partially reduced model” in which the outside heat transfer coefficient is neglected. The resulting dimensionless wall energy balance in this case is:

$$\begin{aligned} \frac{\partial \bar{T}_{\mathrm {w}}}{\partial \tau } = \Pi _1 \frac{\partial ^2 \bar{T_\mathrm {w}}}{\partial Z^2} + \Pi _2 \left( \bar{T} - \bar{T}_\mathrm {w} \right) \end{aligned}$$

(30)

Finally, we may also consider a “fully reduced model” in which the wall energy balance is neglected entirely. In this case the model contains one less partial differential equation and the column energy balance is modified such that the temperature driving force applied to the inside heat transfer coefficient is taken directly as $(\bar{T} - \bar{T}_\mathrm {a})$, where $\bar{T}_\mathrm {a}$ is the constant ambient temperature. Figure 15 shows the internal temperature profile for these three energy balance models in comparison to the experimental data for the experimental scenario corresponding to adsorption at an inlet flow rate of $f_\mathrm {in} = 200$ ccm. We can see that removing the term which includes the outside heat transfer coefficient from the wall energy balance has no measurable effect on the column temperature profile. However, when removing the wall energy balance entirely from the modelling, the temperature profile changes and becomes insufficient for description of the experimental data. This indicates that the wall energy balance does play an important role in moderation of the heat within the column, but that heat transfer to the ambient surroundings from the column wall is not an important mechanism of heat transfer. Therefore, the “partially reduced model” appears to be sufficient in this case. This is a useful result for potentially two reasons. Firstly, practitioners need not waste time identifying and applying an appropriate correlation for evaluating the outside heat transfer coefficient. Secondly, in the case where the outside heat transfer coefficient would be fitted against the experimental data, one can neglect this parameter and reduce the number of forward dynamic models which must be evaluated to carry out the fitting. This would reduce, potentially significantly, the computational burden of the fitting exercise.

Fig. 15

a Internal temperature profiles as compared to experimental measurements (solid blue symbols) using either the full wall energy balance model (solid red line), the partially reduced wall energy balance model (dashed black line) or the fully reduced wall energy balance model (dashed red line). b Transient profiles of heat fluxes within the column wall for the adsorption experiment with an inlet flow rate of $f_\mathrm {in} = 200$ ccm. Shown are the fluxes due to conduction (red), heat exchanged between the gas-phase and the wall (blue) and heat exchanged between the column wall and the surroundings (grey) (Color figure online)

We have identified that the outside heat transfer coefficient is not necessary for the description of this experimental breakthrough system. However, before neglecting the parameter entirely we wish to gain some understanding as to why this parameter is not relevant to the system. Figure 15 shows the various heat fluxes of the full wall energy balance as functions of time, at the location of the thermo-couple ($Z = 1/4$). The term $Q_\mathrm {cond}$ is the heat flux owing to conduction in the column wall and the terms $Q_\mathrm {in}$ and $Q_\mathrm {out}$ are the heat fluxes owing to the transfer of heat from the column to the wall, and from the wall to the surroundings, respectively. We can see, as anticipated, that the heat flux for the transfer of heat from the wall to the surroundings is very small in magnitude compared to the other heat fluxes in the column wall. We can see that initially heat transfer in the wall is dominated by conduction. This is because as heat is transferred from the adsorption front into the column wall upstream of the location of the thermo-couple, conduction in the wall disperses this heat longitudinally away from the position of the adsorption front. As the adsorption front reaches the location of the thermo-couple, heat is transferred from the front into the column wall. We can see from the corresponding inversion of the conduction profile that this heat is removed almost entirely by longitudinal conduction within the column wall. Owing to the conservation of energy principle, we understand that this heat must be leaving the system somewhere. We propose that in the present formulation of the 1D DCB model that the boundary condition of tight thermal contact between the wall and the surroundings (Table 4) is causing the model to predict the loss of heat from the system almost exclusively from the ends of the column wall. This is because this boundary condition fixes the temperature of the column wall to the ambient temperature at both ends of the column and essentially provides a heat sink for heat transferred to the ends of the column by conduction. By using this boundary condition, we provide a route for heat to escape the system which has a very low thermal resistance in comparison to loss of heat to the ambient air surrounding the column. This conclusion is supported by forward modelling exercises in which we disable longitudinal conduction in the column wall by setting the thermal conductivity of the wall to $K_\mathrm {w} = 0$. In this case, the outside heat transfer coefficient empirically regains a degree of control over the shape of the tail of the internal column temperature profile.

We propose that there are two potential resolutions to this conflict. Firstly, one could explore alternative boundary conditions for the closure of the wall energy balance such that the outside heat transfer coefficient regains relevance. Secondly, one can make peace with this modelling inadequacy and exclude the outside heat transfer coefficient from the model entirely to reduce the overall computational effort of analysing the dynamic experiments.

7 Conclusions

We have shown how Bayesian inference can be applied for the quantification and propagation of uncertainties in dynamic column experiments with a single adsorbing component. We have also integrated a global variance-based sensitivity analysis using the Sobol method with the uncertainty quantification exercise to identify opportunities to improve the robustness of the numerical modelling and to simplify the model formulation.

We have found that there are moderate uncertainties in the analysis of the DCB system. The outlet mole fraction profile, internal temperature profile and internal adsorption profiles all experience uncertainties on the order of approximately $\pm 15\%$ for both adsorption and desorption experiments. We would suggest that these uncertainties are intolerably large for the parametrisation of system specific physical processes and for the validation of the numerical model through comparison to experimental data. The global sensitivity analysis of the system has revealed that uncertainties in the dynamic model outputs owe significantly to uncertainties in the parameters which describe the temperature dependence of the equilibrium state of the system. We propose that these uncertainties could be effectively reduced by including isotherms in the equilibrium data set at more temperatures to provide both a better range of temperatures, and improved granularity within the specified temperature range. This aspect of the results in particular should attract significant further attention to improve the robustness of dynamic modelling throughout the adsorption community. We found that the outside heat transfer coefficient has essentially no influence over the simulated temperature profile, and that the model boundary conditions should be modified if this parameter is not to be excluded from the modelling.

We also make the following additional recommendations for the procedure of analysing DCB experiments. Firstly, the choice of isotherm model should not be made solely based on the quality of fit to the experimental equilibrium data. We have shown that the decision runs deeper than this and must also include considerations relating to the uncertainty in relevant dynamic model outputs, in addition to the performance of the isotherm against the equilibrium data. Secondly, we have shown quantitatively that heat transfer coefficients should not be determined from internal temperature profiles measured during desorption experiments, through the comparison of parametric posterior distributions obtained from both adsorption and desorption experiments. Finally, we propose that more careful attention should be given in general when choosing the data for fitting dynamic models to experimental measurements to ensure accurate parametrisations of the physical processes are prioritised over forcing the models to fit the experimental data to the highest degree. We believe that this practice masks inadequacies in the modelling workflow which are better off addressed, rather than ignored.

Appendices

Appendix A Non-dimensionalisation of 1D DCB model

In dimensional form, the 1D DCB model is defined as follows. The overall material balance is:

$$\begin{aligned} \frac{\partial p}{\partial t} - \frac{p}{T}\frac{\partial T}{\partial t} = -T\frac{\partial }{\partial z}\left( \frac{pv}{T} \right) - \frac{RT\rho _{\mathrm {b}}}{\epsilon }\frac{\partial q_1}{\partial t} \end{aligned}$$

(A1)

The component material balance for $\hbox {CO}_2$ is:

$$\begin{aligned}&\frac{\partial y_1}{\partial t} + \frac{y_1}{p}\frac{\partial p}{\partial t} - \frac{y_1}{T}\frac{\partial T}{\partial t} = \frac{T}{p}D_{\mathrm {L}}\frac{\partial }{\partial z}\left( \frac{p}{T} \frac{\partial y_1}{\partial z} \right) - ...\nonumber \\&\frac{T}{p}\frac{\partial }{\partial z}\left( \frac{y_1 p v}{T} \right) - \frac{RT \rho _{\mathrm {b}}}{p \epsilon }\frac{\partial q_1}{\partial t} \end{aligned}$$

(A2)

The pressure drop along the column is given by Darcy’s law, which is:

$$\begin{aligned} -\frac{\partial p}{\partial z} = \frac{150}{4 r_{\mathrm {p}}^2} \left( \frac{1-\epsilon }{\epsilon } \right) ^2 \mu v \end{aligned}$$

(A3)

The column energy balance is:

$$\begin{aligned}&\left[ \frac{\rho _{\mathrm {b}}}{\epsilon } \left( C_{\mathrm {p,s}} + \omega _{\mathrm {a}} C_{\mathrm {p,a}}q_1 \right) \right] \frac{\partial T}{\partial t} = \frac{K_{\mathrm {z}}}{\epsilon }\frac{\partial ^2 T}{\partial z^2} - ... \nonumber \\&\frac{\omega _{\mathrm {g}} C_{\mathrm {p,g}}}{R}\frac{\partial }{\partial z}(vp) - \frac{\omega _{\mathrm {g}} C _{\mathrm {p,g}}}{R}\frac{\partial p}{\partial t} - \frac{\omega _{\mathrm {a}} \rho _{\mathrm {b}}}{\epsilon }C_{\mathrm {p,a}}T\frac{\partial q_1}{\partial t} + ... \nonumber \\&\frac{\rho _{\mathrm {b}}}{\epsilon }\left( (-\Delta U_1 + RT)\frac{\partial q_1}{\partial t} \right) - \frac{2 h_{\mathrm {in}}}{\epsilon r_{\mathrm {in}}}(T - T_{\mathrm {w}}) \end{aligned}$$

(A4)

And the wall energy balance is:

$$\begin{aligned}&\rho _{\mathrm {w}} C_{\mathrm {p,w}} \frac{\partial T_{\mathrm {w}}}{\partial t} = K_{\mathrm {w}} \frac{\partial ^2 T_{\mathrm {w}}}{\partial z^2} + \frac{2r_{\mathrm {in}}h_{\mathrm {in}}}{r_{\mathrm {out}}^2 - r_{\mathrm {in}}^2}(T-T_{\mathrm {w}}) - ...\nonumber \\&\frac{2r_{\mathrm {out}}h_{\mathrm {out}}}{r_{\mathrm {out}}^2 - r_{\mathrm {in}}^2}(T_{\mathrm {w}}-T_{\mathrm {a}}) \end{aligned}$$

(A5)

In Eq. A4, the molecular weight of the gas phase, $\omega _\mathrm {g}$, is given by the following relationship:

$$\begin{aligned} \omega _\mathrm {g} = y_1 \omega _1 + (1 - y_1)\omega _2 \end{aligned}$$

(A6)

Where $\omega _1$ and $\omega _2$ are the molecular weight of $\hbox {CO}_2$ and He, respectively. The molecular weight of the adsorbed phase, $\omega _\mathrm {a}$, is equal to the molecular weight of $\hbox {CO}_2$.

The non-dimensional variables used in the 1D DCB model (Table 3) are defined as follows:

$$\begin{aligned} \bar{p}= & {} \frac{p}{p_0}, \bar{T} = \frac{T}{T_0}, \bar{T}_{\mathrm {w}} = \frac{T_{\mathrm {w}}}{T_0}, \bar{T}_{\mathrm {a}} = \frac{T_{\mathrm {a}}}{T_0}, x_i = \frac{q_i}{q_{\mathrm {s,}0}} \\ \bar{v}= & {} \frac{v}{v_0}, Z = \frac{z}{L}, \tau = t\frac{v_0}{L} \\ p_0= & {} p_{\mathrm {F}}, T_0 = T_{\mathrm {F}}, v_0 = v_{\mathrm {F}}, q_{\mathrm {s,}0} = q_{\mathrm {s},1} \end{aligned}$$

The dimensionless groups of the model are defined as follows:

$$\begin{aligned} \psi= & {} \frac{R T_0 \rho _\mathrm {b} q_{\mathrm {s},0}}{p_0 \epsilon } \end{aligned}$$

(A7)

$$\begin{aligned} Pe= & {} \frac{v_0 L}{D_\mathrm {L}}\end{aligned}$$

(A8)

$$\begin{aligned} \alpha _1= & {} \frac{k_1 L}{v_0}\end{aligned}$$

(A9)

$$\begin{aligned} \Omega _1= & {} \frac{ \left( \frac{K_\mathrm {z}}{v_0 L} \right) }{\rho _\mathrm {b} \left( C_\mathrm {p,s} + \omega _\mathrm {a} C_\mathrm {p,a} q_{\mathrm {s},0} x_1 \right) }\end{aligned}$$

(A10)

$$\begin{aligned} \Omega _2= & {} \frac{ \left( \frac{\omega _g C_\mathrm {p,g} p_0}{R T_0} \right) }{\frac{\rho _\mathrm {b}}{\epsilon } \left( C_\mathrm {p,s} + \omega _\mathrm {a} C_\mathrm {p,a} q_{\mathrm {s},0} x_1 \right) }\end{aligned}$$

(A11)

$$\begin{aligned} \Omega _3= & {} \frac{\omega _\mathrm {a} C_\mathrm {p,a} q_{\mathrm {s},0}}{\left( C_\mathrm {p,s} + \omega _\mathrm {a} C_\mathrm {p,a} q_{\mathrm {s},0} x_1 \right) }\end{aligned}$$

(A12)

$$\begin{aligned} \Omega _4= & {} \frac{ \left( \frac{2 h_\mathrm {in} L}{r_\mathrm {in} v_0} \right) }{\rho _\mathrm {b} \left( C_\mathrm {p,s} + \omega _\mathrm {a} C_\mathrm {p,a} q_{\mathrm {s},0} x_1 \right) }\end{aligned}$$

(A13)

$$\begin{aligned} \sigma _1= & {} \frac{ \left[ \frac{q_{\mathrm {s},0}}{T_0} \left( -\Delta U_1 + R T_0 \bar{T} \right) \right] }{C_\mathrm {p,s} + \omega _\mathrm {a} C_\mathrm {p,a} q_{\mathrm {s},0} x_1}\end{aligned}$$

(A14)

$$\begin{aligned} \Pi _1= & {} \frac{K_\mathrm {w}}{\rho _\mathrm {w} C_\mathrm {p,w} v_0 L}\end{aligned}$$

(A15)

$$\begin{aligned} \Pi _2= & {} \frac{2 r_\mathrm {in} h_\mathrm {in}}{r_\mathrm {out}^2 - r_\mathrm {in}^2} \cdot \frac{L}{\rho _\mathrm {w} c_\mathrm {p,w} v_0}\end{aligned}$$

(A16)

$$\begin{aligned} \Pi _3= & {} \frac{2 r_\mathrm {out} h_\mathrm {out}}{r_\mathrm {out}^2 - r_\mathrm {in}^2} \cdot \frac{L}{\rho _\mathrm {w} c_\mathrm {p,w} v_0} \end{aligned}$$

(A17)

Maximum entropy principle

The maximum entropy principle states that the prior distribution which best represents our initial knowledge of the parametric distribution is that which maximises the “Shannon entropy” of the prior distribution, subject to constraints defined by our initial knowledge. This concept follows naturally from the physical idea of entropy, in which systems with a larger entropy tend to require a smaller amount of information to be described. Therefore, by maximising the Shannon entropy of the prior distribution, we incorporate as little information as possible into our choice of the distribution, outside of constraints which we specifically apply. This avoids a potential situation arising in which we bias the information described by the prior distribution by our choice of the form of the distribution. The Shannon entropy, $H(\theta _j)$, of the marginal prior distribution, $P(\theta _j)$, for parameter $\theta _j$, is defined as [38]:

$$\begin{aligned} H(\theta _j) = -P(\theta _j)\log (P(\theta _j)) \end{aligned}$$

(A18)

There are two constraints on our choice of the prior distribution which maximises the entropy $H(\theta _j)$. Firstly, whatever the choice of probability distribution is, it must normalise to unity:

$$\begin{aligned} \int _{\theta _j} P(\theta _j) \, d\theta _j = 1 \end{aligned}$$

(A19)

Secondly, in the context of this study, we are aware of the fitted values of the model parameters from the parameter extraction exercise carried out in Sect. 3. Therefore, we can assume that the mean of the prior distribution should take the fitted parameter value, $\theta _j^{\mathrm {nom}}$. So, it follows that the first central moment of the prior distribution should be:

$$\begin{aligned} \int _{\theta _j} \theta _j \cdot P(\theta _j) \, d\theta _j = \theta _j^{\mathrm {nom}} \end{aligned}$$

(A20)

Subject to the constraints of Eqs. A19–A20, we can find the best choice of prior distribution by solving the following optimisation problem:

$$\begin{aligned} \max _{P(\theta _j)} H(\theta _j) = -P(\theta _j)\log (P(\theta _j)) \end{aligned}$$

This problem can be solved by application of the conditions of Karush, Kuhn and Tucker (KKT) [39], which derive the maximum of a functional constrained by equality conditions as the stationary point of the corresponding Lagrangian, $\nabla \mathcal {L}(P(\theta _j)^*, \varvec{\lambda }^*) = 0$. Solution of the above optimization problem by application of the KKT conditions leads to an exponential marginal prior distribution for parameter $\theta _j$:

$$\begin{aligned} P(\theta _j) = \frac{1}{\theta _j^{\mathrm {nom}}}\exp \left( -\theta _j/\theta _j^{\mathrm {nom}} \right) \end{aligned}$$

(A21)