A qualitative approach to adsorption mechanism identification on microporous carbonaceous surfaces

Abstract

The paper presents results of research on identification of localized and other adsorption mechanisms, on geometrically heterogeneous graphite-like carbonaceous surfaces. It attempts to get an insight into properties of individual adsorptive molecule movement near attractive adsorption sites, arising from adsorbent surface geometrical heterogeneities. In particular, a shape and volume of space occupied by the continuously moving molecule mass center are investigated. To this aim, kinematic equilibrium of the particle moving near a hypothetical microporous carbonaceous adsorbent wall is considered, and then compared with thermodynamic equilibrium. The proposed approach enables to examine effects of certain surface geometry on the shape and volume of space occupied by adsorbed particles, and so to outline temperature conditions for the localized adsorption mechanism predomination. Thus, it provides a cognitive basis to answer the question, what particular mechanism (localized or other—e.g. mobile) should be assumed for a class of adsorption systems in order to select the most appropriate mathematical adsorption model. Hence, it makes it possible for more reliable examination of real porous structures, based on adsorption measurements.

1 Introduction

Practical identification of material porous structure from experimental adsorption measurements requires a mathematical description of adsorption mechanism. A number of theoretical investigations were elaborated in order to reliably describe the adsorption equilibrium, where different aspects of the adsorption mechanism are stressed (Dąbrowski 2001; Sing et al. 1985). Nevertheless, the mechanism itself is a basic assumption of any mathematical model, and its arbitrary selection is most commonly related to the surface description: heterogeneous for localized mechanism and homogeneous for others.

The classical approach is based on a lattice surface model that leads to the Langmuir (Langmuir 1916), Fowler–Guggenheim (Fowler and Guggenheim 1940) and BET formulas for localized adsorption, while the mobile adsorption is described by Volmer (Volmer 1925) or Hill-de Boer (1968; Hill 1946) equations. On the other hand a potential theory of adsorption [for example Dubinin-Radushkievitch model (Dubinin 1989)] is successfully employed, assuming formation of a quasi liquid like phase near the solid surface, i.e. based on mobile adsorption mechanism. Recently, this approach is intensively developed in the form of Density Functional Theory formalism [DFT, (Jagiełło and Olivier 2013; Lastoskie and Gubbins 2000)], where the adsorbate molecules are treated with the same formulae as describing the liquid bulk phase, but affected by the solid surface attractive forces.

Furthermore, in our earlier works we proposed a new approach for the localized adsorption modeling, in which a clustering based mechanism is exposed. From a formal viewpoint, it is a far generalization of BET multilayer adsorption (i.e. adsorbate clusters may be viewed as localized layers). Geometrical and energetic constraints of the clusters formation are taken into account, as well as configurational effects coming from the clusterization mechanism. Resultant general formula, referred to as a uniBET model may be adapted to random microporous structures, yielding LBET class adsorption models. The latter is applicable to the microporous heterogeneous structures examination, by employing a multivariant fitting procedure (Kwiatkowski et al. 2011, 2014).

An elaboration of a comprehensive mathematical model describing adsorption phenomena and taking into account localized and other mechanisms is almost virtually impossible [due to chemical and structural diversity of the porous materials (Jagiełło and Olivier 2013)]. Hence, the mechanism in the abovementioned models is commonly assumed intuitively, based on a presumed picture of pore shape and size. For regular structures (nanotubes, slit-like pores, etc.) mobile adsorption may be more appropriate, while for irregular or random pores localized adsorption mechanism seems to be closer to a physical reality. Nevertheless, even in relatively regular structures there are local irregularities (rows, niches, cones, etc.). The question is, how far such places affect the adsorbate molecule behavior near the solid surface and in what extent the local shape of the surface affects the particle movement making it closer to the localized adsorption mechanism.

This paper attempts to answer such questions by computer analysis of adsorptive molecule movement constraints, due to the surface attractive forces. In particular, a shape and volume of the space occupied by the continuously moving molecule mass center are investigated. Subsequently, conditions for the localized and other adsorption mechanisms are outlined, when compared to the liquid bulk phase properties. To this aim, kinematic equilibrium of individual adsorbate particle near the adsorbent wall is taken under considerations, and then examined in contrast with thermodynamic equilibrium. The adsorbent surface is represented by a set of carbon atoms forming predefined graphite-like nanostructure, and hence included geometrical heterogeneity generates attractive adsorption sites (e.g. nanocone, nanocubes). Such calculations enable to examine the effects of particular surface geometry on the shape and volume of adsorbed particles, and so identify a temperature conditions for particular adsorption mechanism domination. The results of these investigations may be useful in selection of the most appropriate mathematical adsorption model, for examination of real porous structures based on adsorption measurements. Hence, it makes it possible to evaluate the porous structure properties more reliably.

2 Theoretical basis

2.1 Kinematics and Maxwell–Boltzmann averaging

Let us consider a movement of an individual particle of a volatile phase (adsorptive molecule) near an adsorbent solid wall, in time intervals t _int between collisions with other adsorptive molecules. The averaged, in time t, molecule movement is limited by an equipotential boundary surface U _bdry (t). On this surface a kinetic energy of two degrees of freedom k _B τ(t) is compensated by a corresponding decrease in an average solid–fluid potential U _avge (t). Thus, the equilibrium of the molecule movement may be described kinematically by the following formulae:

$$t_{int} U_{bdry} - \int\limits_{0}^{{t_{int} }} {U_{avge} (t)} dt - k_{B} \int\limits_{0}^{{t_{int} }} {\tau (t)} dt = 0$$

(1)

where k _B stands for a Boltzmann constant.

Let us assume that the mass center of this particle moves within a space of volume V _fi (free space) and may be found at any phase-space variables v with the same probability (i.e. v ≤ V _fi ). Hence, time averages t over the particle movement after a suitable lapse of time, frequently longer than t _int , correspond to macro scale ensemble averages and the volume in space is preserved, see (Hansen and McDonald 2006). Thereby, kinetic energy $k_{B} \tau \left( t \right)$ averaged in time may be equivalently represented by an energy k _B τ _i averaged over the movement space in volume v. Thus, the kinetic energy is expressed in units [K] and τ _i denotes an average particle “temperature”:

$$\tau_{i} = \frac{1}{{V_{fi} }}\int\limits_{0}^{{V_{fi} }} {\tau (v)} dv$$

(2)

Subsequently, the average solid–fluid potential U _avge (t) and boundary potential U _bdry (t) may be equivalently described by analogous formulas leading to the U _avge (V _fi ) and U _bdry (V _fi ).

At the boundary, when considering individual particle, the potential is generated by the solid–fluid adhesive forces producing component U _bdry (V _fi ). Nevertheless, when considering the macro scale, at the boundary, potential is also generated by possible collisions of adsorptive particles in the volatile phase and depends on an external pressure p (i.e. expressed as a pV potential).

Total effects of interactions of the adsorbate particle with volatile phase, represented by the pressure p, may be partitioned into subsystems using a collision probability s _pi /s _p of an individual i-th particle. Kinematically, interactions with other particles represented by the pV potential may be related to the free volume V _fi . Hence, the interaction force p·s _pi should be recalculated to an effective pressure p _fi , and then multiplied by the volume V _fi :

$$p_{fi} = \frac{{s_{pi} }}{{s_{fi} }}p,\quad{\text{and}}\quad pV \to \sum\limits_{i = 1}^{N} {\frac{{s_{pi} }}{{s_{fi} }}V_{fi} p} ,$$

(3)

where s _pi is an open surface, limiting the particle movement in volume V _pi and corresponding to the open surface s _fi , limiting the particle mass center movement in volume V _fi . For a convenience, the relationship s _fi /V _fi may be denoted as a specific surface area of the space of particles mass center a _fi .

Hence, the kinematic equilibrium of the i-th particle takes the form:

$$p\frac{{s_{pi} }}{{a_{fi} }} + U_{bdry} (V_{fi} ) - U_{avge} (V_{fi} ) - k_{B} \tau_{i} = 0$$

(4)

The values for the particle volume V _pi and the surface ratio s _pi /s _fi may be roughly evaluated by replacing the real free space of the adsorbate molecule with the sphere of the same volume V _fi and corresponding diameter d _fi . Then the volume V _pi is calculated as a sphere with the diameter d _pi , increased by the adsorbate hard sphere core diameter σ _ff :

$$d_{pi} = d_{fi} + \sigma_{ff} ,\quad d_{fi} \mathop = \limits^{def} \left( {\frac{6}{\pi }V_{fi} } \right)^{{\frac{1}{3}}} ,\quad V_{p\,i} = \frac{\pi }{6}d_{pi}^{3} ,\quad \frac{{s_{pi} }}{{s_{fi} }} = \left( {\frac{{d_{pi} }}{{d_{fi} }}} \right)^{2}$$

(5)

In our study solid is represented by a set of carbon atoms spaced like in a graphite sheet and forming a nanostructure of a predefined shape (nanotube, nanocone or nanocubic niche etc.). Hence, the carbon-fluid potential at a given k-th position of adsorbate molecule mass center is calculated by summing up the LJ_12-6 potential u _C-fk (Lennard-Jones 1931). The latter is performed over all set of carbon atoms forming the solid wall, with a corresponding carbon-fluid intermolecular distance r _C-fk :

$$u_{{C - f_{k} }} = 4\varepsilon_{C - f} \left[\left( {\frac{{\sigma_{C - f} }}{{r_{{C - f_{k} }} }}} \right)^{12} - \left( {\frac{{\sigma_{C - f} }}{{r_{{C - f_{k} }} }}} \right)^{6} \right]$$

(6)

where ε _C-fk and σ _C-fk are the potential well-depth and intermolecular diameter, respectively, both calculated applying Lorentz-Berthelot (Berthelot 1898; Lorentz 1881) mixing rules from pure-species quantities.

The boundary potential U _bdry (V _fi ) is taken arbitrary as a fixed value of $\sum\limits_{C} {u_{{C - f_{k} }} }$. Hence, the average potential U _avge (V _fi ) is:

$$U_{avge} (V_{fi} ) = \frac{1}{{V_{fi} }}\int_{0}^{{V_{fi} }} {U_{bdry} (v)dv}$$

(7)

The values for V _fi , corresponding to a given U _bdry , may be evaluated with analytical or Monte-Carlo calculations. The analytical calculations run initially by searching consecutive points k at an equipotential surface s _fi of a given U _bdry . If $\sum\limits_{C} {u_{{C - f_{k} }} }$ ≈ U _bdry the k-th point is accepted as belonging to the surface s _fi (more precisely, to a volume δs _fi ·δr _C-fk ). Then, the volume V _fi is determined, as a volume of space limited by all points found at the s _fi surface. Starting with a minimum potential U _bdry for which V _fi  ≈ 0, the calculations run step by step with an increasing U _bdry by a small value δU _bdry . In the Monte-Carlo technique u _C-fk is calculated many times for randomly chosen points k (shots). The point k is accepted as an admissible n _adm if respects geometrical constraints of the solid and as a successful n _v if additionally fulfills the relation $\sum\limits_{C} {u_{{C - f_{k} }} }$ ≤ U _bdry . Having an appropriately large number of admissible shots n _adm  > 10⁶ with a number n _v of successful shots, one can calculate the volume V _fi corresponding to a given U _bdry : V _fi  ≈ n _v /n _adm . In both techniques the values for U _avge (V _fi ) are calculated by numerical integration of the U _bdry (V _fi )– see Eq. (7). Subsequently the corresponding particle volume V _pi is calculated according to Eq. (5).

So far as a movement of a single particle is considered only, one should assume that there are no particles in volatile phase, i.e. p = 0. In this case, having the values for U _avge (V _pi ) and U _bdry (V _pi ) one can calculate with Eq. (4) the values for τ _i corresponding to a given V _pi . For a convenience, the quantities in Eq. (4) may be also related to one mole of particles, enabling to calculate the kinematic equilibrium temperature τ _i (corresponding to a given V _fi , V _pi , and so to U _avge (V _pi ), U _bdry (V _pi )):

$$\tau_{i} = \left( {\frac{{U_{bdry} (V_{pi} ) - U_{avge} (V_{pi} )}}{{k_{B} }}} \right) \times \frac{{N_{A} }}{{N_{A} }} = \frac{{U_{m} (V_{{m_{pi} }} ) - U_{{m_{adh} }} (V_{{m_{pi} }} )}}{R}$$

(8)

and

$$V_{{m{}_{fi}}} \mathop = \limits^{def} N_{A} V_{fi} ,\quad V_{{m_{pi} }} \mathop = \limits^{def} N_{A} V_{pi} ,\quad U_{m} (V_{{m_{pi} }} )\mathop = \limits^{def} N_{A} U_{bdry} (V_{{m_{pi} }} ),\quad\,U_{{m_{adh} }} (V_{{m_{pi} }} )\mathop = \limits^{def} N_{A} U_{avge} (V_{{m_{pi} }} )$$

(9)

where N _A is an Avogadro constant and R is a gas constant.

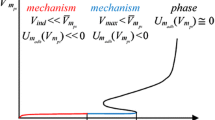
The functions U _m (V _mpi ) and U _madh (V _mpi ) are schematically shown in Fig. 1. Subsequently, the inverse relationship V _mpi (τ _i ) calculated with Eq. (8) is schematically shown in Fig. 2.

Fig. 1

Schematic profile of solid–fluid potential U _madh (V _mpi ) function (dashed line) and boundary solid–fluid potential U _m (V _mpi ) function (solid line) for an individual particle moving in a space of volume V _mpi

Fig. 2

Hypothetical V _mpi (τ _i ) relationship for one mole of individual particles moving in the free volume space V _mfi (τ _i ) calculated with Eq. (8). V _ind stands for the maximum volume V _mpi (τ _i ) of one mole of individual particles, at the temperature τ _ind . V _max stands for the maximum occupied volume at the individual spaces V _mpi (τ _i ) or shared volume of space V _mpi (τ _i ) with j molecules, at the temperature τ _max . The intervals 0 < τ _i  ≤ τ _ind and τ _ind  < τ _i  ≤ τ _max corresponds to the localized or possible mobile mechanisms, respectively

Let us denote V _ind as a maximum volume of a free movement space (e.g. close to an averaged volume of particle movement at a critical point), thus it is not likely that this space may be shared with other molecules. The corresponding temperature τ _ind is found with Eq. (8) and τ _ind  = arg {min {V _mpi (τ _ind ) = V _ind }}. When the particle temperature is appropriately low, i.e. τ _i  ≤ τ _ind and so V _mpi (τ _i ) ≤ V _ind , one may assume that it occupies a localized site, so the localized monolayer adsorption takes place. If the temperature is τ _i  > τ _ind , but is still appropriately low, that the particle may be captured into an interaction potential well, one may assume that the particle may easily occupy an individual spaces V _mpi (τ _i ) or joint a space V _mpi (τ _i ) containing j molecules. Thus, maximum volume occupied by individual particles j (depending on pressure p) may be expressed in general form V _max  = V _mpi (τ _i )·j, and so the corresponding maximum temperature τ _max  = arg{V _mpi (τ _i ) = V _max  ≫ V _ind }. If the space of volume V _max covers a large fraction of the solid surface, adsorption mechanism may be seen as a purely mobile, otherwise it may be closer to the clustering based or to locally mobile adsorption (based on forming a local 2D fluid). Nevertheless, the derived formulas are legitimate only for characterization of localized adsorption mechanism properties. Thus they don’t decide on the mechanism in the temperature range τ _ind  < τ _i  ≤ τ _max (i.e. it may be mobile or clustering based mechanism). Finally, particles of the temperature τ _i  > τ _max are treated as belonging to the volatile phase (not adsorbed).

While accepting the abovementioned criteria, one should consider that the total volume V _mpi and potentials U _madh (V _mpi ), U _m (V _mpi ) are additive at appropriately low temperature range τ _i  ≤ τ _ind . Moreover, excess energy evolved due to the interaction of the captured particle with solid wall is totally withdrawn to keep the constant temperature T in isothermal adsorption. Hence, the quantities in Eq. (4) may be averaged over all set of molecules (e.g. containing N particles) with Maxwell–Boltzmann distribution function f(τ _i ,T) at a given temperature T. If the individual particles temperature is τ _ind  < τ _i  ≤ τ _max , the additivity of the total volume of adsorbed individual particles is no longer valid. Nevertheless, for a consistency of the proposed description it is useful to evaluate the number of particles j sharing occupied volume also in the range V _ind  < V _mpi (τ _i ) ≤ V _max . Assuming, that the volume V _ind corresponds to the maximum separated volume of one mole of individual particles, the upper bound for a volume V _mpi (τ _i ) of the number of particles, may be evaluated with simple expression j = V _mpi (τ _i )/V _ind . As well, the potentials U _madh (V _mpi ) and U _m (V _mpi ) may be seen as proportionally shared in terms of the number of j particles. Thus, the following expressions are valid:

$$j = \frac{{V_{{m_{pi} }} }}{{V_{ind} }},\quad U_{m} (V_{{m_{pi} }} ) = \frac{{U_{m} (V_{{m_{pi} }} > V_{ind} )}}{j},\quad U_{{m_{adh} }} (V_{{m_{pi} }} ) = \frac{{U_{{m_{adh} }} (V_{{m_{pi} }} > V_{ind} )}}{j}$$

(10)

Hence, it enables for the averaging of the quantities in Eq. (4) also up to the limit τ _i  = τ _max .

The integration of the distribution function f(τ _i ,T) up to the limits τ _ind and τ _max leads to the fraction w _ind and w _max of volatile phase particles, at the particular temperature T. Following adsorption mechanism identification criteria w _ind is a localized mechanism fraction and so w _max correspond to the other mechanisms, e.g. possible mobile mechanism (see Fig. 3):

Fig. 3

Hypothetical relationship for ${{w_{ind} } \mathord{\left/ {\vphantom {{w_{ind} } {w_{max} }}} \right. \kern-0pt} {w_{max} }}$ ratio as a function of temperature T, describing the statistical significance of the localized and possible mobile mechanisms in real adsorption system

$$w_{ind} \mathop = \limits^{def} \int_{0}^{{\tau_{ind} }} {f(\tau_{i} ,T)d\tau_{i} } ,\quad w_{max} \mathop = \limits^{def} \int_{0}^{{\tau_{max} }} {f(\tau_{i} ,T)d\tau_{i} }$$

(11)

where the remaining part (1 − w _max ) is the fraction of one mole of individual particles of volatile phase π. The values obtained in Eq. (11) refer to the idealized adsorptive volatile phase fractions that may be adsorbed with particular mechanism, but it does not specify liquidlike phase particles properties.

At the intervals between collisions, each i-th particle in the adsorption system is at the kinematic equilibrium and the average temperature of adsorbed molecules is expressed as:

$$T_{k} \mathop = \limits^{def} \frac{1}{{N_{ind} }}\sum\limits_{i = 1}^{{N_{ind} }} {\tau_{i} } = \frac{1}{{w_{ind} }}\sum\limits_{n = 1}^{{N_{ind} }} {f(\tau_{n} ,T)\tau_{n} \Delta \tau_{n} }$$

(12)

where N _ind is a number of particles corresponding to the particular temperature τ _i , fulfilling the constraint τ _i  ≤ τ _ind .

Hence, by virtue of Eqs. (8) and (12) the following equation is valid:

$$\begin{aligned} T_{k} = \frac{1}{{w_{ind} R}}\sum\limits_{n = 1}^{{N_{ind} }} {f(\tau_{n} ,T)\left( {p\frac{{s_{pn} }}{{a_{{m_{fn} }} }} + U_{{m_{n} }} (V_{{m_{pn} }} ) - U_{{m_{adh,n} }} (V_{{m_{pn} }} ) + } \right)\Delta \tau_{n} } \hfill \\ = \frac{1}{R}\left( {p\left\langle {\frac{{s_{pn} }}{{a_{{m_{fn} }} }}} \right\rangle + \overline{U}_{m} (\overline{V}_{{m_{p} }} ) - \overline{U}_{{m_{adh} }} (\overline{V}_{{m_{p} }} )} \right) \hfill \\ \end{aligned}$$

(13)

where $\bar{ \cdot }$ refers to the quantities at the given temperature T _k , averaged over the interval τ _i   $\in$  (0; τ _ind ). The averaging is performed for all quantities in analogy to the following formulae:

$$\overline{V}_{{m_{p} }} \mathop = \limits^{def} \frac{1}{{N_{ind} }}\sum\limits_{i = 1}^{{N_{ind} }} {V_{{m_{pi} }} } = \sum\limits_{n = 1}^{N} {f(\tau_{n} ,T)V_{{m_{pn} }} \Delta \tau_{n} }$$

(14)

Moreover, Eq. (13) implies that relationship V _mpi (T _k , p = 0) may be seen as the upper bound for a volume V _mpi (T _k , p). It may be easily examined by solving nonlinear system, of Eq. (13) and equilibrium vapor pressure estimation with quasipolynomial Riedel equation (Vetere 1991). Thus, enabling to find corresponding temperature T _k at the pressure p:

$$\ln p = A\ln T_{k} + \frac{B}{{T_{k} }} + C + DT_{k}^{2}$$

(15)

where p is expressed in units [kPa] and A, B, C, D are empirical constants that may be taken from KDB (CHERIC 2015; Kang et al. 2001).

2.2 Thermodynamics

Let us assume that τ _ind  = ∞ and adsorption system, held at a constant temperature T, consists of N _ind separated subsystems, each containing one molecule i. The volume of any molecular system at its equilibrium state minimizes free enthalpy G of the system:

$$\left. {\frac{\partial G}{{\partial V_{p} }}} \right|_{T} = 0,\;\,G = U_{ads} + pV_{p} - TS_{ads}$$

(16)

where U _ads , S _ads , V _p denote the total energy, entropy and volume of adsorbate molecules, respectively.

For such a system internal entropy and energy are additive, so the following equations are valid:

$$S_{ads} = S_{conf} + \sum\limits_{i = 1}^{{N_{ind} }} {S_{i} } ,\quad S_{i} = - k_{B} \ln \frac{\delta V}{{V_{fi} }} = k_{B} \ln V_{fi} + S_{0} ,\quad U_{ads} = \sum\limits_{i = 1}^{{N_{ind} }} {U_{avge} } (V_{fi} )$$

(17)

where S _conf denotes the configurational entropy of the system, S _i stands for the i-th particle internal entropy (it was assumed that finding of an individual particle in any infinitesimal volume δV is equally probable), S ₀ is a constant of no importance and U _avge (V _fi ) is defined in Eq. (7).

The configurational entropy does not depend on adsorbate molecules volume, so ∂S _conf  / ∂V _p  = 0. In turn, effects of any change in free volume V _fi of an i-th particle are limited to this particle internal entropy and temperature. Hence, the entropy term and its total differential should be written in the following form:

$$TS_{ads} = TS_{conf} + T\sum\limits_{i = 1}^{{N_{ind} }} {S_{i} } ,\quad\,\frac{\partial }{{\partial V_{p} }}\left( {TS_{ads} } \right) = T\sum\limits_{i = 1}^{{N_{ind} }} {\frac{{\partial S_{i} }}{{\partial V_{p} }}} = T\sum\limits_{i = 1}^{{N_{ind} }} {\frac{{\partial S_{i} }}{{\partial V_{fi} }}\frac{{\partial V_{fi} }}{{\partial V_{p} }}}$$

(18)

Thus, by virtue of Eqs. (7), (17) and (18), free enthalpy total differential may be expressed:

$$\left. {\frac{\partial G}{{\partial V_{p} }}} \right|_{T} = \sum\limits_{i = 1}^{{N_{ind} }} {\left. {\frac{{\partial V_{fi} }}{{\partial V_{p} }}\frac{{\partial G_{i} }}{{\partial V_{fi} }}} \right|_{T} } = p + \sum\limits_{i = 1}^{{N_{ind} }} {\frac{{\partial V_{fi} }}{{\partial V_{p} }}\frac{1}{{V_{fi} }}\left( {U_{bdry} (V_{fi} ) - U_{avg} (V_{fi} ) - k_{B} T} \right)} = 0$$

(19)

Let us take that any change in the total volume V _p splits into the volumes V _pi and V _fi in proportion to the surfaces s _p , s _pi and s _fi of corresponding spaces (i.e. any change in volume may be expressed by small change dr). Hence, the differentials fulfill the relations:

$$\frac{{\partial V_{fi} }}{{\partial V_{p} }} = \frac{{s_{fi} }}{{s_{p} }},\;\frac{{\partial V_{pi} }}{{\partial V_{p} }} = \frac{{s_{pi} }}{{s_{p} }},\quad {\text{where}}\;s_{p} = \sum\limits_{i = 1}^{{N_{ind} }} {s_{pi} }$$

(20)

Moreover, the total effect of interactions of adsorbate particles N _ind with volatile phase, represented in Eq. (19) by the pressure p, may be partitioned onto the subsystems using the collision probability s _pi /s _p of an individual i-th particle:

$$p = \sum\limits_{i = 1}^{{N_{ind} }} {\frac{{s_{pi} }}{{s_{p} }}p}$$

(21)

For a convenience, let us again relate the quantities obtained in Eq. (19) to one mole of particles according to Eq. (9). By virtue of Eqs. (20) and (21) into Eq. (19) the thermodynamic equilibrium may be expressed in the following form:

$$\left( {\sum\limits_{i = 1}^{{N_{ind} }} {s_{pi} p + \frac{1}{{N_{ind} }}\sum\limits_{i = 1}^{{N_{ind} }} {a_{fi} } U_{bdry} (V_{fi} )} - \frac{1}{{N_{ind} }}\sum\limits_{i = 1}^{{N_{ind} }} {a_{fi} } U_{avge} (V_{fi} ) - \frac{1}{{N_{ind} }}\sum\limits_{i = 1}^{{N_{ind} }} {a_{fi} } k_{B} T} \right) \times \left( {\frac{{N_{A} }}{{N_{A} }}} \right)^{2} = 0$$

(22)

Subsequently, taking into account quantities defined in Eq. (9), the thermodynamic equilibrium temperature T _t may be obtained:

$$T_{t} = \frac{1}{R}\frac{{\sum\limits_{i = 1}^{{N_{ind} }} {\left( {ps_{pi} + a_{{m_{fi} }} U_{m} (V_{{m_{pi} }} ) - a_{{m_{fi} }} U_{{m_{adh} }} (V_{{m_{pi} }} )} \right)} }}{{\sum\limits_{i = 1}^{{N_{ind} }} {a_{{m_{fi} }} } }}$$

(23)

In order to evaluate the adequacy of kinematic considerations to the analysis of adsorbed particles properties, let us calculate the thermodynamic temperature T _t . Thus, let us assume that the distributions of the quantities U _madh (V _mpi ) and U _m (V _mpi ) and corresponding s _pi and a _mfi is the same as in the kinematic equilibrium, at the temperature T _k (see Eq. (13)):

$$T_{t} = \frac{1}{R}\frac{{\sum\limits_{n = 1}^{N} {f(\tau_{n} ,T)a_{{m_{fn} }} \left( {p\frac{{s_{pn} }}{{a_{{m_{fn} }} }} + U_{{m_{n} }} (V_{{m_{pn} }} ) - U_{{m_{adh,n} }} (V_{{m_{pn} }} )} \right)\Delta \tau_{n} } }}{{\sum\limits_{n = 1}^{N} {(\tau_{n} ,T)a_{{m_{fn} }} \Delta \tau_{n} } }}$$

(24)

where N stands for the number of the available τ _n , found with Eq. (8).

The relationship V _mp (T _t ) may be viewed as a realistic description of adsorbate volume in real localized adsorption systems. Moreover, the comparison of Eqs. (24) and (13) provides information that the particle temperature distribution in real systems is the Maxwell–Boltzmann distribution, modified with a _mfn weights.

2.3 Adsorption mechanism domination

In real adsorption system, it is not likely that adsorption will take place only with purely localized or purely mobile mechanism. In turn, intuitively both mechanisms are expected, even if single heterogeneity is considered as a model (e.g. cavity, corner). Hence, the particular mechanism domination may be evaluated based on the molecules fractions w _ind and w _max , see Eq. (11). One may consider the ratio of the obtained fractions, as follows:

$$\frac{{w_{ind} }}{{w_{max} }}\mathop \approx \limits^{def} 1\;{\text{for purely localized mechanism}},\;\frac{{w_{ind} }}{{w_{max} }}\mathop \approx \limits^{def} 0\;{\text{for purely mobile mechanism}}$$

(25)

The relationships in Eq. (25) are exceptional cases and most likely in real adsorption systems they might not be observed. Nevertheless, at the given temperature T of experimental adsorption measurements, it is possible to select the most appropriate mathematical adsorption model based on ${{w_{ind} } \mathord{\left/ {\vphantom {{w_{ind} } {w_{max} }}} \right. \kern-0pt} {w_{max} }}$ ratio (see Fig. 3).

The localized mechanism in uniBET model, elaborated in our team, may be considered as a mixing of molecules being in the reference liquidlike state, with cells placed at the adsorbent surface, see e.g.: (Duda et al. 2013; Milewska-Duda et al. 2000; Milewska-Duda and Duda 2001). In such a view a key parameter is an effective adhesion energy E _adh , related to a measurable monolayer adsorption energy Q _A with a Huggins formula (Flory 1953):

$$Q_{A} = E_{vap} - \zeta E_{adh}$$

(26)

where E _vap is the cohesion (evaporation) energy of the adsorbate in its reference state and ζ is a surface texture parameter describing possible contact of adsorbate with neighboring adsorbent molecules (intermolecular effective contact ratio). Adhesion energy E _adh is evaluated for a pair of molecules being in a full contact, by combining, via Berthelot rule, adsorbate and adsorbent cohesion energies:

$$E_{adh} = 2\delta_{c} \sqrt {E_{vap} V_{m} }$$

(27)

where δ _c is a solubility parameter and E _vap is evaluated with PVT relationship for V _m , a molar volume of adsorbate in its reference state (for vaporous substances it is the liquid state), see (Milewska-Duda and Duda 2009).

In order to get an insight into adequacy of the kinematic evaluations in Eq. (13) one may calculate the ζ parameter. Thus, taking the values for E _adh (V _mp ) found with Eq. (27), V _mp and corresponding effective adhesion energy U _madh (V _mp ) calculated with Eq. (10) and averaged with Eq. (14):

$$\zeta = \frac{{\overline{U}_{{m_{adh} }} (\overline{V}_{{m_{p} }} )}}{{\overline{E}_{adh} (\overline{V}_{{m_{p} }} )}}$$

(28)

Despite the simplifications involved in Eq. (10) for the volume V _ind  < V _mpi  < V _ind , the parameter ζ found with Eq. (28) may be viewed as a basis for validation of the proposed approach, when compared to empirical values published e.g. in (Duda et al. 2013).

3 Results and discussion

Accuracy of the proposed description was evaluated performing the calculations for interaction of nitrogen with carbon atoms of materials surface. The modeled materials were open carbon nanocone (CNC), graphite sample (GS) with a defect in a form of a cavity, soft activated carbon (AC) composed of graphite crystallites and capped single-walled carbon nanotube (SWCNT). Commonly, an adsorbent structure is modeled as continuous carbon surface, e.g. in DFT formalism. However, in our view more detailed discreet distribution of carbon atoms may be of significance. Hence, it was assumed that the surface consists of carbon atoms spaced like in a graphene and forming a structure of a predefined shape, thus also a geometrical heterogeneity. In particular, CNC model is composed of the wrapped graphene sheet, respecting geometrical requirements for a seamless connection. The cone height is 4.0 nm and a base is 2.5 nm diameter with a disclination angle 240°. The cone itself may be seen as a geometrical heterogeneity. SWCNT model was constructed in the similar manner, and so the graphene layer is wrapped yielding armchair nanotube of 4.0 nm diameter. In order to produce geometrical heterogeneity the tube was capped, so the total length is 6.0 nm. Due to a steric constraints cap is built of a 5-, 6- and 7-membered carbocycles, see (Robinson and Marks 2014) for more details. In turn, GS model is simply graphite constructed of six graphene layers with randomly placed cavity. The cavity itself was designed by removal of the carbon atoms in two top layers (so even deeply penetrating nitrogen particle still may interact with four graphene layers). The cavity shape is a circle-like with a diameter that varies at the top layer from 1.1 nm to 1.6 nm and at the second layer from 0.8 nm to 1.9 nm. Finally, AC model, intended to be the most realistic one, was designed assuming a crystallographic structure of the activated carbon. An individual microcrystallite is built from four graphene layers, each of 1.5 nm length and 1.2 nm width. Then, AC structure was reconstructed as consisting of randomly and loosely packed six microcrystallites (like in soft activated carbon, see (Gauden et al. 2008)). The particular structures realizations are shown as supplementary data (http://www.jmol.org/ 2013) (Fig. 4).

Fig. 4

Adsorbent models (model parameters are given in brackets, all distances are measured between the center of carbon atoms), from left: open CNC of 4.0 nm height and 2.5 nm diameter; armchair, one-side capped SWCNT of 6.0 nm height and 4.0 nm diameter, six-layers GS with a cavity at the two top layers, soft AC consisting of six microcrystallites, respectively

All calculations and plots were performed with our own software working on MATLAB^® platform, applying Monte-Carlo method (Sect. 2.1). Parameters used in the study are gathered in Table 1. Resultant parameters of adsorption mechanism identification are gathered in Table 2.

Table 1 Calculation parameters used in the study

Table 2 Calculated adsorption mechanism (localized versus other) identification parameters

It was expected that structural diversity of AC, CNC and GS materials would generate energetical heterogeneity, so that a depth of a potential well U _m (V _mpi ) would be deep enough to produce a temperature τ _i  < τ _ind (see Fig. 2). The results presented in Figs. 5a–c and 6a–c confirms this expected feature, while referring to Fig. 2. Thus, maximum individual volume V _ind  = V _c was taken as a reasonable value, and then the corresponding temperature τ _ind was identified.

Fig. 5

Interaction potential U _m (V _mpi ) (solid line) and adhesion energy U _madh (V _mpi ) (dashed line) for: a AC, b CNC, c GS and d SWCNT models

Fig. 6

Calculated volume V _mpi and corresponding temperature τ _i for: a AC, b CNC, c GS and d SWCNT models. Dot corresponds to the values of τ _ind and V _ind , and asterisk to the τ _max and V _max

Moreover, in case of CNC model it was intuitively expected that geometrical heterogeneity will produce only one adsorption site, i.e. at the cone top. This may be observed in low range of potentials in Fig. 7a and g, where equipotential lines are continuous and individual. In turn, for GS (Fig. 7b, e) and AC (Fig. 7c, f) materials due to the structural heterogeneity of the cavity, and microcrystallites distribution, more than one separated active site was expected. This may be observed at the equipotential surface cross-sections, where more than one local minimum of separated volume were identified. It should be also noticed in Fig. 7 that despite a sufficiently large number of successful shots in Monte-Carlo method, the discontinuities and slight differences in the minimum values of the potential, may be observed. This is due to interpolation of random, scattered configurations v in order to determine an equipotential surface, and may be easily eliminated in analytical calculations. Anyway, the results quality of the Monte-Carlo method is good enough to perform these analyses.

Fig. 7

U _m (V _mpi ) equipotential surface cross-sections, interpolated from random, scattered configurations (colorbar correspond to the values of the potential). Cross-sections for: AC model, at the AC width 2.4 nm (b) and along AC length (e), CNC model, at the CNC height 1.3 nm (a) and along CNC center (g), GS model, at the GS width 1.4 nm (c) and through the cavity center (f) and for SWCNT model, at the SWCNT height 1.3 nm (d) and along SWCNT center (h) (Color figure online)

What concerns an identification of the other mechanism (e.g. possible mobile mechanism), it was found out there may be observed a temperature range, wherein two volume values correspond to one value of the temperature (see Fig. 2). It indicates coexistence of two phases: dilute liquidlike and bulk, and also facilitates a determination of a temperature τ _max . Thus, the latter was identified as a corresponding to the maximum volume of dilute liquidlike phase V _max , for the phases coexistence region.

SWCNT material was designed as a model with relatively small expected energetical heterogeneity (at the nanotube cap), resulting in adsorbate condensation not exceeding the critical volume (Zhao et al. 2001). Accordingly, the highest minimum value of the potential U _m (V _mpi ) was obtained for SWCNT (Fig. 5d), and so the structural diversity produces relatively shallow potential well-depth. Qualitatively, it occurs at the equipotential surface cross-sections, where indistinct and connected with each other lines may be observed see Fig. 7d and h. Therefore, identification of the separated volume V _ind corresponding to the localized adsorption mechanism is ambiguous (see Fig. 6d).

Very interesting results, providing a comparison of the kinematic and thermodynamic temperatures with a liquid nitrogen thermal expansion curve are shown in Fig. 8. They compare the curves corresponding to a given V _mpi , see Eq. (13) T _k  (V _mpi , p = 0), T _k  (V _mpi , p) and Eq. (24) T _t  (V _mpi , p), with the thermal expansion curve found with (Milewska-Duda and Duda 2009). This comparison brings strong confirmation of the adequacy of the proposed approach. Moreover, it provides an information that the pressure effect on the volume is insignificant, when the indistinguishability of the curves T _k  (V _mpi , p = 0) and T _k  (V _mpi , p) is noticed, (less than 1 % of a difference, see Table 2).

Fig. 8

The calculated temperatures T _k  (V _mpi , p) (dashed line), T _t  (V _mpi , p) (dash-dotted line) and liquid nitrogen thermal expansion (solid line) at the volume V _mpi , for: a AC, b CNC, c GS and d SWCNT models. Asterisk corresponds to the critical temperature T _c at the critical volume V _c

For CNC (Fig. 8b) and GS (Fig. 8c) materials, the T _t curves are almost in perfect agreement with calculated nitrogen expansion curve. It means that for such structures the classical localized adsorption assumption (i.e. vaporous adsorbate is in a liquid state) is fully acceptable. Nevertheless, the T _t curve for AC (Fig. 8a) seems to suggest that this assumption is valid only in the low temperature range. On the other hand, for SWCNT model (Fig. 8d) the obtained results give an evidence for a possible mobile mechanism (or other), and so obtained volume immediately exceeds V _c and differs from nitrogen liquid expansion curve.

Found with the LBET models and approved in our earlier works (Duda et al. 2013) values for ζ ratio vary around 0.50–0.48 and 0.32–0.40 for the nitrogen adsorption on heterogeneous and homogenous active carbon, respectively. A quite satisfactory agreement of these empirical data and the values calculated in this study may be observed in Fig. 9. The most effective contact ratio was obtained for CNC and GS materials, but ζ significantly exceeds the values obtained in our earlier works. This is due to obvious differences in the structural heterogeneity in both cases. AC structure is geometrically the most consistent and gives the results almost in perfect agreement. Again, as expected, for SWCNT the lowest values of ζ ratio were obtained. Those results are consistent with determined experimentally weak adsorption on SWCNT (Zhao et al. 2001). Hence, determined values for structure parameter ζ are in a good agreement with earlier assumed mechanism identification criteria. This consistency of the ζ values, evaluated with the newly derived formulas and obtained on the basis of experimental examination of adsorption isotherms with LBET models, constitutes ζ as a validation parameter.

Fig. 9

Calculated intermolecular effective contact ratio ζ and corresponding temperature T, for: AC (dash-dotted line), CNC (dotted line), GS (solid line) and SWCNT (dashed line) models

Nevertheless, it has to be pointed out that below a freezing temperature this description is inadequate, since the energy in Eq. (26) is calculated with PVT relationship, dedicated for liquid bulk phase only. However, the attention should be also paid to the invariance of ζ parameter, that may be observed over a certain values of T < T _B , see Table 2, ζ _const . Let us remind that ζ is really important parameter that provides information on the pore shape and gets an intuitive view on the material structure. Thus, the way the particle detects structure diversity (pore shape structure ζ) became an invariant to the temperature parameter, for the specific pair adsorbate-adsorbent. Therefore, it may make it possible to evaluate the properties of another system, without any additional experimental measurements. This may be achieved by interrelation of a two particles (i.e. by volume, diameter) and then application in Eq. (26). Moreover, it may be also exploited, to improve identification of the adsorbent structure, by simultaneous fitting of two or more isotherms measured at different temperatures for the same pair adsorbate-adsorbent.

Calculations were completed with the analysis of adsorption mechanism predomination (Fig. 10), according to Eq. (11) in the temperature range 0–300 K. The most interesting point concerns the normal boiling temperature T _B , at which nitrogen experimental adsorption is most commonly measured. Hence, at this temperature the localized adsorption mechanism should be assumed for materials where geometrical heterogeneities are close to those modeled in AC, GS and CNC structures. Whereas for SWCNT-like structures other mechanism based mathematical models are certainly more appropriate.

Fig. 10

Ratio w _ind /w _max , implying predomination of the particular mechanism, at the temperature T range 0-300 K, AC (dash-dotted line), CNC (dotted line), GS (solid line) and SWCNT (dashed line) models

4 Conclusions

Presented in this paper novel approach and numerical tools, aimed at qualitative adsorption mechanism identification, are significant development of the works lead in Authors’ team. The proposed kinematic description enables for adsorption mechanisms identification, in comparison to the adsorbate critical properties. It was shown that the real particles temperature distribution comes from the thermodynamic equilibrium, corresponding to kinematically determined adsorbate particles volume distribution.

The obtained results are sufficient to get an insight into the adsorption mechanism, and hence performed calculations provide a reliable picture of individual particles movement near the solid surface. In particular, it was shown, that substantial geometrical heterogeneity generates localized attractive adsorption sites, whereas small surface deformations results in mainly possible mobile adsorption.

The numerical tool is also comprehensive in terms of model complexity, since it has been shown that geometrical constraints mainly influence calculations efficiency. Therefore, the properties may be evaluated also even if more than one localized adsorption site is expected.

It has been also demonstrated, that nitrogen volume in the adsorption phase up to the critical volume, may be properly approximated as liquid phase volume. However, the shape of the particle movement significantly differs from a sphere-like space. In order to check the description consistency, the texture parameter ζ was constituted as validation parameter. It was shown, that the comparison of the results derived from new formulas and on the basis of experimental examination of adsorption isotherms with LBET models, provides the approach validation. It should be also stressed that ζ becomes temperature invariant over the boiling temperature and it may bring benefits in further researches according to the discussion presented in the paper.

Analysis of the mechanisms predomination with w _ind /w _max ratio is of practical importance. It enables to select the appropriate mathematical model not only intuitively, but on the basis of the calculations performed for the modeled geometrical heterogeneities (e.g. similar as in AC, GS and CNC structures). In particular the results shown in our study suggest that nitrogen adsorption up to boiling temperature is of localized nature in the tested microporous structures of different shape, except for nanotubes.