Effect of adsorbate properties on adsorption mechanisms: computational study

Abstract

The paper presents results of research on identification of localized and mobile adsorption mechanisms of several selected adsorbates, on geometrically heterogeneous graphite-like carbonaceous surface. The proposed approach is intended to examine effects of surface geometrical heterogeneity on shape and volume of space occupied by the selected adsorbate molecules. In particular, the continuously moving individual molecule mass center properties, near adsorbent surface are investigated. When compared to the corresponding liquid phase properties it enables to outline the conditions for localized and mobile adsorption mechanisms. To this aim, the kinematic and thermodynamic equilibrium conditions are taken under the study, providing information on particular mechanism predomination. Therefore, the approach gives a cognitive basis for selection of the most appropriate mathematical adsorption model to reliable examination of material porous structure (comprising similar geometrical heterogeneity). Numerous simulation results for selected adsorbates H₂, CO₂, CH₃OH and C₆H₆ are presented, and adsorption mechanism identification is discussed.

1 Introduction

Practical evaluation of adsorption system properties requires mathematical model selection, to describe empirical data obtained from experimental measurements. Nevertheless, due to structural and energetical diversity of adsorbents structure, the complete mathematical description is almost virtually impossible and requires an adsorption mechanism assumption, i.e. localized or mobile (Jagiełło and Olivier 2013). Therefore, a significant interest has been concentrated on elaboration of reliable description of adsorption equilibrium, where different aspects of localized and mobile adsorption mechanisms are stressed (Dąbrowski 2001; Sing et al. 1985).

The author’s team is working on mathematical modeling of solid–fluid interaction, in particular in materials of carbonaceous origin. So far, team’s work was concentrated on development and applicability of the new clustering based approach aimed at microporous structure characterization i.e. LBET class adsorption model (Duda et al. 2013; Duda and Milewska-Duda 2005). The background for the model design was to especially consider the surface geometrical heterogeneity and energy distribution effects on the adsorption system properties (Duda et al. 2005). Recently, the author’s team works were also focused on the examination of structural diversity effects, on the molecule behavior near the adsorbents surface, with special regard in what extent the local surface deformation reduces the particle movement making it closer to the localized mechanism (Ziółkowska and Duda 2015). Having in mind that system properties are closely related to the surface geometrical heterogeneity and energy distribution (Rudzinski and Everett 1992) for adsorbents of irregular, randomly distributed porous structure localized adsorption may be assumed. On the other hand for highly regular porous structures (e.g. slit-like pores, zeolites) mobile mechanism seems to be more appropriate. Nevertheless, currently the particular adsorption mechanism is mostly selected intuitively based on presumed picture of surface geometrical heterogeneity. Thus, it is useful to outline the conditions for localized and mobile adsorption mechanisms in order to select the most appropriate mathematical adsorption model, for reliable porous structure characterization.

The aim of this paper is to show, how the recently elaborated in author’s team approach works, when applied to the several selected adsorbates H₂, CO₂, CH₃OH and C₆H₆. In particular, the space and volume of the individual adsorbate particle mass center movement near adsorbent solid wall is considered, then localized and mobile mechanisms conditions are outlined, when compared to the liquid bulk phase properties. Hence, the approach complexity was taken under the study in terms of its applicability to various adsorbates. The practical information that may be drawn from computer analysis aimed at adsorption mechanism identification is presented.

2 Examination of surface geometrical heterogeneity effects

The approach presented in this paper is based on the analysis of adsorptive molecule movement constraints arising from adsorbents surface attractive forces. More precisely, the mass center of individual particle of volatile phase movement is considered in time intervals between collisions with other adsorptive molecules. It is assumed that the molecule mass center moves within a free space, and finding of its mass center at any point of this space is equally probable. Hence, time averages after a suitable lapse of time correspond to the macro scale ensemble averages, see (Ziółkowska and Duda 2015).

In the free space of volume V _fi , the averaged i-th molecule movement is limited by an equipotential surface U _bdry (V _fi ), at which molecule translation is limited to the surface. Therefore, at the boundary movement accounts for two degrees of freedom and kinetic energy represented by the temperature k _B τ _i , is equilibrated by the average potential decrease U _avge (V _fi ). If individual particle is considered (i.e. there are no particles in volatile phase), U _bdry (V _fi ) is the only component of the potential generated at the boundary, coming from solid–fluid adhesive forces. Nevertheless, when considering macro scale the pV potential also has to be taken into account, as a component coming from possible collisions with other particles of volatile phase. Therefore, for practical calculations, it is necessary to relate the pV component to the free volume V _fi . Kinematically such a relationship may be obtained applying collision probability s _pi /s _fi of an individual i-th particle, leading to the formulae:

$$pV \to \sum\limits_{i = 1}^{N} {\frac{{s_{pi} }}{{s_{fi} }}V_{fi} p}$$

(1)

and i-th particle kinematic equilibrium condition reads:

$$p\frac{{s_{pi} }}{{a_{fi} }} + U_{bdry} \left( {V_{fi} } \right) - U_{avge} \left( {V_{fi} } \right) - k_{B} \tau_{i} = 0$$

(2)

where s _fi is the open surface bounding free space of volume V _fi , s _pi and V _pi correspond appropriately to the particle movement. The relationship s _fi /V _fi is a specific surface area of the space of particle mass center movement, denoted as a _fi . If accepting the assumption that the particle mass center movement corresponds to the sphere-like spaces, the values for the particle movement (i.e. d _pi , s _pi , V _pi ) may be evaluated equivalently by calculating the sphere diameter d _pi as a diameter d _fi of volume V _fi increased by the hard sphere core diameter σ _ff .

The rigorous examination of surface heterogeneity effects requires discrete representation of the adsorbents structure. Hence, the material (model) taken under study is a nanostructure of a predefined shape comprising the heterogeneity formed by the carbon atoms at fixed positions. For such a representation the carbon-fluid potential at a given k-th position is calculated by summing up 12–6 Lennard-Jones potential $u_{{C - f_{k} }}$ over the set of carbon atoms (Lennard-Jones 1931):

$$u_{{C - f_{k} }} = 4\varepsilon_{C - f} \left( {\frac{{\sigma_{C - f} }}{{r_{{C - f_{k} }} }}} \right)^{12} - \left( {\frac{{\sigma_{C - f} }}{{r_{{C - f_{k} }} }}} \right)^{6}$$

(3)

where $\varepsilon_{{C - f_{k} }}$ and $\sigma_{{C - f_{k} }}$ are the potential well-depth and intermolecular diameter, calculated applying Lorentz–Berthelot (Berthelot 1898; Lorentz 1881) mixing rules from pure-species quantities and $r_{{C - f_{k} }}$ is carbon-fluid intermolecular distance.

A fixed value of 12–6 Lennard-Jones potential sum $\sum\limits_{C} {u_{{C - f_{k} }} }$ is taken as an arbitrary value of a boundary potential U _bdry (V _fi ), enabling to calculate an average potential U _avge (V _fi ) as:

$$U_{avge} \left( {V_{fi} } \right) = \frac{1}{{V_{fi} }}\int_{0}^{{V_{fi} }} {U_{bdry} \left( v \right)dv}$$

(4)

The free space of volume V _fi corresponding to an arbitrary assumed value of U _bdry may be determined employing analytical or Monte-Carlo calculation technique, both employed in the approach. In our earlier paper (Ziółkowska and Duda 2015) it was shown that Monte-Carlo calculations is a more convenient technique, due to time efficiency, and it is accurate enough to perform analysis. Thus, the volume V _fi corresponding to a given boundary potential is calculated as a ratio of admissible shots n _adm , respecting model geometrical constraints, and successful shots n _v , fulfilling the relation $\sum\limits_{C} {u_{{C - f_{k} }} \le U_{bdry} }$. Hence, while having sufficiently large number of admissible shots, the free volume V _fi may be calculated as: V _fi  ≈ n _v /n _adm .

Furthermore for a convenience, the values for U _bdry (V _fi ) and U _avge (V _fi ) may be recalculated for the particle volume V _pi and then related to one mole of particles with the Avogadro constant N _A . Hence, the following relationships are obtained:

$$V_{{m_{fi}}} \mathop {=} \limits^{def} N_{A} V_{fi},\quad V_{{m_{pi}}} \mathop {=} \limits^{def} N_{A} V_{pi},\quad U_{m} \left({V_{{m_{pi}}}} \right)\mathop {=}\limits^{def} N_{A} U_{bdry} \left({V_{{m_{pi}}}} \right),\quad U_{{m_{adh}}} \left({V_{{m_{pi}}}} \right)\mathop {=} \limits^{def} N_{A} U_{avge} \left({V_{{m_{pi}}}} \right)$$

(5)

As far as individual particle movement is considered only (i.e. p = 0), and the values for $U_{m} \left( {V_{{m_{pi} }} } \right)$ and $U_{{m_{adh} }} \left( {V_{{m_{pi} }} } \right)$ were obtained, the kinematic equilibrium temperature τ _i may be calculated with Eq. (2):

$$\tau_{i} = \frac{{U_{m} \left( {V_{{m_{pi} }} } \right) - U_{{m_{adh} }} \left( {V_{{m_{pi} }} } \right)}}{R}$$

(6)

The analysis of inverse relationship $V_{{m_{pi} }} \left( {\tau_{i} } \right)$ makes possible to gain information on adsorption mechanisms, see Fig. 1. When adsorption below the critical volume V _c is considered, a fully accepted practice is to approximate the volume of adsorption phase as liquid phase. In such a volume, close molecules packing makes it virtually impossible to share the volume with any other particles. Hence, the volume of a free movement space $V_{{m_{pi} }} \left( {\tau_{i} } \right) \le V_{c}$ may be seen as localized site bounded by the maximum volume V _ind  = V _c . The individual particle temperature τ _i , that corresponds to the V _ind may be then calculated as $\tau_{ind} = \arg \left\{ {\hbox{min} \left\{ {V_{{m_{pi} }} \left( {\tau_{ind} } \right) = V_{ind} } \right\}} \right\}$. In turn, if the particle temperature is within a certain range, such that τ _ind  < τ _i  ≤ τ _max , the temperature is still appropriately low that the particle may be captured into the interaction potential well. Nevertheless, due to weaker interactions the molecules packing decrease, and so enabling the particle to occupy individual spaces $V_{{m_{pi} }} \left( {\tau_{i} } \right)$ but also to share the volume $V_{{m_{pi} }} \left( {\tau_{i} } \right)$ with other j particles. Thus, the general form for the maximum volume of, individual or j particles, free movement space (depending on pressure p) is $V_{max} = V_{{m_{pi} }} \left( {\tau_{i} } \right)j$ and the volume range $V_{ind} < V_{{m_{pi} }} \left( {\tau_{i} } \right) \le V_{max}$ may be seen as a corresponding to the possible mobile mechanism. Analogously, the temperature τ _i corresponding to the volume V _max is calculated as $\tau_{max} = \arg \left\{ {V_{{m_{pi} }} \left( {\tau_{i} } \right) = V_{max} \gg V_{ind} } \right\}$. Finally, if the temperature τ _i  > τ _max , then the particle may be seen as volatile phase fraction.

Fig. 1

Hypothetical inverse relationship $V_{{m_{pi} }} \left( {\tau_{i} } \right)$ calculated with Eq. (6) for one mole of individual particles moving in the free volume space $V_{{m_{fi} }} \left( {\tau_{i} } \right)$. V _ind stands for the maximum volume of individual particle free movement space at the temperature τ _ind . The temperature range τ _i  ≤ τ _ind correspond to the localized mechanism. V _max is the maximum volume of individual or j particles movement space at the temperature τ _max . The temperature range τ _ind  < τ _i  ≤ τ _max correspond to the possible mobile mechanism and τ _i  > τ _max , to the volatile phase fraction (Ziólkowska and Duda 2015)

As far as isothermal adsorption is considered only, the excess energy evolved due to particle interaction with surface carbon atoms may be assumed to be withdrawn, in order to hold the constant temperature T (if the particle is captured into the potential-well). The latter together with the additivity assumption of $V_{{m_{pi} }} ,\;U_{{m_{adh} }} \left( {V_{{m_{pi} }} } \right)\;{\text{and}}\;U_{m} \left( {V_{{m_{pi} }} } \right)$ in temperature range τ _i  ≤ τ _ind , enables for averaging of the system parameters. Hence, the quantities in Eq. (2) may be averaged over all set of molecules (e.g. containing N or one mole of particles) with Maxwell–Boltzmann distribution function f(τ _i ,T) at a given temperature T. Nevertheless, when the temperature range τ _ind  < τ _i  ≤ τ _max is taken under considerations, the additivity of the total volume $V_{{m_{pi} }}$ is no longer valid assumption. However in order to keep the description consistent, the number of particles j sharing the occupied volume $V_{ind} < V_{{m_{pi} }} \left( {\tau_{i} } \right) \le V_{max}$ may be roughly evaluated, assuming V _ind to be the maximum separated volume of one mole of individual particles. Hence, the particle number j may be evaluated as a ratio $j = V_{{m_{pi} }} \left( {\tau_{i} } \right)/V_{ind}$. Subsequently, volume $V_{{m_{pi} }} \left( {\tau_{i} } \right)$ and potentials $U_{{m_{adh} }} \left( {V_{{m_{pi} }} } \right),\;U_{m} \left( {V_{{m_{pi} }} } \right)$ may be recalculated as proportionally shared in terms of the particles number at the range corresponding to the volume $V_{{m_{pi} }} \left( {\tau_{i} } \right) > V_{ind}$.

Due to surface structural diversity in real adsorption systems, it is expected that adsorption may take place with both, localized and possible mobile mechanisms. Hence, the analysis of the mechanism predomination is of practical importance and may be performed employing Maxwell–Boltzmann distribution function. The function f(τ _i ,T) integration, up to the limits of localized mechanism τ _ind and possible mobile mechanism τ _max , leads to the volatile phase particles fractions of the particular mechanism w _ind and w _max , at the temperature T:

$$w_{ind} \mathop {=} \limits^{def} \int_{0}^{{\tau_{ind}}} {f\left({\tau_{i},T} \right)d\tau_{i}},\quad w_{\max} \mathop {=} \limits^{def} \int_{0}^{{\tau_{\max}}} {f\left({\tau_{i},T} \right)d\tau_{i}},\quad\pi \mathop {=} \limits^{def} 1 - w_{\max}$$

(7)

where the remaining part π is a fraction of particles in volatile phase. As a matter of fact, the values obtained in Eq. (7) do not specify properties of liquidlike phase particles.

The ratio of the obtained fractions w _ind and w _max may be considered as follows:

$$\frac{{w_{ind}}}{{w_{max}}}\mathop {\approx}\limits^{def} 1\;{\text{for}}\;{\text{purely}}\;{\text{localized}}\;{\text{mechanism}},\quad \frac{{w_{ind}}}{{w_{max}}}\mathop {\approx}\limits^{def} 0\;{\text{for}}\;{\text{purely}}\;{\text{mobile}}\;{\text{mechanism}}$$

(8)

Hence, at the given selected temperature T (e.g. experimental adsorption measurements temperature) it is possible to identify predominating mechanism, based on w _ind /w _max ratio (see Fig. 2).

Fig. 2

Schematic curves of w _ind /w _max ratio versus T and identified predominating mechanisms (Ziółkowska and Duda 2015)

Assuming that temperature distribution is the Maxwell–Boltzmann distribution, for each i-th particle being in the kinematic equilibrium (i.e. at the intervals between collisions with other particles of volatile phase), the averaged kinematic temperature T _k may be defined:

$$T_{k} \mathop {=} \limits^{def} {\frac{1}{{N_{ind}}}}\sum\limits_{i = 1}^{{N_{ind}}} {\tau_{i}} = {\frac{1}{{w_{ind}}}}\sum\limits_{n = 1}^{{N_{ind}}} {f\left({\tau_{n},T} \right)} \tau_{n} \varDelta \tau_{n}$$

(9)

where the averaging is performed for N _ind particles of temperature τ _i , fulfilling the constraint τ _i  ≤ τ _ind .

Hence, by virtue of Eqs. (2) and (9) temperature T _k may be expressed by the following equation:

$$\begin{aligned} T_{k} = & \frac{1}{{w_{ind} R}}\sum\limits_{n = 1}^{{N_{ind} }} {f\left( {\tau_{n} ,T} \right)} \left( {p\frac{{s_{pn} }}{{a_{{m_{fn} }} }} + U_{{m_{n} }} \left( {V_{{m_{pn} }} } \right) - U_{{m_{adh,n} }} \left( {V_{{m_{pn} }} } \right) + } \right)\Delta \tau_{n} \\ = & \frac{1}{R}\left( {p\left\langle {\frac{{s_{pn} }}{{a_{{m_{fn} }} }}} \right\rangle + \overline{U}_{m} \left( {\overline{V}_{m} } \right) - \overline{U}_{{m_{adh} }} \left( {\overline{V}_{{m_{p} }} } \right)} \right) \\ \end{aligned}$$

(10)

where $\bar{ \cdot }$ refers to the averaged quantities in Eq. (2) at the given temperature T _k , in analogy to the following formulae:

$$\overline{V}_{{m_{p}}} \mathop {=} \limits^{def} \frac{1}{{N_{ind}}}\sum\limits_{i = 1}^{{N_{ind}}} {V_{{m_{pi}}}} = \sum\limits_{n = 1}^{N} {f\left({\tau_{n},T} \right)} V_{{m_{pn}}} \varDelta \tau_{n}$$

(11)

From Eq. (10), the obtained inverse relationship $V_{{m_{pi} }} \left( {T_{k} ,p = 0} \right)$ may be seen as the upper bound for a volume $V_{{m_{pi} }} \left( {T_{k} ,p} \right)$. In our previous paper (Ziólkowska and Duda 2015) it was shown that curves corresponding to $T_{k} \left( {V_{{m_{pi} }} ,p = 0} \right)$ and $T_{k} \left( {V_{{m_{pi} }} ,p} \right)$ are almost indistinguishable, so the pressure effect on the volume is insignificant and may be neglected. Moreover, it was revealed that real particles temperature distribution comes from the thermodynamic equilibrium, corresponding to the Maxwell–Boltzmann distribution, modified with the $a_{{m_{fn} }}$ weights, see Eqs. (10) and (12). Therefore, the thermodynamic temperature T _t is calculated assuming the same distribution of the quantities $U_{{m_{adh} }} \left( {V_{{m_{pi} }} } \right),U_{m} \left( {V_{{m_{pi} }} } \right)$ and corresponding s _pi and $a_{{m_{fi} }}$ in the kinematic equilibrium, at the temperature T _k :

$$T_{t} = \frac{1}{R}\frac{{\sum\limits_{n = 1}^{N} {f\left( {\tau_{n} ,T} \right)a_{{m_{fn} }} \left( {p\frac{{s_{pn} }}{{a_{{m_{fn} }} }} + U_{{m_{n} }} \left( {V_{{m_{pn} }} } \right) - U_{{m_{adh,n} }} \left( {V_{{m_{pn} }} } \right)} \right)\Delta \tau_{n} } }}{{\sum\limits_{n = 1}^{N} {\left( {\tau_{n} ,T} \right)a_{{m_{fn} }}\Delta \tau_{n} } }}$$

(12)

where τ _n comes from Eq. (6) and the pressure p (kPa) is calculated by solving of nonlinear system of Eq. (12) and Riedel equation with empirical constants A, B, C, D:

$$\ln p = A\ln T_{k} + \frac{B}{{T_{k} }} + C + DT_{k}^{2}$$

(13)

Hence, the resultant temperature T _t calculated with Eq. (12) in comparison to the kinematically determined temperature T _k calculated with Eq. (10) enables for evaluation of adequacy of kinematic considerations.

The averaged volume $\overline{V}_{{m_{p} }} \left( {T_{k} } \right)$ may be seen as a realistic adsorbate molar volume in adsorption system of predominating localized mechanism and may be employed for calculations of surface texture parameter ζ, applied in our previous paper as a validation parameter (Ziółkowska and Duda 2015). This comes from the elaborated in our team LBET class adsorption models implementations (Duda et al. 2013; Milewska-Duda et al. 2000; Milewska-Duda and Duda 2001) where localized mechanism is viewed as a mixing of molecules being in the reference liquidlike state with cells placed at the adsorbent surface. Thus, ζ describes possible contact of the adsorbate with neighboring adsorbent molecules (intermolecular effective contact ratio) and may be calculated taking the values for molar adhesion energy $\overline{E}_{adh} \left( {\overline{V}_{{m_{p} }} } \right)$ and effective adhesion energy $\overline{U}_{{m_{adh} }} \left( {\overline{V}_{{m_{p} }} } \right)$, calculated with Eq. (11) (divided for j molecules if the volume $\overline{V}_{{m_{p} }}$ is shared at the range $V_{ind} < V_{{m_{pi} }} \left( {\tau_{i} } \right) \le V_{max}$):

$$\zeta = \frac{{\overline{U}_{{m_{adh} }} \left( {\overline{V}_{{m_{p} }} } \right)}}{{\overline{E}_{adh} \left( {\overline{V}_{{m_{p} }} } \right)}}$$

(14)

$\overline{E}_{adh} \left( {\overline{V}_{{m_{p} }} } \right)$ is the molar adhesion energy of the full contact adsorbate–adsorbent molecules and may be evaluated applying Berthelot rule by combining adsorbate and adsorbent cohesion energies involving the solubility parameter δ _c of adsorbent matter:

$$\overline{E}_{adh} = 2\delta_{c} \sqrt {E_{vap} \overline{V}_{{m_{p} }} }$$

(15)

where $\overline{V}_{{m_{p} }}$ stands for the adsorbate molar volume and E _vap is the adsorbate cohesion (evaporation) energy, both referring to the adsorbate reference state (for vaporous substances it is the liquid state). The latter is evaluated with PVT relationship for liquid bulk phase (Milewska-Duda and Duda 2009).

3 Numerical analysis

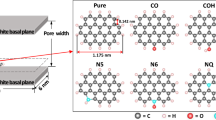
In our earlier paper (Ziółkowska and Duda 2015) it was shown that presented approach makes it possible to get a picture of shape and volume of space occupied by the nitrogen molecules and to outline the conditions for localized and possible mobile adsorption mechanisms for the pores of presumed structure. Moreover, depending on the type of geometrical heterogeneity it is possible to detect the number of the produced adsorption sites, e.g. for carbon nanocone only one site is produced at the top, whereas at the graphite sample with a defect in the form of cavity more than one active site was detected. However, having in mind that the probing molecule size may significantly affect the structure diversity evaluation, to check the reliability of the proposed approach further calculations were performed for selected adsorptives of different size: H₂, CO₂, CH₃OH and C₆H₆. Due to interesting results obtained earlier (Ziółkowska and Duda 2015) for graphite sample (GS) model (i.e. almost perfect agreement of thermodynamic temperature curve and thermal expansion curve for nitrogen calculations) the researches presented in this paper were performed for this model (Fig. 3). All calculations parameters used in the study are gathered in Table 1.

Fig. 3

The material structure, graphite sample model, composed of carbon atoms at fixed positions (i.e. chemical heterogeneity is neglected), predefining geometrical heterogeneity in the form of cavity of 0.7 nm depth and diameter: at the top layer 1.1–1.6 nm and at the second layer 0.8–1.9 nm

Table 1 Calculation parameters used in the study, Lennard-Jones pure species parameters for: graphite sample model (Siderius and Gelb 2011) and H₂, CO₂, C₆H₆ (Bird et al. 2001), CH₃OH (Wilhelm and Battino 1971)

All calculations and plots were performed on MATLAB^® platform, employing software elaborated in author’s team with the Monte-Carlo calculation technique described in Sect. 2. The evaluated adsorption mechanism identification parameters are gathered in Table 2.

Table 2 Calculated adsorption mechanism (localized vs. mobile) identification parameters

Following proposed criteria for adsorption mechanisms identification, both localized and possible mobile mechanisms were identified for all adsorptive–graphite sample model pairs, see Fig. 1. Localized mechanism was identified at the rapidly growing interaction potential region $U_{m} \left( {V_{{m_{pi} }} } \right) \ll 0$, where well-depth is deep enough to produce τ _i  < τ _ind and the corresponding volume of one mole of individual particles does not exceed the critical volume, $V_{{m_{pi} }} < V_{ind}$ (see Figs. 4, 5). This feature is strongly confirmed when analyzing equipotential surface cross-sections presented in Fig. 6. At the lowest range of potentials, for each investigated pair, the equipotential lines are closed and continuous, so the implied volume of space is occupied by individual particle (one mole of particles). Moreover, it should be noticed that for CO₂ and CH₃OH more than one localized adsorption site is observed, what may result from the accepted molecule diameter (see Table 1). As the molecule diameter decrease, the cavity may be penetrated more precisely, enabling to detect even slight structure defects. On the other hand, C₆H₆ molecule diameter is almost the size of the cavity diameter ($\sigma_{{C_{6} H_{6} }} = 0.56\,{\text{nm}}$ and cavity diameter 0.8 nm) making it impossible, due to strong potential interaction, to access further cavity parts. Hence, for C₆H₆ molecule only one adsorption site was detected. It should be also noticed that in Fig. 5 the surface cross-section lines discontinuities may be found. This is an effect of the interpolation of random, scattered configurations and as discussed in Sect. 2 may be accepted for analysis presented in this paper.

Fig. 4

Interaction potential $U_{m} \left( {V_{{m_{pi} }} } \right)$ (solid line) and adhesion energy $U_{{m_{adh} }} \left( {V_{{m_{pi} }} } \right)$ (dashed line) for interaction of a H₂, b CO₂, c CH₃OH and d C₆H₆ with carbon atoms of graphite sample model

Fig. 5

Calculated volume $V_{{m_{pi} }}$ and corresponding temperature τ _i for: a H₂, b CO₂, c CH₃OH and d C₆H₆. Determined values of τ _ind , V _ind , and τ _max , V _max are denoted with dot and triangle markers, respectively

Fig. 6

The equipotential surface cross-sections, interpolated from random, scattered configurations and corresponding to the colorbar $U_{m} \left( {V_{{m_{pi} }} } \right)$ values obtained for H₂ (1st row subfigures), CO₂ (2nd row subfigures), CH₃OH (3rd row subfigures) and C₆H₆ (4th row subfigures). First column cross-sections correspond to the model width values where $U_{m} \left( {V_{{m_{pi} }} } \right)$ reaches its minimum, the second column correspond to the model width at 1.4 nm. Finally, at the third column the cross-sections through the cavity center are presented, on the background of three top layers where the cavity is formed. Possible discontinuities of the cross-sections lines are the consequence of applied Monte Carlo method and interpolation of the configurations

What concerns possible mobile mechanism, τ _max was identified as a value corresponding to the maximum volume V _max . The determination of the latter one is based on the interesting feature, observed for all calculated adsorptives. Thus, there exist a certain temperature range where two volume values are produced for one temperature value, see Fig. 1. This may be seen as a coexistence of two phases: dilute liquidlike and bulk, and so V _max is determined as maximum volume of dilute liquidlike phase for the region of coexisting phases.

Interesting information may be drawn when comparing the kinematic $T_{k} \left( {V_{{m_{pi} }} ,p = 0} \right)$, Eq. (10) and thermodynamic temperatures $T_{t} \left( {V_{{m_{pi} }} ,p} \right)$, Eq. (12) with appropriate adsorbate liquid thermal expansion curve, evaluated with formulae in (Milewska-Duda and Duda 2009). In our previous paper it was shown (Ziółkowska and Duda 2015), that graphite sample model gives results of T _t almost in perfect agreement with nitrogen expansion curve, enabling to conclude that for such structures the classical localized adsorption assumption (i.e. vaporous adsorbate is in a liquid state) is fully acceptable. Nevertheless, results for CO₂, CH₃OH and C₆H₆, presented in Fig. 7, are not in such a good agreement with calculated liquid expansion curve. This may be result of numerical problems encountered when more than one attractive adsorption site is identified and comes from the difficulty in determination of the volume corresponding to the particular site. It means that, when considering individual geometrical heterogeneity the produced well-depth may result in implying different volume of space (i.e. the volume does not have to be proportionally shared for each site). Thus, the identification of the volume corresponding to the particular adsorption site is ambiguous and has to be overcome in further research in order to evaluate thermodynamic temperature T _t more reliably.

Fig. 7

Calculated kinematic temperature $T_{k} \left( {V_{{m_{pi} }} ,p = 0} \right)$ (dashed line), thermodynamic temperature $T_{t} \left( {V_{{m_{pi} }} ,p} \right)$ (dash-dotted line) corresponding to $V_{{m_{pi} }}$ values and liquid thermal expansion curve (solid line) for a H₂, b CO₂, c CH₃OH and d C₆H₆. The dot marker corresponds to the critical parameters: T _c and V _c

Having in mind that the demonstrated numerical problems are related to the volume determination for individual attractive adsorption site, one may consider the reliability of the identification of adsorption mechanism. Nevertheless, it has to be taken into account that the numerical problems were found only when individual attractive site is considered. Thus, having in mind that the volume is considered as an additive, the evaluated value $V_{{m_{pi} }}$ is the total volume and fulfills accepted constraint $V_{{m_{pi} }} < V_{ind}$. Thereby, the adsorption mechanism is identified properly for the material comprising such a geometrical heterogeneity.

However, the accuracy in volume evaluation for one adsorption site has an impact when determining surface structure parameter ζ, in particular the molar adhesion energy $\overline{E}_{adh} \left( {\overline{V}_{{m_{p} }} } \right)$. Hence, when analyzing the results for ζ presented in Fig. 8 it has to be taken into account that the calculated energy $\overline{E}_{adh} \left( {\overline{V}_{{m_{p} }} } \right)$ is overall adhesion energy. In our previous studies we did not perform the calculations of effective contact ratio for H₂ (applying a model equivalent to the presented researches). When analyzing the relationship for CH₃OH, the inconsistency of the description may be seen. In low range of temperatures this results from inadequate description of the adhesion energy in such range, since the energy is calculated with PVT relationship, dedicated for liquid bulk phase only. On the other hand, at the higher temperatures range the effective contact ratio value is surprisingly low, corresponding rather to the possible mobile mechanism than localized. This is an interesting feature that most probably results from the identified numerical problems, since in Fig. 6 it may be seen that the adsorption sites are of a significantly different size, and so the volume. When compared the remaining results with earlier works (Milewska-Duda and Duda 2002) the ζ overestimation may be seen, due to obvious differences in the structural heterogeneity. Nevertheless, results are in a good agreement with earlier assumed adsorption identification criteria and may be approved as validation parameter, when compared to the results of experimental examination of adsorption isotherms with LBET models. Moreover, notice that ζ parameter became almost invariant to the temperature (Table 2, ζ _const ). This is really important property and may be exploited, to improve identification of the adsorbent structure, by simultaneous fitting of two or more isotherms measured in different temperatures for the same pair adsorbate–adsorbent.

Fig. 8

Intermolecular effective contact ratio ζ and temperature T for H₂ (solid line), CO₂ (dotted line), CH₃OH (dashed line) and C₆H₆ (dash-dotted line). The description is consistent at the range above adsorbate freezing point (marked with dots), due to evaluation of the energy in Eq. (14) with PVT relationship dedicated for liquid bulk phase only

The analyses were completed with identification of the predominating adsorption mechanism at the temperature range 0–300 K with Eq. (7). It may be seen that for H₂ both mechanisms may occur. Localized mechanism predomination may be clearly seen for hydrogen at the temperature up to 115 K. For CO₂, CH₃OH and C₆H₆ only localized mechanism domination is observed. This is an obvious feature coming from the classical localized adsorption assumption (i.e. vaporous adsorbate is in a liquid state) and the fact that the tested range is blow the critical temperature range (i.e. these adsorbates in whole temperature range fulfill the localized mechanism constraints). Hence, w _ind /w _max ratio implies that for materials where geometrical heterogeneities are close to those modeled in graphite sample localized adsorption mechanism should be assumed, and so the corresponding appropriate mathematical model (Fig. 9).

Fig. 9

Adsorption predomination indicated via w _ind /w _max ratio at the temperature range 0–300 K for H₂ (solid line) and CO₂, CH₃OH, C₆H₆ (dashed line)

4 Conclusions

Presented in this paper results of research aimed at adsorption mechanism identification are further development of the approach elaborated in author’s team. The obtained results are sufficient to get an insight into H₂, CO₂, CH₃OH and C₆H₆ adsorption mechanisms. Performed calculations provide a reliable picture of individual particles movement near the solid surface. In particular, it was verified that that substantial geometrical heterogeneity generates localized attractive adsorption sites.

The numerical tool is comprehensive in terms of model complexity and ability to properties evaluation even when more than one adsorption site for localized mechanism is expected. Nevertheless, the application of the tool met obstacles coming from the difficulty of the volume determination for the particular site, thereby distorting true picture of thermodynamic equilibrium properties.

It has been demonstrated, that selected adsorbates H₂, CO₂, CH₃OH and C₆H₆ volume may be approximated as a liquid volume at the given temperature. Moreover, depending on the molecule size different structure diversities may be detected, especially when analyzing equipotential surface cross-sections.

The practical information driven by analyses of w _ind /w _max gives a basis to answer what particular mechanism predominates while adsorption of H₂, CO₂, CH₃OH and C₆H₆ in material of structure similar to the modeled graphite sample and so, what particular mathematical model should be chosen in order to examine reliably material porous structure.