${\mathcal{H}}$-matrix approximability of inverses of FEM matrices for the time-harmonic Maxwell equations

Abstract

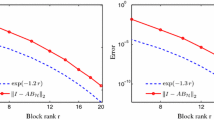
The inverse of the stiffness matrix of the time-harmonic Maxwell equation with perfectly conducting boundary conditions is approximated in the blockwise low-rank format of ${\mathcal{H}}$-matrices. Under a technical assumption on the mesh, we prove that root exponential convergence in the block rank can be achieved, if the block structure conforms to a standard admissibility criterion.

Appendix: Regular decompositions

The following lemma follows from the seminal paper [12]. The notation follows [12] in that $H^{s}_{\overline {{{{\varOmega }}}}}(\mathbb {R}^{3})$, $s \in \mathbb {R}$ denotes the spaces of distributions in $H^{s} (\mathbb {R}^{3})$ supported by $\overline {{{{\varOmega }}}}$, and that $C^{\infty }_{\overline {{{{\varOmega }}}}}(\mathbb {R}^{3})$ is the space of $C^{\infty }(\mathbb {R}^{3})$-functions supported by $\overline {{{{\varOmega }}}}$.

We introduce the space

$${\mathbf{H}}^{s}_{\overline{{{{\varOmega}}}}}(\text{curl}) := \left\{\mathbf{E} \in {\mathbf{H}}_{\overline{{{{\varOmega}}}}}^{s}(\mathbb{R}^{3}) \colon \nabla \times \mathbf{E} \in \mathbf{H}_{\overline{{{{\varOmega}}}}}^{s}(\mathbb{R}^{3})\right\}$$

equipped with the norm $\|\mathbf {E}\|_{{\mathbf {H}}_{\overline {{{{\varOmega }}}}}^{s}(\text {curl})}:= \|\mathbf {E}\|_{\mathbf {H}_{\overline {{{{\varOmega }}}}}^{s}(\mathbb {R}^{3})}+ \|\nabla \times \mathbf {E}\|_{\mathbf {H}_{\overline {{{{\varOmega }}}}}^{s}(\mathbb {R}^{3})}$.

Remark A.1

From [12, p. 301], for any $s \in \mathbb {R}$, the space $\mathbf {H}^{s}_{\overline {{{{\varOmega }}}}}(\mathbb {R}^{3})$ is naturally isomorphic to the dual space of H^−s(Ω). Hence, for s ≥ 0, we have the alternative norm equivalence $\|\mathbf {v}\|_{\mathbf {H}_{\overline {{{{\varOmega }}}}}^{s}(\mathbb {R}^{3})} \sim \|\mathbf {v}\|_{\widetilde {\mathbf {H}}^{s}({{{\varOmega }}})} = \|\mathbf {v}^{\star }\|_{{\mathbf {H}}^{s}(\mathbb {R}^{3})}$, where v^⋆ is the zero extension of a function v defined on Ω.

Lemma A.2

Let Ω be a bounded Lipschitz domain. There exist pseudodifferential operators T₁ and T₂ of order − 1 and a pseudodifferential operator L of order $-\infty$ on $\mathbb {R}^{3}$ with the following properties: For each $s \in \mathbb {R}$, they have the mapping properties ${{T}}_{1}:\mathbf {H}_{\overline {{{{\varOmega }}}}}^{s} (\mathbb {R}^{3})\rightarrow {H}_{\overline {{{{\varOmega }}}}}^{s+1}\left (\mathbb {R}^{3}\right )$, ${\mathbf {T}}_{2}:\mathbf {H}_{\overline {{{{\varOmega }}}}}^{s} (\mathbb {R}^{3})\rightarrow \mathbf {H}_{\overline {{{{\varOmega }}}}}^{s+1}\left (\mathbb {R}^{3}\right )$, and $\mathbf {L}:\mathbf {H}_{\overline {{{{\varOmega }}}}}^{s}(\mathbb {R}^{3}) \rightarrow \mathbf {C}^{\infty }_{\overline {{{{\varOmega }}}}}\left (\mathbb {R}^{3}\right )$ and for any $\mathbf {u}\in \mathbf {H}_{\overline {{{{\varOmega }}}}}^{s}\left (\text {curl}\right )$, there holds the representation

$$\mathbf{u}=\nabla T_{1}\left(\mathbf{u}-\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) \right) +\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) +\mathbf{Lu}.$$

(A.1)

Proof

In [12, Theorem 4.6], operators T₁, T₂, T₃, L₁, L₂ with the mapping properties

$$\begin{array}{@{}rcl@{}} T_{1}&:&\mathbf{H}_{\overline{{{{\varOmega}}}}}^{s}\left(\mathbb{R}^{3}\right)\rightarrow {H}_{\overline{{{{\varOmega}}}}}^{s+1}\left(\mathbb{R}^{3}\right),\\ \mathbf{T}_{2}&:&\mathbf{H}_{\overline{{{{\varOmega}}}}}^{s}\left(\mathbb{R}^{3}\right)\rightarrow\mathbf{H}_{\overline{{{{\varOmega}}}}}^{s+1}\left(\mathbb{R}^{3}\right),\\ \mathbf{T}_{3}&:&H_{\overline{{{{\varOmega}}}}}^{s}(\mathbb{R}^{3})\rightarrow\mathbf{H}_{\overline{{{{\varOmega}}}}}^{s+1}\left(\mathbb{R}^{3}\right) , \\ \mathbf{L}_{\ell}&:&\mathbf{H}_{\overline{{{{\varOmega}}}}}^{s}\left(\mathbb{R}^{3}\right) \rightarrow \mathbf{C}_{\overline{{{{\varOmega}}}}}^{\infty}\left(\mathbb{R}^{3}\right) , \quad \ell=1,2, \end{array}$$

are defined, and it is shown that

$$\begin{array}{@{}rcl@{}} \nabla T_{1} \mathbf{v} +\mathbf{T}_{2}\left(\nabla \times \mathbf{v}\right) & =\mathbf{v}-\mathbf{L} _{1}\mathbf{v}, \end{array}$$

(A.2a)

$$\begin{array}{@{}rcl@{}} \nabla \times \mathbf{T}_{2} \mathbf{v} +\mathbf{T} _{3}\left(\nabla \cdot \mathbf{v}\right) & =\mathbf{v} -\mathbf{L}_{2}\mathbf{v}. \end{array}$$

(A.2b)

Taking $\mathbf {v}=\mathbf {u}-\mathbf {T}_{2}\left (\nabla \times \mathbf {u}\right )$ in (A.2a), we obtain

$$\begin{array}{@{}rcl@{}} \nabla {T}_{1}\left(\mathbf{u}-\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) \right) +\mathbf{T}_{2}\left(\nabla \times \left(\mathbf{u}-\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) \right) \right) =\mathbf{u} -\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) -\mathbf{L} _{1}\left(\mathbf{u}-\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) \right) . \end{array}$$

(A.3)

Since ∇×u is divergence-free, we obtain from (A.2b) with the choice v = ∇×u

$$\begin{array}{@{}rcl@{}} \mathbf{T}_{2}\left(\nabla \times \left(\mathbf{u}-\mathbf{T} _{2}\left(\nabla \times \mathbf{u}\right) \right) \right) & =&\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) -\mathbf{T} _{2}\left(\nabla \times \mathbf{u}-\mathbf{L}_{2}\nabla \times \mathbf{u}\right) \\ & =&\mathbf{T}_{2}\left(\mathbf{L}_{2}\left(\nabla \times \mathbf{u}\right) \right) =:\mathbf{L}_{3}\mathbf{u}, \end{array}$$

where, again, L₃ is a smoothing operator of order $-\infty$ mapping into $\mathbf {C}^{\infty }_{\overline {{{{\varOmega }}}}}(\mathbb {R}^{3})$. Inserting this into (A.3) leads to

$$\nabla T_{1}\left(\mathbf{u}-\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) \right) +\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) =\mathbf{u}-\mathbf{L}_{1}\left(\mathbf{u}-\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) \right) -\mathbf{L}_{3}\mathbf{u}.$$

Choosing $\mathbf {Lu}:=\left (\mathbf {L}_{1}\left (\mathbf {u} -\mathbf {T}_{2}\nabla \times \mathbf {u}\right ) \right ) +\mathbf {L} _{3}\mathbf {u}$, we arrive at the representation (A.1). $\square$ 

Corollary A.3

Let ${{{\varOmega }}} \subset \mathbb {R}^{3}$ be a bounded Lipschitz domain. Then, for every s ≥ 0, there is a constant C (depending only on Ω and s) such that every $\mathbf {u} \in {\mathbf {H}_{0}^{s}}(\text {curl},{{{\varOmega }}})$ can be decomposed as u = z + ∇p with $\mathbf {z} \in \mathbf {H}_{\overline {{{{\varOmega }}}}}^{s+1}(\mathbb {R}^{3})$ and $p \in {H}_{\overline {{{{\varOmega }}}}}^{s+1}(\mathbb {R}^{3})$ together with

$$\|\mathbf{z}\|_{\mathbf{H}_{\overline{{{{\varOmega}}}}}^{s+1}(\mathbb{R}^{3})} \leq C \|\mathbf{u}\|_{\mathbf{H}_{\overline{{{{\varOmega}}}}}^{s}(\text{curl})}, \qquad \|\nabla p\|_{\mathbf{H}_{\overline{{{{\varOmega}}}}}^{s}(\mathbb{R}^{3})} \leq C \|\mathbf{u}\|_{{\mathbf{H}}_{\overline{{{{\varOmega}}}}}^{s}(\mathbb{R}^{3})}.$$

(A.4)

Proof

From Lemma A.2 we can write u = z + ∇p with

$$\begin{array}{@{}rcl@{}} \mathbf{z} := \mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) +\mathbf{Lu}, \qquad p := T_{1}\left(\mathbf{u}-\mathbf{T}_{2}\left(\nabla \times \mathbf{u}\right) \right) . \end{array}$$

The stability estimate for z follows from the mapping properties of the operators T₂ and L. The mapping properties of T₁ yield

$$\begin{array}{@{}rcl@{}} \|\nabla p \|_{\mathbf{H}^{s}_{\overline{{{{\varOmega}}}}}(\mathbb{R}^{3})} & \lesssim \|\mathbf{u} - \mathbf{T}_{2}(\nabla \times \mathbf{u})\|_{{\mathbf{H}^{s}_{\overline{{{{\varOmega}}}}}(\mathbb{R}^{3})}} \lesssim \|\mathbf{u} \|_{{\mathbf{H}^{s}_{\overline{{{{\varOmega}}}}}(\mathbb{R}^{3})}} + \|\nabla \times \mathbf{u} \|_{{\mathbf{H}^{s-1}_{\overline{{{{\varOmega}}}}}(\mathbb{R}^{3})}} \lesssim \|\mathbf{u} \|_{{\mathbf{H}^{s}_{\overline{{{{\varOmega}}}}}(\mathbb{R}^{3})}}, \end{array}$$

where the last step follows from the mapping property $\nabla \times :\mathbf {H}^{s}_{\overline {{{{\varOmega }}}}}(\mathbb {R}^{3}) \rightarrow \mathbf {H}^{s-1}_{\overline {{{{\varOmega }}}}}(\mathbb {R}^{3})$. $\square$