Skip to main content
SpringerLink
Log in

Approximation of the high-frequency Helmholtz kernel by nested directional interpolation: error analysis

  • Published:
Numerische Mathematik Aims and scope Submit manuscript

Abstract

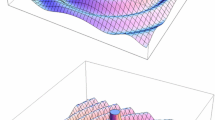
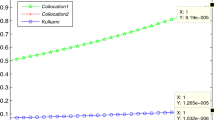
We present and analyze an approximation scheme for a class of highly oscillatory kernel functions, taking the 2D and 3D Helmholtz kernels as examples. The scheme is based on polynomial interpolation combined with suitable pre- and post-multiplication by plane waves. It is shown to converge exponentially in the polynomial degree and supports multilevel approximation techniques. Our convergence analysis may be employed to establish exponential convergence of certain classes of fast methods for discretizations of the Helmholtz integral operator that feature polylogarithmic-linear complexity.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3

Similar content being viewed by others

References

  1. Abramowitz, M., Stegun, I.A.: Handbook of Mathematical Functions. Applied Mathematics Series 55. National Bureau of Standards, U.S. Department of Commerce (1972)

  2. Bebendorf, M., Kuske, C., Venn, R.: Wideband nested cross approximation for Helmholtz problems. Numer. Math. 130(1), 1–34 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  3. Börm, S.: Directional \(\cal{H}^2\)-matrix compression for high-frequency problems. https://arxiv.org/abs/1510.07087

  4. Börm, S.: Approximation of integral operators by \({\cal{H}}^2\)-matrices with adaptive bases. Computing 74(3), 249–271 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  5. Börm, S.: Efficient Numerical Methods for Non-local Operators: \({\cal{H}}^2\)-Matrix Compression, Algorithms and Analysis, volume 14 of EMS Tracts in Mathematics. EMS (2010)

  6. Börm, S., Börst, C., Melenk, J.M.: An analysis of a butterfly algorithm. https://arxiv.org/abs/1703.01941 (2017)

  7. Börm, S., Löhndorf, M., Melenk, J.M.: Approximation of integral operators by variable–order interpolation. Numer. Math. 99(4), 605–643 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  8. Brandt, A.: Multilevel computations of integral transforms and particle interactions with oscillatory kernels. Comput. Phys. Commun. 65, 24–38 (1991)

    Article  MathSciNet  MATH  Google Scholar 

  9. Candès, E., Demanet, L., Ying, L.: A fast butterfly algorithm for the computation of Fourier integral operators. Multiscale Model. Simul. 7(4), 1727–1750 (2009)

    Article  MathSciNet  MATH  Google Scholar 

  10. Cheng, H., Crutchfield, W.Y., Gimbutas, Z., Greengard, L.F., Ethridge, J.F., Huang, J., Rokhlin, V., Yarvin, N., Zhao, J.: A wideband fast multipole method for the Helmholtz equation in three dimensions. J. Comput. Phys. 216(1), 300–325 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  11. Darve, E.: The fast multipole method: numerical implementation. J. Comput. Phys. 160(1), 195–240 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  12. Demanet, L., Ferrara, M., Maxwell, N., Poulson, J., Ying, L.: A butterfly algorithm for synthetic aperture radar imaging. SIAM J. Imaging Sci. 5(1), 203–243 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  13. DeVore, R.A., Lorentz, G.G.: Constructive Approximation. Springer, Berlin (1993)

    Book  MATH  Google Scholar 

  14. Engquist, B., Ying, L.: Fast directional multilevel algorithms for oscillatory kernels. SIAM J. Sci. Comput. 29(4), 1710–1737 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  15. Greengard, L., Huang, J., Rokhlin, V., Wandzura, S.: Accelerating fast multipole methods for the Helmholtz equation at low frequencies. IEEE Comput. Sci. Eng. 5(3), 32–38 (1998)

    Article  Google Scholar 

  16. Kunis, Stefan, Melzer, Ines: A stable and accurate butterfly sparse Fourier transform. SIAM J. Numer. Anal. 50(3), 1777–1800 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  17. Li, Y., Yang, H., Ying, L.: Multidimensional butterfly factorization. Preprint available at https://arxiv.org/abs/1509.07925 (2015)

  18. Messner, M., Schanz, M., Darve, E.: Fast directional multilevel summation for oscillatory kernels based on Chebyshev interpolation. J. Comput. Phys. 231(4), 1175–1196 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. Michielssen, E., Boag, A.: A multilevel matrix decomposition algorithm for analyzing scattering from large structures. IEEE Trans. Antennas Propag. 44, 1086–1093 (1996)

    Article  Google Scholar 

  20. Olver, F.W.J.: Asymptotics and Special Functions. Academic Press, Cambridge (1974)

    MATH  Google Scholar 

  21. Rivlin, T.J.: The Chebyshev Polynomials. Wiley-Interscience, New York (1990)

    MATH  Google Scholar 

  22. Rokhlin, V.: Diagonal forms of translation operators for the Helmholtz equation in three dimensions. Appl. Comput. Harm. Anal. 1, 82–93 (1993)

    Article  MathSciNet  MATH  Google Scholar 

  23. Sauter, S.A.: Variable order panel clustering. Computing 64, 223–261 (2000)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institut für Informatik, Christian-Albrechts-Universität zu Kiel, D-24118, Kiel, Germany

    Steffen Börm

  2. Institut für Analysis und Scientific Computing, Technische Universität Wien, A-1040, Vienna, Austria

    Jens M. Melenk

Authors
  1. Steffen Börm
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jens M. Melenk
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Steffen Börm.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Börm, S., Melenk, J.M. Approximation of the high-frequency Helmholtz kernel by nested directional interpolation: error analysis. Numer. Math. 137, 1–34 (2017). https://doi.org/10.1007/s00211-017-0873-y

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00211-017-0873-y

Mathematics Subject Classification

Search

Navigation