Comprehensive Analysis of Deterministic and Stochastic Eco-Epidemic Models Incorporating Fear, Refuge, Supplementary Resources, and Selective Predation Effects

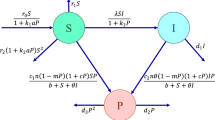
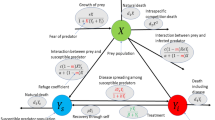
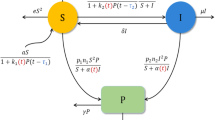
Abstract

In this investigation, we delve into the dynamics of an ecoepidemic model, considering the intertwined influences of fear, refuge-seeking behavior, and alternative food sources for predators with selective predation. We extend our model to incorporate the impact of fluctuating environmental noise on system dynamics. The deterministic model undergoes thorough scrutiny to ensure the positivity and boundedness of solutions, with equilibria derived and their stability properties meticulously examined. Furthermore, we explore the potential for Hopf bifurcation within the system dynamics. In the stochastic counterpart, we prioritize discussions on the existence of a globally positive solution. Through simulations, we unveil the stabilizing effect of the fear factor on susceptible prey reproduction, juxtaposed against the destabilizing roles of prey refuge behavior and disease prevalence intensity. Notably, when disease prevalence intensity is too low, the infection can be eradicated from the ecosystem. Our deterministic analysis reveals a complex interplay of factors: the system destabilizes initially but then stabilizes as the fear factor suppressing disease prevalence intensifies, or as predators exhibit a stronger preference for infected prey over susceptible ones, or as predators are provided with more alternative food sources. Moreover, for the stochastic system, the oscillations tend to cluster around the coexistence equilibrium of the corresponding deterministic model when white noise intensity is low. However, with increasing white noise intensity, oscillation amplitudes escalate. Critically, very high levels of white noise can lead to the eradication of infection from the ecosystem.

Appendices

Appendix A

For any solution $(S(t),I(t),P(t))$ of system (1) with the positive initial values $(S_{0},I_{0},P_{0})$, we have

$$\begin{aligned} S(t) =&S_{0}\exp \biggl[\displaystyle \int ^{t}_{0}\biggl\{ \frac{r_{0}}{1+ k_{1}P(u)}-r_{1}-r_{2}S(u)- \frac{\lambda I(u)}{1+k_{2}P(u)}\\ &{}- \frac{n(1-mP(u))P(u)}{b+S(u)+\theta I(u)}\biggr\} du \biggr], \\ I(t) =&I_{0}\exp \left [\displaystyle \int ^{t}_{0}\left \{ \frac{\lambda S(u)}{1+k_{2}P(u)}- \frac{n\theta (1-mP(u))P(u)}{b+S(u)+\theta I(u)}-d\right \}du\right ], \\ P(t) =&P_{0}\exp \biggl[\displaystyle \int ^{t}_{0} \biggl\{ r_{3} \biggl(1-\frac{P(u)}{K} \biggr)+n(1-mP(u)) \frac{c_{1}S(u)+c_{2}\theta I(u)}{b+S(u)+\theta I(u)}\\ &{}-\delta _{1}- \delta _{2} P(u)\biggr\} du \biggr]. \end{aligned}$$

Positivity of the solutions of system (1) is guaranteed from the above expressions. Let $\Phi =S+I+P$, then the time derivative of $\Phi$ will be

$$\begin{aligned} \dot{\Phi} =&\frac{r_{0}S}{1+k_{1}P}+r_{3}P\left (1-\frac{P}{K} \right )- \frac{(1-c_{1})(1-mP)nSP+(1-c_{2})n\theta (1-mP)IP}{b+S+\theta I} \\ &-d I-\delta _{1} P-\delta _{2}P^{2}-r_{1}S-r_{2}S^{2} \\ \leq & r_{0}S+r_{3}P-r_{1}S-d I-\delta _{1} P-r_{2}S^{2}. \end{aligned}$$

For $\delta >0$, we have $\dot{\Phi}+\delta \Phi \leq S(-r_{2}S+r_{0}-r_{1}+\delta )-I(d- \delta )-P(\delta _{1}-r_{3}-\delta )$. For $0<\delta \leq \min \{d,\delta _{1}-r_{3}\}$, we get $\dot{\Phi}+\delta \Phi \leq S(-r_{2}S+r_{0}-r_{1}+\delta )$. Note that the maximum value of $\displaystyle S(-r_{2}S+r_{0}-r_{1}+\delta )$ is $\displaystyle \frac{(r_{0}-r_{1}+\delta )^{2}}{4r_{2}}$, which is always positive; denote this number by $\kappa$. Thus, we get $\displaystyle \dot{\Phi}+\delta \Phi \leq \kappa$. By the theorem of differential inequality, we have

$$\begin{aligned} 0< \Phi (S,I,P)\leq \frac{\kappa (1-e^{-\delta t})}{\delta}+\Phi (S_{0},I_{0},P_{0})e^{- \delta t}. \end{aligned}$$

Thus, for sufficiently large values of t, we have $0<\Phi (t)\leq \kappa /\delta$.

Appendix B

Jacobian matrix $V=[V_{ij}]_{3\times 3}$ of system (1) has the following entries:

$$\begin{aligned} &V_{11}=\frac{r_{0}}{1+k_{1} P}-r_{1}-2r_{2}S- \frac{\lambda I}{1+k_{2}P}- \frac{n(b+\theta I)(1-mP)P}{(b+S+\theta I)^{2}}, \\ & V_{12}=-\frac{\lambda S}{1+k_{2}P}+ \frac{n\theta (1-mP)SP}{(b+S+\theta I)^{2}}, \\ & V_{13}=- \frac{r_{0}k_{1} S}{(1+k_{1}P)^{2}}+ \frac{\lambda k_{2}IS}{(1+k_{2}P)^{2}}-\frac{nS(1-2mP)}{b+S+\theta I}, \\ & V_{21}=\frac{\lambda I}{1+k_{2}P}+ \frac{n\theta (1-mP)IP}{(b+S+\theta I)^{2}}, \ V_{22}= \frac{\lambda S}{1+k_{2}P}- \frac{n\theta (b+S)(1-mP)P}{(b+S+\theta I)^{2}}-d, \\ & V_{23}=-\frac{\lambda k_{2}IS}{(1+k_{2}P)^{2}}- \frac{n\theta (1-mP)I}{b+S+\theta I},\ V_{31}= \frac{n(1-mP)P\{bc_{1}+(c_{1}-c_{2})\theta I\}}{(b+S+\theta I)^{2}}, \\ &V_{32}= \frac{n\theta (1-mP)P\{bc_{2}+(c_{2}-c_{1}S)\}}{(b+S+\theta I)^{2}}, \\ &V_{33}=r_{3}\left (1-\frac{P}{K}\right )-\frac{r_{3}P}{K}+ \frac{n(1-2mP)(c_{1}S+c_{2}\theta I)}{b+S+\theta I}-\delta _{1}-2 \delta _{2} P. \end{aligned}$$

• 1. The three eigenvalues, after evaluating the matrix $V$ at the equilibrium $E_{0}$, are obtained as $r_{0}-r_{1}$, $-d$ and $r_{3}-\delta _{1}$. Clearly, one eigenvalue is always negative while the other two will be negative if the conditions in (4) hold. Thus, the equilibrium $E_{0}$ is stable in view of conditions in (4).

• 2. At the equilibrium point $E_{1}$, eigenvalues of the Jacobian matrix $V$ are obtained as $-(r_{0}-r_{1})$, $\displaystyle \frac{\lambda (r_{0}-r_{1})}{r_{2}}-d$ and $\displaystyle r_{3}-\delta _{1}+ \frac{nc_{1}(r_{0}-r_{1})}{br_{2}+r_{0}-r_{1}}$. Note that in view of the feasibility condition of the equilibrium $E_{1}$, one eigenvalue is negative while the other two will be negative if the conditions in (5) hold. Thus, the conditions stated in (5) lead to stability of the equilibrium $E_{1}$.

• 3. The Jacobian matrix of the system (1) at the equilibrium $E_{2}$ has one eigenvalue as $\displaystyle r_{3}\left (1-\frac{2P_{2}}{K}\right )-\delta _{1}-2 \delta _{2} P_{2}$ whereas the others two are the roots of the following quadratic equation:

  $$\begin{aligned} &\Lambda ^{2}-\left \{\frac{r_{0}}{1+k_{1}P_{2}}-r_{1}-n\left ( \frac{1}{b}+\frac{\theta}{d}\right )(1-mP_{2})P_{2}\right \}\Lambda \\ & \hspace{2cm}+\frac{n^{2}\theta (1-mP_{2})^{2}P_{2}^{2}}{bd}-\left ( \frac{r_{0}}{1+k_{1}P_{2}}-r_{1}\right ) \frac{n\theta (1-mP_{2})P_{2}}{d}=0. \end{aligned}$$

  In view of the conditions in (6), the equilibrium $E_{2}$ is stable as under those conditions, eigenvalues are either negative or have negative real parts. Therefore, if the conditions in (6) are satisfied, the equilibrium $E_{3}$ is locally stable.

• 4. At the equilibrium $E_{3}$, the Jacobian matrix $V$ has one eigenvalue as $\displaystyle r_{3}-\delta _{1}+ \frac{n(C_{1}S_{3}+C_{2}\theta I_{3})}{b+S_{3}+\theta I_{3}}$ whereas the others two are the roots of the following quadratic equation:

  $$\begin{aligned} \Lambda ^{2}-\left (r_{0}-2r_{2}S_{3}-r_{1}-\lambda I_{3}\right ) \Lambda +\lambda ^{2}S_{3}I_{3}=0. \end{aligned}$$

  If the conditions in (7) hold, all the eigenvalues are either negative or negative real parts, and hence the equilibrium $E_{3}$ is stable locally.

• 5. The Jacobian matrix of the system (1) at the equilibrium $E_{4}$ immediately gives one eigenvalue as $\displaystyle \frac{\lambda S_{4}}{1+k_{2}P_{4}}- \frac{n\theta (1-mP_{4})P_{4}}{b+S_{4}}-d$. The other two eigenvalues are the roots of the following quadratic equation: $\Lambda ^{2}-(F_{1}+F_{2})\Lambda +(F_{1}F_{2}-F_{3}F_{4})=0$,

  where

  $$\begin{aligned} &F_{1}=-r_{2}S_{4}+\frac{n(1-mP_{4})S_{4}P_{4}}{(b+S_{4})^{2}}, \ F_{2}=- \left [\frac{r_{3}}{K}+\delta _{2}+\frac{c_{1}mnS_{4}}{b+S_{4}} \right ]P_{4}, \\ &F_{3}=-\frac{r_{0}k_{1}S_{4}}{(1+k_{1}S_{4})^{2}}- \frac{n(1-2mP_{4})S_{4}}{b+S_{4}},\ F_{4}= \frac{bc_{1}n(1-mP_{4})P_{4}}{(b+S_{4})^{2}}. \end{aligned}$$

  If the conditions in (8) hold, all the eigenvalues are either negative or have negative real parts. Thus, the equilibrium $E_{4}$ is stable under the conditions stated in (8).

• 6. The matrix obtained after evaluating the Jacobian matrix of system (1) at the equilibrium $E_{*}$ is $V_{E^{*}}=[m_{ij}]_{3\times 3}$, whose entries are as follows:

  $$\begin{aligned} &m_{11}=-r_{2}S^{*}+ \frac{n(1-mP^{*})S^{*}P^{*}}{(b+S^{*}+\theta I^{*})^{2}}, \ m_{12}=- \frac{\lambda S^{*}}{1+k_{2}P^{*}}+ \frac{n\theta (1-mP^{*})S^{*}P^{*}}{(b+S^{*}+\theta I^{*})^{2}}, \\ &m_{13}=-\frac{r_{0}k_{1} S^{*}}{(1+k_{1} P^{*})^{2}}+ \frac{\lambda k_{2}S^{*}I^{*}}{(1+k_{2}P^{*})^{2}}- \frac{n(1-2mP^{*})S^{*}}{b+S^{*}+\theta I^{*}}, \\ &m_{21}=\frac{\lambda I^{*}}{1+k_{2}P^{*}}+ \frac{n\theta (1-mP^{*}) I^{*}P^{*}}{(b+S^{*}+\theta I^{*})^{2}}, \ m_{22}= \frac{n\theta ^{2}(1-mP^{*}) I^{*}P^{*}}{(b+S^{*}+\theta I^{*})^{2}}, \\ & m_{23}=-\frac{\lambda k_{2}S^{*}I^{*}}{(1+k_{2}P^{*})^{2}}- \frac{n\theta (1-2mP^{*})I^{*}}{b+S^{*}+\theta I^{*}},\\ & m_{31}= \frac{n\{bc_{1}+(c_{1}-c_{2})\theta I^{*}\}(1-mP^{*})P^{*}}{(b+S^{*}+\theta I^{*})^{2}}, \\ &m_{32}= \frac{n\theta \{bc_{2}+(c_{2}-c_{1})S^{*}\}(1-mP^{*}) P^{*}}{(b+S^{*}+\theta I^{*})^{2}}, \\ & m_{33}=-\left [\frac{r_{3}}{K}+\delta _{2}+ \frac{mn(c_{1}S^{*}+c_{2}\theta I^{*})}{b+S^{*}+\theta I^{*}}\right ]P^{*}. \end{aligned}$$

  The characteristic equation corresponding to the matrix $J_{E^{*}}$ is given by

  $$\begin{aligned} \Lambda ^{3}+A_{1}\Lambda ^{2}+A_{2}\Lambda +A_{3}=0, \end{aligned}$$

  (11)

  where

  $$\begin{aligned} & A_{1}=-(m_{11}+m_{22}+m_{33}), \\ & A_{2}=m_{22}m_{33}-m_{23}m_{32}+m_{11}m_{33}-m_{13}m_{31}+m_{11}m_{22}-m_{12}m_{21}, \\ & A_{3}=m_{12}(m_{21}m_{33}-m_{11}(m_{22}m_{33}-m_{23}m_{32})-m_{23}m_{31})-m_{13}(m_{21}m_{32}-m_{22}m_{31}). \end{aligned}$$

  In view of Routh-Hurwitz criterion, roots of the equation (11) will be either negative or have negative real parts if and if only if the three conditions in (9) hold. Therefore, the equilibrium $E_{*}$ is locally asymptotically stable if and only if the conditions mentioned in (9) are satisfied.

Appendix C

Let the critical value of $\theta$ (say $\widehat{\theta}$) be such that

$$\begin{aligned} A_{1}(\widehat{\theta})A_{2}(\widehat{\theta})-A_{3}(\widehat{\theta})=0. \end{aligned}$$

(12)

Thus, at $\theta =\widehat{\theta}$, the characteristic equation (11) can be rewritten as $(\Lambda +A_{1})(\Lambda ^{2}+A_{2})=0$. This equation has three roots, a pair of purely imaginary roots $\Lambda _{1,2}=\pm i\sqrt{A_{2}}$ and a negative root $\Lambda _{3}=-A_{1}$. Thus, Hopf bifurcation occurs in the system (1).

Now, we consider a point $\theta$ in an $\epsilon -$ neighborhood of $\widehat{\theta}$, then the above roots become function of $\theta$, namely $\Lambda _{1,2}=\eta (\theta )\pm i\rho (\theta )$. Thus, from equation (12), after separating real and imaginary parts, we get

$$\begin{aligned} \eta ^{3}-3\eta \rho ^{2}+A_{1}(\eta ^{2}-\rho ^{2})+A_{2}\eta +A_{3} =&0, \end{aligned}$$

(13)

$$\begin{aligned} 3\eta ^{2}\rho -\rho ^{3}+2A_{1}\eta \rho +A_{2}\rho =&0. \end{aligned}$$

(14)

Since $\rho (\theta )\neq 0$, from equation (14), it follows that $\rho ^{2}=3\eta ^{2}+2A_{1}\eta +A_{2}$. Substituting this in equation (13), we get

$$\begin{aligned} 8\eta ^{3}+8A_{1}\eta ^{2}+2\eta (A^{2}_{1}+A_{2})+A_{1}A_{2}-A_{3}=0. \end{aligned}$$

(15)

Since $\eta (\widehat{\theta})=0$, from the above equation, we get

$$\begin{aligned} \left [\frac{d\eta}{d\theta}\right ]_{\theta =\widehat{\theta}}= - \left [\frac{1}{2(A^{2}_{1}+A_{2})}\frac{d}{d\theta}(A_{1}A_{2}-A_{3}) \right ]_{\theta =\widehat{\theta}}. \end{aligned}$$

The right side of the above equation does not vanish provided $\displaystyle \left [\frac{d}{d\theta}(A_{1}A_{2}-A_{3})\right ]_{ \theta =\widehat{\theta}}\neq 0$.

Appendix D

Letting $S(t)=e^{x}$, $I(t)=e^{y}$ and $P(t)=e^{z}$, the system (10) transforms into the following form:

$$\begin{aligned} &dx=\left [\frac{r_{0}}{1+k_{1}e^{z}}-r_{2}e^{x}-r_{1}- \frac{\sigma ^{2}_{1}}{2}-\frac{\lambda e^{y}}{1+k_{2}e^{z}}- \frac{n(1-me^{z})e^{z}}{b+e^{x}+\theta e^{y}}\right ]dt+\sigma _{1}d \beta _{1}(t), \\ &dy=\left [\frac{\lambda e^{x}}{1+k_{2}e^{z}}- \frac{n\theta (1-me^{z})e^{z}}{b+e^{x}+\theta e^{y}}-d- \frac{\sigma ^{2}_{2}}{2}\right ]dt+\sigma _{2}d\beta _{2}(t), \\ &dz=\left [r_{3}\left (1-\frac{e^{z}}{K}\right )+ \frac{n(1-me^{z})(e^{x}+\theta e^{y})}{b+e^{x}+\theta e^{y}}-\delta _{1}- \delta _{2}e^{z}-\frac{\sigma ^{2}_{3}}{2}\right ]dt+\sigma _{3}d \beta _{3}(t) \end{aligned}$$

(16)

with initial value $(x_{0},y_{0},z_{0})=(\ln S_{0},\ln I_{0},\ln P_{0} )$. Obviously, the coefficients of system (16) are locally Lipschitz continuous. Thus, there is a unique maximal local solution $(x(t),y(t),z(t))$ of system (16) for $t\in [0,\tau _{e})$, where $\tau _{e}$ denotes the explosion time. Therefore, $(S(t),I(t),P(t))=(e^{x(t)},e^{y(t)},e^{z(t)})$ is the unique positive local solution of the system (16) with positive initial value $(S_{0},I_{0},P_{0})$ on the interval $[0,\tau _{e})$.

Now, for the global positive solution, we need to verify $\tau _{e}=\infty$ a.s. Since $(S(t),I(t), P(t))$ is always positive, from the first equation of the system (10), we can write

$$\begin{aligned} dS(t)\leq S(t)(r_{0}-r_{2}S(t))dt+\sigma _{1}S(t)d\beta _{1}(t). \end{aligned}$$

Now, we consider the following stochastic differential equation:

$$\begin{aligned} d\Phi _{1}(t)=\Phi _{1}(t)\left [r_{0}-r_{2}\Phi _{1}(t)\right ]dt+ \sigma _{1}\Phi _{1}(t)d\beta _{1}(t), \ \Phi _{1}(0)=S_{0}. \end{aligned}$$

(17)

Then, $\displaystyle \Phi _{1}(t)= \frac{e^{\left (r_{0}-\frac{\sigma _{1}^{2}}{2}\right )t+\sigma _{1}\beta _{1}(t)}}{\frac{1}{S_{0}}+r_{2}\int _{0}^{t}e^{\left (r_{0}-\frac{\sigma _{1}^{2}}{2}\right )s+\sigma _{1}\beta _{1}(s)}ds}$ is the unique solution of system (17). Thus, from the comparison theorem of stochastic differential equation, we have $S(t)\leq \Phi _{1}(t)$, $t\in [0,\tau _{e})$ a.s.

From the second equation of system (10), we can write

$$\begin{aligned} dI(t)\leq I(t)[(\lambda S(t)-d)]dt+\sigma _{2}I(t)d\beta _{2}(t). \end{aligned}$$

Consider the following auxiliary system:

$$\begin{aligned} d\Phi _{2}(t)=\Phi _{2}(t)[\lambda \Phi _{1}(t)-d]dt+\sigma _{2}\Phi _{2}(t)d \beta _{2}(t), \ \Phi _{2}(0)=I_{0}. \end{aligned}$$

(18)

Then, $\displaystyle \Phi _{2}(t)=I_{0}e^{\int _{0}^{t}\left (\lambda \Phi _{1}(s)-d- \frac{\sigma _{2}^{2}}{2}\right )ds+\sigma _{2}\beta _{2}(t)}$ is the unique solution of system (18). Thus, from the comparison theorem of stochastic differential equation, we have $I(t)\leq \Phi _{2}(t)$, $t\in [0,\tau _{e})$ a.s.

Similarly, for the following auxiliary system:

$$\begin{aligned} &d\Phi _{3}(t)=\Phi _{3}(t)\left [\left \{r_{3}-\delta _{1}+ \frac{n\Phi _{1}(t)+\theta \Phi _{2}(t)}{b+\Phi _{1}(t)+\theta \Phi _{2}(t)} \right \}-\delta _{2}\Phi _{3}(t)\right ]dt+\sigma _{3}\Phi _{3}(t)d \beta _{3}(t), \\ & \Phi _{3}(0)=P_{0}.\\ &\Phi _{3}(t)= \frac{\exp \left [\int _{0}^{t}{\left (r_{3}-\delta _{1}-\frac{\sigma _{3}^{2}}{2}+\frac{n\Phi _{1}(s)+\theta \Phi _{2}(s)}{b+\Phi _{1}(s)+\theta \Phi _{2}(s)}\right )ds+\sigma _{3}\beta _{3}(t)}\right ]}{\frac{1}{P_{0}}+\delta _{2}\int _{0}^{t}\exp \left [\int _{0}^{s}{\left (r_{3}-\delta _{1}-\frac{\sigma _{3}^{2}}{2}+\frac{n\Phi _{1}(\tau )+\theta \Phi _{2}(\tau )}{b+\Phi _{1}(\tau )+\theta \Phi _{2}(\tau )}\right )d\tau +\sigma _{3}\beta _{3}(s)}\right ]ds} \end{aligned}$$

(19)

is the unique solution. Thus, from the comparison theorem of stochastic differential equation, we have $P(t)\leq \Phi _{3}(t)$, $t\in [0,\tau _{e})$ a.s. Using the positivity of $S(t)$, we get the following inequality:

$$\begin{aligned} dS(t)\geq S(t)\left [(r_{0}-r_{1}-n)-r_{2}S(t)\right ]dt+\sigma _{1}S(t)d \beta _{1}(t). \end{aligned}$$

Clearly,

$$\begin{aligned} \phi _{1}(t)= \frac{\exp \left \{(r_{0}-r_{1}-n-\frac{\sigma _{1}^{2}}{2})t+\sigma _{1}\beta _{1}(t)\right \}}{\frac{1}{a_{10}}+r\int _{0}^{t}\exp \left [(r_{0}-r_{1}-n-\frac{\sigma _{1}^{2}}{2})s+\sigma _{1}\beta _{1}(s)\right ]ds} \end{aligned}$$

is the unique solution to the initial value problem

$$\begin{aligned} &d\phi _{1}(t)=\phi _{1}(t)\left [(r_{0}-r_{1}-n)-r_{2}\phi _{1}(t) \right ]dt+\sigma _{1}\phi _{1}(t)d\beta _{1}(t),\ \phi _{1}(0)=a_{10}. \end{aligned}$$

Hence, by comparison theorem of stochastic differential equation, we get $S(t)\geq \phi _{1}(t)$ for $t\in [0,\tau _{e})$ a.s. and $I(t)\geq \phi _{2}(t)$ for $t\in [0,\tau _{e})$ a.s., where

$$\begin{aligned} \phi _{2}(t)=a_{20}\exp \left [\int _{0}^{t}\left (\lambda \phi _{1}(s)-n \theta -d-\frac{\sigma _{2}^{2}}{2}\right )ds+\sigma _{2}\beta _{2}(t) \right ] \end{aligned}$$

is the unique solution of the following auxiliary equation:

$$\begin{aligned} &d\phi _{2}(t)=\phi _{2}(t)\left [(\lambda \phi _{1}(t)-n\theta -d) \phi _{2}(t)\right ]dt+\sigma _{2}\phi _{2}(t)d\beta _{2}(t),\ \phi _{2}(0)=a_{20}. \end{aligned}$$

Again, $P(t)\geq \phi _{3}(t)\ for \ t\in [0,\tau _{e})$ a.s., where

$$\begin{aligned} \phi _{3}(t)= \frac{\exp \left \{(r_{3}+n-\delta _{1}-\frac{\sigma _{3}^{2}}{2})t+\sigma _{3}\beta _{3}(t)\right \}}{\frac{1}{a_{30}}+(\frac{r_{3}}{K}+\delta _{2})\int _{0}^{t}\exp \left \{(r_{3}+n-\delta _{1}-\frac{\sigma _{3}^{2}}{2})s+\sigma _{3}\beta _{3}(s)\right \}ds} \end{aligned}$$

is the unique solution of the auxiliary equation

$$\begin{aligned} &d\phi _{3}(t)=\phi _{3}(t)\left [(r_{3}+n-\delta _{1})-\left ( \frac{r_{3}}{K}+\delta _{2}\right )\phi _{3}(t)\right ]dt+\sigma _{3} \phi _{3}(t)d\beta _{3}(t),\ \phi _{3}(0)=a_{30}. \end{aligned}$$

Therefore, we get

$$\begin{aligned} \phi _{1}(t)\leq S(t)\leq \Phi _{1}(t), \ \phi _{2}(t)\leq I(t)\leq \Phi _{2}(t),\ \phi _{3}(t)\leq P(t)\leq \Phi _{3}(t),\ \forall \ t \in [0,\tau _{e})\ \textit{a.s.} \end{aligned}$$

From the above, it is clear that the values of $\Phi _{1}(t)$, $\Phi _{2}(t)$, $\Phi _{3}(t)$, $\phi _{1}(t)$, $\phi _{2}(t)$ and $\phi _{3}(t)$ will not be explored at any finite time, and are well defined for any large values of $\tau _{e}$. Hence, $(S(t),I(t),P(t))$ is a global solution of system (10).