Abstract
Persistence and stability properties are considered for a class of forced positive nonlinear delay-differential systems which arise in mathematical ecology and other applied contexts. The inclusion of forcing incorporates the effects of control actions (such as harvesting or breeding programmes in an ecological setting), disturbances induced by seasonal or environmental variation, or migration. We provide necessary and sufficient conditions under which the states of these models are semi-globally persistent, uniformly with respect to the initial conditions and forcing terms. Under mild assumptions, the model under consideration naturally admits two steady states (equilibria) when unforced: the origin and a unique non-zero steady state. We present sufficient conditions for the non-zero steady state to be stable in a sense which is reminiscent of input-to-state stability, a stability notion for forced systems developed in control theory. In the absence of forcing, our input-to-sate stability concept is identical to semi-global exponential stability.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The present paper considers boundedness, convergence, persistence and stability properties for a class of forced positive nonlinear delay-differential systems. The forcing arises from exogenous terms which, depending on the context, are interpreted as a control action or disturbance. Specifically, we consider the system
where the matrix \(A\) is Metzler (all off-diagonal entries are nonnegative) and asymptotically stable, the vectors \(b\) and \(c\) are nonnegative, \(h\geq 0\) is the length of the delay and \(f\) is a nonnegative nonlinearity which may depend on a forcing function \(u\) and \(v\) represents additive nonnegative forcing.
As is well known, positive dynamical systems, or simply positive systems, are dynamical systems where the evolution map leaves a positive cone invariant. The archetypal positive cone is the nonnegative orthant of Euclidean space, equipped with the partial order of component wise inequality.Footnote 1 There are a multitude of scientific and engineering contexts where positive systems arise, including communications, logistics, economics, biology, chemistry and ecology, each motivated by the natural requirement that certain system variables (such as prices, population densities, concentrations) are nonnegative by their very nature. The study of positive systems described by linear dynamic equations is grounded in the seminal work by Perron and Frobenius in the early 1900s on irreducible and primitive matrices, and the generalisation to compact operators by Krein and Rutman in 1950. Extensions of these results to various nonlinear settings can be found in the literature (see, for example, [26]). For more information, we refer the reader to the numerous monographs and textbooks devoted to the study of positive systems, including [2, 19, 25, 26].
Delay-differential equations are a class of functional differential equation [21, 28, 37] in which the derivative of the unknown function \(x\) at time \(t\) depends not only on \(x(t)\), but also on \(x(\tau )\) for certain times \(\tau < t\). They are known to play an important role in many application areas, including mathematical ecology [37], where they, for example, arise in models which feature delayed population density dependence. One famous example is the so-called Nicholson model, proposed in [18], as a model for Australian blowfly populations, and based on the experimental work of Nicholson [32]. Naturally, differential-delay models in population dynamics enjoy certain positivity properties [37].
The model (1.1) has both a linear and a structured nonlinear delayed component and can be thought of as the feedback interconnection of a linear system with delayed output \(c^{T}x(t-h)\) and the nonlinearity \(f\). Differential and difference equations of this structure (with and without delay) have been analysed in great depth in control theory (where they are also known as Lur’e systems, after the Soviet scholar A.I. Lur’e), originally in the unforced case [23, 29, 47], and more recently in the presence of forcing [17, 22, 35, 36]. Positive systems of the form (1.1) arise also in biology, ecology and chemistry, including the Nicholson blowfly equation and the Mackey-Glass equation [24, 30]. In the absence of delays, systems of Lur’e type have been studied in a population dynamics context in the papers [3, 9, 10, 12–14, 33, 39, 44] which, with the exception of [3], consider the discrete-time case.
When studying the dynamic behaviour of (1.1), a natural question is whether solutions are bounded, persistent or stable. In typical cases (though not always), zero is a steady state (equilibrium) of system (1.1) when unforced (\(u\) constant, \(v=0\)). Generally speaking, persistency, which is now a well-established concept [13–15, 38, 39], captures the extent to which non-zero solutions are bounded away from 0 which corresponds to the avoidance of extinction in population models.
Under fairly natural assumptions, the unforced version of (1.1) admits two steady states — 0 and a unique non-zero non-negative steady state \(x^{\mathrm{s}}\). If the system is persistent, then, obviously, 0 is not stable and the immediate stability question is: do there exist natural and easily checkable conditions under which the non-zero steady state \(x^{\mathrm{s}}\) is stable, and attracts all (non-zero) solutions in the absence of forcing? Furthermore, what are the effects of the potentially persistent forcing terms? The motivation for including these terms is to study a framework where disturbances (unintended effects), such as temporal parameter variation, or control actions (intended effects) can be accommodated.
Our main results relate to persistence and stability of (1.1). For the former, our main result is Theorem 4.3 which provides sufficient conditions for (1.1) to be semi-globally persistent, uniformly with respect to time. Here the term “semi-global” refers to initial conditions as well as forcing functions. Furthermore, under mild additional assumptions, we show that the sufficient persistency conditions of Theorem 4.3 are necessary, see Proposition 4.4. In relation to stability, our main result is Theorem 5.2, which provides estimates of \(x(t)-x^{\mathrm{s}}\) in terms of the initial condition and the forcing functions \(u\) and \(v\). The stability conditions are based on the interplay of the constant \(-c^{T}A^{-1}b\) and an associated sector condition for \(f\). The concept of a sector condition is ubiquitious in the theory of Lur’e systems [22, 23, 29, 47] and is related to that of an enveloping condition [6, 34] in the difference equations literature. In the absence of any forcing, our stability results guarantee that \(x^{\mathrm{s}}\) is semi-globally exponentially stable. The theoretical results are illustrated by detailed discussions of three classes of examples from population dynamics and chemical reaction networks, namely: delayed recruitment models, dispersal of a population with unique breeding region (modelled by a so-called Nicholson system) and self-regulated biochemical reactions.
The feature which distinguishes our work from much of the literature on population dynamics is the inclusion of the forcing terms \(u\) and \(v\) (modelling disturbances, control actions or certain parameter variations) in the stability analysis to estimate the effects these terms may have on the unforced dynamics. To do so, we make use of concepts and techniques from the field of nonlinear control theory, namely the input-to-state stability paradigm [8, 42, 43], initiated in [40], and one of the major developments in nonlinear control theory over the last 30 years. To make the paper understandable to readers without any background in control theory, we explain and state the relevant control theoretic concepts and results in some detail.
The paper is organised as follows. Sections 2 and 3 gather mathematical preliminaries and introduce the model we consider, respectively. Sections 4 and 5 comprise the technical heart of the paper and contain persistence and stability results, respectively. Three classes of examples are considered in depth in Sect. 6. Some technical aspects are relegated to the Appendices.
2 Preliminaries
As usual let ℕ, ℤ, ℝ and ℂ denote the positive integers (natural numbers), integers, real numbers and complex numbers, respectively. Furthermore,
For \(M=(m_{ij})\in {\mathbb{R}}^{n\times q}\), we write \(M\geq 0\) if \(M\in {\mathbb{R}}_{+}^{n\times q}\), \(M>0\) if \(M\geq 0\) and \(M\neq0\) and \(M\gg 0\) if \(m_{ij}>0\) for all \(i\) and \(j\). If \(M\gg 0\), then we also say that \(M\) is strictly positive. The matrix \(M\) is said to be Metzler if it is square and \(m_{ij}\geq 0\) for \(i\neq j\). We recall that a square matrix is called Hurwitz if every eigenvalue has negative real part.
The \(i\)-th canonical basis vector of \({\mathbb{R}}^{n}\) is denoted by \(e_{i}\), that is, \(e_{i}\) is the vector in \({\mathbb{R}}^{n}\) the \(i\)-th component of which is equal to 1 and with all other components being equal to 0. Obviously, \(e_{i}>0\), but \(e_{i}\) is not strictly positive. For the purposes of this paper, it is convenient to endow \({\mathbb{R}}^{n}\) with the 1-norm \(\|\cdot \|_{1}\), that is, for \(z=(z_{1},\ldots ,z_{n})^{T}\in {\mathbb{R}}^{n}\), the norm \(\|z\|_{1}\) is given by \(\|z\|_{1}=\sum _{i=1}^{n}|z_{i}|\). Since the 1-norm on \({\mathbb{R}}^{n}\) is used throughout, we will simply write \(\|z\|:=\|z\|_{1}\). Occasionally, the maximum norm \(\|z\|_{\infty }=\max _{1\leq i\leq n}|z_{i}|\) will also be used.
For \(r=1,\infty \) and \(h>0\), we define
An element \(\zeta \in M^{r}([-h,0],{\mathbb{R}}^{n})\) will be written in the form \(\zeta =(\zeta ^{0},\zeta ^{1})\) with \(\zeta ^{0}\in {\mathbb{R}}^{n}\) and \(\zeta ^{1}\in L^{r}([-h,0],{\mathbb{R}}^{n})\) and the norm of \(\zeta \) is defined by
For brevity, we will set \(M^{r}:=M^{r}([-h,0],{\mathbb{R}}^{n})\). Obviously, \(M^{\infty }\subset M^{1}\). A number of other function spaces will be introduced when needed and, for ease of reference, are listed in Appendix A.
For a function \(z:[-h,a]\to {\mathbb{R}}^{n}\), where \(a\geq 0\) and \(h>0\), we define \(z_{t}:[-h,0]\to {\mathbb{R}}^{n}\) by \(z_{t}(s):=z(t+s)\) for all \(s\in [-h,0]\) and for any \(t\in [0,a]\). The space of continuous functions \(C([-h,0],{\mathbb{R}}^{n})\) endowed with the supremum norm is continuously embedded in \(M^{r}\) via the map \(z\mapsto (z(0),z_{0})\). In the case \(r=1\), the embedding is dense.
Consider the following linear system with output delay
where \(A\in {\mathbb{R}}^{n\times n}\), \(b,c\in {\mathbb{R}}^{n}\), \(h\geq 0\), \(v_{\mathrm{f}}\) and \(v\) are forcing (input, control, disturbance) functions and \(y\) is the so-called output (measurement, observation). In the rest of this paper, the input \(v_{\mathrm{f}}\) will be generated by nonlinear output feedback (see below). The impulse response associated with the delay-free linear system
will be denoted by \(G\), that is,
Note that if \(x(0)=0\), then the output (or response) of system (2.2) corresponding to a Dirac delta input \(v_{\mathrm{f}}\) is given by \(G\), hence the terminology. Denoting the corresponding transfer function (the Laplace transform of \(G\)) by \({\mathbf{G}}\), we have that
where \(s\) is a complex variable. It is clear that \({\mathbf{G}}\) is a rational function which vanishes at \(\infty \).
Application of nonlinear output feedback of the form \(v_{\mathrm{f}}(t)=N(t,y(t))\) to (2.1) leads to
where \(v\in L^{1}_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}^{n})\). It is assumed that \(N:{\mathbb{R}}_{+}\times {\mathbb{R}}\to {\mathbb{R}}\) is locally integrable in its first variable, that is, for each \(z\in {\mathbb{R}}\), the function \(t\mapsto N(t,z)\) is locally integrable, and \(N\) is locally Lipschitz in its second variable, in the sense that, for every \(z\in {\mathbb{R}}\), there exist a locally integrable function \(\lambda :{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}\) and an open interval \(J\subset {\mathbb{R}}\) containing \(z\) such that
Let \(0<\tau \leq \infty \). A function \(x:[-h,\tau )\to {\mathbb{R}}^{n}\) is said to be a solution of (2.3) on the interval \([-h,\tau )\) if \((x(0),x_{0})=\xi \), \(x|_{[0,\tau )}\in W^{1,1}_{\mathrm{loc}}([0,\tau ),{\mathbb{R}}^{n})\) and \(x\) satisfies the differential equation in (2.3) for a.e. \(t \in [0,\tau )\). Here \(W^{1,1}_{\mathrm{loc}}([0,\tau ),{\mathbb{R}}^{n})\) is the local version of the Sobolev space \(W^{1,1}([0,\tau ),{\mathbb{R}}^{n})\). It is well known that each equivalence class in \(W^{1,1}_{\mathrm{loc}}([0,\tau ),{\mathbb{R}}^{n})\) has a unique locally absolutely continuous representative \(x\), where we recall that \(x:[0,\tau )\to {\mathbb{R}}^{n}\) is locally absolutely continuous if, and only if, there exists \(y\in L^{1}_{\mathrm{loc}}([0,\tau ),{\mathbb{R}}^{n})\) such that \(x(t)=x(0)+\int _{0}^{t} y(s)\mathrm{d}s\) for all \(t\in [0,\tau )\).
If \(h=0\) (in which case we may identify \(M^{1}\) with \({\mathbb{R}}^{n}\) and the initial condition in (2.3) reduces to \(x(0)=\xi ^{0}\in {\mathbb{R}}^{n}\)), then it is well known that (2.3) has a unique maximally defined solution \(x:[0,\tau )\to {\mathbb{R}}^{n}\), and, if \(\tau <\infty \), then \(\|x(t)\|\to \infty \) as \(t\to \tau \), see, for example [41, Appendix C.3] or [48, §10, Supplement II]. Furthermore, if \(N\) satisfies an affine-linear bound in the sense that there exist nonnegative locally integrable functions \(\alpha \) and \(\beta \) such that \(|N(t,z)|\leq \alpha (t)+\beta (t)|z|\) for all \(t\geq 0\) and \(z\in {\mathbb{R}}\), then the maximal interval of existence is equal to \([-h,\infty )\).
In the next result, we consider the case wherein \(h>0\). In particular, it turns out that if the function \(t\mapsto N(t,\xi ^{1}(t-h))\) is integrable on \([0,h]\), then blow up in finite time is not possible.
Proposition 2.1
Assume that \(h>0\) and let \(\xi =(\xi ^{0},\xi ^{1})\in M^{1}\). Define \(w:[0,h]\to {\mathbb{R}}\) by \(w(t):=N(t,\xi ^{1}(t-h))\) for all \(t\in [0,h]\).
(1) If \(w\in L^{1}([0,h],{\mathbb{R}})\), then there exists a unique solution of (2.3) on the interval \([-h,\infty )\).
(2) Assume that \(b\neq0\). If \(w\notin L^{1}([0,h],{\mathbb{R}})\) and \(h<\tau \leq \infty \), then (2.3) does not have a solution on \([-h,\tau )\).
Proposition 2.1 is well known, but it is hard to find a precise reference, and therefore we provide a proof in Appendix B.
It follows from the assumptions imposed on \(N\) that \(w\in L^{1}([0,h],{\mathbb{R}})\) if \(\xi ^{1}\in L^{\infty }([-h,0], {\mathbb{R}})\). Consequently, for every \(\xi \in M^{1}\) with \(\xi ^{1}\in L^{\infty }([-h,0],{\mathbb{R}})\), the initial-value problem (2.3) has a unique solution on \([-h,\infty )\). If there exist \(\alpha \in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}_{+})\) and \(\beta \in L^{1}_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}_{+})\) such that \(|N(t,z)|\leq \alpha (t)|z|+\beta (t)\) for all \((t,z)\in {\mathbb{R}}_{+}\times {\mathbb{R}}\), then \(w\in L^{1}([0,h],{\mathbb{R}})\) for every \(\xi ^{1}\in L^{1}([-h,0],{\mathbb{R}})\), and thus, in this case, the initial-value problem (2.3) has a unique solution on \([-h,\infty )\) for every \(\xi \in M^{1}\).
The following so-called input-to-state stability result will play an important role in the paper.
Proposition 2.2
Assume that there exists \(l\geq 0 \) such that
For each initial condition \(\xi \in M^{1}\) and each \(v\in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}^{n})\) there exists a unique solution of (2.3) on \([-h,\infty )\), and the following statements hold.
(1) Let \(\tau >0\). There exists a constant \(\Gamma \geq 1\) (depending on \((A,b,c)\), \(l\), \(h\) and \(\tau \)) such that, for each \(\xi \in M^{1}\) and each \(v\in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}^{n})\), the unique solution \(x:[-h,\infty )\to {\mathbb{R}}^{n}\) of (2.3) satisfies
(2) If \(A\) is Hurwitz and \(l\|G\|_{L^{1}}<1\), then there exist constants \(\Gamma \geq 1\) (depending on \((A,b,c)\), \(h\) and \(l\)) and \(\gamma >0\) (depending on \((A,b,c)\) and \(l\)) such that, for each \(\xi \in M^{1}\) and each \(v\in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}^{n})\), the unique solution \(x:[-h,\infty )\to {\mathbb{R}}^{n}\) of (2.3) satisfies
(3) If \(A\) is Hurwitz and \(l\|G\|_{L^{1}}<1\), then, for each \(\xi \in M^{1}\) and each \(v\in L^{\infty }({\mathbb{R}}_{+},{\mathbb{R}}^{n})\) with \(\lim _{t\to \infty }\|v\|_{L^{\infty }(t,\infty )}=0\), the unique solution \(x:[-h,\infty )\to {\mathbb{R}}^{n}\) of (2.3) is convergent to 0, that is, \(x(t)\to 0\) as \(t\to \infty \).
Corollary 2.3
Assume that \(A\) is Hurwitz and there exist constants \(a\geq 0\) and \(l>0\) with \(l\|G\|_{L^{1}}<1\) and such that
Then there exist constants \(\Gamma \geq 1\) (depending on \((A,b,c)\), \(h\) and \(l\)), \(\gamma >0\) (depending on \((A,b,c)\) and \(l\)) and \(\theta \geq 0\) (depending on \((A,b,c)\), \(a\) and \(l\)) such that, for each initial condition \(\xi \in M^{1}\) and each \(v\in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}^{n})\), the unique solution \(x:[-h,\infty )\to {\mathbb{R}}^{n}\) of (2.3) satisfies
The proofs of the above proposition and the corollary can be found in Appendix B.
3 A Class of Forced Positive Delay-Differential Systems
In the rest of the paper, we will be interested in non-negative systems of the form (1.1), that is, \(A\) is Metzler and \(b\), \(c\), \(f\) and \(\xi \) are non-negative. More specifically, we will make the following assumptions.
-
(L1)
\(A\in {\mathbb{R}}^{n\times n}\) is Metzler and Hurwitz.
-
(L2)
\(b,c\in {\mathbb{R}}_{+}^{n}\), \(b\neq0\) and \(c\neq0\).
In the context of (L1), it is interesting to note that a Metzler matrix \(A\) is Hurwitz if, and only if, \(A\) is invertible and \(-A^{-1}\geq 0\). Furthermore, if \(A\) is Metzler and the spectral abscissa \(a\) of \(A\) is positive (implying in particular that \(A\) is not Hurwitz), then (1.1) (see also (3.2) below) has exponentially growing solutions. Indeed, as is well-known, there exists non-zero \(\eta \in {\mathbb{R}}_{+}^{n}\) such that \(A\eta =a\eta \), and so, with \(\xi =(\eta ,0)\) and non-negative \(u\), \(v\), and \(f\), it is immediate that the solution \(x\) of (3.2) satisfies
We mention that if (L1) and (L2) hold, then \(G(t)=c^{T}e^{At}b\geq 0\) for all \(t\geq 0\) and thus
An application of the feedback law \(w=f(u,y)\) to the linear system (2.1) leads to the following initial-value problem
where \(h\geq 0\) and \(f:U\times {\mathbb{R}}_{+}\to {\mathbb{R}}_{+}\) is a nonlinearity, where \(U\subset {\mathbb{R}}\) is compact. The functions \(v\in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}_{+}^{n})\) and \(u\in L({\mathbb{R}}_{+},U)\), where \(L({\mathbb{R}}_{+},U)\) denotes the space of Lebesgue measurable functions \({\mathbb{R}}_{+}\to U\), should be considered as forcing terms (which, depending on the context, are interpreted as a control, input or disturbance). The nonlinearity is continuous and locally Lipschitz in its second argument uniformly with respect to its first argument, that is: for all \(z\in {\mathbb{R}}_{+}\), there exists a relatively open set \(Z\subset {\mathbb{R}}_{+}\) and a constant \(\lambda >0\) such that \(z\in Z\) and
Given \(\xi \in M^{1}([-h,0],{\mathbb{R}}_{+}^{n})\), \(u\in L({\mathbb{R}}_{+},U)\) and \(v\in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}_{+}^{n})\), a function \(x:[-h,\tau )\to {\mathbb{R}}^{n}\), where \(0<\tau \leq \infty \), is said to be a solution of the initial-value problem (3.2) on the interval \([-h,\tau )\) if \((x(0),x_{0})=\xi \), \(x|_{[0,\tau )}\in W^{1,1}_{\mathrm{loc}}([0,\tau ),{\mathbb{R}}^{n})\), \(x(t)\geq 0\) for all \(t\in [0,\tau )\) and \(x\) satisfies the differential equation in (2.3) for a.e. \(t\in [0,\tau )\).
For the following, it is convenient to define
Lemma 3.1
Assume that
(1) If \(A\) is Metzler and \(b,c\geq 0\), then, for all \(\xi =(\xi ^{0},\xi ^{1})\in M^{1}_{+}\), all \(v\in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}_{+}^{n})\) and all \(u\in L({\mathbb{R}}_{+},U)\), the initial-value problem (3.2) has a unique (non-negative) solution \(x\) on \([-h,\infty )\).
(2) Let \(\beta >0\). Assume that (L1) and (L2) hold and \(\sigma {\mathbf{G}}(0)<1\). Then there exists \(\rho >0\) (depending on \(\beta \), \((A,b,c)\), \(f\) and \(h\)) such that, for all \(v\in L^{\infty }_{+}\) and all \(\xi =(\xi ^{0},\xi ^{1})\in M^{1}_{+}\) with \(\|\xi \|_{M^{1}}+\|v\|_{L^{\infty }}\leq \beta \) and all \(u\in L({\mathbb{R}}_{+},U)\), the unique solution \(x\) of (3.2) satisfies \(\|x(t)\|\leq \rho \) for all \(t\geq 0\).
Proof
(1) Let \(\xi =(\xi ^{0},\xi ^{1})\in M^{1}_{+}\), \(v\in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}_{+}^{n})\) and \(u\in L({\mathbb{R}}_{+},U)\) be given. Define a function \(N_{u}:{\mathbb{R}}_{+}\times {\mathbb{R}}\to {\mathbb{R}}_{+}\) by
The hypotheses on \(f\) imply that \(N_{u}\) satisfies the assumptions imposed on \(N\) in Sect. 2. Furthermore, for \(l>\sigma \), there exists \(a\geq 0\) such that
Consequently, the function \(t\mapsto N_{u}(t,c^{T}\xi ^{1}(t-h))\) is integrable on \([0,h]\) and statement (1) of Proposition 2.1 guarantees that the initial-value problem
has a unique solution \(x\) on \([-h,\infty )\). It is sufficient to show that \(x(t)\geq 0\) for all \(t\geq 0\), because in this case \(x\) is also a solution of (3.2). By the variation-of-parameters formula,
Consequently, using the Metzler property of \(A\) and the non-negativity of \(b\), \(c\), \(N_{u}\), \(\xi \) and \(v\), an application of the above identity for \(k=0\) shows that \(x(t)\geq 0\) for all \(t\in [0,h]\). This argument can now be repeated with \(k=1\) and \((x(h),x_{h})\) taking the role of \(\xi \), to obtain that \(x(t)\geq 0\) for all \(t\in [h,2h]\). Continuing in this way, we obtain that \(x(t)\geq 0\) for all \(t\geq 0\).
(2) Assume that \(\sigma {\mathbf{G}}(0)<1\) and choose \(l>\sigma \) such that \(l{\mathbf{G}}(0)<1\). By (3.1), \(l\|G\|_{L^{1}}<1\). Also note that (3.3) holds for every \(u\in L({\mathbb{R}}_{+},U)\). Therefore, by Corollary 2.3, there exist constants \(\Gamma \geq 1\), \(\gamma >0\) and \(\theta \geq 0\) (depending on \((A,b,c)\), \(a\), \(l\) and \(h\)) such that, for each initial condition \(\xi \in M^{1}_{+}\), each \(v\in L^{\infty }_{+}\) and each \(u\in L({\mathbb{R}}_{+},U)\), the unique solution \(x:[-h,\infty )\to {\mathbb{R}}^{n}\) of (3.4) satisfies
The claim now follows as every solution of (3.2) is also a solution of (3.4). □
Typical scenarios for \(f\) are given by:
-
\(f(w,z)=g(wz)z\), where \(g:(0,\infty )\to {\mathbb{R}}_{+}\) is continuous and such that \(\lim _{z\to 0}g(z)z\) exists and is finite;
-
\(f(w,z)=g(wz)\), where \(g:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}\) is continuous;
-
\(f(w,z)=wg(z)\), where \(g:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}\) is continuous.
In each of the above cases, \(U\) is a compact subset of \({\mathbb{R}}_{+}\).
We impose a further positivity assumption on the linear system underlying (3.2).
-
(L3)
For every \(i\in \{1,\ldots ,n\}\), there exists \(\tau _{i}>0\) such that \(c^{T}e^{A\tau _{i}}e_{i}>0\).
For a good understanding of hypothesis (L3), it is useful to recall some basic facts about observability, see, for example, also [29, 41]. The observed system
is said to be observable if, for all \(x^{0}\neq0\), the function \(t\mapsto y(t) = c^{T}e^{At}x^{0}\) is not identically equal to 0. In the following, the above observed system will be denoted by \((c^{T},A)\). It is well-known that \((c^{T},A)\) is observable if, and only if, \(\mathrm{rank}\,O(c^{T},A)=n\), where
is the so-called observability matrix (see, for example, [29]). Furthermore, we recall that
Hypothesis (L3) simply means that, for each \(i\in \{1,\ldots ,n\}\), the observation \(y\) of (3.5) corresponding to the initial condition \(x(0)=e_{i}\) does not vanish identically on \({\mathbb{R}}_{+}\), or, equivalently, \(e_{i}\notin \ker O(c^{T},A)\). Conversely, assuming that \(A\) is Metzler and \(c\) is non-negative, the condition that \(e_{i}\notin \ker O(c^{T},A)\) for all \(i\in \{1,\ldots ,n\}\), implies that (L3) holds. As will be shown further below (see Corollary 4.5), under natural assumptions, (L3) is equivalent to \(c^{*}\)-persistency of (3.2). The following result provides a number of important characterizations of (L3).
Proposition 3.2
Assume that \(A\) is Metzler and \(c\in {\mathbb{R}}_{+}^{n}\), \(c\neq0\). Let \(\nu \in {\mathbb{R}}\) be such that
Under these conditions, assumption (L3) is equivalent to each of the following properties.
(1) There exists \(\tau >0\) such that \(c^{T}e^{A\tau }\gg 0\).
(2) There exist \(d\in {\mathbb{R}}_{+}^{n}\) and \(\tau >0\) such that \(c^{T}e^{(A+dc^{T})\tau }\gg 0\).
(3) \(c^{T}e^{A t}\gg 0\) for all \(t>0\).
(4) \(c^{T}(\nu I-A)^{-1}\gg 0\).
(5) \(\ker (c^{T}(\nu I-A)^{-1})\cap {\mathbb{R}}_{+}^{n}=\{0\}\).
(6) \(\ker O(c^{T},A)\cap {\mathbb{R}}_{+}^{n}=\{0\}\).
(7) There exists \(d\in {\mathbb{R}}_{+}^{n}\) such that \(A+dc^{T}\) is irreducible.
(8)  is irreducible, where
is irreducible, where  .
.
It is not difficult to find examples which show that (L3) does not enforce observability. Indeed, consider
and note that \(A\) is Metzler and Hurwitz (the eigenvalues of \(A\) are −3, −2 and −1) and
Since \(\ker O(c^{T},A)=\{\rho (0,1,-1)^{T}:\rho \in {\mathbb{R}}\}\), we see that \((c^{T},A)\) is not observable, but (L3) holds since \(\ker O(c^{T},A)\cap {\mathbb{R}}_{+}^{3}=\{0\}\).
As for characterization (7), we point out that (L3) does not imply that \(A+dc^{T}\) is irreducible for all non-zero \(d\in {\mathbb{R}}_{+}^{n}\). A counterexample is given by
for which it is easily shown that (L3) holds and \(A+dc^{T}\) is reducible.
Proof of Proposition 3.2
To prove the characterizations of condition (L3), we proceed in several steps, the roles of which are outlined in the diagram below:

Thus, it suffices to establish Steps 1–8 above.
To this end, set \(g(t):=c^{T}e^{At}\) for all \(t\geq 0\). Obviously, the \(i\)-th component \(g_{i}\) of \(g\) is given by \(g_{i}(t)=c^{T}e^{At}e_{i}\) and \(g_{i}(t)\geq 0\) for all \(t\geq 0\) and all \(i\in \{1,\ldots ,n\}\).
Step 1: (L3) ⇔ (1). Trivially, (1) implies (L3). Conversely, assume that (L3) holds. Then, for each \(i\in \{1,\ldots ,n\}\), the function \(g_{i}\) is not identically equal to 0. Since \(g_{i}\) is analytic, for each \(i\in \{1,\ldots ,n\}\), there exists \(\theta _{i}>0\) such that \(g_{i}(t)\neq 0\) for all \(t\in (0,\theta _{i}]\). Setting \(\tau :=\min (\theta _{i})\), we have that \(g_{i}(\tau )>0\) for all \(i\in \{1,\ldots ,n\}\), and thus, \(g(\tau )\gg 0\).
Step 2: (1) ⇔ (3). Obviously, (3) implies (1). Assume that (1) holds. Then, since the functions \(g_{i}\) are analytic, there exists \(\theta >0\) such that \(g_{i}(t)\neq 0\) for all \(t\in (0,\theta ]\) and all \(i\in \{1,\ldots ,n\}\), and so \(g(t)\gg 0\) for all \(t\in (0,\theta ]\). Now let \(t>\theta \) and let \(k\in {\mathbb{N}}\) be such that \(0\leq t-k\theta <\theta \). Then
As \(c^{T}e^{A\theta }\gg 0\) and \(e^{A(k-1)\theta }e^{A(t-k\theta )}\) is a non-negative invertible matrix, we conclude that \(g(t)=c^{T}e^{At}\gg 0\) for all \(t>\theta \).
Step 3: (3) ⇔ (4). Since
it is clear that (3) implies (4). Conversely, if (4) holds, then, by the above identity, for every \(i\in \{1,\ldots ,n\}\), \(g_{i}\) is not the zero function. Hence (L3) holds, and so, invoking Steps 1 and 2, we see that (3) is satisfied.
Step 4: (4) ⇔ (5). This is clear.
Step 5: (3) ⇔ (6). Trivially, (3) implies (6). Conversely, assuming (6), the identity (3.6) shows that, for every \(i\in \{1,\ldots ,n\}\), \(g_{i}\) is not the zero function. Therefore (L3) holds, and so (3) is satisfied by Steps 1 and 2.
Step 6: (2) ⇔ (6). As (1) and (6) are equivalent (by Steps 2 and 5), we conclude that (2) is equivalent to \(\ker O(c^{T},A+dc^{T})\cap {\mathbb{R}}_{+}^{n}=\{0\}\). Noting that \(\ker O(c^{T},A)=\ker O(c^{T},A+dc^{T})\), we obtain that (2) is equivalent to (6).
Step 7: (6) ⇔ (7). Assume that (7) holds, that is, there exists \(d\in {\mathbb{R}}_{+}^{n}\) such that \(A+dc^{T}\) is irreducible. Then, as \(A+dc^{T}\) is Metzler, we have that \(e^{(A+dc^{T})t}\gg 0\) for all \(t>0\), see, for example, [46, Theorem 8.2]. Consequently, \(c^{T}e^{(A+dc^{T})t}\gg 0\) for all \(t>0\). It now follows from Step 5 that (6) holds. Conversely, assume that (6) is satisfied. Seeking a contradiction, suppose that there does not exist a vector \(d\in {\mathbb{R}}_{+}^{n}\) such that \(A+dc^{T}\) is irreducible. Then, in particular,  is reducible, where
is reducible, where  . Hence there exist non-empty disjoint subsets \(I\) and \(J\) of \(\{1,\ldots ,n\}\) such that \(I\cup J=\{1,\ldots ,n\}\) and
. Hence there exist non-empty disjoint subsets \(I\) and \(J\) of \(\{1,\ldots ,n\}\) such that \(I\cup J=\{1,\ldots ,n\}\) and
where the \(a_{ij}\) are the entries of \(A\) and the \(c_{j}\) are the components of \(c\). For a pair \((i,j)\in I\times J\) we have that \(i\neq j\), and so \(a_{ij}\geq 0\). As \(c_{j}\geq 0\), we conclude from (3.7) that \(a_{ij}=0\) for all \((i,j)\in I\times J\) and \(c_{j}=0\) for all \(j\in J\). Writing \(O(c^{T},A)=(o_{ij})\), we have that
Hence,
By the same argument, with \(o_{1j}\) replaced by \(o_{2j}\), we see that \(o_{3j}=0\) for all \(j\in J\). Continuing this line of reasoning, we conclude that, for each \(j\in J\), the \(j\)-th column of \(O(c^{T},A)\) is equal to 0, whence \(\ker O(c^{T},A)\cap {\mathbb{R}}_{+}^{n}\neq\{0\}\), which is impossible.
Step 8: (7) ⇔ (8). It is clear that (8) implies (7). Conversely, suppose that (7) holds, that is, \(A+dc^{T}\) is irreducible for some \(d\in {\mathbb{R}}_{+}^{n}\). Then \(A+\alpha dc^{T}\) is irreducible for all \(\alpha >0\), and since there exists \(\alpha >0\) such that  , we conclude that
, we conclude that  is irreducible. □
is irreducible. □
It is worthwhile noting that
as follows from (3.6) and arguments used in the above proof. If \(A\) is not only Metzler, but also Hurwitz, then the identity is valid for \(\nu =0\), and thus,
For the analysis of the behaviour of the solutions of (3.2), it is useful to consider the following linear system of homogeneous delay-differential equations
where \(q\geq 0\). It is well-known that (3.9), a special case of (1.1), induces a strongly continuous solution semigroup on \(M^{1}\) which we shall denote by \(\big ({\mathcal{T}}_{q}(t)\big )_{t\geq 0}\) (see, for example, [7, Sect. 2.4]), that is, if \(x^{\xi }:[-h,\infty )\to {\mathbb{R}}^{n}\) denotes the unique solution of (3.9), then \({\mathcal{T}}_{q}(t)\xi =(x^{\xi }(t),x^{\xi }_{t})\) for all \(t\geq 0\).
We record some consequences of the assumptions (L1)–(L3) in the proposition below.
Proposition 3.3
Assume that (L1) and (L2) are satisfied, set
and define a functional \({\mathcal{F}}\in {\mathcal{L}}(M^{1},{\mathbb{R}})\) by
The following statements hold.
(1) \(-c^{T}A^{-1}b>0\) if, and only if, \(b\notin \ker O(c^{T},A)\).
(2) If (L3) holds, then \(-c^{T}A^{-1}b>0\).
(3) The functional ℱ is non-negative, that is, \({\mathcal{F}}(\zeta )\geq 0\) for all \(\zeta \in M^{1}_{+}\).
(4) If (L3) holds, then \(\inf _{\zeta \in M^{1}_{+},\,\|\zeta ^{0}\|=1}{\mathcal{F}}(\zeta )>0\).
(5) If \(c\gg 0\), then \(\inf _{\zeta \in M^{1}_{+},\,\|\zeta \|_{M^{1}}=1}{\mathcal{F}}( \zeta )>0\).
(6) If \(b\notin \ker O(c^{T},A)\), then \({\mathcal{F}}({\mathcal{T}}_{p}(t)\xi )={\mathcal{F}}(\xi )\) for all \(t\geq 0\) and \(\xi \in M^{1}\).
We note that statement (6) says that the functional ℱ is constant along orbits of the semigroup \(({\mathcal{T}}_{p}(t))_{t\geq 0}\), or, equivalently, ℱ is a first integral of the linear delay-differential system \(\dot{x}(t)=Ax(t)+pbc^{T}x(t-h)\).
Proof of Proposition 3.3
(1) As \(A\) is Hurwitz, (3.8) holds and the claim follows immediately from the non-negativity of \(b\).
(2) If (L3) holds, then by statement (6) of Proposition 3.2, \(\ker O(c^{T},A)\cap {\mathbb{R}}_{+}^{n}=\{0\}\). As \(b>0\), we see that \(b\notin \ker O(c^{T},A)\), and so \(-c^{T}A^{-1}b>0\) by statement (1).
(3) This follows immediately from (L1) and (L2).
(4) By statement (5) of Proposition 3.2, \(-c^{T}A^{-1}\gg 0\), and the claim follows from this.
(5) This is immediate.
(6) Since \(b\notin \ker O(c^{T},A)\), it follows from statement (1) that \(-c^{T}A^{-1}b>0\) and so \(p=1/{\mathbf{G}}(0)=-1/(c^{T}A^{-1}b)<\infty \). For \(\xi \in M^{1}\), let \(z:[-h,\infty )\to {\mathbb{R}}^{n}\) be the unique solution of the initial-value problem (3.9) with \(q=p\). Then \({\mathcal{T}}_{p}(t)\xi =(z(t),z_{t})\) for all \(t\geq 0\), and so
Consequently, \((\mathrm{d}/{\mathrm{d}}t){\mathcal{F}}({\mathcal{T}}_{p}(t)\xi )=c^{T}A^{-1} \dot{z}(t)+c^{T}\big (z(t)-z(t-h)\big )\) for almost all \(t\geq 0\), and so
as \(p{\mathbf{G}}(0)=1\). This shows that \({\mathcal{F}}({\mathcal{T}}_{p}(t)\xi )={\mathcal{F}}(\xi )\) for all \(t\geq 0\). □
For the rest of this paper, it will always be assumed that (L1) and (L2) hold, in which case, by Lemma 3.3, the constant \(p\) defined in (3.10) satisfies \(0< p\leq \infty \) (and \(p<\infty \) if (L3) holds).
4 Persistence Results
We consider persistence properties of the initial value problem (3.2). Assume that (L1) and (L2) hold and that \(f(w,z)\geq 0\) for all \(w\in U\) and \(z\geq 0\). If \(x:[-h,\infty )\to {\mathbb{R}}^{n}\) is a solution of (1.1), then we set \(\check{x}(t):=(x(t),x_{t})\) for all \(t\geq 0\).
In the following, let \(\Phi :M^{1}\to {\mathbb{R}}\) by a bounded linear functional and let \(D\subset M^{1}_{+}\times L({\mathbb{R}}_{+},U)\times L^{\infty }_{+}\). We say that the system (3.2) is uniformly \(\Phi \)-persistent with respect to \(D\) if there exist \(\tau \geq 0\) and \(\delta >0\) such that, for all \((\xi ,u,v)\in D\), the solution \(x\) of (3.2) has the property that
It is clear that if (3.2) is uniformly \(\Phi \)-persistent with respect to \(D\) (and thus (4.1) holds), then for all \((\xi ,u,v)\in D\), the solution \(x\) of (3.2) satisfies
where \(\eta :=\inf \{\|\zeta \|_{M^{1}}:\Phi (\zeta )\geq \delta \}>0\). In the following, we shall associate with a vector \(d\in {\mathbb{R}}_{+}^{n}\) a corresponding bounded linear functional \(d^{*}\) which is given by
Of particular interest will be \(d^{*}\)-persistence when \(d=c\).
We now introduce two assumptions on the nonlinearity \(f\). Recall that \(p=1/{\mathbf{G}}(0)=-1/(c^{T}A^{-1}b)\).
-
(N1)
\(U\subset {\mathbb{R}}\) is compact, \(f(w,z)>0\) for all \(w\in U\) and \(z>0\) and
$$ \limsup _{z\to \infty }\big(\max _{w\in U}f(w,z)/z\big)< p\,. $$ -
(N2)
(N1) holds, \(p<\infty \) and
$$ \liminf _{z\downarrow 0}\big(\min _{w\in U}f(w,z)/z\big)>p\,. $$
Obviously, the interpretation of (N1) and (N2) depends on the particular context, but we refer the reader to [14, Sect. 3] for more discussion of these types of conditions for a class of ecological population models. Briefly, the quantity \(p\) acts as a stability threshold for the linear delay system (3.9). Indeed, if \(q< p\), then solutions of (3.9) converge to zero exponentially by statement (2) of Proposition 2.2 and (3.1). If \(p<\infty \) (that is, \({\mathbf{G}}(0)>0\)) and \(q\geq p\), then the trivial solution of (3.9) is not exponentially stable. Indeed, in this case, there exists \(s_{*}\geq 0\) (with \(s_{*}=0\) if, and only if, \(q=p\)) such that \(q {\mathbf{G}}(s_{*})e^{-s_{*} h} = 1\) from which it follows via a routine calculation that
A well-known result (see, for example, [7, Theorem 5.1.7]) now yields that the trivial solution of (3.9) is not exponentially stable. We conclude that the “smallest” parameter value for which an additive perturbation of the form \(qbc^{T}x(t-h)\), where \(q\geq 0\), destabilizes \(\dot{x}=Ax\) is given by \(q=p\).
We remark that the case \(p=\infty \) (or, equivalently \({\mathbf{G}}(0)=0\)) is of little interest in the current context, because, in this case, under reasonable assumptions, persistency cannot be expected. For example, assuming that (L1) and (L2) hold and \(f(w,0)=0\) for all \(w\in U\), it is not difficult to show that if \(p=\infty \), then, for all triples \((\xi ,u,v)\in M^{1}_{+}\times L({\mathbb{R}}_{+},U)\times L^{\infty }_{+}\) such that \(v(t)\to 0\) as \(t\to \infty \), the solution of (3.2) approaches 0 as time goes to infinity.
For \(\beta >0\) and \(r=1,\infty \), we set
We note that \(D^{\infty }(\beta )\subset D^{1}(\max (1,h)\beta )\).
The next result shows that \(c^{*}\)-persistence implies \(e_{i}^{*}\)-persistence whenever \(-e_{i}^{T}A^{-1}b>0\).
Proposition 4.1
Assume that (L1), (L2) and (N1) hold, let \(\beta >0\), \(r=1,\infty \) and \(D\subset D^{r}(\beta )\). If (3.2) is uniformly \(c^{*}\)-persistent with respect to \(D\), then (3.2) is uniformly \(e_{i}^{*}\)-persistent with respect to \(D\) for each \(i\in \{1,\ldots ,n\}\) such that \(-e_{i}^{T}A^{-1}b>0\).
Proof
Assume that (3.2) is uniformly \(c^{*}\)-persistent with respect to \(D\). Together with statement (2) of Lemma 3.1 this implies that there exist \(\delta _{2}>\delta _{1}>0\) and \(\tau \geq 0\) such that, for all \((\xi ,u,v)\in D\), the solution \(x\) of (3.2) satisfies
Setting \(y(t)=c^{T}x(t-h)\) for all \(t\geq 0\) and \(\kappa :=\inf \{f(w,z):w\in U,\,\,\delta _{1}\leq z\leq \delta _{2} \}>0\), it follows from the variation-of-parameters formula that, for all \(t \geq \tau + h\),
and thus
If \(i\in \{1,\ldots ,n\}\) is such that \(-e_{i}^{T}A^{-1}b>0\), then, as \(e^{A(t-\tau -h)}\to 0\) as \(t\to \infty \), there exists \(\sigma \geq \tau +h\) such that
showing that (3.2) is uniformly \(e_{i}^{*}\)-persistent with respect to \(D\). □
If (L1) holds, then choosing \(\alpha >0\) such that \(A+\alpha I\geq 0\), we have that
Therefore, if \(e_{i}^{T}b>0\), then \(-e_{i}^{T}A^{-1}b>0\). We note that the positivity of \(-e_{i}^{T}A^{-1}b\) does not imply that of \(e_{i}^{T}b\): indeed, for the simple example
we have that \(-A^{-1}b=(1,1)^{T}\) and so \(-e_{1}^{T}A^{-1}b=1\), whilst \(e_{1}^{T}b=0\).
The following lemma will be a key tool for the persistency analysis of (3.2).
Lemma 4.2
Assume that (L1)–(L3) and (N2) are satisfied and let \(\beta >0\). Then there exists \(q>0\) such that, for all \((\xi ,u,v)\in D^{1}(\beta )\cup D^{\infty }(\beta )\), the solution \(x\) of (3.2) satisfies
Furthermore, the following statements hold.
(1) There exists \(\eta >0\) such that, for all \((\xi ,u,v)\in D^{\infty }(\beta )\), the solution \(x\) of (3.2) satisfies
(2) Under the additional assumption that \(f\) is bounded, there exists \(\eta >0\) such that, for all \((\xi ,u,v)\in D^{1}(\beta )\), the solution \(x\) of (3.2) satisfies (4.3).
Proof
Let \(\beta >0\). It is clear from statement (2) of Lemma 3.1 that there exists \(\rho >0\) such that, for all \((\xi ,u,v)\in D^{1}(\beta )\cup D^{\infty }(\beta )\), the solution \(x\) of (3.2) satisfies
For the rest of the proof, we set
Setting \(y^{\dagger }:=\rho \|c\|_{\infty }\), it follows that
By (N2), there exists \(y^{\#}\in (0,y^{\dagger })\) such that
Furthermore, by the properties of \(f\),
Setting \(q:=\min (p,p_{1})>0\), we have that
and consequently,
Hence, for all \((\xi ,u,v)\in D^{1}(\beta )\cup D^{\infty }(\beta )\), the solution \(x\) of (3.2) satisfies
and thus
establishing (4.2).
(1) Let \((\xi ,u,v)\in D^{\infty }(\beta )\) and let \(x\) be the corresponding solution of (3.2). It follows from (4.4) and the differential equation in (3.2) that there exists \(\lambda >0\) such that, for all \((\xi ,u,v)\in D^{\infty }(\beta )\),
Note that, on the interval \([h,2h]\), the above bound holds because the \(L^{\infty }\)-norm of \(\xi ^{1}\) is uniformly bounded for all \((\xi ,u,v)\in D^{\infty }(\beta )\).
By (4.5), there exists \(\varepsilon \in (0,y^{\#})\) such that
We set \(I_{1}:=[0,y^{\#}+\varepsilon ]\) and \(I_{2}:=[y^{\#}-\varepsilon ,y^{\dagger }]\). By (4.6), the family of all \(y\) generated by data \((\xi ,u,v)\in D^{\infty }(\beta )\) is equi-continuous on \([h,\infty )\), and therefore, there exists \(\tau >0\) such that, for every \(t\geq h\) and every such \(y\),
and
Let \(t\geq h\). We distinguish two cases.
Case 1: \(y(t)\in [0,y^{\#}]\). By (4.8), \(y(t+s)\in I_{1}\) for all \(s\in [0,2\tau ]\) and, invoking (4.7), we obtain
Let us first assume that \(h>0\). Then, without loss of generality, we may further assume that \(2\tau \leq h\). Let \(z:[-h,\infty )\) denote the unique solution of the linear initial-value problem
Note that \((z(s),z_{s})={\mathcal{T}}_{p}(s)\check{x}(t)\) for all \(s\geq 0\). Invoking (4.10), we conclude that, for all \(s\in [0,2\tau ]\),
where, in the last step, we have used that \(2\tau \leq h\). Now \(e^{As}z(0)+p\int _{0}^{s}e^{A(s-\theta )}bc^{T}z(\theta -h)\mathrm{d} \theta =z(s)\) for all \(s\in [0,2\tau ]\) and thus,
Noting that, for \(s\in [0,2\tau ]\) and \(\theta \in [-h,0]\), \(x(t+s+\theta )\geq z(s+\theta )\) if \(s+\theta \geq 0\) (as follows from (4.11)) and \(x(t+s+\theta )=z(s+\theta )\) if \(s+\theta <0\) (by the initial condition for \(z\)), we see that \(x_{t+s}\geq z_{s}\) for all \(s\in [0,2\tau ]\). Together with (4.11) this yields
Consequently, an application of statement (6) of Proposition 3.3 yields,
If \(h=0\), then \(\check{x}(t)=x(t)\), \({\mathcal{T}}_{p}(t)=e^{(A+pbc^{T})t}\) and \(z(s)=e^{(A+pbc^{T})s}x(t)\), and (4.11) follows easily from the variation-of-parameters formula and (4.10). We conclude that (4.12) continues to hold in the delay-free case.
Case 2: \(y(t)\in (y^{\#},y^{\dagger }]\). By (4.9), \(y(t+s)\in I_{2}\) for all \(s\in [0,2\tau ]\), and so
Hence,
If \(h>0\), then, without loss of generality, we may assume that \(\tau \leq h\), and so
For \(s\in [0,\tau ]\) and \(\theta \in [-h,\tau -h]\), we have that \(s+\theta +h\in [0,2\tau ]\). Combining the last inequality with (4.13) and setting \(\eta :=(y^{\#}-\varepsilon )\tau >0\), we arrive at
Furthermore, if \(h=0\), then, with \(\kappa _{1}:=\inf \{\|z\|:z\in {\mathbb{R}}_{+}^{n},\,\,c^{T}z\geq y^{\#}-\varepsilon \}\), it follows from (4.13) that \(\|x(t+s)\|\geq \kappa _{1}\) for all \(s\in [0,2\tau ]\), and so
where \(\kappa _{2}=\min _{1\leq i\leq n}(-c^{T}A^{-1}e_{i})>0\). The positivity of \(\kappa _{2}\) is a consequence of (L3) and Proposition 3.2. We see that (4.14) continues to hold in the delay-free case (now with \(\eta =\kappa _{1}\kappa _{2}\)).
Combining (4.12) and (4.14) from Cases 1 and 2, respectively, we obtain
Consequently, with \(t=t_{0}+k\tau \), where \(t_{0}\geq h\) and \(k\in {\mathbb{Z}}_{+}\), and \(s=\tau \), it follows that
and thus,
For \(t\geq t_{0}\), let \(k\in {\mathbb{Z}}_{+}\) be such that \(t=t_{0}+k\tau +s\), where \(0\leq s<\tau \). The last inequality together with (4.15) leads to
establishing (4.3).
(2) Assume now that \(f\) is bounded. Then the \(L^{\infty }\)-norm of the function \([0,h]\to {\mathbb{R}},\,t\mapsto f(u(t),c^{T}\xi ^{1}(t-h))\) is uniformly bounded for all \((\xi ,u,v)\in D^{1}(\beta )\). Combining this with (4.4), we see that there exists a suitable \(\lambda >0\) such that (4.6) is satisfied for all \((\xi ,u,v)\in D^{1}(\beta )\), and the arguments of the proof of statement (1) continue to apply. □
An inspection of the above proof shows that (L3) was used only in the delay-free case: if \(h>0\), then Lemma 4.2 remains true without assuming (L3).
For \(\beta >\alpha >0\) and \(r=1,\infty \), we set
and note that the following inclusions hold: \(E^{r,0}(\alpha ,\beta )\subset E^{r}(\alpha ,\beta )\), \(E^{\infty }(\alpha ,\beta )\subset E^{1}(\alpha , \max (1,h)\beta )\) and \(E^{\infty ,0}(\alpha ,\beta ) \subset E^{1,0}(\alpha ,\max (1,h) \beta )\).
We are now in the position to state and prove our main results on persistence.
Theorem 4.3
Assume that (L1), (L2) and (N2) are satisfied. Let \(\beta >\alpha >0\) and \(\tau >0\).
(1) If (L3) holds, then there exists \(\delta >0\) such that, for all \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\), the solution \(x\) of (3.2) satisfies
(2) If (L3) holds and \(f\) is bounded, then there exists \(\delta >0\) such that, for all \((\xi ,u,v)\in E^{1,0}(\alpha ,\beta )\), the solution \(x\) of (3.2) satisfies (4.16).
(3) If \(c\gg 0\), then there exists \(\delta >0\) such that, for all \((\xi ,u,v)\in E^{\infty }(\alpha ,\beta )\), the solution \(x\) of (3.2) satisfies
The following result can be considered as a “converse” of Theorem 4.3.
Proposition 4.4
Assume that (L1) and (L2) are satisfied and that there exists \(u^{\dagger }\in U\) such that \(f(u^{\dagger },0)=0\). Let \(\beta >\alpha >0\).
(1) If the solution \(x\) of (3.2) satisfies
for all \((\xi ,u,v)\in E^{1,0}(\alpha ,\beta )\cap E^{\infty ,0}(\alpha , \beta )\), then (L3) holds.
(2) Assume that \(h\beta \geq \alpha \). If the solution \(x\) of (3.2) satisfies (4.17) for all \((\xi ,u,v)\in E^{\infty }(\alpha ,\beta )\), then \(c\gg 0\).
The next corollary is an immediate consequence of Theorem 4.3 and Proposition 4.4.
Corollary 4.5
Assume that (L1), (L2) and (N2) are satisfied and there exists \(u^{\dagger }\in U\) such that \(f(u^{\dagger },0)=0\). Let \(\beta >\alpha >0\).
(1) (3.2) is uniformly \(c^{*}\)-persistent with respect to \(E^{\infty ,0}(\alpha ,\beta )\) if, and only if, (L3) holds.
(2) If \(f\) is bounded, then (3.2) is uniformly \(c^{*}\)-persistent with respect to \(E^{1,0}(\alpha ,\beta )\) if, and only if, (L3) holds.
(3) If \(h\beta >\alpha \), then (3.2) is uniformly \(c^{*}\)-persistent with respect to \(E^{\infty }(\alpha ,\beta )\) if, and only if, \(c\gg 0\).
Statements (1) and (2) of Corollary 4.5 provide a considerable improvement of the results in [3] where, for the undelayed case and under the assumption that \(A+bc^{T}\) is irreducible, persistence-like properties were proved.
Proof of Theorem 4.3
(1) Assume that (L3) holds. As \(\theta >0\), Proposition 3.2 yields that
and hence \(c^{T}e^{A\theta }\xi ^{0}\geq \kappa \|\xi ^{0}\|\). It follows from the variation-of-parameters formula that, for all \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\), the solution \(x\) of (3.2) satisfies
and thus, setting \(\kappa _{1}:=(\alpha \kappa )/\|c\|_{\infty }>0\), we conclude that \(\|x(\theta )\|\geq \kappa _{1}\). Therefore, by statement (4) of Proposition 3.3,
Invoking statement (1) of Lemma 4.2, we see that there exists \(\eta >0\) such that, for all \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\), the solution \(x\) of (3.2) satisfies
showing that (3.2) is uniformly ℱ-persistent with respect to \(E^{\infty ,0}(\alpha ,\beta )\).
Seeking a contradiction, suppose that there does not exist \(\delta >0\) such that (4.16) holds for all solutions \(x\) of (3.2) with data \((\xi ,u,v)\) in \(E^{\infty ,0}(\alpha ,\beta )\). Then there exist \((\xi _{k},u_{k},v_{k})\in E^{\infty ,0}(\alpha ,\beta )\), \(k\in {\mathbb{Z}}_{+}\), such that the corresponding solutions \(x^{k}\) satisfy
and therefore, there exist \(t_{k}\geq \theta \) such that \(c^{T}x^{k}(t_{k}+\theta )\to 0\) as \(k\to \infty \). It follows from the variation-of-parameters formula that
Moreover, if \(h>0\), then an application of (4.2) shows
Consequently,
where we have made use of the strict positivity of \(c^{T}e^{At}\) on \((0,\theta ]\) (guaranteed by Proposition 3.2) and Lemma B.1 in Appendix A. But (4.20) implies that \({\mathcal{F}}\big ((x^{k}(t_{k}),x^{k}_{t_{k}})\big )\to 0\) as \(k\to \infty \), in contradiction to (4.19).
(2) The proof is identical to that of statement (1), we only need to invoke statement (2) (instead of statement (1)) of Lemma 4.2.
(3) Assume that \(c\gg 0\). Then, trivially, (L3) holds, and moreover,
As the \(L^{\infty }\)-norm of \(\xi ^{1}\) is uniformly bounded for all \((\xi ,u,v)\in E^{\infty }(\alpha ,\beta )\), it follows from the properties of \(f\) that there exists \(q>0\) such that
Since, by the variation-of-parameters formula,
we conclude that
Consequently, for all \((\xi ,u,v)\in E^{\infty }(\alpha ,\beta )\), the solution \(x\) of (3.2) satisfies
with \(\kappa \) given by (4.18) and
where the positivity of \(\lambda \) follows from (4.21). By the strict positivity of \(c\), there exists \(\lambda _{1}>0\) such that, for all \((\xi ,u,v)\in E^{\infty }(\alpha ,\beta )\), \(\|c^{T}\xi ^{1}\|_{L^{1}(-h,0)}\geq \lambda _{1}\|\xi ^{1}\|_{L^{1}(-h,0)}\). Using (4.22), we may conclude that there exists \(\lambda _{2}>0\) such that, for \((\xi ,u,v)\in E^{\infty }(\alpha ,\beta )\), the solution \(x\) of (3.2) satisfies,
Therefore, by statement (5) of Proposition 3.3,
Appealing to statement (1) of Lemma 4.2, we see that there exists \(\eta >0\) such that, for all \((\xi ,u,v)\in E^{\infty }(\alpha ,\beta )\), the solution \(x\) of (3.2) satisfies
showing that (3.2) is uniformly ℱ-persistent with respect to \(E^{\infty }(\alpha ,\beta )\). The proof can now be completed by invoking a contradiction argument identical to that used in the proof of statement (1). □
Proof of Proposition 4.4
(1) We prove this by contraposition. To this end, assume that (L3) does not hold. Then, by statement (6) of Proposition 3.2 and (3.6), there exists \(z>0\) such that \(c^{T}e^{At}z=0\) for all \(t\geq 0\). Setting \(\xi ^{0}:=(\alpha /\|z\|)z\), we have that \(\|\xi ^{0}\|=\alpha \) and \(c^{T}e^{At}\xi ^{0}=0\) for all \(t\geq 0\). Defining \(x:[-h,\infty )\to {\mathbb{R}}^{n}\) by \(x(t)=0\) for \(t\in [-h,0)\) and \(x(t)= e^{At}\xi ^{0}\) for \(t\geq 0\), we have that \(f(u^{\dagger },c^{T}x(t-h))=0\) for all \(t\geq 0\), and so, \(\dot{x}(t)=Ax(t)+f(u^{\dagger },c^{T} x(t-h))\) for all \(t\geq 0\), showing that \(x\) solves (3.2) with \(\xi =(\xi ^{0},0)\), \(u(t)\equiv u^{\dagger }\) and \(v(t)\equiv 0\). Moreover, \(x(t)\to 0\) as \(t\to \infty \), by the Hurwitz property of \(A\), and, as \(\|\xi \|_{M^{1}}=\|\xi \|_{M^{\infty }}=\|\xi ^{0}\|=\alpha \), we see that \((\xi ,u^{\dagger },0)\in E^{1,0}(\alpha ,\beta )\cap E^{\infty ,0}( \alpha ,\beta )\). We conclude that there exists a data triple in \(E^{1,0}(\alpha ,\beta )\cap E^{\infty ,0}(\alpha ,\beta )\) for which (4.17) does not hold.
(2) Assume that \(h\beta \geq \alpha \). Again we prove the claim by contraposition. To this end, let us assume that \(c\) is not strictly positive. Then there exists \(z>0\) such that \(c^{T}z=0\). Define a function \(\xi ^{1}(t)=(\beta /\|z\|)z\) for all \(t\in [-h,0]\). Obviously, \(c^{T}\xi ^{1}(t)=0\) for all \(t\in [-h,0]\). Let \(x\) be the solution of (3.2) with \(\xi =(0,\xi ^{1})\), \(u(t)\equiv u^{\dagger }\) and \(v(t)\equiv 0\). By the variation-of-parameters formula, we have that
Consequently, \(x_{h}\) is the zero function and therefore \(x(t)=0\) for all \(t\geq 0\). Now \(\|\xi \|_{M^{\infty }}=\beta \) and \(\|\xi \|_{M^{1}}=h\beta \geq \alpha \), showing that \((\xi ,u^{\dagger },0)\in E^{\infty }(\alpha ,\beta )\). We have now shown that there exists a data triple in \(E^{\infty }(\alpha ,\beta )\) for which (4.17) does not hold. □
5 Stability Results
We consider stability properties of the initial value problem (3.2). Particularly, we formulate conditions under which (3.2) (in the absence of forcing) admits a unique, constant non-zero solution. We then provide conditions under which this solution is stable in a sense we describe.
In the following, let \(p\) be the constant given by (3.10) and let \(u^{\mathrm{s}}\in U\), where \(U\subset {\mathbb{R}}\) is compact. The number \(u^{\mathrm{s}}\) plays the role of a target or nominal value for the variable \(u\). Further below, we will be interested in the steady states (equilibria) of (1.1) when \(u=u^{\mathrm{s}}\) and \(v=0\) and that is the motivation for the superscript “s”.
The nonlinearity \(f\) appearing in (1.1) is assumed to satisfy the following conditions.
-
(N3)
Condition (N2) holds,
$$ |f(u^{\mathrm{s}},z)-f(u^{\mathrm{s}},y^{\mathrm{s}})|=|f(u^{\mathrm{s}},z)-py^{\mathrm{s}}| < p|z-y^{ \mathrm{s}}|\quad \forall \: z>0,\,z\neq y^{\mathrm{s}}\,, $$(5.1)where \(y^{\mathrm{s}}\) is the unique positive number such that \(f(u^{\mathrm{s}},y^{\mathrm{s}}) =py^{\mathrm{s}}\), and
$$ \limsup _{z\to y^{\mathrm{s}}} \frac{|f(u^{\mathrm{s}},z)-f(u^{\mathrm{s}},y^{\mathrm{s}})|}{|z-y^{\mathrm{s}}|} = \limsup _{z\to y^{\mathrm{s}}} \frac{|f(u^{\mathrm{s}},z)-py^{\mathrm{s}}|}{|z-y^{\mathrm{s}}|}< p\,. $$(5.2)
The existence of \(y^{\mathrm{s}}>0\) such that \(f(u^{\mathrm{s}},y^{\mathrm{s}})=py^{\mathrm{s}}\) follows from the continuity of \(f\) and (N2), whilst uniqueness of \(y^{\mathrm{s}}\) is a consequence of (5.1).
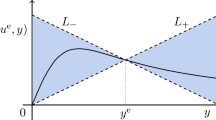
Note that (5.1) is a sector condition and means that the graph \(F\) of \(y\mapsto f(u^{\mathrm{s}},z)\) is “sandwiched” between the lines \(L_{+}=\{(z,pz):z\geq 0\}\) and \(L_{-}=\{(z,-pz + 2py^{\mathrm{s}}):z\geq 0\}\), see Fig. 1 for an illustration.
Illustration of the sector condition (5.1). The dashed lines have gradient \(\pm p\)
Obviously, the only points the graph \(F\) has in common with \(L_{+}\) or \(L_{-}\) are \((y^{\mathrm{s}}, py^{\mathrm{s}})\) and, the origin \((0,0)\) if \(f(u^{\mathrm{s}},0)=0\). Condition (5.2) implies that the intersections of \(F\) with \(L_{+}\) and \(L_{-}\) at the point \((y^{\mathrm{s}}, py^{\mathrm{s}})\) are non-tangential, whilst (N2) ensures that if \(f(u^{\mathrm{s}},0)=0\), then \(F\) is non-tangential to \(L_{+}\) at \((0,0)\). Finally, it follows from the continuity of \(f\), assumption (N2), (5.1) and (5.2) that, for every \(\delta >0\), there exists \(q\in (0,p)\) such that
In the following lemma we will consider the delay-differential equation
that is, (1.1) with \(u = u^{\mathrm{s}}\) and \(v =0\). We say that \(x^{\mathrm{s}}\in {\mathbb{R}}_{+}^{n}\) is a steady state (or equilibrium) of (5.4) if \(Ax^{\mathrm{s}}+bf(u^{\mathrm{s}},c^{T}x^{\mathrm{s}})=0\). Obviously, \(x^{\mathrm{s}}\) is an steady state if, and only if, the constant function \(t\mapsto x^{\mathrm{s}}\) is a solution of (5.4).
Lemma 5.1
Assume that (L1)–(L3) and (N3) hold, and set
where \(p\) is given by (3.10), and \(y^{\mathrm{s}}\) is as in (N3). Then \(x^{\mathrm{s}}>0\), \(c^{T}x^{\mathrm{s}}=y^{\mathrm{s}}\), and \(x^{\mathrm{s}}\) is the unique non-zero steady state of (5.4). Furthermore, if \(A+bc^{T}\) is irreducible, then \(x^{\mathrm{s}} \gg 0\).
Proof
Assumptions (L1)–(L3) ensure that \(p<\infty \) and
where \(\kappa >0\) is such that \(A+\kappa I \geq 0\). It follows immediately from the definitions of \(x^{\mathrm{s}}\) and \(p\) that \(c^{T}x^{\mathrm{s}}=y^{\mathrm{s}}\). Consequently, since \(y^{\mathrm{s}}>0\), we conclude that \(x^{\mathrm{s}}\neq 0\), and so \(x^{\mathrm{s}}>0\). To show that \(x^{\mathrm{s}}\) is a steady state, we invoke (N3) to note that
As for uniqueness, let \(x^{\dagger }\) be an another non-zero vector in \({\mathbb{R}}^{n}_{+}\) satisfying
Then \(c^{T}x^{\dagger }={\mathbf{G}}(0)f(u^{\mathrm{s}},c^{T}x^{\dagger })\), and thus, \(f(u^{\mathrm{s}},c^{T}x^{\dagger })=pc^{T}x^{\dagger }\). Now \(c^{T}x^{\dagger }\neq0\) (otherwise, due to (5.6), 0 would be an eigenvalue of \(A\) which is not possible by (L1)), and so, since \(y^{\mathrm{s}}\) is the unique positive solution of the equation \(f(u^{\mathrm{s}},y)=py\), we see that \(c^{T}x^{\dagger }=y^{\mathrm{s}}=c^{T}x^{\mathrm{s}}\), whence
Let us now additionally assume that \(A+bc^{T}\) is irreducible. As
we see that
Since \(A+pbc^{T}\) is Metzler and irreducible, \(e^{(A+pbc^{T})t}\gg 0\) for all \(t>0\) (see, for example, [46, Theorem 8.2]), and as \(x^{\mathrm{s}}>0\), it now follows from (5.7) that \(x^{\mathrm{s}}\gg 0\). □
It is convenient to define, for given \(u^{\mathrm{s}}\in U\) and \(\rho >0\), the following function \(\varphi _{\rho }:U\to {\mathbb{R}}_{+}\),
We are now in the position to state a stability theorem relating to the non-zero steady state associated with the system (3.2).
Theorem 5.2
Let \(u^{\mathrm{s}}\in U\) and let \(\beta > \alpha >0\). Assume that (L1), (L2) and (N3) are satisfied.
(1) If (L3) holds, then there exist \(M\geq 1\), \(\mu ,\rho >0\) (depending on \((A,b,c)\), \(f\), \(h\), \(\alpha \) and \(\beta \)) such that, for every \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\), the unique solution \(x\) of (3.2) satisfies
(2) If \(c\gg 0\), then there exist \(M\geq 1\), \(\mu ,\rho >0\) (depending on \((A,b,c)\), \(f\), \(h\), \(\alpha \) and \(\beta \)) such that, for every \((\xi ,u,v)\in E^{\infty }(\alpha ,\beta )\), the unique solution \(x\) of (3.2) satisfies (5.8).
Note that whilst the above criterion guarantees stability independent of the delay parameter \(h\), the “quality” of the stability will in general depend on \(h\) because of the \(h\)-dependence of the constants \(M\), \(\mu \) and \(\rho >0\).
Proof of Theorem 5.2
(1) Let \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\) and let \(x\) be the corresponding solution of (3.2). By statement (2) of Lemma 3.1, it follows that \(\| x(t) \|\) is bounded on \([0, \infty )\), uniformly with respect to \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\). As for all \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\), \(\|\xi \|_{M^{\infty }}+\|v\|_{L^{\infty }}\leq \beta \), we conclude that \(\| x(t) \|\) is bounded on \([-h, \infty )\), uniformly with respect to \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\). Therefore, there exists \(\rho >0\) such that, for all \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\),
Furthermore, by statement (1) of Theorem 4.3, there exists \(\delta >0\) such that, for all \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\),
We rewrite the delay-differential equation (1.1) as follows
where
Observe that, by construction and (5.9),
As was already pointed out, there exists \(q\in (0,p)\) such that (5.3) holds. Let \(\eta \in \{0,\delta \}\) and define a function \(N_{\eta }:{\mathbb{R}}\to {\mathbb{R}}\) by
where \(l_{0}=p\) and \(l_{\delta }=q\). By (N3) and construction of \(N_{\eta }\),
Furthermore, assuming without loss of generality that \(\delta \leq y^{\mathrm{s}}\) and invoking the estimate (5.3) yields that
Setting \(\theta (t):=x(t) - x^{\mathrm{s}}\) for all \(t\geq 0\), it is straightforward to show that
An application of statement (1) of Proposition 2.2 to (5.14) shows that there exists \(\Gamma _{0}\geq 1\) such that
Noting that, by (5.10), \(c^{T}\theta (t+2h)\geq \delta -y^{\mathrm{s}}\) for all \(t\geq 0\), it is routine to verify that the left-translated function \(\theta ^{\ell }\) defined by \(\theta ^{\ell }(t):=\theta (t+3h)\) satisfies
Note that (5.16) is a special case of (2.3). As \(q< p=1/\|G\|_{L^{1}}\), statement (2) of Proposition 2.2 together with (5.13) guarantee the existence of \(\Gamma \geq 1\) and \(\gamma >0\) such that
Consequently,
The conjunction of (5.12), (5.15) and (5.17) establishes (5.8) with \(\mu :=\gamma \) and \(M:=\Gamma \Gamma _{0}e^{3\gamma h}(1+h)\).
(2) The existence of a positive constant \(\delta \) such that, for all \((\xi ,u,v)\in E^{\infty }(\alpha ,\beta )\), (5.10) holds is guaranteed by statement (3) of Theorem 4.3. Otherwise, the proof is identical to that of statement (1). □
In the following corollary of Theorem 5.2, we consider the situation wherein the forcing terms \(u\) and \(v\) in (3.2) are convergent.
Corollary 5.3
Let \(u^{\mathrm{s}}\in U\) and assume that (L1), (L2) and (N3) are satisfied.
(1) If (L3) holds, then, for every \((\xi ,u,v)\in M^{\infty }_{+}\times L({\mathbb{R}}_{+},U)\times L^{\infty }_{+}\) such that \(\|\xi ^{0}\|>0\), \(\lim _{t\to \infty }\|u-u^{\mathrm{s}}\|_{L^{\infty }(t,\infty )}=0\) and \(\lim _{t\to \infty }\|v\|_{L^{\infty }(t,\infty )}=0\), the unique solution \(x\) of (3.2) satisfies \(x(t)\to x^{\mathrm{s}}\) as \(t\to \infty \).
(2) If \(c\gg 0\), then, for every \((\xi ,u,v)\in M^{\infty }_{+}\times L({\mathbb{R}}_{+},U)\times L^{\infty }_{+}\) such that \(\|\xi \|_{M^{1}}>0\), \(\lim _{t\to \infty }\|u-u^{\mathrm{s}}\|_{L^{\infty }(t,\infty )}=0\) and \(\lim _{t\to \infty }\|v\|_{L^{\infty }(t,\infty )}=0\), the unique solution \(x\) of (3.2) satisfies \(x(t)\to x^{\mathrm{s}}\) as \(t\to \infty \).
Proof
We prove only statement (1), as the proof of statement (2) is very similar to that of statement (1). To this end, assume that (L3) holds, let \((\xi ,u,v)\in M^{\infty }_{+}\times L({\mathbb{R}}_{+},U)\times L^{\infty }_{+}\) such that \(\|\xi ^{0}\|>0\), \(\lim _{t\to \infty }\|u-u^{\mathrm{s}}\|_{L^{\infty }(t,\infty )}=0\) and \(\lim _{t\to \infty }\|v\|_{L^{\infty }(t,\infty )}=0\) and let \(x\) be the solution of (3.2). By statement (1) of Theorem 4.3, there exist \(\delta ,\theta >0\) such that \(c^{T}x(t)\geq \delta \) for all \(t\geq \theta \) and hence \(\|x(t)\|\geq \delta /\|c\|_{\infty }:=\alpha \) for all \(t\geq \theta \). Furthermore, it follows from statement (2) of Lemma 3.1, that \(\sigma :=\sup _{t\geq 0}\|(x(t),x_{t})\|_{M^{\infty }}<\infty \). Let \(\tau \geq 0\) and set \(x^{\tau }(t):=x(t+\tau )\), \(u^{\tau }(t):=u(t+\tau )\) and \(v^{\tau }(t):=v(t+\tau )\) for all \(t\geq 0\). It is clear that \(x^{\tau }\) is a solution of (3.2) with \(\xi \), \(u\) and \(v\) replaced by \((x(\tau ),x_{\tau })\), \(u^{\tau }\) and \(v^{\tau }\), respectively. Choosing \(\beta \geq 2\max (\alpha ,\sigma ,\|v\|_{L^{\infty }})\), we have that \(\big ((x(\tau ),x_{\tau }),u^{\tau },v^{\tau }\big )\in E^{\infty ,0}( \alpha ,\beta )\) for every \(\tau \geq \theta \). Consequently, by statement (1) of Theorem 5.2, there exist \(M\geq 1\) and \(\mu ,\rho >0\) such that, for all \(t \geq 0\) and all \(\tau \geq \theta\),
Hence, for all \(t \geq 0\) and all \(\tau \geq \theta\),
As
it follows that \(x(t)\to x^{\mathrm{s}}\) as \(t\to \infty \). □
The estimate (5.8) in Theorem 5.2 can be simplified in the case that \(f\) is Lipschitz in its first variable, which is recorded as the following theorem.
Theorem 5.4
Let \(u^{\mathrm{s}}\in U\), let \(\beta >\alpha >0\) and assume that \(f\) is Lipschitz in its first variable, uniformly with respect to the second variable, that is, there exists \(\lambda >0\) such that
Furthermore assume that (L1), (L2) and (N3) are satisfied.
(1) If (L3) holds, then there exist \(M\geq 1\) and \(\mu >0\) (depending on \((A,b,c)\), \(f\), \(h\), \(\alpha \) and \(\beta \)) such that, for every \((\xi ,u,v)\in E^{\infty ,0}(\alpha ,\beta )\), the unique solution \(x\) of (3.2) satisfies
(2) If (L3) holds and \(f\) is bounded, then there exist \(M\geq 1\) and \(\mu >0\) (depending on \((A,b,c)\), \(f\), \(h\), \(\alpha \) and \(\beta \)) such that, for every \((\xi ,u,v)\in E^{1,0}(\alpha ,\beta )\), the unique solution \(x\) of (3.2) satisfies (5.19).
(3) If \(c\gg 0\), then there exist \(M\geq 1\) and \(\mu >0\) (depending on \((A,b,c)\), \(f\), \(h\), \(\alpha \) and \(\beta \)) such that, for every \((\xi ,u,v)\in E^{\infty }(\alpha ,\beta )\), the unique solution \(x\) of (3.2) satisfies (5.19).
Proof
By invoking (5.18), we obtain the following estimate for the function \(d\) defined in (5.11)
which replaces (5.12). Otherwise the proof is very similar to that of Theorem 5.2 and we omit the details. □
Statement (2) considers data triple \((\xi ,u,v)\in E^{1,0}(\alpha ,\beta )\) and so allows for unbounded \(\xi ^{1}\). Note that there is no counterpart to statement (2) in Theorem 5.2: the reason is that in general there does not exist a finite \(\rho \) such that (5.9) holds if \(\xi ^{1}\) is not essentially bounded (see proof of Theorem 5.2).
Nonlinearities which satisfy (N3) and (5.18) are quite common in mathematical ecology as the following example shows.
Example 5.5
(1) Consider the so-called Beverton-HoltFootnote 2 nonlinearity \(g(z)=az/(1+kz)\) for \(z\geq 0\), where \(a,k>0\) are parameters, and let \(p\in (0,\infty )\) be given. We assume that \(U\) is of the form \(U:=[u^{-},u^{+}]\subset (0,\infty )\) with \(u^{\mathrm{s}}\in [u^{-},u^{+}]\) and define \(f_{1}(w,z):=g(wz)\) and \(f_{2}(w,z)=wg(z)\) for \(w\in [u^{-},u^{+}]\) and \(z\geq 0\). It follows from [13, Table 5.1] that if \(au^{-} >p\), then (N3) holds for \(f_{1}\) and \(f_{2}\) with \(y^{\mathrm{s}}=(au^{\mathrm{s}}-p)/(pku^{\mathrm{s}})\) and \(y^{\mathrm{s}}=(au^{\mathrm{s}}-p)/(pk)\), respectively.
Furthermore, \(f_{1}\) and \(f_{2}\) are obviously bounded and so are
Setting \(\lambda _{i}:=\sup \{|({\partial f_{i}}/{\partial w})(w,z)|:w\in [u^{-},u^{+}], \,z\geq 0\}<\infty \), \(i=1,2\), it follows from the mean-value theorem for differentiation that (5.18) holds.
(2) This example focuses on the nonlinearities \(f_{1}\) and \(f_{2}\) induced by the Ricker-type function \(g(z)=aze^{-z}\) via \(f_{1}(w,z)=g(wz)\) and \(f_{2}(w,z)=wg(z)\) for \(w\in [u^{-},u^{+}]\) and \(z\geq 0\), where \(u^{+}>u^{-}>0\). Under the assumption
it is well-known that, for every \(u^{\mathrm{s}}\in [u^{-},u^{+}]\), (N3) is satisfied for \(f_{1}\) and \(f_{2}\) with \(y^{\mathrm{s}}= \ln (au^{\mathrm{s}}/p)/u^{\mathrm{s}}\) and \(y^{\mathrm{s}}= \ln (au^{\mathrm{s}}/p)\), respectively, see [13, Table 5.1]. As in the Beverton-Holt example, a mean-value argument can be used to show that (5.18) holds. \(\Diamond \)
If the nonlinearity \(f\) does not satisfy the sector condition (N3), then it may still satisfy some sector condition and we will now explore this in some more detail. For which purpose, assume, for simplicity, that \(f(w,z)=f(z)\) does not depend on \(w\). For \(q>0\), we denote by \(S_{q}\) the set of all locally Lipschitz functions \(f:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}\) for which there exist affine-linear functions \(l_{+},l_{-}:{\mathbb{R}}\to {\mathbb{R}}\) with slopes \(q\) and \(-q\), respectively, and \(y^{\sharp }>0\) (all depending on \(f\)) such that
and, furthermore,
Note that \(l_{+}(y^{\sharp })=l_{-}(y^{\sharp })=f(y^{\sharp })\), \(l_{+}(0)=f(y^{\sharp })-qy^{\sharp }\), \(l_{-}(0)=f(y^{\sharp })+qy^{\sharp }\), and, by (5.21),
Obviously, this looks similar to (5.1), but here \(z=0\) is included, and, in general, \(f(y^{\sharp })\neq qy^{\sharp }\). If \(f\in S_{q}\), then we say that \(f\) satisfies a sector condition with abscissa \(y^{\sharp }\) and slope \(q\).
The set \(S_{q}\) constitutes a rich class of functions. For example:
-
any bounded differentiable function \(f:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}\) such that \(\limsup _{z\to \infty }|f'(z)|< q\) is an element in \(S_{q}\);
-
any locally Lipschitz function \(f:{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}\) such that \(f(z)\) converges to a finite limit as \(z\to \infty \) and for which there exist \(\tilde{q}\in (0,q)\) and a sequence of intervals \([y_{k},z_{k}]\subset (0,\infty )\) such that \(y_{k}\to \infty \) as \(k\to \infty \), \(\inf _{k\in {\mathbb{N}}}(z_{k}-y_{k})>0\) and
$$ \limsup _{h\to 0}\left |\frac{f(z+h)-f(z)}{h}\right |\leq \tilde{q} \quad \forall \,z\in \bigcup _{k\in {\mathbb{N}}}[y_{k},z_{k}]\,, $$is in \(S_{q}\).
Example 5.6
Consider the functions \(f_{1}, f_{2}: {\mathbb{R}}_{+} \to {\mathbb{R}}_{+}\) given by
which are plotted in Fig. 2. Since
the function \(f_{1}\) does not even satisfy (N2), for any \(p>0\), and so (N3) cannot hold. The function \(f_{2}\) does not satisfy (N3) when \(p=1\), see Fig. 2(b).
However, the functions \(f_{1}\) and \(f_{2}\) are clearly bounded and differentiable, with
and so belong to \(S_{q}\) for all \(q>0\). Figure 2 illustrates graphically that \(f_{1}, f_{2} \in S_{1}\). \(\Diamond \)
The next result shows that if \(f\in S_{p}\), then there exists a constant forcing function \(v\) such that the resulting forced system has nice stability and convergence properties
Proposition 5.7
Assume that (L1) and (L2) are satisfied and \({\mathbf{G}}(0)>0\). Consider (3.2) with \(f\in S_{p}\) (where \(p=1/{\mathbf{G}}(0)\)). Let \(y^{\sharp }\) be a sector abscissa of \(f\), set \(x^{\sharp }:=-A^{-1}bpy^{\sharp }\) and assume that \(\psi :=py^{\sharp }-f(y^{\sharp })\geq 0\). Under these conditions, there exist constants \(\Gamma \geq 1\) (depending on \((A,b,c)\), \(f\), \(h\) and \(y^{\sharp }\)) and \(\gamma >0\) (depending on \((A,b,c)\), \(f\) and \(y^{\sharp }\)) such that, for all \((\xi ,v)\in M^{1}_{+}\times L^{\infty }_{+}\), the unique solution \(x:[-h,\infty )\to {\mathbb{R}}^{n}\) of (2.3) satisfies
Furthermore, if \(\lim _{t\to \infty }\|v-\psi b\|_{L^{\infty }(t,\infty )}=0\), then \(x(t)\to x^{\sharp }\) as \(t\to \infty \).
We emphasize here that \(x^{\sharp }\) is not a steady state of the unforced system \(\dot{x}(t)=Ax(t)+bf(c^{T}x(t-h))\), but of the modified equation \(\dot{x}(t)=Ax(t)+ b\big (f(c^{T}x(t-h))+\psi \big )\).
In the context of scalar (\(n=1\)) instances of (3.2), in the absence of the forcing term \(u\), it has been shown in the chaos control literature (see, for example, [24]) that constant additive control may enforce convergence in systems which show chaotic behaviour when unforced. Proposition 5.7 identifies a general scenario in which the application of such control action results in dynamics which are stable in the sense of (5.23).
Proof of Proposition 5.7
As \(f\in S_{p}\), the function \(N:{\mathbb{R}}\to {\mathbb{R}}\) defined by
satisfies
Let \((\xi ,v)\in M^{1}_{+}\times L^{\infty }_{+}\) and let \(x\) be the unique solution \(x\) of (3.2). Setting \(e(t):=x(t)-x^{\sharp }\), it follows that
Since \(c^{T}e(t-h)=c^{T}x(t-h)-y^{\sharp }\geq -y^{\sharp }\) for all \(t\geq 0\), the above equation can re-written as
The claim now follows from (5.24), the fact that \(p=1/{\mathbf{G}}(0)=1/\|G\|_{L^{1}}\) and statements (2) and (3) of Proposition 2.2. □
We conclude the section by mentioning that Proposition 5.7 may be extended to the case wherein \(f = f(u,z)\) does depend on two arguments, provided that \(f(u^{\sharp }, \cdot ) \in S_{p}\) for some \(u^{\sharp }\in U\). For the sake of brevity, we do not give a formal statement.
6 Examples
The results presented in the previous sections allow the analysis of mathematical models arising in a great variety of contexts. To demonstrate this, we consider three different models in this section. The first two are related to population dynamics and the last one to self-regulated biochemical reactions.
6.1 Delayed Recruitment Models
Recruitment models typically assume that the dynamics of sexually mature individuals of a population are driven by the difference between the rate at which new members are recruited and the mortality rate. If the maturation process takes a constant time \(h>0\), competition occurs only in a specific age cohort and the mortality rate is constant, then the following population model is obtained
Here \(x(t)\) denotes the number of mature individuals at time \(t\), \(\mu >0\) is the mortality rate, the production function \(f\) depends on the competition between individuals, \(u(t) \in U:=[u^{-},u^{+}]\subseteq (0,\infty )\) and \(v(t)\ge 0\) are forcing terms which model the effect of environmental fluctuations affecting recruitment. A derivation of (6.1) without forcing may be found in, for example, [4] and we refer the reader to [20, Sect. 1] for an interesting discussion on delays in population models.
Example 6.1
Consider (6.1) with \(f:U \times {\mathbb{R}}_{+} \to {\mathbb{R}}_{+}\) given by
where \(k>0\), see part (1) of Example 5.5. This corresponds to a so-called contest competition setting, in which resources available are monopolized by some individuals. In this situation the production function \(f\) tends to the maximum \(a/k\) as \(z \to \infty \), uniformly in \(w\). Model (6.1) with \(f\) given by (6.2) is a special case of (1.1) with \(n=1\), \(A=-\mu \), \(b= 1\) and \(c= 1\). It is straightforward to verify that assumptions (L1), (L2) and (L3) are satisfied and, trivially, \(p=1/{\mathbf{G}}(0)=\mu \). We have shown in Example 5.5 that, for every \(u^{e}\in [u^{-},u^{+}]\), condition (N3) holds, provided that \(u^{-}>\mu \). Thus, we can use Theorem 4.3, Corollary 5.3 and Theorem 5.4 to obtain persistence, convergence and stability results, respectively, for the forced equation (6.1) with \(f\) given by (6.2). For instance, Theorem 5.4 implies that the deviation of \(x(t)\) from \(x^{\mathrm{s}}\) is bounded in the uniform manner (5.19), whereas Corollary 5.3 shows that the equation satisfies a converging-input converging-state property — namely, that if \(\lim _{t\to \infty }\|u-u^{\mathrm{s}}\|_{L^{\infty }(t,\infty )}=0\) and \(\lim _{t\to \infty }\|v\|_{L^{\infty }(t,\infty )}=0\), then \(x(t) \to x^{\mathrm{s}}\) as \(t \to \infty \). \(\Diamond \)
The above example shows that, under contest competition, the mature population tends to a constant value, provided that the forcing functions \(u(t)\) and \(v(t)\) converge as \(t\to \infty \). However, it is known that this is not the case if resources are equally allocated among individuals, that is, under so-called scramble competition (characterized by a unimodal production function which tends to zero at high population sizes, see [4, 5]). In this case, even in the absence of fluctuating external forcing, the solutions of model (6.1) might show persistent fluctuations which, in many practical situations, are undesirable. Interestingly, a constant control, which adds a constant amount of mature individuals to the population per unit time, can have a stabilizing effect. This was shown in the context of (6.1) with a specific \(f\) (Mackey-Glass equation) in [24]. In the example below, we obtain the stabilizing effect of constant control action as a consequence of Proposition 5.7.
Example 6.2
Consider model (6.1) with \(\mu =1\), so that \(p=1\), and where the production function \(f\), assumed to be independent of its first variable, is given by
for fixed parameters \(a, k >0\) and \(s>0\). Whilst \(f\) trivially satisfies (N2) whenever \(a > k\), Fig. 3(a) illustrates that condition (N3) does not hold for \(f\) with
and, consequently, Corollary 5.3 does not apply for these values. Nevertheless, for any fixed \(a>0\) and \(k>0\), the bounded and differentiable function \(f\) belongs to \(S_{q}\) for any \(q>0\), since \(|f'(z)|\to 0\) as \(z\to \infty \). In particular, \(f\in S_{1}\) and \(y^{\sharp }=2.65\) is a sector abscissa, see Fig. 3(b). As \(\psi = y^{\sharp }- f(y^{\sharp })\approx 1.75>0\), Proposition 5.7 applies. In this scalar example where \(A=-1\), \(b =1\) and \(p=1\), we simply have that \(x^{\sharp }:= -A^{-1}bp y^{\sharp }= y^{\sharp }\).
Consider (6.1) with \(f\) given by (6.3), (6.4) and
where \(\zeta : [-25,0] \to {\mathbb{R}}_{+}\) is defined by
Numerical results are provided in Fig. 4: for the model data (6.3)–(6.5), solutions were computed numerically using the delay-differential equation solver dde23 in Matlab. Figure 4(a) shows plots of two solutions \(x_{1}\) and \(x_{2}\) of (6.1) corresponding to the initial conditions \(\xi _{1}\) and \(\xi _{2}\), respectively, and forcing term \(v(t)\equiv 0\). In both cases persistent fluctuations are observed.
Numerical solutions of the delay-differential equation (6.1) from Example 6.2, with model data (6.3)–(6.5). The dotted line corresponds to \(x^{\sharp }\). In panels (a) and (c) the solid and dashed-dotted lines correspond to initial conditions \(\xi _{1}\) and \(\xi _{2}\), respectively. In panel (b), the solid and dashed-dotted lines correspond to forcing terms \(v_{1}\) and \(v_{2}\), respectively. Only initial condition \(\xi _{1}\) is used. (a) Persistent fluctuations are observed with \(v=0\). (b) Bounded oscillations around \(x^{\sharp }\) are observed with \(v_{1}\) and \(v_{2}\) as in (6.6). (c) Convergence is observed with constant \(v = \psi \)
Figure 4(b) shows simulations of (6.1) with two oscillatory forcing terms
In this simulation, only one initial condition is used from (6.5), namely \(\xi _{1}\). As ensured by Proposition 5.7, bounded oscillations around \(x^{\sharp }\) are observed which, as expected, increase with increasing \(k\).
Figure 4(c) shows simulations of (6.1) with constant forcing term \(v(t) \equiv \psi \). As ensured by Proposition 5.7, we observe that the addition of sufficiently large constant forcing has the effect of making solutions converge to a positive limit. \(\Diamond \)
6.2 Dispersal of a Population with a Unique Breeding Region
Consider the following model of a population spatially structured over \(n\) discrete patches
Here \(x_{i}(t)\) is the density of the population in patch \(i\in \{1,\dots , n\}\) at time \(t \geq 0\), \(d_{i}>0\) is the mortality rate in patch \(i\in \{1,\dots , n\}\), \(a_{ij}\ge 0\) are the dispersal or migration rates of the population from patch \(j\) to patch \(i\), where \(a_{ii}:=0\) for \(i\in \{1,\dots ,n\}\). Furthermore, \(h>0\) is the maturation time, the birth function \(f\colon [u^{-},u^{+}] \times {\mathbb{R}}_{+} \to {\mathbb{R}}_{+}\) is given by
the constant \(c_{i}\ge 0\) measures the contribution of the population in patch \(i\) to the number of births in patch 1 and it is natural to assume that there exists \(j\in \{1,\dots ,n\}\) such that \(c_{j}>0\); finally, \(u(t)\in [u^{-},u^{+}] \subset (0,\infty )\) and \(v_{i}(t)\geq 0\) model disturbances.
The model (6.7) is a so-called Nicholson system, as the case \(n=1\) reduces to the well-known Nicholson’s blowfly equation [18]. A related Nicholson system is studied in [11]. However, the results in [11] focus on the case wherein the birth of new individuals occurs in every patch. Here, we consider a different situation commonly seen in nature, in which there is a single breeding patch.
System (6.7) is a special case of (1.1) with
The matrix \(A\) is Metzler by construction and, since, without newborns, the population should become extinct, it is natural to assume that \(A\) is Hurwitz. Under this assumption, (L1) and (L2) hold. Verifying condition (L3) in general without further assumptions on \(A\) and \(c\) seems analytically cumbersome. Proposition 3.2 provides characterisations of (L3) which may be used in specific situations. The Ricker nonlinearity \(f\) satisfies (N3) provided (5.20) holds, see Example 5.5.
Example 6.3
Consider (6.7) with \(n=3\), \(d_{1}=d_{2}=d_{3}=2\), \(a_{12}=a_{21}=a_{31}=1\) and \(a_{13}=a_{23}=a_{32}=0\), so that
We note that \(A\) is Metzler and Hurwitz and
since \(c=(c_{1},c_{2},c_{3})^{T} >0\) by assumption. From the block-structure of \(A\) it is immediate that property (7) of Proposition 3.2 holds if, and only if, \(c_{3} >0\). In other words, (L3) is satisfied if, and only if, \(c_{3} >0\). Consequently, if \(c_{3}>0\) and (5.20) holds then the stability results Theorems 5.2 and 5.4 are applicable. Moreover, we note that \(-A^{-1}b\gg 0\), and so, if \(c_{3}>0\), then, for every \(i\in \{1,2,3\}\), (6.7) is uniformly \(e_{i}^{*}\)-persistent with respect to \(E^{r,0}(\alpha ,\beta )\) (\(r=1, \infty \) and \(\beta >\alpha >0\)) as follows from Proposition 4.1.
We now explore the case wherein \(c_{3}=0\), that is, (L3) does not hold. Then, by Corollary 4.5, the population is not uniformly \(c^{*}\)-persistent with respect to \(E^{\infty ,0}(\alpha , \beta )\), \(E^{1,0}(\alpha ,\beta )\) or \(E^{\infty }(\alpha ,\beta )\) for any \(\beta >\alpha >0\). Indeed, by inspection of the model structure, for all initial conditions \(\xi \) with \(\xi ^{0}_{i} =0\) and \(\xi ^{1}_{i} = 0\) for \(i \in \{1,2\}\), all functions \(u:{\mathbb{R}}_{+}\to [u^{-},u^{+}]\) and for \(v=0\), the first two components of the solution \(x\) are equal to 0, showing that the system fails to be \(c^{*}\)-persistent. Interestingly, if we consider the dynamics of just the first two states, which decouple from the third, then we obtain the subsystem
which is another special case of (6.7) and (6.8) with
Since \(c_{1} + c_{2} >0\) as \(c>0\), it is straightforward to show that (L3) always holds for the subsystem (6.9). It is routine to calculate that
Consequently, if (5.20) holds, then subsystem (6.9) is ultimately \(c^{*}_{\mathrm{s}}\)-persistent and Theorems 5.2 and 5.4 are applicable to (6.9). Finally, Proposition 4.1 guarantees that (6.9) is also ultimately \(e_{1}^{*}\)- and \(e_{2}^{*}\)-persistent. \(\Diamond \)
6.3 Self-Regulated Biochemical Reactions
Consider a chain of chemical reactions which converts a (first) substance with concentration \(s_{1}\) into an end-product with concentration \(s_{n}\) via several intermediate substances with concentrations \(s_{2}\), …, \(s_{n-1}\). Let \(\tau _{i}\ge 0\) be the time needed for a substance \(s_{i}\) to affect the production of the next substance in the chain \(s_{i+1}\). The existence of delays is common in biochemical reactions of gene expression and are related to transcriptional and translational processes [31]. We assume that the reaction is self-regulated in the sense that an increase of concentration of substance \(n\) in the chain induces or represses the production of the first substance. More specifically, we consider the following model
where \(d_{i}>0\), \(i=1,\dots , n\) is the decay rate of substance \(i\) and \(a_{i-1}>0\), \(i=2,\dots ,n\), is the production rate of substance \(i\) from substance \(i-1\). The nonlinearity \(f\colon U\times {\mathbb{R}}_{+} \to {\mathbb{R}}_{+}\) is the self-regulation function for the reaction, where \(U=[u^{-},u^{+}]\subset (0,\infty )\) and the functions \(u\) and \(\omega _{i}\) model external disturbances. Without delays and external disturbances, model (6.10) was proposed in [16] and further studied in [45]. The authors of [3] also studied a version of (6.10) with additive forcing, but without delays and for \(f\) not depending on \(u\). With delays, model (6.10) was first considered in [27], although without considering forcing terms.
System (6.10) is not in the form of (1.1) but, by setting \(h:= \sum _{j=1}^{n} \tau _{j}\),
it is routine to check that
which is a special case of system (1.1), with
We see immediately that assumptions (L1) and (L2) are satisfied. Assumption (L3) also holds, as follows from Proposition 3.2 by noting that \(A+b c^{T}\) is irreducible. Hence, Proposition 3.3 implies that \({\mathbf{G}}(0)>0\). Owing to the particular structure of \(A\), \(b\) and \(c\), the latter can also be seen directly by noting that
Depending on whether an increase of the concentration \(x_{n}\) of substance \(n\) inhibits or activates the production of the first substance, the function \(f\) is assumed to be decreasing or increasing in its second variable, respectively, see [1]. We illustrate the stability theory developed in Sect. 5 in the case of an increasing \(f\), namely,
Before we do this, we state a simple lemma which provides a sufficient condition for (N3) to hold. The proof is straightforward and is left to the reader.
Lemma 6.4
Assume that \(f:[u^{-},u^{+}]\times {\mathbb{R}}_{+}\to {\mathbb{R}}_{+}\) is of the form \(f(w,z)=wg(z)\), where \(g \colon {\mathbb{R}}_{+} \to {\mathbb{R}}_{+}\) is bounded and \(g(0)>0\). Let \(u^{\mathrm{s}} \in [u^{-},u^{+}]\). The following statements hold.
(1) The nonlinearity \(f\) satisfies (N2).
(2) If, additionally, \(g\) is differentiable and \(\sup _{z\geq 0}|g'(z)|< p/u^{\mathrm{s}}\), then the function \(z\mapsto f(u^{\mathrm{s}},z)\) is globally Lipschitz with Lipschitz constant smaller than \(p\) and \(f\) satisfies (N3).
Writing \(f\) given by (6.12) as \(f(w,z)=wg(z)\) with
elementary calculations show that
and thus, by Lemma 6.4, \(f\) satisfies (N3) if
Example 6.5
Consider system (6.11) with nonlinearity (6.12), \([u^{-},u^{+}]=[0.2,1.5]\), \(u^{\mathrm{s}}=0.25\) and parameter values
If \(d_{1}=2\), then
and so, by Lemma 6.4, (N3) holds. Consequently, the stability theory developed in Sect. 5 is applicable to this example.
If we reduce \(d_{1}\) to \(d_{1}=1\), but keep the other parameter values as in (6.13), then \(p=1\), and statement (2) of Lemma 6.4 does not apply. In fact, condition (N3) does not hold in this case as Fig. 2(b) shows. Furthermore, in this case, the system with \(u(t)\equiv u^{\mathrm{s}}\) and \(v=0\) seems to be bi-stable, see the simulations in Fig. 5(a) with initial conditions given by
where
All numerical solutions in this example were computed using the dde23 command in Matlab.
Numerical solutions of the system of delay-differential equations (6.11) for parameter values given by (6.13), with \(d_{1}=1\) and \(u(t)\equiv u^{\mathrm{s}} = 0.25\). Each solid and dashed-dotted line corresponds to a component of \(x\). Dotted lines correspond to (the equal) components of \(x^{\sharp }\). (a) Bi-stability of (6.11) with forcing \(v =0\). (b) Bounded oscillations around \(x^{\sharp }\) with almost periodic forcing \(v\) as in (6.15). (c) Convergence of states to \(x^{\sharp }\) with convergent forcing term \(v\) as in (6.16)
Nevertheless, the function \(z\mapsto f(u^{\mathrm{s}},z)\) was considered in Example 5.6, and shown to belong to \(S_{1}\). Furthermore, \(y^{\sharp }= 2.453\) is a sector abscissa of \(f(u^{\mathrm{s}}, \cdot )\) with \(\psi =y^{\sharp }-f(u^{\mathrm{s}},y^{\sharp })\approx 0.5>0\), see Fig. 2(b). Consequently, Proposition 5.7 guarantees that \(x^{\sharp }= -A^{-1}b y^{\sharp }\), in this case given by
is “stable” in the sense of (5.23). To illustrate this result numerically, Fig. 5(b) plots a numerical simulation of (6.11) with parameter values given by (6.13) and \(d_{1}=1\), \(u(t)\equiv u^{\mathrm{s}} = 0.25\), and with oscillatory forcing term \(v\) given by
The initial conditions are given by (6.14a), (6.14b). Bounded oscillations around \(x^{\sharp }\) are observed.
Moreover, Proposition 5.7 ensures that, for every \((\xi ,v)\in M^{1}_{+}\times L^{\infty }_{+}\) such that \(\lim _{t\to \infty }\|v-\psi b\|_{L^{\infty }(t,\infty )}=0\), the unique solution \(x\) of system (6.11) satisfies \(x(t)\to x^{\sharp }\) as \(t\to \infty \). Thus, Fig. 5(c) plots a numerical simulation of the same model, only now with a convergent forcing term \(v\) given by
Convergence \(x(t) \to x^{\sharp }\) as \(t \to \infty \) is observed. Hence, the inclusion of such a convergent additive control removes the bi-stability and forces the solutions to converge to a limit \(x^{\sharp }\) independently of the initial condition in \(M^{1}_{+}\) and delay \(h \geq 0\). \(\Diamond \)
Notes
Note that the terms “positive” and “nonnegative” are often used interchangeably in this context.
Also called a Hollings type II or Michaelis-Menten nonlinearity.
References
Allwright, D.J.: A global stability criterion for simple control loops. J. Math. Biol. 4, 363–373 (1977)
Berman, A., Plemmons, R.J.: Nonnegative Matrices in the Mathematical Sciences. SIAM, Philadelphia (1994)
Bill, A., Guiver, C., Logemann, H., Townley, S.: Stability of non-negative Lur’e systems. SIAM J. Control Optim. 54, 1176–1211 (2016)
Blythe, S.P., Nisbet, R.M., Gurney, W.S.C.: Instability and complex dynamic behaviour in population models with long time delays. Theor. Popul. Biol. 22, 147–176 (1982)
Brauer, F., Castillo-Chavez, C.: Mathematical Models in Population Biology and Epidemiology. Springer, New York (2012)
Cull, P.: Enveloping implies global stability. In: Allen, L.J.S., Aulbach, B., Elaydi, S., Sacker, R. (eds.) Difference Equations and Discrete Dynamical Systems, pp. 71–85. World Sci. Publ., Hackensack (2005)
Curtain, R.F., Zwart, H.J.: An Introduction to Infinite-Dimensional Linear Systems Theory. Springer, New York (1995)
Dashkovskiy, S.N., Efimov, D.V., Sontag, E.D.: Input-to-state stability and allied system properties. Autom. Remote Control 72, 1579–1614 (2011)
Eager, E.A., Rebarber, R.: Sensitivity and elasticity analysis of a Lur’e system used to model a population subject to density-dependent reproduction. Math. Biosci. 282, 34–45 (2016)
Eager, E.A., Rebarber, R., Tenhumberg, B.: Global asymptotic stability of plant-seed bank models. J. Math. Biol. 69, 1–37 (2014)
Faria, T., Röst, G.: Persistence, permanence and global stability for a \(n\)-dimensional Nicholson system. J. Dyn. Differ. Equ. 26, 723–744 (2014)
Franco, D., Logemann, H., Perán, J.: Global stability of an age-structured population model. Syst. Control Lett. 65, 30–36 (2014)
Franco, D., Guiver, C., Logemann, H., Perán, J.: Semi-global persistence and stability for a class of forced discrete-time population models. Physica D 360, 46–61 (2017)
Franco, D., Guiver, C., Logemann, H., Perán, J.: Boundedness, persistence and stability for classes of forced difference equations arising in population ecology. J. Math. Biol. 79, 1029–1076 (2019)
Freedman, H.I., So, J.W.-H.: Persistence in discrete semidynamical systems. SIAM J. Math. Anal. 20, 930–938 (1989)
Goodwin, B.C.: Oscillatory behavior of enzymatic control processes. Adv. Enzyme Regul. 3, 425–439 (1965)
Guiver, C., Logemann, H., Opmeer, M.R.: Infinite-dimensional Lur’e systems: input-to-state stability and convergence properties. SIAM J. Control Optim. 57, 334–365 (2019)
Gurney, W.S.C., Blythe, S.P., Nisbet, R.M.: Nicholson’s blowflies revisited. Nature 287, 17–21 (1980)
Haddad, W.M., Chellaboina, V., Hui, Q.: Nonnegative and Compartmental Dynamical Systems. Princeton University Press, Princeton (2010)
Hadeler, K.P., Bocharov, G.: Where to put delays in population models, in particular in the neutral case. Can. Appl. Math. Q. 11, 159–173 (2003)
Hale, J.K., Verduyn Lunel, S.M.: Introduction to Functional Differential Equations. Springer, New York (1993)
Jayawardhana, B., Logemann, H., Ryan, E.P.: The circle criterion and input-to-state stability: new perspectives on a classical result. IEEE Control Syst. Mag. 31, 32–67 (2011)
Khalil, H.K.: Nonlinear Systems, 3rd edn. Pearson, Harlow (2014)
Kiss, G., Röst, G.: Controlling Mackey-Glass chaos. Chaos 27, 114321 (2017)
Krasnosel’skij, M.A., Lifshits, J.A., Sobolev, A.V.: Positive Linear Systems: The Method of Positive Operators. Heldermann Verlag, Berlin (1989)
Krause, U.: Positive Dynamical Systems in Discrete Time. de Gruyter, Berlin (2015)
Landahl, H.D.: Some conditions for sustained oscillations in biochemical chains with feedback inhibition. Bull. Math. Biophys. 31, 775–787 (1969)
Logemann, H., Ryan, E.P.: Volterra functional differential equations: existence, uniqueness, and coninuation of solutions. Am. Math. Mon. 117, 490–511 (2010)
Logemann, H., Ryan, E.P.: Ordinary Differential Equations: Analysis, Qualitative Theory and Control. Springer, London (2014)
Mackey, M.C., Glass, L.: Oscillation and chaos in physiological control systems. Science 197, 287–289 (1977)
Monk, N.A.M.: Oscillatory expression of Hes1, p53, and NF-\(\kappa \)B driven by transcriptional time delays. Curr. Biol. 13, 1409–1413 (2003)
Nicholson, A.J.: An outline of the dynamics of animal populations. Aust. J. Zool. 2, 9–65 (1954)
Rebarber, R., Tenhumberg, B., Townley, S.: Global asymptotic stability density dependent integral population projection models. Theor. Popul. Biol. 81, 81–87 (2012)
Rubió-Massegú, J., Mañosa, V.: On the enveloping method and the existence of global Lyapunov functions. J. Differ. Equ. Appl. 13, 1029–1035 (2007)
Sarkans, E., Logemann, H.: Input-to-state stability for Lur’e systems. Math. Control Signals Syst. 27, 439–465 (2015)
Sarkans, E., Logemann, H.: Input-to-state stability for discrete-time Lur’e systems. SIAM J. Control Optim. 54, 1739–1768 (2016)
Smith, H.L.: An Introduction to Delay Differential Equations with Applications to the Life Sciences. Springer, New York (2011)
Smith, H.L., Thieme, H.R.: Dynamical Systems and Population Persistence. Am. Math. Soc., Providence (2011)
Smith, H.L., Thieme, H.R.: Persistence and global stability for a class of discrete-time structured population models. Discrete Contin. Dyn. Syst., Ser. A 33, 4627–4646 (2013)
Sontag, E.D.: Smooth stabilization implies coprime factorization. IEEE Trans. Autom. Control 34, 435–443 (1989)
Sontag, E.D.: Mathematical Control Theory: Deterministic Finite Dimensional Systems. Springer, New York (1998)
Sontag, E.D.: Input-to-state stability: basic concepts and results. In: Nistri, P., Stefani, G. (eds.) Nonlinear and Optimal Control Theory, pp. 163–220. Springer, Berlin (2006)
Terrell, W.J.: Stability and Stabilization. Princeton University Press, Princeton (2009)
Townley, S., Rebarber, R., Tenhumberg, B.: Feedback control systems analysis of density dependent population dynamics. Syst. Control Lett. 61, 309–315 (2012)
Tyson, J.J., Othmer, H.G.: The dynamics of feedback control circuits in biochemical pathways. Prog. Theor. Biol. 5, 1–62 (1978)
Varga, R.S.: Matrix Iterative Analysis, 2nd edn. Springer, Berlin (2000)
Vidyasagar, M.: Nonlinear Systems Analysis, 2nd edn. Prentice-Hall, Englewood Cliffs (1993)
Walter, W.: Ordinary Differential Equations. Springer, New York (1998)
Acknowledgement
D. Franco was supported by grant MTM2017-85054-C2-2-P (AEI/FEDER, UE) and ETSII-UNED grant 2021-MAT10.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix A: List of Function Spaces Used
For ease of reference, we provide a list of the function spaces introduced in the paper.
-
\(C([-h,0],{\mathbb{R}}^{n})\) = space of continuous functions \([-h,0] \to {\mathbb{R}}^{n}\) equipped with supremum norm, where \(h>0\).
-
\(L({\mathbb{R}}_{+},U)\) = space of Lebesgue measurable functions \({\mathbb{R}}_{+}\to U\), where \(U\subset {\mathbb{R}}\) is compact.
-
\(L^{r}(J,{\mathbb{R}}^{n})\) = space of Lebesgue measurable functions \(J \to {\mathbb{R}}^{n}\) which are integrable (\(r=1\)) or essentially bounded (\(r=\infty \)), where \(J\subset {\mathbb{R}}\) is an interval.
-
\(L^{r}_{\mathrm{loc}}(J,{\mathbb{R}}^{n})\) = local version of \(L^{r}(J,{\mathbb{R}}^{n})\).
-
\(W^{1,1}_{\mathrm{loc}}([0,\tau ),{\mathbb{R}}^{n})\) = local version of the usual Sobolev space \(W^{1,1}([0,\tau ),{\mathbb{R}}^{n})\), where \(0<\tau \leq \infty \).
-
\(M^{r}= M^{r}([-h,0],{\mathbb{R}}^{n})={\mathbb{R}}^{n}\times L^{r}([-h,0],{ \mathbb{R}}^{n})\), where \(r=1,\infty \) and \(h>0\).
-
\(M^{1}_{+}={\mathbb{R}}_{+}^{n}\times L^{1}([-h,0],{\mathbb{R}}_{+}^{n})\), \(L^{\infty }_{+}=L^{\infty }({\mathbb{R}}_{+},{\mathbb{R}}_{+}^{n})\).
-
\(D^{r}(\beta )=\{(\xi ,u,v)\in M^{r}_{+}\times L({\mathbb{R}}_{+},U) \times L^{\infty }_{+}:\|\xi \|_{M^{r}}+\|v\|_{L^{\infty }}\leq \beta \}\), where \(r=1,\infty \) and \(\beta >0\).
-
\(E^{r}(\alpha ,\beta )=\{(\xi ,u,v)\in D^{r}(\beta ):\|\xi \|_{M^{1}} \geq \alpha \}\), where \(r=1,\infty \) and \(\beta >\alpha >0\).
-
\(E^{r,0}(\alpha ,\beta )=\{(\xi ,u,v)\in D^{r}(\beta ):\|\xi ^{0}\| \geq \alpha \}\), where \(r=1,\infty \) and \(\beta >\alpha >0\).
Appendix B: Proofs of Results Not Given in the Main Text
Proof of Proposition 2.1
(1) We recursively define a function \(x:[-h,\infty )\to {\mathbb{R}}^{n}\) by defining it on the intervals \([(k-1)h,kh]\) for all \(k\in {\mathbb{Z}}_{+}\) as follows: set \(x(t):=\xi ^{1}(t)\) for all \(t\in [-h,0)\), \(x(0):=\xi ^{0}\), and, for every \(k\in {\mathbb{Z}}_{+}\) and all \(t \in [0,h]\),
Note that, for \(k=0\), the integral on the right-hand side of (B.1) is well-defined because, by assumption, the function \(t\mapsto N(t,c^{T}\xi ^{1}(t-h))\) is integrable on \([0,h]\). For \(k\geq 1\), the integral is also well-defined because \(x\) is continuous on \([(k-1)h,kh]\) and hence, invoking the Lipschitz property of \(N\), we see that \(t\mapsto N(t+kh,c^{T}x(t+(k-1)h))\) is integrable on \([0,h]\). Consequently, the recursive definition of \(x\) via (B.1) results in a well-defined function on \([-h,\infty )\). It is clear that \(x|_{[0,\infty )}\in W^{1,1}_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}^{n})\) and \(x\) is a solution of (2.3) on \([-h,\infty )\). This solution is unique, because if \(\tilde{x}\) is a solution of (2.3) on \([-h,\infty )\), then, for every \(k\in {\mathbb{Z}}_{+}\), (B.1) holds with \(x\) replaced by \(\tilde{x}\), and, since \(\tilde{x}(t)=\xi ^{1}(t)=x(t)\) for all \(t\in [-h,0)\) and \(\tilde{x}(0)=\xi ^{0}=x(0)\), we conclude that \(\tilde{x}=x\).
(2) If \(x\) is a solution of (2.3) on \([-h,\tau )\) for some \(\tau >h\), then \(bw=\dot{x}-Ax-v\in L^{1}([0,h],{\mathbb{R}}^{n})\), and, as \(b\neq0\), it follows that \(w\in L^{1}([0,h],{\mathbb{R}})\), establishing the claim. □
We note that in the above proof the Lipschitz property has not been used in the argument establishing uniqueness. In fact, an inspection of the proof shows that Proposition 2.1 holds if \(N\) is measurable in its first argument and continuous in its second and, for every \(z\in {\mathbb{R}}\), there exist a locally integrable function \(\nu :{\mathbb{R}}_{+}\to {\mathbb{R}}_{+}\) and an open interval \(J\subset {\mathbb{R}}\) containing \(z\) such that \(|N(t,z)|\leq \nu (t)|z|\) for all \(z\in J\) and \(t\geq 0\). These conditions are weaker than the assumptions imposed on \(N\) in Sect. 2. However, the latter are required in the delay-free case.
Proof of Proposition 2.2
Let \(\xi \in M^{1}\) and \(v\in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}^{n})\). Invoking (2.4), we see that \(t\mapsto N(t,c^{T}\xi ^{1}(t-h))\) is integrable on \([0,h]\), and thus, by Proposition 2.1, the initial-value problem (2.3) has a unique solution \(x\) defined on \([-h,\infty )\). It is clear that \(x\) satisfies the variation-of-parameters formula
(1) It follows easily from (2.4) and (B.2) with \(t_{0}=kh\), where \(k\in {\mathbb{Z}}_{+}\), that there exists \(\Gamma _{0}\geq 1\) (depending only on \((A,b,c)\), \(l\) and \(h\))
The claim can now follows by a routine argument which is based on the repeated application of the above estimate, starting with \(k=0\) and stopping with the smallest \(k\) such that \(kh\geq \tau \).
(2) By the Hurwitz property of \(A\) and the assumption that \(l\|G\|_{L^{1}}<1\), there exists \(\mu >0\) such that \(A+\mu I\) is Hurwitz and
We define a function \(g:{\mathbb{R}}_{+}\to {\mathbb{R}}^{n}\) by
and note that \(g^{T}(t)b=G(t-h)\) for all \(t\geq h\). Setting \(y(t):=c^{T}x(t-h)\) for \(t\geq 0\), it follows from (B.2) that
Consequently, setting \(\tilde{y}(t):=e^{\mu t}y(t)\), \(\tilde{v}(t):=e^{\mu t}v(t)\) and \(\tilde{g}(t):=e^{\mu t}g(t)\) for all \(t\geq 0\),
where \(\tilde{N}(t,z):=e^{\mu t}N(t,e^{-\mu t}z)\) for all \(t\geq 0\) and all \(z\in {\mathbb{R}}\). We note that
It follows from (B.4) and (B.5) that
where \(\kappa _{0}:=\int _{0}^{\infty }\|\tilde{g}(t)\|_{\infty }{\mathrm{d}}t\). Hence,
where \(\tilde{G}(t)=e^{\mu t}G(t)\) for all \(t\geq 0\). By (B.3), \(l\|\tilde{G}\|_{L^{1}}<1\), and so
where
As \(\|\tilde{y}\|_{L^{1}(0,t)}\leq \|c\|_{\infty }e^{\mu }h\|\xi ^{1}\|_{L^{1}(-h,0)}\) for all \(t\in [0,h]\), we arrive at
where \(\kappa :=\kappa _{1}+(1+\|c\|_{\infty }e^{\mu h})\kappa _{2}\).
Finally, to derive an estimate for \(x(t)\), we use again (B.2) to obtain
The claim now follows with \(\gamma =\mu \) from a straightforward argument based on (B.5)–(B.7) and the fact that \(\|\tilde{v}\|_{L^{1}(0,t)}\leq \mu ^{-1}e^{\mu t}\|v\|_{L^{\infty }(0,t)}\).
(3) Assume that \(A\) is Hurwitz and \(l\|G\|_{L^{1}}<1\). Let \(\xi \in M^{1}\), let \(v\in L^{\infty }({\mathbb{R}}_{+},{\mathbb{R}}^{n})\) be such that \(\|v\|_{L^{\infty }(t,\infty )}\to 0\) as \(t\to \infty \) and let \(x\) be the unique solution of (2.3). For \(\tau \geq 0\) we set \(x^{\tau }(t)=x(t+\tau )\), \(v^{\tau }(t)=v(t+\tau )\) and \(N^{\tau }(t,z)=N(t+\tau ,z)\) for all \(t\geq 0\). By (2.4), for every \(\tau \geq 0\),
It is clear that \(x^{\tau }\) solves the initial-value problem (2.3) with \(N\), \(\xi \) and \(v\) replaced by \(N^{\tau }\), \((x(\tau ),x_{\tau })\) and \(v^{\tau }\), respectively. Hence, invoking statement (2), there exist \(\Gamma \geq 1\) and \(\gamma >0\) such that, for all \(\tau \geq 0\),
As \(x\) is bounded on \([0,\infty )\), we have that \(\sigma :=\sup _{t\geq 0}\|(x(t),x_{t})\|_{M^{1}}<\infty \), and so, for \(\tau \geq 0\),
Since \(\|v\|_{L^{\infty }(\tau ,\infty )}\to 0\) as \(\tau \to \infty \), we conclude that \(x(t)\to 0\) as \(t\to \infty \). □
Proof of Corollary 2.3
Let \(\tilde{l}>l\) and such that \(\tilde{l}\|G\|_{L^{1}}<1\). Then, by (2.5), there exists \(r>0\) such that
We introduce a modified nonlinearity \(\tilde{N}\) by setting
This nonlinearity satisfies
and we have that
Let \(\xi \in M^{1}\) and \(v\in L^{\infty }_{\mathrm{loc}}({\mathbb{R}}_{+},{\mathbb{R}}^{n})\) and let \(x\) be the corresponding solution of (2.3). Setting \(d(t):=N(t,c^{T}x(t-h))-\tilde{N}(t,c^{T}x(t-h))\) for all \(t\geq 0\), then we have that \(\|d\|_{L^{\infty }}\leq \theta \) and
An application of statement (2) of Proposition 2.2 to the above system yields the claim. □
The following simple lemma was used in the proof of Theorem 4.3.
Lemma B.1
Let \(a>0\), \(\beta >0\) and \(k\in C([0,a],{\mathbb{R}}_{+})\) such that \(k(s)>0\) for all \(s\in [0,a)\). Consider the functional
For every \(\varepsilon >0\), there exists \(\gamma >0\), such that, for all \(w\in L^{\infty }([0,a],{\mathbb{R}}_{+})\) with \(\|w\|_{L^{\infty }}\leq \beta \), we have
Proof
Let \(\varepsilon >0\) and \(w\in L^{\infty }([0,a],{\mathbb{R}}_{+})\) with \(\|w\|_{L^{\infty }}\leq \beta \). Choose \(a_{0}\in (0,a)\) such that \(\beta a_{0}\leq \varepsilon /2\) and set
Since
it follows that
and the claim follows with \(\gamma :=(\nu \varepsilon )/2\). □
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Franco, D., Guiver, C. & Logemann, H. Persistence and Stability for a Class of Forced Positive Nonlinear Delay-Differential Systems. Acta Appl Math 174, 1 (2021). https://doi.org/10.1007/s10440-021-00414-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10440-021-00414-5
Keywords
- Delay-differential systems
- Density-dependent population models
- Environmental forcing
- Forced systems
- Input-to-state stability
- Persistence
- Positive systems
- Semi-global exponential stability