Abstract
In this paper a method to rigorously compute several non trivial solutions of the Gray-Scott reaction-diffusion system defined on a 2-dimensional bounded domain is presented. It is proved existence, within rigorous bounds, of non uniform patterns significantly far from being a perturbation of the homogenous states. As a result, a non local diagram of families that bifurcate from the homogenous states is depicted, also showing coexistence of multiple solutions at the same parameter values. Combining analytical estimates and rigorous computations, the solutions are sought as fixed points of a operator in a suitable Banach space. To address the curse of dimensionality, a variation of the existing technique is presented, necessary to enable successful computations in reasonable time.
Similar content being viewed by others
1 Introduction
Formation and self-organisation of patterns are fascinating phenomena that occur in several natural systems, as for instance in semiconductors, ferroelectric and magnetic materials, in combustion systems, in biological processes and chemical reactions. See [30] for a survey.
Since the seminal work of Turing [28], who first proposed a reaction-diffusion system to account for morphogenesis, systems of reaction-diffusion equations are widely considered to describe and analyse the formation and the dynamics of patterns. A prototype is the Gray-Scott system, a model for the interaction of a pair of reactions involving cubic autocatalysis [12]. It consists in the following reaction-diffusion system
where \(U\) and \(V\) are the concentrations of chemical reactants \(\mathcal{U}\) and \(\mathcal{V}\), \(d_{1}\), \(d_{2}\) are the diffusion coefficients, \(F\) is the feed rate and \((F+\kappa)\) the removal rate of \(\mathcal{V}\).
Experiments and numerical investigation reported by Pearson [24] and in [16, 25] reveal a rich and complex structure in the solutions for the Gray-Scott equation, including self-replicating patterns, oscillating patterns, spots annihilation, irregular patterns, spatio-temporal chaos. Since then, the behaviour and the dynamics of the patterns in the Gray-Scott system has been extensively studied through experimental observations, numerical techniques and analytic approach.
In two dimensional domains, particular solutions like single spot solutions, ring-like solitons and stripe patterns have been found and analysed in [15, 19, 20, 31]. Also, an hybrid analytic-numerical approach is adopted in [6] to detect multi-spot quasi equilibrium patterns.
In this paper analytical theory and rigorous numerics are combined in a computer assisted technique, that allows to successfully treat non-local problems while preserving the mathematical rigorousness. We prove existence, together with precise bounds, of several non homogenous stationary patterns, arranged on continuous branches, for the 2-dimensional Gray-Scott system defined on a bounded domain \(\varOmega\) and with no-flux boundary condition. Because of the extreme difficulty in studying non linear differential equations by purely analytical approach, any new methodology that demonstrates qualitative and quantitative properties of solutions for systems of nonlinear PDEs is a valuable achievement by its own. Moreover, the results of this work can contribute to the interesting discussion concerning the genesis of localised patterns and the underlying mechanisms that drive the transition from one dynamics to another. For instance, they can be useful to understand the self-replicating pattern dynamics, that is, the itinerary process that moves a localised trigger to a stable stationary or oscillating pattern by multiple splitting of the pulses. Attempts to answer these questions are presented in [22, 23]. Looking at the global bifurcation diagram of stationary solutions, in [22] it has been suggested that a hierarchy structure of saddle-node points is responsible for the occurrence of self-replicating pattern dynamics. In [23] the relationship between different bifurcation branches of steady states is considered as a criteria for the onset of spatio-temporal chaos. The spatio-temporal chaotic dynamics emerges by unfolding an itinerant heteroclinic cycle. Also, self-destruction and spots annihilation can be explained as an orbit starting close to an unstable pattern whose unstable manifold is connected to the homogenous state. From these considerations, it is evident that the bifurcation diagram of steady states together with the stability analysis plays a key role in the comprehension of the mechanism behind the complex pattern dynamics.
In order to introduce the results, let us present more in details the system we are dealing with. Following [13], the Gray-Scott system is equivalent to the following
For any choice of \(\lambda\) and \(\gamma\), problem (2) admits a stable uniform stationary solution \((u,v)=(1,0)\) called \(p_{1}\) and, for \(\lambda\geq4\), two branches of uniform stationary solutions denoted by \(p_{2}(\lambda)\) and \(p_{3}(\lambda)\). Local bifurcation analysis predicts the values of \(\gamma\) where families of non-constant stationary solutions bifurcate from the homogeneous states. We investigate various bifurcation branches of non-constant solutions emanating from the homogenous states and the goal is to prove existence of several non constant patterns, providing explicitly the numerical data together with the enclosing bounds.
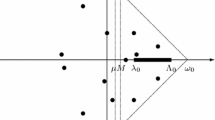
Looking at Fig. 1, we prove the following:
Bifurcation diagrams of rigorously computed non-uniform stationary solutions for the Gray-Scott system (2) on the domain \(\varOmega=[0,1,1]\times[0,0.8]\) and \(\lambda=4.5\). The branches of solutions bifurcate from the homogenous state (a) \(p_{2}(\lambda)\) and (b) \(p_{3}(\lambda)\). The horizontal axis represents the parameter \(\gamma\) and the vertical axis represents the distance, measure with the squared \(L^{2}\)-norm, of the \(v\)-component of the solution from the \(v\)-component of the steady state (Color figure online)
Theorem 1
Let \(\lambda=4.5\) and \(\varOmega=[0, 1.1]\times[0, 0.8]\) be fixed.
-
Any bullet in Fig. 1(a) represents a non-uniform stationary solution for system (2) belonging to branches that bifurcate from the homogenous state \(p_{2}(\lambda)\).
-
Any bullet in Fig. 1(b) represents a non-uniform stationary solution for system (2) belonging to branches that bifurcate from the homogenous state \(p_{3}(\lambda)\).
Clearly, by changing the parameter \(\lambda\) and the size of the rectangular domain \(\varOmega\), many non-constant solutions on different branches can be computed and rigorously validated. Also, most of the families depicted in Fig. 1 can be easily extended.
The computational methods used to prove Theorem 1 has roots in the radii-polynomial technique, introduced in [8] with the aim at solving nonlinear differential problems. In this paper a variant of the computational method is presented. It consists in the introduction of a sharpening parameter that allows to obtain more precise estimates of the nonlinear terms without enlarging the dimension of the finite dimensional approximation. Indeed, using the computational technique in the form it has been developed so far, the computational cost and the time required for the enclosure of a single solution stated in Theorem 1 would be so large as to be practically unfeasible.
The paper is organised as follows. In Sect. 2 we discuss the stationary solutions for system (2) and, for fix \(\lambda\), we find the bifurcation values \(\gamma_{{{\boldsymbol{k}}}}\) for branches of non uniform solutions. Section 3 concerns the radii polynomial technique. First we present the computational method in the general form together with the notion of radii polynomials. Then, in Sect. 3.2 some fundamental formulas for the analytic estimates of the convolution sums are recalled. In Sect. 4 we adapt the computational method to the Gray-Scott system. We rephrase the differential system into an equivalent fix point problem and we introduce the Banach space within which we look for the solutions. Then we write the radii polynomials as they would be without the modifications. In Sect. 4.3 we explain in more details the reason why the radii polynomials technique, so far presented, fails in proving the existence of the solutions we are interested in. In Sect. 4.4 the sharpening parameter is introduced and the new scheme to bound the nonlinear terms is discussed. Finally, in Sect. 5 we are concerned with the computational results.
2 Some Analytical Preliminaries: Bifurcation Values
Stationary patterns of (2) consist in solutions of the elliptic problem
Throughout this paper we denote by \(h_{{{\boldsymbol{k}}}}\) the eigenvalues of
and by \(\phi_{{{\boldsymbol{k}}}}\) the associated eigenfunctions. We restrict our analysis to the case of rectangular domain, \(\varOmega=[0,L _{1}]\times[0,L_{2}]\). Denoting \(x=(z,y)\in\varOmega\), the eigenvalues and eigenfunctions are explicitly given as
for any \({{\boldsymbol{k}}}=(k^{(1)},k^{(2)})\in\mathbb{N}^{2}\).
For any value of \(\lambda\) and \(\gamma\), system (3) admits the uniform state \((u,v)=(1,0)\), denoted by \(p_{1}\). At \(\lambda=4\) a bifurcation occurs and two branches of uniform solutions are created. The set of uniform solutions is the following:
Remark 1
Note that for any uniform solution \((u_{*},v_{*})\), except \(p_{1}\), it holds \(u_{*}v_{*}=1\).
For each \(\lambda>4\) we now detect the values of \(\gamma\) where families of not uniform solutions bifurcate from the homogenous state. Denote by \((u_{*}, v_{*})\) any of the constant stationary solutions \(p_{2}(\lambda)\), \(p_{3}(\lambda)\). For any \({{\boldsymbol{k}}}\in \mathbb{N}^{2}\setminus\{(0,0)\}\), define
a perturbation of the steady state in the direction of the eigenfunction \(\phi_{{{\boldsymbol{k}}}}\). Following the standard bifurcation theory, a bifurcation occurs at value \(\gamma_{{{\boldsymbol{k}}}}\) if for any \(\varepsilon\) small enough it exists a solution for (3) of the form \((u_{{{\boldsymbol{k}}}}(\varepsilon ),v_{{{\boldsymbol{k}}}}(\varepsilon); \gamma(\varepsilon))\), being \(\gamma(\varepsilon)=\gamma_{{{\boldsymbol{k}}}}+\varepsilon\gamma ' + o(\varepsilon)\).
Inserting \((u_{{{\boldsymbol{k}}}}(\varepsilon), v_{{{\boldsymbol{k}}}}( \varepsilon))\) and \(\gamma(\varepsilon)\) into the elliptic problem (3) and using the fact that \((u_{*},v_{*})\) is a solution for any \(\gamma\), we obtain the following
Neglecting the infinitesimal terms, for Remark 1, it remains to solve the system
whose solution is given by
and
We summarise the result in the next lemma.
Lemma 1
For any \({{\boldsymbol{k}}}\in\mathbb{N}^{2}\setminus\{(0,0)\}\), a branch of non-constant stationary solutions for (2) bifurcates from the uniform solution \((u_{*}, v_{*})\) at value \(\gamma_{{{\boldsymbol{k}}}}\) given in (7). The proper perturbation to be applied to the steady state \((u_{*},v_{*})\) is \((a\phi_{{{\boldsymbol{k}}}},b\phi_{{{\boldsymbol{k}}}})\) where \(a\), \(b\) solve (6).
3 The Computational Method
The method here presented is one of the so called verification methods [27]. Suppose we are looking for solutions of \(f(x)=0\) where \(f\) is defined in some Banach space \((X,\|\cdot\|_{X})\). The goal of a verification methods is to prove the existence of a genuine solution \(x^{*}\) of \(f(x)=0\) in the neighbourhood of a numerical approximate solution \(\bar{x}\), providing explicit and rigorous bounds for \(\|x^{*}-\bar{x}\|_{X}\). In this paper we adopt the radii polynomial technique that relies on the Banach fixed point theorem. In the last ten years the radii polynomial technique has been exploited to study a variety of problems in areas ranging from, but not restricted to, ODEs, PDEs, delay differential equations and dynamical systems. See for instance [1, 3–5, 8, 10, 17] and reference therein. In [29] the radii polynomial technique has been applied to the 1-dimensional Gray-Scott system to establish the existence of symmetric homoclinic orbits to the steady state \(p_{1}=(1,0)\). More recently, in [1] bifurcation branches of solutions for a system of one dimensional reaction diffusion equations have been rigorously validated using a similar technique.
Of course there are many other methods for computer assisted and rigorous computational study of differential equations, based for instance on topological arguments like the Conley index theory, covering relations with cone conditions, the Shauder fixed point theorem. We refer to [2, 7, 14, 21, 33] and the references therein for a more detailed discussion of topological tools applied to rigorous computations.
Before presenting the technique, let us fix some notation. Boldface is used to denote multi-indices as \(\boldsymbol{k}=(k^{(1)},\dots, k ^{(d)})\in\mathbb{Z}^{d}\). When applied to multi-indices, the absolute value \(|\cdot|\) acts component-wise, \(|\boldsymbol{k}|:=(|k^{(1)}|, \dots,|k^{(d)}|)\). Inequality in between multi-indices is intended component-wise, that is for \(\boldsymbol{k},\boldsymbol{n}\in \mathbb{Z}^{d}\), \(\boldsymbol{k}<\boldsymbol{n}\) means \(k^{(j)}< n^{(j)}\) for all \(j=1,\dots, d\). The same for ≥,≤,>. In the following we will introduce the multi-indices \(\boldsymbol{m}\), \(\overline{\boldsymbol{M}}\) and \(\boldsymbol{M}\) all in \(\mathbb{N} ^{d}\), respectively called finite dimensional parameter, FFT dimension parameter and computational parameter, satisfying \(\boldsymbol{m}\leq\overline{\boldsymbol{M}}\leq\boldsymbol{M}\). Associated to them, we define the set of indices \(F_{\boldsymbol{m}}\), \(F_{\overline{\boldsymbol{M}}}\), \(F_{\boldsymbol{M}}\) as \(F_{ \boldsymbol{m}}:=\{ \boldsymbol{k}\in\mathbb{Z}^{d} \, :\, | \boldsymbol{k}|<\boldsymbol{m}\}\) and similarly for the others. Note that the difference \(F_{\boldsymbol{M}}\setminus F_{\boldsymbol{m}}= \{\boldsymbol{k}\in\mathbb{Z}^{d}\,|\, \exists j : m^{(j)}\leq|k ^{(j)}| < M^{(j)} \}\) contains all the indices having at least one (at not necessarily all) component \(k^{(j)}\) satisfying \(m^{(j)}\leq|k ^{(j)}|< M^{(j)}\). The same remark applies to \(F_{\boldsymbol{M}} \setminus F_{\overline{\boldsymbol{M}}}\) and \(F_{\overline{ \boldsymbol{M}}}\setminus F_{\boldsymbol{m}}\). Given a sequence \(x=\{ x_{\boldsymbol{k}}\}_{\boldsymbol{k}\in\mathbb{Z}^{d}}\), we denote \(x_{F_{\boldsymbol{m}}}=\{x_{\boldsymbol{k}}\}_{\boldsymbol{k} \in F_{\boldsymbol{m}}}\) and \(x_{I_{\boldsymbol{m}}}=\{x_{ \boldsymbol{k}}\}_{\boldsymbol{k}\notin F_{\boldsymbol{m}}}\).
3.1 Overview of the Radii Polynomial Method
We describe the technique in the context of solving the PDE
defined on a bounded domain \(\varOmega\subset\mathbb{R}^{d}\), subjected to prescribed boundary conditions. Here \(L:D(L)\subset H\to H\) is a linear operator densely defined on a Hilbert space \(H\) and \(p\) is the degree of nonlinearity, \(c_{p}\in\mathbb{R}\).
The first step of the method consists in writing an equivalent problem
defined on a suitable Banach space, so that the zeros of \(f(x)\) correspond univocally to solutions of (8). Assume that the Hilbert space \(H\) admits an orthogonal basis formed by the eigenfunctions of \(L(u)\), say \(\{\phi_{\boldsymbol{k}}\}_{ \boldsymbol{k}}\) with eigenvalues \(\{h_{\boldsymbol{k}}\}_{ \boldsymbol{k}}\) and assume that the domain of \(L\) is given by
By expanding (8) on the basis \(\{\phi_{\boldsymbol{k}}\} _{\boldsymbol{k}}\), it follows that the solutions of (8) correspond to the zeros of \(f(x)\), \(x=\{x_{\boldsymbol{k}}\}_{ \boldsymbol{k}}\), given by
If the eigenfunctions basis \(\{\phi_{\boldsymbol{k}}\}_{ \boldsymbol{k}}\) is of the form of a Fourier basis, as it will be in our case, the inner product \(\langle u^{p},\phi_{\boldsymbol{k}}\rangle _{H}\) is equal to convolution products of the Fourier coefficients \(\{x_{{{\boldsymbol{k}}}} \}_{{{\boldsymbol{k}}}}\), that is
For a vector \(\boldsymbol{s}=(s^{(1)},\dots, s^{(d)})\in\mathbb{N} ^{d}\), let the weight \(\omega_{\boldsymbol{k}}^{\boldsymbol{s}}\) be defined as
Define the \(\boldsymbol{s}\)-norm of a sequence \(x=\{x_{\boldsymbol{k}} \}_{\boldsymbol{k}}\) as \(\|x\|_{\boldsymbol{s}}:= \sup_{\boldsymbol{k}\in\mathbb{Z}^{d}}\{\omega_{\boldsymbol{k}}^{ \boldsymbol{s}}|x_{\boldsymbol{k}}| \}\) and introduce the Banach space
The space \(X^{\boldsymbol{s}}\) is the space of sequences algebraically decaying, with decay rate \(\boldsymbol{s}\), and it is the space where we look for solutions of \(f(x)=0\). This choice is motivated by the fact that any solution \(u\) of the PDE (8) is expected to be smooth and the sequence of Fourier coefficients of a smooth function decays exponentially fast to zero. Therefore, it is reasonable to look for the solution \(\{x_{\boldsymbol{k}}\}_{\boldsymbol{k}}\) in the space of sequences that decay at least as fast as \(\{\frac{1}{ \omega^{\boldsymbol{s}}_{\boldsymbol{k}}}\}_{\boldsymbol{k}\in \mathbb{Z}^{d}}\), \(\boldsymbol{s}\geq2\).
Denote by \(B(x,r):=\{y\in X^{\boldsymbol{s}}\, : \, \|y-x\|_{ \boldsymbol{s}}\leq r\}\) the ball in \(X^{\boldsymbol{s}}\) of radius \(r\) centred at \(x\).
The proof of the existence of solutions for \(f(x)=0\) relays on a contraction mapping argument applied to an operator \(T\), defined below, whose fixed points are in one to one correspondence with the zeros of \(f\). The operator \(T\) depends on the Frechet derivative of \(f\) evaluated at a numerical approximate solutions \(\bar{x}\).
For a choice of \(\boldsymbol{m}=(m^{(1)},\dots, m^{(d)})\in \mathbb{N}^{d}\), denote by \(f^{(\boldsymbol{m})}\) the finite-dimensional system \(f^{(\boldsymbol{m})}:=\{f_{\boldsymbol{k}}^{(\boldsymbol{m})} \}_{\boldsymbol{k}\in F_{\boldsymbol{m}}} \) where, for any \(\boldsymbol{k}\in F_{\boldsymbol{m}}\)
Let \(\bar{x}_{F_{\boldsymbol{m}}}\) be a numerical solution for \(f^{(\boldsymbol{m})}(x)=0\) and denote by \(\bar{x}\) the embedding of \(\bar{x}_{F_{\boldsymbol{m}}}\) into \(X^{\boldsymbol{s}}\), i.e. \(\bar{x}=(\bar{x}_{F_{\boldsymbol{m}}},0_{I_{\boldsymbol{m}}})\). Let \(Df^{(\boldsymbol{m})}\) be the Jacobian matrix of \(f^{(\boldsymbol{m})}(x)\) at \(\bar{x}_{F_{\boldsymbol{m}}}\) and compute \(J^{-1}_{\boldsymbol{m}}\) a non singular approximate inverse of \(Df^{(\boldsymbol{m})}\). Then, define \(J^{-1}\) the operator that maps \(x=\{ x_{\boldsymbol{k}}\}_{\boldsymbol{k}}\) to
By construction, \(J^{-1}\) is an approximate inverse of \(Df(\bar{x})\). Note that for the tail part, that is for \(\boldsymbol{k}\notin F_{ \boldsymbol{m}}\), the operator \(J^{-1}\) does not rely on numerical computations, rather it is defined taking into account the linear contribution of \(f_{\boldsymbol{k}}\) only. The fixed point operator is defined as \(T:X^{\boldsymbol{s}}\to X^{\boldsymbol{s}} \)
Clearly, since \(J^{-1}\) is injective, fixed points of \(T\) correspond to zeros of \(f(x)\).
The goal of the technique is to detect a ball \(B(\bar{x},r)\subset X ^{\boldsymbol{s}}\) within which \(T\) is a contraction. That is done through the notion of the radii polynomials, a finite set of inequalities in the variable \(r\), the verification of which implies that \(T\) is a contraction on some ball \(B(\bar{x} ,r)\). They are defined as combination of the following bounds.
Let \(\{Y_{\boldsymbol{k}}\}_{\boldsymbol{k}}\) and \(\{Z_{ \boldsymbol{k}}(r)\}_{\boldsymbol{k}}\) be two sequences such that, for any \(\boldsymbol{k}\in\mathbb{Z}^{d}\),
Furthermore, for a choice of a computational parameter \(\boldsymbol{M}=(M^{(1)},\dots,M^{(d)})\), assume that \(Y_{ \boldsymbol{k}}=0\) for any \({{\boldsymbol{k}}}\notin F_{ \boldsymbol{M}}\) and it exists \(\tilde{Z}_{\boldsymbol{M}}(r)\) such that
Definition 1
Define the finite radii polynomials \(\{p_{\boldsymbol{k}}(r)\}_{ \boldsymbol{k}\in F_{\boldsymbol{M}}}\) by
and the tail radii polynomial by
Lemma 2
If there exists \(r>0\) so that \(p_{\boldsymbol{k}}(r)<0\) for all \(\boldsymbol{k}\in F_{\boldsymbol{M}}\) and \(\tilde{p}_{\boldsymbol{M}}(r)<0\), then there is an unique \(x\in B( \bar{x},r)\) such that \(f(x)=0\).
Proof
The result follows as an application of the Banach fixed point theorem on the operator \(T\). See for instance [8, 32]. □
Before discussing some analytical estimates used in the construction of the bounds \(Y_{{{\boldsymbol{k}}}}\) and \(Z_{{{\boldsymbol{k}}}}\) let us close this section with a remark.
Remark 2
-
The method requires that the eigenvalues and eigenfunctions of the linear operator \(L(u)\) are explicitly known. That is the reason why we consider only rectangular domain \(\varOmega\) with Neumann boundary conditions. However, only few and trivial modifications are required if periodic boundary conditions are posed.
-
The fact that the polynomial nonlinearity is transformed into convolution sums is a peculiarity of the exponential function basis. When a different complete function basis is chosen the polynomial \(u^{p}\) may be translated in something similar to the convolution sum, as in the case of the Chebyshev function basis (that are nothing more that Fourier series in disguise [18]), or in something completely different as in the case of Hermite functions.
3.2 Analytical Estimates of the Convolution Sums
One of the fundamental steps of the technique is the definition of the bounds \(Y\) and \(Z\) satisfying the inequalities (10) and (11). In the construction of these bounds it is required the computation of several convolution sums of the form
and sharp estimates for convolutions series
A deep and systematic analysis of the latter series is done in [9], where analytical estimates have been proved for any convolutions terms.
The former one (12) is a finite sum and the Fast Fourier Transform (FFT) can be used to faster the computation. Nevertheless, the computational time dramatically increases as far as \(\boldsymbol{M}\), and in particular the dimension \(d\), increase. Moreover, aiming at a rigorous enclosure, these operations must be performed in interval arithmetics regime, hence requiring an even larger computational resources. For instance, if \(d=3\) and \(M=200\), the rigorous computation of (12) involves computing the FFT of sequences of size \(10^{9}\), that is a serious computational task.
These complications and in particular the curse of dimensionality have been addressed in [11]. In that work the authors improved the analytical estimates of [9] and introduced the FFT parameter \(\overline{\boldsymbol{M}}\) with the aim of reducing the computational cost required to enclose the solution of the finite sum (12). For convenience, we report the results that will be used in the sequel of this paper. The detailed construction of the various parameters is given in the Appendix.
The first estimate concerns the upper bound of the convolution series (13) when the indices are free to move in the full set \(\mathbb{Z}^{d}\).
Lemma 3
Let \(\alpha_{\boldsymbol{k}}^{(n)}\) be defined as in (33). Then, for any \(\boldsymbol{k}\in\mathbb{Z}^{d}\),
Proof
See Lemma 2.1 in [9]. □
Now, we consider the case when some of the indices are restricted to take value outside a certain set. Suppose \(\overline{\boldsymbol{M}}=( \overline{M}^{(1)},\dots, \overline{M}^{(d)})\) has be defined so that \(\overline{M}^{(j)}\geq6\) and \(\boldsymbol{M}\geq\overline{ \boldsymbol{M}}\). The notation \(\{\boldsymbol{k}_{1},\dots, \boldsymbol{k}_{\ell+1}\}\not\subset F_{\overline{\boldsymbol{M}}}\) means that at least one of the \(\boldsymbol{k}_{j}\) is not in \(F_{\overline{\boldsymbol{M}}}\). Such a set corresponds to the complement of \(\{\boldsymbol{k}_{1},\dots,\boldsymbol{k}_{\ell+1}: \boldsymbol{k}_{j}\in F_{\overline{\boldsymbol{M}}}\}\).
Lemma 4
Let \(\varepsilon_{\boldsymbol{k}}^{(n)}\) be defined as in (35). For any \(\boldsymbol{k}\in F_{\overline{ \boldsymbol{M}}}\) and \(\ell=0,\dots, n-1\)
Proof
See Lemma 2.2 in [9]. □
4 The Radii Polynomials for the Enclosure of Stationary Solutions of the Gray-Scott System
In this section we apply the technique, presented in Sect. 3.1, to the problem of enclosing non constant solutions of the Gray-Scott system (3). In Sect. 4.3 we perform an a priori analysis of the resulting polynomials and we realise that the presence of \(\overline{ \boldsymbol{M}}\), although important, is not sufficient to assure successful computation of the solutions for the Gray-Scott equation in the parameter range we are interested in. Hence, in Sect. 4.4 the new approach for the definition of the \(Z\) bound is presented.
4.1 Algebraic Formulation in Banach Space
For the reader’s convenience, let us rewrite system (3)
We consider the domain \(\varOmega=[0,L_{1}]\times[0,L_{2}]\), \((z,y)\in\varOmega\), and look for solutions of (3) in the form
where \(\mathbb{Z}^{2}_{*}:=\mathbb{Z}^{2}\setminus\{(0,0)\}\), \(\phi_{{{\boldsymbol{k}}}}(z,y)\) is given in (5) and
Note that:
-
(i)
The sequence \(\{\phi_{\boldsymbol{k}}\}_{\boldsymbol{k} \in\mathbb{N}^{2}}\) is a complete basis for \(\{ u\in L^{2}(\varOmega) \}\cap\{\partial_{\nu}u =0, (z,y)\in\partial\varOmega\}\). Therefore in the expansion of the function \(u\) and \(v\) (14) it would be enough to consider \(\boldsymbol{k}\in\mathbb{N}^{2}\). However, the equivalent choice \(\boldsymbol{k}\in\mathbb{Z}^{2}\) together with the symmetry conditions (15) allows to easily expand the product \(uv^{2}\).
-
(ii)
The boundary conditions in (3) are automatically satisfied by any \(u\), \(v\) given in (14).
Again from (5), we remind that
Since
to solve system (3) it corresponds to solve the infinite dimensional algebraic system
where
In each \(g_{\boldsymbol{k}}\) we replace the second line with the sum of the first and the second and we obtain the equivalent system
From the second equation it follows
thus, plugging \(v_{\boldsymbol{k}}\) into the first equation, we end up with a system of equations in the variables \(\{u_{\boldsymbol{k}}\} _{\boldsymbol{k}}\) only. However, to easy the notation, we continue to use the variable \(v_{\boldsymbol{k}}\), having in mind that any \(v_{\boldsymbol{k}}\) is function of \(u_{\boldsymbol{k}}\). Let us define
and, given a sequence \(x=\{x_{\boldsymbol{k}}\}_{\boldsymbol{k}}\), we adopt the notation \(qx\) for the sequence \(qx=\{q_{\boldsymbol{k}}x _{\boldsymbol{k}}\}_{\boldsymbol{k}}\). In particular \(v=qu\). Also, introduce
Remark 3
The values of the parameters \(\lambda\) and \(\gamma\) of interest in this work are such that \(\lambda\gamma<1\). In this situation it holds \(|q_{{{\boldsymbol{k}}}}|\leq\hat{q}\) for any \({{\boldsymbol{k}}} \in\mathbb{Z}^{2}\).
The system we need to solve is
where
in the unknown \(u=\{u_{\boldsymbol{k}}\}_{\boldsymbol{k}\in \mathbb{Z}^{2}}\). We look for solutions in the Banach space
\(\boldsymbol{s}\geq2\), where the \(\boldsymbol{s}\)-norm is the same as in Sect. 3.1. Introduce
to denote the coefficients of the linear terms in \(f_{{{\boldsymbol{k}}}}\).
4.2 Construction of the Polynomial Bounds
To avoid unnecessary verbosity, most of the technicalities are skipped, rather we report the explicit definition of the bounds \(Y\) and \(Z\). For more details we refer to [11].
Choose the finite dimensional parameter \({{\boldsymbol{m}}}\), the computational parameter \(\boldsymbol{M}\) so that \(\boldsymbol{M} \geq3(\boldsymbol{m}-1)-1\) and the FFT dimension parameter \(\overline{\boldsymbol{M}}\) so that \(\boldsymbol{m}\leq\overline{ \boldsymbol{M}}<\boldsymbol{M}\).
Suppose that a numerical solution \(\bar{u}_{F_{\boldsymbol{m}}}\) is computed so that \(f^{(\boldsymbol{m})}(\bar{u}_{F_{\boldsymbol{m}}}) \approx0\). Denote by \(\bar{u}\) the embedding of \(\bar{u}_{F_{ \boldsymbol{m}}}\) into \(X\), i.e. \(\bar{u}=(\bar{u}_{F_{\boldsymbol{m}}},0_{I _{\boldsymbol{m}}})\), and define \(\bar{v}=q\bar{u}\). Compute the finite dimensional matrix \(J_{\boldsymbol{m}}^{-1}\) and the infinite dimensional operator \(J^{-1}\) as in (9). For this, it is convenient to report the Jacobian matrix \(Df(u)\). Having in mind that the \(v_{{{\boldsymbol{k}}}}\) is function of \(u_{{{\boldsymbol{k}}}}\), it holds
The construction of \(Y_{\boldsymbol{k}}\) readily follows from the definition (10):
The last line is due to the choice of \({\boldsymbol{M}}\), for which \((\bar{u}*\bar{v}*\bar{v})_{\boldsymbol{k}}=0\) for any \({{\boldsymbol{k}}} \notin F_{{\boldsymbol{M}}}\).
The polynomial \(Z_{\boldsymbol{k}}(r)\) is defined as
For each \({{\boldsymbol{k}}}\in F_{\boldsymbol{m}}\) the bound \(Z^{(0)}_{\boldsymbol{k}}\) is defined as
and it is rigorously computed, since only a finite number of computations are involved.
Combining rigorous computation and the analytical estimates, all the other bounds can be defined as:
and
Define
so that \(\tilde{\mu}_{\boldsymbol{M}}\leq|\mu_{\boldsymbol{k}}|\) for any \(\boldsymbol{k}\notin F_{\boldsymbol{M}}\).
The tail coefficient (11) is given by
with \(\tilde{Z}^{(j)}_{\boldsymbol{M}}\geq Z_{\boldsymbol{k}}^{(j)} \omega_{\boldsymbol{k}}^{\boldsymbol{s}}\) for any \(\boldsymbol{k} \notin F_{\boldsymbol{M}}\). It is enough to define
with \(\tilde{\alpha}_{\boldsymbol{M}}^{(3)}\) given in (34).
4.3 A Priori Analysis of the Radii Polynomials
According to Lemma 2, the existence of a stationary solution for the Gray-Scott equation is assured if the radii polynomials are all negative for some positive value of \(r\). A careful analysis of the coefficients of the polynomials clarifies under which conditions the computation will be successful and feasible.
For \(\boldsymbol{k}\in F_{\boldsymbol{M}}\) the polynomial \(p_{ \boldsymbol{k}}(r)\) is of the form \(p_{\boldsymbol{k}}(r)=a_{0}+a_{1}r+a _{2}r^{2}+a_{3}r^{3}\). The constant term \(a_{0}\) is always positive and it is related to the accuracy of the numerical solution. It can be lowered if a better approximate solution is produced, for instance by increasing the finite dimensional projection \(\boldsymbol{m}\).
Also \(a_{2}\) and \(a_{3}\) are positive and they are related to the rate of expansion of the operator \(T\) due to superlinear terms in the function \(f(x)\). A necessary condition for the polynomial \(p_{ \boldsymbol{k}}(r)\) to be negative somewhere is that \(a_{1}\) is negative. Looking to the case \(\boldsymbol{k}\in F_{\boldsymbol{M}} \setminus F_{\boldsymbol{m}}\), the coefficient \(a_{1}\) is of the form \(a_{1}=\frac{1}{|\mu_{\boldsymbol{k}}|}Z_{\boldsymbol{k}}^{(1)}-\frac{1}{ \omega_{\boldsymbol{k}}^{\boldsymbol{s}}}\). Since \(Z_{\boldsymbol{k}} ^{(1)}\) decays like \(C\omega^{-\boldsymbol{s}}_{\boldsymbol{k}}\) (because of the properties of the convolutions), it is enough that \(|\mu_{\boldsymbol{k}}|\) is increasing to ensure, for \(\boldsymbol{m}\) large enough, that \(a_{1}\) is negative. The coefficients \(\mu_{\boldsymbol{k}}\mbox{ s}\) are related to the eigenvalues of the linear operator in the PDE. In particular, high order linear operators yield larger \(\mu_{\boldsymbol{k}}\) and enhance the contractivity of \(T\), that translates into a smaller value for \(a_{1}\) and a possible choice of smaller \(\boldsymbol{m}\). Besides that preliminary theoretical argument, a crucial issue is the feasibility of the computation. Indeed, it is necessary to choose the various parameters \(\boldsymbol{m}\), \(\boldsymbol{M}\) and \(\overline{\boldsymbol{M}}\) relatively small, so to abet practical computation. In particular, since the convolution product is the most costly computation, and it appears several times in (20), it is fundamental to keep \(\overline{\boldsymbol{M}}\) as small as possible.
Let us now inspect how the growth rate of \(\mu_{\boldsymbol{k}}\) influences the choice of \(\overline{\boldsymbol{M}}\) in the context of the PDE under investigation. Looking at the polynomial \(p_{ \boldsymbol{k}}(r)\) with \(\boldsymbol{k}\in F_{\boldsymbol{M}}\setminus F_{\overline{\boldsymbol{M}}}\), we realise that
must be negative. The parameter \(\overline{\boldsymbol{M}}\) must be chosen large enough so that \(\mu_{\boldsymbol{k}}\) remains reasonable larger than \(\alpha^{(3)}_{\boldsymbol{k}}\) for any \(\boldsymbol{k} \notin F_{\overline{\boldsymbol{M}}}\). Again, as a general statement, a larger growth for \(\mu_{\boldsymbol{k}}\) allows a smaller choice of \(\overline{\boldsymbol{M}}\). For two-dimensional PDE problems the coefficient \(\alpha^{(3)}_{\boldsymbol{k}}\) rapidly grows to large values, hence the parameter \(\overline{\boldsymbol{M}}\) needs to be selected quite large. Our situation is even worst due to the presence of \(\hat{q}=\gamma^{-1}\) that multiply the effect of \(\alpha^{(3)} _{\boldsymbol{k}}\). To have a quantitative idea, consider the family of solutions labelled with \((0,3)\) in Fig. 1(a). It bifurcates at the value \(\gamma\approx0.0087\). Taking into account all the constant factors and the \(\boldsymbol{s}\)-norm of \(\bar{u}\) and \(\bar{v}\) (\(\boldsymbol{s}=(2,2)\)) it is necessary to choose \(\overline{\boldsymbol{M}}=(\overline{M}_{1},\overline{M}_{2})\) with both \(\overline{M}_{1}\), \(\overline{M}_{2}\) larger than 250. To perform cubic convolutions of sequences with around \((500)^{2}\) terms is extremely computationally expensive. We underline that it is the combination of the high dimensionality of the problem and the presence of a small constant \(\gamma\) in front of the linear term that makes the computation of the radii polynomials not affordable. Indeed the method was successfully applied in [9] to prove equilibria for the \(2D\) and \(3D\) Cahn-Hilliard equation with constant factor in the range \(\gamma\approx[0.05, 0.1]\) and \(\gamma\approx[0.3,1]\) respectively. Rather, in [11] it is proven existence of solutions for the Allen-Cahn equation with much smaller factor \(\gamma\approx0.001\) but only for the one dimensional case.
In conclusion, we are not claiming that the technique fails in proving the solutions we are interested in, but that, just for one tentative enclosure, one needs to perform a number of computations so large that can not be addressed by a standard computer in reasonable time. Therefore, to the goal of proving Theorem 1, the method so far described is not feasible. To overcome these hurdles, in the next section we introduce some modifications.
4.4 New Definition of the Bound \(Z^{(j)}_{\boldsymbol{k}}\) and \(\tilde{Z}_{\boldsymbol{M}}\)
The following procedure aims at sharpening those terms in \(Z^{(1)} _{\boldsymbol{k}}\), \(Z^{(2)}_{\boldsymbol{k}}\) and \(\tilde{Z}_{ \boldsymbol{M}}\) that involve \(\hat{q}\). At first, we are concerned with the factors \(\hat{q}\|\bar{u}\|_{\boldsymbol{s}}\|\bar{v}\|_{ \boldsymbol{s}}\varepsilon_{\boldsymbol{k}}^{(3)}\), \(\hat{q}\|\bar{u}\|_{ \boldsymbol{s}}\|\bar{v}\|_{\boldsymbol{s}}\frac{\alpha_{ \boldsymbol{k}}^{(3)}}{\omega_{\boldsymbol{k}}^{\boldsymbol{s}}}\) appearing in \(Z^{(1)}_{\boldsymbol{k}}\). Although it was not said explicitly, the role of these terms is to provide a bound for the series
and
The first is obtained applying Lemma 4 and the uniform estimates \(|\bar{u}_{\boldsymbol{k}}|\leq\|\bar{u}\|_{\boldsymbol{s}} \omega_{\boldsymbol{k}}^{-\boldsymbol{s}}\), \(|\bar{v}_{\boldsymbol{k}}| \leq\|\bar{v}\|_{\boldsymbol{s}}\omega_{\boldsymbol{k}}^{- \boldsymbol{s}}\) and \(|q_{\boldsymbol{k}_{3}}|\leq\hat{q}\). Similarly, the second bound has been defined applying Lemma 3.
Rather than uniformly estimate each coefficient \(|\bar{u}_{ \boldsymbol{k}}|\), \(|\bar{v}_{\boldsymbol{k}}|\) as done above, we can separate in the series (22) the significative contributions from the smaller one. Indeed, it could be the case that few of the \(\bar{u}_{\boldsymbol{k}}\)’s and \(\bar{v}_{\boldsymbol{k}}\)’s are large, while the others are extremely small. Such a behaviour is expectable, for instance, when the aimed solution belongs to a branch bifurcating from the constant state. Typically, in this situation, only one mode is dominating.
For a given \(\epsilon\), let us define
We refer to \(\epsilon\) as the sharpening parameter and we assume that \(\epsilon<\min\{ \|\bar{u}\|_{\boldsymbol{s}},\|\bar{v}\|_{ \boldsymbol{s}}\}\) so that both \(F_{\boldsymbol{m}}(\bar{u},\epsilon )\), \(F_{\boldsymbol{m}}(\bar{v},\epsilon)\) are not empty. They are clearly finite, being subsets of \(F_{{{\boldsymbol{m}}}}\).
The series (22) is decomposed into
The effect of the sharpening parameter is twofold. First, it allows to isolate the main contribution of the series, given by the first sum on the right hand side of (25) that will be rigorously computed. All the others sums are uniformly bounded by means of the bound \(\varepsilon^{(3)}_{\boldsymbol{k}}\), see Lemma 4. We note that anytime the index \(|\boldsymbol{k}_{1}|\) ranges outside \(F_{\boldsymbol{m}}(\bar{u},\epsilon)\) (resp. \(|\boldsymbol{k}_{2}|\) ranges outside \(F_{\boldsymbol{m}}(\bar{v},\epsilon)\)) it holds \(|\bar{u}_{\boldsymbol{k}_{1}}|\leq\epsilon\omega^{-\boldsymbol{s}} _{\boldsymbol{k}_{1}}\) (resp. \(|\bar{v}_{\boldsymbol{k}_{2}}|\leq \epsilon\omega^{-\boldsymbol{s}}_{\boldsymbol{k}_{2}}\)). The last estimate is a much sharper than \(|\bar{u}_{\boldsymbol{k}}|\leq\| \bar{u}\|_{\boldsymbol{s}}\omega_{\boldsymbol{k}}^{-\boldsymbol{s}}\) previously adopted.
Explicitly, we obtain
For the series (23) the same strategy and Lemma 3 lead to
The advantage of this approach is to enfeeble the effect of \(\gamma^{-1}\) hidden in \(\hat{q}\). On the other side we have to calculate one more sum at any stage, requiring further computational time. However, if the mass of \(\bar{u}\) is concentrated in few Fourier coefficients, such a computation is pretty fast. Inserting these newly defined bounds, we redefine \(Z^{(1)}_{\boldsymbol{k}}\) by replacing in (20)
Concerning the bound \(Z^{(2)}_{\boldsymbol{k}}\), we aim at replacing the terms \(6\|\bar{v}\|_{\boldsymbol{s}}\hat{q}\varepsilon_{ \boldsymbol{k}}^{(3)}\), \(3\hat{q} \|\bar{v}\|_{\boldsymbol{s}}\frac{ \alpha_{\boldsymbol{k}}^{(3)}}{\omega_{\boldsymbol{k}}^{ \boldsymbol{s}}}\), and similarly the terms \(2\|\bar{u}\|_{ \boldsymbol{s}}\hat{q}^{2}\varepsilon_{\boldsymbol{k}}^{(3)}\), \(\| \bar{u}\|_{\boldsymbol{s}}\hat{q}^{2}\frac{\alpha_{\boldsymbol{k}} ^{(3)}}{\omega_{\boldsymbol{k}}^{\boldsymbol{s}}}\). The former are defined so that
Arguing as before, i.e. collecting the largest contributions in the series, and using the bound \(q_{\boldsymbol{k}}\leq\hat{q}\) and Lemma 4, we write
Similarly, the same procedure provides bounds for the second of (26) and for the terms \(2\|\bar{u}\|_{\boldsymbol{s}} \hat{q}^{2}\varepsilon_{\boldsymbol{k}}^{(3)}\), \(\|\bar{u}\|_{ \boldsymbol{s}}\hat{q}^{2}\frac{\alpha_{\boldsymbol{k}}^{(3)}}{ \omega_{\boldsymbol{k}}^{\boldsymbol{s}}}\). We omit the details. Collecting all the terms, we reformulate
Since the sequence \(Z^{(3)}_{\boldsymbol{k}}\) does not involve \(\bar{u}_{\boldsymbol{k}}\), \(\bar{v}_{\boldsymbol{k}}\), we keep the same \(Z^{(3)}_{\boldsymbol{k}}\) bounds as reported before.
It remains to define the tail bound \(\tilde{Z}_{\boldsymbol{M}}\). By definition, we have to find a constant \(\tilde{Z}_{\boldsymbol{M}} ^{(1)}\) so that
For \(\boldsymbol{k}\notin F_{\boldsymbol{M}}\), \(Z_{\boldsymbol{k}} ^{(1)}\) is now given by
According to [9] the last two terms in (28) can be easily bounded in terms of \(\tilde{\alpha}^{(3)}_{\boldsymbol{M}}\) given in (34). The first one is less than \(2\hat{q} S _{\boldsymbol{k}}\) where
Having in mind that \(\boldsymbol{k}=(k^{(1)},k^{(2)})\), \(\boldsymbol{k}_{1}=(k_{1}^{(1)},k_{1}^{(2)}), \boldsymbol{k}_{2}=(k _{2}^{(1)},k_{2}^{(2)})\), \(\boldsymbol{M}=(M^{(1)},M^{(2)})\), \(\boldsymbol{s}=(s^{(1)},s^{(2)})\), let us introduce the following quantities.
Definition 2
For a choice of \(\boldsymbol{s}\), \(\epsilon\) and \(\boldsymbol{M}\), define
The next lemma provides an uniform bound for \(\omega_{\boldsymbol{k}} ^{\boldsymbol{s}}S_{\boldsymbol{k}}\) for any \(\boldsymbol{k}\notin F_{\boldsymbol{M}}\).
Lemma 5
Let \(\hat{k}\), \(\hat{M}\), \(\chi^{(1)}(\boldsymbol{M},\epsilon)\), \(\chi^{(2)}(\boldsymbol{M},\epsilon)\) be as in Definition 2. Then
Proof
See the Appendix. □
Denoting by \(\eta\) the right hand side of (29) we can define
For \(\tilde{Z}_{\boldsymbol{M}}^{(2)}\) and \(\tilde{Z}_{\boldsymbol{M}} ^{(3)}\) we adopt the same bounds as in (21). Hence the tail bound \(\tilde{Z}_{\boldsymbol{M}}\) is now given by
5 Results
In this section we report the results obtained by applying the radii polynomial technique, in the form discussed in the previous section, for the enclosure of non constant solutions for system (3). All the rigorous computations and the visualisation have been performed in Matlab with the interval arithmetic package Intlab [26].
We remind that the domain \(\varOmega\) is given as the rectangular \(\varOmega=[0,L_{1}]\times[0,L_{2}]\). The various computational parameters have been chosen homogeneous, that is
In any computation the decay rate \(\boldsymbol{s}\) is fixed equal to \(\boldsymbol{s}=(2,2)\). We do not investigate the performance of the enclosure as \(\boldsymbol{s}\) varies. At this regard, an interesting analysis has been performed in [1].
For convenience, let us recall the homogenous states
First we discuss how to compute the numerical solutions, then we report some details about the rigorous enclosure.
5.1 Computing the Numerical Solution
For a choice of the domain sizes \(L_{1}\), \(L_{2}\) and of the parameter \(\lambda\) we numerically compute several patterns lying on the same family bifurcating from one of the homogenous state \(p_{2}(\lambda)\), \(p_{3}(\lambda)\). Each solutions is intended in Fourier space, that is, we numerically find a zero of a finite \(\boldsymbol{m}\)-dimensional projection of system (16) in the unknowns \(\mathcal{X}= \{ \gamma, \{u_{\boldsymbol{k}}\}_{\boldsymbol{k}\in F_{ \boldsymbol{m}}}, \{ v_{\boldsymbol{k}}\}_{\boldsymbol{k}\in F_{ \boldsymbol{m}}} \} \).
According to the analysis performed in Sect. 2, for a choice of \(\boldsymbol{k}\) we set that value \(\gamma= \gamma_{{{\boldsymbol{k}}}}\) and we perturb the homogenous state in the direction of the eigenfunction \(\phi_{\boldsymbol{k}}\). This perturbed state, together with \(\gamma_{{{\boldsymbol{k}}}}\), is now considered as initial data for a Newton iteration scheme. Once a first non homogenous state is computed, we adopt a numerical continuation scheme to compute other solutions on the same branch. We slightly move \(\gamma\) in the direction of the branch, we perturb the previous computed state along the tangent direction and we look for a new solution in the unknowns \(\{u_{\boldsymbol{k}}\}_{\boldsymbol{k} \in F_{\boldsymbol{m}}}\). There are different parameters one can play with that influence the outcome of the process. For example the length of the increment of \(\gamma\), the size \(\boldsymbol{m}\) of the finite dimensional projection and also the accuracy requested for the numerical solution. In our computations we assume that the numerical solution \(\bar{x}\) is achieved when the sup-norm of \(f^{(\boldsymbol{m})}( \bar{x})\) is less than \(10^{-10}\). The parameter \(\boldsymbol{m}=(m,m)\) ranges in between \(12\leq m\leq23\) and different \(\Delta\gamma\)-step are considered.
5.2 Rigorous Enclosure Results
5.2.1 Example 1. Global Bifurcation Diagrams for \(\lambda=4.5\), \(\varOmega=[0,1.1]\times[0,0.8]\)
Here we discuss the results stated in Theorem 1 and depicted in Fig. 1. A magnification of Fig. 1(a) is given in Fig. 2. Any bullet in the figures represents a validated non-constant pattern. The graphs depict \(\gamma\) against the squared \(L^{2}\) norm of the \(v-v_{0}\), where \(v_{0}\) denotes the \(v\) component of the homogenous state. The different families are labelled according to the bifurcation point, that is the \((k^{(1)},k^{(2)})\)-branch is the one that bifurcates from the homogenous state at value \(\gamma_{(k^{(1)},k^{(2)})}\).
Table 1 reports the parameters \(m\), \(\overline{M}\), \(M\) and the sharpening coefficient \(\epsilon\) used in the computation of the solutions marked in Fig. 2 together with the enclosure radius. Since \(\boldsymbol{s}=(2,2)\), the value of \(r\) provides also a bound for the \(C^{2}\) distance of the exact solution from the numerical approximation.
From the data in the Table 1, we realise that larger finite dimensional parameter and larger computational parameter are required when \(\gamma\) decreases and the size of \(\boldsymbol{k}\) increases. The role of \(\gamma\) is already discussed in Sect. 4.3. Although the introduction of the sharpening coefficient \(\epsilon\) enables to weaken the aftereffect of \(\gamma\), a dependence between the parameters is still present and a smaller \(\gamma\) requires a larger \(\overline{M}\) and \(M\). On the other side, \(\boldsymbol{k}\) denotes the Fourier coefficient of \(u\) and \(v\) that has been initially perturbed at the bifurcation point. Due to the nonlinear effects, such a perturbation is spread on the neighbourhood coefficients. Hence a larger \(\boldsymbol{k}\) requires larger \(m\) and \(\overline{M}\) to take into account a large number of contributing coefficients. Also, further the solution is from the bifurcation point, more important is the effect of the nonlinearity.
A similar analysis, here skipped, can be performed for the enclosure of the patterns bifurcating from the homogenous state \(p_{3}(\lambda)\) and reported in Fig. 1(b). In Fig. 3 some of such patterns are plotted.
Plot of the \(v\)-component of solutions for the Gray-Scott equation in 2D. Each solution belongs to a different branch of families depicted in Fig. 1(b), where \(\varOmega=[0, 1.1]\times[0, 0.8], \lambda=4.5 \). For each figure we report the value of \(\gamma\) and the label \(\boldsymbol{k}\) of the branch. (a) \(\gamma= 0.0226, \boldsymbol{k}=(1,0) \), (b) \(\gamma=0.0122\), \(\boldsymbol{k}=(0,2)\), (c) \(\gamma=0.0215\), \(\boldsymbol{k}=(1,1)\), (d) \(\gamma=0.0061\), \(\boldsymbol{k}=(0,3)\), (e) \(\gamma=0.0052\), \(\boldsymbol{k}=(2,3)\), (f) \(\gamma=0.0080\), \(\boldsymbol{k}=(3,1)\), (g) \(\gamma=0.0096\), \(\boldsymbol{k}=(1,2)\), (h) \(\gamma=0.0043\), \(\boldsymbol{k}=(3,3)\) (Color figure online)
5.2.2 Example 2. Effect of the Sharpening Parameter
We now investigate the role of the newly introduced sharpening parameter \(\epsilon\). Remember that the small is \(\epsilon\) the higher is its effect, in the sense that the sets \(F_{\boldsymbol{m}}(\bar{u}, \epsilon), F_{\boldsymbol{m}}(\bar{v}, \epsilon)\) given in (24) are larger. Consider the solution in correspondence to \(\gamma=0.0108\) on the \((1,2)\) bifurcating branch in Fig. 1(b). In Fig. 4 both the components \(u\) and \(v\) of the pattern are depicted. For different choices of \(\epsilon\), in Table 2 we list the computational parameters \(\overline{M}\) and \(M\) needed to obtain a successful validation of the numerical solution. The finite dimensional projection parameter is \(m=13\). We see that for large \(\epsilon\) extremely large values for the computational parameters are requested. The last row in the table concerns a value close to the largest possible choice of \(\epsilon\), according to the condition \(\epsilon\leq\min\{\| \bar{u}\|_{\boldsymbol{s}},\|\bar{v}\|_{\boldsymbol{s}}\}\). Therefore, if the sharpening parameter is not considered at all, that is, if we follow the approach of [11], even larger computational parameters must be selected and a rigorous enclosure of the solution would be practically impossible.
Plot of the \(u\) (left) and \(v\) (right) component of the pattern discussed in Example 2. The solution belongs to the family \((1,2)\) reported in Fig. 1(b) at \(\gamma=0.0108\) (Color figure online)
6 Conclusion
In this paper a new development of the radii polynomial technique is proposed with the aim of rigorously computing non-uniform patterns for the two dimensional Gray-Scott system. It is demonstrated that the new approach succeeds in enclosing several complex patterns, solutions that could not be proved following the previous approach present in the literature. We plan to develop further the technique and to investigate in different directions. For instance, the three dimensional case may be considered. We propose to combine the method with the theory introduced in [1] to compute parameter dependent smooth branches of solutions. Then a systematic analysis of the bifurcation branches of non-uniform patterns may be performed, to prove whether some branches undergo secondary bifurcations or reconnect to the uniform solution. Also, a more challenging project is to rigorously prove existence of heteroclinic connections and homoclinic cycles.
References
Breden, M., Lessard, J.-P., Vanicat, M.: Global bifurcation diagrams of steady states of systems of PDEs via rigorous numerics: a 3-component reaction-diffusion system. Acta Appl. Math. 128(1), 113–152 (2013)
Capiński, M.J., Simó, C.: Computer assisted proof for normally hyperbolic invariant manifolds. Nonlinearity 25(7), 1997–2026 (2012)
Castelli, R., Lessard, J.-P.: Rigorous numerics in Floquet theory: computing stable and unstable bundles of periodic orbits. SIAM J. Appl. Dyn. Syst. 12(1), 204–245 (2013)
Castelli, R., Teismann, H.: Rigorous numerics for NLS: bound states, spectra, and controllability. Physica D 334, 158–173 (2016)
Castelli, R., Lessard, J.-P., Mireles James, J.D.: Parameterization of invariant manifolds for periodic orbits (I): efficient numerics via the Floquet normal form. SIAM J. Appl. Dyn. Syst. 14(1), 132–167 (2015)
Chen, W., Ward, M.: The stability and dynamics of localized spot patterns in the two-dimensional Gray–Scott model. SIAM J. Appl. Dyn. Syst. 10(2), 582–666 (2011)
Day, S., Hiraoka, Y., Mischaikow, K., Ogawa, T.: Rigorous numerics for global dynamics: a study of the Swift-Hohenberg equation. SIAM J. Appl. Dyn. Syst. 4(1), 1–31 (2005) (electronic)
Day, S., Lessard, J.-P., Mischaikow, K.: Validated continuation for equilibria of PDEs. SIAM J. Numer. Anal. 45(4), 1398–1424 (2007) (electronic)
Gameiro, M., Lessard, J.-P.: Analytic estimates and rigorous continuation for equilibria of higher-dimensional PDEs. J. Differ. Equ. 249(9), 2237–2268 (2010)
Gameiro, M., Lessard, J.-P.: Rigorous computation of smooth branches of equilibria for the three dimensional Cahn-Hilliard equation. Numer. Math. 117(4), 753–778 (2011)
Gameiro, M., Lessard, J.-P.: Efficient rigorous numerics for higher-dimensional PDEs via one-dimensional estimates. SIAM J. Numer. Anal. 51(4), 2063–2087 (2013)
Gray, P., Scott, S.K.: Autocatalytic reactions in the isothermal, continuous stirred tank reactor: oscillations and instabilities in the system A + 2B → 3B, B → C. Chem. Eng. Sci. 39, 1087–1097 (1984)
Hale, J.K., Peletier, L.A., Troy, W.C.: Stability and instability in the Gray-Scott model: the case of equal diffusivities. Appl. Math. Lett. 12(4), 59–65 (1999)
Kokubu, H., Wilczak, D., Zgliczyński, P.: Rigorous verification of cocoon bifurcations in the Michelson system. Nonlinearity 20(9), 2147 (2007)
Kolokolnikov, T., Wei, J.: On ring-like solutions for the Gray-Scott model: existence, instability and self-replicating rings. Eur. J. Appl. Math. 16(02), 201–237 (2005)
Lee, K.J., McCormick, W.D., Ouyang, Q., Swinney, H.L.: Pattern formation by interacting chemical fronts. Science 261(5118), 192–194 (1993)
Lessard, J.-P., Kiss, G.: Computational fixed point theory for differential delay equations with multiple time lags. J. Differ. Equ. 252(4), 3093–3115 (2012)
Lessard, J.-P., Reinhardt, C.: Rigorous numerics for nonlinear differential equations using Chebyshev series. SIAM J. Numer. Anal. 52(1), 1–22 (2014)
McGough, J.S., Riley, K.: Pattern formation in the Gray–Scott model. Nonlinear Anal., Real World Appl. 5(1), 105–121 (2004)
Morgan, D.S., Kaper, T.J.: Axisymmetric ring solutions of the 2D Gray–Scott model and their destabilization into spots. Physica D 192(1–2), 33–62 (2004)
Nakao, M.T.: Numerical verification methods for solutions of ordinary and partial differential equations. Numer. Funct. Anal. Optim. 22(3–4), 321–356 (2001)
Nishiura, Y., Ueyama, D.: A skeleton structure of self-replicating dynamics. Physica D 130(1–2), 73–104 (1999)
Nishiura, Y., Ueyama, D.: Spatio-temporal chaos for the Gray–Scott model. Physica D 150(3–4), 137–162 (2001)
Pearson, J.E.: Complex patterns in a simple system. Science 261(5118), 189–192 (1993)
Reynolds, W.N., Pearson, J.E., Ponce-Dawson, S.: Dynamics of self-replicating patterns in reaction diffusion systems. Phys. Rev. Lett. 72(17), 2797–2800 (1994)
Rump, S.M.: INTLAB—INTerval LABoratory. In: Tibor, C. (ed.) Developments in Reliable Computing, pp. 77–104. Kluwer Academic, Dordrecht (1999). http://www.ti3.tu-harburg.de/rump/
Rump, S.M.: Verification methods: rigorous results using floating-point arithmetic. Acta Numer. 19, 287–449 (2010)
Turing, A.M.: The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B, Biol. Sci. 237(641), 37–72 (1952)
van den Berg, J.B., Mireles-James, J.D., Lessard, J.-P., Mischaikow, K.: Rigorous numerics for symmetric connecting orbits: even homoclinics of the Gray-Scott equation. SIAM J. Math. Anal. 43(4), 1557–1594 (2011)
Vanag, V.K., Epstein, I.R.: Localized patterns in reaction-diffusion systems. Chaos, Interdiscip. J. Nonlinear Sci. 17, 037110 (2007)
Wei, J.: Pattern formations in two-dimensional Gray–Scott model: existence of single-spot solutions and their stability. Physica D 148(1–2), 20–48 (2001)
Yamamoto, N.: A numerical verification method for solutions of boundary value problems with local uniqueness by Banach’s fixed-point theorem. SIAM J. Numer. Anal. 35(5), 2004–2013 (1998) (electronic)
Zgliczyński, P., Mischaikow, K.: Rigorous numerics for partial differential equations: the Kuramoto-Sivashinsky equation. Found. Comput. Math. 1(3), 255–288 (2001)
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
1.1 A.1 Definition of the \(\alpha\)’s and \(\varepsilon\)’s Constants
Suppose \(s\geq2\), \(M\geq6\). For \(k\geq3\) let be defined
Then, for all \(k\in\mathbb{Z}\), define \(\alpha^{(2)}_{k}=\alpha^{(2)} _{k}(s,M)\) as
and
Also
By recursion, for \(n\geq3\), define \(\alpha^{(n)}_{k}=\alpha^{(n)} _{k}(s,M)\) as
where
Define
For \(n\geq2\), \(s\geq2\), \(M\geq\overline{M}\geq6\), define
where \(\alpha_{k}^{(1)}=1\), and for \(k<0\)
For the multidimensional case, suppose that \(\boldsymbol{s}=(s^{(1)}, \dots, s^{(d)})\) with \(s^{(i)}\geq2\), \(\overline{\boldsymbol{M}}=( \overline{M}^{(1)},\dots,\overline{M}^{(d)})\), \(\boldsymbol{M}=(M ^{(1)},\dots, M^{(d)})\) with \(6\leq\overline{M}^{(i)}\leq M^{(i)}\) have been fixed. Then, for \(\boldsymbol{k}=(k^{(1)},\dots,k^{(d)}) \in\mathbb{Z}^{d}\), let be defined
and
1.2 A.2 Proof of Lemma 5
Lemma
Let \(\epsilon\) be fixed and \(\hat{k}\), \(\hat{M}\), \(\chi^{(1)}(\boldsymbol{M},\epsilon)\), \(\chi^{(2)}(\boldsymbol{M}, \epsilon)\) be as in Definition 2. Then
Proof
It holds
If both \(|k^{(1)}|\geq M^{(1)},|k^{(2)}|\geq M^{(2)}\),
Hence
If \(|k^{(1)}|< M^{(1)}\) and \(|k^{(2)}|\geq M^{(2)}\) we have
Similarly, in case \(|k^{(1)}|\geq M^{(1)}\) and \(|k^{(2)}|< M^{(2)}\)
□
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Castelli, R. Rigorous Computation of Non-uniform Patterns for the 2-Dimensional Gray-Scott Reaction-Diffusion Equation. Acta Appl Math 151, 27–52 (2017). https://doi.org/10.1007/s10440-017-0101-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10440-017-0101-x
Keywords
- Rigorous numerics
- 2-Dimensional Gray-Scott reaction diffusion equation
- Contraction mapping theorem
- Pattern dynamics