A Finite Element Dual Porosity Approach to Model Deformation-Induced Fluid Flow in Cortical Bone

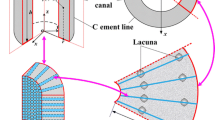
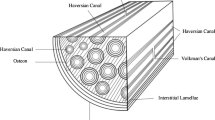
Abstract

Fluid flow through the osteocyte canaliculi network is widely believed to be a main factor that controls bone adaptation. The difficulty of in vivo measurement of this flow within cortical bone makes computational models an appealing alternative to estimate it. We present in this paper a finite element dual porosity macroscopic model that can contribute to evaluate the interstitial fluid flow induced by mechanical loads in large pieces of bone. This computational model allows us to predict the macroscopic fluid flow at both vascular and canalicular porosities in a whole loaded bone. Our results confirm that the general trend in the fluid flow field predicted is similar to the one obtained with previous microscopic models, and that in a whole bone model it is able to estimate the zones with higher bone remodeling.

Appendix A: Dual Porosity Model

For saturated porous media (like cortical bone tissue), the equilibrium equations can be written as

$$ \frac{\partial \tau_{ij}}{\partial x_{j}}+F_{i}=0 $$

(4)

where F _i is the body force per unit volume and τ _ij is the total stress that can be expressed as

$$ \tau_{ij}=\sigma_{ij}-\alpha_1 p_1\delta_{ij}-\alpha_2 p_2\delta_{ij} $$

(5)

being σ _ij the effective stress, p ₁ and p ₂ the pore fluid pressures in the two levels of porosity (here PV and PLC), α₁ and α₂ the effective stress coefficients and δ _ij the Kronecker’s delta. For an elastic and isotropic bone matrix, the effective stress can be written as

$$ \sigma_{ij}=2G\varepsilon_{ij}+\lambda\varepsilon_{kk}\delta_{ij} $$

(6)

with ɛ _ij the global strain tensor and λ and G the so called Lame’s constants, that are expressed in terms of the Young’s modulus E and the Poisson’s ratio ν as λ = Eν/(1 + ν)(1 − 2ν) and G = E/2(1 + ν).

The governing equation for the solid phase is obtained combining Eqs. (4), (5) and (6) getting:

$$ 2G\frac{\partial \varepsilon_{ij}}{\partial x_j}+\lambda \frac{\partial \varepsilon_{jj}}{\partial x_i}-\alpha_1\frac{\partial p_1}{\partial x_i}-\alpha_2\frac{\partial p_2}{\partial x_i}+F_i=0 $$

(7)

For small deformations, strains are related to displacements by the well-known Cauchy strain tensor

$$ \varepsilon_{ij}=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right) $$

(8)

with $\user2{u}$ the displacement vector. Substituting Eq. (8) into (7), the governing equation of the solid phase can we written as a function of displacements as

$$ G\frac{\partial^2u_i}{\partial x_j\partial x_j}+(\lambda+G)\frac{\partial^2u_j}{\partial x_i\partial x_j}-\alpha_1\frac{\partial p_1}{\partial x_i}-\alpha_2\frac{\partial p_2}{\partial x_i}+F_i=0 $$

(9)

The definition of the effective stress parameters α₁ and α₂ can be determined in terms of physically measurable parameters. Following the procedure of Khalili and Valliappan,15 a representative planar volume of cortical bone is subjected to external principal stresses σ _ii and to internal vascular pressure p ₁ and lacuno-canalicular pressure p ₂. These stresses can be decomposed in four components, as it is shown in Fig. 12: (I) equal PV, PLC and external hydrostatic pressure p ₁; (II) zero PV pressure and equal PLC and external hydrostatic pressure (p ₂ − p ₁); (III) external hydrostatic pressure $(\overline{\sigma} -p_2)$, being $\overline{\sigma} =\sigma_{ii}/3$; and (IV) external deviator stress $\widetilde{\sigma_{ij}}=\sigma_{ij}-\overline{\sigma}\delta_{ij}$. The total volumetric strain of this representative bone volume may be calculated, according to Nur and Byerlee,21 as

$$ \varepsilon_{ii}=\varepsilon_{ii}^{\rm I}+\varepsilon_{ii}^{\rm II}+ \varepsilon_{ii}^{\rm III}+\varepsilon_{ii}^{\rm IV} $$

(10)

being

$$ \varepsilon_{ii}^{\rm I}=\frac{p_1}{K_{\rm s}} $$

(11a)

$$ \varepsilon_{ii}^{\rm II}=\frac{p_2-p_1}{K_{\rm v}} $$

(11b)

$$ \varepsilon_{ii}^{\rm III}=\frac{\overline{\sigma}-p_2}{K} $$

(11c)

$$ \varepsilon_{ii}^{\rm IV}=0 $$

(11d)

where K _s, K _v and K are the drained bulk modulus of the bone matrix, the vascular porosity and the cortical bone, respectively. Introducing Eq. (11) into (10) and rearranging, the volumetric strain results

$$ \varepsilon_{ii}=\frac{\overline{\sigma}}{K}-\left(\frac{1} {K_{\rm v}}-\frac{1}{K_{\rm s}}\right)p_1-\left(\frac{1}{K}-\frac{1}{K_{\rm v}}\right)p_2 $$

(12)

Figure 12

Stress decomposition of a representative bone element. The component normal to the plane, σ₂, is not shown for simplicity

Applying now the definition of effective stress, it can also be written as

$$ \varepsilon_{ii}=\frac{1}{K}(\overline{\sigma}-\alpha_1 p_1 -\alpha_2 p_2) $$

(13)

Comparing Eqs. (12) and (13) yields

$$ \alpha_1=\frac{K}{K_{\rm v}}-\frac{K}{K_{\rm s}} \quad \alpha_2=1-\frac{K}{K_{\rm v}} $$

(14)

Note that when the lacuno-canalicular porosity is reduced to zero (i.e. K _v = K), the stress effective coefficients are those used in single porosity models (α₁ = 1 − K/K _s, α₂ = 0).

The governing equations for fluid flow in PV and PLC can be obtained from the mass conservation equations for the fluid. Darcy’s law has been considered here as the constitutive equation, that is,

$$ v_{\alpha i}=-\frac{k_\alpha}{\mu}\frac{\partial p_\alpha}{\partial x_i}\quad \alpha=1,2 $$

(15)

being k the permeability of the pore network and μ the viscosity of the fluid. Subindex α takes the value 1 for the PV and 2 for the PLC, and v _αi represents the relative fluid velocity in each network with respect to the bone matrix, that can be expressed in terms of the porosity ϕ_α, the absolute velocity v _αif and the velocity of the bone matrix v _is as

$$ v_{\alpha i}=\phi_\alpha (v_{\alpha i{\rm f}}-v_{i{\rm s}})\quad \alpha=1,2 $$

(16)

Mass conservation of the fluid in the PV and PLC networks can be written as

$$ -\frac{\partial}{\partial x_i}(\rho_{\rm f}\phi_\alpha v_{\alpha i{\rm f}})=\frac{\partial}{\partial t}(\phi_\alpha \rho_{\rm f})-(-1)^\alpha \Gamma \quad \alpha=1,2 $$

(17)

where Γ corresponds to the leakage term that represents the rate of flow between canaliculi and Haversian canals. Substitution of Eq. (16) into (17) yields

$$ -\frac{\partial}{\partial x_i}(\rho_{\rm f} v_{\alpha i})-\frac{\partial}{\partial x_i}(\rho_{\rm f}\phi_\alpha v_{i{\rm s}})=\frac{\partial}{\partial t}(\phi_\alpha \rho_{\rm f})-(-1)^\alpha \Gamma \quad \alpha=1,2 $$

(18)

which, introducing the Lagrangian material derivative relative to the solid (d _s()/dt = ∂()/∂t + v _is∂()/∂x _i ) can be rearranged as

$$ -\frac{\partial}{\partial x_i}(\rho_{\rm f} v_{\alpha i})=\phi_\alpha\frac{d_{\rm s} \rho_{\rm f}}{dt}+\rho_{\rm f}\frac{d_{\rm s} \phi_\alpha} {dt}+\rho_{\rm f}\phi_\alpha\frac{\partial v_{i{\rm s}}}{\partial x_i} -(-1)^\alpha \Gamma \quad\alpha=1,2 $$

(19)

According to the definition of compressibility one can write for the fluid

$$ \frac{1}{\rho_{\rm f}}\frac{d_{\rm s}\rho_{\rm f}} {dt}=\frac{1}{K_{\rm f}}\frac{d_{\rm s} p_\alpha}{dt} \quad \alpha=1,2 $$

(20)

Substituting Eqs. (15) and (20) into (19) divided by ρ_f it results in

$$ \frac{1}{\rho_{\rm f}}\frac{\partial}{\partial x_i}\left(\rho_{\rm f}\frac{k_\alpha}{\mu}\right)\frac{\partial p_\alpha}{\partial x_i}=\frac{\phi_\alpha}{K_{\rm f}}\frac{d_{\rm s} p_\alpha}{dt}+\frac{d_{\rm s} \phi_\alpha} {dt}+\phi_\alpha\frac{\partial v_{i{\rm s}}}{\partial x_i}-(-1)^\alpha\frac{\Gamma}{\rho_{\rm f}}\quad \alpha=1,2 $$

(21)

Equations (9) and (21) conform the governing equations system for cortical bone. However, in order to completely solve these equations another relationship is needed to establish the term d _sϕ_α/dt. This relationship can be derived from the definition of porosities

$$ \phi_\alpha =\frac{V_\alpha}{V} \quad\alpha=1,2 $$

(22)

where V is a representative volume of cortical bone, and V ₁ and V ₂ are the volumes of PV and PLC in that representative volume. Differentiation of Eq. (22) yields

$$ d\phi_\alpha=\frac{1}{V}(dV_\alpha -\phi_\alpha dV) \quad\alpha=1,2 $$

(23)

The last term in Eq. (23) is actually related to the volumetric strain of the matrix

$$ \frac{dV}{V}=tr \varepsilon=\frac{\partial u_{i{\rm s}}} {\partial x_i} $$

(24)

and, for the first terms in the right-hand side of Eq. (23), which correspond to the variation in fluid content of each porosity ζ_α, Khalili and Valliappan15 showed that they can be expressed as

$$ \frac{dV_1}{V}=\zeta_1=\alpha_1\frac{\partial u_{i{\rm s}}}{\partial x_i}+\frac{\alpha_1-\phi_1}{K_{\rm s}}dp_1+\frac{\chi} {K}d(p_1-p_2) $$

(25a)

$$ \frac{dV_2}{V}=\zeta_2=\alpha_2\frac{\partial u_{i{\rm s}}}{\partial x_i}+\frac{\alpha_2-\phi_2}{K_{\rm s}}dp_2+\frac{\chi} {K}d(p_2-p_1) $$

(25b)

$$ \chi=\alpha_1\alpha_2-\phi_1\phi_2\frac{\alpha_1+\alpha_2} {\phi_1+\phi_2} $$

(25c)

Applying (23) in (21) and considering that, in general, v _is∂()/∂x _i ≪ ∂()/∂t and then d _s()/dt ≈ ∂()/∂t, it results into

$$ \frac{k_1}{\mu}\frac{\partial^2p_1}{\partial x_i\partial x_i}=\left(\frac{\phi_1}{K_{\rm f}}+\frac{\alpha_1-\phi_1} {K_{\rm s}}+\frac{\chi}{K}\right) \frac{\partial p_1}{\partial t}-\frac{\chi}{K}\frac{\partial p_2}{\partial t}+\alpha_1\frac{\partial v_{i{\rm s}}} {\partial x_i}-\frac{\Gamma} {\rho_{\rm f}} $$

(26a)

$$ \frac{k_2}{\mu}\frac{\partial^2p_2}{\partial x_i\partial x_i}=\left(\frac{\phi_2}{K_{\rm f}}+\frac{\alpha_2-\phi_2} {K_{\rm s}}+\frac{\chi}{K}\right) \frac{\partial p_2}{\partial t}-\frac{\chi}{K}\frac{\partial p_1}{\partial t}+\alpha_2\frac{\partial v_{i{\rm s}}}{\partial x_i}+\frac{\Gamma} {\rho_{\rm f}} $$

(26b)

and recovering Eq. (9) the complete set of governing equations for the bone cortical tissue becomes

$$ G\frac{\partial^2u_i}{\partial x_j\partial x_j}+(\lambda+G)\frac{\partial^2u_j}{\partial x_i\partial x_j}-\alpha_1\frac{\partial p_1}{\partial x_i}-\alpha_2\frac{\partial p_2}{\partial x_i}+F_i=0 $$

(27a)

$$ \frac{k_1}{\mu}\frac{\partial^2p_1}{\partial x_i\partial x_i}=a_{11}\frac{\partial p_1}{\partial t}+a_{12}\frac{\partial p_2}{\partial t}+\alpha_1\frac{\partial^2 u_i}{\partial t\partial x_i}-\frac{\Gamma}{\rho_{\rm f}} $$

(27b)

$$ \frac{k_2}{\mu}\frac{\partial^2p_2}{\partial x_i\partial x_i}=a_{21}\frac{\partial p_1}{\partial t}+a_{22}\frac{\partial p_2}{\partial t}+\alpha_2\frac{\partial^2 u_i}{\partial t\partial x_i}+\frac{\Gamma}{\rho_{\rm f}} $$

(27c)

$$ \frac{\Gamma}{\rho_{\rm f}}=\gamma (p_1-p_2) $$

(27d)

where γ is the so-called leakage parameter, which modulates the regulating role that bone lining cells perform on bone surfaces controlling the flux of fluid between compartments and the interstitial fluid pressure.16 The rest of the parameters are defined as

$$ \begin{array}{c} a_{11}=\phi_1/K_{\rm f} + (\alpha_1 -\phi_1)/K_{\rm s} + \chi/K \\ a_{12}=a_{21}=-\chi/K \\ a_{22}=\phi_2/K_{\rm f} + (\alpha_2 -\phi_2)/K_{\rm s} + \chi/K \\ \alpha_1=K/K_{\rm v}-K/K_{\rm s} \\ \alpha_2=1-K/K_{\rm v} \end{array} $$

(28)