On the money creation approach to banking

Abstract

We study today’s two-tier money creation and destruction system: Commercial banks create bank deposits (privately created money) through loans to firms or asset purchases from the private sector. Bank deposits are destroyed when households buy bank equity or when firms repay loans. Central banks create electronic central bank money (publicly created money or reserves) through loans to commercial banks. In a simple general equilibrium setting, we show that symmetric equilibria yield the first-best level of money creation and lending when prices are flexible, regardless of monetary policy and capital regulation. When prices are rigid, we identify the circumstances in which money creation is excessive or breaks down and the ones in which an adequate combination of monetary policy and capital regulation can restore efficiency. Finally, we provide a series of extensions and generalizations of the results.

1 Introduction

1.1 Motivation and approach

Money is predominantly held by the public in the form of bank deposit contracts.¹ These deposits—which are claims on banknotes—are typically created by the banks’ lending decisions. How is such inside money creation controlled, and how can it be steered towards socially desirable levels? These long-standing questions are the focus of this paper.²

For several reasons, the constraints on asset and inside money creation—thereafter simply called “money creation”—in the commercial banking system in today’s architectures have received renewed attention recently (see McLeay et al. 2014). First, the price of reserves, i.e. the short-term interest rate, has generally replaced traditional quantity instruments in the form of reserve requirements, which do not restrict lending directly.³ Moreover, exceptionally, some central banks purchase securities or lend to banks at low and even negative interest rates. Whether such policies trigger a corresponding money creation and foster economic activities is unclear.

We develop a sequential general equilibrium model to study these issues. In particular, we build the simplest general equilibrium model for which the feature that competitive commercial banks create money by granting loans is crucial. In this setting, we investigate the functioning of money creation in various circumstances and we examine which combinations of central bank policy rates and capital requirements lead to a socially efficient money creation and intermediation of households’ endowments to the production sectors. The main issues are as follows:

• Does a two-tier process with private money creation through competitive commercial banks via deposit/loan creation to firms and with public money creation by central banks via deposit/loan creation to commercial banks yield efficient allocations when prices are flexible?

• How do price rigidities affect the functioning of the two-tier money creation process?

• Can capital regulation, together with central bank interest rate setting, alleviate potential inefficiencies?

• How do financial frictions impact the functioning of the two-tier process?

While there are many papers about the role of bank deposits playing the role of money and papers with a different focus, this paper is the first paper with a general equilibrium approach to the two-tier process of private and public money creation, as we discuss in more detail below in Sect. 1.3.

The details of the model are as follows: Bank deposits are essential to buy physical goods, and these deposits are created by banks in the lending process for firms that can only obtain funds through monitored lending. The central bank sets an interest rate (or policy rate) at which banks are able to refinance themselves and which they can earn by holding reserves at the central bank. Regulatory authorities impose bank capital requirements. Households sell their endowment of investment goods to firms and choose a portfolio of bank equity, bank deposits, and bonds. Consumption goods are produced by firms and they are sold to and consumed by households. With the proceeds, banks and firms pay dividends and reimburse bonds and loans. Money in the form of bank deposits is destroyed when firms repay their loans, and money in the form of central bank reserves is destroyed when banks repay their central bank liabilities.

1.2 Main insights

The analysis of our model produces three main insights. First, with perfectly flexible prices, i.e. prices adjusting perfectly to macroeconomic conditions, equilibria with money creation are associated with the first-best allocation, regardless of the central bank’s monetary policy. If prices are rigid, there exist central bank policies for which money creation collapses or explodes. In the only equilibrium possible, in these cases, there is no financial intermediation, and an inefficient allocation occurs. Appropriate central bank policy can restore socially efficient money creation and lending. Second, with price rigidities and the zero lower bound, there may not exist a feasible central bank monetary policy inducing socially efficient money creation and lending. Capital regulation, in the form of a minimum equity ratio, and monetary policy can jointly limit money creation, and, under normal economic conditions, restore the existence of equilibria with socially efficient money creation and lending. Third, when prices are rigid, the central bank’s choice of zero interest rates and appropriate capital regulation can only avoid a slump in money creation and lending if economic conditions are sufficiently favorable.⁴ The functioning of the economy is illustrated in a simple example in Appendix C.

We also investigate how these insights translate (i) in the presence of financial frictions at the bankers’ level, (ii) when bonds are denominated in nominal terms, (iii) when there are more than two states of the world, (iv) when we also consider asymmetric equilibria with banks, (v) when there are real costs for monitoring activities, (vi) when the lending rates or the real deposit rates cannot be written contingently on the state of the economy, and (vii) when a reserve requirement and a haircut rule for borrowing against the central bank are imposed by government authorities. While our results continue to hold for extensions (ii), (iii), (v), and (vi), we obtain three further insights: First, in the presence of financial frictions, there are equilibria with banks only when capital regulation is adequately combined with monetary policy. Second, we demonstrate that there are inefficient asymmetric equilibria with banks when prices are flexible and suitable capital requirements eliminate these inefficient equilibria with banks, so that only efficient equilibria with banks remain. Finally, we show that the impact of a reserve requirement coupled with a haircut rule on money creation is identical to the impact of a minimum equity ratio requirement.

One important remark is in order. The features of our model entail results of the knife-edge type. For instance, money creation is either at optimal level, unlimited, or collapses to zero. This has the advantage of illustrating in the most simple and most transparent way both the forces at work and appropriate monetary policy and capital regulation. Moreover, it should motivate to construct smoother versions of the model.⁵

1.3 Relation to the literature

Our paper is inspired by the long-standing issue of the limits on money creation by commercial banks in a world with fiat money. The historical debate on banks as money creators and on endogenous money is discussed in Jakab and Kumhof (2015). Independently of this paper, Jakab and Kumhof (2015) construct a DSGE model in which a bank can create money. They show quantitatively that shocks have greater effects on bank lending and on the real economy than in the corresponding loanable-funds model. We focus on the welfare properties of general equilibrium models when private banks compete with regard to money creation—both in the absence and presence of price rigidities. Conceptually, our research is connected to four further strands of the literature.

First, the literature has established that fiat money can have positive value in a finite-horizon model when, first, there are sufficiently severe penalties when debt to governments—such as tax liabilities—is not paid and, second, when there are sufficiently large gains from using and trading money.⁶ To this literature, we add the two-tier structure with privately and publicly created monies. Commercial banks create bank deposits (privately created money) when they grant loans to firms, thus enabling them to buy investment goods. Bank deposits will be used later by households to buy consumption goods.⁷ The central bank creates reserves (publicly created money) when it grants loans to commercial banks, thus enabling them to settle claims on privately created money among banks. The publicly created money is often called “central bank money”.

In our model, following the above literature, fiat money in the form of bank deposits has value due to three reasons. First, firms can only acquire investment goods if they obtain loans from banks in the form of bank deposits and thus there are large gains from using money. Second, banks face large penalties when they cannot pay back the central bank money and default against the central bank. Third, all money is destroyed at the end of the economy.

Second, beside the banks’ role in money creation, the existence of banks in our model is justified by their role as delegated monitors, which goes back to Diamond (1984), where the existence of financial intermediaries relies on economies of scale in monitoring borrowers under moral hazard. Furthermore, Boot and Thakor (1997) provide a rationale explaining why financial markets and banks can coexist. They show that high-quality firms can borrow directly from the financial markets and that the moral hazard problem can be alleviated by banks’ monitoring activities. Similarly, Bolton and Freixas (2000) develop a model based on asymmetric information with equity and bond issues as well as bank loans. They also show that safe firms borrow from the bond market, whereas riskier firms are financed by banks. Based on these insights, we construct our model on the assumption that there are two different types of firms. The first type encompasses opaque firms, which are risky and need to be monitored by banks to obtain financing. The second type comprises firms, which are safe and can obtain financing directly from households through bond issues.

Third, a large body of literature on banks in partial or general equilibrium has provided important insights on how appropriate capital regulation may reduce excessive risk-taking, stabilize credit cycles, and liquidity provision.⁸ We examine the role of capital regulation with regard to money creation.

Fourth, our modeling of heterogeneous banks and of an interbank market relates to the approach of Tsomocos (2003) and Goodhart et al. (2006), who develop a tractable general equilibrium model to study financial fragility and derive conclusions regarding monetary, regulatory, and fiscal policies. While in their model, banks lend to firms the money they have first borrowed from the central bank, we develop a general equilibrium model in which banks create inside money by granting loans to firms before any borrowing from the central bank. Banks then have to borrow from the central bank or from the interbank market to finance any outflow of deposits that is greater than the inflow.

Fifth, some of the frictions we examine, such as price rigidities, and constraints, such as the zero lower bound, are, of course, discussed in large and important branches of the macroeconomic literature, which we cannot survey in this paper. We focus on how price rigidities and the zero lower bound affect the interplay of competitive issuance of private money by banks and public money by the central bank (monopoly), and thus our focus is quite different from the above-mentioned literature.

1.4 Structure of the paper

The set-up of the model is outlined in Sect. 2. Section 3 derives the resulting equilibria and their welfare properties. Section 4 analyzes the role of capital regulation when prices are perfectly rigid and the central bank policy rate is constrained by the zero lower bound. Section 5 presents extensions and generalizations of the model and concludes. The Appendices A.2 to C contain detailed analyses of the stages, proofs and an example.

2 Model

We consider a two-period general equilibrium model with two production sectors and one investment good. In Period $t=0$, investment takes place in both sectors. At the beginning of Period $t=1$, the production technologies transform the investment good into a consumption good. The gross rates of return are impacted by a macroeconomic shock. At the end of Period $t=1$, consumption takes place. There are firms in both sectors, commercial banks, the central bank and the government. Households own firms and commercial banks.

We next describe the details of the model. We use bold characters for real variables (for the amount of investment or consumption goods) to distinguish them from nominal variables. All nominal variables are expressed in the numeraire, which will be the central bank monetary unit. Furthermore, we differentiate individual quantities from aggregate quantities by using lower case letters for the former and capitals for the latter.

2.1 Agents

In Sect. 2.1 we describe the agents in the economy in more detail.

2.1.1 Entrepreneurs

Two different technologies are employed by firms to transform the investment good into a consumption good. These firms are run by entrepreneurs, who only play a passive role and simply maximize the value of shareholders. Firms are owned by households. There is a moral hazard technology called hereafter “Sector MT” or simply “MT”. Entrepreneurs running the firms employing this technology are subject to moral hazard and need to be monitored.⁹ We use $\mathbf{K }_\mathbf{M }\in [\mathbf{0 },\mathbf{W }]$ to denote the aggregate amount of investment good invested in MT, where $\mathbf{W }> 0$ denotes the total amount of the investment good in the economy. An investment of $\mathbf{K }_\mathbf{M }$ produces $\mathbf{K }_\mathbf{M }\mathbf{R }_\mathbf{M }$ units of the consumption good, where $\mathbf{R }_\mathbf{M }> 0$ denotes the real gross rate of return.

We define a real gross rate of return—also called hereafter “real gross rate” or simply “gross rate”—as being the amount of the consumption good produced by investing one unit of the investment good. Similarly, we define a nominal gross rate of return—also called hereafter “nominal gross rate” or simply “gross rate”—as being the amount of money (deposits or central bank money) which has to be repaid to the creditor by the debtor per unit of nominal investment.

There is a frictionless technology referred to hereafter as “Sector FT” or simply “FT”. Entrepreneurs running the firms employing this technology are not subject to any moral hazard problem.¹⁰ We use $\mathbf{K }_\mathbf{F }\in [\mathbf{0 },\mathbf{W }]$ to denote the aggregate amount of investment good invested in FT and $\mathbf{f }(\mathbf{K }_\mathbf{F })$ to denote the amount of consumption good produced by FT. We assume f$(0) = 0$, $\mathbf{f }' > 0$ and $\mathbf{f }'' < 0$.

Firms in MT and FT are owned by households, and as long as they are positive, the resulting profits from both technologies, denoted by $\Pi _M$ and $\Pi _F$, are paid to owners as dividends. The shareholders’ values are given by $\max (\Pi _M, 0)$ and $\max (\Pi _F, 0)$, respectively. The assumption that one technology is linear and one is concave ensures that there will be an interior solution for the mix of bond and bank financed firms.¹¹

2.1.2 Bankers

There is a continuum of banks labeled $b \in [0,1]$, owned by households, and operated by bankers who maximize shareholders’ value. At the very beginning, banks are only labels or indices. By granting loans $l_M^b$ to firms in MT, Bank b simultaneously creates deposits $d_M^b = l_M^b$.¹² We use $D_M = L_M$ to denote aggregate private deposits and aggregate loan volume, respectively. $d_M^b$ is the distribution of MT firms’ deposits across banks. When MT firms buy investment goods, these deposits will be transferred to households. The accounts of households are distributed uniformly across banks. Households convert a share $\varphi \in (0,1]$ of their initial deposits $D_M$ into an amount $E_B = \varphi D_M$ of bank equity and keep the remaining deposits to buy some amount of the consumption good. In order to allow banks to start with money creation, households commit to this conversion at the beginning.

We assume that each bank receives the same amount of equity financing, denoted by $e_B$.¹³ The aggregate amount is denoted by $E_B$. As the measure of banks is 1, the aggregate amount is numerically identical to the individual amount $e_B$. When $E_B > 0$ banks are founded¹⁴ and can engage in money creation and lending activities. For simplicity, we assume that banks can perfectly alleviate the moral hazard problem when investing in MT by monitoring borrowers and enforcing contractual obligations and that monitoring costs are zero.¹⁵ Banks provide (nominal) loans to firms in Sector MT at a nominal lending gross rate $R_L$. The individual and aggregate amounts of loans are denoted by $l_M^b$ and $L_M$, respectively. We can express the ratio of individual lending by Bank b to average lending by banks as $\alpha _M^b := \frac{l_M^b}{L_M}$.¹⁶

Bank equity holders are protected by limited liability. The profits of Bank b are denoted by $\Pi _B^b$. If positive, they are paid as dividends to equity holders in the form of deposits. The bank shareholders’ value and the nominal gross rate of return on equity are given by $\max (\Pi _B^b,0)$ and $\frac{\max (\Pi _B^b,0)}{E_B}$, respectively.

2.1.3 Households

There is a continuum of identical and risk-neutral households represented by [0, 1]. They are the only consuming agents in the economy. We can focus on a representative household initially endowed with $\mathbf{W }$ units of the investment good and ownership of all firms and banks in the economy. It sells a part of its endowment of the investment good to firms in MT against bank deposits. Then it chooses a portfolio of bank equity and bank deposits and lends the remaining endowment of the investment good directly to firms in FT against bonds.¹⁷ The dividends from firm ownership and bank equity investment as well as the repayments from bonds and bank deposits are used to buy the consumption good. The details of this process are set out in Sect. 2.4.

2.2 Macroeconomic shock, contracts, and prices

A macroeconomic shock $s=l,h$ occurs at the beginning of Period $t=1$ after the investment good has been allocated to the two technologies during Period $t=0$. It affects the real gross rate of return from production in Sector MT. Specifically, an investment of $\mathbf{K }_\mathbf{M }$ in MT produces $\mathbf{K }_\mathbf{M }\mathbf{R }_\mathbf{M }^\mathbf{h }$ and $\mathbf{K }_\mathbf{M }\mathbf{R }_\mathbf{M }^\mathbf{l }$ with probability $\sigma$ in the good state and $1-\sigma$ in the bad state of the world, respectively ($0< \sigma < 1$), where $\mathbf{R }_\mathbf{M }^\mathbf{s }$ is the real gross rate of return in State s ($s=l,h$). We assume that $0< \mathbf{R }_\mathbf{M }^\mathbf{l }< \mathbf{R }_\mathbf{M }^\mathbf{h }$.

Banks monitor entrepreneurs running firms in MT and plagued by moral hazard (see Sect. 2.1.1) and offer state-contingent loans with nominal lending gross rates $(R_L^s)_{s=l,h}$. The lending interest rates are given by $(R_L^s - 1)_{s=l,h}$.

We focus on a complete market setting in the sense that all contracts can be conditioned on macroeconomic events.¹⁸ All nominal contracts are stipulated in terms of the unit of the central bank money. As the output in FT is not stochastic, the real gross rate of return on bonds, denoted by $\mathbf{R }_\mathbf{F }$, is risk-free.

We will use interchangeably the notations ${\mathbb {E}}[X]$ and ${\overline{X}}$ to denote the expected value of some variable X. We make the following assumptions throughout our paper:

$$\begin{aligned} \mathbf{f }'(\mathbf{W })< \overline{\mathbf{R }}_\mathbf{M }< \mathbf{f }'(\mathbf{0 }). \end{aligned}$$

In words, the above assumption ensures that the expected total production can never be maximized by allocating the entire amount of the investment good to one sector of production.

2.3 Institutional set-up

2.3.1 Monies and interbank market

We have two types of money (privately created and publicly created monies) which are representative of the modern money architecture. A first type of money is privately created by commercial banks through loans to firms (or other banks), held at banks in the form of deposits by households or firms and destroyed when households buy bank equity and when firms repay loans. We call the first type of money “private deposits”. A second type of money is publicly created by the central bank—called hereafter “CB”—via loans to banks. It is held at the central bank in the form of deposits by banks. We call this second type of money “CB deposits”.

The essential rules linking publicly created and privately created monies are illustrated as follows. When households use private deposits to make payments, these deposits typically move from one bank (account of buyer, say $b_j$) to another bank (account of seller, say $b_i$). To settle the transfer of private deposits, Bank $b_j$ becomes liable to $b_i$. These banks now have two options. Either $b_j$ obtains a loan from Bank $b_i$, or it refinances itself at the CB and transfers the central bank money received, CB deposits, to Bank $b_i$. The institutional rule is that one unit of central bank money settles one unit of liabilities of privately created money, and both types of money have the same unit. This fixes the “exchange rate” between central bank money and privately created money at 1.¹⁹ Finally, we assume that there are no transaction costs for paying with private or CB deposits.

The prices of the investment and the consumption goods in units of both privately created and publicly created monies are denoted by $p_I$ and $(p_C^s)_{s=l,h}$, respectively. We also integrate an interbank market in which banks can lend to and borrow from each other. Arbitrage arguments entail that the interbank gross rate is equal to the households’ deposit gross rate, which we denote by $(R_D^s)_{s=l,h}$.²⁰

2.3.2 Role of public authorities

Two public authorities—a central bank and a government—ensure the functioning of the monetary architecture. We purposely impose favorable conditions on the working of the monetary architecture and the public authorities involved. These authorities fulfill three roles.

First, banks can obtain loans from the central bank and can thus acquire CB deposits at the same policy gross rates $(R_{CB}^s)_{s=l,h}$ at any stage of economic activities, where $(R_{CB}^s - 1)_{s=l,h}$ are the central bank interest rates. As a short-cut we often write $(R_{CB}^s)_{s}$ for $(R_{CB}^s)_{s=l,h}$. This implies that banks do not have to worry about the exact flow of funds at any particular stage. Only their net position at the final stage matters. Banks can also borrow from, or deposit at, the central bank contingently on the state of the world s.

Second, the government imposes heavy penalties on those bankers whose bank defaults on obligations to any public authority.²¹ As a consequence, no bank will default on its liabilities against the central bank in any state of the economy. A bank, however, may default on households’ deposits. In such cases, the government has a third role. It makes deposits safe by levying lump-sum taxes on households to bail out banks that default on households’ deposits. In practice, making deposits safe is a necessary condition for their use as money and it protects unsophisticated households. Thus, we integrate implicit insurance of bank deposits into our framework. Later we will introduce a third public authority, i.e. bank regulators, and bank regulation in the form of a capital requirement.

We explore equilibrium outcomes for different policies—the central bank policy gross rate and the capital requirement—and for each combination of these outcomes we determine the associated level of welfare expressed in terms of household consumption. We assume that the central bank and the bank regulators aim at maximizing the welfare of households.

Fig. 1

Timeline

2.4 Timeline of events and bank profits

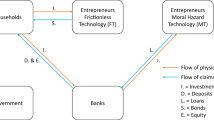
We next describe the timeline of events. For this purpose, we divide each period into several stages. An overview of the timeline is given in Fig. 1.

In Appendix A, we describe every detail of these events, as this ensures the consistency of the evolution of stocks and flows across the stages. For now, we focus on two ingredients of the model that are central for the definition and analysis of equilibria. First, an equilibrium with banks (and thus positive lending to Sector MT) requires $\mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s = R_L^s p_I$, so that entrepreneurs in Sector MT make zero profit. This is a direct consequence of the linear MT technology. Second, the expression of Bank b’s profits is as follows:

$$\begin{aligned} \Pi _B^{b,s}&= (1 - \alpha _M^b) L_M R_{CB}^s + \alpha _M^b L_M R_L^s - d_H R_D^s \nonumber \\&= (1 - \alpha _M^b) L_M R_{CB}^s + \alpha _M^b L_M R_L^s - (L_M - E_B) R_D^s \nonumber \\&= \alpha _M^b L_M (R_L^s - R_{CB}^s) + L_M (R_{CB}^s - R_D^s) + E_B R_D^s. \end{aligned}$$

(1)

Since banks are maximizing return on equity and operate under limited liability, their problem is given by:

$$\begin{aligned} \max _{\alpha _M^b \ge 0} \{ {\mathbb {E}}[\max (\alpha _M^b L_M (R^s_L - R^s_{CB}) + L_M (R^s_{CB} - R^s_D) + E_B R^s_D,0)]\}. \end{aligned}$$

(2)

The bank’s problem is the central element for our analysis and has three terms. The first term is the profit from private money creation and loan activities of Bank b. As all deposits created will move to other banks in the payment process, the bank has to settle the liabilities by central bank money, and thus public money, at interest rate factor $R^s_{CB}$. The intermediation margin $R_L^s - R_{CB}^s$ thus determines whether these activities generate profits or losses. The second term describes the consequences from deposits of other banks moving to Bank b. The intermediation margin $R_{CB}^s - R_D^s$ applies to this part. The third term stems from the reduction of bank debt when some of the deposits are transformed into bank equity and thus the bank has to pay less to debtors.

Two important remarks are in order. First, households have accounts distributed equally across all banks. If one bank creates more money (i.e. deposits) and loans than the average, then fewer deposits flow back to this bank than it has created when firms buy investment goods from households and pay with deposits to household accounts. The bank has to borrow this difference from the central bank, as it has to settle the ensuing liabilities with other banks. Hence, central bank borrowing is endogenous and a result of the money creation decision of an individual bank.

Second, by definition of $\alpha _M^{b}$, we always have $\int _{b \in [0,1]}{\alpha _M^{b} \mathrm {d}{b}}=1$. Hence, at the aggregate level net, borrowing of the banking system from the central bank is zero. This is a fundamental property of the two-tier system. At the aggregate level, the banking system cannot be a net borrower from the central bank at the stage when loans and money are created, since the banking system could not pay the interest rate on central bank money and some or all banks would need to default on the central bank. For individual banks, this is possible, since higher money creation than the average in the economy will lead to higher claims on central bank money in Period 1.

Finally, it may be useful to display all the interactions in figures: Fig. 2 summarizes the agents’ interactions during Period $t=0$. Figure 3 summarizes the agents’ interactions during Period $t=1$.

Fig. 2

Flows and interactions between agents during period $t=0$

Fig. 3

Flows and interactions between agents during period $t=1$

2.5 Definition of an equilibrium with banks

We look for symmetric equilibria with banks in the sequential market process described in Sect. 2.4. In a symmetric equilibrium with banks, all banks take the same decision regarding money creation and lending and thus have identical balance sheets in equilibrium. Moreover, the policy gross rates $(R_{CB}^s)_s$ are set by the central bank, so equilibria with banks are dependent on this choice. The gross rate of return on equity of an individual bank is equal to the shareholders’ value per unit of equity, and it is denoted by $R_E^{b,s} = \frac{\max (\Pi _B^{b,s},0)}{e_B}$.

Definition 1

Given the central bank policy gross rates $(R_{CB}^s)_s$, a symmetric equilibrium with banks in the sequential market process described in Sect. 2.4 is defined as a tuple

$$\begin{aligned} {\mathcal {E}} := \,&\Bigl ((R^s_E)_s,(R^s_D)_s,(R^s_L)_s,\mathbf{R }_\mathbf{F }, \\&p_I,(p^s_C)_s, \\&E_B,D_H,({\tilde{D}}^s_H)_s,L_M,S_F, \\&\mathbf{K }_\mathbf{M },\mathbf{K }_\mathbf{F }\Bigr ) \end{aligned}$$

consisting of positive and finite gross rates of return, prices, savings, bank deposits $D_H$ at the end of Stage C of Period $t=0$, bank deposits $({\widetilde{D}}_H^s)_s$ in Stage E of Period $t=1$, and the corresponding physical investment allocation, such that

• households hold some private deposits $D_H > 0$ at the end of Stage C,²²

• households maximize their expected utility

  $$\begin{aligned}&\max _{\{D_H,E_B,S_F\}} \left\{ E_B {\mathbb {E}} \left[ \frac{R^s_E}{p^s_C} \right] + D_H {\mathbb {E}} \left[ \frac{R^s_D}{p^s_C} \right] + \mathbf{f }(S_F)\right\} \\&\quad \text {s.t.} \quad E_B + D_H + p_I S_F - T= p_I \mathbf{W }, \end{aligned}$$

  taking gross rates of return $(R^s_E)_s$ and $(R^s_D)_s$ as well as prices $p_I$ and $(p^s_C)_s$ and lump sum taxation T as given,

• firms in MT and FT, as well as each bank $b \in [0,1]$, maximize their expected shareholders’ value, given respectively by

  $$\begin{aligned}&\max _{\mathbf{K }_\mathbf{M }\in [\mathbf{0 },\mathbf{W }]} \{ {\mathbb {E}}[\max (\mathbf{K }_\mathbf{M }(\mathbf{R }_\mathbf{M }^\mathbf{s }p^s_C - R^s_L p_I),0)] \}, \\&\max _{\mathbf{K }_\mathbf{F }\in [\mathbf{0 },\mathbf{W }]} \{ {\mathbb {E}}[\max ((\mathbf{f }(\mathbf{K }_\mathbf{F }) - \mathbf{K }_\mathbf{F }\mathbf{R }_\mathbf{F }) p^s_C,0)] \}, \\ \text {and} \quad&\max _{\alpha _M^b \ge 0} \{ {\mathbb {E}}[\max (\alpha _M^b L_M (R^s_L - R^s_{CB}) + L_M (R^s_{CB} - R^s_D) + E_B R^s_D,0)]\}, \end{aligned}$$

  taking gross rates of return $(R^s_D)_s$, $(R^s_L)_s$, and $\mathbf{R }_\mathbf{F }$, as well as prices $p_I$ and $(p^s_C)_s$ as given,

• all banks choose the same level of money creation, and

• markets for investment and consumption goods clear in each state. The market clearing conditions are:

  $$\begin{aligned} \mathbf{K }_\mathbf{M }= \frac{L_M}{p_I}, p_C^s = \frac{{\tilde{D}}_H^s}{\mathbf{K }_\mathbf{M }\mathbf{R }_\mathbf{M }^\mathbf{s }}, \text {with} \quad {\tilde{D}}_H^s := D_H R_D^s + \Pi _B^s, \end{aligned}$$

  where $\Pi _B^s$ are aggregate bank profits,

• the budgets of the monetary and fiscal authorities are balanced.

Three remarks are in order: First, ${\tilde{D}}_H^s$ are the aggregate deposits households have when they buy consumption goods and after they have received the profits from banks given by $\Pi _B^s$. Second, we always require that the budget of the monetary-fiscal authority is balanced. Hence, any shortfall on the fiscal side (when it would need to bailout banks) and on the monetary side (when banks are unable to pay back their borrowed reserves) is financed by lump-sum taxation of households. Formal details on the budget balance are given in Appendix A, and, in particular, in Stage D of Subcase II.b. Third, we have not specified the objective of the monetary-fiscal authority. All our results can be rephrased, however, by assuming that the monetary-fiscal authorities maximize welfare, i.e. the utility of the representative household. At the end of Sect. 4, we will discuss the results from this perspective.

In the remainder of the paper, we will use superscript $^*$ to denote equilibrium variables. Henceforth, for ease of presentation, an equilibrium with banks given $(R_{CB}^s)_s= l, h$ is an equilibrium in the sense of Definition 1.

3 Equilibria with banks

3.1 Individually optimal choices

In this subsection we prepare the characterization of equilibria with banks by determining the individually optimal choices of banks, households, and firms. We first consider the problem of firms in the MT sector and the resulting equilibrium condition. Since the technology is linear and there is limited liability, the representative firm’s demand of loans in sector MT is given by

• an infinite amount if $\mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s > R_L^s p_I$ for some $s = l,h$,

• any non-negative amount if $\mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s = R_L^s p_I$ for $s = l,h$,

• zero if $\mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s < R_L^s p_I$ for $s = l,h$.

Due to the Inada Condition that holds in the other sector, according to Lemma 4 in the Appendix A we can thus conclude that in any equilibrium with banks,

$$\begin{aligned} \mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s = R_L^s p_I \,\, \text {for } s = l,h. \end{aligned}$$

(3)

We note that we have assumed that contracts can be conditioned on the aggregate shock. This implies that although $\mathbf{K }_\mathbf{M }$ is chosen ex ante, the zero profit condition in sector MT in the above equation holds state by state. Otherwise, demand for the investment good would be zero or infinite, since the technology is linear. Moreover, note that in each state, revenues in nominal terms are given by $\mathbf{K }_\mathbf{M }\mathbf{R }_\mathbf{M }^\mathbf{s }p^s_C$, where $\mathbf{K }_\mathbf{M }\mathbf{R }_\mathbf{M }^\mathbf{s }$ is the amount of consumption goods that are produced. The firm borrows a real amount of $\mathbf{K }_\mathbf{M }$ investment goods and thus needs an amount of money equal to $\mathbf{K }_\mathbf{M }p_I$ from banks. This amount has to be paid back with interest and leads to the repayment obligations $\mathbf{K }_\mathbf{M }R^s_L p_I$. Then, in each state, the zero profit condition is

$$\begin{aligned} \underbrace{\mathbf{K }_\mathbf{M }\mathbf{R }_\mathbf{M }^\mathbf{s }}_\text {consumption good produced} {\cdot }\,\, p^s_C = R^s_L p_I \cdot \underbrace{ \mathbf{K }_\mathbf{M }}_\text {capital good acquired}, \end{aligned}$$

which implies (3). We next establish how deposit gross rates are related to policy gross rates. Since banks can grant loans to, or borrow from, other banks, we obtain

Lemma 1

In any equilibrium with banks, the nominal gross rates on the interbank market are equal to $R^s_{CB}$ for all states s=l,h.

The proof of Lemma 1 can be found in Appendix B.2. It is based on a simple arbitrage argument: Any differential in the gross rates could be used in the interbank market by borrowing or lending to infinitely increase expected shareholders’ value. We next investigate the optimal choice of money creation by an individual bank. For convenience, we denote circumstances in which no finite amount of money creation is optimal by “$\infty$”. We obtain

Proposition 1

If $R_D^s = R_{CB}^s$ in all states $s=l,h$, the privately optimal amounts of money creation and lending by an individual bank are represented by a correspondence denoted by²³${\hat{\alpha }}_M : {\mathbb {R}}_{+}^4 \times (0,1) \rightarrow {\mathcal {P}}({\mathbb {R}} \cup \{+\infty \})$. Define $\varphi _\circ$ as

$$\begin{aligned} \varphi _\circ = \frac{\sigma }{1-\sigma }\frac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}. \end{aligned}$$

Then the value of ${\hat{\alpha }}_M \bigl ( (R_L^s)_s, (R_{CB}^s)_s,\varphi \bigr )$ is given in the last column of Table 1 if all the conditions in a row are fulfilled.

The proof of Proposition 1 can be found in Appendix B.2. There are several observations to make. First, the banks’ behavior depends only on $(R_L^s - R_{CB}^s)_{s=l,h}$, which is the intermediation margin, on average lending by banks, and on their capital structure $\varphi$. If the intermediation margin is zero in all states, it is obvious that banks are indifferent between all lending levels. For positive intermediation margins in all states, banks would like to grant as many loans as possible. For negative intermediation margins, banks are not willing to grant any loans. Finally, if the intermediation margin is positive in one state and negative in the other state, banks can use shareholders’ limited liability and depositors’ bailout by the government to maximize their expected gross rate of equity return by defaulting against households in one state and by making large profits in the other. This strategy is only profitable in the following two cases: (i) when the expected intermediation margin is non-negative, i.e., banks can weakly increase their expected shareholders’ value even if they do not use limited liability and depositors’ bailout by the government, (ii) when the expected intermediation margin is negative and banks can sufficiently leverage on limited liability, which occurs when the banks’ equity ratio is sufficiently low. Next we turn to the households’ investment behavior.

Since households are risk-neutral, the representative household’s optimal portfolio choice solely depends on the expected real gross rates of return ${\mathbb {E}}\left[ \frac{R_{E{}}^{s}}{p_C^{s{}}}\right]$, ${\mathbb {E}}\left[ \frac{R_{D{}}^s}{p_C^{s{}}}\right]$, $R_F$ when choosing $E_B$, $D_H$, and $S_F$. The correspondences representing households’ optimal choices for different constellations of expected real gross rates of return are given in Lemma 5 in Appendix B.1. We next turn to the firms’ behavior.

Lemma 2

Demands for the investment good by firms in MT and FT are characterized by two correspondences denoted by $\hat{\mathbf{K }}_\mathbf{M }\in {\mathcal {P}}({\mathbb {R}} \cup \{ + \infty \})$ and $\hat{\mathbf{K }}_\mathbf{F }: {\mathbb {R}}_{+}\rightarrow {\mathcal {P}}( [\mathbf{0 },\mathbf{W }] )$, respectively:

$$\begin{aligned}&\hat{\mathbf{K }}_\mathbf{M }= [ \mathbf{0 }, \mathbf{+\infty }] \\ \text {and} \quad&\hat{\mathbf{K }}_\mathbf{F }(\mathbf{R }_\mathbf{F }) = \left\{ \begin{array}{ll} \{ \mathbf{0 }\} &{} \text {if} \,\,\, \mathbf{f }'(\mathbf{0 }) \le \mathbf{R }_\mathbf{F }, \\ \{ \mathbf{f }'^{-1}(\mathbf{R }_\mathbf{F }) \} &{} \text {otherwise.} \end{array} \right. \end{aligned}$$

The proof of Lemma 2 can be found in Appendix B.2. We note that in Sector MT, firms are indifferent between any investment level $\mathbf{K }_\mathbf{M }$, as the condition in Lemma 4, $\mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s = R_L^s p_I$ for $s=l,h$, implies that these firms make zero profits at any level of $\mathbf{K }_\mathbf{M }$.

Table 1 Results of Proposition 1

3.2 Characterization of equilibria with banks

The preceding lemmata enable us to characterize all equilibria with banks.

Theorem 1

Given the policy rates $(R_{CB}^s)_{s=l,h}$, all equilibria with banks take the following form:

$$\begin{aligned}&R_E^{s*} = R_D^{s*} = R_L^{s*} = R_{CB}^s, \quad \mathbf{R }_\mathbf{F }^\mathbf{* }= \overline{\mathbf{R }}_\mathbf{M }, \end{aligned}$$

(4)

$$\begin{aligned}&p_I^* = p, \quad p_C^{s*} = p \frac{R_{CB}^s}{\mathbf{R }_\mathbf{M }^\mathbf{s }}, \end{aligned}$$

(5)

$$\begin{aligned}&E_B^* = \varphi ^* p \Bigl (\mathbf{W }- \mathbf{f }'^{-1} \bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ) \Bigr ), \quad D_H^* = (1-\varphi ^*) p \Bigl (\mathbf{W }- \mathbf{f }'^{-1}\bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ) \Bigr ), \end{aligned}$$

(6)

$$\begin{aligned}&{\tilde{D}}_H^{s*} = p \Bigl (\mathbf{W }- \mathbf{f }'^{-1} \bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ) \Bigr ) R^s_{CB}, \end{aligned}$$

(7)

$$\begin{aligned}&L_M^* = p \Bigl ( \mathbf{W }- \mathbf{f }'^{-1} \bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ) \Bigr ), \quad S_F^* = \mathbf{f }'^{-1} \bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ), \end{aligned}$$

(8)

$$\begin{aligned}&\mathbf{K }_\mathbf{M }^\mathbf{* }= \mathbf{W }- \mathbf{f }'^{-1} \bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ), \quad \mathbf{K }_\mathbf{F }^\mathbf{* }= \mathbf{f }'^{-1} \bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ), \end{aligned}$$

(9)

where the price of the investment good denoted by $p \in (0,+\infty )$ and the aggregate equity ratio $\varphi ^* \in (0,1)$ are arbitrary. Equilibrium profits of firms and banks are given by

$$\begin{aligned}&\Pi _M^{s*} = 0, \quad \Pi _F^{s*} = p \frac{R_{CB}^s}{\mathbf{R }_\mathbf{M }^\mathbf{s }} \left( \mathbf{f }\Bigl ( \mathbf{f }'^{-1} \bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ) \Bigr ) - \mathbf{f }'^{-1} \bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ) \overline{\mathbf{R }}_\mathbf{M }\right) , \end{aligned}$$

(10)

$$\begin{aligned}&\Pi _B^{s*} = \varphi ^* p \Bigl (\mathbf{W }- \mathbf{f }'^{-1} \bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ) \Bigr ) R_{CB}^s. \end{aligned}$$

(11)

The proof of Theorem 1 can be found in Appendix B.2. We now look at the equilibrium conditions in detail. First, all nominal gross rates are equal to the policy gross rates set by the central bank, as expressed in (4). The equilibrium with banks is unique in real terms, i.e. the physical investments in both sectors expressed in (9), and thus with respect to the real values of lending and saving expressed in (8), where we divide $L_M^*$ by p.

As expressed in (6) the initial split of investments in banks into deposits and equity is indeterminate. In fact, in an equilibrium with banks any capital structure of banks can occur. Equation (7) reflects macroeconomic uncertainty, as the dividends and the deposit gross rates depend on the state of the world. Equations (10) and (11) represent the profits of firms and banks. The representative firm’s profits in Sector FT are paid in terms of the consumption good, while banks’ dividends are paid in the form of bank deposits.

Finally, the second equation in (5) relates the prices of the consumption good in different states to the price of the investment good. The latter is not determinate. The economic system is nominally anchored by the price of the investment good and by the central bank interest rate. While these parameters determine prices and interest rates, the asset structure and the payment processes are additionally determined by the capital structure of banks.

Here, more remarks are in order. First, no bank defaults in equilibrium. Indeed, the profits of any bank in State s are given by $\varphi ^* p \Bigl (\mathbf{W }- \mathbf{f }'^{-1} \bigl ( \overline{\mathbf{R }}_\mathbf{M }\bigr ) \Bigr ) R_{CB}^s$ and are thus positive. The reason is twofold. On the one hand, loan interest rates equal deposit interest rates in each state of the world. On the other hand, low gross rates of return $\mathbf{R }_\mathbf{M }^\mathbf{l }$ trigger a high price $p_C^{l*}$ for the consumption good, which enables firms in Sector MT to pay back their loans, which, in turn, enables banks to pay back depositors.

Second, the theorem shows that in any equilibrium with banks, private money creation is naturally limited. Since $R_L^{s*} = R_{CB}^s$ in both states $s=l,h$, banks have no incentive to increase money creation, as they would be forced to refinance themselves at the gross rates $(R_{CB}^s)_s$ to cover additional money creation. Third, the capital structure of banks has no impact on the physical investment allocation, so there is no need to regulate bank equity capital. Fourth, the physical investment allocation is independent of the central bank’s policy gross rates. Monetary policy is neutral.

Finally, it is important to stress that both conditions for the positive value of bank deposits are fulfilled: First, there are large gains from using and trading money, since MT firms can only produce if they obtain bank deposits and can buy investment goods. Second, banks do not default against the central bank because of sufficiently large penalties, and thus pay back any borrowed central bank money. If there were no penalties, banks could, for instance, pay larger dividends to equity holders in the form of deposits, but could not pay back the ensuing liabilities against the central bank when their deposits are used to buy consumption goods and flow to other banks.

There are important implications and a variety of further consequences of Theorem 1, which we summarize in the next subsection.

3.3 Welfare properties and implications

3.3.1 The first welfare result

We start with the characterization of the optimal investment allocation. Since house-holds are list-neutral the social planner’s problem is given by

$$\begin{aligned}&\max _{(\mathbf{K }_\mathbf{M },\mathbf{K }_\mathbf{F })} {\mathbb {E}}[\mathbf{K }_\mathbf{M }\mathbf{R }_\mathbf{M }^\mathbf{s }+ \mathbf{f }(\mathbf{K }_\mathbf{F })] \\&\quad \text {s.t.} \quad \mathbf{K }_\mathbf{M }+ \mathbf{K }_\mathbf{F }= \mathbf{W }. \end{aligned}$$

It is clear that household utility is maximized at $\mathbf{K_F^{FB}} := \mathbf{f }'^{-1} (\overline{\mathbf{R }}_\mathbf{M })$. This is called the “first-best allocation”. From Theorem 1, we immediately obtain

Corollary 1

For any policy gross rates $(R^s_{CB})_s$, the equilibria with banks yield the first-best allocation.

This result requires a careful interpretation. We have a model that deviates from a standard Arrow-Debreu setting in two ways. In particular, we consider one friction and two potential distortions that are at the center of the role of competitive money creation by banks:

• Moral hazard of entrepreneurs (and thus impossibility for households to invest directly into sector MT),

• Two-tier money creation and destruction: competitively by commercial banks via deposit/loan creation to firms and by central banks via deposit/loan creation to commercial banks,

• Guarantees of deposits by governments and thus bailout by governments in case of default, financed by taxes.

Alleviating moral hazard of entrepreneurs is standard in rationalizing the need for financial intermediaries. The two-tier money creation and destruction process is the object we want to analyze. The guarantee of deposits and the associated bailout of banks in case of default make deposits safe and thus are the precondition for bank deposits to be a medium of exchange.

On purpose, we make two assumptions that allow for the possibility that competitive money issuance by banks in the two-tier structure might achieve the first-best allocation: We assume that banks can eliminate moral hazard in MT at no cost, and taxation to fund the bailout of defaulting banks is lump-sum taxation and thus non-distortionary.

Given these favorable manifestations of the underlying frictions and distortions, it is a priori unclear what competitive money creation by banks and money creation by the central bank can achieve. Corollary 1 shows that we obtain the first-best allocation. This holds regardless of the central bank’s policy rate. The intuition follows from the explanation of Theorem 1: In equilibrium, money creation of banks is limited and no bank defaults. Furthermore, monetary policy only affects nominal interest rates and not physical investments.

As a direct consequence, the central bank that has the objective to maximize welfare is indifferent between any policy gross rates $(R_{CB}^s)_{s=l,h}$, as they all implement the first-best allocation. Essentially, Theorem 1 is a first welfare theorem for an economy with private money creation. It is a benchmark for the results we derive in the next section.

The preceding result is a new addition to Modigliani–Miller-type results. We show that for any liability structure of banks and any interest rate setting of central banks, competitive money creation by banks yields the first-best allocation. The result combines activities of the private sector and the public sector in one irrelevance result. It thus complements the original Modigliani–Miller Theorem, which shows that alternative corporate liability structures are irrelevant, and the public sector result by Wallace (1981), who has identified environments in which both the equilibrium consumption allocation and the path of the price level are independent from the path of the government’s portfolio if fiscal policy is held constant. Our result is also complementary to Chamley and Polemarchakis (1984), who show an irrelevance result for open market operations by the public sector. In particular, when government liabilities (including money) are held in private portfolios only as stores of value and do not provide additional liquidity services, real variables are not affected when the central bank engages in open market operations with real assets and no subsidies are distributed or taxes are levied. Our irrelevance result combines actions of the public sector in setting interest rates for bank refinancing and competitive loan and deposit issuance by banks with a given liability structure.

3.3.2 Unconditional nominal interest rates

We stress that the welfare theorem does not depend on whether the policy gross rates—and as a consequence, all nominal interest rates—depend on the state of the world. Indeed, another immediate consequence is given by

Corollary 2

Suppose that $R_{CB}^s$ is the same in both states s of the world. Then the nominal lending and deposit gross rates are not contingent on the states of the world, and the resulting allocation is first-best.

The corollary implies that the nominal gross rate of return on deposits does not need to depend on the macroeconomic shock to guarantee the first-best allocation. The reason is that in the event of a negative macroeconomic shock, firms in Sector MT compensate for lower real production gross rates of return by higher prices for the consumption good, thereby avoiding default against banks and rendering non-contingent deposits safe even without government intervention. The reason why the prices of the consumption good increase when a negative macroeconomic shock occurs is detailed below.

3.3.3 Nominal indeterminacy

The equilibria with banks described in Theorem 1 are indeterminate in two respects, with regard to (a) the price of the investment good and (b) the capital structure of banks. As to the former, it anchors the prices of the consumption goods. Since the market clearing condition for the investment goods is $\mathbf{K }_\mathbf{M }= \frac{L_M}{p_I}$ and $L_M$ is the aggregate money creation by banks, and banks in equilibrium are indifferent between different levels of money creation, the equilibria with banks are simply parametrized by the price of the investment good. All of these equilibria yield the same allocation for investment and consumption goods. Hence, it is sufficient to look at the equilibria with $p_I = 1$, as we do in the following. However, setting $p_I = 1$ in general as price normalization is not appropriate, since it would dictate the money creation banks would need to settle on. For other possible money creation choices, this would require rationing.

The indeterminacy of the capital structure in equilibrium is a macroeconomic manifestation of the Modigliani–Miller Theorem. As banks do not default in equilibrium and the gross rates of return on equity and deposits are the same, households are indifferent between equity and deposits. Moreover, different capital structures of banks have no impact on money creation and lending by banks. Finally, we note in the following corollary that with price normalization $p_I = 1$ and some capital structure choice $\varphi ^*$, all equilibrium values are uniquely determined.

Corollary 3

Given $p_I = 1$ and some $\varphi ^* \in (0,1)$, all equilibrium values are uniquely determined when the central bank sets the policy gross rates $(R_{CB}^s)_s$.

The relationship between the policy gross rates and the prices of the consumption good in different states of the world is contained in the following corollary:

Corollary 4

In any equilibrium with banks (and thus positive but finite money creation), the following holds:

• (i) If $R_{CB}^s$ does not depend on the state s of the economy, i.e. if $R_{CB}^l = R_{CB}^h$,

  $$\begin{aligned} \text {then} \quad p^h_C < p^l_C \quad \text {and} \quad \frac{p_C^l}{p_C^h} = \frac{\mathbf{R }_\mathbf{M }^\mathbf{h }}{\mathbf{R }_\mathbf{M }^\mathbf{l }}. \end{aligned}$$

• (ii) For central bank policy gross rates $(R_{CB}^s)_s$ characterized by

  $$\begin{aligned} \frac{R_{CB}^h}{R_{CB}^l} = \frac{\mathbf{R }_\mathbf{M }^\mathbf{h }}{\mathbf{R }_\mathbf{M }^\mathbf{l }}, \end{aligned}$$

  the price of the consumption good is independent of the state ($p_C^h = p_C^l$).

We note that central bank policy gross rates described in (ii) imply $R_{CB}^l < R_{CB}^h$. Corollary 4 stems from the equilibrium condition in (5) and is based on the following intuition: If $R_{CB}^s$ is independent of the state of the world and State l occurs, the households possess a comparatively large amount of deposits in Period $t=1$ when production has occurred, which causes the price of the consumption good to rise, as its supply is low. When the central bank chooses lower interest rates in bad states, the amount of created money declines in line with the supply of the consumption good. As a consequence, the price of the consumption good remains constant across states.

In the next section we explore potential cases of friction that may move allocations away from the first-best allocation and may even cause a collapse of the monetary system. We also explore whether monetary policy or capital regulation might help to restore efficiency. We note that constellations with unlimited money creation could not happen in a banking model that only comprises a real sector, as in such models, lending is constrained by the funding of banks with the investment good.

4 Price rigidities and capital requirements

4.1 Absence of capital requirements

In Section 4 we explore what happens when there are price rigidities and possibly the zero lower bound for the central bank interest rate. We also examine how capital requirements can improve equilibrium allocations. For this purpose, it is useful to introduce three types of situation:

(i):

money creation is positive and limited, but aggregate investment is distorted between sectors,

(ii):

money creation is zero, and physical investment occurs only in Sector FT, and

(iii):

money creation would be unlimited if banks existed. There thus exists only an equilibrium in which no household offers equity to banks and this unlimited money creation does not take place. All investment goods are channeled to Sector FT, and no lending to Sector MT occurs.

We assume in this section that nominal prices are perfectly rigid in the sense that they do not depend on the state of the world, and we assume that they are equal to some value $p_C$. One rationale is that prices have to be announced before macroeconomic shocks are realized, which implies $p_C^h = p_C^l$. For ease of presentation, we set to $p_C=1$, but the conclusions hold for any rigid price of the consumption good.²⁴ Moreover, we set $p_I = 1$, but the conclusions hold for any given price $p_I$. Throughout Sect. 4, the concept of price rigidities refers to $p_C^s = p_I = 1$ for both states $s=l,h$. While this is a stark scenario, the logic can be applied to any sort of commodity price rigidity. The price rigidities resolve the nominal price indeterminacy, but also require rationing schemes, since markets may not clear.

The outcome will depend on whether the central bank chooses its policy according to:

$$\begin{aligned} R_{CB}^s = \mathbf{R }_\mathbf{M }^\mathbf{s }. \end{aligned}$$

(12)

We first observe that if the central bank chooses the real gross rates of return as its policy gross rates according to (12), we recover the first-best equilibria with banks in Theorem 1 since in this case, the prices $p_C^s = p_I = 1$, $s = l, h$, are market clearing prices when we allow that all prices are flexible.

We next investigate circumstances where the central bank does not or cannot choose the policy gross rates according to (12). This occurs, for example, if $\mathbf{R }_\mathbf{M }^\mathbf{l }< 1$, i.e. the real gross rate of return in the bad macroeconomic state is sufficiently low, since due to the zero lower bound, the policy gross rate $R_{CB}^l$ cannot be set smaller than one.²⁵

Since with price rigidities, rationing may occur, we have to specify rationing rules for the market for investment goods and consumption goods. Regarding both markets, we assume that there is proportional rationing, i.e. market participants’ demand or supply is reduced proportionally to clear the markets. We will comment at the end of this section on the robustness of these rationing rules.

From the considerations of Proposition 1, we obtain

Proposition 2

Suppose prices are rigid and $R_{CB}^s \ne \mathbf{R }_\mathbf{M }^\mathbf{s }$ for some state s of the world. Then either there is no money creation, or it is unlimited.²⁶ In both cases, no equilibrium with banks exists and in all equilibria, all investments are channeled to Sector FT.

Proposition 2 follows from two considerations. First, money creation incentives of banks are governed by the return considerations outlined in Proposition 1. In addition, potential rationing does not change these incentives. For instance, if borrowers from banks are rationed in the market for investment goods and it is profitable for banks to issue more loans (and deposits), this incentive remains if borrowers are proportionally rationed, since still more loans and more money creation to the borrowers of a bank will lead to more investment goods for these borrowers, and thus more loans will be taken up from the bank under consideration.

Second, in a symmetric equilibrium with banks, an individual bank cannot grant more loans and generate more money creation than the average. Otherwise, money creation is unlimited, as all banks would try to create more money than the average. As a consequence, the monetary system would break down. In the case where no loan is granted, no money is created and only investment in Sector FT is possible, which constitutes an inefficient allocation. Moreover, we note that the equilibrium allocation of Proposition 2 is inefficient, as expected output is maximized only when investment is channeled to both sectors. Expected loss in output and therefore consumption is given by

$$\begin{aligned} \bigl (\mathbf{W }- \mathbf{f }'^{-1} (\overline{\mathbf{R }}_\mathbf{M }) \bigr )\overline{\mathbf{R }}_\mathbf{M }+ \mathbf{f }\bigl (\mathbf{f }'^{-1} (\overline{\mathbf{R }}_\mathbf{M })\bigr ) - \mathbf{f }(\mathbf{W }). \end{aligned}$$

An important remark is in order: Proposition 2 holds for any other type of rationing scheme as long as a higher amount of bank deposits in the hands of a firm in sector MT, borrowed from banks, translates into a higher amount of investment goods for this firm. It does not hold in one extreme case, when rationing is done on a per-capita basis, i.e. all rationed firms obtain the same amount of investment goods, irrespective of their demand. In this extreme case, banks never have incentives to issue more money than the average of banks.²⁷

Table 2 Possible constellations with price rigidities

The possible constellations with price rigidities are depicted in Table 2.

4.2 Capital requirements

We next investigate the extent to which whenever there is a difference between $R_{CB}^s$ and $\mathbf{R }_\mathbf{M }^\mathbf{s }$ for some state s a capital requirement can restore both the existence of an equilibrium with banks in the sense of Theorem 1 as well as efficiency. A capital requirement is defined as follows:

Definition 2

A minimum bank equity ratio $\varphi ^{reg}$ ($\varphi ^{reg} \in (0,1)$) requires each bank to hold more equity at the end of Period $t=0$ than the fraction $\varphi ^{reg}$ of its total assets. In other words, the realized equity ratio of each bank b, which we denote by $\varphi ^b$, has to be larger than $\varphi ^{reg}$.

We first establish a lemma describing how a capital requirement impacts money creation by an individual bank.

Lemma 3

Suppose the average capital structure in the economy is $\varphi$ and $\varphi ^{reg} \le \varphi$. Then the capital requirement $\varphi ^{reg}$ imposes an upper bound on individual money creation:

$$\begin{aligned} \alpha _M^b \le \frac{\varphi }{\varphi ^{reg}} \quad \hbox { for all banks}\ b. \end{aligned}$$

The proof of Lemma 3 can be found in Appendix B.2. We next determine the optimal money creation choice by banks when the government sets a capital requirement. When $R_{CB}^s \ne \mathbf{R }_\mathbf{M }^\mathbf{s }$ for some state s of the economy, money creation is either limited by the threat of default against the central bank, by the capital requirement, or it is not profitable. The detailed characterization of the correspondence describing these three situations is given in Lemma 6 in Appendix B.1. We use Lemma 6 to derive general conditions under which equilibria with banks exist when $R_{CB}^s \ne \mathbf{R }_\mathbf{M }^\mathbf{s }$ for some state s of the world.

Proposition 3

Suppose that prices are rigid and $R_{CB}^s < \mathbf{R }_\mathbf{M }^\mathbf{s }$ for some state s. Then there exists an equilibrium with banks if the central bank policy gross rates $(R_{CB}^s)_s$ and the capital requirement level $\varphi ^{reg}$ are set as either (i) or (ii):

• (i) ${\overline{R}}_{CB} = \overline{\mathbf{R }}_\mathbf{M }$ and $\max \left\{ \frac{R_{CB}^h - \mathbf{R }_\mathbf{M }^\mathbf{h }}{R_{CB}^h}, \frac{R_{CB}^l - \mathbf{R }_\mathbf{M }^\mathbf{l }}{R_{CB}^l} \right\} \le \varphi ^{reg}$.

• (ii) ${\overline{R}}_{CB} > \overline{\mathbf{R }}_\mathbf{M }$ and $0< \varphi ^{reg} = \max \left\{ \frac{1-\sigma }{\sigma } \frac{\mathbf{R }_\mathbf{M }^\mathbf{l }- R_{CB}^l}{R_{CB}^h}, \frac{\sigma }{1-\sigma } \frac{\mathbf{R }_\mathbf{M }^\mathbf{h }- R_{CB}^h}{R_{CB}^l}\right\} < 1$.

The proof of Proposition 3 is given in Appendix B.2. From Proposition 3 and its proof we can derive the welfare properties of equilibria with banks when a capital requirement is imposed. These welfare properties are summarized in the following corollary:

Corollary 5

Suppose that prices are rigid and $R_{CB}^s < \mathbf{R }_\mathbf{M }^\mathbf{s }$ for some state s. Then the central bank policy gross rates $(R_{CB}^s)_s$ and the capital requirement level $\varphi ^{reg}$ implement a socially efficient equilibrium with banks if and only if

$$\begin{aligned} {\overline{R}}_{CB} = \overline{\mathbf{R }}_\mathbf{M }\quad \text {and} \quad \max \left\{ \frac{R_{CB}^h - \mathbf{R }_\mathbf{M }^\mathbf{h }}{R_{CB}^h}, \frac{R_{CB}^l - \mathbf{R }_\mathbf{M }^\mathbf{l }}{R_{CB}^l}\right\} \le \varphi ^{reg}. \end{aligned}$$

The intuition for Proposition 3 and Corollary 5 runs as follows: Let us thus focus on $R_{CB}^s < \mathbf{R }_\mathbf{M }^\mathbf{s }$ for some state s. Then, banks would like to expand money creation to high, if not unlimited, levels because potential losses in the other state $s' \ne s$ would be bounded due to limited shareholder liability. Now, capital requirement can be effective by constraining money creation. Two cases may occur.

When ${\overline{R}}_{CB} = \overline{\mathbf{R }}_\mathbf{M }$ and capital requirements as given in the corollary and proposition, no bank has any incentive to push money creation above average, since first, losses in some state $s'$ exactly offset gains from money creation in the other state $s \ne s'$, and second, the minimum capital requirement is set at a level that prevents banks from defaulting against depositors and thus from leveraging on limited shareholder liability. By preventing default against depositors, such a minimum capital requirement induces socially efficient money creation and lending.

When ${\overline{R}}_{CB} > \overline{\mathbf{R }}_\mathbf{M }$ (and, as assumed, $R_{CB}^s < \mathbf{R }_\mathbf{M }^\mathbf{s }$ for some state s), banks would expand money creation above average in the absence of a capital requirement, since for an increasing money creation level, the shareholders’ value increases in some state s, while it stays at zero in the other state $s'$. Thus, the capital requirement directly limits money creation by preventing banks from granting any above-average amount of loans. In this case, even though such a minimum capital requirement restores a potential equilibrium with banks, it does not implement a socially efficient allocation.

The inefficiency in this case results from banks’ default against depositors. When they make their investment decision, households do not take into account the impact of banks’ default on the lump-sum taxes levied to bail them out. From the proof of Proposition 3 it is straightforward that the equilibria with banks’ default can be ranked in terms of welfare according to the capital requirement level $\varphi ^{reg}$. The intuition runs as follows: A larger equity ratio reduces the amount of taxes levied to bail out banks, which in turn improves households’ investment decision making. Therefore, the intensity of the inefficiency associated with banks’ default declines in the capital requirement level $\varphi ^{reg}$.

4.3 The zero lower bound and capital requirements

As a special case of the preceding considerations, we obtain the consequences when the central bank is constrained by the zero lower bound and prices are assumed to be rigid, i.e. when $p_C^{s*} = p_I^* = 1$ for all states $s=l,h$. From Corollary 5 we obtain

Corollary 6

Suppose that prices are rigid, $\mathbf{R }_\mathbf{M }^\mathbf{l }< 1 \le \overline{\mathbf{R }}_\mathbf{M }$, and the central bank is constrained by the zero lower bound ($R_{CB}^s \ge 1$ for all states $s=l,h$). Then there exist central bank policy gross rates $(R_{CB}^s)_s$ and capital requirement levels $\varphi ^{reg}$ such that the allocation of the resulting equilibrium with banks is socially efficient.

• (i) The central bank policy gross rates have to satisfy ${\overline{R}}_{CB} = \overline{\mathbf{R }}_\mathbf{M }$. One example is

  $$\begin{aligned} R_{CB}^l = 1, \quad R_{CB}^h = \frac{\overline{\mathbf{R }}_\mathbf{M }- (1-\sigma )}{\sigma }. \end{aligned}$$

• (ii) The regulatory capital requirement levels $\varphi ^{reg}$ have to satisfy

  $$\begin{aligned} \varphi ^{reg} \ge \frac{R_{CB}^l - \mathbf{R }_\mathbf{M }^\mathbf{l }}{R_{CB}^l}. \end{aligned}$$

The proof of Corollary 6 can be found in Appendix B.2. Corollary 6 shows that price rigidities and the zero lower bound can be countered by a suitable combination of monetary policy and capital regulation. The capital requirement ensures that money creation is sufficiently constrained for no individual bank to default. The central bank policy gross rates $R_{CB}^l = 1$, $R_{CB}^h = \frac{\overline{\mathbf{R }}_\mathbf{M }- (1-\sigma )}{\sigma }$ ensure that in the good state gains from money creation are sufficiently high to offset losses in the bad state. In other words, setting $R_{CB}^h < \mathbf{R }_\mathbf{M }^\mathbf{h }$ generates sufficient incentives for banks to lend and to create money. The capital requirement, in turn, ensures that money creation does not become excessive. We note that any monetary policy that satisfies ${\overline{R}}_{CB} = \overline{\mathbf{R }}_\mathbf{M }$ achieves the same purpose and induces a socially efficient allocation. In Appendix C we illustrate our results with a simple numerical example.

From Corollary 5 and the proof of Proposition 3 we also immediately obtain

Proposition 4

Suppose that prices are rigid, $\overline{\mathbf{R }}_\mathbf{M }< 1$, and the central bank is constrained by the zero lower bound ($R_{CB}^s \ge 1$ for all states $s=l,h$). Then there exist no central bank policy gross rates $(R_{CB}^s)_s$ and capital requirement level $\varphi ^{reg}$ making the allocation of the resulting equilibrium with banks socially efficient. We derive two cases:

• If $1 < \mathbf{R }_\mathbf{M }^\mathbf{h }$, there exist central bank policy gross rates $(R_{CB}^s)_s$ and a capital requirement level $\varphi ^{reg}$ implementing equilibria with banks.

  • (a) The central bank policy gross rates have to satisfy $R_{CB}^h < \mathbf{R }_\mathbf{M }^\mathbf{h }$. An example is

    $$\begin{aligned} R_{CB}^l = R_{CB}^h = 1. \end{aligned}$$

  • (b) The regulatory capital requirement level $\varphi ^{reg}$ has to satisfy

    $$\begin{aligned} \varphi ^{reg} = \frac{\sigma }{1-\sigma } \frac{\mathbf{R }_\mathbf{M }^\mathbf{h }- R_{CB}^h}{R_{CB}^l}. \end{aligned}$$

• If $\mathbf{R }_\mathbf{M }^\mathbf{h }\le 1$, there are no central bank policy gross rates $(R_{CB}^s)_s$ and capital requirement level $\varphi ^{reg}$ implementing an equilibrium with banks.

Proposition 4 states that in a depressed economy characterized by $\overline{\mathbf{R }}_\mathbf{M }< 1$, where prices are rigid and the central bank is constrained by the zero lower bound, money creation can only be induced by a suitable combination of monetary policy and capital regulation if $\mathbf{R }_\mathbf{M }^\mathbf{h }> 1$.

If $\mathbf{R }_\mathbf{M }^\mathbf{h }\le 1$, the only possible equilibrium is the equilibrium without banks, which is inefficient, as all investments are channeled to FT. The reason is that under any feasible monetary policy and even with no capital requirement, money creation and lending are not profitable in such cases.

If $\overline{\mathbf{R }}_\mathbf{M }< 1$ but $1 < \mathbf{R }_\mathbf{M }^\mathbf{h }$, the central bank and the bank regulators can only make banking profitable and thus trigger money creation and lending by inducing profits in the good state and letting them default against depositors in the bad state. From the proof of Proposition 3 we deduce that the policy gross rates inducing the equilibrium with banks with highest welfare are given by $R_{CB}^s = 1$ for $s=l,h$. Moreover, a capital requirement has to be imposed on banks to prevent unlimited money creation.

The equilibria associated with the policy gross rates $R_{CB}^s = 1$ for $s=l,h$ in the case $1 < \mathbf{R }_\mathbf{M }^\mathbf{h }$ are inefficient. Hence, the central bank and the bank regulators will implement such a policy only if the welfare induced by the policy described in Proposition 4, (a) and (b), is higher than the welfare associated to the equilibrium without banks. A sufficient condition for this is $\mathbf{f }(\mathbf{W }) < \overline{\mathbf{R }}_\mathbf{M }\mathbf{W }$.

The above result in the cases $\overline{\mathbf{R }}_\mathbf{M }< 1$ and $\mathbf{R }_\mathbf{M }^\mathbf{h }> 1$ can be interpreted in terms of Forward Guidance.²⁸ The central bank announces that it will set the policy gross rates at 1 in both states of the world, even if the real gross rate $\mathbf{R }_\mathbf{M }^\mathbf{h }$ is larger than one. This announcement means that banks can expect positive profits in the good state of the world, thereby making money creation and lending profitable. This stimulates money creation and lending at the zero lower bound. However, in the bad state of the world money creation is associated with bank failures, so expected social welfare is lower than in the first-best allocation.

In summary, price rigidity does not cause a welfare loss unless the central bank does not or cannot set the policy rates appropriately. The latter situation occurs when the zero lower bound prevents the equalization of the policy rate and the real rate of return in the bad state. In such an environment, money creation either is unlimited or it is not attractive. Both cases result in a collapse of the banking system and in an equilibrium without banks. When money creation is profitable, capital requirements are a suitable tool to control the incentive to create money and to restore the existence of equilibria with banks.

4.4 Optimal policies

The analysis in the paper reveals three results on optimal policies by the monetary-fiscal authority. First, with flexible prices, any monetary policy leads to the first-best allocation. Second, with rigid prices and no zero lower bound constraint and no capital requirements, we obtain the first-best allocation if and only if the relative magnitudes of central bank interest rates across states equal the relative magnitudes of real interest rates across states. Third, if the central bank interest rates cannot match the relative magnitudes of real interest rates across states, but expected real interest rates are non-negative, a judicious combination of central bank interest rate setting and capital requirements can achieve a first-best allocation. Fourth, if expected real interest rates are negative, no combination of monetary policy and capital requirements can induce an equilibrium with the first-best allocation. If the real interest rate is positive in one state of the world, a judicious combination of monetary policy and capital requirements leads to second-best allocations in the sense that banks are active in equilibrium, but the amount of investment goods channeled to sector MT is inefficient.

5 Conclusion

The integration of money creation by commercial banks into a general equilibrium setting allows to investigate the interaction between monetary policy and capital regulation. Our main findings are as follows: In a general equilibrium economy without price rigidities, any policy rate set by the central bank implements equilibria with banks that are first-best. In these equilibria, money creation is naturally limited, so there is no need for capital regulation. However, if prices are rigid, equilibria with banks only exist for certain values of the central bank policy rates. Moreover, the central bank policy rates may cause unfavorable situations: Either money creation is unlimited, or lending may not be profitable and money may not be created at all. Both types of failure are associated with inefficient equilibria.

In addition, when the central bank policy is constrained by the zero lower bound, there may not even exist a central bank monetary policy with positive and finite money creation. Capital regulation in the form of a minimum equity ratio is an effective tool for limiting money creation, so it can restore the existence of equilibria with banks and also social efficiency. Finally, when prices are rigid, Forward Guidance together with capital regulation can only stimulate money creation and lending if economic conditions are sufficiently favorable.

Numerous extensions can be performed. In our working paper Faure and Gersbach (2018), we discuss how the results might be extended (i) in the presence of financial frictions at the bankers’ level, (ii) when bonds are denominated in nominal terms, (iii) when there are more than two states of the world, (iv) when we also consider asymmetric equilibria with banks, (v) when there are real costs for monitoring activities, (vi) when the lending rates or the real deposit rates cannot be written contingently on the state of the economy, and (vii) when a reserve requirement and a haircut rule for borrowing against the central bank are imposed by government authorities. While our results continue to hold for extensions (ii), (iii), (v), and (vi), we obtain three further insights: First, in the presence of financial frictions, there are equilibria with banks only when capital regulation is adequately combined with monetary policy. Second, there exist inefficient asymmetric equilibria with banks when prices are flexible and suitable capital requirements eliminate these inefficient equilibria with banks, so that only efficient equilibria with banks remain. Finally, we show that the impact of a reserve requirement coupled with a haircut rule on money creation is identical to the impact of a minimum equity ratio requirement.

Numerous further extensions and generalizations along the line of Magill and Quinzii (1992) deserve scrutiny. We outline the main ones here. Risk aversion of households and more sophisticated portfolio decisions between bank equity and deposits are an obvious candidate. Integrating an active government that provides public goods financed by taxation or debt would provide an opportunity to examine the potential and limits of Quantitative Easing. A more elaborate model of this kind could also provide insights into the role of collaterals and haircuts, as well as their impact on investments. Further down the line, variants of the model could be used in a dynamic setting with more than one period. This would be useful for investigating the impact of monetary policy and capital regulation on inflation and price stability.

Appendices

Appendices

1.1 A Sequence of events

In this Appendix we describe every detail of the sequence of events. We first start with the periods and then describe more complex stages in detail.

1.2 A.1 The periods

1.2.1 A.1.1 Period t = 0

It is convenient to describe the sequence of economic activities via the balance sheets of households and banks. The economy starts with the balance sheets in Table 3.

Table 3 Balance sheets at the beginning of period $t=0$

$E_H$ denotes the households’ equity, which represents the ownership of the investment good and both production technologies at the beginning of Period $t=0$.²⁹

Stage A: Foundation of Banks.

Either banks are not founded because no household invests in bank equity and the only possible allocation is given in Sect. A.1.2, or households found banks by pledging to convert a predefined share $\varphi \in (0,1]$ of their initial deposits $D_M$ into an amount $E_B = \varphi D_M$ of bank equity before production in Stage C. When banks are founded, the gross rate of return on equity is equal to shareholders’ value per unit of equity, and it is denoted by $R_E^{b,s} = \frac{\max (\Pi _B^{b,s},0)}{e_B}$. In the remainder of Sect. 2.4, we focus on the case where banks are founded (unless specified otherwise).

Stage B: Granting of Loans by Banks.

Bank b grants loans $l_M^b = \alpha _M^b L_M$ to firms in MT at the contingent nominal lending gross rates $(R_L^s)_s$, which simultaneously creates $d_M^b$ private deposits at Bank b and aggregate private deposits $D_M$.³⁰ The resulting balance sheets are given in Table 4.

Stage C: Payment Process, Investment in FT, and Payment of Bank Equity.

Table 4 Balance sheets at the end of Stage B

Households sell an amount of the investment good to firms in MT. Then they invest in FT by buying $S_F$ bonds denominated in real terms at the real gross rate of return $\mathbf{R }_\mathbf{F }$, meaning that such a bond costs one unit of investment good and promises the delivery of $\mathbf{R }_\mathbf{F }$ units of the consumption good once production has occurred.³¹ Finally, at the end of Period $t=0$, households pay for the equity $E_B$ pledged in Stage A with deposits, which reduces the amount of deposits in the economy. The resulting amount of deposits is denoted by $d_H$ for an individual bank and $D_H = L_M - E_B$ for the aggregate banking system. At the end of Stage C and depending on their lending decisions, some banks labeled $b_i$ have claims $d_{CB}^{b_i}$, and the other banks have liabilities $l_{CB}^{b_j}$ against the central bank. These processes are detailed in Appendix A.2. The balance sheets are displayed in Table 5.³²

Table 5 Balance sheets at the end of Stage C

A summary of the agents’ interactions during Period $t = 0$ is given in Fig. 2.

1.2.2 A.1.2 Period t=1

In Period $t=1$ we distinguish between two cases, when either no bank is founded by households, or banks are founded by households. The latter case can again be divided into two subcases: Either no bank defaults, or some banks default.

Case I: No Bank Is Founded.

When no bank is founded, we have $E_B = 0$. This could constitute an equilibrium, as no household can found a bank individually. We call this an equilibrium without banks. In such circumstances, no money creation takes place, the central bank is inactive, no investment in MT is possible, and the investment good is allocated entirely to Sector FT, which leads to the following allocation: $\mathbf{K }_\mathbf{M }^\mathbf{* }= \mathbf{0 }, \mathbf{K }_\mathbf{F }^\mathbf{* }= \mathbf{W }$.³³ where $^*$ denotes equilibrium variables. This is an inefficient allocation, as households are risk-neutral and the assumption on the production function $\mathbf{f }(\cdot )$ has stipulated that $\mathbf{f }'(\mathbf{W }) < \overline{\mathbf{R }}_\mathbf{M }$.³⁴

Case II: Banks are Founded.

When banks are founded, they grant loans to firms in MT, and we can considerably simplify the description of Period $t=1$ by making the observation given by Lemma 4:

Lemma 4

An equilibrium with banks (and thus positive lending to Sector MT) requires $\mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s = R_L^s p_I$. It implies $\Pi _M^s = 0$ for $s=l,h$.

Lemma 4 is a direct consequence of the MT technology. If for some state s, $\mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s > R_L^s p_I$, firms in MT would demand an infinite amount of loan, as their shareholders’ value per loan unit would be positive in one state, be at least zero in the other state,³⁵ and scale with the level of borrowing. If $\mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s < R_L^s p_I$ for both states of the world, firms would forgo borrowing from banks.³⁶

Subcase II.a: No Bank Defaults.

Suppose next that no bank defaults. Then the following stages occur:

Stage D: Production. The macroeconomic state s is realized. Firms produce and repayments contingent on s fall due. Using bank balance sheets in Table 5 as well as the expression of the net position of Bank b against the CB given by Eq. (14) in Appendix A.2, we derive the expression of Bank b’s profits as follows:

$$\begin{aligned} \Pi _B^{b,s}&= (1 - \alpha _M^b) L_M R_{CB}^s + \alpha _M^b L_M R_L^s - d_H R_D^s \nonumber \\&= (1 - \alpha _M^b) L_M R_{CB}^s + \alpha _M^b L_M R_L^s - (L_M - E_B) R_D^s \nonumber \\&= \alpha _M^b L_M (R_L^s - R_{CB}^s) + L_M (R_{CB}^s - R_D^s) + E_B R_D^s. \end{aligned}$$

(13)

Table 6 Balance sheets at the end of Stage D if no bank defaults

Profits from firms in the real sector are given by

$$\begin{aligned} \Pi _M^s&= \mathbf{K }_\mathbf{M }(\mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s - R_L^s p_I), \\ \Pi _F^s&= (\mathbf{f }(\mathbf{K }_\mathbf{F }) - \mathbf{K }_\mathbf{F }\mathbf{R }_\mathbf{F }) p_C^s. \end{aligned}$$

The balance sheets are given in Table 6, where $R_H^s$ denotes the resulting nominal gross rate of return on household ownership of the investment good and of both production technologies.

Stage E: Dividend Payment, Repayment of Debt, and Payment Process. Households obtain dividends from their equity investment³⁷ and buy the amount of consumption good produced. All debts are paid back. These processes are detailed in Appendix A.3. The resulting balance sheets are given in Table 7.

Table 7 Balance sheets at the end of Stage E if no bank defaults

Subcase II.b: Some Banks Default.

Finally, we consider the scenario where some banks default. In this case, Stages D and E have to be modified as follows:

Stage D: Production and Government Taxation. The macroeconomic state s is realized. Firms produce, and repayments fall due. Two cases can occur. First, if $- d_H R_D^s \le \Pi _B^{b,s} < 0$, Bank b defaults on households but not on the central bank. Second, if $\Pi _B^{b,s} > 0$, Bank b does not default. We note that the case $\Pi _B^{b,s}< -d_H R_D^s < 0$ cannot occur, as banks would default on households and the central bank. Due to the heavy penalties incurred for default against governmental authorities banks will avoid the latter case under all circumstances.

Consider now a non-defaulting bank b. If $R_{CB}^s > R_L^s$ for some state s, there then exists an upper bound on $\alpha _M^b$ given by

$$\begin{aligned} \alpha _M^b \le \alpha _{DH}^s := \frac{R_{CB}^s - (1-\varphi )R_D^s}{R_{CB}^s - R_L^s}, \end{aligned}$$

such that this bank does not default on households in State s. $\alpha _{DH}^s$ is the critical amount of money creation at which a bank is just able to pay back depositors in State s. $\alpha _{DH}^s$ is obtained from Eq. (13) by setting $\Pi _B^{b,s} = 0$ and using $D_{H} = L_{m}$ and $\varphi = \frac{E_B}{L_M}$. From now on, consider a defaulting bank b. If $R_{CB}^s > R_L^s$ for some state s, there exist a lower bound $\alpha _{DH}^s$ and an upper bound $\alpha _{DCB}^s$ for $\alpha _M^b$ given by

$$\begin{aligned} \alpha _{DH}^s < \alpha _M^b \le \alpha _{DCB}^s := \frac{R_{CB}^s}{R_{CB}^s - R_L^s}, \end{aligned}$$

which mark two default points. For $\alpha _M^b \in (\alpha _{DH}^s, \alpha _{DCB}^s]$, Bank b defaults against households but not against the central bank in State s. For $\alpha _M^b > \alpha _{DCB}^s$, the bank would default against households and the central bank in State s. $\alpha _{DCB}^s$ is the critical amount of money creation at which a bank is just able to pay back the central bank in State s. $\alpha _{DCB}^s$ is obtained from Eq. (13) by setting $\Pi _B^{b,s} = -D_H R_D^s$. The lump-sum tax levied to bail out Bank b in State s is denoted by $t^{b,s}$. Aggregate tax payments in State s by households are then given by

$$\begin{aligned} T^s = \int _{b \in [0,1]}{t^{b,s} \mathrm {d}b}. \end{aligned}$$

Furthermore, we use $\Pi _B^{+,s}$ to denote the aggregate profits of non-defaulting banks in State s. The balance sheets possible are given in Table 8.

Table 8 Balance sheets at the end of Stage D if some banks default

In Table 8, the labels $b_{i'}$ and $b_{j'}$ denote banks with a non-negative and negative net position against the CB, respectively. The exact expressions of $d_{CBT}^{b_{i'}}$ and $l_{CBT}^{b_{j'}}$ are not needed for the subsequent analysis, but for completeness they are given in Appendix A.4. We note that the balance sheets in Table 8 are structurally identical to the ones in Subcase II.a of Sect. A.1.2. Therefore, the description of Stage E is similar to the one laid out in Appendix A.3. A summary of the agents’ interactions during Period $t = 1$ is given in Fig. 3, page 12.

1.3 A.2 Stage C

We examine the detailed payment process, investment in FT, and payment of bank equity in Stage C through a series of substages. For this purpose, we index all variables changing in some substage by an integer starting from 1.

Stage C, Substage 1: Borrowing of Banks from the CB

In order to have enough CB deposits to guarantee payments using bank deposits, Bank b borrows from the central bank the amount of³⁸

$$\begin{aligned} d_{{CB}_1}^b := l_M^b = \alpha _M^b D_M. \end{aligned}$$

As a result, an aggregate amount of CB deposits amounting to $D_{{CB}_1} := D_M > 0$ is created. The balance sheets of banks and households are given in Table 9.

Table 9 Balance sheets at the end of Stage C, Substage 1

Stage C, Substage 2: Sale of an Amount of Investment Good to MT

We assume that firms in MT buy the largest possible amount of investment good they can afford and do not hold deposits in the production stage D:³⁹

$$\begin{aligned} \mathbf{K }_\mathbf{M }= \frac{L_M}{p_I}. \end{aligned}$$

In order to settle these payments, each bank b transfers $d_M^b = \alpha _M^b D_M$ to other banks and receives the same amount $d_{H_1} := D_M$ from other banks in the form of CB deposits. We note that $d_{H_1}$ does not depend on the individual bank b due to our assumption that households keep deposits evenly distributed across all banks at all times. The corresponding aggregate amount is denoted by $D_{H_1}$. This transaction impacts CB deposits of Bank b as follows:

$$\begin{aligned} d_{CB_2}^b := d_{CB_1}^b - \alpha _M^b D_M + D_M = D_M. \end{aligned}$$

The balance sheets of banks and households are given in Table 10.

Table 10 Balance sheets at the end of Stage C, Substage 2

Stage C, Substage 3: Investment in FT

When buying $S_F$ bonds from firms in FT, households deliver $\mathbf{K }_\mathbf{F }= S_F$ units of the investment good against the promise to obtain $\mathbf{K }_\mathbf{F }\mathbf{R }_\mathbf{F }$ units of the consumption good from FT after production has taken place. The balance sheets of banks and households are given in Table 11.

Table 11 Balance sheets at the end of Stage C, Substage 3

Stage C, Substage 4: Netting of CB Deposits and CB Loans

Now banks can net their CB deposits and CB loans, as no further payment has to be made before production. We use

$$\begin{aligned} \delta ^b := d_{CB_2}^b - l_{CB_1}^b = (1 - \alpha _M^b) L_M \end{aligned}$$

(14)

to denote the net position of Bank b against the CB. We distinguish banks with claims against the central bank from banks that are debtors of the central bank:

$$\begin{aligned}&B_I := \{b_i \in [0,1] \quad \text {s.t.} \quad \delta ^{b_i} \ge 0\} \\ \text {and} \quad&B_J := \{b_j \in [0,1] \quad \text {s.t.} \quad \delta ^{b_j} < 0\}. \end{aligned}$$

Net claims against the central bank are denoted by $d_{CB}^{b_i} := \delta ^{b_i}$ for all $b_i \in B_I$ and net liabilities by $l_{CB}^{b_j} := -\delta ^{b_j}$ for all $b_j \in B_J$. Table 12 reports the balance sheets of banks and households.

Stage C, Substage 5: Payment of Bank Equity

Now households pay equity $E_B = \varphi D_M > 0$ pledged in $t=1$, thereby destroying the corresponding amount of bank deposits. We use $D_H = (1-\varphi ) D_M$ to denote the remaining amount of deposits. Hence, $D_{H_1} = E_B + D_H$. The balance sheets of two typical banks representing a net depositor and a net borrower from the central bank are displayed in Table 5.

Table 12 Balance sheets at the end of Stage C, Substage 4

1.4 A.3 Stage E

We examine the detailed dividend payment, payback of debt, and payment process of Stage E through a series of substages. Similarly to Appendix A.2, when a variable changes in some substage, we increase the index by 1 starting with the last index from Appendix A.2.

Stage E, Substage 1: Borrowing of Banks from the CB

In order to have enough CB deposits to guarantee payments using bank deposits, Bank b borrows from the central bank the amount of $l_{CB_3}^{b,s} = d_{CB_3}^{b,s} := D_H R_D^s + \Pi _B^{b,s}$. We use the notations

$$\begin{aligned} d_{CB_4}^{b_i,s}&:= d_{CB_3}^{b_i,s} + d_{CB}^{b_i} R_{CB}^s \\ \text {and} \quad l_{CB_4}^{b_j,s}&:= l_{CB_3}^{b_j,s} + l_{CB}^{b_j} R_{CB}^s. \end{aligned}$$

The balance sheets of banks and households are given in Table 13.

Table 13 Balance sheets at the end of Stage E, Substage 1

Stage E, Substage 2: Dividend Payment

Bank profits are paid as dividends to households. This creates bank deposits, and households’ deposits at Bank b become ${\tilde{d}}_H^s := D_H R_D^s + \Pi _B^s$. The aggregate amount of households’ deposits is then denoted by ${\tilde{D}}_H^s$. In order to settle these payments, each bank b transfers $\Pi _B^{b,s}$ to other banks and receives $\Pi _B^s$ from other banks in the form of CB deposits. These processes impact CB deposits of Banks $b_i$ and $b_j$ as follows:

$$\begin{aligned}&d_{CB_6}^{b_i,s} := d_{CB_4}^{b_i,s} - \Pi _B^{b_i,s} + \Pi _B^s = d_{CB}^{b_i} R_{CB}^s + D_H R_D^s + \Pi _B^s \\ \text {and} \quad&d_{CB_5}^{b_j,s} := d_{CB_3}^{b_j,s} - \Pi _B^{b_j,s} + \Pi _B^s = D_H R_D^s + \Pi _B^s . \end{aligned}$$

The balance sheets of banks and households are given in Table 14.

Table 14 Balance sheets at the end of Stage E, Substage 2

Stage E, Substage 3: Repayment of Debt and Distribution of Profits

From the repayment of debt $S_F \mathbf{R }_\mathbf{F }$ and the distribution of profits $\Pi _F^s$, both in terms of the consumption good, households obtain $\mathbf{f }(\mathbf{K }_\mathbf{F })$ units of the consumption good. The balance sheets of banks and households are given in Table 15.

Table 15 Balance sheets at the end of Stage E, Substage 3

Stage E, Substage 4: Sale of the Consumption Good Produced by MT

Firms in MT sell all of their consumption goods. Households buy it with their private deposits consisting of their wealth in terms of equity and deposits.⁴⁰ The supply of $\mathbf{K }_\mathbf{M }\mathbf{R }_\mathbf{M }^\mathbf{s }$ units of the consumption good meets the real demand $\frac{{\tilde{D}}_H^s}{p_C^s}$. Hence, the equilibrium price is given by

$$\begin{aligned} p_C^s = \frac{{\tilde{D}}_H^s}{\mathbf{K }_\mathbf{M }\mathbf{R }_\mathbf{M }^\mathbf{s }}. \end{aligned}$$

In order to settle these payments, each bank b transfers ${\tilde{d}}_H^s$ to other banks and receives an amount $d_{M_1}^{b,s} := \alpha _M^b {\tilde{d}}_H^s$ from other banks in the form of CB deposits. By summing over all banks $b \in [0,1]$ in the expression of banks’ profits in Eq. (13), we obtain $L_M R_L^s = D_H R_D^s + \Pi _B^s$, which means that $d_{M_1}^{b,s} = \alpha _M^b L_M R_L^s$. These operations impact CB deposits of Banks $b_i$ and $b_j$ as follows:

$$\begin{aligned}&d_{CB_8}^{b_i,s} := d_{CB_6}^{b_i,s} - {\tilde{d}}_H^s + d_{M_1}^{b_i,s} = \alpha _M^{b_i} L_M R_L^s + d_{CB}^{b_i} R_{CB}^s \\ \text {and} \quad&d_{CB_7}^{b_j,s} := d_{CB_5}^{b_j,s} - {\tilde{d}}_H^s + d_{M_1}^{b_j,s} = \alpha _M^{b_j} L_M R_L^s. \end{aligned}$$

The balance sheets of banks and households are given in Table 16.

Table 16 Balance sheets at the end of Stage E, Substage 4

Stage E, Substage 5: Repayment of Loans by Firms in MT

Firms in MT pay back their loans, and bank deposits are destroyed. The balance sheets of banks and households are given in Table 17.

Table 17 Balance sheets at the end of Stage E, Substage 5

Stage E, Substage 6: Netting of CB Deposits and CB Loans

Banks net their CB deposits and CB loans. Using the expression of bank profits given by Eq. (13), we obtain

$$\begin{aligned} d_{CB_8}^{b_i,s} - l_{CB_3}^{b_i,s}&= \alpha _M^{b_i} L_M R_L^s + (1-\alpha _M^{b_i}) L_M R_{CB}^s - \bigl ( (L_M - E_B) R_D^s + \Pi _B^{b_i,s} \bigr ) = 0, \\ d_{CB_7}^{b_j,s} - l_{CB_4}^{b_j,s}&= \alpha _M^{b_j} L_M R_L^s - (\alpha _M^{b_j} - 1) L_M R_{CB}^s - \bigl ( (L_M - E_B) R_D^s + \Pi _B^{b_j,s} \bigr ) = 0. \end{aligned}$$

1.5 A.4 Net positions of banks against the CB after a bailout

In Table 8 the label $b_{i'}$ denotes banks with a non-negative net position against the CB. For completeness, the net position is given by

$$\begin{aligned} d_{CBT}^{b_{i'}} := \left\{ \begin{array}{l@{\quad }l} d_{CB}^{b_{i'}} R_{CB}^s - T^s &{} \text {if} \, d_{CB}^{b_{i'}} R_{CB}^s - T^s \ge 0 \, \text {and} \, \Pi _B^{b_{i'},s} \ge 0, \\ d_{CB}^{b_{i'}} R_{CB}^s - T^s + t^{b_{i'},s} &{} \text {if} \, d_{CB}^{b_{i'}} R_{CB}^s - T^s + t^{b_{i'},s} \ge 0 \, \, \Pi _B^{b_{i'},s}< 0, \, \\ t^{b_{i'},s} - T^s - l_{CB}^{b_{i'}} R_{CB}^s &{} \text {if} \, l_{CB}^{b_{i'}} R_{CB}^s + T^s - t^{b_{i'},s} \le 0 \, \, \Pi _B^{b_{i'},s} < 0, \\ \end{array} \right. \end{aligned}$$

where $T^s$ are the tax payments introduced in Sect. A.1.2 representing the households’ deposit withdrawals to pay taxes in State $s=l,h$ and $t^{b_{i'},s}$, the possible bailout in State $s=l,h$ if Bank $b_{i'}$ defaults against households. Similarly, the label $b_{j'}$ denotes banks with a negative net position against the CB:

$$\begin{aligned} l_{CBT}^{b_{j'}} := \left\{ \begin{array}{l@{\quad }l} l_{CB}^{b_{j'}} R_{CB}^s + T^s &{} \text {if} \, \Pi _B^{b_{j'},s} \ge 0, \\ T^s - d_{CB}^{b_{j'}} R_{CB}^s &{} \text {if} \, d_{CB}^{b_{j'}} R_{CB}^s - T^s< 0 \, \text {and} \, \Pi _B^{b_{j'},s} \ge 0, \\ T^s - t^{b_{j'},s} - d_{CB}^{b_{j'}} R_{CB}^s &{} \text {if} \, d_{CB}^{b_{j'}} R_{CB}^s - T^s + t^{b_{j'},s}< 0\, \text {and} \, \Pi _B^{b_{j'},s}< 0, \, \\ l_{CB}^{b_{j'}} R_{CB}^s + T^s - t^{b_{j'},s} &{} \text {if} \, l_{CB}^{b_{j'}} R_{CB}^s + T^s - t^{b_{j'},s} > 0 \, \text {and}~ \Pi _B^{b_{j'},s} < 0. \end{array} \right. \end{aligned}$$

1.6 A.5 Interbank borrowing and lending

In Appendix A.5 we describe how banks settle payments between agents and how banks can borrow and lend to each other, thereby creating bank assets and liabilities. Ultimately, we will be able to investigate the implications of this process for the gross rates of return on private and CB deposits in equilibrium. For ease of presentation, we omit the superscript s as the same considerations hold for both states of the world.

We use an example with two banks, $b_j$ and $b_i$. and focus only on changes in the balance sheets.Assume that Bank $b_i$ grants a loan to Bank $b_j$. Then four entries in the balance sheets are created, as shown in Table 18.

Table 18 Balance sheets representing interbank lending and borrowing (1/4)

$L_i$ represents the amount of loans granted by Bank $b_i$ to Bank $b_j$, and $D_j$ the amount of deposits held by Bank $b_j$ at Bank $b_i$. We have assumed a competitive interbank market with a single gross rate of return for lending and borrowing. Since banks cannot discriminate between deposits owned by households and deposits owned by other banks, the corresponding gross rates are both equal to $R_D$.

We next investigate the relationship between $R_{CB}$ and $R_D$. Assume first that some buyers pay with their deposits at Bank $b_j$ and that the sellers deposit the money at Bank $b_i$. In order to settle the transfer, Bank $b_j$ has two options. If $R_{CB} < R_D$, it will borrow from the CB and transfer CB deposits to Bank $b_i$. Suppose now that $R_{CB} > R_D$. Then Bank $b_j$ directly becomes liable to Bank $b_i$. The buyers’ deposits at Bank $b_j$ are replaced by a loan Bank $b_i$ grants to Bank $b_j$. This loan is an asset for Bank $b_i$ that is matched by the liability corresponding to the new sellers’ deposits. As assumed in Sect. 2.3.1, Bank $b_i$ has the right to require Bank $b_j$ to repay its liabilities with CB deposits, which Bank $b_i$ will do as $R_{CB} > R_D$. The balance sheets at the end of the process look exactly the same, no matter whether or not Bank $b_j$ became liable to Bank $b_i$ in the first place. Therefore, independently of $R_D$, the refinancing gross rate is equal to $R_{CB}$. However, assuming that no bank participating in the interbank market makes any loss by doing so requires $R_D = R_{CB}$, which we show next.

Here we prove that $R_D = R_{CB}$. By contradiction, assume first that $R_D < R_{CB}$. Bank $b_j$, for example, would borrow from Bank $b_i$ at the gross rate of return $R_D$ and from the central bank at the gross rate of return $R_{CB}$, as shown in the balance sheets in Table 19.

Table 19 Balance sheets representing interbank lending and borrowing (2/4)

Using deposits at Bank $b_i$, Bank $b_j$ can now repay CB liabilities. To carry out this payment, Bank $b_i$ has to borrow from the central bank at the gross rate of return $R_{CB}$. The balance sheets are given in Table 20.

Table 20 Balance sheets representing interbank lending and borrowing (3/4)

Bank $b_j$ would make positive profits from this operation, while Bank $b_i$ would make losses. As we assumed that no bank participating in the interbank market makes any loss by doing so, $R_D < R_{CB}$ cannot occur in any equilibrium with banks.

Now assume that $R_{CB} < R_D$. Then Bank $b_j$ would like to repay its liabilities against Bank $b_i$ using CB deposits. This would result in the balance sheets given in Table 21.

Table 21 Balance sheets representing interbank lending and borrowing (4/4)

Bank $b_j$ would make positive profits from this operation, while Bank $b_i$ would make losses. As we assumed that no bank participating in the interbank market makes any loss by doing so, $R_D > R_{CB}$ cannot occur in any equilibrium with banks.

B Auxilliary results and proofs

1.1 B.1 Auxilliary results

In this subsection we present two auxillary results that will help to prove the main results. The first result describes the households’ optimal investment choices.

Lemma 5

The representative household’s optimal portfolio choices are represented by three correspondences denoted by

$$\begin{aligned} {\hat{E}}_B&: {\mathbb {R}}_{+}^7 \times [0,\mathbf{W }] \rightarrow {\mathcal {P}}(\mathbb {R_+} \cup \{ + \infty \}), \\ {\hat{D}}_H&: {\mathbb {R}}_{+}^7 \times {\mathbb {R}}_{+}\times [0,\mathbf{W }] \rightarrow {\mathcal {P}}(\mathbb {R_+} \cup \{ + \infty \}), \\ {\hat{S}}_F&: {\mathbb {R}}_{+}^7 \rightarrow {\mathcal {P}}(\mathbb {R_+} \cup \{ + \infty \}), \end{aligned}$$

and given by

$$\begin{aligned}&\Bigl ( {\hat{E}}_B\bigl ( (R_E^s)_s, (R_D^s)_s, p_I, (p_C^s)_s, S_F \bigr ), \nonumber \\&\qquad {\hat{D}}_H\bigl ( (R_E^s)_s, (R_D^s)_s, p_I, (p_C^s)_s, E_B, S_F \bigr ), \nonumber \\&\qquad {\hat{S}}_F\bigl ( (R_E^s)_s, (R_D^s)_s, p_I, (p_C^s)_s \bigr ) \Bigr ) \nonumber \\&\quad = \left\{ \begin{array}{l} \bigl ( \{0\}, \{0\}, \{\mathbf{W }\} \bigr ) \\ \qquad \qquad \qquad \text {if} \, \max \left( {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] , {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] \right) \le \frac{\mathbf{f }'(\mathbf{W })}{p_I}, \\ \bigl ( \{0\}, \{p_I \mathbf{W }\}, \{ 0 \} \bigr ) \\ \qquad \qquad \qquad \text {if} \, \max \left( \frac{\mathbf{f }'(\mathbf{0 })}{p_I}, {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] \right)< {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] , \\ \bigl ( \{p_I \mathbf{W }\}, \{ 0 \}, \{ 0 \} \bigr ) \\ \qquad \qquad \qquad \text {if} \, \max \left( \frac{\mathbf{f }'(\mathbf{0 })}{p_I}, {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \right)< {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] , \\ \bigl ( [0,p_I \mathbf{W }], \{ p_I \mathbf{W }- E_B \}, \{ 0 \} \bigr ) \\ \qquad \qquad \qquad \text {if} \,\,\, \frac{\mathbf{f }'(\mathbf{0 })}{p_I}< {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] = {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] , \\ \bigl ( \{ 0 \}, \{ p_I \left( \mathbf{W }- S_F \right) \}, \{ \mathbf{f }'^{-1}\left( p_I {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \right) \} \bigr ) \\ \qquad \qquad \qquad \text {if} \, \max \left( \frac{\mathbf{f }'(\mathbf{W })}{p_I}, {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] \right)< {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \le \frac{\mathbf{f }'(\mathbf{0 })}{p_I}, \\ \bigl ( \{ p_I \left( \mathbf{W }- S_F \right) \}, \{ 0 \}, \{ \mathbf{f }'^{-1}\left( p_I {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] \right) \} \bigr ) \\ \qquad \qquad \qquad \text {if} \, \max \left( \frac{\mathbf{f }'(\mathbf{W })}{p_I}, {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \right)< {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] \le \frac{\mathbf{f }'(\mathbf{0 })}{p_I}, \\ \bigl ( [0,p_I \left( \mathbf{W }- S_F \right) ], \{ p_I \left( \mathbf{W }- S_F \right) - E_B \}, \{ \mathbf{f }'^{-1}\left( p_I {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \right) \} \bigr ) \\ \qquad \qquad \qquad \text {if} \,\,\, \frac{\mathbf{f }'(\mathbf{W })}{p_I} < {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] = {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \le \frac{\mathbf{f }'(\mathbf{0 })}{p_I}. \\ \end{array} \right. \end{aligned}$$

(15)

The proof of Lemma 5 is given in Appendix B.2.

The second auxilliary result describes the optimal choice of money creation by banks when they are subject to capital regulation.

Lemma 6

Suppose that banks have to comply with a minimum equity ratio $\varphi ^{reg}$ at the end of Period $t=0$. If $R_D^s = R_{CB}^s$ in all states $s=l,h$, the privately optimal amounts of money creation and lending by an individual bank are represented by a correspondence denoted by ${\hat{\alpha }}_M^{reg} : {\mathbb {R}}_{+}^4\times [\varphi ^{reg},1) \rightarrow {\mathcal {P}}({\mathbb {R}}_{+}\cup \{+\infty \})$ and given by

$$\begin{aligned}&{\hat{\alpha }}_M^{reg} \bigl ( (R_L^s)_s, (R_{CB}^s)_s,\varphi \bigr ) \\&\quad = \left\{ \begin{array}{ll} \{ \frac{\varphi }{\varphi ^{reg}} \} &{} \text {if} \,\,\, (R_L^s \ge R_{CB}^s \, \text {for all states} \, s=l,h \\ &{} \text {with at least one strict inequality) or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L> {\overline{R}}_{CB}, \, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \text {and} \, \frac{\varphi }{\varphi ^{reg}} \le \alpha _{DCB}^l) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L > {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l< R_L^l, \, \text {and} \, \frac{\varphi }{\varphi ^{reg}} \le \alpha _{DCB}^h) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L = {\overline{R}}_{CB}, \, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \text {and} \, \alpha _{DH}^l< \frac{\varphi }{\varphi ^{reg}} \le \alpha _{DCB}^l) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L = {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l< R_L^l, \, \text {and} \, \alpha _{DH}^h< \frac{\varphi }{\varphi ^{reg}} \le \alpha _{DCB}^h) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \alpha _{DH}^l< \frac{\varphi }{\varphi ^{reg}}< \alpha _{DCB}^l, \\ &{} \text {and} \, \varphi ^{reg}< \frac{\sigma }{1-\sigma } \frac{R_L^h - R_{CB}^h}{R_{CB}^l}) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l< R_L^l, \, \alpha _{DH}^h< \frac{\varphi }{\varphi ^{reg}}< \alpha _{DCB}^h, \\ &{} \text {and} \, \varphi ^{reg}< \frac{1-\sigma }{\sigma } \frac{R_L^l - R_{CB}^l}{R_{CB}^h}), \\ \{\alpha _{DCB}^l\} &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \alpha _{DCB}^l \le \frac{\varphi }{\varphi ^{reg}}, \\ &{} \text {and} \, \varphi< \frac{\sigma }{1-\sigma } \frac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}), \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L \ge {\overline{R}}_{CB}, \, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \text {and} \, \alpha _{DCB}^l \le \frac{\varphi }{\varphi ^{reg}}), \\ \{\alpha _{DCB}^h\} &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l< R_L^l, \, \alpha _{DCB}^h \le \frac{\varphi }{\varphi ^{reg}}, \\ &{} \text {and} \, \varphi< \frac{1-\sigma }{\sigma } \frac{R_L^l - R_{CB}^l}{R_{CB}^h - R_L^h}), \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L \ge {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l< R_L^l, \, \text {and} \, \alpha _{DCB}^h \le \frac{\varphi }{\varphi ^{reg}}), \\ \left[ 0,\frac{\varphi }{\varphi ^{reg}}\right] &{} \text {if} \,\,\, (R_L^s = R_{CB}^s \, \text {for all states} \, s=l,h) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L = {\overline{R}}_{CB}, \, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \text {and} \, \frac{\varphi }{\varphi ^{reg}} \le \alpha _{DH}^l) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L = {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l < R_L^l, \, \text {and} \, \frac{\varphi }{\varphi ^{reg}} \le \alpha _{DH}^h), \\ \end{array} \right. \end{aligned}$$

$$\begin{aligned}&{\hat{\alpha }}_M^{reg} \bigl ( (R_L^s)_s, (R_{CB}^s)_s,\varphi \bigr ) \\&\quad = \left\{ \begin{array}{ll} \{0,\frac{\varphi }{\varphi ^{reg}}\} &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \alpha _{DH}^l< \frac{\varphi }{\varphi ^{reg}}< \alpha _{DCB}^l, \\ &{} \text {and} \, \varphi ^{reg} = \frac{\sigma }{1-\sigma } \frac{R_L^h - R_{CB}^h}{R_{CB}^l}) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l< R_L^l, \, \alpha _{DH}^h< \frac{\varphi }{\varphi ^{reg}}< \alpha _{DCB}^h, \\ &{} \text {and} \, \varphi ^{reg} = \frac{1-\sigma }{\sigma } \frac{R_L^l - R_{CB}^l}{R_{CB}^h}), \\ \{0,\alpha _{DCB}^l\} &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \alpha _{DCB}^l \le \frac{\varphi }{\varphi ^{reg}}, \\ &{} \text {and} \, \varphi = \frac{\sigma }{1-\sigma } \frac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}), \\ \{0,\alpha _{DCB}^h\} &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l< R_L^l, \, \alpha _{DCB}^h \le \frac{\varphi }{\varphi ^{reg}}, \\ &{} \text {and} \, \varphi = \frac{1-\sigma }{\sigma } \frac{R_L^l - R_{CB}^l}{R_{CB}^h - R_L^h}), \\ \{0\} &{} \text {if} \,\,\, (R_L^s \le R_{CB}^s \, \text {for all states} \, s=l,h \\ &{} \text {with at least one strict inequality) or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \alpha _{DCB}^l \le \frac{\varphi }{\varphi ^{reg}}, \\ &{} \text {and} \, \frac{\sigma }{1-\sigma } \frac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}< \varphi ) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l< R_L^l, \, \alpha _{DCB}^h \le \frac{\varphi }{\varphi ^{reg}}, \\ &{} \text {and} \, \frac{1-\sigma }{\sigma } \frac{R_L^l - R_{CB}^l}{R_{CB}^h - R_L^h}< \varphi ) or \\ &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \alpha _{DH}^l< \frac{\varphi }{\varphi ^{reg}}< \alpha _{DCB}^l, \\ &{} \text {and} \, \frac{\sigma }{1-\sigma } \frac{R_L^h - R_{CB}^h}{R_{CB}^l}< \varphi ^{reg}) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l< R_L^l, \, \alpha _{DH}^h< \frac{\varphi }{\varphi ^{reg}}< \alpha _{DCB}^h, \\ &{} \text {and} \, \frac{1-\sigma }{\sigma } \frac{R_L^l - R_{CB}^l}{R_{CB}^h}< \varphi ^{reg}) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^l< R_{CB}^l, \, R_{CB}^h< R_L^h, \, \text {and} \, \frac{\varphi }{\varphi ^{reg}} \le \alpha _{DH}^l) \, \text {or} \\ &{} \text {if} \,\,\, ({\overline{R}}_L< {\overline{R}}_{CB}, \, R_L^h< R_{CB}^h, \, R_{CB}^l < R_L^l, \, \text {and} \, \frac{\varphi }{\varphi ^{reg}} \le \alpha _{DH}^h). \\ \end{array} \right. \end{aligned}$$

The proof of Lemma 6 is given in Appendix B.2.

1.2 B.2 Proofs

Proof of Lemma 1

As set out in Sect. 2.3.1, banks can lend to, and borrow from, each other at the gross rates $(R_D^{s*})_s$ contingently on State s. Similarly, as explained in Sect. 2.3.2, they can also borrow from, or deposit at, the central bank at the policy gross rates $(R_{CB}^s)_s$ contingently on State s. Suppose now, by contradiction, that $R_D^{s*} \ne R_{CB}^s$ for some state s. If $R_D^{s*} < R_{CB}^s$, all banks would like to become liable to other banks and use the money obtained to hold assets against the central bank, contingently on State s. Similarly, if $R_D^{s*} > R_{CB}^s$, all banks would like to become liable to the central bank and use the money obtained to hold assets against other banks, contingently on State s. As we assumed that no bank participating in the interbank market makes any loss by doing so, both cases cannot hold in an equilibrium with banks. $\square$

Fig. 4

Expected gross rate of return on equity of Bank b as a function of $\alpha _M^b$ when ${\overline{R}}_L < {\overline{R}}_{CB}$ and $R_{CB}^h < R_L^h$ for three typical relationships between the capital ratio $\varphi$ and $\frac{\sigma }{1-\sigma } \frac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}$. The corresponding areas of default and no default are depicted for $\varphi = \frac{\sigma }{1-\sigma } \frac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}$, including the critical value $\alpha _{DH}^l$

Proof of Proposition 1

Let $b \in [0,1]$ denote a bank. As $R_D^s = R_{CB}^s$ in all states $s=l,h$ by Lemma 1, the expected shareholders’ value of Bank b is given by

$$\begin{aligned} {\mathbb {E}}[\max (\alpha _M^b L_M (R^s_L - R^s_{CB}) + E_B R^s_D,0)]. \end{aligned}$$

Suppose that ${\overline{R}}_L < {\overline{R}}_{CB}$.

• Suppose first that $R_L^s \le R_{CB}^s$ for all states $s=l,h$ with at least one strict inequality. In this case, Bank b’s expected shareholders’ value is decreasing in the volume of loans. Therefore, its choice is $\alpha _M^b = 0$.

• Suppose now that $R_L^l < R_{CB}^l$ and $R_{CB}^h < R_L^h$. For these constellations Fig. 4 depicts three typical cases representing the expected gross rate of return on equity as a function of $\alpha _M^b$. The three different cases are given by the comparison between the capital ratio $\varphi$ and $\frac{\sigma }{1-\sigma } \frac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}$.

  For $\alpha _M^b \le \alpha _{DH}^l$, Bank b does not default on depositors, and its expected shareholders’ value is decreasing with $\alpha _M^b$, as illustrated in Fig. 4. However, for $\alpha _{DH}^l < \alpha _M^b$, Bank b defaults on depositors in the bad state. Then Bank b can further increase expected shareholders’ value by granting more loans, as illustrated in Fig. 4. The reason is that shareholders are protected by limited liability and due to depositors’ bailout by the government, the deposit gross rate of return of Bank b received by households in the bad state is $R_D^l$.

  However, money creation levels $\alpha _M^b > \alpha _{DCB}^l$ cannot be optimal for Bank b, as it would default on the CB and its banker would be subject to heavy penalties. Therefore, Bank b compares expected shareholders’ value with $\alpha _M^b = 0$ given by

  $$\begin{aligned} E_B {\overline{R}}_{CB} \end{aligned}$$

  and expected shareholders’ value with $\alpha _M^b = \alpha _{DCB}^l$ given by

  $$\begin{aligned} \sigma \left( \alpha _{DCB}^l L_M (R_L^h - R_{CB}^h) + E_B R_{CB}^h \right) . \end{aligned}$$

  This comparison leads to the threshold of the equity ratio $\varphi$

  $$\begin{aligned} \frac{\sigma }{1-\sigma } \frac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}, \end{aligned}$$

  below which Bank b chooses $\alpha _M^b = \alpha _{DCB}^l$ and above which it chooses $\alpha _M^b = 0$. At the threshold, Bank b is indifferent between $\alpha _{DCB}^l$ and 0.

• Suppose now that $R_L^h < R_{CB}^h$ and $R_{CB}^l < R_L^l$. Analogously to the previous case,

  $$\begin{aligned} \frac{1-\sigma }{\sigma } \frac{R_L^l - R_{CB}^l}{R_{CB}^h - R_L^h} \end{aligned}$$

  is the equity ratio below which Bank b chooses $\alpha _M^b = \alpha _{DCB}^h$ and above which it chooses $\alpha _M^b = 0$.

Suppose now that ${\overline{R}}_L = {\overline{R}}_{CB}$.

• Suppose first that $R_L^s = R_{CB}^s$ for all states $s=l,h$. In this case, Bank b cannot influence its expected shareholders’ value by varying its amount of loans. Therefore, $[0,+\infty )$ constitutes the set of Bank b’s optimal choices.

• Suppose now that $R_L^l < R_{CB}^l$ and $R_{CB}^h < R_L^h$. In this case, for $\alpha _M^b \le \alpha _{DH}^l$, Bank b does not default on depositors, and its expected shareholders’ value is constant and equal to $E_B {\overline{R}}_D$. However, for $\alpha _{DH}^l < \alpha _M^b$, Bank b defaults on depositors in the bad state. Then Bank b can further increase expected shareholders’ value by granting more loans. The reason is that shareholders are protected by limited liability and due to depositors’ bailout by the government, the deposit gross rate of return of Bank b received by households in the bad state is $R_D^l$. However, levels of money creation $\alpha _M^b > \alpha _{DCB}^l$ cannot be optimal for Bank b, as it would default on the CB and its banker would be subject to heavy penalties. Therefore, Bank b chooses the highest level of lending for which it does not default on the CB. This means that Bank b chooses $\alpha _M^b = \alpha _{DCB}^l$.

• Suppose finally that $R_L^h < R_{CB}^h$ and $R_{CB}^l < R_L^l$. Analogously to the previous case, Bank b chooses $\alpha _M^b = \alpha _{DCB}^h$.

Suppose finally that ${\overline{R}}_L > {\overline{R}}_{CB}$.

• Suppose first that $R_{CB}^s \le R_L^s$ for all states $s=l,h$ with at least one strict inequality. In this case, Bank b can increase expected shareholders’ value by granting more loans. Accordingly, its choice is $\alpha _M^b = +\infty$.

• Suppose now that $R_L^l < R_{CB}^l$ and $R_{CB}^h < R_L^h$. In this case, for $\alpha _M^b \le \alpha _{DH}^l$, Bank b does not default on depositors, and it can increase expected shareholders’ value by increasing its lending level. However, for $\alpha _{DH}^l < \alpha _M^b$, Bank b defaults on depositors in the bad state. Then Bank b can further increase expected shareholders’ value by granting more loans. The reason is that shareholders are protected by limited liability and due to depositors’ bailout by the government, the deposit gross rate of return of Bank b received by households in the bad state is $R_D^l$. However, levels of money creation $\alpha _M^b > \alpha _{DCB}^l$ cannot be optimal for Bank b, as it would default on the CB and its banker would be subject to heavy penalties. Therefore, Bank b chooses the highest level of lending for which it does not default on the CB. This means that Bank b chooses $\alpha _M^b = \alpha _{DCB}^l$.

• Suppose finally that $R_L^h < R_{CB}^h$ and $R_{CB}^l < R_L^l$. Analogously to the previous case, Bank b chooses $\alpha _M^b = \alpha _{DCB}^h$.

We can summarize the choices of lending levels by banks, given gross rates $(R_L^s)_s$, policy choices $(R_{CB}^s)_s$, and their equity ratio $\varphi$, with the correspondence ${\hat{\alpha }}_M \bigl ( (R_L^s)_s, (R_{CB}^s)_s,\varphi \bigr )$ given in the proposition. $\square$

Proof of Lemma 5

Suppose first that $\max \left( {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] , {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] \right) \le \frac{\mathbf{f }'(\mathbf{W })}{p_I}$. Now we define the auxiliary function

$$\begin{aligned} g_1(S_F) := \mathbf{f }(\mathbf{W }) - \left( \mathbf{f }(S_F) + p_I (\mathbf{W }- S_F) \max \left( {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] , {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] \right) \right) . \end{aligned}$$

It is easy to verify that, for all $S_F \in [0,\mathbf{W })$, $g_1'(S_F) < 0$. Moreover, $g_1(\mathbf{W }) = 0$. Therefore, $g_1(S_F) > 0$ for all $S_F \in [0,\mathbf{W })$, which establishes the first case in Eq. (15).

Suppose now that $\max \left( \frac{\mathbf{f }'(\mathbf{0 })}{p_I}, {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] \right) < {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right]$. Next we consider the function

$$\begin{aligned} g_2(S_F) := p_I \mathbf{W }{\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] - \left( \mathbf{f }(S_F) + p_I (\mathbf{W }- S_F) {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \right) , \end{aligned}$$

which shares similar properties to $g_1$: for all $S_F \in [0,\mathbf{W }]$, $g'_2(S_F) > 0$, $g_2(0) = 0$, and thus $g_2(S_F) > 0$ for all $S_F \in (0,\mathbf{W }]$. Accordingly, we can apply the same argument to $g_2$ as previously for $g_1$ and obtain the second case in Eq. (15). With similar arguments we also obtain the third and fourth cases.

Suppose finally that $\max \left( \frac{\mathbf{f }'(\mathbf{W })}{p_I}, {\mathbb {E}}\left[ \frac{R_E^s}{p_C^s}\right] \right) < {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \le \frac{\mathbf{f }'(\mathbf{0 })}{p_I}$. Now we consider

$$\begin{aligned} g_3(S_F) := \,&\mathbf{f }\left( \mathbf{f }'^{-1}\left( p_I {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s} \right] \right) \right) + p_I \left( \mathbf{W }- \mathbf{f }'^{-1}\left( p_I {\mathbb {E}} \left[ \frac{R_D^s}{p_C^s} \right] \right) \right) {\mathbb {E}} \left[ \frac{R_D^s}{p_C^s} \right] \\&- \left( \mathbf{f }(S_F) + p_I (\mathbf{W }- S_F) {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \right) . \end{aligned}$$

We observe that $g_3$ is strictly convex in $S_F$, $g_3'(0) = - \mathbf{f }'(\mathbf{0 }) + p_I {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \le 0$, and $g_3'(\mathbf{W }) = -\mathbf{f }'(\mathbf{W }) + p_I {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] > 0$. Hence, on $[\mathbf{0 },\mathbf{W }]$, $g_3$ takes the minimum at $S_F = \mathbf{f }'^{-1}\left( p_I {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \right)$, and it holds that $g_3\left( \mathbf{f }'^{-1}\left( p_I {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \right) \right) = 0$. Therefore, $g_3(S_F) > 0$ for all $S_F \ne \mathbf{f }'^{-1}\left( p_I {\mathbb {E}}\left[ \frac{R_D^s}{p_C^s}\right] \right)$, which proves the fifth case in Eq. (15). With similar arguments we also obtain the last two cases. $\square$

Proof of Lemma 2

Demands for the investment good by firms in MT and FT are directly derived from the following shareholders’ value-maximization problems:

$$\begin{aligned}&\max _{\mathbf{K }_\mathbf{M }\in [\mathbf{0 },\mathbf{W }]} \{ {\mathbb {E}}[\max (\mathbf{K }_\mathbf{M }(\mathbf{R }_\mathbf{M }^\mathbf{s }p^s_C - R^s_L p_I),0)] \} \\&\text {s.t.} \, \mathbf{R }_\mathbf{M }^\mathbf{s }p_C^s = R_L^s p_I \, \text {for all states} \, s = l,h \\ \text {and} \quad&\max _{\mathbf{K }_\mathbf{F }\in [\mathbf{0 },\mathbf{W }]} \{ {\mathbb {E}}[\max ((\mathbf{f }(\mathbf{K }_\mathbf{F }) - \mathbf{K }_\mathbf{F }\mathbf{R }_\mathbf{F }) p^s_C,0)] \}. \end{aligned}$$

$\square$

Proof of Theorem 1

Let ${\mathcal {E}}^*$ be an equilibrium with banks.

Then all banks choose the same level of money creation and lending denoted by $\alpha _M^*$. At the aggregate level, however, the amount borrowed by banks from the CB has to equal the amount deposited by banks at the CB, meaning that $\int _0^1 \alpha _M^b \mathrm {d}b = 1$, which translates into $\alpha _M^* = 1$. The result of Lemma 1 implies that we can apply Proposition 1. Thus, given gross rates of return $(R_L^{s*})_s$, policy choices $(R_{CB}^s)_s$, and the equity ratio $\varphi ^*$, all banks $b \in [0,1]$ choose a lending level $\alpha _M^b \in {\hat{\alpha }}_M\bigl ((R_L^{s*})_s,(R_{CB}^s)_s,\varphi ^* \bigr )$, as given in Proposition 1. The only gross rates of return in Proposition 1 rationalizing $\alpha _M^* = 1$ are

$$\begin{aligned} R_L^{s*} = R_{CB}^s \end{aligned}$$

for all states $s=l,h$. A direct consequence of this relation, Lemma 1, and the expression of profits in Eq. (13) is that

$$\begin{aligned} R_E^{s*} = R_D^{s*} = R_L^{s*} = R_{CB}^s \end{aligned}$$

(16)

for all states $s=l,h$. Moreover, due to Lemma 1 and the tie-breaking rule introduced in Sect. 2.3.1, the interbank lending market is not used in an equilibrium with banks. Finally, $\Pi _M^{s*} = 0$ for all states $s=l,h$ (see Sect. A.1.2), which translates into

$$\begin{aligned} \mathbf{R }_\mathbf{M }^\mathbf{s }p_C^{s*} = R_L^{s*} p_I^* \end{aligned}$$

for all states $s = l,h$. Given gross rates of return $(R_E^{s*})_s$ and $(R_D^{s*})_s$ as well as prices $p_I^*$ and $(p_C^{s*})_s$, households choose $E_B^* \in {\hat{E}}_B\bigl ( (R_E^{s*})_s, (R_D^{s*})_s, p_I^*, (p_C^{s*})_s, S_F^* \bigr )$ given $S_F^*$, $D_H^* \in {\hat{D}}_H\bigl ( (R_E^{s*})_s, (R_D^{s*})_s, p_I^*, (p_C^{s*})_s, E_B^*, S_F^* \bigr )$ given $E_B^*$ and $S_F^*$, and $S_F^* \in {\hat{S}}_F\bigl ( (R_E^{s*})_s, (R_D^{s*})_s, p_I^*, (p_C^{s*})_s \bigr )$. These correspondences are given in Lemma 5 in Appendix B.1. Only the first, the fourth, and the seventh cases of the definition of the correspondences ${\hat{E}}_B$, ${\hat{D}}_H$, and ${\hat{S}}_F$ correspond to equal nominal gross rates of return $R_E^{s*}$ and $R_D^{s*}$ and are hence consistent with the equality of nominal gross rates of return in Eq. (16). However, the assumption $\mathbf{f }'(\mathbf{W })< \overline{\mathbf{R }}_\mathbf{M }< \mathbf{f }'(\mathbf{0 })$ plus $\mathbf{R }_\mathbf{M }^\mathbf{s }p_C^{s*} = R_L^{s*} p_I^*$ rule out the first and fourth cases. As in an equilibrium with banks $E_B^*, D_H^* > 0$, we thus obtain

$$\begin{aligned}&E_B^* \in (0,p_I^* \left( \mathbf{W }- \mathbf{f }'^{-1}(\overline{\mathbf{R }}_\mathbf{M }) \right) ), \\&D_H^* = p_I^*\left( \mathbf{W }- \mathbf{f }'^{-1}(\overline{\mathbf{R }}_\mathbf{M }) \right) - E_B^*, \text { and} \\&S_F^* = \mathbf{f }'^{-1}(\overline{\mathbf{R }}_\mathbf{M }). \end{aligned}$$

Finally, $\mathbf{R }_\mathbf{F }^\mathbf{* }$ can be determined by using Lemma 2 and equating the demand for the investment good $\mathbf{K }_\mathbf{F }^\mathbf{* }$ to its supply $S_F^*$. With the help of the equity ratio $\varphi ^*$, we can then rewrite all equilibrium variables as given in Theorem 1.

In turn, it is straightforward to verify that the tuples given in Theorem 1 constitute equilibria with banks as defined in Sect. 2.5. $\square$

Proof of Lemma 3

Let ${\mathcal {E}}^*$ be an equilibrium with banks for which a minimum equity ratio $\varphi ^{reg}$ is imposed on banks at the end of Period $t=0$. If $\alpha _M^b \ge 1$ for some bank $b \in [0,1]$, the minimum equity ratio imposes the following constraint on money creation $\alpha _M^b$:

$$\begin{aligned}&\frac{E_B^*}{\alpha _M^b L_M^*} \ge \varphi ^{reg}, \quad \text {or equivalently} \\&\alpha _M^b \le \frac{\varphi ^*}{\varphi ^{reg}}. \end{aligned}$$

If $\alpha _M^b \le 1$, the previous constraint becomes

$$\begin{aligned}&\frac{E_B^*}{L_M^*} \ge \varphi ^{reg}, \quad \text {or equivalently} \\&\varphi ^* \ge \varphi ^{reg}. \end{aligned}$$

$\square$

Proof of Lemma 6

Let $b \in [0,1]$ denote a bank and assume that a minimum equity ratio $\varphi ^{reg} \le \varphi$ is imposed on banks at the end of Period $t=0$. Using Lemma 3 and the property $R_D^s = R_{CB}^s$ for all states $s=l,h$, Bank b’s maximization problem simplifies to

$$\begin{aligned} \max _{\alpha _M^b \in \left[ 0,\frac{\varphi }{\varphi ^{reg}} \right] } \left\{ {\mathbb {E}}[\max (\alpha _M^b L_M (R^s_L - R^s_{CB}) + E_B R^s_{CB},0)] \right\} . \end{aligned}$$

As the arguments used in this proof to investigate the impact of lending on shareholders’ value are similar to the ones given in the proof of Proposition 1, we refer readers to the proof of Proposition 1 for further details.

Suppose that ${\overline{R}}_L < {\overline{R}}_{CB}$.

• Suppose first that $R_L^s \le R_{CB}^s$ for all states $s=l,h$ with at least one strict inequality. In this case, expected shareholders’ value of Bank b is decreasing in the volume of loans. Therefore, its choice is $\alpha _M^b = 0$.

• Suppose now that $R_L^l < R_{CB}^l$ and $R_{CB}^h < R_L^h$.

  • Suppose first that $\alpha _{DCB}^l \le \frac{\varphi }{\varphi ^{reg}}$. Then the equity ratio requirement does not impose an additional constraint on Bank b, and its optimal choice of money creation is

    $$\begin{aligned} \begin{array}{lll} &{} \alpha _M^b = 0 &{} \text {if} \, \dfrac{\sigma }{1-\sigma } \dfrac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}< \varphi , \\ &{} \alpha _M^b \in \{ 0, \alpha _{DCB}^l \} &{} \text {if} \, \varphi = \dfrac{\sigma }{1-\sigma } \dfrac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}, \\ \text {and} &{} \alpha _M^b = \alpha _{DCB}^l &{} \text {if} \, \varphi < \dfrac{\sigma }{1-\sigma } \dfrac{R_L^h - R_{CB}^h}{R_{CB}^l - R_L^l}. \end{array} \end{aligned}$$

  • Suppose now that $\alpha _{DCB}^l > \frac{\varphi }{\varphi ^{reg}}$. Then either $\alpha _{DH}^l < \frac{\varphi }{\varphi ^{reg}}$ and expected shareholders’ value of Bank b is decreasing for $\alpha _M^b \in [0,\alpha _{DH}^l]$ and increasing for $\alpha _M^b \in [\alpha _{DH}^l,\frac{\varphi }{\varphi ^{reg}}]$, or $\alpha _{DH}^l \ge \frac{\varphi }{\varphi ^{reg}}$ and expected shareholders’ value is decreasing for $\alpha _M^b \in [0,\frac{\varphi }{\varphi ^{reg}}]$. Therefore, if $\alpha _{DH}^l \ge \frac{\varphi }{\varphi ^{reg}}$, the choice of Bank b is $\alpha _M^b = 0$. Suppose that $\alpha _{DH}^l < \frac{\varphi }{\varphi ^{reg}}$. Then the choice of Bank b can be derived by comparison between expected shareholders’ value for $\alpha _M^b = 0$ and for $\alpha _M^b = \frac{\varphi }{\varphi ^{reg}}$. Using the expression for profits in Eq. (13) and rearranging terms establishes that the choice for Bank b is

    $$\begin{aligned} \begin{array}{lll} &{} \alpha _M^b = 0 &{} \text {if} \, \dfrac{\sigma }{1-\sigma } \dfrac{R_L^h - R_{CB}^h}{R_{CB}^l}< \varphi ^{reg}, \\ &{} \alpha _M^b \in \{ 0, \frac{\varphi }{\varphi ^{reg}} \} &{} \text {if} \, \varphi ^{reg} = \dfrac{\sigma }{1-\sigma } \dfrac{R_L^h - R_{CB}^h}{R_{CB}^l}, \\ \text {and} &{} \alpha _M^b = \frac{\varphi }{\varphi ^{reg}} &{} \text {if} \, \varphi ^{reg} < \dfrac{\sigma }{1-\sigma } \dfrac{R_L^h - R_{CB}^h}{R_{CB}^l}. \end{array} \end{aligned}$$

• The analysis for $R_L^h < R_{CB}^h$ and $R_{CB}^l < R_L^l$ is similar to the previous one.

Suppose now that ${\overline{R}}_L = {\overline{R}}_{CB}$.

• Suppose first that $R_L^s = R_{CB}^s$ for all states $s=l,h$. Then $[0,\frac{\varphi }{\varphi ^{reg}}]$ constitutes the set of Bank b’s optimal choices.

• Suppose now that $R_L^l < R_{CB}^l$ and $R_{CB}^h < R_L^h$.

  • Suppose now that $\alpha _{DH}^l < \frac{\varphi }{\varphi ^{reg}}$. Then the expected shareholders’ value of Bank b is constant for all $\alpha _M^b \in [0,\alpha _{DH}^l]$ and increases with $\alpha _M^b$ in the interval $[\alpha _{DH}^l,\frac{\varphi }{\varphi ^{reg}}]$. Therefore, Bank b chooses $\alpha _M^b = \min (\alpha _{DCB}^l, \frac{\varphi }{\varphi ^{reg}})$.

  • Suppose now that $\alpha _{DH}^l \ge \frac{\varphi }{\varphi ^{reg}}$. Then Bank b’s expected shareholders’ value is constant for all $\alpha _M^b \in [0,\frac{\varphi }{\varphi ^{reg}}]$. Therefore, $[0,\frac{\varphi }{\varphi ^{reg}}]$ constitutes the set of Bank b’s optimal choices.

• The analysis for $R_L^h < R_{CB}^h$ and $R_{CB}^l < R_L^l$ is similar to the previous case.

Suppose finally that ${\overline{R}}_L > {\overline{R}}_{CB}$.

• Suppose first that $R_L^s \ge R_{CB}^s$ for all states $s=l,h$ with at least one strict inequality. In this case, Bank b can increase expected shareholders’ value by granting more loans. Therefore, its choice is $\alpha _M^b = \frac{\varphi }{\varphi ^{reg}}$.

• Suppose now that $R_L^l < R_{CB}^l$ and $R_{CB}^h < R_L^h$. In this case, Bank b can increase expected shareholders’ value by granting more loans. Therefore, its choice is $\alpha _M^b = \min (\alpha _{DCB}^l, \frac{\varphi }{\varphi ^{reg}})$.

• The analysis for $R_L^h < R_{CB}^h$ and $R_{CB}^l < R_L^l$ is similar to the previous case.

We can summarize our findings with the correspondence ${\hat{\alpha }}_M^{reg}$ given in the lemma.

$\square$

Proof of Proposition 3

Let ${\mathcal {E}}^*$ be an equilibrium with banks for which a minimum equity ratio $\varphi ^{reg}$ is required to be held by banks at the end of Period $t=0$. We first note that a direct consequence is that $\varphi ^* \in [\varphi ^{reg},1)$.

Then all banks choose the same level of money creation and lending denoted by $\alpha _M^*$. At the aggregate level, however, the amount borrowed by banks from the CB has to equal the amount deposited by banks at the CB, meaning that $\int _0^1 \alpha _M^b \mathrm {d}b = 1$, which translates into $\alpha _M^* = 1$. The result of Lemma 1 implies that we can apply Lemma 6. Thus, given gross rates of return $(R_L^{s*})_s$, policy choices $(R_{CB}^s)_s$, and the equity ratio $\varphi ^*$, all banks $b \in [0,1]$ choose a lending level $\alpha _M^b \in {\hat{\alpha }}_M^{reg} \bigl ((R_L^{s*})_s,(R_{CB}^s)_s,\varphi ^* \bigr )$ as given in Lemma 6. Therefore, the only gross rates of return and capital structure $\varphi ^*$ in Lemma 6 in Appendix B.1 rationalizing $\alpha _M^*=1$ are such that

Note first that in Cases f) to l), the expected gross rate of return on equity achieved by any bank b when choosing $\alpha _M^b = 1$ is higher than the expected gross rate of return on equity when choosing $\alpha _M^b = 0$. Since the latter is equal to the expected deposit gross rate, we can conclude that in all cases f) to l) the expected gross rate of return on equity is larger than the expected deposit gross rate. Moreover, for Cases a) to e), the expected gross rate of return on equity is equal to the expected deposit gross rate.

Given gross rates of return $(R_E^{s*})_s$ and $(R_D^{s*})_s$ as well as prices $p_I^* = p_C^* = 1$, households choose $E_B^* \in {\hat{E}}_B\bigl ( (R_E^{s*})_s, (R_D^{s*})_s, p_I^* = 1, p_C^* = 1, S_F^* \bigr )$ given $S_F^*$, $D_H^* \in {\hat{D}}_H\bigl ( (R_E^{s*})_s, (R_D^{s*})_s, p_I^* = 1, p_C^* = 1, E_B^*, S_F^* \bigr )$ given $E_B^*$ and $S_F^*$, and $S_F^* \in {\hat{S}}_F\bigl ( (R_E^{s*})_s, (R_D^{s*})_s, p_I^* = 1, p_C^* = 1 \bigr )$. These correspondences are given in Lemma 5 in Appendix B.1.

In Cases f) to l), Lemma 5 implies that $D_H^* = 0$, which is excluded from the definition of an equilibrium with banks. Therefore, Cases f) to l) do not correspond to possible equilibria with banks.

In Cases a) to e), expected gross rates of return ${\overline{R}}_E^*$ and ${\overline{R}}_D^*$ are equal, and only the first, the fourth, and the seventh cases of the definition of the correspondences ${\hat{E}}_B$, ${\hat{D}}_H$, and ${\hat{S}}_F$ in Appendix B.1 are consistent with ${\overline{R}}_E^* = {\overline{R}}_D^*$.

In Cases a) to c), the assumption $\mathbf{f }'(\mathbf{W })< \overline{\mathbf{R }}_\mathbf{M }< \mathbf{f }'(\mathbf{0 })$ together with $\overline{\mathbf{R }}_\mathbf{M }= {\overline{R}}_E^* = {\overline{R}}_D^*$ rule out the first and fourth cases. As in an equilibrium with banks $E_B^*, D_H^* > 0$, we obtain

$$\begin{aligned}&E_B^* \in (0, \left( \mathbf{W }- \mathbf{f }'^{-1}(\overline{\mathbf{R }}_\mathbf{M }) \right) ), \\&D_H^* = \left( \mathbf{W }- \mathbf{f }'^{-1}(\overline{\mathbf{R }}_\mathbf{M }) \right) - E_B^*, \text { and} \\&S_F^* = \mathbf{f }'^{-1}(\overline{\mathbf{R }}_\mathbf{M }). \end{aligned}$$

In Cases d) and e), the assumption $\mathbf{f }'(\mathbf{W }) < \overline{\mathbf{R }}_\mathbf{M }$ together with $\overline{\mathbf{R }}_\mathbf{M }< {\overline{R}}_E^* = {\overline{R}}_D^*$ rule out the first case. As in an equilibrium with banks $E_B^*, D_H^* > 0$, we obtain

$$\begin{aligned}&E_B^* \in (0, \left( \mathbf{W }- S_F^* \right) ), \\&D_H^* = \left( \mathbf{W }- S_F^* \right) - E_B^*, \\&S_F^* = \left\{ \begin{array}{ll} \mathbf{f }'^{-1}\bigl ({\overline{R}}_{CB}^*\bigr ) &{} \text {if} \, \mathbf{f }'(\mathbf{0 }) \ge {\overline{R}}_{CB}^*, \\ 0 &{} \text {otherwise.} \end{array} \right. \end{aligned}$$

In turn, it is straightforward to verify that the tuples found in this proof constitute equilibria with banks as defined in Sect. 2.5. $\square$

Proof of Corollary 6

Corollary 6 immediately results from Corollary 5 and from the observation that ${\overline{R}}_{CB} = \overline{\mathbf{R }}_\mathbf{M }$, $\mathbf{R }_\mathbf{M }^\mathbf{l }< 1 \le \overline{\mathbf{R }}_\mathbf{M }$, and $R_{CB}^s \ge 1$ for all $s=l,h$ together imply that $R_{CB}^h > \mathbf{R }_\mathbf{M }^\mathbf{h }$. $\square$

Table 22 Parameter values

Table 23 Variable values with policy gross rates $(R_{CB}^l,R_{CB}^h) = (1.02,1.02)$ on the left side and $(R_{CB}^l,R_{CB}^h) = (0.98,1.06)$ on the right side

C Example

We illustrate our results with an example. In this example we use the normalization $p_I^* = 1$, and we set households’ portfolio choice to $\varphi ^* = 0.4$. We use the parameter values given in Table 22. We note that all assumptions on parameters and the function $\mathbf{f }(\cdot )$ are fulfilled, including the assumption that $\mathbf{f }'(\mathbf{W })< \overline{\mathbf{R }}_\mathbf{M }< \mathbf{f }'(\mathbf{0 })$. We now distinguish two cases:

• Either the central bank sets $(R_{CB}^l,R_{CB}^h) = (1.02,1.02)$. Then we obtain the variable values given on the left side of Table 23.

• Or the central bank sets $(R_{CB}^l,R_{CB}^h) = (\mathbf{R }_\mathbf{M }^\mathbf{l },\mathbf{R }_\mathbf{M }^\mathbf{h })$. Then we obtain the variable values given on the right side of Table 23.

In the case of price rigidities characterized by $p_C^{s*} = 1$ for $s=l,h$, the policy presented in Corollary 6 yields the following values:

$$\begin{aligned}&R_{CB}^l = 1, \quad R_{CB}^h = 1.04, \quad \text {and} \quad \varphi ^{reg} = 0.02. \end{aligned}$$