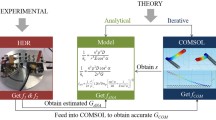
Abstract
Nature and technology often adopt structures that can be described as tubular helical assemblies. However, the role and mechanisms of these structures remain elusive. In this paper, we study the mechanical response under compression and extension of a tubular assembly composed of 8 helical Kirchhoff rods, arranged in pairs with opposite chirality and connected by pin joints, both analytically and numerically. We first focus on compression and find that, whereas a single helical rod would buckle, the rods of the assembly deform coherently as stable helical shapes wound around a common axis. Moreover, we investigate the response of the assembly under different boundary conditions, highlighting the emergence of a central region where rods remain circular helices. Secondly, we study the effects of different hypotheses on the elastic properties of rods, i.e., stress-free rods when straight versus when circular helices, Kirchhoff’s rod model versus Sadowsky’s ribbon model. Summing up, our findings highlight the key role of mutual interactions in generating a stable ensemble response that preserves the helical shape of the individual rods, as well as some interesting features, and they shed some light on the reasons why helical shapes in tubular assemblies are so common and persistent in nature and technology.
Graphic Abstract
We study the mechanical response under compression/extension of an assembly composed of 8 helical rods, pin-jointed and arranged in pairs with opposite chirality. In compression we find that, whereas a single rod buckles (a), the rods of the assembly deform as stable helical shapes (b). We investigate the effect of different boundary conditions and elastic properties on the mechanical response, and find that the deformed geometries exhibit a common central region where rods remain circular helices. Our findings highlight the key role of mutual interactions in the ensemble response and shed some light on the reasons why tubular helical assemblies are so common and persistent.

Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Many biological structures can be modeled as tubular assemblies of helical rods, such as the tail sheaths of bacteriophage viruses [1, 2], the cellulose filaments in the tendrils of climbing plants [3], the bundles of microtubules and motors in all eukaryotic flagella and cilia [4, 5], the envelopes of shape-shifting unicellular organisms such as Lacrymaria Olor [6] and the pellicle of euglenids, a family of unicellular algae [7,8,9,10] (see Fig. 1).
From a technological viewpoint, tubular structures composed of helical fibers exhibit programmable shape-shifting capabilities. This makes them adaptable to changing functional needs, by varying their conformation and properties. Exploiting these features, they have been employed in a broad range of domains, e.g., deployable antennas in aerospace engineering [11], tubular vascular stents in biomedical engineering, sheaths of McKibben artificial muscles and, more generally, helically-arranged fibers in soft robotics and bio-robotics [12,13,14,15]. In all these examples, the system consists of a tubular network of helical rod-like structures. Understanding the mechanical behavior of these systems requires knowledge of how single helices deform under external loads, and how they interact with each other to produce the ensemble response.
In this work, we address these questions by focusing on the response under compression and extension of a tubular assembly made of 8 helical rods. The specific geometry of this assembly, inspired by Ref. [11], is further described below. The behavior of the assembly is analyzed through numerical simulations, adopting a Kirchhoff rod model, that is, an inextensible and unshearable Cosserat rod [16]. For this purpose, the finite element software COMSOL Multiphysics\(^{\textregistered }\) v5.4 is used in equation mode. Specifically, the principle of virtual work is implemented to model the nonlinear response of interacting helical rods in the large deformation regime, under prescribed end-displacements.
Helical structures have been studied extensively and, in particular, their treatment using Kirchhoff rod theory has been discussed in many textbooks and research papers (e.g., see Refs. [16] and [17] and the many references cited therein). Recent contributions to the literature on the mechanics of helical rods include [18,19,20,21,22]. With respect to this recent literature, the main differences of our research consist in the type of structure analyzed, and in the generality of the allowed deformations, i.e., rods are not assumed to remain circular helices a priori and can deform into helical shapes with non-constant curvature and torsion. Another relevant source is the book by Costello [23], where the behavior of wire ropes made of bundles of helical strands is investigated. The main novelties introduced in our work are the type of assembly considered, the presence of large deformations, and the study of the effect of boundary conditions in structures of finite length, whose deformed shapes may deviate from that of circular helices.
Concretely, in this paper we consider a tubular assembly consisting of 8 rods, arranged in 4 pairs of circular helices with opposite chirality and same axis, connected by pin-joints. Friction between the rods, contact and deformations of the cross sections are not accounted for. Rods are subjected to boundary constraints only at their edges. We first examine the response of the assembly in compression and extension in some specific examples that highlight how the rods in an assembly deform all in the same fashion, i.e., as a coherent ensemble. Then, focusing on the behavior in compression, we analyze how the geometry of the deformed configurations is affected by different constraints. We find that, depending on boundary constraints, the rods can either remain circular helices along the whole length of the assembly, or develop edge layers with perturbed geometry around a bulk region where circular helical shapes persist. We then study how the relation between axial force and axial strain is affected by different hypotheses on the elastic properties of the individual rods. In particular, we consider rods that are stress-free in the initial configuration (as circular helices) and rods that are stress-free when straight. Finally, we analyze the effect of modeling the rods as ribbons, and find that this may produce dramatic changes in the stiffness of the assembly, which become evident in a numerical extension experiment.
Our results show that, when arranged in tubular assemblies, helical rods stabilize each other, and that they respond collectively in a way that may be very different from the response they would exhibit if they were loaded individually. This stable collective response is made possible by the mutual interactions between rods, represented by the reactions at pin-joints. This is particularly evident in compression experiments: an individual helical rod typically buckles away from the helix axis; on the contrary, in the assembly, rods deform in such a way that the structure remains symmetric with respect to its initial axis. The deformed shapes of rods with same (opposite) chirality are then identical modulo rigid rotations (reflections). In other words, the rods of the assembly deform cooperatively into helical structures wound around one common axis, that is, the initial axis of the assembly. This collective behavior promotes the stability and persistence of helical shapes in a tubular assembly and, in turn, suggests why these shapes are so commonly observed in nature and technology.
The remainder of this paper is organized as follows. Section 2 introduces the system under investigation and describes its model in terms of kinematics and equilibrium equations, and it delves into the theory of cylindrical deformations; it then describes the finite element method (FEM) implementation of our model and it outlines the investigated problems where different boundary conditions are applied. In Sect. 3, we discuss the main results of our study: we compare the solutions for several boundary conditions, and we analyze cylindrical deformations in the case of zero intrinsic curvatures and torsion, with an example of a zero-stiffness structure. Moreover, the impact of choosing an alternative constitutive model for the rods, namely Sadowsky’s ribbon model, is examined. Section 4 reports our conclusions and outlook for future work.
2 Analytical formulation and computational model
We consider an assembly of initial height \(h_0\) composed of 8 helical rods, i.e., they can be described as circular helices when unloaded. Our goal is to study its equilibrium configurations under compression or extension, enforced by prescribing its height h, with no other forces applied.
The 8 helices are made of the same material, they have the same cross-section and length L, initial radius \(a_0\), initial pitch \(p_0\), and same axis, as shown in Fig. 2. The rods are organized in 4 pairs of 2 helices with opposite chirality, that is, a right-handed and a left-handed one. In each pair, the terminal ends (tip and base) of the two helices are linked together, and they initially lie on the circumference given by the initial radius. Terminal ends of different pairs are distinct. At crossings, helices are linked to each other by pin-joints, which allow relative rotations along the cross-sectional axis with the largest moment of inertia.
2.1 Geometry and kinematics
Let \(\lbrace {\varvec{e}}_1,\, {\varvec{e}}_2,\, {\varvec{e}}_3 \rbrace \) be the global Cartesian reference frame, with \({\varvec{e}}_3\) along the axis of the assembly. Following the Kirchhoff rod theory, each rod is described by a curve and a local three-dimensional reference frame along it. For all helices, we choose the curves joining the centroids of their cross-sections as reference curves. In their initial configurations, a right-handed and a left-handed helix belonging to the same pair can be described by the curves
respectively. Here, \(s \in [0, \, L]\) is the arc-length, \(a_0 = a(h_0) > 0\) is the radius of the helix, \(b_0 = b(h_0) = p_0 /(2\uppi )\), \(c_0 = \sqrt{a_0^2 + b_0^2}\), and \(\theta _1,\, \theta _2\) are offset angles with respect to \({\varvec{e}}_1\). The 8 helices composing the assembly have the following offset angles:
We can then define a local orthonormal reference frame for each helix, given by
where \({\varvec{e}}_{r}^\text{ R }(s)\) and \({\varvec{e}}_{\phi }^\text{ R }(s)\) (\({\varvec{e}}_{r}^\text{ L }(s)\) and \( {\varvec{e}}_{\phi }^\text{ L }(s)\)) are the radial and tangential unit vectors for the right-handed helix (left-handed helix) at arc-length s, respectively. Using this notation, Eq. (1) can be simplified as
We then define the directors of the Kirchhoff rod, choosing \({\varvec{d}}^\text{ R,L}_3(s;h)\) equal to the tangent unit vector to the solution curves \(\varvec{\gamma }^\text{ R,L }(s;h)\) and with the generic position \({\varvec{r}}(s;h)\) reconstructed as
In the initial configuration, directors are described by
and we can compute initial curvatures and torsion as
2.1.1 Parametrization in terms of quaternions
In numerical simulations, we parametrize directors via quaternions [24], i.e., \({\varvec{q}}(s)=(q_1(s), q_2(s), q_3(s))\), \(q_4(s)\), which are four redundant parameters used to avoid singularities. Starting from the identity
the rotation tensor \({\varvec{R}}\) can be expressed, according to Rodrigues’s formula, as
where \({\varvec{a}}\) and \(\alpha \) are the axis and angle of rotation at s, respectively, and \({\varvec{A}}\) is the skew-symmetric tensor corresponding to \({\varvec{a}}\). Quaternions are then defined as
and are therefore constrained by
which causes the dependency of one component from the others. We can then rewrite Eq. (10) as
where \({\varvec{Q}}\) is the skew-symmetric tensor corresponding to \({\varvec{q}}\), and we finally express directors as
2.2 Balance of forces and moments
In the absence of external actions, the balances of forces and moments read
where \({\varvec{M}}\) is the internal moment and \({\varvec{T}}\) is the internal force. The internal moment for a pair of rods (one right-handed and one left-handed) can be written as
We assume the following constitutive equations:
where \(\kappa ^\text{ R}_{s_{1}},\, \kappa ^\text{ R}_{s_{2}},\, \varOmega _s^\text{ R }\) (\(\kappa ^\text{ L}_{s_{1}},\, \kappa ^\text{ L}_{s_{2}},\, \varOmega _s^\text{ L }\)) are the intrinsic curvatures and torsion of each right-handed (left-handed) helix, i.e., those exhibited in the rest configuration; \(B_1,\, B_2\) represent the bending stiffnesses of each rod along \({\varvec{d}}^\text{ R,L}_1, {\varvec{d}}^\text{ R,L}_2\), and \(B_3\) their torsional stiffness along \({\varvec{d}}^\text{ R,L}_3\). According to linear elasticity, we have that
where \(E_Y\) represents the Young modulus of each rod, \(I_1,\, I_2\) the principal moments of inertia of its section along \({\varvec{d}}^\text{ R,L}_1, {\varvec{d}}^\text{ R,L}_2\), G its shear modulus and J its torsional constant.
Since the initial configuration is stress-free, we substitute the intrinsic curvatures and torsion with the ones calculated in Eq. (7), that is,
2.3 Theory of cylindrical deformations
Given a helical assembly, cylindrical deformations are families of configurations parametrized by the axial strain \(\varepsilon = h / h_0 -1 \), where each rod behaves as a circular helix, i.e., a rod with constant non-zero torsion, one constant non-zero curvature, and the other one vanishing. For such deformations, the configurations of a rod can be described by the maps in Eq. (4) with h replacing \(h_0\), that is, \(\varvec{\gamma }^\text{ R,L }(s;h)=\varvec{\gamma }_0^\text{ R,L }(s;h)\). Moreover, let us assume that
so that the energy of each helix reads
which is independent of chirality, because of Eq. (7). The length of each rod can be expressed as
with n the number of turns of the helix, which is constant because of the symmetry of the problem. Then
and because of the inextensibility, we obtain
Rearranging Eq. (4), we can express b for both right-handed and left-handed helices as
and exploiting Eq. (26), we obtain
According to the Kirchhoff rod theory and Eqs. (27) and (28), we can write
For what concerns the loads, substituting Eqs. (19) and (29) into Eq. (18), and considering Eq. (22), we get
The internal moment at \(s = L\) is equal to the external one applied on the considered helix, and the sum of their internal moments at \(s = L\) corresponds to the external moment \({\varvec{Q}}(h)\) applied to the pair, that is,
Since the rods deform as circular helices, the directors are given by Eq. (6), with h replacing \(h_0\). Moreover, due to symmetry we have that
so that we can rewrite \({\varvec{Q}}(h)\) into the local reference frame \(\lbrace {\varvec{e}}_r(L),\,{\varvec{e}}_{\phi }(L),\,{\varvec{e}}_z \rbrace \) as
Under the assumptions of circular helices and of a symmetric structure, only radial rotations are allowed at terminal ends, so that the external work performed by moments vanishes:
Hence, the only external load expending work is the external force needed to balance the reaction to height variations. From the energy balance of the assembly
the external force \(F(h)_\text{ tot }\) can be computed as
The energy of the system can be written as the one of a single helix times the number of helices, regardless of chirality. Therefore, the average force per helix \(F_z\) is computed by differentiating Eq. (23), that is,
We differentiate curvature and torsion as
We substitute Eqs. (29) and (40) into Eq. (39), which reads
Finally, according to
we non-dimensionalize Eqs. (27)-(30),(42) as
where \(K_3 = B_3/B_1\). By setting the intrinsic curvatures equal to the initial ones, according to Eq. (47) we have
2.4 Weak-form of the balance equations
In order to find the equilibrium configuration of the assembly at a prescribed height, we enforce the balance of forces and moments according to the weak formulation of Eq. (16) given by
where \(\delta E\) is the virtual variation of the internal energy of the system, and \({\tilde{q}}_1, {\tilde{q}}_2, {\tilde{q}}_3, {\tilde{q}}_4\) are test functions for the quaternions. For each rod, using constitutive equations we express its elastic energy as
and applying the virtual variation operator \(\delta \) we obtain
where \({\tilde{\kappa }}_1^{(i)}\), \({\tilde{\kappa }}_2^{(i)}\), \({\tilde{\varOmega }}^{(i)}\) are the curvatures and torsion corresponding to the test functions of the quaternions. The additional constraint of Eq. (11) can be imposed using a Lagrange multiplier \(\eta ^{(i)}\). Hence, the total energy of the system reads
with virtual variation resulting in
Thus, the final equilibrium equation reads
2.5 Constraints and boundary conditions
We investigated the response of the assembly as we vary the height h of the assembly by imposing the \({\varvec{e}}_3\)-component of the position vector at the terminal ends of the helices. We studied four cases, corresponding to the following sets of boundary conditions applied at the edges \(s = 0,\, L\) of each rod:
-
1.
displacement components along \({\varvec{e}}_1,{\varvec{e}}_2\) are set to zero, rotations are set to zero;
-
2.
displacement components along \({\varvec{e}}_1,{\varvec{e}}_2\) are set to zero, only radial rotations (i.e., with axis \({\varvec{e}}_{r}^\text{ R } ={\varvec{e}}_{r}^\text{ L }\)) are allowed and free;
-
3.
displacement components along \({\varvec{e}}_1,{\varvec{e}}_2\) are free, only radial rotations are allowed and free;
-
4.
displacement components along \({\varvec{e}}_1,{\varvec{e}}_2\) are set to zero, rotations are free.
Rotations are prescribed by setting Dirichlet boundary conditions on the quadruplet \(q_1\), \(q_2\), \(q_3\), \(q_4\), specifying appropriate constants. The components of the position vector are imposed by choosing integration constants to reconstruct \({\varvec{r}}(s;h)\) from the tangent vector, see Eq. (5), or by enforcing weak constraints using Lagrange multipliers, i.e., by adding the term
to Eq. (55), where \(\lambda _i\) and \({\overline{r}}_i\) are the Lagrange multiplier and the imposed value for i-th coordinate of \({\varvec{r}}(L)\), respectively. In particular, \(\tilde{{\varvec{r}}}(L)\) is expressed in terms of \((\tilde{{\varvec{q}}},{\tilde{q}}_4)\) by applying the virtual operator \(\delta \) to Eq. (5). Since the resulting equation must hold for every \(\lambda _i\), the constraint equation \(r_i(L) = {\overline{r}}_i\) is enforced for every i.
In all cases we imposed no relative translation between helices at the pin-joints connecting them. Moreover, since directors \({\varvec{d}}^\text{ R}_2, {\varvec{d}}^\text{ L}_2\) must remain aligned at crossings, relative rotations were allowed only about the axis of the pin-joint. These constraints were enforced using Langrange multipliers, by imposing zero relative displacement between helices at pin-joints and the orthogonality of \({\varvec{d}}^\text{ R}_2\) with respect to \({\varvec{d}}^\text{ L}_1,\, {\varvec{d}}^\text{ L}_3\), which corresponds to the parallelism of \({\varvec{d}}^\text{ R}_2, {\varvec{d}}^\text{ L}_2\).
2.6 Numerical aspects
The governing equations of the rod model, along with boundary conditions, were implemented and solved in COMSOL Multiphysics\(^{\textregistered }\) v5.4. In particular, the weak form PDE mode was adopted, using a custom implementation of the equations of the model. Regarding the mesh, upon checking that the numerical solution was insensitive to further refinement, each rod of the assembly was divided into 10 elements. Quadratic shape functions were used to discretize the quaternions fields.
In all the boundary value problems a continuation approach was followed, so that the position of one boundary point was varied gradually. Indeed, at each boundary displacement step, the system of non-linear algebraic equations resulting from the finite elements procedure was solved by a quasi-Newton iterative algorithm, taking as initial guess the numerical solution at the previous step. A direct solver (PARDISO) was chosen to solve the linearized system obtained at each continuation step.
3 Results and discussion
We report and discuss the main findings on the response under compression and extension of the assembly described in Sect. 2, as extracted from FEM simulations. We compare computational results with analytical predictions, and we explore the special case of naturally-straight rods, i.e., with \(\kappa _{s_{1}} = \kappa _{s_{2}} = \varOmega _s = 0\), and the consequences of a different constitutive model, that is, the Sadowsky’s ribbon model. To allow meaningful comparisons, the main variables are non-dimensionalized according to Eqs. (43)-(45).
Inter-penetration is not explicitly forbidden in our model, and this is clearly an issue in regimes of extreme compression. Indeed, our ideal assembly is allowed to degenerate into a single circular ring while, in the physical system, the thickness of the rods would put a limit to the minimal height to which the ensemble can be compressed. To thoroughly explore these regimes, our model should be extended to take self-contact into account.
3.1 Stabilization effect due to ensemble response
Single helical rods are known to be unstable under compression, with critical loads determined by their slenderness and material properties. It is then remarkable how helices, when they form assemblies, tend to stabilize each other through mutual interactions, which collectively determine the ensemble response of the structure. Indeed, the higher stability of helical assemblies is arguably a key factor for their recurrence in natural and artificial structures. In this regard, Fig. 3 compares the behavior of a single right-handed helix and of the 8-helix assembly at \(\varepsilon = -0.5\), with boundary conditions corresponding to Case 1. The single helix buckles away from the vertical axis, that is, its helix axis in the initial configuration; on the contrary, in the assembly, rods deform in such a way that the structure remains symmetric with respect to its initial axis. Therefore, because of axisymmetry, the deformed configuration of rods with same (opposite) chirality can be obtained from one another via a rotation (reflection). Thus, the mid-line of each rod remains confined to a surface of revolution around the initial axis of the assembly. The resulting envelope surface, termed in this way because it represents an envelope for the deformed shape of all rods, provides a useful tool to describe the way in which rods deform cooperatively and collectively, i.e., as an ensemble, into helical structures wound around a common axis, given by the initial axis of the assembly.
This type of collective mode of response, in which the deformed configurations of the individual rods are identical modulo rigid rotations or reflections, arises also under extension, as reported in Figs. 4 and 5. In the next subsection, we examine in detail the impact of different boundary conditions on the response of the assembly in the case of compression, in which we can observe the most dramatic differences between the response of a single helix and the one of the assembly (compare Figs. 3 and 4).
3.2 Comparison of equilibrium configurations corresponding to different boundary conditions
Equilibrium configurations in compression corresponding to the boundary conditions reported in Sect. 2.5 exhibit distinct height-radius profiles and thus different envelope surfaces, as shown in Fig. 6. However, all cases have an interesting common feature: solutions tend to overlap within a bulk region, while they depart from each other only at boundary layers, as one can appreciate from the insets in Fig. 6. Notably, the equilibrium solution for Case 3, corresponding to free radial displacement and radial rotations at terminal ends, results in a cylindrical deformation, i.e., a constant radius profile (see Sect. 2.3), which agrees with computational results in Ref. [11].
Comparison of radius profiles (\(\varepsilon = -0.5\)) for Case 1 (orange), Case 2 (green), Case 3 (blue), Case 4 (red). Both axial coordinate and radius are normalized by current height. Dashed black lines represent the lateral view and radius profile for the corresponding theoretical cylindrical transformation. Insets show magnified views of the edge and bulk regions
Comparison of a \({\hat{\kappa }}_1\), b \({\hat{\kappa }}_2\) and c \({\hat{\varOmega }}\) profiles (\(\varepsilon = -0.5)\) for Case 1 (orange), Case 2 (green), Case 3 (blue), Case 4 (red, dashed). Dashed black lines are a \({\hat{\kappa }}_{s_{1}}\), b \({\hat{\kappa }}_{s_{2}}\), and c \({\hat{\varOmega }}_s\)
3.2.1 Curvatures and torsion
Curvatures and torsion profiles (Fig. 7) are symmetric with respect to the arc-length coordinate, consistently with the symmetry of the problems. They exhibit discontinuities at pin-joints, which correspond to concentrated moments exchanged between the helices. Figure 8 illustrates the balance of moments at pin-joints for the first right-handed helix, which is consistent with the absence of external couples and shows a symmetric pattern as well. All cases show a bulk region in the center of the assembly, where curvatures and torsion tend to be constant with similar values across cases, and two boundary layers, where they tend to differ (Fig. 7b) or to oscillate around the bulk value (Fig. 7a). Remarkably, Case 3 shows constant curvatures and torsion profiles, without boundary layers. Hence, in this case rods remain circular helices under compression, while the other cases approach the helical assembly of Case 3 in their bulk regions, and they deviate from it as one moves towards the edges, where they exhibit boundary layers.
3.2.2 External forces
Figure 9 reports a comparison of the axial force versus compressive axial strain \(\vert \varepsilon \vert \) curves for the four cases treated, with \(\varepsilon = 0\) and \(\varepsilon = -1\) corresponding to the initial and a planar circle-like configurations, respectively. All cases show similar trends for the vertical force as a function of \(\vert \varepsilon \vert \). Indeed, all force profiles are non-linear and monotonic, with higher forces for higher compressions and, for a given strain, they have similar values. As compression increases, the required external force grows, since it is balanced by a growing elastic restoring force.
3.3 Case of zero intrinsic curvatures and torsion with an example of zero-stiffness structure
In previous cases rods were modeled with linear constitutive equations, setting intrinsic curvatures and torsion equal to the initial ones. This choice implies that the initial equilibrium configuration is stress-free.
Normalized axial force-compressive strain profiles for computational results (orange), for theoretical ones of Eq. (57) (blue stars), and for computational results when \(\kappa _{s_{1}} = \kappa _{s_{2}} = \varOmega _s = 0,\,\, K_3 = 1\) (red). Insets compare the initial geometric configuration with the one for \(\varepsilon = -0.8\)
A different scenario arises when \(\kappa _{s_{1}} = \kappa _{s_{2}} = \varOmega _s = 0\), that is, for naturally straight rods, since the initial configuration now requires forces and moments to be in equilibrium. Then, we can obtain the force-strain curve of a single circular helix by simplifying Eq. (48) as
Figure 10 compares the force profile for an assembly with \(\kappa _{s_{1}} = \kappa _{s_{2}} = \varOmega _s = 0\) and boundary conditions corresponding to Case 3 as given by numerical simulations, with that of Eq. (57), highlighting their perfect matching. Moreover, starting from this model we can envision a zero-stiffness structure. Indeed, according to Eq. (57), the vertical force is linear with respect to the normalized height \({\hat{h}}\) with a coefficient proportional to \(K_3 - 1\), where \(K_3\) is the ratio of torsional and bending stiffnesses. Therefore, by setting \(K_3 = 1\) we obtain an assembly requiring a constant zero force for any compression ratio, as confirmed numerically (Fig. 10). Deformed configurations form an energetic plateau, where bending and torsional energies are interchangeable.
3.4 Comparison with Sadowsky’s ribbon model
Using the constitutive Eqs. (19) and (20) and assuming a rectangular cross-section, Kirchhoff’s rod model allows for a maximum stiffness for the force-strain relation (57) given by
where \(\beta \) is a geometric parameter which increases with increasing aspect ratio of the cross-section, and that tends to 1/3 when the aspect ratio tends to infinity [25]. We therefore considered an alternative model for the elasticity of the rods, namely, the model for ribbon-like structures proposed by Sadowsky [26] and re-examined in Refs. [27,28,29], in order to investigate the impact of the choice of different constitutive models on the force-strain response. When the rods are modeled as narrow elastic ribbons, the energy density of each rod is described as
where
with w the width of the ribbon, t its thickness, \(E_Y\) its Young’s modulus and \(\nu \) its Poisson ratio. It is assumed that \(t \ll w\ll L\), where L is the length of the rod, and that intrinsic intrinsic curvatures and torsion are equal to zero [27,28,29]. The energy density of Eq. (59) is not strictly convex (see Fig. 12), and this causes convergence problems in the numerical simulations. To circumvent this issue, we added a corrective term to the energy density and defined
where \(\zeta >0\) is a regularization parameter. The energy density of Eq. (61) is strictly convex for all \(\zeta >0\), and Sadowski’s energy (59) is recovered in the limit \(\zeta \rightarrow 0\). The choice \(\zeta = 0.2B\) guaranteed convergence in all the numerical simulations we conducted. Given the boundary conditions of Case 3, we simulated the extension of the assembly from \(h = h_0 = 0.01\,L\) to \(h = L\) and we compared the results with those for a rod model assuming \(\kappa _s =~0,\,\varOmega _s=~0\), \(\nu = 0.3\), and \(w \gg t \), which corresponds to \(K_3\approx ~1.54\), i.e., maximum stiffness according to Eq. (58). Both models adopt the same material and geometric parameters.
In the case of the ribbon model, to obtain the response of the assembly in the absence of the regularizing term we need a procedure to send \(\zeta \) to zero. This is, however, easy when considering the boundary conditions of Case 3, because the equilibrium configurations that we obtain using the regularized energy, Eq. (61), are given by cylindrical deformations for any imposed height h. At a certain h, the same cylindrical deformation (modulo rigid body motions or change of chirality) is an equilibrium solution for any \(\zeta > 0\), and it is unique thanks to the convexity of the energy density. The axial forces experienced by rods are insensitive to \(\zeta \) because the correction term in Eq. (61), when evaluated on circular helices, contributes with zero axial force (see Eq. (57), \(K_3 = 1\)). In these configurations, the (constant) internal moments are given by
where we have written only the non-zero components. At each h, the same cylindrical deformation is an equilibrium solution also for the non-regularized (\(\zeta =0\)) energy density of Eq. (59), under the same axial force and internal moments given by \(M_1(h,0)\), \(M_3(h,0)\). This can be easily verified by checking that it satisfies the differential equilibrium equations, Eqs. (16) and (17).
The axial force-axial strain profiles obtained using the two models are compared in Fig. 11. Since a ribbon is a shell-like structure with no stretches of the mid-surface allowed, while no such constraint is present in the rod model, it is not surprising that the ribbon model leads to a stiffer response of the assembly. What we find surprising, and do not fully understand, is the magnitude of the discrepancy in the prediction of the response using the two different models. It would be interesting to investigate this issue further, and to compare analytical predictions with experimental results, obtained for rods of rectangular cross-section with different aspect ratios w/t. One could then establish which model, if any, better captures the experimentally observed response, and in which regime of geometric or material parameters. Another interesting feature of the ribbon model is that it leads to a discontinuity in the tangent of the axial force-axial strain profile, i.e., in the axial stiffness of the assembly.
Normalized axial force-axial strain profiles for a rod model with \(\kappa _s =~0,\,\varOmega _s=~0,\, K_3 \approx 1.54\), corresponding to maximum stiffness (orange), and for Sadowsky’s ribbon model (blue). Insets compare the geometric configurations obtained in the two models at a certain level of axial force; the initial configuration is reported as a reference
This is caused by a discontinuity of the second derivative of the energy density, which occurs at \(|\kappa _1| = |\varOmega |\), as illustrated in Fig. 12 (\(\zeta = 0\)). Indeed, in the region \(|\kappa _1|< |\varOmega |\) the energy density of a rod becomes degenerate (independent of \(\kappa _1\)) and the energetic landscape is no longer strictly convex. A signature of this degeneracy is visible in the \(|{\hat{\kappa }}_1|-|{\hat{\varOmega }}|\) trajectories traced by evaluating at the pin-joints of one rod the equilibrium solutions obtained by using Sadowski’s energy density without regularizing terms, Eq. (59), in a numerical simulation of extension (\(h_0 = 0.01\,L\), see Fig. 12). As long as the solution remains in the strictly convex region \(|\kappa _1| > |\varOmega |\), we obtain circular helices (i.e., constant curvature and torsion) represented at each h by a single point \((|{\hat{\kappa }}_1(h)|,|{\hat{\varOmega }}(h)|)\) along the curve given by Eqs. (29) and (30), namely,
As soon as the solution crosses the line \(|{\hat{\kappa }}_1| = |{\hat{\varOmega }}|\), the trajectories “fray” (that is, the single point at each h degenerates into a point cloud) indicating that the rod is exploring zero-energy perturbations, i.e., changes of \({\hat{\kappa }}_1\) at constant \({\hat{\varOmega }}\) (see the inset in Fig. 12). After a few steps, the simulation stops converging.
Energetic landscape of Sadowsky’s ribbon model (\(\zeta = 0\)), over which we drew the \(|\hat{\kappa _1}|\)-\(|{\hat{\varOmega }}|\) curves evaluated at the pin-joints of a rod, as traced by solutions of the equilibrium problem. The inset highlights their “fraying” in the non-convex region (\(|\hat{\kappa _1}| < |{\hat{\varOmega }}|\))
4 Conclusions and outlook
Focusing on a concrete example, we have shown that, when arranged in assemblies, helical shapes stabilize each other thanks to the interactions arising from mutual constraints. The pin-jointed helices of our example respond collectively to extension and compression, preserving the axial symmetry of the initial configuration. They can remain cylindrical, i.e., each rod can deform as a circular helix. This is the case of rods with ends free to displace, yet constrained to radial rotations. On the other hand, when ends are constrained from moving, the assembly forms edge layers, where rods behave like perturbed helices, and a bulk region, where circular helices are preserved. These circular helix configurations characterize the response of an assembly of infinite length [23]. Our results suggest that, boundary conditions incompatible with the geometry of a circular helix generate a perturbation in the form of boundary layers which act as transitions from imposed constraints to a bulk region where rods deform as circular helices. In future work, it would be interesting to study the dependence of the extension of the edge layers from the geometric and material parameters of the system, e.g., from the initial height of the assembly.
Moreover, we are interested in considering the use of different models for the prediction of the response of tubular helical structures, to overcome the limitations of the ones we have adopted so far. It would be interesting to experimentally validate the axial force-axial strain profiles in Fig. 11, in order to verify which model, and in which regime, best reproduces the physical behavior of the assembly, as it has been done for knots in Ref. [29]. Our observation on the ill-posedness of the Sadowsky’s model, corrected as in Ref. [28], also raises the question of deriving less degenerate Sadowsky-type energies for narrow ribbons, in which higher order terms may provide a physically meaningful correction and lead to a less singular behavior.
At a more general level, the collective behavior we have discussed highlights the crucial role of mutual interactions among the rods in promoting the stability and persistence of helical shapes in a tubular assembly, hinting at why they are so recurrent in natural and artificial systems. The pellicle strips of Euglena shown in Fig. 1b, in which adjacent strips slide along their common edge, provide another example of stabilization of helical shapes due to mutual interactions in a tubular assembly [9, 30]. It would be interesting to see whether this argument can be extended further to other, less specific types of interactions among the fibers of the assembly, such as in the microtubule meshwork of Lacrymaria shown in Fig. 1a.
References
Falk, W., James, R.D.: Elasticity theory for self-assembled protein lattices with application to the martensitic phase transition in bacteriophage T4 tail sheath. Phys. Rev. E 73(1), 011917 (2006)
Kostyuchenko, V.A., Chipman, P.R., Leiman, P.G., et al.: The tail structure of bacteriophage T4 and its mechanism of contraction. Nat. Struct. Mol. Biol. 12(9), 810 (2005)
Guo, Q., Dong, J.J., Liu, Y., et al.: Macroscopic and microscopic mechanical behaviors of climbing tendrils. Acta Mech. Sin. 35(3), 702–710 (2019)
Alberts, B., Johnson, A., Lewis, J., et al. (eds.): Garland Science. Taylor & Francis, New York (2014)
Cicconofri, G., Noselli, G., DeSimone, A.: The biomechanical role of extra-axonemal structures in shaping the flagellar beat of Euglena gracilis. eLife (2021, in press). https://doi.org/10.7554/eLife.58610
Coyle, S.M., Flaum, E.M., Li, H., et al.: Coupled active systems encode an emergent hunting behavior in the unicellular predator lacrymaria olor. Curr. Biol. 29(22), 3838–3850 (2019). e3
Arroyo, M., DeSimone, A.: Shape control of active surfaces inspired by the movement of euglenids. J. Mech. Phys. Solids 62, 99–112 (2014)
Cicconofri, G., Arroyo, M., Noselli, G., et al.: Morphable structures from unicellular organisms with active, shape-shifting envelopes: variations on a theme by Gauss. Int. J. Non-Linear Mech. 118, 103278 (2020)
Noselli, G., Arroyo, M., DeSimone, A.: Smart helical structures inspired by the pellicle of euglenids. J. Mech. Phys. Solids 123, 234–246 (2019)
Noselli, G., Beran, A., Arroyo, M., et al.: Swimming Euglena respond to confinement with a behavioural change enabling effective crawling. Nat. Phys. 15(5), 496–502 (2019)
Olson, G., Pellegrino, S., Banik, J., et al.: Deployable helical antennas for CubeSats. In: 54th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, p. 1671 (2013)
Tondu, B.: Modelling of the Mckibben artificial muscle: a review. J. Intell. Mater. Syst. Struct. 23(3), 225–253 (2012)
Hassan, T., Cianchetti, M., Moatamedi, M., et al.: Finite-element modeling and design of a pneumatic braided muscle actuator with multifunctional capabilities. IEEE/ASME Trans. Mechatron. 24(1), 109–119 (2019)
Boxerbaum, A.S., Shaw, K.M., Chiel, H.J., et al.: Continuous wave peristaltic motion in a robot. Int. J. Robot. Res. 31(3), 302–318 (2012)
Connolly, F., Walsh, C.J., Bertoldi, K.: Automatic design of fiber-reinforced soft actuators for trajectory matching. Proc. Natl. Acad. Sci. USA 114(1), 51–56 (2017)
Antman, S.S., Renardy, M.: Nonlinear problems of elasticity. SIAM Rev. 37(4), 637 (1995)
Goriely, A.: The Mathematics and Mechanics of Biological Growth, vol. 45. Springer, Berlin (2017)
Zhao, Z.L., Zhao, H.P., Wang, J.S., et al.: Mechanical properties of carbon nanotube ropes with hierarchical helical structures. J. Mech. Phys. Solids 71, 64–83 (2014)
Zhao, Z.L., Zhao, H.P., Chang, Z., et al.: Analysis of bending and buckling of pre-twisted beams: a bioinspired study. Acta Mech. Sin. 30(4), 507–515 (2014)
Zhao, Z.L., Li, B., Feng, X.Q.: Handedness-dependent hyperelasticity of biological soft fibers with multilayered helical structures. Int. J. Non-Linear Mech. 81, 19–29 (2016)
Zhao, Z.L., Zhou, S., Xu, S., et al.: High-speed spinning disks on flexible threads. Sci. Rep. 7(1), 1–11 (2017)
Zhao, Z.L., Zhou, S., Feng, X.Q., et al.: Pump drill: a superb device for converting translational motion into high-speed rotation. Extreme Mech. Lett. 16, 56–63 (2017). https://doi.org/10.1016/j.eml.2017.09.001
Costello, G.A.: Theory of Wire Rope. Springer, Berlin (1997)
Zupan, E., Saje, M., Zupan, D.: The quaternion-based three-dimensional beam theory. Comput. Methods Appl. Mech. Eng. 198(49–52), 3944–3956 (2009)
Ugural, A.C., Fenster, S.K.: Adv. Strength Appl. Elast. Elsevier, Amsterdam (1981)
Sadowsky, M.: Ein elementarer beweis für die existenz eines abwickelbaren möbiusschen bandes und zurückführung des geometrischen problems auf ein variationsproblem. In: Sitzungsber. Preuss. Akad. Wiss., vol. Mitteilung vom 26 Juni, p. 412–415 (1930)
Dias, M.A., Audoly, B.: A non-linear rod model for folded elastic strips. J. Mech. Phys. Solids 62, 57–80 (2014)
Freddi, L., Hornung, P., Mora, M.G., et al.: A corrected Sadowsky functional for inextensible elastic ribbons. J. Elast. 123(2), 125–136 (2016)
Moulton, D.E., Grandgeorge, P., Neukirch, S.: Stable elastic knots with no self-contact. J. Mech. Phys. Solids 116, 33–53 (2018)
Riccobelli, D., Noselli, G., Arroyo, M., et al.: Mechanics of axisymmetric sheets of interlocking and slidable rods. J. Mech. Phys. Solids 141, (2020)
Funding
Open access funding provided by Scuola Superiore Sant’Anna within the CRUI-CARE Agreement.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Excutive Editor: Xi-Qiao Feng.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Quaglierini, J., Lucantonio, A. & DeSimone, A. Mechanics of tubular helical assemblies: ensemble response to axial compression and extension. Acta Mech. Sin. 37, 173–186 (2021). https://doi.org/10.1007/s10409-021-01068-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10409-021-01068-0