1 Introduction

Pressure-driven, rarefied, single-gas flows through circular tubes of finite length have attracted considerable attention, mainly due to their great engineering impact in numerous technological fields, e.g., gaseous microfluidic devices (Colin 2014), vacuum gas flows and pumping (Jousten 2016), lubrication (Breuer 2005), porous media (Ho et al. 2019), vacuum metrology (Naris et al. 2018), high altitude micro-propulsion systems (Tantos and Valougeorgis 2015), and fusion reactors (Vasileiadis et al. 2016). Rarefied gas flows in channels may be in the whole range of the Knudsen number and, therefore, their theoretical treatment and modeling must be based on kinetic theory (Cercignani 1989). The flow setup may be computationally investigated via the deterministic solution of kinetic model equations (Aristov et al. 2012; Misdanitis et al. 2012; Pantazis and Valougeorgis 2013) or alternatively via the stochastic direct simulation Monte Carlo (DSMC) method (Lilly et al. 2006; Varoutis et al. 2008, 2009). Both numerical approaches are reliable and provide accurate results (Sharipov 2012; Aristov et al. 2014).

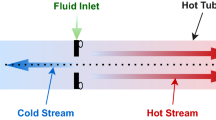
The flow configuration is relatively simple and consists of a tube of radius R and length L, connecting the upstream and downstream containers maintained, far from the tube ends, at pressures \(P_1\) and \(P_2\), respectively, while the tube and containers’ walls are at uniform temperature \(T_0\). The flow setup is fully defined in terms of the following three dimensionless parameters (Varoutis et al. 2009):

  • Tube aspect ratio: \(l=L/R\)

  • Pressure ratio (downstream over upstream): \(p=P_2/P_1\)

  • Gas rarefaction parameter: \(\delta =(R\,P_1)/(\mu _0\,v_0)\)

In the definition of the reference gas rarefaction parameter, \(P_1\) is taken as the reference pressure, while \(\mu _0\) and \(v_0\) are the gas viscosity and most probable molecular speed at reference temperature, respectively. Also, \(\delta\) is proportional to the inverse Knudsen number (Kn) and for monatomic gases is related to the Reynolds (Re) and Mach (Ma) numbers as \(\delta =0.55\,Re/Ma\) (Sharipov 2015). The main output quantity of great practical interest is the reduced flow rate \(W=W(p, l,\delta )\). Then, the mass flow rate is readily deduced as \({\dot{M}}=W \,{\dot{M}}_0\), where \({\dot{M}}_0 = \sqrt{(}\pi ) R^2 P_1/v_0\) is the mass flow rate through an orifice (\(l=0\)) at the free molecular limit (\(\delta =0\)) (Varoutis et al. 2008). Based on these data, the derivation of closed-form algebraic expressions approximating the mass flow rate is very useful in technological applications.

In the case of very long tubes, as well as of tubes with moderate length, the dimensionless flow rate depends only on the gas rarefaction parameter, i.e., \(W=W(\delta )\), and the so-called infinite capillary theory supplemented by the end effect theory may be employed in a computationally efficient manner (Sharipov 2015; Pantazis et al. 2014). Based on these data, many investigators have proposed several simple and accurate closed-form expressions for the mass flow rate. A detailed review on this topic is given in Gallis and Torczynski (2012).

However, in the general case of nonlinear flow, where the tube aspect ratio and/or the pressure ratio are arbitrary, the required computational effort is significantly increased, due to the number and range of the involved parameters \(\{ p, l, \delta \}\), as well as the size of the computational domain. In addition to the capillary, the domain includes adequately large regions upstream and downstream of the capillary to properly impose the incoming distributions, adequately far from the capillary ends (Tatsios et al. 2019). Thus, in this case, owing to the large computational effort, the derivation of closed-form expressions for the mass flow rate or the conductance (volumetric flow rate) is even more important. Several approximate algebraic expressions have been proposed, but they behave well within a narrow range of the involved parameters. Furthermore, they are not always easily applied, since in some cases they must be employed in an iterative manner, while in others, they are written in terms of a large number of fitting parameters that are defined with the aid of auxiliary expressions obtained via interpolation techniques.

For example, Fujimoto and Usami (1984) provided an equation that involves three fitting parameters and it is valid for \(Re<2800\) and \(Kn>0.25 \times 10^{-3}\). By combining semi-analytical results in the free molecular and continuum limits, Livesey (2004) proposed several equations for the gas flow in a tube of arbitrary length that behave well in a wide range of pressures (one for each pressure range). In both studies, iterative procedures are needed. More recently, Hashemifard et al. (2019) developed semi-empirical model equations to calculate the flow rate through short tubes, which are valid, as stated by the authors, for \(0 \le \delta \le 4 \times 10^3\), \(0 \le p \le 0.7\) and \(0 \le l \le 26\). Although an iterative procedure is not required, the proposed expressions are not easily employed because they include nine fitting parameters. Similarly, Yoshida et al. (2021) proposed a modified Knudsen equation, pointing out that it may be used in all flow regimes. As stated, the proposed equation shows differences within \(20\%\) with respect to experimental measurements in tubes with \(R=[5-50]\,\upmu\) m and \(1.4 \le l \le 520\). Again, this equation is rather complicated, since it involves the determination of seven flow rates corresponding to separate flow regimes.

While all above efforts represent significant advances, none of them has yielded relatively simple closed-form expressions for the mass flow rate that can describe accurately the whole range of gas rarefaction. It turns out that conventional interpolation techniques, such as mean square methods, may reproduce well the trend of \(W=W(p, l,\delta )\) for each parameter separately, but it is very hard to find general equations that work properly for all involved parameters.

Considering that machine learning (ML) has been the dominant choice in most prediction-based scientific and technological applications (Mohammad Nejad et al. 2021), it is reasonable to investigate the feasibility of ML to satisfactory deduce the dependency of W on the involved parameters. Machine learning is a subset of Artificial Intelligence (AI), primarily incorporated for complicated data science and statistical applications, in supervised, unsupervised, or reinforcement learning manners (Kontolati et al. 2022; Jiang et al. 2020). It is characterized by its ability to be trained on data and derive predictions on unseen data, inside and outside the available data range, both in classification and regression problems (Chowdhury et al. 2021; Rudy et al. 2017; Brunton 2021; Karniadakis et al. 2021).

Classical ML techniques, such as Random Forest Regression (RFR), Linear Regression (LR), and Multi-Layer Perceptrons (MLP), seem to work satisfactory and can recover successfully the correct reference results (Karakasidis et al. 2022). Since these approaches are focused on estimating complex “black-box” predictive models, their predictions are difficult to rationalize and reveal any physical meaning behind the data (Lee et al. 2022). More importantly, their implementation requires some programming effort and they do not deduce closed-form expressions. Alternative ML techniques, such as the Symbolic Regression (SR) based on Genetic Programming (GP) principles, may be more general, interpretable and suggest analytical models that would potentially allow the extraction of physics-based descriptions solely from data (Koza 1994). In general, SR can result in equations, which are explainable to humans, cheaper to evaluate, and easier to integrate in existing physical science problems (Papastamatiou et al. 2022; Sofos et al. 2022; Xiong et al. 2020; Udrescu and Tegmark 2021). In addition, there is a lack of works on the use of GP-based SR in reduced order modeling for kinetic theory, which has motivated our study.

Based on all above, in the present work, ML techniques are employed in the pressure driven rarefied gas flow through a circular tube in order to accurately predict the dimensionless flow rate in terms of the parameters characterizing the flow. The investigation refers to nonlinear flows through tubes and is based on corresponding data developed by kinetic theory and modeling. Relatively simple and accurate closed-form expressions, easily accessible in design and optimization, are derived via the SR method. To have a more complete view on the topic, a classical ML technique, namely the RFR method, is also considered. Closing the introductory section, it is noted that other ML techniques could possibly have been used as well. One alternative option is the gradient descent method on a predefined equation up to some depth, parametrized with a neural network instead of genetic algorithms (Sahoo et al. 2018) or on a latent embedding of an equation (Kusner et al. 2017). Another potential ML technique is the Monte Carlo Tree Search method, in which an asymptotic constraint is used as input to a neural network, guiding the search for symbolic representations of the underlying equation (Li et al. 2019). Furthermore, there are several algorithms for SR of partial differential equations (PDEs) on gridded data based on a genetic algorithm or sparse regression of coefficients over a library of PDE terms (Both et al. 2021; Rackauckas et al. 2021; Chen et al. 2021; Vaddireddy et al. 2020) or algorithms based on neural operator networks (Lu et al. 2021; Li et al. 2021; Patel et al. 2022). These would also be interesting options to apply when the problem is described by gridded PDE data.

2 Methods

The adopted computational framework is outlined in Sect. 2.1 and the utilized dataset is described, in detail, in Sect. 2.2. The employed ML approaches, namely the RFR and SR methods, are presented in Sects. 2.3.1 and 2.3.2, respectively.

2.1 Computational framework

The general flow diagram of the computational framework followed here is shown in Fig. 1. Kinetic based simulations construct a database of the reduced flow rate W as the dependent (target) variable and \(\{ p, l, \delta \}\) as the three independent (input) variables. The dataset is divided into training and testing subsets and it feeds the RFR and SR models, which, in turn, extract numerical predictions and analytical expressions, respectively, to fully describe the data behavior. In order to have a more complete view on the performance and accuracy of the proposed methods, an additional step towards validation is also considered by comparing the RFR and SR models with kinetic results, not included in the original testing and training datasets. The final outcomes of the current framework include (i) computationally cheaper RFR models relative to the intense kinetic simulations and (ii) SR-based analytical equations, that are, in both cases, capable of providing predictions of W vs \(\{ p, l, \delta \}\) not yet tabulated in the database. All components of Fig. 1 are discussed in the next sections.

Fig. 1
figure 1

Computational framework with preprocessing, RFR, SR, and validation stages

Full size image

2.2 Dataset description

The dataset refers only to rarefied nonlinear flows and more specifically it consists of 22,344 dimensionless flow rates W computed for \(0 \le l \le 5\), \(0 \le p \le 0.9\), \(0 \le \delta \le 10^3\). For parameters \(\{ p, l, \delta \}\) outside the specific ranges, the dimensionless flow rate may be computed employing other kinetic type approaches (Valougeorgis et al. 2017), such as the fully developed methodology with the end effect correction (\(l>5\)) (Pantazis et al. 2014) and linear kinetic modeling (\(0.9<p<1\)) (Pantazis and Valougeorgis 2013), as well as hydrodynamic type approaches with slip and jump boundary conditions (\(\delta <10^3\)). In the latter case, hybrid modeling may also be needed (Docherty et al. 2014).

The specific dataset is based on the deterministic solution of kinetic model equations and has been originally developed to accommodate modeling and simulation of gas distribution networks of arbitrary complexity in the exhaust systems of fusion reactors (Vasileiadis et al. 2016; Vasileiadis and Valougeorgis 2020). Various statistical properties of the dataset, such as the mean, minimum and maximum values and the standard deviation, are given in Table 1, while the complete dataset is available in the supplementary material. The dataset and the scripts implementing the RFR and SR methods are also available on Github https://github.com/labTP-UTH/symbolicRegression.git.

Table 1 Dataset statistical properties
Full size table

A more complete view of the data behavior is shown in Fig. 2, where the flow rate vs \(\delta\) for the limiting values of \(p=[0,0.9]\) and \(l=[0,5]\) is plotted. As expected, W is decreased as l and/or p are increased in the whole range of \(\delta\). Also, W increases with \(\delta\) and, more specifically, it increases for \(\delta < 0.1\) very slowly (remains almost constant), for \(1\le \delta \le 10^2\) significantly (approximately linearly proportional to \(\log \delta\) ) and for \(\delta >10^2\) again slowly reaching gradually the continuum flow rate at the hydrodynamic limit (\(\delta > 10^3\)). The exact values of \(\delta\), determining the limits of each of the three regions, depend on l and p. Surely, the intermediate regime is the one more difficult to capture with a closed-form expression.

Fig. 2
figure 2

Dimensionless flow rate W vs gas rarefaction parameter \(\delta\) for the limiting values of the pressure ratio p and tube aspect ratio l, based on the employed dataset

Full size image

An essential preprocessing step is the calculation of the correlations between the dataset features \(\{ p, l, \delta ; W\}\), which are shown through the correlation matrix in Fig. 3. Values close to 1 or \(-1\) denote high positive and negative correlation, respectively, while values equal to zero denote no correlation. It can be seen that there is no correlation between the inputs \(p, l, \delta\) and they can all be seamlessly incorporated in the regression calculations. The input features p, l are both negatively correlated to the output W, indicating a reduction of the pressure and aspect ratios with increasing W. On the contrary, \(\delta\) is positively correlated to W and, thus, it increases as W increases.

Fig. 3
figure 3

The correlation matrix of the dataset used in the current ML framework. Values close to 1 or \(-1\) denote high positive and negative correlation, respectively, while zeros denote no correlation at all

Full size image

In addition to the prescribed dataset, additional data have been produced for \(l=10\) and \(p=0.95\), based again on the deterministic solution of kinetic model equations. These data are exclusively used in Sect. 3.3 to test the capability of the ML results to capture the correct behavior of W outside the specified training and testing dataset.

2.3 Machine learning

2.3.1 Random forest regression (RFR)

The dataset is fed to an RFR model, in order to provide numerical predictions for the reduced flow rate W. The RFR architecture employs a collection of decision trees (DT); each tree is in itself a regression model and it is trained on a different random subset of the training data, as demonstrated in Fig. 4. A number of DTs are read in parallel from the upper root node, passing through the internal nodes and stopping to a terminal node (the leaf of the tree). Each node is a decision point, where one of the three input variables \(\{ p,l,\delta \}\) is examined if it is greater or smaller than a threshold. If an error criterion (e.g., the MSE) is fulfilled, the process moves on the next node, where another input variable, (or the same, with a different threshold) is considered for new decision tests, until it ends up in the final leaf. The output from a RFR is extracted by averaging the individual predictions of DTs, which anticipates the possibility of over-fitting (Breiman 2001). RFRs have shown a remarkable accuracy in prediction tasks dealing with middle to large datasets (Shah et al. 2019), they can easily be adapted to nonlinear data (Schonlau and Zou 2020) and, recently, they have been applied successfully to Lennard–Jones channel liquid flows (Sofos and Karakasidis 2021) and rarefied gas flows (Ding et al. 2022).

In the present work, the RFR algorithm from the publicly available package Scikit-Learn (Pedregosa et al. 2011) is used. Only \(80\%\) as the implied dataset is designated to train the RFR to predict W, while the remaining \(20\%\) is used as the test set (unseen data). Essentially, the RFR will approximate the results shown in Fig. 2. Important hyper-parameters that have to be decided are the number of DTs to create the forest and the number of leaves that denote the steps needed until the process reaches the final leaf. It has also been shown that one can improve its performance by hyper-parameter tuning (Probst et al. 2019). In the present work, the default values of the Scikit-Learn package have been used, with a total of 30 DTs in the forest.

Fig. 4
figure 4

The RFR model, consisting of various DTs providing different predictions. The final prediction is an averaged value of all DTs’ outputs

Full size image

2.3.2 Symbolic regression (SR)

SR is a novel ML technique that approximates the relation between an input and an output through analytic mathematical formulae derived from a GP-based, natural evolution process. A graphical demonstration of the adopted SR method is given in Fig. 5. An expression is represented as a tree, where leaves are numerical constants or variables and (non-leaf) nodes are mathematical operators applied to their child node(s). This structure makes it possible to apply evolution-mimicking operations in GP, namely mutation and crossover. An initial parent is randomly constructed and transformed to similar or different child structures. To guide the evolution of the expressions in a desirable direction, a fitness function (e.g., mean absolute error, or mean square error) is employed, which determines whether newly created individuals (expressions) survive into the next generation. In general, individuals with higher fitness values survive. This cycle of evaluating, selecting, crossing over and mutating defines one generation of the method.

Fig. 5
figure 5

SR evolution from a parent to child tree structures. A parent tree is created randomly from a pool of mathematical expressions, input features and numerical variables. Child structures are created by substituting nodes or branches of the parent tree

Full size image

Here, SR is used to obtain explicit equations for the reduced flow rate of rarefied gas pipe flows of the form \(W=W(p,l,\delta )\). For this reason, the open source PySR package (Cranmer et al. 2020) has been exploited. The symbolic operators considered here as building blocks to compose the equations are \(\lbrace +, -, \times , /, (\cdot )^2, (\cdot )^3, \exp , \ln , x^y \rbrace\), as well as real constants. The following custom defined operators have also been used: \(\lbrace \textrm{Lin}(x)=1-x, \, \textrm{Ln1}(x)=\ln (\mid x+1 \mid ), \, \textrm{Ln2}(x)=\ln (\mid (x-1)/100 +1\mid ),\, \textrm{Exp1}(x)=(1-x)e^{-y} \rbrace\). These custom operations are basic functions that reproduce certain basic, expected trends of the reduced flow rates and they are adopted here to assist SR. The operators \(\lbrace \exp , \ln , x^y \rbrace\) and all the custom operators are weighted properly, since they are more complex operations.

Equation selection is made manually as follows. Initially, the computational output consists of multiple candidate equations at different levels of complexity. Complexity (COMP) is scored by counting the number of occurrences of each operator, constant and input variable. At first, we select several equations, for which there is a fractional drop in the mean square error, chosen as a loss function, over the increase in complexity from the next best model (Cranmer et al. 2020). Any equation having relative error with respect to the simulation data less than a predefined threshold value (e.g., \(10\%\) or \(20\%\)) is considered a potential analytical model and the one with the smallest complexity is finally chosen. It is found experimentally that, in this way, the best solutions are produced, fulfilling the objectives of the problem under investigation.

SR may lead to complicated expressions that are difficult to interpret, containing undesirable features, such as for example, nested operations. For this reason, constraints are applied in order to control nesting of all operators without permitting nesting of the same operators at all, unless otherwise stated. For example, two consecutive “\(\textrm{exp}\)” operations, \(\textrm{exp}(\textrm{exp}(\cdot ))\), are not allowed. In this context, the complexity of any expression acting on each operation is limited below \(COMP \le 9\). Extensive experimentation revealed that smaller samples of the current dataset are sufficient for obtaining accurate mathematical formulas, i.e., having relative error smaller than predefined limits, using SR. For large datasets and in cases for which all data points are not needed, a sample of approximately 1000 data points is usually used (Cranmer 2023; Cranmer et al. 2020). Here, it is found that random samples of about 1000 to 5600 data points are more than adequate in order to obtain SR-based mathematical equations. The rest of the data is used for comparison purposes against the kinetic results as testing dataset, in order to ensure the accuracy of the SR equations for the whole dataset. The training of the SR model is repeated several times (typically of about 10 times) using different random samples. It is noted that approximately the same skeleton equation is always obtained, which ensures further the validity of the present SR model.

For the purposes of the present work, we mainly anticipate to obtain closed-form and accurate SR-based equations that can be easily used in engineering calculations. In this context, a compromise between accuracy, complexity and total number of the proposed equations is made, while simultaneously ensuring the validity of the equations for the range of the relevant parameters.

3 Results and discussion

The RFR-based numerical predictions and the SR-based analytical expressions of the flow rate W, with regard to the prescribed dataset, within the specified range of parameters, namely \(0 \le p \le 0.9\), \(0 \le l \le 5\), \(0 \le \delta \le 10^3\), are presented in Sects. 3.1 and 3.2, respectively. Complimentary, the capability of the ML procedures to capture the correct behavior of W outside this range is briefly discussed in Sect. 3.3.

The predicted flow rates via the RFR and SR approaches are denoted as \(W_p^{(RFR)}\) and \(W_p^{(SR)}\), respectively. For both ML algorithms, representative accuracy measures (metrics) are provided, including the coefficient of determination \(R^2\), the mean average error MAE, the mean square error MSE and the average absolute deviation AAD. Training and testing data are examined separately. In addition, the RFR and SR relative errors between the predicted flow rates and the ones in the dataset, defined as \(RE^{(RFR)}=\left( W_p^{(RFR)}-W \right) /W\) and \(RE^{(SR)}=\left( W_p^{(SR)}-W \right) /W\), respectively, are computed and discussed.

3.1 Predicted flow rates via random forest regression

The feature importance of the dataset is demonstrated in Fig. 6, which provides a visual representation of the contribution of each input feature p, l or \(\delta\) to the prediction of the target variable W. The feature importance plot accounts the number of times a feature is used to make a split across all the trees in the forest, as well as the improvement in prediction accuracy resulting from the use of a feature in the RFR. Features that are more important achieve higher scores, revealing a greater impact on the prediction of the model. In contrast, features with lower scores will probably be less important or even redundant and they could potentially be removed from the model without significantly affecting its performance (Karakasidis et al. 2022). For the current dataset, the parameter \(\delta\) has a prominent impact on the flow rate W, exhibiting an importance of about \(60\%\), followed by about 25 and \(15\%\) importance for p and l, respectively.

Fig. 6
figure 6

A feature importance plot of the current dataset (higher feature importance depicts higher effect on the dependent variable)

Full size image

After training the RFR algorithm on the available data, as described in Sect. 2.3.1, a comparison between the values of \(W_p^{(RFR)}\) and the corresponding kinetic ones of W is performed by providing the identity plot in Fig. 7a and the prediction residuals \((W_p^{(RFR)}-W)\) in Fig. 7b. In Fig. 7a, the identity plot depicts the actual responses, i.e., the RFR predictions \(W_p^{(RFR)}\) vs the kinetic database W. Obviously, the better the prediction is, the closer the data point is to the diagonal line. It can be seen that the predicted data \(W_p^{(RFR)}\) fit almost perfectly on the expected data W for both training and testing data. Very few outliers are visible, exhibiting a rather insignificant deviation. In Fig. 7b, the scatter plot of the residuals indicates that the RFR predictions for both the train and test data resemble a normal distribution. This is an evidence that training and testing of the RFR model are uniformly tuned (Vabalas et al. 2019). It is also shown that all absolute residuals \(|W_p^{(RFR)}-W |\) fall below 0.05.

Representative accuracy measures for the RFR algorithm are summarized in Table 2. More specifically, \(R^2\) approaches 1, while MAE and MSE obtain very small values for both train and test datasets. The spreading of the predictions based on the test set is somehow greater than that produced from the train set, as indicated by the increase of AAD. All measures have similar values for training and testing data, providing an evidence that no over-fitting occurs from the RFR (Rokach 2016).

Fig. 7
figure 7

a RFR predictions (\(W_{p}^{{RFR}}\)) vs kinetic database (W) of the reduced flow rate; b Prediction residuals (\(W_{p}^{(RFR)}-W\)) and the corresponding distribution, while training and testing the RFR model

Full size image
Table 2 Accuracy measures for the application of RFR on the training and testing datasets
Full size table

A more detailed view on the departure between RFR-based predicted flow rates and the associated kinetic ones from the dataset is shown in Fig. 8, where the relative error \(RE^{(RFR)}\) on a percentage basis vs \(\delta\) is provided for all values of p and l (whole dataset). The maximum absolute value of \(RE^{(RFR)}\) is about \(12.5\%\). The extreme values of the relative error occur at intermediate values of the gas rarefaction parameter \(1\le \delta \le 30\), while for a significant portion of the data, \(RE^{(RFR)}\) is quite small.

Fig. 8
figure 8

Percentage relative error of the RFR-based predictions of the flow rates with regard to the kinetic ones for the whole dataset

Full size image

Overall, the application of the RFR seems capable of providing accurate predictions on the reduced flow rate dataset that fit to the original kinetic simulation results. An inherent advantage of the method is the fast execution, both in training and testing tasks. Therefore, RFR could pose as an interesting option to bypass time-consuming simulations in similar problems. However, the role of kinetic simulations cannot be completely negated, as some simulations will be required for generating the data to train the RFR models. Nevertheless, once trained the use of RFRs can lead to significant cost and effort savings. As pointed above the RFR leads directly to numerical predictions and thus in order to obtain closed-form expressions providing interpretability and accessibility in engineering computations, the SR approach is investigated in the next section.

3.2 Predicted flow rates via symbolic regression

Following the procedure described in Sect. 2.3.2, the SR model may deduce multiple various closed-form expressions of the form \(W=W(p,l,\delta )\) at different levels of complexity. Intuitively, over-simplified equations tend to underfit, whereas the opposite is true for over-complex equations. The objective is to yield simple expressions with high accuracy and, therefore, the relative error \(RE^{(SR)}\) between the SR-based predictions \(W_p^{(SR)}\) and the kinetic dataset W is required to vary within predefined threshold accuracy limits.

After some extensive experimentation, within the guidelines described in Sect. 2.3.2, it has been decided to propose (a) one closed-form expression, valid across the whole spectrum of the input parameters and (b) three closed-form expressions, each one valid in a specific range of the gas rarefaction parameter. The maximum absolute relative errors have been set in the former and latter cases to be less than 20 and \(10 \%\), respectively. The specified threshold limits are considered acceptable for engineering purposes. All equations are valid in the whole range of p and l.

The proposed closed-form expression, which is valid in the whole dataset spectrum with absolute relative error \(|RE^{(SR)} |< 0.2\), is given by

$$\begin{aligned} \begin{aligned}&W_p^{(SR)} = \left( 1 - p\right) \left( 1.04 - e^{- \frac{1.73}{0.667+ l}}\right) \\&\quad \left[ 1 + \frac{\left( 1 - (0.00137 + 0.0352 l)^{\delta /100}\right) \left( 4.95 \times 0.0107^{\delta /100} + 22.4^{p} + p l + l\right) }{1.81 + 0.226^{l}}\right] \end{aligned} \end{aligned}$$
(1)

Smaller relative errors could be possibly achieved by allowing the SR model to distill equations with higher complexity. Here, in order to obtain more accurate prediction of the flow rate, while the expressions remain relatively simple, the initial dataset is divided into three smaller sub-datasets with respect to \(\delta\) and the SR procedure is repeated. As an outcome, one equation for each of the three gas rarefaction subregions, with absolute relative error \(|RE^{(SR)} |< 0.1\), is obtained and proposed:

  • \(0\le \delta \le 10\):

    $$\begin{aligned} \begin{aligned}&W_{p,I}^{(SR)} = \left( 1 - p \right) \frac{ 1.92 + 0.0479 l }{1.932+l} \Bigg \lbrace 1 - \delta \,\, \biggl [ \left( 0.3 \times 0.675^{l} - 0.775^{\delta \left( 1- p\right) }\right) \\&\quad \times \left( 0.28 \times 0.65^{l} - 0.0653 ( p + l + 0.4)^{p - 1.012}\right) - 0.165 p -0.074 \biggr ] \Bigg \rbrace \end{aligned} \end{aligned}$$
    (2)

  • \(10\le \delta \le 10^2\):

    $$\begin{aligned} \begin{aligned}&W_{p,II}^{(SR)}=(p + 0.124)^{p^{6}} \left\{ - 0.0377 l + 1.27 \left( 1 - p^{2}\right) e^{p^{2}} - 0.143 \left[ l \left( 1 - p\right) - 0.334\right] e^{- l \left( 1 - p\right) } \right. \\&\quad \left. +0.217 \left( 1 - 0.417 l e^{- 0.0254 \delta } \right) ^{2} - 0.0377\right\} e^{- \frac{7.55 p^{2} +1.58 l}{\delta }} \end{aligned} \end{aligned}$$
    (3)

  • \(10^2\le \delta \le 10^3\):

    $$\begin{aligned} W_{p,III}^{(SR)} =&\left[ 1.285+\left( 0.195 +2.103 p^{10} \right) e{\frac{(4.676 l - l^{2}) \left( 1 - 0.16 l\right) ^{2} - 0.151 \delta }{\delta \left( 1 - 0.16 l\right) ^{2}}} \right] \\&\quad e^{[{- p \left( p + p^{0.308}\right) \left( 0.0419 - 0.0002089^{p} + p^{5} \right) - \frac{4.676 l}{\delta }}]} \end{aligned}$$
    (4)

Equations (2), (3) and (4) are valid in the whole range of p and l. The performance of the SR-based closed-form expression (1), as well as of expressions (2), (3) and (4) is summarized in Table 3, where their representative statistical metrics are tabulated. As in the RFR analysis, the training and testing datasets are treated separately. The coefficient of determination \(R^2\) approaches 0.99 for Eq. (1) and 1.0 for Eqs. (2), (3) and (4), while for all the equations, the values of the mean average error MAE and the mean square error MSE are sufficiently small of the order of \(10^{-2}-10^{-5}\). The complexity levels are also included mainly for completeness purposes. In the last column of Table 3, the maximum absolute values of the relative error \(RE^{(SR)}\) are given and as seen, in all expressions, they are smaller than the imposed threshold accuracy limits. The metrics of the SR model equations calculated on the subsets of the training and testing data are similar indicating that the tendency for over-fitting is rather small for the proposed SR-based equations with the current levels of complexity (Li et al. 2019).

Table 3 Accuracy measures for Eqs. (1), (2), (3) and (4) obtained via SR on the training and testing datasets
Full size table

The evaluation of the proposed SR-based expressions is continued in Fig. 9 by providing the identity plots for all four expressions. In all cases, the identity plots reveal a very good fitting of the predictions \(W_p^{(SR)}\) based on the SR Eqs. (1–4) and the kinetic database W. In accordance to Table 3, the smallest spreading of predictions is in Eq. (2), followed by the ones in Eqs. (3) and (4), while the largest spreading is in Eq. (1). As it is observed, the deviation of the predictions with respect to the diagonal is more apparent for large values of flow rates. Therefore, the presence of outliers in this region of W is not expected to contribute significantly to increased values of the relative error \(RE^{(SR)}\). On the contrary, spreading of predictions at small values of \(W_p^{(SR)}\) may lead to large relative errors.

Fig. 9
figure 9

SR predictions (\(W_p^{(SR)}\)) vs kinetic database (W) of the reduced flow rate for training and testing datasets based on Eq. (1) (a), Eq. (2) (b), Eq. (3) (c), and Eq. (4) (d)

Full size image

The relative error \(RE^{(SR)}\) on a percentage basis for the flow rates obtained by Eqs. (1), (2), (3) and (4) with regard to the kinetic ones, as a function of \(\delta\) for all p and l cases is shown in Fig. 10. As expected, always the absolute relative errors are smaller or equal to the associated maximum ones in Table 3. In the closed-form expression (1), which is valid in the whole range of \(\delta\), it is seen that \(RE^{(SR)}\) remains very small for \(\delta \le 1\) and then it grows, staying, however, always within the values of \(\pm 17\%\). Closed-form expression (2), which is proposed for \(0 \le \delta \le 10\), works very well in the whole range of the sub-dataset (within \(\pm 4\%\)). In closed-form expressions (3) and (4), which are proposed for \(10 \le \delta \le 10^2\) and \(10^2 \le \delta \le 10^3\), respectively, the variation of \(RE^{(SR)}\) vs \(\delta\) remains almost the same and it is always within \(\pm 9\%\). Although it cannot be seen in Fig. 10, it is noted that with regard to the other two parameters p and l, the maximum deviations from the kinetic database are observed at \(0.8 \le p \le 0.9\) and \(3.5 \le l \le 5\). In general, all the SR-based equations exhibit a better performance for most of the input data parameters in each specific regime and only small fractions of data have absolute relative errors close to the specified maximum ones.

Fig. 10
figure 10

Percentage relative error of the SR-based predictions of the flow rates with regard to the kinetic ones: a Eq. (1), b Eq. (2), c Eq. (3), and d Eq. (4)

Full size image

Closing this section, it may be useful to consider the case of \(\delta =l=0\). As it is well known, in the specific case of free molecular limit (\(\delta =0\)) through and orifice (\(l=0\)), the flow setup is amenable to analytical treatment and the dimensionless flow rate is given by \(W=1-p\). By substituting \(\delta =l=0\) in the closed-form expressions (1) and (2), which are valid at \(\delta =0\), it is readily deduced that \(W_{p,I}^{(SR)} = 0.965\,(1-p)\) and \(W_{p,II}^{(SR)} = 0.994\,(1-p)\), respectively. In both cases the proposed expressions recover sufficiently the analytical ones. Unfortunately, for \(\delta >0\), no analytical expressions of the flow rate are available for orifices or short tubes and, therefore, it is not possible to perform similar comparisons. In the next section, however, some comparisons are performed with numerical results based on linear and nonlinear kinetic modeling.

3.3 Comparison between SR-based and kinetic flow rates outside the prescribed range of input parameters

A comparison between the predicted flow rates via the SR-based closed-form expressions, with corresponding linear and nonlinear kinetic results for flow input parameters not included in the original dataset, is performed. More specifically, the predicted \(W_p^{(SR)}\), in the former case are compared with the ones in Pantazis and Valougeorgis (2013), while in the latter one with kinetic results, which have been particularly produced here for the purposes of the present work.

As the pressure ratio approaches unity (\(p\longrightarrow 1\)), the flow setup is linearized and may be treated via the linearized kinetic model equations. In this case, the dimensionless flow rate \(W_{LIN}\) depends only on \(\delta\), l and is related to the nonlinear one as \(W=(1-p)W_{LIN}\). The complete analysis of the linear flow configurations with the associated results may be found in Pantazis and Valougeorgis (2013). The comparison is performed for the following set of parameters: \(p=0.95\), \(l=[0,0.5,1,2,5,10]\), \(\delta =[0,0.1,1,2,5,10]\). The values of \(p=0.95\) and \(l=10\) are outside the working ranges of the pressure and tube aspect ratios. The above input set of parameters are introduced in the proposed closed-form expressions (1) and (2), which are valid in the specific range of \(\delta\) and the computed \(W_p^{(SR)}\) are compared to the corresponding ones in table 2 in Pantazis and Valougeorgis (2013). The estimated relative errors \(RE^{(SR)}\) for Eqs. (1) and (2) are plotted in Fig. 11a, b, respectively. As it is seen, they remain for \(l \le 5\), as well as for \(l=10\), within the associated imposed maximum threshold values (\(\pm 20\%\) for Eq. (1) and \(\pm 10\%\) for Eq. (2)).

Fig. 11
figure 11

Percentage relative error of the SR-based predictions of the flow rates with regard to linear kinetic ones in table 2 in Pantazis and Valougeorgis (2013) for \(p=0.95\): a Eq. (1), b Eq. (2)

Full size image

The next comparison refers again to closed-form expression (1), but for a wider range of \(\delta\) and more specifically for the following set of parameters: \(l=10\), \(p=[0.1,0.5,0.9]\), \(\delta =[0.1,10,20,50,10^2]\). The value of \(l=10\) is outside the examined tube aspect ratio, while the values of \(\delta\) and p are inside the original input data. Based on the set of parameters the flow is considered nonlinear and to perform the comparison the corresponding values of W are computed based on deterministic nonlinear kinetic modeling (the same with the one used for the original dataset). The computed relative errors, between the kinetic results and the ones via closed-form expression (1), are tabulated in Table 4. Again, the comparison is considered satisfactory since the maximum relative error remains within the imposed maximum threshold values.

Table 4 Percentage relative error of the SR-based predictions of the flow rates via Eq. (1) with regard to nonlinear kinetic ones for \(l=10\)
Full size table

It is noted that the above results may be considered indicative but not conclusive about the capability of closed-form expressions (1) and (2) predict the behavior of the flow rate outside the investigated database.

4 Conclusions

Machine learning (ML) techniques, namely the Random Forest Regression (RFR) and Symbolic Regression (SR), have been employed to compute the flow rate of rarefied gas flow through circular tubes in a wide range of the involved parameters. An available database, built via deterministic kinetic modeling, is divided into training and testing regions and feeds the ML models. The kinetic database consists of the flow rate W, as the dependent (target) variable, and the gas rarefaction parameter \(\delta \in [0,10^3]\), the pressure ratio \(p \in [0,0.9]\) and the tube aspect ratio \(l \in [0,5]\), as the three independent (input) variables. In turn, the RFR and SR models extract numerical predictions and analytical expressions, respectively, to fully describe the data behavior.

The application of SR leads to the extraction of relatively simple and accurate closed-form expressions of the flow rate, which may be very useful in engineering applications, circumventing the need of computationally demanding kinetic modeling and simulations. In particular, the proposed closed expression in the whole range of the dataset, may reproduce the kinetic flow rates, with an absolute relative error of less than \(17\%\). In addition, more accurate predictions have been obtained by dividing the dataset into three subsets in terms of \(\delta\) and providing one SR-based closed-form expression of each subset. Then, in all cases the absolute relative error is reduced to less than \(9\%\).

Complementary, the RFR has been also found capable of providing accurate numerical predictions of the flow rate that fit well the original kinetic database, with an absolute relative error of less than \(12.5\%\). Therefore, RFR could pose as an interesting option to bypass time-consuming kinetic simulations in similar problems and lead to significant computational cost and effort savings. However, the RFR predictions are strictly numerical and no symbolic expressions may be deduced. The results obtained from the RFR analysis serve here as reference for comparisons against those from SR. For instance, it turns out that RFR exhibits a better accuracy relative to SR when the whole range of parameters is considered, but the SR method has the potential to achieve higher accuracy by extending the search space to more complex expressions.

Based on the present results, it is believed that the implementation of the SR and RFR models, in other investigations related to rarefied gas dynamics, such as gas–surface interaction and interaction between particles in single gases and gas mixtures, is very promising and has a lot of potential. Other ML approaches should be also applied.