1 Introduction

Lab-on-a-chip technology provides the possibility to integrate laboratory instruments into small devices (a few centimeters or less) for the trapping, sorting, separation and characterization of biological particles (Lim et al. 2010; Valijam et al. 2018). These types of particle manipulation techniques are essential in point of care and clinical diagnostic (Zoupanou et al. 2021). Many different techniques have been developed to manipulate particles, for example, optophoresis (Ghorbanzadeh et al. 2015), magnetophoresis (Zborowski et al. 2003), acoustophoresis (Augustsson et al. 2012) and dielectrophoresis (Valijam and Salehi 2021). Dielectrophoresis (DEP) is a commonly used separation technique of biological particles because of its label-free nature, low cost, sensitivity and efficiency (Ramirez-Murillo et al. 2021). DEP works on polarizable particles and in the presence of non-uniform electric fields. Thus, DEP depends on the size and dielectric properties of the particles as well as of the suspended medium. When a dielectric particle is placed in a medium in the presence of a non-uniform electric field, a net force acts on the particle. If the polarizability of the particle is larger than the medium an attractive force pulls the particle toward the strong region of the field, whereas smaller particle polarizability, in relation to the medium, repels the particle from the same region. This leads to either positive (pDEP) or negative (nDEP) (Kuzyk 2011).

To create DEP forces, two main approaches are commonly used, the electrode-based or the insulator-based method. Fabrication of insulator-based devices is time-consuming and the introduction of insulating materials requires high voltage (800 V) and thereby an increase in the Joule heating effect, which affects cell viability (Shake et al. 2013). Electrode-based DEP devices can indeed run on lower voltage and use either 2D or 3D configuration of the electrodes. These electrodes are utilized inside the channel to induce the electric fields. Typically, these are interdigitated, quadrupole, curved, castellated, top and bottom and wall patterned electrodes. There are several examples of how these types of electrodes have been successfully used to separate cells in micro-fluidic channels. For example, Shayestehpour et al. (Shayestehpour et al. 2018) used top and bottom electrodes (quarter-of-ellipse electrodes) at 10 V to separate dead and live cells. Yankai Jia et al. (Jia et al. 2015) successfully separated gold-coated polystyrene particles and yeast cells employing sidewall electrodes with a voltage of 12.5 V. To improve the non-uniformity of the electric fields using sidewall electrodes they also utilized obstacles. Furthermore, by using castellated electrodes inside a microchannel, breast cancer cells (MDA-MB 231) were separated from healthy cells (Becker et al. 1995). Utilizing quadruple electrodes Frank Grom et al. (Grom et al. 2006) trapped hepatitis A virus particles by a combination of DEP and electrohydrodynamic flow forces. The electrodes were then operated with 14 V to generate electric fields which accumulated the particles. To separate 1 and 5 µm microbead particles, curved electrodes operated at 30 V were used (Khoshmanesh et al. 2009). Finally, Anas Alazzam et al. (Alazzam et al. 2011) successfully used interdigitated comb-like electrodes for continuous separation of malignant cells from blood using 20 V. Even though these studies showed successful separation of particles, they used high voltages to generate the non-uniform fields, which could generate Joule heating and thereby affect cell viability.

To reduce the Joule heating effect and minimize cell damage, we design and propose in this work microfluidic devices that utilize interdigitated electrodes that can run at low voltage and still achieve cell separation over a short distance, 2 mm. A detailed analysis of cell separation and trajectories is accomplished through 3D finite element simulation modeling (FEM). We investigated different top and bottom arrangements of the electrodes to choose the optimum design for the separation of MDA-MB-231 cells (interchangeable with CTCs in this work) and normal red blood cells (RBCs) at low voltage (± 6 V). Also, we design our device to allow for simultaneous brightfield imaging of the channel with minimal influence of the electrodes. We also investigate the influence of channel height on cell separation and find the maximum height that can be used and still separate cells. The suggested device is not only capable of separating particles at high speed, which increases throughput but also enables the possibility of fabricating devices with higher channel height to reduce the separation time.

2 Materials and methods

2.1 Designing the channel

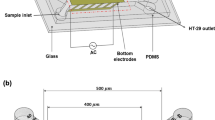
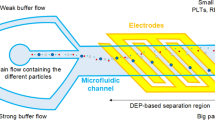
The proposed design to separate cells with different dielectric properties consists of three parts (layers), as illustrated in Fig. 1. To the first layer, which consists of glass, we added two inlets, one for injection of a buffer and the other for injection of a suspended cell mixture. Also, we added two outlets to collect separated cells. The array of interdigitated coplanar gold electrodes is positioned on the top and bottom layers. These electrodes can be made by standard techniques such as, thin-film deposition, etching, photolithography, lift-off, etching, etc. (Martinez-Duarte 2012). In short, 2D planar metal electrodes can be made fairly straightforward using a defined microelectrode pattern, a positive photoresist that is spun down to a preferred thickness using a spin coater, which thereafter is soft-baked. By aligning the mask and exposing it to a UV source an inverse pattern is made where the electrodes will be located. Next, via thin-film deposition, metal can be deposited on top of the substrate (Li et al. 2014). To fit these standard procedures, we make in our design, each electrode with dimensions 100 µm long, 20 µm wide, and 100 nm thick (Tajik et al. 2019). The gap between the electrodes is 100 µm. Note that in our design, we do not want the electrodes to cover the whole width of the channel; we only want the electrodes to protrude into the channel by 20 µm. Therefore, the electrodes are not positioned symmetrically on the top and bottom layers, which work as the outer parts of a sandwich construction. On top of these electrodes, the second layer, the microchannel, is positioned. This second layer can be manufactured in polydimethylsiloxane (PDMS). PDMS is a bio-inert polymer that is thermally stable and optically clear. A microchannel can easily be made in PDMS using, for example, soft lithography, laser engraving, or 3D printing (Li et al. 2014; Dahlberg et al. 2018). This channel will then be positioned and bonded between the two glass slides. We design the channel to have a width and initial height of 150 µm and 35 µm, and to be 2 mm long.

Fig. 1
figure 1

A Schematic of the proposed microfluidic device that consists of three layers. (Left) the first layer consists of the inlets, outlets and top gold electrodes. (Middle) the microchannel imprinted in PDMS using soft lithography or 3D-printing. (Right) gold electrodes on the bottom layer. B Illustration of the proposed separation device seen from above with RBCs (blue) and CTCs (red). The method consists of two stages, in the first stage, particles are focused close to the sidewall of the channel using a defined volume rate of the buffer flow. In the second stage, the top and bottom gold electrodes create the DEP force, which results in particle separation based on their size and dielectric properties. Thus, particles with different properties either deflected toward outlet C or continue straightly toward outlet D. In the illustration, the size of the particles is enlarged for improved visualization

Full size image

To improve the efficiency of the separation, we first focus particles regardless of their size and dielectric properties along the sidewall before the electrodes, see Fig. 1B. This focusing is done by regulating the fluid velocity of inlets A and B. Increasing the fluid velocity in A results in a compressed stream of particles along the sidewall, forcing particles to pass between the pair of electrodes. After this first stage of focusing, particles will be exposed to a non-uniform DEP force in the second stage created by the electrodes placed on the top and bottom slides of the channel. The top layer electrodes are connected to the positive AC voltage, and the bottom electrodes are connected to the negative voltage. Depending on the cell size and dielectric properties as well as applied voltage, cells will migrate in the x-, y- and z-direction of the channel, thus separating different cell types.

2.2 Theory of dielectrophoresis forces

When polarizable particles are placed in a suspension medium and an inhomogeneous electric field, they will migrate due to the dielectrophoretic force (DEP) (Rashed and Williams 2020). For a spherical particle, the magnitude of the DEP force is then given by,

$$F_{{{\text{DEP}}}} = 2\pi r^{3} \varepsilon_{0} \varepsilon_{{\text{m}}} {\text{Re}} [{\text{CM}}({\text{f}})]\nabla \left| {\vec{E}} \right|^{2} ,$$
(1)

where r is the radius of the particle, εm and ε0 are the medium and vacuum permittivity. Re[CM(f)] is the real part of the Clausius–Mossotti factor and ∇|E|2 is the gradient of the electric field. The CM factor varies between −0.5 and 1.0 and the sign of this factor results in either a positive or negative DEP. Thus, if CM > 0, particles will experience a positive force, pDEP, and are pushed to the maxima of the electric fields, which are at the edges of the electrodes. However, if the CM < 0, a negative force, nDEP, will repel the particles and move them away from the electrodes (Jia et al. 2015). The CM factor is defined as,

$${\text{CM}}({\text{f}}) = \frac{{\varepsilon_{{\text{p}}}^{*} - \varepsilon_{{\text{m}}}^{*} }}{{\varepsilon_{{\text{p}}}^{*} + 2\varepsilon_{{\text{m}}}^{*} }},$$
(2)

where\({{ \varepsilon }_{\mathrm{p}}^{*} \mathrm{and} \varepsilon }_{\mathrm{m}}^{*}\) are the complex permittivity of the particle and medium, respectively. They are, in turn defined as,

$$\varepsilon_{{\text{p}}}^{*} = \varepsilon_{{\text{p}}} \varepsilon_{0} - j\frac{{\sigma_{{\text{p}}} }}{\omega }$$
(3)
$$\varepsilon_{{\text{m}}}^{*} = \varepsilon_{{\text{m}}} \varepsilon_{0} - j\frac{{\sigma_{{\text{m}}} }}{\omega },$$
(4)

where \(\sigma_{{\text{p}}}\) and \(\sigma_{{\text{m}}}\) are the conductivity of the particle and medium. Further, ω = 2πf is the angular frequency and j = \(\sqrt{-1}\).

Biological particles such as bacteria, RBCs, and CTCs have, in general, complicated organization of their inner structures. However, previous works have shown that it is possible to model these types of cells as a simple single-shell model to assess their electric properties with good accuracy (Çetin and Li 2011). In this model, the center core of the cell (cytoplasm) is surrounded by the lipid membrane. We used this approach to represent the cells in this work, see Fig. 2A. We can, therefore, replace the complex permittivity of the modeled particle with the complex equivalent permittivity of the particles, εeq*, which is defined as,

$$\varepsilon_{{{\text{eq}}}}^{*} = \varepsilon_{{{\text{cm}}}}^{*} \frac{{\left( {\frac{r}{{r_{{}} - th_{{{\text{cm}}}} }}} \right)^{3} + 2\left( {\frac{{\varepsilon_{{{\text{cp}}}}^{*} - \varepsilon_{{{\text{cm}}}}^{*} }}{{\varepsilon_{{{\text{cp}}}}^{*} + 2\varepsilon_{{{\text{cm}}}}^{*} }}} \right)}}{{\left( {\frac{{r_{{}} }}{{r_{{}} - th_{{{\text{cm}}}} }}} \right)^{3} - \left( {\frac{{\varepsilon_{{{\text{cp}}}}^{*} - \varepsilon_{{{\text{cm}}}}^{*} }}{{\varepsilon_{{{\text{cp}}}}^{*} + 2\varepsilon_{{{\text{cm}}}}^{*} }}} \right)}}.$$
(5)
Fig. 2
figure 2

A Schematic representation of a single-shell model in which the cytoplasm and outer membrane are considered. B The real part of the Clausius–Mossotti factor with frequency for different cells. The dashed lines at (a) and (b) represent the outer range of the 20 kHz and 70 kHz frequency span, respectively. At 80 kHz and 366 kHz particles will not be exposed to a DEP force

Full size image

In this equation, thcm is the thickness of the shell, εcp* is the complex permittivity of the particles, and εcm* is the complex permittivity of the outer shell.

Using this approach, we simulated MDA-MB-231 cells and RBCs as spherical particles, and we defined their physical and electrical properties as described in the literature (Sano et al. 2011; Zhang and Chen 2020). Despite that RBCs have a biconcave shape, previous works support that modeling them as spherical particles gives reliable results (Karimi et al. 2019; Nguyen et al. 2021). A summary of the parameters used in our simulation is shown in Table 1.

Table 1 Physical and dielectric properties of MDA-MB-231 cells, RBC, and medium
Full size table

Using these parameter values, we derived the CM factor using the single-shell model for CTCs and RBCs versus frequency, as shown in Fig. 2B. We see that at 80 kHz and 366 kHz, the DEP force on the CTCs and RBCs are zero. At these frequencies, cells will not move. Thus, according to the simulated data and consistent with previous works (Valijam and Salehi 2021), the applied frequency to the electrodes should preferably be in the range of 20–70 kHz to induce a nDEP force on RBCs and MDA-MB231 cells. In addition, the maximum nDEP in this range of frequencies is found when the frequency is 70 kHz.

Since cells are going to be circulating in a flow channel, we modeled the drag force using the Stokes drag force model. For spherical cells inside a channel that is exposed to a creeping flow, the drag force can be modeled as (Rashed and Williams 2020),

$$F_{{{\text{Drag}}}} = 6\pi r_{{{\text{ext}}}} \eta (\vec{u} - \vec{u}_{{\text{p}}} ),$$
(6)

where the external radius of the particle is rext, η is the viscosity of the medium, \(\overrightarrow{u}\) and \(\overrightarrow{{u}_{\mathrm{p}}}\) are the flow velocity and the velocity of the particle, respectively.

2.3 Numerical simulation

To predict the movement of our particles and the flow field inside the microchannel, we performed numerical simulations using COMSOL Multiphysics 5.5. We used the laminar flow module to solve the Navier–Stokes equation (Eq. 7). In addition, we assumed that the fluid was incompressible and we applied a non-slip boundary condition to the channel walls. Thus, we end up with the following equation,

$$\rho (\vec{u} \cdot \nabla )\vec{u} + \rho \frac{{\delta \vec{u}}}{\delta t} = \nabla \cdot [ - P\vec{I} + \mu (\nabla \vec{u} + (\nabla \vec{u})^{T} )] + \vec{F},$$
(7)

where P and \(\overrightarrow{F}\) are the pressure and applied forces, respectively. For the inlets and outlets, we assumed a constant flow and zero pressure. The total force acting on a particle can thereby be described as a combination of the DEP force, drag force, gravity, and inertial forces as

$$F = F_{{{\text{DEP}}}} + F_{{{\text{Drag}}}} + F_{{{\text{inertial}}}} + F_{{{\text{gravity}}}} \approx F_{{{\text{DEP}}}} + F_{{{\text{Drag}}}} ,$$
(8)

where the gravity and inertial force are insignificant at the time scale of an experiment and due to the low weight of the particles, see thorough derivations of the total force in refs (Liu et al. 2020; Guo et al. 2022). Using these sets of equations, we ran a 3D simulation with 425 268 tetrahedral mesh elements. To assess the efficiency and purity of the separation of cells for different device configurations, we defined these as in reference (Gao et al. 2020), that is.

$${\text{Efficiency}} = \frac{{{\text{Number}}\,{\text{of}}\,{\text{specific}}\,{\text{cell}}\,{\text{types}}\,{\text{(outlet)}}}}{{{\text{Number}}\,{\text{of}}\,{\text{total}}\,{\text{cell}}\,{\text{types(inlet)}}}}$$
(9)

and

$$\begin{gathered} {\text{Purity}} = \frac{{{\text{Number}}\,{\text{of}}\,{\text{specific}}\,{\text{cell}}\,{\text{types}}\,{\text{(outlet)}}}}{{{\text{Number}}\,{\text{of}}\,{\text{total}}\,{\text{cell}}\,{\text{(outlet)}}}}. \hfill \\ \hfill \\ \end{gathered}$$
(10)

3 Results and discussion

3.1 Assessing the drag force and DEP force in the microfluidic channels

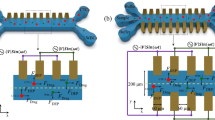
To characterize and compare the results of different positions of the electrodes, we ran computational simulations as described in the methods section. The different arrangements of the electrodes should affect the motion of particles in the channel since the properties of the electric field (DEP force) will change. In the first case, we positioned the top (T) and bottom (B) electrodes exactly above each other, see Fig. 3A, B. In the second case, we shifted the top electrodes by L/2 along the + x-axis (L = 100 µm). In the last case, the top electrodes were moved L along the + x-axis in comparison to the first configuration, implying that they are now exactly between a pair of bottom electrodes, except for the first and last electrodes. We used the same voltage for all electrodes, and we set the top to be positive and the bottom to be negative to generate non-uniform electric fields. This type of configuration thereby changes the gradient of the electric fields allowing for a DEP force. With this, we could study the velocity, electric field properties, DEP force, and drag force of CTCs and RBCs modeled using the parameter values in Table 1. Note that the arrangement of the electrodes is such that the electrodes are not covering the whole width of the channel, making it possible to visualize the center of the channel, see Fig. 3A.

Fig. 3
figure 3

A Arrangements of the top (T0-T4) and bottom (B0-B4) gold electrodes. These electrodes are not covering the whole width of the channel, they are only reaching 20 µm into the channel (y-axis), making the central part clearly visible in a brightfield microscope. Both gap and length of the electrodes are defined as L and they are connected to an AC voltage. B Examples of how the electrodes are positioned and shifted. The top shows aligned electrodes, the middle shows electrodes shifted by L/2, and the bottom shows electrodes shifted by L

Full size image

The inlet flow velocities of our fluid device were first decided via various simulations to find an optimal ratio. These were found to be 134 μm/s for injection of cells in inlet B and 853 μm/s for introducing the buffer fluid from inlet A. The buffer fluid velocity can easily be controlled and tuned to facilitate the focusing of cells toward the electrodes. To inlet B, we simulated the injection of 1830 RBCs and 1830 CTCs that were randomly distributed into the channel. Since the fluid flow and the localized electric field varies in the fluid channel, the magnitude of the force experienced by a cell strongly depends on its position. We, therefore, start by analyzing the drag and DEP forces.

To study the drag force of particles in the channel, we first assess the velocity field, which is related to the drag force via Eq. 6. In Fig. S1, an example of the velocity field in the channel, including a cross-section slice, is shown. Note that, since we are not using any contraction and expansion regions in the channel, the velocity flow inside the channel was uniform and laminar. Compressed sections in a flow channel result in a local increase of the fluid velocity, whereas expansion regions result in a decrease (Valijam and Salehi 2021). In addition, we noted that the thin gold electrodes (100 nm in height) modeled on the bottom and top glass slides did not affect the fluid flow. Thus, since all designs have the same flow channel geometry profiles, except the shifted electrodes, the same fluid field was obtained in all geometries resulting in similar fluid drag forces for all configurations. In Fig. 4, we show an example of the induced drag force in the y-direction on a CTC and an RBC moving through the channel. The results show that when cells initially move from inlet B and are exposed to the buffer liquid from inlet A, which pushes the cell close to the side wall via pN forces (after 100 µm), the cell trajectory stabilizes and moves along a streamline in the channel. At the end of the flow channel, the force in the y-direction increases since the fluid changes direction due to outlets C and D. Considering that the flow profile in the channel is parabolic, as seen in Fig. S1, also implies that particles will move at different velocities depending on where they are located in the x–y plane. Therefore, they will cross the channel at different times.

Fig. 4
figure 4

The drag force in the y-direction acting on an RBC and CTC moving in the flow channel. The flow velocity at the B and A inlets were 134 μm/s and 853 μm/s, respectively

Full size image

To characterize the electric field distribution from the electrodes for the different configurations, we first analyzed the electric field contours from our simulations, see Fig. 5A, B and C. In Fig. 5A, B and C, we show the sideview (z- and x-axis) of electrodes energized using ± 7 V. This indicates that the density of the electric fields is higher near the electrodes' edges and decays rapidly when moving away from the electrodes. Also, it is clear that the position of the top and bottom electrodes relative to each other is important. In the first arrangement, where the top and bottom electrodes are aligned (Fig. 5A), the electric fields were confined within T0-B0, T1-B1, T2-B2, T3-B3 and T4-B4 (see Fig. 3 for definitions), thus there is no overlapping of electric fields between pairs of electrodes. However, by introducing a shift (L/2) of the electrodes, a stronger non-uniform electric field is achieved (Fig. 5E). This non-uniform field increases further when electrodes are shifted with L, resulting in electric fields confined between T0-B0-B1, T1-B1-B2, T2-B2-B3, T3-B3-B4 and T4-B4-B5 (Fig. 5C). Shifting generates a broad region with non-uniform fields and increases the area in which particles are exposed to the electric fields. That shifting also enhances the y-component of the electric field (Fig. 5D, E, compare with 5F). In conclusion, cells moving in the flow chamber will experience broader regions with non-uniform electric fields when electrode pairs are shifted relative to each other, which will help separate cells with different dielectric properties.

Fig. 5
figure 5

A–C shows the electric potential distribution generated by the electrodes for different configurations and D–F shows the y-component of the electric fields in the center plane inside the channel

Full size image

Since the DEP is proportional to the gradient of the electric field squared, we further assessed the DEP forces acting on cells that move in the flow channel by considering the dielectric properties of the particles (Table 1). In Fig. 6, we plot the y-component of the DEP force for the three proposed configurations. We see that the magnitude of the DEP force on a CTC cell and an RBC were higher in the arrangement with an L shift, which is in line with simulation data shown in Fig. 5.

Fig. 6
figure 6

DEP force imposed on RBCs and CTCs when electrodes are energized using ± 7 V. The panels show, top to bottom electrodes shift along the x-axis, A 0, B L/2 and C L

Full size image

As shown in Fig. 6, due to the bigger radius of the CTCs and according to Eq. 1, CTCs experience a higher nDEP force than RBCs for all designs. The higher DEP force, therefore, deflects CTCs further away from the electrodes. Also, by looking at Fig. 5D, E and F, we observe that the gap between electrodes T0/T1, and B0/B1, results in significantly reduced electric fields in local regions. Thus, there is a weak DEP force induced on particles in these regions. Shifting electrodes reduces these regions with low electric fields and should therefore improve the DEP force. Indeed, we see that the third configuration with shifted electrodes produces the highest DEP force for CTCs. However, we also see that the DEP force acting on cells reduces when cells move away from the electrodes, that is, they experience a smaller y-component of electric fields as they flow toward the centrum of the channel. Thus, different configurations result in various regions with different magnitudes of DEP force that need to be considered when making designs.

3.2 Separation performance of MDA-MB-231 and RBC cells

So far, we have considered and evaluated how the drag force and DEP force act on CTCs and RBCs in a 2 mm flow channel. To extend our analysis and look at the separation performance for different conditions, we now consider the random mixture of 3660 RBCs and CTCs injected into inlet B and the number of cells that exits via the two outputs C and D, see Fig. 7. Preferably, we want the CTCs to exit via outlet C. Again, we energize the electrodes with ± 7 V at a frequency of 70 kHz. For the three designs, the height is set to 35 μm, recall that in a thin flow channel, it is easier to separate particles since the DEP force will be stronger. With no electrode shift, the DEP force is not strong enough to deflect CTCs to outlet C; both cell types exit via outlet D (Fig. 7A). With a L/2 shift, all RBCs exit via outlet D and 60% of the CTCs exit via C. Finally, with an L shift, CTCs and RBCs are completely separated, thus all CTCs exit via C and all RBCs exit via D. Thus, we concluded that the third design could efficiently separate CTCs and RBCs at ± 7 V and with a channel height of 35 μm.

Fig. 7
figure 7

Separation of CTCs from RBCs for various shifts of top and bottom electrodes. A 0, B L/2 and C L). The amplitude and frequency of sinusoidal voltage assigned to the top and bottom electrodes were ± 7 V operated at 70 kHz, respectively

Full size image

3.3 Effect of the applied voltage, channel height, and electrode shape

As found in the simulations above, the third design resulted in the best separation of CTCs and RBCs when energizing the electrodes with ± 7 V at 70 kHz. To find the optimum voltage, in this work defined as the lowest possible to reduce Joule heating but still able to efficiently separate cells, we investigated the separation performance of the cells running different voltages for the third design, in the above figures considered as the C panel. Four different voltages (± 5.5 V, ± 6 V, ± 6.5 V, ± 7 V) at frequency 70 kHz were tested by analyzing the magnitude of the negative DEP force.

First, we tested the separation efficiency of the CTCs and RBCs using the lowest voltage, ± 5.5 V. We quantified the efficiency and purity of the separation using Eqs. 9 and 10. For a ± 5.5 voltage, we see that all RBCs exit via outlet D (Fig. S2A), whereas only 25% of the CTCs exit via output C (Fig. S4A). When increasing the amplitude to ± 6 V, CTCs and RBCs were separated well, and all CTCs exit via outlet C and RBCs via outlet D, as wanted (Fig. S2B, Fig. S4A). This was also the case when the voltage was increased to ± 6.5 V and ± 7 V, all CTCs deflected toward outlet C and the RBCs to outlet D (Fig S2C and D, Fig. S4A). Our simulation results, therefore, suggest that ± 6 V is the lowest voltage that can be used and still separate the cell mixture with high efficiency and purity.

The channel height is an important factor that influences the throughput and separation efficiency of CTCs and RBCs (Tajik et al. 2019). Increasing the height of the channel allows for higher volume throughput allowing more particles to be separated. However, the height is also a limiting factor since the DEP force is reduced with increasing distance between electrodes making separating harder for high fluid channels. Therefore, to find the highest possible channel that could separate cells using the conditions mentioned above, low voltage (± 6 V) operated at 70 kHz, we investigated the performance of 35 µm, 40 µm, 50 µm, 60 µm, 70 µm high fluid channels. We found that for the lowest channel, 35 µm, cells were separated with a 100% high efficiency and purity, this was also the case for 40 µm and 50 µm channel height (Fig. S3A,B and C, Fig. S4B). When the height was increased to 60 µm, CTCs were only partially separated, and the separation efficiency was 55% (Fig. S3D, Fig. S4B). The separation efficiency was further decreased when the height of the channel was increased to 70 µm, no CTCs could be separated from the RBCs, and all exited via outlet D (Fig. S3E, Fig. S4B). Thus, we concluded that 50 µm is a suitable height that still can separate cells and have a sufficient throughput of 0.9 µl/min. In comparison to other works, this throughput is slightly higher. For example, in another chip design using a DEP-based separation they reached an efficiency of 0.5 µl/min (Marchalot et al. 2015). An additional paper reached 0.1 µl/min at (± 9 V) and 3.2 MHz (Alshareef et al. 2013). In supporting Movie S1, we show how particles move in a 50 µm high channel and low voltage (± 6 V) operated at 70 kHz.

After optimization of the voltage, we investigated the influence of the electrode shape on separation efficiency. Therefore, we designed and compared rectangular, triangular, and semicircular electrodes positioned in a top and bottom arrangement, see Fig. 8A–C). All electrodes were designed with the same length at the base (100 µm) and width (20 µm), however, due to the different shapes the area differs. We show the electric field distribution for each shape in the center plane in Fig. 8A–C and the corresponding electric field along the x-axis in Fig. 8D. An analysis of the electric field distribution in the separation region shows that the rectangular electrodes produced significantly higher non-uniform electric fields, in general, the field is more than twice as high. The higher fields produced by the rectangular electrodes directly implied that particles experienced a higher DEP force compared to the other geometries (triangular and semicircular). This is indicated by the weaker separation performance of the triangular and semicircular shaped electrodes when energized at the same voltage as the rectangular, see Fig. S5, We, therefore, conclude that the suggested shape used in our initial design was the most suitable to separate cells.

Fig. 8
figure 8

Distribution of the electric fields at the center of the channels for different electrode shapes that are arranged in a shifted position A rectangular B triangular C circular. D Electric field distribution for the different shapes. Rectangular electrodes (blue) produce more than twice as high electric fields in comparison to the circular (yellow) and triangular (red) electrodes

Full size image

The separation efficiency is strongly influenced by the electric field strength, which further generates Joule heating inside the channel. Joule heating can, in turn, change the conductivity and permittivity of the solution and harm biological cells since they are sensitive to temperature fluctuations (Becker et al. 1995; Matsuura et al. 2015). To estimate the temperature dependence on the applied voltage, we first calculated the temperature of the fluid by using the approximative equation (Castellanos et al. 2003),

$$\Delta T \approx \frac{{\sigma_{{\text{m}}} V^{2} }}{{2k_{{\text{m}}} }},$$
(11)

where V is the magnitude of the applied voltage, σm is the conductivity of the fluid and km is thermal conductivity. We compared the temperature difference for ± 6 V and ± 7 V. Thus, we first set the voltage to 12 V (± 6 V), the conductivity to 55 mS/m, and the thermal conductivity of the medium to 0.60 Jm−1S−1 K−1. This calculation shows that increasing the voltage to ± 7 V from ± 6 V increases the temperature inside the channel by 0.54 K. This is a significant increase in temperature that could affect cell viability, therefore, we suggest using ± 6 V instead of ± 7 V. This however, did not tell us about the heat distribution in the channel. To further analyze how heat distributes in the channel, while energizing the electrodes with ± 6 V and 70 kHz, we simulated the heat distribution in COMSOL. In the simulation, we set the room temperature to 293.15 K to represent a general room temperature. An analysis of the results shows that the maximum temperature of the fluid is 305.35 K close to the electrodes, see Fig. 9A. Even though a cell would move into this higher temperature, it will only be exposed to such temperature for about 0.5 s. Thus, the fairly low temperature increase and the short time under is significantly lower than what is needed to cause irreversible cell damage.

Fig. 9
figure 9

A shows a heat map of the center plane of the 50 µm height channel when energizing the electrodes by ± 6 V. B shows the temperature of the center line in the channel

Full size image

According to the results of our simulations, the maximum height and width of the channel that can be used and still achieve 100% separation of CTCs and RBCs are 50 µm and 150 µm, respectively, when operating the top and bottom electrodes with ± 6 V. Our findings is in line with the work by Alazzam et al. (Alazzam et al. 2017), which presented a separation device with a channel height and width of 35 µm and 50 µm, respectively. However, they generated the DEP force from bottom electrodes operated at ± 7.5 V and they used 20 electrodes. Thus, our simulations suggest that it is possible to completely separate MDA-MB231 and RBCs with a lower voltage by using a different setup of the electrodes and fewer. Our five pairs of gold electrodes placed on the top and bottom of the channel, that are shifted and only reach into the channel by a fraction of the channel width, did provide a strong enough DEP force to separate the particles at a low Joule heating effect.

4 Conclusions

In this study, the aim was to design a mm-long lab-on-the-chip microfluidic device that utilizes DEP forces for continuous separation of RBCs from CTCs (MDA-MB-231). We investigated the separation efficiency for different electrode configurations, electrode shapes, and channel heights using numerical simulations in COMSOL multiphysics simulations. We found that using five pairs of shifted top and bottom interdigitated electrodes energized with ± 6 V at 70 kHz, this design can perfectly separate CTCs from RBCs with a channel height of 50 µm over a 2 mm distance. The low voltage used together with a sufficient channel height minimizes the Joule heating effect and should thereby minimize cell damage. We suggest that the proposed design would be effective for separating CTCs and RBCs and, thus, used as a device for the early detection of CTCs.