Hybrid molecular-continuum simulations of water flow through carbon nanotube membranes of realistic thickness

Abstract

We present new hybrid molecular-continuum simulations of water flow through filtration membranes. The membranes consist of aligned carbon nanotubes (CNTs) of high aspect ratio, where the tube diameters are ~1–2 nm and the tube lengths (i.e. the membrane thicknesses) are 2–6 orders of magnitude larger than this. The flow in the CNTs is subcontinuum, meaning standard continuum fluid equations cannot adequately model the flow; also, full molecular dynamics (MD) simulations are too computationally expensive for modelling these membrane thicknesses. However, various degrees of scale separation in both time and space in this problem can be exploited by a multiscale method: we use the serial-network internal-flow multiscale method (SeN-IMM). Our results from this hybrid method compare very well with full MD simulations of flow cases up to a membrane thickness of 150 nm, beyond which any full MD simulation is computationally intractable. We proceed to use the SeN-IMM to predict the flow in membranes of thicknesses 150 nm–2 μm, and compare these results with both a modified Hagen–Poiseuille flow equation and experimental results for the same membrane configuration. We also find good agreement between experimental and our numerical results for a 1-mm-thick membrane made of CNTs with diameters around 1.1 nm. In this case, the hybrid simulation is orders of magnitude quicker than a full MD simulation would be.

Introduction

Water scarcity is a major and increasing problem in both developing and developed countries. Desalination is the most attractive source of potable water, since sea water and brackish water make up ~98 % of the world’s available water (Humplik et al. 2011). Membranes of aligned nanotubes offer a radical opportunity to make significant savings in energy and capital costs in state-of-the-art reverse osmosis desalination facilities, as they have much higher pure water permeabilities than conventional membranes. The high permeability arises from the smooth internal structure of nanotubes, producing low-friction fluid transport. Substantial reductions in water–surface friction have been demonstrated with decreasing tube radius (<10 nm) (Falk et al. 2010), which explains the many orders of magnitude flow enhancement over continuum fluid theory that is observed in both experiment (Holt et al. 2006; Majumder et al. 2005; Majumder and Corry 2011) and simulation (Thomas and McGaughey 2009; Kannam et al. 2012; Nicholls et al. 2012; Walther et al. 2013; Ritos et al. 2014).

A conventional macroscopic approach, such as the Navier–Stokes–Fourier (NSF) equations, is an inadequate flow model for these types of problems. Even with heavily modified versions of the NSF equations including slip, constitutive, and compressibility adjustments for water flow in carbon nanotubes, the accuracy is acceptable only for tube diameters larger than a few nanometres; for smaller diameters, such as the 1.1- and 2-nm-diameter CNTs considered in this paper, enhanced NSF equations are still inaccurate and unreliable (Holland et al. 2014). Molecular dynamics (MD) is currently the best method available to model these non-equilibrium and non-continuum liquid flow problems. Despite MD’s accuracy, its high computational cost makes it impractical for applications of engineering interest. For example, a supercomputer with thousands of processors can require several weeks to run MD simulations of membranes of a thickness that is comparable with experiments. This computational resource may not be readily available, and in any case it makes engineering design of membranes currently unfeasible.

In this paper we describe a recently developed hybrid molecular-continuum method (Borg et al. 2013) for investigating water flow through CNT membranes of realistic thickness. The hybrid method exploits the scale separation in the problem by running MD subdomain simulations in vital parts of the computational domain that provide refinement to an overall set of macroscopic flow equations. This approach reduces not only the overall computational expense of the simulation but also the computational resources that are required. We use full MD simulations of membranes up to 150 nm thick as validation cases. Simulations of larger membranes with thicknesses from 1 μm up to 1 mm are also presented, as these can provide insight into the performance of desalination membranes at realistic scales.

One of these larger hybrid simulations is directly compared with experiment, highlighting possible sources of errors and inaccuracies in both the experimental and computational approaches. The linear dependence of the flow enhancement with the length of the CNT, that was initially addressed in Walther et al. (2013), is also discussed alongside the results from these hybrid simulations.

The paper is organised as follows. Section 2 is an overview of recent advances in hybrid molecular-continuum methods. In Sect. 3, the most advanced hybrid method for solving water flow through CNT membranes is presented. In Sect. 4, we describe the configuration of the MD micro-elements used in the hybrid method. Results are presented in Sect. 5, and conclusions are drawn in Sect. 6.

Hybrid molecular-continuum methods

The filtration/desalination membrane problem is shown in Fig. 1a; bundled open-ended carbon nanotubes (CNTs) connect two rigid graphene sheets. For practicality we take this ideal configuration: the tubes are perfectly aligned, and there is repeatability in the spacing, diameter, and length of the CNTs throughout the membrane. As a result, the simulation of one tube (highlighted in Fig. 1a) is sufficient to calculate the overall membrane performance, as indicated in Fig. 1b. In a desalination application, a pressure higher than the osmotic pressure is applied to an inlet reservoir containing a salt water solution. The small pores in the membrane act as a molecular sieve, rejecting the larger hydrated salt ions and allowing only water molecules to flow through. To make the hybrid implementation in this paper simpler, we only consider the flow of pure water through the entire membrane. Salt rejection percentages sufficient to produce drinkable water have been shown to occur for CNT diameters smaller than 1 nm (Corry 2008). In this work we consider somewhat larger diameters (i.e. 1.16 and 2.034 nm) for the purpose of comparing our results with data in the literature.

Fig. 1

a Ideal filtration/desalination CNT membrane, b configuration problem, c domain decomposition (DD), d heterogeneous multiscale method (HMM), and e serial-network internal-flow multiscale method (SeN-IMM)

The thicknesses of membranes that are considered in experiments are typically ~3–6 orders of magnitude larger than the CNT diameters (i.e. membrane thicknesses are in the μm–mm scales). This makes molecular dynamics simulations of the entire tube too computationally costly. However, these desalination membranes are multiscale flow problems, so we can exploit computationally cheaper hybrid molecular-continuum methods. Length-scale separation exists in the streamwise direction for the majority of the membrane (except in the entrance and exit regions), while high timescale separation exists if the flow is (quasi) steady.

Various hybrid molecular-continuum methods for liquids have been proposed in the literature, but not all of these are applicable to this membrane problem. Hybrid methods are commonly classified into two categories: domain decomposition (DD) (e.g. O’Connell and Thompson 1995; Nie et al. 2004) and the heterogeneous multiscale method (HMM) (Ren and Weinan 2005). DD solves boundary or interface problems; the interface is typically modelled by an MD solver, which is coupled to a continuum fluid solver at an overlapping region via fluid state or flux properties. DD would have some serious difficulties with the membrane system here, as the overlap needs to be located in regions of bulk-fluid equilibrium that, for liquids, are usually around 4–5 nm from any interface. As mentioned above, CNT diameters for desalination applications are smaller than this limit, meaning that the MD portion for DD would need to extend the entire diameter and length of the computational domain as illustrated in Fig. 1c. So there would be no computational savings in using DD over a full MD simulation. A review of advances in DD for liquids can be found in Mohamed and Mohamad (2010).

The heterogeneous multiscale method (HMM) (Ren and Weinan 2005), also known as the point-wise coupling method (Asproulis et al. 2012), is more appropriate for scale-separated problems where boundary and constitutive information are unknown. This missing information is generated concurrently by MD in the simulation. The continuum solver is defined everywhere in the domain, and MD supplies microscopic refinement at every node of the computational mesh, as shown in Fig. 1d. Like DD, HMM also has some serious disadvantages when applied to the membrane problem. The major issue arises from the combination of the large number of grid points that are required in order to obtain a good approximation of the hydrodynamic variables in the transverse direction (e.g. velocity profiles) and the large MD element sizes. The size of each MD element centred at each grid point is typically constrained by the minimum distance between periodic boundaries (typically ~5 nm) that prevents finite size effects. Consequently each MD box is larger than the CNT diameter and overlaps others due to the small spacing of the macroscopic grid points. This not only makes HMM computationally very costly but also brings its accuracy into question when solving for transverse fluid properties in high confinement. A full discussion of the difficulties in using HMM for problems with mixed degrees of scale separation is given in Lockerby et al. (2013) and Borg et al. (2013).

The internal-flow multiscale method (IMM) (Borg et al. 2013; Patronis et al. 2013; Patronis and Lockerby 2014) has been recently developed for high-aspect-ratio geometries confined at the nano-/micro-scale for both liquid and rarefied gas flows. The method consists of placing periodic channel micro-subdomains at regular locations along the tube or channel, with cross sections chosen to match the local geometry, as illustrated in Fig. 1e. The MD subdomains are coupled to a simple one-dimensional macroscopic fluid equation for mass conservation. A continuous macroscopic description of pressure and density in the streamwise direction is also used. The macroscopic equations do not require constitutive relationships or boundary conditions, apart from inlet/outlet boundary conditions on pressure and density that are typically fixed by the problem. Fluid and wall conditions are instead generated in the MD subdomains, and since these cover the entire cross section, there is no need to collocate large MD subdomains with macroscopic grid points in the transverse direction, as in HMM.

Continuum $\rightarrow$ MD coupling is achieved by applying an external body force to liquid molecules within each subdomain, and this communicates streamwise pressure gradients from the macro- to the micro-description. Macroscopic density variations are transferred to the micro-description through the use of density controllers which can delete or introduce molecules during an MD simulation.

MD $\rightarrow$ continuum coupling is enabled through measurements of coarse-grained properties, such as the mass flow rates in individual micro-subdomains, which are then used to evaluate overall macrocontinuity errors. For steady-state problems, the IMM converges to a solution in approximately 2–3 iterations of the couplings, which is very efficient. Recently, the IMM has also been extended to treat unsteady/transient flows (Borg et al. 2015; Lockerby et al. 2015).

The original motivation for IMM was to solve serial-channel fluid problems of high aspect ratio, in particular where length-scale separation (between molecular and hydrodynamic effects) exists in the streamwise direction, but there is no such scale separation in the transverse direction. While IMM can be used to solve the majority of the flow in the CNT—see Fig. 1e—the problem that arises is how to model the exit and entrance regions of the membrane, which, because of abrupt streamwise changes in geometry, do not exhibit any clear scale separation. These ‘junctions’ typically play an important role in a flow system because their losses have a consequent effect on the through-membrane flow rate, which is an important variable in fluidic membrane design. Owing to the very low friction in the CNTs, modelling the junction pressure losses in CNT membranes is especially important because they dominate the pressure losses for a wide range of membrane thicknesses (Nicholls et al. 2012; Walther et al. 2013).

As with HMM, locally refining the junction regions with more IMM subdomains will substantially increase the computational cost, while not necessarily improving accuracy. The serial-network IMM (SeN-IMM) (Borg et al. 2013) has been developed instead to solve serial-channel flow problems with varying scale separation. This method is an extension of IMM and models the non-scale-separated junctions using MD subdomains, with IMM subdomains in the long channel. SeN-IMM has been validated for various channel network configurations with flows of a simple Lennard–Jones fluid. The method has also been extended to consider general nanofluidic branching networks (Stephenson et al. 2014). Validation of these hybrid methods was by comparison with full MD simulations (with an error <1–5 % in the hybrid results).

Hybrid method for CNT membranes

In this paper we apply the SeN-IMM to water–CNT membrane systems. Both the full MD (for validation purposes) and the hybrid simulation set-ups of the membrane problem are shown in Fig. 2. All the simulations are under the same flow assumptions as in the original presentation of the SeN-IMM by Borg et al. (2013), i.e. that the flows are low speed, low Reynolds number, isothermal, compressible, and steady state.

Fig. 2

a The full MD simulation, b the SeN-IMM hybrid configuration, c the combined reservoirs and tube MD micro-element, and d the tube MD micro-element. Figures are not to scale

In the hybrid method, a membrane of thickness L is segmented into three parts (see Fig. 2b): two reservoir junctions (i.e. an entrance and an exit) and the carbon nanotube which is treated using IMM. In this case, because the carbon nanotube is of constant cross-sectional area, and the pressure variations are expected to be linear, one micro-subdomain in the IMM is sufficient. For future consideration of carbon nanotubes with gradually varying cross-sectional area and defects, the IMM would allocate more MD subdomains. Also note that each reservoir junction contains also a part of the CNT in order to contain the entrance/exit effects and allow the flow to fully develop. A single flow development length $\delta l$ is chosen for both entrance/exit parts for simplicity, and this is estimated from laminar macroscopic theory as described in Borg et al. (2013). The remaining carbon nanotube of length $l = L - 2\delta l$, which spans almost the entire thickness of the membrane, can be treated using IMM. Any computational saving that the SeN-IMM provides is achieved only from replacing long scale-separated channel sections with shorter, but hydrodynamically equivalent, periodic channels. The junction micro-elements provide no computational advantage, except that smaller MD simulations in SeN-IMM can converge far quicker to steady state than they would in a large MD system. We find that the density variation along the nanotube remains linear for the full range of CNT lengths considered in this paper, and so the original CNT of length l can accurately be represented in the IMM using just one micro-element of reduced length $l^{\prime}$.

At the heart of this multiscale method lies the conservation of mass. The mass flow rate through each micro-element must be identical for a steady-state flow, i.e.

$${\dot{m}}_i = {\mathrm{const}} = \overline{{\dot{m}}},$$

(1)

where ${\dot{m}}_{i}$ denotes the mass flow rate measured in the $i{\text{th}}$ of $\varPi$ micro-elements. In the cases studied here, there are always three micro-elements, so $\varPi =3$. The mean mass flow rate $\overline{\dot{m}}$ along all of the elements can be considered as the principal output of the multiscale simulation. During the first iteration of SeN-IMM, the mass flow rates in every micro-element are unequal, but a solution to Eq. (1) is approached after consecutive iterations of the hybrid algorithm.

The inputs to the hybrid problem are the absolute pressure at the inlet or the outlet reservoir, the overall temperature (assumed constant throughout at 298 K), and the total pressure difference $\Delta P$ across the membrane. By conservation, the addition of all micro-element pressure drops gives the total pressure difference:

$$\Delta P = \sum _{i=1}^{\varPi } \Delta P_i,$$

(2)

where $\Delta P_i$ is the pressure drop along the $i{\mathrm{th}}$ micro-element. Note that the pressure drop along the central CNT of length l is given by $\Delta P_2 = \Delta P_{2}' \ l/l'$, where $\Delta P_{2}'$ is the linearly interpolated pressure drop applied to the MD subdomain of length $l^{\prime}$.

For convenience, the two water reservoirs are modelled as a single micro-element, instead of two separate ones, as shown in Fig. 2c. This enables periodic boundary conditions to be used in all directions. The outer membrane walls are graphene sheets with dimension $10.5 \times 10.2$ nm, while the connecting tube is a CNT of length $2\delta l + l_{{\rm B}} = 12.6$ nm, where $l_{\mathrm{B}} = 2.5$ nm is a buffer region added to apply the pressure loss from the missing CNT of length l. All simulations are for a (15, 15) CNT of diameter $D = 2.034$ nm, unless specified otherwise.

As in HMM, there is no explicit communication between the individual MD simulations, only the constraints applied by the macroscopic solver, Eqs. (1) and (2). In addition, no constitutive relations or slip boundary conditions are required in the continuum definition as these are contained within the flow rates extracted from the micro-elements. The continuum $\rightarrow$ MD solver constraint consists of applying pressure drops along individual micro-elements that satisfy Eq. (2). The MD $\rightarrow$ continuum step consists of mass flow rate measurements produced from all the micro-elements. In order to conserve overall mass flux, the applied individual pressure drops must subsequently be adjusted. To be able to enforce this, we need an expression relating pressure drop to mass flow rate. Given the reasonable assumption that, in the steady state, ${\dot{m}}_i$ varies monotonically with $\Delta P_i$, a straightforward iteration scheme towards a common mass flow rate in each of the micro-elements is provided by:

$$\Delta P_i^{n+1} = \Delta P_i^n + \psi _i \left( \overline{\dot{m}}^{n+1} - \dot{m}_i^n \right) ,$$

(3)

where $\psi _i$ is a relaxation parameter for each micro-element and n is the iteration index. Inspection of Eq. (3) reveals that as the mass flow rate in each micro-element converges to the mean [and Eq. (1) is then satisfied], the pressure drop in each micro-element will cease to be updated. The mean mass flux is implicitly defined, i.e. it is evaluated at the updated iteration index $n+1$. This means that Eq. (3) represents $\varPi$ equations with $\varPi +1$ unknowns. The missing equation is provided by the pressure difference constraint, Eq. (2). The system of linear equations given by Eqs. (2) and (3) can then be solved using LU decomposition or similar.

At each iteration, before the system of equations can be solved, the individual relaxation parameters $\psi _i$ for each micro-element need to be determined. We base these on approximating a linear relationship between $\Delta P_i$ and $\dot{m}_ i$ at a previous iteration:

$$\psi _i = \frac{\Delta P_i^n}{\dot{m}_i^n}.$$

(4)

Note, this approximation does not affect the accuracy of the converged solution, only the speed of convergence. By substituting Eq. (4) in Eq. (3), the latter can be reduced to a simpler form:

$$\Delta P_i^{n+1} = \Delta P_i^n \frac{ \overline{\dot{m}}^{n+1}}{\dot{m}_i^n}.$$

(5)

We can also determine the mean mass flow rate at the updated iteration ($n+1$) by substituting Eq. (5) in Eq. (2), giving:

$$\overline{\dot{m}}^{n+1} = \frac{\Delta P}{\sum _{i=1}^{\varPi }\left( \Delta P_i^n/\dot{m}_i^n\right) }.$$

(6)

The algorithm requires initial estimates for the pressure drops along micro-elements (i.e. at $n=0$). We estimate these according to: $\Delta P_i = f L_i \Delta P/ L$, where $L_i$ is the streamwise length of the $i{\mathrm{th}}$ micro-element, L is the total length of the system, and f is a user-defined weighting factor. The weighting factor is needed as the total pressure drop contains the entrance and exit losses, which will be explicitly included in the junction micro-elements. In addition, a sensible selection of f increases the stability of the method by avoiding over-corrections that may lead to a reversal of the flow direction. This weighting factor solely affects convergence and does not alter the accuracy of the method or the final result.

Then all the micro-element MD simulations are performed with the pressure differences $(\Delta P_i)$ calculated as above and imposed through body forces as explained below, until a steady state is reached in all subdomains, after which the mass flow rates are measured. The mass flow rates are used in Eqs. (5) and (6) to determine the new pressure drops for the next iteration and the overall mass flow rate. These steps are repeated until a convergence criterion is met:

$$\zeta _i^{n+1} < \zeta ^{\mathrm{tol}},\quad \mathrm{with} \; \zeta _i^{n+1} = \frac{| \overline{\dot{m}}^{n+1} -\dot{m}_i^n | }{\overline{\dot{m}}^{n+1}},$$

(7)

where $\zeta ^{\mathrm{tol}}$ is a predetermined tolerance used for all micro-elements.

Molecular dynamics

The two micro-elements, i.e. the combined reservoirs (Fig. 2c) and the shortened CNT (Fig. 2d), as well as the full MD simulation (Fig. 2a) are simulated using the mdFoam molecular dynamics solver. This software has been validated over a broad range of applications (Macpherson and Reese 2008; Ritos et al. 2013; Dongari et al. 2011) including flow of water through carbon nanotubes (Nicholls et al. 2012; Ritos et al. 2014; Nicholls et al. 2012). In all our simulations we use the TIP4P/2005 water model (Abascal and Vega 2005; Vega and Abascal 2011) with a Lennard–Jones potential for water–carbon interactions that has the following intermolecular parameters: ${\sigma _{\mathrm{CO}} = 0.319}$ nm and $\epsilon _{\mathrm{CO}} = 0.427\,{\hbox {kJ}}\,{\hbox {mol}}^{-1}$.

The full MD simulation is set up as shown in Fig. 2a, and periodic boundary conditions are set in all directions. A pressure drop of $\Delta P = 200$ MPa is applied across the membrane through an external forcing applied to molecules occupying a small buffer region of length $l_x=5$ nm at the inlet reservoir, given by a Gaussian form:

$$F_x(x) = \frac{\Delta P}{\rho _n \sigma _{{\rm s}} \sqrt{2 \pi }} e^{\left( -x^{2}/2 \sigma _{{\rm s}}^2\right) },$$

(8)

where $\sigma _{\mathrm{s}} = l_x/8$ is the standard deviation of the Gaussian, $\rho _n$ is the fluid number density and $F_x(x) = 0$ outside the buffer region.

A velocity-unbiased Berendsen thermostat (Berendsen et al. 1984) is used only in the reservoir regions with a 66-fs time constant in order to control the temperature at 298 K by rescaling only the molecular velocity components that are normal to the flow. A density controller (Borg et al. 2010) was only used in the initialisation part of the simulation (i.e. the first 0.5 ns) in order to set the density at the inlet to $\rho = 1068\,{\hbox {kg/m}}^3$ using the FADE mass-stat (Borg et al. 2014). This is an indirect way of setting the absolute pressure in the system. After steady state is obtained, the full MD simulation is run for an additional period of between 5 and 10 ns to obtain the mass flow rate and other measurements.

The hybrid technique requires the MD simulations of each micro-element to be run at each iteration of the algorithm described in Sect. 3. The initialisation of the reservoir micro-element follows a similar procedure to that required for full MD simulation, including applying the overall pressure drop $\Delta P = 200$ MPa, and control of density and temperature. An additional forcing region of length $l_{\mathrm{B}} = 2.5$ nm is set up in the middle part of the CNT that connects the reservoirs, which is necessary to replicate the pressure loss over the missing length l of the CNT, as shown in Fig. 2c. The force applied in this region is also spatially distributed using the Gaussian in Eq. (8). In the initial iteration $(n=0)$, this pressure drop is estimated, but will converge with further iterations towards the actual value.

The CNT MD micro-element is shown in Fig. 2d. The water density is set in the CNT by using an interpolation between exit and entrance parts of the reservoirs. This procedure increases the accuracy of the method, as discussed in Borg et al. (2013). The pressure drop over the length $l^{\prime}$ is obtained from the hybrid constraints, and is set along the tube by an external forcing (Eq. 8), applied in a short additional buffer region of length $l_{\mathrm{B}} = 2.5$ nm, as highlighted in the figure. Note that the overall CNT pressure drop is first interpolated as discussed in Sect. 3. In this way the same pressure gradient is achieved along the CNT micro-element, while significant computational savings are achieved as only a fraction of the full membrane thickness is simulated, given by $l/l^{\prime}$. The length of the micro-element remains the same independent of membrane thickness l (or L), and so this leads to increased computational savings as the membrane thickness is increased. At $n=0$ the estimated pressure drop is equal to that chosen in the middle buffer region of the reservoirs micro-element in Fig. 2c.

At every iteration the modified pressure drops in the micro-elements are calculated according to Eq. (5) and the MD simulations are repeated. An initial equilibration time of at least 2 ns is needed to create a fully developed flow inside the CNT and reservoirs, and a production run of at least another 2 ns is needed to reduce the standard deviation (SD) of the mass flow rate measurements to <5 %. The mass flow rate is measured in a flow plane at a point within the CNT (in all micro-elements).

Results and discussion

Validation cases

We consider full MD simulations of the membranes as the reference case. The mass flow rate is the main comparison property, but additional measurements and comparisons of pressure, temperature, density and velocity profiles are available in this paper’s supplementary material. The validation simulations consist of three membranes with thicknesses L of 50, 100, and 150 nm. These lengths are chosen so that full MD simulations can still be performed in a reasonable time. Figure 3a shows how accurately the mass flow rate can be predicted by the SeN-IMM when compared with full MD. The assumption of an initial linear pressure variation along the CNT seems to be very efficient for these systems, as the predicted mass flow rate after the first iteration differs by <5 % from the full MD prediction. Long production runs of at least 2 ns ensure that the mass flow rate and all the other properties have been measured over more than $10^6$ samples, leading to small SEMs (standard errors of the means). The stability of the method can also be observed, and although the measured mass flow rate can deviate at one iteration it converges to a more accurate value at the next iteration.

Fig. 3

a Mass flow rate measurements $\dot{m}_{\mathrm{H}}$ from SeN-IMM iterations for three different lengths of CNT, normalised by the equivalent measurements from the reference full MD simulations $\dot{m}_{\mathrm{MD}}$. Error bars are smaller than the symbol for ±1.96 SEMs (95 % confidence interval). b Axial profile of pressure along the 150-nm CNT membrane. SeN-IMM hybrid results are the values measured in the reservoirs and in the CNT micro-element

The development of the axial profile of pressure, from the high-pressure reservoir to the middle of the CNT to the low-pressure reservoir, is shown in Fig. 3b. The hybrid result is in excellent agreement with full MD. In this validation case the pressure profile shows a linear drop along the CNT, so no compressibility effects are expected. While this figure supports our initial assumption of a linear pressure drop along the CNT, the significant entrance losses should be noted as they would not be explicitly accounted for in any simple linear assumption for the pressure drop along the whole system (i.e. from reservoir to CNT to reservoir).

Figure 4 shows the convergence of SeN-IMM for the three validation cases, which is calculated according to Eq. (7). The convergence limit chosen was $\zeta ^{\mathrm{tol}} = 0.05,$ but the simulations were allowed to proceed beyond this threshold to demonstrate that our method is stable once convergence is reached. The relaxation factor $\psi$, which can vary for each micro-element as well as from iteration to iteration, seems to be responsible for the non-monotonic convergence. This relaxation factor is calculated according to Eq. (4) and can switch between under- and over-relaxation. The accuracy of the method is not affected, as seen in Fig. 3a, although the convergence measure does oscillate.

Fig. 4

Convergence of the SeN-IMM simulations of the three validation cases; the convergence value $\zeta$ is calculated according to Eq. (7)

Computational efficiency and performance

We briefly describe the computational efficiency of the hybrid method and the advantages it offers over conventional full MD simulations. All the comparisons made here are with the GPU version of the mdFoam solver. This version of the code performs all the intermolecular force calculations on GPUs, while the measurement, control, and time-stepping parts of the MD algorithm are performed on CPUs. The SeN-IMM hybrid utilises the same version of the MD solver, and simulations were performed on identical computational nodes of the high-performance computer ARCHIE-WeSt at Strathclyde University. Each node consists of two Intel Xeon X5650 CPUs (12 cores in total), 48 GB of RAM, and an Nvidia M2075 GPU card. Therefore the computational savings reported here are attributed solely to the hybrid implementation, and not to any possible hardware or software differences. For full MD simulations, the GPU version of mdFoam offers 4.5 times speed-up when compared with the CPU parallel implementation (72 cores) when simulating the 150 nm case.

Our performance comparison is based on the simulation time needed to reach the final solution using each method (i.e. full MD and the hybrid), without incorporating initialisation and equilibration times but including all the necessary iterations in the hybrid approach. The length L is used as the size variable. Larger systems not only contain more molecules but also need additional time to reach steady state. In the case of full MD simulations, the time to solution increases linearly with the membrane thickness, as Fig. 5 shows. For the three validation cases, the simulation time to solution is higher for the hybrid than the full MD. However, for the larger systems of $L=1$ and L $=$ 2 μm, the hybrid technique is more efficient, despite the fact that six iterations are needed in order to achieve the desired convergence and accuracy.

Fig. 5

Computational time to solution varying with CNT length in logarithmic and linear scales, respectively

For the 2-μm case, the total simulation time using the hybrid method is just 50 % of that for the equivalent full MD simulation, as Fig. 5b shows. For longer cases still, the computational savings will be even greater, as in the hybrid simulations only the number of iterations and/or time to reach steady state can increase. From these figures, it is estimated that a CNT membrane with a thickness of 100 μm would require around 8000 days of simulation time using the current state-of-the-art full MD solver on a GPU. However, the same result can be achieved using SeN-IMM in ~100 days (see Fig. 5a).

An additional advantage of the fixed MD simulation sizes in SeN-IMM, which are independent of the problem’s actual size, is in the computer memory required. The GPU solver utilises only the GPU memory and not the RAM memory of a node; otherwise, the communication overhead hinders any computational savings. The current GPU cards in ARCHIE-WeSt have 6 GB of memory, which is enough to simulate around 400,000 atoms. This is highlighted in Fig. 6 by the horizontal red line. So full MD simulations are limited to membranes with CNTs shorter than 1 μm. A possible solution would be to use GPUs with larger memory, but the best current GPU cards offer a maximum of only 12 GB memory. Another option would be the parallelisation of the GPU solver to enable it to run on multiple GPUs, although its performance would then be reduced due to the inter-GPU communication overhead.

Fig. 6

Number of simulated atoms varying with the CNT length in the simulated membranes

From this short performance analysis, we conclude that the only viable option to significantly reduce computational time and therefore enable access to multiscale problem sizes of engineering interest is a hybrid approach, like the SeN-IMM.

Enhancement predictions and macroscopic equations

We now present results from our hybrid simulations that would be totally impractical, or at least extremely computationally demanding, to perform using full MD. The main performance measurement of a nanotube membrane is the flow enhancement ($\varepsilon = {\dot{m}}_{\mathrm{act}}/{\dot{m}}_{\mathrm{HP}}$), which provides a comparison of the actual flow rate (e.g. predicted by MD, SeN-IMM or experiment) to that predicted by the no-slip Hagen–Poiseuille (HP) continuum fluid equation.

Simulations of CNT membranes with thicknesses of 1 and 2 μm are performed. The flow enhancement values in these cases, together with the results from the validation simulations, are compared with other computational and experimental studies. A slip and entrance-/exit-loss-modified Hagen–Poiseuille equation, like the one proposed by Walther et al. (2013), is also used in an attempt to calculate the flow enhancement (and the flow rate) in a CNT membrane of any thickness without the need to perform further hybrid or full MD simulations.

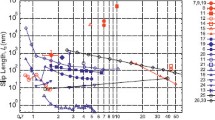
The flow enhancement in CNT membranes of different thicknesses for a given external membrane pressure difference $\Delta P$ is shown in Fig. 7. The reported values include results from our full MD simulations (for $L\,<\,50$ nm) and SeN-IMM simulations (for $L\,\ge\,50$ nm). The enhancement initially increases as the CNT length increases, but then plateaus significantly for $L >150$ nm. This should be expected, unless the flow inside the CNT is completely frictionless.

Fig. 7

Flow rate enhancement $\varepsilon$ for various thicknesses of CNT membranes L. Comparison of our results with previous computational and experimental studies. The error bars for our results are smaller than the symbol. Lines show the enhancement prediction ($\varepsilon _{\mathrm{MHP}}$) of Eq. (11) for the given parameters

Figure 7 also includes flow enhancement data from other computational and experimental investigations. The diameter of the CNT (2.034 nm) is common to all the selected studies. It should be noted that in the experiments this diameter is the dominant one in membranes that contains CNTs of various diameters. This can significantly affect the reported flow values, as viscosity and slip length vary with the diameter of the CNT (Thomas and McGaughey 2008). At the same time, a small variation in the diameter used during the HP flow rate calculation can lead to a great difference in the reported enhancement values. This diameter issue, along with other possible errors during the experimental procedures, may explain the wide differences between reported experimental values in Fig. 7.

Despite the fact that different MD software, water models, interaction potentials, and external applied pressure differences have been used, the previous computational results presented in Fig. 7 are in line with the values we calculate using SeN-IMM. The error bars of our results are smaller than the symbols in Fig. 7, while in previous studies the error bars can be quite significant. In addition, an experimental result for a biological nanochannel (an aquaporin) is also included in this figure.

In the study of Walther et al. (2013), the asymptotic behaviour of the flow enhancement was predicted using results from a CNT membrane and periodic CNT simulations. Here the same behaviour is seen in membrane simulations using SeN-IMM. These results strengthen the hypothesis that the enhancement levels-off after a linear growth with the CNT length. For the CNT diameter we have studied here, the enhancement limit is $\varepsilon _{\mathrm{max}} \approx 350$, independent of the CNT length.

In the work of Walther et al. (2013), a modified Hagen–Poiseuille equation was developed in order to predict the flow enhancement in CNT membranes of various thicknesses. The no-slip Hagen–Poiseuille equation is simply

$$\Delta P = \frac{8\mu L \dot{Q}_{\mathrm{HP}}}{\pi R^4},$$

(9)

while the modified Hagen–Poiseuille (MHP) equation, incorporating slip and entrance/exit losses, takes the form (Walther et al. 2013):

$$\Delta P = \frac{\mu C \dot{Q}_{\mathrm{MHP}}}{R^3} + \frac{8\mu L \dot{Q}_{\mathrm{MHP}}}{\pi \left( R^4 + 4R^3 L_s \right) },$$

(10)

where the coefficient C represents the sum of both fluid entrance and exit losses, $L_{\mathrm{s}}$ is the flow slip length, and $\dot{Q}_{\mathrm{MHP}}$ is the modified volumetric flow rate. From Eqs. (9) and (10) the modified flow enhancement factor is therefore:

$$\varepsilon _{\mathrm{MHP}} = \frac{8 L \left( R + 4 L_{\mathrm{s}} \right) }{8 L R + C \pi R^2 + C \pi R 4 L_{\mathrm{s}}}.$$

(11)

This depends on the length L and radius R of the CNT; it also depends on two parameters: the slip length $L_{\mathrm{s}}$ and the entrance/exit losses coefficient C. If both these parameters are zero, then the no-slip Hagen–Poiseuille prediction is reproduced.

Using Helmholtz’s minimum-energy theorem, Weissberg showed that $C < 3.47$ for $L/R \rightarrow \infty$ (Weissberg 1962). Substituting into Eq. (11) the values of flow enhancement calculated from our MD and SeN-IMM simulations produces the continuous red line in Fig. 7, with optimum fitting parameters $C = 2.49$ and $L_{\mathrm{s}} = 108.5$ nm. The black dashed line in this figure indicates the flow through a membrane if the nanotubes are frictionless, while the horizontal blue dashed line indicates the flow through a membrane without entrance or exit losses. For membranes with a thickness <150 nm, the enhancement value is almost independent of the frictional properties of the nanotube (i.e. the slip length).

This analysis indicates that the flow enhancement, and therefore the flow rate of water through CNT membranes of any thickness, can be estimated using Eq. (11) provided the parameters C and $L_{\mathrm{s}}$ are known. The value of C can be calculated by performing MD simulations of thin membrane cases, while $L_{\mathrm{s}}$ can be obtained from simulations of simple periodic CNT cases. In addition to the predictive capabilities that Eq. (11) provides, it also highlights the critical membrane thickness above which frictional losses dominate the flow.

Direct comparison with experimental results can be troublesome, as Fig. 7 shows, due to the CNT diameter issues outlined above and other possible experimental errors. Recent experimental work by Qin et al. (2011) managed to reduce a source of errors in CNT membrane experiments by performing flow rate measurements of water passing through a single CNT. One of these experimental cases is replicated here in an attempt to evaluate the performance of the SeN-IMM in terms of accuracy and computational efficiency. The diameter of the chosen CNT in Qin et al. (2011) is $D = 1.1$ nm, while its length is $L = 1$ mm. For a CNT of this length an MD simulation would be intractable. Our SeN-IMM simulation is for a CNT membrane with a tube diameter of $D=1.16$ nm, very close to the experimental value. Characteristic snapshots of the membrane are shown in Fig. 8, and the unique ordered ring formation of water molecules within the CNT is seen. A continuum fluid description of water flow through such a narrow CNT would not be suitable in these circumstances. Basic water properties (e.g. viscosity, density, hydrogen bonding) are highly altered by the confinement.

Fig. 8

Snapshots from the entrance and exit SeN-IMM micro-elements of the case replicating the experiment of Qin et al. (2011). a Cross-sectional snapshot at the entrance to the CNT membrane. All the water molecules inside the CNT are visualised. b Cross-sectional snapshot half way along the entrance/exit micro-element. Only one layer of water molecules is shown; dashed blue lines indicate the existence of hydrogen bonds according to the geometrical criterion of Luzar and Chandler (1996). c Axial snapshot of the entrance and exit micro-elements. The central section of the CNT is not visualised in order to show more clearly the ordering of the water molecules inside it (colour figure online)

The same methodology was used as for the previous hybrid simulations, with the only differences being the reduced CNT diameter and the external pressure difference, which is reduced to $\Delta P = 100$ MPa. The flow enhancement values reported by Qin et al. (2011) are also calculated under some assumptions. The first is that two van der Waals diameters of carbon (or, equivalently, twice the thickness of the CNT wall) is subtracted from the overall CNT diameter, i.e. $D_r = 1.16 - 0.33 = 0.83\,\hbox {nm}$. The second assumption is that the viscosity of bulk water (1 mPa s) is used in all calculations, although it is known that the water viscosity inside such a narrow CNT differs significantly (Thomas and McGaughey 2008; Ritos et al. 2014). The bulk water density ($\rho = 997.5\,{\hbox{kg/m}}^3$) is also used in any transformations from volumetric to mass flow rate, and vice versa.

Figure 9 shows the flow enhancement measurements that the SeN-IMM simulations predict at successive iterations. The dashed line is the experimental flow enhancement value reported in Qin et al. (2011). The SeN-IMM solution oscillates in the first three iterations, but levels-off after around 4–7 iterations, although some oscillations still remain. The convergence behaviour can also be seen in Fig. 10a where the convergence parameter $\zeta$ is below 1 when the number of iterations is >4, while Fig. 10b shows a less noisy, quicker convergence of the pressure difference along the CNT. The reason for this prolonged time to converge and its noisy character is that this simulation contains a higher level of statistical noise, compared with the thinner membranes described earlier in this paper. A thicker membrane has a much smaller pressure gradient (for a constant overall pressure drop), and so the thermal molecular velocities would be much higher than the mean flow velocity (or mass flow rate) that we are trying to measure. This is a limitation of molecular dynamics, and as such it is inherited by our hybrid method. In these simulations we have smoothed the statistical fluctuations by running the MD subdomain simulations for much longer averaging times.

Fig. 9

Flow enhancement measurements at each iteration of the SeN-IMM. Blue dashed line is the experimental flow enhancement ($580 \pm 10$) determined by Qin et al. (2011) (colour figure online)

Fig. 10

a Convergence of the SeN-IMM simulation according to Eq. (7). b Pressure difference along the CNT, excluding entrance/exit losses, calculated from the SeN-IMM simulation according to Eq. (5). Note that due to the relatively great length of the CNT in this application ($L = 1\,{\hbox {mm}}$), pressure losses can completely be attributed to frictional losses in the CNT

Despite the issue of a fluctuating convergence, the results produced by our SeN-IMM oscillate around a flow enhancement of $\varepsilon = 787$ at the seventh iteration (which is below the convergence threshold of 5 %), while the experimental value from Qin et al. (2011) is $580\,\pm \,10$, as shown in Fig. 9. This is in good agreement with experimental results despite the assumptions made during both the calculations and the experiment. Further simulations of similar systems are, however, necessary before a solid opinion can be formed regarding the accuracy and capability of the SeN-IMM for solving this type of large problem.

Finally, it should be noted that the SeN-IMM simulation took around two weeks per iteration (on one ARCHIE-WeSt node using a GPU): a total of 116 days was needed to perform all seven iterations shown in Fig. 9 and provide the final result. Using the same hardware, we estimate that a full MD simulation of the same case would require around 247 years!

Conclusions

We have presented results from applying a hybrid molecular-continuum method to steady liquid flow problems that have mixed degrees of scale separation. The serial-network internal-flow multiscale method (SeN-IMM) was used for the first time to investigate the flow behaviour of water in aligned CNT membranes. We validated the method against full MD simulations of increasingly thick membranes, up to the point where the computational cost of the MD simulations became too high. In all cases the mass flow rates and other flow properties from the hybrid simulations matched exceptionally well those measured from the full MD simulations, while the computational performance of the hybrid improves as the size of the flow problem increases.

SeN-IMM simulations of two larger systems—well beyond the reach of molecular dynamics—were compared with previous computational studies, and showed satisfactory agreement. A modified Hagen–Poiseuille equation proposed by Walther et al. (2013) was used as a tool to approximate the flow enhancement in aligned CNT membranes of any length. Finally, the SeN-IMM was used to calculate the flow rate and enhancement in a 1-mm-thick CNT membrane, replicating the experiment performed by Qin et al. (2011). The results were in good agreement, considering the assumptions and errors during both the experimental and computational processes.

When SeN-IMM is applied to problems of this size, it is several orders of magnitude more computationally efficient than MD. However, these larger simulations are still computationally intensive and so the range of our results was limited by the amount of computational resource that was available. Furthermore, it is evident that statistical noise due to the low-pressure gradients affects the rate of convergence, as well as the uncertainty of the predictions. We propose as future work the comparison of the SeN-IMM simulation method presented in this paper with additional experimental results.

The results presented here, along with previous publications on simpler fluid systems (Borg et al. 2013; Stephenson et al. 2014), show that SeN-IMM is a useful computational tool for the study of multiscale flows.