1 Introduction

Continuous processing of fine chemicals in micro reactors offers a number of distinct advantages over batch-wise production in stirred tank reactors, especially for gas–liquid reactions, viz., oxidations and hydrogenations. Gas-to-liquid and liquid-to-solid mass transfer rates are easily one to two orders of magnitude higher in micro channels because of the high surface to volume ratios (Kreutzer et al. 2001). High heat transfer rates prevent hot spot formation and thermal runaways of exothermal reactions. Additionally slug/Taylor flow results in plug flow behaviour (Kreutzer et al. 2005; Muradoglu et al. 2007). Reaction conditions are therefore much better controlled, which generally can lead to higher selectivities and yields.

For solid phase catalyzed reactions, the rate of reaction is determined by the mass transfer of the reactants to the catalytic surface and by the kinetic activity of the catalyst. The mass transfer in micro channels is usually large enough for the reaction to run in the chemically/kinetically limited regime with a typical overall mass transfer coefficient (k ov a) of 10 s−1 (Kreutzer et al. 2001, Nijhuis et al. 2001). The intrinsic reaction rate constant for solid-phase catalyzed gas–liquid reactions (k r) is typically in the order of 1 s−1 for a catalyst deposited as a coating or washcoat. For a monolayer of catalyst on the wall of a micro channel, the intrinsic reaction rate constants are even much lower \((10^{-5}{-}10^{-4}\,\text{m}_{\text{liq}}^3\,\text{m}_{\text{reac}}^{-3}\,\text{s}^{-1}).\) Therefore, an increase of the catalytic surface area of a micro channel directly translates into higher production rates. The catalytic surface area per unit of channel volume can be increased by reducing the channel diameter and by increasing the channel length, at the cost of a higher pressure drop. Another option is to use mesoporous materials deposited on the micro channel wall, such as washcoats (Nijhuis et al. 2001; Roumanie et al. 2005; Degenstein et al. 2006; Hayes et al. 2004; Kapteijn et al. 2005; Janicke et al. 2000; Srinivasan et al. 1997) or zeolites (Zamaro et al. 2005; Kiwi-Minsker and Renken 2005). However, for these materials the diffusion of the reactants into the pores then may become rate limiting. Alternatively, micro packed-beds can be used to increase the catalytic surface area (Losey et al. 2001; Ajmera et al. 2006; Hotz et al. 2008); this however increases the pressure drop over the channel significantly. Alternatively, micro pillars in micro channels can be used (Losey et al. 2002; Krishnamurthy and Peles 2007; Krishnamurthy and Peles 2009). These pillars increase the catalytic specific surface area, have an open structure, and are well-defined, whereas micro packed-beds have a more random distribution over the channel. This may result in maldistribution of the flow.

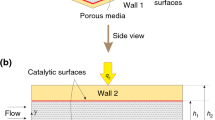
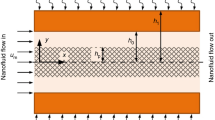
Rectangular micro channels containing, for example, 3-μm pillars with a pitch of 27 μm (Fig. 1) have a number of 1.3 × 104 pillars per cm of channel length for a channel of 1 mm in width, where the pillar pitch is defined as the inter pillar distance in the flow direction (x pillar). For this channel geometry, the catalytic specific surface area is increased with a factor of 1.14. Micro channels containing 3-μm pillars with a pillar pitch of 7 μm have 11.5 × 104 pillars per cm of channel length for a channel of 1 mm in width and increase the catalytic specific surface area with a factor of 1.33. The catalytic surface area can be increased even more by growing carbon nano fiber layers on the pillars (Wenmakers et al. 2008; Thakur et al. 2008) or by making the pillars mesoporous (Tiggelaar et al. 2009), which is part of our future research program. The open structure of the pillars also increases the hydrodynamical accessibility of the catalyst deposited on the pillars. Besides the increase of surface area, this micro pillared channel can also be used for separations through surface affinity.

Fig. 1
figure 1

Schematical overview of the pillared micro reactor (50 μm × 1 mm × 6.6 cm) where liquid slugs and gas bubbles run through the channel in slug/Taylor flow. The first axial part (3.3 cm) of the micro channel is empty and the second part (3.3 cm) contains a hexagonal array of 3-μm pillars having a height of 50 μm. Different pitches (x pillar and y pillar) are used

Full size image

However, primer to performing a catalytic reaction, a comprehensive understanding of the hydrodynamics of these pillared micro channels is required for a proper design of the micro reactor to perform reactions as well as for separation purposes. The hydrodynamics of gas–liquid flow through channels with pillars with larger diameters and pillar hold-ups has already been described in detail (Jensen 2006; Krishnamurthy and Peles 2007, 2009). However, little is known about the hydrodynamics of a micro pillared system with pillars smaller than 20 μm. The present article will experimentally determine the applicability of known design equations on the hydrodynamic behaviour of gas–liquid flows through pillared micro channels and determine whether these equations can be used for a proper design of such a system. In the first part, flow regime maps as a function of superficial gas and liquid velocities for (x, y)-pitches are presented and compared with flow maps for round and rectangular micro channels without pillars. Another important hydrodynamic parameter is the gas hold-up, the amount of gas present in the reactor, since this gives the gas–liquid interfacial area. Therefore, in the second part of this work, the gas hold-up is determined as a function of gas and liquid superficial velocities. In the final part, a model for calculating the pressure drop for the pillared micro channel as a function of channel and pillar geometry is derived and validated with experiments. We will show that the pressure drop hardly increases for low pillar hold-ups and large (x, y)-pitches (Fig. 1), when compared with channels without pillars. Furthermore, the derived model is compared with two-phase pressure drop models used in the literature for gas–liquid flow through rectangular channels with micro pillars (Lockhart and Martinelli 1949; Krishnamurthy and Peles 2007, 2009) with diameters larger than the pillars used in this work.

2 Theory

2.1 Two-phase flow regimes and gas hold-up

The two-phase flow regimes observed in micro channels are significantly different from the regimes observed in larger channels as gravitational forces can be neglected and capillary forces play a dominant role. Since the flow regime determines the mass transfer and the residence time in the channel, it is an important parameter in the design of the pillared micro channel as chemical reactor. Triplett et al. (1999) defined five major flow regimes in the flow map for two-phase flow in micro channels as can be seen in Fig. 2: (1) bubbly flow where bubbles with a diameter smaller than 75% of the tube diameter flow through the liquid (Fig. 2a); (2) slug/Taylor flow, where gas and liquid slugs, longer than 75% of the channel diameter, move alternatingly through the channel, separated from the wall by a thin liquid film (Fig. 2b); (3) churn flow, where the gas slug is regularly broken up by a slug of gas bubbles with a diameter smaller than 50% of the channel diameter (Fig. 2c); (4) slug/annular flow, similar to annular flow, but the annulus diameter is regularly reduced (Fig. 2d), and (5) annular flow, where a gas bubble with a length much larger than the width of the micro channel flows along a liquid film along the wall (Fig. 2e). Because of the short diffusion lengths in the slug/Taylor and bubbly flow to the pillars in the micro channel used in this work, these will be the preferred flow regimes.

Fig. 2
figure 2

Flow regimes in micro channels (Kreutzer et al. 2005; Triplett et al. 1999): a bubbly flow, b slug/Taylor flow, c churn flow, d slug/annular flow, e annular flow

Full size image

2.2 Two-phase gas hold-up

The gas hold-up ɛG in circular micro channels and rectangular micro channels with aspect ratios of 1–2 (width:height) is well-described for slug/Taylor and bubbly flow by the Armand correlation (Armand 1946; Warnier et al. 2008):

$$\varepsilon_{\text{G}} = 0.833\frac{{u_{{\text{G}},{\text{s}}}}}{u_{{\text{G}},{\text{s}}}+u_{{\text{L}},{\text{s}}}} $$
(1)

where u G,s and u L,s are the superficial gas and liquid velocities. It is unknown whether the Armand correlation can be applied for micro channels with a large aspect ratio with or without pillars. This will be investigated in the present article.

2.3 Pressure drop in the pillared micro channel

2.3.1 Liquid-phase pressure drop

The micro channel used in this work consists of an empty part and a part containing pillars (Fig. 1). Therefore, the pressure drop in the liquid phase consists of two contributions: (1) the contribution due to drag on the wall, and (2) the pressure drop due to friction with the pillars in the channel part containing the pillars.

The pressure drop contribution due to friction of the liquid with the wall in the empty part of the micro channel can be derived from the 3D momentum equation for rectangular ducts with a no slip condition at the wall assuming Newtonian behaviour of the liquid phase as was done by Shah and London (1978) for fully developed flow. However, because of the large aspect ratio (small height in relation to the width and length), the momentum equation for flow between two flat plates can be used (Bird et al. 2002):

$$ -\left(\frac{{\text{d}}P}{{\text{d}}x}\right)_{{\text{L}}}^{{\text{wall}}}=\frac{12\mu_{{\text{L}}}u^{0}_{{\text{L}},{\text{s}}}}{h_{{\text{c}}}^2} $$
(2)

where P is the pressure, μL is the dynamic viscosity of the liquid, x is the flow direction, and h c is the channel height. The superficial liquid velocity at 1 bar, u 0L,s , is defined as:

$$ u_{{\text{L}},{\text{s}}}^0 = \frac{F_{{\text{v}},{\text{L}}}^0}{{\text{w}}_{\text{c}} h_{\text{c}}} $$
(3)

where F 0v,L is the liquid volumetric flow rate in an empty channel measured at 1 bar and w c is the channel width. For the geometries used in this work, a comparison with the solution of Shah and London (1978) showed less than 3% error in the simplified Eq. 2.

The pressure drop contribution due to the pillars, for Re L < 0.3, is described by a liquid flowing through a hexagonal array of cylinders, where the Reynolds number is defined as:

$$ Re_{\text{L}} = \frac{\rho_{{\text{L}}} u_{{\text{L}},{\text{s}}}^{0} d_{{\text{pillar}}}}{\mu_{{\text{L}}}} $$
(4)

with ρL the density of the liquid and d pillar the diameter of the pillars. The equations of motion reduce to the creeping flow case and the pressure drop can be described by the Darcy-Brinkman equation (Liu et al. 2007):

$$ -\left(\frac{{\text{d}}P}{{\text{d}}x}\right)_{{\text{L}}}^{{\text{pillar}}}=\frac{4\mu_{{\text{L}}} u_{{\text{L}},{\text{s}}}^{0} Da^2}{w_{{\text{c}}}^2\left(1-\frac{\tan h \left(\frac{Da}{\sqrt{\overline{\mu_{{\text{L}}}}}} \right)}{\frac{Da}{\sqrt{\overline{\mu_{{\text{L}}}}}}}\right)} $$
(5)

where Da is the Darcy constant and \(\overline{\mu_{\text{L}}}\) is defined as:

$$ \overline{\mu_{\text{L}}}=\frac{\mu_{{\text{e}},{\text{liq}}}}{\mu_{{\text{L}}}}= \left(1+2.5\varepsilon_{{\text{s}}}\right) $$
(6)

with μe,liq being the effective viscosity of the liquid (Goharzadeh et al. 2005). The pillar hold-up ɛs, is given by:

$$ \varepsilon_{{\text{s}}}=\frac{\pi d_{{\text{pillar}}}^2}{4\left(x_{{\text{pillar}}}+d_{{\text{pillar}}}\right) \left(y_{{\text{pillar}}}+d_{{\text{pillar}}}\right)} $$
(7)

where x pillar is the distance between the pillars in the flow direction and y pillar is the distance between the pillars in the channel width direction as is defined in Fig. 1. The Darcy constant is given by:

$$ Da=\frac{w_{{\text{c}}}}{2\sqrt{2K}} $$
(8)

where K is the permeability of the system. The permeability of a unit cell of a hexagonal array of cylinders can be calculated using the following equation (Sangani and Acrivos 1982a, b):

$$ K=\frac{3\left(x_{{\text{pillar}}}+d_{{\text{pillar}}}\right) \left(y_{{\text{pillar}}}+d_{{\text{pillar}}}\right)}{2\left(-0.5\ln\left(\varepsilon_{{\text{s}}} \right) -0.745 + \varepsilon_{{\text{s}}}-0.25 \varepsilon_{{\text{s}}}^2\right)} $$
(9)

For Re L > 0.3, however, the creep flow equations can not be applied, since not every pillar can be seen as a separate unit cell. In the regime for Re L > 3, the pillared micro channel can be described as a packed-bed and the pressure drop in the pillared micro channel can be expressed using the laminar term in the Ergun equation, the Blake-Kozeny equation (Bird et al. 2002; Ergun 1952):

$$ -\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{L}}}^{{\text{pillar}}}=\alpha \frac{\mu_{{\text{L}}} u_{{\text{L}},{\text{s}}}^0}{d_{{\text{pillar}}}^2}\frac{\varepsilon_{{\text{s}}}^2}{\left(1- \varepsilon_{{\text{s}}}\right)^3} $$
(10)

Assuming that the drag force on the wall is independent of the drag force due to the pillars, the total pressure drop in the micro channel in the liquid phase is given by the summation of the drag force contributions in the empty and in the pillared parts of the micro channel:

$$ -\left({{\Updelta P}\over {\Updelta L}}\right)_{{\text{L}}}^{{\text{tot}}}= \frac{12\mu_{{\text{L}}}u_{{\text{L}},{\text{s}}}^0}{h_{{\text{c}}}^2}+\alpha\frac{\mu_{{\text{L}}} u_{{\text{L}},{\text{s}}}}{2d_{{\text{pillar}}}^2}\frac{\varepsilon_{{\text{s}}}^2} {\left(1-\varepsilon_{{\text{s}}}\right)^3} $$
(11)

where α is an experimentally determined constant. For packed-beds with ɛs > 0.3, the coefficient α was empirically found to be 150 (Ergun 1952). For the pillared micro channel, this constant is determined from experimental data in this work.

2.3.2 Gas-phase pressure drop

For the single-phase pressure drop in the gas phase, the compressibility of the gas as a function of the pressure has to be taken into account. The Knudsen number in this work is always smaller than 1 × 10−2, therefore, the continuum momentum equation can be used for the gas-phase. The Knudsen number is defined as:

$$ Kn=\frac{k_{{\text{B}}} T}{\sqrt{2} \pi d_{{\text{gas}}}^2 P x_{{\text{pillar}}}} $$
(12)

where k B is the Boltzmann constant, T is the temperature, P is the pressure, d gas is the characteristic molecular diameter of the gas component and x pillar is the distance between the pillars in the flow direction. Similar for the liquid-phase, the momentum equation for the pressure drop in the empty part of the channel reduces to (Arkilic et al. 1997):

$$ -\left(\frac{{{\text{d}}}P}{{{\text{d}}}x}\right)_{{\text{G}}}^{{\text{wall}}}=\frac{12\mu_{{\text{G}}}u_{{\text{G}},{\text{s}}}} {h_{{\text{c}}}^2} $$
(13)

where μG is the viscosity of the gas and u G,s is the superficial velocity of the gas which is a function of pressure and therefore of the channel length.

Because of the higher superficial gas velocity compared to the liquid velocity used in this work \((3\,\text{m/s}<\text{u}_{{\text{G}},{\text{s}}}^0 < 20\,\text{m/s}),\) the Reynolds number of the gas phase is larger than the Reynolds number for the liquid phase (Re G > 1). Therefore, the contribution of the single-phase pressure drop in the gas-phase by the pillared part of the micro channel can be described using the Blake-Kozeny equation with expansion of the gas, which is given by:

$$ -\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{G}}}^{{\text{pillar}}}=\alpha \frac{P^0}{P}\frac{\mu_{{\text{G}}} u_{{\text{G}},{\text{s}}}^0}{d_{{\text{pillar}}}^2}\frac{\varepsilon_{{\text{s}}}^2} {\left(1-\varepsilon_{{\text{s}}}\right)^3} $$
(14)

where P is the pressure dependent on the axial position in the micro channel, P 0 is the reference pressure at standard conditions (T = 298 K, P = 1 bar), and u 0G,s is the superficial gas velocity at these conditions.

The total pressure drop in the channel in the gas phase is given by the summation of the drag force contributions due to the no-slip condition at the wall for the empty part of the micro channel, and the summation of the drag force contribution due to the no-slip condition at the wall and at the pillars for the pillared part of the micro channel:

$$ -\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{G}}}^{{\text{tot}}}=\frac{\sqrt{P_2^2+\left[\frac{24\mu_{{\text{G}}}} {h_{{\text{c}}}^2}+\alpha\frac{\mu_{{\text{G}}}}{d_{{\text{pillar}}}^2}\frac{\varepsilon_{{\text{s}}}^2} {\left(1-\varepsilon_{{\text{s}}}\right)^3}\right]\Updelta L u_{{\text{G}},{\text{s}}}^0P^0}-P_2}{\Updelta L} $$
(15)

where P 2 is the pressure at the end of the channel.

2.3.3 Two-phase pressure drop

The two-phase pressure drop in the pillared micro channel can be obtained by combining the single-phase pressure drop in both the liquid and the gas-phase neglecting the pressure drop due to the interaction of the gas and liquid phases:

$$ -\left(\frac{{{\text{d}}}P}{{{\text{d}}}x}\right)_{{\text{TP}}} = \varepsilon_{{\text{L}}}\left( \frac{\Updelta P}{\Updelta L}\right)_{{\text{L}},{\text{TP}}}^{{\text{tot}}} + \varepsilon_{{\text{G}}}\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{G}},{\text{TP}}}^{{\text{tot}}} $$
(16)

where the two-phase superficial gas and liquid velocities in this case are defined as:

$$ \left(u_{{\text{L}},{\text{s}}}^0\right)_{{\text{TP}}} = \frac{u_{{\text{L}},{\text{s}}}^0}{\varepsilon_{{\text{L}}}} $$
(17)

and

$$ \left(u_{{\text{G}},{\text{s}}}^0\right)_{{\text{TP}}} = \frac{u_{{\text{G}},{\text{s}}}^0}{\varepsilon_{{\text{G}}}} $$
(18)

The superficial velocities in the two-phase system will be larger compared to the single-phase systems. However, the contribution of the turbulent term in the pressure drop equation is still less than 10% and can be neglected. Since both gas and liquid pressure drop contributions are only linearly dependent on the gas or liquid velocity, the gas and liquid hold-ups drop out of the equation and are only indirectly present due to the gas and liquid velocities. This will reduce Eqs. 11 and 15 to the overall two-phase pressure drop in the pillared micro channel:

$$ -\left(\frac{{{\text{d}}} P}{{{\text{d}}} x}\right)_{{\text{TP}}}=\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{L}},{\text{TP}}}^{{\text{tot}}} + \frac{P}{P^0}\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{G}},{\text{TP}}}^{{\text{tot}},0} $$
(19)

where \(\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{G}},{\text{TP}}}^{{\text{tot}},0}\) is defined as:

$$ \left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{G}},{\text{TP}}}^{{\text{tot}},0} = \frac{12\mu_{{\text{G}}}u_{{\text{G}},{\text{s}}}^0}{h_{{\text{c}}}^2} + \frac{\alpha}{2} \frac{\mu_{{\text{G}}}u_{{\text{G}},{\text{s}}}^0}{d_{{\text{pillar}}}^2}\frac{\varepsilon_{{\text{s}}}^2} {\left(1-\varepsilon_{{\text{s}}}\right)^3} $$
(20)

Another well-known correlation to describe the two-phase pressure drop is the Lockhart–Martinelli correlation in which the pressure drop is empirically related to the single-phase pressure drops of both the gas and liquid (Lockhart and Martinelli 1949). Although Lockhart and Martinelli (1949) state that their approach can not be applied for slug/Taylor flow, a similar approach is still often used in the literature to describe the two-phase pressure drop in micro reactors. For example, Krishnamurthy and Peles (2007, 2009) use a modified Lockhart–Martinelli approach to describe the two-phase pressure drop in micro reactors containing pillars. The Lockhart–Martinelli parameter is given by:

$$ \chi=\left[\frac{\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{L}}}^{{\text{tot}}}}{\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{G}}}^{{\text{tot}},0}}\right]^{0.5} $$
(21)

where \(\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{G}}}^{{\text{tot}},0}\) is defined as in Eq. 20. The two-phase pressure drop in packed-beds is then given by the equation proposed by Larkins et al. (1961):

$$ \log\frac{\left(\frac{{{\text{d}}} P}{{{\text{d}}} x}\right)_{{\text{TP}}}^{{\text{tot}}}} {\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{L}}}^{{\text{tot}}} +\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{G}}}^{{\text{tot}}}}=\frac{0.416}{0.666+\left(\log\chi\right)^2} $$
(22)

Krishnamurthy and Peles (2007) empirically derived a different equation to describe the two-phase pressure drop:

$$ \left(\frac{{{\text{d}}} P}{{{\text{d}}} x}\right)_{{\text{TP}}}^{{\text{tot}}} = \left[1+\frac{0.358 Re_{{\text{d}}}}{\chi}+\frac{1}{\chi}\right]\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{L}}}^{{\text{tot}}} $$
(23)

The Reynolds number Re d for the liquid phase in this case is defined as:

$$ Re_{{\text{d}}} = \frac{\rho_{{\text{L}}} F_{{\text{v}},{\text{L}}}^0 d_{{\text{h}}}}{A_{{\text{min}}}\mu_{{\text{L}}}} $$
(24)

where A min is the minimum cross-sectional flow area and d h is the hydraulic diameter of the rectangular channel. The single-phase pressure drops to determine the Lockhart–Martinelli parameter are given by Krishnamurthy and Peles (2007):

$$ -\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{L}}}^{{\text{pillar}}} = \frac{N\left(F_{{\text{v}},{\text{L}}}^0\right)^2 \rho_{{\text{L}}}\, f}{2 A_{{\text{min}}}^2} $$
(25)
$$ -\left(\frac{\Updelta P}{\Updelta L}\right)_{{\text{G}}}^{{\text{pillar}}} = \frac{N \left(F_{{\text{v}},{\text{G}}}^0\right)^2 \rho_{{\text{G}}}\, f}{2 A_{{\text{min}}}^2} $$
(26)

In these equations, N is the number of pillar rows per channel length, ρG is the density of the gas, and F 0v,G is the volumetric gas flow rate in an empty channel at 1 bar. The friction factor f is given by:

$$ f = 1166.6 Re_{{\text{d}}}^{-1.489} $$
(27)

It should be noted that in the model used by Krishnamurthy and Peles (2007), the acceleration of the gas in the reactor length due to expansion of the gas is not taken into account. The validity of the model based on the Blake-Kozeny equation (Eq. 19), as well as the Lockhart–Martinelli models based on the empirically determined correlation by Larkins et al. (1961) (Eq. 22) and the correlation used by Krishnamurthy and Peles (2007) (Eq. 23) for the pressure drop in a water–nitrogen system is tested in this work.

The flow regimes, especially the slug/Taylor flow and bubbly flow regime, the gas hold-up, and the pressure drop are important parameters for a proper design of the pillared micro channel. It is therefore important to have a good model for determining these parameters. The flow regimes and pressure drop will determine the ideal working window for this type of micro channel as a chemical reactor. In the next section, the flow regimes, gas hold-up, and pressure drop are experimentally determined.

3 Experimental

In the present work, rectangular micro channels having a length of 6.6 cm, a width of 1 mm, and a depth of 50 μm were used. The channels were etched in silicon wafers by the MESA+ Institute for Nanotechnology (University of Twente, the Netherlands). The micro channel had a semi-2D configuration in order to increase the number of pillars in the channel, since the depth is limited to 50 μm in the etching process. Round micro pillars of 3 μm in diameter and 50 μm in height were fabricated in the second axial length part of the channels (3.3 cm). The first axial length part (3.3 cm) was empty to compare the flow regime of an empty channel with a pillared channel. The different configurations are shown in Fig. 3 and summarized in Table 1. The channels and pillars were etched in silicon in one step using the Bosch process (Tiggelaar et al. 2009). Powder blasting of the wafer was done to create the inlet and outlet holes for the flow channels. Finally, anodic bonding with a Pyrex wafer was used to complete the chips. Gas was introduced using a Bronkhorst F-201C mass flow controller and the liquid was fed to the channel by an ISCO 100 DM syringe pump. The gas and liquid were introduced into the micro channel with a cross shaped mixer with a bore of 25 μm. All parts were connected using 1/32 inch stainless steel tubing with an internal diameter of 150 μm (Fig. 4).

Fig. 3
figure 3

SEM pictures of micro channels (1 mm × 50 μm × 6.6 cm) containing pillars (3 μm in diameter) etched in silicon wafers by the MESA+ Institute of Nanotechnology (University of Twente, the Netherlands); a front view of a micro channel with a pitch of 12 μm, b top view of a micro channel with a pitch of 17 μm, c side view of a micro channel with a pitch of 12 μm, d schematical overview of the hexagonal pillar configuration

Full size image
Table 1 Configuration, solid hold-up, and surface area of 3-μm pillars in the pillared micro channels
Full size table
Fig. 4
figure 4

Schematical representation of the pillared micro channel set-up. The inlet and outlet holes were connected with 1/32 inch tubing with an internal diameter of 150 μm. The tee and cross junctions had a bore of 25 μm. Pos (1) and Pos (2) are the positions 1 cm from the beginning of the empty part and 1 cm from the end of the pillared part of the micro channel, respectively

Full size image

Nitrogen/water systems were investigated at 1 bar and 294 K for superficial gas velocities of 0.3–15 m/s (0.02 < Re G < 1.25) and superficial liquid velocities of 0.01–1.67 m/s (0.03 < Re L < 5). Video analysis of the two-phase flow in these water/nitrogen systems was performed using a Redlake Motio Pro X-3 high speed camera connected to a Zeiss Axiovert 200 MAT inverted microscope. The maximum frame rate of the camera was 10,000 frames s−1, but for video analysis, a frame rate of 3,000 frames s−1 was sufficient to determine the gas bubble velocity. The images were recorded at a resolution of 1152 × 296 pixels and with an exposure time of 65 μs. The pixel size was 3.8 μm. Each acquisition consisted of 5,000 frames. The videos of the slug/Taylor flow were analyzed with a Matlab script as described by Warnier et al. (2008). For comparison of the empty and the pillared parts of the micro channel, images were recorded at two positions: (1) 1 cm from the inlet of the channel in the empty part, and (2) 1 cm from the outlet of the channel in the pillared part (see Fig. 4). The pressure before and after the channel was measured with Sensor Technics 26 PC Series temperature compensated and calibrated pressure sensors to determine the pressure drop.

4 Results and discussion

4.1 Two-phase flow regimes

Figures 5 and 6 display typical images of the flow regimes obtained in the micro channels for the nitrogen/water system. The flow map for the empty part of the channel is displayed in Fig. 7a. It can be seen that the flow map is in good agreement with flow maps found in literature for round channels with larger hydraulic diameters (Triplett et al. 1999). Slug, slug/annular, and bubbly flows were observed in the empty part of the micro channel. Similar flow regimes were found in the pillared part of the micro channel (pitch 17 μm), and in the pillared part also churn flow was observed (Fig. 7b).

Fig. 5
figure 5

Flow regimes of nitrogen and water in the empty part of the micro channel at position 1: a slug flow, c slug/annular flow, e bubbly flow; and the pillared part of the channel with a pitch of 17 μm at position 2: b slug flow, d slug/annular flow, f bubbly flow

Full size image
Fig. 6
figure 6

Flow regimes of nitrogen and water in the empty part of the micro channel at position 1: a slug flow, c slug/annular flow, e bubbly flow; and the pillared part of the channel with a pitch of 7 μm at position 2: b pulse flow, d pulse flow, f pulse flow

Full size image
Fig. 7
figure 7

Flow map of a nitrogen/water system in a 1 mm × 50 μm channel with a pillar pitch of 17 μm in the empty part (a) and the pillared part (b) of the micro channel. The flow regime transition lines according to Triplett et al. (1999) are indicated by dash dotted lines

Full size image

Due to the relatively large pillar pitch of 17 μm, the fluid flow will be fully developed before the next pillar and therefore every pillar can be seen as a separate unit cell. The fluid flow around the pillar will behave as creep flow and the flow regimes are only determined by the capillary force. The flow maps for the empty and the pillared parts of the micro channel are therefore similar to the flow maps found in literature at similar flow conditions (Kreutzer et al. 2005; Triplett et al. 1999; Warnier et al. 2008).

For the channel with pillars having a pitch of 7 μm, the flow regimes in the empty part of the channel (position 1) are similar to the channel containing pillars with a pitch of 17 μm. Comparing with the flow maps found for the channel containing pillars with a pitch of 17 μm, the flow regimes in the flow map for the empty part of the channel containing pillars with a pitch of 7 μm were shifted to higher gas and liquid superficial velocities u 0L,s and u 0G,s (Fig. 8). However, for the superficial gas and liquid velocities corrected for the local pressure, u L,s and u G,s, the flow map is similar to the flow map for the empty part of the channel with pillars having a pitch of 17 μm and similar to the flow maps found in literature (Kreutzer et al. 2005; Triplett et al. 1999; Warnier et al. 2008).

Fig. 8
figure 8

Flow map of a nitrogen/water system in a 1 mm × 50 μm channel with a pillar pitch of 7 μm in the empty part (a) and in the pillared part (b) of the micro channel. The flow regime transition lines according to Triplett et al. (1999) are indicated by dash dotted lines

Full size image

In the pillared part of the micro channel with a pillar pitch of 7 μm (position 2), the flow regime differs from the flow regime in the empty part of the micro channel. In this channel, the pillar pitch is too small for the fluid velocity profile to fully develop before the next pillar. Therefore, the pillars will have interaction and the regular flow regimes are broken up to form a pulsing regime. In this regime, the gas is randomly divided over the channel width. Furthermore, it appears that not the full depth of the channel is used for the flow. Some of the gas bubbles were observed out of the focal plane of the microscope as can be seen in Fig. 6. This regime is comparable with the pulsing flow regime observed in co-current gas–liquid flow in packed-beds. The pulsing flow regime was observed for all superficial gas and liquid velocities (Fig. 8b).

4.2 Two-phase gas hold-up

The 2D gas hold-up obtained from the top view of the micro channel was determined for the slug/Taylor flow regimes, assuming gas bubbles that have a height (nearly) equal to the height of the micro channel. The volume of the liquid film at the top and bottom of the gas bubble was therefore neglected. The hold-up was calculated by dividing the area occupied by the gas bubbles by the total frame area. The gas interstitial velocity was determined from the bubble velocity u b:

$$ u_{{\text{G}},{\text{s}}}=\varepsilon_{{\text{G}}} u_{{\text{b}}} $$
(28)

It can be seen from Fig. 9 that, as expected, for increasing \(\frac{u_{{\text{G}}}}{u_{{\text{G}}}+u_{{\text{L}}}}\), the 2D gas hold-up increases.

Fig. 9
figure 9

The 2D gas hold-up in the empty and pillared parts of the micro channel with a pillar pitch of x = 17 μm as a function of the relative superficial gas velocity

Full size image

The Armand (1946) correlation predicts the gas hold-up for the empty and the pillared parts of the micro channel with a pillar pitch of 17 μm within 3% error:

$$ \varepsilon _{{\text{G}}}=\left(\frac{A_{{\text{b}}}}{A_{{\text{c}}}}\right)\frac{u_{{\text{G}},{\text{s}}}}{u_{{\text{G}},{\text{s}}}+u_{{\text{L}},{\text{s}}}} = 0.833\frac{u_{{\text{G}},{\text{s}}}}{u_{{\text{G}},{\text{s}}}+u_{{\text{L}},{\text{s}}}} $$
(29)

The Armand constant, defined as the dimensionless cross-sectional bubble surface area \(\frac{A_{{\text{b}}}}{A_{{\text{c}}}}\) (Warnier et al. 2008) is according to Armand (1946) equal to 0.833. This value is very close to the value of 0.81 obtained for the micro channel with a pillar pitch of 17 μm. Thus, it can be concluded that the thickness of the liquid film at the top and bottom of the micro channel is very small (δ < 1 μm). The volume occupied by the liquid film on the top and bottom of the gas bubble can therefore be neglected when determining the gas hold-up.

4.3 Pressure drop in the pillared micro channel

4.3.1 Liquid-phase pressure drop

In Fig. 10, the liquid-phase pressure drop in the micro channels with different pillar pitches is plotted versus the superficial liquid velocity. The measured pressure drop in the micro channels with a pitch of 27 μm is predicted by the Darcy-Brinkman equation (Eq. 5) within 2% error as can be seen in Fig. 10a, whereas the Blake-Kozeny equation (Eq. 11) gives a slight overestimation of the pressure drop, within 20% error. The modeled pressure drop using the empirically found correlation used by Krishnamurthy and Peles (Eq. 25) (2007) underpredicts the liquid-phase pressure drop by 30%. Due to the low Reynolds numbers, the fluid velocity profile will be fully developed before the next pillar and each pillar can be seen as a separate unit cell. The models to calculate pressure drop based on the interaction between pillars such as the Blake-Kozeny equation (Ergun 1952) and the correlations used by Krishnamurthy and Peles (2007) will therefore under or overestimate the pressure drop.

Fig. 10
figure 10

Comparison of the Blake-Kozeny equation (α = 177) (Ergun 1952), Darcy-Brinkman equation (Liu et al. 2007) and the equation used by Krishnamurthy and Peles (2007) with the experimental data for the single-phase pressure drop in the pillared micro channel with pitches of 27, 17, 12, and 7 μm as a function of the superficial liquid velocity

Full size image

For the micro channels with pillar pitches of 17, 12, and 7 μm, the measured pressure drop is much higher than the Darcy-Brinkman model predicts (Fig. 10). With these pitches, the pillars can not be considered as separate unit cells due to the small pillar pitches and the Darcy-Brinkman equation can not be used. In this case the Blake-Kozeny equation (Eq. 11) can be applied. From the experimental data for pillar pitches of 17, 12, and 7 μm, a Blake-Kozeny constant α of 177 is fitted, which is close to the Blake-Kozeny constant of 150 for packed-beds (Ergun 1952). The empirically determined model to calculate the single-phase pressure drop in the liquid phase used by Krishnamurthy and Peles (2007) resulted in an error of 45 and 70% for the pillar pitches of 17 and 12 μm, respectively. The single-phase pressure drop in the liquid phase for the channel containing pillars with a pitch of 7 μm, however, resulted in an error of over 85%. The model used by Krishnamurthy and Peles (2007) seems to be invalid for smaller pillar diameters (typically larger than 100 μm). This is probably caused by a dependency of the constants fitted in the correlation used by Krishnamurthy and Peles on the pillar diameter.

It can also be seen in Fig. 11 that the pressure drop for the micro channel with a pillar pitch of 27 μm is similar to the pressure drop in an empty channel and is modeled accurately by the Darcy-Brinkman equation (Eq. 5). However, when the solids hold-up is increased, the pressure increases rapidly due to the non-developed flow and the pressure drop is in good agreement with the Blake-Kozeny equation (Eq. 11) with a constant α of 177.

Fig. 11
figure 11

Single-phase pressure drop of water in pillared micro channels with a superficial liquid velocity u 0L,s  = 0.082 m/s as a function of the solids hold-up ɛs

Full size image

The value for α is empirically determined and is valid for similar systems. It is independent of the pillar hold-up and pillar pitch, within the boundary limits for Re used in this work. The value may, however, depend on pillar diameter and channel geometry. This is not investigated in this work.

4.3.2 Gas-phase pressure drop

In Fig. 12, the single-phase pressure drop in micro channels with different pillar pitches is plotted versus the superficial gas velocity. Furthermore, the Blake-Kozeny equation (Eq. 15) with expansion using the Blake-Kozeny constant obtained from the single-phase liquid pressure drop (α = 177) is compared with the experimental data. The Blake-Kozeny model is in good agreement with the experimental data for the pillar pitches of 17 and 27 μm (Fig. 12). The Blake-Kozeny equation predicted the pressure drop within an error of 10%. The empirically determined model to calculate the single-phase pressure drop in the gas phase used by Krishnamurthy and Peles (2007) resulted in an error of 40% for pitches of 27 and 17 μm and an error of 85% for pitches of 7 μm. This is due to neglecting the expansion of the gas at different pressures over the length of the channel by the correlation used by Krishnamurthy and Peles (2007) and by the dependency of the empirically determined constants on the pillar diameter. It can be concluded that the model used by Krishnamurthy and Peles (2007) can not be applied to calculate the pressure drop in a pillared micro channel with pillar diameters smaller than 100 μm.

Fig. 12
figure 12

Comparison of the Blake-Kozeny equation (α = 177) (Ergun 1952) and the equation used by Krishnamurthy and Peles (2007) with the experimental data for the single-phase pressure drop in the pillared micro channel with pitches of 27, 17, and 7 μm as a function of the superficial gas velocity at 1 bar

Full size image

4.3.3 Two-phase pressure drop in the pillared micro channel

The two-phase pressure drop was determined in the micro channels with pillar pitches of 7 and 17 μm. In Fig. 13, the pressure drop for a low liquid superficial velocity (u L,s = 0.05 m/s) is plotted versus the superficial gas velocity. It can be seen that with increasing superficial gas velocities, higher pressure drops are obtained. Furthermore, much larger pressure drops at similar superficial gas velocities were observed in the channel with a pillar pitch of 7 μm than in the micro channel with a pillar pitch of 17 μm. The derived model for the two-phase pressure drop in Eq. 19 slightly underestimates the pressure drop found with experiments but predicts the experimentally obtained pressure drop within 30% error. The correlation used by Krishnamurthy and Peles (2007) to calculate the two-phase pressure drop underestimates the data within 40% error. This is probably due to the dependency of the empirically determined constants in the equations used by Krishnamurthy and Peles (2007) on the pillar diameter as well as neglecting the expansion of the gas at different pressures in the channel.

Fig. 13
figure 13

Comparison of the two-phase Blake-Kozeny equation (α = 177) (Ergun 1952) and the Lockhart–Martinelli correlation with the equation used by Larkins et al. (1961) and Krishnamurthy and Peles (2007) with the experimental data for the two-phase pressure drop of a nitrogen–water system with u 0L,s  = 0.05 m/s in the pillared micro channel with pitches of 17 and 7 μm as a function of the superficial gas velocity at 1 bar

Full size image

For the two-phase pressure drop in the channel containing pillars with a pitch of 7 μm, the pressure drop model in Eq. 19 underestimates the experimentally obtained data within an error of 35%. The empirical Lockhart–Martinelli correlation (Eq. 21) using the Larkins equation (Eq. 22) (Larkins et al. 1961) overestimates the pressure drop with a factor of 2 to 3. The correlation used by Krishnamurthy and Peles (2007) to calculate the two-phase pressure drop in the channel containing pillars with a pitch of 7 μm underestimates the data within 85% error.

For a superficial gas velocity of u 0G,s  = 0.78 m/s, the pressure drop is plotted versus the superficial liquid velocity in Fig. 14. It can be seen that the pressure drop in the channel with a pillar pitch of 7 μm is much larger than the pressure drop in the micro channel with a pillar pitch of 17 μm. The two-phase pressure drop model in Eq. 19 predicts the experimentally determined pressure drops in the micro channel with a pillar pitch of 17 μm within 20% error. The Lockhart–Martinelli correlation using the Larkins et al. equation (Eq. 22) overestimates the pressure drop with a factor of 2 to 3. The correlation used by Krishnamurthy and Peles (2007) underestimates the data within an error of 50%.

Fig. 14
figure 14

Comparison of the two-phase Blake-Kozeny equation (α = 177) (Ergun 1952) and the Lockhart–Martinelli correlation with the equation used by Larkins et al. (1961) and Krishnamurthy and Peles (2007) with the experimental data for the two-phase pressure drop of a nitrogen–water system with u G,s = 0.78 m/s in the pillared micro channel with pitches of 17 and 7 μm as a function of the superficial liquid velocity

Full size image

The experimental two-phase pressure drop in the channel with a pillar pitch of 7 μm is 40% higher than the pressure drop predicted by Eq. 19, whereas the equation used by Krishnamurthy and Peles (2007) predicted the data with an error up to 95%. This higher experimentally found pressure drop in the channels with a pillar pitch of 7 μm is attributed to the presence of a static liquid hold-up stabilized by the capillary forces between the closely spaced pillars. The reduced through-flow area increases the gas-phase contribution to the two-phase pressure drop. This was also observed in the two-phase pulsing flow regime in the channel containing pillars with a pitch of 7 μm.

5 Conclusions

In the present work, a rectangular pillared micro channel has been developed to increase the catalytic support area with a maximum factor of two. Similar flow maps for the empty part of the micro channel and the part containing pillars with a pitch of 17 μm were observed. The structured flow regimes were not influenced by the pillars. For a pillar pitch of 7 μm, a pulsing flow regime was observed in the part of the channel containing the pillars. In comparison with the flow regimes observed in the empty part of the channel, the pulsing flow had a larger gas–liquid interfacial area, but is less structured.

The 2D gas hold-up in the empty part of the channel with a pillar pitch of 17 μm was compared with the empty part at similar superficial gas velocities. The gas hold-up was in good agreement with the Armand correlation and from this validity, it could be concluded that the thickness of the liquid film at the top and bottom of the channel is very small. The volume occupied by the liquid film can therefore be neglected in determining the gas hold-up.

The single-phase pressure drop over the micro channel was determined for different pillar configurations. The Darcy-Brinkman equation was derived to model the pressure drop in the micro channel with a pillar pitch of 27 μm. The data was well-represented by the model with an error of less than 2%. For pillar pitches of 17, 12, and 7 μm, the pillars can no longer be seen as separate unit cells and a large pressure drop increase was observed. For these pillar configurations, the known Blake-Kozeny equation for packed-beds with a constant of α = 177 can be used for the liquid phase and for the gas phase. This constant is close to the Blake-Kozeny constant used in packed-beds (α = 150) and not dependent on the pillar pitch and pillar hold-up. The correlation found by Krishnamurthy and Peles (2007) seems to be invalid for pillar diameters smaller than 100 μm.

Three models were used to predict the two-phase pressure drop, a theoretical model derived in this work and two different Lockhart–Martinelli correlations. The theoretical model predicted the experimentally obtained data for the two-phase pressure drop in the micro channel containing pillars with a pitch of 17 μm within 30% and for a pitch of 7 μm within 40%. The Lockhart–Martinelli correlation based on the Larkins et al. (1961) equation and on the Krishnamurthy and Peles (2007) equation had a maximum error of 95%. The theoretically derived model is therefore the best design equation to predict two-phase pressure drops in these pillared micro channels within 40% error.

The open structure and higher production rate per reactor volume make the pillared micro channel an efficient system for performing heterogeneously catalyzed gas–liquid reactions. To increase the catalytic surface area even more, micro structures with larger surface areas can be used, such as carbon nano fibers. These fibers have a large open volume and specific surface area and more catalyst can be deposited in the pillared micro channel.