Numerical study of liquid inclusion oscillations inside a closed 1D microchannel filled with gas

Abstract

The motion of a liquid inclusion inside a 1D microchannel filled with gas and externally heated is simulated. An incompressible formulation is used for the liquid, while a low Mach approximation is considered for the gas flow. Gas–liquid interfaces are captured using an Arbitrary Lagrangian Eulerian method. The whole liquid–gas system is shown to behave as a damped oscillator. Natural frequency of the linearized system and associated eigenmodes are first identified. Forced oscillations are investigated for different heating conditions (temperature or heat flux) at the microchannel ends. Detailed analyses are performed which reveal the main thermo-mechanical effects involved in the oscillations. The relevant parameters governing the dynamics are found out through a dimensionless analysis. Finally, heating conditions leading to non decaying oscillations of the liquid inclusion are proposed.

Appendix: Numerical methods

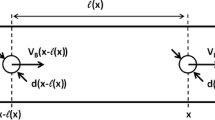
The domains Ωⁱ moving with time, an Arbitrary Lagrangian Eulerian (ALE) method (see, e.g., Navti et al. 1997; Medale and Jaeger 1997) is used for the resolution of the governing equations of the flow. Specifically, linear transformations are used to map $\Upomega^1\cup\Upomega^{\rm l}\cup\Upomega^2$ to a reference mathematical domain $[0, 1] \cup [1, 2]\cup[2,3]$. The spatial discretization uses a high-order spectral element for each sub-domain, with order p for the temperature, density, velocity and order p − 2 for the hydrodynamic pressure (Canuto et al. 1990). The mapping being time dependent, it yields additional correction terms in the governing equations to account for the mesh velocity. The time integration of the flow involves diverse time discretizations and numerical methods for the inversion of the resulting discrete operators. The complete numerical methodology is detailed elsewhere, and we simply provide here a quick overview of the structure of a time step. For simplicity, we temporarily drop the domain indexes that instead will denote the time level. We assumed the solution known at time level nΔt, where Δt is the time-step of the simulation. The whole procedure for the determination of the solution at t = (n + 1)Δt is

• 1. Set guessed estimates P ⁿ⁺¹ for the thermodynamic pressure at the end of the time step.

• 2. Using P ⁿ⁺¹, update velocities and positions of the interface using a semi-implicit Newmark time-scheme. It yields the ALE mapping (geometry and mesh velocities).

• 3. Prediction step

  • The energy equations in the sub-domains are solved for a provisional temperature field T*, using an implicit time-scheme and Schwartz methods for the enforcement of continuity conditions across the interfaces. Other variables are taken to their respective values at t = nΔt.

  • Provisional thermodynamical pressures P* and density fields ρ* in the two gas domains are then determined using equation (8) and the state equation, respectively.

  • Momentum equations in the gaseous domains are then solved for the provisional velocities u* and hydrodynamic pressures Π*. The latter is determined, through the resolution of an elliptic problem, as to yield $\frac{\partial}{\partial x}(\rho u)*$ consistent with an estimate of $\frac{\partial}{\partial t} \rho$ based on ρⁿ and ρ*.

• 4. Correction step

  • Solve the energy equation for T ⁿ⁺¹ as in the prediction step, but using the provisional values for the other variables.

  • Set thermodynamical pressures P ⁿ⁺¹ and density fields ρⁿ⁺¹ in the two gas domains.

  • Set the velocities u ⁿ⁺¹ and hydrodynamic pressures Πⁿ⁺¹. The latter now being determined to yield $\frac{\partial}{\partial x}(\rho u)^{n+1}$ consistent with an estimate of $\frac{\partial} {\partial t} \rho$ based on ρⁿ and ρⁿ⁺¹.

• 5. If the computed thermodynamical pressures P ⁿ⁺¹ are different from the ones used at step 1, restart from step 2 for a new iteration.

In the computation presented in this study, three to four iterations were needed for the convergence of the thermodynamical pressure P ⁿ⁺¹.