Submarine landslides and tsunami genesis in Sagami Bay, Japan, caused by the 1923 Great Kanto earthquake

Abstract

The 1923 Great Kanto earthquake occurred on September 1, in Japan, and caused severe damage mainly in the Kanto region. Tsunamis were observed over wide regions from the east coast of the Izu Peninsula to the west coast of the Boso Peninsula, and particularly, the damage in Atami was devastating. Many earthquake fault models including those of Kanamori (1971) and Ando (1971) were proposed based on the records of land deformation. However, such fault models cannot sufficiently explain the tsunami elevation and its initial sea-level motion on the coasts. Hence, the detailed mechanisms remain elusive. This study examines the possibility that a leading mechanism of the tsunami in the 1923 Great Kanto earthquake was a large-scale submarine landslide that occurred at Sagami Bay and at the mouth of Tokyo Bay based on the records of depth data measured by the Imperial Japanese Navy (1924) before and after the earthquake. We first show that the tsunami calculated by each fault model was inconsistent with the waveform at Yokosuka, the coastal tsunami elevations, and initial sea-level motion. Then, based on statistical analysis of the depth changes at the 1923 Great Kanto earthquake, we found that the seafloor bathymetric changes represented large-scale submarine landslides that may correspond to long-runout submarine liquefied sediment flows. The seafloor gradient over a 40 km flow-out distance was equal to or less than 0.4$^\circ$. Through the identification of the submarine landslide source by tsunami backpropagation analysis and utilizing an analytical solution of a high-density gravity flow and a sensitivity analysis, we conducted a range of numerical simulations of the 1923 Great Kanto earthquake tsunamis using a fault model and a submarine landslide tsunami source model due to a high-density liquefied gravity flow. The results quantitatively accounted for the discrepancy between the observed tsunami records with maximum tsunami elevations over 12 m and the fault-model–based simulations with maximum tsunami elevations of 2 to 5 m and explained consistently the maximum tsunami elevation distributions as well as the time-series tsunami waveforms. These results may thus facilitate and deepen our understanding of the earthquake-induced submarine landslide tsunami risk as cascading multi-geohazards.

Introduction

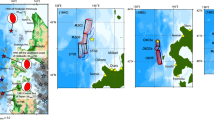
The 1923 Great Kanto earthquake occurred on September 1 and caused severe damage mainly in Tokyo, Kanagawa, Chiba, and Shizuoka in Japan. The earthquake struck the Kanto and the Sagami Bay area, and the moment magnitude was estimated to be M_w = 7.9–8.1 (Kanamori 1971; Namegaya et al. 2011) (Fig. 1). The Kanto earthquake also caused severe fire damage. The number of casualties reached 100,000 (Moroi and Takemura 2004), and the scale of the damage was enormous compared to the 2011 Tohoku earthquake with 20,000 casualties. The following tsunami caused extensive damage along the coast from the east region of the Izu Peninsula to the west coast of the Boso Peninsula and was particularly severe in Atami such that a 12 m tsunami elevation was recorded around the coastal zone (Imperial Japanese Navy 1924). Ground deformations showed a marked uplift of 1.8 to 3 m along the southern Boso Peninsula, the southern tip of the Miura Peninsula and the coast of Sagami Bay. The land area around the eastern to the southern Izu Peninsula subsided from 0.3 to 0.75 m (Land Survey Department 1930).

Fig. 1

a Tectonic map (yellow line, plate boundary; orange dashed line, volcanic front) and the target area of this study (red frame), which is located at a complex region adjacent to the Pacific, Philippine Sea, Okhotsk, and Eurasian plates. b The 1923 Great Kanto earthquake with M_w = 7.9–8.1 is considered to have been caused by a fault movement in the Sagami Trough region (e.g., Kanamori 1971; Ando 1971). The distribution area of the Sagami Trough and the detailed epicenter map of the 1923 Great Kanto earthquake (Takemura and Ikeura 1994). The first earthquake occurred near Odawara, deep in Sagami Bay, and the second earthquake near the southern part of the Miura Peninsula, as shown by the two red circles. The fault area (broken blue line) extended over Tokyo, Kanagawa, and Chiba

Kanamori (1971) and Ando (1971) quantitatively analyzed the fault motion mechanism of the 1923 Kanto earthquake based on the seismic waveform data and geodetic data, including detailed fault parameters such as strike, dip, and slip. Then, a number of studies proposed detailed analysis models considering the slip and direction characteristics of the fault area (Ando 1974; Matsu'ura et al. 1980; Matsu'ura and Iwasaki 1983; Ishibashi 1980, 1985; Wald and Somerville 1995; Kobayashi and Koketsu 2005; Namegaya et al. 2011; Nakadai et al. 2023), to reproduce the values of uplift and subsidence records (Land Survey Department 1930). These existing fault models are understood as a primary mechanism of this earthquake and tsunami (e.g., Namegaya et al. 2011), whereas Nakadai et al. (2023) showed that the agreement with the tsunami records is limited to a narrow area in Tokyo Bay and the east coast of the Izu Peninsula. However, there has been no detailed discussion based on the quantitative tsunami elevation distributions and their initial sea-level motion over the coastal area in Sagami Bay, and thus, their validity has remained unclear. The Central Disaster Management Council, Cabinet Office, Government of Japan (2013) has proposed a “Tsunami Fault Model” with corrected slip parameters for subdivided fault areas for this earthquake in order to prepare for a megathrust earthquake tsunami in the future. However, there are many places where tsunami fault model simulations are not consistent with the tsunami records (Cabinet Office, Japan 2013). These discrepancies between the existing models and the observed tsunami records will be quantified and elucidated in this study.

The greatest mystery in understanding the fault dynamics of the 1923 Great Kanto earthquake stems from the large-scale changes in water depth observed by weight measurement based on the sea depth coordinates of the triangulation survey from Sagami Bay to the mouth of Tokyo Bay after the earthquake (Imperial Japanese Navy 1924; Fig. 2). Bathymetric surveys were conducted immediately after the earthquake and in January the following year. In Fig. 2, the blue areas denote deepened water depths and the red areas denote shallowed areas. This map was created based on the Tokyo datum, and the deepening and shallowing depth changes reached as high as 200 m. These survey points were based on land reference points and a triangulation method. Mogi (1959) analyzed possible errors caused by the measurement method through the creation of a water depth change map similar to that of the Imperial Japanese Navy (1924) using the survey data by acoustic depth measurement from 1949 to 1955 and the survey records by weight measurements from 1913 (before the earthquake) in Sagami Bay. Although there was an error in the weight measurement method due to the influence of a drifting of the wire due to the tidal current, it was suggested that the deepening distributions could not be ignored and were significant. This study closely examines such seafloor ground dynamics before and after the 1923 Great Kanto earthquake through analysis of the spatial correspondence between the detailed seafloor topography obtained with a current acoustic depth measurement technology and the depth changes following the earthquake.

Fig. 2

Depth change map of Sagami Bay before and after the 1923 Great Kanto earthquake, where the deepened areas are highlighted in blue and the shallowed areas in red (Imperial Japanese Navy 1924)

Landslides and tsunamis are one of the most important cascading multi-geohazards that can cause substantial damage to infrastructures and loss of human life (Locat and Lee 2002; Sassa and Sekiguchi 2012; Sassa 2023; Heidarzadeh et al. 2023). Although the origins of the landslides that trigger tsunamis range widely from earthquakes to volcanoes, rainfalls, rising water levels, and among others, the importance of earthquake-induced submarine landslides has recently been emphasized in the 2018 Indonesia Sulawesi earthquake and tsunami disasters, where the cascading strong strike-slip fault earthquake, liquefaction, coastal and submarine landslides, and multiple tsunamis caused more than 2000 fatalities (Sassa and Takagawa 2019). In Sagami Bay as the origin of the 1923 Great Kanto earthquake, Ogawa (1924) was the first to point out the possibility that a submarine landslide caused a large-scale subsidence and uplift of the submarine topography in Sagami Bay. He showed a similarity to the cases at Lake Zurich (1875) and Lake Zug (1435, 1887, 1894) in Switzerland, suggesting that submarine landslides might have caused an increase in tsunamis, with the associated discussion by Terada (1924). Subsequently, several researchers reported submarine landslides in Sagami Bay (Ohkouchi 1990; Kusunoki et al. 1991; Watanabe 1993; Kato et al. 1993; Kasaya et al. 2006). The Imperial Japanese Navy (1924) reported a submarine cable–cutting accident caused by a submarine landslide. However, no in-depth quantitative analysis of the bathymetric changes before and after the 1923 Great Kanto earthquake has been made in the past.

Our preliminarily investigations of the seafloor ground deformations of the 1923 Great Kanto earthquake and associated tsunamis were published in Murata et al. (2020, 2021) and Ebisuzaki (2021). Specifically, Murata et al. (2020, 2021) proposed and evaluated the digitizing method for water depth records observed by the weight measurement. Ebisuzaki (2021) analyzed that the dominant mechanism of “tsunami earthquakes” is large-scale liquefaction and submarine landslides induced by seismic motion based on the historical tsunami earthquake events including the 1923 Great Kanto earthquake. However, this paper presents and discusses four innovations, namely:

• (a) Elucidating the gap between the observed tsunami data and the previous simulations from various sources available in the literature.

• (b) Presenting the in-depth analysis of the bathymetric changes before and after the Great Kanto earthquake and uncovering the occurrence of submarine landslides in light of the state-of-the-art understanding of the liquefied gravity flow.

• (c) Conducting the tsunami simulations based on an optimum fault model and a submarine landslide model due to a high-density liquefied gravity flow.

• (d) Quantitatively accounting for the gap and explaining the maximum tsunami elevation distributions, arrival times, and the time-series tsunami waveforms.

Temporal characteristics of the 1923 Great Kanto earthquake tsunami are indeed noteworthy. With reference to Fig. 1, the arrival time of the tsunami as backwash at Atami and Manazuru on the eastern coast of the Izu Peninsula was 5 to 6 min after the earthquake (Imperial Japanese Navy 1924). Then, leading waves came from the northeast direction. The tsunami reached Aihama and Tateyama in the southern part of the Boso Peninsula, the ebb and flood tides were repeated within about 15 min after the earthquake, with the first wave coming from the northwest (Ikeda 1925). The local tsunami arrival times and incident directions were significantly different on each coast that divided Sagami Bay into east and west. Such temporal behavior of tsunamis indicates that short-frequency components are dominant and have strong directivity occurring in a local area, showing characteristics common to submarine landslide–induced tsunamis (e.g., Tappin et al. 2014; Sassa and Takagawa 2019).

The organization of this paper is as follows. We first present an overview of the rupture process of the 1923 Great Kanto earthquake fault models and tsunami predictive accuracy of each model. Next, based on statistical analysis of the depth changes and comparison with the current seafloor topography, we clarify the bathymetric changes and associated seafloor ground dynamics before and after the earthquake. Third, a submarine landslide model will be presented through the identification of a submarine landslide source by tsunami backpropagation analysis and utilizing a theoretical relationship between size, velocity, and slope angle of a high-density gravity flow based on the present understanding of the characteristics of large-scale submarine liquefied sediment flows. The numerical simulations and parameterization of the 1923 Great Kanto earthquake tsunamis will then be presented using a fault model and a submarine landslide tsunami source model due to a high-density liquefied gravity flow. Here, the submarine landslide tsunami source scheme proposed by Watts et al. (2005) and the numerical tsunami simulator developed at the Port and Airport Research Institute (STOC-ML, Tomita et al. 2006) were used. The comparison between the simulated results and the observed overall maximum tsunami elevation distributions along the coasts of Sagami Bay, Tokyo Bay, and the Pacific Ocean, their arrival times, and the available time-series tsunami waveforms in Yokosuka (Aida 1970) will be discussed in detail, showing submarine landslides as a major source of the 1923 Great Kanto earthquake tsunamis.

Existing research and tsunami prediction accuracy of each model

Overview of the rupture process of the 1923 Great Kanto earthquake fault model

In Fig. 1, the source fault areas proposed by each existing model generally spread from the western part of the Kanagawa region to the sea beyond the Boso Peninsula (WNW-ESE) and are distributed on a surface dipped to the NNE direction. The slip direction was sideslip at the bottom of the fault. However, a reverse dip-slip fault along the dip occurred near the top of the fault, and asperities were distributed around the epicenter in western Kanagawa and the southern Miura Peninsula (Wald and Somerville 1995; Kobayashi and Koketsu 2005). Takemura and Ikeura (1994) argued that the rupture started near the Odawara region in western Kanagawa and transitioned to near the Miura Peninsula (Fig. 1) based on short-period data obtained from seismograms. Matsu'ura et al. (1980) and Nyst et al. (2006) proposed a segmented fault surface considering slip directional characteristics. In any case, the rupture process of each existing model starts at a depth of approximately 15 km near the Odawara in the western Kanagawa region. The rupture area extends over a region of 130 km in length and 70 km in width in the eastern coastal area of the Boso Peninsula. In addition, each fault model explains the horizontal and vertical movements in the land displacement records before and after the earthquake (e.g., Namegaya et al. 2011; Nakadai et al. 2023).

Tsunami predictive accuracy

Existing fault models have been evaluated using land deformation records; however, their consistency with the observed tsunami records is limited (Nakadai et al. 2023). Here, we present a set of numerical simulations of the 1923 Kanto earthquake tsunami using existing fault models, compare them with the records from various coastal points, and discuss their predictive accuracy.

The numerical tsunami simulator developed at Port and Airport Research Institute (STOC-ML, Tomita et al. 2006) was used. The governing equations of the STOC-ML are the continuity equation and the Reynolds-averaged Navier–Stokes equations as the momentum equations. STOC-ML is a quasi-three-dimensional model with the water area divided vertically into multi-levels where the hydrostatic pressure is computed and applied at each level on a general shallow water equation. The simulation time was equal to 180 min and the simulation time step was set to be 0.1 s. The numerical simulation domain was horizontally divided into a uniform mesh grid of 270 m based on the rectangular coordinate system (Fig. 3a).

Fig. 3

a Coastal point map showing the area of analysis in this study (No. 1 to No. 53). b Observed and calculated maximum tsunami elevations at each coastal point (No. 1 to No. 53). Here, black circles denote the observed records and each color line denotes the calculated results from each fault model (F1 to F9) shown in Table 1. c Observed and calculated time-history waveforms, where the black solid line denotes the observed records and each color line denotes the calculated results by each fault model at Yokosuka tide gauge (No. 30). The tsunami amplitudes are extracted and digitized from the tide records shown in Aida (1970). d Residual sum of squares RSS results for each fault model at Yokosuka (No. 30)

Table 1 shows each fault model used for the numerical simulation. We selected a total of eight fault models (F1 to F8) and included a tsunami fault model (F9) of the Cabinet Office, Japan (2013). The tsunami fault model considers tsunami data from several coastal locations and the amount of ground movement on land. The topographic data used for the tsunami propagation simulation was from the Cabinet Office, Japan (2013), and not the coastal topography 100 years ago. The reason is that there has been essentially no or little change in the coastal topography due to port development in a coastal area of Sagami Bay and Yokosuka that we focus on here. For the purpose of comparison, tsunami waveforms are extracted from the tide records (Aida 1970). In the present analysis, since the tsunami records, except for the Yokosuka record, represent the trace heights above sea level observed near the coast, we treated each record as the water surface elevation of tsunami observed at the shoreline. The record of maximum tsunami elevation on each coast has local variations within each observation point area. Here, the sea area in front of each coast is defined as the tsunami elevation time series analysis domain, where the 50th, 25th, and 75th percentiles of the waveforms obtained from multiple coordinates in 9 neighboring cells are evaluated. The maximum tsunami elevation at each coastal point was calculated by using the 50th-percentile time-history waveform obtained from the multiple coordinates in 9 neighboring cells. The above simulation conditions and the numerical treatment were the same for both the fault model–based simulations and the landslide tsunami simulations described later in the “Numerical simulations of the 1923 Great Kanto earthquake tsunamis using a fault model and a submarine landslide source model” section. Supplementary material 1 of this paper summarizes the numerical calculation conditions and the detailed parameters of each fault model.

Table 1 The eight fault models and the tsunami fault model considered in this study

Figure 3a shows an overview of all the coastal points (No. 1 to No. 53) of this simulation. The tsunami record at each coastal point has been collected from the earthquake disaster survey reports (Imperial Japanese Navy 1924; Meteorological Observatory 1924; Ikeda 1925), field survey results (Hatori et al. 1973, Hatori 1976; Aida 1993; Yoshida et al. 2012), and tsunami trace database (The International Research Institute of Disaster Science (IRIDeS), Tohoku University, Japan 2010: https://tsunami-db.irides.tohoku.ac.jp/tsunami/mainframe.php). Figure 3b shows the observed and simulated maximum tsunami elevations at each point number (No. 1 to No. 53) shown in Fig. 3a. Figure 3c indicates the comparison of the simulated and observed results of the time-history waveforms at Yokosuka (No. 30). In both Fig. 3b and c, the black solids and lines represent the observed records and the blue solids and lines represent the simulated results from each model (F1 to F9). The time-history waveforms of each model (Fig. 3c) show 50th-percentile waveforms. The influence of ground deformation on the tsunami data at each coastal point was considered by subtracting the amount of uplift or subsidence obtained from each fault model. Figure 3d shows the results of the analysis on the residual sum of squares (RSS) in the time-history waveforms in order to evaluate the degree of agreement between the observed record and the simulated results from each model.

The maximum tsunami elevations simulated from each fault model generally explain the records at the coastal points north of the Tokyo Bay mouth (No. 27 to No. 38) as shown in Fig. 3b. By contrast, the simulated maximum tsunami elevations for the costal points (No. 1 to No. 25 and No. 41 to No. 48) show marked and significant discrepancies with the observed tsunami records, including the southern Miura Peninsula (No. 23), the eastern coast of Sagami Bay (e.g., No. 19) to the eastern coast of the Izu Peninsula (No. 4), and Mera (No. 47) at the southern tip of the Boso Peninsula. These results clearly indicate that each fault model is insufficient to explain the observed tsunami records. Further, the Imperial Japanese Navy (1924) reported that the initial tsunami undertow then leading waves reached Atami (No. 12) at 5 to 6 min after the earthquake, and the tsunami struck around Yuigahama (No. 18) at 10 to 13 min after the earthquake. However, each fault model cannot reproduce these heights, arrival times, and the initial motions of the tsunami at Atami (No. 12) and Yuigahama (No. 18) (see Supplementary Material 1 of this paper).

It is also evident from the comparison of the time-history waveforms at Yokosuka (No. 30) that the simulated and observed record shows marked discrepancies (Fig. 3c). Although there exists a limited period, from 0 to 28 min, having a low average RSS-value equal to 5.89, the general RSS shows much higher values in the periods from 28 to 43 min, 43 to 55 min, and 80 to 96 min, with the corresponding average RSS_28–43 = 19.81, RSS_43–55 = 20.05, RSS_80–96 = 33.97, respectively, giving rise to the overall average RSS-value as high as 91.28 (Fig. 3d). This means that each fault model is incapable of accounting for the observed tsunami time-history waveforms in Yokosuka.

Overall, the above results clearly demonstrate that the observed tsunami records cannot be explained solely by the fault models. Hence, the in-depth analysis of the seafloor bathymetric changes, associated ground dynamics, and their contributions to the 1923 Great Kanto earthquake tsunamis will be presented and discussed hereafter.

Depth changes of the seafloor and associated submarine landslide characteristics before and after the 1923 Great Kanto earthquake

The number of the survey points recorded using the weight measurement method before and after the earthquake is limited and sparse compared to current sounding data. Therefore, the accuracy of the depth changes may not be guaranteed even with spatial interpolation. Here, we utilize the current terrain information on the same coordinate points and analyze the statistical deviations for each group area. Specifically, we analyze the survey errors of the depth changes and the seafloor ground dynamics on the basis of the probability density distributions. Each difference between the weight measurements before and after the earthquake and the current echo-sounding data is the explanatory variables. The ground slope angle grid is a dependent variable. Statistical analysis was performed on each coordinate point using attributes as covariates.

Extraction and digitalization of the coordinate points were evaluated by comparing the current coastal topography based on the map information of the measurement point and the coastline. In Fig. 4a, the depth change records are divided into four groups (A, B1, B2, C) based on the current topography and geological features. The total number of records of the water depth change was 359, among which Group A with 110 records had the most significant number of valid survey data. Depth change areas are often distributed in the deep-sea area with a more than 1000-m depth that runs north–south along Sagami Bay. Supplementary Material 2 of this paper describes and summarizes the grouping details (A to C) shown in Fig. 4a, the method of extracting and digitizing each survey point using a geographic information system, and the interpolation results by an inverse distance weighting method using the water depth data of each survey point.

Fig. 4

a Grouping results based on the current topography and geological features of the depth changes (Imperial Japanese Navy 1924). b Probability density distributions of the depth changes before and after the 1923 Great Kanto earthquake. The left and right figures show the results of analysis for Group A and Group B-1, respectively. Each ground angle shown in Fig. 4 denotes the angle of a slope in degrees with a horizontal plane for a unit length equal to 90 m. The upper and lower figures represent the water depth differences between the current seafloor topography and the before and after earthquake, respectively

Figure 4b shows representative results of the probability density distributions of Group A and Group B-1. Other group results are summarized in Supplementary Material 2. The horizontal axis shows the water depth difference between the current topography and the topography before/after the earthquake at each ground angle. dh = 0.0, + , − , mean no depth change, shallowing, and deepening on the seafloor, respectively. Here, the ground angle denotes the angle of a slope in degrees with a horizontal plane for a unit length equal to 90 m. The distributions show dispersion when the effects of deepening and shallowing coexist at a same ground angle. Comparing the water depth difference between the post-earthquake and the present topography shown in the lower panel of Fig. 4b indicates that dh is dominantly equal to 0 in Group A and B-1, meaning that the water depth has not significantly changed since the earthquake. In contrast, comparing the water depth difference between the pre-earthquake and the present topography shown in the upper panel of Fig. 4b shows that dh becomes negative in Group A and positive in Group B-1. The former indicates that the sediments outflowed, and the latter indicates that the sediments deposited. The highest-probability depth changes and the associated dominant sediment outflows are observed at a gentle slope with 0 to 5° in Group A. Group A also shows a trend of deepening at some steeper degrees. The corresponding outflow areas extend over a wide area as shown in Fig. 4a. Group B-1 shows depositional tendency at essentially all ranges of slopes.

The results of collations showing the outflow and deposition are summarized in Fig. 5a. Here, the blue points show deepening areas (outflow) and the red points show shallowing areas (deposition). The blue dotted line denotes a submarine cable with its cutting positions marked, which are located at the vicinity of the sediment outflow areas. The representative cross-sectional seafloor ground dynamics derived from the water depth change profiles before and after the earthquake along Lines 1, 2, and 3 in Fig. 5a are shown in Fig. 5b. The concrete procedure for the interpolation of the seafloor topography before and after the earthquake is summarized in Supplementary Material 2. Figure 5a confirms that the deepening outflow areas generally correspond to the submarine canyons in the Sagami Trough, and the shallowing depositional areas are distributed along the cliffs, seafloor slopes, and a submarine canyon. In Fig. 5b, Line 1 shows an overall sediment outflow over the entire area with the flow thickness up to 142.7 m, Line 2 shows a general depositional tendency, and Line 3 shows the trend of outflow and deposition alternately. The outflow areas along Line 1 have gently sloping grounds with 0.33$^\circ$ from 25 to 35 km and 0.37$^\circ$ from 45 to 55 km. This means that the dominant sediment outflows and the landslides took place over a very gentle slope. The bathymetric changes and the associated submarine landslide characteristics shown in Figs. 5 and 6 indicate the widespread long-distance run-out, sharing an important feature of the submarine liquefied sediment flows. Namely, the seafloor gradient in the dominant flow area from 20 to 60 km was equal to or less than 0.4$^\circ$ as described above. A liquefied gravity flow can develop over a very mild slope with less than 1$^\circ$ (Field et al. 1982; Sassa and Takagawa 2019), which are consistent with the present observations. The dynamics of such submarine liquefied sediment flows features a phase change process in which the transitory fluid-like particulate sediment reestablishes a grain-supported framework accompanying pore fluid migration during the course of flowage (Sassa and Sekiguchi 2010, 2012). However, the transient high-density liquefied flow has been shown to be characterized by a high-density fluid whose density is equivalent with that of liquefied soil, with the associated theoretical framework showing consistent predictions and agreement with the observed flow behavior from laboratory to field (Sassa and Sekiguchi 2010, 2012). This relevant feature of the liquefied gravity flow will be referred to in the “Submarine landslide source model for the 1923 Great Kanto earthquake tsunamis” section.

Fig. 5

Results of analysis of the seafloor ground dynamics in Sagami Bay before and after the 1923 Great Kanto earthquake. a Results of collations with the detailed topographic map showing the areas of the sediment outflows and depositions, b cross-sectional seafloor ground dynamics derived from the water depth change profiles before and after the earthquake along Lines 1, 2, and 3 in a

Fig. 6

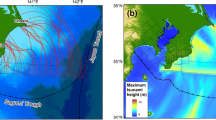
a Results of tsunami backpropagation analysis using the tsunami records of Atami (No. 12) and Yokosuka (No. 30). b Detailed seafloor topography at/around the extracted tsunami source (ETS) area as a result of the backpropagation analysis and its relationship with the previously reported traces of submarine landslides (Hydrographic and Oceanographic Department; Japan Coast Guard: JCG 2000; Watanabe 1993). c A-A’ cross-section of Manazuru Knoll slope

In Fig. 5b, Line 2 shows a shallowing depositional trend in steep seafloor slopes with 30$^\circ$ or more. A detailed examination of the slope angle near the survey point using the results shown in Fig. 5a indicates that the deposition was over a gentle slope just below the steep slope. In other words, the shallowing depositional tendency of Line 2 in Group B-1 is considered to be a phenomenon where the sediment flowed down from the top of the slope and deposited at the foot of the cliff. Line 3 is located along the submarine canyon at the mouth of Tokyo Bay, where the seafloor ground outflowed and deposited repeatedly. Furthermore, the submarine cables were broken at six locations in the area near Line 3 as shown in Fig. 5a (marked with x, Imperial Japanese Navy 1924). This strongly suggests that the large-scale sediment transport phenomenon of the liquefied ground caused the cable to break.

Submarine landslide source model for the 1923 Great Kanto earthquake tsunamis

Identification of a submarine landslide source by tsunami backpropagation analysis

Imperial Japanese Navy (1924) reported that the initial tsunami undertow then leading waves reached Atami (No. 12) or Manazuru (No. 13) 5 to 6 min after the earthquake, and the tsunami struck around Yuigahama (No. 18) 10 to 13 min after the earthquake. However, each fault model shown in the “Existing research and tsunami prediction accuracy of each model” section above cannot explain the arrival times and initial undertow of the tsunami at Atami (No. 12) and Yuigahama (No. 18) (Supplementary Material 1). Table 2 shows relevant information on the tsunami arrival times for each coastal point, where Atami (No. 12) and Manazuru (No. 13) located in the western part of Sagami Bay show relatively early tsunami initial movements (Imperial Japanese Navy 1924; Meteorological Observatory 1924; Ikeda 1925). Here, a range of tsunami backpropagation analysis was performed based on the assumption that the propagation times required for the distances between the tsunami source locations and observation stations are equivalent irrespective of the directions. This analysis was conducted by considering hypothetical tsunami sources at the location of a tsunami observation point and drawing the tsunami travel time contours propagating backwards from that observation point to the open sea. Then, the area where all reverse travel time contours from all points met was extracted as the source of the tsunami. The backpropagation analysis is a powerful tool for pinpointing the location of tsunami source (e.g., Hayashi et al. 2011; Heidarzadeh et al. 2023). The results of this analysis for Atami (No. 12) and Yokosuka (No. 30) are shown in Fig. 6a. This figure also shows the propagation diagram using the tsunami arrival information at Atami (No. 12) and Yokosuka (No. 30). The blue lines indicate the tsunami backpropagation diagram extracted from Atami (No. 12) and Yokosuka (No. 30) (Atami diagram line = 5 min, Yokosuka diagram line = 29 min). The overlapping area exists in the southeastern region off Cape Manazuru (hereafter referred to as ETS, extracted tsunami source). In other words, ETS highlights a secondary tsunami source area that cannot be explained by the existing fault models as described above. Furthermore, the ETS corresponds to the area where the seafloor sediments extensively outflowed showing large-scale submarine landslides, as shown in Fig. 5a.

Table 2 Information on tsunami arrival times

Figure 6b shows the visualization result of the detailed seafloor topography at/around the extracted tsunami source (ETS) just mentioned. The double circles indicate the deepening outflow area (blue) and the shallowing deposition area (red) as shown in Fig. 5a and the area with no essential change (white, Imperial Japanese Navy 1924). The yellow- and green-shaded areas represent the locations showing the traces of submarine landslides reported previously (Hydrographic and Oceanographic Department; Japan Coast Guard: JCG 2000; Watanabe 1993). In Fig. 6b, the Sagami Trough crosses the Sagami Bay from north to south. The Manazuru Knoll and the Sagami Knoll are distributed along the submarine canyon from Atami Bay, which is located at the northwestern end of the Sagami Trough. The ETS strongly suggests that the submarine landslide tsunami occurred in this area. A close examination of Fig. 6a and b shows that the submarine landslide source area marked by the orange-shaded zone in Fig. 6b is smaller in size than the ETS area in Fig. 6a. The reasoning for this limited submarine landslide source stemmed from the fact that the left-side area of the ETS corresponded to the area with no essential change characterized by the white circles, indicating that this area cannot be regarded as a landslide source, and that a steeper slope and a shallower water depth generally exhibit a more significant effect on tsunami generation (Grili and Watts 2005; Watts et al. 2005). Figure 6c shows the ETS cross-sectional (A-A’) geometry with the average slope angle equal to $\theta =$8.45$^\circ$.

Overall, based on the ETS area evaluated by the tsunami backpropagation analysis, overlapping with the results of the present seafloor ground dynamics analysis as well as the previously reported traces of submarine landslides, and detailed bathymetric survey data, the submarine landslide source in Sagami Bay for the 1923 Great Kanto earthquake tsunami has been identified as the orange-shaded area in Fig. 6b as described above. The submarine landslide source shows that submarine landslides occurred just above the Manazuru Knoll, located in the western part of Sagami Bay, as part of the widespread submarine liquefied sediment flows described above, which were induced by the strong seismic motion of the 1923 Great Kanto earthquake. Furthermore, the literature on many carcasses of deep-sea fish after the earthquake in the sea area off the east coast of the Izu Peninsula (Imperial Japanese Navy 1924) reinforces the start of the large-scale submarine landslides originating from the southern slope of the Manazuru Knoll in Sagami Bay. According to Kato et al. (1987), the turbidite layer supplied from the Sagami Bay seafloor is thickly deposited on the Katsuura Basin located off the southern coast of the Boso Peninsula.

Analytical solution on the terminal velocity of a high-density liquefied gravity flow on a southern slope of Manazuru Knoll

The submarine landslide characteristics as presented in the “Depth changes of the seafloor and associated submarine landslide characteristics before and after the 1923 Great Kanto earthquake” section indicate an important feature of the submarine liquefied gravity flows which can be characterized by a high-density fluid whose density is equivalent with that of liquefied soil. On this basis, we adopt here a theorical solution of a gravity flow. By employing the analytical solution by Ross (2000) and considering the mass density of a liquefied soil (Sassa et al. 2001), the terminal velocity of a liquefied gravity flow is given by:

$${u}_{{\text{f}}}={F}_{{\text{r}}}{\left(2{g}^{{\prime}2}V{\text{tan}}\theta \right)}^\frac{1}{4}$$

(1)

$$g{\prime}=\frac{\rho -{\rho }_{0}}{\rho }g$$

(2)

where ρ is the mass density of a liquefied soil, ρ₀ is the mass density of the ambient fluid, u_f is the terminal velocity of a liquefied gravity flow on a submarine slope (m/s), F_r is the Froude number, g is the gravitational acceleration (m/s²), V is the volume of the gravity flow, and $\theta$ is the seabed ground angle ($^\circ$). Here, the gravity-flow volume consists of submarine landslide length l (m) and thickness h (m) per a unit width of a submarine landslide.

The scale of the submarine landslide, the orange shaded area in the ETS on the southern slope of the Manazuru Knoll, can be estimated as length l = 3 km and width w = 5 km from the detailed topographical interpretation in Fig. 6b. The thickness h of the submarine landslide was set equal to 140 m which essentially corresponded to that of the large-scale submarine liquefied sediment flows as shown in Fig. 5b. The seafloor ground angle was set to be $\theta$ = 8.45$^\circ$ from Fig. 6c. Table 3 shows the parameterized submarine landslide scale on the southern slope of the Manazuru Knoll. The specific gravity of the submarine landslide was set equal to 1.85 of a liquefied gravity flow, namely with the mass density of a liquified soil (Sassa et al. 2001; Sassa and Sekiguchi 2012). Here, the specific gravity represents the ratio of the mass density of a liquefied soil to that of the ambient fluid. Figure 7 shows the relationship between the gravity-flow volume (horizontal axis) and the terminal velocity u_f (vertical axis) corresponding to the high-density liquefied gravity flow based on Eqs. (1) and (2) and Table 3. Here, the ground angles determine the terminal velocities for a given flow volume, and the red line shows the terminal velocity on the southern slope of the Manazuru Knoll. For the purpose of comparison, the blue line shows the terminal velocity for the average slope angle equal to 0.6$^\circ$ in the entire Sagami Bay. Considering the scale of the gravity flow as represented by l × h/2 = 3000 × 140/2 = 210,000 m² as schematically shown in Fig. 7, the terminal velocity for the liquefied gravity flow on the southern slope of the Manazuru Knoll becomes equal to 32.2 m/s. This value will be referred to in the “Numerical simulations of the 1923 Great Kanto earthquake tsunamis using a fault model and a submarine landslide source model” section.

Table 3 Details of submarine landslide parameters corresponding to a high-density liquefied gravity flow

Fig. 7

Terminal velocity versus volume of a high-density liquefied gravity flow on the southern slope of Manazuru Knoll as determined by the analytical solution that takes account of the mass density of a liquefied soil

Numerical simulations of the 1923 Great Kanto earthquake tsunamis using a fault model and a submarine landslide source model

Methods for the submarine landslide tsunami simulations

On the basis of the results presented in the “Existing research and tsunami prediction accuracy of each model,” “Depth changes of the seafloor and associated submarine landslide characteristics before and after the 1923 Great Kanto earthquake,” and “Submarine landslide source model for the 1923 Great Kanto earthquake tsunamis” sections, the “Numerical simulations of the 1923 Great Kanto earthquake tsunamis using a fault model and a submarine landslide source model” section presents a series of the numerical simulations of the 1923 Great Kanto earthquake tsunamis using a fault model and a submarine landslide tsunami source model. Here, the dimensions of the submarine landslide source correspond to those of a high-density liquefied gravity flow as described above. The simulated results will be compared and discussed in light of a range of coastal tsunami records. The submarine landslide tsunami source scheme adopted a slump model based on empirical formulas developed by Grilli and Watts (2005) and Watts et al. (2005). This scheme, via their shape parameters, can evaluate the influence of landslide flow on the shape of the initial tsunami wave form approximated by a simultaneous dipole Gaussian. Accordingly, the present analysis addressed a parametrization of a shape parameter to examine the influence of the landslide flow characterized by the high-density liquefied gravity flow on the tsunami generation in the Sagami Trough, corresponding to Case 1 to 5 in Table 4. The validity of the initial water-level fluctuation amplitude from a landslide tsunami has been shown by Watts et al. (2005) and Grilli and Watts (2005) based on the hydraulic and numerical experiments using a fully nonlinear potential flow model (FNPF), and also by several studies on past submarine landslide tsunami events (e.g., Tappin et al. 2008, 2014). As described in the “Tsunami predictive accuracy” section, the tsunami simulation program and its numerical conditions were the same as used for the fault-model–based simulations, and the 50th, 25th, and 75th percentiles of the waveforms were obtained from multiple coordinates in 9 neighboring cells at each coastal point (see the “Overview of the rupture process of the 1923 Great Kanto earthquake fault model” section and Supplementary Material 1 for details). As for the fault model, the fault model F8 by Namegaya et al. (2011) was used as an optimal fault model, which showed the lowest overall RSS-value among the eight fault models (F1 to F8) and the tsunami fault model (F9) shown in Fig. 3d.

Table 4 Numerical simulation parameters for submarine landslide–induced tsunamis

Table 4 shows the dimensions of the submarine landslides and parameters and coefficients set in the analysis. The hydrodynamic coefficients were set equal to those used in Watts et al. (2005). The water depth at the submarine landslide source before the earthquake, h = 740 m, was derived from the detailed seafloor topography in Fig. 6b, by considering the flow thickness equal to 140 m as described above. The submarine landslide took place on the southern slope of the Manazuru Knoll and flowed down through the Sagami Trough. With reference to Fig. 6a, the flow direction was set at 75$^\circ$ with the north–south direction as a primary axis. The associated sensitivity analysis on the flow direction is described in Supplementary Material 3. The flow section on the southern slope of the Manazuru Knoll was set to be 3300 m long. This was based on the topographic interpretation, and considering the possible most significant section that could have affected the tsunami excitation, and importantly, taking account of the consistency with the liquefied gravity flow. Namely, the corresponding terminal velocity calculated by the source model of Watts et al. (2005) was equal to 31.48 m/s, which essentially corresponded to the terminal velocity of a high-density liquefied gravity flow on the southern slope of the Manazuru Knoll as shown in Fig. 7. The liquefied gravity flow is assumed here to have reached its terminal velocity immediately following the occurrence of the 1923 Great Kanto earthquake.

Results and discussion

Figure 8a indicates the simulated and observed maximum tsunami elevations at each coastal point shown in Fig. 3a. Here, the solid circles represent the observed records, the simulated results by an optimal fault model are marked with F8, and the simulated results by the fault model and the submarine landslide source models are denoted by Cases 1 to 5, respectively. Figure 8b shows the simulated and observed tsunami time-history waveforms in Yokosuka (No. 30). Here, the simulated results denote the 50th-percentile (median) waveforms, where the solid line represents the observed waveforms marked with “Record,” the simulated results by the optimal fault model, and by the fault model, and the submarine landslide source models marked with “FLT + SL” are denoted in the same way as in Fig. 8a. The difference here is that the simulated results by the submarine landslide source models are denoted by Cases 1’ to 5’ marked with “SL” in Fig. 8b. The observed records are the same as shown in Fig. 3b and c.

Fig. 8

a Simulated and observed maximum tsunami elevations at each coastal point (No. 1 to No. 53) shown in Fig. 3a. The black circles denote the observed records, F8 denotes the simulated results by an optimal fault model with the lowest RSS values shown in Fig. 3d, and Cases 1 to 5 denote the simulated results by the fault model and the submarine landslide source models shown in Table 4. b Comparison of the simulated and observed time-history waveforms in Yokosuka (No. 30). The black solid line denotes the observed records, the F8 and Cases 1 to 5 marked with “FLT + SL” denote the same as in a. Cases 1’ to 5’ denote the simulated results by the submarine landslide source models without the fault model, marked with “SL.” All of the simulated results in a and b denote those from the 50th-percentile (median) waveforms at each coastal point

In Fig. 8a, it is clear that the simulated maximum tsunami elevations obtained by the optimal fault model (F8) disagree substantially with the observed tsunami records except for the regions at north of the Tokyo Bay mouth (No. 27 to No. 38) with the lowest observed maximum tsunami elevations up to 2 m. In contrast, the simulated results by the optimal fault model and all the submarine landslide source models (Cases 1 to 5) improve the predictions significantly by amplifying the tsunami components, including the areas of Atami (No. 12), Oiso (No. 15), Yuigahama (No. 18), around the southern tip of Boso in Sunosaki (No. 43), and Mera (No. 47). Indeed, in Atami (No. 12) with the highest observed maximum tsunami elevations, the simulated maximum values of the 50th-percentile waveforms give rise to an increasing tendency, in comparison to 1.6 m by the optimal fault model (F8), from 4.46 m in Case 1 to 10.35 m in Case 5, where the latter shows a general agreement with the observed maximum tsunami elevation of about 12 m in Atami (No. 12).

At around the Tokyo Bay mouth (Uraga, No. 27, to Kanaya, No. 38), the simulated results are essentially the same with and without the submarine landslide sources. The wavelength of the tsunami induced by a submarine landslide is known to be typically shorter than that of the tsunami induced by a fault motion (Brink et al. 2014). Accordingly, a shorter-period component may be dominant in the former compared with a longer-period component in the latter and can thus more significantly attenuate through reflection and refraction over the coastal topography, which may be consistent with the observed small tsunami elevation especially on the north of Cape Futtsu (No. 36).

A comparison of the time-history waveforms (Fig. 8b) in Yokosuka (No. 30), located in the south of Cape Futtsu, indicates that the submarine landslide–induced tsunami propagated from the leading wave component (SL, Cases 1’ to 5’). This may correspond to the thrust wave component of the SL tsunami generated offshore by the submarine landslide on the southern slope of the Manazuru Knoll. This tsunami generation process is consistent with the characteristics of the SL tsunami, in which the first wave is dominant as a forward wave component in the flow direction of the landslide (e.g., Haugen et al. 2005). Moreover, it accounts well for the start of the significant gap between the fault model prediction and the tsunami record at t = 28–30 min. Indeed, the fault model (F8) results are distributed in antiphase to the observed waveform at 28–42 min, 43–55 min, and 80–96 min. However, the present models (FLT + SL) show consistent phases with the observed record. Consequently, the submarine landslide components improve the time-history predictions considerably with increasing SL tsunami components from Case 1 to 5 (FLT + SL).

On the basis of the results and comparisons presented above, a summary of the results of the present simulations adopting the optimal fault model (F8) and a suitable submarine slide source model (Case 5) is shown in Fig. 9. For the purpose of a closer examination, all the results are shown here in terms of the 25th-, 50th-, and 75th-percentile variabilities.

Fig. 9

a Simulated and observed maximum tsunami elevations at each coastal point (No. 1 to No. 53). The black circles denote the observed records, F8 denotes the simulated results by an optimal fault model shown in Fig. 8a, and Case 5 denotes the simulated results with the 50th-, 25th-, and 75th-percentile variabilities. b Comparison of the simulated and observed time-history waveforms in Yokosuka (No. 30). The black solid line denotes the observed records. FLT and SL + FLT denote the simulated results by F8 and Case 5, respectively. c Comparison of the observed tsunami records and the simulated time-history waveforms with each percentile in Yuigahama (No. 18), Atami (No. 12), Oshima (No. 1), Mera (No. 47), Manazuru (No. 13), and Shimoda (No. 2). The light red areas indicate the observed tsunami records with an upper to lower limit at each coastal point. Here, all of the simulated results in time series denote those for the 50th percentile (solid lines), the 25th percentile (lower dotted lines), and the 75th percentile (upper dotted lines)

In Fig. 9a, the observed maximum tsunami elevations increase from Shimoda (No. 2) to Atami (No. 12) at the southern tip of the Izu Peninsula. These geographically increasing maximum tsunami elevations are well explained by the present simulations considering the 25th- to 75th-percentile variabilities. Moreover, the present simulations well explain the observed local maximum tsunami elevations from Enoshima (No. 17) to Zushi (No. 19) in the area of the eastern coast of Sagami Bay, Koyatsu (No. 42) and Sunosaki (No. 43) to Nojimasaki (No. 48) located in the southern part of the Boso Peninsula facing the Pacific Ocean. Essentially, the present results generally conform well to the observed maximum tsunami elevation distributions along the whole coast.

It is important to note in Fig. 9a that there are a few or a limited number of coastal points where the simulated results exhibited a certain discrepancy with the observed maximum tsunami elevations, notably Jogashima (No. 24). This could be closely related with another possible submarine landslide source. The basis of this is such that Jogashima is located above the regions where the submarine cable-cutting accidents are previously reported as in Fig. 5a, and with reference to Fig. 1, the epicenter of the 1923 Great Kanto earthquake migrated from the first in the western Sagami Bay to the second in the southern Miura Peninsula, the latter of which may have caused this second submarine landslide source in this area, such as the submarine landslides along Line 3 shown in Fig. 5b. The results shown in Figs. 8 and 9a also indicate that the shape parameters of Watts et al. (2005) adopted in Cases 1 to 5 had a significant effect on the tsunami generation. Such parameterization may depend on a number of factors which could involve multiple landslide sources and a more realistic modelling on the multi-phased physics of the submarine landslide processes and their consequence in light of the submarine liquefied flows undergoing flow stratification, deceleration, and redeposition (Sassa and Sekiguchi 2010, 2012).

Figure 9b shows the simulated and observed time-history waveforms at Yokosuka (No. 30). It is seen that the present results (FLT + SL) account well for the observed tsunami time-history waveforms. With reference to the observed tsunami arrival times shown in Table 2, the simulated time-history waveforms at Yuigahama (No. 18), Mera (No. 47), Atami (No. 12), Manazuru (No. 13), Oshima (No. 1), and Shimoda (No. 2) are summarized in Fig. 9c. In these graphs, the red shaded areas indicate the observed tsunami records at each location. The tsunami arrival times at 28 to 30 min after the earthquake in Yokosuka (No. 30) in Table 2 agree with the timing when the submarine landslide–induced tsunami arrived, as shown in Figs. 8 and 9b. At Yuigahama (No. 18), the present results (FLT + SL) show 6.23 m (50th percentile) and 9.33 m (75th percentile) at 11 to 12 min after the earthquake, and at Atami (No. 12), the present results show a tsunami backwash with − 1.3 m (50th percentile) and − 2.8 m (75th percentile) at 4.5 min after the earthquake and a local leading tsunami with 9.83 m (50th percentile) and 13.77 m (75th percentile). These simulated tsunami initial motions with their arrival times as well as the local tsunami elevations accord well with the observed records at each coastal point shown in Table 2 and Fig. 9c. Furthermore, the observed tsunami records at Manazuru (No. 13), Oshima (No. 1), Mera (No. 47), and Shimoda (No. 2) can be reasonably well explained by the present results (FLT + SL) in terms of the tsunami arrival times and the local tsunami elevations as shown in Fig. 9c and Table 2. The optimal fault model (FLT) is incapable of accounting for these tsunami records, in particular, cannot explain as high as 13 m tsunami record at Oshima (No. 1) at all, whereas the present FLT + SL results conform to this distinct tsunami record locally.

The results of the RSS analysis of each model (FLT and FLT + SL) for the Yokosuka record are shown in Table 5 to quantitatively evaluate its consistency with the observed time-history waveforms. It is evident that the present FLT + SL results show substantially lower RSS-values compared with those by the optimal fault model (F8) after the submarine landslide-induced tsunami arrived in Yokosuka at 28 min after the earthquake. This means that the submarine landslide contributed markedly to the time-history waveforms of the observed tsunami.

Table 5 Results of RSS analysis of the F8 model and FLT + SL model for the observed time-history waveforms in Yokosuka (No. 30)

Overall, the above results demonstrate that the submarine landslides as represented by a high-density liquefied gravity flow played a pivotal role in the observed time-history waveforms, initial tsunami motion (arrival times), and the maximum tsunami elevation distributions along the whole coast in the Izu Peninsula and the Miura Peninsula facing Sagami Bay, the Miura Peninsula and the Boso Peninsula facing Tokyo Bay, and the Boso Peninsula facing the Pacific Ocean for the tsunami damage of the 1923 Great Kanto earthquake.

Conclusions

The present study investigated submarine landslides and tsunamis in Sagami Bay at the 1923 Great Kanto earthquake that caused severe and extensive damages from the east coast of the Izu Peninsula to the west coast of the Boso Peninsula involving the devastating damage in Atami, Japan. The principal findings and conclusions obtained from this study are as follows.

The comprehensive gap between the predictions by the existing nine fault models and the observed tsunamis was quantified by showing that the fault models can explain the observed low tsunami elevation areas at around Tokyo Bay mouth, however, are incapable of accounting for the observed time-history waveforms in Yokosuka, the observed tsunami initial motions with their arrival times at Atami and Yuigahama, and the observed maximum tsunami elevation distributions along the whole coast including the southern Miura Peninsula, the eastern coast of Sagami Bay to the eastern coast of the Izu Peninsula, and the southern tip of the Boso Peninsula. These results clearly indicate that each fault model is insufficient to explain the observed tsunami records.

The results of the in-depth statistical analysis of the water depth density distributions before and after the 1923 Great Kanto earthquake demonstrated that the seafloor bathymetric changes, that took place before and after the earthquake, represented large-scale submarine landslide phenomena. The seafloor gradient in the dominant flow area over a 40 km flow-out distance was equal to or less than 0.4$^\circ$. These bathymetric changes and the associated submarine landslide characteristics indicated the widespread long-distance run-out, sharing an important feature of the submarine liquefied gravity flows that can develop over a very gentle slope with less than 1$^\circ$.

Through the identification of the submarine landslide source by tsunami backpropagation analysis and utilizing an analytical solution of a high-density liquefied gravity flow and a sensitivity analysis, a range of numerical simulations of the 1923 Great Kanto earthquake tsunamis was conducted using an optimal fault model with the lowest residual sum of squares (RSS) values among the nine existing models with the observed time-history waveforms, and the submarine landslide tsunami source models due to a high-density liquefied gravity flow.

The present results demonstrate that the submarine landslides as represented by a high-density liquefied gravity flow played a pivotal role in consistently accounting for the observed time-history waveforms, the observed initial tsunami motions and their arrival times, and the observed maximum tsunami elevation distributions along the whole coastal areas along three peninsulas involving Izu, Miura, and Boso Peninsulas facing Sagami Bay, Tokyo Bay, and the Pacific Ocean, thereby showing submarine landslides as a major source of the 1923 Great Kanto earthquake tsunamis.

Since a better integrated understanding of the landslide dynamics and landslide-water interactions is crucial to reducing landslide tsunami disaster risk globally (Sassa et al. 2022), it is hoped that the findings and conclusions obtained in the present study may facilitate and deepen our understanding of the earthquake-induced submarine landslide tsunami risk as cascading multi-geohazards.