Introduction

An underrated problem in engineering practice is the run-up of debris flows against obstacles to ensure retention capacity and structural safety. Few practical guidelines provide an approximation for estimating potential run-up heights (e.g., Lo 2000; Kwan 2012), and these models predict debris-flow run-up based on different approaches tested by small scale experiments and simulations (e.g., Ng et al. 2017; Rickenmann et al. 2019; Song et al. 2021). However, results are often compared using the Froude number, the dimensionless ratio of gravitational and inertial forces (Eq. 1) (e.g., Iverson et al. 2016; Rickenmann et al. 2019).

$$Fr= \frac{{v}_{0}}{\sqrt{g{h}_{0}}}$$
(1)

In Eq. 1, \({h}_{0}\) and \({v}_{0}\) denote the height and velocity of the incoming flow, and \(g\) accounts for the gravitational acceleration. It is important to note that the use of the Froude number to characterize debris-flow processes (either from real events or based on experiments) assumes kinematic similarity, i.e., that the velocity at any point in the model flow is proportional to a constant scale factor. No account is taken of the various stresses that may characterize the flowing mixture nor of the disproportionate effects of drag forces and time scales (Iverson 1997; Iverson et al. 2016). Particularly for debris flows in the low Froude regime (Armanini et al. 2020; Song et al. 2021), where bulk resistance is often either frictionally or collisionally induced, anisotropic, i.e., non-hydrostatic, stress conditions appear to prevail during run-up processes (Scheidl et al. 2019; Nagl et al. 2021). Some experimental investigations also indicate different resisting processes at lower Froude regimes that are influencing the run-up of debris flows (Rickenmann et al. 2019; Armanini et al. 2020). As frequently reported from field observations (Pierson 1986; Marchi et al. 2002; Hu et al. 2011; McArdell et al. 2023; Lapillonne et al. 2023), such debris flows, whose dynamics can be characterized by Froude numbers between 0.2 and 3, are reasonably common (Fig. 1).

Fig. 1
figure 1

Measured Froude numbers of natural debris flows

Full size image

However, run-up models are mainly validated by small-scale experiments (e.g., Choi et al. 2015; Rickenmann et al. 2019) where the range of Froude number is often higher than in natural debris flows (Phillips and Davies 1991). To this end, there are no real-time measurements of natural debris flows available to validate prediction models for run-up estimations. In this paper, we present real-time measurements of natural debris-flow run-ups on a monitoring structure together with related flow characteristics. Three debris flows with multiple surges were used to analyze the run-up against a vertical monitoring structure, providing a solid database for investigating and analyzing existing run-up prediction models. The presented real-time run-up measurements are further compared with existing data of run-up experiments from literature.

Debris-flow run-up models

In the following, we briefly present three main approaches (Fig. 2) for estimating the run-up height of debris flows. The first two models, based on energy and mass momentum conservation, refer to the run-up at a vertical obstacle. The third model refers to the potential run-up height of a counter slope, which in this study is assumed to be normal to the flow direction.

Fig. 2
figure 2

Sketch of different conceptual approaches to modelling the run-up height of debris flows

Full size image

All described models are estimating the run-up factor, the relation between run-up height (\(H\)), and incoming flow height (\({h}_{0}\)). They all indicate a dependency on the Froude number.

Energy conservation principle (point mass model)

The most used method to predict the run-up height \(H\) is based on the energy conservation principle, where all kinetic energy of an infinitesimal rigid body is assumed to convert to potential energy at impact. This classical approach does not account for any basal friction and is rooted in hydraulic theory (Chanson 2004).

$$\frac{H}{{h}_{0}}=1+\frac{{Fr}^{2}}{2}$$
(2)

The assumption of energy conservation is reasonable, if a smooth gradual run-up can be expected during impact. Based on a comprehensive energy model for debris flows (Pudasaini and Kröner 2008; Pudasaini and Domnik 2009), Faug (2021) proposed an extended run-up prediction model by accounting for anisotropic stress (\(k\)) and bulk flow (\(\rho\)) variations between the incoming (\({k}_{0}, {\rho }_{0}\)) and impacted (\({k}_{1}, {\rho }_{1}\)) flow. Here, \(k\) reflects a stress coefficient often corresponding to Rankine’s earth pressure theory—reflecting the ratio of normal to longitudinal stress conditions.

$$\frac{H}{{h}_{0}}=\frac{1}{{k}_{0}}\frac{{\rho }_{0}}{{\rho }_{1}}\left({k}_{1}+\frac{{Fr}^{2}}{2}\right)$$
(3)

In this study, we assume that the stress coefficient due to the impact \({k}_{1}\) is greater than the stress coefficient of the inflowing mass, which we define as \({k}_{0}=1\) for further analyses.

Scheidl et al. (2023) recently determined high variability in bulk density ratios upon impact based on small-scale debris-flow experiments. On average, they observed 20% higher bulk densities at impact for granular debris flows and even higher for debris-flow mixtures with a high proportion of fine material. However, bulk density ratios between inflowing and impacting flows \(\left(\frac{{\rho }_{0}}{{\rho }_{1}}\right)\) have not yet been fully explored, and uncertainties are still high. Thus, for this study, we assume \(\frac{{\rho }_{0}}{{\rho }_{1}}=1\).

Based on these assumptions, Eq. 3 can now be written,

$$\frac{H}{{h}_{0}}={k}_{1}+\frac{{Fr}^{2}}{2}$$
(3a)

whereas the run-up factor depends beside the dynamic flow on the anisotropic stress condition, reflected by \({k}_{1}\).

Mass and momentum conservation principle (moment jump model)

The run-up height can also be estimated by assuming a balance of mass and momentum between the incoming and impacting flow. The compression of a continuous, uniform flow at impact causes a wave to propagate upwards as a result of an abrupt change of the macroscopic momentum and the conversion to internal pressure. With a focus on snow avalanches, Hákonardóttir et al. (2003) and Jóhannesson et al. (2009) formulated this phenomena, considering bulk density variations of incoming and impacted flow.

$${\frac{{\rho }_{1}}{{\rho }_{0}}\left(\frac{H}{{h}_{0}}\right)}^{2}-\frac{H}{{h}_{0}}-1+{\left(\frac{{\rho }_{1}}{{\rho }_{0}}\frac{H}{{h}_{0}}\right)}^{-1}-2{Fr}^{2}=0$$
(4)

Iverson et al. (2016) adapted the model to debris flows, accounting for stress anisotropy. Assuming equal bulk flow densities of the incoming and impacted flow \(\left(\frac{{\rho }_{0}}{{\rho }_{1}}=1\right)\), Eq. 4 gets to:

$${\left(\frac{H}{{h}_{0}}\right)}^{2}-\frac{H}{{h}_{0}}-1+{\left(\frac{H}{{h}_{0}}\right)}^{-1}-\frac{2{Fr}^{2}}{{k}_{1}}=0$$
(4a)

Armanini et al. (2011) pointed to the dependence of the Froude number on the behavior of an impacting surge. If the flow regime is supercritical, a vertical jet is developed; instead, in the subcritical regime, the flow converts to a horizontal backwater effect or bow shock wave (Chen et al. 2021).

Constant discharge principle (smooth momentum flux model)

Another model based on Takahashi and Yoshida (1979) described a momentum equilibrium equation by incorporating momentum flux for coarse-grained debris flows decelerating due to a rapid change of slope. This model, also known as the leading-edge model (Prochaska et al. 2008; Takahashi 2014), assumes a constant upstream discharge, with deposition starting at the point where the channel abruptly levels out. Iverson et al. (2016) modified the model by redirecting the flow momentum upslope by centripetal forces, the basal flow resistance only depending on the adverse slope \(\left({\theta }_{1}\right)\), the effective basal friction (\({\phi }_{{\text{e}}}\)), and the precise treatment of longitudinal to normal pressure ratio by considering anisotropic stress conditions (\({k}_{1}\)) at run-up or run-out, respectively.

$$\frac{H}{{h}_{0}}=\frac{{\left(Fr+\frac{{k}_{1}}{2}{Fr}^{-1}{cos}^{3}{\theta }_{1}\right)}^{2}}{\left(1+\frac{tan{\phi }_{{\text{e}}}}{tan{\theta }_{1}}\right)}$$
(5)

Like the energy concept-based models, the smooth momentum flux model considers gradual deceleration of the debris-flow head instead of an abrupt deceleration associated with a momentum jump. As described by Iverson et al. (2016), in the limiting case with \({\theta }_{1}=90^\circ\), the absence of a slope-normal weight component implies that no basal friction is engaged, and the predictions of the smooth momentum flux model is directly related to the Froude number (Eq. 5a):

$$\frac{H}{{h}_{0}}={Fr}^{2}$$
(5a)

Method

Field site

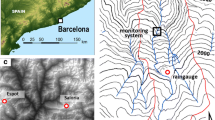
All the measurements presented in this study were carried out on natural debris flows, using a special monitoring structure in the Gadria torrent in northern Italy (Nagl et al. 2018). With an area of about 6.3 km2 and an altitude difference from 2950 to 1394 m a.s.l., the Gadria torrent is located in a typical, small and steep, alpine headwater catchment (Fig. 3b). Metamorphic rock and a high fragment of rocks and glacial deposit lead to frequent debris-flow events. Near the monitoring structure, the channel has a trapezoidal form with a fixed channel bed of a longitudinal slope of 6° and a rock-riprap channel bank. The channel bed is 40 m upstream and 10 m downstream from the structure secured with concrete riprap to ensure no erosion during a debris-flow event.

Fig. 3
figure 3

a Debris-flow monitoring structure, with its size in relation to the channel as well as situation of the ultra-sonic sensors (USS-1, USS-2) to measure run-up as well as flow height, respectively. b Map of the monitoring site

Full size image

Monitoring structure and instrumentation

The monitoring structure represents the main exposed part of a debris-flow barrier—a typical mitigation measure to protect from mass wasting processes in alpine regions. The structure consists of a 1-m wide concrete element in the middle of the channel, with a height of 3 m above the ground (Fig. 3). The structure is connected to a foundation below the bottom of the channel bed and is secured by pre-dam, situated upslope. The effective width of the measuring barrier is 1.0 m with a rectangular shape and is in a plausible relationship to the averaged 50 grain size of 0.15 m and the bed width of the channel cross-section (8.5 m) of typically observed debris-flow events at Gadria, which force a run-up by a redirection of the momentum of the impacted mass.

Measurements of both run-up height (\(H\)) as well as flow height (\({h}_{0}\)) are based on two vertical-oriented ultra-sonic sensors, which are situated in front (USS-1) and 2 m aside of the structure (USS-2) in the transverse direction, respectively (Fig. 3). Both sensors were sampled at 100 Hz.

Studies have recently highlighted the importance of so-called “dead zones,” i.e., the accumulation of sediment in the form of a ramp in front of the obstacle, which mutually influence run-up observations (Albaba et al. 2018; Faug 2021). The uncertainty of the influence of ramping cannot be excluded in this study either, as we cannot detect the processes inside the debris-flow matrix during impact. However, we argue that for the observed events in the Gadria torrent, the influence of a potential ramp is small in relation to the measured maximum run-up height, as the fluid part of the debris-flow tail significantly lowers a potential deposit in front of the measuring barrier before the next debris-flow surge. Splashing debris is another phenomenon that might influence measurements of run-up heights, especially in very fine-grained debris flows with higher flow dynamics—which contrast with the debris flows observed in this study (c.f. Fig. 1). To limit the influence of splashing debris, the raw flow height data measured at 100 Hz were binned to 1 Hz (c.f. Nagl et al. 2020).

Additionally, a Mobotix M15 was used to determine the surface velocity by manual particle tracing. It should be noted that there will be a degree of uncertainty in the calculation of surface speed due to the variation in frame rate (Theule et al. 2018). In 2019, a second camera (Dahua., IPC-HFW5231E-Z12E)—only used for visual observations—was installed. Both cameras are equipped with infrared spots for day and night observations and are mounted on the side of the structure.

Results

Debris-flow events

This research is based on three observed debris-flow events which occurred in three consecutive summers from 2018 to 2020—triggered due to convective rainfalls (Tables 1, 2, 3, and 4).

Table 1 The debris flow of 2018 run-ups of eight surges. Flow depth above force plate 1 (beside the barrier) and above force plate 2 (in front of the barrier) with the maximum surface velocity. The run-up factor and Froude number of the impacting surges (numbers in bold emphasis are excluded)
Full size table
Table 2 The debris flow of 2019 run-ups of 15 surges. Flow depth 1 (beside the barrier) and flow depth 2 (in front of the barrier) with the maximum surface velocity. The run-up factor and Froude number of the impacting surges
Full size table
Table 3 The debris flow of 2020 run-ups of 15 surges. Flow depth 1 (beside the barrier) and flow depth 2 (in front of the barrier) with the maximum surface velocity. The run-up factor and Froude number of the impacting surges
Full size table

The first event was observed on 21 July 2018 and exhibited several surges with a maximum flow height (h0) of around 1.5 m and velocities up to 3.6 m/s. The second debris-flow event was observed on 11 June 2019, and again multiple surges could be observed with flow heights (h0) up to 2.5 m and velocities of 4.2 m/s. The third debris flow could be observed on 2 August 2020, with a maximum velocity of around 8.2 m/s and flow heights (h0) of around 2.3 m.

All three debris-flow events showed a sediment-laden precursory surge (c.f. Fig. 4), which exhibited a pronounced run-up due to the considerably higher liquid content compared to the following main debris-flow surges. All main debris-flow surges, however, showed the typical granular front with intermediate finer debris. While a reasonably comparable sequence of debris-flow surges can be observed in both the 2018 and 2019 events, the 2020 debris-flow event reveals an inactive phase of about 20 min following the first main debris-flow surge (Fig. 4). For the 2020 debris-flow event, additionally, a boulder was deposited in front of the barrier during the first main debris-flow surge and remobilized after the inactive phase.

Fig. 4
figure 4

Flow depth measurements of three debris flows from 2018 and 2020 in the Gadria torrent. The black line shows flow depth measurements beside the barrier (flow height 1) and the grey line in front of the barrier (flow height 2). Before each debris flow, a sediment-laden precursory surge (Pre.S) was observed

Full size image

It is acknowledged that deposited material in front of the barrier can influence the flow depth differences. For this reason, we excluded the last three surges of the 2018 event at time steps 655 s, 680 s, and 700 s. In this case, a visual assessment revealed that the surges were excessive due to a subsequent surge (c.f. Fig. 4).

In general, our observations indicate that run-up can be distinguished by the different surge characteristics. The run-up heights created by the precursory sediment-laden surges are up to nine times greater than the impacting flow height, while the run-up factors of the main debris flows are about four, at similar Froude numbers. We therefore differentiate in this study between precursory surges and debris-flow surges to highlight the transition of flow types, based on our observations.

Comparison of run-up factors \(\left(\frac{H}{{h}_{0}}\right)\)

In this study, we calculated run-up factors for 7, 15, and 20 main debris-flow surges during the 2018, 2019, and 2020 debris-flow events, as well as for the sediment-laden precursory surges of the 2018, 2019, and 2020 events.

In Figs. 5 and 6, we compare the run-up factors, as observed in this study, with those predicted by theoretical models (Eqs. 2–5), based on the associated Froude range. In addition, we display run-up factors from experiments conducted by Armanini et al. (2020), Rickenmann et al. (2019), and Song et al. (2021) (inlets in Figs. 5 and 6). Armanini et al. (2020) investigated the impact behavior and run-up of pure water (W1) and water sediment mixtures (M1). Rickenmann et al. (2019) applied three different water–sediment mixtures (M2_1/M2_2/M2_3) to mimic debris-flow material, with M2_1 the muddiest mixture and M2_3 the most granular mixture. For this study, we combine the datasets to M2. The run-up dataset from Song et al. (2021), denoted with M3, is based on mono-sized glass beads dispersed in a Newtonian fluid (glycerol-water-mixture). All three studies cover a wide Froude range up from 0.1 to 8.62. However, only the study of Song et al. (2021) showed some data in the Froude range below 1.

Fig. 5
figure 5

Observed run-up factors of the three debris-flow events 2018/2019/2020 as well as predicted run-up factors from theoretical energy conservation models (Eqs. 2 and 3a) for the associated Froude ranges. The inlet displays the same data together with the experimental results as given by Armanini et al. (2020), Rickenmann et al. (2019), and Song et al. (2021) for an extended Froude range

Full size image
Fig. 6
figure 6

Observed run-up factors of the three debris-flow events 2018/2019/2020 as well as predicted run-up factors from theoretical mass and momentum conservation models (Eqs. 4a and 5) for the associated Froude ranges. The inlet displays the same data together with the experimental results as given by Armanini et al. (2020), Rickenmann et al. (2019), and Song et al. (2021) for an extended Froude range

Full size image

Figure 5 shows observed run-up factors and those proposed from the literature with predicted run-up factors for the respective Froude ranges, based on energy conservation (Eqs. 2 and 3a).

From Fig. 5, it is notable that the simple mass point model, based on energy conservation (Eq. 2), predicts quite well the observed run-up factors in the lower Froude regime (\(Fr\) < 1.5). The run-up factors given from the literature can also be mapped with the modified mass point model (Eq. 3a) accounting for different stress anisotropies at impact (\(0.7\le {k}_{1}\le 2\)). Only the proposed run-up factors of Song et al. (2021) show generally higher run-up factors compared to all other presented run-up factors at higher Froude ranges (Fig. 5 inlet).

Figure 6 compares the observed run-up factors and the run-up factors suggested from the literature with the predicted run-up factors for the respective Froude ranges, based on mass and moment conservation (Eqs. 4a and 5a).

In Fig. 6, the applied theoretical model based on mass and momentum conservation (Eq. 4a) overestimates the observed run-up factors even when different anisotropic stress conditions at impact are considered (\(0.7\le {k}_{1}\le 2\)). However, the smooth momentum flux model (Eq. 5a) based on the constant discharge principle achieves a better approximation.

To assess the performance of the applied theoretical models (Eqs. 2–5a) regarding the observed run-up factors, we estimated the root-mean-squared-error (RMSE), given by:

$$RMSE= \sqrt{\sum\limits_{i=1}^{n}\frac{{\left({\widehat{y}}_{i}-{y}_{i}\right)}^{2}}{n}}$$
(6)

In Eq. 6, \({\widehat{y}}_{{\text{i}}}\) and \({y}_{{\text{i}}}\) refer to the predicted and observed run-up factors, respectively. The number of all observations is given by \(n\). Table 4 lists the RMSE results of the different applied model approaches, once by using the dataset of main debris-flow surges only, and once by accounting also for the sediment-laden precursory surges.

Table 4 Performance of theoretical run-up models, given by root-mean-squared-error (RMSE), when predicting observed run-up factors of both the main debris-flow surges only and the main debris-flow surges together with sediment-laden precursory surges. The results are ranked according to the RMSE values of the main debris-flow surges
Full size table

The results in Table 4 generally show that the predicted run-up factors are diverging from the observed run-up factors when sediment-laden precursory surges are considered. For RMSE values greater than one, it can be assumed that the prediction model cannot reproduce the observed data at all.

In principle, the extended point mass model (Eq. 3a), based on energy conservation and accounting for \({k}_{1}=1.3\) and with precursory surge \({k}_{1}=1.1\), reproduces the observed data best; it seems that a general consideration of anisotropic stress conditions improves its performance. This is different with the momentum jump model (Eq. 4a), where a reduce in performance is achieved if \({k}_{1}<1\) is considered. The reduced smooth momentum flux model (Eq. 5a), however, shows a medium performance compared to both the point mass as well as momentum jump models with \({k}_{1}=0.7\).

Discussion

All observed events showed two different surges that have transitions in flow composition. It is only after a precursory sediment-laden and fluid dominated surge when a sequence of mainly granular debris-flow surges occurred. While most of the main debris-flow surges were observed at Froude values below 2, the sediment-laden precursory surges exceeded Froude values of 2. The two surges appear to differ significantly in their rheological characterization.

In the sediment-laden precursory surges, the liquid phase appears to be the dominant component, recognizable from the higher mobility and the tendency to splash. Here, it can be assumed that bulk flow resistance is controlled by viscos forces acting between the liquid phase of the debris flow and the suspended particles. It is therefore obvious that in the event of an abrupt change in momentum due to impact, the resulting run-up height cannot solely be explained by mechanical energy conservation, but rather by the approach of mass and momentum conservation with the description of a reflecting wave or a vertical jet (c.f. Fig. 2 center). Because of the limited data on sediment-laden precursory surges, it is not possible to discuss the performance of the different run-up prediction models used in this study. However, the associated run-up heights or, as proposed in this study, the normalized run-up factors are in a good agreement with the run-up factors found in literature.

For the main debris-flow surges, either frictional, collisional, or rather viscous-induced bulk flow resistances can be assumed—depending on the rheological characterization. A precise distinction which mechanisms of bulk resistance are predominant for the considered debris flow can be determined with dimensionless numbers, in particular Savage and Bagnold numbers (Iverson 1997; Sanvitale and Bowman 2017). However, this requires detailed flow parameters for which to this end, the collection is not yet realizable. Run-up estimations for debris flows with mainly viscos behavior might, in principle, be best approximated by models based on mass and momentum concepts. Frictional or collisional induced resistance to flow causes a higher influence of particles in the moving mixture, which is why these conditions are often attributed to granular debris flows at lower Froude numbers. In this case, the sudden change in momentum on impact and the resulting run-up height is rather gradual. Thus, models based on energy conservation or considering boundary conditions such as basal friction might result in better run-up predictions.

The comparison of observed run-up from main debris-flow surges with prediction models based on energy conservation seems to be plausible, especially in the low Froude ranges (Fr < 3). This confirms the assumption of Faug (2021) and is consistent with the experimental results of Scheidl et al. (2023), according to which granular debris flows in low Froude areas show low energy dissipation due to a smooth, gradual run-up. Further, the consideration of the stress anisotropy with \(0.7\le {k}_{1}\le 2\) in energy conservation-based prediction models (Eq. 3a) envelops the scattering of the observed run-up factors as well as the run-up factors given from the literature with increasing Froude number.

The prediction model based on mass and momentum conservation (Eq. 4a) rather overestimates the observed run-up factors of the main granular surges at lower Froude ranges and underestimates the values quoted from the literature at higher Froude ranges. Here, a better prediction performance of the observed run-up factors seems to be achieved under the assumption of anisotropic stress conditions \({k}_{1}>1\).

The reduced smooth momentum flux model (Eq. 5) significantly underestimates the observed run-up heights from the main debris flow. However, as shown by Rickenmann et al. (2019) and extended in this study with run-up data from literature, the smooth momentum flux model appears to provide the conservative estimate of run-up heights (upper bound of theoretical models) for values of \(Fr\) larger than about 2.

According to Fig. 5 and Table 4, a best-fit of the observed run-up factors is given by the extended point mass model (Eq. 3a) considering \({k}_{1}=1.3\) for debris flows and with precursory surges \({k}_{1}=1.1\). This indicates a compaction of the mass (induced increased bulk resistance), which leads to lower run-up measurements at similar Froude numbers. However, it should be noted that the monitoring structure is passable and wide enough to cause a lateral deflection of part of the flow; thus, the increased kinetic energy due to the dilatant behavior is not immediately verifiable. Another reason for the measured higher run-ups could thus be the fact that the granular front of the main debris flow deposits coarse material in front of the barrier, causing the following waves to “ramp up.” Rickenmann et al. (2019) argue that especially at low Froude numbers, such a static deposition in front of the obstacle diverts part of the incoming flow momentum upwards and prevents the formation of a fully developed reflecting wave as assumed for the momentum jump model. This might also be the reason why, in general, predictions based on mass and momentum conservation do not cover the observed run-up heights well.

Conclusion

In this study, the run-up heights at a vertical obstacle due to subsequent surges of three debris-flow events were determined. The highest run-up factors, i.e., run-up heights normalized to flow heights, were observed by sediment-laden precursory surges with Froude values greater than 2. However, all subsequent debris-flow surges showed a pronounced granular behavior and occurred mostly in Froude ranges below 2.

The results also show that a prediction model based on energy conservation can best reproduce the observed run-up factors. This suggests that debris flows in low Froude ranges can be expected to convert kinetic energy to potential energy at the maximum run-up height, resulting in a smooth gradual run-up. However, this smooth gradual run-up may also be enhanced by preceding debris deposition and the formation of ramps, which may also prevent the formation of a reflection or shock wave as assumed in models based on conservation of mass and momentum. These models have mainly overestimated the run-up factors of the observed natural debris flows. The reduced smooth momentum flux model, which accounts for run-up at a vertical wall, is a direct function of the Froude number and reflects a conservative estimate of run-up heights for debris flows at \(Fr>2\).