Highly energetic rockfalls: back analysis of the 2015 event from the Mel de la Niva, Switzerland

Abstract

Process-based rockfall simulation models attempt to better emulate rockfall dynamics to different degrees. As no model is perfect, their development is often accompanied and validated by the valuable collection of rockfall databases covering a range of site geometries, rock masses, velocities, and related energies that the models are designed for. Additionally, such rockfall data can serve as a base for assessing the model’s sensitivity to different parameters, evaluating their predictability and helping calibrate the model’s parameters from back calculation and analyses. As the involved rock volumes/masses increase, the complexity of conducting field-test experiments to build up rockfall databases increases to a point where such experiments become impracticable. To the author’s knowledge, none have reconstructed rockfall data in 3D from real events involving block fragments of approximately 500 metric tons. A back analysis of the 2015 Mel de la Niva rockfall event is performed in this paper, contributing to a novel documentation in terms of kinetic energy values, bounce heights, velocities, and 3D lateral deviations of these rare events involving block fragments of approximately 200 m³. Rockfall simulations are then performed on a “per-impact” basis to illustrate how the reconstructed data from the site can be used to validate results from simulation models.

Introduction

Rockfall runout distances depend on many factors, such as the geometry of the terrain and the rock’s perceived surface roughness of the encountered materials (Noël et al. 2021; Bourrier et al. 2012; Jones et al. 2000; Pfeiffer and Bowen 1989; Pfeiffer and Higgins 1990). The resulting reach angles from the horizontal and vertical traveled distances of the rock can thus vary greatly from site to site (Labiouse 2004; Volkwein et al. 2011). It is therefore important to use low or calibrated site-specific reach angle values to maintain a safety margin when predicting rockfall runout distances for regional preliminary susceptibility zoning using geometrical models such as Flow-R (Horton et al. 2013), CONEFALL (Jaboyedoff and Labiouse 2011), or QPROTO (Castelli et al. 2021; Scavia et al. 2020).

For detailed susceptibility zoning, hazard zoning, risk assessments, and mitigation designs, it is common and sometimes mandatory to complete the analysis with process-based models like CRSP (Pfeiffer and Bowen 1989; Jones et al. 2000; Andrew et al. 2012), RocFall (Stevens 1998; Rocscience Inc. 2022), RockFall Analyst (Lan et al. 2007), STONE (Guzzetti et al. 2002), HY-STONE (Agliardi and Crosta 2003; Crosta and Agliardi 2004; Frattini et al. 2008; EG4 Risk 2022), Rockyfor3D (Dorren 2008, 2015; EcorisQ 2022), RAMMS::ROCKFALL (Christen et al. 2012; Leine et al. 2014; Bartelt et al. 2016; Caviezel et al. 2019), RockGIS (Matas et al. 2017, 2020), Pierre3D (Gischig et al. 2015), or RocPro3D (Cottaz et al. 2010). These models attempt to better emulate the rockfall dynamics to different degrees. As no model is perfect, their development has often been accompanied and validated with the valuable collection of rockfall databases covering the range of site geometries, rock masses, velocities, and related energies that the models were designed for. Additionally, such rockfall data can also serve as a base for assessing a model’s sensitivity to different parameters, evaluating their predictability and helping calibrate model’s parameters from back calculations and analyses.

The process-based rebound model from Pfeiffer and Bowen (1989) has been calibrated with empirical data from 4 different sites with heights ranging from 20 to 100 m, with average slopes from 30 to 45° and from approximately 200 rocks with diameters from 0.3 to 1.5 m (Jones et al. 2000). After performing rockfall experiments and sensitivity analyses, they noted that the slope profile geometry and perceived surface roughness at impact are the main elements controlling the runouts of their model (Jones et al. 2000; Pfeiffer and Higgins 1990). These geometric controlling factors can be objectively considered from detailed terrain models, as shown in Noël et al. (2021). The Pfeiffer and Bowen (1989) model, used with slight adjustments in CRSP 4 (Jones et al. 2000) and in RocFall 8 (Rocscience Inc 2022) and from which Rockyfor3D 5.2 (Dorren 2015) is derived, should be valid for simulating rockfalls for sites and rocks sharing features in the same range as the tested sites. However, the observed differences between CRSP 4 and RocFall 8 (Noël et al. 2021) remind us of the importance of independently calibrating the parameters for each software program using back analysis from events on sites sharing the same features (Volkwein et al. 2011; Labiouse 2004).

Rockyfor3D’s rebound model (Dorren 2008, 2015) has additionally been calibrated from rockfall experiments on one site with two similar parallel slopes, both 38° on average and 186 and 138 m tall, with the second being forested (Dorren et al. 2005; Dorren and Berger 2006). The 202 rocks used out of 218 have a mean diameter of 0.95 m and volumes that range from 0.1 to 1.5 m³ with an average of 0.49 m³. The average reconstructed velocities are approximately 10 m·s^–1, with a maximum of 30.6 m·s^–1 and a maximum translational kinetic energy of approximately 1000 kJ. To transform the 2D parabolas to 3D, the simulation model applies probabilistic lateral deviations around the vertical axis function of the incident velocity and on the aspect direction of the terrain or on the impact position of a tree stem based on these rockfall data.

The RAMMS::ROCKFALL model (Christen et al. 2012; Leine et al. 2014; Bartelt et al. 2016) is based on rockfall experiments covering a similar range of energies and volumes (Caviezel et al. 2019, 2020, 2021; Sanchez and Caviezel 2020). Their database can be distinguished from many others by the precise acquisition of the accelerations experienced by the rock bodies during impact thanks to inboard accelerometers and gyroscopes installed in the experimental rocks (Caviezel and Gerber 2018; Volkwein and Klette 2014). This should allow a better understanding of the dynamics of the different motion phases of rockfall.

If the rockfall physics is relatively well captured, the process-based rebound models should behave predictably and independent of the site’s conditions and produce results that are closer to reality. However, because of the limited available empirical rockfall data to which the simulation software and models can be compared, one can mostly hypothesize here. This highlights the need for open and shared data to properly assess a model’s predictability, evaluate its sensitivity, and adjust its parameters on a per-site basis using back analysis. This is especially true if models are used beyond the range of empirical data used for their development or if they simply lack calibration and validation, as highlighted by Valagussa et al. (2015). Such shared data could also be used for the development of more objective rockfall simulation methods that are less dependent on time-consuming back analyses.

Similar to the rockfall experiments previously mentioned for the development of simulation models, many rockfall experiments were performed in a similar range of volumes (mostly between 0.03 and 2 m³ and up to 10 m³) to better understand the effectiveness of ditches, trees, and barrier designs (Table 10–1 of Turner and Schuster 2012). As the involved rock volumes/masses increase, the complexity of conducting field-test experiments increases to a point where such experiments become impracticable. Some have thus also documented to a certain extent natural events involving larger volumes and estimated the involved energies and bounce heights analytically from back analyses and calculations (e.g.,Evans and Hungr 1993; Domaas 1995; Paronuzzi 2009; Wyllie 2014a; Wei et al. 2014; Gerber 2019). However, to the author’s knowledge, none have reconstructed rockfall data in 3D from real events involving block fragments of approximately 500 metric tons.

In this paper, the flexible computer-assisted videogrammetry trajectory reconstruction method (CAVR) described in Noël et al. (2022a) is used to reconstruct the trajectories of the 2015 Mel de la Niva rockfall event in 3D, contributing to a novel documentation in terms of kinetic energy values, bounce heights, velocities, and 3D lateral deviations of such rare events involving block fragments of approximately 200 m³. The video footage of the event captured by the officials from the canton of Valais and the BEG SA Geological Office is first described, followed by the rock block fragment characteristics and 3D terrain model used as inputs for the CAVR method. Observations related to the elongated impact marks visible on the 3D terrain model are then described, followed by those related to the reconstructed 3D trajectories and the block fragment behavior. Finally, rockfall simulations are performed to illustrate how the reconstructed data from the site can be used to validate results from simulation models on a “per-impact” basis.

The 2015 Mel de la Niva rock fall event

Mel de la Niva (Figs. 1 and 2) is a mountain located in Val d’Hérens in Switzerland. Its summit, rising 2756 m above sea level, is part of the Tsaté nappe and is locally composed of gray carbonate–silicate schist with veins of white quartz. Its northeast facing cliff near the summit is known to be an active source of rockfalls, with some events even reaching the La Borgne River at the bottom of the valley near the village of Evolène (Steck et al. 2001).

Fig. 1

Photo of the Mel de la Niva Mountain taken immediately after the 2015 rockfall event from a helicopter when flying back from a witnessing position near the summit. Note the brown projections draped on the ground after each impact mark and the curvature of the paths (photo courtesy of the Valais Canton)

Fig. 2

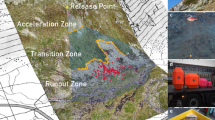
Isometric 3D view of the site and 2D vertical profile showing the projected positions and elevations of the two main rock block fragments from the 2015 rockfall event and the one from the 2013 event. The reach angles of the block fragments measured in line of sight with their source cliff are also shown on the 2D profile

In August 2013, hundreds of cubic meters of rock collapsed from the source cliff, generating a block fragment that propagated downslope and stopped in a gully at approximately 200 m from a mountain cabin after traveling a horizontal distance of approximately 1500 m and a difference of elevation of approximately 1000 m (Fig. 2). The roads, transport, and waterways service of the canton of Valais then undertook to monitor the stability of a portion of the cliff in collaboration with the BEG SA Geological Office. In mid-October 2015, during week 42, significant movements were recorded on the installed extensometers leading to the evacuation of the hamlet of Arbey and the closure of an access road. A few days later, on October 19, a section of the cliff collapsed (Fig. 3), generating several rockfalls (Fournier 2015). Two large block fragments traveled more than a kilometer downslope (~ 1.0 km for block 1, and ~ 2.0 km for block 2, Fig. 2). The total volume of the event combined with smaller failures that occurred after the 2013 event was evaluated to be approximately 8000 m³ from a comparison of 3D terrain models done by the BEG SA.

Fig. 3

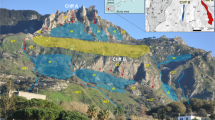
Part of the Mel de la Niva cliff that collapsed in 2015 shown on a picture taken a few minutes before the event in (a) and on a coarse 3D textured meshed model on the other windows in (b) and (c). This simple 3D model for quick measurements and visualization purposes is made by structure from motion photogrammetry (SfM) with the software Agisoft Metashape Professional (Agisoft LLC 2018) from a selection of ten pictures acquired with a DJI Phantom 4 Pro drone in September 2019 (8721 tie points, 39,570 projections, ground resolution of 8.79 cm/pix, 0.40 m of Z error, and 1.17 m of XY error)

Video footage

This event was captured from near the summit and the opposite side of the valley by officials from the canton of Valais and the BEG SA who were on site. Beautiful footage of the failure with a wide field of view (FOV) of approximately 80° was acquired at 29.97 fps and a resolution of 1080 × 608p based on the metadata of the shared edited video file. It shows a clear toppling behavior of the rock mass (Fig. 4).

Fig. 4

Selected frames seconds apart of the video footage captured near the source cliff showing the toppling failure of the 2015 rockfall event. The cropped part of the video has a field of view (FOV) of approximately 65°

The propagation of block 2 was then captured from the same point of view with the same camera, wide FOV, and applied edits (presumably to rotate the video file originally captured vertically). From the other side of the valley (WGS 84: 46.11118, 7.50853), the propagation of the two main block fragments was captured with a Canon IXUS 140/PowerShot ELPH 130 IS camera at 25 fps, HD resolution (1280 × 720p), and a FOV of approximately 18° (it changed during the capture with the optical zoom). This point of view, two to three kilometers away from the propagating block fragments, is excellent for tracking them once they leave the dust cloud caused by the event. Its 25-fps original footage was then used as the time reference for reconstructing the trajectories once stabilized and cropped to an approximate FOV of 10° (Fig. 5). The edited footage, with a wide FOV from the other point of view, was added for block 2 and synced to 25 fps.

Fig. 5

Stacked frames every second showing the position of the propagating block fragments on the video footage captured from the other side of the valley two to three kilometers away. The cropped portion of the HD footage has a field of view (FOV) of approximately 10°

Even though the quality of the footage is not optimal for reconstructing trajectories due to the relatively wide FOV used, it is sufficient for timing the impacts due to the visible projections that follow them one or two frames later. It is also sufficient for estimating the average angular velocity per cluster of successive impacts by counting the number of block rotations for the corresponding period. The video footage is then sufficient for identifying which impact is involved at a given time relative to the surrounding terrain features to apply the CAVR trajectory reconstruction method described in Noël et al. (2022a). The impact position is refined from the visible impact marks on a 3D detailed terrain model, as later described.

Rock block geometries

To obtain the geometric characteristics of the rock block fragments, their 3D geometry was acquired by structure from motion photogrammetry (SfM) with Metashape Professional (Agisoft LLC 2018) (from approximately 40 photos per block fragment acquired with a DJI Phantom 4 Pro drone, a ground resolution approximately 0.4 to 2 cm/pix, 50,000 to 500,000 Tie points and 113,000 to 1 700,000 projections, a Z error of approximately 0.5 to 0.7 m, and an XY error of 0.5 to 1.3 m) and with a handheld mobile terrestrial LiDAR scanner (TLS) (GeoSLAM Zeb Revo). The 3D SfM models were scaled based on the mobile TLS acquisitions. Since the shape of the block fragments for that site seems strongly controlled by the schistosity, the hidden base of the block fragments was reconstituted by interpolation while ensuring that it would be parallel to the largest visible face. The block fragments have a volumetric density of 2626 kg·m^–3 based on weighted samples. By assuming a homogeneous mass distribution of the filled 3D models from the obtained volumetric density, the principal axes and moment of inertia (I₁, I₂, and I₃) and mass centers were identified with MeshLab (Cignoni et al. 2008). The 3D models were then aligned so that their principal axes correspond to the x-y-z references of the 3D working environment. The d₁-d₂-d₃ block dimensions were then simply obtained from the block fragment bounding boxes aligned on the principal axes of inertia while ensuring that the 3D models were not affected by artifacts. The geometric characteristics of the block fragments are summarized in Table 1.

Table 1 Table summarizing the geometric characteristics of the blocks

Block 1 is very flat and slightly elongated, while block 2 is moderately flat and slightly elongated (Fig. 6). Their volumes, masses, and principal moment of inertia fall close to those estimated from ellipsoids constructed from the d₁, d₂, and d₃ diameters along the principal axes of inertia (Fig. 7). Since the 3D acquisitions, processing, and reconstruction of the occluded faces are time-consuming, practitioners could quickly estimate such characteristics from ellipsoids with the d₁, d₂, and d₃ diameters measured in the field when encountering similar deposited block fragments. However, estimating these characteristics from rectangular prisms for such block fragments should be avoided. Indeed, this would overestimate their masses and principal moments of inertia by almost doubling and quadrupling them, respectively (Fig. 7). However, such overestimation safely leads to conservative simulation results that at least double the expected energy/intensity for land use zoning, risk assessments, and the design of mitigation measures.

Fig. 6

Shapes of block fragments 1 and 2 in the Sneed and Folk (1958) diagram using the terminology from Blott and Pye (2007). For the shape context, the four largest artificial reinforced concrete rocks used by the WSL Institute for Snow and Avalanche Research SLF featured in Noël et al. (2022a) and the 31 natural rocks used at the Riou Bourdoux site featured in Hibert et al. (in review) are shown in turquoise and dark yellow respectively. Additionally, the six rocks from the rockfall experiment performed at the Tschamut site in 2014 (Volkwein et al. 2018; Volkwein and Gerber 2018) and the seven largest block fragments from the 2019 event at La Verda, Rougemont, for which their site is featured in Noël et al. (2021) are shown in blue and purple respectively

Fig. 7

Comparison of the block fragment masses and principal moments of inertia (I) obtained from the 3D models with those that one would obtain by estimating them from simplified block shapes in the form of ellipsoids and rectangular prisms

Digital terrain model

A detailed 3D terrain model composed of 104 M dense points was then generated by SfM (Agisoft LLC 2018) at high quality settings, unlimited key and tie point limits, and no depth filtering from 123 photos. The photos were acquired on September 17, 2019, with a DJI Phantom 4 Pro. With 1.5 million identified tie points and 5 million projections, the reprojection error is 4 cm on average on the ground, the XY error is 3.8 m, and the Z error is 4.5 m. At least 9 photos overlap for all parts of the model covering the two trajectories of the rocks from the 2015 event.

The position and scale of the model were then refined (scaled by 98.9% and its angle with the horizontal plane adjusted by 0.6°) using the iterative closest point (ICP) algorithm to align its part without trees on the 2013 reference terrain model from the swissALTI^3D product by ^©swisstopo. The aligned detailed SfM terrain model has an average distance with its reference model of 0.02 m and a standard deviation (S.D.) of 0.60 m. Given the size of the involved rock block fragments and impact marks, this terrain model precision is sufficient for estimating the relative separating distances of the impacts to their neighbors required for the CAVR reconstruction method described in Noël et al. (2022a).

Three terrain samples of the 3D model were also reprocessed with the same settings but constrained to smaller bounding boxes. In this way, smaller terrain geometrical features are also processed by SfM to obtain the detailed surface roughness of the main terrain types affected by rockfalls: (1) the active scree slopes of colluvium accumulated mostly from rockfall events and partly remobilized by snow avalanches and debris flows; (2) the blocky meadows where the active processes are less energetic or less frequent, and fines can slightly accumulate and thin vegetation settle in; and (3) the grassy alpine montane meadow where the morainic gray fine sediments are present, partly covered here and there by rockfall block fragments, and reshaped in small terrasses by livestock grassing. The perceived surface roughness affecting the initial geometry of rockfall impacts prior to scarring for the three samples is described in Noël et al. (2021).

Even if the impact marks are almost four years old, they remain clearly visible when contrasted with their surrounding grassy terrains. On the scree slopes, however, they are less easy to distinguish from their surrounding rocky textured terrain. Artificial colors and shadings were then applied to complement the real RGB textures from the photos (Noël et al. 2022a). In this way, the impact marks are clearly visible even with similar surrounding RGB textures (Fig. 8).

Fig. 8

Two impact marks from block 1, numbered p8 and p9, visible on a photo taken in September 2019 in (a) and on the artificially colored 3D SfM terrain model in (b). A block fragment from a previous rockfall event that occurred before 1977 based on the oldest orthophoto covering the site lies next to impact mark p9

Mapped rockfall paths and block fragments

For definition, rockfall trajectories are composed of a series of vertical parabolas during the freefalling phases and come with back-calculated values such as bounce heights, velocities, and energies. They can be expressed in 2D vertical profiles or in 3D. Their mapped projections on the horizontal plane are called paths in this paper. Partial trajectories or paths that do not cover the whole traveled distance by the block fragments from their source to their deposited location are qualified as segments.

Since the video footage for the 2015 Mel de la Niva event is not detailed enough for selecting the impact locations with precision, it is important that the impact locations can be determined in a different way for the 3D trajectory reconstruction using the CAVR method (Noël et al. 2022a). For that purpose, the visible impact marks are of great help (Fig. 8). Indeed, the center of the impact marks can be used as the impact locations. Additionally, their elongated shapes tell us about the general travel direction of the rocks when they impact the ground, which helps locate the next and previous neighbor impact marks.

To the surprise of the authors, the aligned series of impact marks from the 2015 event were not alone: Many other impact marks from older events were also highlighted by the artificial shading and colors applied on the detailed 3D model, revealing the previous activity state of the site. The absence of video footage for such previous events means that their 3D trajectories cannot be reconstructed with their related velocities and other characteristics based on the CAVR method.

The 2D paths used by the block fragments from older events can, however, be estimated by linking their elongated respective impact marks. Including the 3D reconstructed trajectories from the 2015 event, a total of 13 path segments were mapped, with 12 associated block fragments found (the deposited location of the 2005 block fragment is unknown) (Fig. 9). Their paths were validated and completed from the available orthophotos of the SWISSIMAGE Journey through time dataset from ^©swisstopo (years: 1977, 1983, 1988, 1995, 1999, 2005, 2007, 2010, 2013, 2016, 2017). The years shown on the paths correspond to the years of the corresponding orthophotos when the paths appear or to the known events from 1980, 2013, and 2015. In the first case, the associated rockfall events could have occurred during the period separating their orthophotos and the preceding ones.

Fig. 9

Mapped path segments, deposited block fragments, their related sizes [d₁; d₂; d₃ (if measured)], and the close-up placements for the detailed views of the reconstructed trajectories of the 2015 event in Fig. 10. The paths whose rockfall event years are known are displayed in (a) with the years 1980, 2013, and 2015. The others have the years corresponding to the oldest orthophotos available from ^©swisstopo, where the paths are visible. The mapped deposited block fragments from the BEG SA Geological Office are shown with transparent red circles and triangles in (a) and (b). The hillshade and elevation contours are derived from the 2013 swissAlti^3D product from ^©swisstopo

Interestingly, the paths form a curved shaped fan where the block fragments seem to have deviated laterally to different degrees from the steepest downward slope gradient and were only very little or not channelized by the present gullies, as also observed by Wyllie (2014b) at other sites. For this site, a triangle drawn on the map in the horizontal plane including the source and the 12 associated blocks would have an angle at the source of 41.7° (lateral deviations inside ± 20.9°).

The d₁-d₂-d₃ dimensions of the block fragments were estimated from the 3D models. They are limited to d₁-d₂ when estimated from the orthophotos, assuming the blocks lie with their d₃ dimension vertical. It is interesting to note that the block fragment that almost reached the river (8.1-6.9 m) is similar in shape but smaller than blocks 1 and 2 from the 2015 event and close to the size of the 2013 block fragment (7.8-5.6-2.8 m, ~ 64 m³). Similarly, for the 1999 paths, smaller block fragments reached longer runouts than the 12.2-8.5-5.8 m large block. In that case, they could be fragments from the larger block that detached from it in the first 500–600 m from the source, given the similar path directions.

The 2015 reconstructed trajectories

With the position and time of the impact points estimated, the 3D trajectories could be reconstructed with the CAVR method (Noël et al. 2022a). The offset of the center of mass of the block fragments was applied using 100% of their respective d₁/2, since it was applied on the SfM terrain model with the impact marks, therefore without the need to move the block fragments further in the terrain model. This does not affect the reconstructed values relative to the incident and returned velocity components, such as the total apparent kinematic coefficient of restitution (${COR}_{v}$) and the total deviation angle (${\theta }_{dev}$) described in Noël et al. (2022a). One should, however, bear in mind that the angles relative to the terrain might be slightly influenced by the impact marks. This might thus affect the related normal and tangential components. The reconstructed trajectories and mapped deposited block fragments still completely fulfill the needs by showing the main paths used by rockfalls, their runouts, how the energies/velocities evolve along these paths, and how the block fragments deviate with their bounce heights and lateral propagation.

Impact marks

The mapped 2D paths from the projected 3D reconstructed trajectories at the center of mass of the block fragments are shown in Fig. 10 with the normal vectors to the terrain used to properly offset the parabola segments from the chosen center of the impacts simplified to single points as in Noël et al. (2022a). The normal vectors to the detailed terrain model, partly affected by the impact marks, are shown with white bars locally pointing in the direction of the steepest downslope gradient. They thus show the local aspect direction of the terrain in the vicinity and are usually perpendicular to the topographic contours. The impact points are accompanied with a pair of values under brackets as follows: p. number [${\Delta \theta }_{trend}$ ${\theta }_{N}$]. The first value, ${\Delta \theta }_{trend}$, corresponds to the angular difference in the horizontal plane between the trend direction of the incident parabola and the aspect/dip direction of the terrain, and ${\theta }_{N}$ corresponds to the block fragment lateral deviation around the normal vector that makes the returned velocity vector deviate from being coplanar with the incident velocity and the normal vectors, thus resisting the terrain orientation, as described in Noël et al. (2022a). The impact marks are shown in close-ups on the generated orthophoto from the SfM model and on the 3D terrain model with artificial colors and shading in supplementary materials with their associated estimated time from the video footages.

Fig. 10

Projected paths seen from above from the 3D reconstructed trajectories of blocks 1 and 2 of the 2015 rockfall event from the Mel de la Niva colored based on their translational velocities overlaid on the 3D terrain model with artificial colors and shading. The normal vectors to the terrain of lengths corresponding to the d₁ diameters of the block fragments are shown at each impact in white. The ${\Delta \theta }_{trend}$ and ${\theta }_{N}$ reconstructed angles as described in Noël et al. (2022a) are shown under brackets for each impact

Most impact marks left by block 1 are clearly visible on the video footage and on the 3D terrain model. Only the position of impact points p2 and p3 is slightly less precise due to the lack of impact marks. The surrounding distinct outcrop features, both visible in the video and on the 3D terrain model, permit a precise alignment of the video footage, where the timed impacts are visible and overlaid on the 3D model. There, the minimal local precision from the viewpoint, as conceptually shown in Noël et al. (2022a), with the semimajor axis of a conic section, is locally constrained by the gully’s width and by the directions deduced from the previous and following elongated impact marks, improving the precision of these two estimated positions from the video footage. Point p9 has the widest impact mark and corresponds to a drastic slope change from approximately 28° to 10°. The block fragment from an event visible on the 1977 orthophoto sits next to this impact mark (Fig. 8). A large dark cloud of projected material following that impact is visible in the video footage and occluded the impact point p10, whose time is thus roughly estimated.

For block 2, most impact points are visible from the impact marks imprinted on the terrain. The time of the impact points is estimated from the video footage captured from both locations until the block fragment enters the forest. Then, only the footage captured from the opposite side of the valley is used. The part where the block fragment crosses the forest is less precise, as some occluded impact marks might be missing between points p28 and p31. The deduced velocities for that segment might thus be marginally increased. Indeed, the slightly longer trajectory composed of two vaulted parabolas between p28, p29, and p31 compared to a shorter trajectory built with three or four flatter parabolas requires a marginally higher velocity to connect the bounding timed impact points p28 and p31. Additionally, the effect of the forest is neglected since its effect is marginal for such a large block (Jonsson 2007; Rickli et al. 2004; Collins et al. 2022).

Between some impact marks left by the two block fragments, there is an occasional relatively small scar left by a slight contact of the rotating block fragment when its next upcoming longest tip grazes the terrain surface. Such slight contact was ignored during the reconstruction process and was assumed to not have affected the falling directions and velocity significantly due to the small interaction with the ground.

There is a slight bulge visible on the lateral and bottom sides of some of the impact marks from the 2015 events. The dynamic aspect of the impacts might have played an important role, as a part of the bulge seems to be missing due to the dynamic projection of the bulging soil sheared during the sudden load of the impacting block fragment. Additionally, the width of these impact marks exceeds the shortest diameter of their related block fragments, even though they were falling with their rotation aligned around their d₃-axes like wheels. Indeed, for block 1, impacts p4, p5, and p9 have widths of 7.3, 7.9, and 9.3 m, respectively, while impacts p6, p7, and p8 are closer to d₃, with widths of approximately 4.8, 5.1, and 6.1 m, respectively. For block 2, impacts p1, p2, p5, p7, and p31, for example, have widths of approximately 9.9, 8.3, 7.6, 7.4, and 7.7 m, respectively. Additionally, there are slightly more bulges and/or projected soil on the lateral side facing downslope for impact marks with high ${\Delta \theta }_{trend}$. All this accelerated displaced soil mass under general shear failure might have “absorbed” some of the kinetic energy through momentum transfer while providing some lift to the blocks as an opposite reaction inducing some deviation.

Lateral deviations

Concerning the lateral deviations, it is interesting to note how the trajectory of block 1 gradually deviates from the steepest downslope gradient, crossing the topographic contours perpendicularly from p1 to p3, and then obliquely with an increasing ${\Delta \theta }_{trend}$. Most lateral deviations (${\theta }_{N}$) are positive, meaning that the block fragments deviate against the steepest downslope direction as defined in Noël et al. (2022a). The lateral deviations add up to a cumulative value that roughly corresponds to the local ${\Delta \theta }_{trend}$, unless the local slope aspect changes drastically. When looking downslope, these positive deviation values from p4 correspond to the curvature to the left side of the trajectory.

The same happens to block 2, but this time curving to its right when looking downslope. This is especially true for the first impacts up to p6 inclusively. Then, the aspect direction of the terrain increases from approximately NE to ENE and catches up with the trend of the trajectory that then does not deviate much up to approximately p27 inclusively. The ${\Delta \theta }_{trend}$ then increases along with the lateral deviation, and both are particularly high at p31. The lateral deviation is briefly inverted for p32, lowering the trend direction of the trajectory. Then, the lateral deviation induces a rise in the trend direction again, inducing a curvature to the right. This happens to the following impacts until the block fragment topples laterally to its right side in the same upslope direction as the lateral deviation. The curved path from the older events in Fig. 9 suggests similar behaviors.

Bounce heights and energies

The unfolded 2D vertical profiles of the reconstructed 3D trajectories with their related translational velocity and kinetic energy, bounce heights, total deviations (${\theta }_{dev}$), and local terrain slopes are shown in Fig. 11. The vertical terrain profiles along the reconstructed trajectories are extracted from the 2013 terrain model from ^©swisstopo. The bounce heights correspond to the vertical difference in heights between the 2013 terrain model and the center of the reconstructed trajectories. Due to slight differences between the SfM and 2013 terrain models and the amount of scarring at the impact marks, the bounce heights from the center of mass at each impact can be less than the radius of the block fragments. This is especially visible for impact point p9 of block 1, where the translational kinetic energy goes from 322 to 146 MJ with the trajectory being vertically deflected to a more horizontal path with a lower plunge. The remaining kinetic energy is “consumed” in the last 100 m, with the block fragment tipping on its lateral side in the last 25 m.

Fig. 11

2D vertical profiles of the unfolded 3D reconstructed trajectories shown in black with their related information of interest. The terrain profiles from the 2013 swissALTI^3D product by ^©swisstopo are drawn in gray without vertical exaggeration (to scale). The terrain slope along the profiles is shown with purple curves and crosses showing the impact-to-impact average slope (${\beta }_{s}$). The bounce heights in blue are expressed vertically to the terrain from the center of mass of the rock block fragments. The total deviations (${\theta }_{dev}$) correspond to the angle between the incident and returned velocity 3D vectors that are almost coplanar with vertical planes. Note the characteristic rockfall sawtooth velocity and energy profiles shown with the same colors as in Fig. 10 and in magenta, respectively

Additionally, it is interesting to note that this block fragment never leaves the ground by more than 4 m. Indeed, its maximal bouncing height of 9.4 m from its center minus its radius leaves the block surface close to the ground. This combined with the angular velocity of the block fragment gives the visual sense that it is constantly rolling in contact with the ground, while it is rather bouncing with a large rolling component, or in other words making “rolling bounces.” This is confirmed by the intact texture of the terrain left in between most impact marks (see the close-ups with orthophoto in supplementary material).

The same can be seen for block 2, even during the closely spaced rolling bounces from p8 to p25 at a horizontal distance of 764 to 1055 m. Since the bounce height for that segment does not exceed the longest radius of the block fragment, the block barely leaves the terrain during the freefalling transition with its longest and shortest axes parallel to the ground at each half rotation around its d₃-axis. During each of these closely spaced impacts, the block fragment has its tips along its longest axis in contact with the ground. The numerous small energy losses during this phase, where the trajectory undergoes little deviation, do not prevent an overall gain in kinetic energy from 259 MJ immediately after impact point p8 to 388 MJ immediately after p25.

Shortly after this phase of closely spaced rolling bounces, block 2 is freefalling from p25 to p26 while entering a gully just before crossing the forest. It reaches its maximal translational kinetic energy of 625 MJ at the bottom of the gully. It then loses 332 MJ in less than a second from 1133 to 1159 m, thus generating important contact forces through impact points p26, p27, and p28, while being vertically deflected out of the gully before pursuing its course through the forest. At the exit of the forest, the same process is repeated over approximately 1 s, with impact points p33 and p34 deflecting the block fragment vertically out of a gully again and lowering its kinetic energy from 426 to 126 MJ. The block fragment then gradually topples on its lateral side facing upslope and on the general convex side of the trajectory seen from above with the two subsequent last impacts over a 100 m horizontal distance. It then slides downslope over another 100 m back into the gully, where it finally stops.

Interestingly, the impact points with scars much wider than the shortest diameter of the block fragments mentioned in the previous section seem to correspond to impacts with high energy losses and strong vertical deviations. Indeed, for block 1, impacts p4, p5, and p9 with wide scars have translational kinetic energy losses of 136, 146, and 176 MJ, respectively, while narrower impacts p6, p7, and p8 have lower respective losses of 92, 81, and 84 MJ (Fig. 11). For block 2, the wide impacts p2, p5, p7, and p31 have high losses of 125, 177, 132, and 228 MJ, respectively (Fig. 11).

The relatively low reconstructed rebounds are in contrast with what is considered normal in Volkwein et al. (2011) (Fig. 12). Indeed, when the bounce height (f) is calculated from the center of mass relative to the related impact-to-impact line, distance (s), and slope (β_s), as in Volkwein et al. (2011), Glover (2015), and Gerber (2019), a ratio of f/s near 1/8 is considered normal (Volkwein et al. 2011). In contrast, the f/s ratios for block 1 are 1/20 on average (S.D. of 0.15) corresponding to parabolas with very slightly curved vaults. The f/s ratios for block 2 are 1/39 on average (S.D. of 0.04). However, the f/s ratio of 1/8 has the safe advantage of containing all values from the Mel de la Niva 2015 event and 81.6% of the 538 values from all sites shown in Fig. 12. The f/s ratio of 1/6 contains 95.5% of the reconstructed values from all sites. Those ratios from Volkwein et al. (2011) are thus good for quickly estimating heights for the design of mitigation measures such as flexible barriers and embankments from back calculations when suitable given the involved energies.

Fig. 12

Bounce heights (f) as in Volkwein et al. (2011), Glover (2015), and Gerber (2019) as a function of the impact-to-impact distance (s). The reconstructed values from the Riou Bourdoux test site (Hibert et al. in review) and the SLF Chant Sura test site (Noël et al. 2022a) are shown in dark yellow and turquoise, respectively, in Fig. 6. The size of the markers is a function of their incident translational velocities

Angular velocities

The average angular velocity (ω) based on the number of block rotations counted over a given number of video frames is 5.6 rad s^–1 around the d₃-axis for block 1 from p1 to p2. As shown with the red points slightly above the 1:1 line in Fig. 13a, this is 1.2 times the angular velocity that one would predict from the returned tangent translational velocity (v_T2) at p1 divided by d₁/2 (e.g., if predicted with the simulation rebound model from Pfeiffer and Bowen (1989)). The same is true for the two next parabolas from p2 to p3 and p4, with ω values of 6.5 and 6.9 rad s^–1, respectively. The two next parabolas, from p4 to p5 to p6, have ω values of 6.1 and 5.9 rad s^–1, which is 1.1 times what one would obtain from the returned v_T2/(d₁/2). The parabolas from p6 to p7 to p8 have ω values of 5.6 and 5.4 rad s^–1, respectively, slightly above what the returned v_T2/(d₁/2) would give, but by less than 1.1 times. For all those parabolas, the angular energy corresponds to 20% (S.D.: 2%) of the total incident energy just before impact (Fig. 13b) and to 26% (S.D.: 2%) of the total returned energy immediately after impact. This is slightly larger than the 9–19% ratios mentioned in Chau et al. (2002), Bourrier and Hungr (2013), and Lambert and Kister (2017), similar to the assumed ratio of 20% mentioned in Jonsson (2007) and under the maximal theoretical ratio of 29% mentioned in Gerber (2019) and Chau et al. (2002) (40% of the translational energy of a sphere).

Fig. 13

Returned angular velocity (ω₂) as a function of the returned tangential velocity (v_T2) in (a). Incident angular energy (E_ω1) as a function of the total incident kinetic energy (E₁) in (b). The reconstructed values from the Riou Bourdoux test site (Hibert et al. in review) and the SLF Chant Sura test site (Noël et al. 2022a) are shown in dark yellow and turquoise, respectively. The size of the markers is a function of their incident translational velocities

For block 2, the angular velocities around the d₃-axis are averaged over multiple parabolas due to its closely spaced rolling bounces. The values for block 2 are thus omitted in the Fig. 13. The average ω is 4.1 rad s^–1 from p3 to p5, 4.8 rad s^–1 from p5 to p8, 5.5 rad s^–1 from p8 to p18, and 6.1 rad s^–1 from p18 to p26. This increase in angular velocity corresponds with the general increase in translational velocity from p3 to p26 (Fig. 11).

Velocity changes and slope geometry

The velocity of block 1 is rather constant up to impact point p9 despite a variating slope between 20° and 35° (Fig. 11). The largest velocity drops and deviations at impacts seem to happen after long parabolic freefalling phases or following changes in the slope angle of the terrain along the profile that force the trajectory to be deflected to a less steep path, such as for impacts p4, p5, and p9. Looking closer, the velocity and deviation gradually increase from p1 to p4, with a slope generally approximately 35°, and stabilize from p4 to p5, with an average slope of 28°. From approximately 25 m before p5 to 10 m after, the slope rapidly decreases from 27° to 17° and then gradually increases with the three following impacts. The velocity follows a similar pattern for the related impacts, with one of the largest velocity drops at p5, followed by rather moderate drops for the following three impacts. The velocity also gradually decreases during that segment, from p5 to p7 with average slopes of approximately 21°, and then gradually increases with average slopes of approximately 27° until reaching impact p9, where the slope rapidly decreases under 10°. This sharp change in slope is accompanied by a strong velocity drop and deviation. The average slope from p9 to p12 is low, with respective values of 5° and 11°, and the gains from potential energy during the freefalling phases are low and do not compensate for the losses during impact.

For block 2, the velocity gradually increases until impact p25 despite a gradually decreasing slope from approximately 35° to 25°. It is then disturbed by many slope variations inducing important velocity increases during freefalling phases and sharp velocity drops at impacts with important deviations from p25 to p28, p31 to p32, and p33 to p34. Again, the largest velocity drops and deviations at impacts seem to happen after long freefalling phases that steepen the plunge of the trajectory or following changes in the slope angle of the terrain at impact that force the trajectory to be deflected to a gentler plunge. This is especially visible where the impacted slope angle is lower than the average preceding slope and when looking at the cumulative deviation and velocity drop of closely spaced impacts such as p26-p27-p28 and p33-p34.

Looking closer at the trajectory until it crosses the forest, the velocity gradually increases from p1 to p5 despite the relatively high velocity drops and deviations at impacts, helped by the high average slope of approximately 35°. It then slightly decreases from p5 to p8 with high velocity drops and deviations at impact and a decreasing slope from approximately 35° to 27°, always lower by a few degrees at the impact than the preceding average slope. With slight fluctuations, the velocity keeps gradually increasing during the phase of closely spaced rolling bounces with an almost strait trajectory segment and low deviations, even with the slope decreasing from 27° to approximately 25° and the numerous closely spaced impacts. This shows how efficient this phase is at preserving the kinetic energy when undisturbed by topographic changes and suggests that reach or shadow angles of approximately 25° could be attained under perfect conditions for those block fragments and terrain types. This is lower than the 27.5° shadow angle threshold for practical use suggested by Evans and Hungr (1993) but is in line with their few exceptions of 23°, 24°, and 25° mentioned for smooth terrain/substrate surfaces.

Apparent coefficient of restitution components

With the previously observed velocity changes related to the slope geometry and induced deviations, it could be interesting to further explore those changes in terms of ratios of returned velocities over the incident ones and their associated incident angles (${\theta }_{1}$). These ratios are usually called the apparent kinematic coefficient of restitution ($COR$) and are commonly analyzed in terms of ratios of the normal velocity components (${COR}_{N}$) and ratios of the tangential velocity components (${COR}_{T}$).

The ${COR}_{N}$ as a function of their ${\theta }_{1}$ are shown in Fig. 14a. All reconstructed values from the Mel de la Niva site fall under the correlation suggested by Wyllie (2014b). Most reconstructed values from the three sites combined also fall under the suggested correlation, which seems to correspond to a limit beyond which few values are observed. It is interesting to note that many values were reconstructed with more returned normal velocities than their incident normal velocities, as shown by the ${COR}_{N}$ values above one for incident angles below 20°. This was also observed by numerous authors and summarized in Ferrari et al. (2013) and Asteriou (2019). Among them, Paronuzzi (2009), Asteriou et al. (2012), Spadari et al. (2013), and Wyllie (2014b) observed ${COR}_{N}$ values above one for similar incident angles below 25°, 26°, 23°, and 25°, respectively.

Fig. 14

Apparent normal coefficient of restitution (COR_N) as a function of the incident angle (${\theta }_{1}$) in (a). Apparent tangential coefficient of restitution (COR_T) as a function of the incident angle (${\theta }_{1}$) in (b). The reconstructed values from the Riou Bourdoux test site (Hibert et al. in review) and the SLF Chant Sura test site (Noël et al. 2022a) are shown in dark yellow and turquoise, respectively. The size of the markers is a function of their incident translational velocities

Because energy cannot be created, the normal gain must come from somewhere. Such ${COR}_{N}$ values beyond unity mean that there is a transfer from a partial redirection of the tangential velocity away from the terrain (Wyllie 2014b). Given the change in topography due to scarring (e.g., Paronuzzi 2009), a part of the translational velocity may be geometrically redirected away from the terrain for the rock to move out of the impact scar. This contributes to apparent gain in returned normal velocity and thus affects the COR_N. Such deviation induced by a local change in topography leaves impact marks behind and can work independently of the rock block’s elongation, as shown by the ${COR}_{N}$ values above one for the nonelongated blocks used by the WSL at the SLF Chant Sura test site (Noël et al. 2022a).

Additionally, the elongation of the rotating rock bodies may also contribute to such geometric redirection phenomena. Indeed, a forward offset contact point with the ground allows the center of mass of the rock to pivot around (Paronuzzi 2009), acting like the jumpers at pole vaulting that redirect their tangential velocity into a normal jumping component while pivoting around their pole contact point. For example, with a null incident angle before jump, the apparent normal coefficient of restitution of a pole jumper is equal to infinity due to the ratio from an initial incident normal velocity equal to zero.

Such combined geometric phenomena may be predominant at low incident angles in Fig. 14a due to the low incident normal velocity component. This can explain the observation of values above one without breaking the laws of physics. Obtaining COR_N values above one for a sufficient set of reconstructed values at a low incident angle should thus be normal and not the other way around, unless nonelongated rock bodies and rigid surfaces are involved. This may explain the contrast between values reconstructed from laboratory conditions involving small spheres on hard impacted slabs and those from field experiments closer to natural conditions (e.g., Chau et al. 2002; Asteriou et al. 2012; Asteriou and Tsiambaos 2018; Asteriou 2019).

A similar transfer from normal velocity toward tangential and angular velocities due to the asymmetry of elongated blocks could happen. For example, an impact with a high incident angle and a contact point with the ground offset behind the center of mass would allow the block to pivot toward a more tangential direction and higher angular velocity. For such geometric transfer to be predominant on ${COR}_{T}$, the incident tangential velocity component must be small, so the incident angle must be high. This is visible in the reconstructed data from Asteriou et al. (2012) for incident angles beyond 60°. Those impacts at high incident angles are, however, uncommon for the reconstructed data covered in Fig. 14. Therefore, no strong correlation emerges in Fig. 14b between the incident angle and the apparent tangential coefficient of restitution, as for Asteriou et al.’s (2012) values with ${\theta }_{1}$ below 60°.

No clear distinction emerges from the reconstructed values of the different sites (Fig. 14) despite the different materials involved, as discussed in Ferrari et al. (2016). The impacts for the Riou Bourdoux site (Hibert et al. in review) involving limestone rocks and mainly soft black marl terrain material cannot be clearly distinguished from the others. In contrast, the SLF Chant Sura test site (Caviezel et al. 2021; Noël et al. 2022a) also involves hard metagranitoid outcrops and blocky scree. Similarly, Wyllie (2014b) did not find a significant difference for his compiled reconstructed ${COR}_{T}$ between rock, talus, and colluvium materials and concluded that the ${COR}_{T}$ and ${COR}_{N}$ are generally independent of the slope material.

Without a clear geometric control on the ${COR}_{T}$, Wyllie (2014b) suggests that the returned tangential velocities are a function of Coulomb’s friction only acting during the reacting normal ground impulse. This should act conjointly on the angular velocities until no slipping or skidding occurs or until the end of the normal impulse (Wyllie 2014b). Correlations between the total deviations induced by the reacting ground impulse and the velocity changes should thus be expected.

Momentum transfer and deviations

Inducing a given deviation requires a variable impulse from the ground depending on the initial momentum of the block fragment. Therefore, it can be interesting to look at the velocity changes in terms of the ratio of translational momentum returned after the impact over the initial one, which happens to be the same as the total apparent kinematic coefficient of restitution (${COR}_{v}$) given by the ratio of total returned velocity over the incident velocity. The two variables are thus plotted in relation to the other in Fig. 15, with some corresponding numbers of the impact points of block 1 shown. As foreseen from the velocity changes, the lowest ${COR}_{v}$ values seem to correspond to the highest deviations. However, this does not correspond all the time to high velocity or energy drops (Fig. 11) and wide related impact marks. Indeed, a low ${COR}_{v}$ ratio can still be obtained with low returned translational velocity (or momentum) over low incident velocity (or momentum), such as for impact point p10 from block 1.

Fig. 15

Total apparent kinematic coefficient of restitution (${COR}_{v}$) put in relation to the total deviation induced by the impacts with the ground. Some of the impact numbers are shown for block 1. The coefficient of correlation R² from the linear and custom fits are based on the data from the Mel de la Niva site only. The reconstructed values from the Riou Bourdoux test site (Hibert et al. in review) and the SLF Chant Sura test site (Noël et al. 2022a) are shown in dark yellow and turquoise, respectively. The size of the markers is a function of their incident translational velocities

The ${COR}_{v}$ from approximately 0.65 to 1.00 and ${\theta }_{dev}$ from approximately 0° to 50° for this site seems relatively well correlated. A linear fit in the form of y = ax + b on the data from the two block fragments gives a coefficient of determination (R²) of 0.94, with coefficients a and b being – 0.0075 and 1, respectively. Since ${COR}_{v}$ should be close to 0.00 when ${\theta }_{dev}$ is at its maximum at 180°, corresponding, for example, to a strait impact on a horizontal surface that induces a vertical rebound with a near 0 returned velocity, it might be more appropriate to fit the data in the form of Eq. (1) as follows:

$${COR}_{v}=min\left\{1, 1.033-\mathrm{sin}\left(\frac{{\theta }_{dev}}{2}\right)\right\}$$

(1)

Such a fit gives an R² of 0.93 on the data from this site and of 0.76 when combined with the reconstructed data from Noël et al. (2022a) and Hibert et al. (in review), while returning low ${COR}_{v}$ from 0.03 to 0.33 for high deviations beyond 90°. It might, however, be too early to generalize from this set of data, as different block fragment sizes, shapes, impact energy, encountered materials, and saturation might affect the scarring and related reacting ground impulse and direction. This may contribute to the scattering of the combined data from different sites. Nevertheless, such a relation can be useful for validating predicted rebound behaviors in simulations. It also suggests that impacts should be analyzed not only in terms of normal and tangent components but also as a whole, as foreseen by Wyllie (2014b), especially if scarring is involved.

Application to rockfall simulations

The valuable gathered data from the reconstructed 3D trajectories, mapped 2D paths, and deposited block fragments can serve many purposes related to the simulation of rockfalls:

• 1. The data can serve as a reference for the calibration and comparison of existing rockfall simulation models for sites with similar conditions, rock shapes and large sizes.

• 2. The data could be further analyzed to improve the understanding of the impact dynamics for such high energetic rockfalls.

• 3. Newer rockfall simulation models and existing models could be developed further to expand their application range to such high energetic rockfalls.

As an application case, the data are used here for the development and validation of a simplified rolling friction rebound model prototype inspired by Wyllie (2014a, b). The existing rebound model from Pfeiffer and Bowen (1989) used in the simulation software CRSP and slightly revised for the fourth version of the software (Jones et al. 2000; Noël et al. 2021) is used as a comparison reference with the reconstructed rockfall data. The software RocFall (Stevens 1998; Rocscience Inc. 2022) and Rockyfor3D (Dorren 2008, 2015; EcorisQ 2022) are derived from the revised version of the Pfeiffer and Bowen (1989) rebound model. The rebound model of Dorren (2008) is also used as a comparison reference since it is adapted for 3D simulations. In the following sections, the rolling friction rebound model prototype derived from Wyllie (2014a, b) is first described. It is then used conjointly to the revised model from Pfeiffer and Bowen (1989) and to the one from Dorren (2008) to simulate every rebound of the reconstructed 3D trajectories. Finally, the simulated results are briefly compared between each model and with the reconstructed rockfall data.

Simplified rolling friction rebound model

As shown previously, the change in momentum and total deviation induced by the ground impulse seems relatively well correlated, as foreseen by Wyllie (2014b). Therefore, we built the model prototype on some related simplifying assumptions:

• 1. The more a rock body interacts with the ground during impact, the more it deviates and slows down.

• 2. The velocity changes at impact are assumed to be due to the deceleration induced by the ground reacting impulse (Wyllie 2014b). Indeed, for an infinitely short rock–ground interaction period, the force induced by the deceleration becomes infinitely large, while the force due to gravitational acceleration during that period becomes null. Therefore, the frictional and damping–rolling forces can only be applied during the scarring period, while the incident normal velocity of the rock becomes null and then accelerates slightly to its returned normal velocity (Wyllie 2014b).

• 3. Because of the combined deviating effects caused by the ground scarring and the rotating irregular rock on the returned trajectory, it is assumed that the returned velocity comes from the transformation and deflection of the incident tangential velocity. The incident normal component of the momentum is assumed to be lost through plastic and brittle deformation of the scarred ground.

With these simplifying assumptions in mind, the short rock–ground interaction period (${\Delta t}_{impact}$) is defined as a function of an arbitrarily high constant normal deceleration with the ground (${a}_{N}$ = 500 m s⁻²) and the normal incident and returned velocity (${v}_{N1}$ and ${v}_{N2}$) by Eq. (2) as follows:

$${\Delta t}_{impact}=\frac{{v}_{N1}+{v}_{N2}}{{a}_{N}}$$

(2)

Since the returned velocity (${v}_{2}$) is initially unknown, its normal component (${v}_{N2}$) is set to zero for a first estimation of the interaction period. During that period, one or two rock–ground interaction phases may be involved:

• 1. A synchronizing frictional phase in which the angular and translational momenta are balanced through slipping or skidding of the bouncing rock with the ground until it synchronizes its rotation with its tangential velocity, as described by Wyllie (2014b).

• 2. A residual resistive rolling phase until the rock is returned to a freefalling phase, since rolling while scarring must involve some resistance.

The second phase is reached if the synchronizing period (${\Delta t}_{sync}$) of the first phase is shorter than the total rock–ground interaction period (${\Delta t}_{impact}$). Otherwise, the synchronizing period is constrained to the total rock–ground interaction period available. The Mohr‒Coulomb frictional force (${F}_{f}$) acting on the rock body during the first phase is given by Eq. (3) as follows:

$${F}_{f}=m\; {a}_{N}\;\mathrm{tan}({\varphi }^{\mathrm{^{\prime}}})+\;^{c^{\prime}}/_{A_{contact}}$$

(3)

where $m$ is the rock mass; ${\varphi }^{^{\prime}}$ and ${c}^{^{\prime}}$ are the effective friction angle and cohesion of the rock–ground contact, respectively; and ${A}_{contact}$ is the contact surface between the rock and the ground. In this paper, ${\varphi }^{^{\prime}}$ and ${c}^{^{\prime}}$ are, respectively, set to 28° and 30 kPa, which contrasts slightly with the ${\varphi }^{^{\prime}}$ of 31° to 42° from the friction coefficients (μ) given by Wyllie (2014b) and is close to the 28° and 25 kPa for soil at 16% water content from (Carey et al. 2014; Vick et al. 2019). ${A}_{contact}$ is assumed to be constant and approximated by the quarter of the lateral surface of a cylinder by Eq. (4) as follows:

$${A}_{contact}=\frac{\pi }{4} {d}_{1}\; {d}_{3}$$

(4)

The rock body spins at impact if its incident angular velocity times its radius ($r$) are larger than its incident tangential velocity (i.e., ${{\omega }_{1} r>v}_{T1}$). In that case, the returned velocities after the synchronizing period are given by Eqs. (5) and (6) (Tipler and Mosca 2007) as follows:

$${v}_{sync}={v}_{T1}+ \frac{{F}_{f}}{m} {\Delta t}_{sync}$$

(5)

$${\omega }_{sync}={\omega }_{1}-\frac{{F}_{f} r}{I} {\Delta t}_{sync}$$

(6)

where $I$ is the moment of inertia of the rock body (e.g., using ${I}_{3}$ if rotating around the d₃-axis). The addition and subtraction of quantities are reversed if the rock body is skidding (i.e., ${{\omega }_{1} r<v}_{T1}$). Like for a skidding bowling ball (Tipler and Mosca 2007), the synchronizing period is obtained from equating Eq. (5) with Eq. (6) and isolating ${\Delta t}_{sync}$, respectively, giving Eqs. (7) and (8) as follows:

$${v}_{T1}\pm \frac{{F}_{f}}{m} {\Delta t}_{sync} = r \left({\omega }_{1}\pm \frac{{F}_{f} r}{I} {\Delta t}_{sync}\right)$$

(7)

$${\Delta t}_{sync}=\mathrm{min}\left\{ {\Delta t}_{impact},\quad \left| \frac{\left({v}_{T1}\,-\, r\; {\omega }_{1}\right)}{{F}_{f} \;{r}^{2}/I \,+\, \frac{{F}_{f}}{m}}\right|\right\}$$

(8)

Until now, the “losses” to the ground come from the normal velocity becoming null during the rock–ground interaction period. Once the tangent translational and angular velocities are balanced between each other from the synchronization of the first phase, the tangent and angular “losses” begin at the second phase involving rolling with resistance. Both phases probably act conjointly in reality, but splitting them helps simplify the model. The resisting rolling force (${F}_{r}$) is a function of the rolling resistance coefficient ($b$), which we set empirically from half of the reconstructed data for the rebound model to approach the returned reconstructed values. They are given by Eqs. (9) (Hibbeler 2016) and (10) as follows:

$${F}_{r}=m\; {a}_{N} \;^{b}/_{r}$$

(9)

$$b=\left(0.28+{\left(\frac{{v}_{T1}}{50}\right)}^{1.5}\right) r$$

(10)

The returned velocities are given by Eqs. (11) and (12) as follows (Tipler and Mosca 2007):

$${v}_{2}={v}_{sync}-\frac{{F}_{r}}{m\;+\;^{I}/_{r^{2}}} \left({\Delta t}_{impact}-{\Delta t}_{sync}\right)$$

(11)

$${\omega }_{2}= {\omega }_{sync}-\frac{{F}_{r}}{r m\;+\;^{I}/_{r}}\left({\Delta t}_{impact}-{\Delta t}_{sync}\right)$$

(12)

The components of the returned translational velocity are set as an empirically fitted ratio of the apparent coefficient of restitution with Eqs. (13) and (14) as follows:

$${v}_{T2}= {v}_{2} \left(0.132 \frac{{v}_{2}}{{v}_{1}}+1-0.132\right)$$

(13)

$${v}_{N2}=\sqrt{{{v}_{2}}^{2}-{{v}_{T2}}^{2}}$$

(14)

Knowing the returned normal velocity from a first estimation assuming a ${v}_{N2}$ null, refined returned values are obtained once by starting over from Eq. (2). Additionally, the velocity reduction is arbitrarily limited so that ${v}_{2}$ does not fall under 10% of ${v}_{1}$. Finally, inspired by Asteriou and Tsiambaos (2016) and Caviezel et al. (2021), lateral deviations (${\theta }_{N}$) are applied around the normal vector N as a function of the ratio d₁/d₃, the incident angle (${\theta }_{1}$), and the difference between the trend of the incident velocity and the aspect of the terrain (${\Delta }_{aspect}$) by Eq. (15) as follows:

$${\theta }_{N}=-19.38\; \frac{{d}_{1}}{{d}_{3}}\;\mathrm{ sin}\left({\Delta }_{aspect}\right)\;\mathrm{ sin}\left({\theta }_{1}\right)$$

(15)

A slight variation is also added to ${\theta }_{N}$ from a uniformly distributed random number varying from – 8° to 8°. Note that for the simplicity of calculation, the sign of ${\theta }_{N}$ does not correspond to those used in Fig. 10 that follows the definition given in Noël et al. (2022a), but rather follows the conventional “right-hand rule”: A positive lateral deviation around an upward pointing normal vector corresponds to the rock body deviating toward its left. The difference between the trend of the incident velocity and the aspect of the terrain (${\Delta }_{aspect}$) is given by Eq. (16) from their horizontal components, and the sign of ${\Delta }_{aspect}$ is given by the sign of Eq. (17) as follows:

$${\Delta }_{aspect} = \pm {\mathrm{cos}}^{-1}\left(\frac{\overrightarrow{{N}_{xy}}\cdot \overrightarrow{{v}_{xy1}}}{\Vert \overrightarrow{{N}_{xy}}\Vert \Vert \overrightarrow{{v}_{xy1}}\Vert }\right)$$

(16)

$${sign}_{not\_normed}={v}_{x1} {N}_{y}-{v}_{y1} {N}_{x}$$

(17)

With the simplified rolling friction rebound model prototype described, it can now be put to the test by confronting its predicted rebounds to “reality” from the reconstructed data.

Rebound models vs. reconstructed data

The reconstructed data are used here as a reference for the “per-impact” comparison of the described simplified rolling friction rebound model prototype and other models (Fig. 16). All initial incident rebound conditions are defined from the reconstructed data, while the returned values are calculated with the models and compared to the returned reconstructed values. For the revised version of the Pfeiffer and Bowen (1989) rebound model, its terrain material “coefficient of restitution” damping parameters R_N and R_T are set based on the values given in Table 2. Note that they are not the same as the apparent coefficients of restitution COR_N and COR_T as explained in Noël et al. (2021) and Noël et al. (2022a). For Dorren’s (2008) rebound model, the terrain material properties are defined using Rockyfor3D’s “rapid automatic simulation” values (Dorren 2015) (Table 2). For all tested models, the various rock characteristics are set based on the reconstructed data, and their moment of inertia is simplified to those of ellipsoids of d₁-d₂-d₃ dimensions rotating around their d₃-axis. A narrow set of five trajectories per rebound model is also simulated on the Mel de la Niva site for a brief “side-by-side” qualitative comparison using the 2 m 2013 digital terrain model (DTM) from the swissALTI^3D geodata by ^©swisstopo (Fig. 17). Rockyfor3D 5.2.15 simulation software is used to produce the trajectories for the Dorren (2008) model and stnParabel v. August 2021 multiple model simulation freeware (Noël 2020) is used for the two other models with the added roughness from the detailed DTM sample defined in Table 2.

Fig. 16

Predicted returned values compared to the reconstructed data (in red) on a “per-impact” basis. Only one variable is compared per graphic in (c), (d), (e), and (f) with the predicted values by the models in “y” and the “observed” reconstructed values in “x” as a reference. A perfect fit should lie on the red diagonal lines

Table 2 Parameters used for the comparison of the rebound model to the reconstructed rockfall data. The roughness from DTM samples is not applied for the “per-impact” comparison. It is, however, applied for the simulated trajectories on the Mel de la Niva site with the revised Pfeiffer and Bowen (1989) model and the simplified rolling friction model. More details can be found about this in Noël et al. (2021) and from its reproduced figure (Fig. 19) given in the supplementary material

Fig. 17

Sets of five simulated trajectories from three rebound models compared aside the mapped observed rockfall paths shown in red. The yellow and blue trajectories, respectively, using the revised Pfeiffer and Bowen (1989) and simplified rolling friction rebound models were produced with the stnParabel multiple model simulation freeware (Noël 2020). Those using the Dorren (2008) rebound model shown in green were produced with Rockyfor3D v5.2.15 simulation software (EcorisQ 2022)

Pfeiffer and Bowen (1989) COR_v values are lower at low total deviation than the reconstructed values (Fig. 16a). This could be due to the low returned angles (${\theta }_{2}$) and COR_N of the model shown in Fig. 16b, e, resulting in lower total deviations than those observed from the reconstructed data. Despite the well-matched returned velocities in Fig. 16c, d, such low deviations for the chosen damping parameters would result in lower simulated bounce heights, shorter parabolas, more closely spaced simulated impacts, and overall lower energies and runout distances (Fig. 17). This could have important implications when using results from this revised rebound model from Pfeiffer and Bowen (1989) for designing mitigation measures or performing risk and hazard assessments. Therefore, one using RocFall software or stnParabel freeware with this model should carefully adjust the simulation parameters to obtain realistic rebound heights and energies, similar to the adjustments that were needed for boosting the energies and bounce heights for the Rifle site in Noël et al. (2021). On that matter, reconstructed rockfall data (e.g., Caviezel et al. 2020; Hibert et al. in review; Noël et al. 2022a) can be of great help when compared as in Fig. 16, where one can attempt to align the calculated returned values with the reconstructed ones.

Similar behavior can be observed from Dorren (2008) values with the “per-impact” comparison, but to a lower extent and with more scattering (Fig. 16). The effect of the random probabilistic lateral deviation applied around the vertical axis can be seen on the lateral deviations in Fig. 16f. This produces more lateral oscillations and a slightly wider area covered by the simulated trajectories shown in green in Fig. 17 in comparison to the Pfeiffer and Bowen (1989) yellow simulated trajectories. A similar behavior can be seen for the simplified rolling friction model in Fig. 16f. Complemented by the added roughness, its simulated trajectories, shown in blue in Fig. 17, cover an even wider area closer to the observations while displaying fewer lateral oscillations. Similar to the other models, the returned angles do not correlate well with the reconstructed data (Fig. 16e), but the crosses are more evenly distributed above and under the 1:1 line, better distributing the over- and underestimations of the returned angles. Thirty-eight percent of the reconstructed returned angles lie between 10 and 20° and have an average of 15.0°. The simplified rolling friction model is close with an average of 14.1° compared to the averages of 5.3° and 6.7° of the values from the Pfeiffer and Bowen (1989) revised model and the Dorren (2008) model, respectively.

The momentum transfer and deviation correlations shown with COR_v and ${\theta }_{\mathrm{dev}}$ shown in Fig. 16a provide good overall insight into the ability of the models to reproduce the observations or, in other words, to evaluate their predictability for their chosen set of parameters. Indeed, simulating realistic trajectories and associated runout distances involves predicting a series of rebounds with proper velocity changes, bounce heights from the returned angles and velocities and proper impact-to-impact distances. For example, a model failing to reproduce proper impact-to-impact distances due to excessively low returned angles would require a higher COR_v. This would compensate for the resulting overly numerous rock–ground interaction caused by the closely spaced impacts to reproduce comparable runout distances. As a result, its bounce heights and following incident angles would be lower, which would be revealed by lower ${\theta }_{\mathrm{dev}}$ values. Therefore, reproducing proper runout distances not only involves predicting proper velocity/momentum changes but also accompanying them with proper predicted returned angles, leading to proper bounce heights, incident angles and overall proper ${\theta }_{\mathrm{dev}}$. The COR_v of the reconstructed data is 0.75 on average (S.D.: 0.13), exactly as for the simplified rolling friction model. They are accompanied by a similar average ${\theta }_{\mathrm{dev}}$ of 34° (S.D.: 15°) and 33° (S.D.: 14°) respectively. In comparison, the average COR_v and ${\theta }_{\mathrm{dev}}$ of the values from the Dorren (2008) model with the “rapid automatic simulation” parameters are 0.79 (S.D.: 0.11) and 30° (S.D.: 17°), respectively. Those from the Pfeiffer and Bowen (1989) revised model with the chosen parameters are 0.77 (S.D.: 0.08) and 23° (S.D.: 13°), respectively.

It is interesting to note that the various predicted values from the simplified rolling friction model did not produce a worse fit than the others despite using a unique set of fixed parameters (e.g., fixed ${\varphi }^{^{\prime}}$ and ${c}^{^{\prime}}$ vs. customized damping parameters R_N, R_T, Soil type, Rg70, Rg20, and Rg10). The sensitivity analysis summarized in Jones et al. (2000) showed that the revised Pfeiffer and Bowen (1989) model from which Dorren’s (2008) model is derived is already little dependent on the damping parameters R_N and R_T. Jones et al. (2000) thus concluded that the slope geometries and surface roughness are the most important controlling factors. Moreover, Wyllie (2014b) did not observe a significant difference for the apparent coefficients of restitution (COR_N and COR_T) from rock, talus, and colluvium. Therefore, prioritizing the categorization of differentiated sets of damping parameters for these encountered materials is not justified. However, soil with high water content may lower the runout distances (Vick et al. 2019), so using a unique set of fixed parameters in that situation would have the safe drawback of potentially overestimating the runout distances to those expected for dryer conditions.

With the effect of perceived terrain geometry and roughness objectively quantified with the impact detection algorithm from Noël et al. (2021) used in stnParabel, the simplified rolling friction model should require very few inputs or fine tuning from the user. If producing realistic simulated trajectories on various site geometries and characteristics, this objective limited parametrization of the model could save precious time for practitioners. Additionally, it would improve the predictability and objectivity of the simulations. The simplified rolling friction model should, however, be tested on a variety of sites affected by previous events to assess such potential predictability and realism. The authors therefore encourage the reader to confront the model to various real events with the multiple model simulation freeware stnParabel (Noël 2020) and to share their findings to help improve the model. This would also help improve the freeware if any residual glitches are found.

This application case of the reconstructed 3D rockfall data from back calculations and analyses covering an unprecedented range of block sizes and energies showed how the data can be used for quantitatively comparing predicted values from rebound models with a “per-impact” configuration. It was also shown that such a comparison can help develop and further refine rebound models empirically to approach the observations. Finally, it was briefly shown (Fig. 17) how the mapped rockfall paths bring valuable data for confronting models to the observations by “side-by-side” trajectory comparison.

Conclusions

A back analysis of the 2015 Mel de la Niva rockfall event with the 3D reconstruction of the rockfall trajectories using the flexible CAVR method described in Noël et al. (2022a) has been performed in this paper. It used a novel method highlighting the impact marks from artificial colored lighting and shading approaches for mapping previous rockfall paths and documenting the previous state of activity of the site. A potentially time-saving method to estimate the geometric characteristics of the rock block fragments simplified to ellipsoid from simple on-field measurements of d₁-d₂-d₃ has been presented. The back analysis contributes to the novel documentation in terms of kinetic energy values, bounce heights, velocities, and 3D lateral deviations of such rare highly energetic events involving block fragments of approximately 200 m³. Indeed, the reconstruction provided insights into the rarely observed rockfall impacts beyond hundreds of megajoules. The moderately to very flat and slightly elongated shape of the block fragments might have played an important role in the observed lateral deviations. This finding, combined with the fact that the trajectories do not laterally deviate during the freefalling phases, contributed to the paths not systematically following the present gullies or the steepest downward slope direction. Such a complex dynamic process characteristic of rockfalls may be challenging to model when performing 3D process–based rockfall simulations and is neglected with diffusive flow approaches and 2D simulations. The reconstruction of this event provided useful data that could be used to compare and fine-tune existing rockfall simulation software for similar sites and to further develop rebound models as demonstrated. Further work should focus on assessing the sensitivity and predictability of simulation models when confronted with back analyses such as the one featured in this paper but from diverse sites of various geometries affected by previous rockfall events.