Introduction

Tsunamis can be mainly produced in two ways: (1) direct displacement of the seafloor due to a fast motion during an earthquake and (2) mass failure, as a consequence of earthquake shaking or other natural/anthropogenic causes, resulting in so-called “landslide tsunamis” (Ward 2001). Although in different proportions, both mechanisms can play a role during most tsunami events, particularly those generated close to continental shelves.

The Sea of Marmara is particularly prone to landslide tsunami hazards for multiple reasons. First, it experiences large magnitude, relatively shallow earthquakes (Ambraseys 2002), along active segments of the North Anatolian Fault (NAF) system (Gasperini et al. 2021), one of the most seismogenic structures on Earth (Şengör 1979; Barka and Kadinsky-Cade 1988; Barka 1992). Second, it is bounded by steep fast-subsiding slopes, favoring relatively thick and unstable sedimentary sequences piling up over natural sliding planes (Gazioglu et al. 2005; Zitter et al. 2012). Third, it has been affected by dramatic water-level changes during the Pleistocene/Holocene transition, and most probably during previous glacial/interglacial cycles, primarily controlled by the natural Dardanelles and Bosphorus sills (Çağatay et al. 2000, 2003; Polonia et al. 2004). This peculiar physiographic setting could have favored catastrophic inundations, mega-turbidites, and slope instability during eustatic transitions and/or variations of hydrostatic pressure conditions (Sultan et al. 2004). In the Sea of Marmara, gravitative failures could also be enhanced by diffuse presence of geological fluids in the sediments, i.e., CH4, CO2, and others, whose circulation and escape at the seafloor was found to be connected with the earthquake cycle (Tryon et al. 2010; Gasperini et al. 2012, 2018; Ruffine et al. 2015; Géli et al. 2018).

Several oceanographic expeditions carried out in the Sea of Marmara after the Mw = 7.6, 1999 İzmit earthquake, collected an extensive set of high-resolution marine geophysical data. They include morphobathymetric images and seismic reflection profiles, both highlighting the effects of gravitative instability and landslides, shown by slumping scars, actively gliding masses, or chaotic deposits in the sediments (Zitter et al. 2012). In this general framework, unpublished geophysical data led us to recognize a sizeable potential landslide mass in the Çınarcık Basin (eastern Sea of Marmara), close to the entrance of the Gulf of İzmit, which we called the South Çınarcık Landslide (SCL). This submarine landslide body could represent a potential hazard for the Sea of Marmara coasts, particularly in the NE sector between the Armutlu Peninsula and Istanbul (Fig. 1). Our work attempts to define possible scenarios in case of massive failure of this body due to future earthquakes or to other causes.

Fig. 1
figure 1

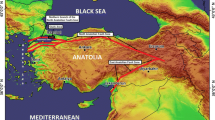
Tectonic map of the Sea of Marmara (modified from Gasperini et al. 2011a). The study area is indicated by a yellow rectangle

Full size image

Backgrounds

The Sea of Marmara is a pull-apart basin (Armijo et al. 2002; 2005; Şengör et al. 2014) formed as a consequence of a wide step-over between two major branches of the NAF (Fig. 1). This peculiar setting has produced a rapidly evolving morphology, dominated by the presence of fast-subsiding basins separated by NE-SW oriented ridges bounding three major left-lateral oversteps (Gasperini et al. 2021). Consequently, the northern edges of these basins are formed by NW–SE oriented normal faults connecting the shelves with the deep depocenters, reaching a dip of 25–27°. Small changes in the Eurasia-Anatolia relative motion vectors have produced complex transtensional and transpressional deformations along the main fault segments, constituting weak “spots” of deformed terrains affected by gravitative instability (Bulkan et al. 2020).

The Sea of Marmara sedimentary infill preserves the record of mass failures and turbidite events mostly localized in the basin depocenters (McHugh et al. 2006; Beck et al. 2007; Çagatay et al. 2012; Drab et al. 2015). The region is prone to periodic large magnitude (M > 7) earthquakes, with average recurrence periods of 250–300 years along each segment (Ambraseys 2002). Most of these high-energy events recorded in the sediments were triggered probably by seismic shaking, as suggested by marine paleoseismological studies and depositional models of seismoturbidites in confined basins (Polonia et al. 2002, 2017). The records of these earthquakes and associated mass flows appear as turbidite/homogenite sequences in the deep Marmara basins (Sarı and Çagatay 2006; McHugh et al. 2006; Çagatay et al. 2012; Drab et al. 2015). Some of these events may have caused large landslides, with the displacement of bodies as large as 10 km3 (Zitter et al. 2012) that probably caused tsunamis.

Historical catalogs report the occurrence of several tsunamis in the Sea of Marmara (Yalçıner et al. 2002), including more than 30 events since AD 120, the latest caused by the 1999 İzmit earthquake. Major effects were reported in the İzmit and Gemlik bays, along the shores of İstanbul, and the Gelibolu Peninsula (Yalçıner et al. 2002). The most recent tsunami observed in eastern Marmara before 1999 occurred in 1963 and was caused by an Ms = 6.3 earthquake. It affected Yalova and Çınarcık, with tsunamis up to about 1 m high along the coastal protection structure in Bandırma (Kuran and Yalçıner 1993).

The tsunami problem in the Sea of Marmara has been addressed in several ways. Most studies focused on the 1999 İzmit earthquake and related tsunami run-up, which may be considered the best studied case ever in the region (Alpar et al. 2001; Altinok et al. 2001; Yalçıner et al. 2002; Hébert et al. 2005; Tinti et al. 2006b). However, due to the prevailing strike-slip regime along the NAF, with main displacements parallel to the seafloor, large tsunamis should necessarily be associated with seismically triggered landslides.

Research on landslide tsunamis evolved less rapidly than those caused by direct earthquake rupture, mainly due to difficulties in obtaining reliable hydrodynamic observations. The 1998 Papua New Guinea tsunami, with more than 2000 casualties and extensive damage, was the first landslide tsunami for which seismological and later marine geophysical data constrained modeling aspects with observations (Geist 2000; Okal and Synolakis 2001; Tappin et al. 2001).

As a fluid mechanics problem, landslide tsunamis were studied using different methods. During the last decades, numerical (Grilli and Watts 1999; Grilli et al. 2002; Hébert et al. 2002; Tinti et al. 2006a), analytical (Pelinovsky and Poplavsky, 1996; Tinti and Bortolucci 2000; Ward 2001), and experimental works (Watts 1998, 2000, 2001; Watts et al. 2005; Liu et al. 2005; Panizzo et al. 2005; Heller and Hager 2011; Sabeti and Heidarzadeh, 2021) improved our understanding of this potentially catastrophic phenomenon. Approaches based on Green’s functions to model tsunami created by large-scale landslides were pioneered by Pelinovsky and Poplavsky (1996) and later improved by Ward (2001). Growing computational resources have enhanced considerably the variety of numerical methodologies adopted. In recent years, the interest on landslide tsunamis has been boosted through a series of works providing new insights on their peculiar characteristics (Heller et al. 2016; Evers et al. 2019; Heidarzadeh et al. 2020; Løvholt et al. 2020; Snelling et al. 2020; Ruffini et al. 2021; Iorio et al. 2021). Comprehensive reviews of the approaches adopted for simulating landslide motion and water interactions, as well as available numerical techniques, can be found in Heidarzadeh et al. (2014), Yavari-Ramshe and Ataie-Ashtiani (2016), and in Kirby et al. (2022) which compares different codes applied to benchmarks with real case.

Tsunami in the Sea of Marmara were simulated using analytical (Özeren et al. 2010) as well as numerical methods (Tinti et al. 2006b). A multidisciplinary example is that of the Tuzla landslide, which included original mathematical modeling for the tsunami waves triggered by submarine mass movement (Özeren et al. 2010). The Tuzla paleo-landslide is particularly significant to our work, since it refers to an event occurred around 17 ka at the opposite (northern) slope of the Sea of Marmara (Fig. 2), in a similar geological setting. After constraining the stratigraphic and morphological characteristics of the landslide, the authors performed mathematical simulations to evaluate the tsunami wavefield possibly created by its collapse. Using a semi-spectral method, they obtained the preliminary characteristics of the dispersive wavefield propagating in the Çinarcik Basin for a 7-km-wide sliding mass, which could have produced waves as high as 0.56 times the average thickness of the sliding mass (over 35 m), corresponding to maximum wave heights of around 20 m in deep water.

Fig. 2
figure 2

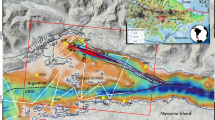
Multibeam echosounder bathymetry of the study area combined with the topography obtained by SRTM data. Top: slope map of the seafloor with location of the MCS profiles used for subsurface interpretation (red lines). Bottom: line-drawing interpretation with main morphostructural features, including the NAF principal displacement zone and the location of Tuzla and South Çınarcık (yellow pattern) landslides. The positions of seismic sections displayed in Figs. 3 and 4 are also reported

Full size image

Prior to this work, no information was available to date regarding a large landslide body located on the opposite side of the Çınarcık Basin, close to the entrance of the İzmit Gulf (Fig. 1).

The SCL case study of this paper uses a numerical approach to model the effects of a sudden collapse towards the deep (> 1200 m) Çinarcik Basin. The workflow develops in subsequent steps, including the landslide body definition (size, morphology, stratigraphic setting, and location in the NAF active tectonic system), followed by numerical simulations designed to understand the main characteristics of the tsunami wavefield generated by the hypothetical mass movement. In the absence of more detailed geotechnical information about the landslide body, we adopted a worst-case scenario strategy, which means that we assumed a massive collapse resulting from a large magnitude earthquake along the Çınarcık or İzmit active NAF segments and simulate generation and propagation of subsequent tsunami through well-tested procedures already applied to other cases.

Methods

To delimit geometry and geomorphological characters of the SCL, we used high-resolution bathymetric and seismic reflection data collected during four oceanographic expedition between 2001 and 2013 in the Sea of Marmara on board of R/V Urania, of the Italian CNR (http://www.ismar.cnr.it/products/reports-campagne?set_language=en&cl=en). The multibeam echosounder data were processed using CARIS Hips and Sips package, which allowed to obtain a 5-m spaced bathymetric grid. The seismic images were selected from a network of multichannel seismic (MCS) reflection profiles collected during the MARMARA-2001 cruise, acquired using an array of 45 + 45 c.i. Sodera G.I. guns as a seismic source, and a 24 channels Teledyne analog streamer (12.5 m of group interval) as a receiver. The seismic data were processed using an industrial package (Disco/Focus) by Paradigm Geophysical following a non-standard sequence to obtain depth-migrated sections. Pre-processing included (1) swell noise removal by time-variant band limited noise suppression; (2) setting acquisition geometry; (3) interactive noisy trace editing; and (4) spherical divergence correction. Processing steps included (5) water column muting; (6) predictive deconvolution with operator length of 255 ms, prediction lag of 12 ms, pre-whitening of 0.2%, filter design window of 0–2 s, and an application window of 0–4 s; (7) DC-bias removal and time variant trace amplitude equalization; (8) time variant band-pass filtering with a frequency band of 4/8–72/96 Hz; (9) CDP sorting and velocity analysis; (10) random and coherent noise reduction by f-k and tau-p velocity filtering in the shot, receiver, and common midpoint domains; (11) bottom surface multiple removal using 2D surface-related multiple elimination (SRME) technique and adaptive filters; (12) normal move out (NMO) and dip move out (DMO) corrections; (13) NMO removal and velocity analysis; (14) NMO and stacking; and (15) finite difference time and depth migration after iteratively smoothing and refining the velocity model. To determine correctly active fault traces, i.e., traces of faults showing an expression as close as possible to the surface, and continuity of internal reflectors, instantaneous attributes sections were also compiled. Seismic data interpretation was performed using the SeisPrho 3.0 software package (Gasperini and Stanghellini 2009). Maps were compiled using GMT 6.0 software (Wessel et al, 2013)

A sequence of codes developed by the tsunami research team at the University of Bologna simulated the landslide tsunami, allowing for separate computation of the landslide motion, the tsunamigenic impulse, and the wave propagation.

The UBO-BLOCK1 code simulates the landslide motion by dividing the mass into interacting volume-conserving blocks, which are allowed to changing shape but not to detach from each other. Body (gravity, buoyancy) and surface (basal friction, drag) forces, as well as dissipative block-block interactions, are accounted to compute the time history of the landslide controlling variables. The resulting motion equations are solved numerically using a finite difference scheme. The simulation is interrupted when the slide velocity becomes small enough, or the mass exits the computational domain. The most important parameter controlling the motion is the basal friction coefficient, primarily influencing the slide velocity and run-out. The code also allows to control the blocks’ center of mass reciprocal distances, in this way mimicking different rheological behaviors of the slide during its failure (see Tinti et al. 1997 for details).

The UBO-TSUIMP code reconstructs the area covered by the slide and its instantaneous variable thickness, converted in tsunamigenic perturbation through a filtering transfer function. This operation depends on the water depth and landslide footprint. Eventually, the code produces the impulse time history for each point of the tsunami computational grid through a space–time interpolation and a smoothing process (further details in Tinti et al. 2006a).

Using the staggered grid technique of the UBO-TSUFD code, we solved the non-dispersive shallow-water equations in a leap-frog finite-difference scheme. Water perturbation is time-dependent, as typical for landslide tsunamis, since the moving body interacts with the water for a time interval within the scale of wave propagation. The boundary conditions depend on the computational domain. A transparency condition is adopted for boundary cells representing the open sea. In the case of dry land, two different behaviors are available, linear, and non-linear. The first does not account for inundation and considers the coast as a “wall” reflecting tsunami. The non-linear version implements flooding of the coastal areas through a moving-boundary technique. This latter option implies longer computation time not only because more terms of the fluid-dynamic equations must be considered, but chiefly because inundation is strongly dependent on sea floor and terrain morphological features that can be adequately represented only by very fine grids. Indeed, the code can handle such grid densification at specific sites by implementing a nested-grid technique. More details about the code and applications to real cases can be found in Tinti and Tonini (2013), Tinti et al. (2011), Zaniboni et al. (2014, 2016, 2019, 2021), and Gallotti et al. (2020, 2021).

The code we use does not treat dispersion. The main effect of dispersion, which implies longer wavelengths to travel with higher speeds, is that of reducing the amplitude of the tsunami front by redistributing its energy over a train of subsequent wave fronts. It is known that the influence of dispersion on the tsunami train and the effects along the coast increase with the distance from the source (Schambach et al. 2020). An estimate of the critical distance \(d\) beyond which dispersion becomes relevant comes from the formula given in Glimsdal et al. (2013):

$$\frac{d}{\lambda }=\frac{\tau {\lambda }^{2}}{\alpha {h}^{2}}$$
(1)

Following suggestions of the authors, in Eq. (1), \(\tau\) is a dispersion coefficient that can be considered equal to 0.1, \(\alpha\) is a coefficient ranging between 4 and 6, and \(h\) is the average water depth. When the ratio \(\lambda /h>20\), a condition always met in case of earthquake-induced tsunamis and often satisfied by landslide tsunamis, the first term in Eq. (1) is around 10, meaning that dispersive effects can be usually neglected in the region with a radius \(d\) shorter than ten times the initial wavelength. This justify the utilization of non-dispersive equations in the near- and intermediate-field. The specific application of Eq. (1) to the case treated in this paper will be discussed in the “Simulation results: tsunami” section.

Results

Delimiting the potential landslide

The high-resolution bathymetric slope map of the eastern Çınarcık basin (Fig. 2) suggests the presence of a lobate body at the entrance of the İzmit Gulf. It presents clear evidence of seafloor roughness and deformations possibly related to creeping/sliding and instability processes. Incipient or relatively recent (10 kyr. time scale) displacements are suggested by the arcuate shape of the body, showing an irregular undulated surface and signs of detachment particularly evident along its southwestern edge (Fig. 2).

The orthogonally oriented MCS profiles IZW-05 M and IZW-08 M across the SCL (Figs. 3 and 4) confirm this picture and led us delimiting the slumping body at depth. They show a topographic high made of deformed sediments delimited towards the north by a canyon. The body appears displaced by a complex system of ruptures branching from a major subvertical strike-slip fault corresponding to the NAF. This setting is more evident in the ESE-WNW section (Fig. 3), but also visible in the SE-NE cut (Fig. 4). The overall picture resembles that of a positive “flower structure,” suggesting transpressive deformations. We note a basal low-angle detachment and a sequence of high-angle normal/gravitative faults pervasively affecting a large mass, with internal reflectors variably deformed by gravity failures, more evidently in the instantaneous attribute’s representation (Figs. 3c and 4c). This would imply an incipient deformation of a sedimentary body that could be totally or partially mobilized by shaking along the basal detachment and/or high angle gravitative faults. Erosion gullies and NAF-related fault scarps at the surface of the sliding mass suggest slow displacement rates or long-term quiescence of the gravitative movements (Fig. 2). However, we cannot exclude that such apparently stable conditions could rapidly change due to a large magnitude earthquake nucleating in the vicinity of the sliding mass, along either the Çınarcık or the İzmit segments. In fact, the latter deformed entirely during the 1999 earthquake, with a coseismic rupture exceeding 120 km and peak ground accelerations (PGAs) reaching 0.4 g near the fault (Scawthorn and Johnson 2000). The 1999 rupture was identified close to the western termination of the segment, which coincides with the gulf entrance (Gasperini et al. 2011b). Such (or similar) PGAs can be very effective in producing large-scale gravitative instability and landslides, widely reported after the 1999 Izmit event (Cetin et al. 2004).

Fig. 3
figure 3

a MCS profile IZW-05 M (location in Fig. 2) across the SCL highlighted by a yellow pattern. b Interpretation line drawing with main morphotectonic features, including detachment of the SCL (dotted line), NAF principal displacement zone (PTDZ), and minor gravity/tectonic fault/fractures. c instantaneous phase representation, highlighting main reflectors displaced by tectonic and gravity deformations

Full size image
Fig. 4
figure 4

a MCS profile IZW-08 M (location in Fig. 2) cutting the SCL orthogonally relative to IZW-05 M (Fig. 3). b Interpretation line drawing with main morphotectonic features, including detachment of the SCL (dotted line), NAF principal displacement zone (PTDZ), and minor gravity/tectonic fault/fractures. c Instantaneous phase representation, highlighting main reflectors displaced by tectonic and gravity deformations

Full size image

Although we note the presence of several gravitative normal faults/failures in the sliding mass, which could imply different possible scenarios of partial collapse even in case of strong accelerations, we analyzed a “worst-case scenario”, i.e., a sudden collapse of the entire body as a possible consequence of earthquake shaking.

Computational grids and landslide simulation setup

The computational grid compiled for the landslide simulation describes the morphology of the eastern part of the Çınarcık Basin and the western end of the İzmit Gulf, encompassing an area of 45 km in the W-E direction and 30 km in the N-S direction, with 50-m spaced nodes, wide enough to account for mass motion and the final deposition in deep water. The tsunami simulation grid is 100-m spaced, covering an area of 85 km (W-E) by 57 km (N-S); it was obtained by integrating our dataset with regional data (EMODnet Bathymetry Consortium 2018). The reconstruction of the sliding mass encompassed a volume of about 3.87 km3, spread over an initial area of 27.5 km2, with maximum thickness of approximately 350 m (see Fig. 5).

Fig. 5
figure 5

Initial sliding mass (hot colors) and computed final deposit (green colors), emplaced at more than 1200 m sea depth. The CoM common trajectory (purple) and lateral boundary (magenta) lines are provided to the simulation code as inputs. Bathymetry contours are drawn at 100-m intervals

Full size image

The application of code UBO-BLOCK1 requires the prescription of the block’s typical trajectory and the lateral boundary of the motion (Fig. 5, in purple and magenta, respectively). While the former was drawn following the maximum slope, the lateral boundary was traced considering the seafloor morphology, which narrows in shallow water followed by spreading in the abyssal plain (Fig. 5).

The coefficients of the code that mainly control slide dynamics are the basal friction coefficient μ and a set of parameters describing block-block contacts and mass deformation accounting for the rheological behavior. Values between 0.02 and 0.06, with 0.01 step intervals, were explored, as reported in Fig. S1, within the typical range of submarine landslide simulations (Janin et al. 2019; Wang et al. 2019; Gargani 2020). We observe that μ influences the landslide run-out (Fig. S1, upper panel) that ranges from 15 to 22 km, as well as the maximum velocity (Fig. S1, lower panel) that varies between 40 and almost 60 m/s. We choose scenarios where the landslide deposit reaches the sub-horizontal seafloor area at a depth of 1200 m, stopping just at its toe: this implies the selection of the higher values for μ, i.e., between 0.04 and 0.06. The respective velocity time-series show differences, both in the peak velocity and in the initial acceleration, factors that are relevant for the tsunami generation process.

Concerning the landslide deformation parameters, these are selected by supposing a considerable elongation of the deposit at the end of its descent along the slope. We assume that the sliding body is made of alternating fine- and coarse-grained marine and lacustrine sediments, as observed and sampled by gravity cores in the near surroundings (Polonia et al. 2004; Dal Forno and Gasperini 2008). Among parameters accounting for this aspect of mass motion, we focus on the block-block interaction coefficient of the landslide model, selecting values that allow the maximum possible deformation, i.e., λ = 1 (see Tinti et al. 1997 for details).

Simulation results: landslide

As mentioned in the previous section, friction coefficients between 0.04 and 0.06, leading to a mass deposition area at the base of the slope, were considered as the most suitable. All results shown hereafter thus refer to μ = 0.05. Figure 5 displays the initial and final landslide body. The deposit extends for more than 8 km in the motion direction, with an average thickness of about 140 m. The slide stops in a flat area at the base of the continental shelf, at over 1200 m water depth, where it loses kinetic energy and reduces its thickness. The fine-grained, low-density material mobilized by the collapse could probably travel some more kilometers farther in deeper water; however, for our purpose, this further motion can be neglected since it is scarcely tsunamigenic. The run-out of the thicker part of the slide exceeds 17 km, as shown in Fig. 6 (upper panel).

Fig. 6
figure 6

Top: profile of the landslide along the CoM trajectory: undisturbed sliding surface (black), initial sliding mass (blue), and final deposit (red), simulated with the code UBO-BLOCK1. Bottom: velocity and Froude number time histories. The mean slide velocity is compared to the block velocities (black dots). The Froude number curve is in blue. The Froude number is the ratio between the horizontal velocity of the slide and the phase velocity of the tsunami

Full size image

The sliding mass undergoes an initial acceleration with the velocity increasing up to 45 m/s in over 3 min (Fig. 6, lower panel). This phase corresponds to the highest Froude number (Fr), a measure of how efficiently the energy is transferred from the mass to the water. In fact, the closer Fr (blue line in Fig. 6, lower panel) is to the critical value (Fr = 1 implies that the slide and wave move at the same velocity), the more tsunamigenic the landslide. The Fr peak is around 0.5, quite far from the resonance condition. Velocity curves of individual blocks (black lines in Fig. 6, lower panel) depart from the mean speed curve (red line), especially in the acceleration phase. This means that it is in this part of the motion that the slide longitudinal deformation mainly occurs. Conversely, in the deceleration stage, block speeds are quite similar. The modelled values of the velocity peaks are compatible with results reported in the literature (Voight et al. 1983; De Blasio et al. 2005; Vanneste et al. 2011; Abadie et al. 2012; Day et al. 2015; Schnyder et al. 2016; Salmanidou et al. 2018; Sun and Leslie 2020).

Simulation results: tsunami

The landslide motion produces a change of the topography at the seafloor that triggers the tsunami (see video animation in S2). Its propagation is simulated by UBO-TSUFD in its linear version. It computes the tsunami propagation up to the coast but does not consider land inundation. This is in line with the aim of assessing the general pattern of the tsunami at a regional scale providing a first picture of the coastal stretches that can be most affected by the event. A detailed study of the flooding over specific coastal areas would in fact require much higher resolutions in the bathymetric grids and more computational efforts.

The most intense tsunami generation phase lasts about 6 min. The coast closer to the slide in the Yalova district is affected by large waves (more than 30 m high) within the first 2 min. A strong positive front propagates quickly westward, driven by the increasing water depth in that direction. To the east, a smaller and slower trough radiates eastward, entering the Izmit Bay towards Kocaeli and Gölkük. In the 4-min field of Fig. 7, a trough follows the positive front moving towards the west, and similar symmetric behavior is visible to the east. We note a train of short waves affecting the southern and northern coasts, with a wavelength shortening effect typical of waves heading to shallower depths. This is shown in the 6- and 10-min fields by a sequence of at least three crest-trough pairs. Between 15 and 20 min, the Istanbul area is affected by crests reaching elevations around 5 m. It is interesting to note the effect of the barrier represented by the Prince’s Islands which shelter the northern Sea of Marmara shelf towards the east. In the opposite direction, the tsunami waves are strongly decelerated by the shallower waters of the İzmit Bay. The 15- and 20-min snapshots show a small negative front advancing very slowly in the basin.

Fig. 7
figure 7

Propagation of the SCL tsunami at different time steps up to 20 min. The black boundary delimits the area swept by the slide

Full size image

Figure 7 leads us to evaluate the effectiveness of a non-dispersive code in our case. In fact, the propagation fields of the westward-moving waves have a length of about 12 km, compatible with a suggestion by Watts et al. (2005) that the wavelength of a landslide tsunami is approximately twice the landslide horizontal dimension. In the source area, the ratio \(\lambda /h\) reaches values close to 20, while it decreases in the deeper central part of the gulf. If we assume 15 as a suitable value of this ratio for the propagating tsunami, Eq. (1) provides \(d/\lambda \approx 6\), meaning that dispersion effects become important at distances over 70 km from the source, implying that the use of a non-dispersive tsunami model gives a good approximation within the domain selected for the simulation.

Plots showing the tsunami travel time (Fig. 8, top) and the maximum water elevation on the coast (Fig. 8, bottom) provide a glance of the most affected coastal stretches within the study area and can be used to draw some conclusions on the tsunami hazard assessment related to SCL.

Fig. 8
figure 8

Top: tsunami travel time, in minutes. The red boundary marks the area swept by the slide. The black labels show the cumulative distance along the coast. Bottom: maximum water elevation at the coastline vs. cumulative distance

Full size image

The maximum water elevation produced by the tsunami is shown as a function of the cumulative distance along the coast (Fig. 8, bottom). The origin of such a reference system is placed at the western bottom corner of the grid. It can be noticed that the entire coastal extension is around 280 km.

The coastal area affected by the highest water elevation (around 45 m) lies on the southern coast between the Çınarcık and Yalova districts (see Fig. 8) and is not the closest to the source. It is reached by the tsunami after more than 3 min. We note that the entire southern coastal stretch around Çınarcık and Yalova is affected by relevant waves (> 20 m water elevation), whose height is due to the large initial thickness of the slide (more than 300 m) and the shallow sea (less than 100 m). The coastal stretch closest to the landslide in the south is affected by up to 25 m water elevation within 1 or 2 min after initiation of the slide (for propagation time, see the top of Fig. 8). On the northern side, the maximum elevation is observed west of Darica (more than 30 m water elevation, 5-min travel time). The whole coast east of Prince’s Islands (220–230 km) is reached after 7–10 min and is heavily impacted by water elevations exceeding 20 m. Further, this plot confirms that the small archipelago protects the Istanbul coasts (especially the eastern part, 240–260 km), impacted by water elevations between 6 and 7 m after more than 15 min. To the East, in the Gulf of İzmit (80–170 km distance, including the industrial districts of Kocaeli and Gölkük), the wave is slowed down considerably, taking more than 40 min to reach the basin eastern extreme (see Fig. 8, top) resulting in smaller water elevations (around 3–4 m).

Figure S3 reports a sensitivity analysis of the tsunami coastal height with respect to the slide friction coefficient: an almost linear correlation can be noted between the slide velocity and the maximum water elevation. In general, the water height ranges within the 50% of the lower values all along the coast.

Discussion

Several factors contribute to consider the SCL as a potential hazard for the eastern Sea of Marmara, including (1) the landslide mass is large (4 by 2 by 0.2 km3); (2) morphobathymetric and seismic reflection data suggest that it is unstable, showing clear signs of recent (< 10 ka) creeping and internal displacement; and (3) it is located where the surface rupture of the last 1999 İzmit earthquake terminated (Gasperini et al. 2011b), which is one of the likely places where the next large-magnitude event along the NAF would nucleate. Several studies suggest that a moderate to large magnitude earthquake is supposed to occur in this region within the next decades (Hubert-Ferrari et al. 2000; Bohnhoff et al. 2013).

Our reconstruction for the SCL collapse should be considered a worst-case scenario, because we assumed a sudden failure of the entire mass. However, our data suggest the existence of multiple potential sliding surfaces without any clear indication for a single, most probable candidate. This could significantly lower the size of the sliding mass and consequently the associated tsunami effects. Further studies should consider other sources involving a retrogressive mechanism favoring a partial collapse of the mass instability. Such alternative, more conservative scenarios are expected to produce smaller tsunami heights but still with relevant impacts on the Marmara coasts. Previous evaluations of tsunami scenarios in the Sea of Marmara, based on historical reports and geological observations (e.g., Latcharote et al. 2016), never reached the tsunami wave heights of our model if we exclude the simulation performed by Özeren et al. (2010) for the Tuzla Landslide. This latter case study is relative to an event dating back to the late Pleistocene (17.0 ka), which affected the slope in a similar geological and physiographic setting. Thus, though probably rare in the historical/geological perspective, events of this magnitude should be considered not likely but possible at the millennia time scale. If this is the case, our reconstruction stresses the need for the acquisition of more geophysical/geological data to recognize local conditions that could favor the occurrence of these destructive events.

Another interesting aspect concerns the destabilizing role of seismic load. Intermediate magnitude earthquakes (up to Mw = 5.5–6) are relatively frequent in the region, while larger events (Mw > 7) show a periodicity of 250–300 years for a given active fault segment (Ambraseys 2002). Minor earthquakes and associated PGAs could however represent possible mechanisms of instability enhancement for large masses close to collapse.

The peculiar physiography of the eastern Sea of Marmara in this region should also be considered. The İzmit Bay, to the east of the study area, is in fact a narrow-elongated gulf characterized by shallow depths (< 200 m). The energy of long waves entering this basin is probably poorly dissipated; this could result in a persistent perturbation affecting the densely populated and industrialized coast (Heller et al. 2016), with associated environmental hazards (Giuliani et al. 2017). Moreover, resonance effects can occur in coastal basins if the incoming waves can excite the characteristic modes of the inlet (see, for example, Bellotti et al. 2012). Therefore, it is interesting to evaluate whether resonance conditions occur for landslide tsunamis in Izmit Bay and assess the consequent amplification of their amplitude and persistence.

Our simulation shows that the Istanbul Metropolitan Area is reached by tsunami waves 10 to 15 min after the landslide collapse. Although such a time-interval is relatively short, a tsunami warning system could lead to evacuate people and trigger safety procedures to limit infrastructural damages. A similar early-warning system could benefit from pioneering studies on multiparameter seafloor observatories in the Sea of Marmara carried out in the recent past (e.g., Embriaco et al. 2014) and from progresses in tsunami detection techniques (Chierici et al. 2010).

Conclusions

Analysis of marine geophysical data enabled us to detect a potentially sliding mass in the southeastern Çınarcık Basin (Eastern Sea of Marmara); we called it the South Çınarcık Landslide (SCL). The SCL shows a basal detachment surface and several normal/gravitative faults. Its size and location, close to the western termination of the Mw = 7.6 1999 İzmit earthquake, suggest that it could represent a major hazard for the eastern Sea of Marmara coasts. In fact, it could be destabilized by ground accelerations in case of future earthquakes nucleating on the Çınarcık segment, along the North Anatolian Fault principal displacement zone, which connects the İzmit segment to the Istanbul Metropolitan Area. Within uncertainties related to the limited geotechnical information, we attempted to simulate a sudden collapse of the landslide body towards the deep Çınarcık basin. Our worst-case scenario implies the formation of tsunamis reaching water elevations of over 5–10 m along the Istanbul coasts. Although our reconstruction is based on incomplete data, it suggests that the problem of landslide tsunami in the Sea of Marmara is largely underestimated, and further geological/geophysical investigations are needed, considering the exposed population, the cultural heritage assets, and the economic values. We stress that landslide tsunami hazard should be integrated in available seismic risk scenarios for the region, since they provide essential elements to devise and implement emergency plans and long-term mitigation strategies.