Stability analysis of laterally confined slope lying on inclined bedding plane

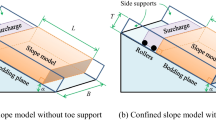
Abstract

A stability analysis of a laterally confined slope model, lying on an inclined bedding plane, was presented to evaluate the lateral shear resistance by considering the loading paths and failure envelopes. Two slope models were prepared on a bedding plane by compaction, one with and one without lateral confinement. The compacted models are related to the geological conditions at shallow depths where brittle deformation can occur and an excavation can induce horizontal field stress that significantly influences the stability of the slope. Three distinct loading paths, controlled by either tilting the angles or increasing the surcharge loads, were applied to achieve the failure of the slope models. Rankine’s passive earth pressure due to compaction was reduced by the shear strength reduction ratio. The shear strength reduction ratio was estimated through the least-squares fitting method based on the results of model tests at failure when the loading paths intersected the failure envelope. Provided that the effect of lateral confinement in a rock mass can be described by the shear strength reduction ratio, the proposed equations will be beneficial for slope stability analyses of laterally confined slopes on bedding planes. A case study of an undercut pit wall in an open-pit mine was demonstrated by showing that the unknown shear strength reduction ratio can be back-analyzed from the rainfall-induced landslide case. Therefore, the design of other undercut slopes with different geometries and groundwater conditions in the rock mass, which have undergone the same geological process as the back-analyzed case, is possible.

Appendices

Appendix 1

The substitution of F_N, expressed in Eq. (2) into Eq. (1) yields

$$R_{B} = \gamma BLT\tan \phi_{i} \cos \alpha + c_{i} BL$$

(30)

The substitution of p_L, expressed in Eq. (7) into Eq. (16) yields

$$R_{L} = \left( {\left( {\frac{1}{2}n_{1} \gamma T\cos \alpha K_{p} + 2n_{2} c\sqrt {K_{p} } } \right)\tan \phi_{s} + c_{s} } \right)LT$$

(31)

The substitution of Eqs. (30) and (31) into Eq. (17) yields

$$R_{I} = \left( {\frac{{2c_{s} }}{\gamma B} + \left( {n_{1} K_{p} \frac{T}{B}\cos \alpha + n_{2} \frac{4c}{{\gamma B}}\sqrt {K_{p} } } \right)\tan \phi_{s} + \tan \phi_{i} \cos \alpha + \frac{{c_{i} }}{\gamma T}} \right)\gamma BLT$$

(32)

The substitution of FS = 1, Eq. (3), and Eq. (32) into Eq. (18), with a minor arrangement, leads to the following equation:

$$\frac{{\left( {n_{1} K_{p} \frac{T}{B}\cos \alpha + n_{2} \frac{4c}{{\gamma B}}\sqrt {K_{p} } } \right)\tan \phi_{s} + \tan \phi_{i} \cos \alpha + \frac{{2c_{s} }}{\gamma B} + \frac{{c_{i} }}{\gamma T}}}{{\sin \alpha + \frac{\Delta W}{{\gamma BLT}}\left( {\sin \alpha - \tan \phi_{r} \cos \alpha } \right)}} = 1$$

(33)

Hence, ΔW/γBLT is formulated from Eq. (33) as follows:

$$\frac{\Delta W}{{\gamma BLT}} = \frac{{\left( {n_{1} K_{p} \frac{T}{B}\cos \alpha + n_{2} \frac{4c}{{\gamma B}}\sqrt {K_{p} } } \right)\tan \phi_{s} + \tan \phi_{i} \cos \alpha + \frac{{2c_{s} }}{\gamma B} + \frac{{c_{i} }}{\gamma T} - \sin \alpha }}{{\sin \alpha - \tan \phi_{r} \cos \alpha }}$$

(34)

To formulate α, all terms related to α are arranged on the left side of Eq. (33) and rearranged to the equation below:

$$\sin \alpha - \tan \beta \cos \alpha = b$$

(35)

where

$$\beta = {\text{atan}}\left( \xi \right)$$

(36)

$$\xi = \frac{{\tan \phi_{r} \frac{\Delta W}{{\gamma BLT}} + \tan \phi_{i} + n_{1} K_{p} \frac{T}{B}\tan \phi_{s} }}{{1 + \frac{\Delta W}{{\gamma BLT}}}}$$

(37)

$$b = \frac{{2\frac{{c_{s} + 2n_{2} c\sqrt {K_{p} } \tan \phi_{s} }}{\gamma B} + \frac{{c_{i} }}{\gamma T}}}{{1 + \frac{\Delta W}{{\gamma BLT}}}}$$

(38)

Multiplying cosβ on both sides of Eq. (35) leads to the following equation, using Eq. (36):

$$\sin \left( {\alpha - \beta } \right) = \eta$$

(39)

where

$$\eta = b\cos \beta$$

(40)

$$\cos \beta = \frac{1}{{\sqrt {1 + \xi^{2} } }}$$

(41)

Hence, α is formulated as follows:

$$\alpha = {\text{atan}}\left( \xi \right) + {\text{asin}}\left( \eta \right)$$

(42)

Appendix 2

Regarding Rankine’s earth pressure theory, effective horizontal stress σ′_h varies with effective vertical stress σ′_v and is limited by the active earth pressure and the passive earth pressure expressed in Eqs. (43) and (44), respectively.

$$\sigma^{\prime}_{h} = \tan^{2} \left( {\frac{\pi }{4} - \frac{\phi }{2}} \right)\sigma^{\prime}_{v} - 2c\tan \left( {\frac{\pi }{4} - \frac{\phi }{2}} \right)$$

(43)

$$\sigma^{\prime}_{h} = \tan^{2} \left( {\frac{\pi }{4} + \frac{\phi }{2}} \right)\sigma^{\prime}_{v} + 2c\tan \left( {\frac{\pi }{4} + \frac{\phi }{2}} \right)$$

(44)

The transition of σ′_h from active earth pressure to passive earth pressure can generally be associated with shear strength reduction ratio r_d and coefficient of lateral earth pressure K through Eqs. (45) and (46).

$$\sigma^{\prime}_{h} = K\sigma^{\prime}_{v} + 2r_{d} c\sqrt K$$

(45)

where

$$\sqrt K = \tan \left( {\frac{\pi }{4} + \frac{{\tan^{ - 1} \left( {r_{d} \tan \phi } \right)}}{2}} \right)$$

(46)

The range in r_d is from − 1 to 1. Consequently, the effective horizontal stress is in the active state when r_d < 0, isotropic when r_d = 0, and in the passive state when r_d > 0. In regards to Eq. (46), r_d can be formulated to the following equation:

$$r_{d} = \frac{1}{2\tan \phi }\frac{K - 1}{{\sqrt K }}$$

(47)

With the substitution of Eq. (47) into Eq. (45), K can be solved as follows:

$$K = \frac{{\sigma^{\prime}_{h} \tan \phi + c}}{{\sigma^{\prime}_{v} \tan \phi + c}}$$

(48)

The removal of K from Eq. (47) can be achieved by substituting Eq. (48) into Eq. (47). Hence, r_d can be calculated by Eq. (49), using material parameters c and ϕ as well as σ′_v and σ′_h measured at the same depth.

$$r_{d} = \frac{{\sigma^{\prime}_{h} - \sigma^{\prime}_{v} }}{{2\sqrt {\left( {\sigma^{\prime}_{v} \tan \phi + c} \right)\left( {\sigma^{\prime}_{h} \tan \phi + c} \right)} }}$$

(49)

Moreover, if both c and ϕ are kept unchanged with depth, r_d could be determined from the changes in effective vertical stress Δσ′_v and horizontal stress Δσ′_h by considering the increment in Eq. (45), as follows:

$$\Delta \sigma^{\prime}_{h} = K\Delta \sigma^{\prime}_{v}$$

(50)

The removal of K from Eq. (50) can be achieved by using Eq. (47) and leads to the following equation:

$$\sqrt {\frac{{\Delta \sigma^{\prime}_{h} }}{{\Delta \sigma^{\prime}_{v} }}} = \tan \left( {\frac{\pi }{4} + \frac{{\tan^{ - 1} \left( {r_{d} \tan \phi } \right)}}{2}} \right)$$

(51)

Concerning Eq. (51), r_d can be solved as shown in Eq. (52) in terms of ϕ and the ratio of Δσ′_v/σ′_h obtained at two different depths.

$$r_{d} = \frac{1}{2\tan \phi }\frac{{\left( {{{\Delta \sigma^{\prime}_{h} } \mathord{\left/ {\vphantom {{\Delta \sigma^{\prime}_{h} } {\Delta \sigma^{\prime}_{v} }}} \right. \kern-\nulldelimiterspace} {\Delta \sigma^{\prime}_{v} }}} \right) - 1}}{{\sqrt {{{\Delta \sigma^{\prime}_{h} } \mathord{\left/ {\vphantom {{\Delta \sigma^{\prime}_{h} } {\Delta \sigma^{\prime}_{v} }}} \right. \kern-\nulldelimiterspace} {\Delta \sigma^{\prime}_{v} }}} }}$$

(52)