Introduction

Offshore pipelines are often buried in the seabed for protection against hydrodynamic forces caused by strong currents/waves or fishing gear (Fredsøe 2016). Due to the long transportation distance and complexity of the seafloor environment, these pipelines may go through a variety of geological conditions, thus they are threatened by offshore geo-hazards. One of the main reported offshore geo-hazards is marine landslides (Parker et al. 2008; Sahdi et al. 2014; Zakeri et al. 2008). A complete study of the available data on offshore pipeline safety during the period from 1967 to 1990 was commissioned by the Marine Board of the National Research Council (Woodson 1991), which reported that 12% of pipeline failures on the Gulf of Mexico (U.S. outer continental shelf region) were caused by seabed movement. Failure of offshore pipelines may cause significant environmental pollution due to the leakage of transported materials in addition to the economic loss and social impact (Randolph and Gourvenec 2011).

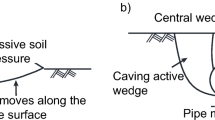
If a segment of a buried pipeline is subjected to seabed movement, the pipeline will deform due to the landslide-induced pressures as schematically shown in Fig. 1 (where qu is the ultimate pressure in the x-direction which is referred to as the lateral direction hereafter). Furthermore, the pipeline displacement is restrained by the passive soil resistance, frictional resistance and pipeline fixities outside of the seabed failure zone (Randolph et al. 2010; Summers and Nyman 1985). During a landslide, a pipeline can bear loads in the vertical, lateral and axial directions. Amongst them, the magnitude of the load in the lateral direction is normally the largest (ASCE 1984; Zakeri et al. 2008). Therefore, knowing the ultimate lateral pressure acting on a buried pipeline due to a marine landslide is crucial in offshore pipeline design.

Fig. 1
figure 1

Schematic illustration of pipeline deformation due to seabed soil movement normal to the pipe axis

Full size image

At the onset of a subaqueous sandy slope failure triggered by either external dynamic or static loads, soil material may undergo partial liquefaction. At this stage, the soil mass starts moving and may still hold geotechnical properties. Then, as the gravitational potential energy converts to internal kinetic energy, the failed soil mass becomes agitated, liquefied and transits into the debris flow, turbidity current and heavy fluid (Boylan et al. 2009). The sliding material at this stage transfers to fluid-like material and the liquefied sand may undergo hindered settling and the advection of grains, and at a certain stage, progressive solidification initiates and some of the grains in the sliding material settle down at the base forming a grain-supported framework (Sassa and Sekiguchi 2010; Sassa and Sekiguchi 2012). Amiruddin et al. (2006) conducted two-dimensional flume tests and observed three distinguishable zones in the sediment gravity flow, namely a zone of dilute sediment clouds atop a zone of highly concentrated sediment, and a solidified soil layer with zero velocities at the base. Eventually, the fluid-like sliding material transforms back to a steady deposit. The evolution of a subaqueous landslide is characterised by multi-phased physics. Sassa and Sekiguchi (2010, 2012) presented an analytical framework that is capable of consistently simulating the dynamics of submarine liquefied/fluidized sediment flows involving flow stratification and deceleration leading to redisposition on the basis of two-phase physics. They stated that for a rational understanding of the processes of subaqueous sediment gravity flows, the integration of fluid dynamics and soil mechanics approaches is necessary.

The induced force acting along the pipeline depends on the landslide velocity, thus on the shear strain rate (Georgiadis 1991; Zhu and Randolph 2011). Regarding the velocity of seabed movement, the soil–pipeline interaction mechanism of submarine-buried pipelines has been commonly investigated from two perspectives, namely the geotechnical approach and the fluid dynamics approach. These two approaches consider two extreme offshore landslides in terms of the slide velocity.

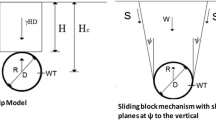
The geotechnical approach is suitable for the case when the relative soil velocity is sufficiently low. The soil holds strength and the soil behaviour can be described within the conventional soil mechanics framework. Researchers have proposed formulae in the form of Eq. 1 for evaluating the ultimate horizontal pressure, qu, acting on a pipeline buried in a sandy material caused by the relative soil–pipe displacement (e.g. Audibert and Nyman 1977; Bea and Aurora 1983; Calvetti et al. 2004; Georgiadis 1991; Guo and Stolle 2005; Summers and Nyman 1985; Trautmann and O'Rourke 1985),

$$ {q}_{\mathrm{u}}={\gamma}_{\mathrm{soil}}^{\prime }{H}_{\mathrm{c}}{N}_{\mathrm{q}} $$
(1)

where \( {\gamma}_{\mathrm{soil}}^{\prime } \) is the soil effective unit weight; Hc is the pipe buried depth from the soil surface to the pipe centre; Nq is the bearing capacity factor for the sand materials estimated by for example Hansen (1961) and Ovesen (1964) as shown in Fig. 2.

Fig. 2
figure 2

Bearing capacity factor for sand material: (a) Hansen (1961) method modified after Audibert and Nyman (1977); (b) Ovesen (1964) method modified after Trautmann and O'Rourke (1985)

Full size image

The fluid dynamics approach has been used to study submarine landslide behaviour (Locat and Lee 2002, Niedoroda et al. 2003, Sahdi et al. 2014, Zakeri 2009a). Based on the fluid dynamics and rheology principles (Pazwash and Robertson 1975), the ultimate lateral pressure can be estimated from Eq. 2.

$$ {q}_{\mathrm{u}}=\frac{1}{2}{C}_{\mathrm{D}}{\rho}_{\mathrm{slide}}{V}_{\mathrm{slide}}^2 $$
(2)

Here, CD is the drag coefficient; ρslide and Vslide are the density and velocity of the flow slide material, respectively. CD is a function of the non-Newtonian Reynolds number (Zakeri 2009b; Zakeri et al. 2008), as shown in Eq. 3, where τ is the mobilised shear stress of the slide material.

$$ {\mathit{\operatorname{Re}}}_{\mathrm{non}-\mathrm{Newtonian}}={\rho}_{\mathrm{slide}}{V}_{\mathrm{slide}}^2/\tau $$
(3)

Sahdi et al. (2014) conducted a series of centrifuge tests simulating submarine landslide flow around a pipe to investigate soil–pipe velocity effects on the impact forces on the pipe. The samples were made of fine-grained soil at various degrees of consolidation. The model pipe moved horizontally through soil samples with various soil–pipe velocities ranging from 0.004 to 4.2 m/s. They recommended a hybrid method in the form of Eq. 4, which is similar to that of the geotechnical approach established by Randolph and White (2012), where NH is the lateral bearing capacity factor.

$$ {q}_{\mathrm{u}}=\frac{1}{2}{C}_{\mathrm{D}}{\rho}_{\mathrm{slide}}{V}_{\mathrm{slide}}^2+{s}_{\mathrm{u}-\mathrm{op}}{N}_{\mathrm{H}} $$
(4)

Sahdi et al. (2014) proposed that su − op is the operative shear strength, which is dependent on the shear strain rate, and CD and NH are constant values (1.06 and 7.35, respectively) to stress that both factors are independent of soil–pipe velocity. Sahdi et al. (2014) argued that the second term (relating to soil strength) of Eq. 4 dominates when Renon − Newtonian =< ~3 and the first term (relating to flow inertia) is significant when Renon − Newtonian > ~3. Randolph and White (2012) proposed that Eq. 4 with CD = 0.4 and NH = 13.0 fits the CFD (computational fluid dynamics) simulation results on the interaction of clay-rich debris and a suspended pipeline from Zakeri (2009b). Randolph and White (2012) and Sahdi et al. (2019) argued that the first term is significant when Renon − Newtonian > ~10. However, it should be noted that the above studies were based on clay-rich material.

The methods outlined above have been proposed and verified based on laboratory tests and therefore, frequently used in practice. However, the available methods provide a wide range of predictions on the landslide-induced loads (Bea and Aurora 1983; Georgiadis 1991; Zakeri 2009b). Accordingly, it is necessary to appreciate that the approaches have their strengths and limitations which originate from the corresponding experiments from which they were developed.

In recent decades, for studying soil–pipeline interaction, many physical models have been designed with either a ‘pulled-pipe’ method or a ‘released-gate’ method. For the previous studies with the ‘pulled-pipe’ method, the pipe is buried under flat ground and is artificially pulled by a mechanical system in a single direction, as illustrated in Fig. 3a (e.g. Almahakeri et al. 2013; Ansari et al. 2019; Audibert and Nyman 1977; Calvetti et al. 2004; Liu et al. 2015; Ono et al. 2017; Robert et al. 2016; Roy and Hawlader 2012; Tian and Cassidy 2011; Trautmann and O'Rourke 1985; Zhang et al. 2002). In reality, the pipes may be pulled by fishing gear or anchors. For the previous studies with the ‘released-gate’ method, a soil flow is triggered by releasing a rotatable/releasable gate which is designed to keep the soil material in its original position (e.g. Zakeri et al. 2012; Zakeri et al. 2008). This method can be employed for the case that a debris flow passes around a pipeline that is either laid on the seabed or suspended above the seabed as demonstrated in Fig. 3b.

Fig. 3
figure 3

Illustration of soil–pipeline interaction at three different cases (θ is the slope angle)

Full size image

Fig. 3c demonstrates the early stage of seabed slope static liquefaction, which can be triggered by either dynamic loads (such as earthquakes, tsunamis and waves) or static loads (such as rapid accumulation of sediments, seabed erosion and dredging), as discussed by Locat and Lee (2002), Ye et al. (2017) and Li et al. (2020). The soil/fluid flow behaviour in the post-liquefaction stage is not much dependent on the triggering mechanism, as the soil/fluid flow is mainly driven by the gravitational forces (Askarinejad et al. 2018a; Iverson 1997; Kumar et al. 2010; Maghsoudloo et al. 2021). However, it is important to note that the soil–pipe interaction mechanisms in Case 1 and Case 2 are different from those in Case 3, owing to the differences in i. the seabed inclination (Case 1 has a flat surface, whilst Case 3 has a certain slope angle); ii. the generated excess pore pressure (EPP) which exists in Case 3 but not necessarily in Case 1; and iii. the soil resistance mobilisation mechanism (soil moves passively in Case 1 and actively in Case 3); iv. the soil properties which have changed dramatically from the initiation of the subaqueous slope failure (Case 3) to the post-failure stage (Case 2) owing to a higher velocity and a more efficient mixing mechanism in Case 2. Therefore, it can be concluded that the soil failure mechanisms and soil (or soil–fluid mixture) properties in the three conditions illustrated in Fig. 3 are all different. Because the geotechnical approach is developed for Case 1 and the fluid dynamics approach is developed for Case 2, neither of them could be applied to Case 3.

Currently, the available literature falls short in providing an approach to investigate the ultimate pressure applied to a pipeline buried in a liquefied slope (Fig. 3c). Teh et al. (2006) investigated the pipeline stability on a liquefied seabed. However, only a flat seabed condition was considered in these experiments with the main focus on the floating/sinking behaviour of a pipeline during seabed liquefaction. Calvetti et al. (2004) built up a model which can simulate buried pipeline movement in the partially liquefied flat seabed by applying hydraulic gradients (i). They applied the ‘pulled-pipe’ method and proposed Eq. 5 as a modification of the geotechnical approach, for considering sand liquefaction effects on qu, where γw is the water unit weight.

$$ {q}_{\mathrm{u}}=\left({\gamma}_{\mathrm{soil}}^{\prime }-i{\gamma}_{\mathrm{w}}\right){H}_{\mathrm{c}}{N}_{\mathrm{q}-\mathrm{sand}} $$
(5)

Zhang and Askarinejad (2019a) investigated the influence of slope geometry on qu by conducting centrifuge tests with pipes buried at various locations in sandy slopes. They proposed Eq. 6 which further considers the effect of pipe position concerning the slope crest to pipe center distance (Lc) and the slope angle (θ), where φ′ is the soil friction angle and Nq is the bearing capacity factor from the Ovesen (1964) method as shown in Fig. 2b. It is important to note that both Eq. 1 and Eq. 6 are only suitable for drained conditions and would not be applied directly to static liquefaction conditions which occur with the accumulation of excess pore pressures.

$$ {q}_{\mathrm{u}}={\gamma}_{\mathrm{soil}}^{\prime }D{\left(\frac{H_{\mathrm{c}}}{D}\right)}^{\omega }{\left(\frac{D}{L_{\mathrm{c}}}\right)}^{1-\omega }{N}_{\mathrm{q}} $$
(6)
$$ \omega =1+\frac{\ln \alpha }{\ln \left({L}_{\mathrm{c}}/D\right)+\ln \left({H}_{\mathrm{c}}/D\right)},\mathrm{where}\ \alpha =\frac{\mathit{\tan}\left({45}^{{}^{\circ}}-{\varphi}^{\prime }/2\right)}{\mathit{\tan}\theta +\mathit{\tan}\left({45}^{{}^{\circ}}-{\varphi}^{\prime }/2\right)} $$
(7)

Based on the analysis above, the application of the existing methods to Case 3 in Fig. 3c needs to be verified based on model tests that can represent the corresponding situation. Thus, a series of centrifuge tests have been conducted in this study to investigate the ultimate lateral pressure of a buried pipeline during the initiation of a marine landslide. The effects of slope angle, pipeline structural stiffness, pipe embedment ratio, non-Newtonian Reynolds number and relative soil velocity on the resultant ultimate pressure on the pipe are discussed and analysed using the experimental data from the centrifuge tests carried out at 50g, where g is Earth’s gravity.

Testing methods

The beam centrifuge at TU Delft was used in this study, which has a nominal radius of 1.22 m and is able to generate a maximum centrifugal acceleration of 300g. The tests presented in this paper were conducted at 50g. The effective centrifuge radius is taken as the distance from the centre of the centrifuge to 1/3 of the sample height (Hsample). The maximum error in the stress profile is less than 2% of the prototype stress (Schofield 1980; Taylor 2014).

Test set-up

Zhang and Askarinejad (2019b, 2021) described an experimental set-up designed for triggering static liquefaction of a submarine slope by steepening the slope angle in the geotechnical centrifuge. The same device is used in this study, as shown in Fig. 4. The device is equipped with a tilting mechanism which increases the inclination of the loose sand sample around the rotating axis in the x-z plane until the sample liquefies or up to a maximum angle of 20°. The slope angle increasing rate is about 0.1°/sec at model scale which is 0.002°/sec at prototype scale. A high-speed camera (DMK 33UP5000) is connected to the strongbox with a holder which enables the observation of soil liquefaction and landslide flow. Fig. 4b schematically illustrates an inclined sample and the locations of seven installed pore pressure transducers (PPTx, where, x is the PPT sequence number from 1 to 7, and the sensor series number is MPXH6400A) which are distributed along the cross-section through the middle of the sample.

Fig. 4
figure 4

Illustration of the test set-up in the centrifuge platform and the tilting mechanism. (a) Sample after preparation: (1) rotation direction; (2) upper-box; (3) linear motor; (4) pipe connection; (5) pipe; (6) high-speed, high-resolution camera; (7) fluidization system; (8) lighting board; (9) rotating axis; (10) centrifuge platform; (11) camera holder; (12) viscous fluid and sand. (b) Sample during tilting with an inclination angle of θ

Full size image

The fluidization method described in Zhang and Askarinejad (2019b, 2021) for making loose and saturated sand samples is adopted in the current study as the sample preparation method. This method includes two main steps: i. applying fluid discharge from the sample base to fluidize the sand grains; ii. closing the inlet to let the sand grains settle down by the gravitational forces. The buried pipeline is modelled by a stainless-steel tube with sealed ends, which has an outer diameter (D) of 0.9 m at prototype scale (18 mm at model scale). In order to reduce the disturbance on the sample, the pipe is installed using the pipe connection system (which is explained in the following section) prior to the fluid discharge during the sample preparation. The three tested embedment ratios (Hc/D) are around 0.83, 1.27 and 1.75.

Pipe external pressure measurement system

Figure 5 shows the pipe holding system designed with two functions, namely keeping the pipe in position and measuring the exerted soil pressure during slope failure. This design permits testing with various pipe embedment ratios and the measurement of the load acting on the pipe in the \( \overline{\mathrm{x}} \)-direction (the main soil movement direction). The top beam is fixed to the upper extension of the strongbox through the screws as shown in Fig. 5. The pipe connection features three threaded rods. The upper partly threaded rod is fixed to the top beam and is attached with a pair of strain gauges (a half Wheatstone bridge). Thus, the bending moment, i.e. force/pressure in the \( \overline{\mathrm{x}} \)-direction can be measured. Calibration tests were conducted to determine the relationships between strain measurements, pipe displacement and loads acting on the pipe in the \( \overline{\mathrm{x}} \)-direction. The middle tube connecting the upper and lower partly threaded rods is facilitated with the inner threads. The pipe vertical position, i.e. pipe embedment ratio, could be adjusted by rotating the middle tube. The strain gauges were attached to the lower partly threaded rods to measure the change of vertical loads. However, the measured vertical loads were marginal.

Fig. 5
figure 5

Pipe connection system

Full size image

The pipeline lateral structural stiffness, depending on the soil passive resistance, the frictional resistance and the distance between two pipeline fixities as demonstrated in Fig. 1, could affect the soil–pipeline behaviour. Hence, the pipeline lateral structural stiffness effect was parametrically studied. For each type of pipe embedment ratios, tests were conducted with two different pipeline lateral structural stiffnesses by using the partly threaded rods with different diameters. Moreover, the pipeline lateral structural stiffness varies with the pipe embedment ratios as well due to the change in the distance between the pipe and the top beam.

Soil geotechnical properties and the viscous fluid

Geba sand is used as the soil material due to its known properties in previous studies (Askarinejad et al. 2018b; De Jager 2018; Maghsoudloo et al. 2017). It is fine, sub-angular and sub-rounded sand with a mean particle size (D50) of 0.117 mm, a uniformity coefficient (Cu) of 1.55, a coefficient of curvature (Cc) of 1.24. The specific gravity is 2.67, and the soil internal friction angle is 34°.

Viscous fluid with kinematic viscosity higher than water has been widely used in geotechnical centrifuge tests to reconcile the time scale difference relating to inertial effects and pore pressure dissipation as discussed in the following section. Therefore, the viscous fluid made of Hydroxypropyl Methylcellulose (HPMC) powder is used in this study as the pore and the submerging fluid. The HPMC concentration is less than 1% which only results in an increase of less than 0.5% in the fluid density compared to the water density (Askarinejad et al. 2017). Each sample was prepared using the fluidization technique explained by Zhang and Askarinejad (2019b, 2021).

Scaling laws

A marine landslide originates from an initially static sediment mass. Mobilisation requires the development of sufficient excess pore pressure, which reduces the soil strength resulting in slope failure. In centrifuge modes, it is well accepted that the scaling factors for kinematic time (\( {t}_{\mathrm{k}}^{\ast } \)) and seepage time (\( {t}_{\mathrm{s}}^{\ast } \)) are different as shown in Eq. 8 (e.g. Garnier et al. 2007; Taylor 2014; Zhang and Askarinejad 2021). The superscript ‘*’ stands for the ratio of ‘model’ to ‘prototype’. The scaling factor for dimensions (N) is 50 in this study. One of the methods to balance the difference in the scaling factors of the kinematic time and seepage time is to use a pore fluid with a viscosity of μf = Nμw (Stewart et al. 1998), where μf and μw are the fluid viscosity of the model fluid and the water viscosity, respectively.

$$ {t}_{\mathrm{k}}^{\ast }=1/N\ \mathrm{and}\ {t}_{\mathrm{s}}^{\ast }=1/{N}^2 $$
(8)

A liquefied subaqueous slope is driven by the gravitational forces, as the soil slides the gravitational potential energy transfers to internal kinetic energy (Iverson 1997). Froude number (Fr, the ratio of the inertial forces to the gravitational forces) is reported as an important dimensionless factor to scale gravity-driven debris flow impacts on structures (Choi et al. 2015; Tobita and Iai 2014). Fr is defined in Eq. 9,

$$ Fr={V}_{\mathrm{slide}}/\sqrt{g{H}_{\mathrm{slide}}} $$
(9)

where Vslide is the soil velocity; Hslide is the depth of the flow slide. Taylor (2014) argued that the scaling factor for the velocity of dynamic behaviour is 1, i.e. \( {V}_{\mathrm{slide}}^{\ast }=1 \). Thus, Fr∗ = 1, as \( {H}_{\mathrm{slide}}^{\ast }=1/N \).

It can be inferred that at the beginning of the slope static liquefaction, the soil mass still has strength, although some certain excess pore pressure exists. With further development of slope failure, the soil mass transforms from soil-strength-dominated material to fluid-dynamics-dominated material. The dimensionless non-Newtonian Reynolds number (Renon − Newtonian in Eq. 3) is used to study the fluid drag forces (Randolph and White 2012; Zakeri 2009a; Zakeri et al. 2008). The soil material used in the model tests is assumed to be the same as that in the prototype, then \( {s}_{\mathrm{u}}^{\ast }={\rho}_{\mathrm{slide}}^{\ast }=1 \). Thus, \( {\mathit{\operatorname{Re}}}_{\mathrm{non}-\mathrm{Newtonian}}^{\ast }=1 \) with the assumption that τ = su as suggested by Sahdi et al. (2014).

It should be noted that Renon − Newtonian is proposed for clay-rich debris flow. A general form of Reynolds number (Eq. 10) is traditionally used to describe complex grain–fluid interactions. D is the characteristic length scale, which is the pipe diameter as suggested by Zakeri et al. (2008). μeff is the effective viscosity of the soil–fluid mixture. Though this study focuses on the initial stage of slope static liquefaction, it is relevant to study the scaling law for Re, as the transition point from soil-strength-dominated material to fluid-dynamics-dominated material is uncertain.

$$ \mathit{\operatorname{Re}}={\rho}_{\mathrm{slide}}{V}_{\mathrm{slide}}D/{\mu}_{\mathrm{eff}} $$
(10)

The effective fluid viscosity (μeff) of a soil–fluid mixture is influenced by the presence of fine particles (Iverson 1997). Thomas (1965) proposed Eq. 11 to predict the effective fluid viscosity of a gravity-driven flow, in which the buoyancy and drag forces dominate the grain–fluid interaction.

$$ {\mu}_{\mathrm{eff}}=\left(1+2.5{C}_{\mathrm{f}\mathrm{ines}}+10.05{C}_{\mathrm{f}\mathrm{ines}}^2+0.00273{e}^{16.6{C}_{\mathrm{f}\mathrm{ines}}}\right){\mu}_{\mathrm{f}} $$
(11)

Cfines is the volume fraction of fine grains in the soil–fluid mixture. μf is the submerging fluid viscosity. The soil material used in the model tests is assumed to be the same as that in prototype, hence \( {C}_{\mathrm{fines}}^{\ast }=1 \) which leads to \( {\mu}_{\mathrm{eff}}^{\ast }={\mu}_{\mathrm{f}}^{\ast } \). In this study, \( {\mu}_{\mathrm{f}}^{\ast }=N \) as the viscous fluid with μf = Nμw is used. Thus, the scaling factor for Reynolds number is 1/N2 as shown in Eq. 12.

$$ {\mathit{\operatorname{Re}}}^{\ast }={\rho}_{\mathrm{slide}}^{\ast }{V}_{\mathrm{slide}}^{\ast }{D}^{\ast }/{\mu}_{\mathrm{eff}}^{\ast }=1/\left(N{\mu}_{\mathrm{f}}^{\ast}\right)=1/{N}^2,\mathrm{if}{\mu}_{\mathrm{f}}^{\ast }=N $$
(12)

Zhu and Randolph (2011) suggested that the shear strain rate (\( \dot{\gamma} \)) can be defined as Eq. 13,

$$ \dot{\gamma}={V}_{\mathrm{slide}}^{\mathrm{relative}}/D $$
(13)

where \( {V}_{\mathrm{slide}}^{\mathrm{relative}} \) is the relative soil movement rate (the difference between the soil velocity and the pipe moving rate). The scaling factor for \( {V}_{\mathrm{slide}}^{\mathrm{relative}} \) is 1 like that for Vslide, hence \( \dot{\gamma^{\ast }}=N \).

Results and discussion

In total, 23 centrifuge tests were performed as summarised in Table 1. These tests are characterised into four groups. Three of them are distinguished by the pipe embedment ratios (Hc/D) which are around 0.83, 1.27 and 1.75. These tests are designed to study the burial depth effect on the ultimate pipe external pressure and are labelled with E1, E2 and E3 in the test ID column of Table 1. For each group of embedment ratios, the pipe was fixed on the pipe connection system (see Fig. 5) with two different diameters for the partly threaded rods (labelled with K1 and K2 in the test ID) aiming to explore the effects of pipeline lateral structural stiffness on the ultimate exerted load by the liquefied soil. The last group of tests was performed only with sand (S01 to S04), i.e. without a buried pipe. The mean relative density of all sand samples is measured to be approximately 55%. In the following sections, all test parameters and results are presented at prototype scale unless stated otherwise.

Table 1 Summary of all the centrifuge tests
Full size table

Slope angle at failure

The slope angle at failure can indicate the onset of sample static liquefaction. The failure angles of all tests with various pipe embedment ratios are presented in Fig. 6. Results show that the average failure angles of the tests with the buried pipe are about 14.0° which is about 2.0° less than that of tests without any pipe. This can be caused by the non-uniformity in the soil fabric around the pipe as a relatively loose zone might be formed below the pipe during the sand grains settlement at the stage of sample preparation and upon the centrifuge spin-up. Moreover, it can be observed that the pipe embedment ratios have a negligible effect on the failure angles.

Fig. 6
figure 6

Failure angles of all centrifuge tests at various embedment ratios

Full size image

Development of EPP and EPP ratios (r u)

Static liquefaction is essentially linked to the rise in EPP and the corresponding reduction in the soil effective stress and the soil strength (Askarinejad et al. 2015; Eckersley 1990; Take et al. 2015). In this study, the change of pore pressure at 7 locations (see Fig. 4b) was recorded. EPP ratio (ru) in Eq. 14 defined by Biondi et al. (2000) is normally utilized to indicate the onset of liquefaction. Here, ∆u is the measured value of EPP, HPPT is the normal distance between the original slope surface and each PPT.

$$ {r}_{\mathrm{u}}=\frac{\Delta u}{\gamma_{\mathrm{soil}}^{\prime }{H}_{\mathrm{PPT}}{\cos}^2\theta } $$
(14)

Figure 7 shows the development of ru at 6 positions from test E2K2_1. Note that PPT7 was only effective in tests from E1K1_1 to E1K1_3. The measurements were conducted at a frequency of 1 kHz. PPT1 detects the change of ru firstly, then PPT2. The values of ru at both PPT1 and PPT2 locations show a linear increase for about 2 sec following by a sudden rise. A possible explanation is that due to the increase of shear stress EPP accumulates, then with the further accumulation of EPP a reduction in the soil strength occurs, which results in local static liquefaction in the vicinity of the PPT1 and PPT2 in about 2 sec.

Fig. 7
figure 7

Development of EPP ratios of test E2K2_1 (note: the onset of slope failure is defined as t = 0 sec, and the slope angle of this test is 14.53°)

Full size image

The peak values of ru are summarised in Fig. 8. At each measuring position, ru with various embedment ratios is in good agreement with that of the tests without a buried pipe. It can be inferred that the existence of the pipe did not influence the development of pore pressure and the testing system could provide good repeatability.

Fig. 8
figure 8

Maximum EPP ratios at all PPT positions of all tests

Full size image

Figure 8 indicates a drop in ru from the slope toe to the slope crest (i.e. from PPT3 to PPT7). The ru at the location of PPT1 is the highest amongst all PPT positions and is larger than 1 which might be due to the kinetic energy of the flow slide right after the onset of static liquefaction. However, the maximum values of ru measured by other sensors are less than 1. This observation is in agreement with the conclusion of Sadrekarimi (2019) who proposed that the magnitude of ru for triggering static liquefaction is essentially associated with modes of shear as well as the principal stress ratio and static liquefaction could happen with ru smaller than 1.

Sadrekarimi (2019) suggested employing ru or EPP as an indicator in the landslide warning system for saturated granular soil material under monotonic loads. However, it seems to be difficult to apply this in the case of seabed static liquefaction considering the quick accumulation of EPP as indicated in Fig. 7. ru rose abruptly only in about 2 sec before the slope failures took place.

Development of liquefied soil layers and soil displacement

Images were taken from one transparent side of the strongbox at an average rate of 36 frames per second before and during slope failure. The frames showing soil movements were analysed using the Particle Image Velocimetry (PIV) technique, as described by White et al. (2003) and Stanier et al. (2015). Nine frames were analysed for each test; Frame 0 and Frame 1 are the frames right before and after the initiation of slope failure, respectively (see Fig. 7).

Figure 9 illustrates the liquefied soil displacement field of a test without the pipe (S04) and a test with the pipe buried with an embedment ratio of 1.78 (E3K2_3). Once the static liquefaction was initiated, sand particles moved swiftly in the direction mainly parallel to the slope surface. Results show that the top layer of the slope near the toe liquefied first in both tests, then the liquefaction zone propagated towards the slope crest and the slope base. This observation indicates the limitation in applying the conventional limit equilibrium approach in catastrophic failure of submerged slopes which assumes that the slip surface appears instantaneously (Puzrin et al. 2004; Tiande et al. 1999). The presence of the buried pipe influences the soil movement regime. Figure 9d indicates that the lower boundary of the liquefaction zone initiated under the pipe and this phenomenon has been observed in other tests with the pipe as well.

Fig. 9
figure 9

Soil displacement field of test S04 (subfigures (a) t = 0.2 sec, (b) t = 1.5 sec and (c) t = 2.9) and test E3K2_3 (subfigures (d) t = 1.4 sec, (e) t = 2.7 sec and (f) t = 4.1 sec). t denotes time and the onset of slope failure is defined as t = 0 sec

Full size image

Figure 10 illustrates the displacement of the soil around the pipe obtained from PIV analysis as well as the pipe displacement for tests with Hc/D around 0.83 and 1.75. The soil and pipe displacement curves for each test have a similar trend–a linear increase in displacement for approximately 4 sec after the initiation of static liquefaction. It should be noted that the decrease in the rate of soil movement at around 4 sec after the initiation of slope failure could be due to the mechanical boundary effects imposed by the strongbox, which hinders the further flow of the soil. Therefore, the results of soil and pipe behaviour in the first 4 sec are analysed and presented in the following subsections.

Fig. 10
figure 10

Examples of pipe displacement and soil displacement around the pipe (note: the onset of slope failure is defined as t = 0 sec)

Full size image

Soil velocity distribution

Understanding the soil velocity profile is important to evaluate the constitutive equations for describing soil flows (Han et al. 2014). Johnson et al. (2012) assumed that for a debris flow, the slide velocity should be the highest at the flow surface and drops through the soil/flow depth. Many researchers adopted Eq. 15 to match the slide velocity (Vslide) profile for a laminar debris flow moving over a rigid bed (e.g. Han et al. 2015; Han et al. 2014; Hotta and Ohta 2000; Iverson 2012), where \( \overline{V_{\mathrm{slide}}} \) is the mean slide velocity, y is the soil depth from flow surface and Hslide is the total flow depth. The parameter β controls the shape of the slide velocity profile, which is plug-flow when β = 1 and simple shear when β = 0.

$$ {V}_{\mathrm{slide}}=\left(2-\beta \right)\overline{V_{\mathrm{slide}}}\left(1-{\left(1-\frac{y}{H_{\mathrm{slide}}}\right)}^{\frac{1}{\left(1-\beta \right)}}\right) $$
(15)

Hotta and Ohta (2000) conducted a series of rolling mill tests with both glass bead mixtures and plastic bead mixtures which are assumed to be similar to natural debris flows. A value of 1/3 for β was used by Hotta and Ohta (2000) for fitting the velocity profiles in the rolling mill. The same value for β was suggested by Han et al. (2014) for describing the vertical debris-flow velocity distribution of Jiasikou debris flow in the high-seismic-intensity zone of the Wenchuan earthquake. The velocity profile with β = 0.5 matches the observations well from the large-scale debris flow tests performed by Johnson et al. (2012).

Based on the PIV analysis, the soil velocity distribution of the tests S03 and S04 are obtained and presented in Fig. 11. It is found that Eq. 16 with β = 0.72 and an amplification factor of 1.06 agrees satisfactorily with the results as shown in Fig. 11. The profiles of soil velocity for the tests with buried pipes are shown in Fig. 11 as well. By comparing them with the results of S03 and S04, it can be seen that the presence of the pipe reduces the soil velocity above the pipe and exaggerates it under the pipe.

Fig. 11
figure 11

Soil velocity distribution along with soil depth

Full size image
$$ {V}_{\mathrm{slide}}=1.06\left(2-\beta \right)\overline{V_{\mathrm{slide}}}\left(1-{\left(1-\frac{y}{H_{\mathrm{slide}}}\right)}^{\frac{1}{\left(1-\beta \right)}}\right)\mathrm{with}\beta =0.72 $$
(16)

Ultimate lateral pressure

The test results indicate that the slope angle, pipeline structural stiffness, pipe embedment ratio and relative soil velocity influence the soil–pipeline interaction mechanism. The effects of these factors on the ultimate lateral pressures (qu) exerted on pipelines are discussed below. The development of lateral pressures on the pipe has the same shape as that of pipe displacement curves (see Fig. 10) as the lateral pressure is a function of pipe displacement and normalised pipeline structural stiffness.

The ultimate lateral pressures (qu) are the maximum stress measurements within the first 4 sec after the initiation of the slope liquefaction to minimise the mechanical boundary effects imposed by the strongbox as discussed previously. qu is believed to be dependent on the residual shear strength of the sliding material, as the soil grains have moved more than 68D50 in 4 sec after the initiation of the liquefaction, which is 8 mm at model scale (0.4 m at prototype scale, see Fig. 10). It should be noted that due to the design of the pipe connection system (see Fig. 5), both the loads on the pipe and the pipe connection system were measured. The error in the ultimate lateral pressures is calculated with the consideration of the cross-section areas of the pipe and that of the pipe connection system (the part buried in the sand) in the direction of the flow slide. The error in qu for the tests with Hc/D = 0.83, 1.27 and 1.75 is 3.2%, 5.1% and 7.0%, respectively.

Slope angle, pipeline structural stiffness and pipe embedment ratio effects

The ultimate pressures exerted on the pipes of all tests are summarised in Fig. 12. Results of the tests with Hc/D around 1.27 and 1.75 show that qu tends to slightly rise with the increase of the slope angle at failure. This observation can be explained by the fact that higher slope angles would result in larger flow energy, hence it causes higher pressures on the structure.

Fig. 12
figure 12

Ultimate lateral pressure on the pipe with various embedment ratios

Full size image

In all cases, a smaller normalised pipeline structural stiffness (K) results in a smaller value of qu. The normalised pipeline structural stiffness represents the stiffness of the pipeline fixity system in the direction parallel to the main soil flow direction (Fig. 1). Under the same external lateral load, a flexible pipeline system (with a smaller value of K) could move further compared to a stiffer pipeline system (with a larger value of K). It can be inferred that reducing the pipeline structural stiffness could increase the pipeline displacement and hence could lessen the relative soil velocity. The effect of relative soil velocity on the development of qu is discussed in the following section.

Based on Eq. 1, qu of tests with Hc/D ≈ 1.75 is expected to be roughly twice that of tests with Hc/D ≈ 0.83. Ono et al. (2017) performed several displacement-controlled ‘pulled-pipe’ tests in saturated sand samples under various excess pore water pressure ratios ranging from 0.2 to 0.9. In their tests, the soil shear strain rate was about 0.01 sec−1. The ultimate lateral resistive force of the tests with Hc/D = 2.0 is approximately twice that of tests with Hc/D = 1.0. However, Fig. 12 shows that the pipe embedment ratio insignificantly affects qu. Two possible causes are (1) the variation in the effective stresses which might affect the sand shear strength prior to liquefaction. The shallower sand layer at a lower effective stress level has a higher dilational tendency than the sand layer below; (2) the difference in the shear strain rate and non-Newtonian Reynolds number as discussed in the following section.

Hybrid approach

Estimation of undrained shear strength of (partially) liquified sand at a very low vertical effective stress level

The studies which have investigated the shearing rate effects on the shear strength of sandy material are mainly focused on the drained condition (e.g. Fukuoka and Sassa 1991; Tika et al. 1996) and very limitedly on the undrained condition (Fang et al. 2020; Saito et al. 2006). It is reported that the shearing rate insignificantly affects the residual strength of granular material both under the drained condition (Tika et al. 1996) and undrained condition (Saito et al. 2006). Saito et al. (2006) compared the effective residual friction angles of silica sand (with a D50 of 0.04 mm) as the results of some ring shear tests under various shearing rate from 0.01 mm/sec to 10 mm/sec under the undrained condition. They found that the effects of the shearing rate were negligible. If the shear strain rate is assumed as the ratio of shearing rate to ring shear apparatus diameter (125 mm), then the shear strain rates in their tests varied from 8 × 10−2 sec−1 to 8 × 10−5 sec−1.

In the current centrifuge tests, the shear strain rates (\( \dot{\gamma} \)) are in the range of 3.9 × 10−2 sec−2 to 8.4 × 10−2 sec−1 (see Table 2). The soil shear strain rate is the ratio of the difference between the soil velocity and the pipe moving rate to the pipe diameter (as defined in Eq. 12). Therefore, the soil residual undrained shear strength (su) is assumed unaffected by the change of the shear strain rate. The vertical effective stress level (\( \left(1-{r}_u\right){\gamma}_{\mathrm{soil}}^{\prime }{H}_{\mathrm{c}} \)) of the centrifuge tests was in the range of 2.0 to 4.4 kPa, when \( {\gamma}_{\mathrm{soil}}^{\prime } \)= 9.2 kN/m3, Hc/D = 0.79~1.78, D = 0.9 m, ru = 0.7. The value of ru is selected as the average excess pore pressure ratios from PPT4 as it is the closest sensor to the pipe (Fig. 4 and Fig. 8). The excess pore pressure in the vicinity of the pipe might be higher than 0.7 due to the structure–soil mixtrue interaction and could lead to a lower vertical effective stress level.

Table 2 Soil shear strain rates and soil residual undrained shear strength
Full size table

The soil residual undrained shear strength under such vertical stress level is difficult to obtain in the laboratory. Instead, for simplicity, su is estimated from Eq. 17 and the soil residual internal friction angle is taken as 34°. The corresponding estimated su values are presented in Table 2. It should be noted that both the possibly existed loose zone below the pipe and the low vertical stress level can affect the soil residual internal friction angle. The real soil residual undrained shear strength could be smaller than the predicated values in Table 2.

$$ {s}_{\mathrm{u}}=\left(1-{r}_u\right){\gamma}_{\mathrm{soil}}^{\prime }{H}_{\mathrm{c}}\tan {\varphi}^{\prime } $$
(17)

Effects of non-Newtonian Reynolds number and shear strain rate effects

The relationship between the normalised lateral pressure on the pipe (qu/su) and the non-Newtonian Reynolds number is presented in Fig. 13. The non-Newtonian Reynolds number is calculated based on Eq. 3 with τ = su, \( {V}_{\mathrm{slide}}={V}_{\mathrm{slide}}^{\mathrm{relative}} \) and ρslide = 1933 kg/m3. By conducting regression analysis, the best-fit values of CD and NH in Eq. 4 are determined as 1.76 and 7.39, respectively (R2 = 0.86). The best-fit results are shown in Fig. 13 as well. Note that the estimation of su is based on the simplified method shown in Eq. 17.

Fig. 13
figure 13

Variation of normalised lateral pressure on the pipe with non-Newtonian Reynolds number

Full size image

Sahdi et al. (2014) proposed that CD = 1.06 and NH = 7.35 yield the best-fit curve for their centrifuge test results and CD = 1.43 and NH = 7.43 yield the best-fit curve for the results of flume tests from Zakeri et al. (2008) and centrifuge tests from Zakeri et al. (2011). Zakeri et al. (2008) used clay–sand slurry as the soil material to study the drag forces induced by the submarine landslides passing through suspended and laid-on-seabed pipelines. Zakeri et al. (2011) investigated drag forces on a pipeline caused by an out-runner block made of kaolin clay. The corresponding predicted values are plotted in Fig. 13 as well. The relationship between qu/su with Renon-Newtonian agrees well with the predication from Sahdi et al. (2014).

The best-fit CD = 1.76 and NH = 7.39 of the current study are very close to the values from Sahdi et al. (2014), CD = 1.06 and NH = 7.35, albeit the best-fit CD is a bit higher. This can be due to: (1) the difference in the sliding material, i.e. (partially) liquefied sand in the present study and clay-rich material in Sahdi et al. (2014); (2) the low effective stress level and high excess pore pressures around the pipe and; (3) the uncertainty in the soil residual undrained shear strength.

The effect of sliding material inertia can be found in Fig. 13. Sahdi et al. (2014) suggested that the sudden increase in the value of qu/su beyond a constant value reflects that the inertial drag term in Eq. 4 is getting prominent. They found that when Renon-Newtonian >~3 the inertial drag term dominates. The inertial drag term is 18% of qu when Renon-Newtonian = 3, CD = 1.06 and NH = 7.35 from Sahdi et al. (2014) according to Eq. 18. Following the same criterion, the best-fit CD and NH from this study result in a value of 2 for Renon-Newtonian as the threshold when the inertial drag term should be considered.

$$ \frac{1}{2}{C}_{\mathrm{D}}{\rho}_{\mathrm{slide}}{V}_{\mathrm{slide}}^2/{q}_u={C}_{\mathrm{D}}{\mathit{\operatorname{Re}}}_{\mathrm{non}-\mathrm{Newtonian}}/\left({C}_{\mathrm{D}}{\mathit{\operatorname{Re}}}_{\mathrm{non}-\mathrm{Newtonian}}+2{N}_H\right) $$
(18)

The effect of shear strain rate is demonstrated in Fig. 14 by subtracting the soil strength term (NHsu) from qu. Here CD = 1.76, NH = 7.39 and ρslide = 1933 kg/m3 are applied. The lower bound in Fig. 14 infers that the inertial drag term is significant when the shear strain rate is larger than 4.5 × 10−2 sec−1, i.e. when the inertial drag term induced pressure is about 20% of the total lateral pressure.

Fig. 14
figure 14

Variation of the percentage of the fluid inertia induced lateral pressure with the shear strain rate

Full size image

Conclusions

The ultimate pressure acting on a model pipe due to the liquefaction of a sloping seabed was investigated by means of centrifuge model tests, exploring the influence of pipe embedment ratio, pipeline structural stiffness, non-Newtonian Reynolds number and shear strain rate. The liquefaction of a submerged slope was triggered by increasing shear stress monotonically. Under the assumption that the soil behaviour after the onset of seabed slope liquefaction caused by static loads is similar to that caused by dynamic loads, the following conclusions could be extrapolated to the dynamic-loads-induced seabed liquefaction (e.g. wave loads, tsunami and earthquake) and other static-loads-induced seabed liquefaction (e.g. dredging, fast sedimentation). The observations from the tests reveal the following conclusions:

  1. 1.

    The onset of static liquefaction tends to take place in the slope surface layer close to the slope toe and then it propagates towards the crest and deeper locations in the slope.

  2. 2.

    It was found that the lateral pressure applied to the pipe in a (partially) liquefied zone is essentially related to the shear strain rate, soil undrained residual shear strength and non-Newtonian Reynolds number. The hybrid method (Eq. 4) unifying the geotechnical and fluid dynamic approaches proposed for soil–pipe interaction in soft clay by Sahdi et al. (2014) was found suitable for (partially) liquefied sand. The best-fit drag coefficient CD and lateral bearing capacity factor NH are 1.76 and 7.39, respectively. When the non-Newtonian Reynolds number >~2 or the shear strain rate > 4.5 × 10−2 sec−1, the inertial drag term would account for more than 20% of the total lateral pressure.

    In the current tests, the pipe was pre-installed prior to the sample preparation. Hence, a loose zone below the pipe might be formed below the pipe during the sample preparation and upon the centrifuge spin-up. Furthermore, the tested vertical effective levels are at a very low level ranging from 2.0 to 4.4 kPa. These facts may cause the predication of su based on Eq. 17 is higher than reality and change the best-fit values of CD and NH.

    More research on the undrained residual shear strength of static liquefied sand with respect to the shear strain rate and the low vertical effective level is required to better define the relationship between the lateral pressure and non-Newtonian Reynolds number and shear strain rate. However, in the absence of more experiments, the findings may be used within the range of tested vertical effective levels (from 2.0 to 4.4 kPa) and shear strain rates (from 3.9 × 10−2 sec−1 to 8.4 × 10−2 sec−1).

  3. 3.

    A stiffer pipeline fixity system would reduce pipe displacement, as it increases the shear strain rate which potentially results in higher lateral pressure.

  4. 4.

    The soil movement profile of a liquefied seabed without a buried structure at the early stages of the onset of static liquefaction is similar to that in a laminar debris flow. The soil velocity distribution along soil depth can be described by Eq. 15.

  5. 5.

    For a liquefied submerged slope, the maximum value of excess pore pressure ratio (ru) is generally smaller than 1. ru is strongly dependent on the measurement locations due to the difference in shearing modes at various points in the slope. A value of ru = 0.4 was observed at a location near the slope crest. Furthermore, the development of the excess pore pressure can happen in less than 2 sec which implies that it is difficult to use excess pore pressure ratios as an indicator in the early warning systems specifically for submerged loose sandy slopes.

The paper focuses on the lateral pressures on buried pipelines due to partially liquefied soil which passes the pipeline axis at right angles. Further research on fully developed liquefied flows with various flow–pipeline interaction angles is necessary to investigate the underwater soil–pipeline interaction mechanism.